Cytoarchitectonic and Dynamic Origins of Giant Positive Local Field Potentials in the Dentate Gyrus

Abstract

To determine why some pathways but not others produce sizable local field potentials (LFPs) and how far from the source can these be recorded, complementary experimental analyses and realistic modeling of specific brain structures are required. In the present study, we combined multiple in vivo linear recordings in rats and a tridimensional finite element model of the dentate gyrus, a curved structure displaying abnormally large positive LFPs. We demonstrate that the polarized dendritic arbour of granule cells (GCs), combined with the curved layered configuration of the population promote the spatial clustering of GC currents in the interposed hilus and project them through the open side at a distance from cell domains. LFPs grow up to 20 times larger than observed in synaptic sites. The dominant positive polarity of hilar LFPs was only produced by the synchronous activation of GCs in both blades by either somatic inhibition or dendritic excitation. Moreover, the corresponding anatomical pathways must project to both blades of the dentate gyrus as even a mild decrease in the spatial synchronization resulted in a dramatic reduction in LFP power in distant sites, yet not in the GC domains. It is concluded that the activation of layered structures may establish sharply delimited spatial domains where synaptic currents from one or another input appear to be segregated according to the topology of afferent pathways and the cytoarchitectonic features of the target population. These also determine preferred directions for volume conduction in the brain, of relevance for interpretation of surface EEG recordings.

Introduction

The processing of information in brain nuclei involves rapid shifts in the correlated firing of neuronal assemblies. Part of this activity is manifested in target regions as fluctuations in the local field potential (LFP), a mesoscopic variable largely contributed by postsynaptic currents (Purpura, 1959; Elul, 1971; Arieli et al., 1995). The advent of multisite recording techniques has enhanced our capacity to analyze LFPs in the study of network dynamics, plasticity, and behavior. Although the biophysical bases of LFPs have been relatively well described (Lorente de Nó, 1947; Freeman, 1975), several issues hampered their interpretation and applicability.

Synchronous activation of presynaptic neurons is necessary but not sufficient for the sum of postsynaptic currents to generate measurable LFPs. The amplitude and polarity of LFPs is critically determined by spatial factors, such as the distribution of coactivated synapses, neuronal morphology, and the architectonic configuration of the cell population (Kajikawa and Schroeder, 2011; Makarova et al., 2011; Ho et al., 2012). Although the arrangement of cells in layers and curved structures is recognized as key feature on a theoretical basis (Woodbury, 1960; Gloor, 1985; Nunez and Srinivasan, 2006), the study requires quantitative explicit modeling and in vivo analysis.

In rodents, the LFP magnitude varies considerably between regions, peaking in the hilus of the dentate gyrus (DG), a region located within the U-shaped structure formed by the granule cell (GC) layer. Anatomical excitatory and inhibitory inputs terminate on the soma and dendrites of GCs forming discrete bands (Hjorth-Simonsen and Jeune, 1972; Han et al., 1993; Amaral et al., 2007; Houser, 2007), although only some appear to contribute to LFPs (Benito et al., 2013). Two assumptions are usually made when interpreting LFPs: (1) the dominant polarity (positive or negative) is determined by the inhibitory or excitatory nature of the synaptic inputs; and (2) the closer the LFP is to the synaptic domain the larger its amplitude. However, several observations in the DG challenge both these assumptions. In this region positively orientated spontaneous LFP events can be observed (Bragin et al., 1995a,b), which are rarely observed in the brain. Moreover, LFP power reaches a maximum in the hilus (i.e., at a distance from the GC layer).

We investigated these apparent paradoxes by combining in vivo analyses and a three-dimensional computer model of the DG. The model allows reproducing the dipole-layer behavior of the GC population and facilitates the study of coherent or topologically organized input distributions. The predictions generated by the model were then evaluated in pharmacological and lesion studies in vivo. The laminar profile of LFPs was recorded by multielectrode arrays and their pathway-specific components were separated by spatially discriminating techniques (Bell and Sejnowski, 1995; Korovaichuk et al., 2010). We found that the large hilar LFPs were produced by synchronous volume-conducted currents generated by two mirrored layers of cells exhibiting a polarized geometry. The striking differences with LFPs recorded in GC domains highlight the role of cytoarchitectonic factors, which may boost the visibility of some inputs compared with others.

Materials and Methods

Experimental procedures.

All experiments were performed in accordance with European Union guidelines (2003/65/CE) and Spanish regulations (BOE 67/8509-12, 1988) regarding the use of laboratory animals, and the experimental protocols were approved by the Research Committee of the Cajal Institute.

Female Sprague Dawley rats (200–220 g, n = 10) were anesthetized with urethane (1.2 g/kg, i.p.) and placed in a stereotaxic device. Surgical and stereotaxic procedures were performed as described previously (Herreras et al., 1988; Canals et al., 2005). A concentric bipolar stimulating electrode was placed in the medial perforant path (MPP) for orthodromic activation of DG GCs (AP: −8, L: 4; V: −3–4 mm). A multisite silicon probe (Neuronexus) connected to a multiple high-impedance headstage was lowered into the hippocampus (AP: 4.5–5.5; L: 2–3 mm). Six animals were analyzed using single-shank probes with 32 contacts, spaced at 50 μm intervals, and four additional animals analyzed using 4-shank probes (200 μm intervals between shanks) with eight linear recording sites spaced at 100 μm intervals. Probes were soaked in DiI (Invitrogen) before insertion for postmortem confirmation of probe placement in histological sections. A silver chloride wire implanted in the neck skin served as a reference for the recordings. Signals were amplified and acquired using Multi Channel Systems recording hardware and software (50 kHz sampling rate).

The excitatory/inhibitory nature of LFP generators was analyzed by injecting neurotransmitter blockers in the vicinity of a recording shank via a glass recording pipette (7–10 μm at the tip) and using a Picospritzer (General Valve; Fernández-Ruiz et al., 2012a). The size of the microdrop was adjusted (∼50–100 pl) to limit the volume of the tissue bathed to a sphere of <500 μm in diameter, as assessed by the selective modulation of evoked potentials in the desired group of recording sites. Bicuculline methiodide (BIC) and 6,7-dinitro-quinoline-2,3-dione (DNQX) were obtained from Sigma-Aldrich, and they were both dissolved in artificial CSF (aCSF) at a final concentration of 1 mm, ∼50 times higher than that usually used in vitro. A single injection ensured stable drug effects for at least 60 s. To better refine the active sites of drugs on GC domains, we performed a second series by injecting smaller drops and monitoring the extension of the injection through the visualization of a transient dip in the recording of sites along the linear probe during injection. This was facilitated by introducing in the pipette KCl (20 mm) substituting an equivalent amount of NaCl. Such procedure was only effective for microinjections of 0.2 mm BIC in the stratum moleculare, because injections in the narrower body layer extended into dendrites and were not evaluated.

Independent component and current source density analyses of LFPs.

The independent component analysis (ICA) is used to reveal spatially stable bouts of activity out of mixed signals (Hutchison et al., 2010). Hilar field potentials are mostly generated by mixed excitatory and inhibitory synaptic currents from nearby GCs. Accordingly they must be separated into pathway-specific components for correct appreciation of the polarity and magnitude of each contributory pathway. The ICA operates on multiple simultaneous recordings and requires spatial immobility of the contributing sources, which is fulfilled by subthreshold synaptic currents on account of the fixed location of the axon terminals. Our ICA-based approach has been described in detail previously (Makarov et al., 2010; Benito et al., 2013). The interpretation of ICA components in laminated brain structures was also described previously in a large-scale multineuronal LFP modeling study of the CA1 region using compartmental units, where the limitations of this approach and potential sources of cross-contamination were discussed (Makarova et al., 2011). Thus, when an ICA-separated LFP component is shown to be pathway-specific, its time course can be considered as a temporal envelope of the global spike output of the population of origin (i.e., afferent spike trains). In some cases, we used such time envelopes as an input parameter for model studies (see below).

Briefly, N simultaneously recorded LFP signals were represented as the weighted sum of the activities of N neuronal sources or LFP-generators: $u\left(t\right)={\displaystyle \sum _{n=1}^N{V}_{n{S}_n}\left(t\right)}$, where {Vn} is the mixing matrix composed of the so-called voltage loadings or spatial distributions of all LFP-generators, and sn(t) is the time course of the n′th LFP-generator. Thus, the raw LFP observed at the k′th electrode tip is a linear mixture of the electrical activity of several independent LFP-generators describing transmembrane current source densities (CSDs) in principal cells I_n = −σΔV_n (where σ is the conductivity of the extracellular space). We used two different algorithms for the ICA: the infomax (Bell and Sejnowski, 1995) implemented in the EEGLAB MATLAB toolbox (Delorme and Makeig, 2004), and the kernel density ICA (Chen, 2006) customary implemented in MATLAB. The performance may differ somewhat depending on the temporal structure of the signals. The ICA returns the activations sn(t) and spatial weights Vn of up to N LFP-generators (N = 32 in experimental recordings). However, only a few generators exhibit significant amplitudes and distinct spatial distributions in the hippocampus (Korovaichuk et al., 2010). Because the location of the recording sites is known, the joint curve of the spatial weights of an LFP-generator (i.e., Vn) is equal to the instant depth profiles of the proportional voltage among sites, as occurs during laminar recording of standard pathway-specific evoked potentials.

Earlier we reported that not all combinations of synaptic inputs or temporal patterns are amenable for ICA separation (Makarova et al., 2011; Benito et al., 2013). In cases of strong covariation of two separate pathways, the ICA is not able to perform well, and mixtures arise as single components. Thus, optimal separation is achieved for irregular LFPs contributed by pathways conveying information with different temporal structures. The ICA of LFP-generators in the DG may have two limitations: (1) time courses s_n(t) may exhibit some degree of correlation due to recruitment of feedback and feedforward couplings, which in general facilitates cross-contamination and may result in the partial merging of sources (Makarova et al., 2011); and (2) moderate extension of spatial modules of coherent activity (Benito et al., 2013) may result in the presence of several low amplitude and highly variable generators corresponding to distant places. To improve the physiological consistency of separated components additional strategies can be adopted over plain ICA. The efficiency of each strategy is best checked in model LFPs obtained in cytoarchitectonically realistic aggregates and known temporal mixtures of synaptic inputs (Makarova et al., 2011). It should be pointed out that model validation of the efficiency of the separation for a particular combination of inputs cannot be generalized as the active pathways may vary in different brain states and regions. Here we also use this technique for crosschecking results of separation. The strong curvatures of the DG in all three dimensions and the moderate spatial coherence of some ICA components (e.g., 0.5–0.8 for the MPP input in sites 500 μm apart; Benito et al., 2013) indeed make difficult the separation. Best results are obtained in the most planar sections of the DG. As a rule of thumb both the separability and accuracy are greatly ameliorated by experimental and analytical strategies aimed at increasing the relative variance of the source of interest (Makarova et al., 2011). An important preprocessing step is the use of the principal component analysis (PCA), which allows reducing the presence of highly variable remote generators (Makarova et al., 2011). The PCA also stabilizes the convergence of the ICA to true stable LFP-generators (Makarov et al., 2010). In this study, we used automatic PCA reduction maintaining 99.0% of the initial LFP variance. The priming of LFPs with evoked activity of specific pathways (Korovaichuk et al., 2010) and/or selecting recording channels that maximize spatial differences of the sources of interest (Benito et al., 2013) may also significantly improve the separation. In addition to, our results in model LFPs suggest (see below) that the time-delayed correlation (few milliseconds) of afferent populations has only slight effect on the quality of separation.

Once extracted from the raw LFPs, each LFP-generator can be analyzed independently by reconstructing virtual LFPs produced by a single generator: u_j(t)= V_j s_j(t). The CSD created by each of these generators can then be evaluated, whose spatial profiles can be compared with those obtained during the specific activation of known pathways. The pathway-specificity of some ICA-isolated components is assessed by their selective capturing of subthreshold evoked synaptic currents and cross-correlation (CC) to spike activity of presynaptic units (Korovaichuk et al., 2010; Fernández-Ruiz et al., 2012a).

CSD analysis calculates the magnitude and location of the net transmembrane current generated by neural elements contained within a small region of tissue (Freeman and Nicholson, 1975). In our experiments, we used a one-dimensional approach suitable for laminated structures with a parallel arrangement of principal cells, and that calculates the CSD from the voltage and conductivity gradients along the main cell axis (Z), assuming negligible net contributions in the XY-plane parallel to the cell body layer (Herreras, 1990).

Analysis of real and simulated LFPs.

The time evolution of the power of an LFP-generator is given by (measured in mV²):

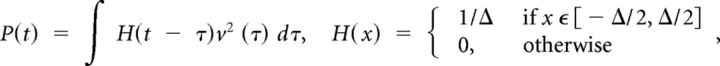where v(t) is the virtual LFP at the electrode with maximal power and Δ is the length of averaging. The overall mean power is then defined by setting Δ equal to the complete time interval (200 s and 2 s for experimental and simulated LFPs, respectively).

The CC index between the activation of the MPP-generator obtained in parallel shanks (or simulated recording tracks) was calculated by pairwise analysis of the generators' activations, obtained separately for each linear array and estimated for the same periods used to calculate the mean LFP power. Although for technical reasons the number of parallel recording shanks in the experiments was limited to four, we plotted one additional track in the model at the open end of the GC layer to examine the effects of blade length asymmetry. The amplitude of MPP-evoked field EPSPs (fEPSPs) was measured for averaged subthreshold evoked potentials in each shank, both in control conditions and after drug treatment.

Mathematical modeling and numerical simulations.

We used a forward approach to model the LFPs produced by neuron currents of known spatial distribution and temporal activation to identify the factors that determine the LFP amplitude and polarity in the DG. Two different modeling strategies were used to accomplish complementary purposes. The first was a standard multicellular aggregate of compartmental GCs of realistic morphology and Hodgkin-Huxley dynamics (Lindén et al., 2011; Makarova et al., 2011), and the second was a finite element method (FEM). Due to excessive computational cost of the former, it was only used to check the efficiency of ICA on multisynaptic LFPs from mixtures of inputs that interact naturally within cells. In this approach, the input consists of a series of instants when synaptic channels are activated in specific dendritic domains, and the temporal envelope of the transmembrane currents is computed from channel kinetics. The FEM model skips this step and uses current sources as an input parameter that has predefined spatial dimensions, locations in the volume and temporal dynamics, saving computational resources. Thus, it is best suited to estimate LFPs following activation of a single input extending over different parts the GC population in multiple spatial combinations, which suits well the main objectives of the present study.

DG model of compartmental GCs.

We simulated a realistic tridimensional neuronal model of the DG made of compartmental GCs (Fig. 1A, top) with identical procedure as in former models of the CA1 aggregate (Varona et al., 2000; Ibarz et al., 2006; Makarova et al., 2010, 2011). Excitatory and inhibitory synaptic inputs of the non-NMDA (τ = 2 ms), and GABAA types (τ = 30 ms) were used to mimic lateral perforant pathway (LPP) and MPP inputs, and perisomatic inhibition, respectively (Fig. 1A1), and were distributed throughout the compartments according to anatomical data (LPP and MPP activated the outer and the middle third compartments of the dendritic arbor, respectively, whereas inhibition was only activated at the soma). These three inputs account for most (>95%) of the LFP variance in the DG (Benito et al., 2013). The synaptic conductances (4–12 nS and 30–60 nS for Glu and GABAA inputs, respectively) were activated in predetermined temporal sequences (irregular, periodic, or mixed) of varying intensity. The transmembrane currents were calculated using the GENESIS simulator with an exponential Euler method (Bower and Beeman, 1998). The DG aggregate was modeled as a folded sheet of GCs (Fig. 1A3) containing an aggregate of 50,384 morphologically identical GC units (1 × 1 mm), with cell density of 100 neurons in a 50 × 50 μm anterolateral lattice. Compartmental currents were estimated in a single GC unit (Fig. 1A2) and the activation of the entire population was then mimicked by replicating the currents in all the neurons of the aggregate using a system of spatial coordinates for the compartments (Fig. 1A3). The LFP was estimated by distance weighed addition of all compartmental currents along a simulated linear track at the center of the population. The conductivity of the tissue was 0.33 S/m (López-Aguado et al., 2001). Calculations of LFPs were programmed in a custom C code.

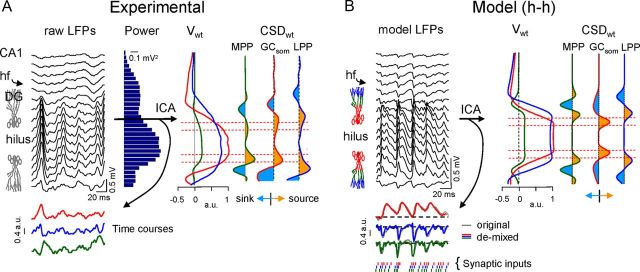
Figure 1.

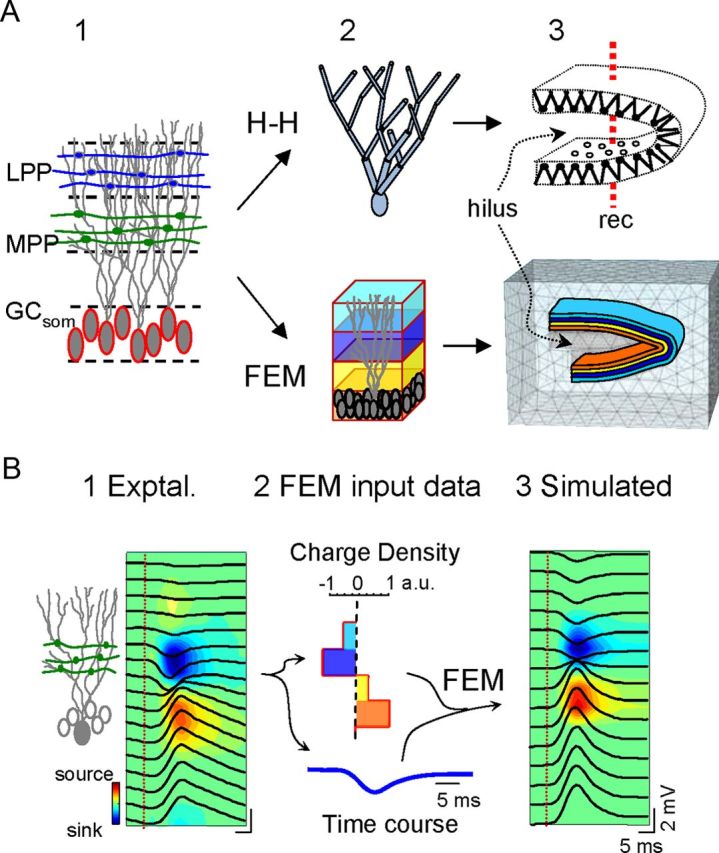
Model reproduction of LFPs in the DG from known synaptic inputs to somato-dendritic domains of GCs. A, Two different approaches were used to address complementary aspects of LFP generation, either using a U-folded layer aggregate of compartmental GCs with explicit membrane electrogenesis and Hodgkin–Huxley kinetics (H–H), or by a FEM that uses predefined volumetric current sources. The compartmental model is best suited to simulate realistic interaction between synaptic inputs in individual cells, and the resultant spatial distribution of transmembrane currents giving rise to macroscopic LFPs. These were estimated in points along a simulated track of recording (A3). Three main synaptic inputs were simulated: the excitatory LPP, MPP, and a somatically targeting inhibition GC_som. In the FEM approach, the gross cytoarchitecture of the GC population (A1) was represented by four stacked rectangular blocks of current, each representing a subcellular domain: one for the somata (bottom block) and three for the dendrites in the stratum moleculare (A2). The blocks were assigned appropriate curvature and dimensions to reproduce a prototypic U-shaped GC population with a central plane of symmetry and slight blade asymmetry (the top blade was longer than the bottom blade). A tetrahedron adaptive recording mesh simulating the conductive extracellular medium was built in and around the cellular component. Note the denser tetrahedron mesh in the cellular component and the interposed region (i.e., the hilus). B, In the FEM model, the block sources required predefined values. By default, we used experimentally obtained spatial distributions and temporal activations from the excitatory MPP. B1 shows the depth profile of an evoked subthreshold fEPSP superimposed to the contour plot of current sources (blue) and sinks (warm colors) estimated by CSD analysis. The charge was distributed throughout all four compartments with identical time course and was balanced at all instants (B2). B3, FEM simulated data. CSD and charge density are given in normalized arbitrary units (a.u.). Vertical red lines indicate the stimulus time.

FEM approach.

FEM allows explicit models to be generated of the geometry and dielectrical properties of the extracellular space and it yields 3D maps of the potential and current distributions in a complex structure over time. As such, we modeled the geometry of the structure of interest establishing the geometry of current sources and their temporal activation, and we fixed the boundary conditions. The volumetric character of FEM current sources allows the electrical currents produced by multiple synchronously activated neurons to be compiled in a few block-like current generators (Fig. 1A, bottom) that jointly obey the principle of charge conservation. This is an important advantage, which makes it suitable to reproduce LFPs in a volume generated by activated sections of layered and/or curved structures made up of units arranged in parallel such as the GC population. Accordingly, the size and geometry of the blocks of current represent the physical extension of the synchronously activated GCs, i.e., the portion of the GC population that elicits postsynaptic currents upon coherent activation of a group of axons from homologous afferent units (Benito et al., 2013). The FEM approach is widely used in magnetoencephalography and scalp electroencephalogram (EEG; Chen and Mogul, 2009; Salvador et al., 2011; Thielscher et al., 2011), although to the best of our knowledge it has not previously been used in the study of LFPs where the modeling approaches included realistic connectivity and/or membrane electrogenesis (Pauluis et al., 1999; Varona et al., 2000; López-Aguado et al., 2002; Lindén et al., 2011; Makarova et al., 2011; Ho et al., 2012).

A three-dimensional FEM model of the rat dorsal DG was constructed using COMSOL Multiphysics software. This model included a cellular portion (colored blocks in Fig. 1A3) that approximated to the dimensions (H, W, L: 0.98 × 1.74 × 2 mm) and curvature of the GC population, and an enclosing volume of the extracellular space equivalent to 2 × 2.7 × 3 mm, which is sufficiently large so as to not distort the field lines in the central region of interest. We tested different surrounding volumes (up to four times longer in each direction) while maintaining boundary conditions. The chosen volume rendered LFPs that were at least 90% of the maximum amplitude obtained with the largest volume (>95% in most tested points). The core set of simulations sought to reproduce the coherent activation of analogous subcellular domains of GCs during activation of a single pathway (we chose the MPP input for testing purposes; Fig. 1B), which behave as laminar dipolar sources. The cellular portion was therefore represented as stacked longitudinal blocks of current sources, each representing a subcellular “population” domain (Fig. 1A). We found that four stacked sheet-like, 60-μm-thick rectangular blocks of current were sufficient to reproduce the gross laminar features of the LFPs generated by GCs, one for the cell bodies and three for the dendritic arbors. These blocks were bent to replicate the U-shape of the GC population in a 2 × 2 mm slab of tissue from the dorsal portion of the hippocampus, with the upper blade slightly longer than the lower blade. For simplicity we simulated this curvature in only one direction, i.e., as a straight U-shaped half tube with open ends. This spatial configuration allowed hilar potentials to be analyzed in the absence of the complex interlaminar volume conduction that occurs in the helicoidal structure of the real DG. In separate sets of simulations, the U-shaped blocks of current were divided into 200, 400, or 800 μm longitudinal sections or strips, mimicking nonoverlapping portions of the GC population, which could be independently activated to analyze the effects of the spatial coherence (topology) and synchrony of the inputs. The use of unique U-shaped blocks or stripped configurations served to evaluate the LFPs produced by one or multiple inputs with predefined extensive or partial synaptic territories on the GC population, respectively. The precise topology of afferent pathways to the GC population is incompletely characterized. Activation of perforant path fibers appears to be well respected by the unique U-shaped block configuration as they sweep all over the GC population in the two DG blades. Other inputs may have a specific topology making synaptic contact with a smaller spatial coverage of the GC population. For simplicity, we used nonoverlapping blocks of current representing inputs with imaginary topological projection of varying synaptic territories. We used Dirichlet boundary conditions by setting the field to the ground value on the external surface of the enclosing volume and imposing charge conservation inside the total volume. A tetrahedrical adaptive grid of the highest resolution (smallest size, 0.05 μm) was used to ensure the correct resolution of field equations in the curved compartments (Fig. 1A3).

In the present model we excluded any possible contribution of the extracellular currents from the GC synapses with hilar cells. Most hilar cells have multipolar dendritic trees (Amaral, 1978) and hence, a closed-field extracellular configuration of the electric field is established by their synaptic activation (Lorente de Nó, 1947). Consequently, the currents do not (or they only poorly) spread beyond their physical limits (Lindén et al., 2011). In consequence, these cells do not add their currents in the extracellular space and they only negligibly contribute to the LFP (even if some subtypes are strongly synchronized). Indeed, the results presented in the experimental section justify their omission from the model.

Maxwell equations describing the relevant phenomena were resolved by FEM, as implemented in COMSOL. This approach assumes a piecewise polynomial approximation for the solution and identifies the polynomial coefficients using an efficient variational technique. The problem region is then converted into a discrete and finite number of tetrahedral elements to which the governing equations are applied, and the resulting equations are ultimately solved (Sadiku, 2001). For the sake of simplicity, the tissue was considered to be isotropic and homogeneous.

Temporal activation of the cellular component (see below) was combined with FEM in a time-dependent analysis performed using the AC/DC module of COMSOL for all nodes in the extracellular volume (containing the hilus and the surrounding volume). The spatial and temporal dynamics of LFP and CSD distributions were evaluated after activation of individual subcellular domains by different inputs (the rationale of the model used is illustrated in Fig. 1B). The temporal activation of a pathway-specific LFP generator, such as the MPP excitatory input, was taken as the input signal, s(t). For simplicity, we used an MPP-evoked fEPSP. The axons of this pathway establish synaptic contact with GCs in the middle third of their dendritic tree (Fig. 1B1, green axons). The spatial distribution of the CSD corresponding to this activation (Fig. 1B1, contour map) was compartmentalized into four spatial blocks that jointly configured the GC population, such that they roughly reproduced the same spatial profile (Fig. 1B2). The sum of charge density was set to zero, as imposed by current conservation law. The electric fields and potentials elicited by these currents were calculated for the entire tissue volume by FEM. Linear profiles of simulated LFPs comparable to those recorded in vivo were built using several linear tracks along the vertical z-axis, which contained 29 registration points spaced at 50 μm intervals and that were placed in the middle of the structure to produce the most homogenous field contribution. LFP profiles were constructed from the instantaneous voltage signal recorded at each simulated recording point (Fig. 1B3).

Results

Excitatory and inhibitory inputs to granule cells both produce large positive LFPs in the hilus

In a sample epoch of an LFP profile spanning both blades of the DG (Fig. 2A), maximum LFP power was observed in the hilus, within the U-shaped fold created by the GC population, and it had decayed noticeably in the dendritic stratum moleculare (0.56 ± 0.02 vs 0.14 ± 0.02 mV²; mean ± SEM measured in 200 s epochs; n = 6 animals). For comparison, the mean power of LFPs in the overlying cortex was 0.018 ± 0.006 mV². Because multiple inputs with different postsynaptic topology in the GC population produced currents that sum unevenly at different sites, we first set out to determine the spatial features of the LFPs contributed by each of the main synaptic pathways in the DG. Although GCs receive inhibitory and excitatory synaptic inputs, the hilar LFPs are predominantly positive-going and reach the highest amplitude in the hilus, away from the active synaptic domains (Bragin et al., 1995a,b). To investigate this apparent paradox, we separated the excitatory and inhibitory contributions to ongoing LFP profiles using ICA (Makarov et al., 2010), allowing us to map the spatial features of LFPs created by an homogeneous input in isolation. The process of separation is based on the differential spatial distribution of the electric fields generated by the transmembrane currents during activation of one or another synaptic pathway that contacts different domains of the GC population. Such differences are maximized in recordings within GC domains, where stronger gradients and different sites of polarity reversal for LFP events are observed in contrast to their uniformity throughout the hilus. Consistent with earlier findings (Benito et al., 2013), we detected three distinct major LFP generators in the DG (Fig. 2A). Two of these (referred to herein as the MPP and LPP generators) corresponded to excitatory inputs from the medial and lateral perforant pathways, whereas the third (the GC_som generator) was a somatic inhibitory input.

Figure 2.

Experimental identification and model reproduction of pathway-specific LFPs in the DG. A, Fragment of raw LFPs recorded across the CA1/DG with a linear probe (only every other site was plotted). Note the large amplitude and dominant positive polarity in the DG. A remarkably steady amplitude of LFPs was observed across the hilus. hf, Hippocampal fissure. The mean power of raw LFPs is shown in the histogram to the right. Three pathway-specific LFP components were separated using an ICA-based method. Each ICA component or LFP generator consists of a spatial distribution of weights (V_wt) that is characteristic of the input and a time course that is specific of the epoch analyzed. The main components were the MPP and LPP inputs, and an inhibitory GC_som. All three LFP generators exhibited a similar CSD distribution (CSD_wt) with strong current sources in the soma layer toward the hilus and sinks in the dendritic layers, albeit with spatial differences. Horizontal red lines indicate the approximate location of GC soma layers. CSD minimized at the hilus. B, The mixing of synaptic currents within individual cells elicited by activation of anatomical afferent excitatory and inhibitory inputs to GCs was essayed through an H–H compartmental model. Each pathway activated only a GC domain (delimited by colored compartments in GC dummies). The illustrated example used an identical time series delayed by 2 ms on each input (instants marked by dashes at the bottom). The resultant model LFPs displayed maximum and steady amplitude throughout the hilus and showed dominant positive polarity. The ICA was able to separate all three components despite the strong temporal overlap of synaptic inputs. Note the almost perfect match of the time courses obtained for each of the pathway-specific components demixed from the composite model LFPs and the time course of each pathway when activated alone (colored and gray traces, respectively).

The excitatory/inhibitory nature of these LFP components has been investigated by local pharmacological blockade of non-NMDA Glu receptors or GABA-A receptors (see Materials and Methods; Benito et al., 2013), findings corroborated by the additional analyses performed here. The mean power for raw LFPs and for each of the ICA-separated LFP components is shown in Table 1. Note that GABA blockade is only effective when injected at the cell body layer, but not in the stratum moleculare, whereas Glu blockade efficiently reduces the MPP and LPP power, and also in part the inhibitory GC_som generator, presumably by decreasing the excitatory drive to somatically targeting local interneurons. The relative contribution of the MPP, LPP, and GC_som generators to the total variance estimated in the profiles spanning from the hippocampal fissure to the outer border of the lower blade was 10.9 ± 4.7, 50 ± 7.8, and 39.1 ± 7.7, respectively (% mean ± SEM, n = 6 animals). Other synaptic inputs, such as commissural excitation of the proximal dendritic layer or dendritic inhibition via the MPP or LPP input, apparently failed to produce LFPs sufficiently large and stable to accumulate enough variance over the periods analyzed, although they may be represented by weaker LFP generators not studied here.

Table 1.

Pharmacological blockade of LFP generators in the DG

	DNQX	BIC1 (som + dend)	BIC2 (dend)
Hilar LFP	20.3 ± 4.8**	71.9 ± 3.2*	110.1 ± 11
MPP	17.7 ± 5.4**	104.9 ± 10.4	108.4 ± 10.7
LPP	10.0 ± 1.6***	138.0 ± 25.2	108.1 ± 9.3
GCsom	55.1 ± 12.8*	32.4 ± 6.2**	109.4 ± 12.9

The values correspond to the mean power of ICA-isolated LFP components after local microinjection of 1 mm DNQX, and 1 or 0.2 mm bicuculline (BIC1, BIC2, respectively). In DNQX and BIC1 the size of microdrop was ∼500 μm in diameter that could not be restricted to any specific strata, thus the injections in the stratum moleculare and the soma layer were pooled. In BIC2, experiments the drop was reduced to within 200–300 μm, and could be restricted to only one domain (the dendrites) when injected in the stratum moleculare. The data are expressed as a percentage of the control (mean ± SEM, Student's t test; α = 0.05, 0.01, and 0.001; n = 5 animals each, except n = 3 in BIC2).

One of the main characteristics of LFP generators is the spatial distribution of the voltage weights (Fig. 2A, V_wt) along the recording track (z-axis). In our experimental conditions, all three generators in the DG exhibited similar spatial distributions: we observed a plateau-like maximum between cell layers throughout the hilus, which declined outwardly and reversed its polarity at different points. The second order derivative of these voltage profiles approximated to stationary CSD profiles along the z-axis (CSD_wt), i.e., the relative strength and polarity of transmembrane currents in the GC layer elicited by a particular synaptic input. We observed the same somatic sink/dendritic source distribution in response to dendritic excitation of MPP and LPP generators (active inward currents in dendritic domains), and somatic inhibition of GC_som (active outward currents in GC somata). The excitatory CSD_wt profiles were consistent with those previously reported for PP-evoked field potentials (Abraham and McNaughton, 1984; Golarai and Sutula, 1996; Canning and Leung, 1997). The CSD_wt tended to disappear in the hilus as the axon is the only GC element in this region and it drains only a negligible amount of somatodendritic synaptic current (Makarova et al., 2008), which means that it does not contribute to hilar LFPs.

The efficiency of the ICA to separate the synaptic sources mixed in natural LFPs in the DG was checked in a realistic multineuronal DG model of compartmental GCs (see Materials and Methods). A variety of temporal patterns for the different excitatory and inhibitory inputs was tested. In general, irregular uncorrelated inputs produced LFPs of which the original sources were efficiently separated (the CC between each demixed LFP generator and its time course when used alone in the model was always larger than 0.95). Only particular combinations of periodic highly correlated inputs appeared to decrease the efficiency. An extreme case using highly correlated inputs at gamma frequency and varying intensity is illustrated in Figure 2B, in which all three pathways were activated with identical but slightly delayed (2 ms) time series (instants are marked by dashes at the bottom). Whether separately or in combination, the LFPs were much larger and positive going in the hilus interposed between GC layers. Note the strong overlap of synaptic activations in all three pathways and the tight matching of demixed activities to their individualized LFPs (superimposed colored and gray traces, respectively). Sample epochs of LFP generators obtained by the ICA of real LFPs were used as the input parameter for the FEM model approach used in all simulations from here on. We assessed that the compartmental and FEM approaches were equivalent to reproduce LFPs.

The spatial features of LFPs for each afferent pathway were determined by virtual LFP reconstruction (see Materials and Methods; sample traces for the GC_som and the MPP generators are shown in Fig. 3A,B, left). Both dendritic excitation and somatic inhibition produced similar large positive-going LFPs across the hilus and smaller negative counterparts in the molecular layers. These observations may be explained by a common orientation of the dipolar sheets of the current sources formed by the GC palisade. We investigated this hypothesis in the FEM model (Figs. 3A,B, right) using the same realistic temporal activation as that obtained in the experimental case (colored traces at the bottom). Both somatic inhibition and dendritic excitation produced positive LFPs in the interposed hilar region and the magnitude of these LFPs was much larger than that of their negative counterparts in cellular layers. Inversion of the polarity of current sources, as if simulating distal dendritic inhibition (Fig. 3D) or somatic excitation, switched the LFP polarity at all sites. Although negative-going LFP fluctuations were also observed in experiments, these were far less frequent than positive LFPs, suggesting that anatomical pathways that generate negative hilar LFPs (e.g., dendritic inhibition) do not fulfill the spatiotemporal requirements to contribute to LFPs as strongly as others (see below).

Figure 3.

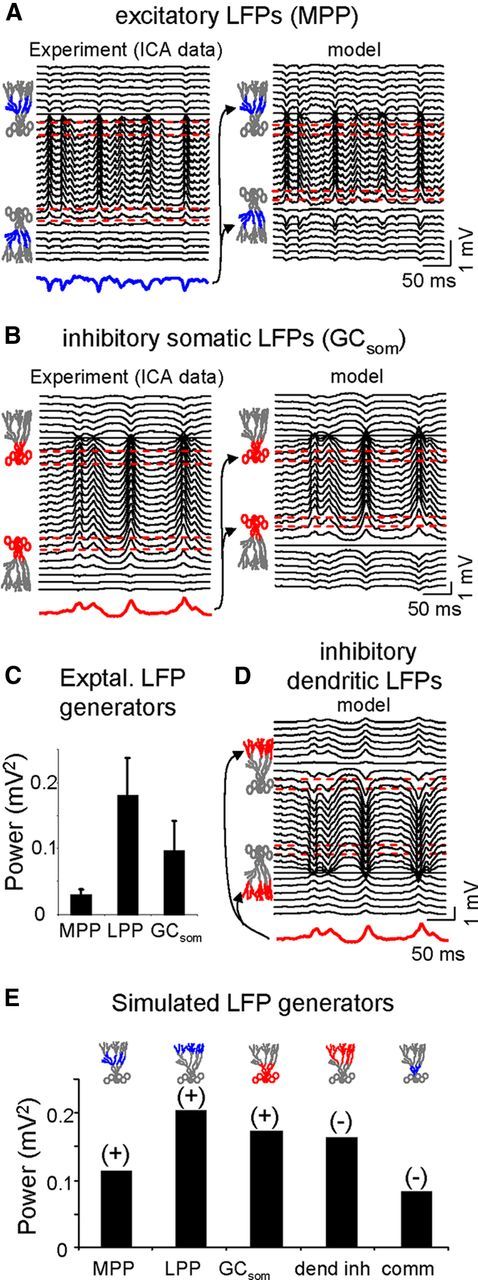
Comparison of the pathway-specific excitatory and inhibitory LFPs in experiments and in the model. The former are virtual reconstructions obtained by multiplying the corresponding spatial weights and temporal activation of ICA-derived components. Model LFPs were obtained using the same temporal activation as those observed in the experiments (in color at the bottom of the LFP). The GC drawing on the left mark the cellular bands used as excitatory (blue) or inhibitory (red) synaptic domains. A, B, sample epochs of dendritic excitatory (MPP) and somatic inhibitory (GCsom) LFPs. Note the precise reproduction of the LFPs by the model, and the large, steady and positive potentials across the hilus in both cases. Negative hilar potentials were only obtained by modeling imaginary cases of distal dendritic inhibition or proximal excitation (D). No such LFP generators were not found in the experiments. C, Population data of the absolute mean power of the experimental LFP generators. E, Absolute power and dominant polarity of the model LFPs in the hilus for each of the experimental cases plus two imaginary cases representing dendritic inhibition and proximal excitatory inputs (commissural-like). All the simulations used identical input activation to reveal the cytoarchitectonic influences. The maximum power was obtained for inputs with stronger dipolar moment (e.g., distal LPP input), regardless of the polarity.

In terms of absolute power for pathway-specific LFPs in the hilus the LPP was the strongest and the MPP the weakest (Fig. 3C, n = 6 animals). Because the absolute power depends on both geometrical and functional factors, and the latter may differ for excitatory and inhibitory inputs during ongoing activity, we ran simulations using the same temporal activation in all cases. Hence, we compared the experimental and other imaginary distributions reproducing anatomical pathways for which we found no significant generator during analysis of real LFPs, including a dendritic inhibition and a proximal commissural-like excitation (colored band in cell drawings in Fig. 3E). The relative power of LFP among simulated generators was similar to those observed in the experiments, although the differences should be attributed to the different temporal dynamics of the inputs in the latter. As expected, we found no difference in the power of hilar potentials in terms of the polarity of the synaptic input as long as the active synaptic zones were the same. The excitatory MPP and LPP inputs and the inhibitory GC_som input elicited positive LFPs across the hilus, whereas distal dendritic inhibition and proximal excitation elicited negative LFPs. However, we noticed that the extension and location of the active synaptic domain produced a clear effect whereby the power was stronger the more distal the input and the narrower the active domain. This result can be explained by the increase of dipolar moment by these geometrical factors.

Cell geometry and layer architecture combine to enhance the positive hilar potentials

A plausible interpretation of the aforementioned observations is that outward somatic currents (either active or passive) add up preferentially in the hilus and they generate positive LFPs. However, to comprehensively interpret the way volume-conducted currents sum or cancel at sites distant of the generating cells, both the cellular geometry and population architecture must be considered. We first explored a key aspect of the former, the number, and orientation of the dendritic arbors. The simulations were repeated using sheet-like blocks of current sources that represented active somatic/perisomatic inhibition in standard GCs with a single polarized dendritic tree (Fig. 4A) or imaginary GCs with two dendritic trees resembling the cellular geometry of the pyramidal cell (Fig. 4B). For simplicity, we limited the architectural model to the planar section of the GC population.

Figure 4.

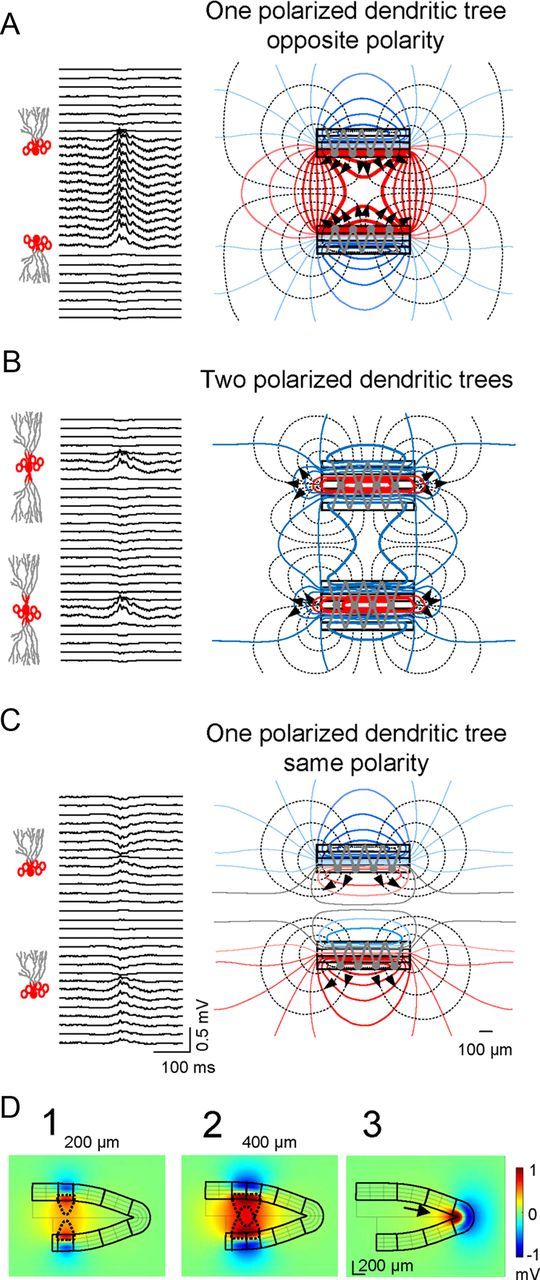
Large positive LFPs in the hilus are produced by mirrored parallel layers or a singlefolded layer of dendritically polarized GCs. A, Model estimate of LFPs using a realistic configuration of parallel layers of GCs with polarized dendritic arbors and a basket cell-type inhibitory input. Note the large amplitude and positive polarity of hilar potentials compared with dendritic sites. The lines of current (black dashed) and isopotential lines (solid colored) to the right show the collective behavior of the cell component (stacked rectangles) as a laminar dipole in which the soma layer oriented toward the hilus acts as the current source and the outer dendritic segment as the current sink. B, Perisomatic inhibitory activation of imaginary GCs with two polarized dendritic trees produced very small negative LFPs in the hilus. Only perisomatic synaptic layers exhibited sizable LFPs with matching polarity. The bulk of the inward currents were directed toward inner synaptic sites, spreading weakly through the outer volume (hence their small potential). C, Mirroring cell layers are required to develop large hilar potentials. The simulation used GC layers with similar orientation. The simultaneous homogeneous somatic inhibition in the two blades cancelled out the hilar LFPs, while distant sites beyond the cell layers developed weak negative and positive potentials. D, Stationary snapshots of the voltage distribution (amplitude and polarity) for the activation of different portions of the GC domains. Large positive potentials (red) were produced by the summation of volume-conducted currents of equal polarity in the hilus generated by two parallel laminas of GCs of different extensions (D1, D2), or by a single-folded lamina (soma-inwards) of GCs (D3). The drop-shaped dashed lines represent the convergence of the volume-conducted currents in the hilus: the wider the activated GC domains the greater the reach of the positive potentials away from cell domains. In the apex (D3), the volume-conducted currents created a headlight effect in the hilus (arrow).

Compared with the realistic morphology with only one dendritic tree (Fig. 4A), a bipolar dendritic arbor led to dramatic changes in hilar potentials, which were smaller in magnitude and largely negative-going (Fig. 4B). Examining the spatial distribution of the current density and potential (dashed and continuous lines in the right panels), large potentials were confined to a narrow cellular domain containing the active synapses. Whereas in the realistic neuronal configuration outward currents exited the cellular compartment through the somatic surface in both blades and they entered the hilus (Fig. 4A, high density of lines of current), in the bipolar dendritic configuration they were cancelled out except in a small region at either edge (Fig. 4B). In all cases, the dominant polarity of the field potential in the hilus was imposed by the direction of the currents in the most proximal cellular compartment (as long as the distance between parallel layers remains within certain limits). We next examined the influence of the relative polarity of dipole layer generators on LFP magnitude by constructing an imaginary model of the DG in which the charge distribution was inverted in the lower blade (i.e., GCs were similarly oriented in both blades; Fig. 4C), This configuration yielded hilar LFPs with the smallest amplitude and displayed a polarity reversal half way between cell layers.

Importantly, the amplitude of hilar potentials grew with the extension of activated GC layers and decayed with their separation. The different expansion of volume-conducted currents for activated strips of 200 and 400 μm is shown in Figure 4D. The LFPs also extended laterally over a considerable distance from the activated GC block (yellowish surfaces). A similar phenomenon occurred in singlefolded layers, such as the curved section at the DG apex (Fig. 4D3, arrow). It can be demonstrated that the enhancement of positive LFPs increases inversely relative to the radius of the GC layer curvature (Woodbury, 1960).

Granule cell cytoarchitecture produces heterogeneous spread of volume-conducted currents

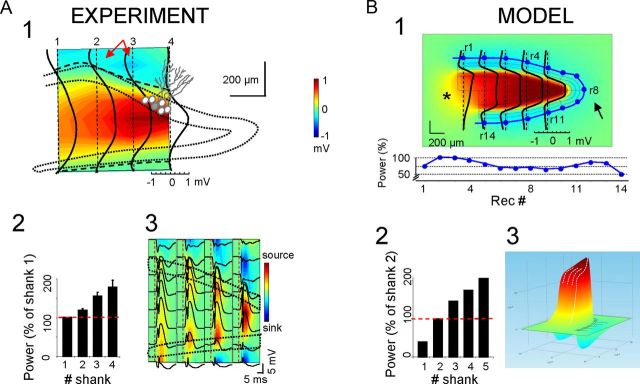
Although the aforementioned simulations explain the polarity of hilar potentials, they do not fully clarify why LFPs are larger in this region than near the synaptic loci or how far can they be recorded from the GC sources. Because architectonic factors should act similarly on each synaptic input, we chose the MPP as a representative LFP generator to be compared in the model and experimental situations. We first characterized the spatial distribution of the MPP generator in vivo (Fig. 5A). Pathway-specific LFPs were obtained by an ICA of raw LFPs recorded with a four-shank multielectrode oriented parallel to the midline (200 μm intershank distance). The MPP-evoked field potentials (Fig. 5A3), and the estimated sinks (blue) and sources (yellow/red) of current, served to identify the synaptic dendritic band for excitatory MPP fibers in both blades. Note the large positive evoked potentials across the hilus, which closely corresponded with ongoing LFPs. The two-dimensional representation of the relative power and polarity of virtual (reconstructed) MPP-LFPs shown (see Materials and Methods) is superimposed upon a scheme of the DG subfields, indicating the regional coverage, relative strength and polarity (Fig. 5A1). In all cases, we observed a strong increase in the power of positive potentials toward the apex. The population data for LFP power (n = 4 animals), estimated along a central line half-way between the cell layers (relative to the value at the most rostral shank) is shown in Figure 5A2.

Figure 5.

Experimental recordings and the model reproduction of positive hilar potentials have spatially heterogeneous proportional amplitude. A1, Surface contour plot of the mean amplitude of MPP-specific LFPs reconstructed from raw LFPs in four parallel linear shanks partially covering the GC layers and the hilus (dashed outline indicates the approximate position of GC somatic layers). Curved dashed lines represent the polarity reversals linking zero-crossing points of individual V_wts of the MPP-specific LFPs obtained separately for each recording track (superimposed solid black traces). Note the increased amplitude of positive hilar potentials toward the apex. The amplitude of negative potentials in synaptic dendritic loci was stronger in planar versus convex sections (red arrows). A2, Population mean power of hilar potentials normalized with respect to the value in the outer shank (mean ± SEM). A3, The spatial map of MPP-evoked potentials and the corresponding CSD reproduce the spatial distribution and heterogeneous amplitude of ongoing MPP potentials. B, The amplitude, polarity and spatial distribution obtained in the model for MPP-like homogeneous activation of the GC population matched those found in vivo (B1, B2). The values of outer negative potentials are plotted along a line equidistant to cell layers (r1–r14 dots marked in surface plot and values in the unfolded lower plot). A notable reduction was observed at sites close to the apex due to increased contamination by the largest nearby positive LFPs, leading to partial cancellation. B3, The three-dimensional representation of the amplitude and polarity helps to visualize the giant positive potentials confined to the hilus. In contrast, smaller negative potentials are generated in synaptic and outer sites. Note that the asymmetrical segregation of positive and negative LFPs in the volume belongs to a single synaptic input.

Identical results were obtained in simulations, when the model was fed with MPP-like current distributions (Fig. 5B; note that we plotted LFPs in five instead of four vertical tracks so that one was placed in a zone with a single blade at the open end). Examination of the lines of current revealed that the increasing concentration of outward currents toward the apex was brought about by the concave structure. We also observed a strong reduction in the negative field potential in the outer layers at the apex (Fig. 5B1; arrow; near recording site r8). This was reflected by the smaller fEPSPs in this section of the molecular layer (sites r6–r10) than in planar sections (sites r2–r5 and r11–r13). We only observed a notable spread of volume-conducted currents out of the GC environment through the open end (asterisk), resulting in positive LFPs of significant amplitude (as much as 0.5 mV up to 400 μm from the cell layers), with a characteristic “headlight” distribution. The power of simulated hilar LFPs along the midline followed the same spatial trend as that seen in vivo (Fig. 5B2), with the apex exhibiting an amplitude ∼5-fold that of the open end (205.3% and 39.3% the value in shank no. 2, respectively; note that there were five shanks in the model instead of four). The pseudo-3D representation of the MPP-LFPs revealed the sharp spatial transition and the relative magnitude of positive and negative LFPs (Fig. 5B3) both in and between cell layers. It is worth mentioning that activation throughout the entire U-shaped GC structure did not simply defined spatial domains of positive and negative LFPs in the volume beyond the cell domains but also it led to a strong imbalance of their relative amplitude that was not evident with partial activation (for instance, compare with the rather symmetrical amplitude of positive and negative field potentials on both sides of the active GC strips; Fig. 3D). Such variation in the relative amplitude of the field potentials recorded at two different sites (the hilus and GC domains) was further explored for its physiological relevance (see below).

Suppressing activity in one blade virtually transforms the DG in a planar structure

The aforementioned experiments suggested that the large amplitude of hilar potentials is due to simultaneous activation of the GCs in the two blades. We investigated this inference experimentally in the animal by local injection of DNQX in the vicinity of a recording shank in the stratum moleculare of the top blade (Fig. 6B1), and in the model by entering activity only in the lower blade (Fig. 6B2). Note the selective blockage of the MPP-evoked fEPSP and the corresponding current sink in the upper blade (upper sink: 30.5 ± 11.3% of control, p < 0.05; lower sink: 98.5 ± 3.5%, p > 0.05: n = 4 animals; Fig. 6A2,A3). As only the lower blade remained active, the DG was virtually converted into a planar structure, and we found that hilar potentials decreased to 20.6 ± 6% the control values (p < 0.01, Student′s t test; n = 4 animals; Fig. 6B,C). Hilar LFPs were also reduced dramatically in the model (10.7–24.7% of control values in tracks 1–5; Fig. 6B,C), whereas the negative LFPs in the synaptic sites of the lower blade appeared to increase, as the removal of positive hilar potentials reduced cancellation (Fig. 6B, red arrows). Notably, after inactivation of the top blade, field potentials in the bottom blade propagated across the top blade and above (Fig. 6B1, compare red ovals), due to the loss of the mutual cancellation of extracellular currents from laminar dipoles of opposing polarity over an identical time course. The faster-than-linear decay of the field potential evident in vivo (curved arrow) was probably due to a small radius of action of the drug.

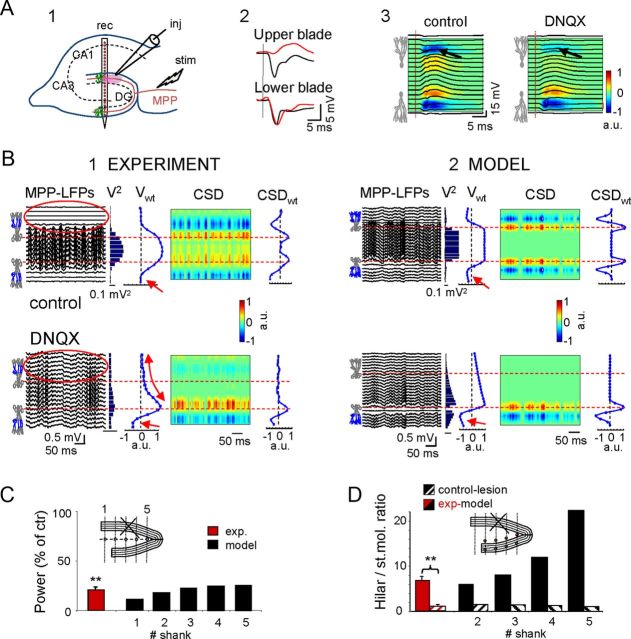
Figure 6.

Deactivation of one blade in vivo and in the computational model converts the DG into a functionally planar structure. A1, Electrode arrangement for the experimental blockade of MPP potentials by local administration of DNQX in the top blade via an injecting/recording pipette (inj) positioned close to the linear probe (rec). A2, MPP-evoked fEPSPs selectively disappeared in the top blade (black and red potentials pertain to vehicle and DNQX administration in the bottom blade, respectively). A3, Superimposed field potentials and CSD across the hilus and cell layers. Note the near complete disappearance of the synaptic sink upon DNQX administration (arrows). B, The top and bottom rows show the results for vehicle versus DNQX treatment (B1) and deactivation of the upper blade in the model (B2), respectively. Similar results were obtained using both approaches. Note the strong reduction of LFP power in the hilus (V²), and the modification of the spatial distribution of MPP potentials (V_wt), which resembled synaptic activation in a single planar layer (linear decay from the active blade). The nonlinear decay observed in vivo (curved arrow) was probably due to incomplete layer ablation by the drug. Despite the intact CSD_wt distribution in the lower blade, the local synaptic sites increased in amplitude (small red arrows) due to reduced cancellation by the absence of positive potentials from the other layer. Note that LFPs were also evident in the deactivated blade (compare red ovals), as the current reached this location volume-conducted through the hilus from the distant active blade. No reversal of polarity was observed for these LFPs. C, Power of the hilar LFPs in experiments and in the model after lesion/inactivation of the top blade expressed as the percentage of control. C, Inset, The sites (in blue) used for estimations in the model. D, Hilar to stratum moleculare ratio of the field potential amplitude in control (homogeneous activation in the two blades) and after inactivation of the top blade. D, Inset, The pairs of sites used for estimation (300 μm apart along recording tracks). Note the increasing boosting effect toward the apex in control and the nearly complete linearization after the inactivation of the top blade (lesion), which then reached values close to 1. C, D, **p < 0.01; Student's t test, n = 4 animals.

We also calculated the ratio of the field potential power in the hilus versus the stratum moleculare (points were separated by 300 μm; Fig. 6D) as a measurement of the boosting effect produced by layer folding and curvatures. In planar structures, this ratio is close to one due to the symmetry of the electric field in laminar dipoles. In experiments, the ratio was calculated in only one shank and it fell from 6.5 ± 1.2 to 1.0 ± 0.1 (n = 4 animals). In the model the ratio increased from ∼4 to ∼22 toward the apex for homogeneous activation in the two blades, and it fell below 1.5 when only the bottom blade was activated (Fig. 6D). These results confirm the central role of layer folding and curvatures in the boosting of hilar potentials.

The influence of the synchrony and spatial extension of synaptic input on hilar potentials

The size of the simulated blocks represents the extension of the synchronously activated GC population. So far, we studied with the model a scenario in which synaptic input is synchronous all over. Such topology of activation appears well suited for the synaptic connections of the perforant path inputs. We then extended the analysis to other possible configurations using different synaptic inputs of varying spatial coverage and position. To this end, tissue strips of GCs of varying size (200, 400, or 800 μm in width) were activated pairwise in both blades (except in the apex) with different (uncorrelated) inputs of an irregular pattern (Fig. 7A). To better evaluate the mixing of currents from different GC sources the activated strips were nonoverlapping, i.e., only one input was injected to each GC strip. The indices of spatial correlation of the resulting LFPs were compared between the model and in vivo studies.

Figure 7.

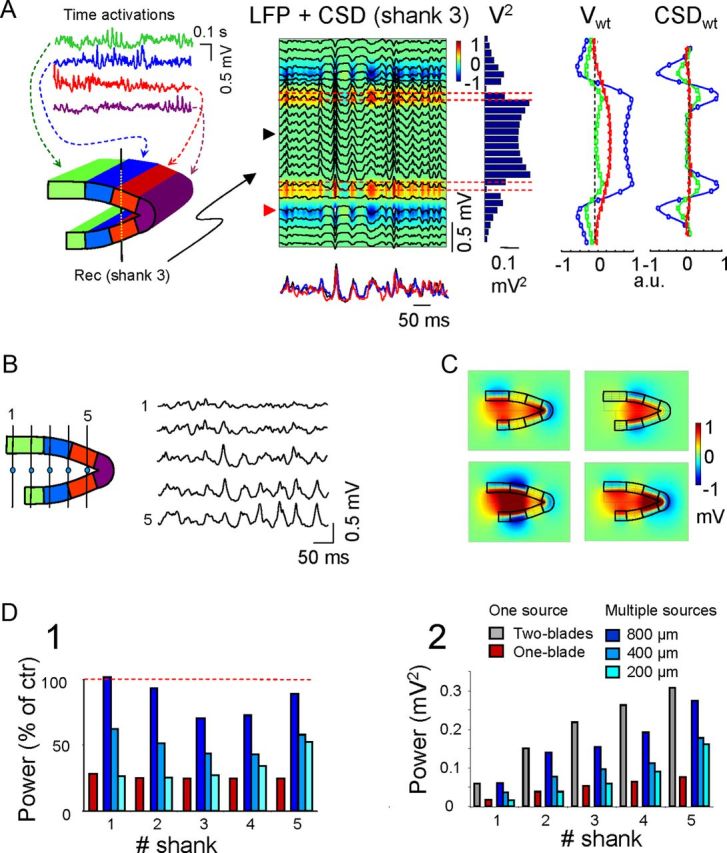
Multiple asynchronous generators of different sizes do not reproduce large coherent hilar LFPs. A, Results obtained for a model configuration using nonoverlapping, 400-μm-wide strip-like mirrored domains of activation (left, colored). Activations (top, colored traces) differed between all the domains. A representative epoch of model LFPs is superimposed on the corresponding CSD map as calculated for the central shank (no. 3). In the histogram of mean LFP power (V²) there is a large reduction in power in the hilus compared with the uniform activation by a single input. Note that recordings alongside the shank no longer match perfectly due to lateral contributions of other GC sources. The superimposed red and black traces below the LFP+CSD panel correspond to the hilar and synaptic sites (reversed and scaled), respectively, whereas the blue trace is the input activation for the blue compartments closer to the recording shank. ICA disentangled the local activity (blue) from that in adjacent domains that had mixed with LFPs by volume conduction (V_wt and CSD_wt). B, Different temporal activations of GC domains produce a variable mixture of volume-conducted currents in the hilus, giving rise to noncoherent hilar LFPs. The model LFPs were estimated along the midline (left, dots). Note the gradual shift of LFPs from sites 1–5, indicating the changing contributions of GC blocks in function of the distance and specific temporal activation. Also, note the increasing mean amplitude toward the apex. C, Snapshots of voltage distribution at four different instants reflect the extremely varying spatial distribution of LFPs contributed by multiple sources in A. Note the extreme variation and regionalization of hilar potentials. D, Change in the mean LFP power (D1) along the hilus normalized (%) to the homogeneous configuration (i.e., coherent input in the two blades), and the change in the absolute power (D2) for the different configurations of GC population activation either in mirrored strips of different sizes (blue bars) or as a single source extending through one or the two blades.

When a representative simulation is considered that involves four inputs to 400-μm-wide spatial modules and recording across the middle shank (no. 3, located across blue modules; Fig. 7A), the LFPs contained a mixed contribution by all four active strips. This can be appreciated by the imperfect matching of LFPs recorded alongside the same recording shank and the time course of the synaptic activation corresponding to the local (blue) strip of activated GCs (superimposed bottom traces under the LFP + CSD; Fig. 7A). The mixture of activities in a recording track contributed by the multiple distant sources can be separated by an ICA of the linear LFPs. In the experiment illustrated, the ICA revealed the three components lying closest to the recording track, each with a distinct spatial distribution and magnitude (Fig. 7A, V_wt profiles). We noticed that the spatial distributions retrieved for distant sources were spatially smoothed counterparts of the local ones, whereas the CSD_wt estimations more accurately reflected the location and laminar arrangement of the original current sources at their corresponding sites, yet with very different power. The strongest component corresponded to activity from the local (blue) GC strips surrounding recording shank 3, whereas the other two captured the volume-conducted activity from adjacent strips (green and red plots). Importantly, hilar LFPs were smaller than those observed during synchronous activation of the DG, and the amplitudes approached those recorded in the GC domains (Fig. 7A, V²).

The multiple current sources contributing to hilar LFPs caused the continuous variation of the spatial coherence of LFPs within the hilus due to the uneven spatiotemporal contribution of the sources. Contrary to the homogeneous activation that produced proportional (scalable) LFPs anywhere in the hilus, regardless of the time course of the input, the blending of volume conducted currents from multiple GC sources rendered LFPs with different time courses in the different tracks, and they were dominated by the activities of the closer GC strips (Fig. 7B). The spatiotemporal distribution of hilar LFPs may become very complex and heterogeneous, as illustrated by sample snapshots of the voltage distribution, magnitude, and polarity at different instants (Fig. 7C). The cytoarchitectonic influence of mirror layers and strong curvatures could still be examined by comparing the mean power of LFPs in different configurations (Fig. 7D). Together, our results revealed a number of spatial effects, several of which are particularly relevant to the interpretation of LFPs: (1) regardless of the number and spatial coverage of the synaptic inputs, the power of hilar LFPs increased toward the apex and always reached a maximum amplitude lower than that induced by a single synaptic input extending throughout the GC population (taken as a reference for data normalization); importantly, even the narrowest mirrored strips produced larger LFPs than a single blade; (2) the loss of power was more accentuated in the narrower activation strips due to the reduced clustering of volume-conducted currents in smaller strips (86 ± 14%, 52 ± 8% and 33 ± 11% of control LFP power averaged over all five recording tracts in DG configurations with 800, 400, and 200-μm-wide strips, respectively; mean ± SEM; Fig. 7D1); (3) compared with homogeneous activation by a single input, the reduction in power in the central tracts was greater for the larger modules (Fig. 7D1, D2; although the absolute value remained unchanged), whereas the apex was less sensitive to module size; and (4) the unbalance of positive and negative relative amplitudes in both sides of the GC domains decreased markedly, and the headlight effect characteristic of the homogeneous activation disappeared. This heterogeneous spatial behavior was a combined function of multiple factors, including the size of spatial modules, layer separation at the open end and the radius of curvature.

Extended synchronous input in both DG blades best reproduces the in vivo hilar LFPs

In the simulations described above we sought to determine the spatial extension of inputs that best fitted our in vivo data. We found that a most reliable parameter is the ratio of LFP power in the hilus versus that in the GC cell domains, as this value is highly sensitive to the size of the spatial coverage of inputs. The hilar/stratum moleculare ratio estimated between points 300 μm apart in the same recording track (Fig. 8A, inset) increased toward the apex due to the shorter distance between the generating GCs in both blades and the proximity to the concave GC section. In any given recording track, this ratio decreased in parallel with the size of the strips (Fig. 8A, blue bars), confirming that this value serves as an index of the spatial extension of synaptic inputs. In all cases, the lowest ratio (close to 1) was observed during activation of a single GC blade (red bars), which resembled activation of a planar layer, whereas the largest ratio was observed when both blades were activated in total synchrony (gray bars, i.e., only one input for the entire U-shaped block). Notably, the contribution of an entire single blade to the hilus was much lower than that of the mirrored activation over a reduced GC strip (Fig. 8A, compare one blade vs 200 μm). Estimating the experimental hilar/stratum moleculare ratio for pathway-specific MPP and LPP LFPs (Fig. 8A, green and red bars; mean ± SEM; n = 4 animals, 200 s epochs) revealed values similar to those observed following full synchronous activation in the model. The ratio was always bigger for the LPP than the MPP inputs.

Figure 8.

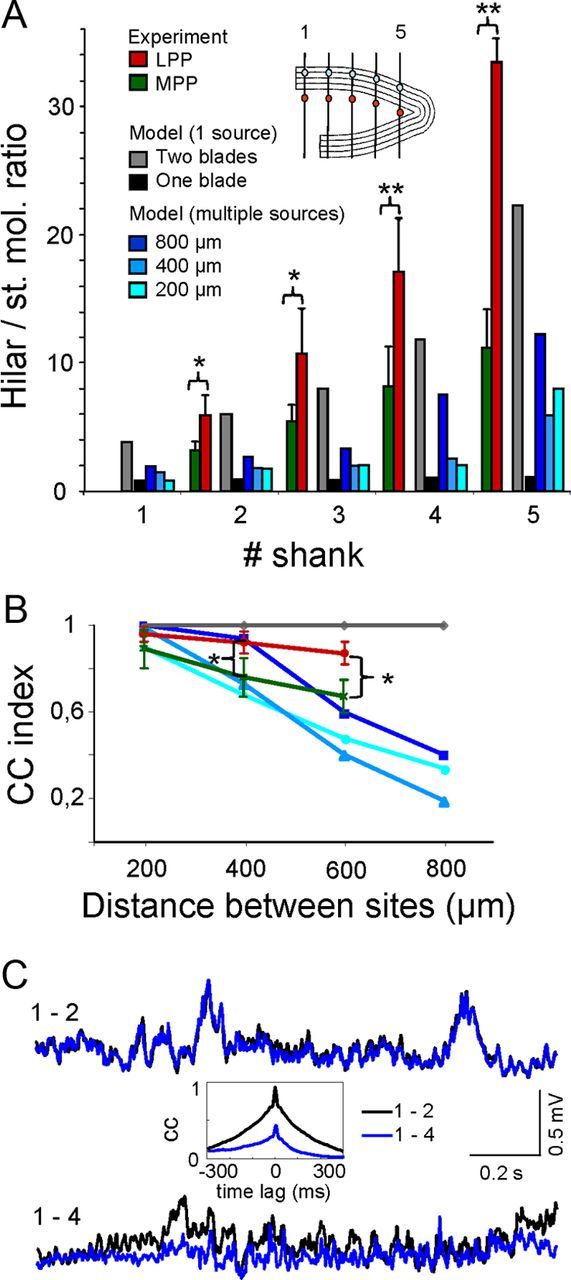
Experimental LFPs are better reproduced by extensive synchronous GC activation in both blades. A, The hilar/GC ratio was measured along the plane of symmetry between hilar and synaptic points of the same shank, as labeled in the scheme (inset). The red and green values correspond to the experimental data for specific reconstructed generators (LPP and MPP, respectively) extracted by the ICA of raw LFPs recorded with four parallel linear multielectrode probes. Note that the two-blade uniform activation of one input produced values similar to those obtained in the experiments. B, CC of LFPs in pairs of sites along the midline in the hilus. Color codes as in A. Only single inputs (gray plot) produced a full correlation anywhere, whereas the experimental values for the LPP and MPP decreased moderately with distance. Experimental values in A and B are the mean ± SEM (Student's t test: α = 0.05, 0.01, and 0.001; n = 4 animals). C, Sample epoch of superimposed activations for the MPP input in adjacent shanks (1–2) and distant shanks (1–4). The reduced correlation in the latter pair is evident in the CCs shown in the inset.

In addition to the spatial coverage, we also analyzed the time course of LFPs as this is another physiologically relevant feature. The divergence or similitude of LFPs recorded at two sites depends on the distance and the time course of the active sources that jointly define the instantaneous intensity. This was estimated from the CC index of LFPs in pairs of sites that were increasingly apart, in the experimental situation and the model (Fig. 8B). In the model, the activation of a single pathway extending throughout the entire GC population (two blades) generated proportional time fluctuations anywhere (Fig. 8B, gray line). However, when two or more synaptic pathways (blocks of different size) were coactivated, the time course of the mixed LFPs varied, hence the CC index decreased. Moreover, the divergence of a given pair of recording sites was inversely proportional to the coverage of the contributing pathways. This effect was mediated by the differential contributions of volume-conducted currents arising from each of the coactivated GC generators located at different locations in the DG, as demonstrated quantitatively by the CC between pairs of points separated by increasing intervals along the midline in the plane of symmetry (Fig. 8B, blue lines). To compare these findings with our experimental data, we superimposed the CC between temporal activations for the MPP and the LPP ongoing activities after their separation by ICA from the ongoing LFPs (green and red lines, mean ± SEM, n = 4 animals, 200 s epochs). When representative epochs of either the MPP or the LPP specific LFPs obtained separately in each of the four recording tracks were cross-correlated we found stronger coherence within LPP than MPP activities (sample traces for the MPP are shown in Fig. 8C).

The simulation data presented here was derived using multiple inputs in nonoverlapping spatial GC domains. Given the complexity of the underlying interactions, we did not present data pertaining to spatially overlapped inputs. However, it can be shown that in cases of complete overlap of multiple inputs, the resulting LFPs maintained their spatial coherence. Thus, the divergence of hilar LFPs arose from the uneven mixing of the volume-conducted currents produced by the differential spatial coverage in nonregular cytoarchitecture, as demonstrated here for nonoverlapping inputs.

Discussion

The geometry of brain structures is neither regular nor chaotic. Numerous neuronal populations are organized in curved layered configurations, whose particular arrangement plays a key role in shaping LFPs. In this study we have used mathematical modeling and in vivo analyses to investigate the generation of LFPs in the DG, a simple example of a curved brain structure. We show that the U-shaped spatial configuration of the GC population favors the spatial clustering of volume-conducted currents away from their physical origin. This projection of synaptic activity to distant sites results in increased activity within highly restricted spatial limits, reaching levels several fold higher than those observed at local sites, albeit with notable heterogeneity. Moreover, the corresponding anatomical pathways (either somatic inhibition or dendritic excitation) must project to both blades of the DG, as even a minimal loss of spatial synchronization leads to a dramatic reduction in LFP power. Our experimental data fulfill several predictions generated by our model, helping to explain why large LFPs recorded away from the source arise from spatially extended synchronous activation in populations with suitable cytoarchitecture.

Addressing the interactions between afferent synchrony and postsynaptic geometry

LFPs are of particular interest as they reflect the degree of synchronization of synaptic inputs, thereby providing insight into output dynamics in afferent populations (Fernández-Ruiz et al., 2012a,b). As individual axons can activate many neurons almost synchronously, the concurrent activation of multiple presynaptic units translates postsynaptically into spatial modules of coherent LFP activity by the merging of their synaptic territories (Elul, 1971). Our former experimental findings demonstrate that spatial modules of pathway-specific LFP activity reflect variations in activation patterns of afferent populations, without the ambiguity inherent to raw LFPs of multisynaptic origin (Fernández-Ruiz et al., 2012a; Benito et al., 2013). However, these advantages only apply to planar structures such as the CA1 region. Indeed, the synchronous spiking of afferent units is insufficient to draw conclusions regarding LFP amplitude and spatial coverage. For instance, only some known local and extrinsic inputs appear to significantly contribute to hippocampal LFPs (Korovaichuk et al., 2010; Benito et al., 2013). A number of functional and geometric factors at the cellular and population levels may enhance or annihilate synaptic currents in the extracellular space (Lorente de Nó, 1947; Makarova et al., 2010). In particular, curved and layered structures, such as the cortex and hippocampus, are prone to the spatial clustering of currents (Woodbury, 1960; Gloor, 1985, Lopes da Silva, 1991; Nunez and Srinivasan, 2006). Thus, elucidating the interplay between cytoarchitectonic and functional factors requires the explicit modeling of individual brain structures.

The spatial heterogeneity of hilar LFPs provides insight into afferent inputs

By mapping LFPs across the DG using both modeling and in vivo approaches, we demonstrate that LFP power is always greatest in the hilus, interposed between cell layer generators, and that it increases toward the apex where the distance between GC layers is reduced and the curvature increased. Blockade of activity in one blade, either pharmacologically or by turning off one blade in the computational model, effectively converted the DG into a planar single-layer structure. Consequently, the LFP power in the hilus dramatically decreased to values similar to those observed in synaptic layers. Coherent activation in mirroring cell layers and/or in a strongly curved single layer is therefore necessary and sufficient to produce the abnormally sized LFPs observed in the hilus. We also demonstrate that the positive polarity of LFPs can only be achieved by somatic inhibition or dendritic excitation in cells with only one dendritic tree. These conditions are only fulfilled by some natural inputs, e.g., the excitatory fibers from the entorhinal cortices and the basket-cell somatic inhibition (Amaral et al., 2007). In the former case, the bifurcation of PP axons sweeping over the GC population in both blades ensures near synchronous activation of extended GC regions. Some DG interneurons have extensive axonal plexus (Halasy and Somogyi, 1993; Han et al., 1993; Houser, 2007) although none are reported to cover entirely the two blades so they could account for the spatial coherence of the somatic inhibitory (GC_som) generator. Therefore this is most likely brought about by the merging of individual synaptic territories into larger spatial modules through correlated fluctuations of activity in a homogeneous subpopulation of interneurons (Whittington et al., 1995; Ho et al., 2012), which may be brought about by a common driving from units in the entorhinal cortex. Different classes of interneurons project into the GC soma (basket cell type) and each of dendritic strata associated with either MPP or LPP inputs (hilar interneurons). Accordingly, it seems plausible that only the former subpopulation fires with sufficient coherence to notably contribute to hilar LFPs, as implied by the generation of negative hilar LFPs following dendritic inhibition in our model.

Fitting in vivo LFP data to that derived from the model may help to reveal the functional topology of connections and provide insight regarding the activity of afferent populations (Benito et al., 2013). For instance, the model shows that the temporal correlation of simulated LFPs in pairs of recordings decreases rapidly with the distance only for input configurations of reduced spatial coverage, which is contrary to our in vivo findings. Furthermore, experimental hilar LFPs were up to 20 times greater than those observed in GC layers, a ratio that, according to the model, could only be reproduced using symmetrically and widely distributed inputs. This does not rule out a possible contribution to LFPs by inputs with smaller synaptic territories. However, although visualization of these pathways is straightforward in planar structures, it is hampered by the selective amplification of activity mediated by the extensive pathways of symmetrical coverage in the particular cytoarchitecture of the GC population.

The present results shed light on specific parameters that should be considered when interpreting LFPs and their association with concomitant spike activity. For instance, because the spatial coherence of LFPs may be due to macroscopic blending of nonoverlapping synaptic territories of functionally coupled neurons (e.g., interneuron networks), it is possible that state-dependent modulation of network coupling disproportionately reduces the visualization of their associated LFPs with respect to individual firing rates, as demonstrated here by reducing the size of the activation strips. These observations are relevant to the study of the cellular mechanisms underlying LFP phenomena including dentate spikes, sharp waves, ripples, and field oscillations, which can appear at different hippocampal loci and with varying degrees of spatial coverage (Bragin et al., 1995a,b; Csicsvari et al., 2000; Bibbig et al., 2007; Reichinnek et al., 2010).

How local are local field potentials? Insights from the DG

It is commonly but erroneously assumed that LFPs are elicited only by the neurons in the vicinity of the recording electrode. Indeed, differential (paired) recordings have demonstrated field potential activity many times lower than that seen in monopolar (grounded) recordings (Gómez-Galán et al., 2012), indicating that most of the activity captured in LFPs is volume-conducted rather than local. The confusion arises when comparing the reduced sensing area of a small electrode to the spatial reach of point sources in conductive media, which is estimated to be a few hundred micrometers (Katzner et al., 2009; Xing et al., 2009; Lindén et al., 2011). In fact, LFPs are generated by currents injected simultaneously into the extracellular space by multiple-cell generators that jointly occupy a large volume (Elul, 1971), and it is the macroscopic summation of very weak currents that allows LFPs to reach a measurable amplitude even at a distance (Wang et al., 2005; Kreiman et al., 2006; Berens et al., 2008; Kajikawa and Schroeder, 2011; and the present study).

The spatial trends described here for the DG are potentially applicable to other structures with similar layered architectures, such as the cortical sulci and gyri in humans and other mammals. It is normally assumed that extracranial EEG is mostly contributed by neurons in the planar sections of the cortex, although extensive mixing of volume-conducted currents in non-neural tissue introduces substantial uncertainty (Srinivasan et al., 2006). Indeed, currents in planar layers only benefit from favorable cytoarchitectonic conditions within the cell layers, because LFPs rapidly fell away (Fig. 3). One should bear in mind that the size of an LFP close to the source does not influence its detection at a distance (e.g., the further reach of LPP compared with MPP potentials due to the different dipolar moments caused by the location of synaptic contacts in the dendritic arbors) nor predicts the polarity or a preferred direction for conduction of their currents in the volume. In the DG, it is the global behavior of the GC aggregate as a laminar dipole that establishes spatial domains of positive or negative LFPs, although the particular curvature promotes uneven spatial cancellation among currents of neighboring GCs ending in a macroscopic strongly unbalanced spatial segregation of net currents and the headlight effect specific for positive LFPs. Importantly, the topology of afferent inputs determines the three-dimensional shape of the activated GC population, thus the activity elicited by different pathways may or may not be contained in LFPs at a distance, which may also be generalized to other structures.

Notes

Supplemental material for this article is available at http://www.mat.ucm.es/∼vmakarov/research.php. Description of the DG model configuration and parameters. This material has not been peer reviewed.