Stochastic Calcium Mechanisms Cause Dendritic Calcium Spike Variability

Abstract

Bursts of dendritic calcium spikes play an important role in excitability and synaptic plasticity in many types of neurons. In single Purkinje cells, spontaneous and synaptically evoked dendritic calcium bursts come in a variety of shapes with a variable number of spikes. The mechanisms causing this variability have never been investigated thoroughly. In this study, a detailed computational model using novel simulation routines is applied to identify the roles that stochastic ion channels, spatial arrangements of ion channels, and stochastic intracellular calcium have toward producing calcium burst variability. Consistent with experimental recordings from rats, strong variability in the burst shape is observed in simulations. This variability persists in large model sizes in contrast to models containing only voltage-gated channels, where variability reduces quickly with increase of system size. Phase plane analysis of Hodgkin-Huxley spikes and of calcium bursts identifies fluctuation in phase space around probabilistic phase boundaries as the mechanism determining the dependence of variability on model size. Stochastic calcium dynamics are the main cause of calcium burst fluctuations, specifically the calcium activation of mslo/BK-type and SK2 channels. Local variability of calcium concentration has a significant effect at larger model sizes. Simulations of both spontaneous and synaptically evoked calcium bursts in a reconstructed dendrite show, in addition, strong spatial and temporal variability of voltage and calcium, depending on morphological properties of the dendrite. Our findings suggest that stochastic intracellular calcium mechanisms play a crucial role in dendritic calcium spike generation and are therefore an essential consideration in studies of neuronal excitability and plasticity.

Introduction

Bursts of calcium spikes are important mechanisms of dendritic information processing in many brain regions (Higley and Sabatini, 2008). Calcium spikes play a crucial role in synaptic integration and thus control the output of neurons. Furthermore, a large amount of voltage-gated calcium influx during calcium bursts may activate calcium-dependent molecular pathways underlying neuronal plasticity. Calcium bursts are generated by interaction of voltage-gated calcium channels and calcium-activated potassium channels, where the interaction is mediated through intracellular calcium mechanisms. A strong depolarizing current is required to initiate bursts of calcium spikes, and the source of depolarization may vary between brain regions. Bursts of calcium spikes in cerebellar Purkinje cells (PCs) are elicited in response to climbing fiber activation (Llinás and Sugimori, 1980; Lev-Ram et al., 1992; Miyakawa et al., 1992). Furthermore, they can also be evoked by injection of a large depolarizing current at the soma (Llinás and Sugimori, 1980; Miyakawa et al., 1992) and occur spontaneously in PCs in cerebellar slices (Womack and Khodakhah, 2002a). Bursts of calcium spikes come in a variety of shapes (Llinás and Sugimori, 1980; Davie et al., 2008), where each burst can consist of a variable number of calcium spikes (generally 1–4 spikes) with varying amplitudes. However, the mechanisms causing calcium burst variability have not been investigated thoroughly, and so the causes of this diversity are unknown. A few of the contributing factors could be ion channel modulation, varying ion channel distributions, and stochastic behavior of both ion channels and calcium-related mechanisms.

Past studies of stochastic effects in neurons have focused on the stochasticity of voltage-gated ion channels and its effect on neuronal excitability but have not included intracellular aspects, such as calcium dynamics. During calcium spike generation, calcium enters the dendrite through noisy pores of the calcium channels, which are often clustered around the calcium-activated potassium channels, making the calcium signal highly localized into nanodomains or microdomains (Fakler and Adelman, 2008; Indriati et al., 2013). The number of calcium and potassium channels per domain are very low; and with stochastic diffusion and buffering of calcium resulting in a highly variable number of ions within these domains, significant spatial stochastic effects in the activation step are expected. Indeed, a simplified model of calcium kinetics has shown that stochastic binding and gating within microdomains have a significant effect on calcium-activated potassium channel activity (Stanley et al., 2011). Therefore, stochastic kinetics in calcium spike generation may underlie the variation in shape and timing of dendritic calcium bursts recorded from PCs.

Because of the difficulty of obtaining enough data to quantitatively study stochasticity and the impracticality of manipulating stochastic processes experimentally, we used a modeling approach. We simulate a realistic and detailed biophysical model of PC dendritic calcium burst generation, with stochastic solution of the calcium kinetics (including channel activation) and voltage-dependent channel gating, coupled to accurate 3D computation of the electrical behavior of the dendrite. Our focus is to investigate the contribution that stochastic effects, in different components of the system, have toward producing intracellular variability in dendritic spike shape.

Materials and Methods

Slice electrophysiology.

Standard techniques were used to prepare 250-μm-thick sagittal brain slices from the cerebellum of 18–25 d postnatal rats of either sex (Davie et al., 2006). All recordings were performed at 31–37.5°C. Simultaneous somatic and dendritic whole-cell patch-clamp recordings were made from PCs under visual control using differential interference contrast optics (Davie et al., 2006). Dendritic recordings were made at distances of 100–160 μm from the soma, measured along the dendritic branches (see Fig. 1A). Dendritic calcium spikes were evoked by injecting 1.1–1.88 nA of current at the soma. All the experiments were performed by Ede Rancz in the laboratory of Michael Häusser (University College London, London, UK).

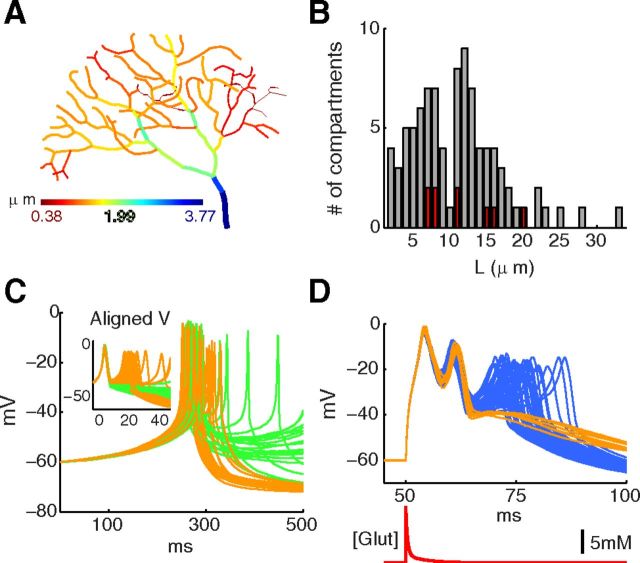
Figure 1.

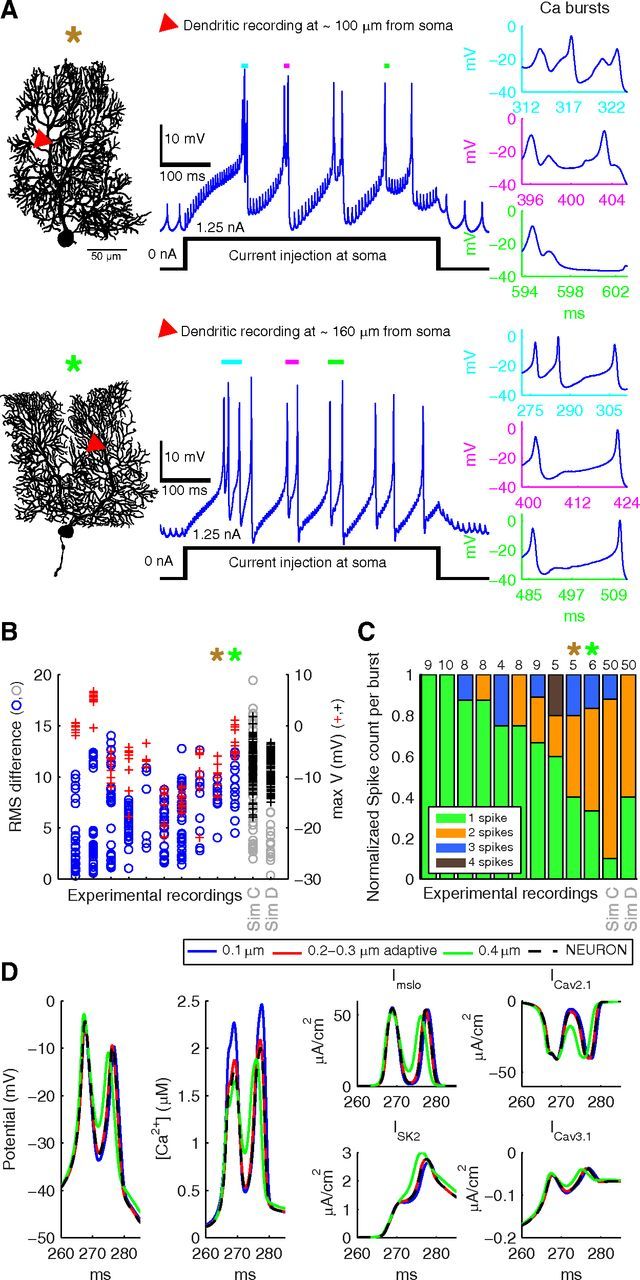
Experimentally recorded dendritic calcium spikes show large variability. A, Example electrophysiological traces recorded from the dendrite of two PCs (shown on left). The bursts of dendritic Ca²⁺ spikes were recorded from the dendrite (recording location is marked with red triangles) while injecting 1.25 nA current at the soma. For both cells, three of the bursts of Ca²⁺ spikes (see Materials and Methods) are enlarged and displayed in cyan, purple, and green insets to show the variability in number of spikes (1–3 spikes per burst), variability in duration of burst (10–40 ms), and variability in spike amplitudes, respectively. The small spikelets in the traces both before and during the current injection are passively propagated somatic action potentials. B, C, Data recorded from 10 different PCs show robust variability of dendritic calcium bursts. B, The circles represent RMS differences (ordinate axis on left hand side) between every pair of bursts of Ca²⁺ spikes in recordings and for the spatial (Sim C) and dendrite (Sim D) models (Figs. 2A, 160 μm; and 10C, respectively). +, Maximum voltage level of every spike (ordinate axis on right hand side) in each recording and for the spatial (Sim C) and dendrite (Sim D) models. C, Variability of spikes count per burst of Ca²⁺ spikes in recordings and for the spatial (Sim C) and dendrite (Sim D) models. Number of bursts detected in each trace are marked at the top of each bar. B, C, Cells marked with brown and green asterisks are shown in A. Data provided by Ede Rancz and Michael Häusser (University College London; see Materials and Methods). D, Three different tetrahedral meshes describing the same cylindrical compartment of length 1 μm and diameter 2 μm are used for spatial deterministic simulations in STEPS and compared with the NEURON benchmark. The 0.2–0.3 μm adaptive mesh was found to give an almost perfect match to the benchmark. Panels show, from left to right, membrane potential, submembrane calcium concentration, and current density for the four different ion channels.

Calcium burst and spike detection.

Calcium bursts in the experimental traces (see Fig. 1A) were detected using an up-threshold of −25 mV. The end of the burst was determined by the voltage level going below −40 mV or after a duration of 40 ms if the voltage level stayed above the down-threshold. The number of spikes in a burst was detected by using up- and down-thresholds of −25 mV for each spike.

Calcium bursts in the voltage traces obtained from simulations were detected using a threshold of −30 mV. The end of the burst was determined by the voltage level going below a threshold of −50 mV or at 40 ms duration if the burst was very broad. The number of spikes in the burst was detected by defining a minimum trough to peak amplitude of 8 mV.

Root mean square (RMS) measure of burst shape variability.

RMS differences (see Fig. 1B) for each neuron were computed in a 40 ms window between every possible pair of bursts of calcium spikes in a recording, after aligning the bursts at −25 mV.

Detailed model of calcium burst generation.

The detailed model of calcium burst generation was adapted for stochastic simulation from the original biophysical model (Anwar et al., 2012) developed in the NEURON simulator framework (Hines and Carnevale, 2001). The model contained 4 types of ion channels: Ca_v2.1 P-type calcium channel (Usowicz et al., 1992; Swensen and Bean, 2005; Anwar et al., 2012), Ca_v3.1 T-type calcium channel (Iftinca et al., 2006; Bittner and Hanck, 2008; Anwar et al., 2012), mslo BK-type calcium-activated potassium channel (Cox et al., 1997; Womack and Khodakhah, 2002b; Anwar et al., 2012), and SK2 SK-type calcium-activated potassium channel (Hirschberg et al., 1998; Solinas et al., 2007; Anwar et al., 2012), plus a leak channel. The channels were implemented as Markov schemes, and conductance densities from the NEURON model were converted into channel densities for a single-channel permeability from the literature (Table 1). The current passing through each open calcium channel was computed using the GHK equation (Hille, 2001).

Table 1.

Single channel and pump model descriptions

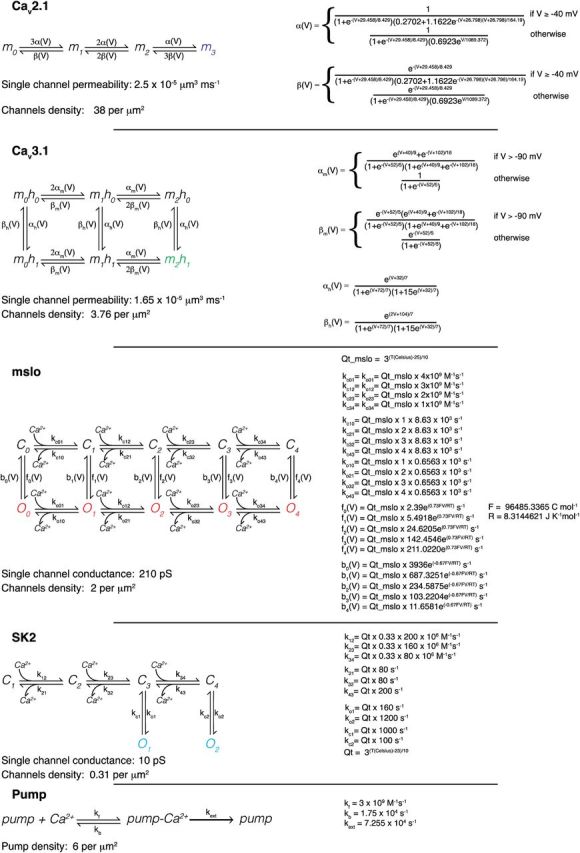
The detailed Ca²⁺ dynamics model included calbindin (CB) and parvalbumin (PV) as buffers. In addition to Ca²⁺, both PV and 80% of CB were diffusible in three dimensions. The kinetics of CB and PV have been described previously (Anwar et al., 2012). The pump kinetics of the model were altered and are shown in Table 1.

The calcium spike generation model ran under the following conditions: temperature 34°C, initial voltage −60 mV, membrane capacitance 1.5 × 10⁻⁸ μF per μm², and axial resistance 2.357 ohm.m. The model fires a spontaneous calcium burst with 2 spikes using deterministic simulation in NEURON (see Fig. 1D).

Model behavior in tetrahedral discretized space.

Spatial discretization in the NEURON simulations consisted of a series of concentric shells with 1D diffusion occurring radially between shells. Only the concentration of calcium in the outermost shell is available for activation of the mslo and SK2 channels. Conversion to tetrahedral subvolume discretization was necessary for implementation of the model in the STEPS simulator (Hepburn et al., 2012). Tetrahedrons should be chosen to fall within a certain size “window” for accurate reaction-diffusion computations (Hepburn et al., 2012), which, because of the fast activation of mslo channels in the model, was found to be rather small: ∼0.1–0.4 μm. In addition, only the concentration of calcium in border tetrahedrons is available for channel activation, introducing more sensitivity to tetrahedron size. To test tetrahedral mesh suitability, several meshes representing a short cylinder of 1 μm length were used in deterministic spatial simulations and compared with the NEURON benchmark. Meshes of fixed tetrahedron size were tested within the acceptable window as well as adaptive meshes, which allow smaller-sized tetrahedrons around borders and larger sizes in central regions, improving simulation time.

Figure 1D shows output from three of the tetrahedral meshes compared with the NEURON benchmark: a mesh of 0.1 μm fixed size tetrahedrons, a 0.2–0.3 μm adaptive tetrahedron size mesh, and a 0.4 μm fixed tetrahedron size mesh. The adaptive mesh, where tetrahedrons were constrained to a size of 0.2 μm to 0.3 μm close to the surface (but allowed to be larger toward the axis of the cylinder), was highly accurate with respect to the NEURON benchmark. In comparison, the 0.1 μm fixed-size mesh is reasonably accurate but shows a small extra polarization between spikes because of a slightly larger activation of mslo by the larger calcium concentration; and in contrast, the relatively large tetrahedron size of 0.4 μm causes a low calcium concentration during the first spike, in turn causing slightly lower activation of mslo and therefore less polarization between the first and second spike. The adaptive mesh contained ∼90% fewer tetrahedrons in total than the next most accurate mesh shown (the 0.1 μm fixed size mesh), an important consideration for runtime. Similar adaptive cylindrical meshes were generated with the same constraints for all cylinder lengths (10, 20, 40, 80, and 160 μm) with output from all of these meshes tested to be highly accurate with respect to the NEURON benchmark (data not shown). All tetrahedral meshes were generated in CUBIT (http://cubit.sandia.gov/).

Dendrite models.

The PC dendrite used in this study was reconstructed with Neurolucida (http://www.mbfbioscience.com/neurolucida) using a 2-Photon image stack from the vermis of the cerebellar cortex of a 4-week-old mouse. It was simulated with the well-mixed approach used in Figure 8 where only radial 1D diffusion is included. Each unbranched segment was modeled as a separate compartment with its own radial diffusion system; all compartments were <40 μm (see Fig. 10B), resulting in a reasonable approximation of a system with full 3D diffusion (see Fig. 8D–F).

Figure 8.

Detailed calcium burst model simulated under well-mixed stochastic conditions captures important features of variability. A, Nonaligned voltage traces (50 iterations for each model size) for the well-mixed stochastic model for various length compartments. The voltage traces plotted in gray, green, orange, and blue represent traces with no spike, 1 spike, 2 spikes, and >2 spikes, respectively. B, Same data, aligned at −30 mV in 50 ms windows. C, The corresponding calcium traces, aligned at threshold of −30 mV in the voltage traces. D–F, Analysis of variability for different model sizes for the spatial model (data from Fig. 2) and the well-mixed model (this figure). All measures are taken relative to the deterministic solution and expressed as the tolerance interval for 90% of the data at 90% confidence for the proper distribution. Lines connect the midpoints. Stars indicate the median. D, RMS of voltage (normal distribution). E, Timing of first spike (γ distribution). F, Time separation between first and second spike if second spike present (γ distribution).

Figure 10.

The stochastic effect of calcium-related mechanisms persists in dendritic morphologies. A, The PC dendrite morphology with 100 compartments used to simulate both spontaneous and synaptically evoked stochastic calcium bursts. The compartments are color-coded according to their diameters. Total length and total surface area of the dendritic tree is 1098 μm and 5716.6 μm², respectively. B, A histogram of lengths of dendritic compartments shows that the distribution of dendrites with small diameters (in red; diameter <0.7 μm as marked in red in Fig. 11) is spread uniformly across the distribution of dendrites with large diameters (in gray; diameter ≥0.7 μm as color coded in different shades of gray in Fig. 11). C, Voltage traces of spontaneous calcium bursts recorded from the first dendritic compartment over 50 trials. The voltage traces shown are classified into bursts with 1 spike (green) and bursts with 2 spikes (orange). Inset, Same data aligned at −30 mV. A second spontaneous burst sometimes occurs. D, Voltage traces of synaptically evoked calcium bursts recorded from the first dendritic compartment of the morphology over 50 trials. The voltage traces are classified into bursts with 2 spikes (orange) and bursts with 3 spikes (blue). The red trace shown below is the glutamate pulse applied to activate AMPA receptors in primary dendrite compartments (blue in A).

The synaptically evoked dendritic calcium burst model was adapted from the detailed model of calcium burst generation (Table 1) by replacing Ca_v3.1 channels on the primary dendrite (see Fig. 11E, black) with 8571 AMPA receptors each with a single-channel conductance of 7 pS (Momiyama et al., 2003). The AMPA receptor model (Destexhe et al., 1994) was obtained from model DB (Accession number 18198). Also, the Ca_v3.1 channel density on spiny dendrites (see Fig. 11E, gray) was reduced from 3.76 per μm² to 1.96 per μm² to avoid spontaneous Ca²⁺ bursting.

Figure 11.

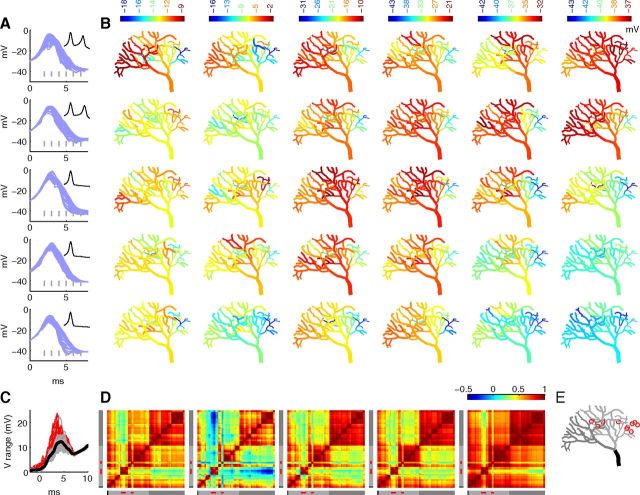
Stochastic calcium bursts in a dendrite model show large spatiotemporal variation of membrane potentials. This figure shows voltage during five different runs of the stochastic well-mixed model of a PC dendrite (A–E). A, B, In the first two runs, the burst consisted of 2 calcium spikes; in the other runs, only 1 calcium spike was generated. A, First 8 ms of the voltage traces recorded from all compartments of the dendritic tree are overlaid. Inset, Complete burst. Gray vertical lines indicate the time points for which the spatial maps are shown. B, Spatial maps of membrane potential throughout the dendrite for each time point marked with gray lines in A. Each time point has its own linear color scale to emphasize differences within single maps. C, Voltage range for all compartments (difference of maximum V and minimum V at each time point across 50 trials). Gray represents compartments with diameter ≥0.7 μm; red represents smaller-diameter ones; black represents mean. D, Spatial correlation of voltage of first 5 time points across 50 trials. Different shades of gray are used in sidebars to highlight subtrees as shown in E. Dendrites with diameter <0.7 μm are marked with red dots. E, Dendritic tree plotted in different shades of gray to highlight two subtrees stemming out of the primary dendritic branch plotted in black. Red circles represent dendrites with diameter <0.7 μm.

Instead of modeling glutamate release from a presynaptic terminal, a pulse of glutamate with peak amplitude of 12 mm and decay time constants of 0.4 ms (86%) and 4.2 ms (14%) was applied to activate the AMPA receptors (Rudolph et al., 2011).

Hodgkin-Huxley (HH) spike generation model.

A leak channel with conductance value of 10 pS per μm² and reversal potential of −50 mV was included with a standard HH model (Hodgkin and Huxley, 1952) in NEURON to generate a spontaneous sodium spike. The conductance per unit area of HH type Na⁺ channels and HH-type K⁺ channels were 1200 pS per μm² and 360 pS per μm² respectively.

The kinetic schemes of the two HH channel types were implemented using Markov schemes for the STEPS simulations. While keeping the conductance per unit area the same as in NEURON, 60 channels of Na⁺ per μm², 18 channels of K⁺ per μm², and 10 channels of leak per μm² were distributed over the surface triangles of the mesh. Each of these channels had single-channel maximal conductance of 20, 20, and 1 pS, respectively.

The HH spike generation model was run under the following conditions: temperature 20°C, initial voltage −65 mV, membrane capacitance 1 × 10⁻⁸ μF/μm², and axial resistance 1 ohm.m.

Simulations.

All simulations, apart from the NEURON benchmark, were run with the STEPS simulator (Hepburn et al., 2012), version 2.0, using tetrahedral meshes generated by CUBIT (http://cubit.sandia.gov/). For simulation in STEPS, channel models were converted to Markov schemes (Hille, 2001) with conformational changes modeled as first-order processes with rate constants as shown in Table 1. Channel gating and calcium dynamics were then solved using either the STEPS implementation of a spatial Stochastic Simulation Algorithm (Gillespie, 1977) or deterministically using the CVODE library (Cohen and Hindmarsh, 1996), or a combination of both. A detailed description of how hybrid simulations, combining stochastic and deterministic solution of different components of the model, were implemented in STEPS can be found at http://steps.sourceforge.net/STEPS/download/Hybrid.pdf.

In addition to reaction–diffusion modeling, STEPS 2.0 also supports efficient, validated computation of the membrane potential on the same mesh (Hepburn et al., 2013). This computation takes input currents from channels residing on the surface of the mesh and returns accurate, spatial voltages throughout the tetrahedral mesh at the resolution of individual mesh nodes (vertices). Where the rate of channel gating depends on local potential across the membrane (Table 1), this voltage was taken across the surface triangle on the mesh within which the channel resided. The membrane potentials were assumed fixed for a 0.02 ms time-step for purposes of the reaction-diffusion computations and updated at the end of each time-step by the membrane potential calculation depending on surface currents that occurred during that reaction-diffusion time-step (for further details, see Hepburn et al., 2013). The time-step of 0.02 ms was tested to be small enough so that lowering it did not appreciably affect results.

The maximum sizes of stochastic models were limited by run time concerns. All model scripts and meshes used in this study are available to download from Model DB (http://senselab.med.yale.edu/ModelDB/showmodel.asp?model=150635).

Results

Dendritic calcium spike bursts are variable in spike number, amplitude, and duration

Bursts of calcium spikes are generated in the dendrites of PCs as a result of strong dendritic depolarization, which may result from strong synaptic input through climbing fiber activation (Llinás and Sugimori, 1980). Similar dendritic calcium bursts can be generated by injecting depolarizing current at the soma. Example dendritic recordings of calcium spikes are shown in Figure 1A. The recordings show several bursts of calcium spikes with highly variable features, such as 1–4 calcium spikes per burst (Fig. 1C), bursts with different durations (Fig. 1A, insets), and bursts with variable spike amplitudes (Fig. 1B; plus signs and axis on right hand side). This caused PCs to have a large range of values for the RMS differences between calcium burst shapes (Fig. 1B; circles and axis on left hand side). Such variability in dendritic calcium bursts is a robust phenomenon as it was observed in all dendritic traces recorded from 10 PCs (Fig. 1B,C). Similar variability in dendritic calcium bursts has been reported previously (Llinás and Sugimori, 1980) but was not quantified.

We wondered whether the stochastic nature of mechanisms involved in the generation of dendritic calcium bursts can explain this variability in dendritic calcium bursts. To investigate this further, we made a stochastic version of a detailed calcium dynamics model of spontaneous dendritic calcium burst generation in PCs (Anwar et al., 2012) with 3D diffusion of calcium and dissected various components of the model to isolate the main factors causing the variability.

Stochastic model of calcium burst reproduces variability

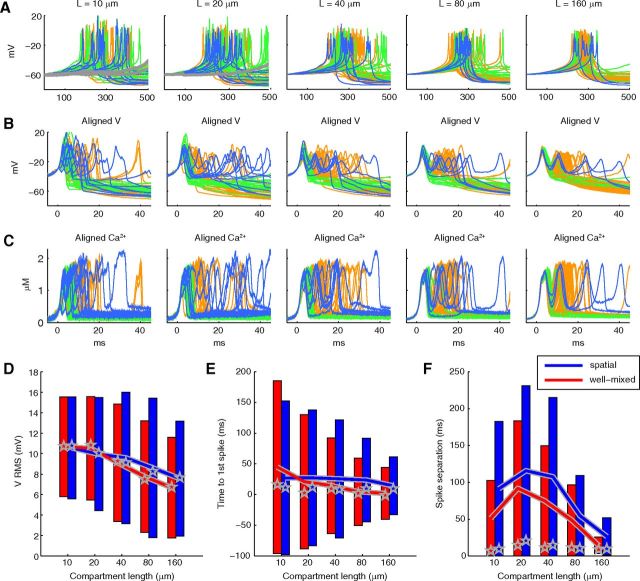
Previous studies on the effects of stochastic kinetics of voltage-gated channels have emphasized the importance of model size (Chow and White, 1996), so we systematically varied the length of unbranched dendritic sections (tetrahedral meshes representing cylinders of diameter 2 μm and length 10, 20, 40, 80, or 160 μm) for simulations. For each length, the spatial distribution of ion channels was maintained from trial-to-trial to make sure that the variability observed was only the result of the stochastic gating of ion channels and stochastic buffering and diffusion of calcium and calcium buffers, and not the result of differences in the spatial distribution of ion channels.

In Figure 2, we compare the effect of dendrite model size on spontaneous stochastic calcium bursts. The stochastic calcium bursts were highly variable for all model sizes, both in timing (Fig. 2A) and in shape. The differences in shape are more visible when the bursts are aligned on their first spike (Fig. 2B), where we can see that the number of spikes varied from 1 to 3 (color coded in Fig. 2), and for the smallest section bursting even sometimes failed. The variability in timing and shape is similar to that observed in experimental traces (Fig. 1B,C: columns Sim C). The submembrane calcium levels in the model show similar large variability during the calcium bursts (Fig. 2C).

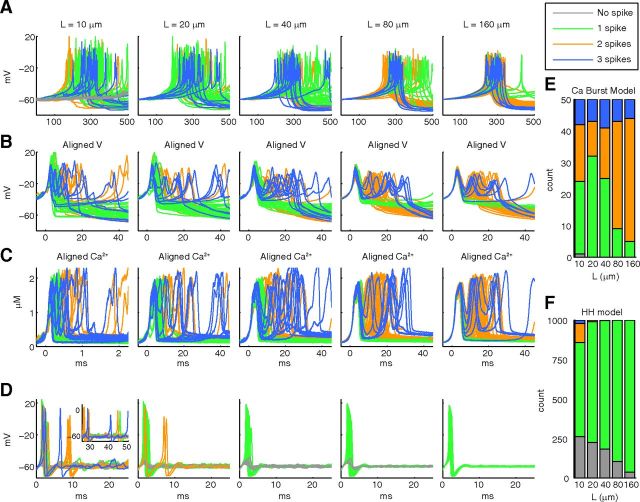
Figure 2.

The stochasticity of a calcium burst model persists with increase in model size, whereas that of a sodium spike model decreases with model size. A, Nonaligned voltage traces (50 iterations for each model size) obtained from simulations of the detailed calcium burst model with stochastic ion channels and stochastic intracellular Ca²⁺ dynamics and 3D diffusion for various length cylindrical meshes. The voltage traces plotted in gray, green, orange, and blue represent traces with no spike, 1 spike, 2 spikes, and >2 spikes, respectively. B, Same data, aligned at −30 mV in 50 ms windows. C, The corresponding calcium traces, aligned at threshold of −30 mV in the voltage traces. D, Spontaneously generated sodium spikes (50 iterations for each model size) using a stochastic HH model in the same meshes. Inset (in panel for 10 μm length), Later part of the respective traces. E, Histogram of number of voltage traces (iterations) with no spike, 1 spike, 2 spikes, and >2 spikes for different length compartments for the calcium burst model shows that variability in burst characteristics persist for large model sizes. F, A similar histogram for the sodium spike model (1000 iterations for each model size) shows a more rapid decrease in variability with increase in model size.

Variability persists in large model sizes in contrast to stochastic HH model

Comparing voltage traces across different lengths for the stochastic calcium burst model, we observe less variability for longer meshes compared with shorter ones. However, even for the longest section (160 μm), significant variability exists in terms of spike numbers (Fig. 2E), shapes, and duration. Particularly, the prevalence of 3 spike cases remained fairly constant with increasing length. Conversely, timing of burst occurrence becomes more consistent with increase in length, suggesting that this may be controlled by a different mechanism.

In contrast, a stochastic implementation of the classic HH model (Hodgkin and Huxley, 1952) on the same meshes (see Materials and Methods) showed a strong dependence on model size (Fig. 2D,F). For small models sizes, variability in the number of spikes (Fig. 2F), jitter in timing of the first spike (Fig. 2D), and difference in peak amplitudes of spikes were present across multiple runs. But for the largest dendritic section, only a very small difference in the peak amplitudes of spikes and rare failures to spike remained.

Consistent with previous studies (Chow and White, 1996), our results confirm that the noise resulting from stochastic fluctuation of voltage-gated ion channels diminishes steeply as the model size becomes larger. This is in contrast to the model of calcium bursts, where a significant variability was observed even for a large model size. To understand these differences better, we examined the relation between variability and model size in phase space.

Phase analysis of HH model identifies two separate causes of spike variability with different dependence on model size

The observed HH spike number variability (Fig. 2D,F) can be separated into two causes: (1) a probability of later spontaneous spikes occurring after the initial spike, resulting in a significant number of trials with multiple (≥2) spikes at 10 μm but disappearing very quickly with increase in length; and (2) a probability of the initial spike failing that diminishes approximately linearly with geometric increase in dendritic length, observed by comparing the number of trials with 0 spikes to those with 1 or more spikes (Fig. 2F). We explain these factors separately by investigating the phase space of the system (Fig. 3).

Figure 3.

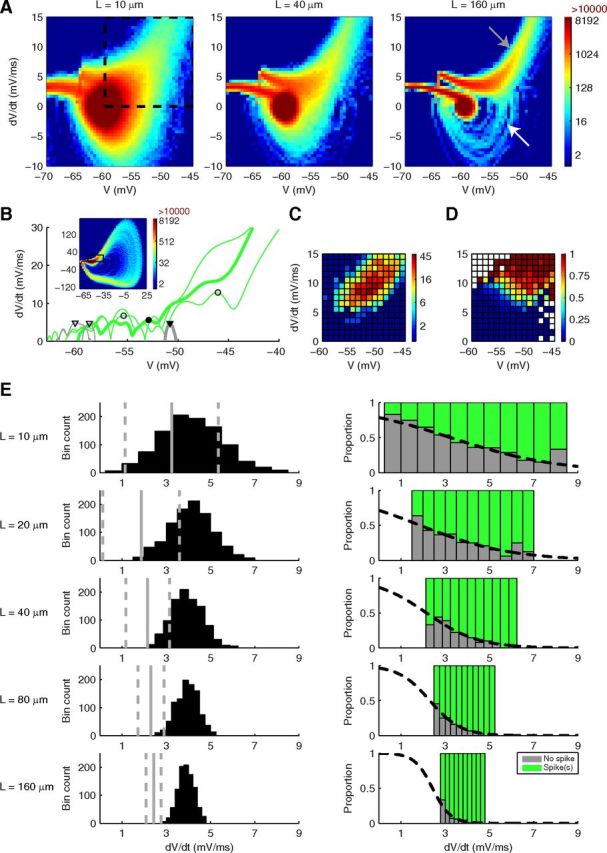
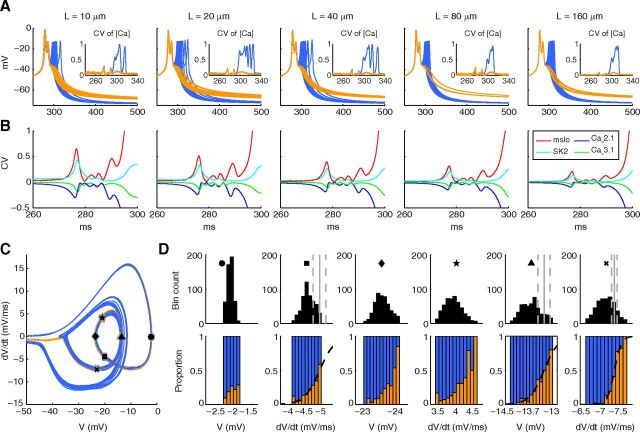
Phase space analysis of HH model explains variability dependence on model size. For phase space analysis, the raw voltage signals were smoothed by convolution with a Hanning window on interval −0.1 ms to 0.1 ms. A, Phase space heat maps of 1000 trials of the HH model are shown for the 10, 40, and 160 μm meshes, showing the spontaneous fluctuations around the baseline and the spike-initiation region. Right, Gray arrow indicates a successful spike. White arrow indicates a failed spike. B, Top, Full phase space heat map of the HH model at 10 μm (expanded from A) showing both initial and spontaneous spikes. Boxed region is shown in more detail in bottom. Bottom, dV/dt peaks of fluctuations are detected for 3 cases that resulted in a spontaneous spike (green, peaks marked by circles) and 3 cases with no spike (gray, peaks marked by triangles). Spontaneous spikes tend to originate from larger dV/dt peaks that occur at higher voltages (circles) compared with peaks that did not result in a spike (triangles), although there is some crossover. C, D, All spontaneous spikes from 5000 trials of the 10 μm model are shown as (C) position by peak dV/dt and V at which each spike originated (color bar scale is number of spikes per bin) and (D) for each phase space bin the probability of a peak resulting in a spontaneous spike (computed as the proportion of dV/dt peaks that resulted in a spontaneous spike divided by those that did not). These panels match the region denoted by a square in A (left). E, Left, For 1000 trials at each mesh length, the distribution in dV/dt at which voltage of −60 mV was first crossed. Right, For these distributions, the proportion of trials by dV/dt position that resulted in a spike (green) or spike failure (gray). Sigmoidal curves were fitted by weighted least-squares fit to define a sigmoidal separatrix. The point at which the value of the sigmoidal is 0.5 is illustrated in the left panels (solid gray line) as the approximate location of a probabilistic phase boundary. Dashed gray lines indicate the points at which the value of the fitted sigmoidal is 0.3 and 0.7.

First, to investigate late spontaneous spikes, we created phase space (dV/dt vs V) heat maps covering the entire 50 ms simulation time for 1000 trials at all dendritic lengths. A complete phase plane is shown in Figure 3B (top, 10 μm cylinder), but we will analyze the baseline region where spike initiation is decided in detail (Fig. 3A: 10, 40, and 160 μm cylinders are shown). We observed a sharp reduction in fluctuations resulting from channel noise with increasing length, giving only small fluctuations around the baseline of −60 mV and 0 V/s at 160 μm after the initial spike, with no spontaneous spikes from 1000 trials. However, at 10 μm we observed much larger fluctuation giving significant crossover into regions of high V and dV/dt and a large number of spontaneous spikes (311 from 1000 trials: some 1 spike cases in Fig. 2F are from spontaneous spikes after an initial failed spike). By recording at 10 μm (for 5000 trials) each dV/dt peak (Fig. 3B) amplitude along with the voltage at which the peak occurred, and whether these peaks resulted in a spontaneous spike or not, we observed a large spike initiation zone (Fig. 3C) suggesting a probabilistic spike threshold. This was confirmed by observing at each location in phase space the proportion of dV/dt peaks that resulted in a late spontaneous spike (Fig. 3D), which showed that spiking probability increased with increase in both V and dV/dt peak but with no deterministic boundary between probabilities of 0 and 1; rather, there was a large region where either outcome was possible. At 10 μm, because of large phase space fluctuations caused by channel noise, we observed significant spontaneous crossover into the zones of high spiking probability. However, because of the sharp decrease in noise in phase space with increasing length (Fig. 3A), there was no significant crossover after the initial spike into the spike initiation zone from the central region for cylinders longer than 20 μm, and very few spontaneous spikes were observed at these lengths. Similar phase analysis would be suitable to explain previous reports of high probability of spontaneous spikes in HH models in small model sizes (Chow and White, 1996).

Because of initial conditions, the HH model is expected to give an initial spike within the first few milliseconds and the second contributor to HH spike number variability is whether this initial spike is successful or if it fails, the probability of failing exhibiting a more graded dependence on model size compared with spontaneous spiking (Fig. 2F), with a small chance (3.7%) of spikes failing even at 160 μm. Arrows in Figure 3A indicate in the phase space for 160 μm the successful spikes (gray arrow) and the failed spikes (white arrow). To investigate the reduction in failed spike probability with increasing length, we recorded, for every trial, the dV/dt at which voltage crossed above −60 mV and display the recorded distribution across 1000 trials for each dendritic section length (Fig. 3E, left panels). We observed, again, that the noise in dV/dt space reduced sharply with increase in length, from a full range of ∼7.5 V/s at 10 μm to 2 V/s at 160 μm with respect to a bin count threshold of 5. Then, for each dV/dt bin and for each length, we separated the trials into those that resulted in a spike or not (Fig. 3E, right panels) and plotted the proportion of failed spikes (gray) to successful spikes (green) by phase position. It is important to note that for some phase positions the outer parts of the histogram apply to very few cases; however, a trend can clearly be seen. We observed a strong dependence of the spike failure probability on phase position, with the probability increasing for smaller dV/dt. This suggested that a “phase boundary” existed between spike success or failure. However, this phase boundary was probabilistic, the dV/dt value only determining the probability of an outcome occurring. This is seen most clearly at 10 μm where at any dV/dt either outcome was still possible. Fitted sigmoidal curves (Fig. 3E, right panels broken lines) allowed us to define the phase boundary as the position with a 50% chance of either success or failure (Fig. 3E, left panels solid vertical gray lines), and also demonstrated how the phase boundary becomes more deterministic with increasing dendritic section length, seen as diminishing size of the 70% to 30% probability window (Fig. 3E, left panel, dotted vertical gray lines). This is the key to understanding the effects of noise in such a system relative to its size: it is the amount of crossover between the distribution of trials (Fig. 3E, left panels) and the sigmoidal separatrix (Fig. 3E, right panels) that is important. If there is a meaningful crossover, the effect of stochasticity is to produce appreciable variability. In our HH model, there is significant crossover at 10 μm because of the wide distribution of dV/dts coupled with a large probabilistic phase boundary, producing significant variability. However by 160 μm, because of the more narrow distribution and more deterministic phase boundary, the variability has almost disappeared.

Next, we compare variability in the HH model to that observed in the stochastic calcium burst model in which the significant difference is the presence of calcium dynamics. We will focus particularly on comparing the variability dependence on model size because, even though the two systems are quite different with different factors affecting variability, the calcium burst model variability exhibits a weaker dependence on model size, particularly with a persisting proportion of 3 spike cases (Fig. 2E).

Wide probabilistic phase boundaries explain persisting variability in the stochastic calcium burst model

To gain insights into why the strong variability in calcium spike number persists in large model sizes, we investigated its phase space at 80 and 160 μm. One possible explanation for large persisting variability could be that the system operates close to phase boundaries between different outcomes (i.e., 1 spike or multiple spikes) and that small fluctuations in the phase space caused by channel noise determines the outcome. However, similar to results shown in Figure 3E, we show in Figure 4 that this is not the case. Location in phase space did not deterministically decide the outcome but rather decided the probability of an outcome, with outcome becoming more certain toward the extremes.

Figure 4.

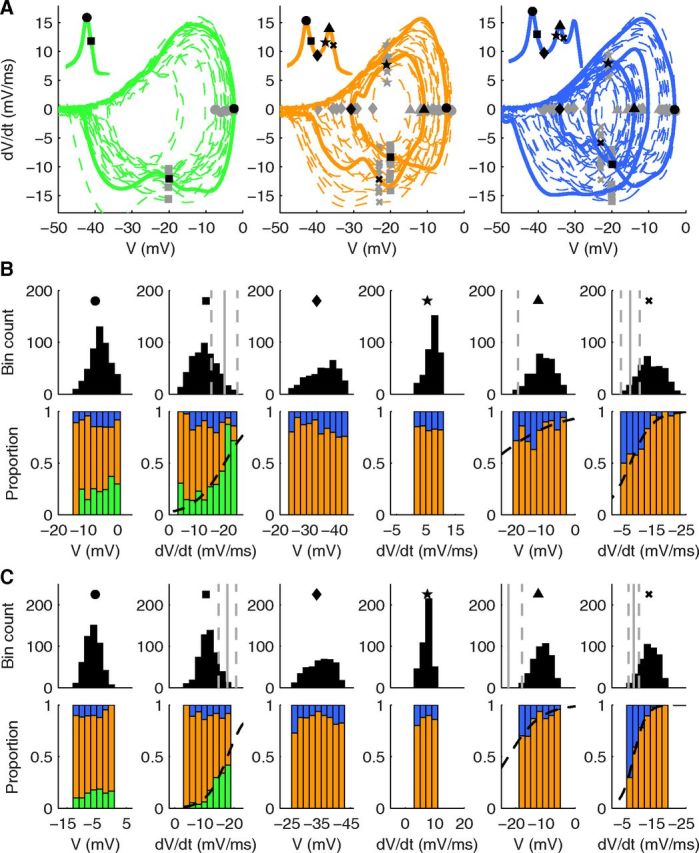
Phase space analysis of stochastic calcium burst model shows wide probabilistic phase boundaries. A total of 500 trials each for the 80 and 160 μm meshes are analyzed. The raw voltage signals were smoothed by convolution with a Hanning window on interval −0.5 ms to 0.5 ms. A, Ten example phase plots from the 160 μm compartment each for 1 spike (green), 2 spike (orange), and 3 spike (blue) trials. Full line indicates one phase plot (voltage trace shown in inset); the other nine are shown as broken lines for clarity. Symbols show six phase positions analyzed further in B and C: circle represents the voltage peak of the first spike (dV/dt = 0); square represents the fall after the first spike to −20 mV; diamond represents the voltage minimum between first and second spike (dV/dt = 0); star represents the rise to second spike at −20 mV; triangle represents the voltage peak of the second spike (dV/dt = 0); cross represents the fall after the second spike to −23 mV. B, C, Histograms represent distribution of all trials as number of trials (top), and proportion of trials that resulted in 1 spike (green), 2 spikes (orange), or 3 spikes (blue) (bottom) for 80 μm (B) and 160 μm (C). The abscissa used (V or dV/dt) depends on the phase position analyzed. For the positions denoted by square, triangle, and cross, sigmoidal curves were fitted by weighted least-squares fit to define a sigmoidal separatrix. The point at which the value of the sigmoidal is 0.5 is illustrated in the top panels (solid gray line, for the triangle in B the boundary falls outside the figure), and the points at which the value of the fitted sigmoidal is 0.3 and 0.7 are shown as dashed gray lines.

In Figure 4A, we plot the phase space for three possible outcomes of the model: 1, 2, or 3 spikes. It is obvious that for each outcome there is a very large trial-to-trial variability in phase space resulting in wide distributions across trials at each of 6 tested phase positions throughout the bursts, with each position either showing a far greater range in dV/dt (in mV/ms) than for the HH model or a very wide range in V (in mV). Similar variability is present in phase plots of the experimental data from Figure 1 (data not shown). In Figure 4B, C (for 80 and 160 μm, respectively) we analyze each of these phase positions by showing a distribution over trials of the relevant value (V or dV/dt, top) and a histogram of the different outcomes versus this value (bottom, color-coded). As for the HH model, some phase positions at the outer parts of the histogram apply to very few cases.

In general, the color-coded histograms demonstrate the main conclusion: most of them show little dependence of the number of calcium spikes on V or dV/dt. For phase positions where there was a relation, it tends to be weak and a mix of possible outcomes remained for almost the full distribution. Next we describe each phase position in more detail. At the first position, at the peak of the first spike (Fig. 4, filled circle), there was no discernible influence of its height on the eventual outcome, despite a wide range in the peak voltages. Conversely, at the next position (filled square), during the fall of the first spike (which is mostly driven by calcium activation of mslo), a tendency exists with a faster fall (more negative dV/dt) favoring a 1 spike outcome. Again, we defined the probabilistic phase boundary as the point at which the probability of one of two outcomes (1 spike or multiple spikes) was equal. This phase boundary did not depend on model size and was located at ∼−18 mV/ms during the first spike fall to −20 mV. Despite only a very small proportion of trials falling to the side of the phase boundary that favored a 1 spike outcome (see distribution at the top of the panel), we observed many more 1 spike cases, which can be explained by the phase boundaries being probabilistic.

At the second spike peak (filled triangle), a weak tendency toward 2 or 3 spike trials could be observed, with a smaller peak actually giving a slightly higher chance of a 3 spike outcome. During the fall of the second spike (cross), we were able to observe a stronger tendency with a probabilistic phase boundary (between 2 spike and 3 spike outcomes), centered at ∼−6 mV/ms, causing a far greater number of 2 spike outcomes. This phase boundary is at a different location compared with the one after the first spike, despite a similar distribution of dV/dt values for the two positions. The shift in phase boundary, which may be linked to activation of SK2 (SK-type) currents, caused the 2 spike cases to become the most prevalent outcome.

The significance of the deflection from the phase boundary for any given trial was somewhat size-dependent, which can be observed as steeper fitted sigmoidal curves at 160 μm compared with 80 μm (Fig. 4C vs Fig. 4B). However, the observed increase in steepness at 160 μm was relatively small, so we do not expect deterministic phase boundaries to appear in even larger models. The larger model size also produced narrower distributions in phase space (top panels), yet there was still a significant number of trials that fell to either side of the sigmoidal separatrix.

Compared with a system consisting of only voltage gating (and no calcium activation), like the HH model, the calcium burst system is more complex with more channel types of varying single-channel conductances and densities, and with different dynamics of activation: both voltage-gated and calcium-activated. All of these components play a different role in burst production, and stochastic local calcium activation can be expected to contribute to noise in the system. Combined, these factors are observed to contribute to significantly noisier behavior at all tested model sizes, noticeable as wide distributions in phase space which, even though there is some observed reduction in phase noise with increase in length, still give wide distributions at 160 μm (somewhat comparable to noise in dV/dt at 10 μm for the HH model at the tested position; Fig. 3E). Because the position in phase is the most important factor in producing spike-number variability in the calcium burst system and the noise gives distributions that are always wide enough to cross probabilistic phase boundaries, there is significant variability at all tested model sizes. These observations can be extrapolated to suggest that significant variability can be expected even in whole-cell systems. The HH system contains only voltage-gated channels that are typically of a relatively large density (and low single-channel conductance), which also share voltage input on a larger scale than the calcium input to calcium-activated channels. These factors cause less noise in phase space compared with the calcium burst system.

With the overall effect of stochasticity well characterized for the calcium bursts model containing voltage-gated calcium channels, calcium-activated channels, and calcium dynamics, we next systematically explore the contribution of each of these components individually to the persistent stochastic effects in large models. We do this by simulating hybrid models where some parts of the model are still solved stochastically whereas the rest is solved deterministically.

Calcium-activated potassium channels are the dominant contributors toward burst variability

As a first step, we estimated the relative contribution of each type of ion channel to the variability of calcium spikes by simulating the calcium burst model using four different hybrid models (Fig. 5). In these models, one channel type was run stochastically and all remaining types of ion channels, as well as intracellular calcium dynamics, were simulated in deterministic mode. All simulations were performed in meshes of a 10 μm dendritic section, where maximal variability was observed.

Figure 5.

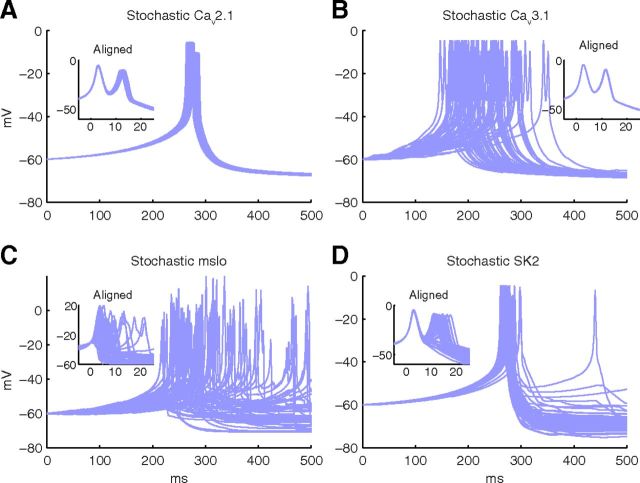
The stochastic effect of Ca²⁺-activated K⁺ channels is large compared with the stochastic effect of voltage-gated Ca²⁺ channels. A–D, Voltage traces for 50 iterations are plotted using a hybrid model (with compartment length of 10 μm) with (A) stochastic Ca_v2.1 channels, (B) stochastic Ca_v3.1 channels, (C) stochastic mslo channels, and (D) stochastic SK2 channels. All other mechanisms, except the mentioned stochastic channels, are simulated deterministically. A–D, Insets, Aligned traces at −30 mV to highlight the variability of spike features in each model over multiple runs.

Comparison of the voltage traces in Figure 5A with the voltage traces for the same mesh in Figure 2A shows that the stochasticity of Ca_v2.1 (P-type) channels has an insignificant contribution toward variable calcium burst generation. The only noticeable difference in the voltage traces in Figure 5A is a small variation in the time of the burst; and after alignment of these traces, a small jitter can also be noticed in the time to second spike. The stochasticity of the other calcium channel, Ca_v3.1 (T-type), has a more interesting effect (Fig. 5B): it causes a larger jitter of the timing of the calcium burst but has no effect on its shape at all (see aligned traces). This suggests that the jitter of burst timing observed in Figure 2A, which strongly declined with model size, is mostly caused by the Ca_v3.1 channel.

Compared with the calcium channels, stochasticity of the calcium-activated potassium channels has more pronounced effects. Indeed, the voltage traces obtained from a hybrid model with stochastic mslo (BK-type) channels (Fig. 5C) look very similar to the traces obtained from the full stochastic model of calcium burst generation (Fig. 2A), suggesting a major contribution of this channel type to calcium spike variability. The contribution of the other Ca²⁺-activated K⁺ channel, SK2, is to produce variability in the number of calcium spikes in the bursts as shown in Figure 5D, inset.

Our results suggest that calcium-activated potassium channels are the major source of variability in calcium bursts, with mslo causing a large variability of both burst timing and burst shape and SK2 specifically causing differences in the number of spikes in the burst. The increased stochastic effect of these two channel types can be explained by their lower density compared with calcium channels, especially for SK2, and the high single-channel conductance of mslo (Table 1).

Ion channel clustering affects burst properties, but not stochasticity

It is well known that mslo channels cluster with Ca_v channels to form nanodomains, where the calcium levels may reach up to 100 μm (Fakler and Adelman, 2008). Pharmacologically, different subtypes of Ca_v have been identified to be selectively coupled with mslo in various cell types: Ca_v1 (Storm, 1987; Prakriya and Lingle, 1999), Ca_v2.1 (Prakriya and Lingle, 1999; Edgerton and Reinhart, 2003; Womack et al., 2004), and Ca_v2.2 channels (Marrion and Tavalin, 1998). The existence of Ca_v-mslo complexes in ratio of 1 mslo to 4 Ca_v channels (Ca_v1.2, Ca_v2.1, and Ca_v2.2) has been suggested by comprehensive proteomic analysis (Berkefeld et al., 2010), but available data for PC dendrites do not provide ratios (Kaufmann et al., 2009; Indriati et al., 2013).

In our model, the ratio of Ca_v2.1 channels to mslo channels is ∼17:1 and there are ∼13 times more surface triangles on the mesh than mslo channels. This implies that a wide range of clustering combinations between these two channel types can be implemented. In our standard model, the arrangement of channels is random and any combination of the channels is possible, although on average one expects a clustering ratio of ∼1.5. To investigate the impact of this clustering ratio on the stochasticity of the model, we varied it systematically. In these simulations, an mslo channel was placed in a surface triangle together with a variable number of Ca_v2.1 channels, whereas Ca_v3.1 and SK2 were distributed randomly in all surface triangles (Fig. 6, schematics). The remaining Ca_v2.1 channels were also distributed randomly in surface triangles without mslo channels. The typical characteristic length of tetrahedral subvolumes next to surface triangles was ∼200 nm. Although calcium nanodomains have typical sizes of ∼20–50 nm (Fakler and Adelman, 2008), it was not possible to reduce surface tetrahedron size to this range because of simulation accuracy and run time concerns (see Materials and Methods; Fig. 1D). Although we do not expect this size discrepancy to influence our conclusion, a full assessment will require different simulation methods (Lee et al., 2012).

Figure 6.

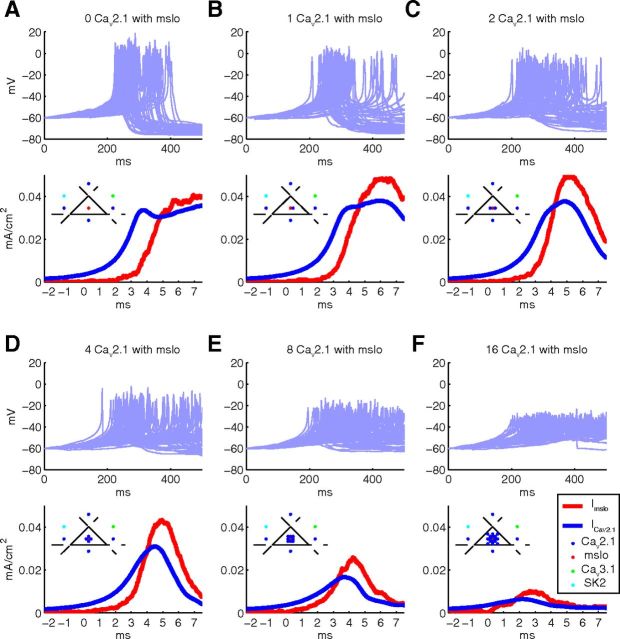
The clustering of Ca_v2.1 channels with mslo channels has a strong effect on dendritic excitability. A–F, Simulations of the stochastic calcium burst model with a variable number of Ca_v2.1 channels clustered together with each mslo channel, sharing the membrane space and submembrane volume. A cylinder of 2 μm diameter and 40 μm length was simulated, and the total number of ion channels were constant for all simulations. Top, Voltage traces for 50 iterations (not aligned). Bottom, Spike-triggered average traces of the Ca_v2.1 and mslo currents. Inset, Schematic of how channels were arranged in the surface triangles of the mesh.

Comparing the results for different cluster sizes with the standard stochastic model (Fig. 2A, 40 μm mesh), a slightly reduced stochasticity was observed when no Ca_v2.1 channels were clustered with the mslo channel (Fig. 6A), but there was no appreciable change in stochasticity for the other cases (Fig. 6B–F). The main effect of clustering is on the excitability of the model: only a limited range of clustering regimens support the generation of full calcium bursts. With an increase in number of Ca_v2.1 channels clustered with mslo channels, there is a decrease in the peak amplitude of calcium spikes. Up to 4 Ca_v2.1 channels clustered with mslo channels, the calcium spikes are still pronounced and identifiable (Fig. 6B–D). But for larger cluster ratios, the calcium spike amplitude is reduced so much that this no longer looks like the physiological traces. The cause of this reduction of spike amplitude can be inferred from the averaged currents (Fig. 6, bottom), with large clustering ratios the mslo channels activate much faster and become larger than the Ca_v2.1 current at earlier time points. The consequent hyperpolarization prevents further activation of the Ca_v2.1 channels and curtails the calcium spike.

Our results clearly show a significant effect of channel clustering on dendritic excitability, but the stochastic properties are not noticeably affected.

Spatial stochastic calcium transport and buffering produce persisting calcium spike number variability to large model sizes

The results of Figure 5 suggest a strong effect of the stochasticity of calcium-activated potassium channels, but the sources of stochasticity in the calcium activation step can be thought of as two separate (though closely related) phenomena: (1) rapidly changing calcium gradients, which are highly localized because of the low diffusion length of calcium in PCs (Santamaria et al., 2006) and caused by stochastic calcium transport and buffering kinetics that produce input patterns that are distinct for each individual channel; and (2) stochastic kinetics in the calcium activation step. Source 2 may be dominant, even in large well-mixed models where the input calcium signal is smooth and global, because of the low channel density and high conductance of calcium-activated potassium channels (Table 1). Source 1 is a distinct and separate source of noise present in spatial models because of the much more local, varying calcium input to calcium-activated channels (see Fig. 9A), but does it play an important role in producing burst variability? To investigate this matter, we first constructed a model in which all channel kinetics were solved deterministically, including activation by calcium, and only calcium diffusion and buffering were solved stochastically (Fig. 7). Although channels behaved deterministically, their discrete locations were maintained from the full stochastic simulations to preserve a spatial element so as to investigate the role that spatial fluctuations in calcium concentrations play in producing spike shape variability.

Figure 9.

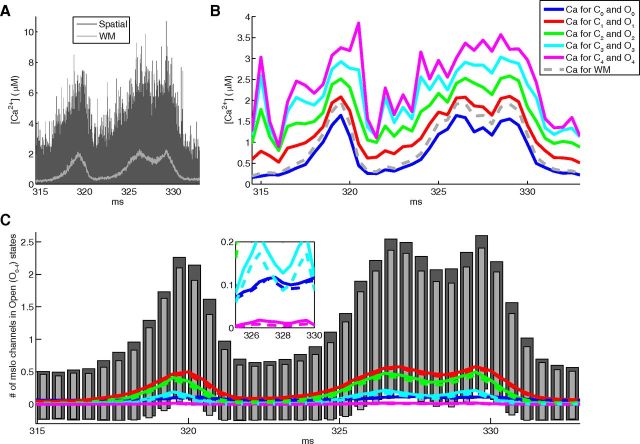
Local calcium concentrations give greater overall mslo activation and larger variability compared with well-mixed conditions. A, Calcium recordings from a stochastic calcium burst simulation at 10 μm, for each of 127 intracellular tetrahedrons connected to a triangle containing an mslo channel. The concentration range across all tetrahedrons is shown at each time point (dark gray) along with the concentration that would be sampled by each channel under well-mixed conditions (light gray). Two simulations mimicking spatial and well-mixed activation of the mslo channel were simulated 10,000 times. B, In the spatial simulation, the observed mean calcium concentration per activated mslo channel shows a dependence on state, with each progressively higher activation state showing a greater mean calcium concentration. C, Mean open state populations across trials for spatial simulations (colored lines) and well-mixed simulations (colored dashes) are compared showing marginally, yet consistently, higher activation in spatial simulations for every state. Total activation is shown as mean ± SD across trials for spatial (dark gray) and well-mixed (light gray) simulations, showing a small yet consistently larger variation in activation for the spatial simulations.

Figure 7.

The stochastic effect of Ca²⁺ dynamics is sustained at large model size. A, The voltage traces (50 iterations for each model size) obtained from simulations of the detailed calcium spike model with deterministic ion channels and stochastic Ca²⁺ dynamics for meshes of varying length. Top insets, CV of resulting intracellular calcium concentration during the burst. The voltage traces and CV are color coded for bursts with 2 spikes (orange) or 3 spikes (blue). B, The corresponding CV of ionic currents during a 40 ms time window covering the calcium burst. A decreasing CV for all currents during the first and second spike with increasing compartment length can be observed. C, D, Phase analysis for the 40 μm compartment at the following: circle represents the peak of the first spike (dV/dt = 0); square represents the fall after the first spike to −20 mV; diamond represents the minimum between first and second spike (dV/dt = 0); star represents the rise to second spike at −20 mV; triangle represents the peak of the second spike (dV/dt = 0); cross represents the fall after the second spike to −23 mV. C, D, Organized similarly to Figure 4A, B, respectively.

The results show very little variability in burst timing, yet significant variation in spike shape, with a significant number of 2 spike and 3 spike cases observed at all lengths, with 3 spike cases being more prevalent (Fig. 7A). In addition, the timing of the third spike was highly variable, which resulted in a high coefficient of variation (CV) of calcium concentration at all lengths. Consistent with the relatively constant shape and timing of the first 2 spikes, the initial CV of the different ionic currents was relatively small but increased strongly for the third spike (Fig. 7B). Congruent with the observations in Figure 5, the CV of calcium-activated potassium currents is always much higher than that of calcium currents.

Similar to Figure 2, there is a small decrease in the variability in spike number with increasing length (going from 42% 2 spike cases at 10 μm to 22% at 160 μm) and corresponding decrease in the CV of the currents. We further observed only a slow decrease in variability of third spike shape with increasing length, causing a consistently high CV of the calcium concentration. We made a phase space analysis of this hybrid system (Fig. 7C,D) and observed the same phenomenon as in Figure 4: there was enough noise in phase space to give significant crossover to the sigmoidal separatrix, and this effect did not reduce quickly with model size.

These results and the accompanying phase space analysis suggest that source 1, local differences in calcium concentrations (caused by stochastic transport and buffering) around spatially separated discrete channels, is a significant contributor toward calcium burst shape variability. If the calcium activation step of the channels (source 2) would also be solved stochastically in this hybrid model, we would have been able to investigate the stochastic effects of all calcium dynamics together and the system would be expected to show significantly noisier behavior. We found, however, no robust way to implement hybrid gating of channels, which would have allowed us to model calcium activation stochastically while keeping voltage gating kinetics deterministic.

Local calcium concentration differences complement the strong variability arising from stochastic channels

We observed that local, stochastic calcium differences around spatially separated deterministic channels produce burst shape variability (Fig. 7), but overall variability was reduced compared with the completely stochastic model (Fig. 2), which includes stochastic ion channels. The stochastic calcium-activated channels are expected to be the dominant source of the increased variability in the completely stochastic model because of their importance for burst variability observed in Figure 5, but how much do the local calcium gradients contribute and how does this depend on model size? To investigate this, we simulated a well-mixed stochastic model, which still included 1D radial diffusion between concentric shells, from submembrane to the core of the dendrite, as in previous models (Anwar et al., 2012), but there was no spatial separation between channels or between calcium ions in the submembrane shell. Using well-mixed models of different lengths, with stochastic channels and stochastic calcium dynamics (Fig. 8A–C), we saw only subtle differences from the spatial stochastic model with 3D diffusion (Fig. 2A–C). Quantitative comparison between the two models indicates that, for small meshes (length up to 20 μm), there is no clear, consistent difference in the level of noise observed from the well-mixed and spatial conditions for the RMS and first spike timing measurements (Fig. 8D,E). In larger meshes (≥40 μm), appreciably greater variability arises from the spatial model, which shows as a greater mean deviation from the deterministic case and a consistently greater range. The measurement of spike separation (Fig. 8F) similarly shows more variability in the spatial model compared with the well-mixed model, but now for all mesh sizes.

Combining the results of Figures 7 and 8 confirms that stochastic calcium activation and stochastic gating are more important toward the calcium burst variability than local differences in calcium concentration. However, the latter still increases variability, which is observable in larger systems where the difference between the spatial and well-mixed model is greatest. To investigate the effects of local calcium concentration on isolated mslo activation, we constructed two models containing only calcium and the mslo channel. Using calcium recordings from the full stochastic model of 10 μm length from each of 127 intracellular tetrahedrons connected to a triangle containing an mslo channel (Fig. 9A), we simulated activation under well-mixed conditions (where every mslo channel received the mean recorded concentration) and under spatial conditions (where each mslo channel received a unique calcium concentration profile from individual tetrahedron recordings). We observed a greater overall activation of mslo under spatial conditions, which is because, although on average mslo channels in the spatial simulation sample the same calcium concentration as the well-mixed simulations, activation is most likely to come from higher-concentration regions introducing a high-concentration bias for higher mslo activation states (Fig. 9B). This can be explained by the kinetic properties of the mslo channel, which favor transition to the open state for higher calcium concentrations: the C₄ → O₄ transition (4 calcium ions bound) is much more likely than the C₁ → O₁ transition (1 calcium ion bound; Table 1). The overall effect was to produce a marginally greater variability in mslo channel activation when sampling the range of concentrations compared with when sampling the mean concentration (Fig. 9C), and this effect can be expected to be more prominent in larger dendritic sections with greater variability in calcium concentration. This explains the larger variability arising from spatial models when simulating longer dendritic sections (Fig. 8).

In conclusion, our analysis shows that the variability of calcium bursts is caused by stochastic activation and gating of calcium-activated channels (Fig. 5C,D), and local differences of calcium concentration caused by stochastic diffusion and buffering also contribute (Fig. 7) through their effect on activation of potassium channels (Figs. 8, 9).

Because the well-mixed model of Figure 8 captures most features of the stochastic system, we will use this approach to simulate larger models that include dendritic branching. A full spatial stochastic simulation of these models would require unacceptably long run times.

Stochastic calcium bursts in a dendrite model manifest large spatial variation of voltage

Even with the run-time improvements of using the stochastic well-mixed model, only part of a PC dendrite could be simulated (Figs. 10, 11). Comparing the dendritic calcium bursts generated in the dendrite model (Fig. 10C) with those in the longest-length cylinder (Fig. 8A,B), we observe a smaller variability for the dendrite model. But the main features are still present: there is a variable number of spikes (1 or 2) and a smaller variability of timing and shape of the burst.

However, such analysis ignores the variability in space, which was not present in the simulations of cylinders of variable length (results not shown). Figure 11 shows very prominent spatial variability of the membrane potential during calcium bursts for five different runs, two of which resulted in 2 spike bursts and three of which resulted in 1 spike bursts. There is large spatial variability in membrane potential, both within a single run and comparing across different runs. The variability in amplitude and peak timing is even larger for the submembrane calcium concentration (results not shown). This variability makes the images quite complex and not easy to interpret; therefore, we analyzed them quantitatively in several ways.

A noticeable feature is that some branches on the right side of the dendrite often show lower membrane potentials (because of higher peak calcium concentrations). These are branches with quite small diameters (Figs. 10A, 11E), where indeed calcium influx is expected to cause larger transients (Cornelisse et al., 2007). But across trials, there is a large variability for these thin branches (Fig. 11C): the voltage range across all trials at any point in time during the first calcium spike is much higher for small-diameter branches (red) than for most other ones (gray), and systematically higher than the mean (black). Overall, the large voltage ranges (up to 27 mV during the peak) are caused by the calcium spike peaking at different times across the dendrite, and this varies across runs.

The lengths of thin compartments are not different from those of larger diameters (Fig. 10B), but their large variability corresponds more to what we observed for short cylinders in Figure 8, whereas the larger-diameter compartments showing less variability approximate the behavior of the longer cylinders. This suggests that differences in electronic coupling between compartments strongly influence their stochastic behavior in the dendrite. Small-diameter compartments have higher axial resistance than large-diameter ones and may therefore be relatively isolated from the voltage transients in the rest of the dendrite. This was verified by computing the spatial correlation between all pairs of compartments in the tree at different points in time (Fig. 11D). Although the correlograms clearly evolve over time, their main features are constant. First, thin compartments (indicated by red points in sidebars) are correlated with each other within two small spatial clusters but are either anticorrelated or weakly correlated with all other compartments. Second, the division of the dendritic tree into two subtrees (Fig. 11E, different shades of gray, D, sidebars) causes strong correlation between all larger-diameter compartments within each subtree and a weaker correlation with those in the other subtree. Based on this, we postulate that the large-diameter compartments within each subtree are strongly coupled and thereby approximate the behavior of the longer cylinder models (Fig. 8A); conversely, thin compartments are relatively isolated from this system and form small clusters that behave more like the shorter cylinders showing significant higher variability (Fig. 8D–F).

Stochastic synaptically evoked dendritic calcium bursts are highly variable

In vivo, large dendritic calcium bursts in PCs are evoked by climbing fiber activity (Schmolesky et al., 2002). The associated complex spikes in the soma have been reported to show variation in waveforms from cell to cell and sometimes also within the cell (Llinás and Sugimori, 1980; Hansel and Linden, 2000; Davie et al., 2008; Mathy et al., 2009). We were therefore interested in whether similar variability would exist for synaptically evoked dendritic calcium bursts in the dendrite morphology. We observe significant variability in dendritic calcium burst shape (Fig. 10D). Because of the strong synaptic stimulus, there is no jitter in timing, but the number of spikes varies between two (8 of 50 trials) and three (42 of 50 trials) (Fig. 10D). As shown in Figure 12 (two 3 spike bursts and two 2 spike bursts), synaptically evoked calcium bursts also have a large spatial and intertrial variability, similar to the spontaneous bursts.

Figure 12.

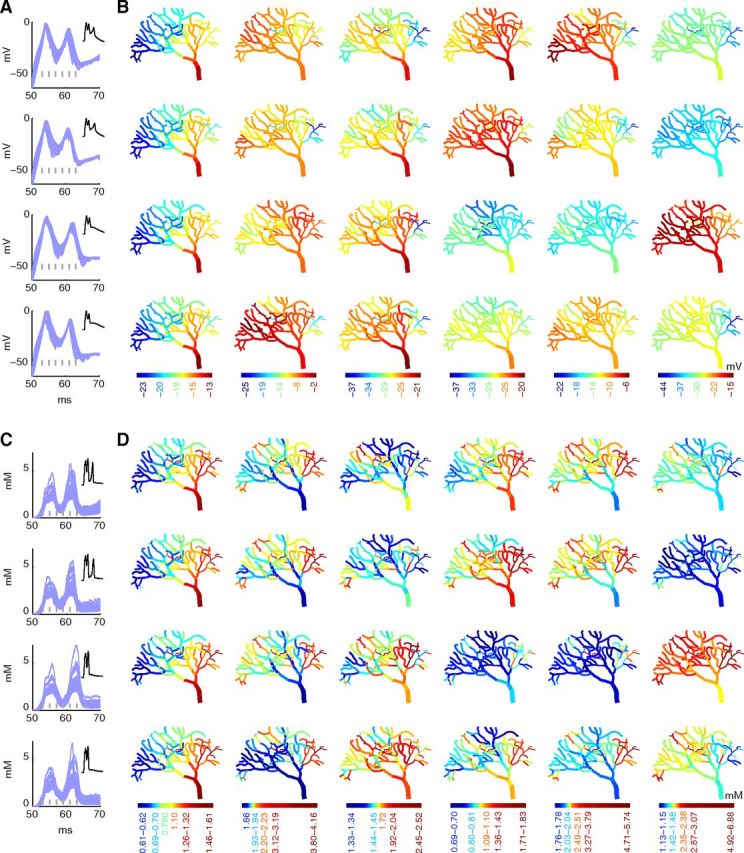
Stochastic synaptically evoked calcium burst model generates differential patterns of voltage and calcium across dendrite. This figure shows voltage and calcium during four different runs of the synaptically evoked dendritic calcium burst model (A–D). A, B, In the first two runs, the burst consisted of 3 calcium spikes; in the other runs, only 2 calcium spikes were generated. A, First 20 ms of the voltage traces recorded from all compartments of the dendritic tree are overlaid. Inset, Complete burst. Gray vertical lines indicate the time points for which the spatial maps are shown. B, Spatial maps of membrane potential throughout the dendrite for each time point marked with gray lines in A. Each time point has its own linear color scale to emphasize differences within single maps. C, D, Calcium traces for calcium bursts shown in A. C, Calcium traces corresponding to the voltage traces recorded from all compartments of the dendritic tree are overlaid. Inset, Complete calcium transient. Gray vertical lines indicate the time points for which the spatial maps are shown. D, Spatial maps of submembrane calcium concentration throughout the dendrite for each time point marked with gray lines in C. Each time point has its own color scale to emphasize differences within single maps. The color scales used in these maps are nonlinear (using histogram equalization) to enhance the contrast.

The activation by the climbing fiber evokes a dendritic calcium burst by depolarizing the primary dendrite first (Fig. 12B; first column), which then depolarizes spiny dendrites attached to it (Fig. 12B; second and later columns). Such a progressive depolarization causes a delay in membrane potential of each compartment to reach its peak amplitude, which depends on distance from the primary dendrite as well as passive properties of all compartments on its way. This progressive spread of depolarization across the dendrite results in spatiotemporal variability of membrane potential, even in a deterministic model (range of peak amplitudes, 4.17 mV; range of time to peak amplitude, 0.4 ms). However, in the stochastic model, the same progressive spread of depolarization allows individual compartments to behave stochastically across different times, resulting in a wider range of spatiotemporal patterns of membrane potentials (ranges of peak amplitudes, 3.41–12.65 mV; ranges of time to peak amplitude, 0.48–1.28 ms). Similarly, the stochastic synaptically evoked dendritic calcium burst results in a large variability of submembrane calcium concentrations across dendritic compartments (Fig. 12C,D). The range of peak calcium concentrations across the dendrite (3.68 μm for deterministic model), which is the result of differences in surface-to-volume ratios of dendritic compartments (Cornelisse et al., 2007), becomes wider in stochastic simulations (2.86–7.06 μm).

In conclusion, we find that dendritic calcium bursts show not only variability in shape and timing across time but also across space: the amplitude and timing of peaks vary greatly within the dendrite, more so for calcium concentration than for membrane potential, and variability is more pronounced in small-diameter branches. This applies to both spontaneous and synaptically evoked calcium bursts. Because these simulations were run in a stochastic well-mixed model, we probably underestimated the variability when 3D diffusion is also present (Fig. 8D–F).

Discussion

Stochasticity in neuronal signaling systems containing calcium-activated channels

Many computational studies of neuronal systems, particularly those on larger spatial scales, involve a bulk representation of the underlying molecular system as a set of differential equations that are assumed to evolve deterministically. This approach is often justified for whole-cell models based on voltage-gated channels in excitable membranes because the fluctuations resulting from stochastic gating kinetics observed in small systems tend to become negligible as system size approaches the whole-cell scale (current study; Chow and White, 1996). However, previous experimental and computational studies have shown that there are occasions when stochastic behavior of voltage-gated ion channels can be important even in a whole-cell context. Voltage-gated channel noise has been shown to give rise to experimentally observed subthreshold fluctuations (Schneidman et al., 1998; Steinmetz et al., 2000; Jacobson et al., 2005) and to make the relation between synaptic input and neuronal output probabilistic (Cannon et al., 2010). Moreover, stochastic effects in spike propagation in thin axons produce timing “jitter” and may make propagation unreliable (Faisal and Laughlin, 2007).

This study makes an important addition to those previous studies by focusing on stochastic effects in a neuronal excitability system that contains stochastic channel activation by calcium molecules diffusing intracellularly. This was made possible by recent software development that tightly couples spatial stochastic reaction-diffusion simulation with membrane excitability calculations within complex morphologies (Hepburn et al., 2013). In dendrites, molecular signals exhibit far greater localization than electrical signals, which means that the calcium-activated channels tend to receive differing discrete local inputs to each other (as opposed to a continuous electrical signal for voltage-gated channels, shared on a large spatial scale), and so one might intuitively expect stochastic effects to be more prominent. Indeed, our results were startlingly different from deterministic behavior and suggest that, for systems with molecular channel activation, stochastic effects are more prominent than for systems containing only voltage-dependent channel activation, and that these effects persist to a significant extent with increasing model size. By isolating individual channel stochasticity, we observed that, indeed, it was the calcium-activated channels that produced considerably more noise in the system. Well-mixed models were found to capture the important stochastic behavior of the system but with an undersampling of noise at larger system sizes, which occurs because channels sample a distribution of local calcium signal in spatial models and only the mean concentration in well-mixed models (Fig. 9). We conclude that consideration of stochastic effects will be crucial for development of our understanding of dendritic neuronal excitability.

The different contributors to variation in dendritic calcium bursts

This study investigated some of the possible contributors to the variability in dendritic calcium bursts that are observed experimentally (Fig. 1A–C). Within this variability, there is cell-to-cell variability, which remains largely unexplored, and dendritic calcium burst variability within a single neuron. Although we did not attempt to fully explain cell-to-cell variability, it is possible that this is partially caused by differing channel arrangements as our results of a prominent effect of clustering (Fig. 6) suggest, and differing morphologies may also play an important role.

The question of dendritic burst variability was addressed by simulation of a detailed biophysical model that included spatial stochastic reaction-diffusion, stochastic currents, and accurate calculations of potential in tetrahedral meshes of cylinders representing dendritic sections. Even with this level of detail, there were undoubtedly simplifications to the real system, such as a uniform channel distribution in our model, yet our results provided valuable insights into the stochastic properties of this system that is statistically similar to the dendritic recordings (Fig. 1B,C). We then extended the results to dendritic morphology by simulating multiple well-mixed compartments based on a reconstruction of a part of a PC dendritic tree. This confirmed our findings and introduced a strong spatial variation component, which was found to depend on dendrite diameter. The modulation of mslo (Weiger et al., 2002; Widmer et al., 2003; Salkoff et al., 2006) and SK2 (Belmeguenai et al., 2010; Hosy et al., 2011; Ohtsuki et al., 2012) may affect the dendritic excitability by changing the characteristic of the calcium bursts (e.g., number of spikes, amplitudes of spikes, shape of afterhyperpolarization). However, we do not expect these modulatory effects to mask the variability resulting from intrinsic stochasticity of those ion channels. Our study suggests that stochastic kinetics contribute strongly to the observed variability in dendritic calcium bursts in PCs, and this probably also applies to dendritic bursting in other neurons (Kamondi et al., 1998; Larkum et al., 1999).

Cause of the persisting stochastic effects in large system sizes

The phase space of calcium bursts in the data and the model was found to exhibit a large variability across trials, in contrast to sodium action potentials that are characterized by a consistent shape with much smaller variability in V and relatively smaller variability in dV/dt (though a faster spike) observed both experimentally (Pinsker and Bell, 1981; Sekerli et al., 2004) and computationally in an HH model (current study). As a system displaying typically only one spike per burst, the significant effects of noise in the HH model are the subthreshold fluctuations that create a probabilistic spiking threshold and can produce spontaneous spikes at small model sizes, but these effects have a strong dependence on model size. This is in contrast to calcium bursts, which often contain multiple spikes per burst with a large variation in dV/dt and V between each spike (Fig. 4), which makes stochastic phase analysis particularly suitable. To our knowledge, no experimental phase space analysis of calcium spikes exists, which may be the result of the large number of trials necessary for complete analysis (because of the large variability).

Phase analysis of both the HH and calcium burst system demonstrates that the probabilistic behavior around a “phase boundary” relative to the variability in the distribution is crucial in determining the importance of stochasticity. We found that, even where mean behavior is relatively far from a phase boundary, if noise produces a skewed distribution where a significant proportion of the trials are relatively close to a phase boundary, then stochastic effects produce significant variability in outcome. In our calcium burst model, these effects did not reduce quickly with length and were observed in larger systems.

Hypothetically, in a system where the mean behavior rests exactly on a phase boundary, on average 50% of trials will result in one outcome (e.g., 1 spike) and 50% will result in the other (e.g., multiple spikes) at any system size because there will always be some noise in the phase space of the system that will push the system into either behavior, with equal probability of both (assuming a uniform distribution). In such a hypothetical system, the variability produced by stochastic effects is therefore independent of system size.

Spatial variability in calcium level and relevance to neuronal signaling and plasticity

Spatial heterogeneity in PCs has been observed previously in the voltage signal (Fujita, 1968; Llinás and Nicholson, 1971) and related calcium transients in distal dendrites (Lev-Ram et al., 1992; Miyakawa et al., 1992). In most of this study, we have modeled the generation of calcium spikes without injection of a depolarizing current. Instead, a relatively large conductance of the Ca_v3.1 channel is used to generate calcium bursts spontaneously. The slower kinetics of Ca_v3.1 calcium current compared with Ca_v2.1 calcium current leads to slow and uniform changes of the membrane potential across the dendrite and determined the jitter of the calcium burst (Fig. 5B). We also confirmed that a dendritic calcium burst triggered by a large synaptic current localized in the primary dendrite shows similar stochastic behavior (Figs. 10D, 12), but we did not explore the spatial heterogeneity with respect to generation of calcium spikes by localized parallel fiber input (Eilers et al., 1995; Rancz and Häusser, 2010). However, we expect that the stochastic effects of mechanisms of calcium spike generation will persist in this case; and indeed, they may become more pronounced because of local differences in morphology and nonuniform expression of voltage-gated channels.

In the dendrite model, we found, apart from variability in spike shapes, tens of millivolts of spatial variation in membrane potentials (Figs. 11, 12) and micromolar spatial variation in submembrane calcium levels (Fig. 12) across trials. The stochastic behavior of intrinsic conductances could affect the spread of local dendritic spikes generated by parallel fiber input, which trigger short-term synaptic plasticity (Rancz and Häusser, 2006). The large spatial variability in submembrane calcium will differentially modulate calcium-activated potassium channels and molecular pathways involved in synaptic plasticity and learning. Experiments have shown that relatively small changes in the amplitude of complex spikes strongly influence the induction of parallel fiber synaptic plasticity (Coesmans et al., 2004), so the large stochastic fluctuations observed in the dendrite model should have pronounced effects on the probability of long-term depression (Antunes and De Schutter, 2012) or long-term potentiation (Jörntell and Hansel, 2006) of the parallel fiber synapse.

Unfortunately, stochasticity is often considered “noise” in experimental designs, and researchers go to great efforts to average it out of their reported results. Here we have demonstrated that it is a fundamental property of dendritic calcium bursts and that it would be impossible to understand why, for example, they can vary between 2 or 3 calcium spikes without considering the underlying stochastic nature of the activation of channels by calcium. This observation may generalize to other aspects of neuron excitability and strongly affect the induction of synaptic plasticity. Therefore, both in experimental studies and modeling of neuronal excitability, stochastic processes should always be considered.

Notes

Supplemental material for this article is available at http://steps.sourceforge.net/STEPS/download/Hybrid.pdf. A detailed description of how hybrid simulations, combining stochastic and deterministic solution of different components of the model, were implemented in STEPS can be found here. This material has not been peer reviewed.