Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2013 Oct 2;33(40):15705–15709. doi: 10.1523/JNEUROSCI.2785-13.2013

Updating Expected Action Outcome in the Medial Frontal Cortex Involves an Evaluation of Error Type

Martin E Maier 1,2,✉, Marco Steinhauser 1
PMCID: PMC6618485  PMID: 24089478

Abstract

Forming expectations about the outcome of an action is an important prerequisite for action control and reinforcement learning in the human brain. The medial frontal cortex (MFC) has been shown to play an important role in the representation of outcome expectations, particularly when an update of expected outcome becomes necessary because an error is detected. However, error detection alone is not always sufficient to compute expected outcome because errors can occur in various ways and different types of errors may be associated with different outcomes. In the present study, we therefore investigate whether updating expected outcome in the human MFC is based on an evaluation of error type. Our approach was to consider an electrophysiological correlate of MFC activity on errors, the error-related negativity (Ne/ERN), in a task in which two types of errors could occur. Because the two error types were associated with different amounts of monetary loss, updating expected outcomes on error trials required an evaluation of error type. Our data revealed a pattern of Ne/ERN amplitudes that closely mirrored the amount of monetary loss associated with each error type, suggesting that outcome expectations are updated based on an evaluation of error type. We propose that this is achieved by a proactive evaluation process that anticipates error types by continuously monitoring error sources or by dynamically representing possible response–outcome relations.

Introduction

Anticipating the outcome of a particular action is an important prerequisite not only for choosing future actions but also for learning from previous actions. Prediction errors reflecting violations or changes in expected outcome have been assumed to form the basis of reinforcement learning (Sutton and Barto, 1998). A crucial role in computing outcome expectation has been ascribed to the medial frontal cortex (MFC) (for review, see Rushworth and Behrens, 2008). Animal studies provided evidence that outcome expectations in the MFC are updated not only by evaluating external cues (Matsumoto et al., 2003; Amiez et al., 2005) but also by evaluating own actions (Amiez et al., 2006; Matsumoto et al., 2007; Seo and Lee, 2007). In humans, errors in choice tasks are accompanied by a negative deflection in the event-related potential, called the error-related negativity (Ne or ERN) (Falkenstein et al., 1990; Gehring et al., 1993). The Ne/ERN peaks ∼50 ms after the error response and is generated in the MFC (Ridderinkhof et al., 2004). Reinforcement-learning frameworks proposed that the Ne/ERN is linked to an update of outcome expectations resulting from the detection of an error (Holroyd and Coles, 2002; Alexander and Brown, 2011; Silvetti et al., 2011).

The present study aimed to investigate whether updating expected outcome after errors involves evaluative processes that go beyond mere error detection. In everyday behavior, actions can fail in various ways and different types of errors can have different consequences. For instance, pouring salt instead of sugar into a coffee has more severe consequences than confusing milk with sugar. In such a case, an adequate computation of expected outcome cannot rely solely on error detection but requires that the type of error is identified. However, although the Ne/ERN indicates that updating outcome expectation based on error detection occurs almost simultaneously with response execution, it is unclear whether information about the error type is already available at this early time point.

Our approach was to use a speeded choice task in which two types of errors can occur (Maier et al., 2008, 2011, 2012; see also van Driel et al., 2012) and to manipulate the amount of monetary loss associated with each error type. Because each error type could occur on each trial, updating the expected outcome on error trials required not only the detection of an error but also an evaluation of the error type. If updating expected outcome were based on an evaluation of error type, the Ne/ERN should be sensitive to the specific error type (i.e., larger Ne/ERNs should be obtained for errors associated with larger monetary loss). Although previous studies have shown that the Ne/ERN varies with the amount of monetary loss (Gehring et al., 1993; Hajcak et al., 2005; Ganushchak and Schiller, 2008; Potts, 2011), in none of these studies was an evaluation of error type necessary to update outcome expectations. Therefore, such a result would demonstrate that complex performance monitoring processes beyond mere error detection inform expected outcome computation already at a very early time point.

Materials and Methods

Participants.

Thirty participants (20 female) between 17 and 27 years of age (mean 21.6 years) were recruited at the Centro Studi e Ricerche in Neuroscienze Cognitive Cesena. They were paid 10 € plus a performance-dependent bonus of up to 10 €. The study was conducted in accordance with institutional guidelines, and informed consent was acquired from all participants.

Behavioral task and procedure.

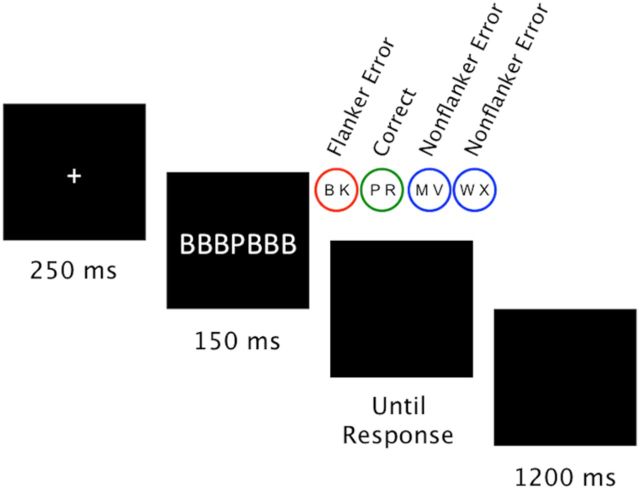
We used a flanker task (Eriksen and Eriksen, 1974) with four response alternatives. On each trial, participants had to respond to a central target letter while ignoring three identical flanker letters on each side of the target. Eight target letters were mapped onto four responses: the left middle finger (B, K), the left index (P, R), the right index (M, V), and the right middle finger (W, X). A total of 48 incongruent stimuli were constructed by combining each target letter with each of the six letters not associated with the target response. A total of 48 neutral stimuli were constructed by combining each target letter with each of the six neutral symbols (§, $, %, &, #, and ?). Letters and symbols subtended a visual angle of 0.26° × 0.33° (width × height) at a viewing distance of 70 cm. The width of the whole stimulus array was 2.10°. A sample trial is depicted in Figure 1. After a 250 ms fixation cross, the stimulus was presented for 150 ms followed by a black screen. When a response was given, this triggered an interval of 1200 ms before the next trial started. This interval was restarted whenever further responses (e.g., spontaneous error corrections) occurred.

Figure 1.

Figure 1.

Open in a new tab

Sequence of events on one trial of the flanker task. Participants had to classify the central target while ignoring the flankers. Because four response alternatives were used, two different types of errors could occur for incongruent stimuli. If participants responded by pressing the button associated with the flankers (button BK in the depicted example), an FE resulted. If participants responded by pressing a button not associated with an element in the stimulus array (buttons MV and WX in the depicted example), an NFE resulted.

With four response alternatives, one can distinguish between two types of errors on incongruent trials. An error response could consist of either the response associated with the flankers (flanker errors [FEs]) or one of the remaining responses not associated with the flankers (nonflanker errors [NFEs]). To manipulate the outcome associated with each error type, committing an error led to a monetary loss, which differed depending on condition and error type. Participants were randomly assigned to one of two experimental groups. In the high FE group, committing an FE was associated with a high monetary loss, whereas committing an NFE was associated with a low monetary loss. In the high NFE group, the assignment of error type and monetary loss was reversed.

The experiment comprised a practice session and a test session, distributed over 2 consecutive days. In each session, participants worked through blocks of 96 trials (one trial for each possible stimulus). At the beginning of the experiment, participants were instructed that (1) they start with 10,000 points; (2) they will lose some of these points depending on their performance during the experiment; and (3) the remaining points will be changed into money (with 1000 points corresponding to 1 €) at the end of the experiment. The practice session started with two blocks without speed pressure to learn the stimulus-response mapping. After this, participants were instructed that the following blocks serve to train their response speed and that, in the test session, they will lose 20 points for each slow response. During blocks 3–10, the error rate was adjusted by an adaptive deadline procedure. At the end of each block, participants were informed about the number of “slow responses” (i.e., the number of responses exceeding a deadline). The deadline was initialized at 1000 ms. After each block, it was decreased by 50 ms whenever the error rate in this block was <15% and was increased by 50 ms whenever the error rate was >25%. The deadline from the last practice block was applied to all blocks of the test session. The test session started with two practice blocks. Then, participants were instructed about the two error types (using the same wording as in our definition described above) and the amount of loss associated with each type. In the test session, participants lost 20 points for each slow response, 1 point for each error on a neutral trial, 10 points for each error type with high loss, and 1 point for each error type with low loss. After each block, participants were informed about the number of errors of each type and the number of slow responses. Twelve test blocks with a total number of 1152 trials were conducted.

Psychophysiological recording.

During the test session, the electroencephalogram (EEG) was recorded with Ag/AgCl electrodes (Fast'n'Easy-Electrodes, Easycap) from 27 electrode sites (Fp1, F3, F7, FC1, FC5, C3, CP1, CP5, P3, P7, O1, AFz, Fz, FCz, Cz, Pz, Fp2, F4, F8, FC2, FC6, C4, CP2, CP6, P4, P8, and O2) and from the right mastoid. The left mastoid was used as reference, and the ground electrode was placed on the right cheek. The electro-oculogram (EOG) was recorded from above and below the left eye and from the outer canthi of both eyes. EEG and EOG were recorded with a bandpass filter of 0.01–100 Hz, amplified by a BrainAmp DC amplifier (Brain Products), digitized at a sampling rate of 1000 Hz, and resampled to 500 Hz offline.

Data analyses.

Trials with response times (RTs) deviating >4 SDs from the condition mean were excluded from RT analyses (<1% of all trials). Frequency data were arcsine-transformed for statistical testing (Winer et al., 1991).

EEG data were analyzed using EEGLAB version 6.03b (Delorme and Makeig, 2004) and custom routines written in MATLAB version 7.0.4 (MathWorks). ERP data were rereferenced off-line to the average of both mastoids and filtered with a 1–20 Hz pass-band. Epochs of 200 ms before and 800 ms after the response were extracted from the continuous EEG and baseline-corrected using a 150 to 50 ms preresponse window. Epochs were excluded if the voltage on an EOG channel exceeded an individually adjusted threshold to remove trials with large EOG peaks or if an epoch contained data that deviated >5 SDs from the mean (joint probability criterion in EEGLAB version 6.03b). The mean percentage of excluded trials was 14.2% (SE 3.42%). Remaining EOG artifacts were corrected using a regression approach (Gratton et al., 1983). The Ne/ERN was quantified as the difference between the most positive peak in an interval of −100 and 0 ms and the most negative peak in an interval of 0 and 120 ms relative to the response. Statistical analysis was restricted to data from channel FCz at which the Ne/ERN was maximal. In addition to mixed-model ANOVAs, post hoc tests between low-loss and high-loss errors on Ne/ERN amplitudes were conducted using one-sided t tests because results from previous studies (e.g., Potts, 2011) suggest the strong directional hypothesis that the Ne/ERN is larger for high-loss relative to low-loss errors. Post hoc t tests on behavioral data were two-sided.

RT matching.

To investigate whether RT differences between error types and conditions influenced the results, we conducted a control analysis on a subset of RT-matched trials. To this end, we matched incongruent trials with correct responses and NFEs to the FE condition, which was the condition with the fewest trials in all participants, using the following algorithm (Steinhauser and Yeung, 2012): First, an FE trial was randomly drawn without replacement. Second, from each of the remaining conditions, the trial providing the closest match to the RT of the drawn trial was selected without replacement and assigned to the RT-matched sample. These steps were repeated until all FE trials were drawn. Because only artifact-free trials were included, mean RTs on RT-matched trials deviate slightly from the results of the initial analysis.

Results

Behavioral data

Task performance

Error rates and correct RTs were subjected to ANOVAs with the variables group (high FE, high NFE) and congruency (neutral, incongruent). Error rates showed a main effect of congruency (F(1,28) = 44.5, p < 0.001), denoting higher error rates on incongruent (22.3%, SE 1.6%) than on neutral trials (18.5%, SE 1.4%) (all other p values > 0.27). The ANOVA on RTs (Table 1) revealed a main effect of congruency (F(1,28) = 119.9, p < 0.001; all other p values > 0.29). Thus, task performance did not differ between the two groups of participants.

Table 1.

Behavioral performance in the flanker task

All trials
 Subset of RT-matched trials
High NFE group
 High FE group
 High NFE group
 High FE group
Mean SE Mean SE Mean SE Mean SE
RT neutral correct (ms) 591 11.9 572 11.1 — — — —
RT incongruent correct (ms) 606 13.0 589 11.5 580 21.8 554 12.3
Relative frequencya FE (%) 10.1 1.20 7.98 0.62 — — — —
Relative frequencya NFE (%) 14.2 1.71 12.3 0.99 — — — —
RT FE (ms) 575 15.7 538 8.83 576 23.3 553 12.5
RT NFE (ms) 574 19.4 559 8.98 573 23.2 557 12.8
Open in a new tab

aRelative frequency is relative to all trials in the incongruent condition.

FE versus NFE

In a second step, we examined proportions of FE and NFE relative to all incongruent trials. To this end, we entered relative frequencies of FE and NFE in the incongruent condition into an ANOVA with the variables group (high FE, high NFE) and error type (FE, NFE). A main effect of error type was revealed (F(1,28) = 80.9, p < 0.001), denoting that NFE occurred more frequently (13.2%, SE 1.0%) than FE (9.04%, SE 0.69%). Crucially, neither the main effect of group (p > 0.28) nor the interaction between group and error type (p > 0.86) was significant, indicating that the two groups differed neither with respect to the overall error rate nor with respect to the proportions of FE and NFE (Table 1). Because of three possible error responses on each trial, the relative proportion of FE among all errors (40.9%, SE 0.92%) was larger than that of each NFE (29.6%, SE 0.46% each; t(28) = 8.24, p < 0.001), thus making FE disproportionally more frequent than NFE (for discussion, see Maier et al., 2011).

An analogous ANOVA on RTs of FE and NFE (Table 1) revealed a main effect of error type (F(1,28) = 4.27, p < 0.05), which was qualified by a significant interaction between error type and group (F(1,28) = 5.18, p < 0.04). RT was shorter for FE than for NFE in the high FE group (t(14) = 3.03, p < 0.01) but comparable in the high NFE group (p > 0.88).

ERP data

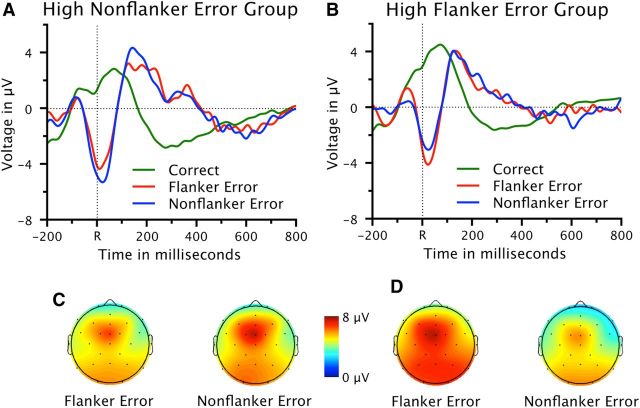
To test the effects of incentives on the Ne/ERN, we compared the Ne/ERN for FE and NFE in both groups of participants. Grand-average waveforms of response-locked ERPs at channel FCz and scalp topographies of peak-to-peak Ne/ERN amplitudes are depicted in Figure 2. Clear Ne/ERNs and maxima of peak-to-peak Ne/ERN amplitudes over channel FCz are visible. An ANOVA with the variables group (high FE, high NFE) and error type (FE, NFE) revealed an interaction between both variables (F(1,28) = 9.45, p < 0.01). In the high FE group, the Ne/ERN for FE (7.63 μV, SE 1.28 μV) was larger than the Ne/ERN for NFE (6.10 μV, SE 1.08 μV) (t(14) = 2.74, p < 0.05). By contrast, in the high NFE group, the Ne/ERN was numerically larger for NFE (7.45 μV, SE 1.25 μV) than for FE (6.66 μV, SE 1.01 μV), although this difference was not significant (t(14) = 1.56, p = 0.07, all other p values > 0.17).

Figure 2.

Figure 2.

Open in a new tab

ERP data. A, B, Response-locked waveforms at electrode FCz for correct trials, FEs, and NFEs, separately for each group. C, D, Scalp topographies of the peak-to-peak Ne/ERN amplitudes, separately for each group. The mean latency of the Ne/ERN peak was 26 ms. R = time point of the button press.

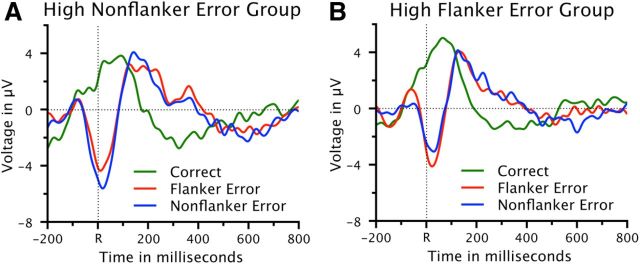
The same analyses were conducted on an RT-matched subset of data to ensure that effects on the NE/ERN amplitude are not the result of differences in RT. An ANOVA on RTs in the RT-matched data (Table 1) with the variables group (high FE, high NFE) and trial type (correct response, FE, NFE) revealed no significant effects (p > 0.26), indicating that RT matching was successful. Grand-average waveforms of response-locked ERPs at channel FCz for RT-matched correct incongruent, FE and NFE trials are depicted in Figure 3. An ANOVA with the variables group (high FE, high NFE) and error type (FE, NFE) on RT-matched peak-to-peak amplitudes yielded an interaction between group and error type (F(1,28) = 11.3, p < 0.01). The Ne/ERN was again larger for FE (7.63 μV, SE 1.28 μV) than for NFE (6.28 μV, SE 0.98 μV) in the high FE group (t(14) = 1.92, p < 0.04). In contrast, in the high NFE group, Ne/ERN amplitudes were now significantly larger for NFE (8.05 μV, SE 1.19 μV) than for FE (6.66 μV, SE 1.01 μV) (t(28) = 3.31, p < 0.01). Thus, analyses of RT-matched trials replicated the findings obtained in the analyses of all trials, with the exception that, in the high NFE group, the difference between FE and NFE was now significant.

Figure 3.

Figure 3.

Open in a new tab

RT-matched ERP data. Response-locked waveforms at electrode FCz for correct trials, FEs, and NFEs for a subset of RT-matched trials, separately for each group. A, High NFE group. B, High FE group. R = time point of the button press.

Discussion

The present study demonstrates that MFC activity is sensitive to the amount of monetary loss in a task in which updating expected outcome requires that the type of error is evaluated. Previous studies manipulating the amount of monetary loss for errors used only a single error type, although the amount of monetary loss was known before the error was committed. In these studies, monetary loss was manipulated between blocks of trials (Gehring et al., 1993; Ganushchak and Schiller, 2008) or was indicated by a cue or the stimulus (Hajcak et al., 2005; Potts, 2011). As a consequence, detection of an error was sufficient to update expected outcome. In the present task, however, updating expected outcome required that the type of error response had to be evaluated because neither the stimulus alone nor error detection was predictive of the outcome. Our results therefore demonstrate that outcome computation receives input from performance monitoring processes that are more complex than mere error detection.

Recent models of reinforcement learning and the MFC (Holroyd and Coles, 2002; Alexander and Brown, 2011; Silvetti et al., 2011) assume that the Ne/ERN directly or indirectly reflects the generation of a negative prediction error and, thus, an update of expected outcome. Although prediction errors are sensitive to both the probability and the value of possible actions, these models were mainly used to account for effects of error probability on the Ne/ERN (i.e., the inverse relation between Ne/ERN and error likelihood) (Gehring et al., 1993). In the present study, however, the pattern of Ne/ERN amplitudes was unaffected by relative frequencies of error types. NFEs were consistently more frequent than FEs and yet showed larger Ne/ERNs when associated with larger monetary loss. Furthermore, the amount of monetary loss had no effect on the relative frequency of each error type across groups. It seems that, in the present paradigm, Ne/ERN amplitude varied more strongly according to error value than according to error probability (see also Maier et al., 2012), possibly reflecting the increased salience of value resulting from the manipulation of monetary loss.

The question arises how information about the error type can be available immediately after the response. An intuitive solution would be a retroactive evaluation process that operates after the detection of an error. This process could evaluate whether the just executed error response corresponds to an FE by comparing the response with a representation of the flanker in working memory. Although such a process is not impossible, it seems rather implausible given the short period between the response and the onset of the Ne/ERN. Instead, we propose a proactive evaluation process that anticipates the error type before a response is executed. Such a process could operate in one or both of two ways:

  1. The evaluation process could monitor possible error sources to anticipate the probability that a given error corresponds to an FE, pFE, or NFE (1 − pFE). Using these probabilities, error detection would allow for an update of expected outcome according to pFE × VFE + (1 − pFE) × VNFE, with VFE and VNFE reflecting monetary loss associated with flanker and NFEs, respectively. Because FEs are more likely when attention is erroneously directed to the flankers, the state of selective attention could be a valid estimator of pFE. Such an account would imply a monitoring mechanism that learns to map specific error sources to action outcomes in the course of an experiment.

  2. The evaluation process could anticipate the outcomes of all possible responses given the stimulus (response–outcome relations) (Alexander and Brown, 2011). The occurrence of a specific response would allow for an update of expected outcome according to the respective response–outcome relation. Although such a mechanism is computationally expensive, it allows for a very parsimonious account of error detection and error type evaluation; both result implicitly as a byproduct of the representation of response–outcome relations. Indeed, the PRO model by Alexander and Brown (2011) implements such a mechanism and assumes that the context-dependent computation of response–outcome relations is a core function of the MFC.

The two possibilities are not mutually exclusive, and further research is necessary to determine which of these two mechanisms is actually involved. A viable approach to test the idea of an error source monitor might be to ask whether Ne/ERN differences across error types are linked to specific error sources, such as impaired selective attention. First evidence for this can be derived from a recent study in which we used multinomial modeling to determine the proportion of FEs that were the result of attention errors (Maier et al., 2012). We found larger Ne/ERN amplitudes on FEs when the estimated proportion of attention errors among FEs was increased. This could reflect that impaired selective attention is used to anticipate that an error will be an FE.

Together, we have shown that the Ne/ERN is sensitive to the amount of monetary loss, even when updating the expected outcome requires an evaluation of error type. Our results add to the literature showing that the MFC is crucially involved in the encoding of action outcomes (Rushworth and Behrens, 2008; Rushworth et al., 2012) and demonstrate that updating expected outcome is not only guided by an evaluation of environmental cues but also by a fast and yet complex evaluation of own actions.

Footnotes

This work was supported by the Deutsche Forschungsgemeinschaft Young Researchers Scholarship MA 4864/1-1 to M.E.M. We thank Barbara Zarrillo for assistance in conducting the experiment and Giuseppe di Pellegrino for helpful comments on an earlier version of this manuscript.

The authors declare no competing financial interests.

References

  1. Alexander WH, Brown JW. Medial prefrontal cortex as an action-outcome predictor. Nat Neurosci. 2011;14:1338–1344. doi: 10.1038/nn.2921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Amiez C, Joseph JP, Procyk E. Anterior cingulate error-related activity is modulated by predicted reward. Eur J Neurosci. 2005;21:3447–3452. doi: 10.1111/j.1460-9568.2005.04170.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Amiez C, Joseph JP, Procyk E. Reward encoding in the monkey anterior cingulate cortex. Cereb Cortex. 2006;16:1040–1055. doi: 10.1093/cercor/bhj046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 2004;134:9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
  5. Eriksen BA, Eriksen CW. Effects of noise letters upon the identification of a target letter in a nonsearch task. Percept Psychophys. 1974;16:143–149. doi: 10.3758/BF03203267. [DOI] [Google Scholar]
  6. Falkenstein M, Hohnsbein J, Hoormann J, Blanke L. Effects of errors in choice reaction tasks on the ERP under focused and divided attention. In: Brunia CHM, Gaillard AWK, Kok A, editors. Psychophysiological brain research. Vol. 1. Tilburg, The Netherlands: UP; 1990. pp. 192–195. [Google Scholar]
  7. Ganushchak LY, Schiller NO. Motivation and semantic context affect brain error-monitoring activity: an event-related brain potentials study. Neuroimage. 2008;39:395–405. doi: 10.1016/j.neuroimage.2007.09.001. [DOI] [PubMed] [Google Scholar]
  8. Gehring WJ, Goss B, Coles MGH, Meyer DE, Donchin E. A neural system for error detection and compensation. Psychol Sci. 1993;4:385–390. doi: 10.1111/j.1467-9280.1993.tb00586.x. [DOI] [Google Scholar]
  9. Gratton G, Coles MG, Donchin E. A new method for off-line removal of ocular artifact. Electroencephalogr Clin Neurophysiol. 1983;55:468–484. doi: 10.1016/0013-4694(83)90135-9. [DOI] [PubMed] [Google Scholar]
  10. Hajcak G, Moser JS, Yeung N, Simons RF. On the ERN and the significance of errors. Psychophysiology. 2005;42:151–160. doi: 10.1111/j.1469-8986.2005.00270.x. [DOI] [PubMed] [Google Scholar]
  11. Holroyd CB, Coles MG. The neural basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. Psychol Rev. 2002;109:679–709. doi: 10.1037/0033-295X.109.4.679. [DOI] [PubMed] [Google Scholar]
  12. Maier ME, Yeung N, Steinhauser M. Error-related brain activity and adjustments of selective attention following errors. Neuroimage. 2011;56:2339–2347. doi: 10.1016/j.neuroimage.2011.03.083. [DOI] [PubMed] [Google Scholar]
  13. Maier ME, di Pellegrino G, Steinhauser M. Enhanced error-related negativity on flanker errors: error expectancy or error significance? Psychophysiology. 2012;49:899–908. doi: 10.1111/j.1469-8986.2012.01373.x. [DOI] [PubMed] [Google Scholar]
  14. Maier M, Steinhauser M, Hübner R. Is the error-related negativity amplitude related to error detectability? Evidence of effects from different error types. J Cogn Neurosci. 2008;20:2263–2273. doi: 10.1162/jocn.2008.20159. [DOI] [PubMed] [Google Scholar]
  15. Matsumoto K, Suzuki W, Tanaka K. Neural correlates of goal-based motor selection in the prefrontal cortex. Science. 2003;301:229–232. doi: 10.1126/science.1084204. [DOI] [PubMed] [Google Scholar]
  16. Matsumoto M, Matsumoto K, Abe H, Tanaka K. Medial prefrontal cell activity signaling prediction errors of action values. Nat Neurosci. 2007;10:647–656. doi: 10.1038/nn1890. [DOI] [PubMed] [Google Scholar]
  17. Potts GF. Impact of reward and punishment motivation on behavior monitoring as indexed by the error-related negativity. Int J Psychophysiol. 2011;81:324–331. doi: 10.1016/j.ijpsycho.2011.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ridderinkhof KR, Ullsperger M, Crone EA, Nieuwenhuis S. The role of the medial frontal cortex in cognitive control. Science. 2004;306:443–447. doi: 10.1126/science.1100301. [DOI] [PubMed] [Google Scholar]
  19. Rushworth MF, Behrens TE. Choice, uncertainty and value in prefrontal and cingulate cortex. Nat Neurosci. 2008;11:389–397. doi: 10.1038/nn2066. [DOI] [PubMed] [Google Scholar]
  20. Rushworth MFS, Kolling N, Sallet J, Mars RB. Valuation and decision-making in frontal cortex: one or many serial or parallel systems? Curr Opin Neurobiol. 2012;22:946–955. doi: 10.1016/j.conb.2012.04.011. [DOI] [PubMed] [Google Scholar]
  21. Seo H, Lee D. Temporal filtering of reward signals in the dorsal anterior cingulate cortex during a mixed-strategy game. J Neurosci. 2007;27:8366–8377. doi: 10.1523/JNEUROSCI.2369-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Silvetti M, Seurinck R, Verguts T. Value and prediction error in medial frontal cortex: integrating the single-unit and systems levels of analysis. Front Hum Neurosci. 2011;5:75. doi: 10.3389/fnhum.2011.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Steinhauser M, Yeung N. Error awareness as evidence accumulation: effects of speed-accuracy trade-off on error signaling. Front Hum Neurosci. 2012;6:240. doi: 10.3389/fnhum.2012.00240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Sutton RS, Barto AG. Reinforcement learning: an introduction. Cambridge, MA: Massachusetts Institute of Technology; 1998. [Google Scholar]
  25. van Driel J, Ridderinkhof KR, Cohen MX. Not all errors are alike: θ and α EEG dynamics relate to differences in error-processing dynamics. J Neurosci. 2012;32:16795–16806. doi: 10.1523/JNEUROSCI.0802-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Winer BJ, Brown DR, Michels KM. Statistical principles in experimental design. London: McGraw-Hill; 1991. [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES