Abstract
Do individual differences in the brain mechanisms for arithmetic underlie variability in high school mathematical competence? Using functional magnetic resonance imaging, we correlated brain responses to single digit calculation with standard scores on the Preliminary Scholastic Aptitude Test (PSAT) math subtest in high school seniors. PSAT math scores, while controlling for PSAT Critical Reading scores, correlated positively with calculation activation in the left supramarginal gyrus and bilateral anterior cingulate cortex, brain regions known to be engaged during arithmetic fact retrieval. At the same time, greater activation in the right intraparietal sulcus during calculation, a region established to be involved in numerical quantity processing, was related to lower PSAT math scores. These data reveal that the relative engagement of brain mechanisms associated with procedural versus memory-based calculation of single-digit arithmetic problems is related to high school level mathematical competence, highlighting the fundamental role that mental arithmetic fluency plays in the acquisition of higher-level mathematical competence.
Introduction
School-entry math skills are a stronger predictor of later academic achievement than early reading or socio-emotional skills (Duncan et al., 2007), and low mathematical competence is associated with lower indices of life success (Parsons and Bynner, 2005). Improvements in mathematical competence are related to growth of gross domestic product (Organisation for Economic Co-operation and Development, 2010, p 17) and are identified as essential for boosting U.S. global competitiveness (National Academies, 2007, p 5). These factors demonstrate the fundamental significance of mathematical competence and highlight the importance of identifying sources of its variability.
A potential source of individual differences in math competence is the neural architecture supporting the performance of simple arithmetic problem solving. Arithmetic fluency, the speed and efficiency with which correct solutions to numerical computations are generated, is thought to represent a scaffold upon which higher-level mathematical skills are built. Initially, students rely on procedural strategies, such as counting aloud, finger counting, or decomposition to solve calculations. These explicit procedures are gradually replaced by more efficient strategies, such as the retrieval of solutions from memory (Ashcraft, 1982). This shift toward memory-based calculation is a hallmark of successful arithmetic development. Indeed, children with mathematical learning difficulties exhibit immature procedural strategies and poor math fact performance (Mazzocco et al., 2008) long after their typically developing peers begin using fact retrieval (Geary, 1993). Thus, it appears that early arithmetic abilities support the acquisition of higher mathematical competence, yet little is known about whether individual differences in arithmetic fluency continue to scaffold broader mathematical competence throughout secondary school and, if so, what neural mechanisms underlie this relationship.
By investigating whether the function of brain circuits underlying simple arithmetic problem solving are predictive of variability in mathematical achievement, it is possible to better understand the mechanisms by which the proposed scaffolding between arithmetic fluency and higher-level skills might occur. A deeper understanding of such mechanisms will support the development of educational interventions that optimally exploit the neurocognitive architectures supporting math achievement and, at the very least, provide some explanation for individual differences in mathematics achievement outcomes.
In the present study, we adopted an educational neuroscience approach (Carew and Magsamen, 2010) using functional magnetic resonance imaging (fMRI) to investigate the relationship between brain activation during single-digit arithmetic and mathematical competence as measured by the Preliminary Scholastic Aptitude Test (PSAT) Math subtest, a nationally administered exam designed to predict college readiness.
If arithmetic fluency serves as a scaffold for mathematical competence, individual differences in performance on the PSAT Math test should be associated with variation in the brain mechanisms associated with retrieval versus procedural calculation: the left inferior parietal lobe (LIP) and bilateral intraparietal sulcus (IPS), respectively (Grabner et al., 2007; Grabner et al., 2009). We predict that individuals with higher PSAT Math scores will demonstrate increased activation of LIP regions during single digit calculations compared to individuals with lower PSAT Math scores, who are expected to exhibit greater activation of the IPS. We predict that such individual differences in brain activation patterns will be specific to PSAT Math and thus unrelated to PSAT Critical Reading scores.
Materials and Methods
Participants
Participants were drawn from a larger, longitudinal study described elsewhere in more detail (Mazzocco and Myers, 2003). When the cohort reached 12th grade, we recruited a sample of these students representative of those with consistently deficient, low average, average, or above average levels of mathematics achievement from kindergarten to grade 9. A total of 43 participants took part in the fMRI experiment. From these participants we requested and received authorization to obtain their official PSAT score report from their high school registrar. Of those participants whose data were not excluded due to excess motion (3 mm total motion in a given run), 33 students sat for the PSAT in grade 10. Thus, a total of 33 participants was included in the final analysis (14 females; mean age: 17 years, 11.5 months).
Tasks
Tasks were presented in separate runs during the scanning session.
Arithmetic verification.
Single digit arithmetic is an elementary mathematical ability, with improvements in efficiency already evident between first and second grade (Geary et al., 1991). Accordingly, it represents an ideal task with which to investigate the neural mechanisms of elementary arithmetic fluency and how these mechanisms relate to individual differences in comprehensive mathematical achievement at the end of secondary education.
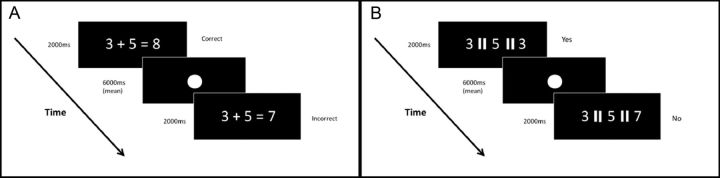
Participants were presented with a series of single digit addition and subtraction equations in the standard a +/− b = c format (Fig. 1A), the solution to which was either correct or incorrect (e.g., 5 + 3 = 8 or 5 + 3 = 7). In the construction of arithmetic trials, all single digit numbers, with the exception of 1, were used as either the left or right operand across the paradigm, and solutions were always a single digit operand. Incorrect solutions deviated from the correct solution by either +1 or −1, and participants were required to indicate via button press whether the presented solution was correct or incorrect. This task, modeled on the task reported by Rivera et al. (2005), had a total of 40 trials presented in a single run comprising 20 subtraction and 20 addition trials. Subtraction and addition trials were intermixed in a pseudorandom order so that the same trial type never occurred for more than three consecutive trials. Each trial was presented for 2 s, followed by a fixation screen comprising a single white dot at the center of the screen (font size, 60). Poststimulus fixation duration was 6 s on average but was varied between trials to improve deconvolution of the hemodynamic response function (HRF). Thus, interstimulus intervals (ISI) could be 4, 5, 6, 7, or 8 s, with a mean ISI across the run of 6 s. Varying the ISI in this way ensures that stimulus onset is not locked with the time to repeat (TR), as trial duration is not consistently an integer multiple of the TR and therefore allows for oversampling of the HRF. ISI length and trial type (subtraction correct and incorrect, addition correct and incorrect) were balanced such that no ISI length was more frequently associated with a given trial type.
Figure 1.
Arithmetic verification (A) and digit matching (B) example stimuli and paradigm timing.
Digit matching.
Participants were presented with three single digits separated by an equal sign (=) and rotated 90° into a vertical rather than horizontal orientation (Fig. 1B). Participants were required to indicate via dual button press whether or not the third digit was identical to either of the preceding digits. Each trial was presented for 2 s, followed by a fixation screen comprising a single white dot at the center of the screen (font size, 60). Stimulus duration and spacing were identical to that for the Arithmetic Verification task described above.
Non-symbolic number comparison.
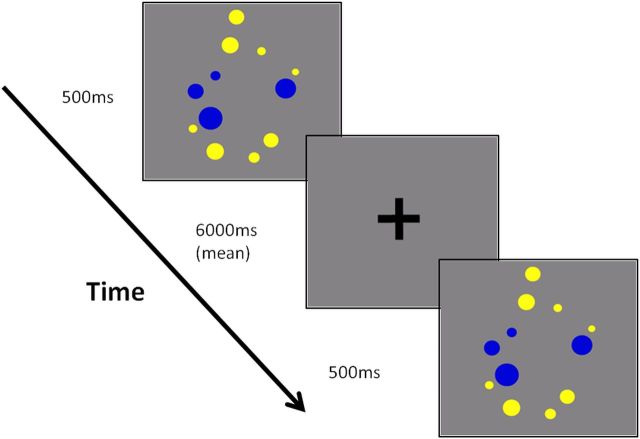
The non-symbolic comparison paradigm used in the present study was based on that reported by Halberda et al. (2008). Participants were presented with a single array of blue and yellow dots in intermixed locations (Fig. 2) and required to select, via button press, whether there were more blue or more yellow dots in the array. Trials varied according to the ratio between the dot sets (ratio calculated as the larger number divided by the smaller number, so that in a trial with 17 yellow dots and 13 blue dots, the ratio was 1.308). A total of 160 trials was presented across two runs, with the number of dots per color ranging from 5 to 21, and ratios ranging from 1.182 to 3.6. Each trial was presented for 500 ms. In half the trials the yellow dots were more numerous, and in the other half the blue dots were more numerous. Trial presentation order was randomized with respect to ratio, but fixed across participants. Poststimulus fixation duration was 6 s on average but was varied between trials to improve deconvolution of the HRF. Thus, an ISI could be 4, 5, 6, 7, or 8 s, with a mean ISI across the run of 6 s. ISI length and trial type (ratio) were balanced such that no ISI length was more frequently associated with a given trial type. Following the method described by Halberda et al. (2008) to limit the influence of non-numerical continuous physical variables, the following controls were put in place. For each ratio, half the trials were “dot-size controlled,” meaning that the size of the average blue dot was equal to the size of the average yellow dot. On these trials, the set with more dots necessarily also had a larger total area on screen. The other half of trials were “area controlled,” meaning that the total number of pixels for blue and yellow dots was equal, resulting in an equivalent total surface area for both sets of dots. Therefore, in this condition the more numerous set therefore had a smaller average dot size.
Figure 2.
Nonsymbolic numerical magnitude comparison example stimuli and paradigm timing.
PSAT.
As our measure of mathematical competence, we used standard scores from the PSAT Math subtest sat during grade 10. The PSAT math subtest is part of a nationally administered test taken by over 3.5 million high school students in the U.S.A. each year as reported by “CollegeBoard.” It is designed to reliably predict college entrance exam scores and serves as the qualifying test for the U.S. Merit-Based Scholarship Program, and it is thus also known as the “National Merit Scholarship Qualifying Test” (PSAT/NMSQT). Therefore, performance on the PSAT is profoundly relevant to higher education success among students in the U.S. Most individuals who take the PSAT are tenth graders, and in most states (including Maryland, where most of the participants resided) tenth graders are enrolled in a mathematics course. Beginning in Grade 11, some students choose not to pursue elective mathematics coursework (Updegraff et al., 1996). Thus, Grade 10 PSAT Math was chosen as a measure of broad achievement outcomes at the latest school grade during which all participants are likely to be receiving ongoing math instruction.
The PSAT Math contains 38 items, including word problems, geometry, algebraic equations, and complex (no single-digit simple calculations) arithmetic, and it therefore represents a broad test of mathematical competence of significant importance to an individual's academic success. As control measure for broad academic achievement, we used standard scores from the Grade 10 PSAT Critical Reading subtest. The PSAT Critical Reading includes reading comprehension questions about full-length and paragraph-length passages, such as speculating on the origin of the passage, as well as questions requiring students to fill in missing words from a range of sentences.
fMRI acquisition parameters
All MR imaging was acquired with a 3T Phillips MRI scanner using an 8-channel head coil with parallel imaging capability. Using multislice 2D SENSE T2* gradient-echo, echo planar imaging (EPI) pulse sequence, functional images were obtained in the axial plane. Higher order shimming was applied to the static magnetic field (B0). The EPI parameters were as follows: echo time, 30 ms; TR, 2000 ms; flip angle, 75°; acquisition matrix, 80 × 80 voxels; field of view (FOV), 240 mm; SENSE factor of 2. This protocol acquired 34 axial brain slices per TR (3 mm thick slices with 1 mm slice gap) and a time course of 176 temporal whole brain image volumes after discarding the first five volumes to ensure steady state. Anatomical scan parameters were performed using an 8-channel head coil, 240 cm FOV, and a 1 mm isotropic MP-RAGE (magnetization-prepared rapid acquisition with gradient echo), which takes 6 min with SENSE factor 2. Axial T1-weighted FSPGR (TR/TE, 215/12), axial diffusion-weighted (10,000/13), and axial T2-weighted FRFSE with fat saturation (3440/68) fast spin echo scans were obtained through the brain.
fMRI analyses
Structural and functional images were analyzed using Brain Voyager QX 2.4.1 (Brain Innovation). Any runs in which head motion exceeded a total of 3 mm were excluded, which resulted in the exclusion of a total of four runs across all participants. All participants were presented with and completed a single run of arithmetic verification, a single run of digit matching, and at least one run of nonsymbolic number comparison. The remaining functional images were corrected for differences in slice time acquisition, head motion, and low-frequency drifts in signal intensity (high-pass filtering). In addition, functional images were spatially smoothed with a 6 mm full width at half maximum Gaussian smoothing kernel. Following initial automatic alignment, the alignment of functional images to the high resolution T1 structural images was manually fine-tuned. The realigned functional dataset was then transformed into Talairach space (Talairach and Tournoux, 1988). A two gamma hemodynamic response function was used to model the expected BOLD signal (Friston et al., 1998).
Statistical maps were corrected for multiple comparisons using false discovery rate (FDR) in the case of whole brain, first level contrasts (e.g., arithmetic verification versus digit matching; see below, this section and Results). In the case of second level covariate analyses (e.g., calculation versus digit matching correlated with PSAT scores), where no voxels survived correction using FDR, cluster-level correction (Forman et al., 1995; Goebel et al., 2006) was used to correct for multiple comparisons. In this method, an initial voxel level (uncorrected) threshold is set. Then, thresholded maps are submitted to a whole-slab correction criterion based on the estimate of the map's spatial smoothness and on an iterative procedure (Monte Carlo simulation) for estimating cluster-level, false-positive rates. After 1000 iterations, the minimum cluster size that yielded a cluster level false-positive rate (α) of 0.05(0.5%) was used to threshold the statistical maps. Put another way, this method calculates the size that a cluster would need to be (the cluster threshold) to survive a correction for multiple comparisons at a given statistical level. Only activations whose size meets or exceeds the cluster threshold are allowed to remain in the statistical maps. Statistical maps resulting from first level contrasts (i.e., calculation > digit matching) were thresholded at FDR corrected p < 0.05. Maps resulting from covariate analyses due to the more complex nature of the analysis were thresholded at p < 0.005 uncorrected and then submitted to cluster-level correction as described above, yielding clusters whose corrected significance level is p < 0.05.
The analysis of nonsymbolic numerical comparison data were carried out at the region of interest (ROI) level. ROIs were defined from the correlation of brain activation during “arithmetic minus digit matching” with PSAT Math scores residualized for PSAT Critical Reading. We performed an ROI GLM in each region, testing for a parametric effect of ratio against baseline. The parametric regressor was defined by assigning as a weight to each correctly solved trial the ratio between the two dot sets (larger set divided by smaller set). In other words, this analysis tested whether a significant relationship between numerical ratio and brain activation (i.e., a positive correlation between ratio and activation) existed in the regions identified by the correlation between arithmetic verification-related activation and PSAT Math scores.
Results
Behavioral data
The two primary behavioral variables of interest from the fMRI tasks were reaction time (milliseconds) for correct responses and percent accuracy across all trials. Paired t tests were used to compare arithmetic verification and digit-matching performance. Reaction time for correctly answered arithmetic verification items (mean = 1540.57; SD = 398.61; range = 887.86–2922.15) was significantly longer than reaction time for digit-matching items (mean = 1093.14; SD = 314.96; range = 683.04–2542.44), t(32) = 10.11; p < 0.001.
Arithmetic verification performance was also significantly more accurate (mean = 96.21; SD = 2.43; range = 87.50–100) than digit matching (mean = 92.12; SD = 2.35; range = 87.50–95), t(32) = 6.89; p < 0.001. Despite this difference, the mean accuracy was high for both tasks.
The sample mean PSAT standard score (possible range = 20–80) was 49.15 (SD = 10.14; range = 35–72) for Math and 45.7 (SD = 9.412; range = 29–68) for Critical Reading. The national norms (average scores) based on over 1.1 million tenth graders who completed the PSAT in 2008, the same year as our sample, were, 44.3 (SD = 11.1) for PSAT Math and 41.9 (SD = 11.4) for PSAT Critical Reading (CollegeBoard, 2008). One-sample t tests, comparing standard scores in the current sample to the national average for the respective test, revealed that the mean PSAT Math score in the current sample was significantly higher than the national average for that year (t(32) = 2.75; p < 0.05), as was the PSAT Critical Reading mean score (t(32) = 2.32; p < 0.05). The current sample was representative of the normative variation, however, because the range of scores observed in the current sample spanned >3 SD, and their means fell within 1 standard deviation of the national average score. Thus, while on average the scores from our sample were higher than the national norm, the scores were within the range of the national norms. Furthermore, the standard scores for PSAT math were normally distributed in our sample (Shapiro–Wilk, p = 0.074), as were the standard scores for PSAT Critical Reading (Shapiro–Wilk; p = 0.622).
To estimate behavioral performance specifically related to arithmetic processing, we calculated difference scores by subtracting accuracy or reaction time for digit matching from accuracy or reaction time for arithmetic verification, respectively (mean reaction time difference = 411.42; SD = 233.68; range = −2.39–953.51; Shapiro–Wilk, p = 0.772; mean accuracy difference = 411.42; SD = 3.41; range = −7.5–10.00; Shapiro–Wilk, p = 0.001)). The difference scores served to isolate variance in performance specific to calculation and were thus closely aligned with the brain-imaging data described subsequently.
Relationship to PSAT scores
Bivariate correlation analyses revealed no significant relationship between accuracy difference score and PSAT Math (r(31) = −0.11, p > 0.05) or PSAT Critical Reading (r(31) = −0.03) p > 0.05. By contrast, reaction time difference was negatively correlated with PSAT Math (r(31) = −0.35; p < 0.05), but for PSAT Critical Reading the correlation was not significant (r(31) = −0.29; p > 0.05). However, the relationship between PSAT Math and RT difference was no longer significant when controlling for PSAT Critical Reading (r(30) = −0.25; p > 0.05). These results suggest that the reaction time difference between arithmetic and digit matching captures variance associated with cognitive processes common to PSAT Math and PSAT Critical Reading, rather than processes specific to arithmetic. Therefore, the relationship between calculation reaction time and PSAT Math does not provide insight into any cognitive mechanisms specific to math competence, but instead it reflects cognitive mechanisms general to academic achievement. Indeed, from these behavioral data alone it could be concluded that there is no domain-specific relationship between performance on single-digit arithmetic verification and individual differences on the PSAT Math test.
fMRI data
Calculation versus digit matching
To confirm that the current arithmetic verification task activated typical calculation brain networks, we conducted whole brain random effects General Linear Model testing for regions showing greater activation for calculation relative to digit matching (incorrect trials were modeled as separate predictors for both conditions and excluded from further analysis). This analysis revealed a number of regions, including the left intraparietal sulcus/superior parietal lobe, bilateral insula, and bilateral superior frontal gyri (p < 0.05, FDR corrected; Table 1), many of which are commonly found to be active during arithmetic verification relative to control tasks (Rueckert et al., 1996; Menon et al., 2000).
Table 1.
Significant regions of difference resulting from contrast of calculation and digit matching
| Contrast | Region | Peak Tal coordinate (x, y, z) | Cluster size (voxels) | Average t-statistic |
|---|---|---|---|---|
| Calculation > Control | Right precentral Gyrus/inferior frontal gyrus | 50, 4, 34 | 1923 | 4.19 |
| Right insula | 34, 19, 5 | 1917 | 4.79 | |
| Left insula | −31, 22, 6 | 929 | 4.09 | |
| Bilateral medial occipital gyrus | 3, −67, 2 | 2780 | 3.93 | |
| Bilateral thalamus/medial dorsal nucleus | −2, −14, 11 | 2290 | 4.17 | |
| Bilateral superior frontal Gyrus/dorsal anterior cingulate cortex | −2, 4, 52 | 8878 | 4.50 | |
| Left superior frontal gyrus | −30, −8, 64 | 506 | 3.88 | |
| Left intraparietal sulcus/ superior parietal | −32, −62, 40 | 2569 | 4.01 | |
| Left precentral gyrus/Inferior frontal gyrus | −49, 3, 30 | 6594 | 4.31 |
PSAT correlations
To create a measure of math competence controlling for the variance related to reading ability (a nonmathematical academic domain), we computed a linear regression with PSAT Math as the dependent variable and PSAT Critical Reading as the independent variable to derive residualized PSAT Math scores. We entered these residualized PSAT Math scores (mean = −3.03E−07; SD = 8.7; range = −15.42–27.65; Shapiro–Wilk, p = 0.193) into a whole brain correlation analysis, testing for an association between the residualized PSAT Math scores and calculation-specific brain activation (i.e., residualized PSAT Math scores were correlated with the difference in brain activation between arithmetic verification and digit matching).
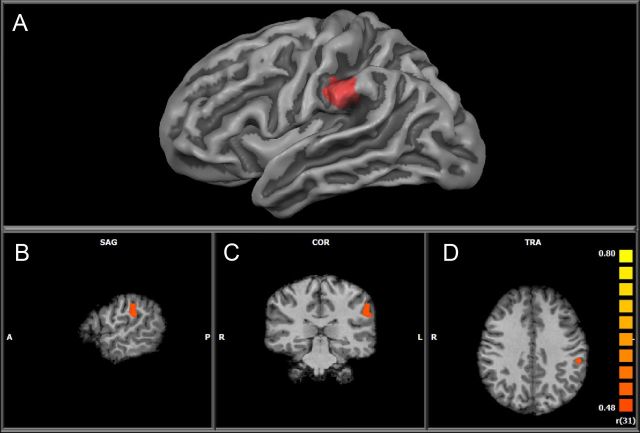
This analysis revealed positive correlations between PSAT Math and individual differences in the brain activation associated with arithmetic verification (arithmetic verification > digit matching) in the left supramarginal gyrus (Talairach coordinates (Tal): − 55, − 30, 30; k = 959; Fig. 3) and the anterior cingulate gyrus (Tal: 1, 23, 21, k = 1090). In other words, greater activation of these brain regions during calculation relative to digit matching was associated with higher PSAT Math scores.
Figure 3.
Positive correlation between calculation activation and PSAT Math standard scores in the left SMG. A, Correlation overlaid on an inflated cortical surface constructed from the average of all participants. B–D, Correlation shown in volume space (radiological convention, left hemisphere shown on right and vice versa) in sagittal (SAG) (B), coronal (COR) (C), and axial (TRA) (D) orientation, respectively.
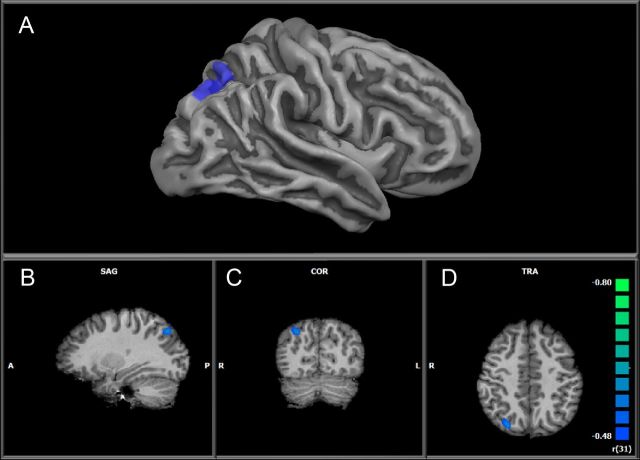
In addition, a negative correlation was revealed between PSAT Math scores and arithmetic activation in the right intraparietal sulcus (Tal: 29, −71, 41; k = 583) (Fig. 4). Specifically, those individuals with lower PSAT Math scores exhibited greater activation of the right IPS during single digit arithmetic relative to digit matching.
Figure 4.
Negative correlation between calculation activation and PSAT Math standard scores in the right IPS. A, Correlation overlaid on an inflated cortical surface constructed from the average of all participants. B–D, Correlation shown in volume space (radiological convention, left hemisphere shown on right and vice versa) in sagittal (SAG) (B), coronal (COR) (C), and axial (TRA) (D) orientation, respectively.
Several studies have shown that regions of the left inferior parietal lobe, including and proximal to the left supramarginal gyrus (SMG) as well as the anterior cingulate cortex (ACC), are associated with arithmetic fact retrieval (Delazer et al., 2005; Grabner et al., 2007; Grabner et al., 2009), while the right IPS has been widely implicated in the representation and processing of numerical magnitude information (Dehaene et al., 2003; Cohen Kadosh et al., 2008) and is associated with procedural problem solving strategies (Delazer, 2003; Delazer et al., 2005). Thus, the current results suggest that individuals with higher PSAT Math standard scores are engaging neural mechanisms associated with memory retrieval to solve single-digit equations, while those with lower scores are engaging systems associated with processing numerical quantity, and likely relying on procedural computations.
To further empirically constrain our interpretation of this finding, we tested the activation of the above regions in a nonsymbolic numerical comparison task completed by the same participants during the same scanning session. Participants were presented with an array of blue and yellow dots and asked to decide whether there were more blue or yellow dots. The numerical ratio between the blue and yellow dot sets was parametrically varied, allowing us to test for the “numerical ratio effect” reliably observed at both the behavioral (Moyer and Landauer, 1967) and brain levels (Pinel et al., 2001; Holloway et al., 2010) and used as a marker of basic numerical magnitude processing. This analysis revealed that activation strength in the right IPS region, whose activity during mental arithmetic negatively correlated with PSAT Math scores, was parametrically modulated by numerical ratio (t(32) = 2.27; p = 0.03; see Materials and Methods for details). Specifically, this region showed greater activation for trials in which the number of blue versus yellow dots was harder to discriminate due to smaller ratio. By contrast, no significant parametric ratio effect was observed in either the anterior cingulate (t(32) = 0.67; p = 0.051) or the left SMG (t(32) = 0.13; p = 0.89), suggesting that these regions were not involved in the processing of numerical magnitude information (although it should be noted that the parametric effect of ratio approached significance in the ACC). These data suggest that the brain circuitry engaged by individuals with lower PSAT scores during single-digit arithmetic is also engaged during basic quantity processing, while brain mechanisms engaged by individuals with higher PSAT Math scores are not. These findings bolster the interpretation that the continued reliance on quantity/procedural mechanisms to solve arithmetic problems is associated with lower math competence even into high school.
Discussion
Summary and interpretation
The present findings reveal that during single-digit arithmetic computations, individuals with higher standardized scores on the PSAT Math test engage calculation brain mechanisms associated with arithmetic fact retrieval in the left SMG and bilateral ACC to a greater extent than individuals with relatively lower PSAT Math scores, who activate quantity-processing mechanisms in the right IPS.
Each of these regions has been previously associated with numerical and mathematical processing. Specifically, the left SMG has been associated with age-related increases in activation during single-digit arithmetic verification (Rivera et al., 2005), and several studies have shown that regions of the left-inferior parietal lobe, including and proximal to the left SMG, are associated with arithmetic fact retrieval relative to procedural calculations (Delazer et al., 2005; Grabner et al., 2007; Grabner et al., 2009).
In addition to its activation during arithmetic retrieval, previous studies have reported involvement of the SMG in the subjective perception of timing (Wiener et al., 2010a), implicit timing mechanisms (Wiener et al., 2010b), and phonological processing during reading (Church et al., 2011). Such findings could suggest a role for the left SMG in the processing of rhythmic, phonologically encoded arithmetic facts in memory (i.e., processing deeply encoded arithmetic facts as a type of rhyme). However, other studies point to a role for the SMG in the processing of semantic associations, both in the context of arithmetic (Grabner et al., 2012) and linguistic processing (Kim et al., 2011), suggesting a more complex and abstract function underlying SMG activity. Thus, SMG's involvement in arithmetic fact retrieval may represent a more “mature” calculation mechanism comprising semantic memory search processes that rely on phonological, timing, and semantic processing mechanisms. However, a great deal of future research is required to fully explicate its precise function.
Likewise, the ACC has previously shown greater activation during arithmetic retrieval relative to number matching and during trained versus novel arithmetic problems (Delazer et al., 2003). This region has a well documented role in conflict-monitoring, and specifically in the top-down regulation of cognitive control (Botvinick et al., 2004), suggesting that the region may play a role in modulating the response to incorrect equations.
By contrast, activation in the right IPS, found here to correlate negatively with PSAT Math scores, is frequently observed during the mental manipulation of numerical quantities in tasks such as numerical comparison (Dehaene et al., 2003; Cohen Kadosh et al., 2008). Indeed, in this study, unlike the ACC and left SMG, activation of the right IPS showed a parametric numerical ratio effect during nonsymbolic number comparison, suggesting that high school students with relatively lower mathematical competence appear to be engaging numerical quantity processing mechanisms to solve single digit calculations to a greater extent than their peers with relatively higher PSAT Math scores. It is possible that these individuals were not relying exclusively on magnitude processing mechanisms to solve the task, but may have developed additional alternative strategies not fully elucidated by the current data.
Consistent with the present findings are data from a recent study using multivoxel pattern analysis in which Cho et al. (2011) showed that activation patterns in brain regions, including the left SMG and right IPS, reliably distinguished between retrieval versus counting calculation strategies in 7–9 year olds. While those findings reveal a brain network related to arithmetic strategy use, the present data are the first to demonstrate that individual differences in the relative engagement of the nodes of that network are associated with performance on a high school mathematical competence test. Thus, we suggest that successful encoding of arithmetic facts contributes, in combination with other factors not investigated in the present study, to the successful acquisition of higher level mathematical competence affecting the ontogenetic construction of brain networks facilitating the learning of higher level mathematical skills.
Developmental scaffolding
The interpretation of the present results is supported by a large body of behavioral research showing that children typically undergo a process of development in arithmetic skill whereby simple calculations are initially computed through procedural strategies, but then gradually come to be solved by memory retrieval (Ashcraft, 1982; Geary et al., 1991). Children with mathematical learning difficulties fail to show this developmental shift (Geary, 1993), suggesting that arithmetic fluency plays a key role in the acquisition of higher math skills. The present data support such a link, providing the first neuroscientific evidence that the functional brain networks associated with arithmetic fluency are related to higher-level math skills. In contrast, behavioral performance measures did not reveal specific associations, thereby highlighting the value added by neuroimaging to our understanding of the cognitive foundations of mathematical competence.
The association between activation of the IPS and poorer math competence may seem counterintuitive, as previous behavioral evidence suggests that numerical magnitude processing serves as a foundation for the acquisition of early arithmetic skills (Halberda et al., 2008). Furthermore, neuroimaging data have revealed that in children with mathematical learning difficulties, the right IPS region thought to support numerical magnitude processing shows atypical responses during numerical magnitude processing (Price et al., 2007; Mussolin et al., 2010). Thus, the functional maturity of the neural substrates for numerical magnitude processing appears to serve as a foundation for early arithmetic learning. The present results, however, in concert with previous findings (De Smedt et al., 2011), demonstrate that while such quantity processing mechanisms may have an important role in the development of elementary arithmetic skills, individuals who continue to rely upon them into adolescence and beyond achieve poorer mathematical competence than their peers who do not. Migration away from quantity-based calculation strategies appears essential for the development of mathematical competence beyond simple arithmetic.
Alternative interpretations
It should be noted that the IPS is also known to be involved in visuospatial working memory, which in turn plays a role in arithmetic performance (Dumontheil and Klingberg, 2012), so the present results could reflect working memory rather than numerical magnitude processing mechanisms. However, arithmetic problem solving involves the mental manipulation of quantities for which both working memory and the engagement of quantity representations are required. Furthermore, the same IPS region found to correlate negatively with PSAT Math scores showed a parametric ratio effect during a nonsymbolic number comparison task that carried no working memory demands. Thus, it is unlikely that working memory can be the sole factor in explaining the present results.
A further constraint on the interpretation of the current data is that they are correlational, and thus it is impossible to draw resolute causal inferences. Since single-digit arithmetic is learned during the very first years of schooling and the PSAT is taken in the last years of high school, it seems logical that single-digit arithmetic skills and their associated neural mechanisms would exert an influence on the acquisition of high school level math skills as opposed to the reverse. However, the present data cannot rule out the possibility that those individuals who scored more highly on the PSAT Math spent more time engaged in practice activities involving mental calculation and thus developed more fluent mental arithmetic processing, which was reflected in the brain activation patterns reported above.
Conclusions and applications
A better understanding of the sources of variability in mathematical skills may inform educational approaches to improving math achievement. Although the present data do not allow us to speculate as to what pedagogical methods are best suited to facilitate the successful encoding of arithmetic facts into memory, they do have important educational implications. In 2005 the Fordham Foundation issued a critique on state mathematics standards (Klein et al., 2005) and reported that even the highest ranked American state curricula spend significantly less time on arithmetic than the “A+ countries” (Singapore, Japan, Korea, Hong Kong, Flemish Belgium, and the Czech Republic). From an educational perspective, our results provide the first neuroscientific evidence demonstrating the fundamental importance of fluency in basic mental arithmetic in the acquisition of college-level mathematical skills. Furthermore, they significantly extend our understanding of the relationship between simple arithmetic and higher level math competence beyond that revealed by behavioral data alone. Specifically, the relationship between PSAT Math and functional brain activation during single-digit arithmetic was significant even when controlling for PSAT Critical Reading, revealing neurocognitive mechanisms specific to PSAT Math not evident from reaction time analysis alone.
In conclusion, the present data are the first to demonstrate that brain mechanisms associated with elementary arithmetic skills are related to performance on a broad ranging, educationally relevant measure of math competence at the end of high school. Thus, the importance of early arithmetic skills for math competence is not only evident at a behavioral level. Their acquisition appears to impact the construction of neurobiological architectures across development, which may in turn support the acquisition of high school-level math skills that have significant consequences for progression into higher education. Finally, the present findings demonstrate how neuroimaging data can inform our understanding of educationally relevant issues and thus demonstrate the power of an educational neuroscience framework.
Footnotes
This research was supported by funding from the Canadian Institutes of Health Research (CIHR), The Natural Sciences and Engineering Research Council of Canada (NSERC), the Canada Research Chairs Program (CRC) to D.A., and Ontario Ministry of Research and Innovation (OMRI) Postdoctoral Fellowship to G.R.P. We thank Carolyn Ahart, who oversaw efforts to obtain the PSAT data, Kate Semeniak, for assistance with collection of behavioral data, and Bea Goffin, for proofreading the manuscript.
The authors declare no competing financial interests.
References
- Ashcraft MH. The development of mental arithmetic: a chronometric approach. Dev Rev. 1982;2:213–236. [Google Scholar]
- Botvinick MM, Cohen JD, Carter CS. Conflict monitoring and anterior cingulate cortex: an update. Trends Cogn Sci. 2004;8:539–546. doi: 10.1016/j.tics.2004.10.003. [DOI] [PubMed] [Google Scholar]
- Carew TJ, Magsamen SH. Neuroscience and education: an ideal partnership for producing evidence-based solutions to guide 21st century learning. Neuron. 2010;67:685–688. doi: 10.1016/j.neuron.2010.08.028. [DOI] [PubMed] [Google Scholar]
- Cho S, Ryali S, Geary DC, Menon V. How does a child solve 7+8? Decoding brain activity patterns associated with counting and retrieval strategies. Dev Sci. 2011;14:989–1001. doi: 10.1111/j.1467-7687.2011.01055.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church JA, Balota DA, Petersen SE, Schlaggar BL. Manipulation of length and lexicality localizes the functional neuroanatomy of phonological processing in adult readers. J Cogn Neurosci. 2011;23:1475–1493. doi: 10.1162/jocn.2010.21515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen Kadosh R, Lammertyn J, Izard V. Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog Neurobiol. 2008;84:132–147. doi: 10.1016/j.pneurobio.2007.11.001. [DOI] [PubMed] [Google Scholar]
- CollegeBoard. Understanding 2008 PSAT/NMSQT scores. New York: CollegeBoard; 2008. PSAT/NMSQT percentiles and mean scores. [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three Parietal Circuits for Number Processing. Cogn Neuropsychol. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Delazer M, Domahs F, Bartha L, Brenneis C, Lochy A, Trieb T, Benke T. Learning complex arithmetic–an fMRI study. Brain Res Cogn Brain Res. 2003;18:76–88. doi: 10.1016/j.cogbrainres.2003.09.005. [DOI] [PubMed] [Google Scholar]
- Delazer M, Ischebeck A, Domahs F, Zamarian L, Koppelstaetter F, Siedentopf CM, Kaufmann L, Benke T, Felber S. Learning by strategies and learning by drill–evidence from an fMRI study. Neuroimage. 2005;25:838–849. doi: 10.1016/j.neuroimage.2004.12.009. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Holloway ID, Ansari D. Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency. Neuroimage. 2011;57:771–781. doi: 10.1016/j.neuroimage.2010.12.037. [DOI] [PubMed] [Google Scholar]
- Dumontheil I, Klingberg T. Brain activity during a visuospatial working memory task predicts arithmetical performance 2 years later. Cereb Cortex. 2012;22:1078–1085. doi: 10.1093/cercor/bhr175. [DOI] [PubMed] [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, Pagani LS, Feinstein L, Engel M, Brooks-Gunn J, Sexton H, Duckworth K, Japel C. School readiness and later achievement. Dev Psychol. 2007;43:1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magn Reson Med. 1995;33:636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Fletcher P, Josephs O, Holmes A, Rugg MD, Turner R. Event-related fMRI: characterizing differential responses. Neuroimage. 1998;7:30–40. doi: 10.1006/nimg.1997.0306. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematical disabilities: cognitive, neuropsychological, and genetic components. Psychol Bull. 1993;114:345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC, Brown SC, Samaranayake VA. Cognitive addition: a short longitudinal study of strategy choice and speed-of-processing differences in normal and mathematically disabled children. Dev Psychol. 1991;27:787–797. [Google Scholar]
- Goebel R, Esposito F, Formisano E. Analysis of functional image analysis contest (FIAC) data with brainvoyager QX: From single-subject to cortically aligned group general linear model analysis and self-organizing group independent component analysis. Hum Brain Mapp. 2006;27:392–401. doi: 10.1002/hbm.20249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabner RH, Ansari D, Reishofer G, Stern E, Ebner F, Neuper C. Individual differences in mathematical competence predict parietal brain activation during mental calculation. Neuroimage. 2007;38:346–356. doi: 10.1016/j.neuroimage.2007.07.041. [DOI] [PubMed] [Google Scholar]
- Grabner RH, Ansari D, Koschutnig K, Reishofer G, Ebner F, Neuper C. To retrieve or to calculate? Left angular gyrus mediates the retrieval of arithmetic facts during problem solving. Neuropsychologia. 2009;47:604–608. doi: 10.1016/j.neuropsychologia.2008.10.013. [DOI] [PubMed] [Google Scholar]
- Grabner RH, Ansari D, Koschutnig K, Reishofer G, Ebner F. The function of the left angular gyrus in mental arithmetic: evidence from the associative confusion effect. Hum Brain Mapp. 2012 doi: 10.1002/hbm.21489. Advanced online publication. Retrieved July 17, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455:665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Price GR, Ansari D. Common and segregated neural pathways for the processing of symbolic and nonsymbolic numerical magnitude: An fMRI study. Neuroimage. 2010;49:1006–1017. doi: 10.1016/j.neuroimage.2009.07.071. [DOI] [PubMed] [Google Scholar]
- Kim KK, Karunanayaka P, Privitera MD, Holland SK, Szaflarski JP. Semantic association investigated with functional MRI and independent component analysis. Epilepsy Behav. 2011;20:613–622. doi: 10.1016/j.yebeh.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein D, Braams BJ, Parker T, Quirk W, Wilson WS. The state of math standards. Washington, DC: Fordham Foundation; 2005. [Google Scholar]
- Mazzocco MM, Myers GF. Complexities in identifying and defining mathematics learning disability in the primary school-age years. Ann Dyslexia. 2003;53:218–253. doi: 10.1007/s11881-003-0011-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MM, Devlin KT, McKenney SJ. Is it a fact? Timed arithmetic performance of children with mathematical learning disabilities (MLD) varies as a function of how MLD is defined. Dev Neuropsychol. 2008;33:318–344. doi: 10.1080/87565640801982403. [DOI] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Preschoolers' precision of the approximate number system predicts later school mathematics performance. PLoS One. 2011;6:e23749. doi: 10.1371/journal.pone.0023749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon V, Rivera SM, White CD, Glover GH, Reiss AL. Dissociating prefrontal and parietal cortex activation during arithmetic processing. Neuroimage. 2000;12:357–365. doi: 10.1006/nimg.2000.0613. [DOI] [PubMed] [Google Scholar]
- Moyer RS, Landauer TK. Time required for judgements of numerical inequality. Nature. 1967;215:1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- Mussolin C, De Volder A, Grandin C, Schlögel X, Nassogne MC, Noël MP. Neural correlates of symbolic number comparison in developmental dyscalculia. J Cogn Neurosci. 2010;22:860–874. doi: 10.1162/jocn.2009.21237. [DOI] [PubMed] [Google Scholar]
- National Academies. Rising above the gathering storm: energizing and employing America for a brighter economic future (Committee on Prospering in the Global Economy of the 21st Century and Committee on Science, Engineering and Public Policy, ed) Washington, DC: National Academy Press; 2007. [Google Scholar]
- Organisation for Economic Co-operation and Development. The high cost of low education performance: the long-run economic impact of improving PISA outcomes. Paris: OECD; 2010. [Google Scholar]
- Parsons S, Bynner J. Does numeracy matter more? London: National Research and Development Centre for Adult Literacy and Numeracy; 2005. [Google Scholar]
- Pinel P, Dehaene S, Rivière D, LeBihan D. Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage. 2001;14:1013–1026. doi: 10.1006/nimg.2001.0913. [DOI] [PubMed] [Google Scholar]
- Price GR, Holloway I, Räsänen P, Vesterinen M, Ansari D. Impaired parietal magnitude processing in developmental dyscalculia. Curr Biol. 2007;17:R1042–R1043. doi: 10.1016/j.cub.2007.10.013. [DOI] [PubMed] [Google Scholar]
- Rivera SM, Reiss AL, Eckert MA, Menon V. Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb Cortex. 2005;15:1779–1790. doi: 10.1093/cercor/bhi055. [DOI] [PubMed] [Google Scholar]
- Rueckert L, Lange N, Partiot A, Appollonio I, Litvan I, Le Bihan D, Grafman J. Visualizing cortical activation during mental calculation with functional MRI. Neuroimage. 1996;3:97–103. doi: 10.1006/nimg.1996.0011. [DOI] [PubMed] [Google Scholar]
- Talairach J, Tournoux P. Co-planar atlas of the human brain. New York: Thieme; 1988. [Google Scholar]
- Updegraff KA, Eccles JS, Barber BA, O'Brien KM. Course enrollment As self-regulatory behaviour: who takes optional high school math courses? Learn Indiv Diff. 1996;8:239–259. [Google Scholar]
- Wiener M, Hamilton R, Turkeltaub P, Matell MS, Coslett HB. Fast forward: supramarginal gyrus stimulation alters time measurement. J Cogn Neurosci. 2010a;22:23–31. doi: 10.1162/jocn.2009.21191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiener M, Turkeltaub PE, Coslett HB. Implicit timing activates the left inferior parietal cortex. Neuropsychologia. 2010b;48:3967–3971. doi: 10.1016/j.neuropsychologia.2010.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]