Abstract
Experiences can alter functional properties of neurons in primary sensory neocortex but it is poorly understood how stimulus–reward associations contribute to these changes. Using in vivo two-photon calcium imaging in mouse primary visual cortex (V1), we show that association of a directional visual stimulus with reward results in broadened orientation tuning and sharpened direction tuning in a stimulus-selective subpopulation of V1 neurons. Neurons with preferred orientations similar, but not identical to, the CS+ selectively increased their tuning curve bandwidth and thereby exhibited an increased response amplitude at the CS+ orientation. The increase in response amplitude was observed for a small range of orientations around the CS+ orientation. A nonuniform spatial distribution of reward effects across the cortical surface was observed, as the spatial distance between pairs of CS+ tuned neurons was reduced compared with pairs of CS− tuned neurons and pairs of control directions or orientations. These data show that, in primary visual cortex, formation of a stimulus–reward association results in selective alterations in stimulus-specific assemblies rather than population-wide effects.
Introduction
The classic concept of plasticity in primary sensory cortex holds that, after development, receptive fields and tuning to visual features (Hubel and Wiesel, 1959; Niell and Stryker, 2008) remain stable, unless the input pattern changes dramatically as in case of neural damage (Kaas et al., 1983, 1990; Keck et al., 2008), monocular deprivation (Dräger, 1978; Gordon and Stryker, 1996), or stripe rearing (Hirsch and Spinelli, 1970; Kreile et al., 2011). Recent work, however, suggests that even subtle paradigms such as repeated exposure and perceptual learning can evoke stimulus-specific experience-dependent plasticity in primary sensory neocortex during adulthood (Schoups et al., 2001; Ghose et al., 2002; Yang and Maunsell, 2004; Frenkel et al., 2006; Gilbert et al., 2009; Xu et al., 2012).
Lasting functional changes in mature visual cortex appear to depend on local plasticity in the V1 network (Hofer et al., 2006, 2009). Mechanistically, NMDA-receptor and endocannabinoid receptor activation, delivery of AMPA receptors to postsynaptic membranes, and changes in spine dynamics have been implicated in V1 experience-dependent plasticity, although in different forms (Sawtell et al., 2003; Frenkel et al., 2006; Keck et al., 2008; Liu et al., 2008; Hofer et al., 2009; Tropea et al., 2010).
As regards reward effects, intracranial electrical reinforcement can trigger plasticity of receptive fields in primary sensory neocortical neurons (Bao et al., 2001). Appetitive conditioning renders a subset of neurons sensitive to the timing of upcoming reward in rat primary visual cortex (Shuler and Bear, 2006), and has been associated with enhanced visual evoked potentials (Hernandez-Peon, 1961; Frankó et al., 2010) and lower detection thresholds for conditioned stimuli (Seitz et al., 2009). Different mechanisms have been suggested to underlie effects of reward on the visual cortex, depending either on mesencephalic dopaminergic efferents (Febvret et al., 1991; Bao et al., 2001; Müller and Huston, 2007; Rivera et al., 2008), cholinergic efferents (Gavornik et al., 2009), or cortical feedback loops (Pennartz, 1997; Pennartz et al., 2000; Roelfsema and van Ooyen, 2005; Roelfsema et al., 2010). Despite these efforts, it remains unknown how the acquisition of a reward association alters representations in neuronal assemblies in visual cortex for stimulus features that are predictive of reward.
Since Hebb (1949) postulated that sensory information is coded by cell-assemblies, it has thus far remained largely unclear what the nature of such assemblies might be, whether their associative plasticity is manifested in altered representations of stimuli and whether this plasticity can be triggered by appetitive reinforcement. Addressing these questions, we investigated the concept of modifiable cell assemblies by examining ensemble changes in V1 orientation tuning as a consequence of the formation of a behaviorally acquired stimulus–reward association. Whereas previous studies focused on population-wide changes in stimulus representations (Weinberger et al., 1993; Bao et al., 2001; Blake et al., 2006), we focused on modifications of tuning curves specifically in subsets of cells that preferentially respond to reward-predicting stimuli. Additionally, we provide evidence suggesting that the effects of reward-feedback are nonuniformly expressed across the spatial layout of direction-tuned cells in primary visual cortex.
Materials and Methods
Animals.
Experiments were done in adult male C57BL/6 mice (Harlan). The average age of the successfully conditioned and imaged animals was 122 ± 16 (SD) d at the moment of imaging, and behavioral training typically started at 6 to 8 weeks of age. Animals were housed individually or in pairs in a large cage (40 cm length × 25 cm width × 25 cm height) and were provided with cage enrichment and nesting material. The day–night schedule was reversed, lights went on at 08:00 P.M. and went off at 08:00 A.M. Access to water and food was ad libitum, except for a six- to eight-hour period around the behavioral experiments when no food was available. Animals were weighed on a regular basis to assure there was no growth delay caused by food restriction. All animal procedures were approved by the animal experiment committee of the University of Amsterdam.
Apparatus for visual conditioning.
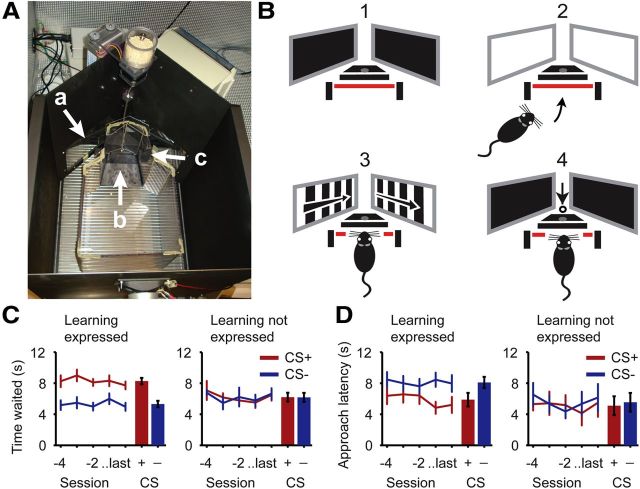
Visual conditioning was done in a custom-built behavioral chamber that measured 35 cm in width, 50 cm in length, and 45 cm in height. The chamber had one photobeam-equipped food pellet delivery tray and two 7” color LCD screens, placed so as to be optimally visible for a mouse that positioned itself in front of the reward tray (Fig. 1A). When the mouse was appropriately positioned, the distance between the screens and eyes was approximately 15 cm. From this position, the screens covered ∼147° of the horizontal visual field and 37° of the vertical visual field in front of the animal. A smaller Plexiglas box (dimensions: 20 cm wide, 25 cm long, and 20 cm high) was placed within the chamber to reduce the size of the area the animal could explore. A ramp (9 cm long, 6–10 cm wide, and 2 cm high) was placed in front of the reward tray, to guide the animal to position itself correctly in front of the screens. Stimuli were directional moving square-wave gratings, spatial frequency 0.05 cycles per degree, temporal frequency 2 Hz and ±100% contrast. Per mouse, one direction was arbitrarily selected as CS+ while a different direction (differing 90 or 180° with the CS+) was assigned as CS−. The CS+ and CS− direction remained the same over sessions and stimuli of other direction than the CS+ or the CS− were never presented to the animal during the entire course of the behavioral experiment.
Figure 1.
Visual conditioning of mice. A, A top-view photograph of the operant chamber that was used for conditioning the mice, with screens (a), a ramp to the reward site (b), and photo beam detectors (c). B, Different trial stages during conditioning in the behavioral setup. Before trial onset, the screens were dark (1) and trial onset was signaled by switching the screens to white (2). When the mouse positioned itself correctly breaking the photobeam (3; red line), the CS+ or CS− was shown. If the CS+ was presented it was followed by a food pellet ∼1 s after stimulus offset (4). C, D, Behavioral performance of 14 mice that expressed the conditioned association and five that did not express the association. Left part of the panels contains data (mean ± SEM) of the last five sessions preceding two-photon imaging. Right side of the panels show in red (CS+) and blue (CS−) bars the mean (±SEM) over these last five sessions. C, Performance in probe trials, which were structured the same as conditioning trials, except that stimulus presentations were not followed by reward (stage 4 was omitted). “Time waited” indicates the time (in seconds) the mouse lingered at the reward site after stimulus presentation in CS+ and CS− probe trials. D, Performance in approach trials, during which white screens indicating trial onset were left out and the moving stimulus was immediately presented (stage 2 was omitted). “Approach latency” indicates the time after stimulus onset (in seconds) until the mouse entered the reward site.
Visual conditioning.
Animals were pretrained on the visual conditioning task in three stages. During the first stage, the animals were habituated to the chamber and food pellets were ad libitum available at the reward tray. In the second stage, food pellets were only delivered when the animal positioned itself correctly at the reward site. In the final pretraining stage, mice were trained to position themselves only in front of the screens when the screens changed from black to uniform white (indication of trial start). Visual conditioning was started when the animals were able to conduct >30 pretraining trials in a single session. A conditioning trial started with both screens changing from black to white. When the animal positioned itself correctly in front of the reward tray, either the CS+ stimulus or the CS− stimulus was presented for 4 s. Delivery of a food pellet followed 1 s after CS+ presentation, while no reward was delivered after presentation of the CS−. Conditioning sessions were done once per day, approximately 6 d a week and consisted of 60 trials per session.
Measurements of stimulus–reward association.
Formation of a stimulus–reward association was measured in CS+ probe trials that were inserted randomly between the normal conditioning trials. Only one out of every three sessions included five CS+ probe trials. In these CS+ probe trials, the CS+ was shown, but no reward was given. Subsequently, the time the animal lingered at the reward site, likely waiting in anticipation of upcoming reward (Schoenbaum et al., 1998; van Duuren et al., 2009), was measured and compared with the time lingered after a randomly selected, temporally proximal CS− trial. This waiting time was defined as the delay between the onset of the stimulus and the departure from the reward tray. Studies on delay-discounting have shown that animals are willing to wait longer when a large reward is expected than when no or a small reward is expected (Rachlin and Green, 1972; Kalenscher et al., 2005; Kalenscher and Pennartz, 2008). Because CS+ probe trials and CS− trials differ only in movement direction of the stimulus, differences in waiting time after stimulus presentation are likely to reflect differences in stimulus-associated expectation of upcoming reward.
Additionally, one out of every three sessions contained eight CS+ and eight CS− approach trials (sessions containing approach trials never included probe trials). During the approach trials, the moving pattern of the CS+ or CS− was shown directly at trial onset (whereas in standard conditioning trials white screens would appear first to signal trial onset and the moving pattern would only appear when the animal had correctly positioned itself in front of the screens). Therefore, the animal was allowed to detect the moving gratings from anywhere in the box and could decide to visit the reward site or not. The pattern stopped as soon as the animal correctly positioned itself in front of the reward tray or when it timed-out after 16 s. In CS+ (but not CS−) approach trials delivery of a food pellet followed directly after the end of stimulus presentation. In the initial phase of the approach trials the difference between CS+ and CS− approach trials was only manifested in the direction of the moving grating. Therefore, faster positioning in front of the reward tray (measured by approach latency) in CS+ trials reflects stronger association between the CS+ and expectation of upcoming reward (Cleland and Davey, 1983; Lovibond, 1983). Sessions containing different trial types were systematically alternated: a session including probe trials was followed by a session with approach trials on the next day, and a session neither containing probe nor approach trials on the following day, and so on.
Animal preparation for imaging.
One day after the last conditioning session, animals were prepared for two-photon microscopy and calcium imaging. Animals were injected subcutaneously with the analgesic Buprenorphine (0.05 mg/kg bodyweight) 30 min before the start of surgery. Anesthesia was induced with 3% isoflurane in 100% O2. During surgery, anesthesia was maintained with 1.3% isoflurane and 1.9% isoflurane in O2. Using fine scissors, skin on top of the head was removed. Local anesthetic, Xylocaine, was applied to the exposed tissue and the skull was cleaned thoroughly. The location of V1 was visually determined and marked, around 4 mm caudal and 2.5 mm lateral from bregma. A custom built head fixation device was attached to the skull using cyanoacrylate glue and reinforced with dental cement. A craniotomy, approximately 2 mm in diameter, was carefully created above V1 using a dentist drill. The exposed dura was left intact and kept moist with buffered aCSF (125 mm NaCl, 5 mm KCl, 1.3 mm MgSO4 * 7 H2O, 2.0 mm NaH2PO4, 2.5 mm CaCl2 * 2 H2O, 10 mm glucose, and 10 mm HEPES in distilled water, pH adjusted to 7.37) (Svoboda et al., 1999).
Multicell bolus loading.
Cells were labeled with the fluorescent calcium indicator Oregon Green BAPTA-1 AM (OGB) and Sulforhodamine 101 (SR101) (Stosiek et al., 2003; Nimmerjahn et al., 2004; Garaschuk et al., 2006). Two to four target sites for dye loading were selected around the center of the craniotomy. Care was taken to avoid dye loading near large blood vessels. A pipette (approximately 6 MΩ resistance) was filled with dye loading solution, containing 12.5 μg of OGB, dissolved in 1 μl of DMSO with 20% pluronic acid, and mixed with 40 μl of pipette solution (150 mm NaCl, 2.5 mm KCl and 10 mm HEPES in distilled water, pH adjusted to 7.37) to reach a final solution of 0.5 mm OGB (Stosiek et al., 2003). Additionally, 2 μl of SR101 stock solution (500 μg of SR101 in 500 μl of pipette solution) was diluted 50 times and 2 μl of this solution was added to the pipette solution to reach a final concentration of 5 μm SR101. The pipette was lowered into the cortex at an angle of 35° to 200–300 μm below cortical surface using a Luigs–Neumann SM-5 manipulator. Dye loading solution was pressure injected under visual guidance into the cortex at 10 to 14 psi for 40 to 80 s at the selected sites within the craniotomy. Next, the cortex was covered with agarose (1.5% in buffered aCSF) and superfused with aCSF (125 mm NaCl, 2.5 mm KCl, 26 mm NaHCO3, 1.25 mm NaH2PO4, 2 mm CaCl2 * 2 H2O, 1 mm MgCl2, and 20 mm glucose in distilled water, bubbled with 95% CO2 and 5% O2 and heated to 37° C) (Stosiek et al., 2003).
Two-photon microscopy.
Images were acquired using a Leica SP5 resonant laser-scanning microscope and a SpectraPhysics Mai Tai High Performance Mode Locked Ti:Sapphire laser with a pico-second pulse width, set to an excitation wavelength of 810 nm. Fluorescence emission was collected non-descanned in two photo-multiplier tubes, one filtered at 525 nm (maximum range 500–550 nm) and the second filtered at 585 nm (maximum range 565–605 nm). This allowed separating the green fluorescent Oregon Green BAPTA 1 (emission peak at 523 nm) from the red fluorescent Sulforhodamine 101 (emission peak at 605 nm). Imaging was done in a square region with a size between 150 × 150 μm and 225 × 225 μm, at a resolution of 512 × 512 pixels and a scan speed of 30 frames per second. Every set of 8 frames was averaged online and saved to disk; the effective sampling frequency was set to 2 Hz.
Visual stimulation during imaging.
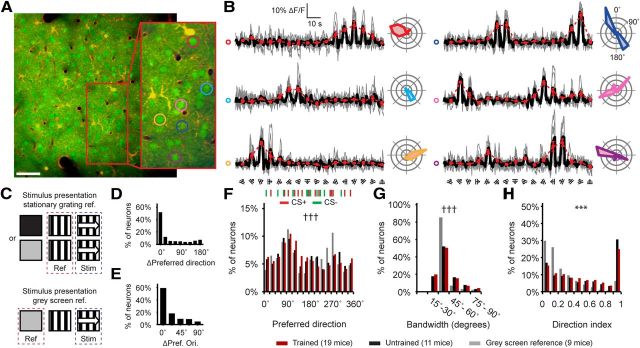
Visual stimuli were presented on a Dell workstation with a 15” TFT screen (Refresh rate 60 Hz) using MatLab (MathWorks) and Psychophysics Toolbox (www.psychtoolbox.org). The screen was positioned 25 cm in front of the monocular region of the right eye. Stimuli consisted of square wave 100% contrast moving gratings with a spatial frequency of 0.05 cycles per degree and a temporal frequency of 2 Hz moving in 16 directions (22.5–360°). Every trial consisted of three 5 s stimulus conditions, each of which comprised 10 two-photon acquisition frames; (1) no stimulation, showing a black screen (for 10 mice) or a gray screen (for 9 mice); (2) presentation of a stationary oriented grating, used as nonmoving reference unless otherwise noted; (3) presentation of a moving grating with the same orientation as the stationary grating (Fig. 2C). For each of the 16 movement directions, five trials were recorded in random order.
Figure 2.
Two-photon calcium imaging of orientation and direction tuning in visually-conditioned and naive adult mice. A, A frame-averaged image of neurons and astrocytes in the primary visual cortex of a trained animal (Scale bar: 50 μm). B, Fluorescence signal (ΔF/F) from within the outlined cell bodies in the inset in A. Trials were randomly presented, but are reorganized by order of movement direction. Single trials are displayed in gray, the mean of all trials is displayed in black. Red curve displays the nonsmoothed tuning curve based on the ΔF/F responses. Polar plots on the right of each curve show the mean fluorescence response (ΔF/F) per movement direction. C, Graphical depiction of the stimulus sequences used for each of the two methods of baselining ΔF/F signals. D, Difference in preferred direction of neurons for which tuning curves could be referenced both against stationary gratings and gray-screens. E, Same as D, but for the difference in orientation of the preferred direction between Stat-ref and Gray-ref tuning curves. F, The distribution of preferred directions for all Stat-ref tuning curves from trained mice (red) and untrained mice (black), and Gray-ref tuning curves from 9 trained mice (gray). Markings at the top of the panel indicate each of the (randomly assigned) CS+ (red) and CS− (green) directions that were used for the experiment. †††Stat-ref (trained) versus Gray-ref (trained); Kolmogorov–Smirnov test, p < 10−6. G, The distribution of the Stat-ref tuning curve bandwidths of neurons measured in trained mice (red), untrained mice (black), and for gray screen referenced data (gray). †††Stat-ref (trained) versus Gray-ref (trained); Kolmogorov–Smirnov test, p < 10−6. H, Idem, for direction index. ***Stat-ref (trained) versus Gray-ref (trained); Mann–Whitney U test, p < 10−6, Kolmogorov–Smirnov test, p < 10−6.
Image and data processing.
Images were saved in lossless TIFF format, realigned using an algorithm that relies on a single step discrete Fourier-transform (Guizar-Sicairos et al., 2008) and smoothed using a 9 pixel (±3 μm) Gaussian smoothing kernel. Cell detection and astrocyte identification was done manually using a custom-built graphical user interface running on the MatLab platform. Astrocytes were subsequently excluded from further analysis. Average fluorescence of the area within the cell body was calculated per frame, resulting in a timeline of mean absolute cell body fluorescence for each neuron.
Tuning curve analysis.
Fluorescence responses to each movement direction were calculated per trial as in Equation 1 and expressed in percentage increase in fluorescence relative to the reference period. Unless otherwise mentioned, we referenced the responses to moving stimuli to the period in which a stationary grating of the same orientation was presented. The value Freference was defined as the average absolute fluorescence over frames 2 to 8 of the reference period that directly preceded the moving-stimulus period. The value Fstimulus was defined as the average absolute fluorescence over frames 2 to 8 of the period in which the moving grating was presented.
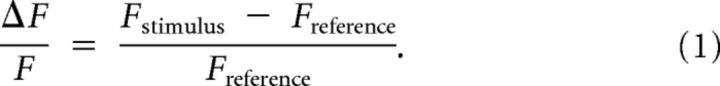 |
To identify neurons that were tuned to movement orientation or direction, the ΔF/F response of each trial (j) was converted into a vector. The angle of this vector represents the stimulus orientation or direction angle θ and its length is equivalent to the magnitude of the ΔF/F response (Li et al., 2008). To detect both neurons that were tuned to one movement direction and neurons that were tuned to two opposite movement directions and thus shared a common orientation, the vectors were calculated in both movement orientation space (Eq. 2) and movement direction space (Eq. 3). Cells were considered to be orientation or direction selective if the mean of the Rorientationθj or the Rdirectionθj vectors of Equations 2 and 3 was significantly different from zero, tested with a Hotelling's T2 test (p < 0.05).
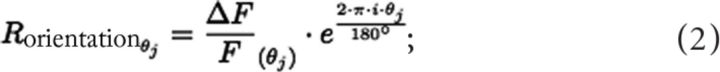 |
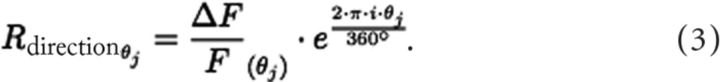 |
Tuning curves were constructed for all neurons that showed significant orientation or direction tuning, by averaging the ΔF/F response over the five trials per movement direction (Rdirectionθj). The preferred movement direction (θPREF) was determined by fitting the average responses over all directions with a two-peaked 360° wrapped Gaussian function (Eq. 4) (Li et al., 2008). Where ROFFSET is the baseline fluorescence, RPREF is the response to the preferred direction θPREF, ROPP is the response to the opposite of the preferred direction (θPREF + 180°), σ is the SD of the fitted Gaussian functions and the function y = ang(x) wraps the angular difference x = θ − θPREF on an interval between 0° and 180°:
 |
The bandwidth of the tuning curve was calculated on smoothed raw-data tuning curves (smoothed using a Hanning-window; kernel = [0.5 1 0.5]). Smoothing was performed to reduce the effects of noise on bandwidth estimation. Bandwidth was defined as the half-width of the tuning curve at 1/ times the maximum response in degrees, calculated using interpolation (Ringach et al., 2002). For asymmetrical tuning curve analysis (see Fig. 6), the half-width at 1/ height was estimated using interpolation on each side of a cell's smoothed tuning curve separately. As this single-sided estimate is more sensitive to noise, a marginally wider smoothing kernel was implemented compared with when bandwidth was estimated by taking the mean for both sides of the tuning curve (Hanning-window; kernel = [0.25 0.5 1 0.5 0.25]).
Figure 6.
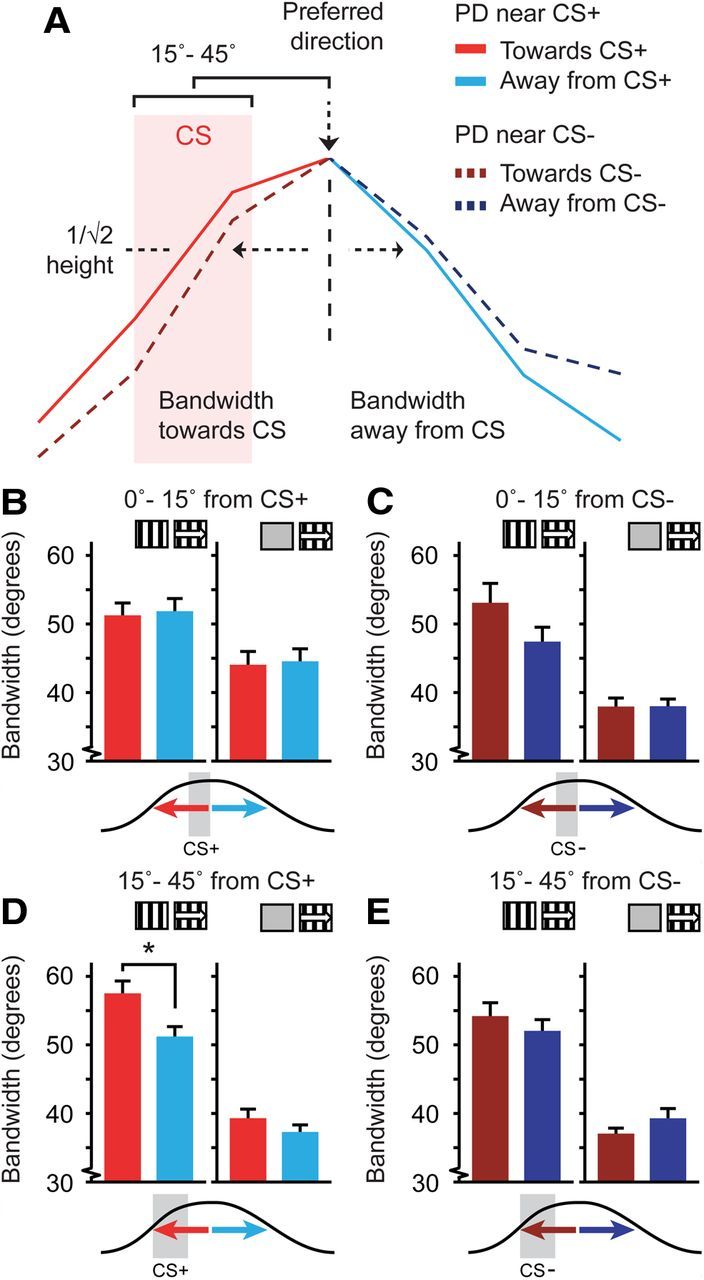
Asymmetry of the tuning curve bandwidth relative to the CS+ direction. A, Representation of two tuning curves recorded from two neurons and the quantification of bandwidth toward (red) and away (blue) from the CS+, CS−, or control directions. The bright solid red/blue tuning curve was taken from a neuron with a preferred direction differing 15–45° from the CS+ that had a broader bandwidth on the side toward the CS+. The dotted dark red/blue curve was taken from a neuron with a preferred direction differing 15–45° from the CS−. B–E, Left, Data for tuning curves referenced against stationary gratings (Stat-ref). Right, Data referenced against gray screens (Gray-ref). Red colors are for bandwidth toward the CS+, blue colors for bandwidth away from the CS+. B, Mean (±SEM) single-sided bandwidth of the tuning curve for neurons with a preferred direction that was similar to the CS+ (angular difference 0–15°). C, Same as B but for neurons having a preferred direction differing 0–15° from the CS−. D, Idem for neurons with a preferred direction differing 15–45° in angle from the CS+ (*p < 0.05). E, As in D, but for neurons having a preferred direction that differed 15–45° from the CS−.
The direction index (DI), indicating whether a tuning curve is bidirectional or peaks only at one direction, was also calculated from raw-data tuning curves. The average response to the opposite direction was subtracted from the average response to the preferred direction and divided by the sum of the responses to the preferred and opposite direction (Eq. 5) (Niell and Stryker, 2008).
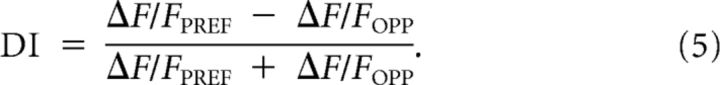 |
The slope of the tuning curve at a direction θ was calculated from the absolute value of the derivative of the normalized fitted tuning curve at that direction and expressed as the percentage of change in response amplitude per degree (Schoups et al., 2001). The response amplitude to a direction was calculated from the normalized fitted tuning curve at that direction and expressed as percentage of maximum response amplitude.
Datasets for control analyses.
From the original dataset, three control datasets were created. Analyses of these datasets served to exclude bias from contamination of cellular signals by local neuropil fluorescence (control dataset #1), the lower fraction of orientation- and/or direction-tuned neurons we found compared with some previous studies (control dataset #2) and a combination of both (control dataset #3). Control dataset #1 contained all neurons and mice that were included in the original dataset. The ΔF/F signals were corrected for neuropil contamination as described in the study by Kerlin et al. (2010). In short, local neuropil fluorescence was estimated per frame by averaging the fluorescence in a circular region between 2 and 5 μm around the cell body (excluding the signal from other cells and blood vessels). This signal was multiplied by the neuropil contamination ratio and then subtracted from the fluorescence of the cell body (for each frame). The neuropil contamination ratio was estimated for each session by dividing the mean fluorescence in the blood vessels by the mean local neuropil fluorescence around those blood vessels. This indicates the ratio of neuropil signal that “leaked” into the blood vessel signal (in our study this ratio typically ranged between 0.5 and 0.8).
Control dataset #2 contained only the recordings from the original dataset that had 35% or more orientation- and/or direction-tuned neurons. Five different mice contributed a total of 1385 orientation- and/or direction-tuned neurons to this highly tuned dataset. The average percentage of tuned neurons in this dataset was 47%. Control dataset #3 was constructed by taking recordings from control dataset #1 (neuropil contamination corrected) that had 35% or more orientation- and direction-tuned neurons. The recordings for this highly tuned, neuropil contamination corrected dataset came from 6 mice and contained 2458 significantly tuned neurons. Statistical analyses of control datasets #1–3 were done following the same procedures as the original dataset and can be found in Table 2.
Table 2.
Control analyses for non-specific neuropil contamination and percentage of orientation- and direction-tuned neurons
| Dataset | Mice (n) | Percentage tuned |
p value for Kruskal–Wallis test |
||||
|---|---|---|---|---|---|---|---|
| Bandwidth |
Direction index |
Slope (15–30 °) | |||||
| Quadrant | Axis | Quadrant | Axis | ||||
| Original | 14 | 19.1% | <10−6 | <10−6 | 2 · 10−5 | 10−5 | 2 · 10−6 |
| Ctrl #1 | 14 | 27.5% | 3 · 10−5 | 0.001 | 0.044 | 0.012 | 3 · 10−5 |
| Ctrl #2 | 5 | 47% | 2 · 10−6 | 3 · 10−5 | 3 · 10−5 | 7 · 10−6 | 5 · 10−6 |
| Ctrl #3 | 6 | 42% | 0.008 | 0.001 | 0.009 | 0.005 | 3 · 10−5 |
Analysis of the original and three additional datasets (Stat-ref; see Methods and Materials) that control for neuropil contamination (#1), lower fraction of orientation- and direction-tuned neurons (#2), and a combination of both (#3). Each dataset was analyzed for quadrant and orientation-axis effects on bandwidth and direction index and for slope of the tuning curve at 15–30° relative to the CS+, CS−, and control directions as presented in Figure 3–5. Values in column 4–8 are p values from the respective Kruskal–Wallis tests. Each control dataset was tested identically to the original dataset.
Statistics.
Parameter values (e.g., bandwidth or direction index in the CS+ quadrant) were averaged across cells (unless mentioned otherwise). Reported numbers of samples (n) refer to cells unless otherwise mentioned, with the exception of the analysis of spatial grouping of CS+ neurons, where the number of samples refers to the number of image planes. Hypotheses were tested using nonparametric tests, i.e., a Kruskal–Wallis test for comparisons between more than two groups and a Mann–Whitney U test or Wilcoxon matched-pairs signed-rank (WMPSR) test for unpaired and paired two-sample comparisons, respectively. In case data were normally distributed, parametric tests were used (ANOVA and post hoc Student's t test). p values were corrected for multiple comparisons using Bonferroni's correction method.
Results
Visual conditioning
Mice were trained on an appetitive visual conditioning task in a custom-built operant chamber, equipped with screens and a reward dispenser (Fig. 1A). The task was designed such that no instrumental action needed to be learned apart from the animal adopting a strategy wherein it positions itself in front of the screens and breaks the photo-beam for minimally 2 s into the period of stimulus presentation. The conditioned stimuli were moving gratings in two pseudo-randomly assigned directions, differing by an angle of 90 or 180°. Nineteen adult mice were trained daily in sessions of 60 trials. In each trial, one of the two moving gratings was shown after the mouse assumed a position in front of the screens. Viewing one direction (CS+) was rewarded with a food pellet whereas the other direction (CS−) was not (Fig. 1B).
Associative learning was assessed in probe trials, in which reward delivery was omitted. Additionally, separate approach trials were included, in which the moving stimulus was presented on the screens while the mouse was roaming in the operant chamber, before it had positioned itself in front of the screens and reward site (see Materials and Methods). Thirteen out of 19 mice waited significantly longer after stimulus presentation in CS+ probe trials and five out of these 13 also approached the reward site significantly faster in CS+ approach trials (WMPSR test, p < 0.05). Out of the six animals that did not express significant learning in the probe trials, one mouse showed significant learning in approach trials (WMPSR test, p < 0.05). Together, this group of animals (n = 14) was classified as expressing the stimulus–reward association in behavior (Fig. 1C,D). The remaining group (n = 5) showed a learning effect neither in probe nor approach trials and was classified as not expressing learning. On average, the best performing mice expressed the conditioned association significantly after 30 training sessions and the worst performers did not show learning of the association after up to 50 sessions. In addition, a control group of 11 untrained adult mice was added to test for overall differences between trained and untrained animals in our setup. The subsequent tuning curve analysis will be mostly focused on the group that expressed learning.
Although it remains unclear for which reason some mice did not express a learned association, four of the five animals that did not express learning were trained on a 180° difference between the CS+ and CS−, while all 14 trained mice that expressed the association were conditioned using stimuli that differed by 90°. Notably, a 180° difference leads to a stimulus contrast only in terms of movement direction, whereas a 90° difference contrasts both orientation and direction of movement. That movement orientation of the gratings acted as dominant conditioning cue is supported by the observed tuning curve effects (see below). Thus, conditioning with the 180° difference was possibly more challenging than the 90° difference, but individual differences in behavior and learning could also provide an explanation. As a cautionary note, we remark that these animals may not have expressed the association because it was in fact not formed, or alternatively, was formed but did not lead to behavioral differences.
Two-photon calcium imaging of orientation and direction tuning in V1
One day after the last conditioning session, we induced general anesthesia and recorded single neuron responses to gratings moving in 16 directions in mouse V1 by calcium imaging of neurons and astrocytes using in vivo two-photon laser scanning microscopy and multicell bolus loading of the calcium indicator Oregon Green BAPTA 1-AM (Stosiek et al., 2003; Nimmerjahn et al., 2004; Garaschuk et al., 2006) (Fig. 2A). To gather large unbiased population samples of neurons from visual cortex layer II/III, imaging planes were acquired at one to three locations and at one to nine different depths per location. The mean number of imaging planes per mouse was 4.9 ± 2.1 (SD), the mean depth was 222 ± 56 μm (SD) from the cortical surface, and the minimum distance between depths on the same location was 20 μm. A total of 24,429 neurons (mean: 814 ± 546 SD per animal) was imaged in 30 animals (17,603 in trained animals and 6826 in untrained animals).
Cellular responses to movement direction were quantified as the relative increase in fluorescence during a presentation of a moving grating, compared with the average fluorescence during the preceding presentation of a stationary grating with the same orientation (duration 5 s; see Materials and Methods, Fig. 2B,C). Referencing the response to moving gratings against the response to nonmoving but otherwise identical gratings was done with the intent of extracting the movement-selective component of the orientational and directional tuning curves. This, however, introduced a potential confound of including a phase-selective response component from simple cells (Hubel and Wiesel, 1959, 1962) in the reference signal, since we did not randomize the phase of the stationary grating. It is therefore possible that our orientation tuning measurements using stationary gratings as reference are confounded by phase selectivity. For instance, a neuron's phase selectivity could give rise to apparent orientation selectivity in a neuron that is not orientation-selective, or two neurons with identical orientation preference but opposite phase preferences could appear to have different orientation preferences. Since the majority of layer 2/3 neurons in mouse striate cortex are simple cells (Niell and Stryker, 2008), this concern applies to the majority of our tuning curve measurements, even though under anesthesia orientation- and phase-selective responses to stationary gratings are generally smaller in amplitude and shorter in duration compared with responses to moving gratings, and individual phase-selective effects are expected to cancel out across larger populations.
The more commonly used alternative is to use a gray screen as baseline, with equal luminance as the moving gratings we used. In nine of the 19 mice, each expressing the conditioned association in their behavioral measures, presentation of these gray screens was interleaved with presentation of the stationary and moving gratings (Fig. 2C). For neurons recorded in those mice, additional tuning curves were constructed by referencing against this mid-gray screen baseline and analyzed in parallel to the stationary grating-referenced tuning curves throughout this study (Gray-ref vs Stat-ref). Referencing against gray screens resulted in somewhat larger responses compared with referencing against stationary gratings because of the aforementioned orientation-selective responses to nonmoving gratings. Given the difference in choice of methodology, it should be noted that there is no a priori prediction that the results obtained by these two approaches should be necessarily the same. These methods may well yield different results, as a stationary-grating reference will emphasize the movement-selective components of the response, whereas a gray-screen reference highlights both static and movement selective components.
In total, we found 4666 out of 24,429 neurons (Stat-ref, 19.1%, n = 30 mice; Gray-ref: 2474 out of 11,661 neurons, 21.2%, n = 9 mice) that were significantly tuned to the orientation and/or direction of movement (Hotelling's T2 test, p < 0.05; significant for orientation tuning, Stat-ref: 2334; Gray-ref: 1290; significant for direction tuning, Stat-ref: 2751; Gray-ref: 1471; same n as above), with no difference between trained and untrained animals (Stat-ref, trained: 19.2%, n = 19 mice; untrained: 18.7%, n = 10 mice). That the Gray-ref analysis produced only a slightly higher percentage of tuned neurons may be explained by the stationary grating responses being smaller in amplitude and more transient than responses to moving gratings, so that generally a significant response remained in the Stat-ref method. The percentage of orientation and direction-tuned neurons is lower than in most previous studies in rat and mouse V1 (Ohki et al., 2005; Niell and Stryker, 2008; Kerlin et al., 2010; Andermann et al., 2011; Ko et al., 2011; Kreile et al., 2011), but these percentages can vary (Ohki et al., 2005; Marshel et al., 2011; Li et al., 2012) and could be a consequence of differences in experimental procedures, statistics, or signal-to-noise ratio of the setup. For instance, testing for orientation tuning using an ANOVA, which is a less stringent test than the Hotelling's T2 test and does not assume a circular relation between test-conditions (orientations and directions), resulted in higher percentages of orientation-tuned neurons (Stat-ref: 6277 out of 24,429 neurons, 25.6%, n = 30 mice; Gray-ref: 3960 out of 11,661 neurons, 34.0%, n = 9 mice).
For every neuron, the preferred movement direction was determined by fitting a tuning curve with a two-peaked 360° wrapped Gaussian function (Li et al., 2008). The resulting overall distribution of preferred directions was similar between trained and untrained animals. Tuning curves referenced against gray-screens had a different distribution compared with Stat-ref data, most notably around a preferred direction of 270° (Kolmogorov–Smirnov test, p < 10−6; Fig. 2F). Still, the majority of the neurons had similar preferred directions and orientations in both the Stat-ref and Gray-ref dataset (Fig. 2D,E). We observed an overrepresentation of preferred directions between 90 and 135° in tuning curves referenced against stationary gratings and around 90 and 270° in the gray screen referenced tuning curves. This range applies to movement along the nasal–caudal axis and may be related to extended exposure to visual flow during behavioral training and in the home cage, and/or the location of the recording sites in the monocular part of V1.
The direction index of the tuning curve was measured on the raw tuning curves and bandwidth (tuning curve half-width at 1/ of the maximum response) was estimated on smoothed raw tuning curves (see Materials and Methods). The median bandwidth in trained animals was 36.9 ± 19.0° SD (untrained: 37.1° ± 17.6°; Gray-ref: 36.0° ± 14.0°). This is different from the median tuning curve bandwidth of 28° that was previously reported (Niell and Stryker, 2008), and is caused by the application of circular smoothing before bandwidth calculation. The median bandwidth in the Gray-ref dataset was very similar to the median found in the Stat-ref dataset (Mann–Whitney U test, p = 0.28), but the distribution was narrower in the Gray-ref dataset (Kolmogorov–Smirnov test, p < 10−6; Fig. 2G). The use of a stationary grating as reference may result in this effect, because for the subset of cells with an orientation-selective component in the reference signal, the difference between gray- and stationary-reference amplitudes will be largest at the preferred orientation/direction, decreasing the maximum response in the latter case and thereby increasing the relative width of the tuning curve. In addition, the direction index was significantly lower in the Gray-ref dataset compared with Stat-ref data (Kolmogorov–Smirnov test, p < 10−6; Mann–Whitney U test, p < 10−6; Fig. 2H), which can be explained by the removal of part of the orientation-, but not direction-selective, component of the tuning curves in the Stat-ref dataset.
Effects of conditioning on the distribution of preferred directions and population response relative to the CS+
In auditory cortex, classical conditioning has been shown to affect the amount of neurons with a preferred frequency at or around the frequency of a conditioned tone (Weinberger et al., 1993; Bao et al., 2001). To investigate whether appetitive visual conditioning resulted in a similar effect on orientation and direction tuning in primary visual cortex, we divided the population of orientation- and direction-tuned neurons into four subsets based on their preferred direction. Each neuron was assigned to the subset for which the angular difference between the subset center (direction of the CS+, CS− and two control directions) and the neuron's preferred direction was between −45 and +45° (Fig. 3A). Thus, one subset included all neurons that had a preferred direction in the quadrant centered at the CS+, a second subset quadrant was centered at the CS−, and the remaining subsets were in quadrants centered at two directions to which the animal was not exposed during visual conditioning. These directions were opposite to the conditioned stimuli and were labeled CS+opp and CS−opp in mice for which the CS+ and CS− were of orthogonal directions, and were orthogonal to the CS+ and CS− in the four “not-expressing learning” mice for which the CS+ and CS− had opposite movement directions.
Figure 3.
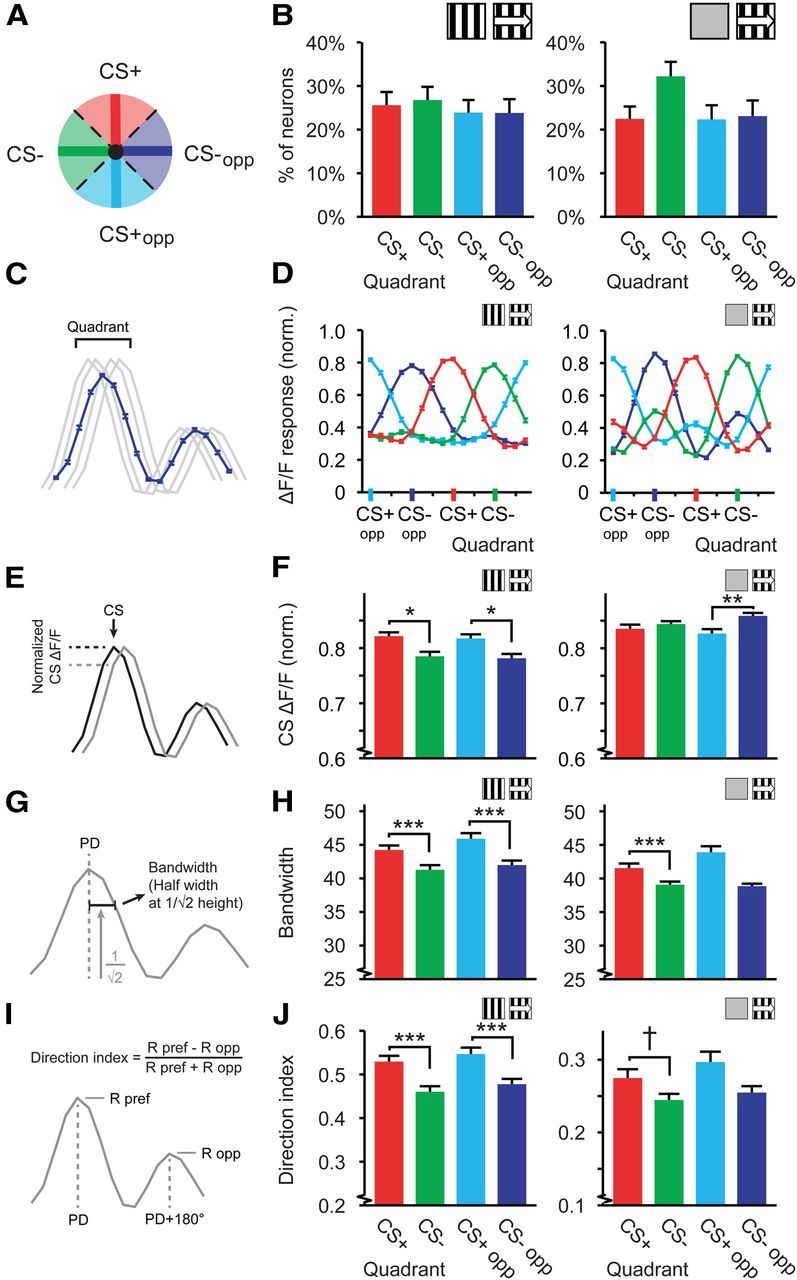
Distributions of tuning curve characteristics relative to the CS+ direction. A, Schematic representation of the quadrant division in a polar plot. B, D, F, H, J, Left, Data for tuning curves referenced against stationary gratings (Stat-ref). Right, Data referenced against gray screens (Gray-ref). B, Average percentage of cells per mouse in each quadrant, mean and SEM over mice. C, Quadrant tuning curves were constructed by averaging the tuning curves of all orientation- and direction-tuned neurons in each quadrant. D, Mean (±SEM) quadrant tuning curves (red, CS+; green, CS−; light blue, CS+opp; dark blue, CS−opp). E, The response of the quadrant tuning curve to a respective reference direction (e.g., response to the CS+ for neurons with a preferred direction in the CS+ quadrant; response to the CS− for neurons with a preferred direction in the CS− quadrant). Black and gray lines represent tuning curves of two neurons with preferred directions equal and similar to the CS+ respectively. F, The mean (±SEM) response of the quadrant tuning curve to each corresponding reference direction (Normalized on its maximum). G, Bandwidth was calculated as half-width of the tuning curve at 1/ times the maximum response in degrees. H, Mean (±SEM) bandwidth of the tuning curves in each quadrant. I, Direction index was defined as the difference between preferred and opposite direction divided by the sum. J, Idem as H, but for direction index. For all panels, data shown are for mice expressing a learning effect. Stat-ref, left panels: 14 mice; Gray-ref, right panels: 9 mice, †p = 0.059, *p < 0.05, **p < 0.01, ***p < 0.001.
To test the homogeneity of preferred directions across quadrants, we calculated the percentage of neurons with a preferred direction in each of the quadrants for each mouse and averaged across mice that expressed the learned association. Although we expected more neurons to have a preferred direction in the CS+ quadrant (Weinberger et al., 1993; Bao et al., 2001), the percentage of neurons did not significantly differ between quadrants per mouse (Stat-ref: ANOVA, F(3,52) = 0.42, p = 0.74; n = 14 mice; Gray-ref: ANOVA, F(3,32) = 2.16, p = 0.11; n = 9 mice; Fig. 3B). This indicates that appetitive visual conditioning using a directional stimulus does not induce an overall population effect by increasing the number of neurons with the CS+ as preferred direction.
An alternative hypothesis is that the summed population response to the CS+ will increase as a consequence of conditioning. Frankó et al. (2010) and Hernandez-Peon (1961) already reported increased visual evoked potentials to conditioned visual stimuli, suggesting that neurons in the visual cortex exhibit stronger activity patterns in response to a reinforced stimulus. To investigate whether this was the case in the current study, we constructed a mean normalized tuning curve for each quadrant and each mouse and averaged these quadrant tuning curves across mice. The mean ΔF/F response of the CS+ quadrant tuning curve to its quadrant center (the CS+) was indeed larger for Stat-ref tuning curves (Kruskal–Wallis test, H(3,2819) = 13.72, p = 0.0033; post hoc: CS+ vs CS−: p = 0.012, CS+opp vs CS−opp: p = 0.011; Fig. 3C–F), but showed a different pattern in Gray-ref tuning curves (Kruskal–Wallis test, H(3,2470) = 9.70, p = 0.021; post hoc: CS+ vs CS−: p = 0.93, CS+opp vs CS−opp: p = 0.0056). Therefore, this result cannot be considered consistent or robust as yet.
Effects of conditioning on tuning characteristics relative to CS+ orientation and direction
Neurons in the mouse primary visual cortex are primarily tuned to moving and stationary oriented bars and edges (Niell and Stryker, 2008). Visual conditioning using directional stimuli may result in specific changes in this tuning for orientation and direction. Therefore, we tested whether characteristics of tuning curves in the different subpopulations of V1 neurons, as defined by quadrants, were altered after visual conditioning. In animals that showed a learning effect, the bandwidth in the four quadrants differed significantly (Stat-ref data, Kruskal–Wallis test, H(3,2819) = 33.83, p < 10−6). Specifically, the subsets of cells with a preferred direction in the CS+ and CS+opp quadrants showed broader orientation tuning than the subsets in the CS− and CS−opp quadrants (Mann–Whitney U test: CS+ vs CS−: p = 5 · 10−6, CS+opp vs CS−opp: p = 0.0002; Fig. 3G,H). Tuning curves referenced against a gray screen showed a similar pattern (Kruskal–Wallis test, H(3,2470) = 20.7, p = 0.00012; Mann–Whitney U test: CS+ vs CS−: p = 0.00014, CS+opp vs CS−opp: p = 0.085; Fig. 3H). These effects were also observed when calculated across mean bandwidth per mouse (Stat-ref: ANOVA, F(3,52) = 6.46, p = 0.0008; n = 14 mice; Gray-ref: ANOVA, F(3,32) = 3.60, p = 0.023; n = 9 mice). Bandwidth in the CS+ quadrant did not differ significantly from that in the CS+opp quadrant, neither was there a difference between the CS− and the CS−opp quadrant (Gray-ref and Stat-ref: p > 0.09).
At least in the Stat-ref dataset, this broadening of orientation tuning was not due to a general loss of selectivity because the neurons were, at the same time, more sharply tuned to direction (Kruskal–Wallis test, H(3,2819) = 24.11, p = 0.00002). Again, the CS+ and CS+opp quadrants were significantly more sharply tuned to direction than the CS− and CS−opp quadrants (Mann–Whitney U test: CS+ vs CS−: p = 0.0006, CS+opp vs CS−opp: p = 0.0007; Fig. 3I,J), while differences between CS+ and CS+opp and between CS− and CS−opp were not significant (p > 0.25). Tuning curves referenced against gray screens showed a similar, but nonsignificant, trend (Kruskal–Wallis test, H(3,2470) = 4.02, p = 0.26; Mann–Whitney U test: CS+ vs CS−: p = 0.059, CS+opp vs CS−opp: p = 0.093; Fig. 3J). The direction index averaged across mice showed a similar pattern (Stat-ref: ANOVA, F(3,52) = 3.49, p = 0.022; n = 14 mice; Gray-ref: ANOVA, F(3,32) = 0.42, p = 0.74; n = 9 mice).
Most main effects of conditioning on tuning curves were expressed for both the CS+ and its opposite direction (Fig. 3F,H,J). An explanation can be found in the two-peak response profile of orientation- and direction-tuned neurons; neurons tuned to the CS+ will also respond (although many to a lesser degree) to the opposite direction of the CS+, and vice versa. To emphasize this effect, neurons were reordered into four mutually exclusive sections by taking the angular difference of their preferred direction to the orientation axis of the CS+ (Fig. 4A). For example, the section of the CS+ axis included neurons with preferred directions between −22.5 and +22.5° from the CS+ but also neurons with preferred directions between −22.5 and +22.5° from the CS+opp (Fig. 4A, red zone).
Figure 4.
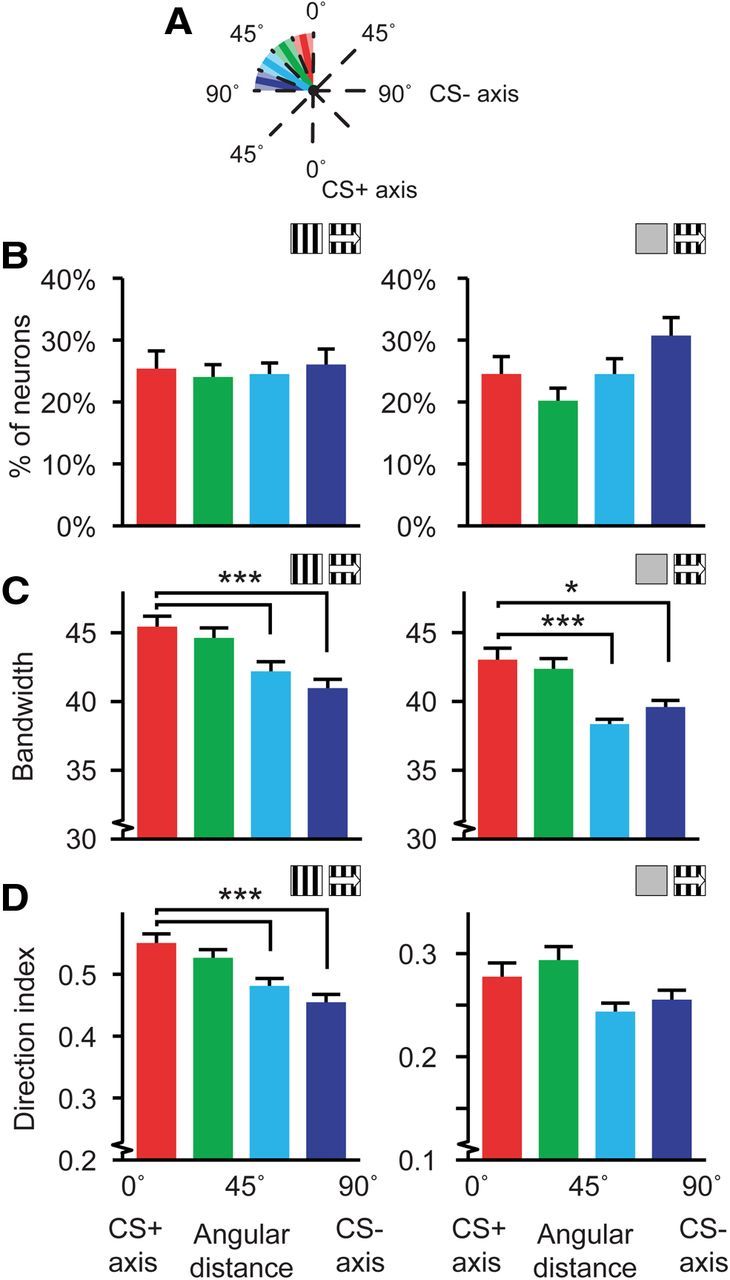
Distributions of tuning curve characteristics relative to the CS+ orientation. A, Schematic representation of the orientation-axis partitioning. Note that the CS+ axis includes neurons with a preferred direction differing within −22.5 and +22.5° from the CS+ and the CS+opp. B–D, Left, Data for tuning curves referenced against stationary gratings (Stat-ref). Right, Data referenced against gray screens (Gray-ref). B, Average percentage of cells per mouse along each orientation-axis, mean and SEM over mice. C, Mean and SEM of the tuning curve bandwidth along the orientation-axis of the CS. D, Idem for direction index. For all panels, data shown are for mice expressing a learning effect (Stat-ref, left panels: 14 mice; Gray-ref, right panels: 9 mice), *p < 0.05, ***p < 0.001.
The percentage of neurons with a preferred direction on each of the four orientation axis zones did not differ significantly across mice (Stat-ref: Kruskal–Wallis test, H(3,52) = 0.04, p = 0.99; n = 14; Gray-ref: Kruskal–Wallis test, H(3,52) = 2.73, p = 0.06; n = 9; Fig. 4B). The mean bandwidth in each of the orientation axis subgroups showed a linear decrease from broader orientation tuning at the CS+ orientation axis subgroup to narrower tuning at the CS− orientation axis zone (Stat-ref: Kruskal–Wallis test, H(3,2819) = 33.48, p < 10−6; Gray-ref: Kruskal–Wallis test, H(3,2470) = 18.20, p = 0.0004; across mice: Stat-ref: ANOVA, F(3,52) = 10.1, p = 2.5 · 10−5; n = 14 mice; Gray-ref: ANOVA, F(3,32) = 3.88, p = 0.018; n = 9 mice). Orientation tuning in the CS+ orientation axis subgroup was significantly broader than the CS+45-67.5° and CS− axis subgroups (Stat-ref: Mann–Whitney U test, p = 3 · 10−6 and p = 2 · 10−6 respectively; Gray-ref: Mann–Whitney U test, p = 0.00028 and p = 0.027 respectively; Fig. 4C). The same effect was found for the direction index in the tuning curves referenced against stationary gratings, with a gradually declining mean direction index toward the angular zone of the CS− orientation axis (Stat-ref: Kruskal–Wallis test, H(3,2819) = 25.85, p = 10−5; CS+ vs CS+45–67.5° and CS−, Mann–Whitney U test, p = 0.0008 and p = 6 · 10−6 respectively; across mice: ANOVA, F(3,52) = 3.03, p = 0.038; n = 14 mice; Fig. 4D), but the orientation axis subgroups did not differ significantly in direction selectivity when tuning curves were referenced against gray screens (Gray-ref: Kruskal–Wallis test, H(3,2819) = 3.37, p = 0.34; across mice: ANOVA, F(3,32) = 0.71, p = 0.56; n = 9 mice; Fig. 4D).
The CS+ specific increase in bandwidth and direction index of the Stat-ref data was exclusively seen in the group that showed a learning effect; no differences between quadrant nor axis-subpopulations were found in the group of mice that did not show a learning effect (quadrant, bandwidth: Kruskal–Wallis test, H(3,560) = 3.76, p = 0.29; direction index: Kruskal–Wallis test, H(3,560) = 0.55, p = 0.91; orientation-axis, bandwidth: Kruskal–Wallis test, H(3,560) = 3.89, p = 0.27; direction index: Kruskal–Wallis test, H(3,560) = 2.32, p = 0.51). These data are only available for Stat-ref tuning curves because all mice for which gray-ref tuning curves could be made expressed a learning effect.
Tuning curve parameters were calculated on smoothed tuning curves, but an alternative method to reduce noise is to use curve fitting (see Materials and Methods) (Li et al., 2008). Curve fitting using a symmetrical two-peaked Gaussian function imposes a symmetrical tuning curve and may obscure possible asymmetrical effects of conditioning, which is why we opted for smoothing. Median bandwidth obtained using the Stat-ref method was similar for fitted and smoothed tuning curves (smoothed: 36.9 ± 19.0° SD; fitted: 36.2 ± 16.3° SD), while the median direction index was lower (smoothed: 0.46 ± 0.35 SD; fitted: 0.36 ± 0.37 SD). Bandwidths and direction indices, estimated for the fitted tuning curves, showed the same conditioning-related differences for quadrant- (Stat-ref; bandwidth: Kruskal–Wallis test, H(3,2819) = 26.48, p < 10−6; direction index: Kruskal–Wallis test, H(3,2819) = 29.01, p = 2 · 10−6) and orientation-axis subgroups (Stat-ref; bandwidth: Kruskal–Wallis test, H(3,2819) = 41.22, p < 2 · 10−6; direction index: Kruskal–Wallis test, H(3,2819) = 33.51, p < 10−6) as smoothed tuning curves. Consequently, tuning curve smoothing did not introduce an artifact that can explain the differences between quadrant and orientation-axes subgroups.
The difference in results obtained using the Stat-ref and Gray-ref methods for the direction index of the various quadrant and orientation axis sub groups (Figs. 3J, 4D) can be related to the baseline difference in direction selectivity in the populations of tuned neurons (Fig. 2H), i.e., the Stat-ref data contained a higher percentage of direction selective neurons compared with the Gray-ref data. For instance, if the conditioning-induced change in direction index was only expressed in direction selective cells, the larger number of nondirection-selective orientation tuned neurons in the Gray-ref data may have obscured the effect. To test this hypothesis, the Gray-ref data and Stat-ref data were split into two groups. One group strongly expressed direction selectivity, having a direction index larger than or equal to 0.33, which implies that the response to the preferred direction was twice or more that of the opposite direction and lies in between the thresholds used in the study by Ohki et al. (2005) and Rochefort et al. (2011). The other group expressed direction selectivity weakly to not at all, having direction indices smaller than 0.33.
In both the Stat-ref and Gray-ref data, broadening of orientation tuning (as expressed in increased bandwidth) was more significant in the strongly direction-selective subset of the data (Table 1, Bandwidth). Post hoc Mann–Whitney U tests on the difference between CS+ versus CS− confirmed that the CS+ tuned cells had larger bandwidths compared with the CS− (strongly direction-tuned subset, Stat-ref and Gray-ref: p < 0.01). In the sharply direction-tuned subset of the Stat-ref dataset, the effect of conditioning on direction selectivity was also more significant than in the less direction selective subset (Table 1, Direction index; post hoc Mann–Whitney U test, CS+ vs CS−, strongly direction tuned subset, Stat-ref: p < 0.005), but in the Gray-ref data, this was not clearly the case. Here, we observed a significant effect for quadrants and orientation-axis in the strongly direction tuned subset and for quadrants in the weakly direction selective subset, as indicated by a Kruskal–Wallis test, but the post hoc tests did not reveal a significant difference between CS+ and CS− for strong or weak direction selectivity (Mann–Whitney U test, CS+ vs CS−, Gray-ref, strongly direction tuned subset, quadrants: p = 0.39; Axis: p = 0.062. Weakly direction tuned subset, Gray-ref, quadrants: p = 0.46; axis: p = 0.15). Therefore, highly direction-selective cells show stronger changes in bandwidth in both Stat-ref and Gray-ref data, while stronger changes in direction index of highly direction-selective cells were only observed in the Stat-ref dataset.
Table 1.
Conditioning related effects on tuning curve parameters for strongly and weakly direction selective groups of neurons
| Dataset | Direction selectivity | Cells (n) |
p value for Kruskal–Wallis test |
|||
|---|---|---|---|---|---|---|
| Bandwidth |
Direction index |
|||||
| Quadrant | Axis | Quadrant | Axis | |||
| Stat-ref | Low (<0.33) | 1120 | 0.021 | 0.033 | 0.14 | 0.12 |
| Stat-ref | High (≥0.33) | 1703 | 1.4 · 10−5 | 4.8 · 10−5 | <10−6 | <10−6 |
| Grey-ref | Low (<0.33) | 1804 | 0.057 | 0.81 | 0.00022 | 0.093 |
| Grey-ref | High (≥0.33) | 670 | 3 · 10−6 | <10−6 | 0.015 | 0.027 |
Analysis of the Stat-ref and Grey-ref datasets, split into subgroups exhibiting high (>0.33) and low (<0.33) direction selectivity of the orientation tuning curves. Columns 4–7 show p values from the respective Kruskal–Wallis tests on differences in bandwidth and direction index of the tuning curves between quadrant and orientation axis subgroups. Column 3 shows the total number of neurons included in each comparison. Each control dataset was tested identically to the original dataset.
Broader orientation tuning amplifies neuronal responses to CS+ like directions
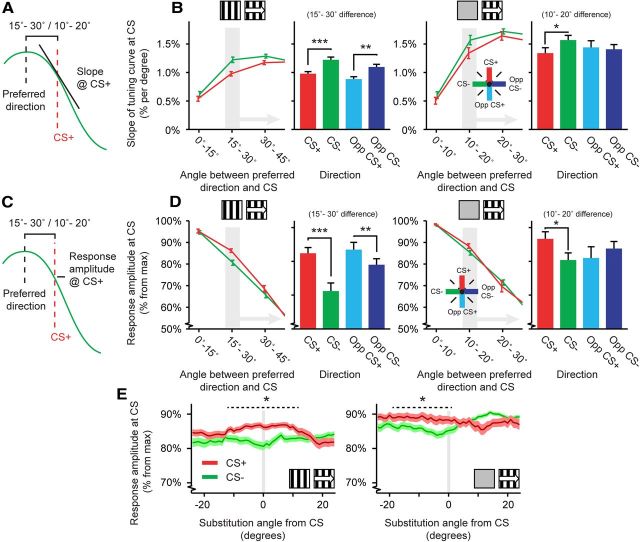
Sharper direction tuning indicates that the selectivity of responses to the CS+ and CS+opp increased, but broader orientation tuning suggests a decrease in tuning specificity. Under certain circumstances, however, broader orientation tuning for neurons with a preferred direction in the CS+ quadrant may increase the neuronal population response to the CS+. If a specific group of neurons with a preferred direction close to, but not exactly at, the CS+ increases the bandwidth of its tuning curve toward the CS+, the relative response of these neurons to the CS+ will become larger.
To examine how the effect of increased bandwidth may be reconciled with increased direction selectivity, we calculated the slope (in percentage per degree; Fig. 5A) and the response amplitude (% of maximum response amplitude; Fig. 5C) for each tuning curve at each of the four reference directions; the CS+, CS−, CS+opp, and CS−opp. The slope of the tuning curve was shallower at the CS+ than CS− in a band of directions (15–30°) relative to the CS+ (Stat-ref: Kruskal–Wallis test, H(3,2819) = 28.94, p = 2 · 10−6; Across mice, ANOVA, F(3,48) = 8.35, p = 0.00014; n = 14 mice; Fig. 5B). Specifically, slopes at both the CS+ and CS+opp were significantly different from the CS− and CS−opp (Mann–Whitney U test: CS+ vs CS−: p = 0.00028, CS+opp vs CS−opp: p = 0.0029; Fig. 5B). Similar to the slope, the response amplitude to the CS+ was significantly increased compared with the CS− (Stat-ref: Kruskal–Wallis test, H(3,2819) = 26.83, p = 6 · 10−6; Across mice, ANOVA, F(3,48) = 7.61, p = 0.00029; n = 14 mice; Fig. 5D). The group of neurons tuned 15–30° away from the CS+ had a significantly larger response amplitude at the CS+ than neurons had at the CS− and CS−opp, respectively (Mann–Whitney U test: CS+ vs CS−: p = 0.00087, CS+opp vs CS−opp: p = 0.0038; Fig. 5D). The differences between CS+ and CS− in slope and response amplitude were also present when tuning curves were referenced against gray screens (Mann–Whitney U test: CS+ vs CS−; slope: p = 0.039; across mice, ANOVA, F(3,32) = 4.57, p = 0.0089; n = 9 mice; response amplitude: p = 0.020; across mice, ANOVA, F(3,32) = 2.85, p = 0.053; n = 9 mice; Fig. 5B,D), but the effects were less strong under those conditions and emerged closer to the CS+ (10–20° away).
Figure 5.
CS+ related effects on slope and response decline in trained animals that expressed learning. A, Schematic description of the measurement of tuning curve slope at the CS+ for cells with a preferred direction 15–30° (Stat-ref) or 10–20° (Gray-ref) away from the CS+ direction. B, D, E, Left, Data for tuning curves referenced against stationary gratings (Stat-ref). Right, Data referenced against gray screens (Gray-ref). B, Line plots, Mean (±SEM) slope of the fitted tuning curve at the CS+ (red) and CS− (green) directions per mouse, as a function of angular distance of the cell's preferred direction to these reference directions. Bar plots, Mean (±SEM) slope of the fitted tuning curve for the subset of neurons with a preferred direction 15–30° (or 10–20° for the Gray-ref dataset) away from the CS+, CS−, CS+opp, and CS−opp. C, Schematic description of the measurement of response amplitude at the CS+ for cells with a preferred direction 15–30° (Stat-ref) or 10–20° (Gray-ref) away from the CS+ direction. D, Same as in B, but showing the mean response amplitude of the tuning curves. E, Mean (±SEM) response amplitude of the tuning curve at the CS+ and the CS− direction after substituting these reference directions with a direction ranging between −24 to +24° in difference. For all panels: *p < 0.05, **p < 0.01, ***p < 0.001.
Control procedures for non-cell-specific effects and differences in exposure to the CS+ and CS−
A potential confound in in vivo two-photon calcium imaging is that changes in tuning properties might not be cell specific but originate from changes in the surrounding neuropil. To control for this possibility, we subtracted local ΔF/F neuropil signals from cellular signals (control dataset #1; Stat-ref method; see Materials and Methods) and found that the original results were reproduced following this operation (Table 2), which indicates that the effects are not likely biased by non-cell-specific signals. Another potential confound could be the lower fraction of orientation- and direction-tuned neurons in the analyzed dataset compared with some other studies. To test whether our main results were affected by this, we created two highly orientation- and direction-tuned datasets (analyzed using the Stat-ref method), one from the original dataset and one from the neuropil contamination-corrected set by selecting only recordings with 35% or more orientation- and direction-tuned neurons and named them control dataset #2 and #3, respectively. The same pattern of results as in the original dataset was found in both of these control datasets (Table 2), leading to the conclusion that neither a relatively low percentage of orientation- and direction-tuned neurons, nor nonspecific neuropil contamination can explain our findings.
The mice were subjected to equal numbers of CS+ and CS− trials, but due to the freely moving aspect of the task, the total duration of exposure to the CS+ stimulus was on average 3238 s (±618 SD) while exposure to the CS− stimulus was on average 2400 s (±438 SD). For both stimuli, this duration of exposure exceeds the range in which build-up of stimulus-selective response potentiation has been described to result in differences in visual responses (Frenkel et al., 2006). Moreover, these differences were not significantly correlated to any of the changes in Stat-ref tuning curves found in this study (bandwidth, quadrant: r = −0.029, p = 0.93; axis: r = 0.12, p = 0.69; direction index, quadrant: r = −0.0066, p = 0.99; axis: r = −0.042, p = 0.89; slope: r = −0.048, p = 0.88; response amplitude: r = −0.076, p = 0.80; n = 14 mice for all cases). This makes it unlikely that the differences in exposure time to the CS+ and CS− stimuli explain the observed changes in orientation and direction tuning.
Specificity of changes in slope and response decline of the tuning curve
The effects reported above, e.g., broader orientation tuning and sharper direction tuning, comprised a subset of neurons tuned to a relatively large range of angles around the CS+ and the CS+opp, as the range of each quadrant was 90°. This suggests that the effect of the increased response amplitude found in the animals expressing a learning effect was not limited to the CS+ direction exclusively. To test the angular specificity of the CS+ effects on response amplitude of the tuning curve, our analysis program substituted the actual CS+ with hypothetical CS+ directions ranging from −24 to +24° relative to the real CS+ direction. In other words, going back to Figure 5D, we calculated the response amplitude at the hypothetical CS+ for neurons with a preferred direction differing 15–30° of this hypothetical CS+, while systematically varying the hypothetical CS+ direction from −24 to +24° (with 0° being the real CS+ direction) and thus determining the range of directions across which the increase in response amplitude occurred. In the Stat-ref dataset, the effects of response amplitude remained significant for substituted directions between −12° and +16° away from the CS+ (Gray-ref dataset: −20° and +1°; Mann–Whitney U test contrasting CS+ and CS−, p < 0.05; Fig. 5E), indicating that the conditioning effect generalized to a range of angles that was ∼20 to 25° wide around the CS+, but not to the entire quadrant.
Asymmetrical broadening of tuning curve bandwidth toward CS+ direction
Classically, orientational and directional tuning curves have a characteristic symmetrical response profile around the preferred direction. Plasticity, however, does not necessarily respect tuning curve symmetry. For instance, adaptation-induced short-term plasticity can boost responses to certain movement directions, while responses of the same neuron to different movement directions are attenuated (Dragoi et al., 2000, 2001). If in our experiments tuning curve plasticity was expressed selectively for the CS+ direction, only the side of the tuning curve that is facing toward the CS+ should be affected and not the other side of the bell-shaped curve facing away from the CS+ (Fig. 6A). Indeed, neurons in the Stat-ref condition that were not precisely tuned to the CS+, but had a preferred direction differing 15–45° in angle from the CS+, had a larger tuning curve bandwidth on the CS+ side of the tuning curve as compared with the other side (WMPSR test, p = 0.025; n = 514; Fig. 6D). This effect of tuning curve broadening toward the CS+ was not observed for the CS− (WMPSR test, p > 0.11, Fig. 6E) or for angular differences <15° (WMPSR test, p > 0.06; Fig. 6B,C). Analysis of Gray-ref tuning curves did not reveal a significant difference in asymmetric bandwidth broadening of neurons with a preferred direction 15–45° from the CS+ (WMPSR test, p = 0.11; n = 140; Fig. 6D), but this could be related to the lower number of neurons in this group (which was less than a quarter compared with the Stat-ref analysis), or may be a direct result of the difference in reference methods.
Spatial grouping of CS+ quadrant neurons
One of the main advantages of using two-photon microscopy over electrophysiology is exact knowledge about the spatial relationships between somata of single neurons. Previous studies on the rat and mouse primary visual cortex did not report an ordered spatial organization of orientation- and direction-tuned neurons relative to the cortical surface (Ohki et al., 2005; Mrsic-Flogel et al., 2007; Ohki and Reid, 2007; Bock et al., 2011; Bonin et al., 2011). If, however, reinforcement-related information feeds back into V1 in a spatially nonuniform fashion, reward-induced plasticity will be expressed by small localized subsets of orientation- and direction-tuned neurons. Such clustering would then be manifested in a tuning similarity between neurons with a preferred direction in the CS+ quadrant or orientation-axis subgroup and their direct neighbors, and will lead to an increased chance that neighboring neurons are classified as belonging to the same quadrant or orientation-axis subgroup.
To assess nearest neighbor tuning similarities without risking a bias caused by a possible over-representation and/or nonuniform distribution of preferred directions, we calculated the relative frequency (normalized between 0 and 1), across each image plane, that two orientation or direction-tuned nearest-neighbor pairs had a preferred direction in the same quadrant or orientation axis and corrected this by subtracting the mean relative frequency derived from 500 random permutations of quadrant/orientation axis identity in the same image plane. For this analysis, we used all imaging planes with at least one neuron in each quadrant, which allows relative frequencies to occur in the full range between 0 and 1. Because direction selectivity was significantly lower in the Gray-ref dataset compared with the Stat-ref dataset (Fig. 2H), the variable “preferred direction” is most likely less informative for gray-screen referenced tuning curves. The preferred orientation, however, should not be dependent on direction selectivity in the Gray-ref case. Therefore, the direction-specific tuning parameter “quadrant membership” and the orientation-specific tuning parameter “orientation-axis membership” were used as grouping variables in parallel, separate analyses on both the Stat-ref and Gray-ref dataset.
Neurons of the Stat-ref dataset with a preferred direction in the CS+ quadrant tended to neighbor another CS+ quadrant neuron more often than predicted by chance (Stat-ref: WMPSR test; CS+ vs shuffled, p = 0.05, n = 50; Fig. 7B). This clustering occurred significantly more often in the CS+ quadrant, compared with the CS− and CS−opp quadrants (Stat-ref, quadrant: Kruskal–Wallis test, H(3,196) = 10.18, p = 0.017; post hoc: CS+ vs CS−: p = 0.002, CS+ vs CS−opp: p = 0.018; n = 50; Fig. 7D). The effect was not significant for orientation-axis subgroups of the Stat-ref dataset (Stat-ref, orientation-axis: Kruskal–Wallis test, H(3,220) = 3.86, p = 0.28; n = 56). When using tuning curves referenced against gray screens, a similar effect of pairwise occurrence was found in the orientation-axis subgroups (Gray-ref, orientation axis: Kruskal–Wallis test, H(3,160) = 9.67, p = 0.022; post hoc: CS+ vs CS−: p = 0.011; n = 41; Fig. 7E), but not for quadrant subgroups (Gray-ref, quadrant: Kruskal–Wallis test, H(3,140) = 4.62, p = 0.20; n = 36). This difference between the Stat-ref and Gray-ref results may be explained by the observation that neurons in the Gray-ref dataset were less selective for movement direction (Fig. 2H), making the preferred movement orientation a more suitable characteristic for measuring tuning similarity for that dataset. Altogether, CS+ preferring neurons were more often colocalized with other CS+ preferring neurons in cortical space when compared with neurons preferring other directions or orientations.
Figure 7.
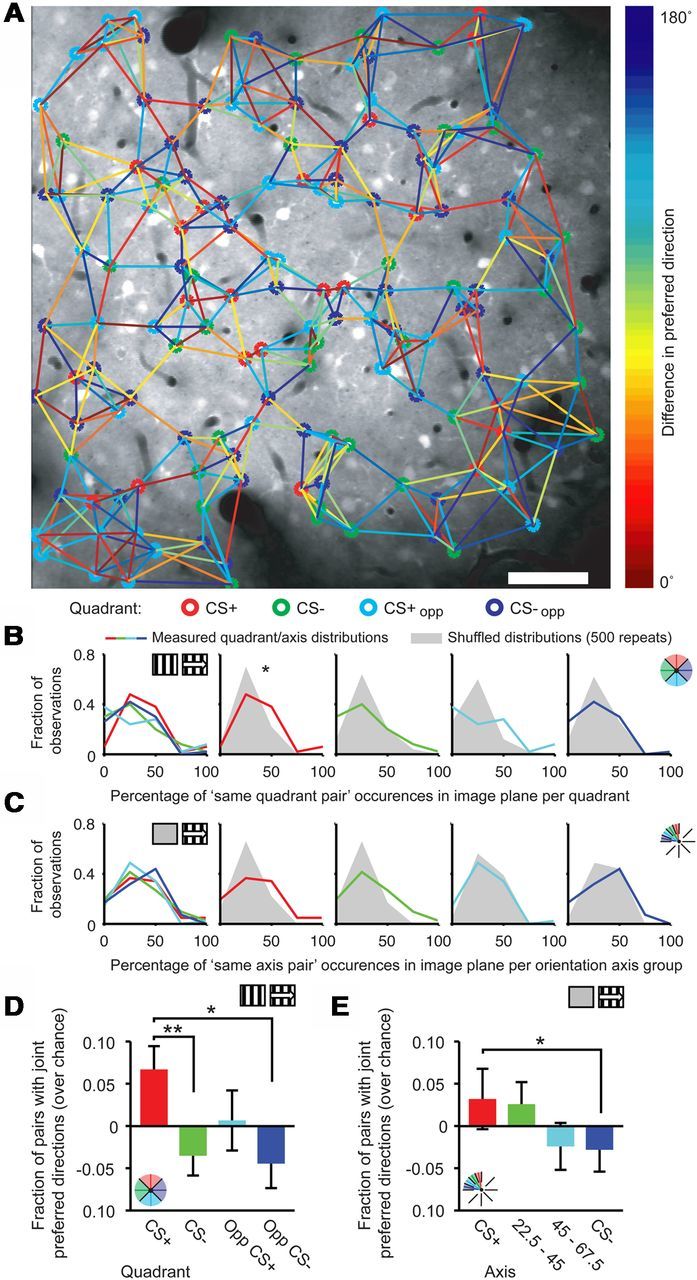
Spatial co-occurrence of neurons by quadrant membership. A, Example of spatial grouping of neurons from different quadrants in one imaging session. Orientation- and direction-tuned neurons were marked with the color of the quadrant they fall into (CS+: red, CS−: green, CS+opp: light blue, CS−opp: dark blue). Tuning difference between each neuron and its five nearest neighbors was drawn as a colored line, the color indicating angular difference in preferred direction of the neurons (color bar). Scale bar, 50 μm. B, Distributions of the normalized frequency of occurrence of same quadrant nearest neighbor pairs that were used to calculate D and E for the Stat-ref dataset. Lines are measured distributions, gray areas represent the data distributions after shuffling quadrant assignment (*p = 0.05). C, As in B, but for Gray-ref data and orientation-axis subgroups. D, Fraction, greater than chance, of nearest neighbor pairs with a preferred direction in the same quadrant subgroup (Stat-ref; *p < 0.05; **p = 0.002). E, Same as D, but for Gray-ref data and orientation-axis subgroups (*p < 0.05).
Discussion
We introduced a new in vivo model for studying molecular and physiological mechanisms underlying reward-dependent cortical plasticity. Appetitive visual conditioning resulted in altered tuning curves for neurons in mouse visual cortex. Departing from the reference method using stationary gratings, neurons with a preferred direction similar to the axis of the CS+ (CS+ or CS+opp direction) expressed broader orientation tuning and sharper direction tuning than cells preferring the CS− axis, which is consistent with a conditioning effect of the orientation of moving stimuli, and not so of much direction, on V1 response properties. Related to this, tuning curves of neurons having a preferred direction 15–30° away from the CS+ axis had a shallower slope and an increased response amplitude at the CS+ and CS+opp directions, which generalized to similar orientations. Finally, CS+ preferring neurons co-occurred in cortical space more often than neurons preferring the CS− and CS−opp. The results obtained using a gray screen as reference will be discussed below.
Methodological considerations
The percentage of significantly orientation- and direction-tuned neurons we observed (19.1%) was lower than in most previous studies (25–75%; Ohki et al., 2005; Niell and Stryker, 2008; Kerlin et al., 2010; Andermann et al., 2011; Bonin et al., 2011; Ko et al., 2011; Marshel et al., 2011). This difference may be due to the fact that we did not exclude recording sessions with a lesser signal-to-noise ratio in the measured regions of interest, or could be a consequence of differences in experimental procedures or statistics (a circular Hotelling's T2 test vs an ANOVA), and was not exclusively the result of using stationary gratings as baseline. Control analyses revealed that our main findings were not dependent on the percentage of tuned neurons, as we replicated the findings in a dataset that contained only recordings with large fractions of orientation- and direction-tuned neurons (Table 2). Second, the mean tuning curve bandwidth in our study was larger than previously reported by, e.g., Niell and Stryker (2008). This is most likely due to the application of circular smoothing before bandwidth calculation. Bandwidth estimation on raw tuning curves is more sensitive to noise than on smoothed tuning curves, therefore, application of circular smoothing can improve data reliability. A further concern for the technique of in vivo multicell calcium imaging is the possibility of nonspecific neuropil contamination. Although nonspecific contamination is unlikely (i.e., we observed our effects only in a selective subset of neurons), we additionally confirmed that the main results of this study remain when we apply a method that controls for neuropil-contamination artifacts (Kerlin et al., 2010).
Tuning curves for orientation and direction of movement were referenced against stationary gratings of the same orientation, which may have introduced a potential confound because of phase-selective responses to stationary gratings, although these effects may cancel out across the population. This referencing, however, highlights direction selectivity and underexposes (nondirectional) orientation selectivity, which was done because the conditioned stimuli were moving gratings, and, thus, learning and plasticity may be associated primarily with moving components. Because of these differences, there was no a priori prediction that both reference methods will give identical results.
The comparisons between reference methods can be unpacked in three components. The first component consists of effects that were of the same nature and were significant according to both methods. These results comprise the increased bandwidth for CS+ and CS+opp quadrant cells (Figs. 3H, 4C), the decrease in tuning curve slope at the CS+ and elevated response amplitude (Fig. 5B,D), and the generalization effect for CS+ substituting angles (Fig. 5E). The second subset consists of results that were significant under the Stat-ref method and showed a trend in the Gray-ref method, or showed a result that can be logically ascribed to a difference in referencing. These effects include the enhanced DI for near CS+ tuned cells (Figs. 3J, 4D) and the spatial co-occurrence of similarly tuned CS+ neurons (Fig. 7B–E). For this subset, we recall that the fraction of direction-selective cells was considerably smaller using the Gray-ref method (Fig. 2H). Finally, a third subset of results reached significance only using the Stat-ref method, whereas the lack of significance, or difference in effect direction, using the Gray-ref method could not be parsimoniously explained. These findings concern the higher ΔF/F response for CS+/CS+opp directions (Fig. 3F) and the asymmetric broadening of the tuning curve toward the CS+ (Fig. 6D). Although we note that the number of mice and cells available in the Gray-ref condition were lower than in the Stat-ref condition (Gray-ref: 9 mice, 2474 cells; Stat-ref: 14 mice, 2823 cells), thus diminishing the statistical power for this method, this third subset must be regarded with caution, as a consistency of results cannot be claimed here.
Comparisons to previous studies
The results in this study differ from those in earlier studies using other conditioning paradigms in primary sensory neocortex. In auditory cortex, conditioning using either footshock or electrical stimulation of the ventral tegmental area (VTA) increased the number of neurons or cortical area that preferably responded to the conditioned tone (Weinberger et al., 1993; Bao et al., 2001). In our study, the percentage of neurons with a preferred direction similar to the CS+ did not increase (Fig. 3B). This difference may lie in the nature and strength of the unconditioned stimuli used, with footshock and VTA stimulation having a potentially more pervasive impact on sensory representations than naturalistic reward. Second, the recordings of these studies were done in cortical layer IV–V (Bao et al., 2001) and layer V–VI (Weinberger et al., 1993) while our study focused on layer II–III. Finally, while neurons in the rodent auditory cortex are topographically organized by preferred sound frequency (Bao et al., 2001), neurons in rodent visual cortex are not spatially organized by preferred movement direction (Ohki et al., 2005; Ohki and Reid, 2007); this contrast may be coupled to different mechanisms for integrating reinforcing feedback or homeostatic mechanisms that compensate for overrepresentation of certain directions (Mrsic-Flogel et al., 2007; Shah and Crair, 2008).
Previous work on perceptual learning in monkeys indicated that orientation-tuned V1 neurons may be involved in perceptual decisions by sharpening their tuning curves to provide finer discrimination of orientation differences (Schoups et al., 2001), although this is not strictly required for perceptual learning to occur (Ghose et al., 2002). Contrasting with these studies, our results show broadened orientation tuning and sharper direction tuning for the subset of V1 neurons with a preferred direction similar to the CS+. In addition to species differences, it should be emphasized that the task in our study did not target fine orientation discrimination, but required mice to associate clearly differently orientated moving gratings to distinct outcomes (reward vs no reward). Computationally, sharpening of V1 tuning curves may be an optimal mechanism to increase the angular resolution, needed to detect small nonmoving orientation differences, while optimal coding for larger orientation differences results in other changes. Furthermore, in the task of Schoups et al. (2001), correct detection of both stimulus orientations led to reward while in our study only one of the two moving stimuli was followed by reward, making reward a critical determinant of differential plasticity.
It should be noted that in our study the mice were anesthetized when tuning curves were measured, making it unlikely that top-down signals (Lamme et al., 1998; Maunsell and Treue, 2006; Roelfsema, 2006; Ekstrom et al., 2008) are directly responsible for the results. Attentional modulation may have been present in the study of Schoups et al. (2001), possibly entailing a sharpening of tuning curves. The expression of effects of visual conditioning outside the behavioral paradigm and under anesthesia suggests that the changes we document are robust, lasting, and independent of top-down signaling.
Implications of selective alterations in CS+ specific assemblies
Our findings have implications for the understanding of groups of functionally related, interconnected neurons, alternatively called cell assemblies (Hebb, 1949; Harris, 2005). Because members of an assembly are thought to respond to a common object or object property, a pragmatic approach to define an assembly in the current study is by the common tuning of member cells to particular stimulus properties. If this criterion is adopted, then our observations suggest that plasticity in visual response patterns only stands out for the assembly commonly tuned to the stimulus feature that had been specifically coupled to reward during prior training.
Earlier studies showed that appetitive conditioning increases visual evoked potentials (Hernandez-Peon, 1961; Frankó et al., 2010) and causes a reduction in the psychophysical detection threshold for stimuli that have been paired with reward (Seitz et al., 2009). Augmentation of the relative population output of the CS+ assembly, by sharper direction tuning in the CS+ assembly and broadening of tuning curves toward the CS+, may serve to facilitate processing of the CS+ in higher cortical areas (Zhang et al., 2012), while the observation of extension of the effects to directions close to the CS+ (Fig. 5G) indicates generalization of the CS+ stimulus (Lissek et al., 2008).
A single mechanism could underlie the changes in tuning curves, amplifying the response of only the near-CS+ tuned assembly to the CS+, and increasing both directional selectivity and convexity of the tuning curve. Given this hypothesis, our results suggest that common tuning to stimulus features in V1 cell assemblies is coupled to selective plasticity for processing these preferred features. Several learning rules, either related to dopaminergic signaling or not, could account for reward-dependent sensorimotor learning (Pennartz, 1997; Schultz et al., 1997; Sutton and Barto, 1998; Pennartz et al., 2000; Dayan and Balleine, 2002; Roelfsema and van Ooyen, 2005). Nevertheless, the plausibility of these algorithms, the nature of the reinforcement signal, and the underlying physiological (cf. Hofer et al., 2011; Ko et al., 2011; Bock et al., 2011) and molecular transduction pathways must await further investigation.
Functional consequences of reward learning were nonuniformly distributed across cortical space and only affected a subset of neurons (Fig. 7). This suggests that the mechanisms conveying reward information do so selectively on local groups of neurons and raises the hypothesis that reinforcement-signaling axons terminate sparsely in V1 (Febvret et al., 1991; Müller and Huston, 2007; Rivera et al., 2008), only affecting neurons located in close proximity to these afferents. Such a mechanism could explain the close proximity of CS+ tuned neighbors, as the effects of reward on the primary visual cortex will be centered around hotspots of reinforcement-gated plasticity. Alternatively, nonuniformities may originate from interactions between uniformly distributed reward inputs and local, history-dependent, cell activity patterns.
In conclusion, we propose that formation of a stimulus–reward association drives a learning mechanism in selective visual cortex assemblies that facilitates relative population output to the conditioned stimulus and similar orientations. These changes may help the visual cortex to maintain a stable, robust representation of conditioned stimuli, generalize across minor variations in stimulus features, and assist bottom-up driven detection of reward-predicting inputs.
Footnotes
This work was supported by SenterNovem BSIK Grant 03053, NWO VICI Grant 918.46.609, and EU Grant FP7-ICT-270108 to CMAP. We thank Francesco Battaglia, Tobias Kalenscher, Carien Lansink, and Martin Vinck for comments on this manuscript; Marcus Leinweber, the laboratory of Tobias Bonhoeffer, Laura Donga, Ruud Joosten and the laboratory of Arthur Konnerth for helping us with techniques for calcium imaging; Steven van Hooser for sharing data-analysis tools; and Emma van Bodegraven for assisting with cell detection.
The authors declare no competing financial interests.
References
- Andermann ML, Kerlin AM, Roumis DK, Glickfeld LL, Reid RC. Functional specialization of mouse higher visual cortical areas. Neuron. 2011;72:1025–1039. doi: 10.1016/j.neuron.2011.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bao S, Chan VT, Merzenich MM. Cortical remodelling induced by activity of ventral tegmental dopamine neurons. Nature. 2001;412:79–83. doi: 10.1038/35083586. [DOI] [PubMed] [Google Scholar]
- Blake DT, Heiser MA, Caywood M, Merzenich MM. Experience-dependent adult cortical plasticity requires cognitive association between sensation and reward. Neuron. 2006;52:371–381. doi: 10.1016/j.neuron.2006.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bock DD, Lee WC, Kerlin AM, Andermann ML, Hood G, Wetzel AW, Yurgenson S, Soucy ER, Kim HS, Reid RC. Network anatomy and in vivo physiology of visual cortical neurons. Nature. 2011;471:177–182. doi: 10.1038/nature09802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonin V, Histed MH, Yurgenson S, Reid RC. Local diversity and fine-scale organization of receptive fields in mouse visual cortex. J Neurosci. 2011;31:18506–18521. doi: 10.1523/JNEUROSCI.2974-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleland GG, Davey GC. Autoshaping in the rat: the effects of localizable visual and auditory signals for food. J Exp Anal Behav. 1983;40:47–56. doi: 10.1901/jeab.1983.40-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Balleine BW. Reward, motivation, and reinforcement learning. Neuron. 2002;36:285–298. doi: 10.1016/S0896-6273(02)00963-7. [DOI] [PubMed] [Google Scholar]
- Dräger UC. Observations on monocular deprivation in mice. J Neurophysiol. 1978;41:28–42. doi: 10.1152/jn.1978.41.1.28. [DOI] [PubMed] [Google Scholar]
- Dragoi V, Sharma J, Sur M. Adaptation-induced plasticity of orientation tuning in adult visual cortex. Neuron. 2000;28:287–298. doi: 10.1016/S0896-6273(00)00103-3. [DOI] [PubMed] [Google Scholar]
- Dragoi V, Rivadulla C, Sur M. Foci of orientation plasticity in visual cortex. Nature. 2001;411:80–86. doi: 10.1038/35075070. [DOI] [PubMed] [Google Scholar]
- Ekstrom LB, Roelfsema PR, Arsenault JT, Bonmassar G, Vanduffel W. Bottom-up dependent gating of frontal signals in early visual cortex. Science. 2008;321:414–417. doi: 10.1126/science.1153276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Febvret A, Berger B, Gaspar P, Verney C. Further indication that distinct dopaminergic subsets project to the rat cerebral cortex: lack of colocalization with neurotensin in the superficial dopaminergic fields of the anterior cingulate, motor, retrosplenial and visual cortices. Brain Res. 1991;547:37–52. doi: 10.1016/0006-8993(91)90572-d. [DOI] [PubMed] [Google Scholar]
- Frankó E, Seitz AR, Vogels R. Dissociable neural effects of long-term stimulus—reward pairing in macaque visual cortex. J Cogn Neurosci. 2010;22:1425–1439. doi: 10.1162/jocn.2009.21288. [DOI] [PubMed] [Google Scholar]
- Frenkel MY, Sawtell NB, Diogo AC, Yoon B, Neve RL, Bear MF. Instructive effect of visual experience in mouse visual cortex. Neuron. 2006;51:339–349. doi: 10.1016/j.neuron.2006.06.026. [DOI] [PubMed] [Google Scholar]
- Garaschuk O, Milos RI, Konnerth A. Targeted bulk-loading of fluorescent indicators for two-photon brain imaging in vivo. Nat Protoc. 2006;1:380–386. doi: 10.1038/nprot.2006.58. [DOI] [PubMed] [Google Scholar]
- Gavornik JP, Shuler MG, Loewenstein Y, Bear MF, Shouval HZ. Learning reward timing in cortex through reward dependent expression of synaptic plasticity. Proc Natl Acad Sci U S A. 2009;106:6826–6831. doi: 10.1073/pnas.0901835106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghose GM, Yang T, Maunsell JH. Physiological correlates of perceptual learning in monkey v1 and v2. J Neurophysiol. 2002;87:1867–1888. doi: 10.1152/jn.00690.2001. [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Li W, Piech V. Perceptual learning and adult cortical plasticity. J Physiol. 2009;587:2743–2751. doi: 10.1113/jphysiol.2009.171488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon JA, Stryker MP. Experience-dependent plasticity of binocular responses in the primary visual cortex of the mouse. J Neurosci. 1996;16:3274–3286. doi: 10.1523/JNEUROSCI.16-10-03274.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guizar-Sicairos M, Thurman ST, Fienup JR. Efficient subpixel image registration algorithms. Opt Lett. 2008;33:156–158. doi: 10.1364/OL.33.000156. [DOI] [PubMed] [Google Scholar]
- Harris KD. Neural signatures of cell assembly organization. Nat Rev Neurosci. 2005;6:399–407. doi: 10.1038/nrn1669. [DOI] [PubMed] [Google Scholar]
- Hebb DO. The organization of behavior. New York: Wiley; 1949. [Google Scholar]
- Hernandez-Peon R. Reticular mechanisms of sensory control. In: Rosenblith WA, editor. Sensory communication. New York: Wiley; 1961. pp. 497–520. [Google Scholar]
- Hirsch HV, Spinelli DN. Visual experience modifies distribution of horizontally and vertically oriented receptive fields in cats. Science. 1970;168:869–871. doi: 10.1126/science.168.3933.869. [DOI] [PubMed] [Google Scholar]
- Hofer SB, Mrsic-Flogel TD, Bonhoeffer T, Hübener M. Lifelong learning: ocular dominance plasticity in mouse visual cortex. Curr Opin Neurobiol. 2006;16:451–459. doi: 10.1016/j.conb.2006.06.007. [DOI] [PubMed] [Google Scholar]
- Hofer SB, Mrsic-Flogel TD, Bonhoeffer T, Hübener M. Experience leaves a lasting structural trace in cortical circuits. Nature. 2009;457:313–317. doi: 10.1038/nature07487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofer SB, Ko H, Pichler B, Vogelstein J, Ros H, Zeng H, Lein E, Lesica NA, Mrsic-Flogel TD. Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex. Nat Neurosci. 2011;14:1045–1052. doi: 10.1038/nn.2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields of single neurones in the cat's striate cortex. J Physiol. 1959;148:574–591. doi: 10.1113/jphysiol.1959.sp006308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaas JH, Merzenich MM, Killackey HP. The reorganization of somatosensory cortex following peripheral nerve damage in adult and developing mammals. Annu Rev Neurosci. 1983;6:325–356. doi: 10.1146/annurev.ne.06.030183.001545. [DOI] [PubMed] [Google Scholar]
- Kaas JH, Krubitzer LA, Chino YM, Langston AL, Polley EH, Blair N. Reorganization of retinotopic cortical maps in adult mammals after lesions of the retina. Science. 1990;248:229–231. doi: 10.1126/science.2326637. [DOI] [PubMed] [Google Scholar]
- Kalenscher T, Pennartz CM. Is a bird in the hand worth two in the future? The neuroeconomics of intertemporal decision-making. Prog Neurobiol. 2008;84:284–315. doi: 10.1016/j.pneurobio.2007.11.004. [DOI] [PubMed] [Google Scholar]
- Kalenscher T, Windmann S, Diekamp B, Rose J, Güntürkün O, Colombo M. Single units in the pigeon brain integrate reward amount and time-to-reward in an impulsive choice task. Curr Biol. 2005;15:594–602. doi: 10.1016/j.cub.2005.02.052. [DOI] [PubMed] [Google Scholar]
- Keck T, Mrsic-Flogel TD, Vaz Afonso M, Eysel UT, Bonhoeffer T, Hübener M. Massive restructuring of neuronal circuits during functional reorganization of adult visual cortex. Nat Neurosci. 2008;11:1162–1167. doi: 10.1038/nn.2181. [DOI] [PubMed] [Google Scholar]
- Kerlin AM, Andermann ML, Berezovskii VK, Reid RC. Broadly tuned response properties of diverse inhibitory neuron subtypes in mouse visual cortex. Neuron. 2010;67:858–871. doi: 10.1016/j.neuron.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko H, Hofer SB, Pichler B, Buchanan KA, Sjöström PJ, Mrsic-Flogel TD. Functional specificity of local synaptic connections in neocortical networks. Nature. 2011;473:87–91. doi: 10.1038/nature09880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreile AK, Bonhoeffer T, Hübener M. Altered visual experience induces instructive changes of orientation preference in mouse visual cortex. J Neurosci. 2011;31:13911–13920. doi: 10.1523/JNEUROSCI.2143-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamme VA, Zipser K, Spekreijse H. Figure-ground activity in primary visual cortex is suppressed by anesthesia. Proc Natl Acad Sci U S A. 1998;95:3263–3268. doi: 10.1073/pnas.95.6.3263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Van Hooser SD, Mazurek M, White LE, Fitzpatrick D. Experience with moving visual stimuli drives the early development of cortical direction selectivity. Nature. 2008;456:952–956. doi: 10.1038/nature07417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Lu H, Cheng PL, Ge S, Xu H, Shi SH, Dan Y. Clonally related visual cortical neurons show similar stimulus feature selectivity. Nature. 2012;486:118–121. doi: 10.1038/nature11110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lissek S, Biggs AL, Rabin SJ, Cornwell BR, Alvarez RP, Pine DS, Grillon C. Generalization of conditioned fear-potentiated startle in humans: experimental validation and clinical relevance. Behav Res Ther. 2008;46:678–687. doi: 10.1016/j.brat.2008.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu CH, Heynen AJ, Shuler MG, Bear MF. Cannabinoid receptor blockade reveals parallel plasticity mechanisms in different layers of mouse visual cortex. Neuron. 2008;58:340–345. doi: 10.1016/j.neuron.2008.02.020. [DOI] [PubMed] [Google Scholar]
- Lovibond PF. Facilitation of instrumental behavior by a pavlovian appetitive conditioned stimulus. J Exp Psychol Anim Behav Process. 1983;9:225–247. doi: 10.1037/0097-7403.9.3.225. [DOI] [PubMed] [Google Scholar]
- Marshel JH, Garrett ME, Nauhaus I, Callaway EM. Functional specialization of seven mouse visual cortical areas. Neuron. 2011;72:1040–1054. doi: 10.1016/j.neuron.2011.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maunsell JH, Treue S. Feature-based attention in visual cortex. Trends Neurosci. 2006;29:317–322. doi: 10.1016/j.tins.2006.04.001. [DOI] [PubMed] [Google Scholar]
- Mrsic-Flogel TD, Hofer SB, Ohki K, Reid RC, Bonhoeffer T, Hübener M. Homeostatic regulation of eye-specific responses in visual cortex during ocular dominance plasticity. Neuron. 2007;54:961–972. doi: 10.1016/j.neuron.2007.05.028. [DOI] [PubMed] [Google Scholar]
- Müller CP, Huston JP. Dopamine activity in the occipital and temporal cortices of rats: dissociating effects of sensory but not pharmacological stimulation. Synapse. 2007;61:254–258. doi: 10.1002/syn.20366. [DOI] [PubMed] [Google Scholar]
- Niell CM, Stryker MP. Highly selective receptive fields in mouse visual cortex. J Neurosci. 2008;28:7520–7536. doi: 10.1523/JNEUROSCI.0623-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nimmerjahn A, Kirchhoff F, Kerr JN, Helmchen F. Sulforhodamine 101 as a specific marker of astroglia in the neocortex in vivo. Nat Methods. 2004;1:31–37. doi: 10.1038/nmeth706. [DOI] [PubMed] [Google Scholar]
- Ohki K, Reid RC. Specificity and randomness in the visual cortex. Curr Opin Neurobiol. 2007;17:401–407. doi: 10.1016/j.conb.2007.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohki K, Chung S, Ch'ng YH, Kara P, Reid RC. Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature. 2005;433:597–603. doi: 10.1038/nature03274. [DOI] [PubMed] [Google Scholar]
- Pennartz CM. Reinforcement learning by hebbian synapses with adaptive thresholds. Neuroscience. 1997;81:303–319. doi: 10.1016/S0306-4522(97)00118-8. [DOI] [PubMed] [Google Scholar]
- Pennartz CM, McNaughton BL, Mulder AB. The glutamate hypothesis of reinforcement learning. Prog Brain Res. 2000;126:231–253. doi: 10.1016/S0079-6123(00)26017-2. [DOI] [PubMed] [Google Scholar]
- Rachlin H, Green L. Commitment, choice and self-control. J Exp Anal Behav. 1972;17:15–22. doi: 10.1901/jeab.1972.17-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringach DL, Shapley RM, Hawken MJ. Orientation selectivity in macaque v1: diversity and laminar dependence. J Neurosci. 2002;22:5639–5651. doi: 10.1523/JNEUROSCI.22-13-05639.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera A, Peñafiel A, Megías M, Agnati LF, López-Téllez JF, Gago B, Gutiérrez A, de la Calle A, Fuxe K. Cellular localization and distribution of dopamine d(4) receptors in the rat cerebral cortex and their relationship with the cortical dopaminergic and noradrenergic nerve terminal networks. Neuroscience. 2008;155:997–1010. doi: 10.1016/j.neuroscience.2008.05.060. [DOI] [PubMed] [Google Scholar]
- Rochefort NL, Narushima M, Grienberger C, Marandi N, Hill DN, Konnerth A. Development of direction selectivity in mouse cortical neurons. Neuron. 2011;71:425–432. doi: 10.1016/j.neuron.2011.06.013. [DOI] [PubMed] [Google Scholar]
- Roelfsema PR. Cortical algorithms for perceptual grouping. Annu Rev Neurosci. 2006;29:203–227. doi: 10.1146/annurev.neuro.29.051605.112939. [DOI] [PubMed] [Google Scholar]
- Roelfsema PR, van Ooyen A. Attention-gated reinforcement learning of internal representations for classification. Neural Comput. 2005;17:2176–2214. doi: 10.1162/0899766054615699. [DOI] [PubMed] [Google Scholar]
- Roelfsema PR, van Ooyen A, Watanabe T. Perceptual learning rules based on reinforcers and attention. Trends Cogn Sci. 2010;14:64–71. doi: 10.1016/j.tics.2009.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawtell NB, Frenkel MY, Philpot BD, Nakazawa K, Tonegawa S, Bear MF. Nmda receptor-dependent ocular dominance plasticity in adult visual cortex. Neuron. 2003;38:977–985. doi: 10.1016/S0896-6273(03)00323-4. [DOI] [PubMed] [Google Scholar]
- Schoenbaum G, Chiba AA, Gallagher M. Orbitofrontal cortex and basolateral amygdala encode expected outcomes during learning. Nat Neurosci. 1998;1:155–159. doi: 10.1038/407. [DOI] [PubMed] [Google Scholar]
- Schoups A, Vogels R, Qian N, Orban G. Practising orientation identification improves orientation coding in v1 neurons. Nature. 2001;412:549–553. doi: 10.1038/35087601. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Seitz AR, Kim D, Watanabe T. Rewards evoke learning of unconsciously processed visual stimuli in adult humans. Neuron. 2009;61:700–707. doi: 10.1016/j.neuron.2009.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah RD, Crair MC. Mechanisms of response homeostasis during retinocollicular map formation. J Physiol. 2008;586:4363–4369. doi: 10.1113/jphysiol.2008.157222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shuler MG, Bear MF. Reward timing in the primary visual cortex. Science. 2006;311:1606–1609. doi: 10.1126/science.1123513. [DOI] [PubMed] [Google Scholar]
- Stosiek C, Garaschuk O, Holthoff K, Konnerth A. In vivo two-photon calcium imaging of neuronal networks. Proc Natl Acad Sci U S A. 2003;100:7319–7324. doi: 10.1073/pnas.1232232100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning: an introduction. Vol. 28. Cambridge: MIT Press; 1998. [Google Scholar]
- Svoboda K, Helmchen F, Denk W, Tank DW. Spread of dendritic excitation in layer 2/3 pyramidal neurons in rat barrel cortex in vivo. Nat Neurosci. 1999;2:65–73. doi: 10.1038/4569. [DOI] [PubMed] [Google Scholar]
- Tropea D, Majewska AK, Garcia R, Sur M. Structural dynamics of synapses in vivo correlate with functional changes during experience-dependent plasticity in visual cortex. J Neurosci. 2010;30:11086–11095. doi: 10.1523/JNEUROSCI.1661-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Duuren E, van der Plasse G, Lankelma J, Joosten RN, Feenstra MG, Pennartz CM. Single-cell and population coding of expected reward probability in the orbitofrontal cortex of the rat. J Neurosci. 2009;29:8965–8976. doi: 10.1523/JNEUROSCI.0005-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberger NM, Javid R, Lepan B. Long-term retention of learning-induced receptive-field plasticity in the auditory cortex. Proc Natl Acad Sci U S A. 1993;90:2394–2398. doi: 10.1073/pnas.90.6.2394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S, Jiang W, Poo MMM, Dan Y. Activity recall in a visual cortical ensemble. Nat Neurosci. 2012;15:449–455. S1–2. doi: 10.1038/nn.3036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang T, Maunsell JH. The effect of perceptual learning on neuronal responses in monkey visual area v4. J Neurosci. 2004;24:1617–1626. doi: 10.1523/JNEUROSCI.4442-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Zhaoping L, Zhou T, Fang F. Neural activities in v1 create a bottom-up saliency map. Neuron. 2012;73:183–192. doi: 10.1016/j.neuron.2011.10.035. [DOI] [PubMed] [Google Scholar]