The Role of Delayed Suppression in Slow and Fast Contrast Adaptation in V1 Simple Cells

Abstract

The sensitivity and rate of neural coding along the early visual pathways adapt to changes in contrast of the retinal image caused by external motion or self-generated eye movements. To identify the functional mechanisms of fast and slow contrast adaptation at the level of the visual cortex, we randomly varied, over both short and long timescales, the contrast of optimal sinusoidal gratings flashed in the receptive field of simple cells. We found that fast contrast-dependent suppression lagged excitation by ∼11 ms and controlled the spike's temporal precision. During slow adaptation to low contrasts, the gain and latency of excitation increased whereas suppression became less visible, resulting in more sensitive but slower and more variable responses. We conclude that delayed suppression controls the response dynamics during both fast and slow contrast adaptation. More generally, we propose that sensory adaptation trades neuronal sensitivity for processing speed by changing the balance between excitation and delayed inhibition.

Introduction

By adapting to the varying statistics of natural environments, sensory neurons can make an efficient use of their limited dynamic range and coding capacities (Barlow and Foldiak, 1989). In the mammalian primary visual cortex (V1), neurons match their dynamic range to the range of contrasts presented in the receptive field for the past few seconds (Ohzawa et al., 1982, 1985). In addition to this slow contrast adaptation, V1 neurons also adapt to the contrast of current stimuli by reducing their gain so that spatial selectivity remains contrast invariant (Sclar and Freeman, 1982; see contrast gain control in Albrecht and Geisler, 1991; and contrast normalization in Heeger, 1992). This fast contrast adaptation could also increase the coding rate at high contrasts by accelerating the response's temporal dynamics (Holub and Morton-Gibson, 1981; Dean and Tolhurst, 1986; Reid et al., 1992; Carandini and Heeger, 1994; Albrecht, 1995; Gawne et al., 1996; Carandini et al., 1997; Mechler et al., 1998; Reich et al., 2001; Alitto and Usrey, 2004) and by lowering the response's variability (Finn et al., 2007; Mechler et al., 1998).

However, despite the central role of fast and slow contrast adaptation in visual processing, their biological substrates remain largely unknown. Slow adaptation likely relies on both intrinsic and cortically based synaptic mechanisms (Maffei et al., 1973; Ohzawa et al., 1985; Carandini and Ferster, 1997; Sanchez-vives et al., 2000; Nowak et al., 2005). In the case of fast contrast adaptation, the relative roles of the spike threshold, subcortical sources, and intracortical synaptic inhibition are still debated (Geisler and Albrecht, 1992; Heeger, 1992; Borg-Graham et al., 1998; Hirsch et al., 2003; Lauritzen and Miller, 2003; Finn et al., 2007; Katzner et al., 2011). Part of the issue may be that “slow” adaptation in V1 actually spans a diversity of timescales, from <1 s (Bonds, 1991; Müller et al., 1999) to seconds (Ohzawa et al., 1982, 1985) to minutes (Sharpee et al., 2006); moreover, the fine dynamics of the fast (<100 ms; Albrecht et al., 2002) contrast gain control are still unknown. As a consequence, the seconds-long stimulus durations used in most previous studies of V1 contrast processing (shortest stimulus presentations: ∼200 ms in Gawne et al., 1996; Reich et al., 2001; Albrecht et al., 2002; Nowak and Barone, 2009) may have activated both slow and fast contrast-dependent nonlinearities and resulted in a mixture of effects in the recorded responses (Nowak and Barone, 2009).

In the present study, we used white noise analysis to characterize independently the functional mechanisms of slow and fast contrast adaptation. Our stimulus design ensured that the contrast responses to ∼13-ms-long individual frames (instantaneous contrast) were affected only by fast contrast adaptation. We also varied the ambient contrast of the stimulus on a slow timescale (∼1 min) to isolate the effects of slow contrast-dependent nonlinearities by comparing the receptive fields (RFs) reconstructed in different adaptation conditions. Our results reveal that delayed nonlinear suppression plays a crucial role in adapting the temporal dynamics of V1 responses to the contrast of visual stimuli.

Materials and Methods

Recording procedures.

Single units were recorded extracellularly in area 17 of anesthetized (Pentothal, 1.0 mg/kg/h) and paralyzed (Flaxedil, 10 mg/kg/h) adult male and female cats, in conformance with the guidelines adopted by the Society for Neurosciences. The orientation, direction, spatial frequency, and size tuning of each neuron was determined quantitatively by presenting pseudorandom sequences of 4-s-long drifting sinusoidal gratings (Michelson contrast: 35%) on a CRT display (refresh rate: 76 Hz, mean luminance: 20 cd/m², subtending 31° × 23° at 57 cm). The precise position and spatial organization of the RF was also measured with sparse noise stimuli. Cells were classified as “simple” based on clearly segregated ON and OFF subregions (Hubel and Wiesel, 1962) and on the relative amplitudes of the DC and first harmonic components of the spike response to an optimal drifting grating (Skottun et al., 1991).

Visual stimulus.

Simple cells were stimulated with ∼52-s-long blocks of flashed sinusoidal gratings. The orientation, spatial frequency, and size of these gratings were optimal for the recorded cell, but their contrast and spatial phase changed at the screen refresh rate (Fig. 1A). Each block consisted in 10 repeats of a sequence of 400 frames, drawn pseudorandomly and with uniform probability from a set of 40 combinations of 10 contrasts and four phases. The four 90°-spaced spatial phases were selected so that one of them was optimal for the cell based on the RF map measured by reverse correlation and, when it was available, the phase tuning of the cell. One of the 10 contrast values was set to zero to provide for blank stimuli and the others spanned a two-octave interval in equal logarithmic steps. The set of contrast values varied across blocks: in the “high contrast range” condition (Hi CT), the contrast varied from 20% to 80%, whereas in the “low contrast range” condition (Lo CT), the contrast varied from 7.07% to 28.28%. In some cells we also presented a “very low contrast range” condition, in which the contrast varied from 2.5% to 10%. The responses measured in this latter condition agreed with the rest of our results, but were not included in the population analysis because only four of the recorded cells displayed sufficient responses for subsequent RF reconstruction. Blocks were separated by 5 s blank images of uniform luminance. To allow for slow contrast adaptation, the initial 8 s of the responses after each block onset were discarded. Each cell was stimulated with 27–60 different blocks.

Figure 1.

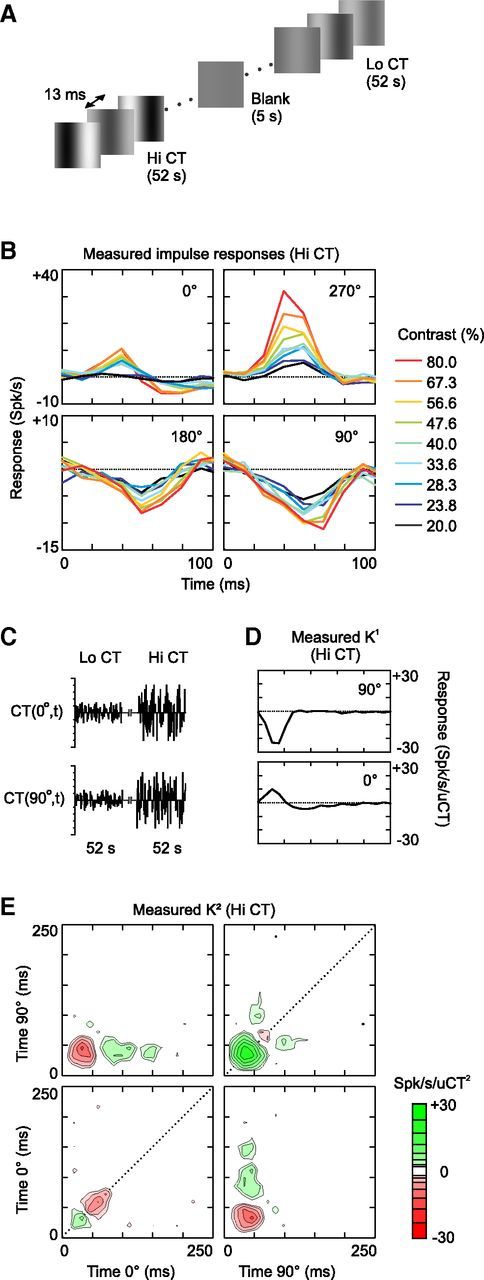
First- and second-order analysis of contrast suppression at Hi CT (cell 1). A, The stimulus was a dynamic sequence of optimal gratings, the spatial phase and contrast of which changed randomly at the screen refresh rate (76 Hz). The range of contrasts presented varied across 52-s-long blocks: in the Hi CT condition, the contrast varied between 20% and 80%; in the Lo CT condition, the contrast varied between 7.07% and 28.28%. B, Impulse responses to each of the 36 combinations of contrast and phase presented in the Hi CT condition. Only the dynamic section (first 100 ms) of the 250-ms-long impulse responses is shown. Each panel contains all of the impulse responses reconstructed at a given spatial phase. The color (see figure key) of the impulse responses indicates the contrast of the corresponding frame. The baseline (K⁰ = 10.7 spikes/s) is indicated by the dotted line. C, The stimulus sequence can also be represented by two variables CT(0°,t) and CT(90°,t), corresponding to the contrasts presented at spatial phases 0° and 90° (positive values) and 180° and 270° (negative values). D, K¹ of cell 1 at Hi CT in the 2D stimulus space described in C. E, K² of cell 1 at Hi CT. The K² is arranged in four quadrants corresponding to the four possible phase combinations (clockwise from top left: 0°/90°, 90°/90°, 90°/0°, and 0°/0°, respectively). The x-axis and y-axis specify the delays (from the gratings onsets) after which a particular interaction is observed or, equivalently, the time at which each grating was flashed before the response at time zero. The z-axis (color scale) measures the strength and polarity of the interaction, in units of spikes per second per square unit contrast; note that a logarithmic color scale was used to represent the large dynamic range of the K². The K² diagonals are indicated by dotted lines.

Data preprocessing.

Spike trains were binned at the stimulus duration (∼13.16 ms). Blocks were separated in two sets of approximately equal size: in the fitting set, spike trains were averaged across multiple repeats of the same stimulus sequence and the resulting mean responses were used to fit the models, whereas in the validation set, single-trial responses were used to measure the models' predictive power (see Validation of the models, below). We followed Rust et al. (2005) in including in our analysis only cells for which at least 50 spikes per spatiotemporal dimension were collected in each adaptation condition. One cell was excluded because variations in the spatial profile of the RF during the course of the recordings suggested incomplete suppression of eye movements. Our study is based on the responses of 29 simple cells in the Hi CT condition (mean 301 spikes per dimensions, 12,000 total spikes), of which 26 were sufficiently responsive at Lo CT (mean 184 spikes per dimensions, 7345 total spikes) for comparison of the RFs across contrast ranges.

Fit of the bank of impulse responses.

We first characterized the contrast responses in the Hi CT condition with a bank of impulse responses. This model assumes that each combination of contrast and phase is an independent variable with its own impulse response; the sum of the impulse responses evoked by each stimulus frame results in the predicted response R̂(t):

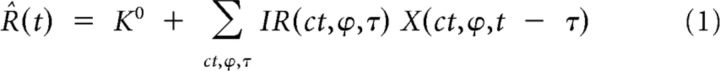where K⁰ is the baseline firing rate, X is the stimulus sequence (X(ct,ϕ,t) = 1 when the frame presented at time t has contrast ct and phase ϕ; X(ct,ϕ,t) = 0 otherwise), and IR represents the 36 independent impulse responses corresponding to each combination of nine contrasts and four phases. The impulse responses were estimated over 20 time samples (∼250 ms). Equation 1 was applied at each time t, resulting in a system of >10,800 linear equations (400 times the number of Hi CT blocks) for 721 coefficients. Because this system had many more equations than coefficients, it had one unique solution that minimized the sum of the squares of the differences between the predicted and the measured responses. The system was solved using the Cholesky factorization implemented by the fast orthogonal algorithm of Korenberg (1988).

Estimation of the second-order kernel.

For nonlinear white noise analysis, the stimulus sequence was represented by two independent variables, CT(0°,t) and CT(90°,t), corresponding to the contrasts of the gratings presented at the spatial phases 0° and 90°, respectively. CT(0°,t) and CT(90°,t) also included negative contrasts, corresponding to gratings presented at spatial phases 180° and 270°, respectively. The first three terms of the Volterra expansion (Marmarelis, 2004) were fitted using both the fitting and the validation datasets according to the following equation:

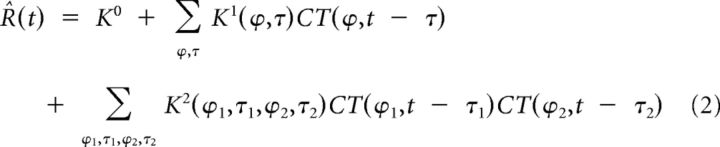where K⁰, K¹, and K² are the zero-, first-, and second-order Volterra kernels, respectively. Equation 2 was applied at each time t and the resulting system of linear equations was solved for the kernels coefficients (1 coefficient for the K⁰, 40 for the K¹, and 800 for the diagonally symmetric K²). We used an orthogonal least-squares algorithm because it produces more robust estimates of the K² coefficients than cross-correlation methods in response to non-Gaussian white noise stimuli (Korenberg, 1988). Note that our stimuli allowed the direct measurement of the diagonals K²(ϕ_i,τ_i,ϕ_i,τ_i) from the responses to gratings of varying contrasts presented at a single spatial phase and a single delay. Because we did not present 45° spatial phases, the K² coefficients corresponding to interactions between 0° and 90° at identical delays τ_i were interpolated from neighboring coefficients at τ_{i − 1} and τ_{i + 1}.

Fit of the linear-nonlinear model.

The linear-nonlinear (LN) model consisted of a linear stage in which CT(0°,t) and CT(90°,t) were convolved with their corresponding 1D filter, followed by a rectifying nonlinearity. The LN model was fitted in three steps. First, the linear part of the LN model was approximated by the K¹ obtained from Equation 2. Second, a sigmoid nonlinearity was added after the linear filter as follows:

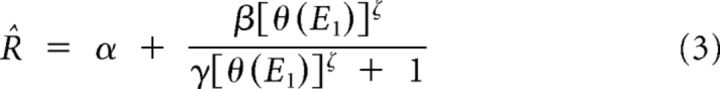where E₁ is the output of the first-order kernel obtained by convolving K¹ with the stimulus and θ(x) is the threshold function, which returns x if x > 0 and 0 otherwise. The parameters α, β, γ, and ζ were estimated by nonlinear least-squares minimization (Levenberg-Marquardt method). Thirdly and finally, the response prediction was further improved by letting all of the 44 parameters of the LN model evolve together, starting from the estimates of the linear filter and the nonlinearity obtained in steps 1 and 2. Only the data from the fitting set were used during this last stage, ensuring that the final fits depended on a dataset different from the one used for validation.

Fit of the multi-LN model.

Multi-LN models consisted of multiple LN branches, the outputs of which were combined by a static output nonlinearity. The multi-LN models were fitted in four steps: (1) the K¹ and K² of the receptive field were computed, (2) the linear filters of the multi-LN model were approximated by the significant eigenvectors of the K², (3) the parameters of the output nonlinearity were estimated, and (4) the estimates of the model parameters were refined by refitting the linear and nonlinear stages together. Both the fitting and the validation sets were used for steps 1 and 2, whereas only the fitting set was used for steps 3 and 4. Steps 2 and 3 have been described in detail previously (Rust et al., 2005).

Step 1: The K¹ and K² were estimated using Equation 2 (see above).

Step 2: The K² was decomposed into a weighted sum of linear filters dimensioned as the K¹ and affected by a quadratic nonlinearity. Equation 2 then becomes:

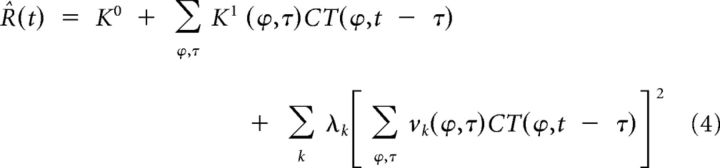The filters v_k are the eigenvectors determined by eigen decomposition of the K². Their contribution to the variance of the K² is measured by the eigenvalues λ_k, which can be positive or negative depending on the excitatory or suppressive effect of the corresponding eigenvectors. As a rule, most of the K² variance was explained by a single eigenvector proportional to the K¹, as expected from the LN model of simple cells. To determine which eigenvectors contributed significantly to the response, we used a bootstrapping procedure (Rust et al., 2005; Schwartz et al., 2006). More precisely, we tested the null hypothesis that the eigenvalues of the measured K² were not significantly different from those expected by chance. First, the K¹ prediction, which corresponds to the first term of Equation 4, was obtained by convolving the K¹ with the stimulus sequence and was subtracted from the mean spike train. Then the K¹-subtracted response was randomly time shifted relative to the stimulus sequence, the K² was estimated, and its eigenvalues were determined. By repeating this calculation 300 times, we obtained the 95% confidence intervals of the K² eigenvalues expected when the stimulus and the response were not correlated. If the largest (or smallest) eigenvalue of the measured K² was not in the confidence interval estimated by bootstrapping, we concluded that the corresponding eigenvector contributed significantly to the K¹-subtracted response. We computed its contribution as the square of the convolution of the stimulus sequence with the eigenvector, scaled by the corresponding eigenvalue. This eigenvector contribution, which corresponds to the third term of Equation 4, was subtracted from the K¹-subtracted response, and we proceeded to determine whether the next largest (or smallest) eigenvalue contributed significantly to the rest of the response. This process was repeated until all of the significant eigenvalues were determined. We never found more than two excitatory and/or two suppressive significant eigenvectors per cell.

Step 3: The output nonlinearity was fitted according to a modified Naka-Rushton equation (Rust et al., 2005):

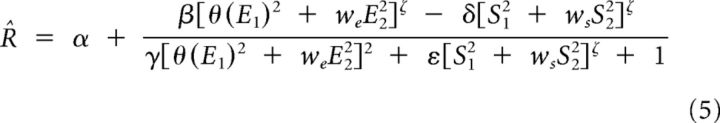where E₂, S₁, and S₂ are the outputs of the excitatory filter e₂ and the suppressive filters s₁ and s₂ determined during step 2. The weights w_e, w_s, δ, and ε were set to 0 when the corresponding filters did not significantly affect the response. δ and ε were clamped to 0 in the case of the multi-LN models without suppression (Fig. 7, Fig. 11).

Figure 7.

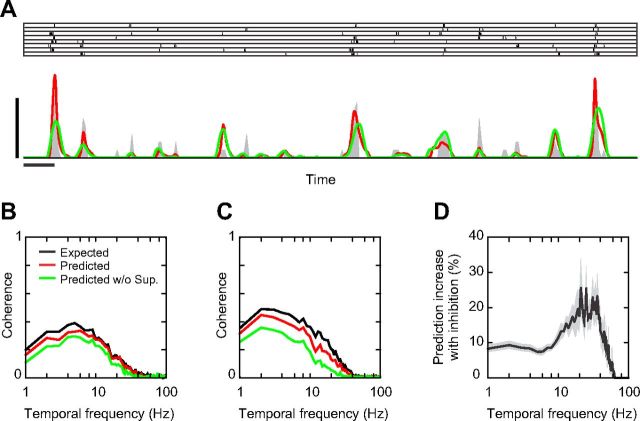
Delayed suppression and temporal spiking precision at Hi CT. A, Two-second-long segment of the trial responses (raster plot), PSTH (dark gray), and predicted responses (red line: full multi-LN model, green line: multi-LN model without suppression) of cell 1 at Hi CT. Horizontal and vertical scale bars indicate 100 ms and 125 Hz, respectively; PSTH bin size, 8 ms. B, Expected (black line) and predicted (red line: full multi-LN model, green line: multi-LN model without suppression) coherences for the neuron shown in A. C, Expected and predicted coherences for cell 2. Same conventions as in B. D, Average improvement of the model prediction with suppression as a function of temporal frequency across the simple cell population, computed as the difference between the predicted coherences with and without suppression, normalized by the expected coherences. Gray area indicates ± 1 SEM.

Figure 11.

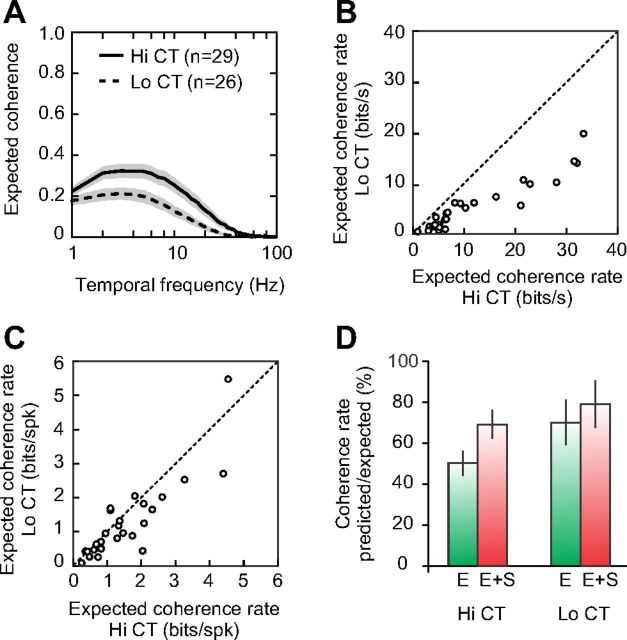
Response precision in different adaptation conditions. A, Expected coherences at Hi CT (solid line) and Lo CT (dashed line). Shaded areas indicate ±1 SEM. B, Expected coherence rates in bits/s measured in each cell at Hi CT (horizontal axis) and at Lo CT (vertical axis). C, The expected coherence rates in B were normalized by the mean firing rate to obtain expected coherence rates in bits per spike. D, Predictive power of the multi-LN model with (red bars) and without suppression (green bars) at Hi CT and Lo CT, computed as the ratio of the predicted over the expected coherence rates.

Step 4: We refined the multi-LN models by letting all of the parameters evolve together, starting from the estimates of the linear filters and of the nonlinearity obtained during steps 2 and 3 (maximum number of parameters: 168 for a multi-LN model comprising two excitatory and two suppressive filters). There are two reasons for this supplementary step: first, the eigenvectors were estimated assuming a square output nonlinearity and not a Naka-Rushton equation. Second, the eigen decomposition imposes that the recovered filters are orthogonal, whereas their potential biological substrates, in particular synaptic inhibition and excitation, may actually be coactivated (Lauritzen and Miller, 2003). This fourth step significantly improved the quality of the fits, prevented spurious orthogonal relationships between the estimated filters, and ensured that the final fits depended on a dataset different from the one used for validation. All fits were done in Elphy (open-source software developed at UNIC by Gérard Sadoc) and relied on Intel mathematical libraries for nonlinear least-squares optimization.

Direction selectivity index.

The direction selectivity index (DSI) was measured from the responses to two gratings drifting in opposite directions for 4 s. Orientation and spatial frequency were optimal for the recorded cell, temporal frequency was set to 2 Hz, Michelson contrast was set to 35%, and the presentation of each grating was repeated at least 5 times. The DSI was defined as follows (DeAngelis et al., 1993):

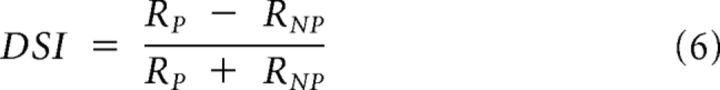where R_P and R_NP are the first harmonics of the trial-averaged responses to the preferred and nonpreferred directions, respectively.

Excitatory and suppressive K².

According to Equation 5, the total excitatory signal e_tot in our models consisted of a weighted sum of the (half-)squared outputs of the excitatory filters: e_tot = θ(E₁)² + w_eE₂².

Conversely, the total suppressive signal, s_tot, consisted of the weighted sum of the squared outputs of the suppressive filters: s_tot = S₁² + w_sS₂².

We reconstructed the second-order kernels for excitation and suppression by replacing the predicted firing rate in Equation 2 with e_tot and s_tot, respectively.

Spatiotemporal tuning of the excitatory and suppressive K².

For a given K² (whether measured, predicted, excitatory or suppressive), second-order interactions selective to motion can be separated from those insensitive to motion by computing the motion K² and the position K², respectively. By definition, pure motion interactions depend on the temporal order in which the two gratings are presented: their sign changes when the gratings spatiotemporal positions are permuted. Conversely, second-order interactions insensitive to motion are not affected by such permutations. Therefore, the motion K² can be computed by subtracting a “flipped” K² (where the temporal axes of each quadrant have been permuted) from the original K², whereas the position K² is obtained by adding the flipped and the original K²:

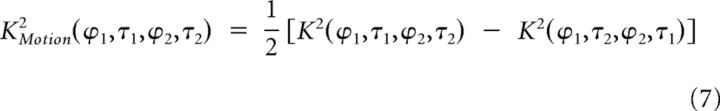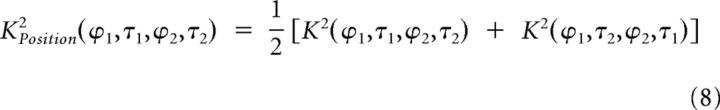To compare the direction preferences of the excitatory and suppressive subunits, we first computed the motion K² of the excitatory and suppressive K², and then computed their Pearson's correlation coefficient. High correlation coefficients indicate similar direction tunings for suppression and excitation, whereas correlation coefficients close to −1 correspond to opposite direction preferences. Similarly, we compared the preference for stationary stimuli of the excitatory and suppressive K² by computing the correlation coefficient between the position K² of excitation and suppression.

Dynamics of the linear filters.

To analyze the time course of the excitatory and suppressive subunits, we picked the largest 1D linear filter of each subunit and computed its envelope as the vector sum of the 1D filter and of its Hilbert transform (DeAngelis et al., 1993). We then interpolated the envelope at 1 ms with a cubic spline and measured the latency of its peak.

Validation of the models: expected and predicted coherences.

The coherence measures in the Fourier space the degree of linear relationship between two signals, w₁(t) and w₂(t), and is defined by:

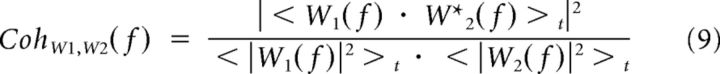where W₁(f) and W₂(f) are the Fourier transforms of w₁(t) and w₂(t) and angular brackets symbolize window averaging (across 1-s-long Hann windows shifted by 0.5 s steps in the present study). The coherence = 1 for linearly related signals, and decreases to <1 when the signals are nonlinearly related and/or corrupted by noise. In particular, the coherence between the recorded response and its prediction by any given model, the predicted coherence, can be used as a measure of the model predictive power across temporal frequencies provided that it is compared with the theoretical maximum given the response noise, the expected coherence (van Hateren and Snippe, 2001). We computed the predicted coherence as the average of the coherences between each trial response R_i(t) and the model prediction, whereas the expected coherence is the average of the coherences computed between each trial response R_i(t) and the mean of the responses to the other trials, R_{j ≠ i}(t). Note that these estimates are biased because of the limited number of repetitions and the fact that coherence can only assume positive values. We corrected for this bias by subtracting shuffled coherences, which were computed as the expected and the predicted coherences except that the trial responses were randomly shifted in time. Finally, the coherence rate, RCoh, quantifies how close the coherence function is to 1 over the entire frequency range:

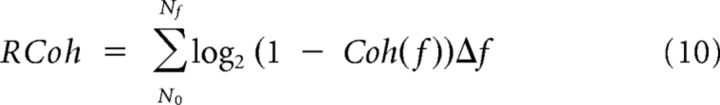The ratio of the predicted over the expected coherence rate measures the proportion of the response signal explained by the corresponding model.

Results

We recorded extracellularly from 29 simple cells in the area 17 of anesthetized adult cats. Each neuron was stimulated by a dynamic sequence of sinusoidal luminance gratings flashed at the orientation, spatial frequency, and size optimal for the cell under study. The contrast and spatial phase of the gratings changed pseudorandomly at the screen refresh rate (76 Hz; Fig. 1A). The range of contrast presented was also varied, in 52-s-long blocks: the contrast of the grating frames was between 20% and 80% during Hi CT conditions and between 7.07% and 28.28% during Lo CT conditions (1.5 octaves below the Hi CT condition). This stimulus design, in which contrast varied over both fast and slow timescales, allowed the independent analysis of fast and slow contrast-dependent nonlinearities: the former were characterized by nonlinear analysis of contrast responses within Hi CT blocks, and the latter were analyzed by comparing receptive fields across adaptation blocks.

Dynamics of fast contrast-dependent suppression in V1 simple cells

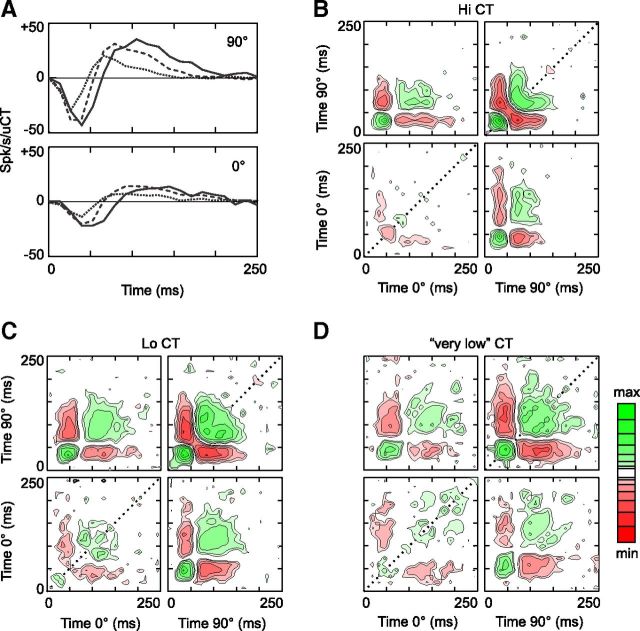
The impact of the fast contrast-dependent nonlinearity on simple cell dynamics can be observed directly by comparing the responses to the contrasts and phases presented in the Hi CT condition (Fig. 1B, cell 1). More precisely, the cell response was modeled as the summed output of a bank of 36 impulse responses, each corresponding to a different combination of contrast and phase (9 contrasts × 4 spatial phases, see Materials and Methods). This is equivalent to measuring the spike-triggered average stimulus with the different combinations of contrast and phase considered as independent variables. At the optimal spatial phase (270°), the peak latency of the impulse responses decreased with contrast, which is consistent with previous results (Gawne et al., 1996; Albrecht et al., 2002). Surprisingly, however, the time course of the impulse responses at the anti-optimal spatial phase (90°) changed in the opposite direction: the trough latency increased with contrast. The time courses of the impulse responses to the 0° and 180° spatial phases were also affected in opposite directions by increasing contrast.

This simple linear analysis is sufficient to reveal the contrast dependence of response dynamics, but not its underlying functional mechanisms, because the visual system does not process different contrasts in independent channels. Alternatively, the visual input sequence can be described by two signed variables, CT(0°,t), representing the contrasts over time at spatial phases 0° and 180° with positive and negative values, respectively, and CT(90°,t), representing the contrasts at 90° and 270° (Fig. 1C). Due to its simplicity, this stimulus space is well suited to nonlinear system identification of contrast and phase processing (Marmarelis, 2004). The first step of this analysis consists of using the Volterra expansion to describe the receptive field by a second-order polynomial as Equation 2 of the Materials and Methods. The coefficients, or kernels, of this polynomial will then serve as a basis for fitting LN and multi-LN models to the receptive field (Rust et al., 2005).

K¹ (Fig. 1D), or the linear receptive field, quantifies the linear response of the cell to individual gratings. It consists of two 1D filters for convolving the inputs CT(0°,t) and CT(90°,t). K² (Fig. 1E) quantifies the nonlinear response due to second-order interactions between gratings. The K² is nearly identical to the spike-triggered covariance matrix described in other studies (Touryan et al., 2002; Rust et al., 2005), except that it was estimated using an orthogonal least-squares algorithm instead of cross-correlation techniques. The K² coefficients indicate whether a given pair of gratings, CT(ϕ₁,τ₁) and CT(ϕ₂,τ₂), facilitates or suppresses the linearly predicted response; the amount of facilitation or suppression equals the coefficient K²(ϕ₁,τ₁,ϕ₂,τ₂) multiplied by the contrast of the gratings. For example, the green region in the upper left quadrant of Figure 1E shows that the response at time 0 is facilitated by the presentation of 0° spatial phase at time −100 ms followed by 90° spatial phase at time −40 ms.

The diagonals of the K² (Fig. 1E, dotted lines) are particularly important for the present study, because they show whether the response to a single grating scales linearly with contrast. These diagonal interactions are facilitatory early in the response (green regions at ∼40 ms) but then become suppressive (red regions at ∼60 ms), suggesting that contrast-dependent suppression is delayed relative to the peak response. Furthermore, the second-order nature of this suppression indicates that it is evoked by both positive and negative contrasts (i.e., it is complex-like). This may explain why, as the contrast increases, the impulse responses to optimal phases are cut short, whereas the suppression caused by anti-optimal phases is prolonged.

LN model prediction of simple cell responses at Hi CT

A popular model of simple cell receptive fields, the LN model, can explain part but not all of the K² structure. Theoretical studies have shown that the K² diagonal of a LN cascade should include only positive coefficients, because the K² diagonal is proportional to the square of the K¹ (Marmarelis, 2004). Therefore, the LN model cannot account for the suppressive interactions we observed along the diagonals of the measured K². To illustrate this, we used part of the recorded responses (the fitting set, see Materials and Methods) to fit a LN model consisting of two impulse responses (based on the K¹) followed by a sigmoid nonlinearity (Fig. 2A). We then predicted the response of the LN model during the rest of the stimulus presentation (the validation set). Finally, the LN prediction was submitted to the same analyses as the observed responses (i.e., we reconstructed the impulse responses and the K² of the LN prediction; Fig. 2B,C). Unlike the bank of impulse responses obtained directly from the observed firing rate (Fig. 1B), the bank of impulse responses predicted by the LN model exhibited no contrast-dependent change in peak or trough latency (Fig. 2B). Moreover, the structure of the measured and the LN-predicted K² were almost identical, except that the latter did not show any evidence of diagonal suppression: instead, diagonal excitation lasted longer in the predicted than in the observed K² (compare Fig. 2C, Fig. 1E). Therefore, as expected, the static nonlinearity of the LN model could not reproduce the phase independence or dynamics of the contrast-dependent nonlinearity.

Figure 2.

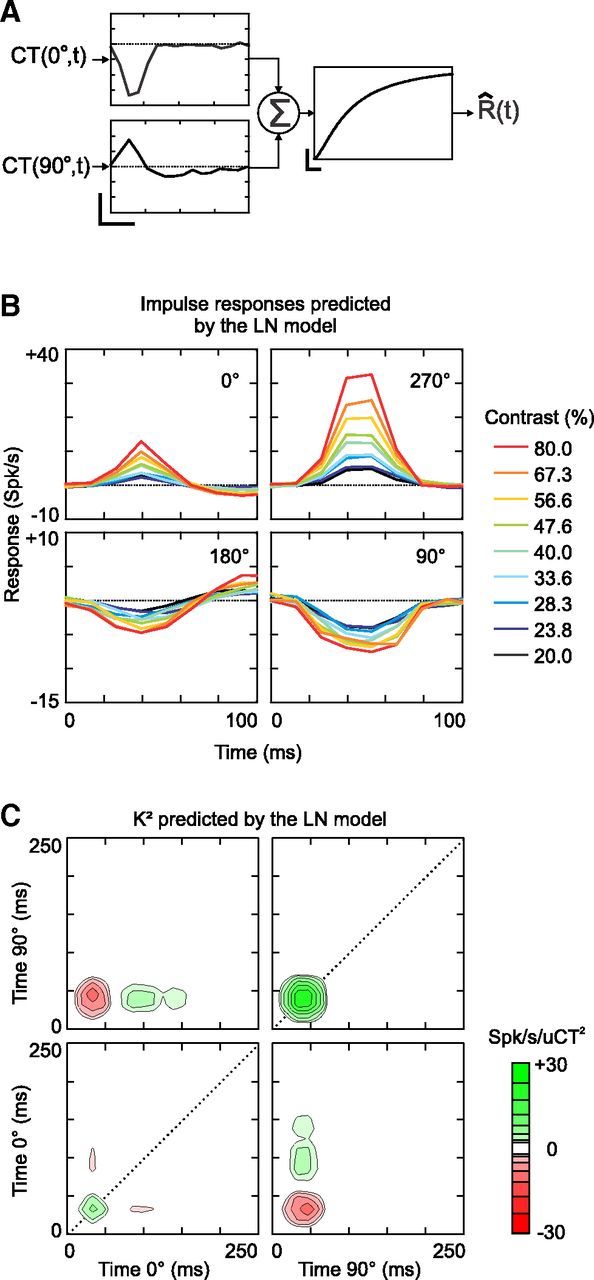
First- and second-order analysis of the response predicted by the LN model of cell 1. A, LN-model of cell 1 in the Hi CT condition. The LN-model consists of two 1D filters receiving the contrast inputs CT(0°,t) and CT(90°,t) (vertical scale bar: 2 spikes/s/uCT; horizontal scale bar: 50 ms), followed by a sigmoid static nonlinearity (vertical scale bar: 100 spikes/s; horizontal scale bar: 1 spikes/s). This nonlinearity corresponds to Equation 3 with parameters α = 0.43, β = 122, γ = 0.26, and ζ = 0.73. B, Impulse responses predicted by the LN model. The impulse responses were computed by solving Equation 1 using the response predicted by the LN model. C, K² predicted by the LN model.

Multi-LN models of simple cell RFs at Hi CT

The properties of nonlinear suppression suggested that simple cells receive delayed suppressive inputs from complex-like subunits. To evaluate this functional mechanism, we fitted the RFs in our population with models consisting of multiple parallel LN branches; the outputs of these branches were combined nonlinearly (multi-LN model, Rust et al., 2005, see Materials and Methods). We proceeded in four steps: after determining the K¹ and K² of the RF (step 1), a set of linear filters was obtained directly by eigen decomposition of the K² (step 2). Each filter consisted of, as for the K¹, a pair of 1D filter corresponding to the inputs CT(0°,t) and CT(90°,t). The contribution of the squared output of each filter to the total K² output was measured by its eigenvalue, which could be positive or negative, as shown in Equation 4 in Materials and Methods. As a result, the signal-dependent variance of the K² was accounted for by a reduced set of filters (never more than two excitatory and/or two suppressive filters in our cell population), the properties and function of which could be analyzed separately. Then (step 3), we fitted the output nonlinearity with a modified Naka-Rushton equation, Equation 5 in Materials and Methods (Rust et al., 2005). Finally (step 4), we refined our estimates of the models by letting all of the parameters (the linear filters as well as the nonlinearity) evolve freely together. We used only part of the response (the fitting set) during this last step; the remaining responses were used for validating the model predictions.

The eigen decomposition of the K² of cell 1 showed that three eigenvalues (one positive and two negative, Fig. 3A) differed significantly from those expected if the stimulus and the spike responses had been uncorrelated (see Materials and Methods). As a result, the multi-LN model (Fig. 3B) comprised one excitatory branch similar to the LN model (Fig. 2A) and two complex-like suppressive branches (i.e., two linear filters, s₁ and s₂, followed by quadratic nonlinearities). s₁ and s₂ had different spatial phase preferences (s₁ was strongest at 90°, whereas s₂ preferred 0°) and, importantly, they were slightly delayed (by ∼10 ms) relative to the excitatory filter, as indicated by the peak latencies of the filter envelopes (Fig. 3B).

Figure 3.

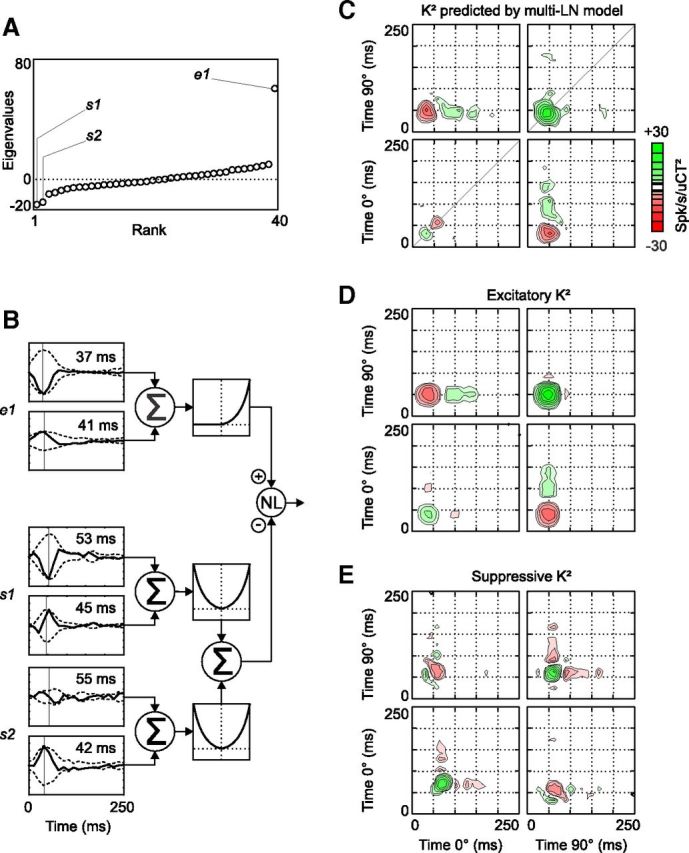
The multi-LN model and its predicted K² at Hi CT (cell 1). A, Graph of the eigenvalues obtained after eigen decomposition of the K² shown in Figure 1E. Three eigenvalues (two negative and one positive) differed significantly from the eigenvalues obtained after randomly time shifting the spike responses relative to the stimulus. B, Schematic illustration of the multi-LN model of cell 1. The linear filters s₁, s₂, and e₁ each consist of two 1D filters. Their envelopes are shown (dotted lines) and the peak latency of each envelope is indicated in inset. The output of e₁ is passed to a half-squaring function, whereas the outputs of s₁ and s₂ are squared. The resulting excitatory and suppressive inputs are combined by a sigmoid nonlinearity (see Materials and Methods), which produces the response prediction. C, K² reconstructed from the response predicted by the multi-LN model in B. D, K² reconstructed from the predicted excitation (i.e., the output of the branch consisting of e₁ followed by the half-squaring nonlinearity). E, K² reconstructed from the predicted suppression, the sum of the squared outputs of s₁ and s₂. This signal then contributes to the subtractive and divisive terms of the output nonlinearity of the multi-LN model. Note that because this suppressive K² is computed before the intervention of the output nonlinearity, green regions in E correspond to interactions that suppress the final predicted firing rate, and red regions facilitate the predicted response. Note also that the diagonal interactions peak at slightly later time in E than in D.

The K² predicted by the multi-LN model (Fig. 3C) improved on the K² predicted by the LN model by displaying diagonal suppression at the 0° spatial phase and by cutting short diagonal excitation at ∼60 ms in the 90°/90° quadrant. This diagonal suppression came from the suppressive filters, as can be seen by reconstructing the K² of the excitatory branch output (Fig. 3D) and comparing it with the K² reconstructed from the pooled output of the suppressive branches (Fig. 3E). The power of the suppressive K² was concentrated in two regions along the diagonal, which counteracted the corresponding regions in the excitatory K², but with a slight delay.

Cell 1 was poorly selective to the direction of motion: its DSI (see Materials and Methods) based on the responses to optimal gratings drifting in opposite directions was 0.42. Accordingly, the excitatory and suppressive filters were not selective to direction either, and suppression in particular depended almost only on the contrast of the presented gratings. The results were slightly different in the case of direction-selective neurons (Fig. 4, cell 2, DSI = 0.99). Contrary to what would be expected from a direction-selective LN model (Marmarelis, 2004), the response was facilitated when the 0° spatial phase was presented after the 90° spatial phase and suppressed when it was presented before, regardless of the delay between the gratings presentations and the spike response (Fig. 4A, top left and bottom right). A similar nonlinear spatiotemporal summation has been reported previously in some direction-selective simple cells (Movshon et al., 1978; Emerson, 1997; Rust et al., 2005). This second cell had a lower F1/F0 ratio in response to drifting gratings than the first one (1.16 vs 1.80, respectively), although both cells were clearly simple.

Figure 4.

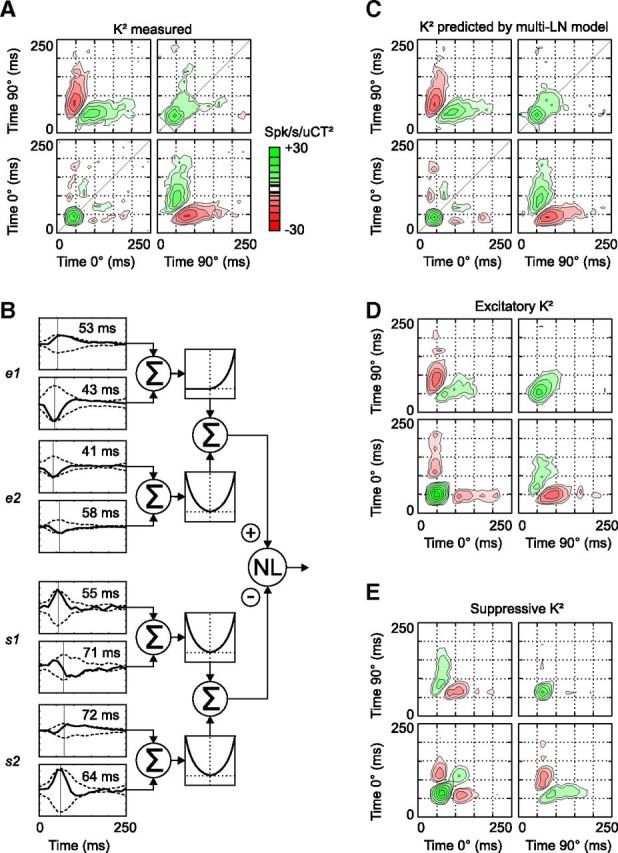
Receptive field and multi-LN model at Hi CT (cell 2). Same conventions as in Figure 3. A, Measured K². B, Multi-LN model of the receptive field of cell 2. C, K² reconstructed from the predicted responses. D, K² reconstructed from the predicted excitation. E, K² reconstructed from the predicted suppression. Note that the suppressive and excitatory filters prefer opposite directions of motion, as indicated by the opposite polarity of the cross-phase interactions in D and E. The delay between excitation and suppression is more pronounced in this cell than in the previous one (Fig. 3).

The multi-LN model of cell 2 (Fig. 4B) showed that both excitatory and suppressive nonlinearities were responsible for the K² structure. In addition to the excitatory filter e₁, which was identical to the K¹, it also comprised a second excitatory filter, e₂, and two suppressive filters, s₁ and s₂. The two excitatory filters were tuned to the same direction but were 90° out of phase (i.e., they formed a quadrature pair). As a result, the total excitation was strongly direction selective and “complex-like” (i.e., it did not show the biphasic temporal modulation characteristic of the LN model; Fig. 4D). The suppressive and excitatory filters were tuned to the opposite direction of motion, as can be seen from the opposite polarity of the cross-phase (0°/90°) quadrants in the excitatory and suppressive K² (Fig. 4D,E). Motion-opponent suppression has been described previously in a similar analysis of macaque simple cell RFs (Rust et al., 2005). However, although this cell was the most direction selective of our sample, the suppressive K² still had most of its power concentrated along the diagonal, indicating that suppression reinforced the cell preference for moving versus static stimuli mainly by suppressing the responses to high contrast stationary stimuli. Finally, the peak latencies of the filter envelopes showed that suppression was delayed relative to excitation by ∼15 ms.

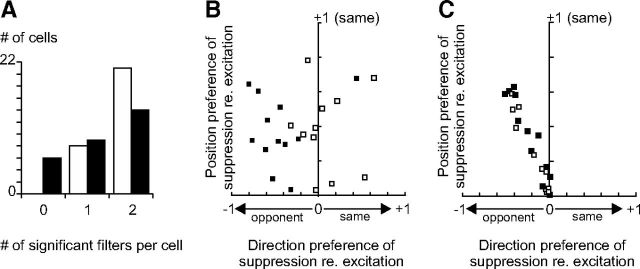
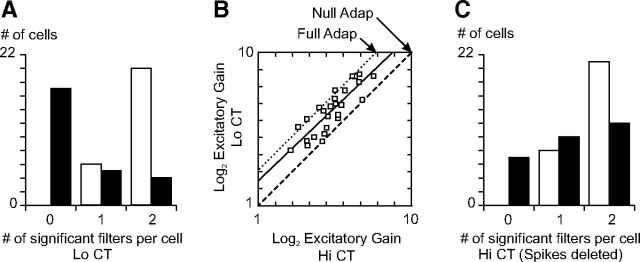
Over our population of simple cells, none of the RFs corresponded to a pure LN model (i.e., a single excitatory filter and no suppressive filters): at high ambient contrast, 79% (23/29) of the recorded cells showed significant suppression, 64% displayed two significant suppressive filters, and 72% two significant excitatory filters (Fig. 5A). On average, suppression was motion opponent (Fig. 5B, horizontal axis, mean ± ci: −0.20 ± 0.17, p < 0.05, t test), but this was more often true in direction-selective than in non-direction-selective neurons (Fig. 5B, solid and open squares, respectively). However, when suppression was present, it always had a non-motion-sensitive component that counteracted excitation along the K² diagonal, thereby decreasing the sensitivity of the cell to the contrast of stationary stimuli (Fig. 5B, vertical axis, mean ± ci: 0.38 ± 0.09, p < 10e-08, t test). Note that suppression was systematically motion opponent in the filters obtained directly after eigen decomposition, likely because the resulting eigenvectors are by definition orthogonal (Fig. 5C). The fourth step of our fitting procedure (joint refitting of the linear and nonlinear parameters of the multi-LN model) alleviated this constraint and revealed balanced excitation and suppression in some non-direction-selective cells (5/11; Fig. 5B).

Figure 5.

Spatiotemporal tuning of the significant excitatory and suppressive filters at Hi CT. A, Histogram of the number of excitatory (white bars) and suppressive (black bars) significant filters per cell at Hi CT. B, Direction and position preference of suppression relative to excitation. Vertical axis: Correlation coefficient (Pearson's r) between the position-specific terms of the excitatory and suppressive K² (position K², see Materials and Methods). Horizontal axis: Correlation coefficient between the motion-specific terms of the excitatory and suppressive K² (motion K²). Open squares indicate non-direction-selective cells having a DSI <0.6; solid squares, direction-selective cells having a DSI >0.6. C, Same as B, except that the fourth step of the multi-LN model fitting (joint refitting of the linear and nonlinear parameters) was omitted. The motion K² of excitation and suppression are now systematically anticorrelated.

Delayed complex-like suppression and response temporal precision at high ambient contrast

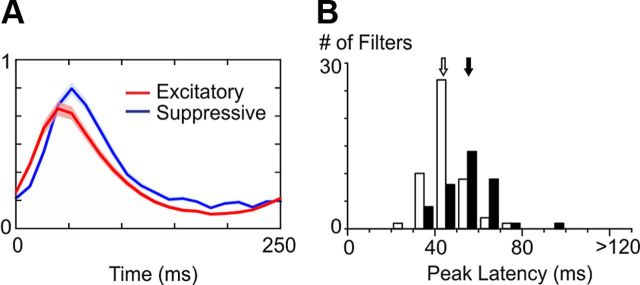
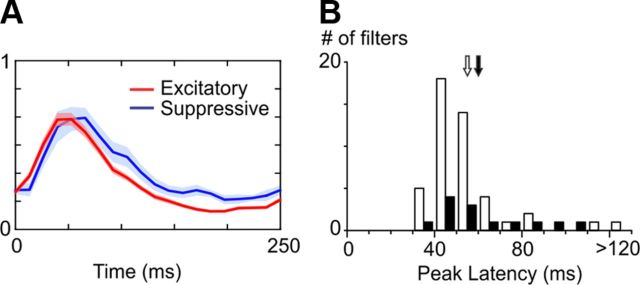
The examples shown in Figure 3 and Figure 4 suggested that suppression is delayed with respect to excitation in the Hi CT condition. This result was confirmed at the population level by comparing the envelopes of the excitatory and suppressive subunits (Fig. 6A; see Materials and Methods). Suppression was slower and peaked on average 11.4 ms later than excitation (Fig. 6B, peak latency of excitation: 44.2 ms ± 8.8 ms, white arrow; peak latency of suppression: 55.6 ms ± 12.3 ms, black arrow; p < 10e-05, unpaired t test). We did not observe any significant difference between the peak latencies of the K¹ envelopes and those of the other excitatory filters.

Figure 6.

Dynamics of the significant excitatory and suppressive filters at Hi CT. A, Average temporal envelopes of the excitatory (red) and suppressive (blue) filters at Hi CT (shaded areas indicate ± 1 SEM). B, Histogram of the peak latencies of the excitatory (white bars) and suppressive (black bars) filter envelopes at Hi CT. Arrows indicate the means of the two distributions (white: excitatory filters, black: suppressive filters).

This delayed suppression may change the temporal precision of the spike output by controlling the duration of the spiking opportunity window (Pouille and Scanziani, 2001; Kremkow et al., 2010). To test this hypothesis, we studied how the predicted responses were affected when the gain of the suppressive filters was clamped to zero during the fitting procedure. Figure 7A shows a 2-s-long segment of cell 1 response at Hi CT (8 repetitions), as well as the response predicted with and without suppression (red and green traces, respectively). To avoid overfitting, the responses were predicted using a different dataset (validation set) from the one used for final estimation of the models' parameters (fitting set, see Materials and Methods). Both models predicted quite well the occurrence of spike events, but without suppression, the peaks of the predicted PSTH tended to be too small in amplitude and too long in duration. Adding suppression to the model resulted in more transient and more accurate predictions of the firing rate waveforms by suppressing the late phase of the responses.

The performances of the two models were compared using the coefficient of determination, or R² (computed as 1 − the ratio of the residual sum of squares to the total sum of squares). In the neuron illustrated in Figure 7A, the R² increased from 0.30 to 0.37 when suppression was included into the model. This difference was significant at the population level: the R² was 0.38 ± 0.19 for the full model compared with 0.33 ± 0.16 for the model without suppression (mean ± SD, p < 0.05, paired t test). The R² for the LN model (0.32 ± 0.15) was not significantly different from the R² for the model without suppression (p = 0.75).

One drawback of the R² is its dependence on the temporal resolution at which the observed and modeled responses are compared. When the bin size is reduced beyond the intrinsic temporal precision of the spike response, the noise component becomes dominant and the resulting variance cannot be reproduced by the models. This issue is especially important for the present study, given the limited number of stimulus sequence repetitions and the potential role of suppression in improving the spike response precision. Therefore, we measured the models' performance at different temporal frequencies as the coherence between the predicted and the observed responses (van Hateren and Snippe, 2001; see Materials and Methods). Moreover, we measured how well the models' predictions fared compared with the theoretical maximum given the response noise by computing the expected coherence (i.e., the coherence between trial responses to the same stimulus sequence). The predicted and expected coherences of cell 1 at Hi CT are shown in Figure 7B. The coherence predicted by the full model (red trace) approached the expected coherence (black trace) even at high temporal frequencies, indicating that the multi-LN model predicted well the transient events of the response. Without suppression, the predicted coherence shifted downward (green trace). The same behavior was observed in the other example cell of this study (Fig. 7C). To quantify this effect in our population, we compared the increase in predicted coherence when suppression was included in the model (i.e., the area between the red and green curves in Fig. 7B,C) to the expected coherence. Among the 23/29 cells that displayed significant suppressive subunits, suppression accounted on average for ∼10% of the expected coherence <10 Hz and ∼20% of the expected coherence at 10–40 Hz (Fig. 7D). Therefore, suppression improves the response prediction over the whole frequency spectrum, but especially at high temporal frequencies.

Effect of slow contrast adaptation on RF sensitivity

The above results showed the involvement of a complex-like, delayed suppression in the fast adaptation of simple cell responses dynamics to high contrast stimuli. We next examined the functional mechanisms of slow contrast adaptation by comparing the RFs measured across different contrast ranges. Figure 8 shows the K¹ and the K² of a third simple cell (F1/F0 = 1.75, DSI = 0.26) measured at Hi CT, Lo CT, and also at “very low” contrasts (contrasts ranging from 2.5% to 10%). As expected (Ohzawa et al., 1982, 1985), neuronal sensitivity adapted to the overall contrast of the stimulus block: when the ambient contrast was lowered, the amplitude of K¹ (Fig. 8A) and K² (Fig. 8B,C,D, note the change in the minimum and maximum of the color scale) increased. However, the effect of slow contrast adaptation was not restricted to the static output nonlinearity of the cell: the response kinetics also slowed down markedly at low ambient contrasts. This deceleration was evident in the K¹, as well as in the expansion of the K² toward the top right corner of each quadrant. Finally, the signature of the fast contrast-dependent suppression (i.e., the delayed suppression along the K² diagonal) was less prominent at Lo CT than at Hi CT and was totally absent at the lowest contrasts tested (Fig. 8D). This example suggests that slow contrast adaptation affects excitation and suppression differentially.

Figure 8.

K¹ and K² measured in three adaptation conditions (cell 3). A, K¹ measured at Hi CT (contrasts ranging from 20% to 80%, dotted line), Lo CT (contrasts ranging from 7% to 28%, dashed line), and very low contrasts (contrasts ranging from 2.5% to 10%, solid line). B–D, K² measured at high, low, and very low contrasts, respectively. The maximum/minimums of the color scale are ±30, ±120, and ±480 spikes/s/uCT² in B, C, and D, respectively.

As we did with the receptive fields measured at Hi CT, we fitted multi-LN models to the RFs measured at Lo CT. We found that the distribution of the significant excitatory filters did not depend on ambient contrast (compare Fig. 9A, Fig. 5A; Wilcoxon rank sum test, p = 0.71). Despite the reduced stimulus power, most neurons (77%) still displayed two significant excitatory filters, because the neuronal sensitivity adapted to the average contrast of the stimulus. Over the population, the gain of excitation, β in Equation 5, increased by 48% from Hi CT to Lo CT. This is half of the change required to maintain the excitation invariant across contrast ranges (Fig. 9B).

Figure 9.

Change in the excitation/inhibition balance across adaptation conditions. A, Histogram of the number of excitatory (white bars) and suppressive (black bars) significant filters per cell at Lo CT. B, Graph of the log₂ excitatory gain at Hi CT versus log₂ excitatory gain at Lo CT. The solid line is the best-fitting straight line (slope: 0.956, y-intercept: 1.50). The dashed line corresponds to no change in gain (null adaptation). The dotted line corresponds to an 8 × increase in gain between Hi CT and Lo CT: this is the gain change that would be expected in the case of perfect adaptation given the 1.5 octave difference in contrast between the two conditions and the squaring nonlinearities of the multi-LN model, as shown in Equation 5. C, Histogram of the number of excitatory (white bars) and suppressive (black bars) significant filters per cell at Hi CT after randomly deleting spikes to match the number of spikes recorded at Lo CT.

Contrary to excitation, however, the distribution of the number of suppressive filters per cell was strongly affected by ambient contrast (Wilcoxon rank sum test, p < 0.001). The proportion of neurons displaying significant suppression fell from 79% to 35% between Hi CT and Lo CT; only 15% (4/26) of the recorded cells still displayed two significant suppressive filters at Lo CT (Fig. 9A). In the minority of cells in which suppression remained significant (9/26), the suppressive filters contributed less to the total variance of the K² at Lo CT than at Hi CT conditions (6.3% at Lo CT vs 10.7% at Hi CT, p < 0.005, paired t test). Therefore, even when suppression remained visible at Lo CT, its strength relative to excitation decreased. The reduction of suppression was not the result of the ∼40% reduction in firing rate between the Lo CT and the Hi CT condition. First, we analyzed only the 26 cells for which we collected at least 50 spikes per spatiotemporal dimensions in both the Hi CT and the Lo CT conditions (Rust et al., 2005). Second, the decrease in firing rate should affect the significance of the excitatory and suppressive filters in the same fashion (Rust et al., 2005) and not differentially as we observed. Finally, as an additional control, we randomly deleted spikes from the Hi CT responses and repeated our analysis (from kernel reconstruction to the determination of the significant filters) on a restricted response set containing as many spikes as in the Lo CT condition. We found that the distributions of both the significant excitatory and suppressive filters were largely unaffected, demonstrating that the number of spikes recorded in the Lo CT condition was not a limiting factor in our analysis (Fig. 9C). We conclude that the adaptation of neuronal sensitivity to slow changes in contrast (Ohzawa et al., 1982, 1985) relies on a shift of the excitation/inhibition balance toward inhibition at Hi CT and toward excitation at Lo CT. One possible explanation for our results could be that inhibitory neurons adapt less to ambient contrast than excitatory neurons.

Effect of slow contrast adaptation on the temporal properties of the response

Our population analysis also confirmed that the ambient contrast of the stimulus block changed the temporal dynamics of the response. Compared with the Hi CT condition, the excitatory filters slowed down in the Lo CT condition, whereas the suppressive filters appeared to be less affected (Fig. 10A). The average peak latency of the excitatory envelopes in the Lo CT condition (55.6 ms ± 27.7 ms, Fig. 10B, white arrow) increased significantly relative to the Hi CT condition (p < 0.01, unpaired t test), whereas the average peak latency of the suppressive envelopes at Lo CT (60.7 ms ± 21.4 ms, black arrow) was not significantly different from the one measured at Hi CT (p = 0.30). As a result, the difference in latency between excitation and suppression was not significant at Lo CT (p = 0.54).

Figure 10.

Dynamics of the significant excitatory and suppressive filters at Lo CT. A, Average temporal envelopes of the excitatory (red) and suppressive (blue) filters at Lo CT (shaded areas indicate ± 1 SEM). B, Histogram of the peak latencies of the excitatory (white bars) and suppressive (black bars) filter envelopes at Lo CT. Arrows indicate the means of the two distributions (white: excitatory filters, black: suppressive filters).

If delayed suppression controls the temporal precision of simple cell responses (Fig. 7), then contrast adaptation, by changing the balance between excitation and delayed suppression, could also affect the response temporal precision. We quantified the precision of the spike responses by computing the expected coherence of each cell in each adaptation condition. We found that when the average contrast of the stimulus decreased, the peak and high cutoff frequency of the coherence function tended to shift downward and leftward (Fig. 11A). This indicates that the spike response, and particularly its high temporal frequency components, became less reliable at low ambient contrasts.

To quantify response reliability across contrast ranges with a single statistic, we computed the expected coherence rates (van Hateren and Snippe, 2001) by integrating the expected coherence over the frequency spectrum (see Materials and Methods). Expected coherence rates were highly variable from one cell to the other, but decreased significantly over the population of 26 neurons that could be analyzed at both Hi CT and Lo CT conditions: from 12.1 ± 10.2 bits/s at Hi CT to 5.4 ± 5.0 bits/s at Lo CT (mean ± SD, p < 10e-05, paired t test). Figure 11B shows that the expected coherence rate (in bits/s) decreased in all of the cells we recorded when the average contrast of the stimulus was switched from high to low. This was not surprising, because the mean firing rate decreased by ∼40% when the stimulus was switched from Hi CT to Lo CT. However, in most cells, the decrease in expected coherence rate held even when the mean firing rate was taken into account (Fig. 11C). The mean of the expected coherence rate, expressed in bits/spike, was significantly different between the two contrast conditions (Hi CT: 1.57 ± 1.13 bits/spike; Lo CT: 1.26 ± 1.12 bits/spike; mean ± SD, p < 0.01, paired t test). Therefore, our data suggest that neurons convey information about the stimulus at a much slower rate (in bits/s) when the average contrast decreases, largely because they fire less. However, the information per spike also decreases, most likely because delayed suppression no longer constrains the spike temporal precision. The loss in spike timing precision is consistent with the switch of the neuronal temporal sensitivity toward slower stimuli, as indicated by the slowdown of the excitatory filters or, equivalently, by the shift of the temporal frequency tunings toward lower frequencies (Holub and Morton-Gibson, 1981; Albrecht, 1995). In summary, when the visibility of the stimulus decreases, the spikes are less numerous and less precise and encode information about slower stimulus components.

Finally, we compared the predictive power of the multi LN models at different adaptation levels by computing the ratio between the predicted and the expected coherence rates (Fig. 11D). The multi-LN models explained a greater proportion of the response signal at Lo CT than at Hi CT, because the responses became more linear when the average contrast decreased. Without suppression, the predictive power of the models decreased from 69% to 50% at Hi CT and from 78% to 70% at Lo CT, confirming that the functional role of suppression was greater at Hi CT than at Lo CT.

Discussion

The goal of this study was to characterize the functional mechanisms responsible for fast and slow contrast adaptation in V1 simple cells. We presented a novel type of noise in which the contrast of optimal gratings is modulated over different timescales (∼10 ms vs ∼1 min) and showed that nonlinear delayed suppression is involved in both processes. On a fast timescale, delayed suppression improves the temporal precision of the responses to high contrast gratings. On a slower timescale, the balance between excitation and delayed suppression changes so that neuronal sensitivity increases at low contrasts at the cost of slower and noisier responses. Our results thus provide a general mechanism by which adaptation can trade neuronal sensitivity against processing speed depending on how easily a sensory stimulus can be detected.

Relationship to previous studies

The nonlinearities of simple cell spatiotemporal processing have been studied with white noise analysis previously, both in the cat (Jacobson et al., 1993; Emerson, 1997; Baker, 2001; Fournier et al., 2011) and in the macaque (Rust et al., 2005). Our results confirm that two excitatory subunits are generally required in direction-selective simple cells (Jacobson et al., 1993; Emerson, 1997; Baker, 2001; Rust et al., 2005). The output of the secondary excitatory subunits is fully rectified and makes simple cell responses more complex, (i.e., less dependent of the absolute spatiotemporal phase of the stimulus; Movshon et al., 1978).

The existence of suppressive subunits in V1 receptive fields is more debated. Suppressive subunits have been reported in the macaque (Rust et al., 2005; Chen et al., 2007), but not in the cat (Mancini et al., 1990; Touryan et al., 2002). Because the retrieval of subunits depends on the number of spikes recorded per stimulus dimension (Rust et al., 2005), we restricted our exploration to only two spatial phases. As a result, 79% of our simple cells showed significant suppression. This suppression was motion opponent in direction-selective cells, as in the macaque (Rust et al., 2005), but not in other neurons when the constraint of orthogonality imposed on the eigenvectors was relaxed. Suppression was always strongest along the K² diagonals, indicating that its main function was to counteract the excitation evoked by high contrast stimuli. The fact that binary stimuli do not allow the reconstruction of the K² diagonals may explain why previous studies did not report delayed suppression (but see Fig. 3 in Rust et al., 2005).

The contrast dependence of V1 responses dynamics is classically attributed to a fast, nearly instantaneous contrast gain control (Carandini et al., 1997; Kayser et al., 2001, Albrecht et al., 2002, but see Reid et al., 1992). However previous studies did not measure the dynamics of contrast responses at the fine temporal scale shown here. Our stimulus design allowed us to characterize the temporal dynamics of fast contrast adaptation precisely and independently from the effects of slow contrast adaptation, which also affected the dynamics of V1 responses. In addition, in our framework, the “slow” contrast adaptation may lump together a collection of nonlinearities having different time constants, from a few hundreds of milliseconds (Gawne et al., 1996; Müller et al., 1999; Reich et al., 2001; Albrecht et al., 2002) to ∼1 mn or more (Sharpee et al., 2006). Other properties of the fast contrast gain control, such as the contrast invariance of orientation tuning, may actually rely in part on slower contrast-dependent nonlinearities (Nowak and Barone, 2009).

The slow contrast adaptation acts largely by modulating the strength of the fast contrast adaptation—that is, by changing the balance between excitation and delayed suppression. Its effects on the dynamics of excitation could be secondary: the breakdown of delayed suppression at low average contrast could result in stronger and slower excitation, especially after amplification by the cortical feedback loop (Somers et al., 1995). Such a nested cascade of adaptive processes could display power law dynamics (Drew and Abbott, 2006) and a similar arrangement could contribute to the timescale invariance found elsewhere in the visual and other sensory systems (Fairhall et al., 2001; Nagel and Doupe, 2006).

Putative biological mechanisms

As functional descriptions, multi-LN models cannot settle whether delayed suppression originates from cortical (Heeger, 1992; Somers et al., 1995; Lauritzen and Miller, 2003), subcortical (Shapley and Victor, 1978), synaptic (Chance et al., 1998), or even intrinsic neuronal sources (Sanchez-Vives et al., 2000; Azouz and Gray, 2003). In particular, their serial structure does not reflect the recurrence of the cortical microcircuit or the diverse intrinsic properties of biological neurons. Nonetheless, our results support some biological mechanisms more than others. We found that the nonlinear suppression, particularly in non-direction-selective neurons, was genuinely contrast dependent (Sclar and Freeman, 1982; Geisler and Albrecht, 1992): it was visible at all spatial phases, whether optimal, null, or even anti-optimal (Fig. 1), contrary to the suppression that would be expected from intrinsic neuronal mechanisms, which should be maximal at high firing rates.

A recent study showed that delayed suppression participates in the precision of LGN spike responses to spatially uniform noise (Butts et al., 2011). Contrast gain controls have been described in both the retina and the LGN (Shapley and Victor, 1978; Baccus and Meister, 2002), and they could participate in the effect we see in V1 (Finn et al., 2007). However, the fast contrast-dependent nonlinearity is weaker at subcortical stages than in the cortex (Ohzawa et al., 1985; Dean and Tolhurst, 1986; Albrecht, 1995; Kayser et al., 2001; Alitto and Usrey, 2004). Moreover, it is unclear how subcortical suppression could account for differences in dynamics between excitation and suppression at the cortical level. In particular, if all of the contrast-dependent changes in V1 dynamics originated from the excitatory thalamocortical pathway, then the responses to both the optimal and anti-optimal phases should accelerate when contrast increases, which is contrary to what we observed.

Intracellular studies have shown that in addition to the push-pull, phase-dependent inhibition that contributes the linear RF of V1 simple cells, these neurons also receive phase-independent synaptic inhibitory inputs (Borg-Graham et al., 1998; see also the DC component in response to drifting gratings in Anderson et al., 2000; Priebe and Ferster, 2005; Liu et al., 2010). This suppression could come from layer 4 complex cells (Hirsch et al., 2003; Lauritzen and Miller, 2003) and participate in the emergence of simple cell properties (Liu et al., 2010; Fournier et al., 2011). Inhibitory inputs from direction-selective interneurons are also the simplest explanation for the motion opponent suppression reported here and in previous studies (Monier et al., 2003; Rust et al., 2005). These results suggest that intracortical inhibition, whether feedforward or recurrent, is the likely source of nonlinear delayed suppression in V1 simple cells. Recent advances in optogenetics may help to specify the cortical circuits involved (Atallah et al., 2012).

The relative increase of nonlinear suppression at high ambient contrast is consistent with a hyperpolarization of the membrane potential relying on both intrinsic and synaptic mechanisms (Carandini and Ferster, 1997; Nowak et al., 2005). The fact that V1 fast-spiking neurons fire more at high contrast than regular-spiking neurons may participate in the contrast dependence of the excitation/inhibition balance (Contreras and Palmer, 2003). Alternatively, inhibitory neurons might not adapt to ambient contrast as much as excitatory neurons or their contrast thresholds could be higher (Somers et al., 1995; Carvalho and Buonomano, 2009). Finally, the greater weight of inhibition at high ambient contrast could also originate from differences in short-term synaptic plasticity between excitatory and inhibitory cortical neurons (Chance et al., 1998; Varela et al., 1999; Beierlein et al., 2003; Kapfer et al., 2007).

Functional significance

Evidence in favor of delayed inhibition has been found in both intracellular and extracellular recordings of V1 neurons (Volgushev et al., 1995; Gillespie et al., 2001; Ringach et al., 2003; Cardin et al., 2010). It has been proposed that delayed suppression refines the neuronal orientation tuning over time by suppressing the unselective component of the response (Celebrini et al., 1993; Ringach et al., 2003) and participates in the increase in spike precision in response to coincident inputs (Cardin et al., 2010). Consistent with these studies, delayed suppression could implement a coarse-to-fine processing of direction over the time course of a single fixation (∼300 ms).

More generally, our results indicate that the contrast dependence of the balance between excitation and delayed inhibition serves a dual purpose: it adapts the neuronal gain to the average contrast of the stimulus (Ohzawa et al., 1982) and it also adjusts the coding rate (Gawne et al., 1996; Mechler et al., 1998; Reich et al., 2001) by controlling the dynamics of the neuronal integration window (Pouille and Scanziani, 2001). As a result, V1 simple cells favor high sensitivity in low contrast conditions and processing speed when the visual signal is strong. It remains to be seen whether delayed inhibition plays a similar role in the adaptation to other types of sensory stimuli (Wehr and Zador, 2003; Tan et al., 2004; Higley and Contreras, 2006; Heiss et al., 2008).