Skip to main content
NCBI home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2013 Jan 30;33(5):2137–2146. doi: 10.1523/JNEUROSCI.3095-12.2013

Neural Correlates of Reinforcement Learning and Social Preferences in Competitive Bidding

Wouter van den Bos 1,✉, Arjun Talwar 1, Samuel M McClure 1
PMCID: PMC6619103  PMID: 23365249

Abstract

In competitive social environments, people often deviate from what rational choice theory prescribes, resulting in losses or suboptimal monetary gains. We investigate how competition affects learning and decision-making in a common value auction task. During the experiment, groups of five human participants were simultaneously scanned using MRI while playing the auction task. We first demonstrate that bidding is well characterized by reinforcement learning with biased reward representations dependent on social preferences. Indicative of reinforcement learning, we found that estimated trial-by-trial prediction errors correlated with activity in the striatum and ventromedial prefrontal cortex. Additionally, we found that individual differences in social preferences were related to activity in the temporal-parietal junction and anterior insula. Connectivity analyses suggest that monetary and social value signals are integrated in the ventromedial prefrontal cortex and striatum. Based on these results, we argue for a novel mechanistic account for the integration of reinforcement history and social preferences in competitive decision-making.

Introduction

Recent work in decision neuroscience has investigated cooperative and strategic behaviors in multiplayer economic games (for review see Rilling and Sanfey, 2011). The bulk of these paradigms have posed the dilemma to cooperate (e.g., trust, reciprocate) or compete (e.g., not trust, defect). In contrast, purely competitive behavior, defined as the pursuit of assets perceived to be scarce and contested, has received far less attention. Competitive motivations are fundamental to social interactions but can have negative consequences not only for one's competitors, but for oneself (Malhotra, 2010). For example, the desire to beat rival bidders can lead auction participants to pay more than an item is worth, leading to monetary losses and opportunity costs (Ku et al., 2005). We hypothesize that in competitive decisions, social preferences interact with monetary outcomes to guide strategy learning.

We used a five-player auction task (Fig. 1) in conjunction with fMRI. In this task, the market value of the goods is the same to everyone, but participants have only approximate estimates of this true market value. Experiments using similar tasks have shown that, although the losses of naive bidders decline over time, even very experienced and professional auction participants persist in overbidding (Dyer et al., 1989; Garvin and Kagel, 1994), even if they know the optimal bidding strategy (van den Bos et al., 2008).

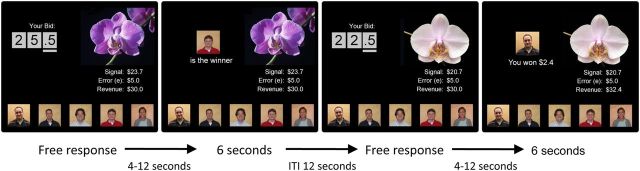
Figure 1.

Figure 1.

Open in a new tab

Common value auction experiment design. On each round, a new object (flower) was presented with a personal estimation of the value and error term indicating how much estimates may differ from the true value. Participants placed bids by adjusting digits beginning from a random initial value. After all bids were submitted, the outcome was shown at a variable delay of 4 to 12 s. Finally, a 6 s display showed either the winner of the auction or the amount of revenue gained or lost if the participant was the winner. The next round started after an intertrial interval (ITI) of 12 s. The revenue on the right side of the screen represents the total sum of money the participant had earned at that point in the task. MUs we displayed as dollar amounts.

Inspired by learning models from psychology (Rescorla and Wagner, 1972), neuroscience (Montague et al., 1996), and economic exchange games (Camerer and Ho, 1998; Zhu et al., 2012), we investigated behavior in this task using a reinforcement learning (RL) model (Sutton and Barto, 1998; McClure and van den Bos, 2011) that captures the dynamics of bidding strategies over time. The basic assumption underlying the model is that participants select bids based on the outcome expected by following a specific strategy.

Recent developments in behavioral game theory (Fehr and Schmidt, 1999; Camerer, 2003) and decision neuroscience (Rilling and Sanfey, 2011) have shown that behavior and neural activity are not only driven by preferences over monetary outcomes but also by social preferences. Consistent with social preference models, we argue that people derive utility from winning and disutility from losing an auction, independent of monetary outcome. Importantly, this hypothesis is supported by recent auction experiments indicating that the joy of winning or the pain of losing increases when the social aspects of the auction environment are emphasized (Delgado et al., 2008), and that overbidding virtually disappears when participants play with computer opponents instead of people (van den Bos et al., 2008). Our RL model incorporates this thesis into an extended value function used in learning bidding strategies.

First, we show that RL accounts for several aspects of behavior and that reward prediction errors estimated from our model correlate with activity in the striatum (Str) and ventromedial prefrontal cortex (VMPFC). Second, we find that behavioral biases associated with winning or losing auctions are predicted by activity in the temporoparietal junction (TPJ) and anterior insula (AI). Together, these findings support a novel brain-based account of behavioral biases in competitive environments.

Materials and Methods

Participants

The studies were conducted at Baylor College of Medicine in Houston, Texas, where 25 volunteers participated in the experiments. The average age of the group was 28.56 years (SD, 7.28 years), and consisted of 13 male and 12 female participants. In accordance with the Institutional Review Boards of Baylor College of Medicine and Stanford University, written informed consent was obtained and it was emphasized that participants could withdraw from the study at any time. For three participants, the scanner failed to start in sync with the other participants in the auction; therefore, only 22 of the 25 fMRI datasets were usable for imaging analyses (11 male, 11 female). All 25 subjects were included in behavioral analyses. We tested for possible gender differences in all analyses, but none was significant for behavioral measures or brain activity. There also were no consistent general trends across gender analyses.

Experimental procedures

At the start of the experiment, each group of five participants received a 15 min long instruction session on the common value sealed bid auction task procedures using a standardized PowerPoint presentation (van den Bos et al., 2008). During the introductory presentation, the following points were explained: the structure of a first price sealed bid common value auction, how to operate the computer to place bids, and the exchange rate between monetary units (MUs) in the game and pay-off in real dollars at the end of the experiment. All participants received $50 dollars for participating in the MRI experiment and received an additional 30 MU endowment to use for bidding in the task. For every 2 MUs won or lost, $1 was added or subtracted from the base pay, respectively. To ensure comprehension of the task, all participants completed the questionnaire (reproduced below in Single-player auction experiment) before continuing on to the experiment.

At the beginning of the experiment, all participants were endowed with 30 MUs, with which they could bid in the auctions. In each auction round, participants were given independent estimates of the value of the item under auction (xi) and were provided with the error term (ε) for that round. They were instructed that estimates were drawn from a uniform distribution with maximum error ε around the true, but unknown, common value x0. During the instructions, we carefully explained that, given the nature of the uniform distribution, value estimates were equally likely to be underestimates or overestimates of the true value. The error term ε was the same for all participants in each round, but changed between rounds (ε ∼{4,5,6,8}). Before the start of the experiment, participants were additionally instructed that x0 was randomly drawn from uniform distribution with lower and upper bounds of xL = 10 MUs and xU = 55 MUs.

After all players submitted their bid, the largest bid was determined and the winning participant's picture was shown to all players (for a detailed timeline and example stimuli, see Fig. 1). Only the winner gained information about the true value of the object and the revenue made in that round (revenue was determined by x0 − bi and was negative when the winning bid was larger than true value x0). The experiment consisted of 40 consecutive sealed bid auctions and took, on average, ∼30 min to complete. In each round there was a new object for auction, represented by a novel picture of a flower, to discourage participants from using previous trials to estimate true values x0. The number of rounds was unknown to the participants to prevent end-game effects.

The participant with the highest (stochastic) estimate of value is likely to be the highest bidder in the auction. Furthermore, since estimates were uniformly distributed around the true value, this highest estimate is also likely to be an overestimate of the true market value. Therefore, if participants do not bid sufficiently less than their estimated value, they are likely to win the auction but lose money in the transaction. Such overpayments are known as the winner's curse (Kagel et al., 1989; Thaler, 1994).

The winners' curse was first identified in auctions for oil drilling rights in the Gulf of Mexico (Capen et al., 1971), and has since been reported in baseball free agency (Blecherman and Camerer, 1998), book publishing (Dessauer, 1981), construction (Dyer and Kagel, 1996), corporate takeovers (Roll, 1986), and 3G spectrum auctions (Binmore and Klemperer, 2002). Laboratory studies have shown that, although the losses of naive bidders decline over time, the winner's curse nonetheless persists even for very experienced or professional auction participants (Dyer et al., 1989; Garvin and Kagel, 1994). Given the persistent and stable biases evident in these experiments, common value auction tasks provide an ideal setting to study biases evident in decision-making in a competitive environment.

Behavioral analyses

We analyzed behavior in terms of “bid factor,” κ, given by the following:

graphic file with name zns00513-3253-m01.jpg

A bid factor of 1 implies that participants bid their signal (bi = xi; i.e., they do not shade their bid). As described above, such bids are likely to produce losses when the auction is won. A bid factor of 0 is optimal (Kagel and Levin, 2002). In particular, based on the signal (xi) and the error (ε), the (optimal) risk-neutral Nash equilibrium (RNNE) bidding strategy can be determined for each round and each participant. The solution is given by the following:

graphic file with name zns00513-3253-m02.jpg

where

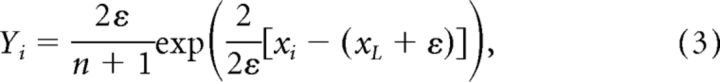graphic file with name zns00513-3253-m03.jpg

n is the number of bidders, and i indexes participants (Kagel and Levin, 2002). Following the methods of our previous study (van den Bos et al., 2008), the participants only received signals from a range where the term Y from Equation 2 is almost zero (Y < 0.001 MU) and can thus be ignored (Lind and Plott, 1991). As a result, the optimal bidding strategy is given by

graphic file with name zns00513-3253-m04.jpg

Thus, as indicated above, in terms of bid factor (κ), the optimal strategy is to bid with κ = 0. As has shown previously, participants learn to bid less than their value estimate (i.e., κ < 1) but generally overbid relative to the optimum (i.e., κ > 0) (van den Bos et al., 2008).

Reinforcement learning model

In developing a learning algorithm, we made several adjustments specifically tailored to the auction environment (McClure and van den Bos, 2011) that are listed below.

Assumption 1: intrinsic utility of winning and losing.

First, we hypothesized that social factors create value for winning and losing that is independent of the monetary outcomes of the task. As a result, winning becomes more valuable by some factor, which we call ρwin, and not winning the auction becomes aversive by some value ρloss:

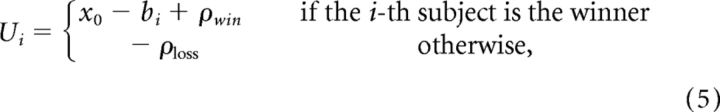graphic file with name zns00513-3253-m05.jpg

where x0 − bi is the amount won (or lost) by the winning bidder.

Next, following the logic of classic reinforcement learning model, we expect that, at the end of every round, participants compute a prediction error based on the difference between the actual outcome (U) and the expected outcome (V) related to their bid factor:

graphic file with name zns00513-3253-m06.jpg

Note that, for simplicity, we have omitted the index i from Ui, Vi, κi, and δi in Equation 6. We continue to do so for these and other subject-specific quantities in the equations below when no confusion is expected.

Because κ is a finely discretized variable, the number of states over which it is necessary to learn state-action values is very large (for modeling purposes, we restrict predicted behavior to the approximate range of bid factors submitted by participants in the experiment: −1 to 2, discretized in steps of 0.01). To converge to a stable strategy in 40 trials, as is observed behaviorally, learning must generalize across unsampled bid factors. This leads to two additional assumptions.

Assumption 2: when losing an auction, participants assume that all bids less than what they submitted would have also lost.

The monetary outcome when losing an auction is zero. If V(κ) is the predicted value of bidding κ, then a reward prediction error signal for all states is produced according to

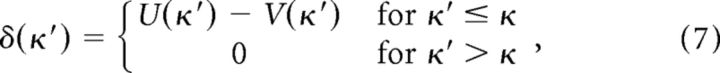graphic file with name zns00513-3253-m07.jpg

following a loss. κ denotes the actual bid factor submitted in a single round of the experiment, and κ′ is used to indicate a range of bid factors. Thus, κ′ ≤ κ indicates all bid factors smaller than that submitted are assigned a nonzero prediction error.

Assumption 3: when winning an auction, participants assume that larger bids would have also won the auction.

Since auction winners are informed of the true value (x0) of the item, then the outcome that would have been obtained for larger bids is also known. Thus, the potential outcomes for higher bids can be known and compared with expectation, giving reward prediction errors according to:

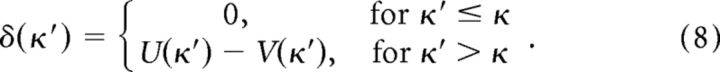graphic file with name zns00513-3253-m08.jpg

Learning based on reward prediction errors is modeled as in most RL methods, with a learning rate α determining the influence of δ on new values of V(κ′):

graphic file with name zns00513-3253-m09.jpg

In the current model, we scaled learning rate so that updating only occurs within a limited range of the bid factor used on any trial to account for the fact that the probability of winning with a given bid factor changes over time. This was implemented by creating an effective learning rate that decreases inversely with distance from κ:

graphic file with name zns00513-3253-m10.jpg

Decisions were then generated by the model using a soft-max decision function, with a parameter m that modifies the likelihood of selecting suboptimal bids:

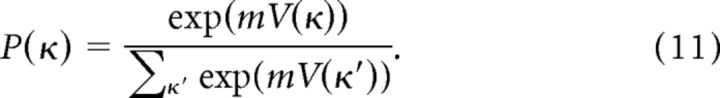graphic file with name zns00513-3253-m11.jpg

The value function, V, was initialized to zero for all values of κ. The denominator sums over all possible values of κ (indexed by κ′ ϵ [−1,2], as discussed in Assumption 1, above). We also experimented with randomized initial values of V(κ), which is commonly used in RL algorithms to encourage initial exploration of strategies. Randomizing initial values did not affect the performance of the model in any notable way. All model-related results are reported for fits conducted with V initialized to zero.

We estimated the parameters (ρwin, ρloss, α, and m) of the RL model using a simplex optimization algorithm in Matlab. The model simulated the performance of five bidders with average bid factors calculated for each round of 40 consecutive auctions in 10,000 runs of the model. A similar round-by-round average bid factor was also calculated for the bids submitted by the 25 participants in the study. Best-fitting model parameters were determined at the group level so as to minimize the sum-squared error between average model performance and the average subject performance. The best fitting model parameters were ρwin = 2.40, ρloss = 0.49, α = 0.138, and m = 10. Group-based estimates of α and m were subsequently used in a second model fitting procedure that was aimed at estimating the individual differences in ρwin and ρloss for the 22 subjects that had usable data in the imaging experiment.

Finally, we compared the performance of the current model with several alternative models using Bayesian model comparisons. To test the null hypothesis that there are no social preferences, we compared the full model to one in which the ρwin and ρloss parameters were both removed. To further explore the role of ρwin and ρloss, we also included the RL models with either ρwin or ρloss removed from the model. These model comparisons indicate that the full model provides the best fit to the data (Fig. 1; Table 1).

Table 1.

Bayesian model comparisons

Model AIC BIC
Full model 5181.0 5185.4
No ρwin 5531.1 5534.5
No ρloss 7560.9 7564.1
No ρwin or ρloss 7917.9 7920.0
Open in a new tab

AIC, Akaike information criterion; BIC, Bayesian information criterion.

Sequential analyses and social utility

For behavioral analyses, we defined two dependent variables to investigate the relation between model parameters and choice behavior: [Δκ | win] and [Δκ | not win]. These two measures of sequential changes in bid factor (κ) were computed by calculating the average change in κ (κt+1 − κt) following either winning or not winning a round in the auction. To test whether the individually estimated parameters for ρwin and ρloss predict different aspects of participants' behavior, both estimates were simultaneously regressed against [Δκ | win] and [Δκ | not win] using multiple regression.

Single-player auction experiment

We hypothesized that the ρwin and ρloss parameters reflect individual social preferences. To further support this hypothesis, we performed an additional behavioral experiment on an independent subject group in which we separately measured model parameters and participants' social and monetary motivations in the task. In this task, participants played an online five-player common value auction. Unbeknownst to participants, the other players were simulated (van den Bos et al., 2008). In particular, competing bids were based on the bid factors, κ, generated by the reinforcement model detailed above, with model parameters that produced the best fit to the behavioral data in the imaging study (ρwin = 2.40, ρloss = 0.49, α = 0.138, and m = 10).

Before participating in the study, subjects were sent an e-mail emphasizing the importance of arriving on time due to the multiplayer nature of the experiment. Upon arrival, subjects were told the other participants of the online auction were seated in different parts of the building. After obtaining written consent, participants were given the explanation of experimental procedures described above and were given a short questionnaire to ensure comprehension. All participants passed this test without error. Participants were instructed that their payoff would be generated according to their revenue. Participants were endowed with 75 MUs and $1 in payoff was added/subtracted from an endowment of $20 for every 5 MU profit/loss in game money. The experiment ended after 70 rounds of auctions and the participants were debriefed.

The study was conducted at Stanford University, where 47 volunteers participated in the experiment. The average age of the group was 23.4 years (SD, 7.28 years) and consisted of only male participants. Seven participants were excluded from the data analysis because during the debriefing they indicated that they did not believe they were playing against real peoples.

At the end of the auction, participants were given a 10-item questionnaire to assess feelings associated with participating in the experiment. For all items, responses were given on a 5-point Likert scale with 1 labeled “very positive” and 5 labeled “very negative.”

  1. Being the winner of an auction made me feel…

  2. Not winning the auction made me feel…

  3. Losing money in the auction made me feel…

  4. Winning money made me feel…

  5. Realizing that another player wins a lot of auctions made me feel…

  6. Realizing that other players win more auctions than I do made me feel…

  7. Not winning an auction over a long period of time made me feel…

  8. Winning an auction without making a profit or a loss made me feel…

  9. The possibility that other players could make more money than I do made me feel…

  10. The possibility that other players could make less money than I do made me feel…

All significantly correlated items were combined, yielding two factors. The first factor concerned monetary outcomes and consisted of questions 3 and 4 (reversed). The second factor concerned the other players winning auctions and money and included questions 5, 6, 7, 9, and 10 (reversed). The nonweighted mean scores of the monetary and social factor were used as predictors for individual differences in ρwin and ρloss. Responses related to monetary and social motivations were correlated within category across subjects (Cronbach's α = 0.66 and 0.79, respectively). Summary monetary and social motivations were uncorrelated across subjects (Spearman's ρ = −0.08, p = 0.65).

fMRI data acquisition and analyses

Imaging was performed on 3.0 tesla Siemens scanners. High-resolution T1-weighted scans were acquired using an MP-RAGE sequence. Functional run details were as follows: echo-planar imaging, gradient recalled echo; TR = 2000 ms; TE = 40 ms; flip angle = 90°; 64 × 64 matrix; 26 4 mm axial slices; yielding voxels with dimension 3.3 × 3.3 × 4.0 mm. Functional data were analyzed using SPM5 (Wellcome Department of Cognitive Neurology, London, UK). First, slice-timing correction was applied to all images. Next, motion correction to the first functional scan was performed using a six-parameter rigid-body transformation. The motion-corrected images was coregistered to each individual's structural MRI using a 12-parameter affine transformation. Images were then resampled into 3 × 3 × 3 mm voxels and spatially normalized to the MNI template by applying a 12-parameter affine transformation. Images were then smoothed with an 8 mm isotropic Gaussian kernel and adjusted for global signal variation using a voxel-level linear model of the global signal. For each experiment, all five participants were scanned simultaneously and stimulus presentation and the timing of all stimuli and response events were acquired using NEMO software (http://www.hnl.bcm.tmc.edu/nemo/index.html), which is specifically designed for multisubject experiments and network-initiated scanning. Head motion was restricted with a pillow and foam inserts that surrounded the head.

Statistical analyses were performed on individual participants' data using the general linear model in SPM5. The fMRI time series data were modeled by a series of events convolved with a canonical hemodynamic response function (HRF). To investigate the neural correlates of different aspects of the outcome phase of the auction, we set up a general linear model (GLM) with regressors for the individual trail-by-trial estimated prediction errors (scaled and signed), win/non-win trials, and revenue change. As is necessarily true, prediction error and revenue change were partially correlated, with an average r2 of 0.04 across our subjects. Similarly, the revenue change and win/non-win trial regressors were also partially correlated with an average r2 of 0.04. However, neither correlations reached significance nor influenced the estimability of the design matrices. Additionally, we used a single regressor for the decision phase because the procedures during this phase—which involved viewing private estimates and error information and deciding on and submitting bids—occurred in rapid succession, too fast to be distinguished temporally. In contrast to the default procedure in SPM, we entered all regressors independently (without serial orthogonalization) into the design matrix. The regressors of interest were those of the outcome phase: the prediction error regressor and the regressors for winning and not winning the auction. Both the decision and the outcome phase regressors were modeled as events of 0 s duration. Additional analyses where the decision phase was modeled by reaction time did not yield qualitatively different results; the results in this paper are based on the null duration model. All regressors were convolved with the canonical HRF and regressed against the BOLD signal. Thresholds were set to p < 0.05 FWE with an extent threshold of 10 continuous voxels for the whole-group analyses.

Functional connectivity analyses.

To explore the interplay between the VMPFC, striatum, and other regions associated with winning and not winning auctions, we assessed functional connectivity using psychophysiological interaction (PPI) analysis (Friston, 1994). The VMPFC and striatum regions were taken from a whole-brain analysis in which BOLD activity was regressed against reward prediction errors for the whole group. Significant voxels within the VMPFC and striatum were used as volumes of interest (VOI). The method used here relies on correlations in the observed BOLD time series data and makes no assumptions about the nature of the neural events that contributed to the BOLD signal. For each participant, the entire time series over the experiment was extracted from the VOIs. Regressors were then created by multiplying the normalized (z-transformed) raw time series with two condition vectors that contained ones for the six TRs following either winning or not winning the auction, and zeros otherwise (Cohen et al., 2005; Kahnt et al., 2009). This produced the two condition vectors for winning and not winning (containing ones and zeros) that were multiplied with the time series of each VOI to produce the interaction terms used as covariates in a whole-brain regression analysis. Additional regressors for the condition (psychological) and time series (physiological) were included as additional covariates of no interest.

Individual contrast images for winning and not winning were computed and entered into second-level one-sample t tests. To find related differences in functional connectivity with the VMPFC/Str and the TPJ/AI, we performed follow-up region of interest (ROI) analyses.

ROI analyses.

We used the Marsbar toolbox for use with SPM5 to perform ROI analyses to further characterize patterns of activation and estimate individual differences in connectivity with the VMPFC and striatum seed regions. Individual connectivity coefficients for winning and not winning were extracted for the target regions of interest (TPJ and AI). Paired-sample, two-tailed t tests were used to test whether the psychophysiological interactions were stronger between winning and not winning. Individual connectivity regression coefficients were also used for subsequent correlation analyses with the ρwin and ρloss model parameters. For the ROI analyses, we performed additional robust regression analyses with the Huber weighting function (using the robustfit algorithm in Matlab) to account for possible effects driven by outliers. Given that these analyses did not change the results (all ps < 0.01), we have decided to report the results of our linear correlation analyses. Effects were considered significant at an α of 0.0125, based on Bonferroni correction for multiple comparisons (i.e., p = 0.05/4 ROIs), unless reported otherwise.

Results

Computational model of bidding behavior

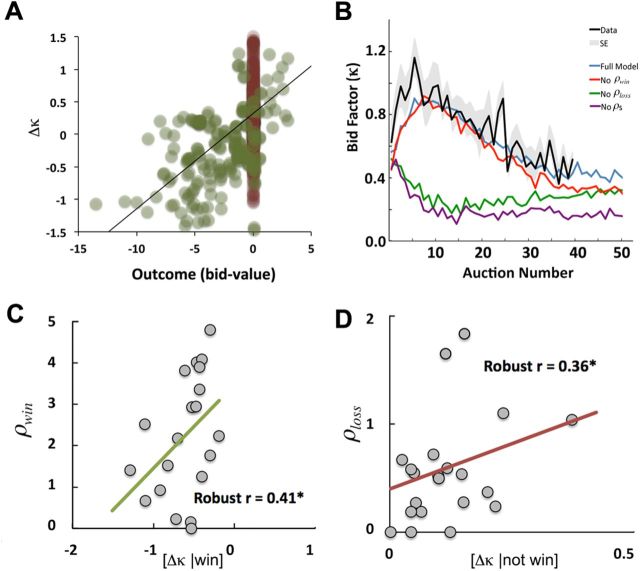
Participants completed 40 rounds of a multiplayer auction task while undergoing functional brain imaging. As expected, trial-by-trial analyses revealed that monetary wins and losses were correlated with increases and decreases in bid factors, indicating that subjects adjusted their bids based on reinforcement (r = 0.46; p < 0.01; Fig. 2A). However, these analyses also suggested that there is some equilibrium point where people lose money, but winning the auction perfectly offsets the loss and results in no change in bidding. In particular, Figure 2A indicates that subjects tended to maintain their bidding strategy when incurring small losses (i.e., Δκ = 0 when outcome is negative). Furthermore, consistent with numerous previous studies, we found that participants' bids during the task were initially much higher than optimal (κ > 0 on first round; t(21) = 3.90, p < 0.001) but with repeated play bid factors declined to an asymptote above the optimal Nash equilibrium (κ ≈ 0.4; at Nash equilibrium κ = 0; Fig. 2B). Finally, we found that the mean bid factor increases sharply in the first several rounds of the experiment. Our learning model captured all of the observed aspects of bidding through time, including the initial rise in mean bids as well as the gradual reduction toward Nash equilibrium (Fig. 2B).

Figure 2.

Figure 2.

Open in a new tab

Bidding behavior in common value auctions. A, Participants adjusted their bids based on the amount of money earned or lost an each round of the experiment. Changes in bidding were analyzed in terms of bid factors (κ, see Materials and Methods) and were directly related to money won or lost. Δκ is the change in bid factor between auction rounds. Green dots represent rounds that are won and red dots the rounds that were not won (revenue change always 0). B, With repeated play, bidding approaches an asymptote above Nash equilibrium. Simulation of the reinforcement model with and without the ρwin and ρloss parameters. The results present the average data of 10,000 simulations; for demonstrative purposes, we have simulated auctions with a total of 50 rounds using the best fitting parameters for each model. These simulations demonstrate that the initial rise in bid factors is governed by ρloss and the positive asymptote depends on both ρwin and ρloss. Bayesian model comparison indicates that the full model has the best fit to the behavioral data (Table 1). C, D, Robust regression of ρwin with [Δκ | win] (r = 0.41, p < 0.01; C), and the robust regression of ρloss with[Δκ | not win] (r = 0.36, p < 0.03; D).

We estimated model parameters using maximum likelihood procedures. The model included two parameters to estimate the utility of winning or losing independent of monetary outcome: ρwin and ρloss. Best fitting estimates of ρwin and ρloss were significantly greater than zero across subjects (ρwin: mean = 2.40, SE = 0.35, p < 0.001; ρloss: mean = 0.49, SE = 0.11, p < 0.01). Moreover, ρwin and ρloss were positively correlated with average bid factor during the course of the experiment across subjects (r = 0.71, p < 0.001 and r = 0.53, p < 0.01, respectively). As will be relevant for interpreting fMRI results below, we found no relationship between ρwin and ρloss across subjects (r = 0.07, p = 0.8), ρwin was not correlated with the prediction error in win trials (r = −0.11, p = 0.27), ρloss was not correlated with the prediction error in non-win trials (r = −0.05, p = 0.48). Finally, a likelihood ratio test indicated that our reinforcement learning model captured behavior well compared with a null hypothesis of random responses within our modeled range of bid factors (D4 ≥ 189.4; p ≈ 0 for all subjects).

Analyses of trial-to-trial changes in behavior further validated our estimates of ρwin and ρloss. Since reward (Eq. 2) is dependent on both ρwin and ρloss, changes in bidding across rounds (summarized at Δκ) should depend on ρwin and ρloss following wins and losses, respectively. To confirm this, we compared trial-to-trial changes in bid factors by regressing ρwin and ρloss against [Δκ | win] and [Δκ | not win]. A robust multiple regression of both ρwin and ρloss on [Δκ | win] fitted significantly (r = 0.50, F(2,18) = 4.01, p < 0.03), but only ρwin (b = 0.43, t(18) = 2.44, p < 0.02) and not ρloss (b = −0.13, t(18) = −0.52, p = 0.53) contributed significantly to the regression. In contrast, in the regression against [Δκ | not win] (r = 0.34, F(2,18) = 4.85, p < 0.02), ρloss contributed significantly (b = 0.32, t(18) = 2.55, p < 0.01), but not ρwin (b = −0.14, t(18) = −0.68, p = 0.50) (Fig. 2B,C). These analyses confirm that ρwin and ρloss capture expected, independent, dynamics of participants' behavior. In addition, we found that changes in bidding across rounds (Δκ) was correlated with the magnitude of monetary gains or losses (r = 0.52, p < 0.001). Together, these results support our hypothesis that participants use both monetary and non-monetary outcomes to adjust their bidding strategy.

Based on previous studies (Fehr and Camerer, 2007; Delgado et al., 2008; van den Bos et al., 2008), we hypothesized that the ρwin and ρloss parameters reflect social preferences related to winning or losing to other participants. To further support this hypothesis, we performed an adjunct behavioral experiment on an independent subject group in which we separately measured model parameters and participants' social and monetary motivations in the task. As in the main study, participants consistently bid significantly higher than optimal (i.e., above Nash equilibrium; mean κ = 0.49, SD = 0.22, t(39) = 14.3, p < 0.001) and overall incurred a net loss of −22.70 MUs (SD = 22.30) over the course of the experiment. Additionally, the model fit of the participants' behavior in this experiment yielded very similar estimates (ρwin = 0.94, ρloss = 0.59, α = 0.178, and m = 9.5) as in the imaging experiment. We measured attitudes using a novel questionnaire in which people rated from “very negative” to “very positive” assertions related to monetary motivations (e.g., “Winning money made me feel… ”) and social motivations (e.g., “Realizing that other players win more auctions than I do made me feel… ”). Next, we performed correlation analyses on the individual estimates of the ρwin and ρloss parameters with the monetary and social construct of the questionnaire. Supporting our hypothesis, the results of these analyses showed that individual differences in both ρwin and ρloss are correlated with self-reported feelings associated with the social impact of winning or losing an auction (Spearman's ρ = 0.37, p < 0.02 and Spearman's ρ = −0.46, p < 0.003, respectively). In contrast, ρwin and ρloss were not related to preferences over monetary gains and losses (Spearman's ρ = −0.18, p = 0.26 and Spearman's ρ = −0.26, p = 0.08, respectively). Importantly, post hoc comparison of correlation coefficients also revealed that the correlations of ρwin and ρloss with the social factor was significantly larger than with the money factor, and vice versa (z = 2.88, p < 0.001 and z = 3.11, p < 0.001, respectively).

Neural correlates of prediction errors

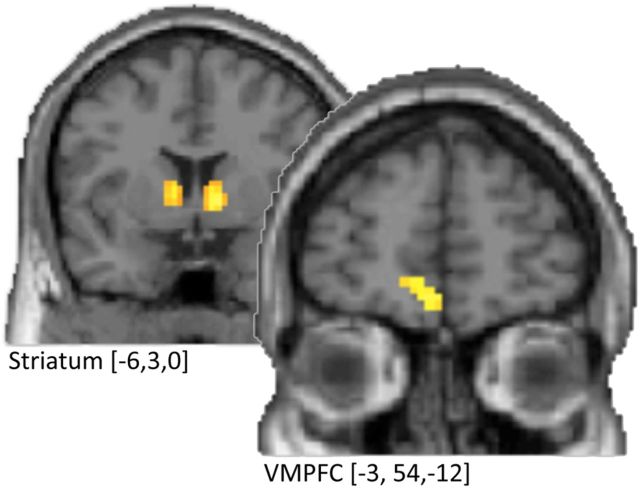
To further investigate the origins of bidding behavior, we performed whole-brain analyses on fMRI data collected as participants performed in the experiment. Given the strength of our reinforcement learning model in capturing behavior, our first interest was the neural basis of this learning process. Following others (Montague et al., 1996; O'Doherty et al., 2003; Li et al., 2006), we identified brain regions related to valuation by identifying areas that correlated with the prediction errors that underlie learning (Eqs. 6–9). We used best-fitting model parameters to generate estimated trial-wise prediction errors and correlated this signal with BOLD responses in a whole-brain analysis. We found significant correlated responses bilaterally in the Str [more specifically, caudate; Montreal Neurological Institute (MNI): −6, 3, 0] as well as the VMPFC (MNI: −3, 54, −12) (Fig. 3, Table 2). These areas have been associated with reward prediction errors in reinforcement learning numerously (for review, see Cohen, 2008).

Figure 3.

Figure 3.

Open in a new tab

Neural correlates of reinforcement learning in common value auctions. Individual trial-by-trial estimates of reward prediction errors correlate with activity in the striatum and VMPFC (p < 0.05, FWE; k > 10).

Table 2.

Brain regions revealed by whole brain contrasts

Anatomical region L/R BA Z MNI coordinates
x y z
Prediction error
    VMPFC L/R 11 6.37 −3 54 −12
    Ventral striatum (caudate head) L/R — 6.45 −6 3 0
Outcome (win > not win)
    Right TPJ R 40 5.05 54 −57 33
    Posterior cingulate cortex L/R 7 5.18 4 −60 35
Outcome (not win > win)
    Anterior insula
        Left L — 5.74 −30 27 0
        Right R — 5.78 45 18 −9
    dACC L/R 32 5.95 3 18 48
    Postcentral gyrus R 2 5.66 59 −24 44
Open in a new tab

MNI coordinates, peak voxels reported. L, Left; R, right.

Neural correlates of ρwin and ρloss

Our second major claim is that the winner's curse persists due to biases in net reward that reflect social preferences. We captured this bias in our model parameters ρwin and ρloss. Here, we demonstrate that these signals arose separately from the right TPJ and AI and affected value through (direct or indirect) connections with the VMPFC and Str.

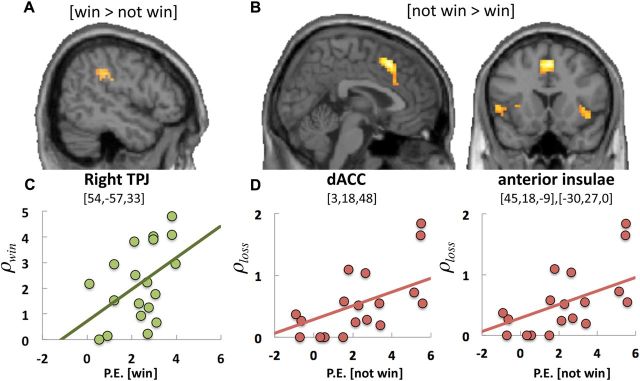
First, we identified brain regions associated with ρwin and ρloss by contrasting brain activity related to winning or not winning the auction. Our regression model controlled for responses related to other aspects of reward, including monetary wins/losses and reward prediction error (for details of the GLM, see Materials and Methods). The contrast [win > not win] revealed an area in the right TPJ (Fig. 4A, Table 1), whereas the opposite contrast [not win > win] was associated with activity in the dorsal anterior cingulate cortex/pre-supplementary motor area (dACC/pre-SMA) and the bilateral AI (Fig. 4B, Table 1).

Figure 4.

Figure 4.

Open in a new tab

Neural correlates of winning and not winning the auction. A, Results of the whole-brain contrast of [win > not win] selectively identified a regions of the right TPJ (p < 0.05; FWE, k > 10). B, In contrast, losing auctions (contrast of [not win > win]) is related to activity in the dACC and bilateral anterior insula (p < 0.05; FWE, k > 10). These responses were related to social preferences. C, D, The value of winning (ρwin) correlated with TPJ activity (parameter estimate of [win]; C), and the disutility of losing (ρloss) predicted the size of the responses in the anterior insula (parameter estimate [not win]; not significant for dACC; D).

To explore how the TPJ, dACC/pre-SMA, and AI are related to bidding behavior, we explored the relationship between brain activity, ρwin, ρloss, and bidding behavior in subsequent ROI analyses.

A robust multiple regression of both ρwin and ρloss on parameter estimate (P.E.) [win] in the TPJ fitted significantly (r = 0.59, F(2,19) = 4.31, p < 0.03), but only ρwin (b = 0.55, t(19) = 3.94, p < 0.002) and not ρloss (b = 0.13, t(19) = 0.09, p = 0.94) contributed significantly to the regression. This indicates that those participants that attributed relatively more utility to winning (regardless of monetary gain or loss) showed more activity in the right TPJ when they won the auction (Fig. 4C). In contrast, a robust multiple regression of both ρwin and ρloss on P.E. [not win] in the AI fitted significantly (r = 0.56, F(2,18) = 3.92, p < 0.03), but only ρloss (b = 0.52, t(18) = 2.83, p < 0.01) and not ρwin (b = 0.14, t(18) = 0.66, p = 0.52) contributed significantly to the regression. Given that the time series between the left and right hemispheres for anterior insula were highly correlated (r = 0.88), parameter estimates of left and right structures were collapsed by averaging time series in subsequent analyses. The results for each AI analyzed separately yielded qualitatively similar results. The robust multiple regression of both ρwin and ρloss on [P.E. not win] in the dACC did not show significant fit (r = 0.22, F(2,18) = 0.89, p = 0.56). These analyses showed that those participants that attributed relatively more negative utility to not winning the auction also showed more activity in the AI when they did not win. In sum, these results indicate that activity in the TPJ and AI is related to how much utility participants attribute to winning or not winning the auction.

Interaction between neural systems

Above, we identified the striatum and VMPFC as regions associated with updating values that govern bidding behavior. Since ρwin and ρloss are assumed to affect learning, we next aimed to determine whether the TPJ and AI showed functional coupling with the VMPFC and Str during the outcome phase of the experiment. We did so through a set of PPI analyses, using the ROIs from the previously reported whole-brain analyses.

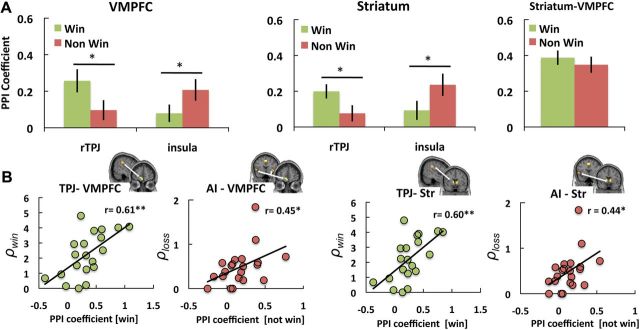
First, we contrasted the level of functional connectivity during the outcome phase of winning and not winning trials. The analyses showed that there was significantly increased TPJ-VMPFC functional connectivity after winning versus not winning an auction (t(21) = 3.11, p < 0.01). In contrast, there was greater AI-VMPFC connectivity after not winning versus winning (t(21) = −2.94, p < 0.01; Fig. 5A). Connectivity analyses of the Str with TPJ and AI showed the same pattern of changed connectivity strength related to winning or not winning (t(21) = 2.83, p < 0.02 and t(21) = 2.744, p < 0.03, respectively; Fig. 5A). However, we found no differences in VMPFC-Str connectivity strength for winning or not winning (t(21) = 0.77, p = 0.45, Fig. 5A). This was true even though VMPFC and Str are significantly functionally connected during the outcome phase (p < 0.001 following both wins and losses).

Figure 5.

Figure 5.

Open in a new tab

Functional connectivity of the VMPFC and striatum. A, Differences in VMPFC and Str task-related connectivity during winning or not winning the auction. Bars represent mean and SEM of the PPI coefficients. B, There is a significant relationship between individual ρwin estimates and TPJ-VMPFC/Str connectivity strength after winning, and a significant relationship between the individual ρloss estimates and AI-VMPFC/Str connectivity strength after not winning the auction. For all plots, significance is indicated as *p < 0.01 and **p < 0.005.

Second, because of our previous results showing that the level of activity in the TPJ and bilateral AI was dependent on outcome and individual differences in social values (ρwin and ρloss), we hypothesized that connectivity strength between these regions and the VMPFC and Str would also be related to ρwin and ρloss. We specifically hypothesized that the connectivity strength of TPJ-VMPFC/Str after winning, and the insula-VMPFC/Str after not winning, would be related to ρwin and ρloss. As predicted, our results indicated that TPJ-VMPFC connectivity strength after winning was correlated with ρwin across subjects (r = 0.61, p < 0.003), and that AI-VMPFC connectivity strength after not winning was correlated with ρloss (r = 0.45, p < 0.008; Fig. 5B). Similarly, TPJ-Str connectivity strength after winning was correlated with ρwin (r = 0.60, p < 0.003), and AI-Str connectivity strength after not winning was correlated with ρloss (r = 0.44, p < 0.01; Fig. 5B).

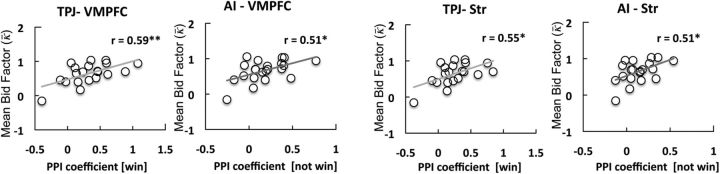
Finally, we hypothesized that connectivity strength between the TPJ/AI and VMPFC/Str would also be related to overbidding (i.e., κ). We found that trial-by-trial changes in bidding behavior (Δκ) are related to connectivity strength with the TPJ and AI. More importantly, we also found that connectivity strength predicted individual differences in overbidding: TPJ-VMPFC connectivity strength after winning and AI-VMPFC connectivity strength after not winning were both correlated with overbidding (mean κ; r = 0.59, p < 0.005 and r = 0.51, p < 0.01, respectively; Fig. 6). Again, the Str showed the same pattern: κ correlated with TPJ-Str connectivity strength after winning (r = 0.55, p < 0.01) and with AI-Str connectivity strength after not winning (r = 0.51, p < 0.01; Fig. 6).

Figure 6.

Figure 6.

Open in a new tab

Functional connectivity of striatum and VMPFC. TPJ-VMPFC/Str connectivity strength after winning and AI-VMPFC/Str connectivity strength after not winning predicted the individual differences in the size of the winner's curse. In the plots, significance is indicated as *p < 0.01 and **p < 0.005.

Together, the PPI analyses indicate a direct relationship between brain areas that represent value as people develop bidding strategies (VMPFC and Str) and regions commonly implicated in social cognition and emotion (AI and TPJ). Furthermore, the strength of connectivity between these networks predicted individual estimates of social preferences (ρwin and ρloss parameters) and, crucially, overbidding. These findings suggest a mechanism for how social preferences may bias bidding behavior toward financially risky choices in competitive environments.

Discussion

Auctions provide an ideal environment to study systematic biases in decision making that arise in competitive environments. We hypothesized that people develop bid strategies essentially by trial-and-error through a process of reinforcement learning. The brain areas we found to be associated with this process, the striatum and VMPFC, have been consistently implicated in this type of learning process. Moreover, reinforcement learning is generally thought to be relatively automatic in nature, underlying basic associative learning processes. Based on this, we propose that competitive strategies do not result from deliberate reasoning alone. Instead, behavior is driven by an adaptive process, which converges on what seems to produce the best results.

Reinforcement learning models are designed to learn which behavior maximizes expected reward (Sutton and Barto, 1998). Relying on associative learning mechanisms to develop a bid strategy therefore does not explain why the suboptimal bidding strategies are so persistent. Recent developments in behavioral game theory (Fehr and Schmidt, 1999; Camerer, 2003) and decision neuroscience (Fehr and Camerer, 2007) have shown that behavior and neural activity are driven in part by social preferences. That is, people not only derive utility from their own monetary outcomes but also from their performance relative to others (Fehr and Schmidt, 1999), from giving to worthy causes (Andreoni, 1990), and from maintaining a positive social image (Benabou and Tirole, 2006). Consistent with social preference models, we assumed that reward is biased by events related to social factors. Namely, we assume that winning and losing per se have value (ρwin and ρlose, respectively). We support this assumption in several ways. First, these values predict various aspects of behavior, both aspects of the evolution of bids across time, and individual differences in trial-by-trial changes in bidding. Second, we have shown that individual differences in both ρwin and ρloss are correlated with self-reported measures of feelings about the social, but not monetary, impacts of winning or losing auctions. Third, we identify brain areas associated with these values in the TPJ and anterior insula. The TPJ is a structure that has often been associated with social cognitive processes such as taking the perspective of others (Saxe and Kanwisher, 2003; Hampton et al., 2008) and processing changes of your position within a social hierarchy (Zink et al., 2008; Chiao et al., 2009). Of course, TPJ activity is more generally associated with the reorientation of attention to salient stimuli (Corbetta et al., 2008). Concluding that responses in TPJ are related to some aspect of social cognition is therefore problematic (Mitchell, 2007). Nonetheless, taking all of the data together supports the hypothesis that winning and losing are socially salient events, particularly for those participants who reported being highly socially motivated.

As for the neural structures associated with losing, the anterior insulae have been associated with negative outcomes in social interactions, such as unfair offers in the Ultimatum Game (Sanfey et al., 2003) and betrayal in the Trust Game (King-Casas et al., 2005). Our findings may therefore reflect the negative affect associated with seeing another person win the auction. However, a recent study aimed at understanding the more fine-grained functional parcellation of the insula suggested that there is a functional difference between dorsal and ventral regions within in the anterior insula (Chang et al., 2012). Whereas the dorso-anterior insula was found to be more consistently involved in higher cognitive processing such as task switching (Dosenbach et al., 2006), the ventro-anterior region associated more often with socio-emotional processing. Our anterior insula regions overlap with both dorso-anterior and ventro-anterior regions, potentially indicating that our observed anterior insular activity reflects not only the socio-emotional processing of the outcome of the auctions but may also be involved in signaling the need for change of the current behavioral strategy.

Interestingly, a recent paper has shown that the right TPJ and bilateral insula are more strongly functionally connected with the VMPFC during charitable donation decisions compared with food purchasing decisions, supporting the idea that social context may modulate the information exchange between these networks (Hare et al., 2010). This idea is further supported by a recent study with macaques that showed that single cells in the VMPFC tracked both magnitude of future rewards and the motivational value of rewards obtained in a social context. More specifically, these neurons were found to track momentary social preferences and social rank of other monkeys (Azzi et al., 2012). Our connectivity analyses suggest a mechanistic account for how such a social modulation of value may occur. First, consistent with several recent studies, our results suggest that activity in TPJ and AI are involved in processing social aspects of outcomes in multiplayer interactions (Rilling and Sanfey, 2011). Second, we show that these areas interact with the Str and VMPFC. Finally, the strength of this interaction was correlated with individual differences in overbidding. Together, these results suggest a novel mechanism for the influence of social and affective processes on competitive behavior.

Our results have implications for psychological and economic models of competitive behavior. One prominent account for competitive behavior states that individuals are (exclusively) driven by the motivation to maximize differences in pay-offs between themselves and their competitors (Messick and McClintock, 1968; Loewenstein et al., 1989). That there are competitive environments in which individuals fail to maximize these differences is often explained in terms of bounded rationality (Eyster and Rabin, 2005). However, the results presented in this paper suggest that in competitive situations, individuals may hold preferences for winning (and avoiding losing), regardless of the (monetary) costs. Based on these results, we hypothesize that the nature and salience of the social context (e.g., the number and identity of the other bidders in the auction) may mediate the interaction between socio-emotional and reward areas to bias competitive decisions. For instance, if the other players are members of a salient outgroup, competitive motivations may increase, whereas if the other players are anonymous others, competitiveness may decrease (van den Bos et al., 2008). Another way of manipulating competitive motivations suggested by the current model would be to temporarily inhibit or excite the TPJ with techniques like transcranial magnetic stimulation.

Recently, a series of neuroimaging studies of social interactions have used depth of social reasoning (theory of mind) to describe individual differences in strategic behavior (Hampton et al., 2008; Coricelli and Nagel, 2009; Yoshida et al., 2010). In contrast to our study, these experiments have revealed an important role for the dorsal medial prefrontal cortex in social reasoning. Although it is unlikely that individual differences in depth of processing underlie individual differences in bidding strategies in first price common value auctions (Gneezy, 2005), they do play a role in different types of auctions. An interesting avenue for future research would be the development of experiments and computational models that could investigate the putative roles of both social preferences and depth of processing in strategic behavior.

Of course, we have only begun to understand what is bound to be a number of complex factors that determine the impact of social values on competitive economic decisions (Seo and Lee, 2012). Nonetheless, functional neuroimaging seems to be a powerful tool, enabling quantification of these factors through measures of the brain systems we have identified.

Footnotes

This work was supported by Netherlands Organization for Scientific Research (NWO) Rubicon Postdoctoral Fellowship 446-11-012 (W.v.d.B.). We thank David Effelsberg and Philipp Golka for their help with the data collection.

The authors declare no competing financial interests.

References

  1. Andreoni J. Impure altruism and donations to public goods: a theory of warm glow giving. Econ J. 1990;100:464–477. [Google Scholar]
  2. Azzi JoCB, Sirigu A, Duhamel JR. Modulation of value representation by social context in the primate orbitofrontal cortex. Proc Natl Acad Sci U S A. 2012;109:2126–2131. doi: 10.1073/pnas.1111715109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Benabou R, Tirole J. Incentives and prosocial behavior. Am Econ Rev. 2006;96:1652–1678. [Google Scholar]
  4. Binmore K, Klemperer P. The biggest auction ever: the sale of the British 3g telecom licenses. Econ J. 2002;112:74–96. [Google Scholar]
  5. Blecherman B, Camerer CF. New York: Brooklyn Polytechnic University; 1998. Is there a winner's curse in the market for baseball players? [Google Scholar]
  6. Camerer CF. Behavioral game theory. Princeton, NJ: Princeton UP; 2003. [Google Scholar]
  7. Camerer CF, Ho TH. Experience-weighted attraction learning in coordination games: probability rules, heterogeneity, and time-variation. J Math Psychol. 1998;42:305–326. doi: 10.1006/jmps.1998.1217. [DOI] [PubMed] [Google Scholar]
  8. Capen EC, Clapp RV, Campbell WM. Competitive bidding in high risk situations. J Petr Tech. 1971;2:641–653. [Google Scholar]
  9. Chang LJ, Yarkoni T, Khaw MW, Sanfey AG. Decoding the role of the insula in human cognition: functional parcellation and large-scale reverse inference. Cereb Cortex. 2012 doi: 10.1093/cercor/bhs065. Advance online publication. Retrieved March 20, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chiao JY, Harada T, Oby ER, Li Z, Parrish T, Bridge DJ. Neural representations of social status hierarchy in human inferior parietal cortex. Neuropsychologia. 2009;47:354–363. doi: 10.1016/j.neuropsychologia.2008.09.023. [DOI] [PubMed] [Google Scholar]
  11. Cohen MX. Neurocomputational mechanisms of reinforcement-guided learning in humans: a review. Cogn Affect Behav Neurosci. 2008;8:113–125. doi: 10.3758/cabn.8.2.113. [DOI] [PubMed] [Google Scholar]
  12. Cohen MX, Heller AS, Ranganath C. Functional connectivity with anterior cingulate and orbitofrontal cortices during decision-making. Brain Res Cogn Brain Res. 2005;23:61–70. doi: 10.1016/j.cogbrainres.2005.01.010. [DOI] [PubMed] [Google Scholar]
  13. Corbetta M, Patel G, Shulman GL. The reorienting system of the human brain: from environment to theory of mind. Neuron. 2008;58:306–324. doi: 10.1016/j.neuron.2008.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Coricelli G, Nagel R. Neural correlates of depth of strategic reasoning in medial prefrontal cortex. Proc Natl Acad Sci U S A. 2009;106:9163–9168. doi: 10.1073/pnas.0807721106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Delgado MR, Schotter A, Ozbay EY, Phelps EA. Understanding overbidding: using the neural circuitry of reward to design economic auctions. Science. 2008;321:1849–1852. doi: 10.1126/science.1158860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dessauer JP. Book publishing. New York: Bowker; 1981. [Google Scholar]
  17. Dosenbach NU, Visscher KM, Palmer ED, Miezin FM, Wenger KK, Kang HC, Burgund ED, Grimes AL, Schlaggar BL, Petersen SE. A core system for the implementation of task sets. Neuron. 2006;50:799–812. doi: 10.1016/j.neuron.2006.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dyer D, Kagel JH. Bidding in common value auctions: how the commercial construction industry corrects for the winner's curse. Man Sci. 1996;42:1463–1475. [Google Scholar]
  19. Dyer D, Kagel JH, Levin D. A comparison of naive and experienced bidders in common value offer auctions: a laboratory analysis. Econ J. 1989;99:108–115. [Google Scholar]
  20. Eyster E, Rabin M. Cursed equilibrium. Econometrica. 2005;73:1623–1672. [Google Scholar]
  21. Fehr E, Camerer CF. Social neuroeconomics, the neural circuitry of social preferences. Trends Cogn Sci. 2007;11:419–427. doi: 10.1016/j.tics.2007.09.002. [DOI] [PubMed] [Google Scholar]
  22. Fehr E, Schmidt KM. A theory of fairness, competition, and cooperation. Quart J Econ. 1999;114:817–868. [Google Scholar]
  23. Friston K. Functional and effective connectivity in neuroimaging: a synthesis. Hum Brain Mapp. 1994;2:56–78. [Google Scholar]
  24. Garvin S, Kagel JH. Learning in common value auctions: some initial observations. J Econ Behav Organ. 1994;25:351–372. [Google Scholar]
  25. Gneezy U. Step-level reasoning and bidding in auctions. Management Sci. 2005;51:1633–1642. [Google Scholar]
  26. Hampton AN, Bossaerts P, O'Doherty JP. Neural correlates of mentalizing-related computations during strategic interactions in humans. Proc Natl Acad Sci U S A. 2008;105:6741–6746. doi: 10.1073/pnas.0711099105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hare TA, Camerer CF, Knoepfle DT, O'Doherty JP, Rangel A. Value computations in ventral medial prefrontal cortex during charitable decision making incorporate input from regions involved in social cognition. J Neurosci. 2010;30:583–590. doi: 10.1523/JNEUROSCI.4089-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kagel JH, Levin D. Common value auctions and the winner's curse. Princeton, NJ: Princeton UP; 2002. [Google Scholar]
  29. Kagel JH, Levin D, Battalio RC, Meyer DJ. First-price common value auctions: bidder behavior and the “winner's curse”. Econ Inquiry. 1989;27:241–258. [Google Scholar]
  30. Kahnt T, Park SQ, Cohen MX, Beck A, Heinz A, Wrase J. Dorsal striatal-midbrain connectivity in humans predicts how reinforcements are used to guide decisions. J Cogn Neurosci. 2009;21:1332–1345. doi: 10.1162/jocn.2009.21092. [DOI] [PubMed] [Google Scholar]
  31. King-Casas B, Tomlin D, Anen C, Camerer CF, Quartz SR, Montague PR. Getting to know you: reputation and trust in a two-person economic exchange. Science. 2005;308:78–83. doi: 10.1126/science.1108062. [DOI] [PubMed] [Google Scholar]
  32. Ku G, Malhotra D, Murnighan JK. Towards a competitive arousal model of decision-making: a study of auction fever in live and internet auctions. Organ Behav Hum Decis Proc. 2005;96:89–103. [Google Scholar]
  33. Li J, McClure SM, King-Casas B, Montague PR. Policy adjustment in a dynamic economic game. PLoS One. 2006;1:e103. doi: 10.1371/journal.pone.0000103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lind B, Plott CR. The winner's curse: experiments with buyers and with sellers. Am Econ Rev. 1991;81:335–346. [Google Scholar]
  35. Loewenstein GF, Thompson L, Bazerman MH. Social utility and decision making in interpersonal contexts. J Pers Soc Psych. 1989;57:426–432. [Google Scholar]
  36. Malhotra D. The desire to win: the effects of competitive arousal on motivation and behavior. Organ Behav Hum Decis Proc. 2010;111:139–146. [Google Scholar]
  37. McClure SM, van den Bos W. The psychology of common value auctions. In: Phelps E, Robbins T, Delgado M, editors. Attention and performance XXIII: decision making. Oxford: Oxford UP; 2011. [Google Scholar]
  38. Messick DM, McClintock CG. Motivational basis of choice in experimental games. J Exp Soc Psych. 1968;4:1–25. [Google Scholar]
  39. Mitchell JP. Activity in right temporo-parietal junction is not selective for theory-of-mind. Cereb Cortex. 2007;18:262–271. doi: 10.1093/cercor/bhm051. [DOI] [PubMed] [Google Scholar]
  40. Montague PR, Dayan P, Sejnowski TJ. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J Neurosci. 1996;16:1936–1947. doi: 10.1523/JNEUROSCI.16-05-01936.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. O'Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal difference models and reward-related learning in the human brain. Neuron. 2003;38:329–337. doi: 10.1016/s0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
  42. Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning II. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
  43. Rilling JK, Sanfey AG. The neuroscience of social decision-making. Annu Rev Psychol. 2011;62:23–48. doi: 10.1146/annurev.psych.121208.131647. [DOI] [PubMed] [Google Scholar]
  44. Roll R. The hubris hypothesis of corporate takeovers. J Busin. 1986;59:197–216. [Google Scholar]
  45. Sanfey AG, Rilling JK, Aronson JA, Nystrom LE, Cohen JD. The neural basis of economic decision-making in the ultimatum game. Science. 2003;300:1755–1758. doi: 10.1126/science.1082976. [DOI] [PubMed] [Google Scholar]
  46. Saxe R, Kanwisher N. People thinking about thinking people: the role of the temporo-parietal junction in “theory of mind”. Neuroimage. 2003;19:1835–1842. doi: 10.1016/s1053-8119(03)00230-1. [DOI] [PubMed] [Google Scholar]
  47. Seo H, Lee D. Neural basis of learning and preference during social decision-making. Curr Op Neurobio. 2012;22:1–6. doi: 10.1016/j.conb.2012.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Sutton RS, Barto AG. Reinforcement learning. Cambridge, MA: MIT; 1998. [Google Scholar]
  49. Thaler RH. The winner's curse: paradoxes and anomalies of economic life. Princeton, NJ: Princeton UP; 1994. [Google Scholar]
  50. van den Bos W, Li J, Lau T, Maskin E, Cohen JD, McClure SM. The value of victory, social origins of the winner's curse in common value auctions. Judg Decis Making. 2008;3:483–492. [PMC free article] [PubMed] [Google Scholar]
  51. Yoshida W, Seymour B, Friston KJ, Dolan RJ. Neural mechanisms of belief inference during cooperative games. J Neurosci. 2010;30:10744–10751. doi: 10.1523/JNEUROSCI.5895-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zhu L, Mathewson KE, Hsu M. Dissociable neural representations of reinforcement and belief prediction errors underlie strategic learning. Proc Natl Acad Sci U S A. 2012;109:1419–1424. doi: 10.1073/pnas.1116783109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zink CF, Tong Y, Chen Q, Bassett DS, Stein JL, Meyer-Lindenberg A. Know your place: neural processing of social hierarchy in humans. Neuron. 2008;58:273–283. doi: 10.1016/j.neuron.2008.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES