Estimating and testing direct genetic effects in directed acyclic graphs using estimating equations

ABSTRACT

In genetic association studies, it is important to distinguish direct and indirect genetic effects in order to build truly functional models. For this purpose, we consider a directed acyclic graph setting with genetic variants, primary and intermediate phenotypes, and confounding factors. In order to make valid statistical inference on direct genetic effects on the primary phenotype, it is necessary to consider all potential effects in the graph, and we propose to use the estimating equations method with robust Huber–White sandwich standard errors. We evaluate the proposed causal inference based on estimating equations (CIEE) method and compare it with traditional multiple regression methods, the structural equation modeling method, and sequential G‐estimation methods through a simulation study for the analysis of (completely observed) quantitative traits and time‐to‐event traits subject to censoring as primary phenotypes. The results show that CIEE provides valid estimators and inference by successfully removing the effect of intermediate phenotypes from the primary phenotype and is robust against measured and unmeasured confounding of the indirect effect through observed factors. All other methods except the sequential G‐estimation method for quantitative traits fail in some scenarios where their test statistics yield inflated type I errors. In the analysis of the Genetic Analysis Workshop 19 dataset, we estimate and test genetic effects on blood pressure accounting for intermediate gene expression phenotypes. The results show that CIEE can identify genetic variants that would be missed by traditional regression analyses. CIEE is computationally fast, widely applicable to different fields, and available as an R package.

1. INTRODUCTION

In genetic association studies, biotechnological developments and collaborative efforts are allowing to analyze larger cohorts and include more detailed intermediate and outcome measures in the analysis (Helgadottir et al., 2016; Pickrell et al., 2016). As a result, many genetic associations have been identified, for example, with obesity traits and type 2 diabetes (Fuchsberger et al., 2016; Locke et al., 2016). Some genetic markers are associated with multiple anthropometric traits (Ried et al., 2016), anthropometric and metabolic traits (Pickrell et al., 2016), and birthweight and type 2 diabetes (Zeng et al., 2017). However, it is unknown if these studies, and association studies in general, truly show evidence of functional genetic effects (e.g., through genetically determined circulating biomarkers on type 2 diabetes, Lotta et al., 2016, or coronary artery disease, Helgadottir et al., 2016), of pleiotropic genetic effects on multiple phenotypes, or if the observed associations are due to indirect effects through some other intermediate phenotypes. Also, the genetic effects might be mediated or confounded by regulatory factors and intermediate phenotypes such as epigenetic markers (Corradin et al., 2016; Feil & Fraga, 2012; Relton & Davey Smith, 2012a; Relton & Davey Smith, 2012b). As an example, Vansteelandt et al. (2009) showed that the effect estimate of a previously found association between a genetic marker and lung function was biased and could not be confirmed when the indirect effect of the genetic marker through weight was removed. In addition, the direct genetic effects can also be masked in traditional statistical methods when there are indirect effects or confounded indirect effects in opposing direction of the direct effect.

This background highlights the importance of using appropriate statistical methods that help disentangling direct and indirect genetic effects through intermediate phenotypes, which is the focus of this paper. Causal diagrams (Pearl, 1995) are helpful for visualizing the research setting, and we consider the directed acyclic graph (DAG) in Figure 1, which includes the direct effect of a genetic marker X on the primary phenotype Y and an indirect genetic effect through a secondary phenotype K. The model further includes measured and unmeasured factors L and U, respectively, which potentially confound the effect of K on Y. The goal of this study is to estimate and test the direct genetic effect ${\alpha }_{XY}$, while removing the indirect effect of X on Y through K, and with robustness against effects of L and U. Without restriction of generality, we assume that there are no factors affecting X and that any factors such as family structure or population stratification are included as covariates in the analysis or have been dealt with using other approaches (Eu‐ahsunthornwattana et al., 2014; Price et al., 2006). Also, we generally assume that ${\alpha }_{LY}=0$ so that L is a factor influencing only K. However, it will be shown that our proposed approach also provides valid inference if L is a measured confounder of $K\to Y$ (${\alpha }_{LY}\ne 0$ and ${\alpha }_{XL}=0$). If both ${\alpha }_{LY}\ne 0$ and ${\alpha }_{XL}\ne 0$, then the effect of L as intermediate phenotype could be removed from Y analogously to K.

Figure 1.

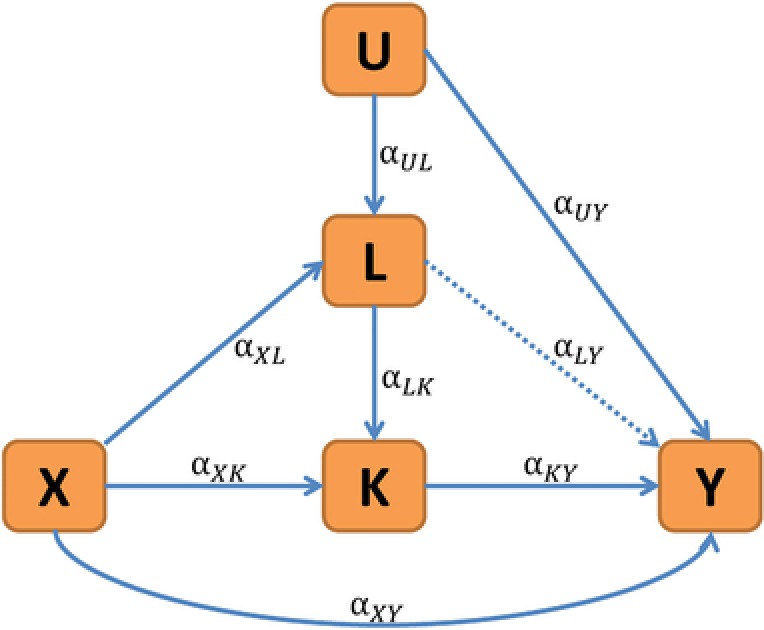
Overview of the directed acyclic graph considered in this study. Y is the primary outcome measure of interest; K is a secondary phenotype; X is the genetic marker of interest and α_XY is the direct effect of interest. It is assumed that ${\alpha }_{\mathrm{LY}}=0$ so that L is a measured predictive factor of K, however, CIEE is also valid if L is a measured confounder of $K\to Y$ (i.e., ${\alpha }_{LY}\ne 0$ and ${\alpha }_{\mathrm{XL}}=0$). U represents unmeasured factors and confounders potentially influencing L and Y.

Two traditional methods for the aim to estimate ${\alpha }_{XY}$ are (i) to include the intermediate phenotypes and factors as covariates in a multiple regression (MR) model of the primary phenotype on the genetic marker, or (ii) to first regress the primary phenotype on the intermediate phenotypes and factors, and then regress the extracted residuals on the genetic marker (regression of residuals, RR). These approaches are frequently used for the analysis of continuous primary phenotypes using a linear regression model, and MR is also a frequently used approach for the analysis of binary or categorical primary phenotypes (using generalized linear regression models), or potentially censored time‐to‐event primary phenotypes (using, for example, proportional hazards (PH) or accelerated failure time (AFT) regression models). However, both traditional approaches can lead to biased point estimates and invalid testing of direct genetic effects on the primary phenotype in some situations, by removing part of the true association or by failing to remove the effect of the intermediate phenotype (i.e., the indirect genetic effect) or unmeasured confounders (Cole & Hernán, 2002; Goetgeluk, Vansteelandt, & Goetghebeur, 2008; Rosenbaum, 1984; Vansteelandt et al., 2009). More elaborate approaches have been proposed to overcome these limitations. The structural equation modeling method (SEM; Bollen, 1989) is a popular approach for modeling DAGs, and has been applied to genetic association studies under similar DAGs as in this study (for example, see Hancock et al., 2015). Further approaches have been developed in studies on causal inference using structural nested models and G‐estimation methods (Goetgeluk et al., 2008; Robins, 1986, 1992; Robins & Greenland, 1994), or the inverse probability weighting method (Robins, Hernán, & Brumback, 2000). A more detailed overview of these approaches can be found in Vansteelandt and Joffe (2014).

Applications of the sequential G‐estimation method to the DAG in Figure 1 have been described for quantitative (i.e., completely observed) primary phenotypes (Vansteelandt et al., 2009) and time‐to‐event primary phenotypes subject to censoring (using PH and AFT regression models, Lipman et al., 2011, and Aalen additive hazard models, Martinussen et al., 2011). These approaches include two steps: first, an adjusted phenotype is obtained by removing the effect of the intermediate phenotype K from the primary phenotype Y. Then, the association of the genetic marker with the adjusted phenotype is tested by accounting for the additional variability obtained due to the estimation in the first stage. Asymptotic properties of the estimator have been provided for the analysis of Aalen additive hazard models (Martinussen et al., 2011) and for the sequential G‐estimation under a more general setting (Goetgeluk et al., 2008). However, it is shown in this study that the sequential G‐estimation method described for time‐to‐event primary phenotypes using the PH and AFT regression models (Lipman et al., 2011) is invalid. In addition, a closed‐form estimate of the standard error of the direct effect estimator was not provided in Vansteelandt et al. (2009) and in Lipman et al. (2011).

In this study, we propose a novel method to estimate and test the direct effect ${\alpha }_{XY}$ of a genetic marker X on the primary phenotype Y under the DAG in Figure 1. The approach is based on the method of estimating equations and called CIEE (Causal Inference based on Estimating Equations), and it can be adapted to other DAGs and to linear models with different error distributions. The standard error of ${\widehat{\alpha }}_{XY}$ is estimated by using the so‐called robust Huber–White sandwich variance estimator, and we use a large‐sample Wald‐type test statistic for hypothesis testing of the absence of the direct effect of X on Y. Using unbiased estimating functions allows drawing on the known asymptotic properties of estimators and test statistics. We provide details of the proposed approach for the analysis of quantitative and time‐to‐event primary phenotypes, and assess the validity of the estimation method and the test statistic across different scenarios in an extensive simulation study. In addition, we compare CIEE in the simulation study with the traditional multiple regression methods (MR and RR), the SEM method (Rosseel, 2012), and the sequential G‐estimation methods (Lipman et al., 2011; Vansteelandt et al., 2009). Finally, in an application to the Genetic Analysis Workshop 19 (GAW19) dataset (Blangero et al., 2016), we estimate and test direct effects of single nucleotide polymorphisms (SNPs) on blood pressure accounting for intermediate gene expression phenotypes and available covariates using CIEE and MR, and discuss the different results obtained. An R package with the implementation of CIEE is publicly available from https://cran.r-project.org/web/packages/CIEE/.

2. METHODS

In this section, we describe the proposed CIEE method for estimating ${\alpha }_{XY}$ under the DAG in Figure 1. We start by introducing CIEE in the simpler analysis of a quantitative primary trait, followed by describing the analysis of time‐to‐event primary traits that requires an additional step. CIEE follows the general idea of the two‐stage sequential G‐estimation method. As a major difference, CIEE is a one‐stage method and estimates all parameters including ${\alpha }_{XY}$ simultaneously by solving the proposed estimating equations.

For the analysis of a quantitative primary phenotype, CIEE yields the same estimate of ${\alpha }_{XY}$ as the G‐estimation method described in Vansteelandt et al. (2009) if the latter is computed using the least squares (LS) estimation. We obtain the asymptotic properties for the direct effect estimator by using the asymptotic theory for estimating functions, show that the estimator of the direct effect is consistent, and derive its asymptotic distribution. As a novel contribution, we obtain a closed form of its standard error that is important for uncertainty quantification. Alternatively, the standard error of the direct effect estimator could be estimated by a nonparametric bootstrap procedure, but it is computationally expensive and has further drawbacks, such that it cannot be directly used for SNPs with low minor allele frequency (MAF).

For the analysis of time‐to‐event primary traits, CIEE contains an additional step and is an extension of the quantitative trait analysis. Since the sequential G‐estimation method described for time‐to‐event primary phenotypes using the PH and AFT regression models (Lipman et al., 2011) is invalid, as is shown in this study, CIEE yields a different estimator and to our knowledge it is the first valid approach for this setting. Furthermore, we give additional empirical details on the properties of CIEE and G‐estimation estimators including the unbiasedness and efficiency through the results of the simulation study for both settings.

2.1. Analysis of a quantitative primary trait with CIEE

First, we focus on the analysis of a (completely observed) normally distributed primary phenotype Y with $n$independent observations. In CIEE, unbiased estimating functions are constructed considering the two linear regression models fitted sequentially in the G‐estimation method (Vansteelandt et al., 2009), which are as follows. In the first stage, the effect of K on Y, α₁, is estimated, adjusting for other factors, by using the LS estimation method under the model

$$\begin{array}{ccc}\hfill Y_i& =& {\alpha }_0+{\alpha }_1{k}_i+{\alpha }_2{x}_i+{\alpha }_3{l}_i+{\epsilon }_i,{\epsilon }_i\sim N\left(0,{\sigma }_1^2\right),\hfill \\ & & i=1,\dots ,n.\hfill \end{array}$$ (1)

Then, to block all indirect paths of X on the primary phenotype Y, the adjusted phenotype $\stackrel{\sim }{Y}$ is obtained by removing the effect of K on Y with

$${\stackrel{\sim }{y}}_i=y_i-\overline{y}-{\widehat{\alpha }}_1\left(k_i-\overline{k}\right)$$ (2)

where ${\displaystyle \overline{y}=\frac{1}{n}\sum _{i=1}^n{y}_i}$ and ${\displaystyle \overline{k}=\frac{1}{n}\sum _{i=1}^n{k}_i}$.

In the second stage, the direct effect of X on Y, ${\alpha }_{XY}$, is tested under the model

$${\stackrel{\sim }{Y}}_i={\alpha }_4+{\alpha }_{XY}{x}_i+{\epsilon }_i^{\prime },{\epsilon }_i^{\prime }\sim N\left(0,{\sigma }_2^2\right)$$ (3)

In CIEE, we formulate unbiased estimating equations $\mathit{U}(\mathit{\theta })=\mathit{}\mathbf{0}$ for a consistent estimation of the unknown parameter vector $\mathit{\theta }=\mathit{}\left(\begin{array}{c}{\mathit{\theta }}_1\\ {\mathit{\theta }}_2\end{array}\right)$with ${\mathit{\theta }}_1={({\alpha }_0,{\alpha }_1,{\alpha }_2,{\alpha }_3,{\sigma }_1^2)}^T$, ${\mathit{\theta }}_2={({\alpha }_4,{\alpha }_{XY},{\sigma }_2^2)}^T$, where

$$U\left(\mathit{\theta }\right)=\left(\begin{array}{c}{\displaystyle \frac{\partial l_1\left({\mathit{\theta }}_1\right)}{\partial {\mathit{\theta }}_1}}\\ {\displaystyle \frac{\partial l_2\left({\alpha }_1,{\mathit{\theta }}_2\right)}{\partial {\mathit{\theta }}_2}}\end{array}\right)$$ (4)

$${\displaystyle l_1\left({\mathit{\theta }}_1\right)=\sum _{i=1}^n\left[-log\left({\sigma }_1\right)+log\left(\phi \left(\frac{y_i-{\alpha }_0-{\alpha }_1{k}_i-{\alpha }_2{x}_i-{\alpha }_3{l}_i}{{\sigma }_1}\right)\right)\right]}$$ (5)

$${\displaystyle l_2\left({\alpha }_1,{\mathit{\theta }}_2\right)=\sum _{i=1}^n\left[-log\left({\sigma }_2\right)+log\left(\phi \left(\frac{y_i-\overline{y}-{\alpha }_1\left(k_i-\overline{k}\right)-{\alpha }_4-{\alpha }_{XY}{x}_i}{{\sigma }_2}\right)\right)\right]}$$ (6)

and φ(.) is the probability density function of the standard normal distribution. To give an intuition on how these estimating equations are obtained, $l_1({\mathit{\theta }}_1)$ is the log‐likelihood function under the model in (1) and $l_2({\alpha }_1,{\mathit{\theta }}_2)$ is the log‐likelihood function under the model in (3) given that α₁ is known. By solving the first five estimating equations based on $l_1({\mathit{\theta }}_1)$ in (5), we are hence fitting the model in (1) to obtain an estimate of θ ₁, that is obtaining the maximum likelihood (ML) estimates under the model in (1). Analogously, solving the last three estimating equations based on $l_2({\alpha }_1,{\mathit{\theta }}_2)$ yields an estimate of θ ₂. Hence, we obtain the estimate of θ, denoted by $\mathit{}\widehat{\mathbf{\theta }}$, by solving $\mathit{U}(\mathit{\theta })=\mathit{}\mathbf{0}$. As a difference to the two‐stage sequential G‐estimation method, we estimate all parameters in θ simultaneously and consider the additional variability obtained in the phenotype adjustment in (2) by using the robust Huber–White sandwich estimator of the standard error of $\mathit{}\widehat{\mathbf{\theta }}$.

Under mild regularity conditions (White, 1982), $\sqrt{n}(\mathit{}\widehat{\mathbf{\theta }}-\mathit{\theta })$ is asymptotically normally distributed with mean 0 and covariance matrix $C(\mathit{\theta })$ that can be consistently estimated with $C_n(\mathit{}\widehat{\mathbf{\theta }})$, where

$$C_n\left(\mathit{\theta }\right)=A_n{\left(\mathit{\theta }\right)}^{-1}{B}_n\left(\mathit{\theta }\right){\left[A_n{\left(\mathit{\theta }\right)}^{-1}\right]}^T$$ (7)

$$A_n\left(\mathit{\theta }\right)=-\frac{1}{n}\left(\frac{\partial U\left(\mathit{\theta }\right)}{\partial {\mathit{\theta }}^T}\right)$$ (8)

$$\begin{array}{ccc}& & B_n\left(\mathit{\theta }\right)\hfill \\ & & =\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left[U_j\left(y_i,k_i,x_i,l_i;\mathit{\theta }\right)·U_k{\left(y_i,k_i,x_i,l_i;\mathit{\theta }\right)}^T\right]}_{j,k=1\dots p}}\hfill \end{array}$$ (9)

with $U_j$ being the j‐th element in equation (4) and $p=8$. The robust Huber–White sandwich estimate of the standard error of ${\widehat{\alpha }}_{XY}$ can then be obtained as $\widehat{SE}({\widehat{\alpha }}_{XY})=\sqrt{\frac{1}{n}{C}_n{(\mathit{}\widehat{\mathbf{\theta }})}_{7,7}}$. Having obtained the estimates of α_XY and its standard error, we use the large‐sample Wald‐type test statistic $W={\widehat{\alpha }}_{XY}/\widehat{SE}({\widehat{\alpha }}_{XY})$ for testing $H_0:{\alpha }_{\mathrm{XY}}=0$ vs. $H_A:{\alpha }_{\mathrm{XY}}\ne 0$. Under H ₀, W has an asymptotic standard normal distribution.

2.2. Analysis of a time‐to‐event primary trait with CIEE

For the analysis of a time‐to‐event primary phenotype T, we consider the right‐censoring scheme with observed time‐to‐events $t_i=min(T_i,C_i)$ and censoring indicators ${\delta }_i=I[T_i\le C_i]$ for a random sample of individuals $i=1,\dots ,n$, where $T_i$ is the time‐to‐event, $C_i$ is the censoring time and I[.] is the indicator function. We assume that censoring is noninformative. We consider the AFT, or the log‐linear, model

$$Y_i=log\left(T_i\right)={\alpha }_0+{\alpha }_1{k}_i+{\alpha }_2{x}_i+{\alpha }_3{l}_i+{\sigma }_1{\epsilon }_i,{\sigma }_1>0$$ (10)

for the phenotype adjustment. The error term in equation (10) can come from any distribution, and here we focus on the log‐linear model with ${\epsilon }_i\sim N(0,1)$ for illustration. The estimating equations can be constructed as described above for a quantitative primary phenotype, but in order to remove the effect of K from Y, the true underlying log‐time‐to‐event $Y_{est}$ needs to be estimated for each censored time.$Y_{est}$ equals the observed log‐time‐to‐event Y for uncensored times. To estimate $Y_{est}$ for a censored time‐to‐event, we obtain the conditional expectation of Y given that it is greater than the observed log‐transformed right‐censoring time and given the covariates (Konigorski, Yilmaz, & Bull, 2014):

$$y_{est,i}={\delta }_i·y_i+\left(1-{\delta }_i\right)·E\left[Y_i|Y_i>y_i,k_i,x_i,l_i\right]$$ (11)

This additional computation is needed since the censored time‐to‐events cannot be directly used to remove the effect of K from Y. Under the AFT model in (10), the estimates of $Y_{est}$ in (11) should roughly behave like the true underlying time‐to‐event in expectation (Lawless, 2003, pp. 284–285). The effect of this additional step on the estimation and testing will be discussed in the Results section under different levels of censoring.

Then, we compute the adjusted phenotypes using

$${\stackrel{\sim }{y}}_i=y_{est,i}-\overline{y_{est}}-{\alpha }_1\left(k_i-\overline{k}\right)$$ (12)

with $y_{est,i}$ obtained from equation (11) and ${\displaystyle \overline{y_{est}}=\frac{1}{n}{\sum }_{i=1}^n{y}_{est,i}}$.

Finally, we model the direct genetic effect on the adjusted phenotype using

$${\stackrel{\sim }{Y}}_i={\alpha }_4+{\alpha }_{XY}{x}_i+{\epsilon }_i^{\prime },{\epsilon }_i^{\prime }\sim N\left(0,{\sigma }_2^2\right)$$ (13)

Hence, the estimating equations for estimating $\mathit{\theta }=\left(\begin{array}{c}{\mathit{\theta }}_1\\ {\mathit{\theta }}_2\end{array}\right)$ with ${\mathit{\theta }}_1={({\alpha }_0,{\alpha }_1,{\alpha }_2,{\alpha }_3,{\sigma }_1)}^T$, ${\mathit{\theta }}_2={({\alpha }_4,{\alpha }_{XY},{\sigma }_2^2)}^T$ are

$$U\left(\mathit{\theta }\right)=\left(\begin{array}{c}{\displaystyle \frac{\partial l_1\left({\mathit{\theta }}_1\right)}{\partial {\mathit{\theta }}_1}}\\ {\displaystyle \frac{\partial l_2\left({\mathit{\theta }}_1,{\mathit{\theta }}_2\right)}{\partial {\mathit{\theta }}_2}}\end{array}\right)=\mathit{}\mathbf{0}$$ (14)

with

$$\begin{array}{ccc}\hfill l_1\left({\mathit{\theta }}_1\right)& =& {\displaystyle \sum _{i=1}^n\left[-{\delta }_{i}log\left({\sigma }_1\right)+{\delta }_{i}log\left(\phi \left(\frac{y_i-{\alpha }_0-{\alpha }_1{k}_i-{\alpha }_2{x}_i-{\alpha }_3{l}_i}{{\sigma }_1}\right)\right)\right.}\hfill \\ & & \left.+\left(1-{\delta }_i\right)log\left(1-\mathrm{\Phi }\left(\frac{y_i-{\alpha }_0-{\alpha }_1{k}_i-{\alpha }_2{x}_i-{\alpha }_3{l}_i}{{\sigma }_1}\right)\right)\right]\hfill \end{array}$$ (15)

and

$${\displaystyle l_2\left({\mathit{\theta }}_1,{\mathit{\theta }}_2\right)=\sum _{i=1}^n\left[-log\left({\sigma }_2\right)+log\left(\phi \left(\frac{y_{est,i}-\overline{y_{est}}-{\alpha }_1\left(k_i-\overline{k}\right)-{\alpha }_4-{\alpha }_{XY}{x}_i}{{\sigma }_2}\right)\right)\right]}$$ (16)

where φ(.) and Φ(.) are the standard normal probability density and cumulative distribution function, respectively. $\mathit{U}(\mathit{\theta })=\mathit{}\mathbf{0}$ are unbiased estimating equations with $\sqrt{n}(\mathit{}\widehat{\mathbf{\theta }}-\mathit{\theta })\stackrel{D}{\to }N(0,C(\mathit{\theta }))$, where $C(\mathit{\theta })$ is estimated as described in the previous section. Here, $l_1({\mathit{\theta }}_1)$ is the log‐likelihood function under the model in equation (10) and $l_2({\mathit{\theta }}_1,{\mathit{\theta }}_2)$ is the log‐likelihood function under the model in equation (13) given that θ ₁ is known. By solving the first five estimating equations based on $l_1({\mathit{\theta }}_1)$ in equation (15), we obtain an estimate of θ ₁, and solving the last three estimating equations based on $l_2({\mathit{\theta }}_1,{\mathit{\theta }}_2)$ yields an estimate of θ ₂. See Supplementary Text 1 for the derivation of $Y_{est}$ in equation (11) and for further explanations on how the estimating equations were constructed.

2.3. Estimation of standard errors using nonparametric bootstrap

As an alternative to the sandwich variance estimator of $\mathit{}\widehat{\mathbf{\theta }}$ based on estimating equations, the nonparametric bootstrap (Efron, 1981) can be used (see also Goetgeluk et al., 2008). In order to obtain the standard error estimate of ${\widehat{\alpha }}_{XY}$, in step 1, a sample of n individuals is randomly selected from the data with replacement. In step 2, the point estimate ${\widehat{\alpha }}_{XY,l}$ is obtained by solving the estimating equations in (4) or (14), depending on the type of the primary phenotype. These two steps are performed B times and the bootstrap standard error estimate of ${\widehat{\alpha }}_{XY}$ can be obtained as the standard deviation of the ${\widehat{\alpha }}_{XY,l},l=1,\dots ,B$.

2.4. Simulation study

In order to evaluate CIEE, simulation studies were performed to firstly investigate the properties of the point estimate of α_XY, and whether the effect of the intermediate phenotype K is successfully removed from the primary phenotype Y, for both quantitative and time‐to‐event phenotypes. Next, the empirical type I error and power estimates of the Wald‐type tests based on CIEE using robust sandwich standard errors and using nonparametric bootstrap standard errors (based on $B=1,000$ resamples) were obtained. For a quantitative primary phenotype, they were compared with the two naïve regression modeling approaches (MR and RR), the sequential G‐estimation method (Vansteelandt et al., 2009) and the SEM method (Bollen, 1989; Rosseel, 2012). Under the AFT model, the results were compared to the naïve MR approach and the extension of the sequential G‐estimation method proposed by Lipman et al. (2011).

The genetic marker X was generated with an additive genetic coding for minor allele frequencies ${\mathrm{MAF}}_X=$ 0.05, 0.1, 0.2, 0.4. The phenotypes and factors were then generated from different subgraphs of the DAG in Figure 1 with different effect sizes, for a sample of $n=1,000$ individuals and using $m=10,000$ replication datasets. A detailed overview of the scenarios and parameter values can be found in Supplementary Table 1. Figure 2 gives a graphical overview of the different scenarios, including models with and without measured and unmeasured confounding factors, under the null hypothesis of no direct genetic effect of X on Y. Under the AFT model, time‐to‐event traits with 10%, 30%, and 50% censoring were considered. The effect sizes were set to simulate realistic situations with small genetic effects and small/moderate effects of the intermediate phenotype and the measured as well as unmeasured factors on the primary phenotype (scenarios 1–5). Under the null model of a quantitative primary phenotype, two additional scenarios (6 and 7) were investigated where scenario 6 contains confounding of the indirect effect through measured factors, and scenario 7 equals scenario 4 but with larger effect sizes. While the data generation contains a nonzero effect of L on Y, the CIEE, SEM, and sequential G‐estimation methods assume ${\alpha }_{\mathrm{LY}}=0$ in the analysis, so that scenario 6 provides an assessment of the robustness of the methods against model misspecification. For a more detailed description of the simulation study scenarios and data generation, see Supplementary Text 2.

Figure 2.

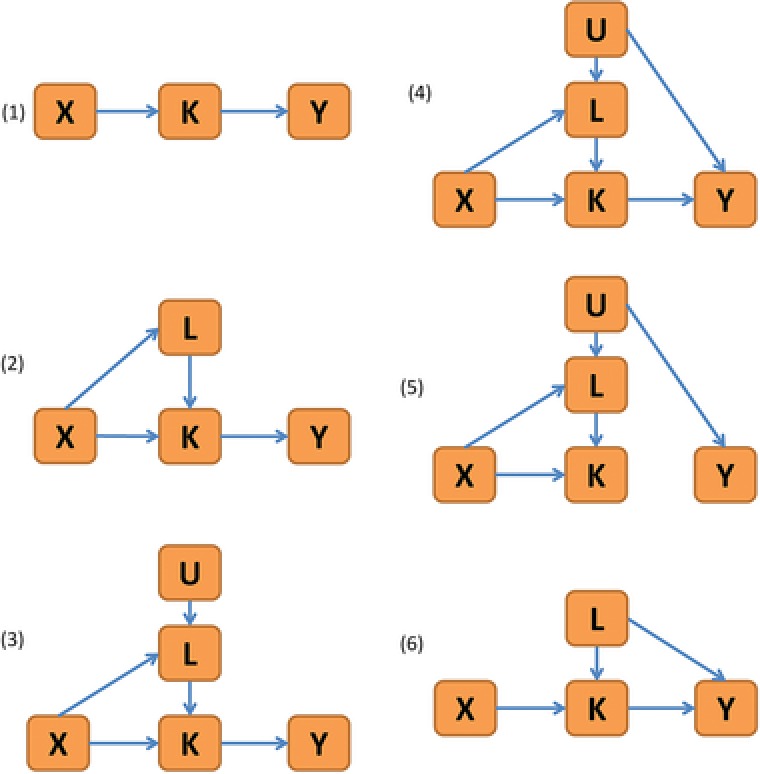
Overview of the scenarios considered in the simulation study for investigation of the type I error. The models are submodels of the DAG in Figure 1 with some of the effects set to 0. Scenario 7 equals scenario 4 in this figure with larger effect sizes. Scenario 6 contains a nonzero effect of L on Y in the data generation, providing a test of robustness against model misspecification. Nonzero direct effects of X on Y are considered under each scenario for investigation of the power of the test statistics.

For the two traditional approaches, MR and RR, estimates of ${\alpha }_{XY}$ were obtained by fitting the following models in the analysis of a quantitative primary trait.

MR: Obtain the LS estimate of ${\alpha }_{XY}$ by fitting

$$Y_i={\alpha }_0+{\alpha }_{XY}{x}_i+{\alpha }_1{k}_i+{\alpha }_2{l}_i+{\epsilon }_i,{\epsilon }_i\sim N\left(0,{\sigma }_1^2\right)$$

RR: First, obtain residuals ${\widehat{\epsilon }}_{1i}=$ $y_i-({\widehat{\alpha }}_0+{\widehat{\alpha }}_1{k}_i+{\widehat{\alpha }}_2{l}_i)$ by fitting

$$Y_i={\alpha }_0+{\alpha }_1{k}_i+{\alpha }_2{l}_i+{\epsilon }_{1i},{\epsilon }_{1i}\sim N\left(0,{\sigma }_1^2\right)$$

using the LS estimation. Second, obtain the LS estimate of ${\alpha }_{XY}$ by fitting

$${\widehat{\epsilon }}_{1i}={\alpha }_3+{\alpha }_{XY}{x}_i+{\epsilon }_{2i},{\epsilon }_{2i}\sim N\left(0,{\sigma }_2^2\right)$$

Then, $H_0:{\alpha }_{\mathrm{XY}}=0$ vs. $H_A:{\alpha }_{\mathrm{XY}}\ne 0$ was tested using the default t‐test in the lm() function in R. For the analysis of a time‐to‐event primary trait, the censored log‐linear regression model in equation (10) was fitted using the survreg() function in the survival R package to obtain the ML estimate of ${\alpha }_{XY}$, and the Wald test was performed for testing the null hypothesis $H_0:{\alpha }_{\mathrm{XY}}=0$.

In order to obtain estimates of ${\alpha }_{XY}$ and its standard error estimate under the SEM method, the sem() function in the lavaan R package (Rosseel, 2012) was used with default settings to fit the DAG based on the following equations:

$$\begin{array}{ccc}& & L_i={\alpha }_0+{\alpha }_1{x}_i+{\epsilon }_{1i},{\epsilon }_{1i}\sim N\left(0,{\sigma }_1^2\right)\hfill \\ & & K_i={\alpha }_2+{\alpha }_3{x}_i+{\alpha }_4{l}_i+{\epsilon }_{2i},{\epsilon }_{2i}\sim N\left(0,{\sigma }_2^2\right)\hfill \\ & & Y_i={\alpha }_5+{\alpha }_6{k}_i+{\alpha }_{XY}{x}_i+{\epsilon }_{3i},{\epsilon }_{3i}\sim N\left(0,{\sigma }_3^2\right).\hfill \end{array}$$

The default Wald‐type test in the sem() function was then used to test $H_0:{\alpha }_{\mathrm{XY}}=0$ vs. $H_A:{\alpha }_{\mathrm{XY}}\ne 0$.

To apply the sequential G‐estimation methods, the functions CGcont() and CGsurvreg() in the R package CGene (Lipman & Lange, 2011), obtained from http://www.inside-r.org/packages/cran/CGene, were used with default values and adapted to the considered log‐linear model for the analysis.

3. RESULTS

3.1. Estimation of coefficients and standard errors

First, the estimates of the direct genetic effect and its standard error were investigated for all methods for the analysis of quantitative and time‐to‐event primary phenotypes, under the null and alternative hypotheses (see Supplementary Tables 2–5). The results showed that the CIEE point estimates of the direct genetic effect are unbiased across all scenarios. Also, the standard error estimates based on the estimating equations’ Huber–White sandwich estimate, nonparametric bootstrap, and the empirical standard deviation of point estimates (Supplementary Table 6) were identical up to 2 decimals. Further checks showed that the effect of K on Y was successfully removed using the CIEE method so that $\stackrel{\sim }{Y}$ was uncorrelated with K (data not shown).

Regarding the naïve approaches, the coefficient estimates under the MR and RR models showed some bias whenever there was unmeasured confounding (scenarios 4, 5, and 7 in Supplementary Table 2). The direct effect can be underestimated as in the scenarios considered here, or overestimated if, for example, the unmeasured confounding effect of U on Y is negative. When the effect of the intermediate on the primary phenotype was only confounded through measured factors in scenario 6, then both methods provided unbiased genetic effect estimates. The SEM genetic effect estimates also showed some bias when there was a higher amount of unmeasured confounding (scenario 7 in Supplementary Table 2), or when the DAG model was misspecified (scenario 6 in Supplementary Table 2, when the estimation falsely assumed ${\alpha }_{LY}=0$ while the data were generated with ${\alpha }_{LY}=0.3$). However, when the model was changed to correctly model an effect of L on Y in scenario 6, then unbiased genetic effect estimates were obtained with the SEM method (data not shown). The standard error estimates of ${\widehat{\alpha }}_{XY}$ obtained through MR, RR, and SEM were close to the CIEE standard error estimates when the amount of unmeasured confounding was small or medium. Under scenario 7, the RR modeling approach underestimated the standard errors.

Among the investigated sequential G‐estimation approaches, the method for analyzing quantitative traits (Vansteelandt et al., 2009) provided the same unbiased genetic effect estimates as CIEE, however, the approach for time‐to‐event traits (Lipman et al., 2011) did not remove the effect of the intermediate phenotype (see Supplementary Text 3 for further details) and provided strongly biased direct effect estimates whenever there was some effect of K on Y (Supplementary Tables 4 and 5). In addition, the sequential G‐estimation methods do not provide a standard error estimate of the estimated direct genetic effect, and therefore, we could only obtain standard error estimates using the nonparametric bootstrap.

3.2. Empirical type I error and power

As a direct consequence of the bias of genetic effect estimates discussed above, all investigated approaches except the proposed CIEE method and the sequential G‐estimation method for quantitative primary traits led to inflated empirical type I errors in some scenarios (see Tables 1 and 2). Inference based on CIEE was valid for SNPs with different MAF, different effect sizes, with a small or moderate amount of censoring in the analysis of primary time‐to‐event traits, and also if unmeasured confounding through L was present. Statistical inference remained valid also for heavy censoring (e.g., 80% censoring) when there was no unmeasured confounding (data not shown). In addition, CIEE was robust against distributional misspecifications. For example, when the quantitative primary trait Y given X, K, L, U was not normally distributed but followed a t₍₄₎, t₍₈₎, or log‐normal distribution, estimates of α_XY remained unbiased and type I errors were valid (Supplementary Table 6).

Table 1.

Empirical type I error estimates under the null model of a quantitative primary phenotype

Scenario	MAFX	CIEE	BS	G‐EST	MR	RR	SEM
1	0.05	5.45%	5.40%	5.03%	5.35%	5.29%	5.04%
	0.1	5.26%	5.18%	5.05%	5.34%	5.23%	5.05%
	0.2	4.83%	4.88%	4.76%	4.94%	4.87%	5.34%
	0.4	5.16%	5.17%	5.12%	5.06%	4.80%	5.24%
2	0.05	5.17%	5.12%	4.77%	4.71%	4.67%	5.57%
	0.1	5.16%	5.13%	5.02%	5.12%	4.99%	4.75%
	0.2	5.01%	4.91%	4.87%	5.16%	4.90%	5.46%
	0.4	5.14%	5.14%	5.06%	4.91%	4.54%	4.86%
3	0.05	5.37%	5.27%	4.89%	4.89%	4.82%	5.18%
	0.1	5.17%	5.11%	4.99%	5.00%	4.87%	4.85%
	0.2	4.89%	4.90%	4.81%	5.25%	4.95%	5.19%
	0.4	5.06%	4.96%	4.97%	4.77%	4.38%	5.21%
4	0.05	5.44%	5.30%	4.98%	5.15%	5.10%	5.32%
	0.1	5.25%	5.21%	4.99%	5.27%	5.13%	4.87%
	0.2	4.81%	4.79%	4.73%	6.03%	5.68%	4.98%
	0.4	5.09%	5.14%	5.03%	5.90%	5.48%	5.43%
5	0.05	5.26%	5.11%	4.83%	4.94%	4.82%	5.42%
	0.1	5.08%	5.02%	4.91%	5.42%	5.23%	5.24%
	0.2	4.91%	4.93%	4.88%	6.01%	5.69%	5.42%
	0.4	5.12%	5.14%	5.07%	6.11%	5.75%	5.40%
6	0.05	5.14%	5.21%	4.57%	5.35%	5.29%	5.62%
	0.1	5.29%	5.27%	5.10%	5.13%	5.08%	5.83%
	0.2	5.03%	4.99%	4.83%	5.25%	5.01%	6.01%
	0.4	5.09%	5.04%	4.96%	4.94%	4.68%	6.33%
7	0.05	5.06%	4.97%	4.61%	36.14%	30.45%	21.33%
	0.1	5.05%	5.16%	4.94%	56.37%	45.31%	33.26%
	0.2	4.97%	4.93%	4.94%	73.78%	54.86%	45.47%
	0.4	5.18%	5.23%	5.17%	82.96%	59.54%	55.24%

Data were generated for $n=1,000$ individuals and $m=10,000$ replicates. CIEE is the proposed method using estimating equations; BS is CIEE using nonparametric bootstrap standard errors; G‐EST is the sequential G‐estimation approach (Vansteelandt et al., 2009); MR is multiple regression; RR is residual regression; and SEM is structural equation modeling.

Table 2.

Empirical type I error estimates under the null model of a time‐to‐event primary phenotype

Scenario	Censoring	CIEE	BS	G‐EST	MR
1	10%	5.29%	5.29%	22.81%	4.82%
	30%	5.24%	5.13%	24.98%	5.00%
	50%	5.29%	5.33%	20.24%	5.28%
2	10%	5.15%	5.45%	34.48%	5.28%
	30%	5.13%	5.29%	37.83%	5.15%
	50%	5.14%	5.20%	30.33%	4.74%
3	10%	5.10%	5.12%	34.54%	5.34%
	30%	4.94%	4.92%	37.25%	5.30%
	50%	4.88%	4.77%	30.66%	4.84%
4	10%	5.23%	5.19%	31.59%	6.07%
	30%	5.15%	5.15%	35.40%	6.17%
	50%	5.24%	5.14%	29.43%	5.68%
5	10%	5.15%	5.27%	4.94%	6.17%
	30%	4.98%	5.08%	4.80%	5.79%
	50%	4.93%	4.84%	4.33%	5.73%

Data were generated for $n=1,000$ individuals and $m=10,000$ replicates. The MAF of the marker X was set to 0.2. CIEE is the proposed method using estimating equations; BS is CIEE using nonparametric bootstrap standard errors; G‐EST is the sequential G‐estimation approach (Lipman et al., 2011); and MR is multiple log‐linear censored regression.

The traditional regression methods provided valid testing whenever there was no unmeasured confounding with RR being consistently more conservative (Table 1). SEM was slightly more robust to small unmeasured confounding but had inflated type I error for larger unmeasured confounding (scenario 7) or when the DAG model was misspecified (scenario 6). The sequential G‐estimation method (Vansteelandt et al., 2009) led to valid type I errors for all considered scenarios when quantitative traits were analyzed. For the analysis of time‐to‐event primary traits, however, the proposed G‐estimation approach (Lipman et al., 2011) provided largely inflated type I errors across almost all scenarios (Table 2).

For the power study, the same scenarios of the type I error study were considered for each type of primary trait, with direct genetic effect sizes (${\alpha }_{XY}$) of 0.1 and 0.2. The results were highly consistent across all scenarios both for the analysis of quantitative traits (Table 3) and time‐to‐event traits (Supplementary Table 7). All approaches had very similar power in each scenario where they had valid type I error. It is noteworthy that CIEE did not lose power compared to the traditional approaches in scenarios 1–3 where they had valid type I error. Furthermore, in the presence of unmeasured confounding in scenarios 4–5, the power of CIEE decreased only minimally while the traditional methods had inflated type I error (as well as lower power) and should not be applied.

Table 3.

Power estimates under the alternative hypothesis models of a quantitative primary phenotype

Scenario	αXY	CIEE	BS	G‐EST	MR	RR	SEM
1	0.1	42.33%	42.26%	41.98%	43.13%	42.63%	42.31%
	0.2	94.62%	94.59%	94.54%	94.81%	94.68%	94.13%
2	0.1	42.52%	42.40%	42.22%	41.55%	40.53%	43.51%
	0.2	94.22%	94.09%	94.09%	94.18%	93.81%	94.15%
3	0.1	42.35%	42.30%	41.98%	42.85%	41.90%	42.32%
	0.2	94.20%	94.17%	94.06%	94.03%	93.68%	94.17%
4	0.1	39.90%	39.74%	39.53%	30.12%	29.30%	35.85%
	0.2	91.88%	91.88%	91.78%	87.92%	87.38%	90.26%
5	0.1	39.04%	38.99%	38.76%	28.79%	28.11%	35.56%
	0.2	92.48%	92.44%	92.38%	87.10%	86.66%	90.46%

In all scenarios, data were generated for $n=1,000$ individuals and $m=10,000$ replicates. The MAF of the marker X was set to 0.2. CIEE is the proposed method using estimating equations; BS is CIEE using nonparametric bootstrap standard errors; G‐EST is the sequential G‐estimation approach (Vansteelandt et al., 2009); MR is multiple regression; RR is residual regression; and SEM is structural equation modeling.

3.3. Application to Genetic Analysis Workshop 19 data

For an application of the proposed approach and to illustrate how its result can lead to different conclusions compared to traditional approaches, we performed a genetic association analysis of the GAW19 data (Blangero et al., 2016). The data contains whole genome‐sequence data, gene expression in lymphocytes measured with microarrays, blood pressure phenotypes, as well as nongenetic covariates from the T2D‐GENES Consortium. We chose systolic blood pressure (SBP) as the primary phenotype Y and gene expression as the secondary phenotype K that could mediate the genetic effect of SNPs X on Y. The primary goal was to identify SNPs with a direct effect on SBP that is not (or only partially) mediated through gene expression, i.e., SNPs with an effect on SBP other than through gene expression. While indirect genetic effects through gene expression are functionally interesting, the rationale for our analysis was that if such indirect effects are in opposite direction of the “direct” genetic effect (through any other intermediate than gene expression), the genetic effects can be masked if they are not modeled. We assume the underlying DAG in Figure 3 and that the covariates age, sex, and smoking are not related to the SNPs under investigation, but can be confounders (denoted by $L_1,L_2,L_3$) of the relationship between K and Y. Twenty percent of the study participants took blood pressure‐reducing antihypertensive medication. Hence, their observed blood pressure is lower than their true untreated blood pressure would be. Adjusting blood pressure for the effect of blood pressure‐lowering medication is crucial when the objective is to identify SNPs that are increasing or decreasing blood pressure. For this situation, performing a censored regression using the AFT model with antihypertensive medication as censoring indicator δ is suggested (Konigorski et al., 2014; Tobin et al., 2005). Hence, this data analysis illustrates an application of CIEE when the primary phenotype is subject to censoring.

Figure 3.

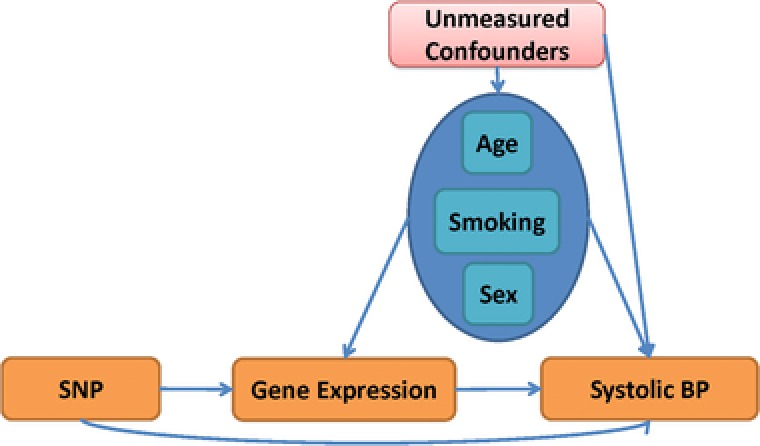
Overview of the assumed DAG for the analysis of the GAW19 data. Systolic blood pressure (BP) is the primary outcome; gene expression is the secondary phenotype and sex, age, and smoking are factors potentially influencing both phenotypes but unrelated to the investigated genetic markers.

In the analysis, we focused on SNPs on chromosome 19, since it contained the gene IL12RB1 whose mRNA expression had the highest dependence with SBP (Kendall's $\tau =0.24$ between gene expression and ${\mathrm{SBP}}_{est}$ adjusted for $L_1,L_2,L_3$ and antihypertensive medication, as described in Konigorski, Yilmaz, & Pischon, 2016). After basic standard quality checks, 113, 890 SNPs with MAF greater than 0.05 were considered for the analysis. Among them, the 45, 200 SNPs lying in cis within 5 kb of genes were analyzed together with the gene expression of their corresponding gene. In brief, 848 genes were included in the analysis and complete data for this analysis was available for 81 unrelated individuals.

Some of the 45, 200 SNPs were considered for their association with more than one gene expression, since they were in close proximity to more than one gene. For each of the 53, 151 tested associations, CIEE was applied under the AFT model in equations (10)–(13) with measured confounders $L_1,L_2,L_3$. Additionally, traditional censored regression models were computed with or without taking gene expression as secondary phenotype into account:

$$\mathrm{MR}1:Y_i={\alpha }_0+{\alpha }_1{l}_{1,i}+{\alpha }_2{l}_{2,i}+{\alpha }_3{l}_{3,i}+{\alpha }_4{k}_i+{\alpha }_{XY}{x}_i+{\epsilon }_i$$

$$\mathrm{MR}2:Y_i={\alpha }_0+{\alpha }_1{l}_{1,i}+{\alpha }_2{l}_{2,i}+{\alpha }_3{l}_{3,i}+{\alpha }_{XY}{x}_i+{\epsilon }_i$$

Results from CIEE, MR1, and MR2 are shown for the five SNPs with the smallest P‐values obtained from testing the absence of the direct genetic effect on Y using CIEE (Table 4). The SNP rs56202530 with the smallest P‐value using CIEE is upstream of the IL27RA gene, and its direct effect on SBP is estimated to be –0.15 ($SE=0.03$, P‐value = 7.2 × 10⁻⁷) using CIEE, and –0.08 ($SE=0.03$, P‐value = 9.5 × 10⁻³) using MR1. This was the only SNP with an adjusted P‐value less than 0.05 using CIEE. The results obtained through MR1 and MR2 were very similar to each other. None of the SNPs in Table 4 were found to be associated with sex, age, or smoking (data not shown). The five SNPs with the smallest P‐values using MR1 are shown in Supplementary Table 8. None of these SNPs returned an adjusted P‐value less than 0.05.

Table 4.

Top five SNPs with the smallest P‐values in the GAW19 genetic association analysis using CIEE

			${\widehat{\alpha }}_{\mathrm{XY}}(\widehat{SE}({\widehat{\alpha }}_{\mathrm{XY}}))$			95% CI for αXY			P‐value			Adjusted P‐value
SNP	MAF	Gene	CIEE	MR1	MR2	CIEE	MR1	MR2	CIEE	MR1	MR2	CIEE	MR1	MR2
rs56202530	0.14	IL27RA	–0.15 (0.03)	–0.08 (0.03)	–0.09 (0.03)	(–0.21; –0.09)	(–0.14; ‐0.02)	(–0.15; ‐0.02)	$7.2\times {10}^{-7}$	$9.5\times {10}^{-3}$	$1.1\times {10}^{-2}$	0.04	1	1
rs3746061	0.05	BTBD2	–0.11 (0.02)	–0.06 (0.04)	–0.06 (0.04)	(–0.15; ‐0.06)	(–0.14; 0.03)	(–0.14; 0.03)	$5.3\times {10}^{-6}$	$2.0\times {10}^{-1}$	$2.2\times {10}^{-1}$	0.28	1	1
rs60458566	0.13	AP2A1	–0.12 (0.03)	–0.08 (0.03)	–0.08 (0.03)	(–0.18; –0.07)	(–0.14; ‐0.02)	(–0.14; ‐0.02)	$8.7\times {10}^{-6}$	$5.9\times {10}^{-3}$	$8.2\times {10}^{-3}$	0.46	1	1
rs62117661	0.09	KLK12	0.26 (0.06)	0.18 (0.04)	0.18 (0.04)	(0.14; 0.37)	(0.10; 0.26)	(0.10; 0.26)	$1.0\times {10}^{-5}$	$8.7\times {10}^{-6}$	$1.4\times {10}^{-5}$	0.55	0.46	1
rs883394	0.25	ACTN4	–0.10 (0.02)	–0.08 (0.02)	–0.06 (0.02)	(–0.15; –0.06)	(–0.12; ‐0.04)	(–0.11; ‐0.02)	$1.1\times {10}^{-5}$	$3.3\times {10}^{-4}$	$6.9\times {10}^{-3}$	0.62	1	1

Top five SNPs with the strongest association with systolic blood pressure obtained through the CIEE genetic association analysis of 113,890 SNPs on chromosome 19, with the shown gene (expression) as intermediate phenotype. The SNP is described by its rs identification number. For these SNPs, point estimates, standard error estimates, approximate 95% confidence intervals (CI), raw P‐values and Bonferroni‐corrected (adjusted) P‐values obtained through CIEE and the multiple regression approaches MR1 and MR2 are shown. MAF is the observed minor allele frequency of the SNP.

In a comparison of the results using CIEE and MR, for the SNPs in Table 4, the estimated direct effects were in the same direction but larger using CIEE while estimated standard errors were similar – leading to different conclusions on the statistical significance of the effect estimates. Assuming the correctness of the underlying DAG in Figure 3 and using the results from the simulation study, the most plausible explanation for the effect estimate differences is that there is unmeasured confounding of the indirect effect $X\to K\to Y$through L in opposite effect direction (e.g., $X\to Y$ negative, $U\to L$ negative, $L\to K,K\to Y,U\to Y$ positive effects). This suggests that using traditional approaches without accounting for indirect effects of secondary phenotypes and confounders might miss true causal SNPs (such as SNPs 1, 2, 3, and 5 in Table 4).

4. DISCUSSION

In this study, we propose a new method called CIEE to estimate the direct genetic effect on a primary phenotype, adjusting for indirect effects through intermediate phenotypes that can also be influenced by measured or unmeasured confounding factors. Multiple influencing factors and multiple intermediate phenotypes can be included in the model. For the analysis of quantitative traits, our novel contribution is that CIEE gives a closed‐form estimate of the standard error and a simpler test statistic, while the estimator of the direct genetic effect amounts to the same as the G‐estimation method using LS estimation (Vansteelandt et al., 2009). For the analysis of time‐to‐event traits subject to censoring, CIEE includes a new approach for the removal of the indirect effect and allows valid inference while the G‐estimation method for the models considered here by Lipman et al. (2011) is invalid. CIEE yields a consistent estimator for the direct effect and its standard error, even when there is unmeasured confounding of the indirect effect through measured factors. Since it is based on established theory of unbiased estimating functions, the approach can be extended to different error distributions. However, the use of robust sandwich standard error estimates also provides valid inference if the error distribution is misspecified, as shown in the simulation study. Also, using the robust sandwich standard error is preferred compared to the nonparametric bootstrap standard error since the latter is computationally intensive and cannot be directly used for SNPs with small MAFs. Of note, when analyzing quantitative traits, CIEE yields estimates equivalent to the LS estimates under the corresponding models, which do not rely on any distribution assumption. Therefore, the resulting direct effect estimate can be used even if the distribution assumption is not satisfied. CIEE is implemented in an R package of the same name and is freely available.

Applying CIEE to genetic association studies can both identify genetic variants that would be missed by traditional analyses, and can prevent false positive results – depending on whether the indirect genetic effect with unmeasured confounders is in the same or opposite direction of the direct effect. In the application of CIEE to the GAW19 data, we investigated genetic associations with SBP by accounting for intermediate gene expression phenotypes. While such “indirect” genetic effects through gene expression can provide valuable functional information and help to filter candidate loci, it has rarely been considered that if such indirect effects are in opposite direction of the direct genetic effect (through any other intermediate than gene expression), the genetic effects can be masked if the direct and indirect effects are not modeled. This was the rationale for our novel application approach and indeed, our results suggest the potential role of a new genetic locus, which would have been missed if a traditional regression analysis was performed. The identified SNP is upstream of the IL27RA gene, which is involved in anti‐inflammatory processes and immune response (Hunter & Kastelein, 2012).

The results of the simulation study also provided a detailed analysis when the standard and other proposed methods provide valid estimation and testing, and when they should not be used. Standard multiple regression approaches (which include linear regression, PH and AFT regression models) were valid in all scenarios as long as there was no unmeasured confounding of the indirect genetic effect. For example, they also provided valid inference when there was measured confounding of the indirect genetic effect – which is in contrast to some claims in the literature (Goetgeluk et al., 2008). The genetic effect estimates obtained from SEM were also affected by unmeasured confounding of the indirect genetic effect that exemplifies that SEM is highly dependent on the correctness of the assumed paths and edges and may lead to biased estimates otherwise. Finally, the sequential G‐estimation method (Vansteelandt et al., 2009) provides equally valid testing compared to CIEE for the analysis of quantitative traits, but the G‐estimation approach proposed by Lipman et al. (2011) for the analysis of time‐to‐event primary phenotypes is not able to remove the effect of intermediate phenotypes leading to biased direct effect estimates and invalid testing. In addition, the sequential G‐estimation methods do not provide a standard error estimate of the estimated direct effect.

For an application of CIEE and any other model to the analysis of DAG models, it should be noted that despite the robustness properties of CIEE, there are still some assumptions that are required for valid testing and estimation. One assumption is that there is no unmeasured confounding of the direct genetic effect, i.e., factors both affecting the genetic marker and primary phenotype. For genetic association studies, this assumption seems plausible and if any such factors (e.g., population stratification) were present, they could be controlled for in an initial step or considered as covariates. Furthermore, an a priori choice of relevant intermediate variables and influencing factor (i.e., distinction between K, L) is important. Finally, while CIEE and the G‐estimation methods are robust against unmeasured confounding of the indirect effect through measured factors, they lead to biased point estimates and inflated type I errors similar to traditional approaches if there is direct unmeasured confounding of the indirect effect (e.g., if U affects K directly and not only through L), i.e., if the DAG is misspecified.

We believe that the application of CIEE to association studies in genetic epidemiology and other biomedical fields can provide new insights about direct effects. In addition, future extensions of CIEE including multiple primary phenotypes in the analysis can provide further possibilities to build more complex and realistic models.

CONFLICTS OF INTEREST

The authors declare no conflicts of interest.

Supporting information

Supplementary Materials

Konigorski S, Wang Y, Cigsar C, Yilmaz YE. Estimating and testing direct genetic effects in directed acyclic graphs using estimating equations. Genet Epidemiol. 2018;42:174–186. 10.1002/gepi.22107