“Master” Neurons Induced by Operant Conditioning in Rat Motor Cortex during a Brain-Machine Interface Task

Abstract

Operant control of a prosthesis by neuronal cortical activity is one of the successful strategies for implementing brain-machine interfaces (BMI), by which the subject learns to exert a volitional control of goal-directed movements. However, it remains unknown if the induced brain circuit reorganization affects preferentially the conditioned neurons whose activity controlled the BMI actuator during training. Here, multiple extracellular single-units were recorded simultaneously in the motor cortex of head-fixed behaving rats. The firing rate of a single neuron was used to control the position of a one-dimensional actuator. Each time the firing rate crossed a predefined threshold, a water bottle moved toward the rat, until the cumulative displacement of the bottle allowed the animal to drink. After a learning period, most (88%) conditioned neurons raised their activity during the trials, such that the time to reward decreased across sessions: the conditioned neuron fired strongly, reliably and swiftly after trial onset, although no explicit instruction in the learning rule imposed a fast neuronal response. Moreover, the conditioned neuron fired significantly earlier and more strongly than nonconditioned neighboring neurons. During the first training sessions, an increase in firing rate variability was seen only for the highly conditionable neurons. This variability then decreased while the conditioning effect increased. These findings suggest that modifications during training target preferentially the neuron chosen to control the BMI, which acts then as a “master” neuron, leading in time the reconfiguration of activity in the local cortical network.

Introduction

Understanding the neuronal code in motor cortical areas has long been a key issue in neuroscience. It should allow scientists to extract the relevant brain firing patterns preceding movement execution (Evarts, 1968) to move a prosthetic device (Humphrey et al., 1970; Schmidt et al., 1978). Multiple demonstrations of neuronal control of a robotic limb or of a cursor in real-time have been achieved in the last decade, giving rise to the new field of brain-machine interfaces (BMI). These pioneering studies are principally based on the decoding of a large neural ensemble activity, i.e., activity from dozens to hundreds of neurons (Taylor et al., 2002; Carmena et al., 2003; Velliste et al., 2008). An alternative way, envisioned already a long time ago (Olds, 1965; Fetz, 1969; Fetz and Baker, 1973; Schmidt, 1980) but transposed to a real robotic device only recently (Moritz et al., 2008), consists in associating prosthesis movement rules with the neural output of a small number of neurons, from 1 to 10. Repeated associations between a self-generated neuronal pattern and an actuator that controls access to reward (such as a prosthetic arm bringing the reward to the mouth) result in the reactivation of the neural process, which thus becomes operant in maximizing reward probability. This strategy, i.e., imposing a predefined association rule between neural activity and reward accessibility, does not require knowing beforehand the exact role and function of the conditioned neurons in terms of motor control; instead it relies on behavioral adaptation and learning—and sometimes on the forced coadaptation of the algorithm rule itself and brain circuits (Gage et al., 2005; Marzullo et al., 2006).

Previous implementations of prosthetic control by one or a few neurons mostly concentrated on optimizing the spatial precision with which a target could be reached. Less importance has been given to the speed of neuronal reaction or success rate during a session (Schmidt, 1980; Gage et al., 2005; Moritz et al., 2008). However, the level of performance of a brain-machine interface should also include measures of speed control and reliability, two parameters important for the design of BMIs useful in everyday life.

In the present study, motor cortex neurons of awake behaving rats underwent operant conditioning one at a time, using a simple activity-based rule to drive a one-dimensional prosthetic actuator toward a fixed reward delivery position. We subjected the same selected neuron to several successive sessions, allowing us to estimate the best performance that can be expected for control of a BMI using the firing rate of a single-unit. After asymptotic training, neuronal reaction times of the conditioned units were fast, mostly under 200 ms. Because we always recorded multiple single neurons simultaneously, we examined the activity of neighboring nonconditioned units as well, and found that the activity patterns underlying control of the BMI were specific to the successfully conditioned neurons.

Materials and Methods

Animal handling and pretraining.

Eight male Wistar rats weighing 250–350 g were obtained from the in-house animal facility of the CNRS Campus of Gif-sur-Yvette (French Agriculture Ministry Authorization B91-272-105). Maintenance, manipulations, and surgery were performed in conformity with French (JO 2001-464) and European legislation (86/609/CEE) on animal experimentation. Before surgery, animals were gently handled by the experimenter, and progressively trained to stay quiet in a harness and drink from a bottle containing a solution of water and glucose (strawberry syrup). While attached in the harness, the posterior limbs laid on a platform, and the forelimbs were free to move. Animals were kept at 85% of their free-feeding weight. The bottle was mounted on a one-dimensional linear actuator (Festo) perpendicular to the rat body, and moved to and away from the rat mouth on a left-right axis (Fig. 1A). During preoperative training, the bottle followed four successive steps: (1) a waiting period of randomized duration from 8–12 s, in the dark, and during which the bottle was kept away from the animal; (2) a fast displacement of the bottle to the mouth position, during which a green light-emitting diode (LED) placed close to the animal was “on”; (3) a period of 3 s of drinking during which a blue LED was “on”; and (4) a return travel back to the initial position. A new waiting period started simultaneously with the start of the bottle return. Two sessions of 10–15 min occurred each day, consisting each of up to 50 repetitions approximately. The LEDs were switched “on” and “off” by a microcontroller (Arduino Diecimila). The whole preconditioning period lasted several weeks, after which the animal was well accustomed to the setup and showed no sign of stress throughout an entire session.

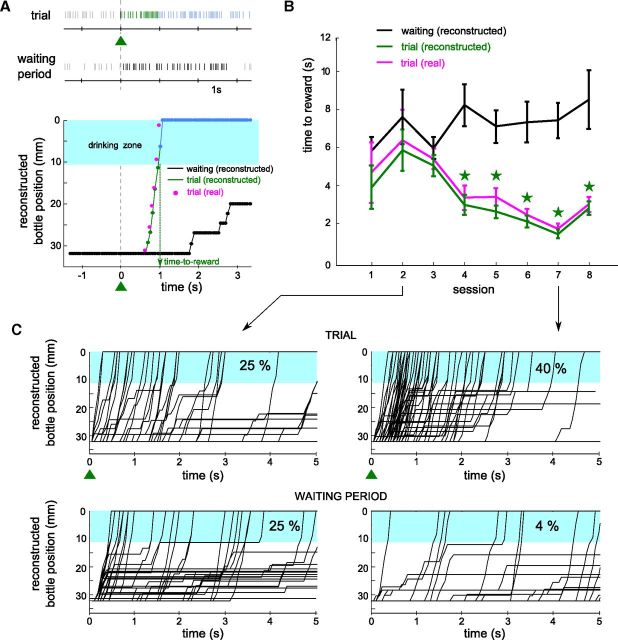
Figure 1.

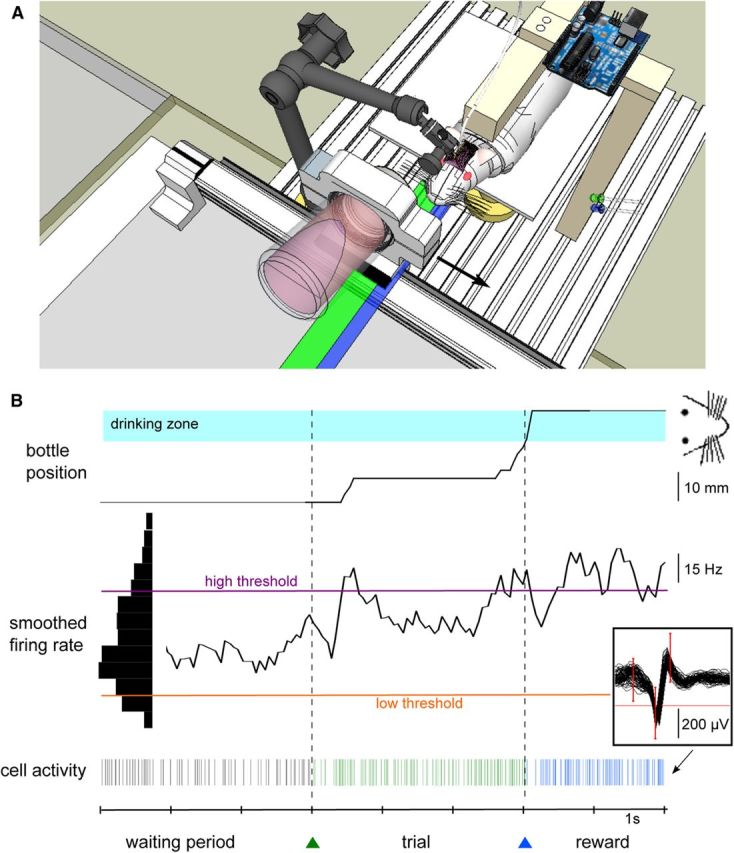
Experimental setup and neuronal control protocol. A, Schematic of the experimental setup. A bottle containing water and syrup is held by a metal piece placed on a one-dimensional linear axis rail, perpendicular to the rat's body. The bottle always starts from the left of the rail and can only move in one direction (black arrow; the green rectangle indicates the bottle course). The rat can drink when the bottle is close enough from the center (“drinking zone”, blue rectangle). Green and blue LEDs shown on the right indicated trial onset and reward, respectively. B, Bottom, Spiking activity of a single neuron (see 60 superimposed action potentials in the inset) during the waiting period (black), the trial (green), and the reward period (blue ticks). The smoothed firing rate of the unit (middle black curve) controls the displacement of the bottle toward the rat from a lateral starting position (top). The speed depended on the difference between the firing rate and two thresholds (purple and orange horizontal lines). The thresholds were set at fixed percentiles of the previous firing rate distribution (black histogram on the left). When close enough to tongue reach, that is, upon entering the drinking zone (blue rectangle), the bottle automatically moved in front of the mouth and stayed there for 3 s. The colored triangles (green and blue) below the time axis represent the colored LEDs that were switched on for the different phases of the experiment. Intertrial intervals (waiting periods) were of a variable randomized duration of 8–12 s.

Surgical procedure.

Two days before surgery, the rat received subcutaneous injections of 0.1 ml of the anti-inflammatory drug meloxicam (Metacam 0.5 mg.kg⁻¹) and 0.1 ml of the antibiotics cevofecin (Convenia 25 mg.kg⁻¹) to prevent pain and infections, respectively. On the day of surgery, we placed the animal in a ventilated box and induced anesthesia with isoflurane at 3%. The animal was then transferred to a stereotaxic frame. Anesthesia was maintained throughout surgery with isoflurane, the level of which was progressively decreased down to ∼1.5%. The ear bars were covered with lidocaine gel (Xylocaine) and we injected 0.3 ml of lidocaine 2% under the head skin before incision. Once the skull was exposed, seven to eight screws were inserted, both to ensure a strong contact between skull and implant, and for electrical grounding (see below). A craniotomy was drilled above the forelimb or hindlimb region of the motor cortex, and the dura was resected. We implanted arrays of 32 electrodes: for six rats, we used microwire arrays of 8 rows and 4 columns with a grid spacing of 0.25 mm (Microprobes for Life Sciences) and for two rats, we used custom-made tetrodes distributed over an area of 0.25 mm². The electrodes were lowered to a cortical depth of ∼1300 μm. We verified in two instances that the electrode tip was indeed in deep layers of the primary motor cortex, by performing electrolytic lesions and Nissl staining of brain slices. Once the microwire array was in place, a ground wire was coiled around one or several of the ground screws (A-M Systems). Gelfoam was applied around the upper part of the electrodes outside the brain to help prevent excessive bleeding. Drops of cyanoacrylate were sparsely spread on the dry skull. The electrode array was then fixed in place with dental acrylic (Henry Schein). Finally, a piece of polyvinyl chloride (PVC, custom-made) was embedded in the dental cement to allow head-fixation in subsequent training sessions (see below). The rat received a saline injection intraperitoneally before the anesthesia was stopped. Food was accessible ad libitum for 5 d during which the rat was closely looked after to check proper recovery. Drops of an oral solution of meloxicam were given if signs of pain or disturbance were noticed.

Head fixation.

The rat was then submitted to the same food control protocol than before surgery. The training sessions were similar and the rat was trained to stay quiet during a strict head-fixation ensured with a 3D articulated arm (NMG700030, Noga). The arm extremity (NFA1100) was designed to match the PVC piece glued to the skull (Fig. 1A). With that device, the rat snout and mouth could be positioned precisely by the experimenter in front of the bottle in the drinking position. The four limbs were still free to move as before.

Data acquisition and control of the behavioral setup during training.

Neuronal activity was recorded and processed in real-time (Cerebus hardware, BlackRock Microsystems). Each electrode output was filtered between 250 Hz and 7.5 kHz and sampled at 30 kHz. Spikes were sorted online (Central software, BlackRock Microsystems). Spike sorting was performed at the beginning of each session, using a template-matching method: assignment of a waveform to a unit depended on whether it crossed all the criterion windows drawn by the experimenter (Fig. 1B, inset). A putative unit was considered as well isolated if less than one percentage of spikes was contained in the first bin (2 ms) of its autocorrelogram. Spikes were considered to be emitted by the same unit from one session to the next when their waveform remained invariant withstanding the precision of the measure. Spikes of nonconditioned neurons were not always successfully isolated throughout all successive sessions for the currently conditioned neuron.

All information was sent to a computer (Dell Intel QuadCore at 2.66 GHz, 3.24 Gb of RAM, OS Windows XP) via a fiber-optic data link. A custom-made software (Eclipse Qt C++) read in the spike information in real-time and commanded the linear actuator holding the bottle through a serial 56k bauds communication. The instantaneous bottle position was recorded on the same file through another serial port whenever the bottle crossed from one spatial bin to another (10 bins spanning the bottle course).

Neuronal control of the bottle position.

Training during neural control sessions broke down into repetitions of the same four steps described above for the pretraining period: waiting, bottle travel to the mouth, drinking, bottle travel back. However, during the second step (the trial), the bottle did not move automatically toward the rat mouth as before electrode implantation, but was now submitted to neural rules on the basis of the ongoing recorded activity. A single unit was chosen as the operantly conditioned neuron for controlling the bottle position. Criteria for selection were stability of recording over days, high signal-to-noise ratio, wide firing rate distribution, and modulation with limb movement. During the experiment, spiking activity was computed every 62.5 ms, and was smoothed over 500 ms by convolving each spike with a continuous filter: h(t) = 2 * (0.5 − t) between 0 and 0.5 s and h(t) = 0 otherwise. When the green LED was turned on (playing the role of a “GO” signal and marking the trial onset), the neuron had to increase the smoothed firing rate above a high threshold f_high to make the bottle move toward the mouth (Fig. 1B). The speed increased when the firing rate f increased according to the relation: v(f) = v₀.(f − f_low)/(f_high − f_low) if f ≥ f_high, v(f) = 0 otherwise. Note that there was no movement of the bottle when the firing rate f crossed the low threshold; f_low only affected the slope of the v(f) function. The low and high thresholds f_low and f_high were re-evaluated every block of three successive trials. Their value was set respectively to 10% and 90–94% of the firing distribution (see below). Once the bottle entered the drinking zone, it was automatically stabilized in the mouth position and the 3 s drinking period started. We carried on the conditioning of the same neuron in the next session unless one of three conditions occurred: (1) the neuron was trained successfully up to the highest level of difficulty (see below); (2) the recording was lost, or the waveform or firing rate changed so that we could no longer ascertain that it was the same neuron; (3) 10 successive sessions were not sufficient to induce successful conditioning.

Task difficulty was gradually increased across sessions to reach the final parameters of neuronal control. Maximum trial length was set to 30 s for the first session and was progressively decreased to 7 s. The speed factor of the bottle v₀ also decreased, from ∼3 cm.s⁻¹ to ∼1 cm.s⁻¹. These parameters were fixed before starting the session. When in the course of one session, a sudden drop in performance or motivation threatened to greatly lower the number of trials, the task could then be made easier or more difficult by modifying the threshold f_high inside the range 90–94% of the firing rate distribution.

Conditioning criterion and conditioning effect.

All spiking activities were analyzed with a custom-made program (Eclipse Qt C++). Results were displayed with the same software or in Matlab (MathWorks).

Performance during a session was measured by counting the number of trials during which reinforcement was obtained. However, we always kept the task difficulty sufficiently low so that the animal received frequent rewards during the session. This was necessary to avoid stress of the head-fixed rat and maintain its behavioral motivation (Schwarz et al., 2010). Thus, we devised a measure of the effect of the conditioning protocol during one session based on the comparison of test and control trials completed under the same set of session parameters. Accordingly, we compared the movements of the bottle during the trials to the virtual movements of the bottle that would have been produced if the neural activity of the waiting period had been used, together with the same activity-to-speed rule as described above for trials. For these reconstructed trajectories, we took the neural activity between 3 and 6 s of each waiting period and concatenated these episodes to obtain periods of activity with a duration as long as the real trials. To confirm the validity of our reconstruction algorithm, we applied it also to the real trial periods and compared the real trajectories and time-to-rewards with the reconstructed ones using trial activity (Fig. 2A,B, magenta vs green curves). Trajectories were most often indistinguishable. We observed small discrepancies due to the fact that whereas the offline algorithm indeed calculates the smoothed neuronal activity precisely every 62.5 ms, the online algorithm was sometimes delayed by a computer clock increment so that the change in bottle speed was delayed as well. Thus, time-to-reward values were consistently slightly longer during the real trials than when simulated offline (Fig. 2B). To eliminate this bias in the rest of our analysis, we always compared the waiting period time-to-reward distribution to the offline (reconstructed) trial time-to-reward distribution, and not the online (real) trial time-to-reward distribution.

Figure 2.

The conditioning effect for a single unit increases across sessions. A, Top, Spiking activity of a neuron submitted to operant conditioning during one trial (first line, green ticks) and the subsequent reward period (first line, blue ticks), and during a waiting period (second line, black ticks). Bottom, Reconstruction of the bottle movements using the spike patterns for each of these periods (green/blue: trial and reward; black: waiting). Additionally, the activity-based position for the trial is compared to the real position of the bottle (magenta points, see Materials and Methods). The blue shaded area represents the drinking zone. B, The mean (± SEM) time-to-reward is plotted for eight several successive sessions using the reconstructed bottle position for the trial and waiting periods (black and green lines) and the real bottle position (magenta line). Stars indicate significant conditioning (p < 0.01, two-tailed unpaired Student's t test; see Materials and Methods). C, Bottle trajectories reconstructed for session 2 (left) and session 7 (right) for the same neuron. We used the trial activity (up) and the waiting period activity (down) for reconstruction. The percentage of trajectories that entered the drinking zone in the first second of the trials is displayed for each dataset.

The neuron was considered successfully conditioned for a session if the distributions of time-to-reward of the waiting and trial periods were significantly different (two-tailed unpaired Student's t test, p < 0.01). To estimate the strength of the conditioning effect, we used the normalized mean difference to capture the distance between the time-to-reward distributions: d′ = (μ_W − μ_T)/√(σ_W² + σ_T²), with μ and σ representing the mean and SD of the times-to-reward for waiting (W) and trial (T) reconstructions. This measure gets larger when the activity of the neuron is modulated quickly and strongly after trial onset. For analyses requiring only one session per neuron, we defined the best session of the neuron as the session with the highest conditioning effect d′.

The three parameters defining the task difficulty, i.e., f_high, the maximum trial length, and the velocity v₀ (see above), were the same for the real trials and for the simulated (reconstructed) trials using the waiting period activity.

Latency of individual trials, mean session latency, and rank of activation.

To compute the latencies of firing rate increases for the individual trials, we convolved the instantaneous firing rate with a filter pattern designed to signal an increase in activity h_inc = [0 1 2 2.5]. The bin width was 100 ms with 20 ms sliding steps. To detect high values, we converted the filtered profile to a z-score waveform, using the mean and SD in the window [−2 s 0 s] during the last five waiting periods. The trial latency was then computed in two steps, by finding: (1) the time after trial onset at which the z-score was first above a value of 3 (p < 0.00135 for a one sided t test), and (2) within that 100 ms window, the time abscissa of the first z-score >3 in the filtered profile calculated with 20 ms bins. If no such variation of discharge was found in 10 s, it meant either that no increase and no reward occurred or that reward occurred without a measurable onset of increase, and the trial latency was left unassigned. We defined the neuronal reaction time of the neuron during one session by finding the mode of the distribution of trial latencies, or the mean of the modes if there were several local maxima.

Response latencies were sometimes not detected on individual trials, even though the neuron exhibited a clear increase in activity when averaged across trials. To quantify the delay of this increase, we defined a mean session latency. A perievent time histogram (PETH) between −2 s and +2 s relative to the trial start was constructed with a sliding window of 100 and 20 ms step. The mean of the PETH was computed within [−2 s; 0 s]. We transformed the raw PETH into an equivalent normalized PETH of z-score values using this mean and the corresponding variance value of a Poisson process. We first searched for the earliest 100 ms duration bins where six successive z-scores were found >2 (p < 0.023). Within this selected time window, the mean session latency was given by the earliest point in time where the first z-score was found >1 using a discretization of 20 ms bins. A second set of z-score thresholds, 5 (p < 1.10⁻⁴) and 2.5 (p < 0.00625), was used to detect high increases in firing rate. If, during a session, a latency could be defined for at least one neuron, we looked at the order of activation of all other neurons simultaneously recorded during that session based on their mean session latency. If several neurons had the same latency, the rank of activation was defined by the rounded mean position of those neurons.

Variability.

For each session, we studied the evolution of the firing variability of a neuron in the waiting periods between the end of one trial and the beginning of the next one. These waiting periods were of randomized duration, between 8 and 12 s. To quantify the trial-to-trial variability, we computed the spike count within each 200 ms bin in the waiting period, with time bins locked to the previous trial end. We calculated the Fano Factor (FF) by dividing for each time bin the variance of the spike count by its mean. This measure gives 1 for an ideal Poisson process, as often reported for cortical neurons during ongoing activity (for review, see Churchland et al., 2006).

Distances between recording sites were assessed from the known topology of the microwire rectangular array. The minimum distance between two recording wires was 250 μm (grid spacing) and the maximal distance was 1.9 mm. Data from the two rats implanted with tetrodes were discarded for analyses involving these distances (see Figs. 5D,E, 6A2,B2), as they could not be estimated accurately. We rarely recorded activity from more than one neuron per electrode per session, so that we could not estimate the average firing properties of nonconditioned neurons at the same location site as conditioned neurons.

Figure 5.

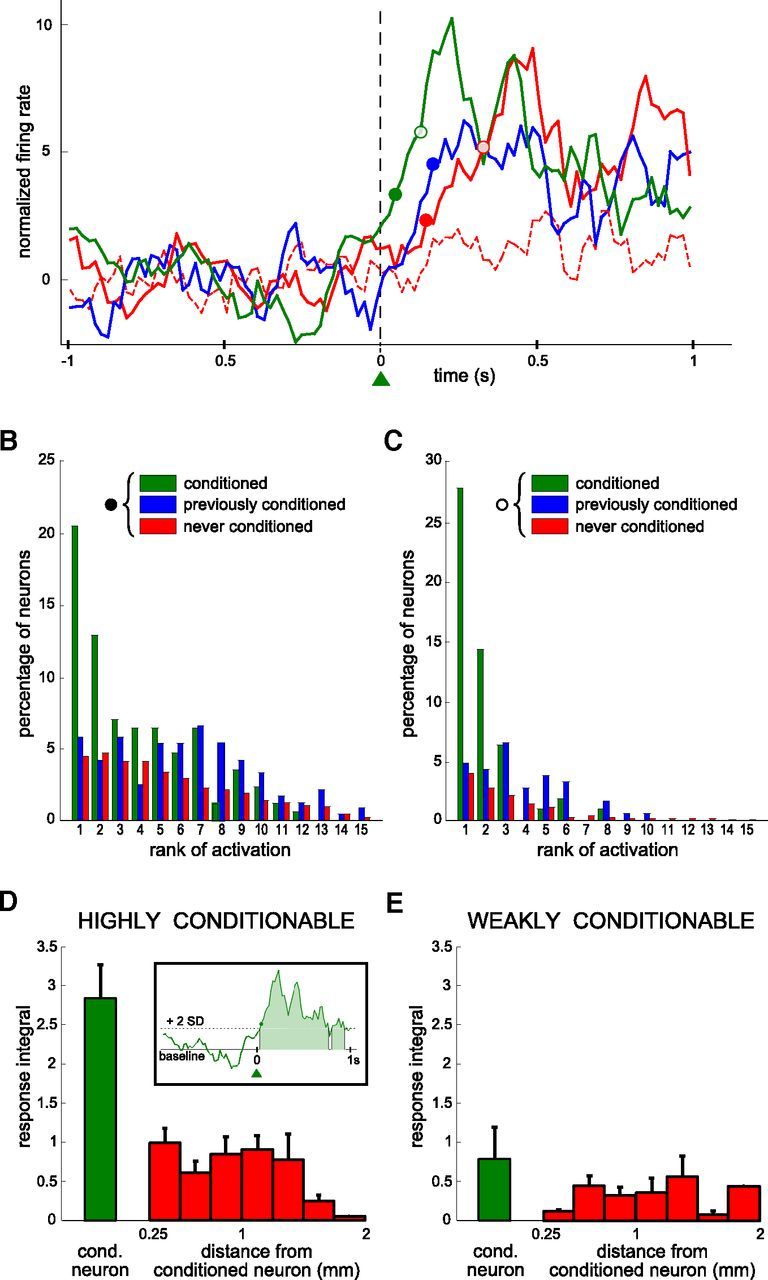
Differences in the rank of activation between conditioned neurons and simultaneously recorded neighboring neurons. A, Perievent time histogram of neuronal activity normalized and centered on trial onset, for four neurons simultaneously recorded during the same session (green: the conditioned neuron; blue: a previously conditioned neuron; red: two neurons never conditioned). Filled and empty circles of different colors represent the session latency for thresholds at 2 and 5 SD (see Materials and Methods). One of the neurons (red dashed line) did not have a measurable latency for that session. The latency of the blue neuron could only be defined for the 2 SD threshold. Additional (n = 20) neurons that were simultaneously recorded during that session have not been included for sake of clarity. Bin size: 20 ms; each value is the z-transform of the firing rate integrated over a sliding window of 100 ms. Latencies were calculated using a 20 ms bin scale (see Materials and Methods). B, C, Distributions of the ranks of activation for all sessions, based on the latencies defined as in A, for thresholds at 2 SD (B) and 5 SD (C). Only sessions where a latency could be measured for at least one neuron are included (B, n = 165 sessions; C, n = 109 sessions). All the neurons are partitioned into three categories (green: conditioned at that session, B, 165 and C, 109 latency values; blue: previously conditioned, B, 237 and C, 183 latency values; red: never conditioned, B, 2758 and C, 1836 latency values). D–E, Response integral for the conditioned (green) and nonconditioned neurons (red) as a function of the distance relative to the recording site of the conditioned neuron. Values are averaged over all sessions during which highly conditionable (D, n = 10 neurons, 111 sessions) and weakly conditionable (E, n = 5 neurons, 44 sessions) neurons were trained. Inset, The response integral was defined by the area between the neuron PETH corresponding to firing rates higher than the baseline activity by 2 SD, during a one-second period following trial onset.

Figure 6.

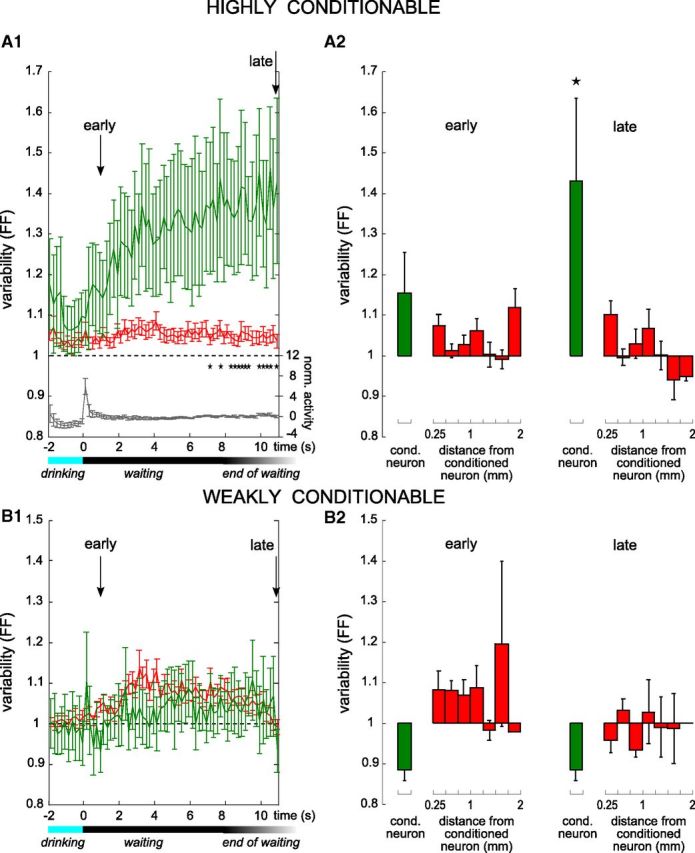
The firing rate variability of the conditioned neuron builds up during the waiting period. A1, B1, Average time course of the trial-to-trial variability of the discharge rate, measured by the FF, for conditioned (green) and never conditioned (red) neurons using 200 ms bins. All sessions during which a highly conditionable neuron (A1, 111 sessions on 10 conditioned neurons) and a weakly conditionable neuron (B1, 63 sessions on 7 conditioned neurons) was conditioned were analyzed separately. Stars indicate a significant difference between the conditioned and nonconditioned neurons at the p < 0.01 level. Arrows indicate the two time points (early and late) during each waiting period, used for the data displayed in A2 and B2. Variability of a Poisson process is represented by the horizontal dotted line at FF = 1. For waiting periods terminating before the end of the time scale, only spikes from the waiting periods themselves were included in the calculation; i.e., the activity recorded after trial onset was not considered. The horizontal black/gray bar below the graphs indicates the range of waiting period durations, and the blue bar indicates the drinking period. In A1, the gray curve displays the mean normalized activity of the conditioned neurons over the same window (scale on the right of the graph). A2, B2, Average variability (FF) in the early (left, t = 1 s) and the late (right, t = 11 s) parts of the waiting period between successive trials for the conditioned (green) and nonconditioned neurons (red) as a function of the distance relative to the recording site of the conditioned neuron, for sessions during which a highly conditionable neuron (A2) or a weakly conditionable neuron (B2) was trained. Stars indicate significant differences with the variability of the population (Mann–Whitney U test, p < 0.01).

Results

General features of neural-based operant conditioning

One hundred seventy-eight single units were recorded from the primary motor cortex of eight rats. Seventeen neurons were trained, one at a time, for neuronal operant conditioning, from 1 to 6 per animal.

Before surgery, the animals were accustomed to sit in a harness and drink from a bottle containing a sweet liquid, while their head was maintained fixed (Fig. 1A). For each trial of this preconditioning period, the bottle moved automatically from its initial position to the drinking zone in front of the mouth. The animal was then allowed to drink during 3 s, after which the bottle returned to the start position and a waiting period of 8–12 s elapsed before the next trial. Once a unit was chosen for neuronal control, this conditioned unit had to increase its firing rate above a high threshold to move the bottle toward the animal until it reached the drinking zone (Fig. 1B, blue area). Liquid reinforcement was then allowed during 3 s. Above the threshold, the speed of the bottle increased linearly with the smoothed firing rate of the unit (see Materials and Methods). Animals were submitted to two training sessions per day, each session consisting of ∼50–100 trials both in the preconditioning and the conditioning period. Task difficulty was progressively adjusted so that a sufficient number of completed trials could be collected during any given session, both for data analysis purposes, and for maintaining a high reward level and motivation of the animal (Schwarz et al., 2010).

To quantify the performance of the conditioned neuron during one session, we compared the spiking activity patterns during the trials to those recorded during the same session in the waiting periods between trials (see Materials and Methods). This comparison was based on the ability of spike patterns to successfully bring the bottle to the drinking position. Figure 2A shows the action potentials of a conditioned neuron during one trial and during a waiting period of same duration, as well as the virtual control trajectories of the bottle calculated with the neural control algorithm using these two firing patterns as inputs (green and black lines, respectively). The firing rate of the unit increased 500 ms after trial onset, resulting in a rapid movement of the bottle toward the drinking zone until it entered it at 1 s. By contrast, the firing activity of the waiting period remained low and resulted in a simulated trajectory of the bottle that was still outside the drinking zone after 3 s. We defined the time-to-reward as the time after onset when the reconstructed position of the bottle first entered the drinking zone. For this conditioned neuron, the average time-to-reward varied little for the first three sessions (Fig. 2B, green curve) and decreased progressively in the following sessions, whereas the average time-to-reward calculated on the waiting period activity remained relatively unchanged (black curve). We defined a successful conditioning session as one for which the average time-to-reward was significantly reduced during trials compared with the one obtained with reconstructed values from the waiting period (two-tailed unpaired Student's t test, p < 0.01; Fig. 2B, green stars). This neuron was thus successfully conditioned from session 4 to session 8, which was its last conditioning session. On Figure 2C, all the trajectories of the second (left) and seventh (right) session are plotted for the trial (top) and waiting (bottom) periods. Bottle movements were similar for both periods during the second session, whereas in the seventh session, many more trajectories entered the drinking zone during trial periods than waiting periods activity (40% vs 4% in the first second of the trials). This analysis was applied to all neurons selected for operant conditioning (n = 17). All but two neurons were successfully conditioned in at least one session.

In addition to determining for each session whether the conditioning protocol had a significant effect, we quantified the magnitude of the associated changes. For example, for the fifth session of the data displayed in Figure 3A (same neuron as Fig. 2B), we plotted the histograms of time-to-reward for the two reconstruction datasets (Fig. 3B). As defined above, a conditioning session was successful when these two distributions were significantly different. We further defined the conditioning effect (d′—see Materials and Methods) as the distance (d) between the means of these two histograms, normalized by the combined SD. At the population level, the percentage of neurons that were successfully conditioned increased with the number of sessions (Fig. 3C, r² = 0.69, p < 7.10⁻⁵). Figure 3D shows that in parallel, the average conditioning effect d′ increased significantly (r² = 0.82, p < 2.10⁻⁶). On average, 896 trials were necessary to reach the maximal task difficulty. This level was successfully achieved in 4 neurons and required 10–25 consecutive sessions per conditioned neuron.

Figure 3.

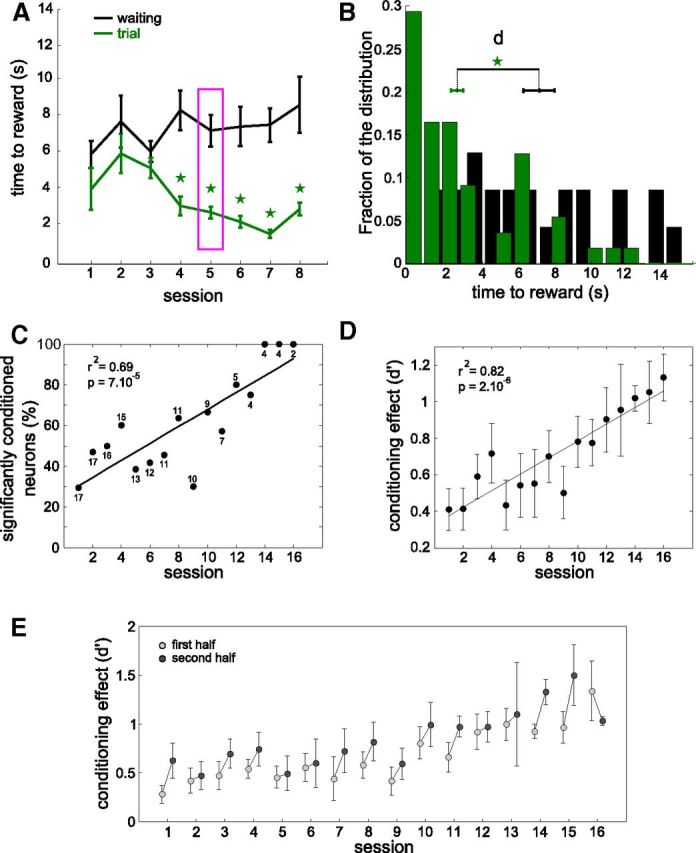
The conditioning effect increases across sessions for the population of conditioned neurons. A, Mean (± SEM) time-to-reward during trial and reconstructed from the waiting periods for 8 successive sessions for a single conditioned neuron (same data as Fig. 2B). B, Histograms of all time-to-reward values for session 5 (indicated by the magenta box in A), comparing the times to get reward during trial (green) with the estimated (virtual) times to get reward during waiting (black). d represents the distance between the two means, and is divided by the pooled SD to yield the conditioning effect d' displayed in D (see Materials and Methods). C, Percentage of neurons successfully conditioned for each session. The total number of neurons used is indicated near each data point. Only sessions with n ≥ 2 neurons were used. D, Mean conditioning effect for each session averaged across all conditioned neurons, by comparing time-to-reward during trial and (reconstructed during) waiting periods. Error bars represent SEM. E, Similar to D, but after dividing each session in two halves. Linear fits for graphs C and D are plotted and the correlation coefficients (r2) and significance levels (p) indicated.

Furthermore, we tested whether there was an improvement of performance within sessions. We divided each session in two equal successive blocks of trials and compared the conditioning effect in the two halves. On average, 15 of 16 sessions of conditioning showed an improvement in the second half of the session compared with the first half (Fig. 3E).

We conclude that neuronal control resulted in rapid movements of the bottle to the drinking zone after trial onset, and that this was learnt progressively from session to session for a given neuron.

Reliable neuronal reaction time at each trial onset

The strength of the conditioning effect does not indicate whether the modulation of activity took place late or early during the trial or even in anticipation of the trial onset. We determined when the activity of the neuron was modulated relative to the trial start, on a trial-by-trial basis, and how regular and consistent were the fast modulations. To that end we selected for each neuron the session with the highest conditioning effect, to estimate a lower bound of best performance that can be achieved with this protocol with sufficient training. For such a session, we constructed a raster plot centered on each trial start and indicated the latency of the neuronal activity increase for each trial (see Materials and Methods), if measurable (Fig. 4A1, magenta dots). On a few trials, the neuron failed to show a significant increase and the rat missed the reward. The average bottle movement and increase of activity during trials for the whole session are displayed below the raster plot (Fig. 4A2,A3), confirming that the activity rose in the first few hundreds of milliseconds. We estimated the neuronal reaction time for that session by determining the mode of the distribution of individual trial latencies (150 ms; Fig. 4A3). Figure 4B shows the distribution of those modes for the population of conditioned neurons, and this for the best session of each neuron as defined above. We observed that the discharge rate of 13 of the 17 conditioned neurons had a peak reaction time shorter than 500 ms, and 8 among them consistently fired in the first 200 ms after trial onset. Among these 8 fastest neurons, 7 had 100% successful trials during the session, and the last one 98%. In total this corresponds to 1 failure per 500 trials. This shows that for nearly half of the neurons that were conditioned, the increase in firing was very reliable and fast, despite the absence of any requirements on the neuronal reaction time during the trial. This performance was only reached in sessions with the highest conditioning effect. When averaging over all sessions and all neurons, the percentage of trials for which the animal obtained the reward was 85%.

Figure 4.

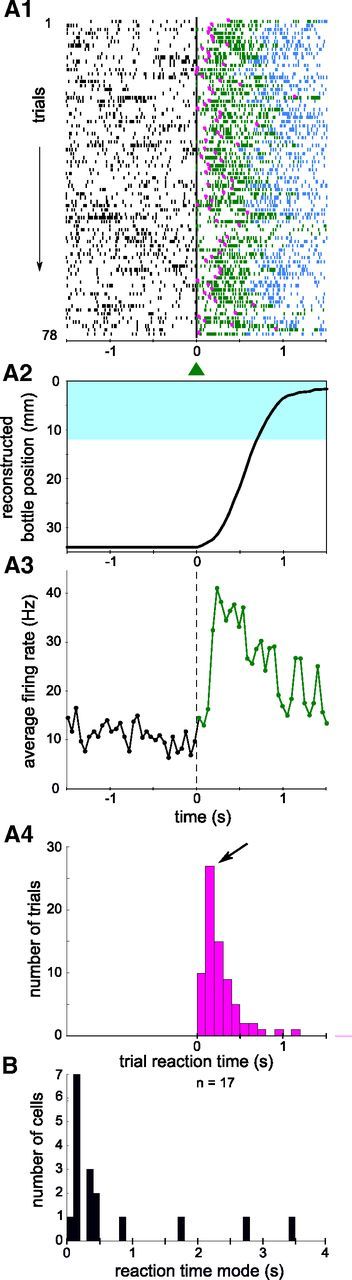
Reaction times of conditioned neurons after learning. A1, Raster plot of the activity of a neuron selected for operant conditioning around trial start (t = 0). Ticks represent spike times and they are colored depending on the experiment phase (black: waiting; green: trial; blue: reward periods). Small magenta dots mark the calculated individual trial latencies. A2, Bottle position averaged over trials for the same session. The blue area represents the drinking zone. A3, Perievent time histogram for the session shown in A1, for the waiting period (black line before 0) and the trials (green line after 0). The activity during reward periods (blue spikes in A1) was not included. Bin size, 50 ms. A4, Distribution of individual trial latencies for the same session, plotted in 100 ms bins. The peak of the distribution, defining the neuronal reaction time, is indicated by an arrow. B, Distribution of the best neuronal reaction time for all 17 conditioned neurons, in 100 ms bins. The session with the highest conditioning effect was used for each neuron (best session, see Materials and Methods).

The conditioned neurons are the first activated in the local network

The conditioned neuron and many neighboring neurons were recorded simultaneously with electrodes arranged in a 250 μm grid around the conditioned neuron electrode. In total, 161 neighboring neurons were recorded in the eight rats (∼15–20 per session). We often observed increases in the firing rate of nonconditioned neurons after trial onset, as displayed by the PETHs of Figure 5A for one conditioned neuron (green line) and three neighboring neurons (blue and red lines). To assess the temporal organization of activity in the local network, we computed the latency of activation of each neuron for each session, if measurable (see Materials and Methods; Fig. 5A, filled and open circles for two levels of sensitivity). Each neuron was assigned a rank of activation based on the response latencies of all the neurons recorded simultaneously. We divided the rank data for all sessions into three categories, depending on whether the neuron was conditioned at that session, had been submitted to operant conditioning previously, or had never been submitted to operant conditioning.

Across all sessions, the conditioned neurons responded faster than neurons from the two other categories. The distribution of ranks for conditioned neurons was significantly shifted toward lower values compared with the distributions for the two other groups (Fig. 5B; Mann–Whitney U test, p < 10⁻⁸ and p < 10⁻²⁸, n = 165 sessions). This was especially true for ranks 1 and 2, which indicates that the conditioned neuron was often among the first neurons to respond. To confirm that the conditioned neuron was reacting both fast and strongly, we raised the threshold of latency detection from 2 to 5 SD above the mean (see Materials and Methods), so that only neurons with highly significant increases in firing rate were now considered for determining the activation order in the network. As expected, fewer neurons responded according to that criterion, and the number of sessions where we could measure the latency of at least one neuron decreased (Fig. 5C, n = 109 sessions). However, taking into account only those sessions, the proportion of conditioned neurons with rank 1 or rank 2 increased from 33% to 42%, whereas it decreased for the two other categories of neurons. This confirmed that the conditioned neuron tended to react more often, faster and more strongly than the surrounding nonconditioned neurons.

We also quantified directly the strength of activation of each neuron by integrating the firing rate above the baseline value in the first second after trial onset, whenever it exceeded the mean by two times the SD value (Fig. 5D, inset). For this analysis, the conditioned neurons were classified in two categories: those that showed significant conditioning in at least half of the sessions, called “highly conditionable” (n = 10), and those that failed in more than half of the sessions, called “weakly conditionable” (n = 7). During all training sessions, conditioned neurons (green) associated with a strong conditioning efficacy (highly conditionable) exhibited on average a larger response integral than nonconditioned neighboring neurons (Fig. 5D, red). The response integral of nonconditioned neurons did not depend on the distance to the conditioned neurons. During training sessions with weakly conditionable neurons, all neurons displayed similar response integrals (Fig. 5E).

Firing rate variability of the conditioned neuron increases before trial onset

Trial-to-trial variability of spiking activity in a neuronal network has been previously proposed to be inversely related to the degree of preparation before a movement (Churchland et al., 2006). In addition, it can facilitate learning and adaptation in a dynamic environment by favoring the exploration of more network states (Faisal et al., 2008). In particular, it is exacerbated at the time and location where sensorimotor learning is supposed to happen (Mandelblat-Cerf et al., 2009). To establish a possible relation between variability in the ongoing activity and success of the conditioning, we quantified the trial-to-trial variability of the firing rate of each neuron during the waiting period using the FF index (see Materials and Methods). At the beginning of the waiting period, there was no significant difference between the conditioned and nonconditioned neurons (Fig. 6A1,B1, early). However, the highly conditionable neurons showed a strong increase of their mean variability index at the end of the waiting period (Fig. 6A1, green curve) compared with the nonconditioned population average (Fig. 6A1, red curve; Mann–Whitney U test, p < 0.01 are noted with stars). No trend was noticeable for the weakly conditionable category (Fig. 6B1). Also, the increase in variability was not accompanied by a concomitant trend of the mean firing rate (Fig. 6A1, gray line).

To assess whether this increase was due to a bias in the selection of conditioned neurons, we looked at the mean variability index during the waiting period for neurons that had been submitted to a conditioning protocol in previous sessions. Indeed, if we just happened to select neurons with a propensity for high variability to start with, we expect all conditioned neurons—currently or previously conditioned—to exhibit the same variability profile in any session. In contrast, the curve for the previously conditioned neurons did not differ significantly from that of the nonconditioned neurons (Mann–Whitney U test, p < 0.01, data not shown). It is thus unlikely that the high variability that we observed was due to a selection bias of the neurons. Similarly, we wanted to assess the possibility that the high trial-to-trial variability emerges from correct patterns of activity triggered in the local network in anticipation of trial start. We averaged the variability for the group of nonconditioned neurons that were responsive after trial onset, i.e., neurons for which the session latency could be measured and thus are most susceptible to participate in patterns of activity related to the task. Again, there was no significant difference with the nonconditioned average (Mann–Whitney U test, p < 0.01, data not shown). This implies that task-related increases in firing did not generate by themselves increased variability before trial onset, because in that case the increased variability should have been visible for these neurons as well. These results suggest that the increase in Fano Factor index before trial onset is a correlate of the learning specific to the currently conditioned neuron.

This was further confirmed by plotting the variability index as a function of the distance between the recorded neuron and the conditioned neuron. Again, the variability increase was found to be selective for the conditioned neuron. The mean variability computed for the neurons located at each distance did not significantly differ from the average variability of the population (Fig. 6A2, late; Mann–Whitney U test, stars indicate significance at the p < 0.01 level). For sessions involving weakly conditionable neurons, no significant difference from the population level was noticeable at any distance either (Fig. 6B2, late). Overall, these data indicates no observable spatial trend of the variability increase depending on the distance to the conditioned neuron. This observation does not contradict the fact that neurons other than the one used to control behavior also modified their activity during the learning process (Fig. 5D), but it excludes a possible gradient of variability, or at least indicates that it is very localized with a length constant smaller than 250 μm. In summary, an increase in the trial-to-trial variability of the firing rate of the conditioned neuron develops during the waiting period, for highly conditionable neurons, but this modification does not seem to involve any specific motor cortex region around it, except possibly a small one.

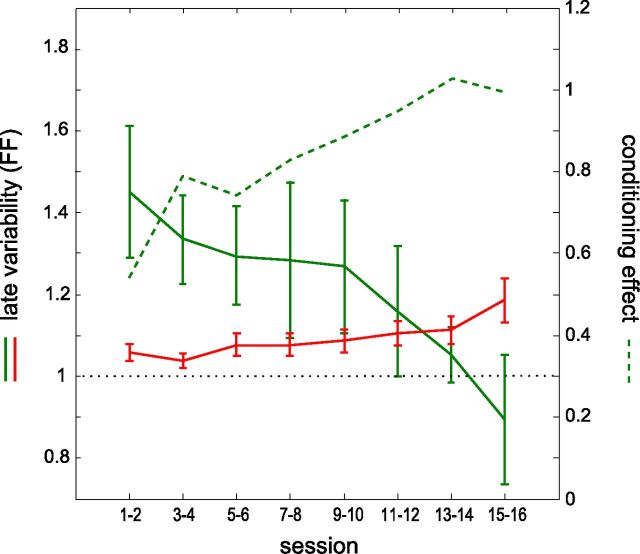
Finally, to examine how the transient increase in variability before trial onset changes in the course of learning, we computed the variability of the highly conditionable neurons at the end of the waiting period as a function of session number and confronted it with the learning curve of those neurons. The late variability was high during the first sessions of the training and progressively decreased throughout the sessions (Fig. 7, solid green curve). During the last sessions, the variability was close to the variability of a Poisson process (FF = 1), that is, it was at the same level than during the early part of the waiting period, and at the same level than that of nonconditioned or weakly conditionable neurons. Interestingly, the curve of performance (Fig. 7, dashed green curve) increased in the first sessions as long as the variability was high, and stabilized in the last sessions when the variability returned to its intrinsic level, confirming that the variability decrease time course was indeed related to the learning process. The time course of the variability throughout sessions for the nonconditioned neurons did not follow the same trend, as it slightly increased over days (Fig. 7, red curve), possibly demonstrating a refocus of learning (Mandelblat-Cerf et al., 2009).

Figure 7.

Time course of variability changes and conditioning effects across successive sessions. Evolution of the trial-to-trial variability of activity measured during the late phase of the waiting period for the conditioned neuron. The measures, taken from highly conditionable neurons only, are averaged for pairs of consecutive sessions, starting from the first day of conditioning (solid green curve). The red curve plots the variability of the simultaneously recorded nonconditioned neurons for those same sessions. Performance is represented by the conditioning effect d' (dashed green line, scale on the right; see Fig. 2D). The dotted line at variability = 1 indicates the variability of a Poisson process.

Discussion

We applied operant conditioning on single neurons in the rat motor cortex, to assess whether the reactivity and response reliability of a single-unit provides an output signal efficient enough for controlling brain-machine interfaces. Our results support the concept that using one neuron at a time may be suitable for BMI control. Most neurons tested (88%) successfully learnt the operant task at least in one of the sessions during which they were submitted to conditioning. The conditioning effect strengthened over successive sessions with the same neuron. The conditioned neurons displayed a number of specific functional modifications compared with simultaneously recorded neurons, notably a larger increase in firing rate, a shorter neuronal reaction time, and a transient change in discharge variability in anticipation of the trial onset.

Improvement in the operant task often required up to 5–10 sessions with the same neuron. This was similar to results reported from the few other operant conditioning studies conducted with rats (Gage et al., 2005; Marzullo et al., 2006). By contrast, operant conditioning of neurons in the primate motor cortex can be achieved much faster, within minutes (Moritz et al., 2008).

Previous operant conditioning studies focused on mean firing rate changes (Olds, 1965; Fetz, 1969) or mean changes at trial onset (Gage et al., 2005; Marzullo et al., 2006). Only a few works reported single trial reaction times, but without quantification for all neurons and trials (Evarts, 1966; Schmidt et al., 1978). Here, we examined the kinetics of activity for each single trial, and focused for each conditioned neuron on the session with the highest conditioning effect. Despite the fact that units had potentially the whole trial of several seconds to increase their firing rate, most of the conditioned units consistently responded within 500 ms, and nearly half of them below 200 ms. These latencies compare to the ones found by Schmidt et al. (1978) when conditioning motor cortex neurons in the hand-arm area or by Evarts (1966) when monkeys performed a fast movement of grasping, while recording pyramidal tract cells in motor cortex.

In the eight neurons exhibiting a reduced latency of the operant response output, we observed a high reliability across trials, such that the percentage of successful trials reached 99.8% for the best sessions recorded for these neurons. This might appear unexpected, in light of recent studies suggesting that the motor representation may be continuously changing at the single cell level, even for a given stable output (Cohen and Nicolelis, 2004; Carmena et al., 2005; Rokni et al., 2007). However, other studies have argued on the contrary for a strong stability of functional properties of motor cortex neurons (Chestek et al., 2007; Stevenson et al., 2011). In our experiments, the decoding rule of the prosthesis was fixed and only one neuron was used. This could have forced the emergence of a stable and precise map, in which the conditioned neuron was the sole operant output. For the sessions that were less reliable, it remains to be determined whether the failures were caused by changes in the internal states like attention or motivational drops, intrinsic stochasticity of some of the conditioned neurons, or a motor strategy limiting the precision of the firing rate.

Most remarkably, we found that the conditioned neuron fired on average before neighboring neurons recorded simultaneously, and exhibited stronger modulations. This was unexpected, because our protocol did not require the conditioned neuron to increase its firing rate first or more strongly. Indeed, if conditioned responses had occurred in synchrony with increased activity in the network a few hundred milliseconds later, this would essentially have produced the same number of drinking reinforcements by the end of the session. Our results show that the neuron responsible for the instrumental control acquires the functional role of a “master” cell, taking the lead of activation of the local cortical network.

We wondered whether conditioned neurons responded to bottle movements, so that a positive sensory feedback might be responsible for the conditioned neurons modulation of activity. PETHs aligned with the onset of bottle movement of each trial showed a phasic peak of response around the movement in the conditioned master neurons only, which was absent in nonconditioned neurons. We cannot exclude that a positive feedback loop triggered by the bottle displacement participates to later phases of maintained activity, but the differential patterns observed between conditioned and nonconditioned cells suggests that the time course of the activity does not reflect simply visual reafference.

Several observations strengthen the concept of a specificity of the conditioned cells developing progressively during learning of the operant task. First, master cells exhibited a surprisingly large firing rate variability in the waiting periods between trials. This was in contrast with the smaller variability observed for nonconditioned neurons and for conditioned neurons that failed to reach a high performance threshold (weakly conditionable neurons). For those categories, the variability was at the level of a Poisson process, as reported in other cortical studies (for review, see Churchland et al., 2006). Examination of the time course showed that the variability of the master cells started at baseline level and increased progressively throughout the waiting period, until it became significantly higher than control values before trial onset. High variability has been reported in the literature in situations involving uncertainty of the action to be executed and a related lack of preparation of the motor plan (Churchland et al., 2006; Afshar et al., 2011). Here, all trials have identical constraints for completion. However, because the duration of the waiting periods was variable, the high variability in firing rate could reflect the building up of expectancy of the next trial start. Alternatively, the high variability of master cells could reflect intrinsic mechanisms of learning. Similar observations have been reported during trace eye blink conditioning (Disterhoft et al., 1988) and in motor cortex during Pavlovian learning (Woody et al., 1991; Saar and Barkai, 2003). Both studies report the same temporal dissociation between an early phase of increased excitability and its extinction during the asymptotic phase of learning (Moyer et al., 1996). Indeed, such excitability process could facilitate learning by exploring patterns of discharge that are not commonly triggered (Rokni et al., 2007; Mandelblat-Cerf et al., 2009). This is further supported by the temporal relationship between the master cell variability and the conditioning effect (Fig. 7), showing that this mechanism is necessary for learning but not for performance afterward. The transient nature of increased excitability also suggests that some regulatory processes restore the normal baseline state, which is an important property for a mechanism supporting memory consolidation (Byrne, 1987). In our case, the fact that the mean variability of the nonconditioned population slowly increases in late sessions additionally suggests that once the master cell has been established, plasticity mechanisms could occur in the local network and consolidate task-related modifications of nonconditioned neurons (Mandelblat-Cerf et al., 2009).

Another indication that the master cell occupies a unique position comes from the unexpected spatial selectivity of both the firing rate response and the increase in variability between trials. Whereas most studies of learning-related changes noticed widespread phenomena (Pascual-Leone et al., 1994), or modifications that are common to all cells tuned for the task (Churchland et al., 2006; Mandelblat-Cerf et al., 2009), in our study the functional modifications are largely restricted to the successfully conditioned neurons. Of course, we do not exclude the possibility of nondetected plastic modifications since our recording sample is limited, but they would be necessarily sparsely distributed in the network, or very close to the master neuron (<250 μm).

Two mechanisms could lead the master neuron to fire earlier and more strongly than others: a change in intrinsic excitability and/or a change in the synaptic circuitry of the pathways that ultimately activate the conditioned neuron. In the motor cortex, enhanced excitability and signal transduction are dependent on neuromodulatory dopamine projections, known to be active during learning and reward (Yasumoto et al., 2002; Schultz, 2007; Hosp et al., 2009; Hosp et al., 2011). A possible interpretation of our results is that dopamine levels may change progressively and affect selectively the neurons of the motor cortex that are involved actively in the task. Other processes could come into play such as the unmasking of latent priming effects revealed when the learning context reappears, tagging (Redondo and Morris, 2011), and state-dependent learning (Shulz et al., 2000). However, it is difficult to explain how such modifications could be restricted only to the master neuron. Alternatively, plasticity changes of the master neuron may reflect synaptic modifications distributed upstream in the sensory and sensorimotor networks recruited by the task (Meftah and Rispal-Padel, 1994). Again, dopamine release triggered by the task reinforcements could be an important factor for the induction of such modifications (Rioult-Pedotti et al., 2000; Bao et al., 2001; Molina-Luna et al., 2009).

In the context of the development of efficient brain-machine interfaces, the demonstration of operant conditioning of the firing rate of a single neuron, almost in real time, should help building bottom-up strategies for higher dimensional control, in particular n-D as required for sophisticated actuators. To design a full BMI with our paradigm, each of several conditioned neurons—or small groups of neurons, to increase reliability even more—should be assigned to control different state variables (kinematic, dynamic, or even higher level parameters) or different task-related values of a prosthetic device (Snyder et al., 1997; Musallam et al., 2004). This requires that neurons can function independently. Such independence has been previously observed for motoneurons (Smith et al., 1974), motor units (Basmajian, 1963), and between motor cortex neurons and muscles (Fetz and Finocchio, 1971; Fetz and Baker, 1973; Moritz et al., 2008). The operant conditioning approach, exploiting the plasticity properties of cortical neurons, should be pursued in parallel to the fruitful advances obtained with the neural ensemble decoding approach. Initially based on the recording of very large populations of neurons, this strategy was recently implemented using a few tens of cortical motor neurons in order for tetraplegic patients to successfully control a robotic arm (Hochberg et al., 2012).

The functional changes induced in the cortical network by operant conditioning may be explained by different but not exclusive scenarios. A first scheme posits that the primary changes are not restricted to the conditioned cell and that the operant control of the bottle is established through dynamic restructuration of correlations in the premotor and motor networks. Such network changes may result both from synaptic and excitability changes, as often observed during classical behavioral (Disterhoft et al., 1986) or cellular (Daoudal and Debanne, 2003) conditioning. Unfortunately in our experiments, the sampling of nonconditioned cells was not dense enough to have a chance to reveal coupling changes in a distributed assembly.

However, the comparison between simultaneously recorded cells in our experiments showed that (1) the conditioning does not result in a spatial gradient centered in the vicinity of the conditioned cell whose activity changes drove the bottle displacement, and (2) that activation latencies point to a temporal reordering of the network activity. This latter observation suggests a second interpretative scheme, where the conditioned neurons would become master units encoding for the causality established through operant conditioning between the cell's firing rate and the bottle movement. Note that this concept, popular in electronics and robotics (e.g., tinkertrons) and invertebrate literature [“orchestra leaders” in the study by Meyrand et al. (1994)], share strong similarities to that of “grand-mother” cells (for review, see Bowers, 2009) and “iconic memory” cells (Sakai et al., 1994), except that the emergence of these highly specialized neurons through learning applies here to anticipation of action/decision rather than perception.