Comparisons among Equations Used for Retinol Isotope Dilution in the Assessment of Total Body Stores and Total Liver Reserves

Abstract

Vitamin A plays an essential role in animal biology and has negative effects associated with both hypo- and hypervitaminosis A. Many notable interventions are being done globally to eliminate vitamin A deficiency, including supplementation, fortification, and biofortification. At the same time, it is important to monitor vitamin A status in nations where preformed vitamin A intake is high because of consumption of animal source foods (e.g., liver, dairy, eggs), fortified foods (e.g., milk, cereals, oil, sugar, margarine), or vitamin supplements (e.g., one-a-day multivitamins) to ensure the population does not reach hypervitaminosis A. To accurately assess population status and evaluate interventions aimed at improving vitamin A status, accurate assessment methods are needed. The primary storage site of vitamin A is the liver; however, routinely obtaining liver samples from humans is impractical and unethical. Isotope dilution using deuterium- or ¹³C-labeled retinol is currently the most sensitive indirect biomarker of vitamin A status across a wide range of liver reserves. The major drawback to its application is the increased technicality in sample analysis and data calculations when compared to less sensitive methodology, such as serum retinol concentrations and dose response tests. Two main equations have emerged for calculating vitamin A body pool size or liver concentrations from isotope dilution data: the “Olson equation” and the “mass balance equation.” Different applications of these equations can lead to confusion and lack of consistency if the underlying principles and assumptions used are not clarified. The purpose of this focused review is to describe the evolution of the equations used in retinol stable-isotope work and the assumptions appropriate to different applications of the test. Ultimately, the 2 main equations are shown to be fundamentally the same and differ only in assumptions made for each specific research application.

Introduction

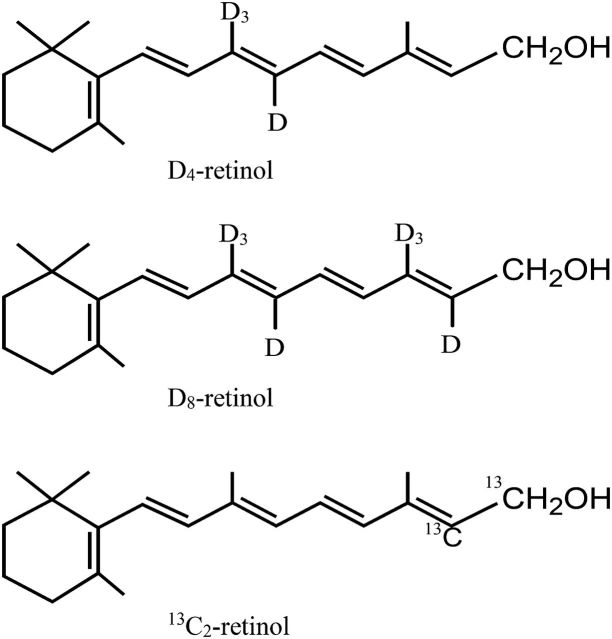
Isotopes of an element differ from each other in the number of neutrons that they contain and are useful for a variety of metabolic and assessment applications. Although the word isotope is often interpreted to mean radioactivity, naturally occurring stable isotopes are not radioactive and are completely safe to use in humans at the doses administered (1). Because of the organic structure (Figure 1) and synthetic procedures for retinol (2, 3), the stable isotopes that have been applied in vitamin A status assessment are the heavy isotopes of hydrogen (²H), namely deuterium, and carbon, namely ¹³C (4). The natural abundance of deuterium is ∼0.015% compared to hydrogen at >99.9%, whereas those of ¹²C and ¹³C are 98.9% and 1.1%, respectively. Only traces of radioactive tritium and ¹⁴C (<0.000000001%) occur naturally.

FIGURE 1.

The chemical structures of the 3 main stable-isotope-labeled retinol molecules used in the assessment of total body stores of vitamin A in humans. The most common form is 10, 19, 19, 19-D₄-retinol, followed by 10, 19, 19, 19, 14, 20, 20, 20-D₈-retinol, and 14, 15-¹³C₂-retinol. D, deuterium.

The seminal work describing the use of the retinol isotope dilution (RID)³ principle to evaluate total body stores (TBS) and total liver reserves (TLR) of vitamin A was that of Bausch and Rietz in 1977 (5). Since that publication, several research groups have used the same principle, modified with different assumptions relevant to each specific application. Over time, different equations have emerged, with 2 major classes of equations used today: 1) the Olson equation (Equation 1), put forth by Furr et al. in 1989 with Olson as the senior author (6); and 2) the mass balance equation (Equation 2) (Figure 2) used directly for RID with ¹³C in 2000 by Tanumihardjo (7), as suggested by Goodman and Brenna in 1992 for use in FA metabolism in conjunction with gas chromatography–combustion isotope ratio mass spectrometry (GC-CIRMS) (8).

FIGURE 2.

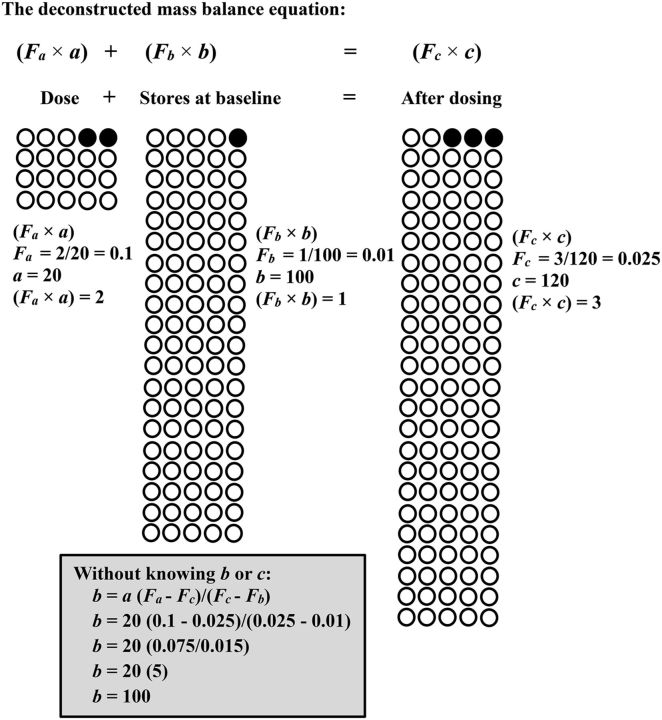
A diagram representing the principle of stable-isotope dilution and the factors in the mass balance equation that correspond to each part of the equation using ¹³C-tracer as an example. Closed circles represent heavy isotopes and open circles represent light (common) isotopes. The variables a, b, and c, which refer to molar quantities in the mass balance equation, are represented in units of atoms as pictured. F_a, F_b, and F_c are calculated by dividing the number of ¹³C atoms by the number of total carbon atoms in a sample. An example solution of b without knowing b or c is shown: (F_a × a) + (F_b × b) = (F_c × c) is numerically verified (2 + 1 = 3) and a + b = c (20 + 100 = 120).

Where “F” is efficiency of absorption and storage of an oral dose, “dose” is quantity of deuterium-retinol dose, “S” is the specific activity of retinol in serum to liver, “a” corrects storage for catabolism, “H:D” is the ratio of unlabeled to labeled retinol, and “−1” accounts for dose addition to the body pool.

where (b or q_end) is quantity of endogenous stores, (a or q_lbl) is quantity of label, and (c or q_tot) is total quantity; c = a + b or q_tot = q_end + q_lbl. The ¹³C atom fraction (isotope abundance) is represented by (F_b or f_end) for endogenous stores, (F_a or f_lbl) for label, and (F_c or f_tot) for the total.

The first published application of the RID test in humans used retinol labeled with 4 deuteriums (6). The equation (Equation 1) that was used to calculate TLR, termed the Olson equation (Equation 1) in 2005 (4, 9), was derived from the Bausch and Rietz equation used in rats (5) with modifications based on another rat study for the serum-to-liver isotopic ratio (S in Equation 1) described below (10).

The Olson equation (Equation 1) was applied in several other studies with the deuterated-RID (D-RID) test [reviewed by Furr et al. (4)]. In 2000, ¹³C₄-retinol was administered to rats for the determination of TBS (7). The switch to ¹³C from deuterium was based on multiple factors and originally began with conversations between Tanumihardjo and Goodman (8) in the mid 1990s. The synthetic procedure is more straightforward because the ¹³C is added at the end of the organic synthetic pathway (3), and it is incorporated into the backbone of the retinol moiety (Figure 1). Therefore, the label does not shift within the molecule. This may not be the case with deuterium, which can shift within or between molecules through proton exchange reactions, although this usually occurs under harsh conditions (11). In addition, isotope ratio MS for ¹³C-enrichment could be employed, which had several advantages: 1) lower doses of labeled retinol could be used, and therefore, perturbation of retinol metabolism was diminished; 2) fewer labeled atoms within the molecule could ultimately be used, which meant fewer isotopic effects in the body and lower synthetic costs; and 3) the retinol did not have to be derivatized before introduction into the gas chromatograph. Instead of applying the Olson equation, the author went back to the original mass balance equation (Equation 2) and made specific assumptions based on the metabolism and storage of retinol in the rat. The ¹³C-retinol isotope dilution (¹³C-RID) test using mass balance (Figure 2) was subsequently applied to rhesus monkeys (12) and multiple groups of humans (13–15).

During the presentation in different venues of the somewhat surprising finding of hypervitaminosis A in a large percentage of Zambian preschool children (15), the authors were questioned by the nutrition community on the use of the mass balance equation (Equation 2) for the basis of calculations instead of the Olson equation (Equation 1) for the calculation of TLR in these children. The purpose of this review is to compare the similarities among the equations used in the calculation of TBS and TLR with use of tritium-, deuterium-, or ¹³C-retinol. Isotope dilution methods are becoming more available for studies involving vitamin A assessment and intervention monitoring, but there is some confusion within the field as to why multiple equations exist. The 2 main equations will be explained in detail and ultimately shown to be the same equation, differing only by assumptions specific to each application. We encourage all future studies using isotope dilution for vitamin A assessment to clearly state the equation adopted and the assumptions appropriate to the unique study or evaluation design for transparency and consistency to move forward with evaluating and optimizing the vitamin A status of the world.

Principle of isotope dilution

The principle of isotope dilution involves giving a tracer dose of vitamin A labeled with either radioactive (tritium and ¹⁴C) or stable (deuterium and ¹³C) isotopes, allowing the tracer to mix with the body pool of vitamin A, and assessing the tracer-to-tracee ratio (TTR) after mixing has occurred. There are key assumptions in the isotope-dilution test as it is applied: 1) the tracer dose mixes completely with the tracee body pool; 2) the tracer behaves indistinguishably from the tracee in the system; 3) the tracer is detectible by analytical methods in the context of the tracee; 4) the tracer does not perturb the system being studied; and 5) the tracee system is a single pool in steady state (tracee mass is constant). By using MS (or decay counting with complimentary analytical techniques), TTR can be determined and TBS or TLR of vitamin A can be estimated.

Definitions and units.

Two commonly used units for isotope content are the isotope ratio (R) and atom fraction or isotope abundance (F). The units are dimensionless, i.e., mol/mol, and relate the number of heavy atoms compared to the number of total atoms (F) or light atoms (R) (16–18). Although a preferred abbreviation for atom fraction is x (18), the purpose of this review is to clarify equations and variables published in the literature for vitamin A assessment (16, 18, 19); therefore, we will use F because it was used in association with the mass balance equation (Equation 2) and the ¹³C-RID test (7, 12–15).

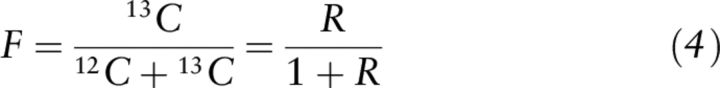Review and applications of the equations

Bausch and Rietz equations.

Bausch and Rietz (5) put forward a number of equations for calculating vitamin A TBS using tritium- and deuterium-labeled retinol. The basic theoretical equation for isotope dilution is the first described for tritiated retinol (Equation 5):

This equation assumes complete equilibration of the tracer dose with the tracee pool with no further intake or excretion of tracee (i.e., a closed system). Because these assumptions are not satisfied in most cases, modifications must be made to the equation to account for the dynamics of the system. For TBS assessment, sampling of plasma is performed once the tracer mixes with the tracee pool. Specific activity changes dramatically for a few days after dosing either orally or intravenously but changes more slowly after the mixing period (5, 7), and these are accounted for with storage assumptions and first-order kinetics (20), which are described below.

Bausch and Rietz state that the test dose will not be completely absorbed and can be metabolized during the mixing period. Therefore, a term needs to be included in the equation to indicate how much of the test dose is absorbed and incorporated into the vitamin A pool. The authors then put forward an equation (Equation 6) for vitamin A liver stores (equivalent to TLR in this review) that includes a term for how much dose was absorbed and stored in the liver based on analytical determination of tritium tracer remaining in the liver.

It is important to note that this factor includes both absorption of the tracer dose and the amount of dose remaining in the pool of choice (e.g., total liver pool) after the mixing period.

The authors next put forward an equation (Equation 7) to calculate vitamin A liver reserves in humans using deuterated retinol with a similar calculation:

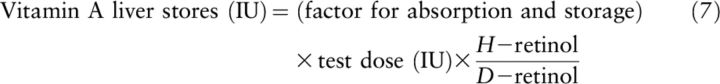Equation 7 needs a correction term (+1) in the final form to account for the large amount of deuterated dose that could not be differentiated from the tracee in the fluorometric analysis of liver content after dosing in comparison to the isotope-dilution method (5):

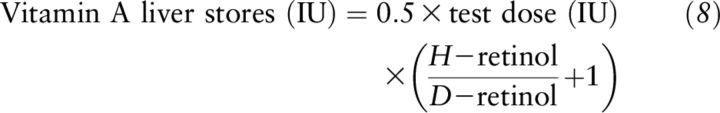The authors clarify that the 0.5 factor for absorption and storage in liver in humans is still arbitrary and needs to be considered in future applications of the RID test (5).

The Olson equation.

The Olson equation (Equation 1) is considered a modified version of Equation 8 by Bausch and Rietz:

where “F” is a factor for efficiency of absorption and storage of an oral dose in the liver and not to be confused with atom fraction notation (F) in this review, “dose” is the quantity of deuterated-retinol dose administered (typically in mmol), “S” is the ratio of specific activity of retinol in serum to that in liver, “a” is an additional factor to correct the dose for catabolism and excretion over time [a = e^−kt, k = ln(2)/half-life of retinol, t is days since dosing] and is discussed further below, “H:D” is the ratio of unlabeled to labeled retinol after mixing, and “−1” accounts for the contribution of dose to the total body pool.

It is noted that the Olson equation (Equation 1) has a correction term “−1,” whereas the Bausch and Rietz equation (Equation 8) has a “+1” correction term, likely due to a typographical error that has been carried throughout recent applications and remains as such in the current user's guide (9) and the DRIs (21). The relative effect of this change (net −2 to unlabeled to labeled retinol ratio term) is modest, is dependent on the ratio being “corrected,” and has a greater percentage change on TBS or TLR with a lower ratio (i.e., lower vitamin A stores). For example, there would be a 6% decrease in calculated stores of Filipino elders with an unlabeled to labeled retinol ratio of 1:0.03 (calculated liver vitamin A concentration was 0.17 μmol/g) (22). Bausch and Rietz gave 2 reasons for needing this correction term: 1) the analytical determination cannot differentiate between hydrogenated- and deuterated-retinol, and 2) the administered dose of deuterated retinol is much larger than the tritiated retinol dose and therefore cannot be neglected for comparison. The first point is more important when validating RID methods and equations against liver samples taken after dosing rather than evaluating status. Furthermore, tracer dose amounts have become smaller as analytical techniques have improved, meaning minimal effects on TBS, and this correction term has recently been suggested to be ignored in future applications of D-RID tests (23).

The correction term for catabolism (i.e., e^−kt) was misprinted (although calculated correctly) in the original 1989 publication (6) but was corrected in a subsequent published erratum (24). Finally, there is redundancy between the “F” and “a” terms in the equation because “F” accounts for the amount of dose absorbed and stored by the liver, and the “a” term corrects for whole-body metabolism, which includes the liver and other losses, during the mixing period. In the original work by Bausch and Rietz, “a” is actually part of “F” (23). This extra factor decreases calculated TLR.

Mass (isotope) balance equation.

The principle of mass balance and isotope dilution dates back decades as a highly sensitive analytical technique (25). More properly called “isotope balance,” the mass balance equation (Equation 2) and principle allows the determination of the amount of substance originally present in a system because “the sum of the amounts of the isotopes of each constituent of the mixture must equal the total in the system” (18). Isotope data have been used in terms of R (25) or F (26). Goodman and Brenna (8) described a novel approach for high-sensitivity tracer detection using ¹³C-labeled molecules coupled with GC-CIRMS for FA metabolism, which was subsequently adopted for the RID test. The equation as applied to the ¹³C-RID test balances the tracer quantity before and after mixing with body stores and allows calculation of TBS of vitamin A. The equation and principle of mass balance for ¹³C-retinol was applied to rats (7), monkeys (12), and humans (13–15):

where a, b, and c are quantities (μmol) of retinol in the dose, TBS, and their sum, respectively; a + b = c. (Note: this a is not the same as factor “a” used in the Olson equation). F_a, F_b, and F_c are the isotope abundance (¹³C/total C) of the dose, baseline serum retinol, and postdose serum retinol, respectively. First, (a + b) is substituted for c, and then the equation is solved for b (TBS at baseline) (26). Factors are included for absorption and total body storage in Equation 9, which are based upon the group being studied because these factors can be affected by individual situations:

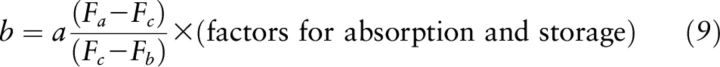TTR.

The TTR (Equation 10) is a value used in stable-isotope dilution calculations (27–29) and is the analogue of specific activity for radioactive tracers (27, 29). It represents the ratio between molecules of tracer and tracee after the mixing period has occurred (29) and takes into account the isotope abundance at baseline and in the tracer dose.

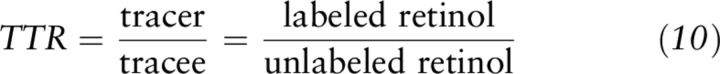The unlabeled to labeled retinol ratio (H:D) (Equation 11) used in the Bausch and Rietz (Equations 7 and 8) and Olson (Equation 1) equations can be represented as:

and Equation 7 put forward by Bausch and Rietz, which assumes small tracer doses, can be rewritten:

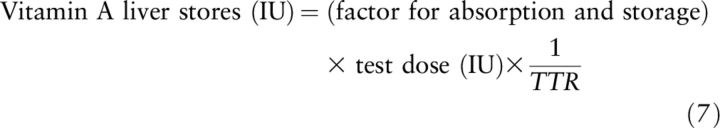Cobelli et al. (27, 28) denote TTR as z(t). Some confusion is generated because in these publications, TTR is defined as the ratio of “tracer and tracee mass,” and one could wonder if these ratios should have units of (mass/mass) instead of (mol/mol). However, in the earlier publication, the authors discuss z(t) as a “molar ratio” (27). In addition, the mass difference between the heavy and light isotopes in isotope dilution is sometimes ignored because of minimal differences (25), which is also the case for most retinol tracers.

Cobelli et al. (28) provides a valuable resource for calculating TTR from F, R, and isotope enrichment. The calculation for TTR in terms of R is presented, whereas similar logic is applied for F (Equation 12). Although the authors refer to their variables as mass, the calculations hold for moles as well, because the mass or molar variables drop from the equation as long as either is used consistently.

where a(t) is the isotope abundance (F) after the mixing period, a_N is the naturally occurring isotope abundance, and a_I is the infusate (dose) isotope abundance. The a_I, a_N, and a(t) from Cobelli et al. (28) correspond to the variables used consistently by the Tanumihardjo research group (F_a, F_b, F_c, respectively) (7, 12–15). This allows substituting these values in Equation 12 to rewrite it as:

Equation 12 can now be substituted into the mass balance equation to rewrite Equation 9:

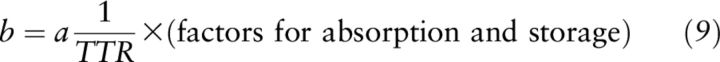Thus, the mass balance equation solved for TBS (Equation 9) and the Bausch and Rietz equation (Equation 7) are fundamentally the same equation (recalling that a is equivalent to “dose”), and differ only by assumptions for absorption and storage of the dose in the whole body or liver to estimate the pool of interest (i.e., TBS or TLR, respectively) (Table 1). The Olson equation (Equation 1), because it is based on the Bausch and Rietz equation (Equation 8), is also fundamentally the same but includes factors for the plasma-to-liver–specific activity ratio and the perturbation to the system (essential for large labeled doses) as well as traditional factors for absorption and storage in the liver.

TABLE 1.

Summary of the equations and assumptions currently used in the calculations of TBS and TLR of vitamin A using stable-isotope dilution techniques¹

Core principle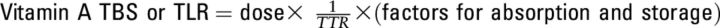
	Mass balance equation (Equation 2)		Olson equation (Equation 1)
	Assumptions used for TBS	Factor used	Assumptions used for TLR	Factor used
Initial assumptions	Amount of tracer absorbed in body	Constant, typically 0.8–1.0	Amount of tracer absorbed and stored in the liver	“F” 0.5
	Amount of tracer stored in body	Constant (time dependent), e−kt, where k = [ln(2)]/half-life of (d), t = time (d)	Amount of tracer stored	”a”, e−kt, where k = [ln(2)]/half-life of retinol (d), t = time (d)
	Contribution of dose to body pool	Ignored due to low tracer dose in applications using mass balance equation	Contribution of dose to body pool	”+1” by Bausch and Rietz
				”−1” in Olson equation
	Specific activity ratio of serum/liver	Eliminated due to low tracer dose, low vitamin A intake, and fasting state in applications using mass balance equation	Specific activity ratio of serum/liver	”S”, 0.65
Additional assumptions used for TLR	Percent of TBS stored in liver	Constant, varies with vitamin A status:
		Marginal status = 0.5
		Adequate status = 0.8–0.9
Additional assumptions used for vitamin A liver concentration	Liver weight as % of body weight	Constant, 4–4.2% for infants, 3% for children, 2.4% for adults	Liver weight as % of body weight	Constant, 4–4.2% for infants, 3% for children, 2.4% for adults

¹“F”, efficiency of absorption and storage of an oral dose in the liver; TBS, total body stores; TLR, total liver reserves; TTR, tracer-to-tracee ratio.

Although other variables of tracer enrichment could be used, TTR (D:H) or 1/TTR (H:D) has been used consistently with the Olson and mass balance equations, although not explicitly stated. Differences in instrumentation and data output have likely contributed to preference of a specific equation (e.g., GC-CIRMS software directly reports isotope abundance, which is used by the mass balance equation). Reporting TTR with calculated TBS or TLR would allow easier comparison among studies.

Correction for plasma-to-liver–specific activity ratio.

The Olson equation uses 0.65 as the factor for the plasma-to-liver–specific activity ratio and is equivalent to S in Equation 1. This factor was based on 1 rat study, which was published in 1984 (10). The total retinol dose administered in that rat experiment was 61 μg, comprised of almost equal amounts of tritiated-retinol and nonradioactive retinol, which is ∼4-times higher than the amount of retinol known to keep rats in balance (30). Furthermore, the rats continued to receive their daily vitamin A doses during the mixing period. Thus, the tracer dose was continually diluted during the mixing period and likely a large amount of the tracer was stored in the liver. In a subsequent human study, this ratio was 0.8 in Bangladeshi surgical patients given large D₄-retinol doses (∼32.5 μmol based on 0.753-μmol/kg body weight) and continued on their vitamin A–containing hospital diets (31), but the equation was not updated for the human application. This factor was not used in current published applications of the ¹³C-RID test for the following reasons: 1) the doses administered are very small compared to the deuterated doses and therefore are not shunted to the liver to disproportionally label the liver pool; 2) the human subjects (13–15) and rats (7) were fed a very low vitamin A–containing diet during the equilibration period; and 3) the ratio was 1.0 after equilibration in rats with varying vitamin A status and hypervitaminotic monkeys (7, 12). Adding another specific activity factor would have underestimated TLR. However, if an intervention or a population evaluation used the ¹³C-RID test and did not control the diet during the mixing period, the 0.8 factor may be appropriate and incorporated into the assumptions because of continued dilution from the daily vitamin A intake into the plasma retinol pool.

Correction for catabolism of the tracer dose.

A correction to most equations used for the calculation of TBS is to account for the catabolism of the tracer dose. This correction corresponds to “a” in the Olson equation (Equation 1), i.e., a = e^−kt, for the D-RID test (6, 24) and was applied to the ¹³C-RID test used in humans (13–15), although it was not used for ¹³C-RID applications in rats (7) and monkeys (12). This correction may be made to the TBS or TLR calculation, i.e., corrected TBS = TBS × e^−kt, where k = ln(2)/(half-life of retinol in days), and t is time in days since dosing. The relation between half-life and TBS has not been fully elucidated, but it appears to be related to age in humans (20, 32), life stage in rats (33), and tends to increase as TBS increase (30).

Depending on the study design, including the number of blood draws, timing of blood draws, treatment groups, and dietary control, the actual half-life of the group being studied may be able to be measured as part of the experimental protocol, usually as part of a negative control group that did not receive substantial amounts of vitamin A during an intervention and maintained tracee pool size (15). If not part of the design, half-lives for retinol that have been used in both RID tests are 140 d in adults [6, 13, discussed in Olson (32)] and 32 d in children with low TBS (14, 20). If this correction is used across treatment groups, it will not affect intervention effects, but may change the prevalence of either hypo- or hypervitaminosis A in a community evaluation depending on the value used. A half-life of 140 d and a 14-d mixing period results in a factor of 0.93, whereas a half-life of 32 d and a 14-d mixing period results in a factor of 0.74.

Deviations from the Olson equation.

In 1999, a change in the definition was made for the Olson equation (Equation 1) (34), which has continued since then by some users (4). The equation was used to define TBS (34) instead of TLR as originally meant (6). Although it appears an assumption was not applied for percentage of TBS in liver in that publication (34), other users of the D-RID test began correcting TLR from the Olson equation (Equation 1) for 90% in the liver (35, 36). The 2005 handbook states that calculation of liver concentration is less than ideal (9). Therefore, applications using the Olson equation (Equation 1) need to consider whether the value for TLR should be corrected up for TBS or down for lower amounts anticipated in the liver during deficiency. The original Olson equation (Equation 1) was meant to reflect TLR, and not TBS, when the 0.5 fraction absorbed and stored in the liver (“F” in Equation 1) and the 0.65 specific activity value is applied (S in Equation 1) (10).

Three-day equations.

A number of studies have evaluated a shortened time period between dosing and blood sampling (3 vs. 14, 20, or 21 d) to minimize field time and the potential for infections, which may interfere with RID tests (9, 23). Comparisons were made by having multiple blood draws (early and standard time points) from the same subjects.

Comparisons between dissimilar variables of early and standard blood draws have compared 3- and 6-d TTR vs. 21-d calculated stores with a linear fit (34), 3-d TTR and 20- or 21-d calculated stores with a nonlinear fit (22), and 3-d TTR and >10-d calculated stores with a different nonlinear fit (20). Although a nonlinear fit should be expected (calculated stores are proportional to 1/TTR), comparison of the plots and best-fit equations, which were of different forms, for Peruvian children given a 14-μmol dose (20) and Filipino elders given a 15-μmol dose (22) indicate discrepancy in the operational range of TTR for isotope dilution.

Comparisons of identical variables at 3-d and longer (14, 20, or 21 d) time intervals generally revealed linear relations between TTR (22), atom percent (37), and calculated TBS (13) in males and females across a wide range of ages and TBS, indicating that a linear function could estimate TBS or TLR based on short mixing periods. Three studies compared different, yet related, variables, and therefore the best fit lines can be compared: Valentine's (13) best fit (reverse calculation) was 3-d TTR × ∼0.27 = 14-d TTR, Ribaya-Mercado's (22) best fit for Filipino subjects (visual approximation) was 3-d TTR × ∼0.29 = 20-d TTR, and Tang's (37) best fit [transforming (deuterated-retinol/total retinol) to TTR and ignoring minimal intercept] was 3-d TTR × ∼0.22 = 21-d TTR. The similarity among the constant correction factors in diverse groups indicates potential for another factor for 3-d RID applications (similar to fraction of dose absorbed) to account for the higher TTR at the early sampling point.

Although short-term predictive equations may work to assess TBS or TLR of a population with comparison to a subset that uses the conventional mixing period to establish the relation (37), it may be more difficult to extrapolate those equations to populations that may differ in aspects that affect the RID test (e.g., vitamin A status, prevalence of infection, life stage). Nonetheless, general agreement across a wide range of subjects holds promise for 3-d RID applications. Early and standard sampling of TTR in diverse populations should determine the following: 1) if a linear relation is maintained; 2) if the relation is similar across differing groups; and 3) if these data could be used to generate another factor that could correct short-term sampling for TBS or TLR determinations. Ideally, this would be another transparent, intuitive factor that could be stated in calculations and subject to improvement as more data are generated.

Discussion

This review specifically focused on the evolution of equations used for the application of stable-isotope methodology to vitamin A status assessment. Historically, the principle of isotope dilution dates back multiple decades, and versions of the mass balance equation date back centuries to Archimedes' Principle. In 1946 the US Atomic Energy Commission made stable isotopes available to analytical chemists, and a variety of applications of isotope dilution emerged (25). With this came the general use of the mass balance equation (Equation 2), although some use very different notations (25, 38) than those used above in Equation 2, but are mathematically identical:

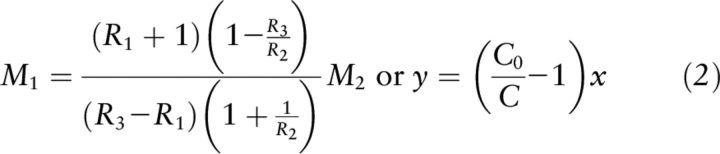where M₁ = b and M₂ = a in Equation 9; R₁ is R_b, R₂ is R_a, and R₃ is R_c, where R_x corresponds with F_x; R is ¹³C/¹²C (25); or y = b and x = a in Equation 9, C₀ and C are atom percent excess of the dose (F_a − F_b)*100 and mixture (F_c − F_b)*100, respectively (38).

Hayes (26) described a more general form of the mass balance equation termed the “master equation” that can be applied to mixtures of isotopically different materials:

where n_x is the molar quantity and F_x is the isotope abundance of the element of interest, and subscript T refers to total sample comprised of subsamples 1, 2, ….

The specific case applied for the ¹³C-RID is a mixture of 2 isotopically differing materials: the labeled dose with TBS. The preferred isotope balance equation and notation by some investigators are based on recommendations by the International Union of Pure and Applied Chemistry (18).

Compared to serum retinol concentrations alone, RID tests offer much more power to evaluate interventions and assess vitamin A status from hypo- through hypervitaminosis A (39). To be more consistent among the different types of RID tests, it is imperative that the equations used be carefully considered and appropriate assumptions described clearly so that the readers understand how the calculations presented may differ from other studies in the literature. A recent application of the D-RID test in Mexican preschoolers used the Olson equation (Equation 1) for TBS instead of TLR and then corrected the value by 90% to calculate liver stores using 3% of body weight for liver weight (35). The values for liver concentration would be ∼37% higher if 0.8 would have been used for the specific activity in humans on a vitamin A–containing diet during the mixing period instead of 0.65, a correction for 90% in the liver was not used, and a direct calculation using 3% body weight for liver weight was made from the Olson equation (Equation 1) for TLR for concentration. Based on continuous improvements in mass spectrometers, the D₄-retinol dose used in the preschoolers (∼5 mg) (35) was 9- to 10-times less than that in the adults (45 mg), which will affect the specific activity (6). [Note: It is unclear whether mass was 5.08-mg acetate ester or based on retinol as in publication (6)].

To reiterate, as long as the assumptions are uniform in the equation used across treatment groups, treatment effects are not affected, but the prevalence of hypo- and hypervitaminosis A is because they are based on liver retinol concentrations (39). Nonetheless, this may not be important at the public health level when used for vitamin A status evaluation. In the application of the ¹³C-RID test in Zambian children (15), a correction for subclinical inflammation was made because C-reactive protein concentrations were known and active infections are known to decrease the amount of tracer dose absorbed (40). Treatment effects did not change, but this individual factor decreased the calculated prevalence of hypervitaminosis A in these children from 61% to 59% (15), which certainly is not that different at a public health level. Due in part to all of the assumptions made, RID tests better estimate the status of the community and not individuals (9).

The synthetic procedure for retinol results in a mixture of deuterated forms (2), which need to be combined in the final MS analysis. This is especially true when D₈-retinol is used and several isotopomers are present in the blood after dosing (35, 36, 41). Furthermore, isotope mass effects in vivo and proton exchange, especially during the derivatization reactions, have not been studied specifically for retinol and should be considered. A simple comparison of mass difference is a 100% increase in weight between hydrogen and deuterium atoms and an 8.3% increase from ¹²C to ¹³C. Not only does deuterium exchange with hydrogen within and between molecules (11), other noncovalent isotope effects occur between molecules that may be of biological interest (42). Although these differences are likely not substantially affecting the calculations of TBS at the group level because of variation among individuals and the global assumptions made in equations, it is something to consider in future work considering the current use of D₈-retinol and perhaps ¹³C₁₀-retinol (43) in different types of isotopic applications. These larger weight differences may affect binding of retinol to retinol-binding protein in the liver, which would preferentially cause a higher isotopic ratio in the liver than the plasma pool. In fact, a study in rats demonstrated a potential isotopic effect using tritiated-retinol as a tracer and inducing inflammation with recombinant human IL-6 (44). The plasma-specific activity, in addition to serum retinol concentrations, decreased during the most intensive administration of the inflammatory agents indicating less mobilization of the tracer (44). The authors state that reduction in retinol-binding protein synthesis is a likely explanation for these findings, but an isotope-by-inflammation interaction could have also occurred and requires more investigation.

In future applications of RID tests for the evaluation of TBS and TLR in populations, it is appropriate to discuss modifications of the equation in obese individuals. In the 1989 paper by Furr et al. (6), 6 individuals in the group of 11 were considered obese and a ceiling value of 2.2 kg was used for liver size instead of 2.4% body weight. In these same 6 individuals, the calculated-to-measured TLR ratio was 1.14 using this liver weight ceiling. Perhaps this extra calculated vitamin A was not in the liver but in the adipose tissue, which was not analytically determined. Adipose tissue is likely a large storage site for vitamin A in obese individuals. In fact, in a variety of adipose storage sites in rats with adequate vitamin A status, the mean retinol concentrations were relatively uniform between 6 and 7.1 μg/g fat (45). If a 120-kg obese individual has 40% body fat, this depot could represent 1 mmol of extra vitamin A not in the liver reserve. Considering the global obesity epidemic, this is certainly a point worthy of future investigation.

The use of isotope dilution in monitoring various interventions will be key considering the lack of sensitivity for other biomarkers in the excessive range of liver reserves (39). An example of this is the evaluation of the sugar fortification program in Nicaragua using the D-RID test (46), where 9 of the 21 children enrolled rose above 1.0-μmol/g liver, indicating hypervitaminosis A, 1 y after program implementation. Many foods are now being fortified across the globe, and continued monitoring is no longer only based on the prevalence of deficiency, but must now include the prevalence of excess (47). We look forward to the widespread use of the RID tests in the near future and encourage users to carefully state the equation adopted and the assumptions appropriate to the unique study or evaluation design.

Abbreviations

D-RID

deuterated retinol isotope dilution

“F”

efficiency of absorption and storage of an oral dose in the liver

F

isotope abundance

GC-CIRMS

gas chromatography–combustion isotope ratio mass spectrometry

RID

retinol isotope dilution

TBS

total body stores

TLR

total liver reserves

TTR

tracer-to-tracee ratio

¹³C-RID

¹³C-retinol isotope dilution