Scapulothoracic rhythm affects glenohumeral joint force

Abstract

Hypothesis

Musculoskeletal computer models provide valuable insights into shoulder biomechanics. The shoulder is a complex joint composed of glenohumeral, scapulothoracic, acromioclavicular, and sternoclavicular articulations, whose function is largely dependent on the many muscles spanning these joints. However, the range of patient-to-patient variability in shoulder function is largely unknown. We therefore assessed the sensitivity of glenohumeral forces to population-based model input parameters that were likely to influence shoulder function.

Methods

We constructed musculoskeletal models of the shoulder in the AnyBody Modeling System (AnyBody Technology, Aalborg, Denmark). We used inverse dynamics and static optimization to solve for glenohumeral joint forces during a simulated shoulder elevation. We generated 1000 AnyBody models by uniformly distributing the following input parameters: subject height, scapulohumeral rhythm, humeral head radius, and acromiohumeral interval.

Results

Increasing body height increased glenohumeral joint forces. Increasing the ratio of scapulothoracic to glenohumeral elevation also increased forces. Increasing humeral head radius and acromiohumeral interval decreased forces. The relative sensitivity of glenohumeral joint forces to input parameters was dependent on the angle of shoulder elevation. We developed an efficient method of generating and simulating musculoskeletal models representing a large population of shoulder arthroplasty patients. We found that scapulohumeral rhythm had a significant influence on glenohumeral joint force.

Conclusions

This finding underscores the importance of more accurately measuring and simulating scapulothoracic motion rather than using fixed ratios or average scapulothoracic motion. This modeling approach can be used to generate virtual populations for conducting efficient simulations and generating statistical conclusions.

Computational modeling and simulation of the human musculoskeletal system has potential for improving the diagnosis and treatment of many conditions that affect human mobility. These models can predict internal muscle forces and joint loads for a wide range of scenarios, from activities of daily living to high-performance or high-risk maneuvers. Internal muscle and joint forces are either difficult or impossible to measure experimentally but are important for biomedical development, especially in designing implants, planning rehabilitative treatment, and identifying areas of risk and failure.

Researchers have developed various shoulder models in the past and have used them to analyze the function of the shoulder girdle, to predict muscle actions, and to estimate joint forces. Previously reported computational models of the shoulder include the Delft Shoulder and Elbow model³¹ and its predecessor,⁴⁰ the Stanford-VA model¹⁸; the AnyBody model³⁴; the UK National Shoulder Model, previously known as the Newcastle Model⁵; the Swedish Shoulder Model¹⁷; and the Garner and Pandy model,¹¹ which was based on geometry from the Visible Human data set. For real-time simulation of forward dynamics, Chadwick et al⁴ used polynomials to approximate muscle lines of action and implicit methods for solving muscle forces.

Despite the potential relevance of shoulder models for patient care, these models have yet to be generally accepted in clinical settings, partly because of lack of confidence in the model's predictive capability.²⁸ In vivo measurements of glenohumeral joint loads now provide valuable experimental measurements for validation to improve the confidence in their models' predictive capabilities.² For the shoulder, it is particularly important to assess the robustness of the model to uncertainties in the inputs and assumptions. These model assumptions are not merely limited to variability in geometry or inertial parameters but are also present in the kinematics often prescribed in simulations.

Scapulothoracic kinematics are an important component of shoulder kinematics, but directly measuring scapular motion accurately in vivo is challenging and involves fluoroscopy²¹ or invasive methods, such as bone pins in the scapula.²⁷ Noninvasive methods, such as skin marker–based motion analysis, are not always accurate because of soft tissue artifact, especially during dynamic motion.²⁹ Consequently, most of the existing shoulder models rely on regression equations to prescribe scapular kinematics. These equations describe scapular motion as a function of thoracohumeral motion and are based on the average scapulohumeral rhythm measured in healthy subject populations.⁴³ The scapulohumeral rhythm is the ratio of the glenohumeral motion to the scapulothoracic motion.

The kinematics of the scapula are commonly prescribed as an input in simulations because predicting scapular motion is complicated and computationally challenging.¹⁷ However, scapular motion is highly variable even in normal subjects, and this variability is further compounded with fatigue.⁷ Potential errors in model assumptions (including scapular kinematics) can significantly influence the model outputs. An important aspect of model validation is the assessment of model robustness to variability in model assumptions. The goal of our study was to quantify the sensitivity of the shoulder model predictions, specifically the glenohumeral joint force, to important model input parameters. We therefore performed a sensitivity analysis using the AnyBody Modeling System (AnyBody Technology, Aalborg, Denmark) and evaluated the effects of variations in height, body mass, humeral head radius, acromiohumeral interval, and scapular motion on glenohumeral joint force. The results are valuable in identifying the importance of relevant model parameters that are most likely to affect the outputs of patient-specific shoulder models.

Materials and methods

Model development

A 3-dimensional rigid multibody musculoskeletal model of the shoulder (Fig. 1) was constructed using the AnyBody Modeling System. The model was based on the Dutch Shoulder Model.⁴⁰ Six segments were modeled: thorax, scapula, humerus, clavicle, ulna, and radius. The thorax was fixed to ground and the 6 segments were connected using 5 joints: the sternoclavicular, the acromioclavicular, the glenohumeral, the elbow, and the scapulothoracic joints. The sternoclavicular, acromioclavicular, and glenohumeral joints were modeled as spherical joints. The elbow joint was treated as a revolute joint. The scapulothoracic joint was modeled by constraining the inferior angle of the scapula and the point where the medial border and the spine of the scapula intersect to an ellipsoid approximating the rib cage.³⁹

Figure 1.

Computer rendering of AnyBody musculoskeletal model.

The following model parameters were computed using a uniform distribution varying between the ranges of 2 standard deviations about the average for each parameter. A base model was constructed to represent a subject with the average body weight of the senior surgeon's patient population (79 kg). The length and mass of each segment were computed on the basis of the subject's height and weight, respectively, using linear scaling (Table I). Scapulohumeral rhythm was defined as the ratio of glenohumeral elevation to scapulothoracic elevation. The scapulohumeral rhythm was varied from a rhythm with no scapular rotation to a ratio of 0.5:1, derived from fluoroscopic measurements.23, 41 Previously published measurements were also used to derive the ranges for humeral head radius3, 32, 35 and acromiohumeral interval.13, 36 The range for body height was obtained from 155 patients who underwent shoulder arthroplasty at the authors' institution. We generated uniform distributions that ranged from the minimum and maximum values listed in Table II.

Table I.

Scaling of body segments based on height and weight

	Base model	Upper arm mass	Lower arm	Scapula
Weight	79 kg	2.80%	1.60%	1.30%
Height (H)	1.7 m	0.211*H − 0.0642	0.1203*H − 0.0646	N/A

N/A, not applicable.

Table II.

Ranges of inputs for sensitivity analysis

Parameter	Minimum	Maximum
Scapulohumeral rhythm	No scapular rotation	1:2
Humeral head radius	20 mm	37 mm
Acromiohumeral interval	0 mm	25 mm
Body height	1.4 m	2 m

Seventeen muscles were represented by a total of 85 muscle elements in the model. Muscles that acted along a direct line of action between origin and insertion required no wrapping (eg, trapezius). For muscles that required wrapping, analytical surfaces such as spheres, ellipsoids, or cylinders were used to simulate the surface of the bone underlying the muscle.¹⁰ The latter group included the rotator cuff muscles as they wrapped around the humeral head.

Simulation approach

Inverse dynamics was used to compute muscle and joint reaction forces during a simulated shoulder elevation. Static optimization was used to minimize maximal muscle activation, where activations are defined as the ratio of the muscle force and maximum force proportional to the physiologic cross-sectional area of the muscle.⁸ Shoulder joint angles were computed using a coordinate system recommended by the International Society of Biomechanics.⁴²

Sensitivity analysis

We performed a sensitivity analysis to document how uncertainties in the different parameters of the shoulder model affect the computed glenohumeral joint reaction force. AnyBody saves model information in an easily editable XML file format. Using Python scripts, we generated a population of 1000 samples uniformly distributed across ranges listed in Table II. We computed the glenohumeral joint force during a simulated shoulder elevation. We normalized the value of each parameter to the mean value. We fit a linear model to the normalized values and computed the coefficients of regression. These coefficients quantified the sensitivity of glenohumeral joint force to each input parameter of interest.

Computer performance

The solution time for a total of 1000 AnyBody models was approximately 10 hours on a desktop PC containing a 6-core hyperthreaded Intel Xeon ES-1650 CPU with 64 GB RAM.

Results

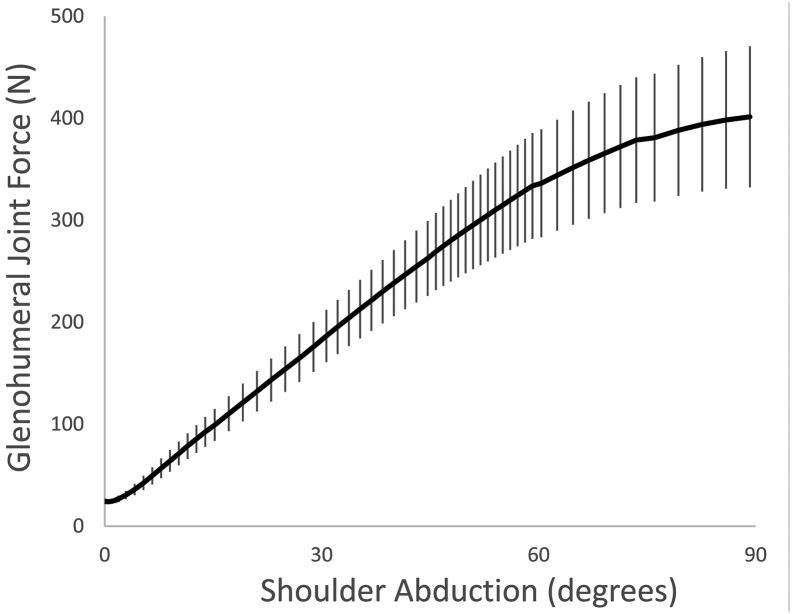
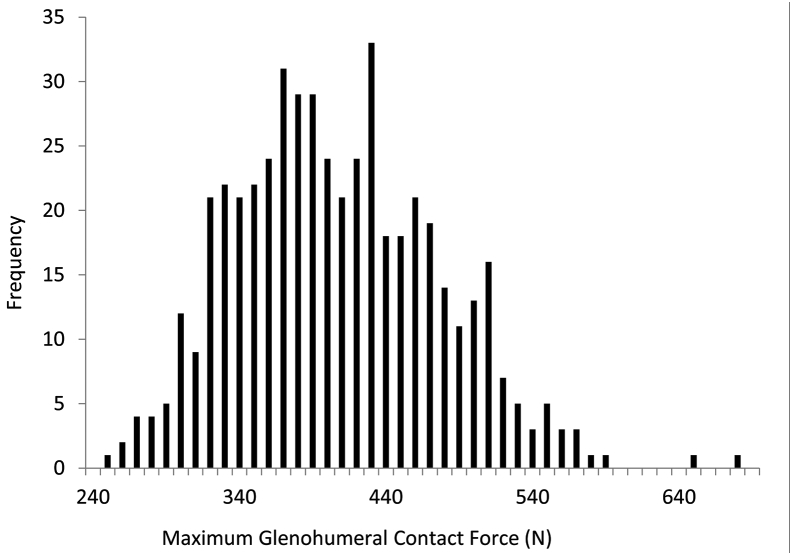
The peak joint force averaged over 1000 simulations was approximately 400 N (Fig. 2). Multiple linear regression analysis of glenohumeral joint force to scapulohumeral rhythm, subject height, size of humeral head, and distance between the acromion and humeral head generated a coefficient of determination (R²) averaging 0.82 (P < .0001) over the range of elevation. Although the input parameters were uniformly distributed, the predicted glenohumeral joint forces approached a more normal distribution (Fig. 3).

Figure 2.

Glenohumeral forces predicted by the shoulder model over the range of elevation. The solid line is the average; vertical bars are standard deviations for all values for the 4 input parameters (height, scapular motion, humeral head radius, and acromiohumeral interval).

Figure 3.

Frequency histogram showing the distribution of peak glenohumeral forces for the entire population of models. Each bar represents the corresponding magnitude of glenohumeral force ±10 N.

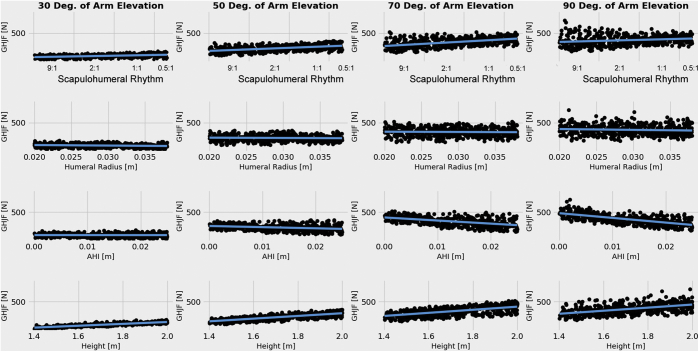
We performed linear regression to determine the sensitivity of glenohumeral force to each input parameter. We plotted the glenohumeral force against the range of each input parameter to determine the sensitivity at 30°, 50°, 70°, and 90° of elevation (Fig. 4).

Figure 4.

The range of the effect of each input parameter on joint force is depicted for different angles of arm elevation. Height and scapular humeral rhythm have the most effect on glenohumeral joint force (GHJF). Note that scapular elevation is 0 at the origin of the x-axis and that the entire shoulder elevation occurs at the glenohumeral joint. Humeral head radius and acromiohumeral interval (AHI) have a smaller negative influence on joint force.

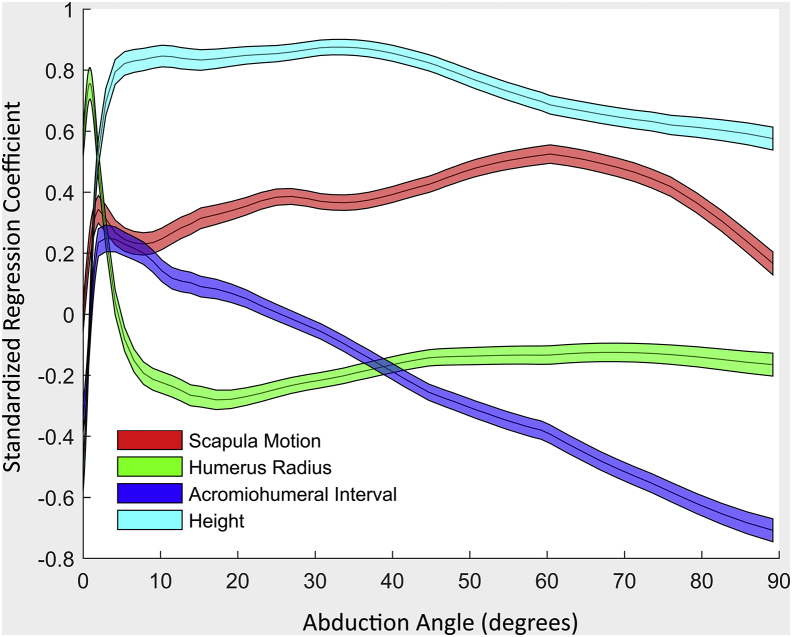
To depict this variation of sensitivity to input parameter and elevation angle, the individual regression coefficients were computed against elevation angle (Fig. 5). The wide variation reflects the dynamic nature of the biomechanics of arm elevation.

Figure 5.

The magnitude of regression coefficients representing the sensitivity of the glenohumeral contact force to each of the specified parameters varied with shoulder elevation angle. The range represents the 95th percentile confidence intervals for each shoulder elevation angle.

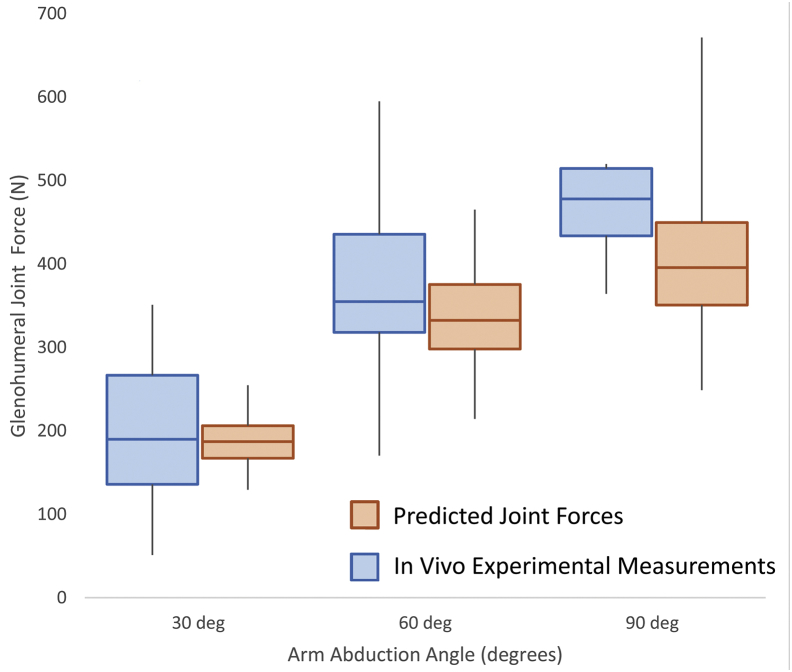
We also compared the range of predicted glenohumeral joint forces with in vivo measurements published for the same activity (Fig. 6)² (https://orthoload.com). The glenohumeral joint forces measured at 30°, 60°, and 90° were well within the ranges predicted for our model population.

Figure 6.

Box plot of glenohumeral forces at 30°, 60°, and 90° elevations, comparing predicted glenohumeral forces vs. those measured in vivo.

Discussion

The shoulder girdle is a highly complex musculoskeletal unit that requires the coordinated activation of dozens of muscles extending from the thoracic wall to the elbow. The scapula is a “floating” bone that is connected to the clavicle by the acromioclavicular joint and coracoclavicular ligaments. Scapular motion is controlled by the scapulothoracic and scapulohumeral muscles. Scapulohumeral rhythm (ratio of scapulothoracic motion to glenohumeral) is an important feature of shoulder function and is often disrupted with shoulder disease.³⁸ Restoring or optimizing scapulohumeral rhythm is important for shoulder function and a major goal in physical therapy and rehabilitation after injury, disease, or surgery. We therefore constructed shoulder models to simulate a population of virtual subjects to assess the effect of scapulohumeral rhythm on glenohumeral joint force and compared the magnitude of this effect relative to important anthropomorphic variables, such as height, size of the humeral head, and distance between the acromion and humeral head.

Overall, the subject's height had the strongest effect on glenohumeral joint force, presumably because of the direct association between bone length and external moment arms of body segments. This association is somewhat artificial as one expects that internal muscle moment arms increase with bone length, which tends to counter the effect of external moment arms. However, in the AnyBody Modeling System, changing the subject's height does not automatically change muscle attachment points.

Scapulothoracic motion had a significant influence on glenohumeral joint force with a coefficient of regression that was almost consistently high throughout the range of arm elevation. Commonly, scapulothoracic motion is modeled as a function of thoracohumeral elevation using mean values derived from healthy populations.⁴³ Scapula motion is highly variable even in normal subjects and is altered significantly in symptomatic shoulder disease.7, 21 Scapulothoracic motion is considered an important clinical factor, and restoration of normal kinematics is an important target for nonsurgical physical therapy and postoperative rehabilitation.³⁸ Our results indicate that accurate prediction of glenohumeral forces requires more careful measurements of scapulothoracic motion and simulation scapulohumeral rhythm in a manner relevant to the population of interest.

We expected reduction in muscle forces, and therefore joint forces, with increasing humeral head radius and acromiohumeral interval because both tend to increase muscle moment arms. We did find a small negative correlation (R² approximately 0.2) between glenohumeral joint force and humeral head radius over the range of shoulder elevation. Acromiohumeral interval also correlated negatively with glenohumeral joint force, but the slope and strength of the correlation varied, being the highest near 90° of arm elevation. This was likely because acromiohumeral interval maximizes muscle moment arm close to 90° of arm elevation.¹⁶ Acromiohumeral interval tends to decrease with severity of rotator cuff disease.14, 15, 20 An increase in joint force with loss of rotator cuff integrity might explain the increase in risk for glenohumeral arthritis in patients with rotator cuff tears.

Population modeling studies more often use a normal distribution to generate cohorts of computational models.24, 25, 26, 33 However, our primary objective was to identify the sensitivity of the joint force to relevant input parameters rather than to estimate the probability of statistical distribution of glenohumeral joint force. Using a normal distribution would tend to bias the inputs toward the mean value and compromise the regression analysis. We did find that the predicted glenohumeral joint force appeared somewhat normally distributed, presumably because of the combinations of input variables with opposite effects.

Improvements in computer CPU speeds, implementation of parallel computing, and software enhancements have greatly reduced the computational time needed for complex computer simulations. Computational modeling has therefore evolved from analyses of single models to subject-specific models and population analysis.1, 6, 12, 19, 30, 33 Subject-specific computer models can have clinical potential, for example, in predicting performance and outcomes in individual patients.9, 22, 30 Population models are valuable for generating large cohorts of virtual patients, simulating clinical studies, and permitting statistical analysis.1, 19 Population modeling was efficient in AnyBody; solving 1000 models took approximately 10 hours on a desktop computer. The Python scripting feature facilitated the automation of the generation, modification, and deployment of models and also enabled monitoring and analysis of the results, making it feasible to simulate large populations for statistical analysis. Although we used a desktop computer for simulation and analysis, high-performance computing clusters could easily be leveraged to replicate even larger virtual populations if needed.

One weakness of this study was the use of a relatively simple muscle model that did not include muscle force-length activation and contraction velocity. However, our objective was not to accurately simulate muscle activations but to determine sensitivity of glenohumeral joint force to model assumptions. The simpler muscle model works reasonably well for activities with low to moderate contraction velocities. Others have estimated the sensitivity of model output to muscle model parameters.²⁴ We also did not simulate glenohumeral contact; the glenohumeral joint was modeled as a spherical joint. Our interest was mainly on the magnitude of the joint force. The location of glenohumeral contact and the direction of the resultant force vector can be important in the biomechanical analysis of shoulder arthroplasty. Simulating contact is feasible in the AnyBody modeling by using the force-dependent kinematics feature.³⁷ However, implementing that feature significantly increased solution times. Direct validation of predicted muscle forces was not possible, so we compared the predicted glenohumeral joint forces with in vivo measured data with reasonable approximation. Finally, we did not simulate the effects of muscle weakness that can be due to age and disease.

Conclusions

We conducted a population analysis of the sensitivity of joint forces to relevant assumptions in a musculoskeletal model of the shoulder. We found that scapulothoracic motion had a significant influence on glenohumeral joint force. This finding underscores the importance of greater emphasis on more accurately measuring and simulating scapulothoracic motion rather than using regressions to represent average scapulothoracic motion. The advantage of this modeling approach using a virtual population is the feasibility of conducting rapid simulations and generating statistical data.

Disclaimer

The Shaffer Family Foundation provided research funding in support of this study.

The authors, their immediate families, and any research foundations with which they are affiliated have not received any financial payments or other benefits from any commercial entity related to the subject of this article.