The load dependence of muscle’s force-velocity curve is modulated by alternative myosin converter domains

Abstract

The hyperbolic shape of the muscle force-velocity relationship (FVR) is characteristic of all muscle fiber types. The degree of curvature of the hyperbola varies between muscle fiber types and is thought to be set by force-dependent properties of different myosin isoforms. However, the structural elements in myosin and the mechanism that determines force dependence are unresolved. We tested our hypothesis that the myosin converter domain plays a critical role in the force-velocity relationship (FVR) mechanism. Drosophila contains a single myosin heavy chain gene with five converters encoded by alternative exons. We measured FVR properties of Drosophila jump muscle fibers from five transgenic lines each expressing a single converter. Consistent with our hypothesis, we observed up to 2.4-fold alterations in FVR curvature. Maximum shortening velocity (v₀) and optimal velocity for maximum power generation were also altered, but isometric tension and maximum power generation were unaltered. Converter 11a, normally found in the indirect flight muscle (IFM), imparted the highest FVR curvature and v₀, whereas converter 11d, found in larval body wall muscle, imparted the most linear FVR and slowest v₀. Jump distance strongly correlated with increasing FVR curvature and v₀, meaning flies expressing the converter from the IFM jumped farther than flies expressing the native jump muscle converter. Fitting our data with Huxley’s two-state model and a biophysically based four-state model suggest a testable hypothesis that the converter sets muscle type FVR curvature by influencing the detachment rate of negatively strained myosin via changes in the force dependence of product release.

INTRODUCTION

Muscle fibers operate against variable resistive force (often referred to as load) while powering locomotion, similar to a manmade motor. For both motor types, the greater the force on a motor, the slower the velocity. However, a muscle’s response to force has an interesting characteristic that sets it apart from manmade motors. In a manmade motor, this relationship is typically linear, whereas in muscle fibers this relationship is hyperbolic. This means that, relative to a linear relationship, as the force on muscle increases, high velocities decrease more quickly and low velocities decrease more slowly. This inverse hyperbolic relationship between the force acting on a muscle and shortening velocity was first mathematically described by A. V. Hill in 1938 (21) with the equation:

$$\left(\text{F}+a\right)\left(v+b\right)=\left({\text{F}}_0+a\right)\left(b\right)$$ (1)

where F is the force on the muscle, F₀ is maximum isometric force, and v is shortening velocity. The parameter a was originally interpreted as shortening heat, and b the rate of energy liberation (21), but subsequent experiments showed that this interpretation of a and b is incorrect (20). Nevertheless, the equation remains an excellent phenomenological description. The ratio a/F₀ determines the curvature of the force-velocity relationship (FVR), where a higher a/F₀ value indicates a more linear, whereas a lower a/F₀ value indicates a more curved FVR.

Experiments and modeling have suggested that myosin molecules are at least partially responsible for the FVR being curved rather than linear. For example, Debold et al. (7) reproduced a hyperbolic FVR curve with a/F₀ similar to muscle fiber measurements, using only a small ensemble of myosin heads and actin in a laser trap. Models of muscle function suggest that myosin cross-bridges impart curvature to the FVR through the force dependence of their chemistry (i.e., mechanochemistry). The most famous of these models is that of A. F. Huxley (24), who reproduced a FVR curve by using a two-state cross-bridge model that included strain-dependent attachment and detachment rates (note that in this model cross-bridge strain is proportional to cross-bridge force). In contrast, models of muscle that do not include force-dependent rate constants produce linear FVRs (23, 27). Optical trapping results have shown that some rate constants of the cross-bridge cycle exhibit force dependence. For example, resistive forces slow ADP release, whereas assistive forces accelerate the rate of ADP release (18, 25, 37, 44). These studies show that force dependence exists at the myosin level but have not shown a causative link to the curved FVR.

Muscle fiber types differ in the curvature of their FVR and, therefore, in their a/F₀ values as well (3, 16). Slower mammalian fiber types generally have greater FVR curvature, but this correlation does not always hold, especially among faster fiber types (4), making the functional reasons for evolving differences in curvature not readily apparent. Determining how much of this fiber-dependent difference in curvature is due to myosin is difficult because many contractile protein isoforms differ between mammalian fiber types. Furthermore, the structural and kinetic mechanisms that cause myosin isoforms to impart different FVR curvatures are not known or have not been experimentally tested. Studies that change the myosin isoforms, while keeping the rest of the muscle fiber identical, would be ideal to answer these questions.

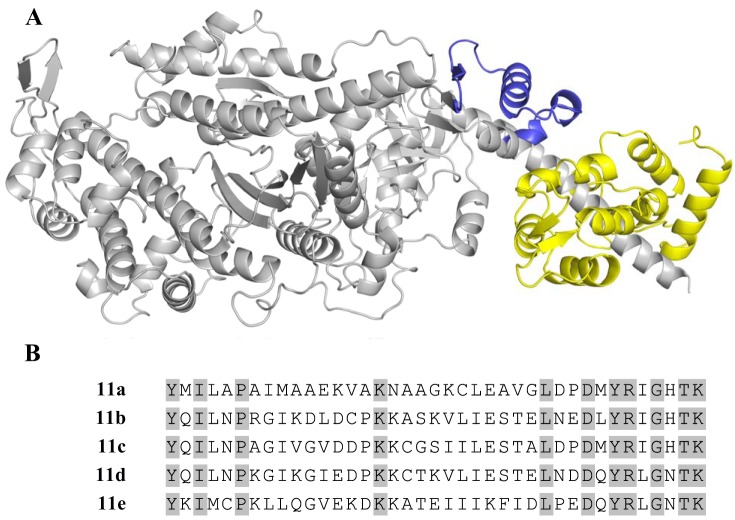
The Drosophila model system provides a unique opportunity to comprehensively and specifically test the effect of myosin isoform variation on muscle performance (36, 39, 40, 42, 48, 49). We can substitute different myosin isoforms and specific subdomains in a Drosophila muscle fiber, while keeping other proteins constant, by exploiting the alternative splicing mechanism by which myosin heavy chain (MHC) isoforms are generated in Drosophila muscles. The single muscle Mhc gene in Drosophila contains four alternatively spliced exons in the catalytic domain: exons 3, 7, 9, and 11. Previous experiments revealed that the converter subdomain has the largest impact on muscle and myosin properties of any of these alternative domains (39–41, 49). Because the converter had the largest impact of the four catalytic domains, we further investigated its influence by creating additional fly lines. The Drosophila converter domain, encoded by exon 11, has five alternatively spliced variants (a, b, c, d, and e; Fig. 1). The resulting transgenic fly lines express a single converter in the indirect flight muscle (IFM) and jump muscles (17). Sinusoidal analysis of the five converters in the IFM showed that they imparted a 2.2-fold range of muscle kinetics (e.g., frequency at which maximum power was generated) and a 2.8-fold range of maximum oscillatory power production and altered at least two rate constants of the myosin cross-bridge cycle (17).

Fig. 1.

The Drosophila myosin converter. A: Drosophila myosin S-1 fragment showing the exon 11 converter (blue) and essential light chain (yellow). The rest of the myosin heavy chain is gray. B: amino acid sequences of the 5 endogenous Drosophila converter domains, with 11 identical amino acids highlighted.

Based on the structure of myosin, we hypothesize that the converter is important for myosin’s force dependence and setting FVR curvature. The converter connects myosin’s catalytic domain with its lever arm, interfacing noncovalently with the relay helix and the essential light chain (ELC). This is a mechanically advantageous position for converting small motions in the catalytic domain into the larger motion of the lever arm (8, 22, 32) and, potentially, for sensing force. The converter might communicate force information (perhaps via intramolecular strain) back to the active site or alter other protein conformational changes that could modulate FVR.

The observed cross-bridge rate changes in myosin isoforms with different converters and the likely role of the converter in myosin’s force dependence suggested an opportunity to test FVR mechanistic hypotheses; however, the IFM is not an ideal muscle type to use for measuring FVR. Therefore, we instead used our Drosophila jump muscle, also known as the tergal depressor of trochanter muscle (TDT) preparation. This muscle preparation, with its high-force generation and long shortening excursions, enables the use of the force clamp technique to measure FVRs (12, 38). With this system, we measured FVR curves from force clamp experiments on Drosophila jump muscle fibers expressing five different converters. We found that the converter alters jump muscle FVR curvature. Fitting of our measurements with A. F. Huxley’s model (16, 24) suggests that the curvature changes are due to the converter altering the detachment rate of negatively strained cross-bridges (g₀). Similar analysis with the four-state model of Walcott et al. (46) suggests that this strained detachment rate is altered by the converter changing force-dependent product release rate. These results support our hypothesis that the converter is at least part of the force-sensing mechanism of myosin and that force sensing alters the shape of muscle FVR.

MATERIALS AND METHODS

Transgenic Drosophila Lines

The control fly line pwMhc2, which expresses the native 11c converter in the jump muscle, contains a wild-type myosin transgene expressed in Mhc¹⁰, a Drosophila line null for myosin (43), and is referred to here as TDT-11c. Four transgenic fly lines were previously created to each express a single converter (17) and are referred to here as TDT-11a, TDT-11b, TDT-11d, and TDT-11e, respectively. Flies were raised at 25°C on a 12:12-h light-dark schedule.

Jump Muscle Mechanics

Muscle fibers were prepared as previously described (12, 38). Briefly, the jump muscle was dissected from a 2- to 3-day-old female fly and chemically demembranated for 1 h. The jump muscle was pared down to six to eight large cell fibers and clipped on either end with aluminum t-clips with approximate final dimensions of 150 µm in length, 100 µm in width, and 50 µm in depth. The prepared fiber bundle was mounted on a mechanics rig between a piezo motor and a force transducer in relaxing solution [pCa (−log₁₀ of the calcium concentration) 8.0, 12 mM MgATP, 30 mM creatine phosphate, 600 U/ml creatine phosphokinase, 1 mM free Mg²⁺, 5 mM EGTA, 20 mM BES (pH 7.0), 200 mM ionic strength, adjusted with Na methane sulfonate, and 1 mM DTT] at 15°C and stretched to a starting sarcomere length of 3.6 µm. The fiber was transferred to pre-activating solution (relaxing solution with pCa 8.0 and no EGTA) for 2 min and then to activating solution (relaxing solution with pCa 5.0 and no EGTA). Isometric tension was measured once force plateaued. One force clamp was then performed (see next section) before the fiber was immediately returned to relaxing solution. The fiber was restretched to the original starting length and the process repeated for additional force clamps. Fibers that exhibited drops in isometric tension >10% during the first four force-clamps were discarded as well as any fibers unable to shorten at loads <5% of isometric tension.

Force-Velocity Relationship

To measure force-velocity properties, force clamps were conducted, starting with low force loads as previously described (Fig. 2) (12). Feedback from the force transducer determined the velocity at which the piezo motor shortened the fiber based on a preset force level. To generate a single force-velocity data point from each force clamp, the average velocity and average force from 5 to 13 ms was calculated, the earliest time after the start of shortening that force was reliably clamped. The force-velocity points were fit to Hill’s equation (Eq. 1). Twelve to 18 fibers for each line were individually fit to the equation using Microsoft Excel add-in Solver (Frontline Systems) to minimize the residual sum of squares.

Fig. 2.

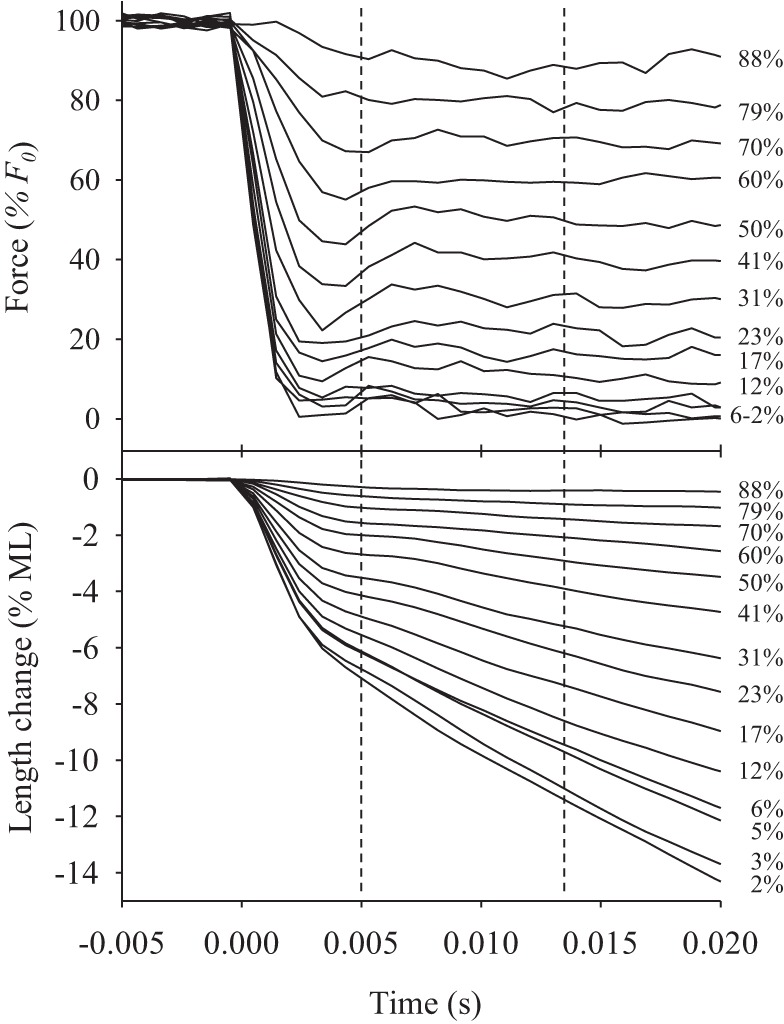
Force clamps. Representative force and length traces were generated while a force clamp experiment was performed on a tergal depressor of trochanter muscle (TDT)-11c jump muscle fiber. In this example, force clamps ranged from 2% to 88% of isometric force as indicated. Vertical dashed lines indicate the time window used to measure force and calculate velocity. F₀, maximum isometric force; ML, muscle length.

Fitting the Force-Velocity Relationship to Cross-Bridge Models

To gain insight into the molecular basis for observed differences in FVRs, we fit our measurements with two different cross-bridge models. The Huxley model (2-state model) is a simplified description of the interaction of myosin with actin, with force-dependent attachment and detachment rates whose mathematical form was likely motivated for mathematical simplicity (24). Like any simplified model, the Huxley model has the advantage of providing qualitative insight while being relatively insensitive to system details, but its disadvantage is a lack of quantitative insight into system details. The four-state model of Walcott et al. (46) is a more complex description of the interaction of myosin with actin, with force-dependent rates whose mathematical form was determined from comparisons with a wide array of actin motility and optical trapping measurements. Like any realistic model, the four-state model has the advantage of providing quantitative insight into system details while having the disadvantage of being sensitive to errors in modeling those details. By analyzing our measurements with both the Huxley and the four-state model, we can get the advantages of both modeling approaches while minimizing the disadvantages.

The Huxley model.

To fit the Huxley model to the data, we used a nondimensional version of Huxley’s force-velocity relationship (derived in appendix a):

$$\Psi =1-V\left[1-\text{exp}\left(-\frac{1}{V}\right)\right]\left[1+\left(\frac{T^{2}V}{2}\right)\right]$$ (2)

The nondimensional parameters in this equation are Ψ = F/F₀, measured force scaled by maximum isometric force; V = v/Φ, the experimentally measured shortening rate, v (in muscle lengths per second) scaled by Φ, which defines the time scale of attachment and detachment at positive cross-bridge strain (in inverse seconds; see appendix a); and t = Φ/Hg₀, Φ scaled by the product of H, the reach of a cross-bridge scaled by the average sarcomere length, and g₀, the time scale of detachment at negative cross-bridge strain (in inverse seconds). Φ is related to the slope of the attachment (df/dx = f₁) and detachment (dg/dx = g₁) rates at positive cross-bridge strain (x) in Huxley’s model by the equation Φ = (f₁ + g₁)h²/L_s, where h is the reach of the myosin head and L_s the sarcomere length (see Fig. A1 for schematic diagram depicting f₁ + g₁ and g₀). Because we measure F, F₀, and v during our force clamp experiments, this equation has two unknown parameters, Φ (required to determine V) and T. We determine these parameters by fitting Eq. 2 to our FVR measurements.

Fitting was accomplished by implementing Eq. 2 in Microsoft Excel add-in Solver (Frontline Systems). Φ and T were determined by minimizing the sum of the squared error. We ensured that our fits converged to a global optimum by testing several different initial values for Φ and T.

The four-state model.

Like the Huxley model, to fit the four-state model to the data, we used a nondimensional version of the force-velocity relationship (derived in appendix a):

$$\text{Ψ}=\frac{D{e}^{-D}\text{exp}\left(\frac{e^{-D}}{DV}\right)}{VD}\underset{-\infty }{\overset{1}{\int }}x\text{exp}\left(-\frac{e^{-Dx}}{DV}\right)dx$$ (3)

The nondimensional parameters in this equation are Ψ = F/F₀ (as in the Huxley model); V = vL_s/2d$k_D^0$ = vL_s/2ζ, the experimentally measured shortening rate, v (in muscle lengths per second) times the half-sarcomere length, L_s/2 (in nm), scaled by the power stroke size, d (in nm) times the ADP release rate in the absence of external force on myosin,$k_D^0$ (in inverse seconds); and D = κδd/k_BT, the product of myosin’s stiffness, κ (in pN/nm), the force-dependence of ADP release, δ (in nm), and power-stroke size, d, scaled by Boltzmann’s constant, k_B, times absolute temperature, T. Like the Huxley model, this equation has two unknown parameters: ζ (required to determine V, which is the measured velocity times the half sarcomere length divided by this parameter, V = vL_s/2ζ) and D. We determined these parameters by fitting Eq. 3 to our FVR measurements.

Fitting was accomplished by implementing Eq. 3 in Matlab, numerically evaluating the integral using global adaptive quadrature (Matlab’s integral function) and varying D and ζ to optimize the model fit to the data (using Matlab’s nonlinear optimization algorithm, fminsearch) by minimizing the sum of the squared error. We ensured that our fits converged to a global optimum by starting our optimization from a random initial guess for D and ζ and then testing several different initial values of D and ζ to make sure the same final values of D and ζ were obtained.

Jump Assay

Two- to three-day-old female flies were tested for jumping ability at 15°C (the same temperature at which the muscle mechanics were performed). The wings of the flies were removed while under CO₂ anesthesia and given at least 2 h to recover and acclimate to the testing temperature. Flies were prompted to jump by using a pen tip, and their jump distances were marked and measured on the testing paper. The longest three jumps out of 10 for each fly were averaged. Ten flies were tested from each line.

Statistical Analysis

The tests used to determine statistical significance are described in each figure caption and table legend along with sample number, age, and sex of the flies. Possible correlations between parameter values were tested by calculating Pearson’s r² values and a t-test to determine whether the best-fit regression line has a slope significantly different from zero.

RESULTS

FVR Curvature, Shortening Velocity, and Isometric Tension

We were able to perform the force clamp technique on jump muscle fibers from all fly lines to characterize their FVR. We consistently clamped the prescribed force, which stabilized within 5 ms from the start of shortening and was maintained for ≥15 ms (Fig. 2). Measuring the average velocity from 5 to 13 ms generated 14 points to create a force-velocity curve. Curves from all five lines displayed a hyperbolic shape of the FVR and were well fit by Hill’s equation (r² > 0.97 for all fibers; Fig. 3). FVR curves can deviate from a single-hyperbola shape, typically showing an inflection point in the high-strain region around 80% of isometric tension (9, 10). However, our current jump muscle FVR curves did not display this deviation, nor did our previous jump muscle FVR curves (12). Even if there is a slight deviation at high force that we did not detect with our measurements, the deviation likely does not differ between the five lines, because their independently measured isometric tension values were not significantly different (Fig. 5).

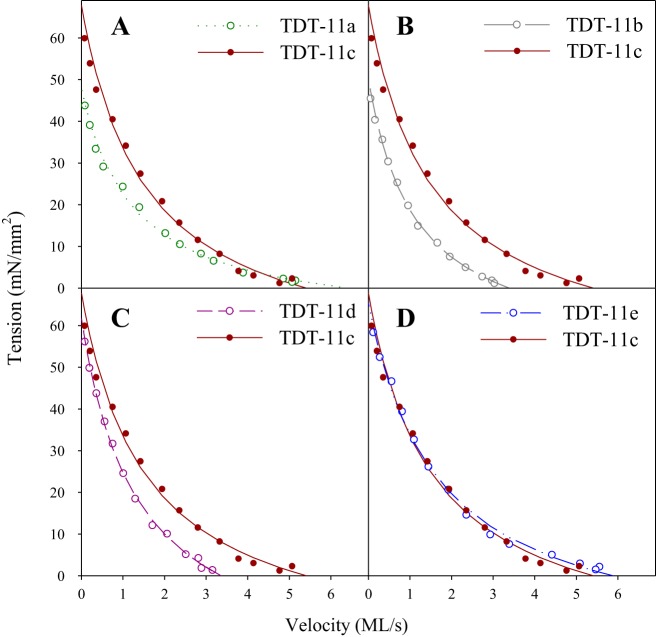
Fig. 3.

Representative force-velocity relationships (FVR). A–D: comparison of representative FVR curves for performed on a tergal depressor of trochanter muscle (TDT)-11c and TDT-11a (A), TDT-11b (B), TDT-11d (C), and TDT-11e (D). The raw data used to generate the TDT-11c curve is shown in Fig. 2. Lines are fits generated using Hill’s equation, which have r² values of 0.994, 0.997, 0.989, 0.998, and 0.996 for TDT-11a, TDT-11b, TDT-11c, TDT-11d, and TDT-11e, respectively.

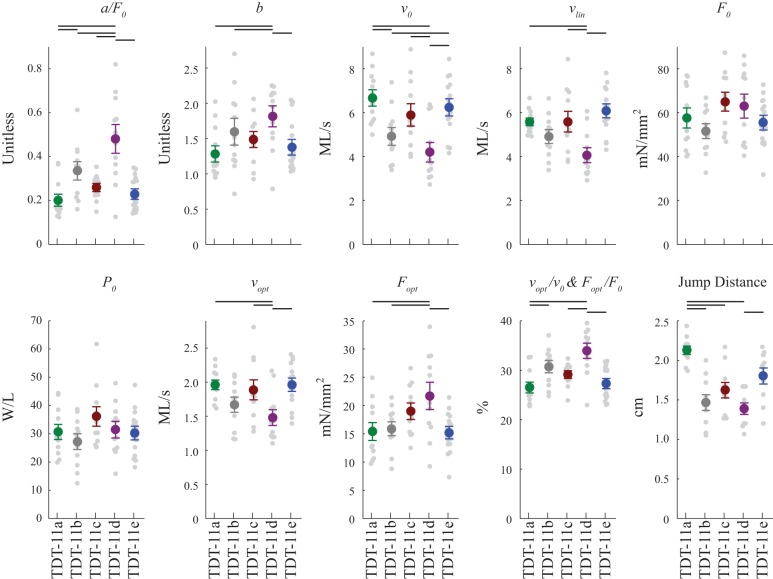
Fig. 5.

Drosophila jump muscle mechanical properties and jump distances. Force-velocity relationship (FVR) parameters were measured using the force-clamp technique and fit using Hill’s equation. a/F₀ is inversely proportional to FVR curvature. The higher the value the more linear the FVR; b is a fit parameter; v₀ is maximum shortening velocity, v_lin is maximum shortening velocity determined by extrapolation to zero force using the four fastest velocities, F₀ is isometric tension measured immediately before each force-clamp, P₀ is maximum power generated, v_opt is the velocity at which maximum power was produced, F_opt is the tension at which maximum power was produced, v_opt/v₀ and F_opt/F₀ are optimal velocity and optimal tension normalized to maximum velocity and isometric tension, respectively. Note that v_opt/v₀ and F_opt/F₀ are algebraically equivalent and have been previously referred to as M (15, 47). Jump distance was measured using flies with their wings removed. Colored circles are means ± SE, with each data point shown by a gray dot. The number of fibers used was 13, 12, 12, 12, and 18 for tergal depressor of trochanter muscle (TDT)-11a, TDT-11b, TDT-11c, TDT-11d, and TDT-11e, respectively. Fibers were from 2- to 3-day-old female flies. Black horizontal bars indicate significant difference between lines by one-way ANOVA followed by Holm-Sidak pairwise comparisons with P < 0.05.

Our force-velocity experiments showed that the converter can alter the degree of curvature of the FVR curve, as indicated by the 2.4-fold range of a/F₀ values (Figs. 4B and 5). TDT-11a fibers displayed the lowest a/F₀ (most curved FVR), 23% lower than the control TDT-11c fibers, whereas TDT-11d fibers displayed the highest a/F₀ (most linear FVR), 85% higher than the control. The relative order of a/F₀, from highest to lowest, was TDT-11d ≥ TDT-11b ≥ TDT-11c ≥ TDT-11e ≥ TDT-11a, with the fiber types that are statistically significant from each other indicated in Fig. 5.

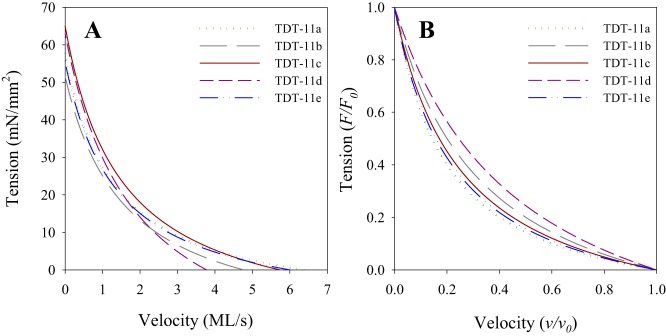
Fig. 4.

Average force-velocity relationships (FVR). A: FVR for all 5 converter lines generated using averaged parameters derived from fitting Hill’s equation to the FVR data from each individual fiber. B: force-velocity curves from A normalized to maximum isometric tension and maximum velocity to better show differences in FVR curvature. The number of fibers used was 13, 12, 12, 12, and 18 for tergal depressor of trochanter muscle (TDT)-11a, TDT-11b, TDT-11c, TDT-11d, and TDT-11e, respectively. Fibers were from 2- to 3-day-old female flies.

Maximum shortening velocity (v₀) was determined by extrapolating the fit of the individual FVR curves for each fiber to zero load. The velocities showed several statistically significant differences (Figs. 4A and 5). TDT-11a fibers displayed the fastest v₀, while fibers expressing 11d displayed the slowest v₀, a 28.8% decrease relative to control TDT-11c fibers. The relative order of v₀ was the exact opposite of a/F₀, that is, the fibers with the greatest degree of curvature had the highest maximum shortening velocity. From fastest to slowest the order of v₀ was TDT-11a ≥ TDT-11e ≥ TDT-11c ≥ TDT-11b ≥ TDT-11d, with a 1.6-fold range. A second method of determining maximum shortening velocity, extrapolating the linear regression of only the four fastest force-velocity points to F = 0 (v_lin), produced similar results as fitting the entire curve. v_lin showed a 1.5-fold range and a relative order of TDT-11e ≥ TDT-11c ≥ TDT-11a ≥ TDT-11b ≥ TDT-11d (Fig. 5). Isometric tension (F₀), measured immediately before performing the first force-clamp of each fiber, was not statistically significant different between any of the lines (Figs. 4A and 5).

Power Generation

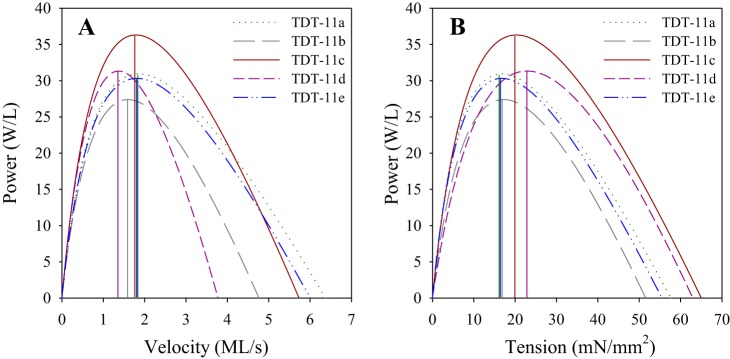
We found no statistically significant differences in maximum power (P₀) between the five lines (Figs. 5 and 6). However, optimal velocity for maximum power generation (v_opt) and optimal tension for maximum power generation (F_opt) displayed some significant differences (Figs. 5 and 6). Fibers expressing 11d displayed the slowest v_opt, a 20.4% decrease relative to control TDT-11c fibers. The relative order of v_opt, from fastest to slowest, was the same as v₀: TDT-11a ≥ TDT-11e ≥ TDT-11c ≥ TDT-11b ≥ TDT-11d, with a 1.3-fold range. In addition to the slowest v_opt, TDT-11d fibers displayed the highest F_opt. F_opt had a 1.4-fold range and relative order, from highest to lowest, of TDT-11d ≥ TDT-11c ≥ TDT-11b ≥ TDT-11e ≥ TDT-11a. Relative optimal velocity, v_opt/v₀, and relative optimal tension, F_opt/F₀, reported as percentages of their respective maxima, displayed the inverse order as v_opt and v₀ (Fig. 5).

Fig. 6.

Power generation. Power curves for all 5 converter lines plotted against velocity (A) and tension (B) to show maximum power-generating ability (P₀), optimal velocities (v_opt), and optimal tensions (F_opt) for maximum power generation. Vertical lines indicate v_opt and F_opt. The number of fibers used was 13, 12, 12, 12, and 18 for tergal depressor of trochanter muscle (TDT)-11a, TDT-11b, TDT-11c, TDT-11d, and TDT-11e, respectively. Fibers were from 2- to 3-day-old female flies.

Huxley Model Fits

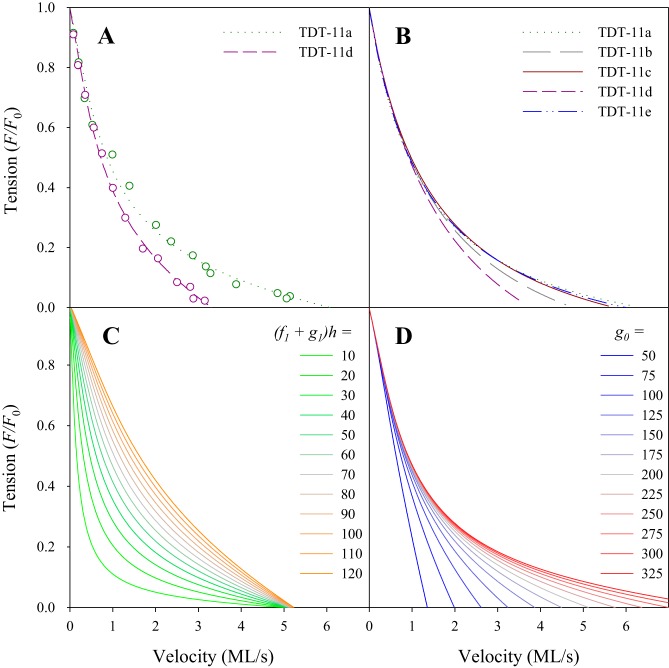
To gain insight into the molecular basis for the converter-dependent differences in FVR curvature, we fit our FVR data to two cross-bridge models. The first equation is from Huxley’s 1957 two-state model (Eq. 2; representative fits shown in Fig. 7). The equation has two unknown parameters: 1) the time scale of attachment and detachment at positive strain: Φ = (f₁ + g₁)h²/L_s, which is required to determine V = v/Φ in Eq. 2 from the measured shortening velocity, v, where f₁ and g₁ are the slope of attachment and detachment rates at positive strain, h is the reach of a cross-bridge, and L_s is the sarcomere length; 2) the time scale at positive strain relative to the time scale at negative strain, T = (f₁ + g₁)h/g₀, where g₀ is the detachment rate at negative strain (see appendix a). The fits show no significant differences in Φ across the five lines (Table 1). In contrast, T values varied significantly across the five lines, showing a 1.6-fold range, with the relative order of TDT-11a ≤ TDT-11e ≤ TDT-11c ≤ TDT-11b ≤ TDT-11d. This order correlates well with FVR curvature, a/F₀ (R² = 0.96 and P = 0.0002). Given a constant cross-bridge reach, h, combined with the observation that Φ is not different between the different converters, the variation in T must arise from converter-dependent differences in the detachment of negatively strained cross-bridges, g₀.

Fig. 7.

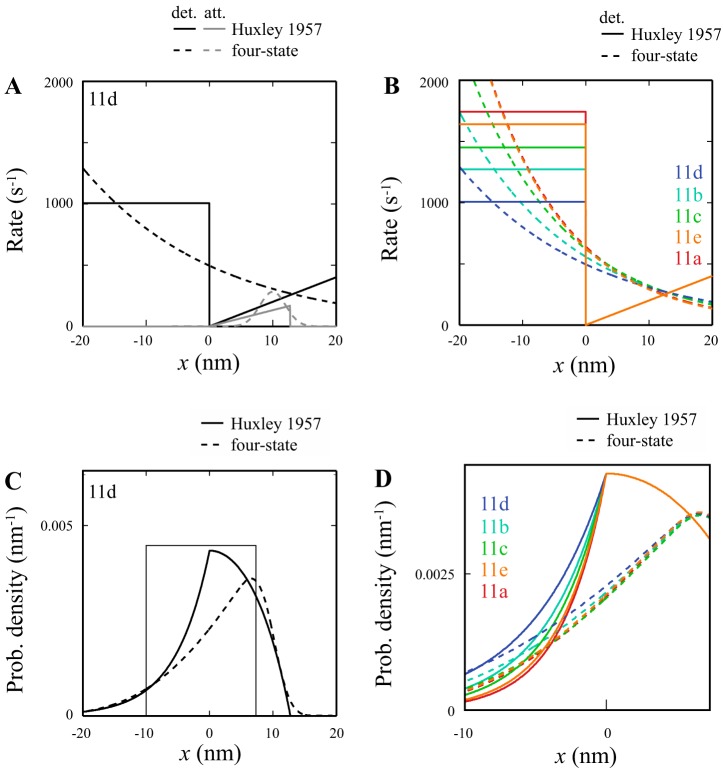
The converter primarily influences the detachment rate at negative strain (g₀). A: Eq. 2, derived from Huxley’s 1957 model, was fit to individual force clamp points (circles). Representative fits for the most curved tergal depressor of trochanter muscle (TDT)-11a and least curved TDT-11d force-velocity relationships (FVR) are shown (same fibers as Fig. 3); r² values were 0.988 and 0.996, respectively. B: FVR of the 5 converter lines fitted with average parameters from Eq. 2. Tension did not vary significantly between any of the 5 converter lines (see Fig. 5) and is thus normalized to maximum isometric tension for illustrative purposes. C: FVR derived by substituting a range of (f₁ + g₁)h values, 10 to 120 s into Eq. 2; g₀ is set to 200 s, approximately the average of the 5 converter fiber types. Tension is normalized to maximum isometric tension. D: FVR derived by substituting a range of g₀ values, 50–325, into Eq. 2; (f₁ + g₁)h is set to 60 s, approximately the average of the 5 converter fiber types. Tension was normalized to maximum isometric tension.

Table 1.

Huxley model parameters

	Φ, s−1	T	(f1 + g1)h, s−1	g0, s−1
TDT-11a (n = 13)	1.45 ± 0.07	0.243 ± 0.018b,d	57.91 ± 2.78	244.2 ± 10.2b,d
TDT-11b (n = 12)	1.54 ± 0.12	0.333 ± 0.024a,d	61.74 ± 4.60	189.2 ± 12.5a,e
TDT-11c (n = 12)	1.59 ± 0.10	0.292 ± 0.014d	63.49 ± 3.97	221.4 ± 16.4d
TDT-11d (n = 12)	1.57 ± 0.29	0.421 ± 0.034a,b,c,e	62.79 ± 11.7	159.3 ± 14.0a,c,e
TDT-11e (n = 18)	1.50 ± 0.06	0.258 ± 0.014d	60.17 ± 2.52	240.5 ± 10.8b,d

Values are means ± SE; n = no. of fibers fitted to the equation. Cross-bridge rate constants were derived from fitting our jump muscle force-velocity data to Eq. 2. All lines were fit well by the equation r² > 0.97 for all fibers. For the mathematical definitions of Φ and T, see appendix a. To obtain (f₁ + g₁)h and g₀ from Φ and T, we used an H (h scaled by sarcomere length, L_s, H = h/L_s) value of 0.025 based on the value used by Gilliver et al. (16) (see materials and methods for equations relating Φ and T to (f₁ + g₁)h and g₀). We also presumed that reach does not vary between the 5 myosin isoforms.

^a,b,c,d,eSuperscripted letters indicate significant difference between fiber types by one-way ANOVA, followed by Holm-Sidak pairwise comparisons with P < 0.05.

f₁, attachment rate of detached myosin; g₁, detachment rate of positively strained attached myosin; g₀, detachment rate of negatively strained attached myosin; Φ, time scale of attachment and detachment at positive cross-bridge strain; T, detachment at negative strain.

Four-State Model Fits

The second equation we fit to our data is from a biophysically based four-state model (Eq. 3; representative fit shown in Fig. A4). Like the Huxley model, this model has two unknown parameters, ζ and D. The parameter ζ, a characteristic velocity scale needed to find nondimensional velocity, V, in Eq. 3 from the measured velocity, v, is defined as myosin’s power stroke size, d, times unloaded ADP release rate,$k_D^0$; the parameter D is the product of myosin’s stiffness, κ, the force dependence of ADP release, δ, and power stroke size scaled by Boltzmann’s constant, k_B, times absolute temperature, T. Both ζ and D varied between the five converter lines in relative order, from highest to lowest, of TDT-11a ≥ TDT-11e ≥ TDT-11c ≥ TDT-11b ≥ TDT-11d. This order is identical to g₀ in the Huxley model and correlates well with FVR curvature (r² = 0.98 and P = 0.001 for ζ, and r² = 0.95 and P = 0.005 for D). Interpretation of the parameters ζ and D is simplified by assuming a 10-nm power stroke (14, 19) that does not differ between the five converter lines. We justify this assumption by noting that lever arm length is unchanged in the different isoforms, and no difference in power stroke size was observed between myosins TDT-11a and TDT-11d (28). We divide ζ by 10 nm to obtain unloaded ADP release rate, $k_D^0$. Rates for the five converter lines ranged from 495 to 640 s⁻¹, a 1.3-fold range, but only TDT-11d was significantly different from TDT-11a, TDT-11c, and TDT-11e (Table 2). Changes in D are attributable to changes in the product of myosin stiffness and the force dependence of ADP release (given a constant power stroke size). Values of D spanned a larger range, 1.6-fold, and displayed more significant differences than $k_D^0$ (Table 2). Thus, in the four-state model, the converter alters FVR curvature by varying myosin stiffness and/or the force dependence of ADP release.

Table 2.

Four-state model parameters

	ζ (103 nm/s)	$k_D^0$, s−1	D
TDT-11a (n = 13)	6.40 ± 0.17d	640 ± 17d	0.76 ± 0.03b,d
TDT-11b (n = 12)	5.57 ± 0.28	557 ± 28	0.57 ± 0.04a,e
TDT-11c (n = 12)	6.20 ± 0.39d	620 ± 39d	0.66 ± 0.02d
TDT-11d (n = 12)	4.95 ± 0.30a,c,e	495 ± 30a,c,e	0.48 ± 0.05a,c,e
TDT-11e (n = 18)	6.27 ± 0.20d	627 ± 20d	0.71 ± 0.02b,d

Values are means ± SE; n = no. of fibers fitted to the equation. Parameters were derived from fitting the force-velocity data to the four-state model (Eq. 3). All lines were well fit by Eq. 3 (r² > 0.97 for all fibers). ζ is defined as myosin’s power stroke size (d ) × unloaded ADP release rate, $k_D^0$. $k_D^0$ is derived from ζ by assuming a 10-nm power stroke size for all 5 converters. The parameter d is the product of myosin’s stiffness (κ) the force dependence of ADP release (δ), and power-stroke size scaled by Boltzmann’s constant (k_B) × absolute temperature (T) (see results and appendix a for more detail).

^a,b,c,d,eSuperscripted letters indicate significant difference between fiber types by one-way ANOVA, followed by Holm-Sidak pairwise comparisons with P < 0.05.

Jumping Distances

All fly lines were able to jump an average distance of ≥1.25 cm (Fig. 5). TDT-11a fibers exhibited the farthest jump distance, significantly farther than TDT-11b, TDT-11c, and TDT-11d flies. TDT-11d flies jumped the shortest distance, i.e., only 65% of the distance of TDT-11a flies. The relative order of jumping distance, from farthest to shortest, was TDT-11a ≥ TDT-11e ≥ TDT-11c ≥ TDT-11b ≥ TDT-11d, the same order as v₀ (from fastest to slowest) and FVR curvature (most curved to least curved).

DISCUSSION

The main goal of this study was to test our hypotheses that the converter is part of the force-sensing mechanism in muscle, and myosin’s force dependence sets the curvature of FVRs. In support of these hypotheses, our results show that the converter influences FVR curvature, as we observed differences in a/F₀ that varied over a 2.4-fold range (Fig. 5). This range is comparable with previous a/F₀ measurements made on different mouse fiber type fibers from inferior rectus, EDL, diaphragm and soleus muscles (2-fold) (29), rat fibers from EDL and soleus (1.8-fold) (4), and human fibers, which are classified as type I through type IIB based on MHC isoform (2.2-fold) (3). Although the mechanisms for these variations in a/F₀ are not known, because our study shows the same range of a/F₀ values, it is possible that changing the converter alone in these mammalian fiber types could be enough to account for their variation in FVR curvature.

However, our results do not definitely show whether the mechanism by which the converter is altering FVR curvature is based on myosin’s force dependence. For example, an alteration to the jump muscle myofilament architecture may have occurred as a result of expressing other converters in the jump muscle that may have influenced our experimental results. However, we think this is unlikely, because we previously found that these five myosins did not alter the myofilament ultrastructure of IFM (17). In general, we find that Drosophila myosin mutants disrupt the structure of the jump muscle less than IFM. For insight into possible ways that changes to the myosin cross-bridge cycle might be altering the FVR, we turn to our modeling results.

Converter Influences FVR Curvature by Altering Detachment Rate of Negatively Strained Myosin Heads

The FVR data for the five converters were well fit by the Huxley 1957 model (Eq. 2; representative fits shown in Fig. 7A). These fits revealed no significant differences in the time scales of attachment and detachment of positively strained cross-bridges, Φ. However, we observed significant differences in the ratio of that time scale to the time scale of detachment of negatively strained cross-bridges, T (Table 1). These differences are highly correlated with the observed converter-dependent differences in FVR curvature. Taken together, these results suggest that a potential molecular mechanism for our observations is that the converter affects the detachment rate of negatively strained cross-bridges, g₀. That is, changes in the converter that increase g₀, such as 11a, result in more curved FVRs, whereas those that decrease g₀, such as 11d, result in more linear FVRs.

In the Huxley model, g₀ affects FVR curvature because the population of negatively strained cross-bridges is dependent on velocity. At zero velocity, there are no negatively strained heads, and thus force is independent of g₀. As velocity increases, the population of negatively strained cross-bridges increases, and g₀, their detachment rate, exerts a greater influence on force. The larger the g₀ value, the fewer negatively strained cross-bridges bind, and thus the greater the force; this results in a more curved FVR (Fig. 7D). Note that in the Huxley model, changing g₀ is not the only way to modify FVR curvature. If the converter instead altered the kinetics of positively strained cross-bridges (i.e., Φ or f₁ + g₁), then FVR curvature would change without modifying maximum shortening velocity (Fig. 7C). Instead, the influence of g₀ is apparent when the similarities between Fig. 7, B and D, are observed. This altered detachment rate of negatively strained cross-bridges supports our hypothesis that the converter affects myosin’s force-sensing ability because, in the Huxley model, these effects occur only when individual cross-bridges experience negative forces. Our analysis with the four-state model provides further support for this result and a connection to myosin’s mechanochemistry.

Like the Huxley model, the four-state model (Eq. 3) gives good fits to the FVR data for the five converters (Fig. A4). Assuming a constant power stroke size, these fits revealed differences in both unloaded ADP release rate, $k_D^0$, and the product of myosin stiffness and the force dependence of ADP release, κδ (proportional to D in Table 1 because the other components of D are constants), with the latter difference both being larger and showing more significant differences (Table 2). With a few assumptions (see appendix b), we can compare both the attachment/detachment rates and the distribution of strain in bound cross-bridges for the Huxley and four-state models. One clear result of this comparison is that, to fit the FVRs of the different myosin isoforms, both models alter curvature by changing the detachment rate of negatively extended myosin. In the Huxley model, fitting the different FVRs is accomplished by changing g₀ (Table 1 and Fig. 7), whereas in the biophysically detailed model, fitting the different FVRs is accomplished by changing D (Table 2 and Fig. B1B). However, the end result is the same; the converters alter FVR by changing the binding probability density when myosin is under negative strain (Fig. B1D).

In the four-state model, it is differences in the product of myosin stiffness and the force-dependence of ADP release, κδ, that cause negatively strained cross-bridges to detach. The dependence is exponential, so that relatively small differences lead to large effects (Fig. B1B). Thus, compared with the linear dependence in detachment given by $k_D^0$, we expect this effect to be dominant. Therefore, we conclude that, in the four-state model, the primary effect of the converter is either a change in myosin stiffness, κ, and/or the force dependence of ADP release, δ.

Evidence that the Converter Affects Myosin’s Force-Dependence

From fits to the FVR data alone, we cannot distinguish between changes in myosin stiffness or force dependence. However, our isometric force measurements suggest that differences in force dependence, and not stiffness, are the primary cause of the different FVRs between the five converter lines. It is generally accepted and included in both the Huxley and the four-state models that isometric force is proportional to myosin stiffness (isometric force is the product of myosin’s stiffness, average strain while bound to actin, and myosin’s probability of being bound to actin) (33). Thus, if the differences in FVR arise from changes in myosin stiffness, isometric force should vary between the five converter lines. Specifically, based on the four-state model, we would expect to see a twofold difference in isometric force between TDT-11d and TDT-11a myosins (Fig. C1). However, we did not see a significant change in isometric force (Fig. 5). Rather, the major differences between the five converter lines occurred at high velocities, i.e., when a high number of myosins are undergoing negative strain and thus most likely to be influenced by myosin’s force dependence. A mathematical version of this argument is presented in appendix c. In appendix d, we discuss whether our interpretation would change if ADP was not the rate-limiting step, as is presumed to be the case in the four-state model.

Although we think it is more likely that the converters in this study are altering myosin’s force dependence rather than stiffness, we do not mean to imply that the converter cannot change myosin stiffness. Köhler et al. (26) and Seebohm et al. (33) showed that HCM point mutations in the converter alter myosin stiffness and isometric force generation. Of the three mutations they investigated, two increased myosin stiffness and muscle force production (723 and 716), and one showed no change in stiffness or isometric force generation; 723 showed a minor increase in v₀, and 716 slightly increased fiber ATPase rate. These results differ from our current study in that we found no significant differences in isometric force, but more substantial changes in v₀, plus substantial differences in ATPase rates were previously observed for two of these myosins (30). Furthermore, our previous work with these five Drosophila converters in IFM showed that the converter can alter at least two rate constants of the cross-bridge cycle (17). Taken together, these results suggest that multiple mechanisms exist by which the converter can alter muscle mechanical properties.

FVR Relevance to Jumping

To test whether the FVR alterations caused by the different converters produce physiologically relevant changes at the organismal level, we measured fly jumping performance. Surprisingly, not only did we observe significant differences between the fly lines, but replacing the native jump muscle myosin converter isoform (11c) with the IFM (11a) converter increased jump distance. Comparing jump distance with FVR parameters reveals that distance strongly correlated with the degree of FVR curvature, a/F₀, and maximum shortening velocity, v₀, but did not correlate with maximum power or the frequency at which maximum power was generated, v_opt. The best correlation was with v₀ (r² = 0.84 and P = 0.028). This result is consistent with our previous work that also showed a strong positive correlation between v₀ and jump distance (12).

FVR Relevance to Muscle Function

The FVR properties of the five converter fiber types generally agree with the physiological demands of the Drosophila muscle types in which the converters are found. The jump muscle’s primary function is to power takeoff for flight using a very rapid shortening contraction. Evolutionary pressure has presumably pushed the jump muscle to make takeoffs occur as fast as possible to avoid predators and perhaps maximize jump distance (6). A relatively high maximum shortening velocity, high v_opt, and a high degree of curvature help it achieve this. To understand how higher curvature helps, one should focus on the high-velocity portion of the FVR curve. In the high-velocity portion of the FVR, high curvature results in large increases in shortening velocity for small decreases in load. As the fly jumps and starts to launch its body into the air, the high curvature of the jump muscle’s FVR allows the muscle velocity to accelerate quickly to a high maximum velocity. Maximum velocity at takeoff would maximize jump distance and how fast the fly is moving during the initial tumbling phase of the escape response (6).

The converter found in the flight muscle, 11a, has evolved for a different type of contractility pattern, but it also functions under relatively low loads. Instead of one shot shortening, asynchronous IFM undergoes the fastest known lengthening and shortening contraction cycles of any muscle type, 175 Hz for Drosophila IFM at 15°C, to power wing beating (40). However, when held isometric at high calcium, the muscle generates very little tension. Low tension helps enable high speed and is probably part of IFM’s adaptations to minimize resistive load during the lengthening portion of its contractile cycle (42). This high-speed approach qualitatively matches TDT-11a exhibiting the fastest shortening velocity and highest v_opt and lowest f_opt. The reason for TDT-11a having the most curved FVR may be similar to that described for jump muscle, because both are high-speed low-force muscles. However, the IFM uses a sinusoidal contraction pattern, and thus we would likely need to measure the negative velocity portion of its FVR to understand fully the implications of TDT-11a’s FVR.

TDT-11d fibers exhibited the highest optimal tension for maximum power, F_opt, and highest F_opt/F₀, but low v_opt and the slowest maximum shortening velocity, v₀. These results agree with 11d’s function in embryonic and larval body wall muscles of Drosophila. These muscles produce slow, sustained cyclical contractions for crawling on or through food sources.

Relating converter 11b to its source muscle characteristics is difficult because 11b has not been localized to a specific muscle type. 11b was detected in an embryonic cDNA screen, but in situ hybridization failed to reveal its exact muscle location (50). Jump muscle fibers expressing 11b displayed average values out of the five fiber types measured in this study for most FVR properties. 11b values most closely matched 11d which makes sense because 11d is also found in embryonic muscles. One should note that adult muscle types have not been screened as thoroughly as the embryonic muscles. Thus, 11b and the other converters may also be expressed in some of the adult muscles such as head, abdominal muscles and heart muscles.

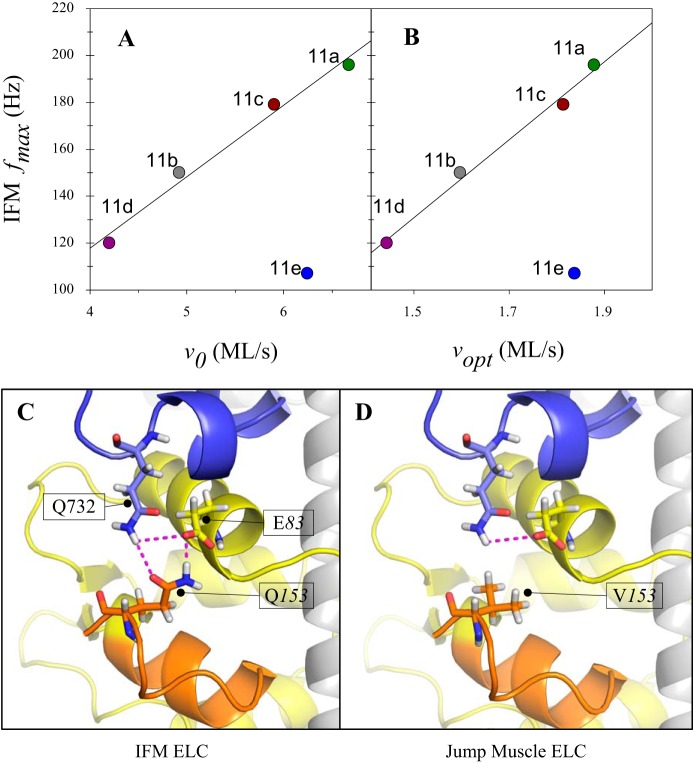
Surprisingly, jump muscle fibers expressing 11e, which is found in the relatively slow embryonic, larval, and pharyngeal muscles, displayed FVR properties most similar to the fast TDT-11a fibers rather than fibers expressing other embryonic converter versions. Another surprising aspect of the 11e converter was that its relative impact on jump muscle mechanics differed from its relative impact on IFM muscle mechanics. We previously expressed these same five Drosophila myosins in the IFM (17), and the results in IFM for all of the converters, except for 11e, strongly correlated with our current jump muscle mechanical results (Fig. 8, A and B). In contrast with the other embryonic converters, expression of the 11e containing myosin in the IFM slowed muscle kinetics, e.g., f_max, relative to the native IFM isoform control, whereas its expression in the jump muscle increased or did not change muscle kinetics, e.g., v₀ and v_opt, relative to the native jump muscle isoform control (Fig. 8, A and B).

Fig. 8.

Mechanism for converter 11e’s different influence on indirect flight muscle (IFM) contraction speed compared with jump muscle shortening velocity. A: IFM frequency at which maximum power was generated (f_max) vs. jump muscle maximum shortening velocity (v₀; r² = 0.98 and P = 0.008, excluding 11e). B: IFM f_max vs. jump muscle optimal velocity for power production (V_opt; r² = 0.97 and P = 0.005, excluding 11e). C: interaction of the exon 11e converter (blue) and the ELC (yellow, variable domain in orange). The IFM isoform of the ELC is shown, with Q153 and E83 of the ELC interacting strongly with Q732 of the 11e converter. D: the non-IFM isoform of the ELC (found in the TDT and other muscles) is shown, with V153 and E83 interacting weakly with Q732 of the 11e converter. The difference in isoform-dependent interaction strength provides a possible explanation for 11e’s imparting fast muscle kinetics (e.g., v_opt and v₀) in the TDT and slow muscle kinetics in the IFM (e.g., f_max). The other 4 versions of the converter have amino acids at this position (732) that do not result in as big of a change in interaction strength when expressed in conjunction with the different essential light chain (ELC) isoforms.

A possible explanation for TDT-11e’s differing behavior between IFM and jump muscles might be because it interacts differently with the myosin essential light chain (ELC) isoforms found in the jump muscle and IFM. Alternative splicing of the last 14 ELC residues generates two Drosophila ELC isoforms (13). The ELC binds to myosin heavy chain just below and in contact with the converter, forming a core part of the myosin lever arm. Comparing sequences suggests different interaction strengths between the 11e converter and the two ELC isoforms (Fig. 8, C and D), whereas interaction strengths of the other four converter versions remain consistent despite different ELC isoforms. Similarly, an explanation for why converter 11e did not alter jump muscle mechanical properties in the same manner as the other two embryonic converter isoforms might be because of differing interactions of 11e with alternative versions of the MHC relay domain, with which the converter also interfaces, compared with the other embryonic converters.

Conclusions

We set out to test our hypotheses that myosin’s converter is part of the force-sensing mechanism in muscle and that myosin’s force dependence sets the curvature of FVRs. By measuring force-velocity relations in muscle fibers that differ only in myosin’s converter domain, we directly show that the converter influences FVR curvature. Analysis of these measurements with two different mathematical models demonstrates that, in the models, increasing FVR curvature arises from an increase in the detachment rate of negatively strained myosin. In the four-state model, these changes are explained by the force dependence of myosin’s detachment from actin. The predictions from these models present a hypothesis that could be further investigated with biochemical and biophysical studies of product release rates and myosin structural modeling. The changes in FVR due to the converter are physiologically relevant, helping match a muscle’s mechanical properties to its locomotory task. Taken together, these data provide support for the idea that the converter influences myosin’s force dependence and that this force dependence sets the curvature of muscle FVRs.

GRANTS

This work was supported by National Institutes of Health Grant AR064274 to D. M. Swank, National Science Foundation Predoctoral Fellowship DGE-1247271 to C. S. Newhard, and National Science Foundation Division of Mathematical Sciences Grant 1413185 to S. Walcott.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

C.S.N. and D.M.S. conceived and designed research; C.S.N. performed experiments; C.S.N., S.W., and D.M.S. analyzed data; C.S.N., S.W., and D.M.S. interpreted results of experiments; C.S.N., S.W., and D.M.S. prepared figures; C.S.N. and D.M.S. drafted manuscript; C.S.N., S.W., and D.M.S. edited and revised manuscript; C.S.N., S.W., and D.M.S. approved final version of manuscript.

APPENDIX A: DERIVATION OF HUXLEY AND FOUR-STATE MODEL EQUATIONS

We fit our force-velocity measurements to two different molecular muscle models: 1) the Huxley model (24) and 2) the four-state model (46). The purpose of this appendix is to derive the equations to which we fit our data. The Huxley model is well known, so the derivation of force as a function of velocity is not new; however, we include it because variable definitions are not consistent throughout the literature, and the final equation to which we fit our experiments is not standard. The derivation of force as a function of velocity is new for the four-state model.

The Huxley Model

The Huxley model assumes that each myosin molecule can exist in two states: 1) a bound state and 2) an unbound state (Fig. A1A). Then, the probability that a given myosin molecule is in one of the two states is governed by partial differential equations (PDEs), given the following four assumptions: 1) binding and unbinding obey mass action kinetics; 2) there are an infinite number of myosin molecules; 3) there are no short-distance interactions between myosin molecules (i.e., the binding of 1 myosin molecule affects, at most, all bound myosin equally, and not just nearby myosin); and 4) binding sites are sparsely distributed on actin, so each myosin molecule can access (at most) only one binding site.

These are the governing PDEs:

$$\frac{\partial n_1}{\partial t}+v\frac{\partial n_1}{\partial x}=f\left(x\right)n_2-g\left(x\right)n_1$$

$$\frac{\partial n_2}{\partial t}+v\frac{\partial n_2}{\partial x}=-f\left(x\right)n_2+g\left(x\right)n_1$$ (A1)

In these equations, x is the position of the binding site on actin relative to the unextended position of myosin, v is the velocity of actin (also equal to the time derivative of x), f(x) is an attachment rate, g(x) is the detachment rate, and n₁(x,t) [or n₂(x,t)] is the probability of a myosin molecule, located a distance x from a binding site, attached (or detached) (Fig. A1B). There is an additional constraint of conservation of probability (i.e., myosin has to be in one of the two states), n₁ + n₂ = 1.

Assuming steady state and using the conservation of probability constraint, we get a single ordinary differential equation (ODE) for n₁:

$$v\frac{d{n}_1}{dx}=f\left(x\right)(1-n_1)-g\left(x\right)n_1$$ (A2)

Attachment and detachment rates.

The Huxley model (24) assumes piecewise linear functions for f(x) and g(x):

$$f\left(x\right)=\left\{\begin{array}{ccc}0& :& x<0\\ f_{1}x& :& 0\le x\le h\\ 0& :& x>h\end{array}\right.$$ (A3)

and

$$\left(x\right)=\left\{\begin{array}{ccc}{g}_0& :& x<0\\ g_{1}x& :& x\ge 0\end{array}\right.$$ (A4)

Note that h, the “reach” of a myosin molecule, has units of distance and that g₀ has units of inverse time, whereas f₁ and g₁ have units of inverse distance times inverse time. Because both attachment and detachment rates depend on the position of the binding site x, and since x can be related to force (see Force below), both attachment and detachment depend on force in this model.

Nonisometric conditions.

The advantage of picking piecewise linear functions is that we can find an analytic solution to the ODE governing n₁ (Eq. A2). To do so, we note that, for shortening, v will be negative (this is a different sign convention than in Ref. 24). As long as v is uniformly negative, there can never be a myosin bound to a binding site with extension greater than h, since myosin can only bind with extension between 0 and h, and once bound, that extension can only decrease, since v < 0.

The solution is then constructed in the following way. Consider Eq. A2 for 0 < x < h:

$$v\frac{d{n}_1}{dx}=f_{1}x\left(1-n_1\right)-g_{1}x{n}_1:0<x<h$$ (A5)

This equation can be separated and integrated to yield

$$n_1=\frac{f_1}{f_1+g_1}+C\text{exp}\left[-\frac{\left(g_1+f_1\right)x^2}{2v}\right]:0<x<h$$ (A6)

The constant of integration, C, is determined by the observation, discussed above, that n₁ = 0 for x > h. Thus, a continuous solution requires that

$$C=-\frac{f_1}{f_1+g_1}\text{exp}\left[\frac{\left(g_1+f_1\right)h^2}{2v}\right]$$ (A7)

so that

$$n_1=\frac{f_1}{f_1+g_1}\left\{1-\text{exp}\left[-\frac{\left(g_1+f_1\right)\left(x^2-h^2\right)}{2v}\right]\right\}:0<x<h$$ (A8)

This process can be repeated to construct the full solution:

$$n_1=\{\begin{array}{ccc}0& :& h<x\\ \frac{f_1}{f_1+g_1}\left\{1-\text{exp}\left[-\frac{\left(g_1+f_1\right)\left(x^2-h^2\right)}{2v}\right]\right\}& :& 0\le x\le h\\ \frac{f_1}{f_1+g_1}\left\{1-\text{exp}\left[\frac{\left(g_1+f_1\right)h^2}{2v}\right]\right\}exp\left(-\frac{g_{0}x}{v}\right)& :& x<0\end{array}$$ (A9)

Force.

To calculate force, we must also know something about the distribution of x values in our ensemble. It is easiest (and also probably correct) to assume that the probability distribution is constant. That is, if binding sites are spaced a distance L apart on the thin filament then, for a given myosin molecule, the probability of finding a binding site between some value x and x + Δx is Δx/L, if −L/2 < x < L/2 and 0 otherwise. Then, the force per molecule is

$$F=\underset{-L/2}{\overset{L/2}{\int }}\frac{1}{L}{n}_1\kappa xdx$$ (A10)

where we assume that myosin is linear elastic with spring constant κ. Using Eq. A9, and solving the integrals, we obtain the following expression for force per molecule:

$$F=\left(\frac{\kappa f_1{h}^2}{2L\left(g_1+f_1\right)}\right)\left\{\left[1-\text{exp}\left(\frac{\left(g_1+f_1\right)h^2}{2v}\right)\right]\times \left[-\frac{2v^2}{h^2{g}_0^2}+\frac{2v}{\left(f_1+g_1\right)h^2}\right]+1\right\}$$ (A11)

Note that, in deriving this expression, we assume that exp(g₀L/2v) ∼ 0, which follows from the assumption that a myosin molecule has access to only one binding site and the assumption that v < 0. This assumption also requires that n₁(L/2) =  n₁(−L/2) ∼0.

Isometric conditions.

We have to consider isometric conditions (v = 0) separately because we divide by v in the derivation of Eq. A11. Under isometric conditions, Eq. A2 becomes

$$0=f\left(x\right)\left(1-n_1\right)-g\left(x\right)n_1$$ (A12)

which then can easily be solved for n₁, and with the equations for f(x) and g(x) (Eqs. A3 and A4), the solution is simply a piecewise constant function:

$$n_1=\left\{\begin{array}{ccc}0& :& h<x\\ \frac{f_1}{f_1+g_1}& :& 0\le x\le h\\ 0& :& x<0\end{array}\right.$$ (A13)

Then, the isometric force per molecule is

$${\text{F}}_{\text{iso}}=\frac{\kappa f_1{h}^2}{2L\left(g_1+f_1\right)}$$ (A14)

Relative force.

Dividing Eq. A11 by Eq. A14, we obtain an equation for the relative force, Ψ = F/F_iso:

$$\psi =1-\left[1-\text{exp}\left(\frac{P}{v}\right)\right]\left(-\frac{v}{P}\right)\left\{1+{\left[\frac{\left(f_1+g_1\right)h}{g_0}\right]}^2\left(-\frac{v}{2P}\right)\right\}$$ (A15)

where P = (f₁ + g₁)h²/2.

Comparing the Huxley model with our measurements.

In our FVR experiments, we measure velocity in muscle lengths per second and define shortening as positive, but here, v is negative when a muscle is shortening. Thus, our experimental velocity measurements, v_exp, are related to v by

$$v_{exp}=-\frac{2v}{L_s}$$ (A16)

where L_s is the sarcomere length in the fiber (assumed constant).

Rewriting Eq. A15 in terms of v_exp, we have

$$\text{Ψ}=1-\left[1-\text{exp}\left(-\frac{\text{Φ}}{v_{\text{exp}}}\right)\right]\left(\frac{v_{\text{exp}}}{\text{Φ}}\right)\left\{1+{\left[\frac{\left({\varphi }_1+{\gamma }_1\right)}{g_0}\right]}^2\left(\frac{v_{\text{exp}}}{2\text{Φ}}\right)\right\}$$ (A17)

where Φ = 2P/L_s = (f₁+g₁)h²/L_s, and we define the following variables: H = h/L_s, φ₁ = f₁h, and γ₁ = g₁h. This equation, with a few different symbols, is used in Gilliver et al. (16).

We can nondimensionalize this equation by defining V = v_exp/ Φ to get

$$\Psi =1-V\left[1-\text{exp}\left(-\frac{1}{V}\right)\right]\left[1+\left(\frac{T^{2}V}{2}\right)\right]$$ (A18)

where T = Φ/Hg₀, a nondimensional ratio of time scales. From our velocity measurements, v_exp, and corresponding measurements of scaled force, Ψ, this equation is specified by two parameters, Φ (to determine V) and T. Thus, by fitting the model to the data, we obtain these two parameters for each muscle fiber type.

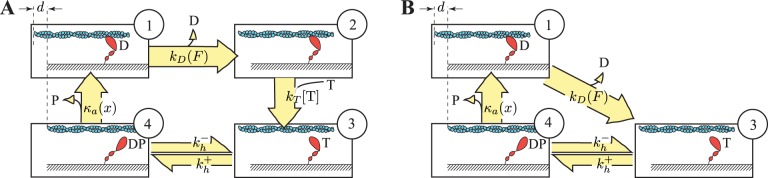
The Four-State Model

The four-state model, developed and tested by Walcott et al. (46), applies to any ATP concentration (Fig. A2A). Our force-velocity measurements were made at or near saturating ATP concentrations. This allows us to reduce the model to three states by presuming that detachment is limited by ADP release (Fig. A2B). Note that for very fast myosin isoforms, this assumption might be violated (see appendix d).

To write a differential equation description of this model, we make three of the same assumptions as for the Huxley model (reactions obey mass-action kinetics; there are an infinite number of myosin molecules, but there are no short-distance interactions between myosin molecules). However, we do not assume sparse binding sites (i.e., that each myosin molecule can access at most 1 binding site), but rather, we assume dense binding sites. Simulations, based on direct experimental measurements (35), suggest that this is a better approximation [see Walcott and Sun (45)].

These are the governing integro-PDEs

$$\frac{\partial {\eta }_1}{\partial t}+v\frac{\partial {\eta }_1}{\partial x}={\kappa }_a\left(x\right)N_4-k_D\left(x\right){\eta }_1$$

$$\frac{d{N}_3}{dt}=k_h^{-}{N}_4-k_h^{+}{N}_3+\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{k}_D\left(x\right){\eta }_{1}dx$$

$$\frac{d{N}_4}{dt}=k_h^{+}{N}_3-\left(k_h^{-}+\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\kappa }_a\left(x\right)dx\right)N_4$$ (A19)

with the additional constraint of conservation of probability

$$\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\eta }_{1}dx+N_3+N_4=1$$ (A20)

These equations, although similar to the equations of the Huxley model (Eq. A1), contain some important differences. In this model, x is the extension of an attached myosin molecule, as opposed to the position of the nearest binding site. The two are equivalent when myosin is in a bound state, but in the four-state model, x does not apply for unbound states; η₁ is a probability density (and has units of inverse distance), whereas n₁ in the Huxley model is a probability (and is dimensionless). More precisely, η₁(x,t)dx is, to first order, the probability of finding myosin in state 1 with extension between x and x + dx. The equivalent expression for the Huxley model is n₁(x,t)dx/L. Another difference is that, when myosin binds to actin, its attachment is governed by a binding rate density, κ_a(x), such that the effective rate constant for myosin in state 4 binding to actin with an extension between x and x + dx is κ_a(x)dx. The equivalent expression for the Huxley model would be f(x)dx/L. The final important difference is the presence of the integrals in Eqs. A19 and A20. All of these differences, discussed above, arise from the assumption that binding sites are densely distributed on actin [discussed in more detail in Srinivasan and Walcott (34)].

In steady state and using the conservation of probability constraint, we get a single integro-ODE for η₁:

$$v\frac{d{\eta }_1}{dx}=\frac{k_h^{+}{\kappa }_a\left(x\right)}{k_h^{-}+k_h^{+}+\underset{-\infty }{\overset{\infty }{\int }}{\kappa }_a\left(x\right)dx}\left(1-\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\eta }_{1}dx\right)-k_D\left(x\right){\eta }_1$$ (A21)

Note that, although we assume identities for the states in the model and thereby connect the reaction rates to biochemical steps [e.g., k_D(x) governs ADP release], these equations apply to any three-state model with a single attached state and approximately irreversible attachment and detachment steps.

Attachment/detachment rates.

Assuming an exponential relationship between ADP release rate and force [as was observed in smooth and cardiac myosin (18, 25, 37, 44), and predicted theoretically (1)], we have

$$k_D\left(x\right)=k_D^0\text{exp}\left(\frac{\delta F}{k_{B}T}\right)=k_D^0\text{exp}\left(-\frac{\delta \kappa x}{k_{B}T}\right)$$ (A22)

where, as in the Huxley model, we assume a linear relationship between force and myosin extension (F = −κx). The parameter $k_D^0$, a constant, is ADP release rate in the absence of force, δ is a distance [interpreted as the distance to the transition state; see e.g., Veigel et al. (44)], and k_BT is Boltzmann’s constant times temperature (4.14 pN nm at room temperature).

If we assume that attachment depends exponentially on the energy required for myosin to bind and that, just after binding, a power stroke of size d occurs, then

$${\kappa }_a\left(x\right)=k_a^0\sqrt{\frac{\kappa }{2\pi k_{B}T}}\text{exp}\left[-\frac{\kappa {\left(x-d\right)}^2}{2k_{B}T}\right]$$ (A23)

which is just a Gaussian centered at d, normalized and then scaled by $k_a^0$, so that

$$\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\kappa }_a\left(x\right)dx=k_a^0$$ (A24)

Nonisometric conditions.

The nondimensionalized version of Eq. A21 is

$$\begin{gathered} V\frac{d{\widehat{\eta }}_1}{dx}=K\left(1-\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\widehat{\eta }}_{1}dX\right)\sqrt{\frac{E}{\pi }}\text{exp}\left[-E{\left(X-1\right)}^2\right] \\ -\text{exp}\left(-2E\Delta X\right){\widehat{\eta }}_1 \end{gathered}$$ (A24)

where X = x/d, E = κd²/2k_BT, V = v/d$k_D^0$, Δ = δ/d, K = $k_a^0$k_h⁺/[$k_D^0$ (k_h⁺ + k_h⁻ + $k_a^0$)], and ${\widehat{\eta }}_1={\eta }_{1}d$.

We estimate that E should be relatively large (∼10), whereas Δ is relatively small (∼0.1). Then, if we choose E = 1/ε and Δ = 0.5Dε, we get

$$\begin{gathered} V\frac{d{\widehat{\eta }}_1}{dx}=K\left(1-\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\widehat{\eta }}_{1}dX\right)\sqrt{\frac{1}{\pi \epsilon }}\text{exp}\left[-\frac{{\left(X-1\right)}^2}{\epsilon }\right] \\ -\text{exp}\left(-DX\right){\widehat{\eta }}_1 \end{gathered}$$ (A25)

where ε is small. Although there is no closed-form solution to Eq. A24 (or Eq. A25), we can approximate the solution by using a matched asymptotic expansion. The end result is

$${\widehat{\eta }}_1~\frac{-DK\left\{\text{exp}\left(-\frac{e^{-D}}{DV}\right)\text{exp}\left(-\frac{e^{-DX}}{DV}\right)-\frac{1}{2}\left[\text{erf}\left(\frac{X-1}{\sqrt{\epsilon }}\right)+1\right]\right\}}{DV-K\text{exp}\left(-\frac{e^{-D}}{DV}\right)E_1\left(-\frac{e^{-D}}{DV}\right)}$$ (A26)

where erf(x) is the error function and E₁(x) is the exponential integral of the first kind as a function of x. This equation is a good approximation of the full numerical solution of Eq. A24 (see Fig. A3).

Force.

Force, in this model, is

$$F=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\kappa x{\eta }_{1}dx=\kappa d\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}X{\widehat{\eta }}_{1}dX$$ (A27)

Using Eq. A26, this gives the following expression

$$F~\kappa d\left[\frac{-KD\text{exp}\left(-\frac{e^{-D}}{DV}\right)}{1-K\text{exp}\left(-\frac{e^{-D}}{DV}\right)E_1\left(-\frac{e^{-D}}{DV}\right)}\right]\underset{-\infty }{\overset{1}{{\displaystyle \int }}}X\text{exp}\left(\frac{e^{-DX}}{DV}\right)dX$$ (A28)

where the integral must be evaluated numerically; it is nevertheless far more computationally efficient than the full numerical solution of Eq. A24.

Isometric conditions.

As in the Huxley model, we must consider isometric conditions separately, because our solution (i.e., Eq. A28) depends on being able to divide by V. When V = 0, the governing equation (Eq. A25) is

$$0=K\left(1-\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\widehat{\eta }}_{1}dX\right)\sqrt{\frac{1}{\pi \epsilon }}\text{exp}\left[-\frac{{\left(X-1\right)}^2}{\epsilon }\right]-\text{exp}\left(-DX\right){\widehat{\eta }}_1$$ (A29)

which can be solved to yield

$${\widehat{\eta }}_1=\frac{K}{1+K\text{exp}\left[\frac{D\left(D\epsilon +4\right)}{4}\right]}\sqrt{\frac{1}{\pi \epsilon }}\text{exp}\left[\frac{-X^2+\left(2+D\epsilon \right)X-1}{\epsilon }\right]$$ (A30)

Using Eq. A27, isometric force is then

$$F_0=\kappa d\frac{K}{1+K\text{exp}\left[\frac{D\left(D\epsilon +4\right)}{4}\right]}\frac{1}{2}\left(\text{Dε}+2\right)\text{exp}\left[\frac{D\left(D\epsilon +4\right)}{4}\right]$$ (A31)

This equation is exact. Assuming small ε, we can simplify it to

$$F_0~\kappa d\frac{K{e}^D}{1+K{e}^D}$$ (A32)

Relative force.

Dividing Eq. A28 by Eq. A32, we obtain an equation for the relative force, Ψ = F/F₀,

$$\text{Ψ}~\left[\frac{\left(e^{-D}+K\right)D\text{exp}\left(-\frac{e^{-D}}{DV}\right)}{DV-K\text{exp}\left(-\frac{e^{-D}}{DV}\right)E_1\left(-\frac{e^{-D}}{DV}\right)}\right]\underset{-\infty }{\overset{1}{{\displaystyle \int }}}X\text{exp}\left(\frac{e^{-DX}}{DV}\right)dX$$ (A33)

We make one further simplification, by noting that K is likely to be small (around 0.05). Then, we have

$$\text{Ψ}~\left[\frac{-D{e}^{-D}\text{exp}\left(-\frac{e^{-D}}{DV}\right)}{DV}\right]\underset{-\infty }{\overset{1}{{\displaystyle \int }}}X\text{exp}\left(\frac{e^{-DX}}{DV}\right)dX$$ (A34)

This equation compares well to the full numerical solution (Fig. A4) and, due to its computational efficiency, allows rapid and robust optimization of fits to our data.

Comparing the four-state model to our measurements.

To use Eq. A34, we must specify two values: 1) the nondimensional velocity V = v/d$k_D^0$ and 2) the nondimensional parameter D. From our velocity measurements, v_exp, and Eq. A16 we may determine v, so we must determine the velocity scale ζ = d$k_D^0$ and D = κdδ/k_BT by fitting Eq. A34 to our experimentally determined force-velocity curves.

APPENDIX B: ASSUMPTIONS AND COMPARISONS OF THE TWO MODELS

To compare the Huxley model to the four-state model, we must identify corresponding variables and parameters in the two models. This process is complicated by the fact that the Huxley model assumes sparse binding sites on actin, while the four-state model assumes dense binding sites (see The Four-State Model in appendix a). So, for example, binding probability in the Huxley model [n₁(x,t), which is dimensionless] has different units than the binding probability density in the four-state model [η₁(x,t), which has units of inverse distance]. However, we can find the appropriate comparison between these two variables by looking at how they affect quantities of relevance to our measurements. For example, in the Huxley model, force is

$$F=\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}\frac{n_1}{L}\kappa xdx$$ (B1)

So, if we define a probability density η_H = n₁/L, then this equation becomes

$$F=\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}{\eta }_H\kappa xdx\approx \underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\eta }_H\kappa xdx$$ (B2)

Note that the latter approximation follows the assumption, central to the Huxley model, that each myosin molecule has access to at most one actin-binding site. Eq. B2 is the same equation for force from the four-state model (Eq. A27), with η_H replacing η₁. Thus, these two variables are comparable between the two models.

With this definition, we can then convert the differential equation for the Huxley model (Eq. A2) to this new variable by dividing by L, to get

$$v\frac{d{\eta }_H}{dx}=\frac{f\left(x\right)}{L}\left(1-n_1\right)-g\left(x\right){\eta }_H$$ (B3)

Comparing this equation to the governing differential equation for the four-state model (Eq. A21), we see that f(x), g(x), and n₁ from the Huxley model correspond to k_h⁺κ_a(x)L/(k_h⁻ + k_h⁺ + k_a), k_D(x) and $\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\eta }_{1}dx$, respectively, from the four-state model. Note that the correspondence between n₁ and $\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\eta }_{1}dx$ is likely reasonable, albeit not exact, since the integral of η_H is the average value of n₁.

From fits to the force-velocity measurements, we can only specify two parameters for each model [Φ = (f₁+ g₁)h²/L_s and T = (f₁ + g₁)h/g₀ for the Huxley model and D = κδd/k_BT and ζ = d$k_D^0$ from the 4-state model]. Therefore, we do not know many of the variables in f(x) and g(x) for the Huxley model or the related functions for the four-state model. However, we can take advantage of previous work to estimate the parameters for the four-state model. For example, from previous work [Walcott et al. (46) and references therein], we can estimate k_h⁻ = 10 s⁻¹, k_h⁺ = 100 s⁻¹, $k_a^0$ = 40 s⁻¹, L = 36 nm, and d = 10 nm.

To compare the Huxley model to the four-state model, we must specify h and f₁ (see Eq. A3). We accomplished this by varying h to match η_H from the Huxley model to η₁ from the four-state model at positive extension. This gave a value of h = 12.75 nm (H = 0.0035). We then determined f₁ by matching the force produced by the four-state model. This gave a value of f₁ = 13.195s⁻¹nm⁻¹ (φ₁ = 168 s; see Eq. A17). With these values, we can compare the two models (Fig. B1A).

One result of this comparison is that the models suggest that the mechanism behind the different experimental FVR curves is the same; curvature is varied by increasing the detachment rate of negatively extended myosin (Fig. B1B). In the Huxley model, this is accomplished by increasing g₀; in the four-state model, it is accomplished by increasing D (Fig. B1C). However, the end result is the same, i.e., a faster decay in binding probability density as x decreases (Fig. B1D).

APPENDIX C: FORCE DEPENDENCE UNDERLIES DIFFERENCES IN FORCE-VELOCITY RELATIONSHIPS

Our initial fitting of the four-state model to the FVR data suggested that the differences between the five myosin isoforms comes from changes in D = κδd/k_BT and (to a lesser extent) ζ = d$k_D^0$ (see Table 2). Given that d does not change, and since k_BT is a constant, the changes in D arise either from differences in myosin’s stiffness, κ, its force dependence, δ, or a combination of the two. We can determine which by looking at isometric force.

The model predicts (Eq. A32; reproduced here for convenience) the following equation for isometric force:

$$F_0~\kappa d\frac{K{e}^D}{1+K{e}^D}$$ (C1)

Recall that

$$K=\frac{k_a^0{k}_h^{+}}{k_D^0\left(k_a^0+k_h^{+}+k_h^{-}\right)}$$ (C2)

Although K could potentially vary between myosins, for simplicity, we assume that the parameters remain constant in it (with $k_h^{-}$= 10s⁻¹, $k_h^{+}$ = 100s⁻¹, $k_a^0$ = 40s⁻¹), except for $k_D^0$, which varies according to our best fits. We can then use our isometric force measurements to test whether the variations in D between myosin isoforms arise from variations in κ, δ, or both.

In particular, suppose that all of the variation in D arises from changes in κ. Then,

$$\frac{F_0}{F_0^d}~\frac{\kappa dK{e}^D}{{\kappa }_{d}d{K}_d{e}^{D_d}}=\frac{DK{e}^D}{D_d{K}_d{e}^{D_d}}$$ (C3)

where the subscript d refers to parameters that are specific to myosin 11d (picked because it has the smallest values of D and $k_D^0$). Alternatively, suppose that all of the variation in D arises from changes in δ. Then,

$$\frac{F_0}{F_0^d}~\frac{\kappa dK{e}^D}{\kappa d{K}_d{e}^{D_d}}=\frac{K{e}^D}{K_d{e}^{D_d}}$$ (C4)

These two equations (Eqs. C3 and C4) generate different predictions: with D arising from changes in κ (Eq. C3), we would expect to see a roughly twofold change in isometric force between 11d and 11a myosin; alternatively, with D arising from changes in δ (Eq. C4), we expect to see only small differences in isometric force between myosin isoforms. Indeed, our measurements show no statistically significant differences in isometric force (Figs. C1 and 5), suggesting that the variation in D arises from changes in δ, myosin’s force dependence.

APPENDIX D: DOES OUR INTERPRETATION CHANGE IF ADP RELEASE IS NOT LIMITING?

The four-state model makes assumptions about the identity of each state, and particularly, that myosin’s detachment from actin is limited by ADP release (or a closely related step such as a myosin isomerization before ADP release). Although there is evidence that ADP release is the rate-limiting step for sinusoidal power production in slower Drosophila myosin isoforms, i.e., EMB and TDT-11d (previously referred to as IFI-11d), experiments have suggested that faster Drosophila myosins, i.e., IFM myosin and IFI-9b, are likely limited by another step, perhaps Pi release or ATP-induced detachment of myosin from actin (42, 48). Furthermore, solution kinetics results compared with actin motility velocities suggest that, under unloaded conditions, some Drosophila isoforms are not limited by ADP release (11, 30). One should note that another step being rate-limiting for unloaded velocity is not unique to Drosophila. Instead, it is likely a general characteristic of myosins found in very fast muscle types, including human extraocular myosin (2, 31). Therefore, it is worth considering how our interpretation would change if we presumed ADP release is not always rate limiting for myosin’s detachment from actin.

Given that ADP release is rate limiting for TDT-11d, the putative rate-limiting step for the myosins faster than TDT-11d must be faster than ADP release in TDT-11d. Defining this value is complicated by the fact that ADP release is force dependent; however, according to the four-state model, negatively strained myosins occasionally experience forces of −3 to −6 pN (extensions of −10 to −20 nm), at which point detachment rate (equivalent to ADP release since ADP release is limiting) is predicted to be ∼750–1,300 s⁻¹ (see 11d trace in Fig. B1B). Thus, the putative rate-limiting step of the faster myosins must be ≥750 to 1,300 s⁻¹, most likely significantly faster. Interestingly, the ATP-induced detachment rates in solution have been measured for several Drosophila myosins and were found to be 1,500–2,700 s⁻¹ (30). If this ATP-induced detachment rate is the putative rate-limiting step for all the myosin isoforms we measured in this study except for 11d, and if ATP-induced detachment is presumed not to be force sensitive [it has been found to be largely insensitive to forces on the scale of a few pN (25, 44)], and if we further presume that shortening velocity is still limited by myosin’s detachment rate from actin, then the four-state model interpretation would change in the following ways. Instead of the exponential increase in detachment rate as cross-bridges experience negative strain, which arises from the force dependence of ADP release, there would be an initial exponential increase in detachment rate that would quickly plateau to a roughly constant value at the force-insensitive ATP release rate of 1,500–2,700 s⁻¹. This would result in negatively strained cross-bridges detaching more slowly, which, if nothing else changed, would lead to lower predicted v₀ values than we measured. To accurately fit our data, the detachment rate of less strained cross-bridges would need to increase either by increasing the detachment rate of unstrained cross-bridges (ζ) or by increasing the force dependence of detachment (D). Increasing the force dependence of detachment, D, is more likely, given that both the four-state model and the Huxley model agree that the force-dependent detachment of negatively strained cross-bridges is what differs between the myosins in this study. Thus, the D values of all myosins, except for TDT-11d, would increase. However, the relative order of D values for the five myosins, from most to least force dependent, would not change.

Fig. A1.

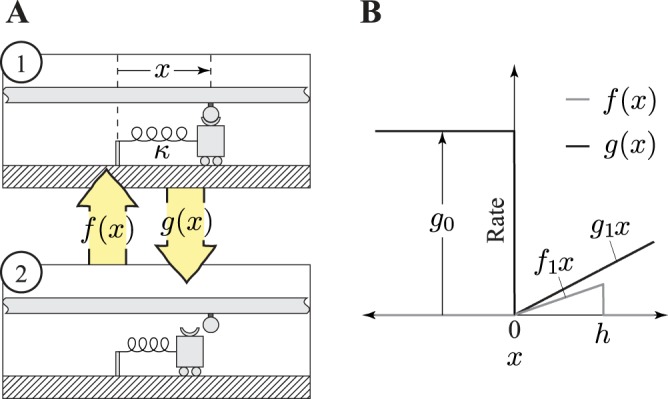
Kinetic scheme of the Huxley model. A: the Huxley model is a 2-state model; myosin is either attached to (1) or detached from (2) actin; x is the distance to a myosin-binding site on actin, and κ is the spring constant of the myosin head. The myosin-attached state shows the spring in the myosin head stretched out and generating force, whereas the detached myosin head does not generate force; f(x) is the attachment rate as a function of distance from the myosin binding site on actin, and g(x) is detachment rate. B: detachment and attachment rates as a function of distance from a myosin binding site. The parameters g₁ and f₁, are the slope of the detachment and attachment rates, respectively, as a function of positive x. Detachment rate assumes a constant value g₀, and the attachment rate is zero when x is negative. The parameter h is the value of x at above which attachment can no longer occur. Lengthening a muscle will increase the x values of attached cross-bridges, whereas shortening decreases x.

Fig. A2.

Kinetic scheme of the 4-state model. A: the full kinetic scheme. Myosin starts strongly bound to actin (state 1) and then releases ADP in a force-dependent process to enter the rigor state (state 2). Detachment in a post-power stroke state (state 3) occurs upon ATP binding. Reversible ATP hydrolysis allows myosin to enter a detached pre-power stroke state (state 4) from which attachment can occur, allowing myosin to enter state 1 and the cycle to continue. B: a reduced kinetic scheme, given a sufficiently high ATP concentration. At high ATP concentrations, the lifetime of state 2 is negligible, and detachment is limited by force-dependent ADP release. D, ADP; P, inorganic phosphate; T, ATP.

Fig. A3.

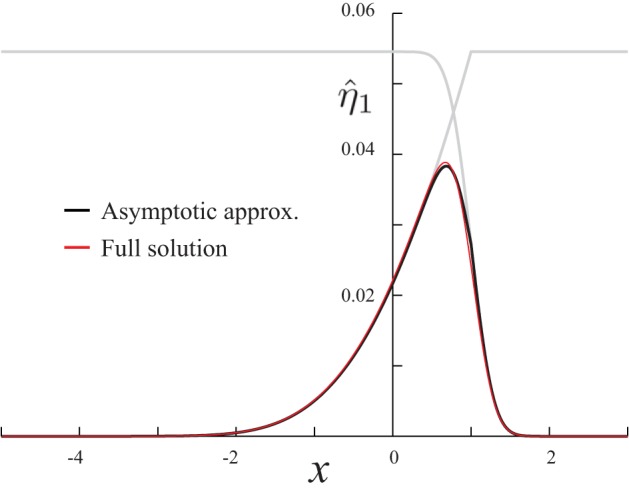
Comparison of the asymptotic approximation (Eq. A26) with the full numerical solution in Eq. A24. Gray lines are the inner and outer approximations of the matched expansion. For these simulations, parameters were K = 0.05, D = 0.46, V = −0.87, and ε = 0.1.

Fig. A4.

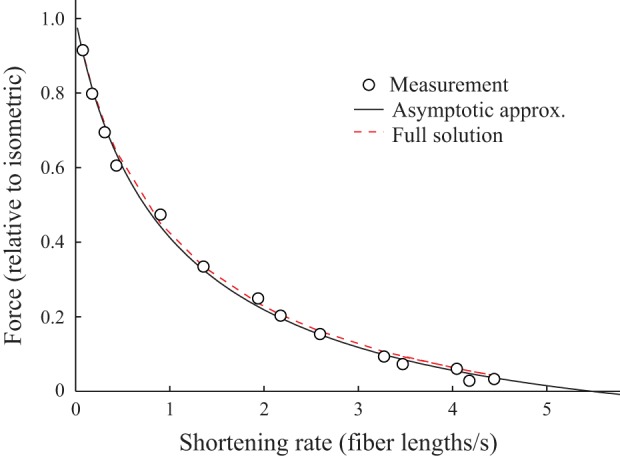
The 4-state model describes force-velocity measurements. This particular fit is with D = 0.79 and ζ = $d{k}_D^0$ = 5.38 μm/s, determined from fitting Eq. A34 to the force-velocity measurements of an 11a muscle fiber (∘). The best fit, based on an asymptotic approximation (solid black line), gives a sum of squared error of 0.0038. The full numerical solution to Eq. A24, then numerically integrated to get force (dashed red line, with K = 0.05 and ε = 0.1), is almost completely obscured by the approximation.

Fig. B1.

Comparisons between the Huxley and 4-state model fits to our force-velocity measurements. In all plots, x is cross-bridge extension. A: myosin attachment (gray) and detachment (black) rates from actin for the Huxley (solid) and 4-state (dashed) model derived from fitting the 11d fiber data. B: the detachment rates for the Huxley and 4-state model for all fibers. C: probability density for the Huxley and 4-state model (η_H, and η₁, respectively) for the model fit to the 11d fiber data. D: probability density rates for the Huxley and 4-state model for all fibers. Negligible differences between myosins occurred above 8 nm; thus we scaled the x-axis to better show the differences between −10 and 8 nm (the axes correspond to the box shown in C). Color indicates the curvature of the force-velocity relationship, with warmer colors being more curved.

Fig. C1.

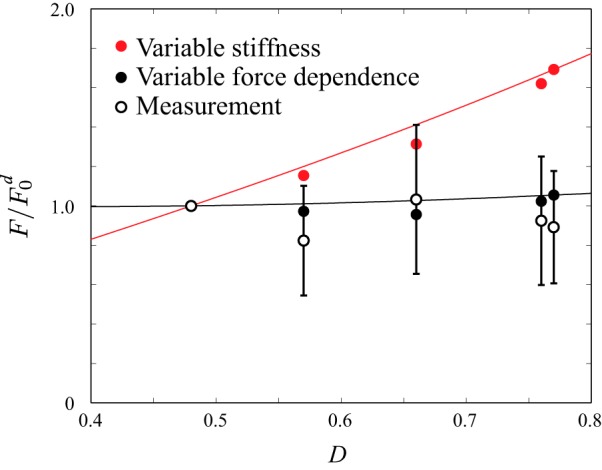
Measurements of isometric force are consistent with myosin isoform-dependent changes in force dependence, not stiffness. Model assuming changes in D occur from changes in myosin stiffness (red circles and fit line; Eq. C3). Model assuming changes in D occur from changes in myosin force dependence (● and fit line; Eq. C4). Experimental measurements of isometric force (○). Error bars show standard deviation. Forces scaled by the force of the myosin 11d isoform, which is predicted to have the smallest value of D.