Abstract
Current theories of deliberative decision making suggest that deliberative decisions arise from imagined simulations that require interactions between the prefrontal cortex and hippocampus. In rodent navigation experiments, hippocampal theta sequences advance from the location of the rat ahead to the subsequent goal. To examine the role of the medial prefrontal cortex (mPFC) on the hippocampus, we disrupted the mPFC with DREADDs (designer receptors exclusively activated by designer drugs). Using the Restaurant Row foraging task, we found that mPFC disruption resulted in decreased vicarious trial and error behavior, reduced the number of theta sequences, and impaired theta sequences in hippocampus. mPFC disruption led to larger changes in the initiation of the hippocampal theta sequences that represent the current location of the rat rather than to the later portions that represent the future outcomes. These data suggest that the mPFC likely provides an important component to the initiation of deliberative sequences and provides support for an episodic-future thinking, working memory interpretation of deliberation.
NEW & NOTEWORTHY The medial prefrontal cortex (mPFC) and hippocampus interact during deliberative decision making. Disruption of the mPFC impaired hippocampal processes, including the local and nonlocal representations of space along each theta cycle and the initiation of hippocampal theta sequences, while sparing place cell firing characteristics and phase precession. mPFC disruption reduced the deliberative behavioral process vicarious trial and error and improved economic behaviors on this task.
Keywords: hippocampus, place cell, prelimbic cortex, theta, vicarious trial and error
INTRODUCTION
The hippocampus is believed to store representations of the past to be used flexibly in imagining the future during deliberative decision making (Cohen and Eichenbaum 1993). Current theories of deliberative decision making suggest that deliberative decisions arise from imagined simulations that require interactions between the hippocampus and prefrontal cortex (Redish 2016). In these theories, the medial prefrontal cortex (mPFC) iteratively engages the hippocampus as it imagines potential outcomes, sorting through numerous contextually relevant options, while ignoring contextually irrelevant options, to determine the best outcome (Depue 2012; Preston and Eichenbaum 2013; Wang et al. 2015). Imaging studies in humans have shown that these same neural networks are activated while imagining the future (Addis et al. 2007; Hassabis et al. 2007; Schacter et al. 2007).
Pyramidal cells in the hippocampus, also known as “place cells,” show firing properties that are spatially specific (O’Keefe and Dostrovsky 1971; O’Keefe and Nadel 1978; Redish 1999). In addition to firing at the rat’s current location, place cells also show rare extra-field firing (i.e., firing occasionally in locations separate from their place field in a sequentially relevant, temporally compressed manner). During this nonlocal firing, the place cells are activated in behaviorally relevant sequences that can represent trajectories the rat previously traversed or could traverse (Davidson et al. 2009; Foster and Wilson 2007; Gupta et al. 2010, 2012; Pfeiffer and Foster 2013; Skaggs and McNaughton 1996). Rodent navigation experiments have found that these place cell sequences are organized on individual theta cycles. Hippocampal theta sequences are time-compressed representations of space (Dragoi and Buzsáki 2006; Foster and Wilson 2007) that advance from the location of the rat ahead to the subsequent goal (Gupta et al. 2012; Wikenheiser and Redish 2015).
Exactly how the mPFC and hippocampus are communicating with each other has yet to be fully elucidated. Numerous studies suggest that these two regions communicate with each other during goal-directed decision making via oscillatory coordination (Colgin 2011). Theta oscillations (6–10 Hz) in the hippocampus are believed to support learning and memory (Buzsáki 2002; Vanderwolf 1969). Studies have shown increased theta coherence between the hippocampus and mPFC during decision making (Benchenane et al. 2010). Similarly, mPFC neurons are phase locked to hippocampal theta oscillations during memory tasks (Hyman et al. 2005; Jones and Wilson 2005; Siapas et al. 2005; Sirota et al. 2008).
Lesions of the mPFC impair behavioral flexibility (Rich and Shapiro 2007) and can “focus” hippocampal place cell activity (Hok et al. 2013). We hypothesized that the mPFC contributes to the ability of the hippocampus to maintain different contextual representations and maintain hippocampal theta sequences that sweep to goal locations during deliberative decision making.
We set out to examine the influence of the mPFC on deliberative decision making by inducing reversible disruptions in the mPFC while examining theta sequences in the hippocampus. We transduced the inhibitory h4MDi DREADD (designer receptor exclusively activated by designer drugs) under a CAMKIIα promoter into the mPFC of 12 rats. DREADDs are a state of the art, chemical-genetic method of silencing neurons by transducing a genetically modulated designer G protein-coupled receptor that is activated by a systemic injection of clozapine N-oxide (CNO; Armbruster et al. 2007). While DREADDs can transfect both excitatory and inhibitory cells under a CAMKIIα promoter (Watakabe et al. 2015), either of these transfections would disrupt mPFC information processing. Each day we systemically injected (subcutaneously) each rat with CNO or vehicle (Veh; see methods) while simultaneously recording from the mPFC and the CA1 region of the hippocampus, as rats made stay/skip decisions on the neuroeconomic spatial foraging task Restaurant Row (Steiner and Redish 2014).
METHODS
DREADD transfection.
Sixteen Brown-Norway rats aged 10–14 mo at the start of the experiment were used in this study. Rats were maintained above their 80% free-feeding weight (see Table 1). Prior to training on the task, 12 rats were transfected with mCitrine- (n = 4) or mCherry- (n = 8) tagged AAV8-CaMKIIα-hM4Di virus (University of North Carolina Vector Core, Chapel Hill, NC) under isofluorane anesthesia. Non-DREADDs control rats (n = 4) were trained on the behavior and given the CNO/Veh sequence injections but received no viral surgery. We transfected the virus bilaterally into the prelimbic cortex. We infused a total of 4 µl 3.4 × 1,012 mol/ml titer at a rate of 200 nl/min into each site. mPFC coordinates for the infusion were 3.0 mm anterior/posterior, 0.7 mm medial/lateral, and 3.6 mm dorsal/ventral. All procedures and protocols were conducted under Biological Safety Level 1 practices and were approved by the University of Minnesota’s Institutional Biological Safety Committee and Institutional Animal Care and Use Committee. DREADDs are localized to cell bodies and axons (Mahler et al. 2014; Zhu and Roth 2014) and silence spontaneous and electrically evoked neuronal firing (Dong et al. 2010), in vivo (Ferguson et al. 2011), by activating G protein inward-rectifying K channels (Lechner et al. 2002; Li et al. 2005). DREADDs silence neuronal activity by both hyperpolarizing the cell body and suppressing presynaptic vesicular release (Zhu and Roth 2014). CNO administration in vitro and in vivo silences presynaptic synapses by suppressing glutamatergic and GABAergic vesicular release (Mahler et al. 2014; Stachniak et al. 2014).
Table 1.
Rats used
| Manipulation + Task | Sample Size |
|---|---|
| Restaurant Row | |
| Hyperdrive & DREADDs+ | n = 7 |
| Behavior & DREADDs+ | n = 2 |
| Behavior & DREADDs− | n = 4 |
| Noncognitive foraging | |
| Behavior & DREADDs− | n = 3 |
Sample sizes for each condition are shown. Some rats were implanted (Hyperdrive), while some were behavior only (Behavior). Some rats were given designer receptors exclusively activated by designer drugs (DREADDs+) and some control rats were not (DREADDs−).
The Restaurant Row task.
An overhead camera recorded the rat’s position via light-emitting diodes (LEDs) attached to a removable backpack worn by the rat (behavior only) or mounted to the hyperdrive. Data were recorded with a Cheetah Digital Lynx SX system (Neuralynx). The task was controlled by software written in-house in MATLAB R2012a (The MathWorks, Natick, MA) using video tracked and time-stamped from the 96-channel Neuralynx Digital Lynx system. Recordings from hyperdrive-implanted rats were collected for 5 min of rest before the run (Pre), while on the maze (Maze), and then again for 5 min of rest after the run (Post).
Restaurant Row is a neuroeconomic spatial decision-making task in which rats make serial stay/skip choices for different flavors of food reward in a naturalistic foraging paradigm (Steiner and Redish 2014). The Restaurant Row task enables direct measures of value from the flavor preferences revealed by individual rats. Rats were trained to run clockwise around a circular maze with four evenly spaced spokes; at the end of each spoke was one of four differently flavored rewards (“restaurants”: plain, chocolate, banana, cherry). The feeder (MedAssociates, St. Albans, VT) dispensed two 45-mg food pellets (Research Diets, New Brunswick, NJ). Flavor locations remained constant throughout training. As the rat entered a restaurant, a tone sounded, where the pitch of the tone indicated the required delay remaining before food would be delivered. Delays were randomized (uniform distribution) between 1 and 30 s on each entry, so the rat did not know what the cost (delay) would be until entering the restaurant. Higher delays had higher frequency tones and counted down every second in decreasing 250-Hz steps. If the rat skipped the restaurant, the tone stopped, the offer was rescinded, and the rat was required to proceed to the next restaurant. Restaurants were primed in serial order, forcing the rats to encounter the restaurants serially. Rats had 1 h to gather all of their food for the day (7 days a week), making this an economic task in which their time was a commodity.
Non-DREADDs control rats (n = 4) and mPFC DREADDs transfected rats [n = 9 (hyperdrive n = 7, behavior only n = 2)] following DREADD transfection surgery and 3 days of recovery, received twice-daily training sessions lasting 30 min each (see Supplemental Fig. S1; Supplemental Material for this article is available online at the Journal website). Training began with 5 days of habituation to the environment. Delays in this phase remained a constant 1 s at all feeder sites. After 5 days of habituation, the randomized list of delays presented to the animals was expanded up to 2-, 3-, 4-, and 5-s delays over 4 consecutive days. Rats then received 10 days of training on which delays were randomly selected from a uniform distribution between 1 and 30 s. After this 19-day sequence of twice-daily, 30-min sessions, rats transitioned to training to a once-daily, 60-min session while presented with the same 1- to 30-s delay. These sessions were presented over a minimum of 5 days until performance was deemed stable by visual inspection. At that time, rats either received hyperdrive implantation surgery or began the injection sequence described below.
Hyperdrive implantation surgery.
After initial task training, six rats underwent a triple-bundle, 24-tetrode, four-reference hyperdrive implantation targeting the prelimbic cortex (A/P 3.0 mm; M/L 0.7 mm; 3 tetrodes), ventral striatum (A/P 1.2 mm; M/L 2.4 mm; 5 tetrodes), and hippocampus (A/P −3.0 mm; M/L 4.0 mm; 16 tetrodes). Ventral striatal data are not analyzed in this paper. One additional rat was implanted with a tetrode/nanowire hyperdrive (targeting the same locations); only the local field potential and behavioral data were used from this rat. Tetrodes were lowered daily until they hit the mPFC and the pyramidal cell layer of CA1. Theta was recorded from the hippocampal fissure, and the references were placed in the corpus callosum.
Injection sequence.
Posthyperdrive surgery rats (n = 7) were retrained daily on the maze as tetrodes were lowered. A 20-day injection sequence (see Supplemental Fig. S1a) followed once the tetrodes had reached their respective areas. Behavior-only rats [mPFC DREADD (DREADDs+) n = 2; no-DREADD controls (DREADDs−) n = 4] were immediately tested on the injection sequence after the initial task training. Experimenters were blind to the identity of the solution (Veh or CNO) injected on any given day. Experimental and control conditions were presented in matched pairs in pseudorandomized order, controlling for first-order sequence effects. The rats were given CNO (5 mg/kg sc) or Veh 20 min before testing. CNO (NIMH Chemical Synthesis and Drug Supply Program) was dissolved in dimethyl sulfoxide (DMSO; Fisher Scientific, Pittsburgh; PA) and 0.9% saline to yield a DMSO concentration of 10%. Veh injections also contained 10% DMSO. The blind was broken once all the data were collected.
Training and injection sequence for the noncognitive foraging control task.
As a control, we ran additional rats (n = 3) on a noncognitive foraging task using a maze similar to Restaurant Row. Following transfection surgery into the mPFC and 2 wk of recovery, rats began daily training sessions lasting 45 min each. The task was controlled by software written in-house in MATLAB R2012a (The MathWorks, Natick, MA), video tracked and time-stamped from the Neuralynx Digital Lynx 16SX system. Rats ran clockwise around a square maze with four feeders located in the center of the sides of the maze. Each feeder (MedAssociates) dispensed two plain 45-mg food pellets (Research Diets). Training began with 13 days of habituation to the environment. Delays in this phase remained a constant 1 s at all feeder sites. After 13 days of training, the rats began an injection sequence of CNO and Veh for 10 days. For each of the 10 days, rats were given an injection 20 min before running the task. The type of injection (CNO or Veh) was determined by a premeditated schedule that was kept constant for all control rats run on this training and injection sequence. Experimenters were blind to the identity of the solution (Veh or CNO) injected on any given day.
Perfusion/histology.
After the end of the experiment, current (100 mA, 10 s) was passed through the electrodes to verify tetrode locations. Three days later, rats were overdosed with pentobarbital sodium (150 mg/kg, Nembutal) and perfused intracardially with formalin. Their brains were transferred to a 30% (wt/vol) sucrose-formalin solution, sectioned on a cryostat, and stained with immunofluorescence for DREADDs or cresyl violet. Immunofluorescence staining was conducted as described in Dong et al. (2010).
Delay threshold.
To quantify the subjective value of the four flavors presented to each rat, we fit a Heaviside step function to the stay/skip decisions as a function of the presented delays by least squares. Separate step functions were fit to the data for each zone, rat, and session. The delay at which the function predicted an equal likelihood of stay or skip for a given flavor was defined as the threshold for that flavor and provided a measure of the subjective value of the flavor for the rat for the session. The median threshold across flavors for a session provided the rat’s overall willingness to wait for food of any kind.
Rate of reinforcement.
To quantify the effectiveness of the rats’ decision making, we calculated the overall session rate of reinforcement for all food. We obtained this measure by dividing the total number of pellets that rats obtained in a session by the total session time. Higher rates imply that rats made objectively better choices, whereas lower rates imply that rats made objectively less-advantageous choices.
Flavor preference.
The degree of flavor preference was inferred from variability in flavor thresholds. We calculated the median absolute deviation (MAD) from the median of the flavor thresholds for a session. Widely varying thresholds imply highly ordered flavor preferences, whereas constant thresholds across flavors imply no flavor preference. The MAD, therefore, provided a measure of the degree to which flavors mattered in the rat’s decision to stay or skip a particular offer.
Vicarious trial and error.
When making difficult decisions, rats often pause and orient back and forth, a behavior termed “vicarious trial and error” (VTE; Muenzinger and Gentry 1931; Muenzinger 1938; Redish 2016; Tolman 1938). To quantify VTE, we calculated the logarithm of the integrated absolute head angle velocity (Log[IdPhi]) in the first 3 s of zone entry (Papale et al. 2012; Schmidt et al. 2013). The Log[IdPhi] values were subsequently Z-scored for each rat across all zone entries made in each drug condition. Large values of Z[Log[IdPhi]] (values over 1) corresponded to trajectories that qualitatively matched the pause-and-orient description of VTE, whereas low values (values below 1) corresponded to smooth passes through the zone. In the case of behavior-only rats (n = 9), position was tracked with backpack-mounted LEDs; in the case of recording rats (n = 7), position was tracked from LEDs mounted to recording head stages.
Running speed.
We computed the running speed as the change in x and y position (dx, dy) using an adaptive windowing of best-fit velocity vectors (Janabi-Sharifi et al. 2000).
Place fields and sequence score.
Spikes were manually clustered on the basis of their waveform properties (MClust 4.2, A. D. Redish, University of Minnesota, Minneapolis, MN) based on automatically derived clusters (Klusta-Kwik, K. Harris, Rutgers University, Newark NJ). Cells firing more than 5 Hz were excluded to filter out likely interneurons. Cells that fired less than 100 spikes on the maze were also excluded. Spikes recorded when the animal ran less than 5 cm/s were excluded. Contiguous bins where the firing rate was ≥6% of the cell’s session maximum firing rate were considered place fields. Fields separated by ≤2 bins were merged. Place field centers were ordered from maze start (zone one entry) to maze start in the direction traveled on the maze. A sequence detecting algorithm was used to identify theta cycles whose spike sequences showed significant spatial and temporal structure (Gupta et al. 2010, 2012). The algorithm detects spatial and temporal structure in the pattern of place cells’ activity by comparing the times and place field centers of spike pairs. The algorithm was run once for the original data set and once for a shuffled data set. The shuffled data set was analyzed in the same way as the original data set; however, the shuffled data set preserved the spike trains but randomly reassigned each spike train to a different cells’ firing field.
Mutual information.
We measured the mutual information (MI) between cell spiking (x) and spatial location (y) of the rat as
Theta oscillations.
Theta oscillations were recorded from a tetrode placed in the hippocampal fissure. Recordings were bandpass filtered with a Hilbert transform between 6 and 10 Hz to obtain the theta signal and 2–4 Hz to obtain the delta signal. Instantaneous amplitude and phase were estimated via the Hilbert transform. The log-transformed ratio of theta to delta power was computed and averaged over each theta cycle. Theta cycles with a theta-delta ratio above the mean were included for analysis. For individual theta cycle analyses, theta cycles were separated from peak to peak.
Coherence.
Coherence was analyzed using a multitaper Fourier analysis (Mitra and Pesaran 1999) using the Chronux toolbox (http://chronux.org). Coherence analyses were limited to the first three seconds of zone entry. The trials were averaged over the day for each rat. Differences in the distributions were analyzed with a two-sample Kolmogorov-Smirnov goodness-of-fit test.
Bayesian decoding.
For each theta cycle that met criteria, the represented path in space was determined using a one-step Bayesian decoding method (Zhang et al. 1998). Bayesian decoding was done as described in Wikenheiser and Redish (2013). Given spike counts from each cell in the ensemble, the posterior probability of the ensemble was computed representing each position in space. We decoded spiking within each theta cycle (peak to peak) in a 40-ms time window using a uniform spatial prior, resulting in a posterior probability distribution across 64 spatial bins. Posterior distributions were normalized to sum to one, and we calculated the decoded position for each time step as the circular mean of the posterior probability distribution. Theta cycles included in the analysis had a theta-delta ratio above the mean, while the rat was running more than 5 cm/s. Only time steps with at least one spike were decoded. To detect sequences, we computed the cumulative sum of the difference between successive decoded positions. Forward sequences had a positive slope and backward sequences had a negative slope. The path length was defined within each theta cycle as the distance between the decoded start and end location. The data presented were computed on theta cycles containing a minimum of five spikes from five different cells. Both easier and stricter criteria results are presented in the supplemental materials.
Decoding quality measures.
We measured the entropy over the decoded posterior probability:
We measured decoding error as the weighted distance between each decoded location bin and the rat’s actual position (weighted by the posterior probability in that bin). We also estimated decoding error as the distance from the maximum posterior probability location and the rat’s actual position and found similar results.
Sequence identification.
To measure the coherent sequence of place cell activity during each theta cycle, we computed the sequence score. The algorithm described here is nearly identical to the algorithm used previously (Gupta et al. 2010, 2012). The sequence score of place cell activity within each theta cycle was calculated as follows: Place field centers were ordered from maze start (zone one entry) to maze start in the direction traveled on the maze. Using the place field centers and spike times, each spike in the theta cycle was pairwise compared with other spikes occurring in the same theta cycle. If the place field center corresponding to spike A was traversed before the place field center for spike B and spike A occurred before spike B, the sequence score was +1, otherwise, the score was −1. For all spikes in a cycle, all pairwise comparisons were summed to determine the cumulative score of the sequence. A positive sequence score indicates a forward sequence.
The basic sequence score was as follows.
-
Given:
Spike time: T vector: [nSpikes × 1]
Spike place field centers: C vector: [nSpikes × 1]
-
Compute:
Time difference for each spike pair: ∆T matrix: [nSpikes × nSpikes]
Field center distance for each spike pair: ∆C matrix: [nSpikes × nSpikes]
Element-wise multiply ∆T and ∆C to create ∆TC matrix: [nSpikes × nSpikes]
Binarized ∆TC. For each element in ∆TC: if element is positive, replace with ‘+1’; if element is negative, replace with ‘−1 ’.
Sum over all elements in ∆TC to get the sequence score.
The scoring algorithm requires each spike to have one place field. Spike bursts were not handled separately. A neuron could contribute multiple spikes to the sequence. If a cell has multiple place fields it is unclear which field is being represented by a spike, therefore, the algorithm assigned each spike from a multifield cell to the place field which best fit with the firing sequence. This was done by maximizing the score over each place field available to a spike. Always picking the place field that optimizes the sequence score could result in artificially high sequence scores. To provide a fair and statistically justified comparison, this same score maximization procedure was conducted for the shuffled control sequences. For spike bursts, the burst was kept together in the shuffle procedure.
Asymmetry index.
The asymmetry index was calculated as described in Belluscio et al. (2012). The theta oscillation was first broad bandpass filtered (1–80 Hz) to determine the local minima and maxima in the theta frequency. Local minima and maxima were then used to determine the duration of the ascending and descending phases. The asymmetry index was calculated as the log ratio of the duration of the ascending phase and descending phase. Negative scores represent asymmetric cycles. A score of zero would represent a symmetric cycle.
Phase locking.
Each spike was assigned a theta phase between 0 and 360°. Measures of significance were made with the Rayleigh’s test of uniformity, which tested each cell’s phase distribution against a uniform distribution (MATLAB circular statistics toolbox).
Statistics and general data analyses.
All statistical tests were two-sided. All behavioral data were analyzed within animal with an ANOVA. Differences between Veh and CNO electrophysiology data were analyzed with nonparametric statistics including Wilcoxon rank sum and signrank. Differences between binned data were measured with paired t-tests corrected for multiple comparisons. Differences in correlations between Veh and CNO data were measured with the Fisher’s r-to-z transformation. To measure significance between Veh and CNO cell phase locking we used the Watson-Williams two-sample test from the circstats toolbox for MATLAB. To measure differences in coherence we used a two-sample Kolmogorov-Smirnov test. To measure differences in sequence scores, controlling for cell count, we used an analysis of covariance (ANCOVA) with the MATLAB aoctool.
Data availability.
The data sets generated and/or analyzed in the current study are available from the corresponding author upon reasonable request.
Code availability.
In-house written code used in the current study is available from the corresponding author upon reasonable request.
RESULTS
DREADDs disrupted representation in the mPFC.
Viral transduction was generally localized to the prelimbic cortex with some spread to the infralimbic cortex and anterior cingulate cortex (Fig. 1A, left and middle). As with all viral manipulations, the DREADD transfections in mPFC cortex were not complete lesions and CNO did not shut down all firing within the mPFC region. Because cortical systems include excitatory-inhibitory normalizing factors, we reasoned that the effect of DREADDs and CNO on neural circuits was better described as a disruption of mPFC information processing.
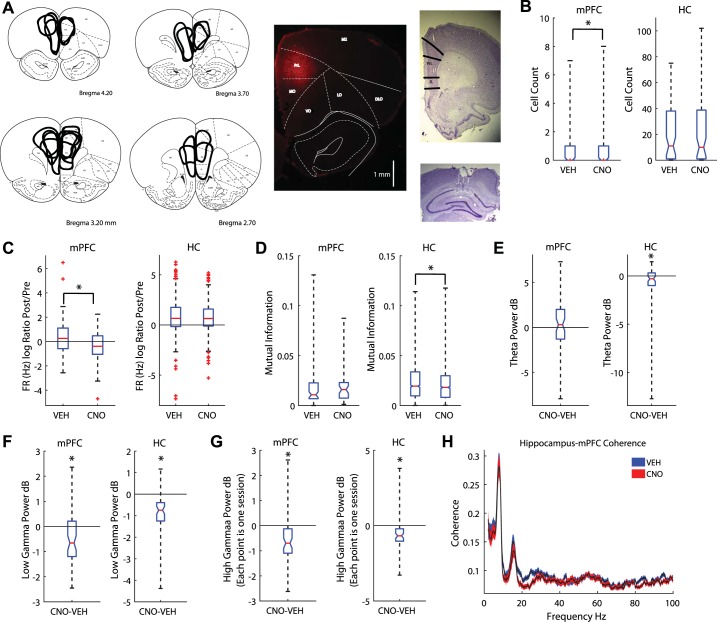
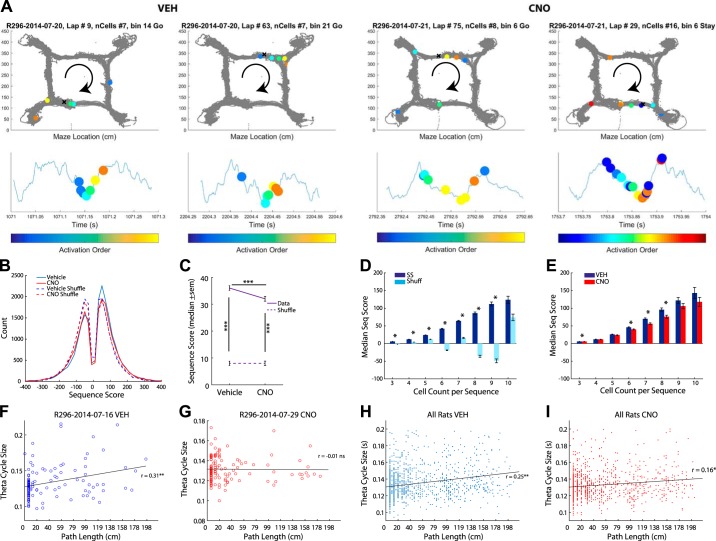
Fig. 1.
Clozapine N-oxide (CNO) altered medial prefrontal cortex (mPFC) and hippocampal local field potentials. A: the mPFC was transduced with the designer receptor exclusively activated by designer drugs (DREADDs) AAV8-CaMKIIa-hM4Di. Summary figure of DREADDs spread (left) and example photo of fluorescence (middle). Tetrodes were targeted toward CA1 (cornu ammonis, bottom right) and the prelimbic cortex of the mPFC (top right). B: CNO reduced the number of cells recorded in the mPFC (left) but had no effect on recordings in the hippocampus [HC; boxplot: median is plotted (red line), whiskers extend to outliers]. C: CNO decreased the firing rate (FR) ratio between premaze rest (Pre) and postmaze rest (Post) in the mPFC (left); it had no effect on hippocampal cells (right). D: we measured the mutual information (MI) between spatial location and spike firing (see methods). CNO had no effect on the MI for neurons in the mPFC (left). However, CNO decreased place cell MI (right). E: we measured the differences in theta power between CNO and vehicle (Veh) days. mPFC disruption did not alter theta power in the mPFC (left) but did reduce it in the hippocampus (right). The median difference between Veh and CNO theta power is plotted for all rats. F: we found a decrease in low gamma power in both the mPFC (left) and hippocampus (right). G: high gamma power also decreased in the mPFC (left) and hippocampus (right). H: coherence plot between the hippocampal and mPFC local field potentials. Blue, Veh; red, CNO. Values are means ± SE. dB, decibels; DLO, dorsolateral orbital cortex; IL, infralimbic cortex; LO, lateral orbital cortex; M2, secondary motor cortex; MO, medial orbital cortex; RrL, prelimbic cortex; VO, ventral orbital cortex. *P < 0.05.
We simultaneously recorded from the mPFC and hippocampal layer CA1 (Fig. 1A, right). CNO reduced the number of mPFC cells recorded, while sparing ensemble size in CA1 (Fig. 1B; Wilcoxon signed-rank test for nonparametric distributions: z = −2.53, P < 0.05). Though CNO had no general effect on firing rate (Wilcoxon rank sum; both P > 0.05); we found the firing rate ratio between the Post and Pre was significantly decreased on CNO days compared with Veh days for mPFC cells (Fig. 1C; Wilcoxon rank sum z = 2.58, P < 0.01), but not hippocampal cells (Fig. 1C; Wilcoxon rank sum z = 0.58, P > 0.10). Further examination revealed that cells in the mPFC that normally increased their firing across the session were more disrupted than cells that did not change or decreased their activity across the session. This was specifically so when examining mPFC cells that were not significantly phase locked to local low gamma oscillations (25–55 Hz; χ2 = 13.71, P < 0.0001). On Veh days, 68% of recorded mPFC cells (32 of 47) were not phase locked to low gamma. In contrast, on CNO days, only 24% of recorded mPFC cells (7 of 29) were not phase locked to low gamma (Table 1). To examine whether DREADDs + CNO disrupted information processing we measured the mutual information between spiking and the rat’s spatial location on the maze (see methods; Rieke et al. 1997). Because different task parameters occur at different locations, spatial location is a good proxy for general task responsiveness. Mutual information between neural firing rate and location remained unchanged in mPFC neurons on CNO days (Fig. 1D; Wilcoxon rank sum, z = −1.22, P > 0.10), but decreased in hippocampal cells (Fig. 1D; Wilcoxon rank sum, z = 2.6, P < 0.01). Therefore, CNO disruption of the mPFC region impaired the mutual information of cell spiking and spatial location of hippocampal cells.
mPFC disruption altered gamma oscillations and hippocampal theta oscillations.
To understand how disrupting mPFC affected global network dynamics, we measured differences in the local field potential at theta (6–10 Hz), low gamma (25–55 Hz), and high gamma (65–115 Hz) frequencies. Gamma oscillations are divided into different frequency ranges, reflecting differences in input and information processing (Colgin et al. 2009). mPFC disruption did not alter theta power in the mPFC [Fig. 1E; paired t-test: t(58) = 0.77, P > 0.10]; however, we did find a small, but significant reduction in the hippocampus [Fig. 1E; paired t-test: t(58) = −2.21, P < 0.05]. Similarly, we found low gamma [Fig. 1F; paired t-test; mPFC: t(58) = −3.99, P < 0.001; hippocampus: t(58) = −8.14, P < 0.001] and high gamma [Fig. 1G; left; paired t-test; mPFC: t(58) = −4.60, P < 0.001; hippocampus: t(58) = −5.38, P < 0.001] decreased in both the hippocampus and prefrontal cortex. Low and high gamma are believed to reflect differences in local and nonlocal spatial processing (Amemiya and Redish 2018; Zheng et al. 2016); therefore, this reduction in gamma power could reflect disruptions in local and nonlocal spatial processing (though see Fernández-Ruiz et al. 2017). Last, we measured the coherence between the hippocampus and mPFC while at the choice point. CNO reduced the coherence between these two structures (2-sample Kolmogorov-Smirnov test, D = 0.27, P < 0.0001). Specifically we found a significant drop in low gamma (Fig. 1H).
mPFC disruption spared hippocampal place cell integrity.
To determine whether mPFC disruption affected hippocampal theta sequences we first set out to measure whether CNO altered place field firing stability within (first half versus second half) and across sessions. We found no differences in the number of place fields within the testing session [Veh: number of Fields difference: 0.05 ± 0.85; paired-sample t-test, t(1211) = 1.92, P = 0.06; CNO: 0.01 ± 0.85; t(1187) = 0.38, P > 0.10], nor did we find any differences between Veh and CNO days (independent sample t-test, Veh versus CNO: t(2398) = −1.08, P > 0.10; Supplemental Fig. S2a). Though we did find a within session difference for place field area on Veh days (\[CNO-Veh: 1.70 ± 26.6; paired-sample t-test, t(1005) =2.02, P < 0.05; CNO: t(993) = 1.7, P = 0.09], we found no differences in this variability between CNO and Veh days [independent sample t-test, t(1998) = 0.49, P > 0.10; Supplemental Fig. S2b]. We found differences in maximum in-field firing rate within the session for both CNO and Veh days [Veh: 3.4 ± 29.0, t(1005) = 3.7, P < 0.001; CNO: 2.5 ± 31.0, paired-sample t-test, t(993) = 2.55, P < 0.05], but no difference between CNO and Veh days [independent sample t-test, t(1998) = −0.66, P > 0.10; Supplemental Fig. S2c). In contrast, we found no differences for mean in-field firing rate for Veh (paired-sample t-test, t(1005) = 0.63, P > 0.10] or CNO days [t(993) = −0.48, P > 0.10], nor did we find any differences between Veh and CNO days [independent sample t-test, t(1998) = −0.79, P > 0.10; Supplemental Fig. S2d]. We found no differences between tuning curve correlations between Veh and CNO days (Veh: r = 0.75 ± 0.15, CNO: r = 0.74 ± 0.15; Wilcoxon rank sum, z = 1.11, P > 0.10; Supplemental Fig. S2e).
Next, we examined the place cell properties between CNO and Veh days. While examining the main place field of a cell we found no difference in maximum in-field firing rate (Wilcoxon rank sum: z = −0.40, P > 0.10; Supplemental Fig. S2f), mean in-field firing rate (z = −0.40, P > 0.10; Supplemental Fig. S2g), or place field size (Wilcoxon rank sum z = 0.39, P > 0.10; Supplemental Fig. S2h). These results held true when we examined all place fields of a cell (not just the main field; data not shown): there were no differences in the number of place fields, place field size, mean in-field firing rate, or maximum in-field firing rate between CNO and Veh days (all P > 0.10]. These data suggest that disrupting the mPFC had no primary effect on place cell firing characteristics and therefore any differences found in theta sequences would not be due to place field instability.
mPFC disruption improved economic behavior.
Restaurant Row is a neuroeconomic spatial decision-making task in which rats make serial stay/skip choices for different flavors of food reward in a naturalistic foraging paradigm (Fig. 2A; Steiner and Redish 2014). Restaurant Row measures preference of the different flavors (value), which we operationally define as willingness to wait: how much of the signaled delays the rats were willing to tolerate. Because of the time constraint, to economically maximize reward on this task, a rat should prefer short delays over long delays. Preferences can be revealed through the thresholds, below which a rat was willing to wait for a given flavor and above which the rat left the zone before receiving the food reward, thus rejecting the offer (Steiner and Redish 2014; Sweis et al. 2018a, 2018b).
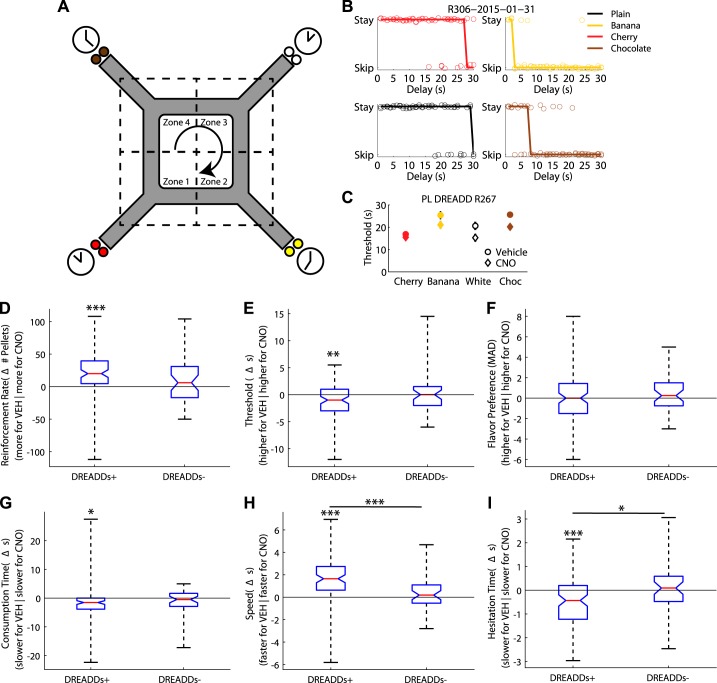
Fig. 2.
Compromising the medial prefrontal cortex (mPFC) with designer receptors exclusively activated by designer drugs (DREADDs) + clozapine N-oxide (CNO) improved optimal foraging behavior on the Restaurant Row task. A: schematic of the Restaurant Row task. On Restaurant Row, rats are required to make serial stay/skip choices (stay and receive the food pellet reward or skip and go to the next restaurant) for different flavored food rewards (color reflects flavor: white, plain; brown, chocolate; yellow, banana; red, cherry; flavor locations were constant throughout training/testing). B: stay-skip plots for 1 day of one rat. Each plot represents the stay/skip choice of the rat at each flavor (black, plain; brown, chocolate; yellow, banana; red, cherry) for the 1- to 30-s delays. Jitter has been added for display purposes. Rats usually waited for trials with short delays and skipped trials with large delays. The delay at which the function predicted an equal likelihood of stay and skip was defined as the threshold (see methods). Thresholds were different for different flavors, revealing a rat’s flavor preferences. C: thresholds for each flavor across training sessions [vehicle (Veh) n = 10; CNO n = 10] for an example rat R267 (session mean ± SE). Circle, Veh; diamond, CNO; white, plain; brown, chocolate; yellow, banana; red, cherry. D: compromising the mPFC with DREADDs administration (DREADDs+) improved foraging optimality by increasing the rats’ rate of reinforcement (number of pellets/h). In contrast, control rats not given DREADDs (DREADDs−) showed no differences in rate of reinforcement. Boxplot of the overall group median difference between Veh and CNO days and data for each DREADD+ rat (left) and DREADDs− (right). E: DREADDs+ rats showed a reduced willingness to wait for food, as measured by a decrease in threshold (see methods). DREADDs− showed no differences in threshold between CNO and Veh days. Group median threshold differences between Veh and CNO days are for DREADDs+ rats (left) and DREADDs− rats (right). F: changes in thresholds were not due to a blunting of flavor preferences as measured by the median average deviation (MAD; see methods) from threshold. CNO had no effect on flavor preferences as measured by the MAD from threshold for DREADDs− rats. Group median threshold differences between Veh and CNO days are plotted for DREADDs+ rats (left) and DREADDs− rats (right). G: CNO decreased the amount of time spent at the feeder before entering a new restaurant (consumption time) for DREADDs+ rats but had no effect on DREADDs− rats. H: DREADD+ rats ran faster on CNO days. CNO had no effect on running speed for DREADDs− rats. I: when a DREADDs+ rat quit a trial (hesitation time), they did so more quickly on CNO days. CNO had no effect on hesitation time for DREADDs− rats. Group median threshold differences between Veh and CNO days are plotted for DREADDs+ rats (left) and DREADDs− rats (right). *P < 0.05, **P < 0.01, ***P < 0.001.
Replicating previous results (Steiner and Redish 2014), rats exhibited individual flavor preferences such that each rat revealed a consistent threshold at each restaurant (Fig. 2B). Flavor preferences differed between rats but were consistent from day to day within rat (Fig. 2C and Supplementary Fig. 3).
To economically optimize food reward on this foraging task, rats should skip long delays, stay for short delays, and stay for more preferable food (revealed through the rat’s choices). While the rats did show a preference for short delays over long delays, they were significantly suboptimal in their food gathering, consistent with previous experiments on foraging tasks (Wikenheiser et al. 2013). Surprisingly, compromising the mPFC with CNO increased the rats’ overall rate of reinforcement by increasing the amount of food reward earned {number of pellets per session; ANOVA: main effect of Condition [F(1,156) = 8.1, P < 0.001] and Rat [F(8,156) = 6.27, P < 0.001], but no Condition*Rat interaction [F(8,156) = 1.01, P > 0.10]; Fig. 2D}. In contrast, control rats (rats with no DREADDs, given CNO/Veh) showed no differences in reward rate under CNO versus Veh {no main effect of Condition [F(1,72) = 2.21, P > 0.10], a main effect of Rat [F(3,72) = 11.28, P < 0.001], and no Condition*Rat interaction [F(3,72) = 0.17, P > 0.10]; Fig. 2D}. Though the mPFC rats significantly increased their rate of reinforcement on CNO days, this was not significantly different from control rats [F(1,230) = 2.12, P > 0.05].
CNO reduced how long mPFC-compromised rats were willing to wait for food {main effect of Condition [F(1,156) = 4.42, P < 0.05] and Rat [F(8,156) = 6.21, P < 0.001], but not a Condition*Rat interaction [F(8,156) = 1.24, P > 0.10]; Fig. 2E}. This shift occurred because mPFC-compromised rats stopped accepting the delays near threshold that these same rats were taking on Veh days. In contrast, control rats showed no differences in threshold between CNO and Veh conditions {no main effect of Condition [F(1,72) = 0.64, P > 0.10], no main effect of Rat [F(3,72) = 0.04, P > 0.10], and no Condition*Rat interaction [F(3,72) = 0.08, P > 0.10]; Fig. 2E}. Though mPFC rats significantly decreased their thresholds on CNO days, this was not significantly different from control rats [F(1,230) = 2.2, P > 0.05]. Compromising the mPFC induced the rodents to lower their willingness to wait out long delays for food and thereby increased their overall rate of reinforcement.
We hypothesized that this effect could be a result of reduced deliberative planning behavior (i.e., no longer deliberating over accepting delays near threshold) or reduced preferences for certain flavors (i.e., no longer waiting for long delays at preferred flavors). Even though the food pellets were theoretically similarly nutritious, rats did show individual flavor preferences (thus suggesting that they were optimizing subjective utility rather than raw number of food pellets). Therefore, a part of the increase in reward rate may have been due to a loss of individual preferences of one flavor over another. To examine this, we measured the MAD across flavor thresholds relative to the session median. Significant differences in the MAD would indicate large variability in threshold changes across flavors (i.e., a large change in threshold for one or two flavors while sparing the others would indicate loss of individual flavor preference), whereas small changes would indicate a consistent change in threshold across flavors. No change was found in the MAD for mPFC-compromised rats {a main effect of Rat [F(8,156) = 6.23, P < 0.001], but no effect of Condition [F(1,156) = 0.27, P > 0.10] nor a Condition*Rat interaction [F(8,156) = 0.18, P > 0.10]; Fig. 2F} or control rats {no main effect of Condition [F(1,72) = 0.03, P > 0.10], a main effect of Rat [F(3,72) = 6.98, P < 0.001], and no Condition*Rat interaction [F(3,72) = 0.44, P > 0.10]; Fig. 2F}, nor were there any differences between mPFC and control rats [F(1,230) = 1.69, P > 0.05]. Additionally, we have found that disrupting the orbitofrontal cortex impaired MAD, specifically altering more preferred flavors over others (Breton et al. 2015). Therefore, the changes seen in threshold and rate of reinforcement in mPFC-compromised rats were not due to altering thresholds for preferred flavors.
Second, we measured flavor preferences as time spent at the feeder after consumption (Sweis et al. 2018b). mPFC-disrupted rats spent less time-consuming reward on CNO days than Veh days {a main effect of Condition [F(1,156) = 8.53, P < 0.01] and Rat [F(8,156) = 17.23, P < 0.001], and a Condition*Rat interaction [F(8,156) = 2.56, P < 0.05]; Fig. 2G}; however, control rats showed no differences between CNO and Veh days {no effect of Condition [F(1,72) = 2.94, P = 0.09), a main effect of Rat [F(3,72) = 8.24, P < 0.001], and no Condition*Rat interaction [F(3,72) = 0.32, P > 0.10]; Fig. 2G}. Though mPFC rats significantly decreased their consumption time on CNO days, this was not significantly different from control rats [F(1,230) = 0.11, P > 0.05]. Taken together, the MAD and consumption time analyses suggest that mPFC disruption had no effect on flavor preference.
A second possibility is that the change in rate of reinforcement may have resulted from reduced deliberative planning behavior. We examined deliberative planning behavior by measuring the reaction time to skip a trial and VTE (see Vicarious trial and error below). mPFC-compromised rats did run faster under CNO {main effect of Condition [F(1,156) = 58.23, P < 0.01] and Rat [F(8,156) = 60.46, P < 0.001], and a Condition*Rat interaction [F(8,156) = 2.78, P < 0.01]; Fig. 2H}, while control rats showed no effect of CNO on running speed (no main effect of Condition [F(1,72) = 0.86, P > 0.10], a main effect of Rat [F(3,72) = 44.46, P < 0.001], and no Condition*Rat interaction [F(3,72) = 0.64, P > 0.10]; Fig. 2H). mPFC rats significantly increased their running speed on CNO days compared with control rats [F(1,230) = 13.13 P < 0.0001].
Compromising the mPFC increased the efficiency with which rats made decisions. First, we measured the mean time spent in the zone before skipping a trial (hesitation time). Hesitation time decreased on CNO trials {main effect of Condition [F(1,156) = 8.1, P < 0.001] and Rat [F(8,156) = 6.27, P < 0.001], but no Condition*Rat interaction [F(8,156) = 1.01, P > 0.10]; Fig. 2I} demonstrating that the rats were quicker about their decisions to skip a trial. In contrast, control rats showed no effect of CNO on hesitation time {no main effect of Condition [F(1,72) = 0.21, P > 0.10], a main effect of Rat [F(3,72) = 37.07, P < 0.001], and no Condition*Rat interaction [F(3,72) = 0.27, P > 0.10]; Fig. 2I}. mPFC rats significantly decreased their hesitation time on CNO days compared with control rats [F(1,230) = 4.00, P < 0.05]. These data suggest that disrupting the mPFC resulted in rats making their decision to quit a trial, or to start the next one sooner.
As a control, we transfected three additional rats and ran them on a noncognitive spatial foraging task (Supplemental Fig. S4a). In this task, rats were trained to run in a circle that was divided into four zones. At the north, south, east, and west coordinates, two food pellets were dispersed when the rat entered the zone. Unlike the mPFC-disrupted rats trained on Restaurant Row, these mPFC disrupted rats showed no change of running speed (Supplemental Fig. S4b). CNO had no effect on running speed [F(1,24) = 1.04, P > 0.10]: though there was a main effect of Rat [F(2,24) = 8.7, P < 0.01], we found no Rat*Condition interaction [F(2,24) = 0.08, P > 0.10]. mPFC disruption also failed to improve behavioral performance {rate of reinforcement; [F(1,24) = 0.74, P > 0.10]; Supplemental Fig. S4c}. Again, we found a main effect of Rat [F(2,24) =8.51, P < 0.01], but no Rat*Condition interaction [F(2,24) =0.40, P > 0.10]. Last, we measured consumption time, and unlike the mPFC DREADD rats trained on the Restaurant Row task, mPFC DREADD rats trained on this noncognitive task again showed no effect of CNO on consumption time [F(1,24) = 0.78, P > 0.10; Supplemental Fig. S4d]. There was a main effect of Rat [F(2,24) = 6.63, P < 0.01]; however, we found no Rat*Condition interaction [F(2,24) = 0.44, P > 0.10].
These data reveal that rats were initially not economically maximizing the Restaurant Row task, but compromising the mPFC made the rats more decisive and, surprisingly, improved the optimality of their behavior, a phenomenon that was specific to cognitive demanding Restaurant Row task.
DREADDs disrupted phase locking in the mPFC.
Theta and low gamma oscillations coordinate neuronal firing by entraining cells to their rhythm and facilitating information transfer across regions (Hyman et al. 2005; Jones and Wilson 2005; Siapas et al. 2005; Sirota et al. 2008). Comparing CNO to Veh days showed that disrupting the mPFC with DREADDs + CNO had no effect on the number of mPFC cells significantly phase locked to hippocampal theta (data not shown); however, CNO significantly altered the phase of which mPFC cells entrained to hippocampal theta [Watson-Williams two-sample test, F(1,110) = 9.80, P < 0.01; Fig. 3A].
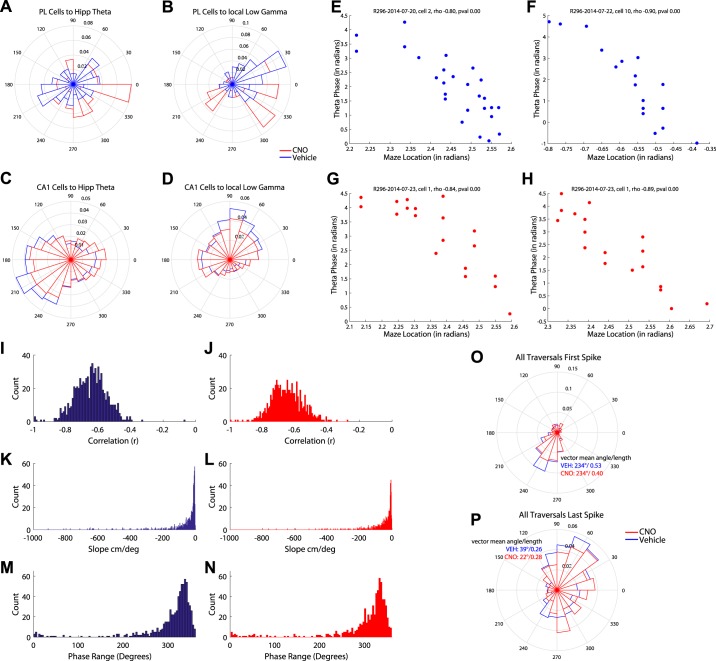
Fig. 3.
Silencing the medial prefrontal cortex (mPFC) altered phase locking. Polar plots are shown for all recorded mPFC and hippocampal cells phase locked to theta and gamma oscillations. A and B: silencing the mPFC with clozapine N-oxide (CNO) altered mPFC cells phase locking to hippocampal theta (A) and local low gamma (B). C and D: similarly, silencing the mPFC altered hippocampal place cell phase locking to local theta (C) and local low gamma (D). E–H: we measured phase precession for individual trials for vehicle (Veh; E and F) and CNO (G and H) days for hippocampal place cells. The correlation between theta phase and spatial location was similar between Veh (I) and CNO (J) days as were the slopes between Veh (K) and CNO (L) days. The theta phase ranges (see methods) were also similar between Veh (M) and CNO (N) days. O: disrupting mPFC impairs the initiation of a sequence. We measured the theta phase relationship of the first and P) last spike of a run through a place field for Veh days (blue) and CNO days (red). mPFC disruption had no effect on the phase locking of the first spike to the theta oscillation; however, it altered the phase locking relationship of the last spike of the field.
mPFC disruption had a larger effect on neuronal phase locking to local low gamma. CNO significantly increased phase locking of mPFC cells to local gamma (Veh = 30%, CNO = 57%, χ2 for proportions = 8.01, P = < 0.005). The data suggest that this increase is likely a result of nonsignificant phase-locked cells being silenced with CNO, though given that CNO and Veh comparisons are across days we cannot conclusively determine this (Table 2). Additionally, CNO significantly altered the phase at which mPFC cells phase locked to local low gamma {Watson-Williams two-sample test [F(1,110) =15.91, P < 0.001]; Fig. 3B}.
Table 2.
Changes in firing rate for mPFC cells significantly and nonsignificantly phase locked to local low gamma oscillations
| CNO* | CNO ns | Veh* | Veh ns | Total | |
|---|---|---|---|---|---|
| Decrease FR | 17 | 11 | 11 | 15 | 54 |
| Increase FR | 8 | 7 | 8 | 32 | 55 |
| No change | 0 | 1 | 1 | 0 | 2 |
| Total | 25 | 29 | 20 | 47 | 111 |
All medial prefrontal cortex (mPFC) cells were categorized as increasing firing rate (FR), decreasing firing rate, or no change in firing rate between the premaze rest and the postmaze rest (within session comparison). These cells were also categorized as to whether they were significantly phase locked to local gamma oscillations. CNO, clozapine N-oxide; Veh, vehicle.
Significantly phased locked; ns, not significantly phased locked.
DREADDs disrupted phase locking in CA1.
The mPFC and hippocampus are hypothesized to iteratively engage each other during decision making (Eichenbaum 2017; Gordon 2011; Wang et al. 2015). We therefore asked how disrupting the mPFC would alter CA1 dynamics. Disrupting the mPFC had no effect on the number of CA1 cells significantly phase locked to hippocampal theta (data not shown); however, it did alter the phase at which cells were entrained to theta {Watson-Williams two-sample test [F(1,2341) = 6.30, P < 0.05]; Fig. 3C}. In contrast, CNO decreased the proportion of significantly phase-locked CA1 cells to local low gamma (Table 2) and altered the phase they entrained to local low gamma oscillations {Watson-Williams two-sample test [F(1,2341) = 6.3, P < 0.01]; Fig. 3D}.
mPFC disruption had no effect on place cell phase precession.
As a rat runs through a cell’s place field, the cell will fire at earlier and earlier phases along the theta oscillation, a phenomenon termed “phase precession.” Theta sequences were once believed to be a result of phase precession (O’Keefe and Recce 1993; Skaggs et al. 1996), though theta sequences and phase precession can be dissociated from each other (Feng et al. 2015). We examined phase precession on a trial-by-trial basis for the predominant place field of each place cell (some cells may have had more than one place field; these fields were excluded from analysis) for Veh (Fig. 3, E and F) and CNO (Fig. 3, G and H) days. As expected, theta phase and spatial position were negatively correlated [Veh: r = −0.65 (SD 0.10) Fig. 3I; CNO: r = 0.63 (SD 0.11); Fig. 3J], though no differences were found between CNO and Veh [2-sample t-test t(1413) = 0.60, P > 0.10]; they had a negative slope [Veh: β = −23.47 (SD 461.28); Fig. 3K; CNO: β = −29.2 (SD 527.8); Fig. 3L, no difference between CNO and Veh (Wilcoxon rank sum z = 1.54, P > 0.10)] and an average phase range around 327° [Veh 327.6 (SD 33.3°); Fig. 3M; CNO 327.4 (SD 35°) Fig. 3N, no difference between Veh and CNO Watson-Williams multisample test for equal means F(1,1416) = 0.816, P > 0.10]. We found no differences in the correlation between theta phase and spatial location for Veh and CNO days. Similarly, we found no differences in the phase precession slope between Veh and CNO days. We measured the differences between only significant trials and still found no differences in slope (data not shown). Nor did we find a difference in the percentage of significant traversals [note that not every traversal shows clear phase precession, potentially due to subtle changes in trajectory (Huxter et al. 2008) or overdispersion (Olypher et al. 2002) between CNO and Veh place cells (Veh = 59.7%, CNO = 59.4%, Wilcoxon rank sum z = 0.37, P > 0.10)]. The phase range was also comparable between Veh and CNO days.
mPFC disruption affected the initiation of sequences more than the conclusion.
Next, we measured the phase of firing of the first spike in each traversal and the last spike in each traversal of a cell’s main place field (43,135 traversals of a place field between 2,179 cells). As expected, place cells fired on the ascending phase of the theta cycle as the rat entered the place field and precessed to firing on the descending phase of the theta cycle upon exiting the place field (Fig. 3, O and P). Disrupting the mPFC did not change the phase of the first spike in the traversal [vector mean angle/length Veh: 234°/0.53, CNO: 234°/0.40; Watson-Williams two-sample test, F(1,11450) =0.0081, P > 0.10; Fig. 3O] but did change the phase of the last spike in the traversal [vector mean angle/length, Veh: 39°/0.26, CNO: 22°/0.28; Watson-Williams two-sample test, F(1,11450) =7.841, P < 0.01; Fig. 3P]. These data suggest that disrupting the mPFC with DREADDs altered hippocampal sequences by impairing place cell spiking that encoded information about the rat’s location in space (local information on the descending phase of the theta cycle) more than about where the rat is going (sweeps forward on the ascending phase of the theta).
Local and nonlocal spatial decoding differed on descending and ascending theta phases.
The theta signal is often depicted as sinusoidal (Fig. 4A, top) but is actually more sawtooth shaped (Fig. 4A, middle; Amemiya and Redish 2018; Belluscio et al. 2012; Buzsáki et al. 1985). Place cell firing is believed to represent local and nonlocal representations of space along different phases of the theta cycle (Fig. 4A; Gupta et al. 2012; Mehta et al. 2002; Sanders et al. 2015; Yamaguchi et al. 2002). Current theories suggest that hippocampal sequences consist of two components, one defining the current location of the animal, and the other defining nonlocal information. These two components appear at different phases of the theta cycle and contribute to an asymmetry in the shape of theta. Because this asymmetry is easily measurable on each individual cycle (Fig. 4B), it is a robust measure that does not rely on large ensemble sizes. To assess the changes between local and nonlocal representations of space we measured the asymmetry index of individual theta cycles (Fig. 4B; Belluscio et al. 2012; see methods). The asymmetry index was calculated as the log ratio of the duration of the ascending phase and the descending phase. A theta cycle with a more negative asymmetry index has a longer descending phase (hypothesized to represent more local information), whereas a theta cycle with a positive asymmetry index has a longer ascending phase (hypothesized to represent more nonlocal information; Belluscio et al. 2012).
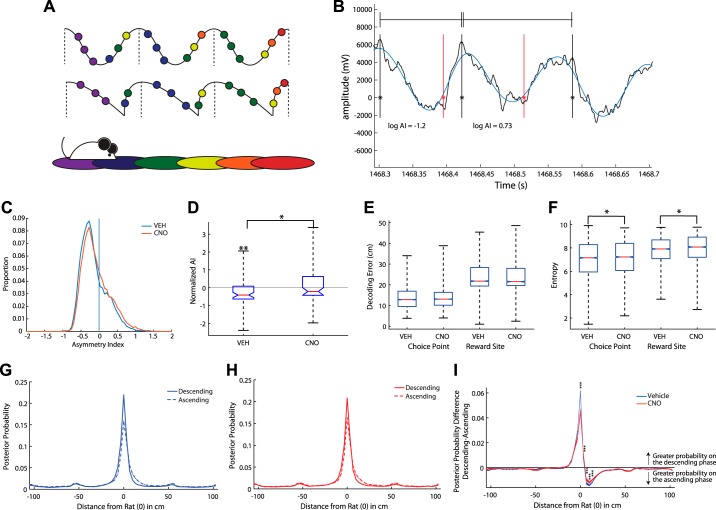
Fig. 4.
Local and nonlocal spatial decoding were found on the descending and ascending theta phases. A: theta oscillations are typically depicted as sinusoidal (top); however, they are often more saw tooth shaped (middle). As a rat runs through space (bottom), the current and upcoming locations are hypothesized to be represented by place cell spiking on the descending and ascending phases of the theta oscillation, respectively. B: an example trace of a raw theta signal (black) and the filtered theta signal (blue). Peaks are marked with a solid black line, troughs are marked with a solid red line. We measured the asymmetry index (AI) of individual theta cycles (peak to peak; Belluscio et al. 2012; see methods). A negative score represented a longer descending phase than ascending phase. C: the AI distribution was positively skewed, suggesting that most of the theta cycles had a negative AI (smaller ascending phase and longer descending phase). D: clozapine N-oxide (CNO) reduced the AI, making theta cycles more symmetric. E: we measured the decoding error at the choice point (for qualified theta cycles) and at the reward site (all theta cycles). We found no difference in decoding error between vehicle (Veh) and CNO days at either location. F: we found less entropy on Veh days. G: we measured the posterior probability along a linearized version of the maze for all ascending and descending phases of qualified theta cycles on Veh days. The maze was divided into 64 bins and the decoded posterior probability was aligned to the rat (at 0). The posterior probability was greater for local representations immediately near the rat on the descending phase of theta than the ascending phase. Areas further ahead of or behind the rat showed greater nonlocal decoding on the ascending phase of theta. H: same as G but for CNO days. As with Veh days, the probability distributions for the ascending and descending phases of theta were significantly different on CNO days. The posterior probability was greater for local representations immediately near the rat on the descending phase of theta than the ascending phase. Most areas further ahead of or behind the rat showed greater nonlocal decoding on the ascending phase of theta. Due to the shape of the maze, we suspect the minor peaks at 50-cm intervals are a result of the linearization of the maze. I: disrupting medial prefrontal cortex with CNO impaired this relationship. We found a reduced posterior probability for both local representations on the descending phase of theta cycles near the rat and nonlocal representations in front of the rat on the ascending phase of theta cycles. *P < 0.05, **P < 0.01; ***P < 0.0008.
The asymmetry index distribution is positively skewed, suggesting more asymmetric cycles (i.e., more local spatial firing; Fig. 4C), consistent with previous studies (Amemiya and Redish 2018; Belluscio et al. 2012). Veh theta cycles were primarily asymmetric [Veh = −0.131 (SD 0.0033), CNO =−0.055 (SD 0.0035)]; however, disrupting the mPFC with CNO resulted in more symmetric theta cycles (Veh: Wilcoxon signrank z = −2.74, P < 0.01; CNO: signrank z = 0.49, P > 0.10; Veh versus CNO: rank sum z = −2.22, P < 0.01; Fig. 4D). To dissociate the effects of running speed we ran a regression examining the asymmetry index with condition and speed as variables and found a significant effect of condition (β = 0.07, P < 0.001) but not speed (β = −0.0004, P > 0.10). This suggests that, under mPFC disruption, CA1 cells spent more time in the part of the theta cycle that is more nonlocal, but it does not necessarily mean that the nonlocal information is sequentially meaningful.
Next, we set out to determine whether CNO altered the rat’s decoding quality with two decoding measures: entropy and decoding error. We measured the entropy over the decoded posterior probability (see methods). We measured decoding error as the weighted distance between each decoded location bin and the rat’s actual position (weighted by the posterior probability in that bin). We also estimated decoding error as the distance from the maximum posterior probability location and the rat’s actual position and found similar results. We measured the decoding error at the choice point (for qualified theta cycles) and at the reward site (all theta cycles). We found no difference in decoding error between Veh and CNO days at either location [i.e., while running or immobile Veh = 13.59 (SD 4.9); CNO = 13.58 (SD 4.56); Wilcoxon rank sum, Choice Point: z = −1.15, P > 0.10; Feeder: z = −0.52, P > 0.10; Fig. 4E]. We did find a small, but significant, increased entropy on CNO days at both the choice point [Veh = 7.09 (SD 1.49); CNO = 7.14 (SD 1.53); Wilcoxon rank sum; z = −2.36, P < 0. 01] and reward sites [Veh = 7.80 (SD 1.1), CNO = 7.9 (SD 1.2), z = −5.40, P < 0.01; Fig. 4F]. Taken together, these data suggest that CNO did not impair the hippocampus’ overall ability to encode position.
We measured the posterior probability along a linearized version of the maze for all ascending (presumed nonlocal) and descending phases (presumed local) of qualified theta cycles on Veh days. The maze was divided into 64 bins and the decoded posterior probability was aligned to the rat (at 0). We performed a two-sample Kolmogorov-Smirnov goodness-of-fit hypothesis test and found that the probability distributions were significantly different between the ascending and descending phases of theta for Veh days (descending versus ascending distributions Kolmogorov-Smirnov test for nonparametric data, D = 0.25, P < 0.05; Fig. 4G). The averaged posterior probability was higher on the descending phase than the ascending phase near the rat on Veh days (−13.2 cm behind the rat to 3.3 cm in front of the rat; all P < 0.0008; mean ± 99.92% CI (bin −16.3 cm to −13.2 cm behind the rat was a trend at P = 0.0026; Fig. 4G). However, as the distance from the rat increased, so did the posterior probability for ascending phase theta cycles (all other locations in front of or behind the rat; all P < 0.0008; Fig. 4G).
CNO days showed similar local/nonlocal representations, probability distributions for ascending and descending theta phases were significantly different on CNO days (descending versus ascending distributions Kstest2 stat = 0.25, P < 0.05; Fig. 4H). The posterior probability was greater for local representations on the descending phase of theta than the ascending phase immediately near the rat (top; 13.2 cm behind the rat to 3.3 cm in front of the rat; all P < 0.0008). Most areas further ahead of or behind the rat showed greater nonlocal decoding on the ascending phase of theta (most bins P < 0.0008, except: −16.5 to −13.2 cm behind the rat was a trend at 0.0017, bins −36.3 to −33 cm behind the rat and −23.1 to −19.8 failed to reach significance; Fig. 4H). This local/nonlocal relationship was significantly decreased from Veh days. CNO days had a smaller posterior probability for both local representations on the descending phase and nonlocal representations in front of the rat on the ascending phase (Veh versus CNO: all P < 0.0008; mean ± 99.92% CI; Fig. 4I). These data support the hypothesis that the descending phase of the theta cycle contains more local information whereas the ascending phase of the theta cycle contains more nonlocal information.
To directly measure the effects of mPFC disruption on CA1 theta sequences, we calculated the coherent sequences of place cell activity during each theta cycle, “the sequence score,” for theta cycles with at least five cells firing spikes (Gupta et al. 2010, 2012; see methods). To determine a sequence score, individual theta cycles had to meet a theta/delta ratio and running speed criteria (see methods). Though CNO days had more qualified theta cycles than Veh days (i.e., CNO days had more theta cycles that met the theta/delta ratio and running speed qualifications; χ2 = 343.77, P < 0.001), there were significantly more cycles with no cell spikes on CNO trials (χ2 = 5482.2, P < 0.001; CNO: 46.5% versus Veh: 38.1%), and CNO trials exhibited significantly fewer sequences (χ2 = 756.3, P < 0.001; Veh: 18.3% versus CNO: 15.9%). Therefore, disrupting the mPFC reduced the number of theta sequences in the hippocampus.
A few examples of theta sequences are shown in Fig. 5A. Consistent with previous experiments (Gupta et al. 2010, 2012), median sequence scores were predominately positive, suggesting a forward trajectory (Fig. 5B). This relationship was slightly but significantly decreased under CNO (χ2 = 22.5, P < 0.001; Veh: 55.2% versus CNO: 53.9%). As expected, the median sequence scores were significantly different from zero (Veh: signrank z = 25.62, P < 0.001; CNO: signrank z =17.39, P < 0.001; Fig. 5C). As a control, we calculated the sequence score of the same cell ensembles after shuffling their firing order within their theta cycle (see methods). Median shuffled sequence scores were not significantly different from zero (all P > 0.05; Fig. 5C), nor were shuffled Veh and CNO data significantly different from each other (all P > 0.05]. Veh sequence scores were significantly different from shuffled Veh data (Veh: rank sum z = 19.16, P < 0.001). Although CNO sequences were also significantly different from shuffled CNO data (CNO: rank sum, z = 12.36, P < 0.001), they were also significantly reduced relative to Veh (rank sum z = 4.65, P < 0.001; Fig. 5C). Therefore, place cell sequences were impaired by mPFC disruption. These analyses were robust to sequence selection criteria; both weaker and stronger criteria found qualitatively similar results (Supplementary Fig. 5, a–d). In theory, the number of cells that fired within a single theta cycle can increase the sequence score. To control for this, we measured the sequence score for cell ensemble sizes ranging from 3 to 10 for Veh data and shuffled Veh data. As can be seen in the shuffled data, increasing the size of the cell ensemble does not necessarily increase the sequence score (Fig. 5D). We did a similar comparison for Veh and CNO days and found that the median sequence scores were lower for CNO days (Fig. 5E). An ANCOVA analysis (see methods) found a significant difference between the slopes of the sequence score as a function of ensemble size between CNO and Veh conditions [F(1) = 213, P < 0.00001].
Fig. 5.
Disrupting the medial prefrontal cortex (mPFC) with designer receptors exclusively activated by designer drugs (DREADDs) altered hippocampal theta sequences. A: examples of sequences (top row) for vehicle (Veh) (left) and clozapine N-oxide (CNO; right) days. Each panel represents a theta sequence. The gray dots represent all trajectories taken. The colored dots represent the place cell location best represented in the sequence. The “x” marks the location of the rat on the maze. The change in color represents cell order in the firing sequence. The same cell firing order (represented in the same colors as the top panel) are plotted along the theta sequence (bottom). B: we measured the sequence score, the coherent sequence of place cell activity, of individual theta cycles for Veh and CNO days (Gupta et al. 2010, 2012; see methods). As a control we calculated the sequence scores of the same data set with the spiking ordered shuffled (see methods for shuffling procedure). C: sequence scores were significantly different from zero. Sequence scores were smaller for CNO days. The real data were significantly different from the shuffled data. The shuffled data, however, were not significantly different from zero or each other. D: larger ensemble sizes do not necessarily produce larger sequence (Seq) scores. We measured the median sequence score for ensembles ranging from 3 to 10 cells for Veh data (dark blue) and shuffled Veh data (light blue). E: examining the median sequence score across different ensemble sizes reveals that CNO (red) theta cycles consistently had lower sequence scores than Veh (dark blue) theta cycles. F and G: examples of correlation between the length of the theta cycle measured against the Bayesian decoded path length for a Veh (F) and CNO (G) day. H: the size of the theta cycle positively correlated with the Bayesian decoded path length on Veh days (I) and CNO days; however, this relationship was significantly reduced in CNO days compared with Veh days. *P < 0.05, ***P < 0.001.
Within each theta cycle, hippocampal sequences proceed to the upcoming goal on both binary decision and foraging tasks (Gupta et al. 2012; Wikenheiser et al. 2013). To investigate the contribution of the mPFC to representations by CA1 sequences we measured the decoded path traced out during significant sequences, which, consistent with previous studies, were predominantly forward (65% forward versus 35% backward; Fig. 5, F and G; Wikenheiser and Redish 2013; Zheng et al. 2016). Previous studies have shown that the size of the theta period correlates with the length of the decoded sequence path on cognitive tasks (Gupta et al. 2012) and we replicated this result on Veh (r = 0.25, P < 0.01; Fig. 5H) and CNO days (r = 0.16, P < 0.01; Fig. 5I). Taken together, these data suggest that look-ahead distance is cognitively driven, not speed driven, on cognitive tasks.
Interestingly, mPFC-disruption reduced the average theta cycle period in CA1 (signrank z = 5.35, P < 0.001; Supplementary Fig. 5e) and reduced the theta period/path length relationship in the CA1 ensembles (Veh versus CNO: z = 2.47, P < 0.05; Fig. 5I). These data suggest that disrupting the mPFC altered normal sequence dynamics in CA1, by disrupting the relationship between local/nonlocal spatial firing and disrupting the relationship between theta cycle size and decoded path length.
Theta cycle correlated with trial delay.
Theta cycle period was positively correlated with trial delay, with longer theta cycles appearing when rats were faced with longer delays (Fig. 6A). Both Veh and CNO days showed this correlation (Veh: signrank z = 5.88, P < 0.001; CNO: signrank z = 5.08, P < 0.001); however, the relationship was significantly reduced on CNO days (Veh versus CNO: rank sum z = 2.94, P < 0.01; Fig. 6B). We performed a stepwise regression with zone delay, running speed, and drug condition (Veh versus CNO) as variables. After accounting for drug condition (β = −0.005, t = −9.46, P < 0.001) and running speed (β = −0.005, t = −140.9, P < 0.001), zone delay (β = −0.001, t = 39.65, P < 0.001) still significantly accounted for the variability in theta cycle size.
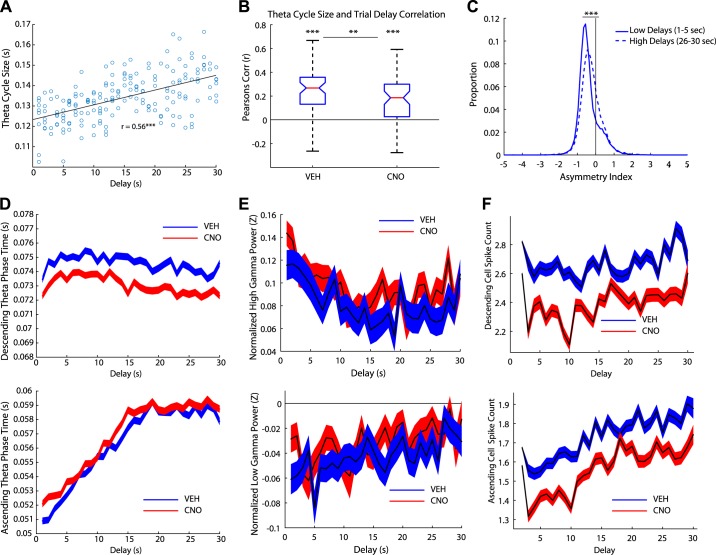
Fig. 6.
Theta oscillations correlated with trial delays. A: an example day of the relationship between theta cycle size and trial delays for one rat on 1 day. B: theta cycle size was positively correlated with trial delay for both vehicle (Veh) and clozapine N-oxide (CNO) days. However, the relationship for CNO days was significantly lower than Veh days. C: distribution of the asymmetry index (AI) for low delays (1–5 s) and high delays (26–30 s) on Veh days. High delays were more symmetric than low delays, suggesting that high delays exhibited more nonlocal activity. D: we measured the duration of the descending theta phase across delays (top). The descending duration decreased across delays (mean ± SE) and was reduced on CNO days. In contrast, the ascending duration increased with delay, suggesting there was more nonlocal activity during longer trial delays (bottom, mean ± SE). The duration of the ascending theta phase increased on CNO days. E: we measured the normalized high gamma power across trial delays (top). High gamma power slightly decreased across delay. In contrast, the normalized low gamma power increased across trial delays (bottom). F: the spike count for all cells was measured across the trial delays during the descending phase (top) and ascending phase (bottom). Spike counts linearly increased on the ascending phase as the trial delay increased. **P < 0.01, ***P < 0.001.
We examined the asymmetry index for low (1–5 s) and high delays (26–30 s) as another measure to examine the relationship between sequences and delay. Low delays were more asymmetric than high delays (Veh: Wilcoxon rank sum z =−37.55, P < 0.001; Fig. 6C). This suggests that low delays had more local spatial firing and high delays had more nonlocal spatial firing, even though the rats traversed the same spatial distance to reach the goal in both conditions. We further explored this by measuring the length of the ascending and descending phases of theta oscillations. The duration of the descending phase time (local representations) decreased across delays (Fig. 6D, bottom). We performed a stepwise regression with zone delay, running speed, and drug condition as variables. After accounting for drug condition (β = −2.60, P < 0.001) and running speed (β = −0.40, P < 0.001), zone delay (β = −0.18, P < 0.001) still significantly contributed to changes in the length of the descending phase across delays.
In contrast, the duration of the ascending time (nonlocal representations) increased with delay (Fig. 6D, top). Again, after factoring out drug condition (β = 2.32, P < 0.001) and running speed (β = −0.64, P < 0.001), the contribution of zone delay (β = 0.45, P < 0.001) remained significant.
Periods of high and low gamma within the theta cycle are believed to reflect local and nonlocal representations, respectively (Bieri et al. 2015). To examine whether low and high gamma oscillations reflected the trial delay we measured gamma power across delay (Fig. 6E top). We ran a stepwise regression on low and high gamma power with drug condition, running speed, and trial delay as variables. After factoring out running speed (β = 0.004, P < 0.001), trial delay still had an effect on high gamma power (β = 0.002, P < 0.001); however, drug condition failed to have an effect. Similarly, after factoring out running speed (β = 0.004, P < 0.001), trial delay still had an effect on low gamma power (β = 0.002, P < 0.001); however, drug condition had no effect (Fig. 6E, bottom).
Next we questioned whether the trial delay could be reflected in the spike count; therefore, we measured the number of spikes on the ascending and descending phase of the theta cycle and binned the data in relation to the delay counting down (i.e., 30 s left, 29 s left, 28 s left, etc.). Place cells increased their firing in a linear manner on the ascending phase of the theta cycle (Fig. 6F, top). In other words, as the delay decreased, so did the firing of the place cells. We ran a stepwise regression with drug condition, running speed, and trial delay as variables. After factoring out drug condition (β = −0.17, P < 0.001) and running speed (β = 0.03, P < 0.001), trial delay still had an effect on the number of spikes in the ascending phase (β = 0.009, P < 0.001). We performed the same analysis on the descending theta phase (Fig. 6F, bottom). After factoring out drug condition (β = −0.32, P < 0.001) and running speed (β = 0.06, P < 0.001), trial delay still had an effect on the number of spikes in the descending phase (β = 0.001, P < 0.001).
Taken together, these data suggest that the hippocampus represented time across the delay. We found that the theta cycle, specifically the ascending phase of the theta cycle, as well as low gamma power, and spike count were all modulated by the trial delay.
Vicarious trial and error.
Disrupting the mPFC improved performance on the Restaurant Row task by diminishing the time spent deciding whether to stay or go at choice points. Furthermore, it disrupted theta sequences in the hippocampus. These data support current models that suggest that prefrontal areas are continuously engaged with the hippocampus, driving the hippocampus to search through contextually appropriate memories to make goal-directed decisions (Wang et al. 2015).
When rats come to binary choices, they sometimes pause and orient back and forth toward the alternate options, a behavior first identified during the 1930s and hypothesized to entail a search-and-evaluate process, termed vicarious trial and error (VTE; Muenzinger and Gentry 1931; Muenzinger 1938; Redish 2016; Tolman 1938). Subsequent studies have confirmed that hippocampal sequences proceed farther ahead during VTE and include sequences running to each alternate goal (Johnson and Redish 2007), both ones that are subsequently chosen and ones that are not (Amemiya and Redish 2016; Papale et al. 2016).
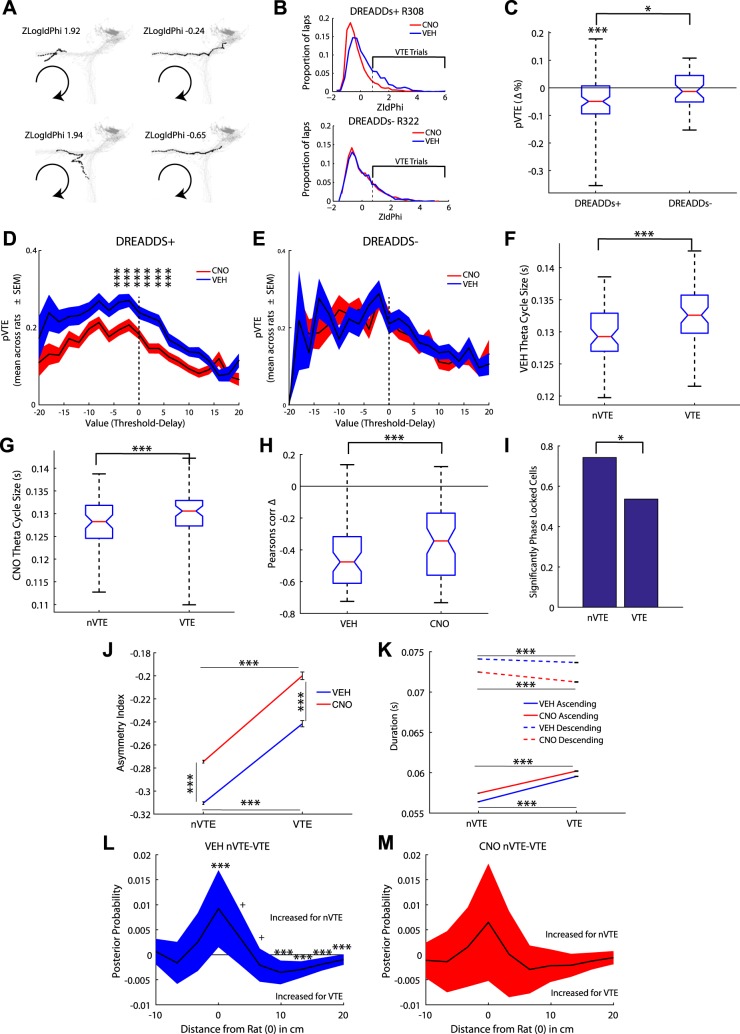
The changes in hesitation time seen above (Fig. 2H) imply that mPFC disruption likely disrupted VTE behavior. We quantified VTE behavior by measuring the z-scored angular displacement (zIdPhi) of the rodent’s head at the choice point upon entering a new zone and cued to the current delay (Papale et al. 2012; Schmidt et al. 2013; Fig. 7A; see methods). Behavioral paradigms with VTE behavior show a positively skewed distribution (Schmidt et al. 2013; Fig. 7B). Compromising the mPFC reduced VTE behavior [t(86) = −5.13, P < 0.001; Fig. 7C]. However, control rats showed no differences in VTE behavior between CNO and Veh conditions (Fig. 7C). mPFC rats significantly decreased their probability of VTE (pVTE) on CNO days compared with control rats [F(1,230) =5.2, P < 0.05].
Fig. 7.
Disrupting the medial prefrontal cortex (mPFC) reduced deliberative vicarious trial and error (VTE) behavior. A: example passes through the choice point. VTE was quantitatively measured as the integrated absolute angular velocity (IdPhi) of the rat’s head across the pass through the choice point (see methods). Large log IdPhi scores are indicative of VTE events (left column) whereas low log IdPhi scores are indicative of non-VTE (nVTE) events (right column). B: On a task with VTE trials, as in Restaurant Row, the IdPhi distribution will be positively skewed, with the size of the shoulder indicative of the proportion of VTE trials. VTE distributions for clozapine N-oxide (CNO) and vehicle (Veh) days for a rat administered designer receptors exclusively activated by designer drugs (DREADDs; DREADDs+; top) and a rat not given DREADDs (DREADDs−; bottom). C: compromising the mPFC reduced VTE behavior. D: on Restaurant Row rats can encounter “good deals” (delay < threshold), “bad deals” (delay > threshold), and “difficult decisions” (delay≈threshold). DREADDs+ rats showed reduced VTE specifically on difficult decisions. E: in contrast, no differences were seen between Veh and CNO days for DREADDs− rats. F and G: the average theta cycle size was measured for VTE and nVTE. Theta cycle size increased on VTE trials on both Veh (F) and CNO (G) days. H: the size of the theta cycle correlated with running speed; however, CNO reduced this relationship. I: we measured the phase locking of hippocampal place cells to hippocampal theta during VTE and nVTE trials. Interestingly, the proportion of significantly phase-locked cells dropped during VTE trials. J: we measured the asymmetry index (AI) of individual theta cycles for VTE and nVTE trials. VTE trials had a smaller AI than nVTE trials for both Veh and CNO trials, suggesting more nonlocal representations of space during VTE. K: we measured the length of the ascending and descending phase of VTE and nVTE trials. The duration of the ascending phase of theta cycles increased during VTE trials on Veh and CNO days. L and M: to further examine this we measured the posterior probability in relation to the rat’s location immediately behind and in front of the rat (rat is at 0). L: the posterior probability was higher for local representations on nVTE trials than VTE trials. In contrast, the decoded probability was higher for nonlocal representations in front of the rat on VTE trials (difference in the mean ± CI 99.50%). M: this relationship was not apparent on CNO days (difference in the mean ± CI 99.50%). +P < 0.08; *P < 0.05, ***P < 0.005.
When an animal reached a restaurant they could encounter a delay much higher than threshold (i.e., a 30-s delay and a 15-s threshold, which is an easy decision to skip), a delay much lower than threshold (i.e., a 5-s delay and a 15-s threshold, which is an easy decision to stay), or a delay near threshold (i.e., a 17-s delay and a 15-s threshold, which is a difficult decision as whether to stay or skip). VTE behaviors appear on the Restaurant Row task particularly at decisions just above threshold (Steiner and Redish 2014; Sweis et al. 2018b). The data from this cohort of rats replicated this earlier finding (Fig. 7D). We conducted several planned comparisons (corrected for multiple comparisons P < 0.0048) examining VTE between CNO and Veh days across different deviations of delay from threshold (value) ranging from −20 s to +20 s from threshold, in 2-s bins. Rats with compromised mPFC showed value-related deficits in VTE specifically during difficult decisions: values between −6 to −4 s [t(86) = −3.37, P < 0.002], −4 to −2 s [t(86) = −3.91, P < 0.001], −2 to 0 s [t(86) = −2.94, P < 0.005], 0 to 2 s [t(86) = −2.94, P < 0.005], 2 to 4 s [t(86) = −3.40, P < 0.002], and 4 to 6 s [t(86) = −3.36, P < 0.002; Fig. 7D] all showed significant decreases in pVTE under CNO. The control group showed no value related pVTE differences between CNO and Veh days (P > 0.20 for all comparisons; Fig. 7E). Comparing the pVTE across different trial values between the DREADD rats and non-DREADD control rats revealed pVTE varied across different trial values {a main effect of Value [−20 to 20 in 2-s bins: F(20,4716) = 20.59, P < 0.001]} across conditions and drugs {no Condition*Value interaction [F(20,4716) = 0.67, P > 0.05] or Drug*Value interaction [F(20,4716) = 1.25, P > 0.05]}. This pVTE distribution (i.e., more pVTE at difficult decisions) was consistent across groups {no main effect of Virus [PFC DREADDs versus non-DREADD Control: F(1,4716) = 1.58, P > 0.05]}, that CNO reduced pVTE {a main effect of Drug [CNO versus Veh: F(1,4716) = 31.62, P < 0.001]}, specifically for the mPFC DREADD rats {a Condition*Drug interaction [F(1,4716) = 18.5, P < 0.001]}. Next we examined whether disrupting the mPFC affected CA1 neural processes during VTE. During VTE, hippocampal place cells sweep serially toward goal locations while theta oscillations are evident in the local field potential (Johnson and Redish 2007). Theta periods were significantly longer on VTE trials than non-VTE (nVTE) trials under both Veh (signrank, z = 5.96, P < 0.001; Fig. 7F) and CNO conditions (z = 6.57, P < 0.001; Fig. 7G). Though the theta cycle size was negatively correlated with running speed for both Veh and CNO days (signrank; Veh: z = −6.58, P < 0.001; CNO: z = −6.57, P < 0.001), CNO significantly reduced this relationship (z = −3.03, P < 0.001; Fig. 7H). 74% of CA1 place cells recorded were phase locked to theta during nVTE trials; however, this proportion significantly dropped to 54% during VTE trials (χ2 for proportions = 86.82, P < 0.001; Fig. 7I).
Nonlocal firing is increased during VTE (Amemiya and Redish 2016; Papale et al. 2016), which would predict a more symmetric asymmetry index in the theta cycle (Amemiya and Redish 2018). We found that the asymmetry index shifted to be significantly more symmetric during VTE trials than nVTE trials for Veh days (nVTE versus VTE: rank sum z = −22.64, P < 0.001), replicating previous results (Amemiya and Redish 2018). VTE trials were also more symmetric on CNO days (nVTE versus VTE: rank sum z = −20.47, P < 0.001; Fig. 7J). This result is consistent with previous studies in our laboratory that have shown more nonlocal cell firing during VTE trials (Amemiya and Redish 2016; Papale et al. 2016). Measuring the length of the descending and ascending phases during VTE and nVTE trials showed that the duration of the ascending phase increased during VTE trials for both Veh (rank sum z = −70.7, P < 0.001) and CNO days (z = −53.11, P < 0.001; Fig. 7K). As can be seen in Fig. 7K the increase in theta cycle size seen on VTE trials results primarily from an increase on the ascending phase, more so than a decrease on the descending phase. Taken together, these data suggest that there are more nonlocal representations of space during VTE trials than nVTE trials. Therefore, we examined the posterior probability of qualified theta cycles (see methods) in relation to the rat. We measured the difference between nVTE and VTE trials (paired t-tests corrected for multiple comparisons). As expected, the posterior probability was significantly greater for local representations for nVTE trials than VTE trials [Current location: t(21154) = 3.36, P < 0.001; up to 3.3 cm ahead of the rat: t(21154) = 1.86, P = 0.063; mean ± 99.5% CI] and nonlocal decoding was higher for VTE trials right in front of the rat [3.3–6.6 cm: t(21154) = −1.76, P = 0.077; 6.6–9.9 cm: t(21154) = −4.19, P < 0.0001; 9.9–13.2 cm: t(21154) = −5.07, P < 0.0001; 13.2–16.5 cm: t(21154) = −4.18, P < 0.0001; 16.5–19.8 cm: t(21154) = −2.74, P < 0.01; Fig. 7L]. Disrupting the mPFC with CNO diminished this relationship: local and nonlocal representations of space were no longer significantly differentially represented on nVTE and VTE trials (all P > 0.50; Fig. 7M). Taken together, the data suggest that disrupting mPFC impaired the initiation of sequence processes in the hippocampus and was mirrored by behavioral deficits in VTE behavior on CNO days.
DISCUSSION
The mPFC supports a myriad of cognitive abilities including working memory, long-term memory consolidation, and executive functions including decision making, attention, and behavioral flexibility (Kesner and Churchwell 2011); studies have shown disruptions in working memory and perseverative errors with mPFC lesions (Guise and Shapiro 2017; Rich and Shapiro 2007). We found that disrupting the mPFC with DREADDs actually improved the rat’s performance on the Restaurant Row foraging task. Given the time constraints on the Restaurant Row task, normal rats did not economically maximize their behavior, partially due to waiting for long delays and partially due to hesitating in the choice zone when skipping long delays. The hesitation within the choice zone was specifically seen when rats showed VTE behaviors characteristic of indecision (Redish 2016). The mPFC disruption engendered by the DREADD+CNO manipulation reduced VTE behavior, suggesting that rats with a disrupted mPFC were more decisive and less deliberative at choice points. This decrease in VTE was particularly noticeable during “difficult decisions” where the offered delay was close to the preference threshold.
Current theories suggest that during deliberative decision making the hippocampus and mPFC are continually engaging each other (Eichenbaum 2017; Gordon 2011; Preston and Eichenbaum 2013; Wang et al. 2015). It is possible that impairing information processing in mPFC disrupted this iterative engagement process. Rats with an intact mPFC were more inclined to take time before making a decision and more inclined to show VTE behaviors, which we interpret as deliberating whether to accept or reject the offer. This was particularly prominent at difficult decisions, where the delay presented was near the threshold for a given flavor. In contrast, rats with disrupted information processing in the mPFC simply skipped the difficult decision and progressed to the next offer.
Given that the rats were continually cued to the delay left to receive the reward (the delay counts down in pitch until the reward has been dispensed), we do not believe that these changes result from disrupted interval timing (Kim et al. 2009, 2013). Previous studies have found that mPFC dysfunction results in a disinhibition of reinforced responses (Gourley and Taylor 2016), but we do not believe a disinhibition of reinforced responses can account for the results found as disinhibiting the mPFC resulted in the animal leaving a zone faster and more often, which was not the behavior that was reinforced.
Because cortical systems include complex excitatory-inhibitory feedback networks, the DREADD+CNO disruption of mPFC should not be expected to necessarily decrease firing in mPFC. We found that some mPFC neurons increased and some decreased their firing rate between the Pre and Post task recordings. As seen in Table 2, we did find that the decrease in recorded mPFC neurons on CNO days were predominantly in neurons that were not significantly phase locked to local low gamma oscillations and typically increase their firing rate on this task (Veh n = 32 versus CNO n = 8), though given the sparse number of tetrodes in the mPFC our cell count for that area is limited, and conclusions must be tempered on the limited number of cells recorded. We did see variability between rats, but our data cannot differentiate whether these were due to inherent individual rat differences or due to differences in DREADD transfection spread. Due to limitations in histology, we were not able to do individual cell counts or to quantify the spread, and therefore we could not correlate the effects seen in behavior or electrophysiology to transfection spread.
Hippocampal theta sequences are believed to support the temporal encoding of spatial information, as well as imagination and planning. Sequences serially sweep to future goal locations during deliberation (Johnson and Redish 2007; Wikenheiser and Redish 2015). We found that hippocampal sequences were disrupted in rats with mPFC disruptions by the DREADD+CNO manipulation. The behavioral data suggest that the animals were more decisive with mPFC disruption, which could have resulted from a reduction of the continual communication between the mPFC and hippocampus of contextually relevant options. An alternative explanation for the improvement in performance could result from a subtle decrease in firing rate for neurons that were not “recruited” during the task. In this scenario, silencing these non-task-engaged neurons with DREADD+CNO could thereby optimize mPFC function.
The electrophysiological data supports the mPFC-hippocampal communication disruption hypothesis: mPFC disruptions resulted in significantly fewer theta sequences in the hippocampus. Previous studies suggest that the mPFC has cognitive control over hippocampal contextual retrieval (Ito et al. 2015; Preston and Eichenbaum 2013). It appears that mPFC disruption reduced the number of theta sequences produced during decision making. One potential hypothesis (Eichenbaum 2017; Gordon 2011; Preston and Eichenbaum 2013; Wang et al. 2015) is that, by impairing the mPFC, the mPFC was no longer “pinging” the hippocampus as often about all the different options and, therefore, the hippocampus was not pulling up as many representations as usual, resulting in fewer theta sequences being generated. These data contribute to the growing literature, suggesting a top-down control of hippocampal activity by the prefrontal cortex in humans and rodents (Maharjan et al. 2018; Oehrn et al. 2018).
mPFC disruption reduced the asymmetry index of the hippocampal theta cycle, suggesting that it altered the dynamics of local and nonlocal spatial representations within a theta cycle (Fig. 4I). Changes in these dynamics were also evident when measuring changes in phase locking of the first and last spike through a place field. Local spatial representations, specifically the initiation of the sequence, was impaired in mPFC disrupted rats, as demonstrated by the changes in phase locking of the last spike of a place field rather than the first spike of the field (Fig. 3P). These impairments in information processing at the sequence level were found even though primary place field characteristics remained intact. This result is similar to a previous study that reported impairments in place cell sequences with cannabinoid manipulations while maintaining place field integrity (Robbe and Buzsáki 2009).
Exactly how the mPFC and hippocampus are communicating with each other remains unclear; the dorsal hippocampus does not have monosynaptic projections to, nor does it receive monosynaptic connections from, the mPFC in the rodent (Jay and Witter 1991). However, recent studies suggest that the nucleus reuniens, which receives bilateral connections from the mPFC and hippocampus, may act as a relay center between these two structures (Hallock et al. 2016; Ito et al. 2015). The lateral entorhinal cortex, which receives projections from the prefrontal cortex and projects to the hippocampus, is another possibility.
Numerous studies have shown that there is increased coherence between the hippocampus and mPFC during decision making and working memory (Benchenane et al. 2010; Jensen 2005; Jones and Wilson 2005; Paz et al. 2008; Sigurdsson et al. 2010). Data suggest that theta oscillations are generated in the hippocampus through extra hippocampal inputs, including the septum and entorhinal cortex (Buzsáki 2002) and potentially through internal generators (Goutagny et al. 2009). The mPFC in turn, is reciprocally connected to the hippocampus via the nucleus reunions (Vertes 2002; Vertes et al. 2007) and the entorhinal cortex (Amaral and Witter 1989; Pignatelli et al. 2012; van Groen et al. 2003) and sends projections to the septum (Gaykema et al. 1991). Though we are not sure why theta oscillations were reduced in power, it is possible that hippocampal theta oscillations were reduced in mPFC disrupted rats via its connections to the external hippocampal inputs that contribute to theta generation.
While at a choice point, animals will often pause and orient toward their potential choices, a deliberative behavior termed vicarious trial and error (VTE). We found that VTE behavior was reduced in mPFC-disrupted rats, making the rats appear more decisive. We particularly noted this decline during difficult decisions, when the threshold was near the delay presented. We found increased local decoding on nVTE trials and more nonlocal decoding in front of the rat on VTE trials, but with disrupted mPFC input this dynamic was abolished.
In summary, disrupting the mPFC with DREADDs impaired decision-making processes in the hippocampus, specifically planning processes in the CA1. Our results imply that rats with an impaired mPFC showed reduced behavioral and electrophysiological correlates of deliberation as seen by less coherent hippocampal theta sequences and reduced VTE behavior. However, on the Restaurant Row task, these behavioral changes increased the rats’ rate of reinforcement. We also found empirical support for a dissociation between local and nonlocal spatial firing along distinct phases of theta oscillations: theta sequences showed more local decoding on the descending phase of the theta cycle and more nonlocal decoding on the ascending phase. Disrupting the mPFC impaired the initiation of the theta cycle, specifically the first spike in the theta sequence, as evidenced by mPFC-disruption-driven phase changes in the last spike fired by the cell in its place field. These data suggest that the mPFC supports the initiation of deliberative sequences and provides support for an episodic-future thinking, working memory interpretation of deliberation that depends on mPFC-hippocampal interactions.
GRANTS
Financial support for this work was provided by National Institute on Drug Abuse (NIDA) grant DA030672 (A. D. Redish), National Institute of Mental Health grant MH080318 (A. D. Redish), as well as a diversity supplement NIDA DA030672S1 (B. J. Schmidt), funding from the Society for Neuroscience Scholars Program (B. J. Schmidt), and an NIH F32 fellowship DA038392 (B. J. Schmidt).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
B.S. and A.D.R. conceived and designed research; B.S. and A.A.D. performed experiments; B.S., A.A.D., and A.D.R. analyzed data; B.S. and A.D.R. interpreted results of experiments; B.S. and A.D.R. prepared figures; B.S. and A.D.R. drafted manuscript; B.S., A.A.D., and A.D.R. edited and revised manuscript; B.S., A.A.D., and A.D.R. approved final version of manuscript.
Supplemental Data
Supplemental Figures S1-S5 - .pdf (1 MB)
ACKNOWLEDGMENTS
The authors thank Dr. Yannick Breton for help with code, data analysis, and an earlier version of this paper and Dr. Bryan Roth, Dr. Daniel Urban, and the University of North Carolina Vector Core for help with viruses, DREADDs setup, and troubleshooting. Technical assistance was provided by Kelsey Seeland, Christopher Boldt, and Ayaka Sheehan.
REFERENCES
- Addis DR, Wong AT, Schacter DL. Remembering the past and imagining the future: common and distinct neural substrates during event construction and elaboration. Neuropsychologia 45: 1363–1377, 2007. doi: 10.1016/j.neuropsychologia.2006.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amaral DG, Witter MP. The three-dimensional organization of the hippocampal formation: a review of anatomical data. Neuroscience 31: 571–591, 1989. doi: 10.1016/0306-4522(89)90424-7. [DOI] [PubMed] [Google Scholar]
- Amemiya S, Redish AD. Manipulating decisiveness in decision making: effects of clonidine on hippocampal search strategies. J Neurosci 36: 814–827, 2016. doi: 10.1523/JNEUROSCI.2595-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amemiya S, Redish AD. Hippocampal theta-gamma coupling reflects state-dependent information processing in decision making. Cell Rep 22: 3328–3338, 2018. [Erratum in Cell Rep 25: 3894–3897.] doi: 10.1016/j.celrep.2018.02.091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armbruster BN, Li X, Pausch MH, Herlitze S, Roth BL. Evolving the lock to fit the key to create a family of G protein-coupled receptors potently activated by an inert ligand. Proc Natl Acad Sci USA 104: 5163–5168, 2007. doi: 10.1073/pnas.0700293104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belluscio MA, Mizuseki K, Schmidt R, Kempter R, Buzsáki G. Cross-frequency phase-phase coupling between θ and γ oscillations in the hippocampus. J Neurosci 32: 423–435, 2012. doi: 10.1523/JNEUROSCI.4122-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benchenane K, Peyrache A, Khamassi M, Tierney PL, Gioanni Y, Battaglia FP, Wiener SI. Coherent theta oscillations and reorganization of spike timing in the hippocampal-prefrontal network upon learning. Neuron 66: 921–936, 2010. doi: 10.1016/j.neuron.2010.05.013. [DOI] [PubMed] [Google Scholar]
- Bieri KW, Bobbitt KN, Colgin LL. Slow and fast γ rhythms coordinate different spatial coding modes in hippocampal place cells. Neuron 82: 670–681, 2015. doi: 10.1016/j.neuron.2014.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breton YA, Schmidt B, Redish AD. Ventral striatum represents reward before the orbitofrontal cortex in the restaurant row task (Abstract). Society for Neuroscience Annual Meeting. Chicago, IL, October 17–21, 2015. [Google Scholar]
- Buzsáki G. Theta oscillations in the hippocampus. Neuron 33: 325–340, 2002. doi: 10.1016/S0896-6273(02)00586-X. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Rappelsberger P, Kellényi L. Depth profiles of hippocampal rhythmic slow activity (‘theta rhythm’) depend on behaviour. Electroencephalogr Clin Neurophysiol 61: 77–88, 1985. doi: 10.1016/0013-4694(85)91075-2. [DOI] [PubMed] [Google Scholar]
- Cohen NJ, Eichenbaum H. Memory, Amnesia, and the Hippocampal System. Cambridge, MA: MIT Press, 1993. [Google Scholar]
- Colgin LL. Oscillations and hippocampal-prefrontal synchrony. Curr Opin Neurobiol 21: 467–474, 2011. doi: 10.1016/j.conb.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser MB, Moser EI. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462: 353–357, 2009. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Davidson TJ, Kloosterman F, Wilson MA. Hippocampal replay of extended experience. Neuron 63: 497–507, 2009. doi: 10.1016/j.neuron.2009.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Depue BE. A neuroanatomical model of prefrontal inhibitory modulation of memory retrieval. Neurosci Biobehav Rev 36: 1382–1399, 2012. doi: 10.1016/j.neubiorev.2012.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong S, Allen JA, Farrell M, Roth BL. A chemical-genetic approach for precise spatio-temporal control of cellular signaling. Mol Biosyst 6: 1376–1380, 2010. doi: 10.1039/c002568m. [DOI] [PubMed] [Google Scholar]
- Dragoi G, Buzsáki G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron 50: 145–157, 2006. doi: 10.1016/j.neuron.2006.02.023. [DOI] [PubMed] [Google Scholar]
- Eichenbaum H. Prefrontal-hippocampal interactions in episodic memory. Nat Rev Neurosci 18: 547–558, 2017. doi: 10.1038/nrn.2017.74. [DOI] [PubMed] [Google Scholar]
- Feng T, Silva D, Foster DJ. Dissociation between the experience-dependent development of hippocampal theta sequences and single-trial phase precession. J Neurosci 35: 4890–4902, 2015. doi: 10.1523/JNEUROSCI.2614-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson SM, Eskenazi D, Ishikawa M, Wanat MJ, Phillips PE, Dong Y, Roth BL, Neumaier JF. Transient neuronal inhibition reveals opposing roles of indirect and direct pathways in sensitization. Nat Neurosci 14: 22–24, 2011. doi: 10.1038/nn.2703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández-Ruiz A, Oliva A, Nagy GA, Maurer AP, Berényi A, Buzsáki G. Entorhinal-CA3 dual-input control of spike timing in the hippocampus by theta-gamma coupling. Neuron 93: 1213–1226.e5, 2017. doi: 10.1016/j.neuron.2017.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster DJ, Wilson MA. Hippocampal theta sequences. Hippocampus 17: 1093–1099, 2007. doi: 10.1002/hipo.20345. [DOI] [PubMed] [Google Scholar]
- Gaykema RP, van Weeghel R, Hersh LB, Luiten PG. Prefrontal cortical projections to the cholinergic neurons in the basal forebrain. J Comp Neurol 303: 563–583, 1991. doi: 10.1002/cne.903030405. [DOI] [PubMed] [Google Scholar]
- Gordon JA. Oscillations and hippocampal-prefrontal synchrony. Curr Opin Neurobiol 21: 486–491, 2011. doi: 10.1016/j.conb.2011.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gourley SL, Taylor JR. Going and stopping: dichotomies in behavioral control by the prefrontal cortex. Nat Neurosci 19: 656–664, 2016. doi: 10.1038/nn.4275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutagny R, Jackson J, Williams S. Self-generated theta oscillations in the hippocampus. Nat Neurosci 12: 1491–1493, 2009. doi: 10.1038/nn.2440. [DOI] [PubMed] [Google Scholar]
- Guise KG, Shapiro ML. Medial prefrontal cortex reduces memory interference by modifying hippocampal encoding. Neuron 94: 183–192.e8, 2017. doi: 10.1016/j.neuron.2017.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta AS, van der Meer MAA, Touretzky DS, Redish AD. Hippocampal replay is not a simple function of experience. Neuron 65: 695–705, 2010. doi: 10.1016/j.neuron.2010.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta AS, van der Meer MAA, Touretzky DS, Redish AD. Segmentation of spatial experience by hippocampal θ sequences. Nat Neurosci 15: 1032–1039, 2012. doi: 10.1038/nn.3138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallock HL, Wang A, Griffin AL. Ventral midline thalamus is critical for hippocampal-prefrontal synchrony and spatial working memory. J Neurosci 36: 8372–8389, 2016. doi: 10.1523/JNEUROSCI.0991-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassabis D, Kumaran D, Maguire EA. Using imagination to understand the neural basis of episodic memory. J Neurosci 27: 14365–14374, 2007. doi: 10.1523/JNEUROSCI.4549-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hok V, Chah E, Save E, Poucet B. Prefrontal cortex focally modulates hippocampal place cell firing patterns. J Neurosci 33: 3443–3451, 2013. doi: 10.1523/JNEUROSCI.3427-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxter JR, Senior TJ, Allen K, Csicsvari J. Theta phase-specific codes for two-dimensional position, trajectory and heading in the hippocampus. Nat Neurosci 11: 587–594, 2008. doi: 10.1038/nn.2106. [DOI] [PubMed] [Google Scholar]
- Hyman JM, Zilli EA, Paley AM, Hasselmo ME. Medial prefrontal cortex cells show dynamic modulation with the hippocampal theta rhythm dependent on behavior. Hippocampus 15: 739–749, 2005. doi: 10.1002/hipo.20106. [DOI] [PubMed] [Google Scholar]
- Ito HT, Zhang SJ, Witter MP, Moser EI, Moser MB. A prefrontal-thalamo-hippocampal circuit for goal-directed spatial navigation. Nature 522: 50–55, 2015. doi: 10.1038/nature14396. [DOI] [PubMed] [Google Scholar]
- Janabi-Sharifi F, Hayward V, Chen SCJ. Discrete-time adaptive windowing for velocity estimation. IEEE Trans Contr Syst Technol 8: 1003–1009, 2000. doi: 10.1109/87.880606 [DOI] [Google Scholar]
- Jay TM, Witter MP. Distribution of hippocampal CA1 and subicular efferents in the prefrontal cortex of the rat studied by means of anterograde transport of Phaseolus vulgaris-leucoagglutinin. J Comp Neurol 313: 574–586, 1991. doi: 10.1002/cne.903130404. [DOI] [PubMed] [Google Scholar]
- Jensen O. Reading the hippocampal code by theta phase-locking. Trends Cogn Sci 9: 551–553, 2005. doi: 10.1016/j.tics.2005.10.003. [DOI] [PubMed] [Google Scholar]
- Johnson A, Redish AD. Neural ensembles in CA3 transiently encode paths forward of the animal at a decision point. J Neurosci 27: 12176–12189, 2007. doi: 10.1523/JNEUROSCI.3761-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones MW, Wilson MA. Theta rhythms coordinate hippocampal-prefrontal interactions in a spatial memory task. PLoS Biol 3: e402, 2005. doi: 10.1371/journal.pbio.0030402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kesner RP, Churchwell JC. An analysis of rat prefrontal cortex in mediating executive function. Neurobiol Learn Mem 96: 417–431, 2011. doi: 10.1016/j.nlm.2011.07.002. [DOI] [PubMed] [Google Scholar]
- Kim J, Ghim J-W, Lee J-H, Jung MW. Neural correlates of interval timing in rodent prefrontal cortex. J Neurosci 33: 13834–13847, 2013. doi: 10.1523/JNEUROSCI.1443-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Jung AH, Byun J, Jo S, Jung MW. Inactivation of medial prefrontal cortex impairs time interval discrimination in rats. Front Behav Neurosci 3: 38, 2009. doi: 10.3389/neuro.08.038.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lechner HA, Lein ES, Callaway EM. A genetic method for selective and quickly reversible silencing of Mammalian neurons. J Neurosci 22: 5287–5290, 2002. doi: 10.1523/JNEUROSCI.22-13-05287.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Gutierrez DV, Hanson MG, Han J, Mark MD, Chiel H, Hegemann P, Landmesser LT, Herlitze S. Fast noninvasive activation and inhibition of neural and network activity by vertebrate rhodopsin and green algae channelrhodopsin. Proc Natl Acad Sci USA 102: 17816–17821, 2005. doi: 10.1073/pnas.0509030102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maharjan DM, Dai YY, Glantz EH, Jadhav SP. Disruption of dorsal hippocampal - prefrontal interactions using chemogenetic inactivation impairs spatial learning. Neurobiol Learn Mem 155: 351–360, 2018. doi: 10.1016/j.nlm.2018.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahler SV, Vazey EM, Beckley JT, Keistler CR, McGlinchey EM, Kaufling J, Wilson SP, Deisseroth K, Woodward JJ, Aston-Jones G. Designer receptors show role for ventral pallidum input to ventral tegmental area in cocaine seeking. Nat Neurosci 17: 577–585, 2014. doi: 10.1038/nn.3664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature 417: 741–746, 2002. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
- Mitra PP, Pesaran B. Analysis of dynamic brain imaging data. Biophys J 76: 691–708, 1999. doi: 10.1016/S0006-3495(99)77236-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muenzinger KF. Vicarious trial and error at a point of choice. I. A general survey of its relation to learning efficiency. J Genet Psychol 53: 75–86, 1938. doi: 10.1080/08856559.1938.10533799 [DOI] [Google Scholar]
- Muenzinger KF, Gentry E. Tone discrimination in white rats. J Comp Psychol 12: 195–206, 1931. doi: 10.1037/h0072238 [DOI] [Google Scholar]
- O’Keefe J, Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res 34: 171–175, 1971. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, Nadel L.. The Hippocampus as a Cognitive Map. Oxford, UK: Clarendon, 1978. [Google Scholar]
- O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3: 317–330, 1993. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
- Oehrn CR, Fell J, Baumann C, Rosburg T, Ludowig E, Kessler H, Hanslmayr S, Axmacher N. Direct electrophysiological evidence for prefrontal control of hippocampal processing during voluntary forgetting. Curr Biol 28: 3016–3022.e4, 2018. doi: 10.1016/j.cub.2018.07.042. [DOI] [PubMed] [Google Scholar]
- Olypher AV, Lánský P, Fenton AA. Properties of the extra-positional signal in hippocampal place cell discharge derived from the overdispersion in location-specific firing. Neuroscience 111: 553–566, 2002. doi: 10.1016/S0306-4522(01)00586-3. [DOI] [PubMed] [Google Scholar]
- Papale AE, Stott JJ, Powell NJ, Regier PS, Redish AD. Interactions between deliberation and delay-discounting in rats. Cogn Affect Behav Neurosci 12: 513–526, 2012. doi: 10.3758/s13415-012-0097-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papale AE, Zielinski MC, Frank LM, Jadhav SP, Redish AD. Interplay between hippocampal sharp-wave-ripple events and vicarious trial and error behaviors in decision making. Neuron 92: 975–982, 2016. doi: 10.1016/j.neuron.2016.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz R, Bauer EP, Paré D. Theta synchronizes the activity of medial prefrontal neurons during learning. Learn Mem 15: 524–531, 2008. doi: 10.1101/lm.932408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer BE, Foster DJ. Hippocampal place-cell sequences depict future paths to remembered goals. Nature 497: 74–79, 2013. doi: 10.1038/nature12112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pignatelli M, Beyeler A, Leinekugel X. Neural circuits underlying the generation of theta oscillations. J Physiol Paris 106: 81–92, 2012. doi: 10.1016/j.jphysparis.2011.09.007. [DOI] [PubMed] [Google Scholar]
- Preston AR, Eichenbaum H. Interplay of hippocampus and prefrontal cortex in memory. Curr Biol 23: R764–R773, 2013. doi: 10.1016/j.cub.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redish AD. Beyond the Cognitive Map: From Place Cells to Episodic Memory. Cambridge, MA: MIT Press, 1999. [Google Scholar]
- Redish AD. Vicarious trial and error. Nat Rev Neurosci 17: 147–159, 2016. doi: 10.1038/nrn.2015.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich EL, Shapiro ML. Prelimbic/infralimbic inactivation impairs memory for multiple task switches, but not flexible selection of familiar tasks. J Neurosci 27: 4747–4755, 2007. doi: 10.1523/JNEUROSCI.0369-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieke F, Warland D, de Ruyter van Steveninick R, Bialek W. Spikes: Exploring the Neural Code. Cambridge, MA: MIT Press, 1997. [Google Scholar]
- Robbe D, Buzsáki G. Alteration of theta timescale dynamics of hippocampal place cells by a cannabinoid is associated with memory impairment. J Neurosci 29: 12597–12605, 2009. doi: 10.1523/JNEUROSCI.2407-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders H, Rennó-Costa C, Idiart M, Lisman J. Grid cells and place cells: an integrated view of their navigational and memory function. Trends Neurosci 38: 763–775, 2015. doi: 10.1016/j.tins.2015.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schacter DL, Addis DR, Buckner RL. Remembering the past to imagine the future: the prospective brain. Nat Rev Neurosci 8: 657–661, 2007. doi: 10.1038/nrn2213. [DOI] [PubMed] [Google Scholar]
- Schmidt B, Papale A, Redish AD, Markus EJ. Conflict between place and response navigation strategies: effects on vicarious trial and error (VTE) behaviors. Learn Mem 20: 130–138, 2013. doi: 10.1101/lm.028753.112. [DOI] [PubMed] [Google Scholar]
- Siapas AG, Lubenov EV, Wilson MA. Prefrontal phase locking to hippocampal theta oscillations. Neuron 46: 141–151, 2005. doi: 10.1016/j.neuron.2005.02.028. [DOI] [PubMed] [Google Scholar]
- Sigurdsson T, Stark KL, Karayiorgou M, Gogos JA, Gordon JA. Impaired hippocampal-prefrontal synchrony in a genetic mouse model of schizophrenia. Nature 464: 763–767, 2010. doi: 10.1038/nature08855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirota A, Montgomery S, Fujisawa S, Isomura Y, Zugaro M, Buzsáki G. Entrainment of neocortical neurons and gamma oscillations by the hippocampal theta rhythm. Neuron 60: 683–697, 2008. doi: 10.1016/j.neuron.2008.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL. Replay of neuronal firing sequences in rat hippocampus during sleep following spatial experience. Science 271: 1870–1873, 1996. [DOI] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL, Wilson MA, Barnes CA. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6: 149–172, 1996. doi:. [DOI] [PubMed] [Google Scholar]
- Stachniak TJ, Ghosh A, Sternson SM. Chemogenetic synaptic silencing of neural circuits localizes a hypothalamus→midbrain pathway for feeding behavior. Neuron 82: 797–808, 2014. doi: 10.1016/j.neuron.2014.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiner AP, Redish AD. Behavioral and neurophysiological correlates of regret in rat decision-making on a neuroeconomic task. Nat Neurosci 17: 995–1002, 2014. doi: 10.1038/nn.3740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweis BM, Abram SV, Schmidt BJ, Seeland KD, MacDonald AW III, Thomas MJ, Redish AD. Sensitivity to “sunk costs” in mice, rats, and humans. Science 361: 178–181, 2018a. doi: 10.1126/science.aar8644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweis BM, Thomas MJ, Redish AD. Mice learn to avoid regret. PLoS Biol 16: e2005853, 2018b. doi: 10.1371/journal.pbio.2005853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolman EC. The determiners of behavior at a choice point. Psychol Rev 45: 1–41, 1938. doi: 10.1037/h0062733 [DOI] [Google Scholar]
- van Groen T, Miettinen P, Kadish I. The entorhinal cortex of the mouse: organization of the projection to the hippocampal formation. Hippocampus 13: 133–149, 2003. doi: 10.1002/hipo.10037. [DOI] [PubMed] [Google Scholar]
- Vanderwolf CH. Hippocampal electrical activity and voluntary movement in the rat. Electroencephalogr Clin Neurophysiol 26: 407–418, 1969. doi: 10.1016/0013-4694(69)90092-3. [DOI] [PubMed] [Google Scholar]
- Vertes RP. Analysis of projections from the medial prefrontal cortex to the thalamus in the rat, with emphasis on nucleus reuniens. J Comp Neurol 442: 163–187, 2002. doi: 10.1002/cne.10083. [DOI] [PubMed] [Google Scholar]
- Vertes RP, Hoover WB, Szigeti-Buck K, Leranth C. Nucleus reuniens of the midline thalamus: link between the medial prefrontal cortex and the hippocampus. Brain Res Bull 71: 601–609, 2007. doi: 10.1016/j.brainresbull.2006.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang JX, Cohen NJ, Voss JL. Covert rapid action-memory simulation (CRAMS): a hypothesis of hippocampal-prefrontal interactions for adaptive behavior. Neurobiol Learn Mem 117: 22–33, 2015. doi: 10.1016/j.nlm.2014.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watakabe A, Ohtsuka M, Kinoshita M, Takaji M, Isa K, Mizukami H, Ozawa K, Isa T, Yamamori T. Comparative analyses of adeno-associated viral vector serotypes 1, 2, 5, 8 and 9 in marmoset, mouse and macaque cerebral cortex. Neurosci Res 93: 144–157, 2015. doi: 10.1016/j.neures.2014.09.002. [DOI] [PubMed] [Google Scholar]
- Wikenheiser AM, Redish AD. The balance of forward and backward hippocampal sequences shifts across behavioral states. Hippocampus 23: 22–29, 2013. doi: 10.1002/hipo.22049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wikenheiser AM, Redish AD. Hippocampal theta sequences reflect current goals. Nat Neurosci 18: 289–294, 2015. doi: 10.1038/nn.3909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wikenheiser AM, Stephens DW, Redish AD. Subjective costs drive overly patient foraging strategies in rats on an intertemporal foraging task. Proc Natl Acad Sci USA 110: 8308–8313, 2013. doi: 10.1073/pnas.1220738110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamaguchi Y, Aota Y, McNaughton BL, Lipa P. Bimodality of theta phase precession in hippocampal place cells in freely running rats. J Neurophysiol 87: 2629–2642, 2002. doi: 10.1152/jn.2002.87.6.2629. [DOI] [PubMed] [Google Scholar]
- Zhang K, Ginzburg I, McNaughton BL, Sejnowski TJ. Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. J Neurophysiol 79: 1017–1044, 1998. doi: 10.1152/jn.1998.79.2.1017. [DOI] [PubMed] [Google Scholar]
- Zheng C, Bieri KW, Hsiao YT, Colgin LL. Spatial sequence coding differs during slow and fast gamma rhythms in the hippocampus. Neuron 89: 398–408, 2016. doi: 10.1016/j.neuron.2015.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu H, Roth BL. Silencing synapses with DREADDs. Neuron 82: 723–725, 2014. doi: 10.1016/j.neuron.2014.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Figures S1-S5 - .pdf (1 MB)
Data Availability Statement
The data sets generated and/or analyzed in the current study are available from the corresponding author upon reasonable request.