Accounting for Substrate Interactions in the Measurement of the Dimensions of Cellulose Nanofibrils

Abstract

Mechanically fibrillated cellulose nanofibrils (CNFs) have attracted special attention as building blocks for the development of advanced materials and composites. A correlation exists between CNF morphology and the properties of the materials they form. However, this correlation is often evaluated indirectly by process-centered approaches or by accessing a single dimensionality of CNFs adsorbed on solid supports. High-resolution imaging is currently the best approach to describe the morphological features of nanocelluloses; nevertheless, adsorption effects need to be accounted for. For instance, possible deformations of the CNFs arising from capillary forces and interactions with the substrate need to be considered in the determination of their cross-sectional dimensions. By considering soft matter imaging and adsorption effects, we provide evidence of the deformation of CNFs upon casting and drying. We determine a substantial flattening associated with the affinity of CNFs with the substrate corresponding to a highly anisotropic cross-sectional geometry (ellipsoidal) in the dried state. Negative-contrast scanning electron microscopy is also introduced as a new method to assess the dimensions of the CNFs. The images obtained by the latter, a faster imaging method, were correlated with those from atomic force microscopy. The cross-sectional area of the CNF is reconstructed by cross-correlating the widths and heights obtained by the two techniques.

Introduction

Alongside developments in colloidal science, bio-based colloids have emerged as promising building blocks for the preparation of materials for a wide range of applications. Particularly, nanoparticles formed from cellulose have captured a widespread interest by the scientific community.^1,2 Nanocelluloses are high aspect-ratio particles that are extracted, principally from plants, by mechanical or chemical means. The term “nanocelluloses” is loosely used to refer to, for instance, cellulose nanofibrils (CNFs) obtained by mechanical fibrillation and TEMPO-mediated oxidation (TO-CNF) as well as cellulose nanocrystals (CNCs) extracted by controlled acid hydrolysis. Other grades of nanocellulose with various functionalities such as carboxymethylated or phosphorylated nanofibrils have also been obtained.³ Herein, the term “CNF” is used to describe nanofibers obtained from partial mechanical fibrillation of bleached wood pulp. Depending on the degree of fibrillation, microfibrillated cellulose (MFC) can also be obtained and a loose distinction is made between nano- and microsizes in the use of the nomenclature. A high degree of fibrillation may lead to fibrils with dimensions close to so-called “elementary fibrils,” as observed in wood.⁴⁻⁶ Thus, it is reasonable to assume that the relatively larger nanofibers in CNF and MFC correspond to bundles of several elementary fibrils with similar orientation within the larger CNFs.

Mechanically fibrillated CNFs are currently one of the most attractive and practical bio-based nanostructures that are used as a single component in hydrogels or aerogels as well as high-performance filaments, films, and nanopapers.⁷ Additionally, CNFs, either native or surface-modified, have been combined with other colloids and polymers to form composites, resulting in a near limitless application potential.^8,9

Considerable fundamental insights have been gained by observing the behavior of nanocelluloses in suspensions.¹⁰⁻¹³ Further understanding of the nanocellulose morphology, however, is required for the prediction of their processability and to design materials with predictable properties. Specifically, assessing accurate morphological description of CNFs is critical in the determination of their aspect ratio as well as surface area and the influence of these characteristics on physicochemical properties such as colloidal stability, hydrated volume, capillary forces,^14,15 light scattering,¹⁶ and reactivity,¹⁷ among others.

However, whereas the morphological characterization of well-defined CNCs^10,18 and TO-CNF¹⁹⁻²² has undergone significant progress,¹³ metrology of conventional CNFs remains a challenge. Such fact arises principally from two factors: (1) as a result of the partial nature of the fibrillation, mechanically fibrillated CNFs are highly polydisperse in size, even after repeated fibrillation cycles. This leads to poor characterization of the finer CNF fraction, usually an important contributor to the active surface area.¹⁶ (2) CNFs tend to aggregate both in suspension and upon drying. Additionally, residual components, such as traces of hemicelluloses, may affect related evaluations. Morphological descriptions of CNFs based on the suspension behavior have relied on dynamic light scattering²³ and rheology.²⁴ Such approaches use a number of assumptions related to the characteristic aspect ratio, hydration, and the effects of shear, all of which can be strongly influenced by a rather small population of the larger particles. On the other hand, imaging is a well-accepted approach to describe the morphological features of nanocelluloses.^4,25,26 Conventional electron microscopy techniques [scanning electron microscopy (SEM) and transmission electron microscopy (TEM)] are commonly applied to image nanocelluloses. However, the low image contrast of SEM is a current technological challenge.⁴ TEM imaging can lead to satisfactory determination of the length of the fibers and, with a decent accuracy, their widths. However, sample preparation and skilled operation are of fundamental importance as the solid support is generally of similar nature of the low-crystallinity, “disordered” cellulose.^4,27,28 Similarly, atomic force microscopy (AFM) relies on proper protocols for the deposition on the solid supports but, in addition, it is subjected to substantial measurement artifacts such as tip convolution, which prevents an absolute assessment of CNF dimensions. This also prevents comparison of results obtained between studies.

The challenges presented above have resulted in significant limitations in the characterization of the morphology of CNFs. Thus far, the correlation between CNF characteristics and associated material properties has been process-centered, that is, indirectly tied to the degree of fibrillation,^29,30 or based on measurements of a single specific dimensionality that may differ across studies.^16,31,32 Because of the simplicity of their extraction as well as their low cost and high performance, mechanically fibrillated CNFs are among the most explored.³³⁻³⁵ Therefore, the lack of standardization in the methods for the quantification of their morphological characteristics sets a limit in our attempts to predict or rationalize their assembly, for example, for developing given targeted performances.

In recent efforts, AFM imaging has been the preferred method to extract the dimensions of nanocelluloses. Nevertheless, especially for CNFs, AFM-based measurements on single particles have been used to describe their morphology based on either the width³¹ or the height^16,32,36 of the observed cross-sectional area. The latter characteristics (width or height) are used as references to propose scaling laws between the properties of materials as a function of the diameter of the fibrillated nanocelluloses.^31,32 Nevertheless, as can be observed in these previous reports, for AFM imaging of CNFs adsorbed on solid substrates, the lateral dimension (width) and out-of-plane height differ significantly.^31,32 Therefore, a major need exists for a standardized, simple, and efficient framework to obtain the detailed morphological features of CNFs.

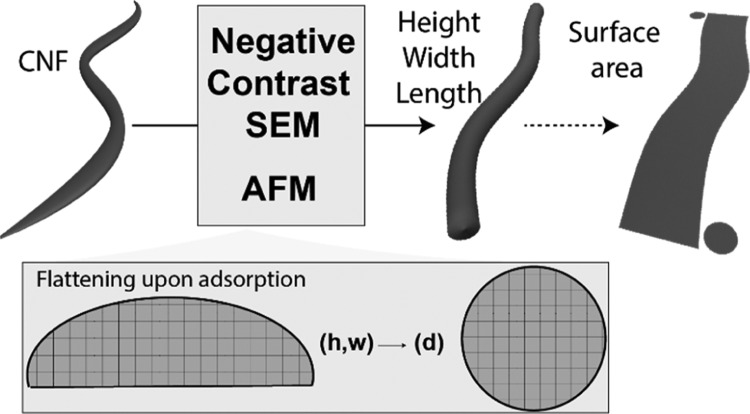
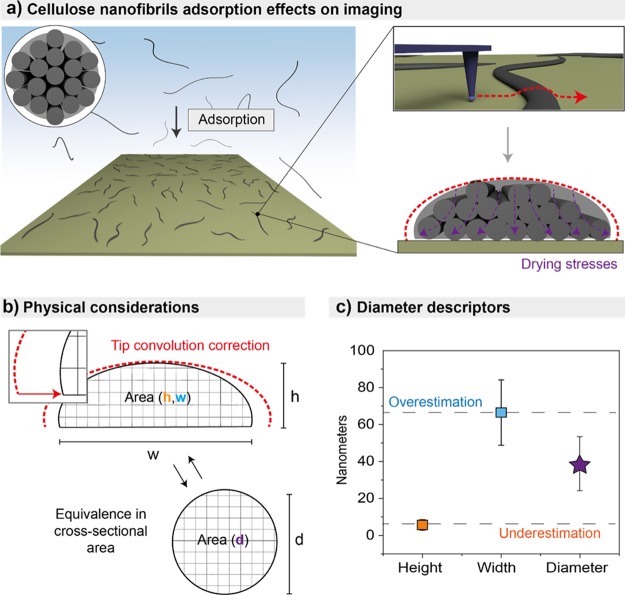
Here, we implemented AFM imaging of CNFs with appropriate consideration toward an improved description of their morphological characteristics (Figure 1a). Our emphasis lies on the analysis and interpretation of the results to provide an accurate evaluation of CNF dimensions. As the raw material, we focused on CNFs produced upon an intermediate degree of fibrillation (6 passes), as is conventionally encountered in the literature and in industrial applications. AFM-based morphological mapping was grounded on associated physical considerations (as described in Figure 1a, top right panel, and 1b). Importantly, as in AFM imaging of synthetic polymeric particles,³⁷⁻³⁹ spreading and flattening of the CNFs onto the solid substrate were observed (Figure 1a, bottom right panel, and 1b). In contrast, the CNFs are generally schematically represented as having a circular cross section. This assumption is based on the structure of the bundle of elementary fibrils that may result from defibrillation, although it remains to be demonstrated. We provide new insight on the adsorption behavior of CNFs onto flat substrates as a result of their disordered domains (i.e., crystallinity <65%) compared, for instance, to highly crystalline CNCs (i.e., crystallinity >70%).^13,40 Therefore, from the cross-sectional area obtained from both the width and the height, the equivalent diameter of the CNFs could be obtained (Figure 1b,c). This enabled an accurate measurement of the CNF diameter, which is compared to those obtained by conventional methods that consider solely width or height as measured by AFM or electron microscopy. A substantial discrepancy between diameter, width, and height is observed (Figure 1c). The results presented are expected to contribute significantly toward the standardization of measurements to obtain dimensionalities directly comparable and, potentially, improved scaling laws.

Figure 1.

Schematic illustration of the methodology used to assess CNF dimensions, including (a) preparation of the supported sample and AFM imaging to obtain the cross-sectional dimensions of CNFs. In the evaluation, the effects of tip convolution should be considered. The effect of drying stresses leading to a substantial flattening of CNFs is also demonstrated and accounted for. (b) Width measurements are cross-correlated with the corresponding height. An equivalent cylindrical cross section can be obtained from the observed noncylindrical cross-sectional area measured for adsorbed CNFs. (c) From the approximated cross-sectional area of the flattened CNF, a significantly different value is obtained for the diameter resulting from the equivalent circular cross section.

We also introduce the use of negative-contrast SEM (NegC SEM) for the characterization of CNFs and correlate the dimensions obtained with those extracted from AFM. Although previously SEM has been deemed poor for imaging nanocelluloses,⁴ we show that NegC SEM enables facile and rapid imaging while maintaining a good contrast. The latter enables a rapid means of obtaining the widths and, more importantly, lengths of the fibrils.

Experimental Section

Materials

Poly(ethylene imine) (PEI) was purchased from Sigma-Aldrich and used as received. Mica discs were purchased from Ted Pella Inc., and silicon wafers were purchased from Okmetic. A kitchen-grade aluminum foil was obtained in the local market. Milli-Q (MQ) water with a resistivity of 18.2 MΩ·cm was obtained from a Millipore (Synergy UV) Milli-Q purification system. CNFs were prepared without any chemical or enzymatic pretreatment prior to mechanical disintegration. A never dried, fully bleached, and fines-free sulfite birch pulp (Kappa number of 1, and DP of 4700) was suspended in distilled water at 1.8% mass fraction (w/v) and disintegrated using a high-pressure fluidizer (Microfluidics M110P) using 6 passes. The CNFs used herein have been previously characterized in depth in terms of chemical composition and surface properties.^50,51

Substrates and Sample Preparation

The initial suspension of the CNFs was diluted to 0.01 mg mL^–1 using Milli-Q water and then mildly tip ultrasonicated (3 min with pulse on/off of 5/1 s at 10% amplitude) to achieve a dispersed, stable suspension. The same suspension was used for SEM and AFM. A stock PEI solution was prepared in Milli-Q water at a concentration of 0.33% (w/v). For SEM imaging, freshly cleaved mica discs were spun-coated with a 4 nm layer of gold, platinum/palladium alloy, or iridium. The metal-coated substrates were dipped in the PEI solution for 1 min, gently rinsed with Milli-Q water, dipped in the CNF suspension for 1 min, and then let to dry at room temperature. For the AFM imaging, the metal coating of the mica substrate was skipped and the other steps were carried out as previously described.

Dip-casting was used to avoid the formation of highly entangled networks usually present after spin-coating. For all measurements, we followed the same dip-casting protocol, thus facilitating the comparison between samples. The thin layer of water (ca. 0.5 mm) after the retraction of the substrate from the CNF suspensions is at least 1 order of magnitude higher than the larger dimensions of the CNFs. This ensures proper sampling, for example, avoiding fractionation or effects that favor the deposition of smaller CNFs.

AFM Measurements

The CNF samples cast on bare mica were imaged on a MultiMode scanning probe microscope (Digital Instruments, Inc., USA) in the tapping mode using a cantilever with an 8 nm radius spherical tip (spring constant of 40 N m^–1 and a resonance frequency of ca. 260 kHz). Typically, images of size in the range 5 μm × 5 μm, 2.5 μm × 2.5 μm, or lower were obtained. From 512 to 1024 lines were taken per images. Images were sampled at 1024–1536 points per lines that were used in most cases to extract width and height features. The resolution for CNFs’ width evaluation was evaluated to be 1.5–2.5 nm based on a half pixel contrast criterion with pixel shortest dimension ranging from 3 to 5 nm. Five hundred CNFs were randomly selected to individually obtain the width and height distributions. In order to analyze the relationship between width and height, we selected 200 CNFs in a broad range of sizes.

Negative-Contrast Imaging Using a Scanning Electron Microscope

High-resolution negative-contrasted images were acquired in a field emission gum electron microscope (FEG-SEM) Zeiss Sigma VP (Germany) using the in-lens detector for imaging. The acceleration voltage used was 1.5 kV, and working distance of 6 mm. All images were acquired at a resolution of 3072 × 2304 pixels or 1024 × 768, depending on the magnification. Five hundred CNFs were randomly selected to individually obtain the width and length distributions. Figure S10 exemplifies the sampling of CNFs for the measurement of their lengths. In order to analyze the relationship between the width and length, we selected 200 CNFs in a broad range of sizes.

Image Analysis

The images acquired using the negative-contrast SEM technique were analyzed with the Fiji version of the ImageJ software. The length and corresponding width of CNFs were individually measured. As a standard measurement, the width was taken at the half-length of the CNF. The analysis of the AFM supporting images was carried using the Gwyddion software. The images were first leveled by a 3-point representative plane segment, and then the height and width were measured from line profiles taken from, preferentially, horizontally rasterized lines.

The dimensions of 200 CNFs were used to describe the height–width and width–length correlations, respectively, for AFM and NegC SEM. For such intrafibril (comparison of the dimensions within the same fibril) descriptions, a broad spectrum of sizes is preferable to describe the dimensionalities scaling as a function of the global size of the CNFs; thus, we selected 200 CNFs of visible different sizes.

Specific Surface Area Calculation

The specific surface area (SSA) distribution as presented in the discussion was obtained by calculating the SSA that would be obtained from each of the individual fibers sampled, with a very high SSA for small fibers and a very low SSA for large fibers. The sampling number was 200.

Results and Discussion

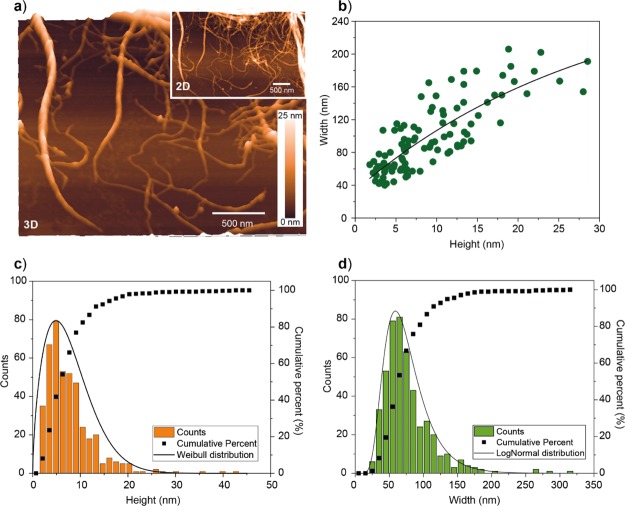
The sample preparation and instrumental techniques utilized herein were similar to those previously reported to characterize such features in a cost- and time-efficient way. Briefly, mica surfaces were dip-coated with a cationic polymer (PEI) and were then immersed in dilute (0.01 mg mL^–1) aqueous suspensions of the CNF. The PEI-coated superhydrophilic surface enabled nearly all water to be removed upon retraction of the sample from the CNF suspension. A ca. 0.5 mm thick layer of water remained within which the larger and smaller CNFs could be adsorbed upon drying, resulting in sparsely adsorbed CNFs. We note that this contrasts with the AFM-based characterization conducted with spin-coated thin films, which are usually highly entangled, making the identification of the CNF end-points nearly impossible.³⁶ AFM imaging was performed using a cantilever typical of those reported in the literature for the same purpose. Specifically, the half-cone angle of the AFM cantilever’s tip was 20° ending with a tip radius of 8 nm (MikroMasch model HQ:NSC15/AL BS). A typical AFM image obtained from the CNF adsorbed on mica is shown in Figure 2a, and additional AFM images are shown in Figure S1. CNFs obtained after 6-pass of microfluidization of bleached sulfite hardwood (birch) fibers were analyzed. Although there was a relatively small proportion of large CNFs, their significant volume is expected to introduce a bias in measurements based on rheology and, particularly, from light scattering studies. In dynamic or static light scattering techniques, for instance, the scattering scales with the sixth power at the nanometer scale. Therefore, larger CNFs would be over-represented, although they may account for a smaller fraction of the SSA. In contrast, in CNF suspensions, the smaller fraction may have a higher contribution to shear thinning than the larger CNFs.⁴¹ Thus, despite the fact that only limited number of particles is factored in microscopy evaluations, compared to scattering or rheological-based measurements, microscopy techniques are more direct and accurate to quantify the detailed morphological characteristics. Thus, such an approach may be more useful in deriving, for instance, the effective surface area of the CNF in the aqueous suspension.

Figure 2.

(a) Representative AFM images obtained from dip casting a 0.01 mg mL^–1 CNF suspension, followed by rapid blotting onto PEI-coated mica used as a solid support. (b) Correlation between the lateral and height dimensions of CNFs obtained from AFM. Distributions of (c) height and (d) width obtained from AFM imaging. The exponential decay fit shown in (b) is given by “width = −257.4 × exp(−height/(29.8)) + 290.7”.

Despite the steps taken for sample preparation (extreme dilution and blotting as well as rinsing), individualized CNFs were scarce. Instead, bundles with fibrils oriented in multiple directions as well as overlapping were common in the suspension. Dewetting and capillary effects during sample drying may also contribute to aggregation and bundle formation. CNFs were identified, and their dimensions were extracted. Specifically, the length was more easily extracted from NegC SEM than that from AFM, simply because of the larger number of images obtained and greater imaging areas. This enables the quantification of CNF length. Branches from clustered CNFs were also used to obtain width and height distributions by AFM and length and width distributions by NegC SEM.

High-resolution images of CNFs spread onto solid supports were analyzed in order to obtain the morphological characteristics independently of their position in the network (Figure 2a; see also Figure S1 containing additional images). The lateral dimension of CNFs obtained from AFM imaging was first evaluated. The values of the height and width were significantly different: 6 ± 3 and 67 ± 18 nm, respectively (Figure 2c,d). The AFM size distributions for CNF height and width followed the Weibull and lognormal distributions, respectively (Figure 2c,d). Although the width and height of given CNFs scale with each other (Figure 2b), the respective mean values diverged by an order of magnitude. This observation suggests other effects occurring during measurements as well as during adsorption and drying of the CNFs, as observed in other studies with adsorbed, soft fibrillar nanomaterials.³⁷⁻³⁹

To evaluate the various effects leading to the discrepancy between width and height, maximum tip-convolution effects were first subtracted from the width measurement (Figure 3). The maximum tip convolution (Figure 3b) for the cantilever tip used herein was calculated as described in Figure 3a, assuming convolution with an object at right angle with the substrate of a given height. Therefore, the values obtained for tip-convolution artifacts are overestimated and are likely to be lower because of a less steep angle between CNFs and the substrate.^42,43 The corresponding tip convolution as a function of height is plotted in Figure 3b. When these values are subtracted to the width described in Figure 2, the light green distribution of points is observed (Figure 3c). An exponential decay was noted for the distribution of the lateral dimensions of the CNFs accessed from the AFM width and height profiles, with their ratio significantly diverging from unity. Interestingly, the values obtained for the width were always larger than 20 nm, with some height values below 3 nm, in the range of size noted for elementary fibrils as extracted from wood analysis.^26,44 This suggests that the CNFs may be bundles of oriented elementary fibrils that are not fully separated upon mechanical shearing.

Figure 3.

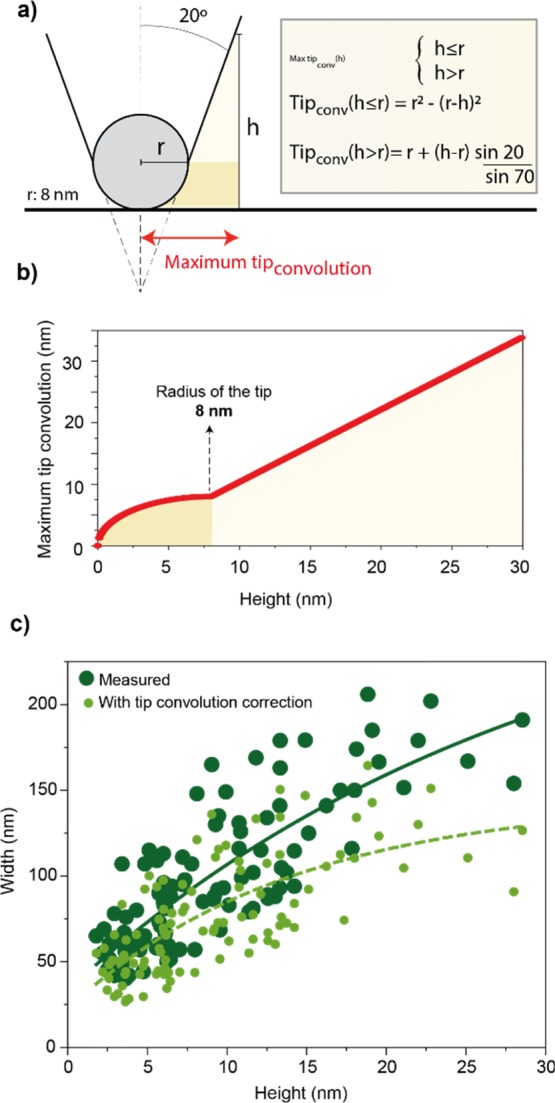
(a) Geometrical considerations and associated fittings governing the maximum tip convolution on the width measured by AFM (tip radius of 8 nm and half cone angle of 20°). (b) Curve of tip convolution as a function of the height of the CNF sample. (c) Correlation between the cross-sectional dimensions of the CNF obtained from AFM measurements, including distributions expected after subtraction of maximum tip convolution (light green). The exponential decay fits shown in (c) are given by “width = −257.4 × exp(−height/(29.8)) + 290.7” for the as-measured values and “width = −122.5 × exp(−height/(13.9)) + 144.7” for the values after tip-convolution correction.

For the tip-deconvoluted average (light green), a small relative difference with the original data is observed for CNFs with a height ≤10 nm. However, the values diverge more significantly for CNFs with a measured height higher than 10 nm. When including the overestimation from AFM tip convolution, the ratio between CNF’s width (lateral dimension after tip deconvolution) and height (from height profiles) was larger than 5 and up to 30. This suggests a significant “flattening” of the CNFs upon drying. This effect can be rationalized by the presence of elementary fibrils in the bundles that are displaced and the presence of disordered and relatively mobile cellulose chains within CNFs that are subjected to the effect of adhesion and capillary forces during drying. The same effect can be observed with a mechanically fibrillated CNF prepared from more extensive processing (12 passes in the microfluidizer, Figure S2). Also, CNCs, with very high crystallinity, display a statistically oblate cross-sectional geometry, however, at much lower extent with an average width-to-height ratio of 1.2.¹⁸ TO-CNF, with considerably low crystallinity and dimensions closer to elementary fibrils, also presents approximately circular cross section (Figure S2). This highlights that for each nanocellulose grade, different considerations may have to be taken into account. Interestingly, compared to the values determined for the largest CNFs, the width–height relations obtained by AFM indicate larger discrepancy for the smaller ones. It can be speculated that the larger CNFs may experience smaller capillary or adhesive forces.

The flattening effect was further evaluated by altering the affinity between CNFs and the substrate. This was performed to assess whether differences in wetting of the substrate may induce distinct degrees of (1) CNF aggregation coming from dip-casting and (2) CNF flattening. The morphological features of CNFs were analyzed from samples deposited onto bare mica, which have a lower affinity with CNFs and thus may lead to lower spreading and flattening. As for (1), the overall distribution of the CNFs was visually similar, regardless the substrate used (no significant differences in sample preparation existed). In contrast, for (2), a smaller width distribution compared to the PEI-coated substrate was determined when the CNF was adsorbed and imaged on bare mica (Figure 4a,b). A higher affinity of CNFs and PEI-coated surface is expected as the zeta potential of the mechanically fibrillated CNF prepared herein is slightly negative.^45,46 Additionally, PEI has been shown to bear a strong adhesive capacity because of multiple interactions.⁴⁷ Both aspects, when combined, may result in a substantially higher flattening when compared to bare mica that would, in contrast, present either a less attractive or even a repulsive interaction potential with the surface of the CNFs.

Figure 4.

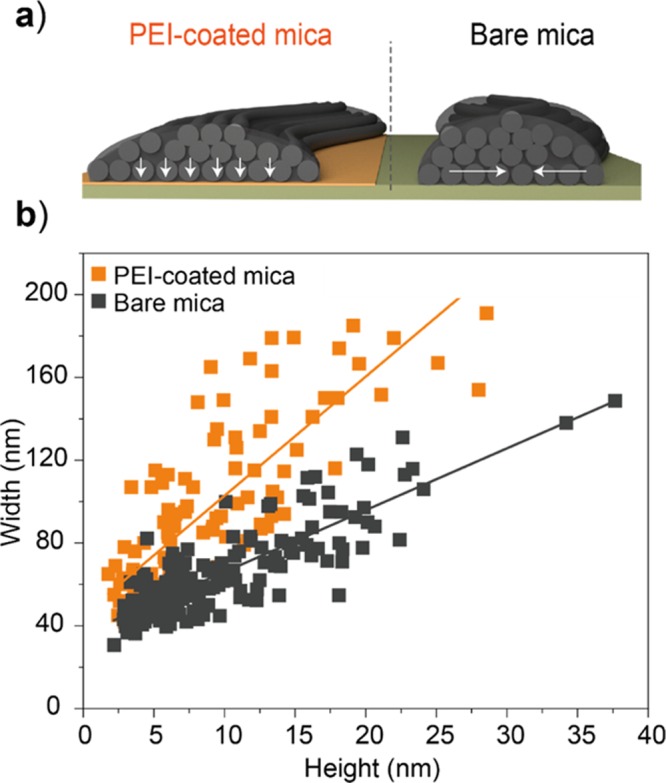
(a) Effect of substrate affinity between the highly adhesive PEI-coated surface and the lower affinity mica surface on adsorption induced spreading of CNFs depicted schematically. (b) Correlation between width and height for CNFs measured on PEI-coated mica or bare mica, highlighting a less oblate cross-sectional area for CNF supported on bare mica. The linear fits in (b) are given by “width = 36.1 + 2.9 × height” for bare mica and “width = 45.3 + 5.7 × height” for PEI-coated mica.

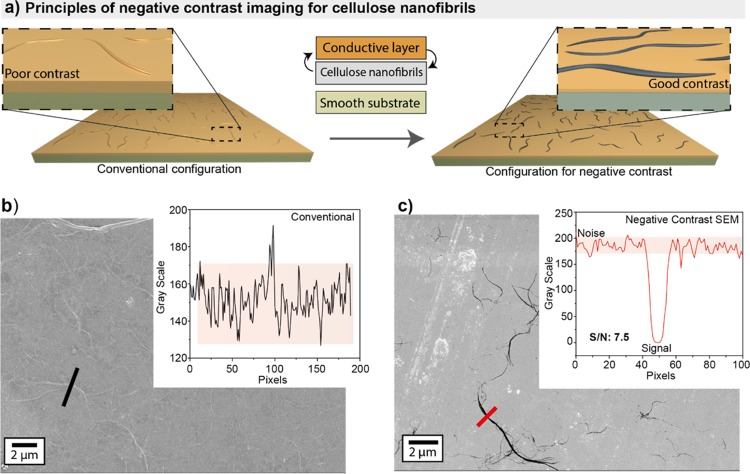
Last, we introduced a negative contrast SEM imaging technique (therein referred to as NegC SEM) to study CNF adsorbed on solid supports coated with a metal, as a conductive layer, for rapid and facile imaging of a large number of CNFs. The metalized mica was coated with PEI, and the CNF was deposited following the same protocols used in AFM evaluations with mica, for comparison. While obtaining high-resolution AFM can be a lengthy process, SEM allows the facile and rapid imaging of considerably larger areas if a good contrast exist (Figure S3). Although previously SEM has been undermined as an imaging technique for nanocelluloses, we show that, by judiciously choosing a metal for coating smooth substrates, a high contrast can be obtained. This makes NegC SEM ideal to obtain the lengths of CNFs and potentially their widths.

SEM detection of electrons reflected normal to the surface using the in-lens detector provided a sharp contrast between CNF and the metal, given the large difference in the dielectric properties of the CNFs and the metallic coating. Compared with the images obtained from a thin-sputtered metal layer onto CNFs or using secondary electron imaging, as is common for SEM imaging of CNFs, the contrast obtained via negative contrast had exceptionally higher signal-to-noise ratio (S/N, Figures 5, and S3–S6). Imaging using secondary electrons, in-lens detection on metal-coated CNF or uncoated CNF deposited onto a metal layer yielded S/N of ca. 1, 1.5, and 7.5 (Figure S5). NegC SEM was most effective for CNF deposited onto thin films of iridium as other surfaces sputtered, for instance, with gold or platinum/palladium alloys, lead to rough surfaces with large cracks (Figure S6). Remarkably, an excellent contrast was achieved when using an inexpensive, “kitchen-grade” aluminum foil as a metal support (Figure S6c). The higher contrast obtained by NegC SEM is further emphasized in Figure 5 (detailed in Figure S7) where CNFs with a lateral dimension <20 nm could be clearly imaged. Interestingly, in all cases, the CNFs’ edges appeared slightly blurred, although they were clearly in focus. This is, for instance, made more evident for CNFs deposited onto thin metallic films with a large number of cracks that appear sharp in the images, highlighting a good focus (Figure S6). This blurring effect may be due to the thickness of the CNFs, which are extremely thin toward their outer edges as also suggested by the AFM analysis.

Figure 5.

(a) Sample preparation using CNFs that are first adsorbed onto a support followed by carting with a thin metal layer (left) and sample preparation whereby the metal coating is first applied onto the substrate followed by deposition of the CNFs (right). (b,c) images obtained with samples prepared as described in panel (a), left and right, respectively. The insets highlight contrast differences.

The distribution of characteristic length and width is shown in Figure 6a,b, yielding median values of 1.46 ± 0.8 μm and 35 ± 12 nm, respectively. The width and length correlated linearly with each other and showed a widened interval of confidence for larger nanofibrils. From the correlation profile in Figure 6c, a length-to-width aspect ratio of ca. 59 was determined from the mean values.

Figure 6.

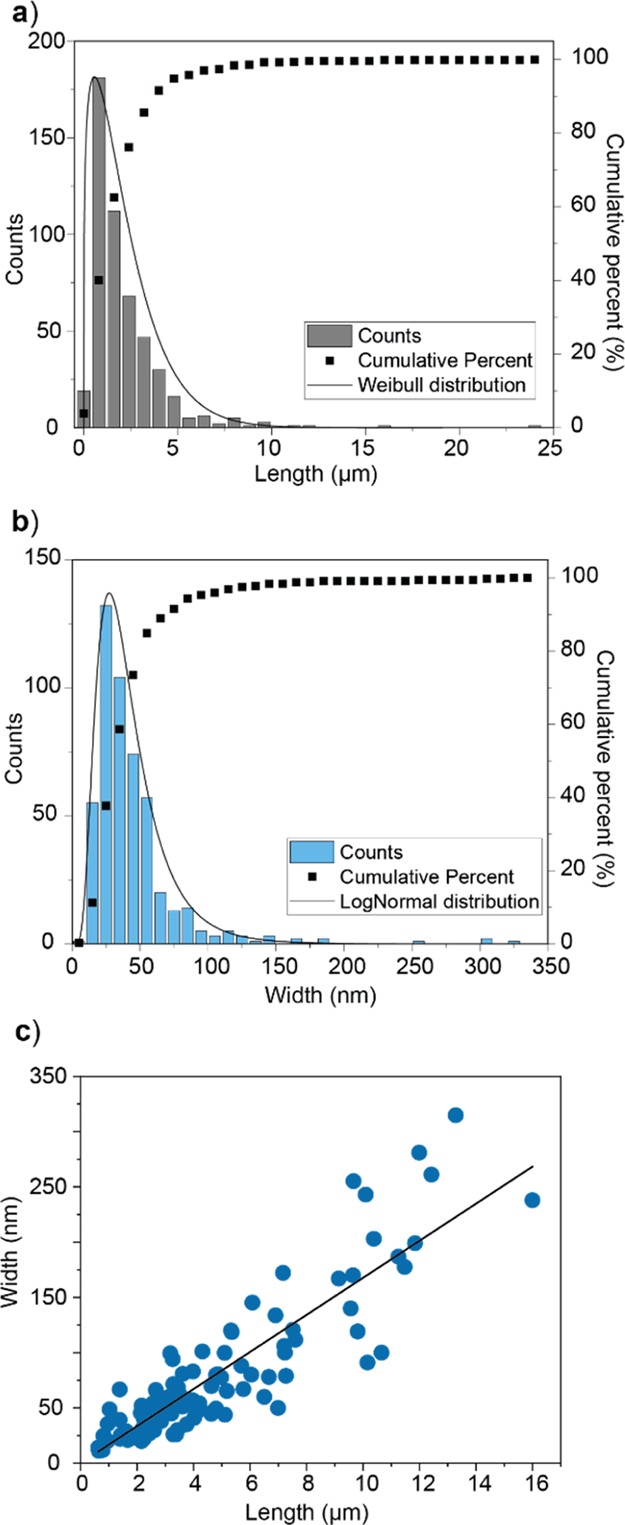
Distribution of (a) length and (b) width of CNF obtained by NegC SEM as described in Figure 5, as well as (c) their linear correlation. The linear fit shown in (b) is given by “width = 16.7 × length”.

From the schematic proposed in Figure 1d and the dimensions distributions obtained thus far, it is possible to obtain the diameter of CNFs by using the equivalent cross-sectional area measured by AFM to estimate the diameter of the equivalent circular cross section. The circular cross section, which is still not agreed upon, was assumed for simplicity and following a vast number of reports that use such geometry.^26,44,48 Using the height obtained from AFM and width obtained from SEM, the diameter of the CNFs is estimated to be ca. 28 ± 12 nm. Using the width obtained from AFM, the diameter is 39 ± 15 nm. Width distribution obtained from NegC SEM and AFM both followed lognormal distributions. The difference may principally arise from the pixel size obtained by AFM being substantially smaller than the one obtained by SEM, where large images were taken to obtain micrometer-sized lengths. Other possible contributions to the width discrepancy between SEM and AFM include higher S/N obtained by AFM (Figure S5) and the effects of swelling during AFM measurements, which were conducted at a higher relative humidity (23%) when compared to the high vacuum atmosphere in the SEM measurement. Additionally, a small sampling bias may be present, where smaller areas were considered for AFM compared to those in SEM. This may result in larger CNFs being underrepresented in AFM measurements. The values reported here for the diameter allow an accurate determination of the aspect ratio of the CNFs, in the present case 49 ± 8 (36 ± 7 by AFM). The cross-sectional analyses and the obtained equivalent diameter enable the estimation of a more accurate aspect ratio of the mechanically fibrillated CNFs, most important in predicting their assembly behavior. On the basis of the precedent discussion, we argue that the CNF aspect ratio obtained from AFM imaging has been overestimated in the literature (reported to reach values up to 1000)⁴⁰ because the measured height is often used as a measure of the diameter. Using the SEM length and the width obtained from SEM (or AFM in combination with the AFM-based height) and to calculate the cross section and associated surface area led to a small difference in values (ca. 4%) for the effective surface area of the suspension: from 472 ± 261 to 457 ± 258 m² g^–1, respectively. Distributions of the SSA values are obtained by calculating the SSA for individual CNFs as shown in the distributions included in Figures 2 and 6, and using the approximations shown in the Figure S8. Briefly, the height and width are converted to an equivalent circular cross section, which combined to the length allow the surface area of an ideal cylinder to be calculated (Figure S9). The SSA values obtained herein do not have any contribution coming from entanglement or fibers overlap, meaning that these values are expected to be higher than the ones experimentally obtained from, for instance, nitrogen adsorption.⁴⁹

Furthermore, because NegC SEM is considerably faster and more user-friendly than AFM, one can potentially use the correlations between dimensions (height/width for AFM and width/length for NegC SEM) to better describe the sample by only using the NegC SEM technique. The accuracy of such estimate is, however, dependent on sampling size, homogeneity, and polydispersity of the sample. With a well-defined sample, the difference between the dimensions obtained from the two techniques can be attributed to humidity and signal-to-noise ratio, which would be constant for all experiments. This may lead, for instance, to a precise estimation of the height from the width obtained in the NegC SEM.

Conclusions

In conclusion, we introduce the combination of AFM and NegC SEM to easily and efficiently assess the morphology and dimensions of CNFs. Our approaches may be applicable to other nanocelluloses (enzyme-pretreated CNF, MFC, fractionated samples, e.g.). More importantly, the importance of the substrate interaction may also be put forward for finer research involving the characterization of smaller bio-based nanofibers such as TO-CNFs, nanochitin, and so forth. The dimensions obtained from AFM (height or lateral dimensions) or TEM/SEM imaging, if used alone, fall short in offering a good description of the morphological features of the CNF. This is due to significant effects arising from the disordered nature of CNFs, that is, in analogy to synthetic macromolecular soft matter, and their interaction with given substrates. Furthermore, the substantial effect of the substrate on the conformation of the CNFs may be put in perspective with neutron or X-ray scattering techniques to better understand the distribution and size of the highly rigid crystalline domains within CNFs. Therefore, we envision that the framework and the findings presented herein will lead to significant advances in the metrology of CNFs and in relating it with the properties of the materials they form, with the potential to be extended to other cellulosic and bio-based colloids.

Glossary

Abbreviations

NegC

negative contrast imaging

SEM

scanning electron microscopy

CNF

cellulose nanofibrils

AFM

atomic force microscopy

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biomac.9b00432.

• Conventional SEM images, signal-to-noise ratio, examples of AFM and SEM images taken for the measurement of the dimensionalities of CNF, negative contrast SEM with other metallic substrates, tip deconvolution calculation, and correlation between height and width from AFM (PDF)

Author Contributions

^§ B.D.M. and B.L.T. contributed equally. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

We acknowledge funding from the ERC Advanced Grant (no. 788489), BioElCell.

The authors declare no competing financial interest.