Abstract
Postinhibitory rebound (PIR) is believed to play an important role in the genesis and maintenance of biological rhythms. While it has been demonstrated during several in vitro studies, in vivo evidence for PIR remains scarce. Here, we report that PIR can be observed in the dorsomedial entorhinal cortex of anesthetized rats, mostly between putatively connected GABAergic interneurons, and that it is more prevalent during the theta (4–6 Hz) oscillation state than the slow (0.5–2 Hz) oscillation state. Functional inhibition was also found to be brain state and postsynaptic cell type dependent but that alone could not explain this brain state dependence of PIR. A theoretical analysis, using two Fitzhugh–Nagumo neurons coupled to an external periodic drive, predicted that the modulation of a faster spiking rate by the slower periodic drive could account for the brain state dependence of PIR. Model predictions were verified experimentally. We conclude that PIR is cell type and brain state dependent and propose that this could impact network synchrony and rhythmogenesis.
Introduction
Neurons releasing GABA can transmit a straight inhibitory signal to their targets, which prevents or delays firing in the postsynaptic cell (Miles et al., 1996). Interestingly, the inhibitory signal can be followed by rebound firing of the target cell, a phenomenon known as postinhibitory rebound (PIR). PIR has been observed in vitro mostly in glutamatergic excitatory neurons such as neurons of deep cerebellar nuclei (Llinás, 1988; Aizenman and Linden, 1999), thalamocortical relay neurons (Llinás, 1988; Huguenard and McCormick, 2007), and stellate cells of entorhinal cortex (Dickson et al., 2000). Its possible underlying mechanisms include the de-inactivation of low-threshold Ca2+ current (Llinás, 1988; Huguenard and McCormick, 2007) or the activation of the Ih current (Dickson et al., 2000). Functional implication of PIR expression is the genesis of rhythms in subcortical regions. Rebound excitation in excitatory relay cells of the thalamus, for instance, along with their reciprocal synaptic connectivity with inhibitory reticular neurons, creates an intrinsic oscillatory unit (Huguenard and McCormick, 2007). Modeling studies also suggest that PIR is central to the genesis of rhythms in interneuron–interneuron networks (Wang and Rinzel, 1992; Coombes and Doole, 1996; Chik et al., 2004; Rotstein et al., 2005). However, whether PIR occurs naturally in vivo remains to be firmly established. Although rebound excitation can be triggered in thalamocortical and cortical neurons by external electrical stimuli (Grenier et al., 1998), a recent study by Alviña et al. (2008) challenged the concept of PIR role in oscillations, reporting that, under physiological conditions in vitro and in vivo, deep cerebellar nuclei neurons rarely show rebound firing.
The difficulty in finding evidence of PIR in vivo may stem from the fact that PIR may be specific to certain neuronal connections and/or its expression could be influenced by the ongoing brain activity. Different behavioral states are associated with the expression of different oscillations—from ultraslow (<0.1 Hz) to very fast (150 Hz)—in the extracellular field potentials (Buzsáki and Draguhn, 2004). Now, the firing pattern of hippocampal GABAergic interneurons depends upon both the type of interneurons (cell specificity) and the type of ongoing oscillation (brain state specificity) (Klausberger and Somogyi, 2008). Since the transfer of information between two neurons depends not only upon the nature of the source and the target cells, but also upon the firing frequency of the presynaptic cell (e.g., via short-term plasticity mechanisms) (Maccaferri et al., 2000; Pouille and Scanziani, 2004), functional inhibition and, consequently or otherwise, a rebound excitation of the target cell may be cell type and brain state dependent.
We tested these hypotheses by performing a cross-correlogram analysis on a database of spike trains of putative pyramidal cell and interneurons recorded in the dorsomedial entorhinal cortex of anesthetized rats during two brain states—theta (4–6 Hz) and slow oscillation (SO) state (0.5–2 Hz) (Quilichini et al., 2010). Modeling was then used to explore the underlying mechanisms, leading to predictions, which were then tested in the database.
Materials and Methods
Data collection.
We used the data published by Quilichini et al. (2010) for our investigations. The data included local field potentials (LFPs) and single-unit recordings made in the dorsomedial entorhinal cortex (EC) of anesthetized rats.
Animal surgery.
All experiments were performed in accordance with experimental guidelines approved by the Rutgers University Animal Care and Use Committee. Experiments were performed on 39 male Sprague Dawley rats (250–400 g; Hilltop Laboratory Animals), which were anesthetized with urethane (1.5 g/kg, i.p.) and ketamine/xylazine (20 and 2 mg/kg, i.m.), and additional doses of ketamine/xylazine (2 and 0.2 mg/kg) were supplemented. The body temperature was monitored and kept constant with a heating pad. The head was placed in a stereotaxic frame, the skull was exposed, and a small hole (1.2 mm in diameter) was drilled −7.0 mm anterior to bregma and 4.0 mm from the midline. The extracellular recording silicon probe was inserted at a 20° angle caudally 5.0–5.2 mm from brain surface to target the dorsomedial portion of entorhinal cortex. Two miniature stainless-steel screws, driven into the skull, served as ground and reference electrodes.
Electrophysiological methods.
Extracellular signal was amplified (1000×) and bandpass filtered (1 Hz to 5 kHz) by a multichannel AC amplifier (Sensorium EPA5; Sensorium). The wide-band signals were digitized at 20 kHz and stored for off-line analysis (64-channel DataMax System; 16 bit resolution; RC Electronics). The extracellular recordings were performed using either a four-shank silicon probe (NeuroNexus Technologies; 32 sites, four shanks, 200 μm shank separation, eight sites per shank, 20 μm vertical separation) staggered to provide a two-dimensional arrangement [see the site layout in the study by Fujisawa et al. (2008)] placed in EC2–EC3 or EC3–EC5, or a single-shank silicon probe (Acreo) with 32 linearly arranged recording sites (at 50 μm intervals) placed almost perpendicular to the layers of the dorsomedial entorhinal cortex. The presence of unit activity in cell body layers and the reversal of theta (3–6 Hz) oscillations when passing from EC2 to EC1 were used to assist on the on-line positioning of the probe (Chrobak and Buzsáki, 1998; Mizuseki et al., 2009) and its final position was confirmed, post hoc histologically, after the experiment. Only experiments with appropriate position of the probe were used for analysis (DiI was applied on the back of the probe before insertion).
Data analysis.
Raw data were preprocessed using a custom-developed suite of programs (Csicsvari et al., 1999). The wide-band signal was downsampled to 1250 Hz for LFP signal analysis. Single units were isolated from the wide-band signal semiautomatically by a custom-developed clustering analysis program KlustaKwik (http://klustakwik.sourceforge.net/) (Harris et al., 2000) and refined manually using custom-made software (http://klusters.sourceforge.net; http://neuroscope.sourceforge.net) (Hazan et al., 2006). Only units showing a clear refractory period and well defined cluster boundaries were included for analysis. The classification between putative principal cells and interneurons was made on the basis of (1) physiological features like their waveform asymmetry and half-width, firing rate, and autocorrelogram (Sirota et al., 2008; Mizuseki et al., 2009; Quilichini et al., 2010), and (2) we took advantage of the simultaneously recorded cells to assess putative monosynaptic connections among neurons revealed by excitatory or inhibitory short latencies in their cross-correlograms (Harris et al., 2000; Barthó et al., 2004; Sirota et al., 2008; Mizuseki et al., 2009).
Recording sessions were divided into brain states of theta and SO periods. LFP theta epochs were visually selected from the raw traces, assisted by the ratios of the whitened power in the theta band (3–6 Hz) and the power of the neighboring bands (1–3 and 7–14 Hz) of EC3 LFP. The theta phase of the EC3 LFP was determined from the LFP filtered in the theta band (adjusted for the dominant theta frequency in each experiment, typically ∼2–6 Hz). The instantaneous phase was computed as the angle of the Hilbert transform and the distribution of the phases in each session was tested for uniformity before unit analysis. The theta phase modulation of action potentials was determined by Rayleigh circular statistics (Fisher, 1993); p < 0.05 was considered significant. Group comparison tests of circular variables were performed using circular ANOVA.
We calculated pairwise cross-correlograms (CCGs) between spike trains of these cells during each brain state separately. The first two bins (0.8 ms binning) were excluded from the CCG computations since the spikes detection algorithm rejects the spikes recorded by the other channels of the spike group within a [−1 1] ms latency from a given spike to prevent assigning the waveforms of this spike, also recorded by surrounding channels, as other spikes. We identified, as a putative PIR, a peak in CCG following an inhibitory trough, as seen in Figure 1, C, D, and F. Statistical significance of the inhibition and the rebound excitation was ascertained using the nonparametric test and criterion used for identifying monosynaptic excitations or inhibitions by Quilichini et al. (2010) and Fujisawa et al. (2008). Essentially, we jittered each spike of each neuron randomly and independently on a uniform interval of [−5 5] ms a 1000 times to form 1000 surrogate data sets. Then we constructed 1000 surrogate CCGs and constructed global maximum and minimum bands at 99% acceptance levels as shown in the CCGs in Figure 1.
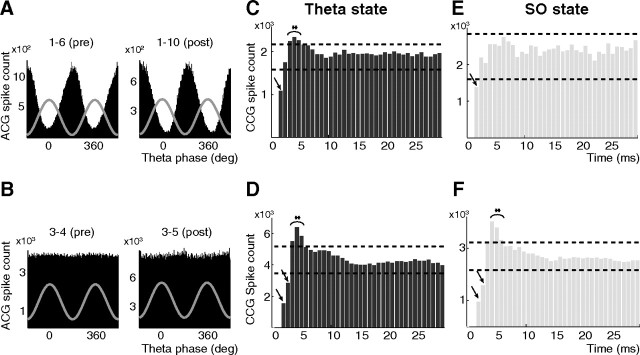
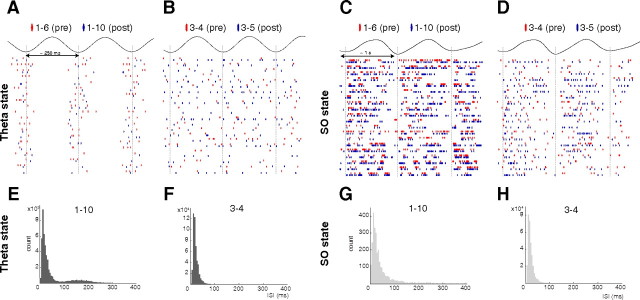
Figure 1.
Brain state dependence of PIR. A, B, Theta phase distribution of the firing of pairs of putative interneurons: neurons 1–6 (presynaptic) and 1–10 (postsynaptic) show a strong preference of their firing at the trough of the theta cycle (wave: average LFP) (A), and for neurons 3–4 and 3–5, no modulation of their firing (B). C–F, CCGs of the spike trains of the two pairs computed during the two states. Spike counts from the first two bins are not taken into account (see Materials and Methods). The arrows and braces indicate statistically significant inhibition and excitation, respectively (dashed lines, 99% global confidence intervals). Note the disappearance of PIR during SO for the 1–6/1–10 pair, while it remains significant for the 3–4/3–5 pair.
The connection strengths (inhibition and rebound excitation) were obtained as the percentage difference between the actual count in the statistically significant bins and the value extracted using a least-square line extrapolated from the counts in the 10–30 ms bins. We used the extrapolation instead of a simple average because in cases in which the firing phase preferences of the pair differed, there was a gradual and, in most cases, linear increase or decrease in the counts of these bins.
Model equations.
We considered two Fitzhugh–Nagumo neurons (Fitzhugh, 1961), each synaptically coupled to an external periodic drive representing the local field potential during theta and SO. We further assumed that neuron 1 is connected to neuron 2 through a fast, inhibitory synapse represented by the sigmoidal function of the membrane potential of the first neuron (Wang and Rinzel, 1992) but that neuron 2 is not connected to neuron 1. The assumptions of instantaneous synapse and unidirectionality were based on observations from the analysis of data.
Thus, the model equations with the corresponding coupling terms are as follows:
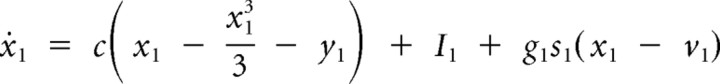 |
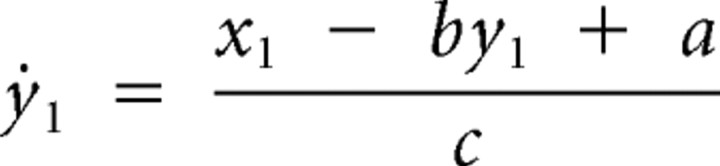 |
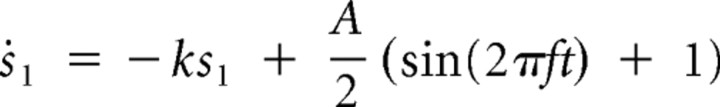 |
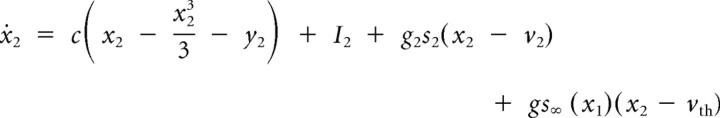 |
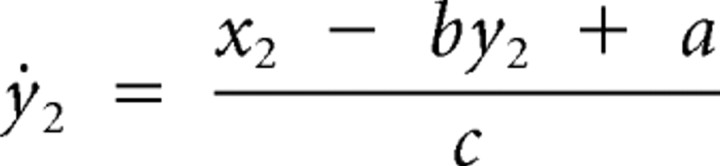 |
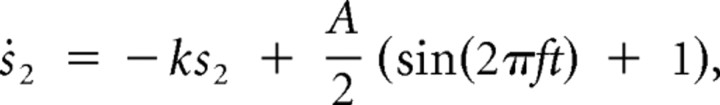 |
where
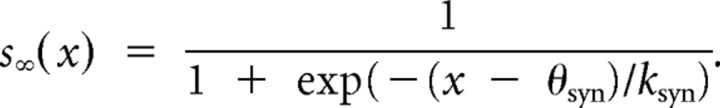 |
Here, x and y represent the membrane potential and the recovery variable that can represent the turn-on of the potassium permeability, respectively, for each neuron. The synaptic variable s represents the fraction of postsynaptic conductance for the coupling with the excitatory extracellular local field potential.
We choose a = 0.45, b = 0.9, and c = 3, and I1 and I2 in the range so that both neurons, in the absence of any other interactions, are in the excitable regime.
In the case of the coupling between the neuron and the drive, the time constant for synaptic decay, k, and the amplitude of the external drive, A, are chosen to be 0.1. v1 and v2 are equal to zero. g1 and g2 are varied for a parameter space analysis.
In the case of the instantaneous inhibitory coupling from neuron 1 to neuron 2, we choose θsyn equal to −0.7. g and vth are chosen so that neuron 2 is sufficiently hyperpolarized when neuron 1 fires an action potential to cause a rebound spike in neuron 2. ksyn determines the timescale of the rebound firing response of neuron 2 to the spikes of neuron 1.
To compare the experimental and theoretical results, we added a noise term to each equation and calculated the CCGs from the simulated spike trains. The noise term was a random variable derived from a Gaussian distribution with zero mean and nonzero variance. The value of the variance was chosen to achieve appropriate background spike count in the CCGs.
Results
Inhibition is brain state dependent
In vivo recordings in the hippocampus show that the firing pattern of a given class of interneurons is brain state dependent (Klausberger and Somogyi, 2008). Hence, the transfer of information between an interneuron and its targets (e.g., the inhibitory action of this interneuron) may also be brain state dependent. Quilichini et al. (2010) isolated a total of 443 single units from 34 separate experiments and identified 125 putative principal cells and 149 putative interneurons, which fired enough spikes during both brain states to calculate autocorrelograms and CCGs. In addition, we identified 12 principal cells and 15 interneurons, which fired exclusively during the theta state, but not during SO. We used all identified units to calculate CCGs between all possible pairs during each brain state separately. The analysis of a total of 12,536 pairs revealed 95 pairs in which the presynaptic cell was a putative GABAergic interneuron (i.e., its firing led to statistically significant transient decreased firing probability of its target cells). The target cell was an excitatory principal cell in 49 of 95 pairs (52%) and another interneuron in 46 of 95 pairs (48%).
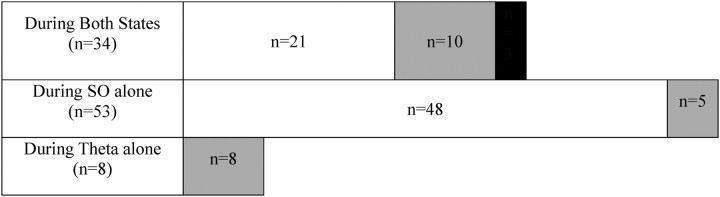
Interestingly, the distribution of functional inhibitory connections was brain state dependent. We identified 87 connected pairs during SO and 42 during theta. Thirty-four pairs were common to both states. Both cells from each of the 95 pairs fired a sufficient number of spikes in both states to perform a statistically significant analysis of inhibitory connections using CCGs. All postsynaptic cells from the eight inhibitory pairs found during only the theta state were interneurons. In contrast, in 39 of 53 (74%) inhibitory pairs observed during only the SO state, the postsynaptic cell was an excitatory principal cell. In the case of 34 pairs that displayed inhibition during both states, 70% of the postsynaptic cells were interneurons. Tables 1 and 2 show this distribution of inhibitory pairs during each state according to the location and type of the postsynaptic cells.
Table 1.
Distribution of cell pairs displaying inhibition according to brain state and the type and location of the postsynaptic cell in the EC
| Percentage of inhibitory connections in | During theta alone (n = 8) |
During SO alone (n = 53) |
During both states (n = 34) |
|||
|---|---|---|---|---|---|---|
| Target cell type |
Target cell type |
Target cell type |
||||
| PC | Int | PC | Int | PC | Int | |
| EC2 | 0 | 63 (n = 5) | 28 (n = 15) | 11 (n = 6) | 6 (n = 2) | 32 (n = 11) |
| EC3 | 0 | 37 (n = 3) | 38 (n = 20) | 13 (n = 7) | 15 (n = 5) | 24 (n = 8) |
| EC5 | 0 | 0 | 8 (n = 4) | 2 (n = 1) | 8 (n = 3) | 15 (n = 5) |
Table lists the percentage of inhibitory cell pairs found during each brain state according to the location and the type of the postsynaptic cell. The postsynaptic cell in 74% of the inhibitory pairs observed during the SO state alone was a putative excitatory principal cell (PC). However, in 70% of the inhibitory pairs observed during both states, the postsynaptic cell was a putative interneuron (Int). All postsynaptic cells of the inhibitory pairs found during the theta state alone were interneurons. This suggests that functional inhibition, and the postsynaptic cell type dependence of the connections, are brain state dependent.
Table 2.
Fraction of postsynaptic cells, from all the cell pairs displaying inhibition during each state, showing rebound excitation
Table shows the fraction of postsynaptic cells, from all the cell pairs displaying inhibition during each state, showing rebound excitation. The color code for column shading is as follows: clear, no rebound excitation; gray, rebound excitation; and black, rebound excitation only during the theta state.
The properties of GABAergic neurotransmission from a given interneuron source depends upon the nature of the postsynaptic target, and it also depends upon the nature of the presynaptic source for a given target (Brown and Hestrin, 2009). We thus assessed the strength of inhibition as a function of the nature of the postsynaptic target, the spatial location of the source (in layers EC 2, 3, and 5), and the nature of the brain state. In a given layer, the average strength of inhibition was independent of the type of postsynaptic cell and the brain state, except for pairs located in EC3 and displaying inhibitory connections during SO only (Tables 3, 4).
Table 3.
Average inhibitory strength displayed by common cell pairs according to brain state and cell type and the layer distribution in the EC of the postsynaptic cell
| Strength (%) in common pairs | During theta state |
During SO state |
||
|---|---|---|---|---|
| Target cell type |
Target cell type |
|||
| PC | Int | PC | Int | |
| EC2 | 68 ± 12 (n = 2) | 53 ± 4 (n = 11) | 59 ± 11 (n = 2) | 50 ± 3 (n = 11) |
| EC3 | 69 ± 9 (n = 5) | 50 ± 6 (n = 8) | 59 ± 4 (n = 5) | 47 ± 5 (n = 8) |
| EC5 | 74 ± 5 (n = 3) | 27 ± 7 (n = 5) | 47 ± 10 (n = 3) | 30 ± 7 (n = 5) |
Values represent mean ± SEM. Table lists the average strength of inhibition displayed by common cell pairs according to the brain state, cell type, and layer location of the postsynaptic cell.
Table 4.
Average inhibitory strength displayed by noncommon cell pairs according to brain state and cell type and the layer distribution in the EC of the postsynaptic cell
| Strength (%) in noncommon pairs | During theta state only |
During SO state only |
||
|---|---|---|---|---|
| Target cell type |
Target cell type |
|||
| PC | Int | PC | Int | |
| EC2 | 0 | 42 ± 5 (n = 5) | 53 ± 4 (n = 15) | 34 ± 3 (n = 6) |
| EC3 | 0 | 35 ± 2 (n = 3) | 58 ± 4 (n = 20) | 40 ± 5 (n = 7)* |
| EC5 | 0 | 0 | 58 ± 6 (n = 4) | 63 (n = 1) |
Values represent mean ± SEM. Tables list the average strength of inhibition displayed by noncommon cell pairs according to the brain state, cell type, and layer location of the postsynaptic cell. We found that the postsynaptic interneurons from the EC3 pairs during SO alone showed significantly lower average inhibition than the corresponding principal cells (*p < 0.01).
Together, these results demonstrate that the connections showing functional inhibition, and in particular, the postsynaptic cell type dependence of them observed in these experiments was brain state dependent.
PIR is mostly present at interneuron–interneuron connections
By definition, PIR corresponds to an inhibition–excitation sequence (i.e., rebound firing after a period of silence). We thus looked for the evidence for PIR among the CCGs of all 95 pairs displaying inhibition. We found that 26 pairs displayed PIR (27%) (Fig. 1C,D,F, for examples). The timescale of the entire interaction was of the order of 5 ms. The average duration of statistically significant inhibition was up to 1.6 ms and of the subsequent rebound duration was ∼2.4 ms. In comparison, the duration of a direct excitation from a principal cell onto its target was 1–2 ms (Quilichini et al., 2010), shorter than PIR. Most PIR cases were unidirectional since only two pairs displayed a reciprocal PIR. Interestingly, 21 of the target cells (81%) displaying PIR were other interneurons. Thus, although 52% of the targets in the pairs showing functional inhibition were principal cells (Tables 1, 2), the latter rarely displayed PIR (10% of interneuron–principal cell connections). Based on CCG analysis, we propose that PIR is found in entorhinal cortex in vivo, and that it is predominantly displayed at interneuron–interneuron connections.
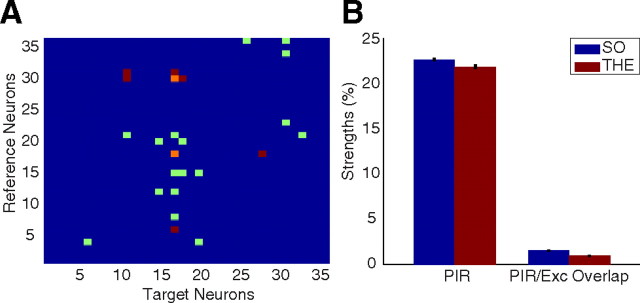
Although CCGs reliably identify connections between neurons (Moore et al., 1970), the evidence they provide is indirect. Therefore, we tested the hypothesis that the inhibition–excitation sequence represents PIR against a competing hypothesis that excitation could be due to the firing of a third-party excitatory cell. As shown in Figure 2, cells showing PIR also receive excitatory connections from other cells. Hence, we calculated the overlap between two sets of spikes of each such postsynaptic neuron: (1) those contributing to the statistically significant rebound excitation bins in the CCG and (2) those contributing to the statistically significant bins in the CCG for regular excitation. We found that the average contribution of third-party excitatory neurons to postsynaptic neurons displaying PIR was over an order of magnitude smaller than the average rebound strength found after inhibition (Fig. 2).
Figure 2.
Verifications for the PIR hypothesis. A, Identified putative connections between all single units from one experiment. Color code: blue, no connection; red, inhibition; green, excitation; and orange, PIR. Some target neurons that display rebound upon inhibition from some interneurons (e.g., interneurons number 18 and 30 onto neuron 17) also receive excitatory connections from some principal cells (e.g., principal cells 8, 12, 15, and 21 onto neuron 17). B, Comparison between average values of the rebound strength and the extent of overlap between two sets of spikes of the target cell: those contributing to the statistically significant peaks in the PIR CCGs and those contributing to the statistically significant peaks in the CCGs for normal excitations. The low strength of overlap suggests that identified excitatory connections cannot account for the rebound excitation observed in the CCG of PIR pairs. The bar diagram considers all PIR pairs in which the target cell is also the target in at least one excitatory connection.
PIR is brain state dependent
Since we observed that pairwise inhibition was brain state dependent, we assessed whether PIR was also different between SO and theta. Fifteen of the 87 connected pairs (17%) displayed PIR during SO (Table 5). In contrast, 21 pairs of 42 (50%) showed PIR during theta (Table 6). Ten pairs showed PIR during both theta and SO states. Thus, PIR seemed more prevalent during the theta state.
Table 5.
All pairs displaying PIR during the SO state
| Exp no. | Reference neuron |
Target neuron |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Shank | Cluster | Layer | Type | Phase modulation in theta | Shank | Cluster | Layer | Type | Phase modulation in theta | |
| 12 | 1 | 4 | 5 | I | UM | 1 | 5 | 5 | E | UM |
| 1 | 4 | 5 | I | UM | 1 | 6 | 5 | I | UM | |
| 1 | 7 | 5 | I | UM | 1 | 4 | 5 | I | UM | |
| 1 | 7 | 5 | I | UM | 1 | 8 | 5 | E | UM | |
| 3 | 4 | 5 | I | UM | 3 | 5 | 5 | I | UM | |
| 3 | 5 | 5 | I | UM | 3 | 4 | 5 | I | UM | |
| 4 | 5 | 5 | I | UM | 4 | 10 | 5 | I | UM | |
| 13 | 4 | 36 | 3 | I | M | 4 | 34 | 3 | E | UM |
| 3 | 25 | 3 | I | M | 3 | 23 | 3 | I | M | |
| 14 | 2 | 12 | 3 | I | M | 2 | 10 | 3 | I | M |
| 16 | 3 | 17 | 2 | I | M | 3 | 16 | 2 | I | UM |
| 3 | 16 | 2 | I | UM | 3 | 8 | 2 | I | M | |
| 25 | 4 | 5 | 2 | I | M | 4 | 6 | 2 | I | M |
| 4 | 6 | 2 | I | M | 4 | 5 | 2 | I | M | |
| 1 | 21 | 2 | I | M | 1 | 7 | 2 | I | M | |
Table shows all pairs displaying PIR during the SO state. Type signifies the type of neuron (I for interneurons and E for excitatory principal cells) identified in the study by Quilichini et al. (2010). Phase modulation (UM for unmodulated and M for modulated) shows whether the cells fire preferentially according to the phase of the theta oscillation. It is shown for comparison with the pairs displaying PIR during the theta state.
Table 6.
All pairs displaying PIR during the theta state
| Exp no. | Reference neuron |
Target neuron |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Shank | Cluster | Layer | Type | Phase modulation | Shank | Cluster | Layer | Type | Phase modulation | |
| 12 | 1 | 4 | 5 | I | UM | 1 | 5 | 5 | E | UM |
| 1 | 4 | 5 | I | UM | 1 | 6 | 5 | I | UM | |
| 1 | 7 | 5 | I | UM | 1 | 4 | 5 | I | UM | |
| 1 | 7 | 5 | I | UM | 1 | 8 | 5 | E | UM | |
| 3 | 4 | 5 | I | UM | 3 | 5 | 5 | I | UM | |
| 3 | 5 | 5 | I | UM | 3 | 4 | 5 | I | UM | |
| 4 | 5 | 5 | I | UM | 4 | 10 | 5 | I | UM | |
| 13 | 3 | 10 | 3 | I | M | 3 | 25 | 3 | I | M |
| 3 | 25 | 3 | I | M | 3 | 10 | 3 | I | M | |
| 3 | 10 | 3 | I | M | 3 | 23 | 3 | I | M | |
| 3 | 25 | 3 | I | M | 3 | 23 | 3 | I | M | |
| 14 | 1 | 16 | 2 | I | M | 1 | 20 | 2 | I | M |
| 1 | 20 | 2 | I | M | 1 | 18 | 2 | I | UM | |
| 16 | 3 | 17 | 2 | I | M | 3 | 16 | 2 | I | UM |
| 18 | 3 | 2 | 3 | I | M | 3 | 3 | 3 | E | M |
| 19 | 3 | 14 | 3 | I | M | 3 | 15 | 3 | E | M |
| 25 | 4 | 5 | 2 | I | M | 4 | 6 | 2 | I | M |
| 26 | 1 | 4 | 2 | I | M | 1 | 9 | 2 | I | M |
| 1 | 9 | 2 | I | M | 1 | 8 | 2 | I | M | |
| 27 | 1 | 6 | 2 | I | M | 1 | 10 | 2 | I | M |
| 1 | 6 | 2 | I | M | 2 | 6 | 2 | I | M | |
Table shows all pairs displaying PIR during the theta state. Type signifies the type of neuron (I for interneurons and E for excitatory principal cells) identified in the study by Quilichini et al. (2010). Phase modulation (UM for unmodulated and M for modulated) shows whether the cells fire preferentially according to the phase of the theta oscillation.
What is so specific about interneuron pairs displaying PIR only during theta? Quilichini et al. (2010) showed that entorhinal cortex neurons, in particular from EC2, display a significant firing preference for a narrow phase range of the theta oscillation. Table 7 shows the percentage of theta phase-modulated cells among all single units isolated and identified as principal cells and interneurons from EC2, EC3, and EC5. We found that 10 of 11 (91%) postsynaptic cells displaying PIR only during the theta state were theta phase-modulated. Four out of five (80%) postsynaptic cells displaying PIR only during the SO state were theta phase-modulated. In contrast, only 2 of 10 (20%) of the postsynaptic cells displaying PIR during both theta and SO states showed a phase preference during theta. We conclude that, while PIR can be expressed in both theta and SO states, its specific occurrence during theta oscillations involve theta phase-modulated interneurons (i.e., specific subsets of interneurons). In keeping with the correspondence between the theta phase modulation of cell firing and its location (Table 7), 7 of 9 (77%) theta phase-unmodulated postsynaptic cells displaying PIR were located in EC5, while all 17 theta phase-modulated cells displaying PIR were located in EC 2 (59%) and in EC3 (41%) as documented in Tables 5 and 6.
Table 7.
Distribution of cells displaying theta phase-modulated firing according to locations in the EC
| Percentage of cells | Principal cells |
Interneurons |
||||
|---|---|---|---|---|---|---|
| EC2 (n = 54) | EC3 (n = 43) | EC5 (n = 40) | EC2 (n = 49) | EC3 (n = 68) | EC5 (n = 47) | |
| Theta phase modulated | 84 (n = 43) | 23 (n = 10) | 21 (n = 8) | 69 (n = 33) | 52 (n = 38) | 21 (n = 10) |
| Theta phase unmodulated | 16 (n = 11) | 77 (n = 33) | 79 (n = 32) | 31 (n = 16) | 48 (n = 30) | 79 (n = 37) |
Table shows the distribution of all single units isolated and identified as principal cells and interneurons by Quilichini et al. (2010) according to their theta phase-modulated firings and locations within the EC. It shows that neurons located mostly in EC2 were theta phase-modulated, while those from EC5 were not.
Why is PIR brain state dependent? One possibility would be that rebound would be stronger during theta. Since theta and SO operate on different timescales, they may recruit different levels of excitatory and inhibitory inputs during each cycle, thus providing conditions favoring PIR expression during theta. We found that average inhibition and rebound excitation strengths were brain state independent (Table 8). However, they were significantly different between theta phase-unmodulated and theta phase-modulated cells. Theta phase-modulated cells showed stronger average inhibition (p < 0.009 during theta state) followed by weaker average rebound excitation (p < 0.002 during theta state) compared with theta phase-unmodulated cells.
Table 8.
Average inhibition and rebound strengths during both brain states
| Strength (%) | Theta phase-modulated neurons |
Theta phase-unmodulated neurons |
||
|---|---|---|---|---|
| Inhibition | Rebound | Inhibition | Rebound | |
| During theta | 42 ± 2 (n = 10) | 16 ± 2 (n = 10) | 29 ± 5 (n = 7)* | 27 ± 2 (n = 7)* |
| During SO | 40 ± 5 (n = 6) | 18 ± 2 (n = 6) | 32 ± 5 (n = 7) | 27 ± 3 (n = 7) |
Values represent mean ± SEM. The table shows the average inhibition and rebound strengths calculated during each brain state. While the pairwise connection strengths between the theta phase-unmodulated cells are significantly different from those of the modulated ones, they do not differ significantly during two different states as can be seen from the table. While the calculation of strengths took them into account, the durations of the inhibition and rebound firing between pairs also did not seem to depend on the state. Typically, duration for statistically significant inhibition was up to 1.6 ms, while the typical rebound duration was ∼2.4 ms.
* indicate statistically significant stronger (p < 0.009) average inhibition and weaker (p < 0.002) average rebound excitation strengths for theta phase-modulated neurons in comparison with theta phase-unmodulated neurons.
Alternatively, the brain state dependent occurrence of PIR may just reflect the brain state dependent occurrence of inhibition, i.e. brain state-dependence of PIR would only be found in cells for which inhibition is also brain state dependent. We found that 8 out of 11 (73%) pairs which displayed PIR during only the theta state did not show significant inhibition during SO, in keeping with the brain state dependence of inhibition reported above. However, postsynaptic interneurons from the remaining 3 pairs displayed inhibition but no rebound excitation from the same presynaptic interneurons during SO. This suggests that, in addition to the brain state dependent occurrence of inhibition, other mechanisms are also involved in the brain state dependent occurrence of the rebound excitation, which prompted us to use a theoretical approach.
Theoretical analysis of PIR
In the model equations, we assumed that the mechanism of PIR is intrinsic to the pair of cells and their connection and investigated the effect of periodic synaptic input on rebound firing. In quantitative terms, and in the context of a purely deterministic model, this translates to the question: how does the number of rebound spikes fired by the postsynaptic neuron for every spike fired by the presynaptic neuron depend on the frequency of the drive?
For a 4 Hz (theta-like) external drive, each neuron showed firing phase preference, and neuron 1 fired two spikes per theta cycle while neuron 2 fired a rebound spike a few milliseconds after each spike of neuron 1 (Fig. 3A,B). For a 0.5 Hz (SO-like) external drive, both neurons fired many more spikes during a preferred phase of the cycle than during theta, but the second neuron fired less spikes than neuron 1 (Fig. 3C,D). During the initial stage of the cycle, neuron 1 fired more spikes than during the latter stage. Such increased instantaneous firing rate suppressed some of the rebound spikes in neuron 2, as neuron 2 could not reach firing threshold between two consecutive spikes of neuron 1 (i.e., it was inhibited again before firing a rebound spike). Indeed, the key parameter, which controls rebound firing is ksyn, the reciprocal of the slope of the sigmoid function in the instantaneous coupling term. The decreased rebound firing during SO is thus due to the fact that instantaneous firing rates during each cycle are more strongly modulated by the slow drive compared with theta. In the case of the fully deterministic model considered here, we assumed nonidentical neurons with nonidentical coupling to the drives to elucidate the effect of this mechanism in the time series of both neurons. To compare the results of the model with the data, we consider a stochastic version of this model by adding Gaussian noise and identical neurons with identical couplings to the drive described later in this section.
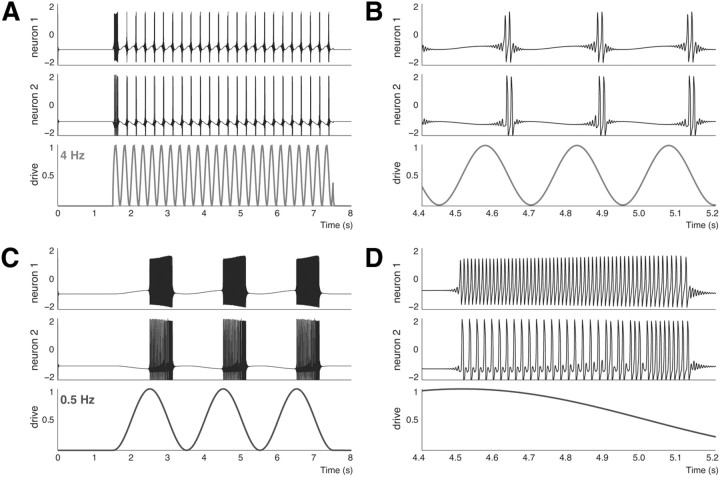
Figure 3.
A, Responses of two neurons to an external sinusoidal drive of 4 Hz. B, Close-up on three theta cycles. Neuron 1 fires only two spikes per cycle, each of which is followed by a rebound spike of neuron 2. Thus, the number of rebound spikes is equal to the number of spikes fired by the presynaptic neuron. C, Responses of two neurons to an external sinusoidal drive of 0.5 Hz. D, Close-up on one cycle of firing activity. Note that the number of rebound spikes is less than the number of spikes fired by the presynaptic neuron. Upon closer inspection of the spikes fired by neuron 1, one can observe that the firing rate of neuron 1 is modulated by the drive. The increased firing by neuron 1 in the first part of the drive reduces the number of rebound spikes that neuron 2 can fire. Here, all the parameters are identical with the case of 4 Hz drive (i.e., I1 = 0.2, I2 = 0.0, g1 = −0.8, g2 = 0.5, g = 0.7, vth = 1.5, ksyn = 0.2).
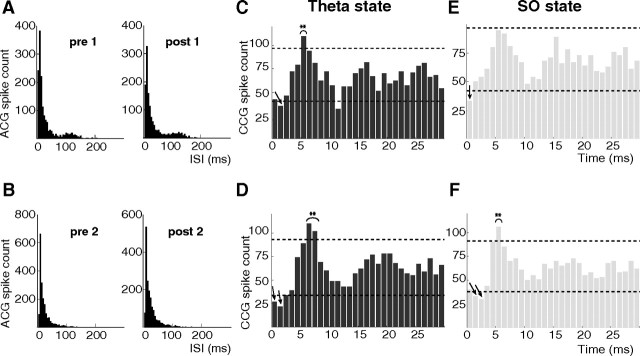
The model predicts that cells should fire short and long high-frequency bursts when driven at 4 and 0.5 Hz, respectively. These predictions were verified in the data. Pairs with PIR fired few spikes during theta, and theta phase-modulated neurons had almost exactly the same phase preference for firing, while, during SO, pairs with PIR fired high-frequency bursts of spikes (Fig. 4A–D). This validates our assumption that the relationship between firing of these neurons and the oscillatory brain states can be modeled as a causal one with each neuron driven by a periodic synaptic drive. The choice of individual neuron model parameters, which yield high intrinsic firing rate (70–100 Hz), is validated by the probability distributions of interspike intervals (ISIs) characterizing theta phase-modulated and -unmodulated neurons in vivo (Fig. 4E–H). Such high firing rates could be due to synchronization with gamma oscillations (40–80 Hz). Indeed, during the theta state, gamma oscillations are nested within theta cycles (Quilichini et al., 2010). However, they were much less prominent during SO, suggesting that the high-frequency firing rate measured during SO is intrinsic to the neurons in which it occurs. The ISI histograms of theta phase-modulated cells displayed at least one additional peak in the theta range since cells tend to fire at every cycle or so (Figs. 4E, 6A).
Figure 4.
Validation of model predictions. Firing patterns (A–D) of theta phase-modulated and theta phase-unmodulated cells in the data that, for sufficiently strong coupling between the drive and the neurons (here phase modulation), cells fire short and long high-frequency bursts when driven at 4 Hz (A) and 0.5 Hz (C), respectively. For weak coupling between the drive and the neurons, the cells do not show any phase modulation during the theta state (B). The most probable ISI (∼10 ms), in the ISI histograms of a theta phase-modulated interneuron (E, G) and a theta phase-unmodulated interneuron (F, H), during both states suggests a high intrinsic firing rate for both types of neurons. The ISI distribution of the theta phase-modulated interneuron during the theta state (E) is bimodal due to phase modulation.
Figure 6.
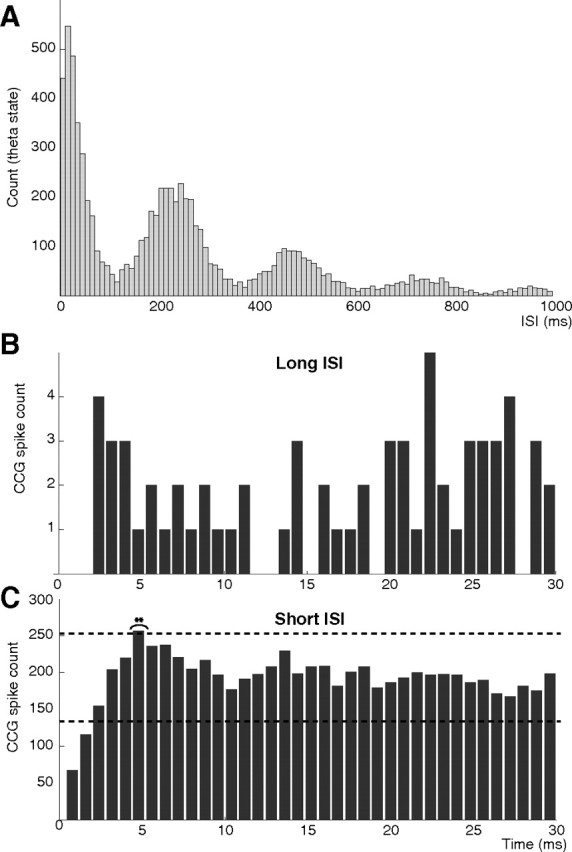
Rebound excitation in theta phase-modulated interneurons is not caused by the synchronization between the neuronal firing rate and the theta rhythm. A, Probability distribution of the interspike intervals of a typical theta phase-modulated interneuron during theta state. Note the peaks at the harmonic of theta frequency, which suggest possible intervals of synchronization between the neuronal firing rate and the theta frequency. B, CCGs obtained using spikes with ISI >100 ms from the spike trains of a pair of PIR displaying theta phase-modulated interneurons—very low number of counts in the CCG show that the correlated firing between isolated spikes of two cells was negligible. C, CCGs obtained using spikes with ISI <100 ms from the spike trains of the same pair of interneurons.
Model simulations with noise: comparison with experimental data
To compare the theoretical and experimental results, we added a noise term to each equation and calculated the CCGs for both external drives. The choice of the parameters was based upon two observations: (1) the rebound excitation strength within a CCG and (2) the different ISI distributions for theta phase-modulated and theta phase-unmodulated neurons during the theta state. We considered a very small value for ksyn to produce fast inhibition and rebound. We then varied the strength of the instantaneous coupling g for given amplitude of noise to obtain the appropriate rebound strengths in the CCG. Next, we assumed identical values for the coupling constants between each neuron and each external drive. The strength of the theta phase modulation of the neuronal firings as observed in the ISI histograms was determined by the coupling between the neuron and the drive. Thus, for sufficiently small coupling between the neuron and the drive, the ISI histogram for each neuron during each state displays a single peak (Fig. 5B) and the corresponding CCGs for both drives are similar (Fig. 5D,F). This mimics the behavior of a pair of theta phase-unmodulated neurons, producing PIR during both theta and SO state. For sufficiently high coupling in the theta regime, ISI histograms display an additional peak at around the theta frequency (Fig. 5A) and the corresponding CCG displays statistically significant PIR when compared with the 0.5 Hz case (Fig. 5C,E). This result corresponds to the brain state dependency of the PIR observed for pairs of theta phase-modulated cells. In these simulations, we assumed equal values of coupling strengths for the drive of both frequencies; this assumption may not be valid in vivo.
Figure 5.
ISI histograms (A) and CCGs obtained using model simulations with Gaussian noise added to each equation for sufficiently high coupling between each neuron with 4 Hz drive (C) and 0.5 Hz drive (E). The secondary peaks in the ISI histograms for the 4 Hz case reflect the theta phase modulation of firing of the neurons. PIR is statistically significant in the 4 Hz case and not in the 0.5 Hz case. ISI histograms (B) and CCGs obtained using model simulations with Gaussian noise added to each equation for sufficiently low coupling between each neuron with 4 Hz drive (D) and 0.5 Hz drive (F). The absence of secondary peaks in the ISI histograms for the 4 Hz case reflects the lack of theta phase modulation of firing of the neurons. PIR is statistically significant in both cases. Here, I1 = 0.0, I2 = 0.0, vth = −1.5, ksyn = 0.01. Mean of Gaussian noise is equal to 0, and the variance is 0.1. g1 = g2 = −1.4; g = −0.08 (A, C, E) and g1 = g2 = −1; g = −0.12 (B, D, F).
Firing rate modulation as a mechanism of brain state dependence of PIR
The theoretical analysis proposes that the expression of PIR is suppressed during SO due to the modulation of the neuronal firing rates. The short timescale of the connection and the firing rates and firing patterns of these neurons during each state in vivo validate the model. Intuitively, however, the prevalence of PIR during the theta state, primarily displayed by theta phase-modulated interneurons mostly from EC2, raises the possibility of an alternative mechanism for PIR: the synchronization between the neuronal firing rate and the theta frequency. Additional peak(s) at harmonics of theta period in the ISI histograms of theta phase-modulated neurons (Fig. 6A shows a prominent example) can include intervals of synchronization and one can hypothesize that it is only in these intervals that one observes PIR in these cells. To test this hypothesis, we separated the spike train of each presynaptic and postsynaptic neuron displaying PIR during the theta state into two groups, those with ISIs greater and smaller than 100 ms, respectively, and reconstructed separate CCGs for each group. As Figure 6, B and C, shows, PIR was only observed from the short ISI spike trains. This result rules the synchronization mechanism out, further supporting the modulation mechanism predicted by the model.
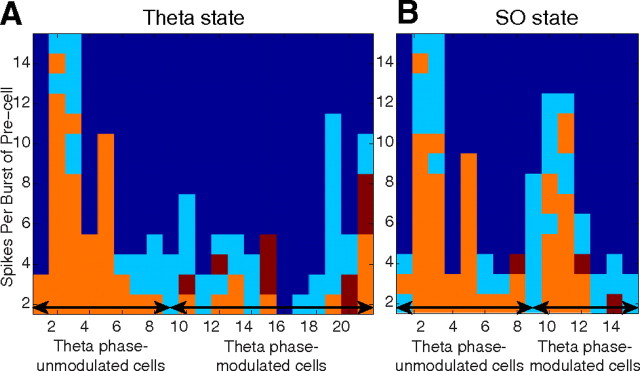
The modulation mechanism proposed by the model can be tested in the data in another way. We divided the spike train of every presynaptic cell into subsets of spikes belonging to bursts with a fixed number of spikes per burst. We used a mean ISI in [0 50] ms, for every presynaptic cell, to define bursts. We then constructed the CCG between each such sub-spike train of the presynaptic cell and the spike train of the postsynaptic cell to identify statistically significant PIR. As Figure 7 shows, the unmodulated cell pairs, mostly from EC5 (first seven, common to both states), displayed statistically significant PIR for several bursts indicating a robust connection between cells. This specific observation provides further evidence that the inhibition–excitation sequence observed in the CCGs of these pairs represents PIR. Interestingly, for the modulated cell pairs, especially those from EC2 (last four in Fig. 7A), PIR was statistically significant for a small number of spikes per burst of the presynaptic cell and only inhibition was significant for higher number of spikes per burst. The ISI histograms formed from spikes belonging to bursts of a given order showed that lower values of ISIs were more probable during long bursts when compared with the short bursts. These observations validate the general mechanism that model proposes: if the presynaptic neuron fires longer bursts with a modulated instantaneous firing rate, the probability of rebound firing of the postsynaptic neuron is reduced.
Figure 7.
Statistical significance (SS) of PIR for all pairs as a function of the number of spikes per burst of the presynaptic cell during theta state (A) and during SO state (B). Color code: Blue, Not enough spikes for obtaining significance/no PIR connection; light blue, PIR is not SS; orange, PIR is SS; red, inhibition is SS but not rebound. There are 21 pairs during theta and 15 during SO that display PIR. For theta phase-unmodulated cells, mostly from EC5 (7 of first 9, common to both states), PIR is SS for several number of spikes per burst of the presynaptic cell, suggesting a robust connection. For theta phase-modulated cells, especially from EC2 during the theta state (18–21 in A), rebound is SS for shorter bursts, while only inhibition is SS for longer bursts.
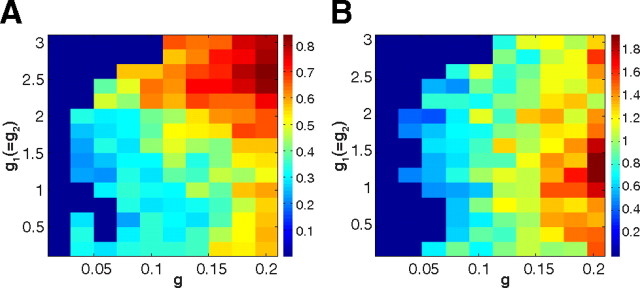
The nonsignificance of the rebound (but not of inhibition) for longer bursts of the presynaptic cell was observed primarily for theta phase-modulated cells. This may be due to the phase preference imposed by the rhythm on the postsynaptic cell. Figure 7B shows examples of theta phase-modulated cells, which show statistically significant PIR for several orders of spikes per burst from the presynaptic cell during SO but not during theta. This suggests that, during the theta state, if some spikes from longer bursts of the presynaptic cell arrive outside the window of phase preference of the postsynaptic cell, the latter cannot fire enough rebound spikes. We investigated this hypothesis in the model by calculating the inhibition and rebound strength, as inferred from the CCGs obtained from simulated spike trains, for a range of values of g1 (=g2) and g. We found that the inhibition strength was highest for high values of g1 (=g2) and g (Fig. 8A), but the rebound strength was highest for smaller values of g1 (=g2) (Fig. 8B) and decreased for increasing modulation. This suggests that a stronger modulation by the underlying rhythm decreases the probability of the postsynaptic cell to fire rebound spikes. We attempted to verify this prediction of the model in the dataset. The coupling parameter g cannot be measured in vivo, but theta phase modulation/unmodulation can be proposed to represent two g values (high and low, respectively). In keeping with the model predictions, the strength of inhibition was higher in theta-modulated cells than in unmodulated ones, while the strength of PIR was higher in unmodulated cells compared with modulated ones (Table 8). We conclude that the strength of functional inhibition and PIR depends upon the strength of the coupling to the rhythm.
Figure 8.
The strength of functional inhibition and PIR depends upon the coupling to the rhythm. Figure shows the strength of functional inhibition (A) and rebound excitation (B), as inferred from the simulated CCGs in the case of a 4 Hz drive, as a function of two coupling strength parameters: (1) g1 (=g2), coupling between the drive and each neuron, and (2) g, the inhibitory coupling from neuron 1 to neuron 2 for a fixed noise level. As g1 (=g2) increases beyond 2, the firing of both neurons is increasingly modulated. Interestingly, we see that, for high values of g and g1 (=g2), the inhibition strength increases but the corresponding rebound strength does not necessarily increase. In fact, for a sufficiently large value of g, as the coupling with the drive increases, the rebound strength decreases, suggesting that, in this case, sufficiently high modulation of neuronal firings by the drive can suppress the number of rebound spikes fired by the postsynaptic cell. Here, I1 = 0.29, I2 = 0.0, vth = −1.5, and ksyn = 0.01. Mean of Gaussian noise is equal to 0, and the variance is 0.1.
Discussion
Our analysis indicates that interneuron firing, in the entorhinal cortex, can trigger rebound firing of their targets, which are mostly other interneurons, in a brain state dependent manner. The entire inhibition–excitation sequence representing PIR typically occurred within 5 ms after the firing of the presynaptic interneuron. The inhibition lasted for 1–2 ms, which is the characteristic timescale of monosynaptic interactions in vivo (Fujisawa et al., 2008), followed by a rebound that lasted for 2–3 ms. Interestingly, studies performed in vitro report that hyperpolarization-induced rebound excitation occurs tens to hundreds of milliseconds after the beginning of the hyperpolarization (Harris-Warrick et al., 1995a,b; Bertrand and Cazalets, 1998). In contrast, our in vivo data suggest that PIR is a very fast event, commensurate with the timescales of other monosynaptic interactions observed in vivo.
The evidence for the PIR from pairwise cross-correlograms is indirect, however, reliable (Moore et al., 1970). Although we cannot rule out that third-party excitatory neurons would systematically produce the increased firing probability that follows the period of inhibition, the analysis of microcircuits suggests that this scheme is unlikely. Another competing hypothesis is that PIR is due to independent correlation of firing of each neuron with respect to the rhythm and not because of an actual connection. We found that these interneurons fire quite sparsely during the theta state and not during every cycle. Hence, this hypothesis is not likely since PIR corresponds to a very tight time correlation between the firing of the two cells. Furthermore, we jittered the spike timings of both neurons while maintaining their theta phase preferences and found that the average CCG of such jitter surrogates did not show the pattern observed in the actual CCG. These arguments make PIR as the most likely explanation for the inhibition excitation sequence we observed in the spike trains of these interneurons.
One important finding of our study is that the postsynaptic cell in pairs displaying PIR was generally another interneuron. The mechanisms responsible for PIR most likely involve ionic channels, such as low-threshold Ca2+ channels and Ih (Llinás, 1988; Dickson et al., 2000; Huguenard and McCormick, 2007). Interestingly, stellate cells found in the superficial layers of entorhinal cortex express a strong Ih current, which can contribute to rebound firing and, in turn, to the theta rhythmicity at the single-cell as well as the network level (Dickson et al., 2000). However, stellate cells are excitatory cells, and to our knowledge, there is no evidence of expression of Ih current in the interneurons of entorhinal cortex. Finally, Ih has slow kinetics, which makes it a less likely candidate given the time course of PIR reported here. The biophysical mechanisms underlying the expression of PIR in vivo, in particular in the entorhinal cortex interneurons, remain to be determined.
The other important finding of our study was the brain state dependence of both inhibition and PIR. The fact that inhibition was not statistically significant in one brain state in a given pair does not necessary mean GABA release failure. Multiple mechanisms could account for the brain state dependence of inhibition, including short-term plasticity, differences in background noise, synaptic strength, membrane potentials, chloride reversal potential, and/or neuromodulator levels during theta and SO. It indicates that, in a permanent regime of brain activity, synaptic connections are differentially recruited (Ostojic et al., 2009). Our results extend the concept that connections are dynamically regulated during transient regimes (i.e., different brain states and behaviors) (Fujisawa et al., 2008).
Since rebound excitation follows inhibition, one would expect to find similar brain state dependent properties for inhibition and rebound. However, this was not the case. Inhibition was more prevalent during SO, while PIR was more evident during the theta state. The postsynaptic cell type (interneuron vs principal cell) dependence of inhibitory connections was brain state dependent; it was not the case for PIR. Cells showing PIR during both states were typically located in EC5 and their firing was not modulated during the theta state, suggesting that PIR is an intrinsic property of these cells or of the connections. Cells displaying PIR only during theta displayed a preference for the phase of theta and were typically located in EC2 and EC3 layers. Thus, the brain state dependent occurrence of PIR was related to the firing pattern of cells during theta, which in turn, was layer specific in the entorhinal cortex. PIR was mostly found between neurons located in the same layer. This does not rule out the existence of long distance and/or translayer connections with PIR. They could not be evidenced with the recording electrodes we used.
Interestingly, we found that the average strength of inhibition and rebound excitation was also related to the firing pattern of cells during theta. Cells showing strong modulation of their firing by the network theta rhythm showed relatively higher inhibition and lower rebound strengths compared with those that were weakly coupled. This suggests that the transmission of information (i.e., inhibition followed or not by rebound firing) from interneurons to their targets also depends upon their functional coupling to the rhythm.
Brain state dependence of PIR could not be fully explained by the brain state dependence of inhibition. We found interneuron–interneuron pairs that displayed PIR during theta state but displayed only inhibition during SO. Typical firing rates of all cells involved in PIR connections were much higher than the theta frequency, and we showed that synchronization between the theta frequency and the neuronal firing rate was not responsible for the prevalence of PIR during the theta state. Instead, as suggested by the model, a possible mechanism responsible for this dynamic regulation of PIR is the modulation of intrinsic high firing rates of neurons by slower rhythms. The model we used for each neuron is phenomenological, that is, it captures, qualitatively, the features of spike generation of a more detailed biophysical model such as the one by Hodgkin and Huxley (1952). The limitation of this model is that the values of its parameters have very little biophysical significance. However, the advantage is its mathematical tractability and ability to elucidate the mechanisms underlying biological phenomena. Also, quantities such as firing rates and spike timings obtained using this model can be compared directly with their experimental counterparts, especially in a study like the present one in which they are the essential measured quantities. Most importantly, such models have a predictive value for the biophysical mechanisms, which can be tested. Our model assumed PIR to be an intrinsic property of the interaction between two neurons, and we approximated the oscillatory local field potential, which typically represents the mean extracellular potential of a population of neurons by a sinusoidal drive. The purpose of these assumptions was to keep the model tractable in terms of number of free parameters. We showed that the slower of the two drives could modulate the firing rates of both neurons more, which, in turn, can suppress some of the rebound firing in the postsynaptic cell. Adding noise to the equations and choosing the appropriate ranges for coupling between the drive and the neuron, we could reproduce the CCG results representing the brain state dependence of PIR to the same degree as observed in vivo. Based on our results, we propose that, during SO, cells firing high-frequency bursts do not have enough time to recover from inhibition and cannot produce rebound. In contrast, during theta, fewer spikes are produced enabling PIR more consistently.
In conclusion, we report that postinhibitory rebound is expressed in vivo, but its expression involves distinct neuronal subnetworks according to the underlying frequency of the ongoing rhythm–brain state. Because PIR shows such time precision (limited jitter), it may actively participate in the appropriate firing timing of specific subsets of neurons and its modulation by the oscillatory brain states could impact network synchronization and the genesis of rhythms.
Footnotes
This work was supported by Institut National de la Santé et de la Recherche Médicale, Agence Nationale pour la Recherche MINOS, and in part by the European Union Seventh Framework Program (FP7/2007–2013) under Grant 269921 (BrainScaleS). P.P.Q. is supported by a Fondation pour la Recherche Médicale fellowship. We used the data collected in G. Buzsáki's laboratory and published by Quilichini et al. (2010) for our investigations. We acknowledge G. Buzsáki and A. Sirota for consenting to the use of this database in the present work.
References
- Aizenman CD, Linden DJ. Regulation of the rebound depolarization and spontaneous firing patterns of deep nuclear neurons in slices of rat cerebellum. J Neurophysiol. 1999;82:1697–1709. doi: 10.1152/jn.1999.82.4.1697. [DOI] [PubMed] [Google Scholar]
- Alviña K, Walter JT, Kohn A, Ellis-Davies G, Khodakhah K. Questioning the role of rebound firing in the cerebellum. Nat Neurosci. 2008;11:1256–1258. doi: 10.1038/nn.2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barthó P, Hirase H, Monconduit L, Zugaro M, Harris KD, Buzsáki G. Characterization of neocortical principal cells and interneurons by network interactions and extracellular features. J Neurophysiol. 2004;92:600–608. doi: 10.1152/jn.01170.2003. [DOI] [PubMed] [Google Scholar]
- Bertrand S, Cazalets JR. Postinhibitory rebound during locomotor-like activity in neonatal rat motoneurons in vitro. J Neurophysiol. 1998;79:342–351. doi: 10.1152/jn.1998.79.1.342. [DOI] [PubMed] [Google Scholar]
- Brown SP, Hestrin S. Cell-type identity: a key to unlocking the function of neocortical circuits. Curr Opin Neurobiol. 2009;19:415–421. doi: 10.1016/j.conb.2009.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- Chik DT, Coombes S, Wang ZD. Clustering through post inhibitory rebound in synaptically coupled neurons. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;70 doi: 10.1103/PhysRevE.70.011908. 011908. [DOI] [PubMed] [Google Scholar]
- Chrobak JJ, Buzsáki G. Gamma oscillations in the entorhinal cortex of the freely behaving rat. J Neurosci. 1998;18:388–398. doi: 10.1523/JNEUROSCI.18-01-00388.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coombes S, Doole SH. Neuronal populations with reciprocal inhibition and rebound currents: effects of synaptic and threshold noise. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1996;54:4054–4065. doi: 10.1103/physreve.54.4054. [DOI] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurkó A, Mamiya A, Buzsáki G. Oscillatory coupling of hippocampal pyramidal cells and interneurons in the behaving rat. J Neurosci. 1999;19:274–287. doi: 10.1523/JNEUROSCI.19-01-00274.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson CT, Magistretti J, Shalinsky MH, Fransén E, Hasselmo ME, Alonso A. Properties and role of Ih in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J Neurophysiol. 2000;83:2562–2579. doi: 10.1152/jn.2000.83.5.2562. [DOI] [PubMed] [Google Scholar]
- Fisher NI. Statistical analysis of circular data. Cambridge, UK: Cambridge UP; 1993. [Google Scholar]
- Fitzhugh R , Impulses and physiological states in theoretical models of nerve membrane. Biophys J. 1961;1:445–466. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujisawa S, Amarasingham A, Harrison MT, Buzsáki G. Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nat Neurosci. 2008;11:823–833. doi: 10.1038/nn.2134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grenier F, Timofeev I, Steriade M. Leading role of thalamic over cortical neurons during postinhibitory rebound excitation. Proc Natl Acad Sci U S A. 1998;95:13929–13934. doi: 10.1073/pnas.95.23.13929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, Henze DA, Csicsvari J, Hirase H, Buzsáki G. Accuracy of tetrode spike separation as determined by simultaneous intracellular and extracellular measurements. J Neurophysiol. 2000;84:401–414. doi: 10.1152/jn.2000.84.1.401. [DOI] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Barazangi N, Guckenheimer J, Gueron S. Dopamine modulation of transient potassium current evokes phase shifts in a central pattern generator network. J Neurosci. 1995a;15:342–358. doi: 10.1523/JNEUROSCI.15-01-00342.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Levini RM, Gueron S, Guckenheimer J. Dopamine modulation of two subthreshold currents produces phase shifts in activity of an identified motoneuron. J Neurophysiol. 1995b;74:1404–1420. doi: 10.1152/jn.1995.74.4.1404. [DOI] [PubMed] [Google Scholar]
- Hazan L, Zugaro M, Buzsáki G. Klusters, NeuroScope, NDManager: a free software suite for neurophysiological data processing and visualization. J Neurosci Methods. 2006;155:207–216. doi: 10.1016/j.jneumeth.2006.01.017. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A qualitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huguenard JR, McCormick DA. Thalamic synchrony and dynamic regulation of global forebrain oscillations. Trends Neurosci. 2007;30:350–356. doi: 10.1016/j.tins.2007.05.007. [DOI] [PubMed] [Google Scholar]
- Klausberger T, Somogyi P. Neuronal diversity and temporal dynamics: the unity of hippocampal circuit operations. Science. 2008;321:53–57. doi: 10.1126/science.1149381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinás RR. The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science. 1988;242:1654–1664. doi: 10.1126/science.3059497. [DOI] [PubMed] [Google Scholar]
- Maccaferri G, Roberts JD, Szucs P, Cottingham CA, Somogyi P. Cell surface domain specific postsynaptic currents evoked by identified GABAergic neurones in rat hippocampus in vitro. J Physiol. 2000;524:91–116. doi: 10.1111/j.1469-7793.2000.t01-3-00091.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miles R, Tóth K, Gulyás AI, Hájos N, Freund TF. Differences between somatic and dendritic inhibition in the hippocampus. Neuron. 1996;16:815–823. doi: 10.1016/s0896-6273(00)80101-4. [DOI] [PubMed] [Google Scholar]
- Mizuseki K, Sirota A, Pastalkova E, Buzsáki G. Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron. 2009;64:267–280. doi: 10.1016/j.neuron.2009.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore GP, Segundo JP, Perkel DH, Levitan H. Statistical signs of synaptic interaction of neurons. Biophys J. 1970;10:876–900. doi: 10.1016/S0006-3495(70)86341-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostojic S, Brunel N, Hakim V. How connectivity, background activity, and synaptic properties shape the cross-correlation between spike trains. J Neurosci. 2009;29:10234–10253. doi: 10.1523/JNEUROSCI.1275-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouille F, Scanziani M. Routing of spike series by dynamic circuits in the hippocampus. Nature. 2004;429:717–723. doi: 10.1038/nature02615. [DOI] [PubMed] [Google Scholar]
- Quilichini P, Sirota A, Buzsáki G. Intrinsic circuit organization and theta-gamma oscillation dynamics in the entorhinal cortex of the rat. J Neurosci. 2010;30:11128–11142. doi: 10.1523/JNEUROSCI.1327-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotstein HG, Pervouchine DD, Acker CD, Gillies MJ, White JA, Buhl EH, Whittington MA, Kopell N. Slow and fast Inhibition and an h-current interact to create a theta rhythm in a model of CA1 interneuron network. J Neurophysiol. 2005;94:1509–1518. doi: 10.1152/jn.00957.2004. [DOI] [PubMed] [Google Scholar]
- Sirota A, Montgomery S, Fujisawa S, Isomura Y, Zugaro M, Buzsáki G. Entrainment of neocortical neurons and gamma oscillations by the hippocampal theta rhythm. Neuron. 2008;60:683–697. doi: 10.1016/j.neuron.2008.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Rinzel J. Alternating and synchronous rhythms in reciprocally inhibitory model neurons. Neural Comput. 1992;4:84–97. [Google Scholar]