Abstract
Perceptual decision making is believed to be driven by the accumulation of sensory evidence following stimulus encoding. More controversially, some studies report that neural activity preceding the stimulus also affects the decision process. We used a multivariate pattern classification approach for the analysis of the human electroencephalogram (EEG) to decode choice outcomes in a perceptual decision task from spatially and temporally distributed patterns of brain signals. When stimuli provided discriminative information, choice outcomes were predicted by neural activity following stimulus encoding; when stimuli provided no discriminative information, choice outcomes were predicted by neural activity preceding the stimulus. Moreover, in the absence of discriminative information, the recent choice history primed the choices on subsequent trials. A diffusion model fitted to the choice probabilities and response time distributions showed that the starting point of the evidence accumulation process was shifted toward the previous choice, consistent with the hypothesis that choice priming biases the accumulation process toward a decision boundary. This bias is reflected in prestimulus brain activity, which, in turn, becomes predictive of future decisions. Our results provide a model of how non-stimulus-driven decision making in humans could be accomplished on a neural level.
Introduction
Recent studies have shown that choice outcomes can be predicted from brain activity before an overt response being made (Das et al., 2010; Bode et al., 2012). One controversial finding has been the existence of choice-related brain activity before the presentation of decision-relevant stimuli (Hesselmann et al., 2008a,b, 2010). To date, there has been no satisfactory explanation for the functional role of this early activity within a formal model of decision making.
Although the role of prestimulus neural activity is unclear, there is evidence that it can bias perceptual decision making. Several studies have linked increased prestimulus activity to improved perceptual decision performance (Supèr et al., 2003; Boly et al., 2007; Schölvinck et al., 2012). One possibility is that coincidentally increased activity levels increase attention to the following stimulus, which then improves accuracy (Hesselmann et al., 2010). Alternatively, evidence accumulation models of perceptual decision making, like the diffusion model (Ratcliff, 1978; Smith and Ratcliff, 2004), might attribute trial-by-trial differences in prestimulus activity to differences in the starting point for the accumulation of stimulus information toward a specific decision boundary. For low stimulus quality, when the rate of evidence accumulation is low, biasing the starting point of the process toward one particular boundary increases the likelihood of reaching that boundary and triggering the associated response. Any prestimulus activity related to starting point biases should therefore be highly predictive of the decision outcome.
Furthermore, it is unclear whether prestimulus choice-related activity is due to random noise (Deco and Romo, 2008; Rolls and Deco, 2011) or whether it has a systematic source. One possibility is that the sequence of preceding choices biases decision outcomes, as suggested by the sequential effects response time (RT) literature (Luce, 1986). For example, basic choice priming might underlie prestimulus activity in a series of perceptual decisions about ambiguous sensory stimuli (Hesselmann et al., 2008a) or stimuli at perceptual threshold (Hesselmann et al., 2008b; Bode et al., 2012).
We used a perceptual decision paradigm in which participants were presented with static, noise-masked images of pianos and chairs (Bode et al., 2012) under four discriminability conditions. On additional, randomly interspersed trials, a briefly presented and strongly masked noise image, which contained no discriminative information whatsoever, was shown. Participants were unaware of the inclusion of these pure noise trials and continued to make object category decisions. We recorded 63-channel electroencephalography (EEG) and performed multivariate pattern classification analyses on the data (Haynes and Rees, 2006; Philiastides and Sajda, 2006; Pereira et al., 2009; Das et al., 2010; Blankertz et al., 2011). This allowed us to decode the decision outcomes directly from brain activity in successive time steps throughout the trial. We hypothesized that when stimuli contain discriminative information (pianos or chairs) poststimulus time windows (∼300 ms; Philiastides and Sajda, 2006) should be predictive for choices. When stimuli do not contain discriminative information (pure noise) we further hypothesized that prestimulus activity would be predictive of choices as this activity may reflect the starting point for the accumulation of evidence.
Materials and Methods
Participants.
Twenty-four right-handed, healthy participants with normal or corrected-to-normal visual acuity gave written informed consent and participated in the study. The experiment was approved by the ethics committee of the German Psychological Society (DGPs) and was conducted according to the Declaration of Helsinki. Two participants who had exceptionally low detection rates and three participants who were strongly biased toward one category in the pure noise condition were excluded. One additional participant's data was unusable due to technical problems with data recording. The remaining 18 participants' (10 female and 8 male, mean age 25.3 years, range 20–32) data were used in the analyses.
Stimuli.
The stimuli were 24 pictures of pianos and 24 pictures of chairs. These were created from freely available pictures from the internet, showing objects in different natural backgrounds. All pictures were transformed into gray-scale (400 × 400 pixels) and presented on a gray background (Bode et al., 2012). Two scrambled masks (premask and postmask) were constructed by dividing every target image into 10 × 10 squares (40 × 40 pixels). Each mask consisted of 100 randomly reorganized squares (400 × 400 pixels), which did not contain any identifiable parts of objects. A neutral stimulus was created for the pure noise condition. For this, one of the masks was Fourier transformed and its phase map was scrambled by adding a random value of +/−1.75*Π to each phase angle. It was then transformed back to an image and contrast-normalized (Bode et al., 2012). For each noise trial, the same image was used to avoid biases due to random variations in similarity to one or the other object category.
Experimental paradigm.
On each trial, participants were presented with a masked image (either an object or pure noise) and made a choice about its category, i.e., between piano and chair. Stimuli were presented at four discriminability levels by varying the ratio of target image duration (66.67, 50.00, 33.33, 16.67 ms) and postmask duration (500 ms minus target image duration). The experiment consisted of five independent runs (or experimental blocks) in which all 24 object images from each category were shown in each discriminability condition. A 100 ms premask preceded the image and served both as an attentional cue for the target as well as a neutral baseline period for the analyses (Fig. 1A). A fifth condition, of 48 trials, was also included, which resembled the shortest object presentation, but in which the pure noise stimulus was shown. Participants were not aware of the nature of these trials and made choices between pianos and chairs. The trial sequence was randomized individually for each run and each participant. Five hundred milliseconds after stimulus presentation, the postmask was replaced by a response mapping screen (1500 ms), which displayed the letters “P” (piano) and “C” (chair) on the left and right side of the fixation cross. The response mapping was randomized from trial to trial, thereby decorrelating motor responses from category choices and ensuring that motor preparation could not be initiated beforehand. Participants responded with the left or right index finger, ensuring bilateral and balanced motor activation. The next trial started after a randomized delay of 700, 950, or 1200 ms. Stimuli were shown on a 17″ VGA monitor at a 60 Hz refresh rate. Stimulus presentation and response recording were controlled by the Cogent2000 1.29 toolbox for MATLAB 7.11 (The MathWorks).
Figure 1.
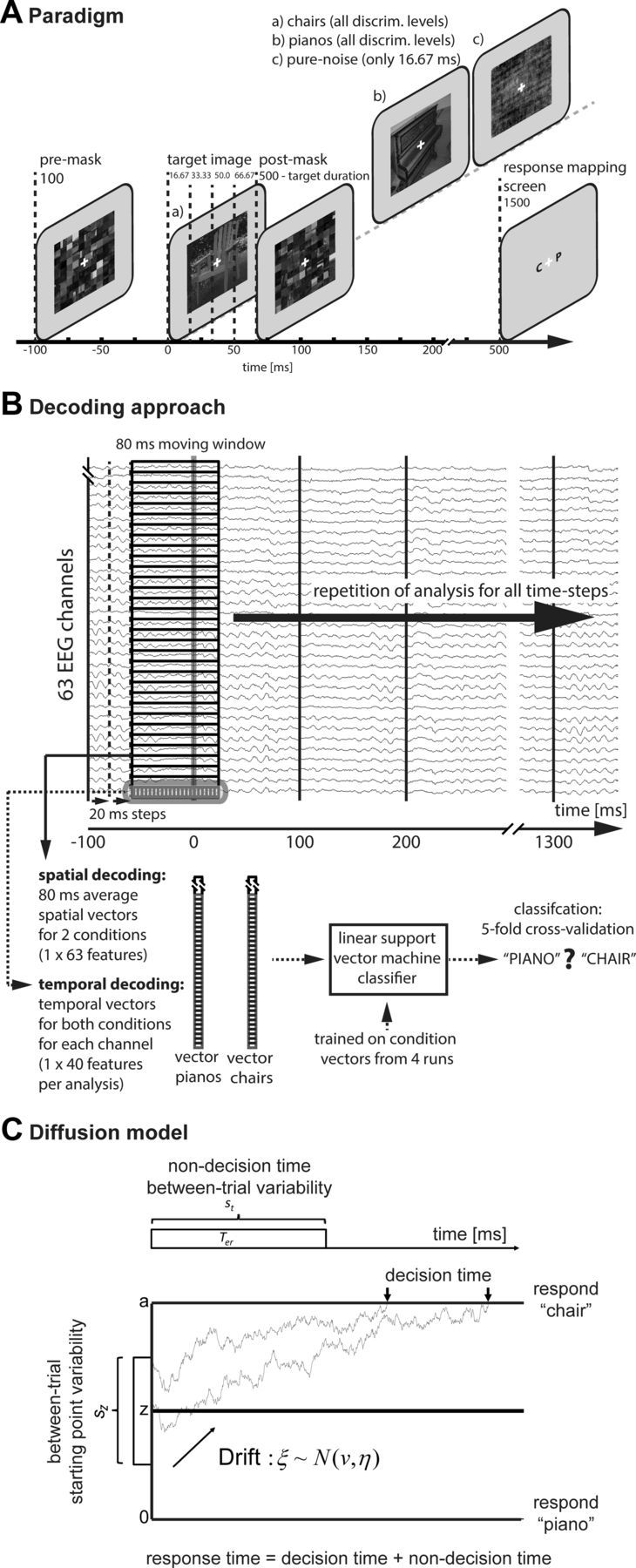
Experimental paradigm and methodology. A, Paradigm. A scrambled premask was presented at −100 ms. At time point 0 ms the target image was presented, followed by a scrambled postmask. In each of the five runs, 24 piano images and 24 chair images as well as 48 pure noise images (16 ms only) were shown in each discriminability condition. Participants were asked to choose the category of the presented image (piano or chair). Response mapping screens were pseudo-randomized. B, Multivariate pattern classification. For spatial decoding, data from all 63 head electrodes for each time step within a given trial were averaged within a time window of 80 ms, resulting in two 63-dimensional spatial vectors (chairs, pianos) per time step and per trial. A linear support vector machine classifier was used for classification of each time step (20 ms moving time-steps) separately. The temporal classification analysis was identical but used all 40 data points within the 80 ms time window as features for separate analyses for each channel. C, The diffusion model decomposes observed response time into time required to make a decision, and time related to nondecision components of processing. The first choice boundary reached by the diffusion process determines the overt response. The time taken to reach the choice boundary determines the decision time. Accumulation of perceptual evidence for one or the other alternatives begins at z. The distance between the absorbing boundaries reflects criterion setting. Evidence accumulation is assumed to be inherently noisy. The mean rate of evidence accumulation on a given trial is determined by the drift of the diffusion process. Drift is assumed to be normally distributed across trials with mean v and standard deviation η. The starting point of the evidence accumulation process is assumed to vary according to a uniform distribution centered at z, with range sz. Two example evidence accumulation paths are shown. The difference in the starting points of the pathways is due to between-trial starting point variability. The highly irregular paths are due to within-trial noise in the accumulation process. The top part of the figure summarizes the nondecision components of overall RT. Non-decision time is modeled as a uniform distribution centered at Ter, with range st.
Data recording, preprocessing, and ERP analysis.
The EEG was recorded from 63 scalp electrode sites (Fp1, Fp2, F7, F3, Fz, F4, F8, FC5, FC1, FC2, FC6, T7, C3, Cz, C4, T8, FPz, CP5, CP1, CP2, CP6, PO9, P7, P3, Pz, P4, P8, FCz, O1, Oz, O2, AF7, AF3, AF4, AF8, F5, F1, F2, F6, TP9, FT7, FC3, FC4, FT8, TP10, C5, IZ, PO10, C6, TP7, CP3, CPz, CP4, TP8, P5, P1, P2, P6, PO7, PO3, POz, PO4, PO8). The active Ag/AgCl electrodes (actiCAP, Brain Products) were referenced against the right mastoid. The vertical electro-oculogram (vEOG) was recorded from an electrode infraorbital to the left eye. The EEG was continuously recorded at a sampling rate of 500 Hz using BrainAmp DC (Brain Products). An on-line bandpass filter (DC–70 Hz) was employed for all channels. The EEG was analyzed off-line with epochs ranging from 100 ms before stimulus onset until 1500 ms afterward. A baseline period of 100 ms before the trial onset was used. All data were screened for technical artifacts (±500 μV), then the influences of eye movements were eliminated by applying the ocular correction algorithm (Gratton et al., 1983), and a second artifact screening was performed in which contaminated trials with max/min amplitudes exceeding ±100 μV were rejected. An off-line, phase shift-free Butterworth low-pass filter (10 Hz, 12 dB/Oct) was applied. The filter had no effect on the latency of the amplitudes and did not lead to temporal distortions. Then, a current source density (CSD) analysis of the event-related potential (ERP) was performed for each of the 63 electrode sites and the grand average of the ERP waveforms was computed separately for each discriminability condition. The CSD signals were computed for each electrode site by taking the second derivative of the distribution of the voltage over the scalp. The CSD analysis accounted for the curvature of the head using a spline algorithm (Perrin et al., 1987, 1989; Pernier et al., 1988). This made the signal independent of the location of the reference electrode as different reference locations can affect the ERP signal differentially (Luck, 2005), but not the CSD signals. The CSD analysis also served as a spatial filter that decreased the blur distortion caused by skull resistance (Katznelson, 1981) and reduced the effect of adjacent currents on the local recordings by emphasizing shallow neural generators. Both the higher topographical accuracy of the CSD signals (Gevins, 1989) and the resulting reduction of redundancies in the signals from adjacent electrode sites increased the accuracy of the pattern classification analysis. Others have shown that the combination of CSD analysis and support vector machine (SVM) classifiers is one of the most effective approaches compared with alternative combinations of filtering and classification methods (Bai et al., 2007).
Multivariate pattern classification.
After preprocessing and transformation into CSD datasets, multivariate pattern classification analyses were performed (Philiastides and Sajda, 2006; Philiastides et al., 2006; Das et al., 2010; Blankertz et al., 2011). First, data from intact trials for all 63 electrodes were sorted into conditions, according to stimulus category or the participant's choice. Because single trial data are inevitably noisy and noise decreases classification performance, signals time-locked to the premask from piano trials and chair trials were averaged individually for each participant within each run and each discriminability condition. As in classical ERP analysis, this procedure reduced the effects of noise from single-trial ERPs and thus provided a better estimate of the underlying activity patterns. The decoding analysis was then performed on the run averaged ERPs. Discussions of single-trial decoding analysis and other approaches to filtering and reduction of dimensionality can be found in the studies by Bai et al. (2007) and Blankertz et al. (2011). For each run, the number of trials in the condition with the smallest number of trials after artifact removal was used for both conditions. For runs without artifacts and with completely balanced choices, the averages would be based on 24 trials per choice option (24 objects from each category were shown in each discriminability condition and the noise image was shown 48 times in the pure-noise condition). This procedure ensured that run-averaged pattern estimates were always based on exactly the same number of trials per condition, thereby avoiding any sample-size biases in the quality of the pattern estimates for the two choices.
The spatial decoding analysis used the spatial configuration of signals across the scalp at a given time point. Signals were averaged within an 80 ms time window for each channel (40 data points) beginning with the onset of the premask. This resulted in two vectors (one for each category) with each channel contributing one data point. A linear SVM classifier with a fixed regulation parameter C = 1 was trained on the vectors for both conditions from four of the five independent experimental runs using LIBSVM (Chang and Lin, 2011). Linear classifiers have been shown to perform extremely well for brain data (Philiastides and Sajda, 2006; Philiastides et al., 2006; Das et al., 2010; Bode et al., 2012; Blankertz et al., 2011). The classifier estimated a decision boundary, which was then used to classify the vectors from the remaining fifth run (Fig. 1B). Subsequently, the classification procedure was repeated with the vectors from each experimental run serving as test data and the remaining four runs serving as training data. The decoding accuracy was calculated as the average accuracy after fivefold cross-validation and assigned to the onset of the respective time window. The time window was then shifted by 20 ms and the procedure was repeated. The time course of spatial decoding accuracies was calculated separately for each discriminability condition for both stimuli and choices. Finally, we computed the average accuracy for five consecutive time windows to obtain average accuracy values for time intervals of 100 ms from −100 to 0 ms (stimulus onset), 0 to 100 ms, 100 to 200 ms, and 300 to 400 ms. t tests were applied to independently test for stimulus encoding as well as for choice encoding in each of these four windows. We expected objects and choices for highly discriminative objects to be encoded in the later time windows only, given that sufficient discriminative information was available. We further tested whether the earliest time window (−100 to 0 ms) encoded choices for the pure noise condition. Decoding accuracies were tested against chance level (50% for a binary choice). To maximize power, we did not use t tests for single time-bins with a family-wise corrected α-level, as this is not common practice in ERP research because it reduces statistical power. Such tests require the data points to be statistically independent, which is not true for ERP analyses and for our ERP-based decoding. Because we had clear a priori hypotheses about whether information encoding should be found before or after stimulus presentation, we were able to reduce the chance of a Type-I error by limiting the number of data comparisons to 100 ms epochs before and after the stimulus presentation using an uncorrected α = 0.05. The ERPs and the decoding accuracies, which were based on the ERPs, were distributed in a very regular way (see Results). This pattern of results provides strong evidence that our findings are unlikely to have been due to Type-I error; such errors arise from repeated random sampling of the same population and so should be distributed randomly through the data. Additionally, a permutation test was applied for which the results were tested against a distribution obtained from randomly assigning the labels to the training data, individually shuffled for each training set. This procedure yields a distribution of accuracies under the null hypothesis for the identical classification procedure that is stricter than the test against baseline (Pereira et al., 2009). For further validation, we also conducted single-trial decoding analyses for relevant time windows. For this, 90% of all trials were randomly drawn and used as training data. The classifier then predicted the omitted 10% of trials. This was followed by a tenfold cross-validation for which each 10% set of trials was used for testing after training on the remaining data. The procedure was repeated 10 times, each time with newly drawn sets of data, to avoid selection biases. All 100 analyses were averaged for each time point, and then for 100 ms time windows, identical to the run average analysis.
The temporal decoding analysis used vectors containing all 40 data points within an 80 ms window at each electrode, thus resulting in 63 separate analyses for each time window (Fig. 1B). Otherwise, the analysis was identical to spatial decoding. Average decoding accuracy after cross-validation was again analyzed for each time window, shifted by time steps of 20 ms. This approach allowed us to test which channels carried maximal information at particular chosen times. This procedure complemented the spatial decoding analysis and provided a more direct way to test for the spatial distribution of information across time compared with, for example, feature weight maps. As this procedure did not involve the spatial distribution of information across the scalp, it provided an independent test of information encoding at single electrode sites, maintaining the independence of the temporal and spatial decoding analyses (for a different approach see Blankertz et al., 2011).
Diffusion model analysis.
The diffusion model (Ratcliff, 1978; Smith and Ratcliff, 2004; Ratcliff and McKoon, 2008) was fitted to the group averaged choice probabilities and RT distributions for correct responses and errors (Fig. 1C). The RT distributions were summarized by their 0.1, 0.3, 0.5, 0.7, and 0.9 quantiles. These were averaged across participants for the two choice alternatives and used to group the RT data into six bins. The data to be accounted for comprised nine pairs of piano–chair RT distributions and their associated choice probabilities (each distribution pair had 11 df, giving 99 df overall). Separate drift rate parameters were estimated for each level of discriminability, and for each stimulus type, although the model still fitted well when drift rates were constrained to be of equal magnitude for pianos and chairs. Diffusion model parameters (Tuerlinckx, 2004; Ratcliff and Tuerlinckx, 2002) were estimated by minimizing a likelihood ratio statistic (G2) where, as follows:
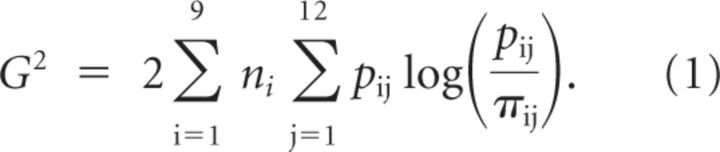 |
In Equation 1, the summation over j runs over the 12 piano-chair joint RT distributions. The summation over i runs over the nine stimulus conditions defined by the factorial combination of the two stimulus types (pianos and chairs) presented at four discriminability levels, plus the pure noise condition (which had only one discriminability level). The number of experimental trials in each condition is given by ni, which was set to 120 (the total number of piano, chair, and noise stimuli presented in each discriminability condition), pij is the observed proportion of responses in bin j in condition i, and πij is the proportion of responses predicted by the diffusion model. We chose to fit the model to the quantile-averaged group data because it was impractical to run sufficient trials to allow fits to individual participant data. Ratcliff and colleagues have repeatedly shown that model parameters estimated from quantile-averaged data correspond fairly closely to the averages of parameters estimated from individual participants. There is no evidence that quantile averaging introduces artifacts into the estimation process. Further discussion, including references, can be found in Smith and Ratcliff (2009).
Diffusion model analysis of sequence effects in choice.
The standard diffusion model described above (by default) assumes starting point variability to be random, not systematic. To directly investigate the effect of previous choices on decision processes, we partitioned the data on the basis of whether the previous response was the same or different as the previous response. Because partitioning the data resulted in very few error responses in the high discriminability conditions, we collapsed across piano and chair stimuli, and refitted the diffusion model to the partitioned data. When organized in this way, the data are interpreted in terms of correct and error responses (rather than piano and chair responses), so we omitted the pure noise data from this analysis. If the previous choice systematically affects decision processes by biasing the starting point of evidence accumulation, it follows that a model with a biased starting point should provide a better fit to the data than an unbiased model. We freely estimated a starting point bias parameter from the partitioned data, which represents the extent to which evidence accumulation is shifted away from an unbiased starting point to a starting point favoring one of the choice alternatives.
Results
Behavioral results
On average, accuracy decreased with decreasing stimulus discriminability, as indicated by significant reductions in d′ values (Fig. 2A). For the lowest object discriminability condition (16.67 ms), d′ was close to zero, representing performance close to chance level. In the pure noise condition, the average choice balance, a measure of response bias, was close to zero and reflected only a slight bias toward piano choices (Fig. 2B). There were no significant mean RT differences between choices for chairs and choices for pianos (all p > 0.10). Incorrect responses were consistently slower regardless of category choice. At the lowest discriminability, no difference between RTs could be found, indicating that participants were mostly unaware of which stimulus was presented.
Figure 2.
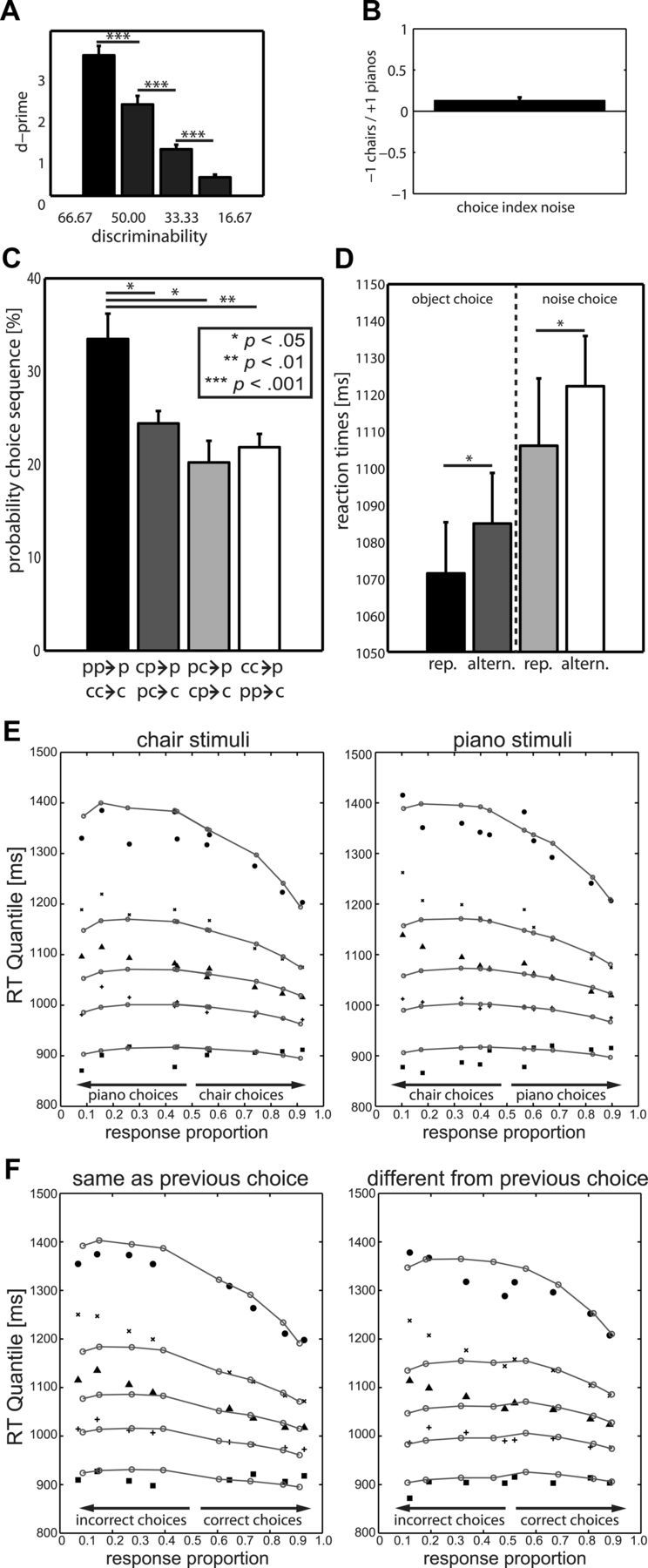
Behavioral results. A, Average d ' (SE) differed significantly between discriminability levels. Error bars indicate SEM. B, Average choice index ([nπ − nch]/[nπ + nch]) indicated a slight but nonsignificant tendency toward piano choices. C, Probability of choosing piano (p) or chair (c) on a pure noise trial as a function of choices made on two consecutive noise trials. Priming effects were significant and even stronger if the same choice had been made on the preceding two trials. D, Repetition trials were faster than alternation trials. E, Diffusion model fit. The correct and error response time quantiles (black symbols) for each discriminability condition for both chair and piano stimuli are plotted together with predictions of the diffusion model (open circles/gray lines). In each panel, the response time quantiles for each discriminability condition are plotted (y-axis) as a function of choice probability (x-axis). The noise condition is redundantly plotted in each panel. F, Diffusion model fit for biased starting point model. Trials are collapsed across piano and chair decisions and sorted with respect to the choice from the previous trial. The correct and error response time quantiles (black symbols) for each discriminability condition are plotted together with predictions of the diffusion model (open circles/gray lines). In each panel, the response time quantiles for each discriminability condition are plotted (y-axis) as a function of choice probability (x-axis).
Choice behavior
To test for effects of choice history priming, we investigated whether choices on pure noise trials were biased by the choices made on the preceding two trials. Looking further back into the sequence of choices was precluded by the low number of longer sequences of consecutive pure noise trials. In sequences of choices culminating in a pure noise trial, there was a significant bias to repeat the previous choice rather than to switch to the alternative choice, regardless of whether it was preceded by pure noise trials or highly discriminable objects (Fig. 2C). In contrast, for highly discriminable objects, the perceptual information in the stimulus was the primary determinant of the choice, eliminating any dependency induced by the choice on previous trials. Regardless of discriminability, and consistent with our hypothesis that the sequences of choices biased the evidence accumulation process, choice repetitions were faster than alternations in all conditions (t(17) = 2.17, p < 0.05; Fig. 2D).
Diffusion model
To investigate whether trial-by-trial dependency in decision making could be accommodated within an evidence accumulation framework, we fitted the diffusion model to the behavioral data. The model provided an excellent quantitative fit to the data, accounting for the choice probabilities and the RT distributions for correct responses and errors. The distributions of correct responses are captured particularly well by the model. Most importantly for our purposes, performance in the pure noise condition is described extremely well by the model. As is usual with RT distribution data, the largest discrepancies in fit are in the extreme tails of the distributions (the 0.9 quantile) and in the error distributions for high discriminability stimuli. Tail quantiles and high discriminability errors are both associated with large errors of estimate: Distribution tails are highly variable because they are based on a small number of very slow responses and there are few errors made to high discriminability stimuli, so these distributions are estimated with low reliability. There is also evidence that some errors may be due to fast guesses: The model tends to overestimates the 0.1 quantile for errors, but not correct responses. The best fitting model had substantial starting point variability, consistent with the idea that the choice history biased the starting point (Fig. 2E, Table 1).
Table 1.
Best-fitting diffusion model parameters for fits to the entire data set (Full) and to the sequential response data (Sequential)
| Parameter | Full G2 = 36.58 |
Sequential G2 = 32.14 |
|
|---|---|---|---|
| Chair stimuli | Piano stimuli | All stimuli | |
| Drift rate (66.67 ms exposure) | 0.442 | −0.405 | 0.400 |
| Drift rate (50.00 ms exposure) | 0.331 | −0.303 | 0.300 |
| Drift rate (33.33 ms exposure) | 0.209 | −0.145 | 0.163 |
| Drift rate (16.67 ms exposure) | 0.047 | −0.083 | 0.065 |
| Noise drift rate (16.67 ms exposure) | −0.054 | — | |
| Drift variability | 0.254 | 0.237 | |
| Boundary separation | 0.111 | 0.107 | |
| Starting point bias | — | 0.004 | |
| Starting point variability | 0.069 | 0.055 | |
| Mean nondecision time | 0.908 | 0.908 | |
| Nondecision time range | 0.225 | 0.219 | |
Note: See the study by Ratcliff and McKoon (2008) for detailed discussion of model parameters. Parameters whose values were fixed across stimulus types are displayed between columns. Note that the full model did not contain a starting point bias by default.
Next, we investigated the dependency of the starting point of the diffusion process on the choice made on the previous trial. We refitted the model after partitioning the data on the basis of whether the choice was the same as on the previous trial, or different from the previous trial. Partitioning the data in this way resulted in very few errors in some of the high discriminability conditions, so we collapsed the data across piano and chair stimulus conditions and fitted the model to the choice probabilities and families of RT distributions, conditioned on the previous response (same or different). Accurate estimation of the parameters of the diffusion model—particularly the mean starting point and starting point variability—depends on having good information about the distributions of error RTs. We therefore chose to fit the model to the collapsed dataset, which provided us with distributions of error RTs in all discriminability conditions. The model for the collapsed data assumes a symmetrical decision process, in both the rates of evidence accumulation for chair and piano stimuli and in the starting point bias for piano and chair responses, conditional on the previous response being either a piano or chair. The symmetry assumption is justified by the previous model fit, which showed little or no difference in the choice probabilities and the distributions of RT for piano and chair responses. This means that little or no information is lost by fitting the model to the collapsed data. We freely estimated a starting point bias and found that there was a shift in mean starting point toward the response boundary associated with the previous choice. For all conditions, at all levels of discriminability, the model accurately predicted the observed choice probabilities. The model additionally provided a very accurate summary of the empirical RT distributions. It shows that the starting point bias was associated with a speeding up of correct responses relative to errors and that correct responses were more likely than errors. The distributions of correct responses were again captured particularly well by the model, although there were some discrepancies in the extreme tails of the RT distributions. Error RT distributions in high discriminability conditions were not fitted as well as were correct responses. The reason for these discrepancies, in both cases, was (as in the previous analysis) measurement error: Tail quantiles of RT distributions are difficult to estimate precisely because of the sparseness of observations in the tail, and there are relatively few observations in the distributions of errors in high discriminability conditions. The important finding is that the inclusion of starting point bias significantly improved the fit over a model that assumed no starting point bias [ΔG2 (1) = 5.86; p < 0.05], supporting the hypothesis that the decision process is systematically biased by previous choices (Fig. 2F, Table 1).
CSD ERP analysis for EEG data
Over the occipital electrode site (Oz, Fig. 3), an early positive component (CSD-P1) after ∼100 ms was found to differ significantly (F(4,68) = 7.85, p < 0.001) between pure-noise and all object conditions (all p < 0.001), but the different object conditions did not differ significantly from each other (all p > 0.10). This was followed by a negative component (CSD-N2) peaking ∼200 ms after stimulus onset that showed a significant modulation by discriminability levels (F(4,68) = 5.50, p < 0.001). The third, negative component peaked at 300 ms after stimulus onset and showed a slow decay until 600 ms, i.e., approximately until the beginning of the response phase. The amplitude of the CSD-N3 varied significantly with the discriminability levels (F(4,68) = 10.23, p < 0.001; Fig. 3A). CSD ERPs appeared to be more sensitive to differences between discriminability conditions than classical ERP analyses. However, neither form of ERP analysis could reveal the decision outcomes. Note that this underscores the importance of the following pattern classification analysis.
Figure 3.
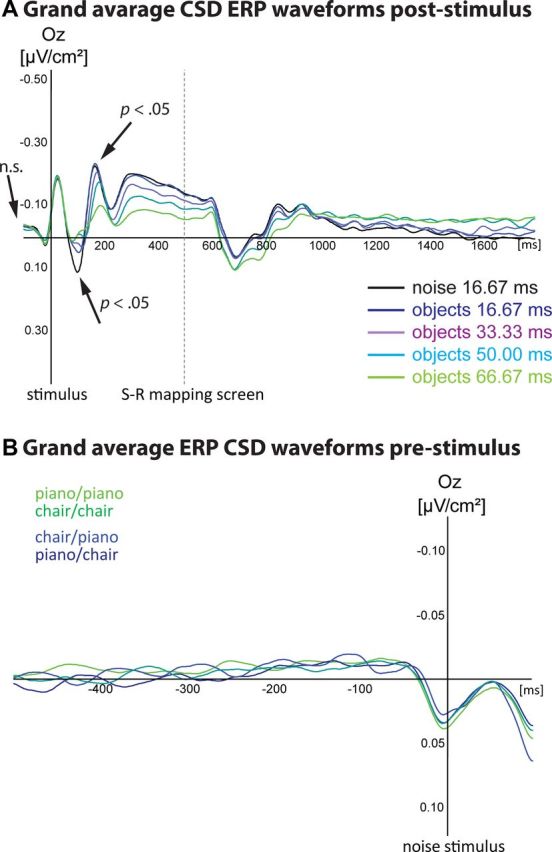
Grand average CSD ERPs. A, The visual inspection of the grand average waveforms indicated strongest differences between discriminability levels at Oz electrode site in the time-periods of 50–150 (CSD-P1), 100–200, (CSD-N1), 300–450 ms (CSD-N3), and 300–600 ms (CSD-P3) (displayed for correct responses and for all pure noise trials). Significant differences between the pure noise condition and all other conditions could be found ∼100 ms poststimulus. The object discriminability conditions did not significantly differ from each other. Differences between discriminability conditions showed a first negative peak ∼200 ms. In the 66.67 ms condition, the CSD-N2 amplitude was significantly smaller compared with the 16.67 ms condition (p < 0.001), the 33.33 ms condition (p < 0.05), and the pure noise condition (p < 0.01). These differences were very pronounced during the following 500 ms. This component was smaller in the 66.67 ms condition compared with the 16.67 ms condition (p < 0.001), the 33.33 ms condition (p < 0.05), and the pure noise condition (p < 0.001). The 33.33 ms condition and the pure noise condition also differed significantly (p < 0.01). No differences between any discriminability conditions were found in the prestimulus interval. No analysis revealed any differences between pianos and chairs for any discriminability condition. 0 ms = stimulus onset; negativity is plotted upwards. B, Grant average ERP CSD waveforms at Oz electrode site preceding the onset of the following pure noise trial. ERP waveforms are displayed separately for each combination of choices (piano–piano, chair–chair, piano–chair, chair–piano). No significant differences were found, confirming that ERPs from the preceding trial were not related to choice outcomes on the following noise trials (p > 0.10). The displayed electrode site was representative for all electrode sites.
Multivariate pattern classification for EEG data
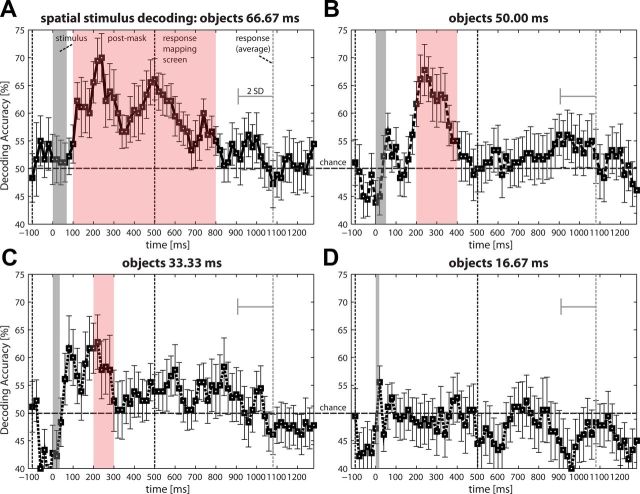
We then analyzed the information in the spatial configuration of activity across all 63 electrode sites at consecutive time points. For the highest discriminability (66.67 ms) condition, information about stimulus identity was encoded in brain activity by the second poststimulus interval (100–200 ms), as confirmed by the baseline test as well as by the permutation test (all p < 0.01). The peak of information encoding was at 240 ms. The decoding accuracies decreased with discriminability. The three highest discriminability conditions showed significant decoding accuracies in the 200–300 ms window, regardless of the statistical test applied (66.67 ms: p < 0.001; 50.00 ms: p < 0.001; 33.33 ms: p < 0.05). By contrast, no information was found for the lowest discriminability condition for any time window (16.67 ms; all p > 0.10; Fig. 4).
Figure 4.
Decoding the presented stimuli from EEG-CSD data. A linear SVM classifier was used on averages of 80 ms windows with 20 ms time-steps (the average accuracy for all classifications within 100 ms time windows was tested using a permutation test; time point 0 = stimulus presentation). Decoding for A, 66.67 ms; B, 50.00 ms; C, 33.33 ms; and D, 16.67 ms target duration. Stimuli could be predicted from the time windows beginning 100 ms after stimulus presentation (66.67 ms) or 200 ms after stimulus presentation (50.00 and 33.33 ms). The range of times during which decoding accuracy was significant above chance decreased with discriminability and no information was found for the lowest discriminability condition (16.67 ms). Note, however, that onset and peak times can only be approximations because these analyses cannot unambiguously resolve the occurrence of information within the averaged time window. Error bars indicate SEM. Significant time windows are highlighted.
The same analyses were then repeated for choices. The results closely mirrored those for stimuli, with accuracy decreasing with discriminability (Fig. 5). Decoding accuracy was significantly above chance in the 200–300 ms interval for the three highest discriminability conditions (66.67 ms, p < 0.01; 50.00 ms, p < 0.01; 33.33 ms, p < 0.05). The permutation test yielded highly similar results (66.67 ms, p < 0.01; 50.00 ms, p < 0.05; 33.33 ms, p < 0.05). Decoding accuracy peaked 260 ms after stimulus onset (Fig. 5A). The lowest discriminability condition (16.67 ms) showed a similar trend (single time bin: p < 0.05, uncorrected for multiple comparisons) (Fig. 5D); however, no time window analysis reached significance for this condition. Previous studies (Philiastides and Sajda, 2006; Philiastides et al., 2006) have performed decoding using single trials instead of using run-average data as reported here. When conducting our analysis using data from single trials, the general pattern of results was the same. The first time window to encode choices was again the 200–300 ms interval (66.67 ms, accuracy 53%, p < 0.05). Decoding accuracy was also significant in subsequent windows (300–400 ms, accuracy 54%, p < 0.01).
Figure 5.
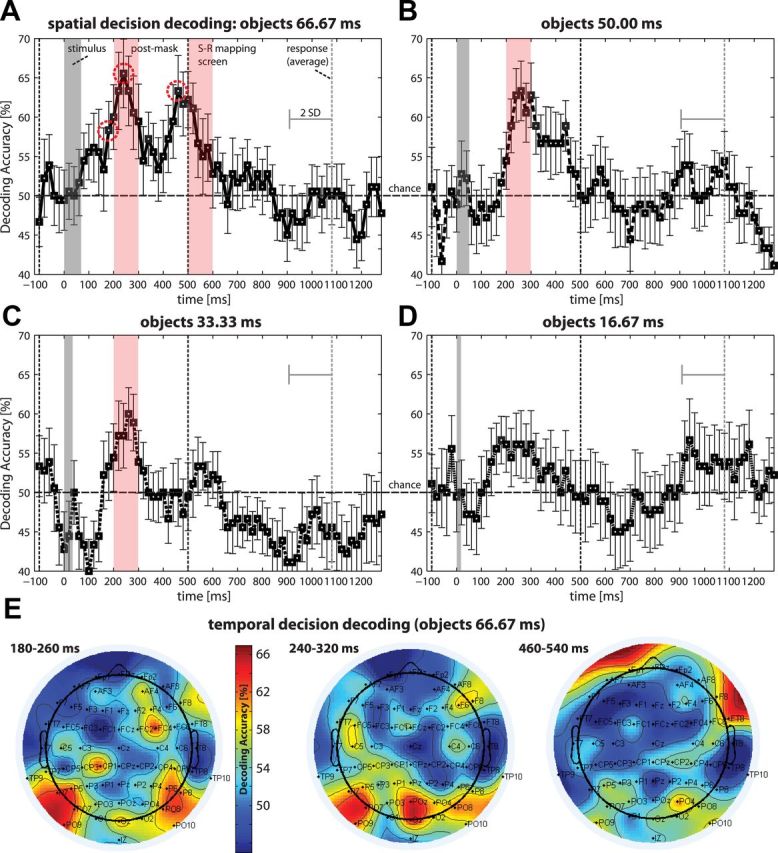
Decoding category choices from EEG-CSD data for object stimuli. A linear SVM classifier was used on averages of 80 ms windows with 20 ms time-steps (the average accuracy for all classifications within 100 ms time windows was tested using a permutation test; time point 0 = stimulus presentation). Decoding for A, 66.67 ms; B, 50.00 ms; C, 33.33 ms; and D, 16.67 ms target duration. Error bars indicate SEM. Significant time windows are highlighted. E, Independent temporal pattern classification using data within each 80 ms window for each channel separately. Scalp maps show decoding accuracy for selected times corresponding to onset and peaks in spatial decoding (highest discriminability). During early stages, mostly occipital and parietal electrodes encoded choices (P7, P5, PO7, PO9, P6, P8, FC4, all p < 0.01; PO8, Oz, all p < 0.05; O2, p = 0.07). Similar channels were predictive during the first peak (POz, Oz, all p < 0.001; P7, PO7, PO9, P6, PO8, O2, all p < 0.05; F6, p = 0.05; P5, p = 0.06; PO4, p = 0.08). During the second peak prefrontal electrodes and parietal channels were predictive (FT8, PO4, all p < 0.01; Fp1, F8, all p < 0.05; PO8, p = 0.07).
Additionally, a complementary, but independent, temporal decoding analysis was performed for the high discriminability condition. This analysis ignored the spatial topography of signals but used all 40 data-points from each electrode site separately to decode choices from signals within the 80 ms time windows. We chose the first onset as well as the two peaks of the spatial choice decoding function under high discriminability as “time-bins of interest” for the temporal decoding analyses. Mostly occipital and parieto-occipital channels and some frontal channels were found to encode choice-information for these periods (Fig. 5E). For the second peak, around the beginning of the response period, anterior prefrontal electrodes showed the highest choice encoding with contributions from several parietal channels.
Separate spatial and temporal decoding analyses were carried out for choices in the pure noise condition. No significant choice encoding after stimulus presentation was found, but activity in the time window preceding stimulus presentation (−100 to 0 ms) predicted choice outcomes (baseline test and permutation test: p < 0.05; Fig. 6A); the peak was found at −40 ms. As this decoding window mainly contained prestimulus activity, this finding most likely reflects information present shortly before and during stimulus presentation. We replicated this finding using different width decoding windows from 60 to 100 ms, ruling out that the finding was an artifact of the decoding window width. We also replicated our finding using single-trial data instead of run-averaged data for decoding (accuracy 54%, p < 0.05). Additionally, the temporal decoding analysis for this time period confirmed that prefrontal channels as well as parietal channels predicted choices (Fig. 6B).
Figure 6.
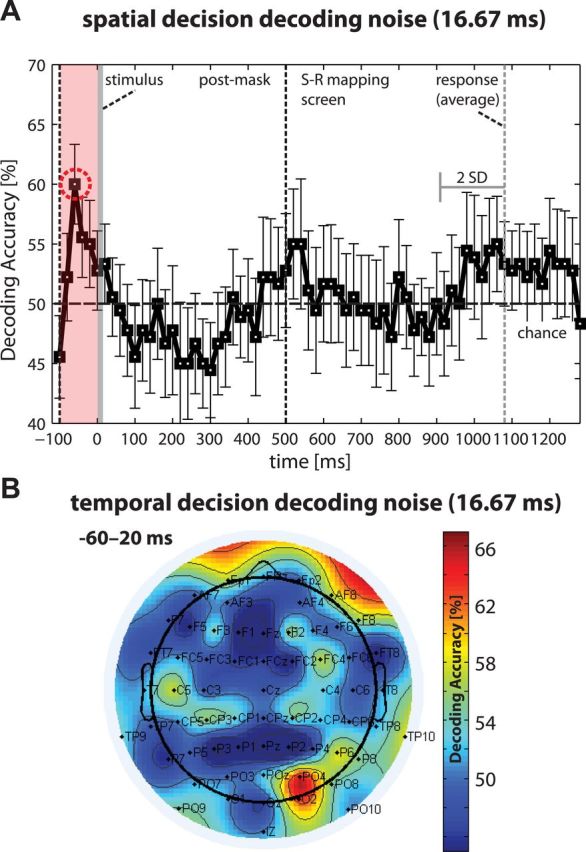
Decoding the category choices from EEG-CSD data for pure noise. A, A linear SVM classifier was used on averages of 80 ms windows with 20 ms time-steps (the average accuracy for all classifications within 100 ms time windows was tested using a permutation test; time point 0 = stimulus presentation). Choices could only be predicted before stimulus presentation (−100–0 ms). Error bars indicate SEM. Significant time windows are highlighted. B, Independent temporal multivariate pattern classification using the data within each 80 ms time window for each channel separately. The scalp map shows decoding accuracy for the selected −60–20 ms window. Occipitoparietal channels (PO4, O2, all p < 0.01; Pz, p < 0.05; PO8, p = 0.07; PO9, p = 0.08) and by trend frontopolar channels (AF8, p = 0.09; Fp1, p = 0.10) were predictive for choice outcomes.
Activity earlier than 100 ms before a noise trial was not predictive of choices (p > 0.10 for all times), nor did any earlier ERP component show differences between choice outcomes (Fig. 3B). The behavioral results show that the choice on the previous trial predicted the next decision, so the EEG on the previous trial implicitly contains information about the subsequent decision. However, we found no evidence that decisions could be predicted from persistent activity associated with the previous trial. Rather, the choice on pure noise trials was only predictable from activity in the last 100 ms of the intertrial interval, immediately preceding the stimulus. Although, arguably, our classification analysis may not have been sensitive enough to detect the neural signatures of decision biases that carried over from the previous trial and persisted throughout the intertrial interval, our analysis suggests that decisions on pure noise trials depend on processes involved in the preparation for the next stimuli that become active immediately before its presentation.
As a control, decoding analyses were run for motor responses instead of category choices, which were decoupled from each other by the use of randomized response mappings. Unlike choices, motor responses could not be decoded until after the presentation of the response mapping screen (high discriminability: peak 79% accuracy at 940–1020 ms, p < 0.0001; pure noise: peak 70% accuracy at 920–1000 ms, p < 0.0001). This confirms that participants made true category choices before the presentation of the response mapping screen and did not prepare random motor responses, as instructed, and that no motor response priming occurred (Fig. 7).
Figure 7.
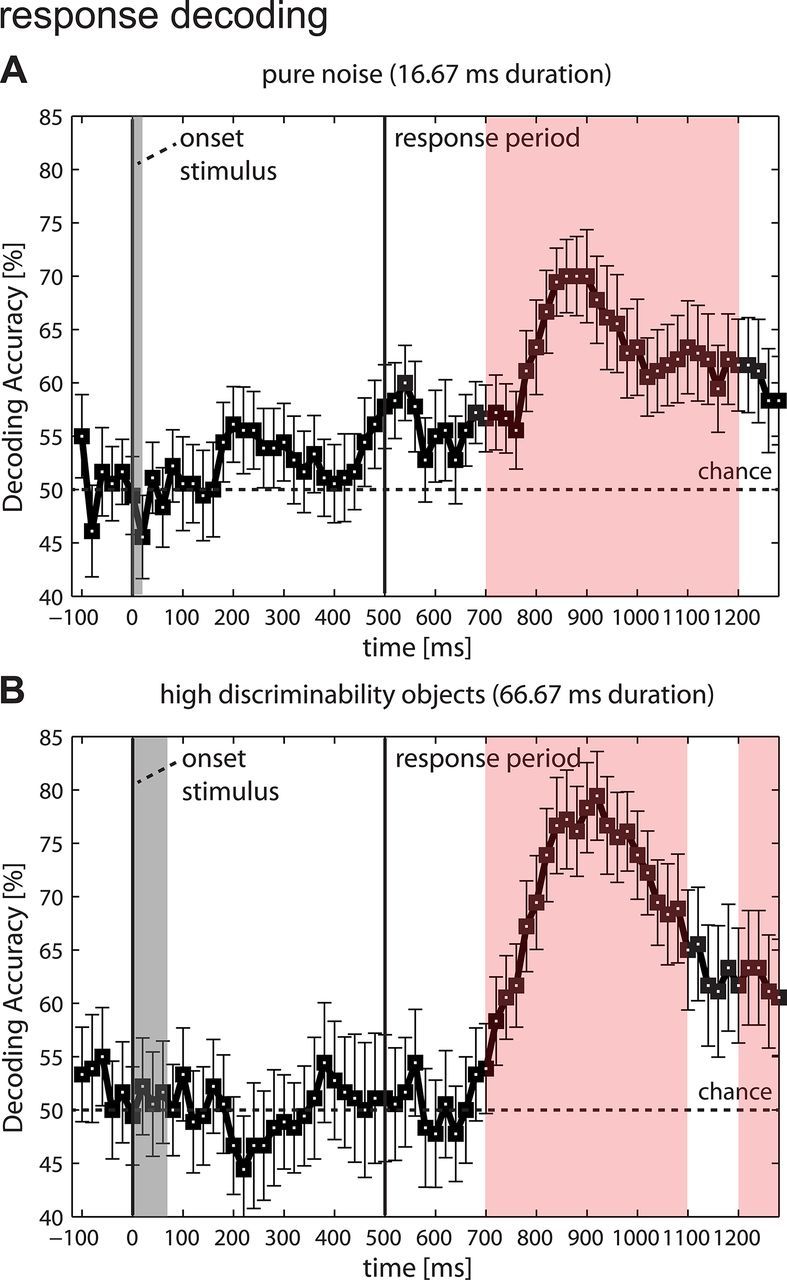
Decoding the motor responses. Displayed are decoding accuracies from spatial motor response decoding analysis (80 ms width, 20 ms moving time steps, left vs right button press, 50% chance level; 100 ms time window analysis using a permutation test). A, Pure noise condition. Responses could only be decoded until after the presentation of the response mapping screen (peak 70% accuracy at 920–1000 ms). B, High discriminability object condition (stimulus duration 66.67 ms). Similar to all other object conditions (illustrated only for highest discriminability condition), motor responses could again only be decoded after the presentation of the response mapping screen (peak 79% accuracy at 940–1020 ms). Thus, participants made true category choices and did not prepare random motor responses. The absence of motor response encoding early in the trial also confirmed that motor response priming cannot explain our choice decoding results. Significant time windows are highlighted.
Discussion
Using a pattern classification approach for EEG data, our study has shown that choice outcomes for perceptual decisions can be decoded from brain activity for stimuli of differing levels of discriminability. When real object stimuli were presented, stimulus and choice information was encoded in spatially distributed brain activity starting around 140–180 ms poststimulus. This finding is consistent with a recent study that used SVM classifiers to predict choices in a face versus car perceptual discrimination task (Das et al., 2010). Our study extended these findings to inanimate object categories, which appear to be encoded in a more distributed fashion in ventral visual cortex (Haxby et al., 2001) as compared with faces, which are represented more locally (Kanwisher et al., 1997). We have thus provided the first evidence that information about choice outcomes is reflected in EEG signals, even when neither of the categories relies on a single focal cortical area. It has been suggested that even modular object representations in the ventral visual cortex, such as faces, may be the result of a combination of correlated and nonlinearly combined property maps (Op de Beeck et al., 2008). Thus, our decoding most likely reflects a difference between two distributed but unique coding schemes for two categories of objects that could be expected for any distinct categories (Haxby et al., 2001). Others have investigated decision-related information in EEG signals using a faces versus cars perceptual discrimination task (Philiastides and Sajda, 2006). That study found two choice-related components, the second (∼300 ms) of which more closely reflected aspects of choice performance (Philiastides et al., 2006). This second component may be linked to stimulus discriminability and the accumulation rate in a diffusion model (Ratcliff et al., 2009). Consistent with these results, using SVM (instead of logistic regression) based on run averages as well as on single trials, we found choices to be encoded ∼300 ms poststimulus, with a tendency toward a later peak and lower accuracy for decreasing discriminability.
We have also shown that choices can be decoded for pure noise stimuli when participants were unaware of the absence of discriminative information, and further, that choices can be predicted on these trials from activity before and around the time of stimulus presentation. This extends earlier fMRI studies that demonstrated prestimulus brain activity, but did not show encoding of choice outcomes (Hesselmann et al., 2008a,b, 2010). Our results do not support the hypothesis that this activity is merely attributable to enhanced attention (Hesselmann et al., 2010). Rather, this activity most likely reflects prestimulus biasing of the decision process, because it was directly related to choice outcomes. This interpretation is further supported by the diffusion model analysis, which provided a good description of our choice and RT distribution data. In the diffusion model, bias affects the starting point for evidence accumulation (Ratcliff, 1978; Smith and Ratcliff, 2004). The best fitting model had substantial starting point variability, and most importantly, the starting point for evidence accumulation was biased toward the response made on the previous trial.
The lowest discriminability condition did not show the same decoding profile as the pure noise condition, even though performance was close to chance level. Instead it showed the same pattern as the other object conditions, but with reduced accuracy. It is likely that there was enough discriminative information on some trials, or for some participants, that the effects of the prestimulus biases were reduced below the detectability threshold for our analysis. Importantly, on these trials, a stimulus object was presented, so decisions on these trials would presumably have been based on weakly or partially encoded stimulus information. This may have washed out any predictive effect of prestimulus biasing activity. It is important to understand that, while we would expect prestimulus biasing activity under all conditions, we would only expect to be able to detect it in the decoding analysis when there was no stimulus information present. Because our analysis partitioned the data according to the choice outcome, it emphasized those features of the EEG that were most predictive of the choice outcome in each condition. In conditions in which stimulus objects were presented, this would have been the stimulus. Under these conditions, trials on which the prestimulus bias and stimulus both predicted the same response would have been averaged with trials on which the prestimulus bias and stimulus predicted opposite responses. Because the response would have been predicted most strongly by the stimulus, the effects of the prestimulus bias would have been largely or wholly averaged out. Consistent with our interpretation, it has been shown that neural activity in the monkey parietal cortex predicts decisions about motion direction in random dot kinematograms before stimulus presentation (Shadlen and Newsome, 2001). This effect was most pronounced for very weak stimuli, leading these authors to interpret their findings as a decision bias, which becomes stronger when less discriminative information is provided by the following stimulus. Similarly, others have demonstrated decision-related prestimulus biases in parietal neurons in monkeys, which were related to the animals' estimation of the relative values of choice options (Platt and Glimcher, 1999).
The prestimulus activity cannot be attributed to stimulus processing because it was found on pure noise trials that contained no discriminative information. Furthermore, any a priori differences between the activity on piano choice trials and chair choice trials are ruled out by the ERP analyses. Why did the starting point for evidence accumulation vary between trials? One possibility is that differences are due to neural noise that biased decision systems during the predecision period (Deco and Romo, 2008; Rolls and Deco, 2011). Although our findings do not contradict this possibility, our behavioral results suggest the existence of a choice priming process that depends on participants' recent choice history. First, participants tended to repeat their most recent choice when presented with a pure noise stimulus, even though the choices themselves may have been mapped to different motor responses. This bias might potentially depend on longer choice sequences than we could evaluate here. Second, choice repetitions were made faster than choice alternations. This would be expected if choice priming shifted the starting point of evidence accumulation on the following trial toward the previous decision boundary. Third, our model-based analysis confirmed the systematic bias toward the previous choice. In a similar vein, repeatedly attending to specific features of highly discriminable objects has been shown to prime attention to the same features in subsequent trials, probably by means of short-term implicit memory formation (Maljkovic and Nakayama, 1994). Furthermore, sequential effects in RT and choice sequences have been extensively described and modeled before, suggesting that participants dynamically control their decision processes to try to optimize performance (Luce, 1986; Remington, 1969; Gao et al., 2009). This interpretation is also consistent with a recent study demonstrating that the neural and behavioral effects of manipulating the prior probabilities of the choice alternatives could be explained by a systematic shift in the starting point of a simple accumulator (Forstmann et al., 2010).
The choice priming hypothesis might also be applicable to recent fMRI studies, which demonstrated the encoding of long-time-scale predecision biases (acting over several seconds) in free decision tasks (Soon et al., 2008; Bode et al., 2011). While the small number of trials per experimental run in these studies did not allow for a conclusive analysis of the underlying response patterns, it is likely that participants' recent choice history influenced which choice was made on a given trial. This, in turn, might have been related to the slow build-up of choice information in the brain (Bode et al., 2011; Lages and Jaworska, 2012).
Another recent study demonstrated the encoding of guesses about low discriminability stimuli in posterior parietal brain regions, using a similar paradigm to ours (Bode et al., 2012). Our findings allow guessing to be reinterpreted as a reflection of the state of the decision system before evidence accumulation. When discriminability is high, sensory evidence in ventral visual pathways will dominate the decision process, consistent with the finding of strong information encoding over visual regions in our study. When discriminability is very low, medial parietal regions, as well as medial prefrontal regions, may become informative about decision outcomes, because the recent choice history might prime the decision system and magnify choice-related preexisting activity. Consistent with this hypothesis, areas in prefrontal cortex and posterior parietal cortex (Heekeren et al., 2004; Philiastides et al., 2011; Ploran et al., 2011), predominantly in monkey parietal area LIP, have been linked theoretically to diffusive information accumulation (Shadlen and Newsome, 2001; Mazurek et al., 2003; Gold and Shadlen, 2007), decision confidence (Kiani and Shadlen, 2009), as well as to the representation of generic categorical associations (Fitzgerald et al., 2011). Our EEG-decoding approach lacks the spatial resolution to identify the sources of information encoding precisely. Nevertheless, the high decoding accuracy in prefrontal and occipitoparietal channels at the beginning of pure noise trials supports the hypothesis that this activity could be related to the memory of participants' previous choices—and thus the trial-by-trial setting, or initialization, of decision parameters.
In summary, using an EEG decoding approach, we directly decoded choice-predictive information from neural activity before stimulus presentation on pure noise trials on which no discriminative information was present. Choice behavior on these trials was shown to be primed by the recent choice history. Modeling of sequential effects in RT and accuracy confirmed that such choice priming biased the starting point of a diffusion process toward a decision boundary, as conceptualized in evidence accumulation models of perceptual decision making.
Footnotes
This work was supported by the University of Cologne, The University of Melbourne, and an Early Career Researcher Grant of The University of Melbourne to S.B. We thank Miriam Kresimon and Bernd Kuderer for help with data acquisition. We thank Carsten Bogler, Carsten Murawski, Ryan Maloney, and Anna He for helpful discussions.
The authors declare no competing financial interests.
References
- Bai O, Lin P, Vorbach S, Li J, Furlani S, Hallett M. Exploration of computational methods for classification of movement intention during human voluntary movement from single trial EEG. Clin Neurophysiol. 2007;118:2637–2655. doi: 10.1016/j.clinph.2007.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blankertz B, Lemm S, Treder M, Haufe S, Müller KR. Single-trial analysis and classification of ERP components—A tutorial. Neuroimage. 2011;56:814–825. doi: 10.1016/j.neuroimage.2010.06.048. [DOI] [PubMed] [Google Scholar]
- Bode S, He AH, Soon CS, Trampel R, Turner R, Haynes JD. Tracking the unconscious generation of free decisions using ultra-high field fMRI. PLoS ONE. 2011;6:e21612. doi: 10.1371/journal.pone.0021612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bode S, Bogler C, Soon CS, Haynes JD. The neural encoding of guesses in the human brain. Neuroimage. 2012;59:1924–1931. doi: 10.1016/j.neuroimage.2011.08.106. [DOI] [PubMed] [Google Scholar]
- Boly M, Balteau E, Schnakers C, Delgueldre C, Moonen G, Luxen A, Phillips C, Peigneux P, Maquet P, Laureys S. Baseline brain activity fluctuations predict somatosensory perception in humans. Proc Natl Acad Sci U S A. 2007;104:12187–12192. doi: 10.1073/pnas.0611404104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Lin CJ. LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol. 2011;2:1–27. [Google Scholar]
- Das K, Giesbrecht B, Eckstein MP. Predicting variations of perceptual performance across individuals from neural activity using pattern classifiers. Neuroimage. 2010;51:1425–1437. doi: 10.1016/j.neuroimage.2010.03.030. [DOI] [PubMed] [Google Scholar]
- Deco G, Romo R. The role of fluctuations in perception. Trends Neurosci. 2008;31:591–598. doi: 10.1016/j.tins.2008.08.007. [DOI] [PubMed] [Google Scholar]
- Fitzgerald JK, Freedman DJ, Assad JA. Generalized associative representations in parietal cortex. Nat Neurosci. 2011;14:1075–1090. doi: 10.1038/nn.2878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forstmann BU, Brown S, Dutilh G, Neumann J, Wagenmakers EJ. The neural substrate of prior information in perceptual decision making: a model-based analysis. Front Hum Neurosci. 2010;4:40. doi: 10.3389/fnhum.2010.00040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J, Wong-Lin K, Holmes P, Simen P, Cohen JD. Sequential effects in two-choice reaction time tasks: decomposition and synthesis of mechanisms. Neural Comput. 2009;21:2407–2436. doi: 10.1162/neco.2009.09-08-866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gevins A. Dynamic functional topography of cognitive tasks. Brain Topogr. 1989;2:37–56. doi: 10.1007/BF01128842. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- Gratton G, Coles MG, Donchin E. A new method for off-line removal of ocular artifact. Electroencephalogr Clin Neurophysiol. 1983;55:468–484. doi: 10.1016/0013-4694(83)90135-9. [DOI] [PubMed] [Google Scholar]
- Haxby JV, Gobbini MI, Furey ML, Ishai A, Schouten JL, Pietrini P. Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science. 2001;293:2425–2430. doi: 10.1126/science.1063736. [DOI] [PubMed] [Google Scholar]
- Haynes JD, Rees G. Decoding mental states from brain activity in humans. Nat Rev Neurosci. 2006;7:523–534. doi: 10.1038/nrn1931. [DOI] [PubMed] [Google Scholar]
- Heekeren HR, Marrett S, Bandettini PA, Ungerleider LG. A general mechanism for perceptual decision-making in the human brain. Nature. 2004;431:859–862. doi: 10.1038/nature02966. [DOI] [PubMed] [Google Scholar]
- Hesselmann G, Kell CA, Eger E, Kleinschmidt A. Spontaneous local variations in ongoing neural activity biases perceptual decisions. Proc Natl Acad Sci U S A. 2008a;105:10984–10989. doi: 10.1073/pnas.0712043105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hesselmann G, Kell CA, Kleinschmidt A. Ongoing activity fluctuations in hMT+ bias the perception of coherent visual motion. J Neurosci. 2008b;28:14481–14485. doi: 10.1523/JNEUROSCI.4398-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hesselmann G, Sadaghiani S, Friston KJ, Kleinschmidt A. Predictive coding or evidence accumulation? False inference and neural fluctuations. PLoS ONE. 2010;5:e9926. doi: 10.1371/journal.pone.0009926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanwisher N, McDermott J, Chun MM. The fusiform face area: a module in human extrastriate cortex specialized for face perception. J Neurosci. 1997;17:4302–4311. doi: 10.1523/JNEUROSCI.17-11-04302.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katznelson RD. EEG recording, electrode placement, and aspects of generator localization. In: Nunez PL, editor. Electric fields of the brain. Oxford: Oxford UP; 1981. [Google Scholar]
- Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science. 2009;324:759–764. doi: 10.1126/science.1169405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lages M, Jaworska K. How predictable are “spontaneous decisions” and “hidden intentions”? Comparing classification results based on previous responses with multivariate pattern analysis of fMRI BOLD signals. Front Psychol. 2012;3:56. doi: 10.3389/fpsyg.2012.00056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luce RD. Response times. New York: Oxford UP; 1986. [Google Scholar]
- Luck SJ. An introduction to the event-related potential technique. Cambridge: MIT; 2005. [Google Scholar]
- Maljkovic V, Nakayama K. Priming of pop-out: I. Role of features. Mem Cognit. 1994;22:657–672. doi: 10.3758/bf03209251. [DOI] [PubMed] [Google Scholar]
- Mazurek ME, Roitman JD, Ditterich J, Shadlen MN. A role of neural integrators in perceptual decision making. Cereb Cortex. 2003;13:1257–1269. doi: 10.1093/cercor/bhg097. [DOI] [PubMed] [Google Scholar]
- Op de Beeck HP, Haushofer J, Kanwisher NG. Interpreting fMRI data: maps, modules and dimensions. Nat Rev Neurosci. 2008;9:123–135. doi: 10.1038/nrn2314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira F, Mitchell T, Botvinick M. Machine learning classifiers and fMRI: a tutorial overview. Neuroimage. 2009;45(1 Suppl):S199–S209. doi: 10.1016/j.neuroimage.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pernier J, Perrin F, Bertrand O. Scalp current density fields: concepts and properties. Electroencephalogr Clin Neurophysiol. 1988;69:385–389. doi: 10.1016/0013-4694(88)90009-0. [DOI] [PubMed] [Google Scholar]
- Perrin F, Bertrand O, Pernier J. Scalp current density mapping: value and estimation from potential data. IEEE Trans Biomed Eng. 1987;34:283–288. doi: 10.1109/tbme.1987.326089. [DOI] [PubMed] [Google Scholar]
- Perrin F, Pernier J, Bertrand O, Echallier JF. Spherical splines for scalp potential and current density mapping. Electroencephalogr Clin Neurophysiol. 1989;72:184–187. doi: 10.1016/0013-4694(89)90180-6. [DOI] [PubMed] [Google Scholar]
- Philiastides MG, Sajda P. Temporal characterization of the neural correlates of perceptual decision making in the human brain. Cereb Cortex. 2006;16:509–518. doi: 10.1093/cercor/bhi130. [DOI] [PubMed] [Google Scholar]
- Philiastides MG, Ratcliff R, Sajda P. Neural representation of task difficulty and decision making during perceptual categorization: a timing diagram. J Neurosci. 2006;26:8965–8975. doi: 10.1523/JNEUROSCI.1655-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philiastides MG, Auksztulewicz R, Heekeren HR, Blankenburg F. Causal role of dorsolateral prefrontal cortex in human perceptual decision making. Curr Biol. 2011;21:980–983. doi: 10.1016/j.cub.2011.04.034. [DOI] [PubMed] [Google Scholar]
- Platt ML, Glimcher PW. Neural correlates of decision variables in parietal cortex. Nature. 1999;400:233–238. doi: 10.1038/22268. [DOI] [PubMed] [Google Scholar]
- Ploran EJ, Tremel JJ, Nelson SM, Wheeler ME. High quality but limited quantity perceptual evidence produces neural accumulation in frontal and parietal cortex. Cereb Cortex. 2011;21:2650–2662. doi: 10.1093/cercor/bhr055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychol Rev. 1978;85:59–108. [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 2008;20:873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: approaches of dealing with contaminant reaction times and parameter variability. Psychon Bull Rev. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Philiastides MG, Sajda P. Quality of evidence for perceptual decision making is indexed by trial-to-trial variability of the EEG. Proc Natl Acad Sci U S A. 2009;106:6539–6544. doi: 10.1073/pnas.0812589106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remington RJ. Analysis of sequential effects in choice reaction times. J Exp Psychol. 1969;82:250–257. doi: 10.1037/h0028122. [DOI] [PubMed] [Google Scholar]
- Rolls ET, Deco G. Predictions of decisions from noise in the brain before the evidence is provided. Front Neurosci. 2011;5:33. doi: 10.3389/fnins.2011.00033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schölvinck ML, Friston KJ, Rees G. The influence of spontaneous activity on stimulus processing in primary visual cortex. Neuroimage. 2012;59:2700–2708. doi: 10.1016/j.neuroimage.2011.10.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J Neurophysiol. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends Neurosci. 2004;27:161–168. doi: 10.1016/j.tins.2004.01.006. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. An integrated theory of attention and decision making in visual signal detection. Psychol Rev. 2009;116:283–317. doi: 10.1037/a0015156. [DOI] [PubMed] [Google Scholar]
- Soon CS, Brass M, Heinze HJ, Haynes JD. Unconscious determinants of free decisions in the human brain. Nat Neurosci. 2008;11:543–545. doi: 10.1038/nn.2112. [DOI] [PubMed] [Google Scholar]
- Supèr H, van der Togt C, Spekreijse H, Lamme VA. Internal state of monkey primary visual cortex (V1) predicts figure-ground perception. J Neurosci. 2003;23:3407–3414. doi: 10.1523/JNEUROSCI.23-08-03407.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuerlinckx F. The efficient computation of the cumulative distribution and probability density functions in the diffusion model. Behav Res Methods Instrum Comput. 2004;36:702–716. doi: 10.3758/bf03206552. [DOI] [PubMed] [Google Scholar]