Adaptation Paths to Novel Motor Tasks Are Shaped by Prior Structure Learning

Abstract

After extensive practice with motor tasks sharing structural similarities (e.g., different dancing movements, or different sword techniques), new tasks of the same type can be learned faster. According to the recent “structure learning” hypothesis (Braun et al., 2009a), such rapid generalization of related motor skills relies on learning the dynamic and kinematic relationships shared by this set of skills. As a consequence, motor adaptation becomes constrained, effectively leading to a dimensionality reduction of the learning problem; at the same time, adaptation to tasks lying outside the structure becomes biased toward the structure. We tested these predictions by investigating how previously learned structures influence subsequent motor adaptation. Human subjects were making reaching movements in 3D virtual reality, experiencing perturbations either in the vertical or in the horizontal plane. Perturbations were either visuomotor rotations of varying angle or velocity-dependent forces of varying strength. We found that, after extensive training with both kinematic or dynamic perturbations, adaptation to unpracticed, diagonal, perturbations happened along the previously learned structure (vertical or horizontal), and resulting adaptation trajectories were curved. This effect is robust, can be observed on the single-subject level, and occurs during adaptation both within and across trials. Additionally, we demonstrate that structure learning changes involuntary visuomotor reflexes and therefore is not exclusively a high-level cognitive phenomenon.

Introduction

The human motor system controls a large number of independent degrees of freedom simultaneously and is capable of learning a seemingly infinite amount of movement skills, vastly surpassing such abilities of any man-made robot (Bernstein, 1967; Shadmehr and Wise, 2005). The computational and neuronal mechanisms of human dexterity and adaptation abilities remain elusive. It has been recently suggested that one of the computational brain mechanisms allowing such a rich movement repertoire might be structure learning (Braun et al., 2009a; Shadmehr et al., 2010; Krakauer and Mazzoni, 2011; Wolpert et al., 2011). Structure learning in this context means learning the similarity of related motor tasks, thus constraining the distribution of likely control parameters and effectively reducing the dimensionality of the control problem (see Fig. 1; discussed below). As a consequence, later adaptation to any motor task belonging to the same structure will be facilitated. Motor skills are never learned in isolation and natural motor tasks are highly structured: when as babies we learn to grasp or when as adults we learn to dance, we have to master a rich set of different, but related, movements, performed in various contexts and postures. The longer one is training, the faster one can acquire new skills of the same type—a phenomenon known as learning to learn. Structure learning is a computational mechanism that can explain the ability of learning to learn (Braun et al., 2010).

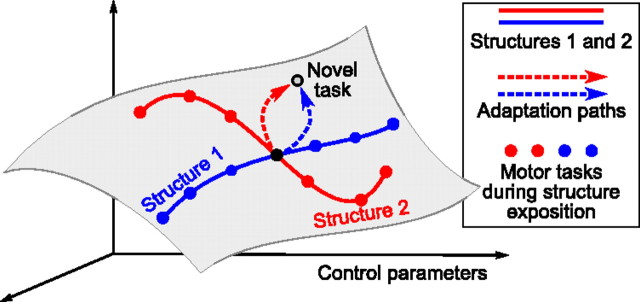
Figure 1.

Structure learning hypothesis predicts bent adaptation paths. Consider a space of control parameters needed to solve different motor tasks. According to the hypothesis of structure learning, adaptation from a certain task (black filled circle) to another task (empty circle) depends on what motor tasks were practiced before (belonging to the red or to the blue structure). The gray manifold represents the parameter subspace relevant for a particular experiment.

It has been shown that structure motor learning can indeed occur when learning visuomotor rotations (Braun et al., 2009a), independent of the exact training regime (Turnham et al., 2012). It has also been shown that structure learning leads to optimal feedback corrections (Braun et al., 2009b) and modifies prior expectations about sensorimotor transformations (Turnham et al., 2011). In addition to being discussed as a theory of motor learning (Shadmehr et al., 2010; Krakauer and Mazzoni, 2011; Wolpert et al., 2011), structure learning might also play a pivotal role in human perception and cognition (Gershman and Niv, 2010; Tenenbaum et al., 2011). In this study, we present new experimental evidence for the structure learning hypothesis and in three experiments address three different questions.

First, does structure learning influence adaptation to novel tasks that were never practiced during training, and in particular to novel tasks that lie outside of the learned structure (Fig. 1)? Second, is structure motor learning a genuine feature of motor control or is it a cognitive phenomenon? Third, does structure learning play a role in learning dynamic tasks? Natural motor tasks often involve precise force control (e.g., steering a bicycle wheel, returning a tennis ball with a racket, or leading a partner in tango); structure motor learning, however, has so far been investigated using only kinematic tasks.

Materials and Methods

Thirty-four naive volunteers (23 males and 11 females) participated in this study. Subjects gave informed consent and were paid for participation. All experiments received ethics approval by Imperial College London.

Experimental setup.

Subjects were looking in 3D glasses (NVIS nVisor SX) and were operating a handle of a 3D manipulandum (Sensable Phantom 1.5 HF) to move a cursor in virtual reality space (see Fig. 2A). 3D glasses were tilted downward by ∼30° so that subjects could lean on them with their forehead. Phantom movements were also tilted by 30°, and to move the cursor along the z-axis subjects had to move their hand 30° downward (these tilts are not shown in Fig. 2A). Subjects were told to hold the Phantom handle as they normally hold a pen, and we made sure that their arm was moving freely during the experiment (i.e., it was not lying on the knee). All the distances given below are measured in hand space.

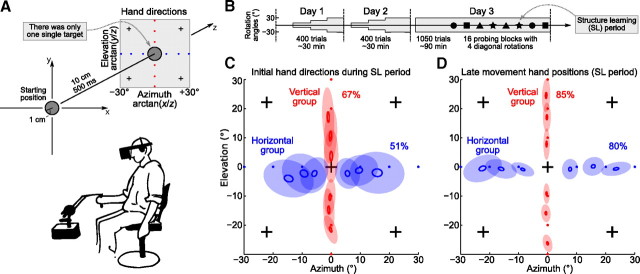
Figure 2.

Visuomotor experiment. A, Subjects were instructed to make fast straight movements between a starting position and a single target (there were no other targets used throughout the experiment). One group of subjects experienced horizontal, and another group vertical, visuomotor rotations, with the angle of rotation randomly chosen from the set {±30, ±20, ±10°} in blocks of five trials (structure learning period). For this and subsequent figures, hand directions were transformed into azimuth-elevation coordinates; the blue (red) dots show ideal hand directions corresponding to different horizontal (vertical) visuomotor rotations. The crosses correspond to visuomotor rotations used for probing after 3 days of training. Below, A subject is holding 3D manipulandum and wearing 3D glasses. B, Paradigm scheme, showing 3 days of experiment (see Materials and Methods). The shaded area shows the exposure to horizontal/vertical rotations, with its width corresponding to the maximal rotation angle (first 10°, then 20°, then 30°). Four different geometric symbols represent four different diagonal rotations used for probing (4 times each). C, Initial hand directions measured at 200 ms after movement onset, on the fifth trial of every structure learning block on the third day of training before probing, in blue for the horizontal group and in red for the vertical one (group averages). The small empty ellipses show SEM, and the large filled ones show SD (N = 30 for each ellipse). The average amount of adaptation for each group is shown as a percentage value. D, The same as above, but for the late movement hand positions, measured at 400 ms after movement onset.

Task.

Subjects had to make repeated straight movements from a starting position to a single target and then back (see Fig. 2A). Throughout all experiments, there was only one single target used, located 10 cm away along the z-axis (radius 1 cm). Subjects were instructed to make movements back and forth between the starting position and this single target as straight as possible and reach the target in the time window of 400–600 ms. They heard a low beep if the movement was too slow and a high beep if it was too fast, but all trials were used for the analysis, regardless of their movement duration. After the target appeared, subjects had to wait for the go cue (target color change) for a random time between 500 and 1000 ms before starting the movement. If they started the movement (speed exceeded 4 cm/s) before the go cue, they had to return to the starting position and start the trial again. To end the trial, subjects had to position the center of the cursor inside the target for 500 ms.

Data recording and analysis.

All position and force data were recorded in some sessions with 200 Hz and in some sessions with 60 Hz. We resampled all the data to 100 Hz with cubic spline interpolation, and then low-passed it with 10 Hz cutoff (third-order Butterworth filter). Velocity was calculated from the resulting position data by a difference filter. Movement onset was detected for every trial as a time point when the speed first exceeded 4 cm/s (excluding false starts before the go cue). Initial movement direction was measured as the difference between hand position at movement onset and hand position 200 ms afterward. For comparison, maximum speed in the first experiment was reached on average (±SD) at 238 ± 65 ms. Late movement hand position was measured at 400 ms after movement onset.

Experiment 1 (visuomotor rotations): paradigm.

One group of six subjects was trained with horizontal visuomotor rotations, and another group of six subjects with vertical ones (see Fig. 2A). We call a rotation “horizontal” when the cursor displacement happened in the horizontal plane (note that this is a rotation around the vertical axis), and vice versa for the “vertical” rotations. For both groups, the angle of rotation was changed in blocks of five trials, pseudorandomly selected from the set of {0, ±10, ±20, ±30°}. The experiment went on for 3 consecutive days to increase the amount of training before the probing phase on day 3 (for a scheme, see Fig. 2B). On day 1, subjects had to complete 100 standard trials to familiarize themselves with the setup, and then the learning started with maximum rotation angle increasing by 10° every 100 trials, so that the full range of angles was covered only during trials 300–400 (total number of trials on day 1 was 400). Day 2 followed the same scheme but with the familiarization block reduced to 30 trials (total number of trials, again 400); it took subjects ∼30 min to complete the sessions on the first 2 days. The experimental session on day 3 consisted of 1050 trials with short breaks after every 210 trials and took subjects around ∼1.5 h to complete. Structure exposition with horizontal/vertical rotations continued throughout the session, interspersed with 16 probing blocks (the first probing block occurred only after the first 250 trials were over). Each probing block consisted of 5 trials with a constant diagonal rotation and was preceded by 10 and followed by 5 washout trials (no rotation). We used 4 different diagonal rotations (±30° for two diagonal axes; see Fig. 2A), and each of them was presented 4 times in pseudorandom order (16 probing blocks in total). Full range of horizontal/vertical rotation angles was covered between every two probing blocks (30 trials).

The pseudorandom sequence of rotation angles was constrained such that no change of angle between subsequent blocks was >30°, to prevent large switches of rotation that could be confusing to subjects. This led to block-to-block lag 1 autocorrelation of 0.55 and trial-to-trial lag 1 autocorrelation of 0.91 (measured on day 3, when the full range of rotations from −30 to 30° was covered). As rotation angle was fixed during each block of five trials, trial-to-trial autocorrelation was much higher than block-to-block one.

Experiment 1 (visuomotor rotations): analysis.

When plotting movement directions (see Figs. 2–4), we transformed them into azimuth-elevation coordinates (see Fig. 2A). The azimuth angle was calculated as arctan(x/z) and the elevation angle as arctan(y/z); see Figure 2A for axes conventions. In the range of angles used in this study, our elevation is only slightly different from the one usually used in spherical coordinates and given by arcsin(y/r). We used our definition to make the transformation symmetric for x and y; as a result, diagonal rotation of 30° was transformed into (22.2, 22.2°).

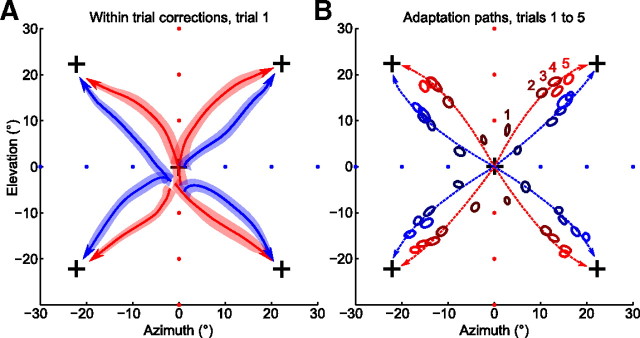
Figure 3.

Adaptation paths are bent toward the learned structure. A, Movement trajectories during the first trial of every probing block, in blue for the horizontal and in red for the vertical group (group averages). Each trajectory starts near (0, 0) because the diagonal rotation was switched on unexpectedly for subjects, and ends near the corresponding cross because subjects had to reach the target to finish the trial. Trajectories are taken from 200 ms after movement onset until the moment when cursor entered the target. The colored bands around average trajectories show SEM; N = 24 for each trajectory. B, Late movement hand positions (400 ms after movement onset) across probing trials, with color (dark to light) showing trial number (1–5) during a probing block. Hand positions for every probing direction and every trial number are significantly different between groups (20 comparisons) (for a scheme of statistical testing, see Fig. 4F): p < 0.001 for 17 pairs, p < 0.01 for 1 pair, p < 0.05 for another 2 pairs. The dashed lines show trajectories corresponding to exponential fits calculated separately for the adaptation of azimuth and elevation (for details, see Materials and Methods).

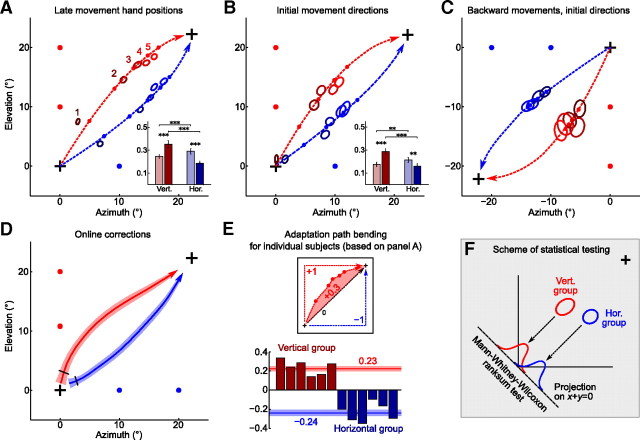
Figure 4.

Adaptation paths are bent toward the learned structure (continued). A, Across-trial adaptation of late movement hand positions: the same data as presented in Figure 3B, but flipped to the first quadrant and averaged over directions (group averages). Ellipses show SEM (N = 96 for each ellipse), with color (dark to light) showing trial number (1–5) during a probing block. The difference between groups is significant for every trial (p < 10⁻¹⁰). The dashed lines show trajectories corresponding to the exponential fits, with small dots on the dashed line showing the positions on trials 1–5, according to the fit. The inset shows learning speeds for both groups with light (dark) bars corresponding to azimuth (elevation) learning speeds. Learning speed is defined as amount of error (from 0 to 1) corrected on each subsequent trial. The asterisks show statistical significance (for details, see Materials and Methods), with three asterisks meaning p < 0.001. B, The same as A, but for initial movement directions (200 ms after movement onset). For trials 2–5, difference between groups is significant with p < 0.001. Two asterisks in the inset mean p < 0.01. C, The same as B, but for initial directions of backward movements. Here, the data were flipped to the third quadrant only for convenience, to show that these are backward movements. Difference between groups is significant for each trial with p < 10⁻⁵. D, Movement trajectories during the first trial, averaged over directions. The black ticks show the time point when the difference between groups becomes significant with p < 0.05. E, For every subject, we computed the degree of bending, calculated as a normalized area between late movement adaptation path and the straight diagonal path. These values are shown for six subjects in the vertical and six subjects in the horizontal group. The horizontal lines show mean value for each group (printed nearby in respective colors) together with SEM. F, Scheme of statistical testing for differences between groups, used in A–D. The data were first projected on a line perpendicular to the perturbation, and then Mann–Whitney–Wilcoxon rank sum test was performed. This way, we were only assessing the difference in bending of adaptation paths, and not in the learning speed.

When plotting adaptation paths (see Figs. 3, 4), we subtracted baseline movement directions for every subject. The baseline value was calculated as the average over the last 5 trials of every 10 trial washout block preceding probing blocks. The average (±SD) baseline initial direction over subjects in azimuth-elevation coordinates was (−0.1 ± 0.9, −2.8 ± 4.5°), so the baseline elevation tended to be slightly negative (reaching −9 and −12° for two subjects). For every subject, we subtracted this value from all initial direction values. The same was done for late movement hand positions as well, even though here the baselines were almost negligible: (−0.1 ± 0.5, 0.0 ± 1.3°). When analyzing backward movements, we also did baseline correction and had to exclude one of the subjects who made extremely curved backward movements (baseline elevation, 46°). Other subjects had initial direction baselines of (0.1 ± 1.0, 0.0 ± 3.0°).

To plot movement trajectories, we transformed each trajectory taken from 200 ms after movement onset until entering the target into the azimuth-elevation coordinates, resampled the resulting trajectory with cubic splines to 20 points equally spaced in time, and then averaged across trials and subjects. To represent the uncertainty, we took the SEM along the direction of largest variance for every point and plotted it perpendicular to the trajectory (see Figs. 3A, 4D). No baseline correction was done for the trajectories, and one can see on Figure 3A that trajectories tend to start below (0, 0), corresponding to the negative baseline elevation.

Experiment 1 (visuomotor rotations): exponential fits and bootstrapping.

To fit trajectories to adaptation paths (shown with dashed lines on Figs. 3B and 4), we made exponential fits to learning curves separately in azimuth and elevation directions, and then plotted the corresponding trajectory. The sequence of errors was fitted with the following formula: e_i(t) = Rexp(−(t − d − 1)/k_i), where i stands for either azimuth or elevation, t is the trial number changing from 1 to 5, R is the azimuth/elevation of the rotation angle (22.2°), d is the offset, and k_i are time constants. For the initial direction fits, the offset d was set to zero. We defined the learning speed λ_i as the amount of error (from 0 to 1) corrected on each subsequent trial; straightforward calculation shows that λ_i = 1 − exp(−1/k_i). The least-squares fit (using the Levenberg–Marquardt algorithm implemented in the MATLAB nlinfit function) was done on the nonaveraged data, and the insets in Figure 4, A and B, show learning speeds λ_i together with 95% confidence intervals.

Note that we follow the definition of learning speed used in the study by van Beers (2009). Sometimes learning speed is defined simply as 1/k_i (and has then the dimension of trial⁻¹), as for example in the study by Huang et al. (2011). Although in the typical range of learning speeds (0.1–0.5) the resulting values are close to each other, they are still slightly different and should not be confused.

To assess statistical significance of difference between two learning speeds (for example, azimuth and elevation learning speeds for the same group, or azimuth learning speeds between the two groups), we used the bootstrapping technique. To calculate p values, we joined all the values from two datasets and drew with replacement the same amount of values for two bootstrapped datasets from the resulting distribution (this was done separately for trials 1–5). Then we fitted the exponents, calculated the learning speeds, and repeated this procedure 5000 times. The p value equals the proportion of times when the difference between the resulting learning speeds is larger than the difference obtained from the real data. These values are shown with asterisks in the insets in Figure 4, A and B.

Experiment 2 (involuntary reflexes).

Experiment 2 consisted of the same training as Experiment 1 but a different probing phase on day 3. It was performed by eight new subjects and seven subjects who had already participated in Experiment 1 and who just did an additional experimental session (four of them performed it on the next day after finishing the Experiment 1, and for three of them it was a month later); we did not find a difference between the reflex forces of the new and the initial subjects (see Fig. 5C, inset; the seven initial subjects are represented by the first four bars in the vertical group, and the first three bars in the horizontal group).

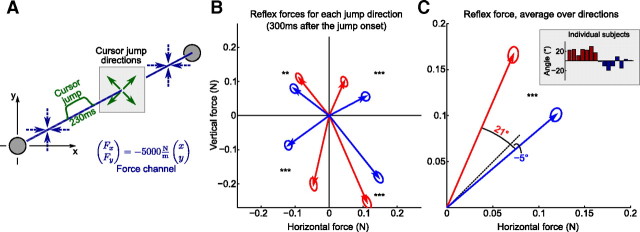
Figure 5.

Cursor jump experiment. A, Subject makes a movement to the target in a “force channel” (blue), with the manipulandum exerting very strong returning forces preventing any deviations from the z-axis. At 3 cm from the origin, cursor was for 230 ms displaced in one of the diagonal directions but still moved in parallel to the z-axis according to the hand movement. The force channel allows to record forces that subjects exert on the channel walls in reaction to the cursor jump. B, Average reaction force at 300 ms after the jump onset for all four jump directions (group averages). Ellipses show SEM (N_HOR = 192 and N_VERT = 168 for each ellipse). The asterisks indicate the statistical significance of the difference between groups, with two asterisks meaning p < 0.01 and three asterisks meaning p < 0.001 (for a scheme of statistical test, see Fig. 4F). C, The same data as on the previous panel, flipped to the first quadrant and averaged over directions (p < 10⁻¹⁷; N_HOR = 768 and N_VERT = 672). The angular values show deviation of the average force responses from the diagonal. The inset shows these angular values for individual subjects (obtained via circular median).

On the probing day, the structure exposition (horizontal/vertical rotations) continued throughout the session, interspersed with eight probing batches. Each probing batch consisted of 18 error-clamp trials and was always preceded by 10 washout trials. During an error-clamp trial subjects' movements were clamped in X and Y directions, so that they could only move along the z-axis directly to the target (see the full description below). During some of the clamped trials, after the cursor crossed 3 cm distance from the starting position, the cursor was smoothly but very quickly displaced away from the z-axis and was then moved in parallel to it for 130 ms before returning back (with total displacement time being 230 ms) (see Fig. 5A). Probing trials were administered in batches of 18 error-clamp trials with 40 trials in between probing batches; each batch was a pseudorandom sequence of three jumps in each of the four diagonal directions and six error-clamp trials without a jump (see Fig. 5A). We took care that two jumps in the same direction never happened in a row, and the pseudorandom sequence was different in each probing batch. Every subject experienced 8 of the 18 trial probing batches (i.e., in total 96 trials with cursor jumps, with 24 of them in each direction).

We recruited additional eight subjects to measure their voluntary reaction time. These subjects had an additional experimental session after the rest of the experiment; this session consisted solely of 10 probing batches (exactly the same as before), and subjects were instructed to exert some force in the direction of the cursor jump as soon as possible after they saw a jump. After a subject reached the target and stayed there for 500 ms, the force channel was abruptly switched off and subject's hand made a swinging movement to the side in the direction of the cursor jump. We disregarded the first two probing batches as subjects needed to familiarize themselves with the task and used only the last eight of them for our analysis.

To plot the average reflex forces (see Fig. 5B,C), we did a subject-wise baseline correction by subtracting the average force produced in the error-clamp trials without cursor jumps [average across subjects: (0.00 ± 0.03, −0.01 ± 0.07) N]. When analyzing the temporal force profiles (see Fig. 6), we did a trial-wise baseline correction, for every trial subtracting the average force during the 50–150 ms interval after the beginning of cursor jump. According to the manufacturer, the 3D glasses have a temporal lag of 16 ms, and we made the corresponding correction for the data presented on Figure 6. All significance tests and calculations of reaction times were done with the unsmoothed data resampled to 1000 Hz.

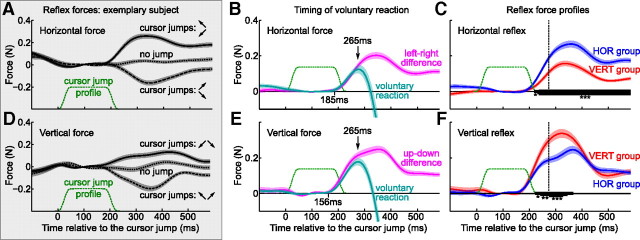
Figure 6.

Timing of force response to cursor jumps. A, Exemplary subject; horizontal force exerted as a reaction to the cursor jumps in the top-left/bottom-left (solid line) and in the top-right/bottom-right (dashed line) directions. The dotted line shows the force during no-jump trials. All of the data are aligned on the jump onset, and the cursor jump profile is shown as a green dashed line (out of vertical scale). N = 48 for each curve. B, The magenta line shows the difference between horizontal forces after cursor jumps in the top-left/bottom-left and in the top-right/bottom-right directions (i.e., between solid and dashed lines in A). Difference was computed for each subject and probing batch, and then averaged over batches and subjects (N = 64 for each curve). The cyan line shows the same, but after the subjects were instructed to push in the direction of the cursor jump. An arrow at 265 ms depicts the voluntary reaction time. A tick at 185 ms marks the beginning of the reflex response (p < 0.05 difference from the baseline, one-sided t test). C, Difference between horizontal forces after cursor jumps in the top-left/bottom-left and in the top-right/bottom-right directions (calculated for each subject and probing batch and averaged over subjects in each group; N_HOR = 64 and N_VERT = 56). The horizontal group is shown in blue, and the vertical group, in red. The thick black lines show the time interval of significant difference between groups (*p < 0.05; **p < 0.01; ***p < 0.001). D–F, The same as A–C for the vertical force.

Experiment 3 (force fields).

This was a variation of the visuomotor experiment with velocity-dependent force fields used instead of visuomotor rotations. One group of eight subjects was trained with horizontal force fields, and another group of six subjects with vertical ones (see Fig. 7A). During a force field trial, there was a force exerted on the subject's hand proportional to subject's velocity along the z-axis; the coefficient of proportionality we call “force gain.” This force always acted in the plane perpendicular to the movement direction and was applied only after movement onset (see Fig. 7A). For both groups, the gain was changed in blocks of five trials, pseudorandomly selected from the set of {0, ±2, ±4, ±6, ±8, ±10} N · s/m (with no switches larger than 4 N · s/m; resulting block-to-block lag 1 autocorrelation, 0.85; trial-to-trial lag 1 autocorrelation, 0.97). The peak speed during the movements was ∼0.25 m/s, so subjects experienced average peak forces up to ∼2.5 N.

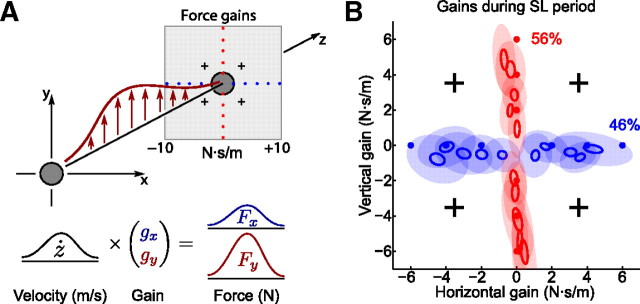
Figure 7.

Force field experiment. A, Subjects were making fast straight movements between two targets, this time experiencing different horizontal or vertical force fields instead of visuomotor rotations. Force was proportional to the velocity along the z-axis, and the gain changed between ±10 N · s/m in blocks of five trials. The red and blue dots on the plane of gains show the gains used for the vertical and horizontal structures. The crosses mark the gains used for probing. B, Gains used by the subjects on the last trial of every block during the structure learning period on the third day (estimated with error-clamp trials) (see Results). The small open ellipses show SEM for group averages, and the large filled ellipses show SD, in blue for the horizontal and in red for the vertical group (N_HOR = 18 and N_VERT = 12 for each ellipse). Note that, on this panel, the axes do not go until 10 N · s/m, and the average adaptation is only ∼50%.

To probe subjects' internal model, we used an error-clamp technique (Scheidt et al., 2000; Smith et al., 2006). During an error-clamp trial subjects' movements were restricted in X and Y directions by the manipulandum, which was applying a returning force of a very stiff spring (spring constant k = 5000 N/m) whenever subject tried to deviate from the Z direction. The force was applied only after movement onset. As a result, subjects moved in a “channel” leading the hand straight to the target, and deviation from the z-axis did not exceed 1 mm (due to specifics of our experimental software, the force channel started working only ∼50 ms after movement onset). We assumed that the restoring force applied by the manipulandum was equal to the force with which subject was pressing on the channel walls. For every error-clamp trial, we estimated subject's horizontal/vertical gains by regressing the horizontal/vertical force outputs to the velocity profile between force onset and the moment of target disappearance (or the moment when the cursor left the target for the first time, if that was earlier) (see Fig. 7A). As during error-clamp trials lateral deviations from straight movement are negligible, these trials are known not to interfere with the learning process (Scheidt et al., 2000).

Before the probing phase (i.e., during random horizontal/vertical force field exposure), the last trial of every block (every fifth trial) was error clamped. The experiment went on for 3 consecutive days, exactly as the visuomotor experiment, with ∼30 min sessions on the first 2 days and ∼1.5 h session on day 3 with short breaks every ∼15 min. The session on the last day consisted of continuing exposure to the horizontal/vertical force fields, interspersed with four probing batches. Each probing batch (always preceded by a 10 trial washout) consisted of 20 probing “triplets” (Sing et al., 2009) with three to five washout trials in between. Each triplet consisted of an error-clamp trial without any additional force field, followed by a velocity-dependent force field trial with a force in one of the four diagonal direction and a gain of 5 N · s/m, and another error-clamp trial without additional force field. Every subject experienced 80 of these probing triplets in total, with 20 of them in each diagonal direction. Across the 20 probing triplets within a probing batch, the sequence of diagonal force directions was pseudorandom with two succeeding triplets always having different force directions.

Of 14 recorded subjects, 4 were excluded from the analysis (see Figs. 7, 8), as they did not show consistent learning during the training phase. In contrast to the 10 “good” subjects (see Fig. 7B), these 4 subjects showed highly asymmetric adaptation patterns during the training phase, with force responses strongly biased upward (2 subjects in the vertical group) or rightward (2 subjects in the horizontal group). To quantify this asymmetry for every subject, we calculated the adaptation value (see Fig. 7B) separately for the forces up and down (left and right) and took the ratio of these values as the “skewness of adaptation” index. For the 10 good subjects, this index was 1.3 ± 0.2 (average ± SD), and for the 4 excluded subjects, it was 3, 4, 5, and 20. As a consequence, these subjects showed poor adaptation during probing, with two of them showing no adaptation at all. However, even if these subjects were included in our analysis, the average results would have stayed the same: structure-specific differences in adaptation between the two groups (see Fig. 8B) remain highly significant (p < 10⁻⁷).

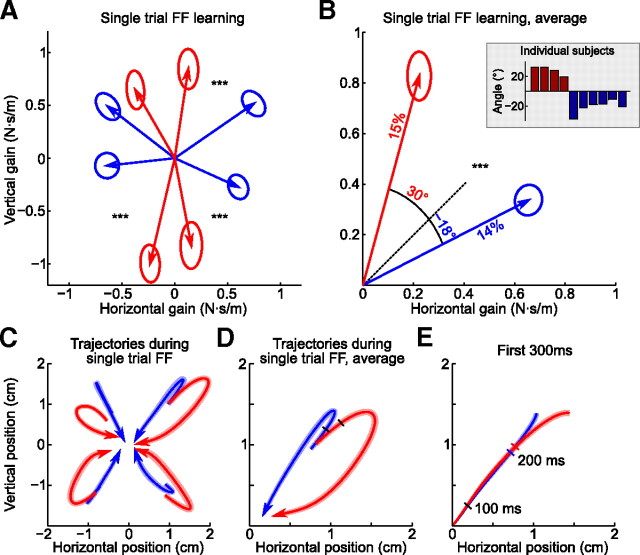
Figure 8.

Effects of structure learning on single-trial force field learning. A, The result of single-trial force field learning for both groups and four diagonal force directions (group averages). Diagonal force field trials were always preceded and followed by error-clamp trials, and this panel shows the difference between gains estimated in the first and in the second error-clamp trials. Ellipses show SEM (N_HOR = 120 and N_VERT = 80 for each ellipse). The difference between groups is significant in three directions of four (p < 0.001) (for a scheme of statistical test, see Fig. 4F). B, The same data flipped to the first quadrant and averaged over directions (p < 10⁻¹¹; N_HOR = 480 and N_VERT = 320). Percentage values show the amount of adaptation achieved after a single trial: the length of projection of the average force onto the diagonal, relative to 5 N · s/m. The angular values show the angular difference between the response force and the diagonal. These angular deviations for single subjects (calculated as circular medians) are shown on the inset. C, Trajectories during force field trials between two error-clamp trials for both groups and all four directions, projected on the XY plane. Plotted trajectories start at 200 ms after movement onset and end at 650 ms. The colored bands around the average trajectories show SEM (N_HOR = 120 and N_VERT = 80 for each trajectory). D, The same trajectories as in C, but averaged over directions. The black ticks show the time point when the trajectories start to be significantly different between groups (p < 0.05; N_HOR = 480 and N_VERT = 320). E, Same trajectories, first 300 ms after movement onset. The ticks mark 100 and 200 ms (the color of the tick corresponds to the group).

Results

Experiment 1: visuomotor rotations

Subjects were looking in 3D glasses and were operating a 3D manipulandum to move a cursor in a virtual reality space (see Materials and Methods). They had to make repeated 10 cm straight arm movements from a starting position to a single target within 400–600 ms and then back (Fig. 2A). After familiarization with the task, one group of subjects was trained with horizontal visuomotor rotations, and another group with vertical ones. For both groups, the angle of rotation changed every five trials, randomly selected from the set of {0, ±10, ±20, ±30°}, and the training continued on 3 consecutive days with ∼30 min of training on the first 2 days and ∼15 min on the last day (Fig. 2B). Note that there was only one single target used throughout all the experiments presented in this manuscript, in contrast to the more common situation when subjects are making center-out reaches to different targets; our subjects were making movements back and forth between the starting position and the single target (Fig. 2A), and it was only the perturbation that was varied.

We used two different measures to assess subjects' movement adaptation: initial hand direction and late movement hand position, measured at 200 and 400 ms after movement onset. Both measures were converted into the azimuth-elevation coordinates (Fig. 2A), so that (0, 0) corresponds to a movement straight to the target along the z-axis. Figure 2, C and D, shows initial hand direction and late movement hand position in the last trial of every five trial training block on day 3, averaged over subjects and over training blocks with the same rotation angle. To quantify the amount of adaptation achieved at the end of training on day 3, we regressed these positional measures (azimuth for the horizontal, and elevation for the vertical group) to the ideal values of {−30… +30°}, so that perfect adaptation would be measured as 100%. For the initial hand directions, adaptation was 51 ± 15 and 67 ± 10% (horizontal/vertical groups) and for the late movement hand positions 80 ± 9 and 85 ± 6% (all values obtained by robust regression; mean ± SD over subjects). Adaptation was higher for the late movement due to feedback corrections: by 400 ms, subjects have already corrected some part of their initial error. Feedback corrections also caused the SDs (size of the filled ellipses in Fig. 2C,D) of the late movement positions to be smaller than those of initial directions.

Adaptation paths

On the third day, we tested how both groups were adapting to four novel, diagonal, rotations of 30° by interspersing continuing exposition to horizontal/vertical rotations with 5 trial probing blocks, always preceded by 10 washout trials without rotation. Every subject experienced 16 probing blocks in total: 4 repetitions of each of the 4 diagonal rotations (administered in pseudorandom order). Ideal hand directions needed to perfectly compensate for these rotations are shown on Figure 2 with four black crosses.

Figure 3A shows trajectories of subjects' hand movements on trial 1 of every probing block, averaged over subjects and repetitions. Trajectories were cut from 200 ms after movement onset to the moment when the cursor entered the target. All trajectories started at around (0, 0) point, showing that subjects could not predict the direction of the diagonal rotations. All trajectories finish near the corresponding cross, as subjects had to bring the cursor to the target to finish the trial. For all four probing directions, the trajectories were markedly different between the two groups: for the vertical group, they were bent toward the vertical axis, and for the horizontal group, toward the horizontal one (see below for statistical tests).

Figure 3B shows the evolution of the late movement hand positions over the course of five trials of every probing block; we refer to trajectory of this evolution as “adaptation path.” Again, in every direction, the adaptation paths were bent toward the learned structure. Hand directions of the horizontal and the vertical group were significantly different for all 4 diagonal rotations and all 5 trials (20 comparisons in total; p < 0.001 for 17, p < 0.01 for 1, p < 0.05 for the remaining 2 tests; Mann–Whitney–Wilcoxon test, applied after projecting 2D data onto 1D line perpendicular to the perturbation) (for a scheme, see Fig. 4F).

As directional errors under a fixed 2D visuomotor rotation are known to decrease approximately exponentially (Krakauer et al., 2000), we made separate exponential fits to the sequences of azimuth and elevation errors for each of the adaptation paths. For every path, this fit was done with three parameters: speed of azimuth learning, speed of elevation learning, and the initial offset from the maximal error (see Materials and Methods for details). The dashed lines on Figure 3A show the adaptation paths corresponding to each fit.

As the adaptation paths were very similar in each of the four quadrants (Fig. 3A,B), we flipped all of them to the first quadrant to increase the sample sizes. Average movement trajectories are shown on Figure 4D; the black ticks show the moment after which the trajectories become significantly different (p < 0.05, Mann–Whitney–Wilcoxon test applied as described above). Adaptation paths corresponding to the late movement hand positions are shown on Figure 4A (p < 10⁻¹⁰ for each of five trials). The inset shows learning speeds in azimuth and elevation directions for both groups, where each speed was calculated from the exponential fit and is defined as the amount of error corrected on each subsequent trial. The learning speed can range from 0 to 1, with 1 meaning that the error disappears after the first trial. For each group, the learning speed corresponding to the direction of learned structure was higher than in the other direction, and also than in the other group.

The same holds true for the adaptation paths corresponding to the initial movement directions as shown on Figure 4B (p < 0.001 for trials 2–5), except for the first trial in which there is no significant difference (p = 0.09) and the initial directions of both groups were very close to (0, 0), as expected.

Finally, we analyzed the initial directions of the backward movements, performed from the target back to the origin. These data were contaminated by large outliers, so we excluded from the analysis all trials in which the directional error exceeded 35° (7% of all the trials) and one of the subjects. The results are shown on Figure 4C (p < 10⁻⁵ for each of the five trials). Note that the initial direction of the backward movement on trial 1 is far from (0, 0) because by the time of the first backward movement subjects have already partially adapted to the rotation during the preceding forward movement (Neitzel et al., 2009). Here, we are not providing an inset with estimations of learning speeds because the learning was very slow (all five ellipses for each group are very close to each other).

All the data described above were averaged across subjects. To quantify the amount of adaptation path bending for each single subject, we calculated the area between the late movement adaptation path (Fig. 4A) and the straight line representing the ideal adaptation path (Fig. 4E). We normalized this value such that an adaptation path going straight up and then straight to the right would get a value of 1 and a path going straight to the right and then straight up would get a value of −1. Note that this calculation was done on the raw data, and not on the trajectories given by exponential fits. As shown on Figure 4E, for every subject in the vertical group the bending degree is positive (mean ± SD, 0.23 ± 0.08), and for every subject in the horizontal group it is negative (−0.24 ± 0.09). This demonstrates that the effect of structure-specific adaptation can be observed on the single-subject level.

Finally, note that these results cannot be trivially explained by incomplete washout. Our paradigm was constructed such that every probing block was preceded by a 10 trial washout, which was in turn preceded by either +20 or −20° rotation block, with equal amounts of both cases for every probing direction. We compared the initial hand directions for the last two washout trials between all washout blocks preceded by a positive and by a negative rotation. The difference was very small and insignificant for both groups (0.1°, p = 0.4, for the horizontal group, and 2.1°, p = 0.07, for the vertical one). To be additionally sure that this small difference did not contaminate our results, we repeated the analysis presented in Figure 4, separately for the subsets of probing blocks preceded by positive and negative rotations. In each case, we calculated the mean degree of adaptation path bending (compare Fig. 4E) and compared them between each other; there was no difference at all (vertical group: 0.23 ± 0.07 and 0.22 ± 0.10, p = 0.8, Mann–Whitney–Wilcoxon test; horizontal group: −0.28 ± 0.12 and −0.21 ± 0.07, p = 0.4). This proves that adaptation path bending is not an artifact of a possibly incomplete washout, but a genuine effect of structure learning.

Experiment 2: involuntary reflexes

We conducted a second experiment in which subjects received the same training as in Experiment 1, but with a different probing phase on the last day: to test whether structure learning modifies involuntary reflex movements, we used a “cursor jump” paradigm recently applied to assess such reflex responses (Franklin and Wolpert, 2008). During probing trials, hand movements were error-clamped by strong spring-like forces preventing any horizontal or vertical deviations from the z-axis, so that subjects could only move in a force “channel” directly to the target (see Materials and Methods). When the hand was 3 cm away from the starting position, the cursor was for 230 ms displaced in one of the four diagonal directions in the plane perpendicular to the z-axis (Fig. 5A). As this was happening in the force channel, we could measure the force that subjects were exerting on the walls of this channel as a reaction to the cursor jump. Probing trials were administered in blocks of 18 error-clamp trials, with each block being a random sequence of 3 jumps in each direction and 6 error-clamp trials without a jump. Every subject experienced 8 of these blocks, with continuing exposition to the horizontal/vertical rotations in between.

Every cursor jump initiated an involuntary force response in the direction opposite to the jump. The average force responses at 300 ms after the jump onset (corresponding approximately to the peak reaction force) are shown on Figure 5B for each cursor jump direction. In all four directions, the horizontal group produces stronger horizontal responses, and the vertical group, stronger vertical responses than the opposite group (p < 0.001 in three cases, p < 0.01 in one case, Mann–Whitney–Wilcoxon test applied after projecting 2D data onto 1D line perpendicular to the perturbation) (for a scheme, see Fig. 4F). The responses flipped to the first quadrant and averaged over four jump directions are shown on Figure 5C (p < 10⁻¹⁷, difference between horizontal and vertical groups); angular deviations of the average force responses from the diagonal are 21 and −5° for the vertical and horizontal groups correspondingly. The inset in Figure 5C shows these angular deviations, calculated for single subjects. The vertical group shows a strong deviation of the force from the diagonal (21°). For the horizontal group, the deviation is smaller (−5°), although consistently ≤0° for most subjects. Most important for our present argument is the difference between groups, which is large (26°) and highly significant.

After these experimental sessions were completed, we asked subjects about their impressions during the cursor jumps trials. All of them reported that they perceived cursor jumps as a “flicker” or even a “glitch” and claimed that they had ignored them; none of the subjects was aware of producing any compensatory force. Still, to completely exclude the possibility that compensatory forces could be influenced by cognitive mechanisms, we conducted another experimental session with eight subjects to measure their voluntary reaction time. This time, we instructed them to exert some force in the direction of the cursor jump as soon as possible after they noticed the jump (Franklin and Wolpert, 2008).

Figure 6 shows the temporal profiles of force responses. Figure 6, A and D, shows the recordings for one exemplary subject. For each cursor jump direction, the average diagonal force response can be decomposed into horizontal and vertical components (Fig. 5B). Figure 6A shows average horizontal forces produced after cursor jumps in the top-left/bottom-left (solid line) and in the top-right/bottom-right (dashed line) directions (all data were trial-wise baseline corrected) (see Materials and Methods). As expected, after cursor jumps to the left, the horizontal restoring force is positive, and after cursor jumps to the right, it is negative. The difference between the left and right responses, averaged over all subjects, is shown in Figure 6B in magenta. After subjects were instructed to produce the force in the direction of the cursor jumps, the same analysis yields the cyan trace in Figure 6B. It is clear that subjects were not able to voluntarily override the initial part of the reaction force. This justifies calling this initial reaction a reflex. The analogous analysis was performed for the vertical force, this time comparing force responses elicited after upward and downward cursor jumps (Fig. 6D,E) instead of leftward and rightward ones.

The cyan curves on Figure 6, B and E, peak at 265 ms; we took this value as the voluntary reaction time. The difference between magenta and cyan curves becomes significant only later, at 285 ms (p < 0.05, Wilcoxon test). If the same significance analysis is done for individual subjects, then the average ± SD voluntary reaction time over subjects is 325 ± 46 ms (with the earliest value over subjects being 275 ms). This is very close to the reaction time of 324 ± 76 ms reported by Franklin and Wolpert (2008). Our “peak” analysis using the average response across subjects results in the most conservative estimation.

Finally, Figure 6, C and F, shows the horizontal and vertical reflex forces, averaged over horizontal and vertical groups of subjects. As we have seen before (Fig. 5), the horizontal group produces stronger horizontal, and the vertical group, stronger vertical force. The differences between groups become significant at 216 ms (with p < 0.05, and at 233 ms with p < 0.001), which is much earlier than the estimated voluntary reaction time (shown with a dashed vertical line). The conclusion is that already the involuntary response is shaped in structure-specific way.

Experiment 3: force fields

To test for structure learning of force fields, we devised an experiment in which subjects were using the same setup as before and were making movements to the same target, but this time experienced velocity-dependent force fields instead of visuomotor rotations. For one group, the perturbing force was always horizontal, and for another group, always vertical (Fig. 7A). For both groups, the perturbing force was proportional to the hand velocity along the z-axis, and the coefficient of proportionality (force gain) was randomly changed every five trials from the set of {0, ±2, ±4, ±8, ±10} N · s/m. The training continued for 3 days, exactly as in the visuomotor experiment (for details, see Materials and Methods). The average peak velocity was ∼0.25 m/s, so subjects experienced average peak forces of ∼2.5 N. Every fifth trial (last trial in every block) was error clamped as described above to assess the subject's forward model. For every such trial, we estimated subject's horizontal/vertical gains by regressing the measured horizontal/vertical force of the subject to the subject's velocity profile during that trial. The gains measured on the third day are shown on Figure 7B, and adaptation was calculated as described above for the visuomotor case; it was 46 ± 8% for the horizontal and 56 ± 13% for the vertical group (mean ± SD over subjects).

On the third day, we tested how subjects adapted to diagonal force fields by using triplets of trials, consisting of a diagonal force field trial with the gain of 5 N · s/m, sandwiched between two error-clamp trials (Sing et al., 2009). These triplets were separated by three to five washout trials (no force, no error clamp), and every subject experienced 80 triplets in total, with 20 triplets using forces in each diagonal direction. The difference in gains between the second and the first error-clamp trials shows the result of the single-trial force field learning. Indeed, for every diagonal force direction, we observed an average compensatory force roughly in the opposite direction produced by subjects during the following error-clamp trial. Figure 8A shows the difference in gains between the first and second error-clamp trials for both groups and for all four force directions. Evidently, the horizontal group produces stronger horizontal responses than the vertical group, whereas the vertical group produces stronger vertical responses than the horizontal group (p < 0.001 for three of four directions, Mann–Whitney–Wilcoxon test applied after projecting 2D data onto 1D line perpendicular to the perturbation) (for a scheme, see Fig. 4F). The same data flipped to the first quadrant and averaged over directions are presented on Figure 8B. The difference between groups is highly significant (p < 10⁻¹¹), with the responses deviating from the diagonal by 30° for the vertical group and by 18° for the horizontal one. The inset of Figure 8B shows these values calculated for single subjects; again, the effect of structure learning can clearly be observed on the single-subject level.

On average, after one trial, subjects adopted the gain of 0.8 N · m/s (16% of the perturbation of 5 N · m/s). The amount of adaptation can be calculated by projecting this value onto the direction of ideal adaptation (i.e., onto the diagonal). This gives 15% adaptation for the vertical group and 14% for the horizontal one.

Additionally, we looked at hand trajectories during the diagonal force field trials in the middle of the probing triplets. As described above, in these trials, the subject's hand was pushed away from the z-axis; this evoked a compensatory movement necessary to bring the cursor to the target. Figure 8, C and D, shows average movement trajectories during 200–650 ms after movement onset. The shape of trajectories was quite different between groups: the horizontal group was faster in correcting the horizontal component of the displacement, whereas the vertical group was faster in correcting the vertical component. At the same time, initial displacement of the hand in response to identical initial force was the same for both groups (Fig. 8E). Hand trajectories become significantly different between groups only after 200 ms (and in the direction perpendicular to the diagonal only after 240 ms). This means that hand stiffness was identical for both groups, and thus our results cannot be explained by differences in hand impedance (Burdet et al., 2001; Franklin et al., 2007).

Discussion

Learning curves and adaptation paths

Most of the experiments in the field of human motor learning are done by making subjects learn to compensate a certain fixed perturbation: usually it is either a visuomotor rotation or a velocity-dependent force. Whatever the perturbation is, subjects gradually improve their performance and the sequence of decreasing errors can be analyzed. These “learning curves” quantify the amount of adaptation of a single parameter (e.g., the rotation angle) across trials. Comparing learning curves in different conditions led to many interesting insights about motor learning (Brashers-Krug et al., 1996; Martin et al., 1996; Krakauer et al., 2000, 2005; Sainburg, 2002; Mazzoni and Krakauer, 2006; Smith et al., 2006; Criscimagna-Hemminger and Shadmehr, 2008; Keisler and Shadmehr, 2010; Sing and Smith, 2010; Huang et al., 2011), including the original evidence for structure learning (Braun et al., 2009a). This is, however, a limited research tool, as all the comparisons are necessarily one-dimensional: one learning curve can only be “faster” or “slower” than another.

An alternative approach to represent learning progress is to plot the evolution of subject's estimated internal model (“adaptation path”) in the appropriate parameter space. If the relevant parameter space has more than one dimension, then adaptation paths can have different shapes, and these shapes can be studied experimentally. A recent study used this approach (Sing et al., 2009), in which subjects were adapting to velocity- and position-dependent forces, and their adaptation paths were plotted in the two-dimensional parameter space of velocity and position gains. Sing et al. (2009) found that adaptation paths are curved in the diagonal direction and suggest that this can be explained by an asymmetric distribution of motor primitives. There is no structure learning involved in that study, and the curved adaptation paths were observed in naive subjects.

Our study is the first to show that, with prolonged training, adaptation paths can change, both in kinematic and dynamic tasks. This is the main reason why we used a 3D setup: the relevant parameter spaces of visuomotor rotations and force fields in 3D naturally become two-dimensional, as perturbations can occur in the plane perpendicular to the movement and thus have a horizontal and a vertical component. Note that, in our experiments, motor tasks from different (horizontal vs vertical) structures involved perturbations in different spatial directions and so possibly induced training with different muscles. It is an interesting topic for future research to investigate whether adaptation path bending will also be observed when perturbations from both structures happen in the same spatial direction (e.g., velocity-dependent vs position-dependent force fields).

Structure learning of force fields

All previous studies about structure motor learning used visuomotor transformations (Braun et al., 2009a,b; Turnham et al., 2011, 2012), and the question whether structure learning also plays a role in learning dynamic tasks, such as learning velocity-dependent force fields, was open. At the same time, humans often have to learn to control movements under new forces in real-world motor tasks. Our Experiment 3 demonstrates that adaptation to new force field tasks is shaped according to the previously experienced structure, and this effect is not due to altered hand stiffness. Thus, human motor system can learn structures of force fields and use this knowledge during adaptation to new dynamic tasks.

Influence of structure learning on involuntary reactions

We showed that structure learning (of different visuomotor rotations) changes the magnitude of the fast force responses, elicited by sudden cursor jumps during a reaching movement. This fast force response is known to be involuntary (Franklin and Wolpert, 2008), in the sense that subjects cannot get rid of it even if they are told to try. Franklin and Wolpert showed that the reflex reaction to cursor jumps is modulated depending on the environment: it becomes stronger in the environment in which subjects have to correct for random perturbations and weaker in the environments in which perturbations do not interfere with the performance and therefore do not have to be corrected. In other words, the strength of this visuomotor reflex can increase or decrease depending on whether it is important in the given environment. In the present study, we show that the modulation of this reflex happens specifically in the direction of external perturbations: training with horizontal (vertical) perturbations leads to increase of the horizontal (vertical) reflex component.

Structure learning is implicit and automatic

Structure learning is a prominent feature of human intelligence and is usually understood as a high-level learning phenomenon (Kemp and Tenenbaum, 2008; Tenenbaum et al., 2011). At the same time, the results of our cursor jump experiment show that structure learning influences involuntary visuomotor reflexes and so cannot be due to conscious efforts or strategies used by the subjects. Involuntary visuomotor reflexes are arguably the most low-level part of the brain-mediated motor system (with only spinal cord reflexes being faster and more basic). Our results demonstrate that structure learning manifests itself not only in the abstract cognitive functions of human brain but also in the most low-level brain-mediated circuits. This is in accordance with studies showing that long-latency reflexes can reflect an internal model of limb dynamics (Kurtzer et al., 2008) and are controlled by the motor cortex (Pruszynski et al., 2011).

Our finding that structure learning in motor control is involuntary is in agreement with the generally accepted view that motor adaptation is an automatic, unconscious, and implicit process (Shadmehr et al., 2010). It is well known, for example, that if a visuomotor perturbation or a force field is introduced gradually, then subjects successfully adapt to it without ever becoming aware of any perturbation (Jakobson and Goodale, 1989; Kagerer et al., 1997; Klassen et al., 2005; Michel et al., 2007). Even though the effects of an explicit cognitive strategy and implicit, “genuine,” motor adaptation are often hard to disentangle, carefully designed experiments allow to separate them (Malfait and Ostry, 2004; Hwang et al., 2006; Mazzoni and Krakauer, 2006). In a similar vein, our present results show that structure learning is part of the implicit motor system.

Possible computational mechanisms of structure learning

It was recently suggested that curved adaptation paths can be explained by a correlated distributions of motor primitives (Sing et al., 2009). Motor primitives, as introduced in the study by Mussa-Ivaldi et al. (1994), are independent units of computation that calculate the output force (or force gain) given the current state; the resulting total force is the weighted sum of forces produced by individual primitives (Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Joiner et al., 2011). Our results can be explained by reorganization of initially symmetric distribution of primitives: practicing tasks belonging to the vertical/horizontal structure could gradually lead to motor primitives accumulating around the vertical/horizontal axis, and this would in turn lead to the subsequent adaptation paths being bent in the vertical/horizontal direction (Sing et al., 2009).

Alternatively, our results can be interpreted as different Bayesian priors acquired by subjects during structure learning. If practicing vertical/horizontal perturbations builds up a vertically/horizontally stretched prior over perturbations, then a suddenly observed diagonal perturbation would be interpreted differently, depending on the prior (Wolpert et al., 2011). A learned structure would then essentially be an acquired bias in estimating the value of a perturbation given a noisy observation.

Yet another, more abstract, way to think about structure motor learning is in terms of Bayesian networks. A Bayesian network is a graphical representation of causal relationships between different variables: an arrow from variable A to variable B means that B is directly influenced by A (Pearl, 2009). For example, in the case schematically presented on Figure 1, a one-dimensional structure in the three-dimensional control parameter space corresponds to a Bayesian network with one hidden variable defining the values of all three control parameters. The value of this hidden variable corresponds to the position along the one-dimensional structure; all three control parameters can be recovered given this value. One can also imagine motor structures corresponding to more complicated Bayesian networks, with several (and not only one) hidden variables influencing control parameters in various combinations. In contrast, a set of perturbations that is not confined to a lower-dimensional structure would correspond to a trivial Bayesian network without any arrows, because all control parameters are statistically independent. From this point of view, what we called structure learning can be seen as learning a Bayesian network with hidden variables, in particular realizing that control parameters are not statistically independent, but instead have one or several hidden common causes. Structure learning of Bayesian networks has recently become an active topic of research bringing together the fields of cognitive psychology and machine learning (Tenenbaum et al., 2011).

These alternatives are not equivalent, but also not mutually exclusive: for example, learning the structure of a Bayesian network leads to a certain prior over the nonhidden node values. The data presented in this manuscript do not allow selecting among these alternatives, and additional work is needed to test whether structure motor learning can indeed be accurately described in any such way. Future work should also show whether similar computational mechanisms are used in other noncognitive brain functions.