Visuomotor Functional Network Topology Predicts Upcoming Tasks

Abstract

It is a vital ability of humans to flexibly adapt their behavior to different environmental situations. Constantly, the rules for our sensory-to-motor mappings need to be adapted to the current task demands. For example, the same sensory input might require two different motor responses depending on the actual situation. How does the brain prepare for such different responses? It has been suggested that the functional connections within cortex are biased according to the present rule to guide the flow of information in accordance with the required sensory-to-motor mapping. Here, we investigated with fMRI whether task settings might indeed change the functional connectivity structure in a large-scale brain network. Subjects performed a visuomotor response task that required an interaction between visual and motor cortex: either within each hemisphere or across the two hemispheres of the brain depending on the task condition. A multivariate analysis on the functional connectivity graph of a cortical visuomotor network revealed that the functional integration, i.e., the connectivity structure, is altered according to the task condition already during a preparatory period before the visual cue and the actual movement. Our results show that the topology of connection weights within a single network changes according to and thus predicts the upcoming task. This suggests that the human brain prepares to respond in different conditions by altering its large scale functional connectivity structure even before an action is required.

Introduction

Humans and other animals can flexibly adapt their behavior to the needs of the current context (Miller and Cohen, 2001; Bunge, 2004; Sakai, 2008). Depending on the situation, the same sensory input can require two completely different actions. An object we might want to pick up in some situation should not be touched under other circumstances. Such contextual modulation requires a flexible control of visuomotor mappings. Standard examples of flexible visuomotor control paradigms are the anti-saccade task (Hallett, 1978; Munoz and Everling, 2004) and the anti-pointing task (Connolly et al., 2000). In pro-trials, the response has to be made toward the visual stimulus, while in anti-trials, a response away from the visual stimulus (to a position mirrored at the fixation spot) is required. Neither stimuli nor responses differ between the compared conditions, but the stimulus–response mapping (pro or anti) changes according to a contextual cue. Individual neurons (Gail et al., 2009; Johnston et al., 2009) and also large scale brain signals (Connolly et al., 2002) have been shown to signal differences in mapping rules in these tasks. More generally, activity changes in prefrontal cortex (PFC) are related to task rules but also demand control (Dove et al., 2000; Brass and von Cramon, 2002; Sakai and Passingham, 2003; Bode and Haynes, 2009; Reverberi et al., 2012). Miller and Cohen (2001) proposed that “bias signals” from the prefrontal cortex “guide the flow of neural activity along pathways between inputs, internal states, and outputs needed to perform a given task.” The pro- and anti-tasks described above require two completely different pathways within a visuomotor network to be activated: information flow within individual hemispheres is sufficient in pro-trials, while both hemispheres need to interact to perform an anti-trial. In other words, our brain needs to modify the interactions between the two hemispheres according to the task demand. It has been shown that prefrontal interactions change depending on the task (Sakai and Passingham, 2003), suggesting the recruitment of different task-specific networks. Importantly, the pro- versus anti-task differs from these studies, as it requires the neural flow of information within a single network of regions to be routed differently for pro- versus anti-trials.

Here, we investigated whether the functional integration in a visuomotor network changed as a function of the task requirements. We hypothesized that the brain would prepare to respond ipsilaterally or contralaterally already during a preparatory phase by changing the functional integration pattern between task relevant visual and motor regions. Hence, it should be possible to predict the task condition (pro or anti) from the functional connectivity pattern in the visuomotor network before the go-signal. We measured brain activity with fMRI in a bilateral visuomotor network and show that the network's functional connectivity structure could be used to predict across subjects whether subjects were planning a pro- or an anti-trial. Importantly, our result provides one of the few examples where a cognitive state can be predicted from brain activity in new subjects.

Materials and Methods

Participants.

Seven healthy adult volunteers participated in the study [four female, three male, all right-handed, 27 ± 6 years old (mean ± SD)]. All subjects had normal or corrected-to-normal vision and gave written informed consent to participate in the study. The experiment was approved by the local ethics review board and conducted according to the Declaration of Helsinki.

Experimental design.

The flexible visuomotor task required subjects to respond with either the ipsilateral or the contralateral hand to a visual stimulus (go-signal) presented in their left or right visual hemifield. The stimulus–response mapping varied between trials: in pro-trials (called “II-trials” in this paper), the response had to be given with the hand on the side of the visual go-signal; in anti-trials (called “X-trials”), with the hand opposite to the go-signal (Fig. 1A). The task condition was indicated by a cue at the beginning of each trial (“II” or “X”, 3 s). After a pause of 2 s, subjects were presented with two clocklike shapes, in the left and right visual field, with eight clock hands each (Fig. 1B) rotating at different velocities. Specifically, all eight hands of each clock rotated in the same direction with their rotational velocities distributed normally around a mean of μ = 50°/s with standard deviation σ = 30°/σ. Negative speeds were inverted so that all clock hands turned in the same direction. At the go-signal, the speeds of all hands of one of the two clocks were set to μ = 50°/s. This continuous visual stimulation during the delay period was chosen to continuously inject visual information into the visual system, which in turn was done to drive fluctuations in the visuomotor network and thus make changes in functional connectivity more visible. Subjects had to detect the go-signal (a synchronization of all hands of one of the two clocks to the same rotational velocity) and respond to this go-signal according to the task condition: with the hand on the side of the go-signal in II-trials or with the opposite hand in X-trials. The time of synchronization was pseudorandomized between 8 and 14 s after the clocks started to turn. During the delay, subjects knew about the task condition and thus could prepare the required mapping (II or X). After each response, subjects received a feedback about their response (correct or error) and their reaction time [horizontal bar with length relative to the reaction time (RT)] to motivate them to respond correctly as quickly as possible. If subjects did not respond to the go-signal within 3 s, they were informed about the miss, and a new trial was started after 1 s. All subjects practiced the relatively difficult task in a 1 h training session several days before scanning and immediately before the fMRI experiment. Short catch trials (4 s delay, 1/5 of all trials) were inserted to force subjects to attend to the clock hands during the whole delay period, but were not used for the analysis. The entire fMRI experiment consisted of four runs with 40 trials each (160 trials in total). Always five consecutive trials (including one catch trial that was not analyzed) formed a mini-block of the same condition (II or X) that was later used in the analysis (Fig. 2A). We used the Cogent 2000 toolbox (http://www.vislab.ucl.ac.uk/cogent_2000.php) for MATLAB (Version R2007b; MathWorks) to present the stimuli and to record the responses.

Figure 1.

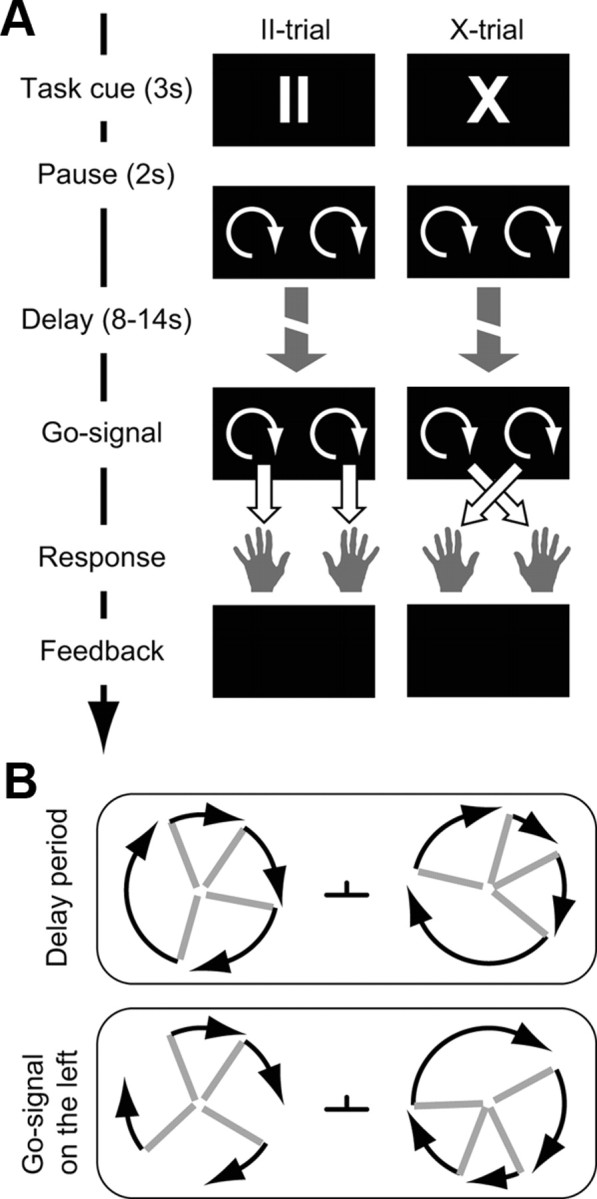
Visuomotor mapping task. A, Time line of a single pro-trial (II, left) and anti-trial (X, right). At the beginning of each trial, the task cue II or X was shown. During an extended delay period (between 8 and 14 s), the subject viewed two rotating clocks and tried to detect the go-signal (when one of the two clocks synchronized its hands; B). During this delay period, the connectivity in the visuomotor network was assessed. B, During the delay period, all clock hands (gray) turned with different velocities. At the go-signal, the hands of one clock synchronized. The black arrows indicate the velocities and were not displayed in the paradigm. For clarity, only four hands per clock are depicted. In the experiment, each clock consisted of eight hands. During the whole experiment, subjects had to fixate on the fixation spot between the two clocks.

Figure 2.

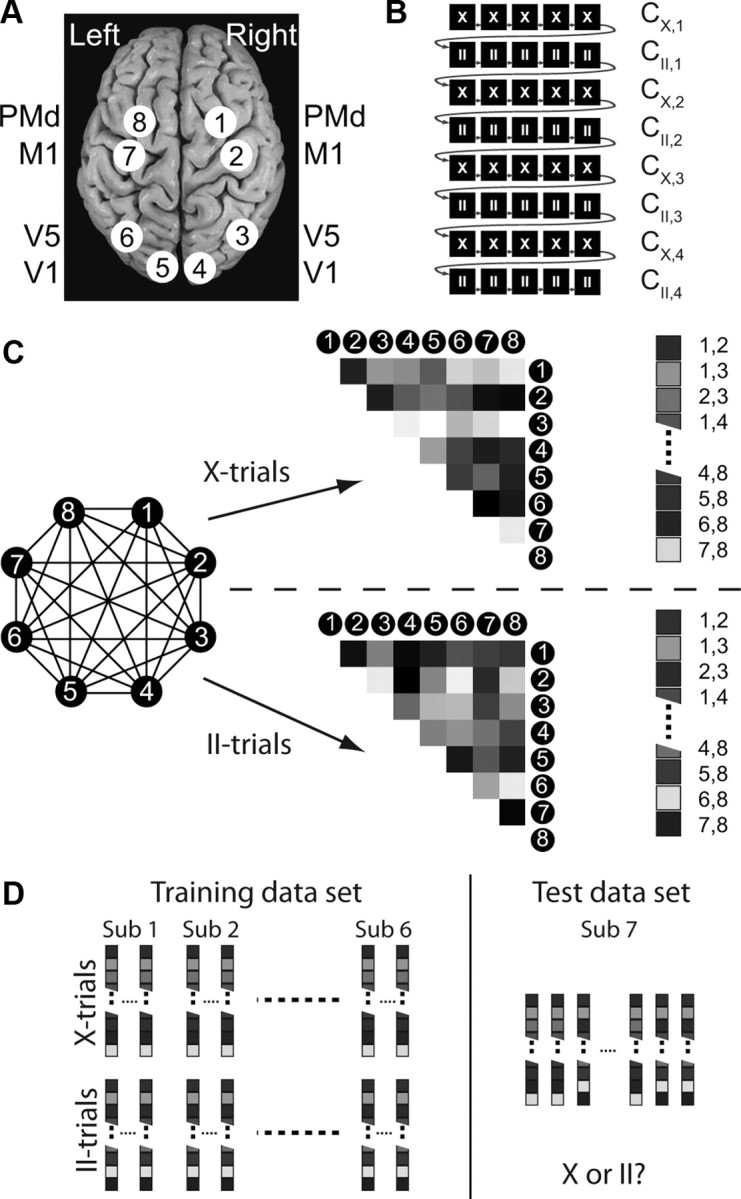
Regions of interest and connectivity graph classification procedure. A, The eight (4 per hemisphere) ROIs are illustrated. B, Illustration of run structure and assignment of data. The two task conditions were presented in miniblocks of five trials. Trials are drawn as black boxes (X, anti-trials; II, pro-trials). Gray arrows indicate the sequence of trials during one run. Note that only a part of one run is shown. All consecutive trials of one miniblock, i.e., one row, were assigned to one subset (without the catch trial) from which the correlation matrix C was computed (e.g., C_X,1 is the correlation matrix for the first subset of the contralateral condition). C, The eight ROIs form a fully connected graph (left). The connectivity structure, i.e., correlation matrix, is calculated for all II and X miniblocks and transformed to vectors of all connections (right), which are then used for the multivariate analysis. Note that the elements on the diagonal of the correlation matrix and the lower half remained empty because of the symmetry of the correlation structure. D, The connectivity vectors of all miniblocks of six subjects were used to train a support vector classifier to distinguish between the connection graphs for the II and the X blocks. The classifier was then tested on the connectivity data from the seventh subject.

Functional localizers of visual and motor cortex.

Functional visual and motor ROIs were individually defined for each subject based on two independent localizer runs at the end of the fMRI experiment: The visual localizer consisted of two circular checkerboards (contrast reversing at 2.5 Hz, 20 s stimulation, 30 s gray background) of the same size and at the same location as the clocks in the main task. Subjects fixated to the center of the screen and had to indicate (button press) small visual events flashed in either the right or the left checkerboard. The motor localizer consisted of alternating blocks (20 s duration, 5 s rest) of right and left index finger tapping paced by a 1 Hz visual cue at the center of the screen. Six repetitions of right and left blocks were performed.

fMRI data acquisition.

Standard functional images were acquired on a 3-tesla Siemens Trio with a 12-channel head coil. We collected four runs of T2*-weighted gradient-echo echo-planar images (EPI): TR, 2000 ms; TE, 30 ms; flip angle, 90°; matrix size, 64 × 64; field of view (FOV), 192 mm; 33 slices (2 mm thick, 1 mm gap, ascending) resulting in a voxel size of 3 × 3 × 3 mm. Finally, a whole-brain EPI image (parameters as above but with 70 slices; TR, 4300 ms) was collected after each session as well as a T1-weighted structural dataset with 1 mm³ resolution (TR, 1900 ms; TE, 2.52 ms; matrix size, 256 × 256; FOV, 256 mm; 192 slices of 1 mm thickness; flip angle, 9°).

Data analysis.

To look at aspects of both specialization and integration, the fMRI data were analyzed twofold. First, we used statistical parametric mapping (SPM) to look for functionally specialized areas in the brain, in which activity might differ between the two task conditions during the delay period. Second, the main analysis focused on functional integration during the delay period, while the subjects prepared their responses, by analyzing the functional connectivity structure in the task-relevant network of brain regions, as identified using the functional localizer tasks (see Functional localizers and definition of regions of interest, below).

Preprocessing of fMRI data.

All functional images were corrected for motion and slice acquisition time and coregistered to each subject's individual structural T1-weighted image via the whole-brain EPI using SPM2 (Wellcome Department of Imaging Neuroscience, Institute of Neurology, London, UK). For the standard GLM analysis, the fMRI data were spatially smoothed with a Gaussian kernel (FWHM, 8 mm), normalized to the standard EPI template of SPM and high-pass filtered (t = 128 s).

Standard average activation analysis.

We looked for differences in brain activation that reflected the task condition (II vs X) using a standard GLM approach. The regressors of the model were defined according to a mixed (event-related and mini-block) design. The presentation of the task cue (II or X), the button presses (left or right), and the display of the feedback were modeled as events, while the visual stimulation during the preparatory period (rotating clocks) was modeled separately for II and X trials using two boxcar functions, which started when the clock hands began to turn and ended with the go-signal. All regressors were convolved with the standard hemodynamic response function to obtain BOLD-regressors for the fMRI data. To find regions whose activation would differ between the two tasks, a linear contrast between the parameter estimates of the X and II delay period was computed for each subject and tested on the group level using a t test on the difference X versus II (or II vs X) over subjects. To illustrate the most prominent differences between X and II trials, a liberal statistical threshold of p < 0.001 (uncorrected) and cluster size 10 was used to define candidate regions. Please note that this threshold is not corrected for multiple comparisons, and thus the resulting activations are not necessarily significant at the whole-brain level. The resulting activations (p < 0.001, k = 10) were then used to create masks and extract the percentage signal change (Δs) in these regions for illustration purposes. The masks consisted of a sphere with a volume of 57 voxels (radius 7 mm) around the peak activation.

Two control analyses looked at the visual and motor activations. Visual activations were computed by contrasting the activation during the delay period with rest. Motor activations resulted from a contrast of left versus right button presses. A threshold of p < 0.001 (uncorrected, k = 10) was applied for both control contrasts.

Functional localizers and definition of regions of interest.

Using the functional localizer data, we defined eight ROIs, four in each hemisphere: two visual areas, primary visual cortex (V1) and V5/hMT+ (also human MT); and two motor related areas, dorsal premotor cortex (PMd) and primary motor cortex (M1). The ROIs were defined in a two-step procedure that combined a priori knowledge about the location of cortical regions in the form of cytoarchitectonic probability maps (Eickhoff et al., 2005., 2007) with the actual functional activation observed in the localizer runs. First, we used the IBASPM (Alemán-Gómez et al., 2006) toolbox to map cytoarchitectonic probability maps (Eickhoff et al., 2005, 2007) from the standard MNI template to the anatomy of individual subjects. We then selected for each voxel in every individual subject the maximum anatomical probability to create binary anatomical masks for the eight ROIs in each subject. Second, these anatomical maps were combined with functional maps from the localizer runs by selecting the 100 most significant voxels in each anatomical ROI for each subject individually. This procedure ensures that the ROIs reflect the general cortical anatomy and also take into account functional activation individually recorded for each subject. For the visual localizer (V1, V5/hMT+), significance was assessed by a t test contrasting stimulus versus rest. For the motor localizer (PMd, M1), we used a t test contrasting left and right button presses and vice versa. This procedure selected within each anatomically defined mask the 100 voxels that were most activated by the corresponding functional localizer. Please note that the data used to create the ROIs were acquired in separate localizer runs and are thus independent from the data that was acquired during the task.

Preprocessing and ROI data selection for connectivity analysis.

For the connectivity analysis, the same preprocessing steps as above were applied, but without smoothing. Additionally, we regressed several potential sources of global effects out of the individual voxels' time courses of each run: the estimated time courses of the movement parameters (6 regressors), a linear regressor, the mean over all voxels (whole-brain regressor), and the time courses of four hand-selected voxels in the left and right ventricles and the white matter in the left and right hemisphere. This denoising procedure has been shown to successfully remove global correlations due to breathing or heartbeat, which could inflate correlations (Van Dijk et al., 2010).

All functional images of the delay period of correct trials (4–7 images/trial, no catch trials) entered the analysis. The hemodynamic delay was taken into account by shifting the delay period by 2 s. This relatively small shift assures that no motor signal enters the analysis. To obtain robust correlation estimates, all consecutive trials of one miniblock were combined into a subset of images (Fig. 2A). Thus, for every subject, we obtained four subsets for each condition and run (4 × 2 × 4 = 32 in total). X subsets consisted on average of 19.5 ± 4.6 images (mean ± SD) and contained at least six images; II subsets consisted of 19.0 ± 4.2 images, at least nine images. The functional connectivity in the visuomotor network was assessed by calculating the correlations between the mean time series in the eight ROIs (28 pairs) within each of the 32 subsets, resulting in 16 correlation matrices for each task condition and subject (Fig. 2C).

Across-subject classification task based on functional connectivity.

A linear SVM (LIBSVM: http://www.csie.ntu.edu.tw/∼cjlin/libsvm) with standard parameters was used in a leave-one-subject-out cross-validation scheme to classify the functional connectivity matrices of the visuomotor network into II versus X conditions. In each fold of the cross-validation, we z-normalized every dimension of the training and test vectors by subtracting the mean and dividing by the standard deviation. Importantly, this normalization procedure was performed using the mean and standard deviation from the training data only, thus preventing any circularity in the analysis. The classifier was then trained on the correlation matrices of six subjects and tested by computing how well it classified II versus X correlation matrices in the subject that was not used to train the classifier. Classifier performance was compared with a binomial distribution B(p,n), with p = 0.5 and n = 224 (32 samples × 7 subjects). In addition, we calculated the 95% confidence interval of the accuracy based on a beta distribution Beta(n_c + 1,n_e + 1), where n_c and n_e are the number of correct and error predictions, respectively, and the term +1 results from the assumption of a flat prior distribution Beta(1,1). See Bishop (2006) for details.

For comparison, an additional classification was performed that relied on the average activation within ROIs rather than on the connectivity within the network. The same data and classification procedure as above were used, but features were defined in the following way: in every block, we extracted the average ROI activity at the four time points at the beginning of the delay period, resulting in a feature vector of 32 dimensions (4 time points × 8 ROIs). These feature vectors were then used to train and test the classifier in exactly the same way as described above. We used four time points to allow for a dimensionality that was close to the one of the main analysis.

Analysis of weight structure.

The structure of the weights of the classifier provides information on the discriminative connectivity pattern, i.e., the pattern of functional connectivity differences between II and X trials that allow for the prediction. We analyzed this pattern to see whether indeed the task-related changes in functional connectivity were in line with the theory of Miller and Cohen (2001). To compare only the directions of weight vectors, the weight vectors from all cross-folds were normalized to length 1 and then averaged. Note that the z-score normalization of the training data to a standard variance of 1 already assures that the weights are approximately normalized. The sign of the weights indicate whether a functional connection is stronger or weaker in either the II or the X task. The labeling of the conditions in our case was such that positive weights were assigned to connections that were stronger in X trials, and negative weights to those that were stronger in II trials. A random permutation test of the signs of the weights of all connections was used to assess a p value of the observed weight structure. In particular, we calculated the fraction of random networks that had more or the equal number of negative weights in ipsilateral connections and thus also more positive weights in contralateral connections than the observed weight distribution.

Influence of individual connections.

The absolute value of the SVM weight w_i of the connection i is linked to how much information about the task condition is present in that particular connection (Mourão-Miranda et al., 2007). A high w_i would suggest that the temporal correlation between the i^th pair of regions consistently differs between the two conditions. Again, the weight vectors from all cross-folds were normalized to length 1 and then averaged across all cross-folds. In two analyses, we assessed the role of individual connections within the network. First, the unique contribution of every single dimension to the classification was tested by removing one dimension from the feature vectors and conducting the classification with this reduced dataset. A drop in accuracy (tested by a t test across subjects) would suggest that this functional connection contributes information that is relevant for the classification of the task condition. Second, we analyzed each element of the correlation matrix separately. For this, we compared the mean correlation (Fisher's Z-transformed) of each region pair for the two conditions (II and X). The matrices from all miniblocks of each condition were averaged for each subject individually and compared using a paired-sample t test across subjects.

Within-subject classification.

To compare the across-subject classification to classifiers that are trained and tested on independent data within the same subject, we classified task condition based on the connectivity pattern and the average activation within ROIs using the same features as for the across-subject classification. Importantly, we now use a leave-one-run-out cross-validation. Please note that this procedure results in fewer training samples and thus a lower performance might be expected.

In addition, within-subject classifiers can make use of the detailed activation pattern within the ROIs, which has been shown to yield substantial information that cannot be obtained from regional averages (Haynes and Rees, 2005; Kamitani and Tong, 2005). We thus wanted to test whether such multivoxel pattern classifiers might be able to classify task condition better than the connectivity-based classification. For each voxel within an ROI, we extracted the average activation over the four first time steps (scans) of the delay period, yielding a 100-dimensional feature vector for each block of the experiment for each ROI. For each ROI, we then trained a multivoxel pattern classifier to predict the task condition in a leave-one-run-out cross-validation. Prediction accuracies were then averaged across subjects to yield the average prediction accuracy of each ROI. Please note that this multivoxel classification differs from the main analysis in two important aspects: it cannot be performed across subjects, and it uses information that is different from the connectivity structure, which was the main interest of this study.

Results

Behavioral results

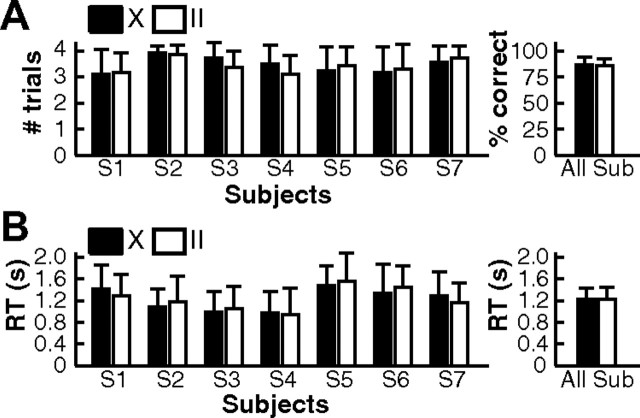
All subjects achieved a good behavioral performance in the task. On average, they responded correctly in more than three of the four trials of a miniblock (Fig. 3A; catch trials were not analyzed). At least one or two trials were correct in each miniblock. A nonparametric Wilcoxon rank sum test was performed to test for differences between the two task conditions. At the group level, there was no significant difference (Wilcoxon test, p = 0.83). When subjects were considered individually, data from six of seven subjects showed no significant difference (p > 0.05), while one subject (S3) showed, on average, slightly more correct trials in X blocks (p = 0.049, not corrected for multiple comparison). RT was defined as the time interval between the go-signal and the button press. Note that RT includes both the time for the difficult detection of the go-signal (synchronization of clock hands) and the actual motor reaction time. The mean RT of subjects ranged from 956 to 1516 ms (mean ± SD: 1230 ± 202 ms; Fig. 3B), suggesting that RT are dominated by the visual detection. RT did not show a significant difference between the two task conditions at the group level (Wilcoxon test, p = 1). Six subjects did not show a significant difference in RT (p > 0.05), while one subject (S6) reacted slightly faster in X trials (p = 0.04, not corrected). Note that none of the single-subject p values (percentage correct or RT) was significant when compared with the Bonferroni-corrected threshold α/n = 0.007. Importantly, the absence of any difference between X and II trials in behavioral measures suggests that the difficulty of the task was mainly influenced by factors that were equal in the two conditions, e.g., the detection of the go-signal.

Figure 3.

Behavioral results. A, Left, Average number of correct trials per miniblock for individual subjects. Short catch trials were not counted. Therefore, there were four trials per block. Right, Percentage of correct trials averaged over subjects. B, Left, Average reaction time for individual subjects. The average and SD were calculated over all correct trials of each individual subject. Right, Group average of reaction times. Black bars, X trials; white bars, II trials. Error bars show the SD.

Task-specific activations

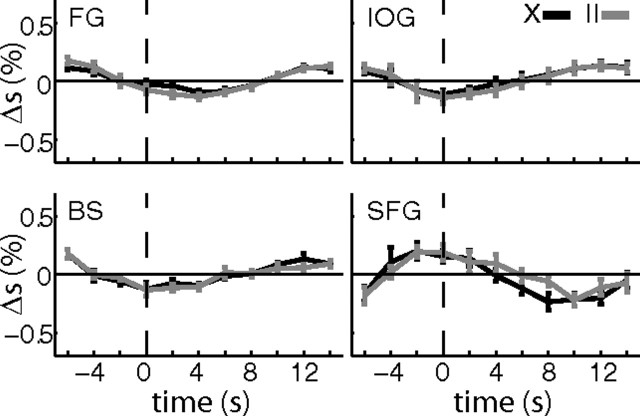
In the following, we will first focus on differences in activation between X and II trials during the delay period. Then results of two control analysis are presented. To illustrate differences in activation between X and II trials, a relatively liberal threshold (p < 0.001, uncorrected) was applied at the voxel level. This analysis revealed four clusters (Table 1) that contained more than k = 10 voxels in which activation differed between the two task conditions during the delay period. One of these clusters was significant at the cluster level (p = 0.026). The peak activation was located in the left superior frontal gyrus (MNI coordinates: −15, 51, 45) in a region that is part of the default network (Raichle et al., 2001) and decreases activity during visual tasks (Shulman et al., 1997). Indeed, the significant contrast resulted from stronger deactivation of that region in X trials compared with II trials (Fig. 4).

Table 1.

Regions with different activation in X and II trials at p < 0.001 (uncorrected)

MNI coordinates	Region	Tmax, k	pcluster, corrected	Contrast
−33, −63, −9	Left fusiform gyrus	11.75, 18	0.095	X > II
39, −75, −3	Right inferior occipital gyrus	8.03, 12	0.330	X > II
−3, −24, −9	Brainstem	6.80, 10	0.487	X > II
−15, 51, 45	Left superior frontal gyrus	7.99, 24	0.029	II > X

Figure 4.

Activation differences during delay period. The activations (p < 0.001, k = 10) of the II versus X (X vs II) contrast were used to create masks and extract the percentage signal change (Δs) in these regions. The masks consisted of a sphere with a volume of 57 voxels (radius, 7 mm) around the peak activation. Average activations (percentage signal change, Δs) are shown for the four regions that showed a significant difference at p < 0.001 (uncorrected, k = 10) between II and X trials. All correct trials of a condition were temporally aligned to the onset of the delay period (dashed vertical line) and then averaged over subjects (n = 7). Average traces of percentage signal change are shown for X trials (black) and II trials (gray). Error bars are SEM. Note that none of the small differences between the two task conditions survived a Bonferroni correction for multiple time points (n = 11). Nevertheless, when fitted with the regressors defined in the GLM, these four regions showed a significant activation. This difference could arise because the GLM regressors take into account the length of the delay period. FG, Right fusiform gyrus; IOG, right inferior occipital gyrus; BS, brainstem; SFG, left superior frontal gyrus.

In addition to the contrasts that look for differences in the task condition, we performed two important control analyses. In these control analyses, the same threshold (p < 0.001, uncorrected) was applied at the voxel level. At this threshold, contrasts of left versus right (right vs left) button presses showed large clusters (both k > 400) around the right (left) central sulcus that were both highly significant (p_cluster < 0.001, corrected) at the cluster level. To assess visual signals induced by the rotating clock hands, a t contrast that compared the visual activation during the delay period with rest was computed and revealed the expected activations in area V5/hMT+. A large cluster was observed in the right hemisphere (k = 106, p_cluster < 0.001, corrected at cluster level), but only few significant voxels in the left V5/hMT+ (not significant at cluster level). These control analyses show that the task indeed elicited reliable cortical activations in the expected regions.

Across-subject prediction of task condition from functional visuomotor network

The main analysis of this study tested with multivariate pattern classification whether the functional connectivity structure in a predefined visuomotor network differed between the two task conditions. First, the correlation matrices between the mean fMRI signals in the eight task-relevant localizer regions were computed. Then, an SVM classifier learned to discriminate between the two conditions (II vs X) on the data of six of the seven subjects (Fig. 2). Finally, the classifier was tested using the connectivity matrices of the seventh subject. This procedure was repeated for each subject in a leave-one-subject-out cross-validation. Thus, successful prediction would mean that task conditions can be predicted in new subjects, whose data were not part of the training data for the classifier. The linear classifier was able to classify the connectivity matrices in the test sets with an accuracy of 58.5% into II and X trials (p < 0.005, binomial test). The 95% confidence interval ranged from 51.9% to 64.8%. Hence, the correlation structure in the visuomotor network contained significant information about the current task condition, even in the delay period, where the visual input was identical for the two conditions and where no motor action or preparation could be taken because the go-signal was not yet shown to the subject.

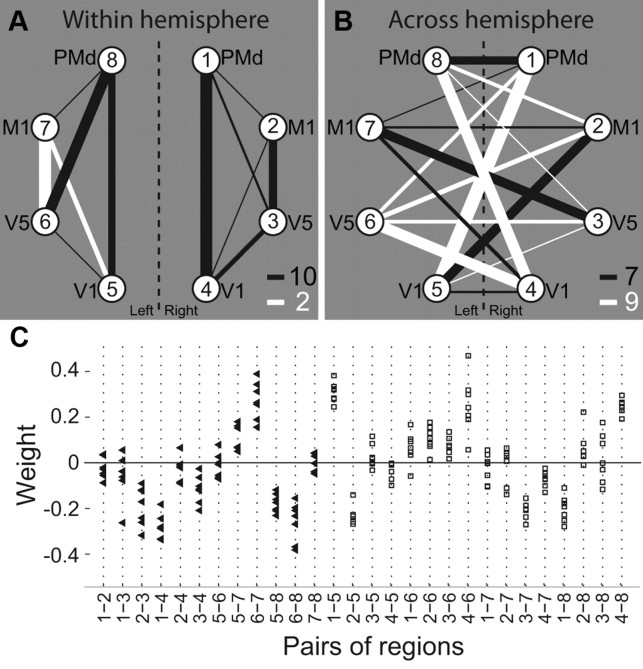
After having shown that the correlation structure yields significant information about the task condition, we investigated in more detail how the preparatory functional connectivity was related to the task and whether specific connections were especially important for this classification. The absolute value of each dimension of the weight vector w⃗ is related to the importance of this dimension for the classification (Mourão-Miranda et al., 2007). We averaged the normalized weight vectors from all seven cross-folds to obtain a single weight value for each of the 28 connections in the visuomotor network. Figure 5 illustrates the result of this procedure for the within (Fig. 5A) and between (Fig. 5B) hemisphere connections. The thickness of the connection lines is proportional to the absolute value weight of the corresponding connection, while the color codes the sign (black, minus; white, plus). Note that the labeling of II trials as −1 and X trials as +1 for the SVM classification was such that higher correlations in II compared with X trials in black connections are suggestive of a II trial, while in white connections, higher correlations in X compared with II trials point toward a classification as an X trial. Interestingly, the majority of white lines are between-hemisphere connections, suggesting a large-scale functional integration between the two hemispheres during the delay period in X trials. In contrast, nearly all within-hemisphere connections have negative weights, suggesting that within-hemisphere functional connectivity is higher during II trials. Note that the connectivity pattern described here is followed by most, but not all, connections. However, a permutation test (see Materials and Methods, above) revealed that the number of positive weights in across hemisphere connections is unlikely to occur by chance (p = 0.040).

Figure 5.

Discriminative weight structure of classifier. A, B, The weights of the support vector classifier are depicted for all connections within hemisphere (A) and between hemispheres (B) for the network of eight ROIs. The nodes of the graph correspond to the ROIs (compare Fig. 2). The line thickness is proportional to the absolute value of the respective dimension of the average weight vector. Hence, it is related to the amount of information about the two conditions that is present in the temporal correlation between the respective region pair. The line color gives information of the sign of the weight corresponding to the connection (black, minus; white, plus). Numbers at the bottom right of A and B indicate the number of black and white lines in the two graphs. The number of black lines in A, and thus, the number of white lines in B, are significantly higher than expected by chance (p = 0.04). C, Illustration of weights versus connections for all cross-folds individually. For every connection (x-axis), the corresponding weight is plotted for all seven cross-folds. Black triangles depict intrahemispheric connections; white squares are interhemispheric connections. Connections are ordered to confirm with A and B: intrahemispheric connections on the left, interhemispheric connections on the right.

The classification on the connectivity matrices was robust against the removal of single connections. A t test did not reveal any significant reduction in accuracy (all p > 0.05, Bonferroni corrected) when any single connection was removed from the connectivity matrix, suggesting that information about task condition was distributed in a pattern of several connections and not attributable to a single, unique dimension. We further tested whether the correlation between any pair of regions in the network showed a significant change with task condition. For this, the difference between the Fisher's Z transformed correlation matrices of the two conditions was tested using a paired t test across subjects. None of the connections survived a statistical threshold of p < 0.05 (Bonferroni corrected for the number of connections). In a post hoc analysis, we asked whether task condition could be predicted by simply considering a single value, namely the difference of the average within-hemisphere and the average between-hemisphere connection strength in the visuomotor network. To obtain comparable results, we again used a leave-one-subject-out cross-validation and computed the threshold that best classified the average within- minus between-hemisphere correlations in the visuomotor network into X and II trials in the training dataset. A test block was then classified as II if the average correlation difference was above the threshold and as X if it was below the threshold. All calculations were performed on Fisher's Z transformed correlations. This simple classifier achieved an accuracy of 51.8%, which is not significant (p > 0.2) and lies outside the 95% confidence interval of the full classification.

Importantly, the average activations within the visuomotor network under consideration did not show any clear differences between the two tasks. Figure 6 illustrates the average percentage signal change in the eight areas of the visuomotor network during the delay period. A sign rank test that compared activations in X and II trials did not reveal any difference that survived a correction for multiple comparisons (all corrected p > 0.17). Hence, there is little to no activation differences in the network depending on the task condition.

Figure 6.

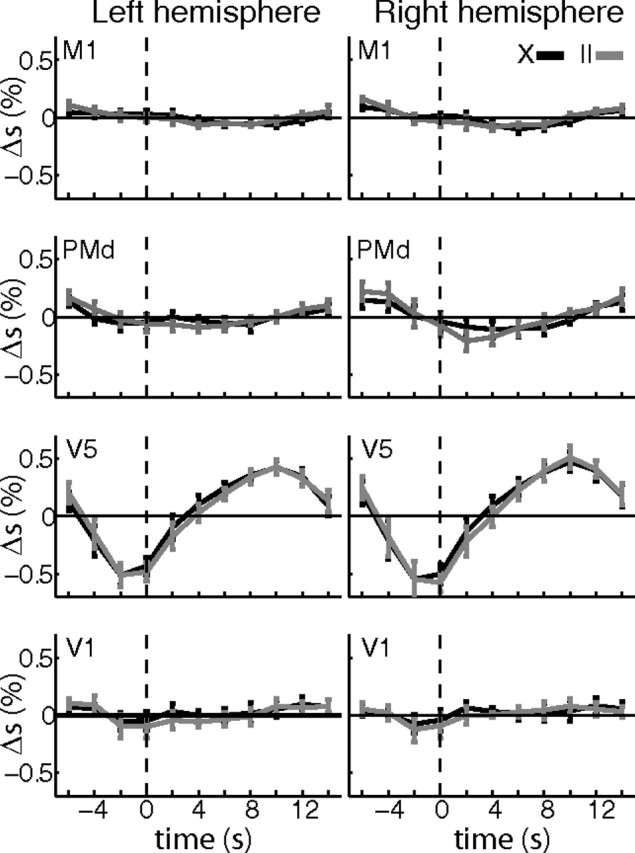
Average activation in visuomotor network. Average activations (percentage signal change, Δs) are shown for the eight regions of the visuomotor network. Normalized (MNI) masks of the eight ROIs were calculated for this purpose. Specifically, we normalized the individual masks of each subject to the MNI template and then selected for each ROI the 50 voxels with the highest overlap between the masks of all seven subjects. The normalized masks were used to extract average time courses from the normalized and smoothed data. Correct trials of a condition were temporally aligned at the onset of the rotating clocks (dashed vertical line) and then averaged over subjects (n = 7). Average traces of percentage signal change (black, X trials; gray, II trials) are shown for the eight regions of the visuomotor network (legend on top right). Error bars show SEM. A sign rank test at a liberal threshold of p < 0.05 yielded only few significant differences in percentage signal change (Δs) between X and II trials, none of which survived a correction for multiple comparisons for the number of time points (Bonferroni, n = 11). Please note that the average traces contain left and right button presses and are aligned to the onset of the visual stimulus and not to the motor response. Hence, motor-related BOLD activity as confirmed by the GLM control analysis is averaged out and cannot be seen here.

Finally, we assessed whether the temporal activation patterns within the ROIs can be used to predict the task condition. Exactly the same classification as for the connectivity matrices was performed but with the mean activation of each region as features. To keep the number of features approximately equal, we used the first four time steps of the delay period in all eight regions, yielding a 32-dimensional feature space. The classification based on these 32 features showed a trend but was not significant (54.9% correct, p = 0.06, binomial test). Although smaller, this value is clearly within the 95% confidence interval of the connectivity-based approach. We thus cannot conclude that the connectivity-based classification performs significantly better. Please note that the original data entering this analysis were very similar to the one in the main analysis, but entered directly instead of looking at correlations between regions. Importantly, the choice of the features that are fed into the classifier is tightly linked to the interpretation of the results. We could not have addressed our hypothesis of a biased functional connectivity in preparation to a task (Miller and Cohen, 2001) had we simply looked at activation-based classification.

Within-subject classifiers based on detailed patterns

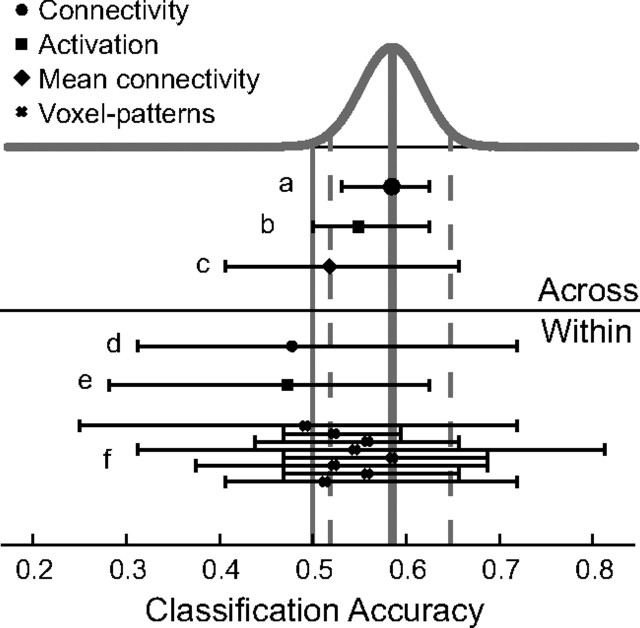
The standard approach in multivariate pattern classification in fMRI is to use within-subject classifiers that do not generalize across subject. However, such classifiers can exploit the activation pattern and thus precise local information at a voxel resolution. Even though these two approaches are difficult to compare, we tested whether such multivoxel classification might perform better than the across-subject classification based on the connectivity pattern and performed a classification analysis using support vector machines on the multivoxel pattern of activation in the regions of interest. For each voxel within a, ROI, we extracted the average activation over the four first time steps (scans) of the delay period, yielding a 100-dimensional feature vector for each block of the experiment. Because detailed patterns are not expected to be the same across subjects, the classification was performed within subject (leave-one-run-out cross-validation) and accuracies were then averaged across subjects for all ROIs individually. Only one of the ROIs (left V1) showed an average accuracy equal to the 58.5% observed in the connectivity-based classification; all the others had lower accuracies. In all regions, the accuracies varied strongly across subjects (e.g., from 46.9% to 68.8% in left V1) so that a sign rank test yielded no significant accuracy in any of the ROIs (all p > 0.05). Interestingly, the connectivity-based classification across subjects as presented above was more consistent across subjects with individual accuracies ranging from 53.1% to 62.5% (mean, 58.5%). Finally, within-subject classification based on either the functional connectivity or average activation within ROIs (same features as for the across-subject classifications, but with a leave-one-run-out cross-validation) did not perform above chance with average accuracies of 47.8% (connectivity) and 47.3% (activation). Thus, within-subject classifiers (even based on fine-grained activation patterns) did not improve the classification in any way and showed results that were relatively inconsistent across subjects and ROIs. Figure 7 summarizes the results of all different classifiers and features that were used here. It is important to emphasize that it was not the goal of this study to maximize classification accuracy but rather to use a specific classifier—the connectivity-based classification across subjects—to answer a specific research question, namely, whether the functional integration in a visuomotor network changes during task preparation and thus allows prediction of upcoming tasks.

Figure 7.

Illustration of different classification schemes. The results of all feature selection and cross-validation schemes used in this study are illustrated. The Beta-distribution, Beta (n_c + 1, n_e + 1), that describes the result of the classifier of the main analysis is plotted on top (gray curve). The average accuracy (solid gray; 58.5%) and the 95% confidence interval (dashed gray; 51.9% and 64.8%) are shown as vertical lines. Chance level (50%) is indicated by the thin vertical solid gray line. Different feature selection methods are indicated by a symbol (key in top left) showing the average accuracy across subjects. Each classifier is further characterized by a horizontal line indicating the full range observed, i.e., from minimum to maximum within-subject accuracy. a, Classification across subjects on connectivity graphs (main analysis). b, Classification across subjects on ROI activation. c, Classification across subjects on average within versus between connectivity. d, Classification within subjects on connectivity graphs. e, Classification within subjects on ROI activation. f, Classification within subjects on voxel pattern within ROIs. In f, ROIs are (from top to bottom): right PMd, right M1, right V5, right V1, left V1, left V5, left M1, and left PMd (compare Fig. 2). Note the large variability in the within-subject classifiers, which might be due to the small number of training samples compared with across-subject classification. It is important to note that it was not the goal of this study to maximize the classification accuracy but to test classification across subjects based on connectivity graphs.

Discussion

In this study, we have analyzed preparatory activity in a flexible visuomotor task with a focus on functional integration in a visuomotor network. We find that the functional weight topology in the studied network of eight cortical regions contains information about the task condition already in the preparatory period, when only the task is known but the side of the go-signal and of the motor response are not known. In contrast, there is hardly any activity that significantly changes with the task condition in single specialized regions.

Behavioral performance of subjects

Our behavioral paradigm was similar to the classic experiment proposed by Poffenberger (1912) to assess conduction delays between the two hemispheres (Marzi, 1999). However, we did not observe any significant differences in behavioral performance (percentage correct and RT) between the II and X conditions. The relatively long RTs suggest that the variance in the measured reaction times (from cue onset to button press) is mainly due to variance in the time needed to detect the go-signal. The small differences between II and X reaction times observed in similar visual-to-motor mapping tasks (Poffenberger, 1912; Simon, 1969) and in anti-saccades (Hallett, 1978) might be invisible due to a much larger variability in detection time for the go-signal in the current study.

Absence of univariate signals indicating the task condition

There were only small differences in univariate activity between II and X trials on the group level. A single cortical area located within the frontal part of the default network survived a statistical threshold at the cluster level. This is in contrast to other fMRI studies (Connolly et al., 2000, 2002) and results from monkey electrophysiology (Everling and DeSouza, 2005) that clearly show differences between pro- and anti-trials. In particular, prefrontal regions are thought to be involved in top-down control (Miller and Cohen, 2001; Bunge, 2004; Sakai, 2008). Prefrontal activation has been associated with “increases in the demand of control” (Miller and Cohen, 2001). A potential reason for the lack of a strong specialized activity in our experiment could be that even during the delay period, subjects were involved in a complex visual detection task, while subjects in many other studies were just waiting to respond to the appearing target. The behavioral results suggest that there is little to no difference in difficulty between the II and X task conditions, which could be the reason for the absence of significant activity in PFC during the preparatory period. It is also conceivable that there is neural activity that signals the upcoming task, but that this activity is too small to be detected with our experimental setting and group size.

However, other contrasts that did not differ between the two task conditions were highly significant at the group level. Area V5/HMT+, a visual region that strongly responds to visual motion (Wilms et al., 2005), was strongly activated during the delay period in the right hemisphere, and motor regions (Yousry et al., 1997) were consistently active during the paradigm. Both visual and motor activations illustrate that considerable BOLD responses were present, in line with our expectations. Despite these clear and reliable cortical activations associated with the task, no difference could be found between the II and X delays, which suggests that the potential differences in univariate signals are small.

Functional integration during preparatory set

It has been suggested that specialization and integration are the two major principles of the functional architecture of the brain (Friston, 2002). Brain regions specialized for sensory processing and motor planning need to interact and integrate their specialized functionality for appropriate behavior in a given situation. In this study, we focused on the question of whether the entire functional connectivity structure in a predefined visuomotor network might reflect the task condition, i.e., the required visuomotor mapping. A classification approach allowed us to predict the task conditions from the functional weight topology during a preparatory delay. Thus, the brain prepares for the upcoming visuomotor mapping by adapting the functional integration to the needs of the task (Miller and Cohen, 2001). Interestingly, the structure of the learned classifier seems to reflect the fundamentally different flow of information required in the two task conditions: in X trials, information needs to cross to the other hemisphere, while in II trials, integration within a single hemisphere is sufficient. The classifier weights suggest that the interactions between areas are biased to serve the upcoming action, as shown by the excess of negative weights in within-hemisphere connections. The functional integration pattern between V1 and PMd consistently follows a hypothetical flow of information from visual to motor areas that is in line with the theory: within hemispheres in II trials and across hemispheres in X trials. Note that the functional interactions in the studied visuomotor network are not necessarily monosynaptic connections but most likely reflect multisynaptic connections via different pathways or common input. It has been shown previously that different lateralized cortical networks are recruited during the execution of different tasks (Stephan et al., 2003) and that prefrontal interactions reflect the upcoming tasks (Sakai and Passingham, 2003). In these studies, the different tasks were fundamentally different (verbal vs spatial) and recruited different brain networks for execution. Our study differs from these findings in considering one single visuomotor network only, whose functional connectivity structure is modulated according to the information flow demands in the task. Please note that the entire visuomotor network needs to be involved in both task conditions. Only the interactions within the network change according to the task. Importantly, the changes in functional connectivity occur during a preparatory period, before execution of the motor command.

There are other physiological measures, like heart rate and respiration, that might change with the task. The inclusion of regressors for white matter and CSF probably reduced such effects (Van Dijk et al., 2010). In addition, it seems unlikely that these large-scale physiological effects would influence interactions in the visuomotor network in a specific way without showing any detectable signal change in the GLM analysis. We cannot rule out that fluctuations in mental preparation during the delay period might have caused the observed correlation structure: if subjects alternated their covert attention between the right and left clock, simultaneous motor imagery of the corresponding movement could create a functional connectivity structure like the one we observe. It would be interesting to see whether a similar preparatory change in functional connectivity is observed with pro- versus anti-tasks that use a simpler go-signal, such as the appearance of a dot, and are thus less attentionally demanding. We see no reason why the functional integration should be specific to the visual stimulation or the difficulty of the task. However, based on previous findings (Connolly et al., 2002), one would expect to observe prefrontal activations that differ between the task conditions when the detection of the go-signal is relatively simple.

Importantly, the information about the task condition was distributed in the network. There was no single connection that was either necessary or sufficient for the classification, as revealed by the knock-out and univariate analyses. Thus, it is the combined integration of the entire network that alters between the two task conditions. The weights of the classifier cannot be replaced by the average within- versus between-hemisphere connectivity. Noninformative connections with low weights in the classifier might increase the noise in the mean within- or between-hemisphere connectivity. Finally, classification based on the mean activation within ROIs did not show significant classification accuracies. The functional connectivity pattern as the input to the classifier not only resulted in better (though not significantly better) accuracy, it also allowed us to interpret our finding in terms of functional integration and thus links our results to an important theory about how different tasks might bias the functional connectivity within cortex (Miller and Cohen, 2001).

It is important to note that the classification here was performed across subjects, which distinguishes our results from most other decoding studies, where classification is usually performed within subjects (Haynes and Rees, 2005, 2006; Kamitani and Tong, 2005). Within-subject classifiers can look at the fine-grained voxel pattern and thus might be more powerful in many cases. However, they cannot generalize to new subjects. Although across-subject classification has to deal with individual subject differences, an additional noise source, none of the within-subject classifications resulted in higher accuracies. Thus, large-scale connectivity structures might be highly suited for robust classification across subject. Although the detailed analysis of large-scale brain networks using graph theory has gained a lot of attention in the last few years (Hagmann et al., 2008; Bullmore and Sporns, 2009), only a few studies have used functional or effective connectivity graphs to classify brain data. Disease states have been successfully predicted from the correlation structure in a predefined network (Craddock et al., 2009). Other studies have successfully used wavelets (Richiardi et al., 2011) or dynamic causal models (Brodersen et al., 2011) to create the connectivity graphs for the classification.

In summary, here we have shown that the human brain prepares for specific stimulus response mappings by altering its large-scale functional connectivity structure. Specifically, the correlation structure in a bilateral network of sensory and motor areas can be used to predict the current task condition during the preparatory phase across subjects. Interestingly, the weight pattern of the linear classifier suggests that the areas that need to work together for a specific mapping increase their functional integration already during a preparatory period.

Notes

Supplemental material for this article is available at http://sites.google.com/site/hayneslab/publications/supplementary-information. A video of the visual stimulation of the paradigm is provided as online material on the authors' website. This material has not been peer reviewed.