Abstract
Introduction:
Many chronic disorders have genomic etiology, disease progression, clinical presentation, and response to treatment that vary on a patient-to-patient basis. Such variability creates a need to identify characteristics within patient populations that have clinically relevant predictive value in order to advance personalized medicine. Unsupervised machine learning methods are suitable to address this type of problem, in which no a priori class label information is available to guide this search. However, it is challenging for existing methods to identify cluster memberships that are not just a result of natural sampling variation. Moreover, most of the current methods require researchers to provide specific input parameters a priori.
Method:
This work presents an unsupervised machine learning method to cluster patients based on their genomic makeup without providing input parameters a priori. The method implements internal validity metrics to algorithmically identify the number of clusters, as well as statistical analyses to test for the significance of the results. Furthermore, the method takes advantage of the high degree of linkage disequilibrium between single nucleotide polymorphisms. Finally, a gene pathway analysis is performed to identify potential relationships between the clusters in the context of known biological knowledge.
Datasets and Results:
The method is tested with a cluster validation and a genomic dataset previously used in the literature. Benchmark results indicate that the proposed method provides the greatest performance out of the methods tested. Furthermore, the method is implemented on a sample genome-wide study dataset of 191 multiple sclerosis patients. The results indicate that the method was able to identify genetically distinct patient clusters without the need to select parameters a priori. Additionally, variants identified as significantly different between clusters are shown to be enriched for protein-protein interactions, especially in immune processes and cell adhesion pathways, via Gene Ontology term analysis.
Conclusion:
Once links are drawn between clusters and clinically relevant outcomes, Immunochip data can be used to classify high-risk and newly diagnosed chronic disease patients into known clusters for predictive value. Further investigation can extend beyond pathway analysis to evaluate these clusters for clinical significance of genetically related characteristics such as age of onset, disease course, heritability, and response to treatment.
Keywords: Unsupervised machine learning, Clustering analysis, Genomic similarity, Multiple Sclerosis
Graphical abstract
1. Introduction
With advancements in genome-wide association study (GWAS) techniques and the advent of low cost genotyping arrays, researchers have developed a significant interest in applying Machine Learning (ML) methods to mine knowledge from patients’ genomic makeup [1,2]. This knowledge has allowed researchers to improve gene annotation and discover relationships between genes and certain biological phenomena [3,4].
The fields of personalized and stratified medicine benefit greatly from ML. For example, many cases in the field of pharmacogenetics have identified genetic variants with clinically actionable impacts on drug response and metabolism [5,6]. Moreover, many chronic disorders (e.g., asthma, diabetes, Crohn’s disease) have genomic etiology, clinical presentation, and response to treatment that vary on a patient-to-patient basis. Such variability reveals a need to identify characteristics within patient populations that have clinically relevant insights. For example, Multiple Sclerosis (MS) is a chronic inflammatory disorder in which progressive autoimmune demyelination and neuron loss occur in the central nervous system. MS varies from patient-to-patient in genomic etiology, disease progression, clinical presentation, and response to treatment. Hence, MS patients, like other chronic autoimmune patients, could benefit from ML methods that advance personalized medicine.
Machine learning methods are commonly classified into supervised and unsupervised methods. Supervised methods, such as Support Vector Machines [7] and Random Forests [8,9], have been extensively used in the field of bioinformatics. These methods classify new objects to a determinate set of discrete class labels while minimizing an empirical loss function (e.g., mean square error). However, supervised methods require the use of a training set that contains a priori information of several objects’ class labels. In contrast, unsupervised methods do not require a training set that contains a priori information of objects’ class labels as input. Unsupervised methods are able to detect potentially interesting and new cluster structures in a dataset. Moreover, they can be implemented when class label data is unavailable. Hence, if the objective of a study is to discover the class labels that best describe a set of data, unsupervised machine learning should be implemented in place of supervised methods [2]. However, it is challenging for existing unsupervised ML methods to identify object memberships that are due to the underlying cluster structures in the dataset, rather than the results of natural sampling variation [10]. Moreover, most current methods require researchers to provide certain input parameters a priori (e.g., number of clusters in the dataset), which can limit their applicability.
In light of the limitations of existing methods and the need to advance personalized medicine, an unsupervised machine learning method to cluster patients based on their genomic similarity is presented. The method integrates statistical analysis that accounts for family-wise-error rate, allowing the method to identify clusters resulting from the underlying structure of the data and not just due to random chance. Moreover, the method takes advantage of the high degree of linkage disequilibrium between Single Nucleotide Polymorphisms (SNP) by pruning correlated nearby SNPs, which helps reduce redundant variants in the dataset. Finally, a gene pathway analysis shows the potential relationships between the clusters in the context of known biological knowledge. The proposed method is capable of clustering patients based on their genomic similarity without a priori information. Moreover, it is capable of identifying the significant variants (i.e., SNPs) between patient sub-groups within a cohort with a common disorder. Successfully identifying distinct genetic subtypes of patients within genomic datasets demonstrates the potential of this method to advance personalized medicine of complex diseases with heritable components, especially autoimmune disorders which have many shared susceptibility loci [11].
2. Literature review
In the last decade, the field of bioinformatics has seen a significant number of publications implementing unsupervised machine learning methods, such as clustering algorithms [12–14]. Clustering algorithms partition data objects (e.g., genes, patients) into groups (i.e., clusters), with the objective of exploring the underlying structure on a dataset [15]. In the medical field, these algorithms have been implemented to identify sets of co-expressed genes [16], compare patients’ prognostic performance [17], cluster patients based on their medical records [18], and identify subgroups of patients based on their symptoms and other variables [19].
In previous work, genomic stratification of patients (i.e., stratified medicine) has been able to match specific therapy recommendations to genetic subpopulations by predicting therapeutic response [5,6]. However, most of these studies implemented class label data (i.e., response to treatment) to cluster patients. In clinical datasets, class label information is not widely available for convenient patient clustering. Unsupervised machine learning methods can be used in such cases to identify clusters within the dataset. Further investigation of genetic subgroups within a cohort of patients can offer a better clinical prediction of age of onset, disease course, heritability, and response to therapy, leading to improved outcomes [20].
2.1. Hierarchical clustering algorithms.
Agglomerative hierarchical clustering algorithms are one of the most frequently used algorithms in the biomedical field [21,22]. Researchers have found that hierarchical clustering algorithms tend to perform better than other algorithms (e.g., k-means, partitioning around Medoids, Markov clustering) when tested on multiple biomedical datasets [23]. The objective of any agglomerative hierarchical clustering algorithm is to cluster a set of n objects (e.g., patients, genes) based on an n × n similarity matrix. These clustering algorithms have grown in popularity due to their capability to simultaneously discover several layers of clustering structure, and visualize these layers via tree diagrams (i.e., dendrogram) [10]. Even though these algorithms allow for easy visualization, they still require preselecting a similarity height cut-off value in order to identify the final number of clusters. In other words, it still requires researchers to know a priori the number of cluster in the dataset.
Agglomerative hierarchical clustering algorithms can be implemented with different linkage methods. For example, Ahmad et al. (2016) [17] implemented the Ward’s linkage method to compare patients’ prognostics performance; while Hamid et al. (2010) [19] implemented the Complete linkage method to identify unknown sub-group of patients. Unfortunately, depending on the underlying structure of the data, different clustering results can be obtained by implementing different linkage methods. Ultsch and Lotsch (2017) [24] demonstrated that neither the Single nor Ward’s linkage methods provided similar clustering results when tested with the Fundamental Clustering Problem Suite (FCPS) datasets [25]. Their results reveal that these linkage methods were able to correctly cluster all the objects in only a subset of the FCPS datasets. Similarly, Clifford et al. (2011) [26] discovered that while testing multiple simulated GWAS datasets, the linkage methods of Median and Centroid were the only ones to consistently be outperformed by the Single, Complete, Average, Ward’s, and McQuitty methods. In light of these, Ultsch and LÖtsch (2017) [24] proposed the use of emergent self-organizing map to visualize clustering of high-dimensional biomedical data into two-dimensional space. Even though, their method allowed for better visualization, it still required preselecting the number of clusters as well as other parameters to perform correctly (e.g., toroid grid size) [24].
2.2. Parameter selection in clustering algorithms.
In order to avoid preselecting input parameters a priori (e.g., the number of clusters), researchers have implemented cluster validation metrics. For example, Clifford et al. (2011) [26] proposed a method that aimed to capture the clustering outcome of multiple combinations of linkage method and similarity metric based on the Silhouette index [27]. The Silhouette index was used to rank the results of the clustering combinations, and select the best cluster set (i.e., cluster set with largest average Silhouette index). Similarly, Pagnuco et al. (2017) [16] presented a method that implemented several linkage methods and implemented modified versions of the Silhouette and Dunn indices [28] to select the final clustering results. Both the Silhouette and Dunn indices served as internal cluster validation metrics (i.e., no external information needed) to guide the selection of the final cluster set. However, the Silhouette index has been shown to have a stronger correlation with external cluster validation metrics, such as the Rand Index, than the Dun index [28,30].
The methods of Clifford et al. (2011) and Pagnuco et al. (2017) did not require selecting the number of clusters a priori due to the internal cluster validation metrics implemented. These metrics allow for algorithmic selection of the number of clusters. Nonetheless, the computational complexity of testing all potential clusters increases linearly with the number of objects in the dataset. Other studies have implemented model-based clustering methods to overcome these limitations. For example, Sakellariou et al. (2012) [29] implemented an Affinity Propagation [30] algorithm to identify relevant genes in microarray datasets. Shen et al. (2009) [31] implemented an Expectation-Maximization algorithm [32] to cluster genes based on an integration of multiple genomic profiling datasets. However, models based methods make underlying assumptions that might not be applicable in certain datasets [33].
Recently, Khakabimamaghani and Ester (2016) [34] presented a Bayesian biclustering method to identify clusters of patients. They benchmarked their method against the multiplicative Nonnegative Matrix Factorization (NMF) algorithm proposed by Lee and Seung (2001) [35]. Their results revealed that their Bayesian biclustering method was more effective in patient stratification than the NMF. While this Bayesian biclustering method did not require selecting the number of clusters a priori, it did require selecting parameters for prior probability distributions. The capability of biclustering algorithms to discover related gene sets under different experimental conditions, have made them popular within the bioinformatics community [36]. One of the first works in this area was presented by Cheng and Church (2000) [37]. They proposed an iterative greedy search biclustering algorithm to cluster gene expression data. Even though their method did not require selecting the number of clusters a priori, it did require the selection of hyperparameters (e.g., maximum acceptable error).
2.3. Statistical significance of clustering results.
Even though the methods of Clifford et al. (2011) and Pagnuco et al. (2017) aimed to find the optimal clustering outcome from multiple algorithms, which resembled the consensus clustering approach (i.e., approach in which a solution is identified by validating multiple outcomes) [38], their methods did not account for possible clustering memberships arising due to random variation. Whether identified clusters memberships are due to underlying cluster structures in the data or are just a result of the natural sampling variation, is a critical and challenging question that needs to be addressed when clustering high-dimensional data [10]. To address this question, Suzuki and Shimodaira (2013) [39] presented the pvclust R package, which calculates probability values for each cluster using nonparametric bootstrap resampling techniques. Even though pvclust allows for parallelized computing, it requires significant time (i.e., 480 mins) when implemented in genomic datasets. This is due to the large number of resampling iterations (i.e., 10,000) required to reduce the error rate [39]. In contrast, Ahmad et al. (2016) [17] applied a non-parametric analysis of variance (ANOVA) Kruskal-Wallis test to compare the clusters within a hierarchical clustering method. Similarly, Bushel et al. (2002) [40] implemented a single gene parametric ANOVA test to assess the effects of genes on hierarchical clustering results. Recently, Kimes et al. (2017) [10] proposed a method based on a Monte Carlo approach to test the statistical significance of hierarchical clustering results while controlling for family-wise-error rate. However, family-wise-error rate can also be controlled while applying repetitive statistical tests by implementing a Bonferroni correction [41].
2.4. Integrating domain knowledge into clustering algorithms
Other frequently used clustering algorithms in the bioinformatics field are k-means and fuzzy c-means. However, these algorithms require initial random assignments of the clusters, which can produce inconsistent results [26]. Hence, they might fail to converge to the same results, even after multiple initiations using the same dataset [21]. In light of these limitations, Tari et al. (2009) [21] proposed the “GO Fuzzy c-means” clustering algorithm. Their method resembles the fuzzy C-mean algorithms [42] and implements Gene Ontology annotation [43] as biological domain knowledge to guide the clustering procedure. Even though this method assigned genes to multiple clusters, which could have improved the biological relevance of the results, it was not capable of discriminating the cluster memberships that were assigned due to random chance. While the algorithm parameters selected in this study might have been reasonable for the dataset analyzed, the authors highlighted that future studies would need to experimentally determine these parameters. Similarly, Khakabimamaghani and Ester (2016) [34] integrated domain knowledge via the selection of parameters for prior probability distributions. However, their results reveal that the selection of these parameters had a direct impact on their clustering results. When analyzing the effects of priors, the authors indicate that “final selected priors favor better sample clustering over better gene clustering” [34]. These findings reveal that the parameters need to be carefully selected since they can bias their method towards better sample clustering rather than better gene clustering results.
Researchers can implicitly integrate domain knowledge to their methods by judiciously selecting the input data of their algorithms [2]. Genomic datasets may include relevant features as well as correlated and non-informative features. The presence of correlated and non-informative features might obscure relevant patterns and prevent an algorithm from discovering the underlying cluster structure of a dataset [19]. Genomic data is generally high-dimensional because the number of features is frequently greater than the number of samples. Additionally, genetic variants are commonly correlated with other variants in close proximity on DNA. Therefore, when clustering genomic data, it is important to prune non-informative and correlated features [2,9].
Highly correlated SNPs are said to be in Linkage Disequilibrium (LD). This characteristic makes it challenging for unsupervised ML algorithms to discover relevant cluster structures in the dataset. GWA studies present significant associations as tag SNPs, implying a true causal SNP can be found within the LD block of a tagged location [11]. LD pruning refers to removing highly correlated SNPs within LD blocks. For example, Yazdani et al. (2016) [44] identified a subset of informative SNPs based on a correlation coefficient. Similarly, Goldstein et al. (2010) [9], implemented several correlation coefficient cut-off values (e.g., 0.99, 0.9, 0.8, 0.5) to remove SNPs with high LD. They achieved this by using the toolsets for Whole-Genome Association and Population-Based Linkage Analyses (PLINK) [45], resulting in a reduction of up to 76% of the original dataset. This reduction decreased the computational complexity of their method [9]. However, researchers have not agreed yet on a standard correlation coefficient cut-off value that can be applied to every genomic dataset to reduce complexity without incurring in significant information loss.
Table 1 shows a summary of the current clustering methods in the field of bioinformatics applied to genomics data. It can be shown that multiple methods prune the SNPs of their datasets based on the degree of LD between nearby SNPs. This is done in order to guide their clustering search and remove potentially non-informative features. However, the vast majority of existing methods still require preselecting the number of clusters and other parameters a priori (e.g., prior probability distributions, toroid grid size). Moreover, the current methods do not commonly implement statistical analysis to test for the significance of their results, or to account for possible family-wise-error rates.
Table 1.
Summary of current methods
| Papers | LD Pruning | Automatic selection of k * | Statistical tests performed | No selection of parameters requiredǂ |
|---|---|---|---|---|
| [9,11,19,21] | X | |||
| [40] | X | X | ||
| [16,26,29,31,34,35,37] | X | |||
| [10, 17, 39, 46], | X | |||
| This work | X | X | X | X |
k is the parameter defining the number of cluster in the dataset.
No parameters or hyperparameters are required to be known or selected a priori by researchers (e.g., prior probability, toroid grid size).
In light of the aforementioned limitations, an unsupervised machine learning method is presented in this work that seeks to identify sub-groups within cohorts of patients afflicted with the same disease. This is done by clustering patients based on their genomic similarity without the need of a priori input parameters. The method presented in this work takes advantage of LD between SNPs by pruning correlated SNPs. In addition, it automatically selects the number of clusters by implementing an internal validation metric. The method ensembles the clustering outcomes of multiple linkage methods via a majority vote approach. Subsequently, it tests for statistical significance among results while accounting for family-wise-error rate. Finally, a gene pathway analysis is performed to support the potential medical significance of the results.
3. Method
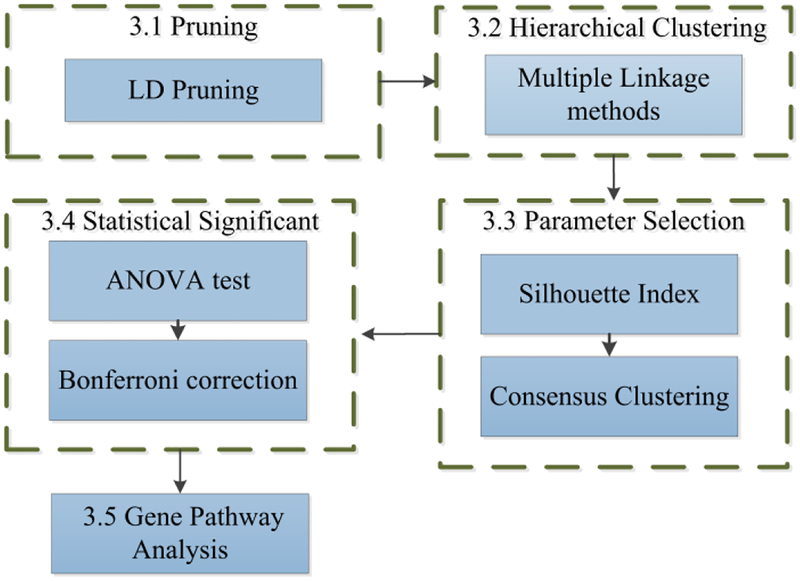
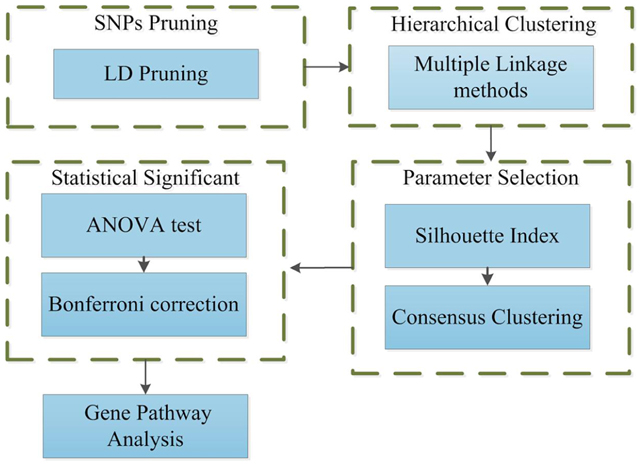
An unsupervised machine learning method is presented that does not require selection of input parameters a priori. The method can help identify patient cluster structures within genomic data and potentially discover valuable differences between them. This knowledge can be used to advance personalized medicine of complex diseases with heritable components, especially autoimmune disorders which have many susceptibility loci. Fig. 1 shows an outline of the method presented in this work.
Figure 1. Outline Method.
3.1. Linkage Disequilibrium Pruning
Pruning SNPs based on LD serves as a feature reduction step. Thus, in the proposed method, SNPs that are strongly correlated to other nearby SNPs are pruned, as previously done in the literature. The degree of LD between SNPs is assessed by calculating the correlation coefficients based on a sliding window method. In this method, cut-off values of (i) 0.999, (ii) 0.99, (iii) 0.9, (iv) 0.8 and (v) 0.5 are employed. Previous studies have shown these cut-off values provide a balance between error reduction and information loss [9]. Hence, five subsets of patients’ genomic data containing different sets of SNPs (i.e., features) are generated. The subsets generated serve as input for the hierarchical clustering step.
3.2. Hierarchical Clustering
The objective of the unsupervised machine learning method presented in this work is to cluster patients based on their genomic similarity. Patients’ genomic similarity can be evaluated using a wide range of distance metrics [26]. The selection of the appropriate distance metric is driven by the type of data under analysis (e.g., ratio, interval, ordinal, nominal or binary scale). For example, the Euclidian distance is appropriated for ratio or interval scale data, while the Manhattan distance for ordinal scale data [47].
Subsequently, the method presented in this work employs an agglomerative hierarchical clustering algorithm. Hierarchical clustering algorithms are frequently used with only one linkage method, which can limit their ability to identify underlying cluster structures in certain datasets [24]. Hence, in this work, multiple linkage methods are implemented. The linkage methods used in this work have been shown to consistently outperform other methods when tested with simulated GWAS datasets [26]. The cluster results obtained by implementing different linkage methods are ensemble in the subsequent steps. This ensemble takes advantage of the performance of multiple linkage methods. Moreover, it helps identify the underlying structure of the data, since the ensemble approach will favor cluster structures identified by the majority (i.e., via a majority vote approach) of the linkage methods. Specifically, the authors propose to implement:
Single Linkage (or Minimum Linkage).
Complete Linkage (or Maximum Linkage).
Average Linkage (or Unweighted Pair Group Method with Arithmetic Mean, UPGMA).
Ward’s Linkage.
McQuitty Linkage (or Weighted Pair Group Method with Arithmetic Mean, WPGMA).
3.3. Parameter Selection
Once the agglomerative hierarchical algorithm is implemented, the Silhouette index is employed as an internal validity metric. This index has been used in previous studies to rank the results of multiple clustering algorithms outcomes and guide the selection of final clusters [16],[26]. Nonetheless, in this method, the index is used to select the number of clusters for all combinations of LD pruning data subsets (see section 3.1) and linkage methods (see section 3.2). The number of clusters that provides the largest average Silhouette index value in each of the combinations is selected.
The computational complexity of testing all possible numbers of clusters increases linearly as the number of objects in a dataset increases. This can be a challenge in datasets that contain a large number of objects, even with parallelized computing. In this work, an optimization approach is presented to identify the number of clusters that maximizes the average Silhouette index. The mathematical formulation of this optimization problem is as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Where,
SI: is the average Silhouette index of the clusters set K
K: is the set of clusters obtained with the hierarchical clustering algorithm for a given number of k disjoint clusters
ni is the number of objects that belongs to cluster Ci, for
i ∊ set of clusters {K}
S(x):is the Silhouette of object x, for x ∊Ci;
a(x)is the average similarity of object x with all other objects that belong to the same cluster of x (i.e., Ci)
b (x): is the average similarity of object x with the objects from the nearest clusters Cw, for w ∊ set of cluster{k},i ≠ w
Eq. (1) represents the objective function that needs to be maximized (i.e., the average Silhouette index). Eq. (2), shows the mathematical representation of the average Silhouette index, while Eq. (3) shows the silhouette of a given object x. Both Eq. (4) and (5) represent the elements that constitute the index of a given object x [27]. Finally, Eq. (6) constrains the search for the number of clusters to be greater than 1 and less than the total number of objects n (i.e., the maximum number of clusters). Since the objective function is non-linear with respect to the parameter k (i.e., number of clusters), this optimization problem needs to be solved with a non-linear optimization algorithm. In the literature, there are several algorithms suitable to solve this type of optimization problem [48]. Nonetheless, the method is not constrained to any specific optimization algorithm.
Once the number of clusters is identified in all datasets combination, the results are aggregated into a final cluster set via a majority vote approach. Table 2 shows an example of this consensus clustering approach in which patient i is assigned to the final cluster 1 since the majority of the cluster results assigned that patient to that given cluster. Similarly, patient n is assigned to the final cluster 2, since the majority of clusters assigned this patient to this cluster
Table 2.
Example of consensus clustering
| No. | LD Pruning | Linkage Method | Patient i cluster | Patient n cluster | |
|---|---|---|---|---|---|
| 1 | 1 | Single | 1 | 2 | |
| 2 | 0.99 | Single | 1 | 2 | |
| 3 | 0.90 | Single | 1 | 1 | |
| 4 | 0.8 | Single | 1 | 2 | |
| 5 | 0.5 | Single | 2 | 1 | |
| ⋯ | ⋯ | ||||
| 24 | 0.8 | McQuitty | 2 | 2 | |
| 25 | 0.5 | McQuitty | 1 | 2 | |
| Final Cluster | 1 | 2 | |||
3.4. Statistical Significance
After the final patient clusters are discovered, a single SNP ANOVA test is performed to reveal the SNPs that are statistically significantly different between the clusters of patients. This step helps validate that the clusters generated are different by at least one associated SNP. To account for family-wise-error-rate a Bonferroni correction is applied by dividing the alpha value by the number of tested SNPs. In the case that no SNPs are found to be statistically significantly different, it can be concluded that the resulting patients’ clusters might have arisen due to random chance.
3.5. Gene Pathway Analysis
The set of SNPs significantly associated with differences between patient clusters can be explored via Gene Ontology (GO) enrichment and mutational burden on molecular pathways. By assigning each SNP to a gene and performing a gene network analysis, (e.g., via STRING-DB software [49]), visualizations of gene networks and estimations of significant enrichment along GO terms could provide evidence for potential biological significance. The significance is assessed by comparing the number of evidence-based relationships between selected genes to the number expected in a set of randomly selected genes. If an enrichment is established, the related genes are examined by their molecular function, biological relevance, and known associations to the disease from GWA studies. While pathway analysis does not provide the rig or of direct experiment or clinical trial, it remains valuable in determining whether selected genes are functionally relevant to the disease studied, as opposed to being a function of other factors such as ethnicity.
4. Application
The performance of the proposed method is first tested on the datasets presented in the Fundamental Clustering Problem Suite (FCPS) [25]. The FCPS contains 10 different datasets designed to assess the performance of unsupervised machine learning algorithms on particular clustering challenges (e.g., outliers, undefined cluster boundaries). The ground truth data of cluster membership are used to test the performance of the method in identifying clusters resulting from the underlying structures in the data and not just from random variation. To measure this performance, the Rand index [50] validation metric is employed. Moreover, the performances of other existing methods in the literature are benchmarked with the same datasets. All the benchmark analyses were performed on a 12 Core i7 3.4 GHz Intel™ computer with 62.8 GB of RAM and Ubuntu 16.04 LTS. The benchmark methods were implemented in R v.3.4 [51] with the used of the packages mclust v.5.3 [52], apcluster v.1.4.4 [53], DatabionicSwarm v.0.9.8 [54,55], NNLM v.0.4.1 [35], and biclust v.1.2.0 [56].
Two genomic datasets are used to compare the performance of the proposed method against other state of the art methods in the literature. The benchmark methods include those that donot require providing the number of cluster a priori. I.e., Clifford et al. (2011) [26]: hierarchical clustering algorithm with silhouette index, Sakellariou et al. (2012) [29]: Affinity Propagation clustering algorithm, Shen et al. (2009) [31]: Expectation Maximization clustering algorithm, and Cheng and Church (2000) [37]: Iterative Greedy Search Biclustering algorithm. Frist, the microarray gene expression data of patients with lymphoblastic and acute myeloid leukemia from Golub et al. (1999) [57] was implemented. The dataset is publically available at the Broad Institute and has been previously used to test the performance of clustering algorithms [23,58]. The dataset is composed of microarray gene expression data of 999 genes for 27 patients with acute lymphoblastic leukemia and 11 patients with acute myeloid leukemia.
Lastly, a dataset of patients diagnosed with MS is employed. DNA samples from 191 Multiple Sclerosis (MS) patients consented via the Pennsylvania State University PRIDE protocol at Hershey Medical Center were subjected to the Immunochip assay (Illumina). Allelic variations were measured at previously described susceptibility loci for multiple immune-mediated disorders [59,60]. The Y chromosome data were filtered out of the dataset to simplify comparisons in a predominantly female cohort. Mitochondrial markers were discarded for analysis as well. Genotype calling was done with Illumina GenomeStudio v.2011.1 (www.illumina.com), and genotype markers were excluded if their GenTrain score was less than 0.8, or if their call rate across the cohort was less than 0.99. Finally, the MS dataset was filtered such that only variants within coding regions (i.e., exons), were considered. Therefore, the MS dataset was composed of 191 patients and 25,482 SNPs.
With the MS dataset, a 10-fold cross-validation analysis was performed with the objective to test the performance of the proposed and the benchmark methods, as well as to provide evidence regarding their propensity of overfitting genomic datasets. In this cross-validation approach, the MS dataset was randomly partitioned into 10 subsets. Subsequently, the methods were used to cluster the patients within these subsets. The clustering results obtained from the 10 subsets were compared to those from the complete dataset. The agreement between the clusters generated with the complete MS dataset and the 10-fold subsets is assessed with the Rand index metric. A match between the clustering results (e.g., average Rand index of 1) will indicate that the proposed method was not overfitting the MS dataset, thus, providing arguments of its generalizability. Moreover, it will support that the method was identifying clusters due to underlying structures in the data and not just due to random variations. Finally, the groups of SNPs identified by the proposed method to achieve statistical significance between clusters generated were examined via gene pathway analysis.
4.1. Linkage Disequilibrium Pruning
For the MS dataset, the pruning of SNPs with a high LD was done based on the correlation-coefficient cut-off values found in the literature, as proposed in section 3.1. LD pruning was performed using the widely used genotype analysis toolset for Whole-Genome Association and Population-Based Linkage Analyses (i.e., PLINK) [45]. This pruning resulted in a reduction of the original dataset as presented in Table 3. These percentages of SNPs removed are consistent with the results found in previous studies.
Table 3.
LD Pruning summary
| R2 cut-off value | Number of SNPs retained | Percentage of SNPs removed |
|---|---|---|
| 0.50 | 5,460 | 78.57% |
| 0.80 | 6,849 | 73.12% |
| 0.90 | 7,421 | 70.88% |
| 0.99 | 8,666 | 65.99% |
| 0.999 | 8,691 | 65.89% |
4.2. Hierarchical Clustering
The FCPS and Golub et al. (1999) [57] datasets contain features that are in ratio scale. Hence, to measure the similarity between the objects in the datasets, the Euclidian distance is implemented. Genotype data can be ordinal or additive scale, depending on whether heterozygous SNPs are treated as a label or as a half-dosage. While additive models are more often used for GWA studies, in this work, ordinal scale was used to demonstrate flexibility in the described clustering method. Hence, the genomic similarity of MS patients based on different subsets of pruned data is evaluated using the Manhattan distance metric. The similarity calculations and the agglomerative hierarchical algorithm with multiple linkage methods were performed in R v.3.4 [51].
4.3. Parameter Selection
The selection of the number of clusters k that maximized the average Silhouette index was performed with a generalized simulation annealing algorithm. This algorithm was selected due to its underlying theory and proven performance in problems with non-linear objective functions [61,62]. The algorithm was implemented via the R package GenSA v.1.1.6 [63]. Nonetheless, other non-linear optimization algorithms or greedy heuristics can also be implemented. Once the number of clusters in every combination of LD pruned data and linkage method are selected, the clustering results are ensemble via a majority vote approach (see section 3.3).
4.4. Statistical Significance
After the final clusters have been selected based on the average Silhouette metric and consensus clustering approach the statistical significance of the results is evaluated. Clusters’ median values for each of the p features in the MS dataset are evaluated via a single SNP non-parametric ANOVA Kruskal-Wallis test [46]. To account for family-wise-error rate, a Bonferroni correction is applied to the significance alpha level of 0.05 (i.e., Bonferroni correction= 0.05/p, for p= 25,482).
4.5. Gene Pathway Analysis
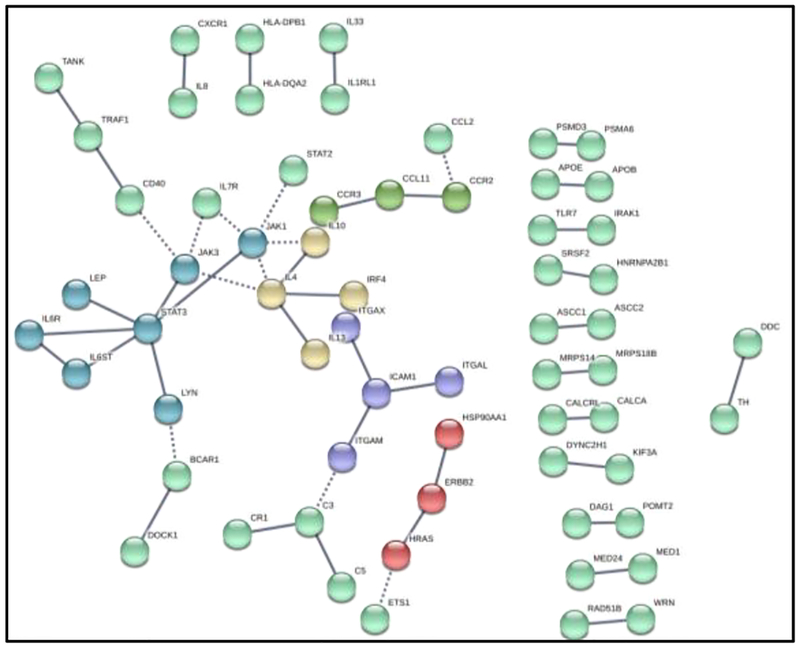
Gene variants that show statistical significance are further analyzed via a gene pathway analysis to explore their potential medical significance. Pathway analysis starts with generating a list of genes determined from the set of SNPs with strong evidence of significance between patient clusters. Inputting the gene set via the STRING-DB software algorithms [49] allows for convenient calculation of pathway enrichment hypothesis tests and visualization of the gene network. STRING-DB determines gene relationships by aggregating several databases into an evidence score. Experimental evidence comes from the BIND [64], GRID [65], HPRD [66], IntAct [67], MINT [68], and PID[69] databases. In addition, STRING-DB pulls from the curated databases KEGG [70], Gene Ontology [43], BioCarta [71], and Reactome [72]. Interaction frequency is tested for enrichment compared to expectation from a random sampling of genes, with p-values and false discovery rates reported for enrichment in specific cellular processes, defined by Gene Ontology references. After statistical testing is done, the gene network is used as a threshold for high confidence interaction and a k-means clustering algorithm is performed for visualization purposes (see Fig. 6).
Figure 6. Gene Pathway Analysis results.
5. Results
5.1. FCPS Benchmark results
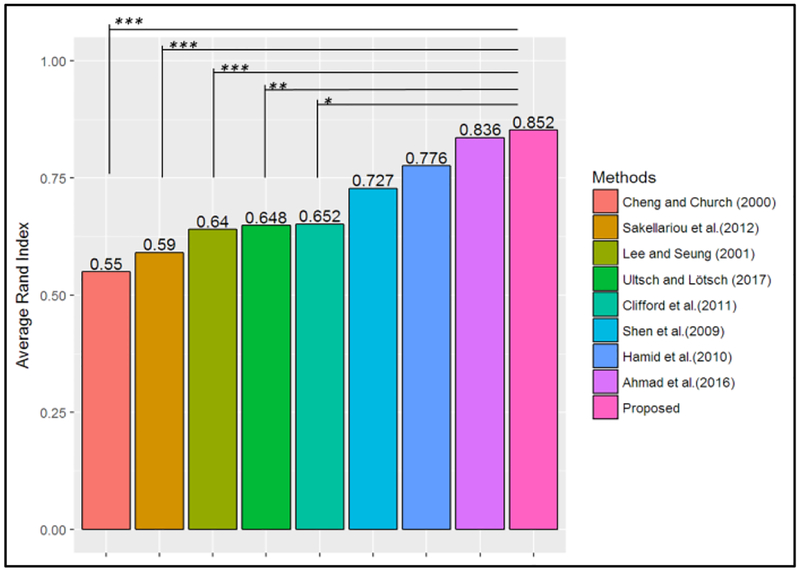
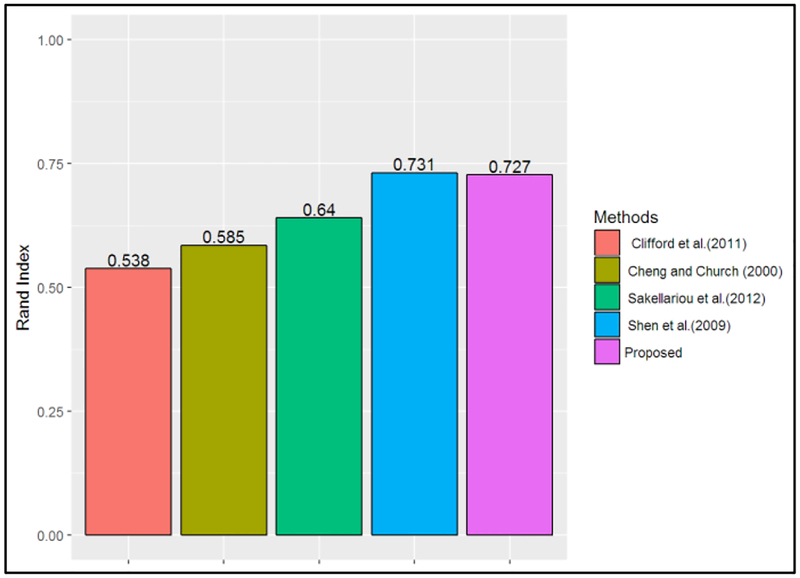
The majority of existing methods in the literature require the selection of parameters a priori (e.g., number of clusters, see Table 1). Hence, to benchmark with multiple methods, the number of clusters provided by the FCPS was used as input when testing these methods. Figure 2 shows the average Rand index obtained in the FCPS datasets by the method proposed in this work (i.e., Proposed) and the methods benchmarked. This plot shows that on average the proposed method outperformed other methods, with an average Rand index of 0.852. The performance is statistically significantly greater than the results of the methods proposed by Cheng and Church (2000), Sakellariou et al. (2012), Lee and Seung (2001), Ultsch and Lotsch (2017), and Clifford et al. (2011). Even though these results indicate that, on average, the proposed method achieved the largest Rand index, there is not enough evidence to conclude that it was statically significantly greater than the Rand index achieved by the methods of Shen et al. (2009), Hamid et al. (2010), or Ahmad et al. (2016), at an alpha level of 0.05. This can be attributed to the relatively small group of validation datasets provided in the FCPS (i.e., 10 datasets).
Figure 2. Average Rand index for FCPS datasets.
Note: p-value: <0.001***, <0.01**, <0.05*
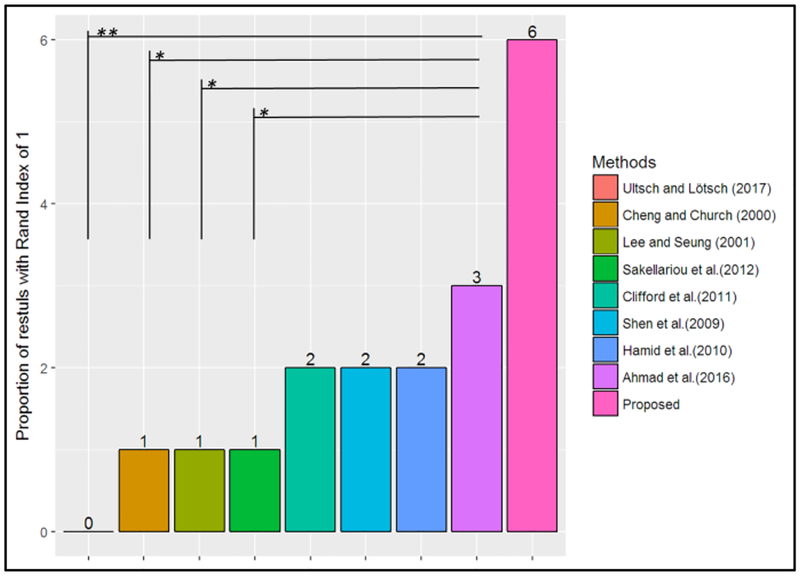
Similarly, Figure 3 shows the proportion of the FCPS datasets that achieved a clustering result with a Rand index of 1 (i.e., perfect clustering) for each of the given methods. The results reveal that the proposed method was able to obtain a Rand index of 1 in 6 out of the 10 FCPS datasets. The results from the Wilcoxon tests indicate that these results are statistically significantly greater than the results of the methods proposed by Ultsch and Lotsch (2017), Cheng and Church (2000), Lee and Seung (2001), and Sakellariou et al. (2012). Even though the results indicate the proposed method correctly clusters the largest percentages of datasets (i.e., 6/10), there is not enough evidence to conclude that this proportion is statically significantly greater than the ones from the other methods benchmarked, at an alpha level of 0.05. Nevertheless, these results provide evidence that the method presented in this work is able to identify true clusters in a wider range of datasets with different underlying structures.
Figure 3. The proportion of results with Rand index of 1 for FCPS datasets.
(i.e., perfect clustering)
Note: p-value: <0.001***, <0.01**, <0.05*
5.2. Genomic dataset Benchmark results
Figure 4 presents the Rand index obtained on the Golub et al. (1999) dataset [57] by the method proposed in this work and the benchmark methods that do not require providing the number of clusters a priori. Fig. 4 indicates that the proposed method performed better than the methods presented by Clifford et al. (2011), Cheng and Church (2000), and Sakellariou et al. (2012).
Figure 4. Rand index for Leukemia dataset.
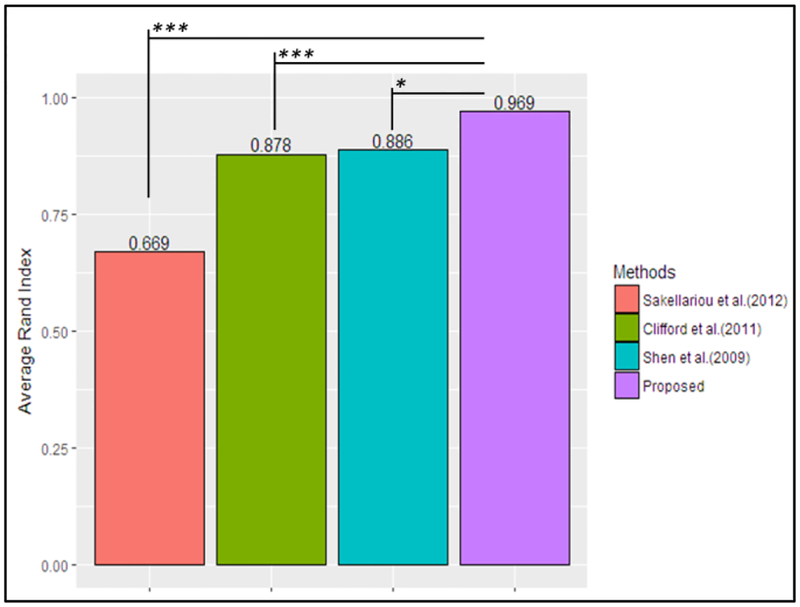
Figure 5 shows the average Rand index obtained with the MS dataset and the 10-fold cross-validation approach by the proposed and benchmark methods. The iterative greedy search Biclustering algorithm proposed by Cheng and Church (2000) was not able to find any cluster structure in the MS dataset; hence it was not included in this plot. The plot shows that on average the proposed method outperformed the other methods, with an average Rand index of 0.969. This is statistically significantly greater than the values obtained with the other methods benchmarked. Moreover, the average Rand index obtained by the proposed method was not significantly different than an average Rand index of 1 (t-value: −1.963, p-value=0.0812), at an alpha level of 0.05. This reveals that on average the proposed method found a perfect match between the clusters of patients obtained with the complete MS dataset and the cross-validation subsets.
Figure 5. Average Rand index for MS dataset.
Note: p-value: <0.001***, <0.01**, <0.05*
Table 4 shows the confusions matrix of the clusters obtained with the proposed method when implementing the 10-fold cross-validation approach. The table indicates that the proposed method was able to group 96.33% of the patients’ in the same clusters when both the complete dataset and the different data subsets were used (i.e., accuracy of 0.96), which is in line with the average Rand index of 0.969 shown in Fig. 5. The Rand index and confusion matrix results indicate that the proposed method identified a similar cluster structure even with different subsets of the MS dataset. This indicates that the proposed method was not overfitting the dataset. Furthermore, it provides evidence that supports that the method was able to identify clusters due to the underlying structure of the data and not just due to random change.
Table 4.
MS dataset 10-fold cross-validation confusion
| Complete Dataset | |||
|---|---|---|---|
| Cluster 1 | Cluster 2 | ||
| Data Subsets | Cluster 1 | 172 | 0 |
| Cluster 2 | 7 | 12 | |
The results from the pathway analysis on the set of statistically significant different SNPs between the MS patient clusters are shown in Fig. 6. The cluster-defining SNPs show significantly more interactions than expected among a random sampling of genes. Out of 515 genes, 1,463 interactions were found, with only 942 expected by chance (p-value: 1.04e-10), among a background set of 4,938 genes present on the Immunochip. The gene interactions in the set shown in Fig. 6 demonstrate a high prevalence of cellular adhesion, cytokine response, and general immune process pathways.
Table 5 shows relationships between genes based on evidence from literature via STRING-DB [49]. The highly connected pathway depicted contains many genes known to be involved in cell adhesion and leukocyte physiology, both of which are processes dysregulated in MS [73]. Additionally, the genes selected show significant Gene Ontology term enrichment in these categories, with false discovery rates less than 0.01. Taken together, pathway analysis reveals that extracting significant features between clusters may be a valid feature reduction technique for downstream analysis. Genes known to be relevant in MS pathophysiology (e.g., interleukin receptors, STAT transcription factors, lymphocyte surface proteins from the CCR family) were highlighted despite no use of supervised methods and label data, implying that the proposed unsupervised method’s value is not just discovering patient clusters, but reducing the dimensionality by nearly 20-fold with few samples (i.e., from over 25,482 features to around 1,500, using 191 samples).
Table 5.
Gene Pathway Analysis results
| Pathway ID | Pathway Description | Count in Gene Set | False Discovery Rate |
|---|---|---|---|
| GO.0051249 | Regulation of lymphocyte activation | 32 | 0.00641 |
| GO.0002823 | Negative regulation of adaptive response | 9 | 0.00749 |
| GO.0006952 | Defense response | 73 | 0.00749 |
| GO.0002694 | Regulation of leukocyte activation | 33 | 0.00804 |
| GO.0050865 | Regulation of cell activation | 35 | 0.00804 |
| GO.0002376 | Immune system process | 93 | 0.00898 |
As a secondary observation, an analysis was done on the MS dataset after pruning samples which showed greater than 0.2 similarity in PLINK’s Identity-By-Descent (IBD) algorithm [74]. This was done to remove potentially related patients from the analysis. IBD identified a total of 11 potentially related patients, from whom 10 were initially assigned to cluster number two. Consequently, after removing these potentially related patients from the MS dataset and applying the proposed method, the number of patients in the second cluster was reduced from 12 to 2, and no pathway enrichment was detected. However, the 120 genes detected still included T-cell relevant proteins such as STAT and JAK, as well as members of the tumor necrosis factor and interleukin families, supporting the claim that the method identified SNPs relevant to the disease process even if the sample size of the smaller cluster (n=2) constrains the power of the pathway analysis. Furthermore, the cross-validation results indicate that the average Rand index achieved after removing potentially related patients (i.e., 0.932) was not significantly different than the initial cross-validation results (i.e., 0.969, see Fig. 5) (t-value: 1.52, p-value: 0.147). This reveals that the proposed method was able to identify the same underlying cluster structure in the MS dataset, and identify patients with similar genomic makeup after the removal of potentially related individuals. These results provide evidence that supports that the method was able to identify clusters due to the underlying structure of the data and not just due to random change.
6. Conclusion and future work
Many chronic disorders have genomic etiology, disease progression, clinical presentation, and response to treatment that vary on a patient-to-patient basis. Such variability creates a need to identify characteristics within patient populations that have clinically relevant predictive value. Unsupervised machine learning methods are suitable to address this type of problem, in which no class label information is available to guide this search. However, it is challenging for existing methods to identify cluster memberships that are due to the underlying structures in the dataset and not just a result of natural sampling variation. Moreover, most current methods require researchers to know and provide input parameters a priori. As a result of these limitations and the need to advance personalized medicine, this work proposed an unsupervised machine learning method to identify genomically distinct patients’ cluster. The method presented in this work integrates statistical analysis to test for significance of clustering results and accounts for family-wise-error rate. Moreover, the method is capable of automatically identifying the number of clusters by implementing an internal validity metric. Similarly, the method takes advantage of the degree of linkage disequilibrium between SNPs by pruning correlated nearby SNPs, as well as implementing a post-clustering gene pathways analysis.
The method is tested with clustering validation datasets previously used in the literature. The benchmark results reveal that proposed method provides, on average, the greatest performance (i.e., average Rand index 0.852). Moreover, results indicate that it was able to obtain cluster results with a Rand index of 1 (i.e., perfect clustering) in 6 out of the 10 Fundamental Clustering Problem Suite (FCPS) datasets. Similarly, the method is applied to a dataset of 38 patients with leukemia, and subsequently to a dataset of 191 Multiple Sclerosis (MS) patients. The results indicate that the method is able to identify genetically distinct patient clusters without the need to select the number of clusters or any input parameter a priori. Moreover, the cross-validation results indicate that the method presented in this work outperformed the other methods found in the literature when en it comes to data overfitting, since the average Rand index obtained was significantly greater than the benchmarked methods and not significantly different than 1. This performance was maintained even after the removal of potentially related patients from the dataset. This indicates that the method was identifying clusters due to the underlying structure of the data and avoided overfitting the dataset. The identification of distinct genetic subtypes of patients demonstrates the potential applicability of this process to advance personalized medicine of complex diseases with heritable components, especially autoimmune disorders.
When applied to genomic data, the method also shows value as a feature reduction strategy. Out of over 25,482 exonic SNPs and 191 patient samples, the clustering of patients yielded a set of SNPs which significantly vary between clusters. These variants represent 515 genes, several of which are known to be involved in MS (CD69, CCRX5, IL-13, STAT3) and cell adhesion (ICAM1, LAMB4). The fact that many highlighted genes are components of the immune system is not surprising due to the nature of the Immunochip assay, but the enrichment of leukocyte-specific genes is evidence that the method can result in functionally relevant feature sets, even without class labels. Notably, 57 genes representing over 10% of the network are involved in cytokine receptor processes. This is greater than expected from random chance, as cytokine receptors constitute a small percentage of all Immunochip genes. The evidence presented in this work alone is insufficient to define genetic subtypes of MS, but the specific SNP set reaching significance may be a valuable resource in experimental studies examining immune cell dynamics and genetics. For example, the hypothesis that these clusters represent different subtypes of MS, can be tested by evaluating clinical criteria such as image results and disease progression, as well as quantitative cytokine profiling and gene expression studies for each cluster, compared against random groupings of patients.
This work demonstrates an iterative unsupervised machine learning method which identifies significant patient clusters within a genomic dataset. Future research should explore the medical significance of the findings shown in this work. Similarly, the method from this work should be implemented in studies collecting SNP array and gene expression microarray data from additional disease cohorts to explore its potential benefits. Further investigation can extend beyond pathway analysis to evaluate these clusters for clinical significance of genetically relelated characteristics such as age of onset, disease course, hereritability, and response to treatment. Once links are drawn bet between clusters and clinically relevant outcomes, the Immunochip can be used to classify high-risk and newly diagnosed chronic disease patients into clusters with predictive value.
Highlights.
Patient clusters based on their genomic makeup
Discovery of significant variantsbetween patient sub-groups
Relationship between the genomic clusters and clinically relevant outcomes
Assign high-risk and chronic disease patients into a discovered cluster
Acknowledgments
The authors acknowledge the NSF I/UCRC Center for Healthcare Organization Transformation (CHOT), NSF I/UCRC grant #1624727, and the Institute for Personalized Medicine at the Pennsylvania State University. Additionally, the authors would like to acknowledge Dr. James R. Broach from the Institute for Personalized Medicine at the Pennsylvania State University, for his valuable contributions. Any opinions, findings, or conclusions found in this paper are those of the authors and do not necessarily reflect the views of the sponsors.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Leung MKK, Delong A, Alipanahi B, Frey BJ, Machine Learning in Genomic Medicine: A Review of Computational Problems and Data Sets, Proceedings of the IEEE. 104 (2016) 176–197. doi: 10.1109/JPROC.2015.2494198. [DOI] [Google Scholar]
- [2].Libbrecht MW, Noble WS, Machine learning in genetics and genomics, Nature Reviews. Genetics 16 (2015) 321–332. doi: 10.1038/nrg3920.Machine. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Upstill-Goddard R, Eccles D, Fliege J, Collins A, Machine learning approaches for the discovery of gene- gene interactions in disease data, Briefings in Bioinformatics. 14 (2013) 251–260. doi: 10.1093/bib/bbs024. [DOI] [PubMed] [Google Scholar]
- [4].Yip KY, Cheng C, Gerstein M, Machine learning and genome annotation: a match meant to be?, Genome Biology. 14 (2013) 205. doi: 10.1186/gb-2013-14-5-205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Ross CJ, Towfic F, Shankar J, Laifenfeld D, Thoma M, Davis M, Weiner B, Kusko R, Zeskind B, Knappertz V, Grossman I, Hayden MR, A pharmacogenetic signature of high response to Copaxone in late-phase clinical-trial cohorts of multiple sclerosis, Genome Medicine. 9 (2017). doi: 10.1186/s13073-0170436-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kulakova O, Tsareva E, Lvovs D, Favorov A, Boyko A, Favorova O, Comparative pharmacogenetics of multiple sclerosis: INF-B versus glatiramer acetate, Pharmacogenomics. 15 (2014) 679–85. [DOI] [PubMed] [Google Scholar]
- [7].Xu W, Zhang L, Lu Y, SD-MSAEs: Promoter recognition in human genome based on deep feature extraction, Journal of Biomedical Informatics. 61 (2016) 55–62. doi: 10.1016/j.jbi.2016.03.018. [DOI] [PubMed] [Google Scholar]
- [8].Zhao Y, Healy BC, Rotstein D, Guttmann CRG, Bakshi R, Weiner HL, Brodley CE, Chitnis T, Exploration of machine learning techniques in predicting multiple sclerosis disease course., PloS One. 12 (2017) e0174866. doi: 10.1371/journal.pone.0174866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Goldstein BA, Hubbard AE, Cutler A, Barcellos LF, An application of Random Forests to a genome-wide association dataset: Methodological considerations & new findings, BMC Genetics. 11 (2010) 49. doi: 10.1186/14712156-11-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Kimes PK, Liu Y, Neil Hayes D, Marron JS, Statistical significance for hierarchical clustering, Biometrics. (2017). doi: 10.1111/biom.12647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Farh KK-H, Marson A, Zhu J, Kleinewietfeld M, Housley WJ, Beik S, Shoresh N, Whitton H, Ryan RJH, Shishkin AA, Hatan M, Carrasco-Alfonso MJ, Mayer D, Luckey CJ, Patsopoulos NA, De Jager PL, Kuchroo VK, Epstein CB, Daly MJ, Hafler DA, Bernstein BE, Genetic and epigenetic fine mapping of causal autoimmune disease variants, Nature. 518 (2015) 337–343. doi: 10.1038/nature13835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Lim S, Tucker CS, Kumara S, An unsupervised machine learning model for discovering latent infectious diseases using social media data, J Biomed Informat. 66 (2017) 82–94. [DOI] [PubMed] [Google Scholar]
- [13].Xu R, Wunsch DC, Clustering algorithms in biomedical research: A review, IEEE Reviews in Biomedical Engineering. 3 (2010) 120–154. doi: 10.1109/RBME.2010.2083647. [DOI] [PubMed] [Google Scholar]
- [14].Prelic A, Bleuler S, Zimmermann P, Wille A, Buhlmann P, Gruissem W, Zitzler E, A systematic comparison and evaluation of biclustering methods for gene expression data, Bioinformatics. 9 (2006) 1122–1129. [DOI] [PubMed] [Google Scholar]
- [15].Jain AK, Murty MN, Flynn PJ, Data clustering: a review, ACM Computing Surveys. 31 (1999) 264–323. doi: 10.1145/331499.331504. [DOI] [Google Scholar]
- [16].Pagnuco IA, Pastorea Juan I.;, Abras G;, Brun M;, Ballarin VL;, Analysis of genetic association using hierarchical clustering and cluster validation indices, Genomics. (2017) 4–11. doi: 10.1016/j.pscychresns.2008.11.004. [DOI] [PubMed] [Google Scholar]
- [17].Ahmad T, Desai N, Wilson F, Schulte P, Dunning A, Jacoby D, Allen L, Fiuzat M, Rogers J, Felker GM, Clinical implications of cluster analysis-based classification of acute decompensated heart failure and correlation with bedside hemodynamic profiles, PloS One. 11 (2016) e0145881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mei K, Peng J, Gao L, Zheng NN, Fan J, Hierarchical Classification of Large-Scale Patient Records for Automatic Treatment Stratification, IEEE Journal of Biomedical and Health Informatics. 19 (2015) 1234–1245. doi: 10.1109/JBHI.2015.2414876. [DOI] [PubMed] [Google Scholar]
- [19].Hamid JS, Meaney C, Crowcroft NS, Granerod J, Beyene J, Cluster analysis for identifying sub-groups and selecting potential discriminatory variables in human encephalitis., BMC Infectious Diseases. 10 (2010) 364. doi: 10.1186/1471-2334-10-364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Redekop W, Mladsi D, The faces of personalized medicine: a framework for understanding its meaning and scope, Value in Health. 6 (2013) S4–S9. [DOI] [PubMed] [Google Scholar]
- [21].Tari L, Baral C, Kim S, Fuzzy c-means clustering with prior biological knowledge, Journal of Biomedical Informatics. 42 (2009) 74–81. doi: 10.1016/j.jbi.2008.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Bellazzi R, Zupan B, Towards knowledge-based gene expression data mining, Journal of Biomedical Informatics. 40 (2007) 787–802. doi: 10.1016/j.jbi.2007.06.005. [DOI] [PubMed] [Google Scholar]
- [23].Wiwie C, Baumbach J, Rottger R, Comparing the performance of biomedical clustering methods, Nature Methods. 12 (2015) 1033–1038. doi: 10.1038/nmeth.3583. [DOI] [PubMed] [Google Scholar]
- [24].Ultsch A, Lotsch J, Machine-learned cluster identification in high-dimensional data, Journal of Biomedical Informatics. 66 (2017) 95–104. doi: 10.1016/j.jbi.2016.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Ultsch A, Clustering with SOM: U*C., in: In Proceedings of the 5th Workshop on Self-Organizing Maps, Paris, 2005: pp. 75–82. [Google Scholar]
- [26].Clifford H, Wessely F, Pendurthi S, Emes RD, Comparison of clustering methods for investigation of genome-wide methylation array data, Frontiers in Genetics. 2 (2011) 1–11. doi: 10.3389/fgene.2011.00088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Rousseeuw PJ, Silhouettes: A graphical aid to the interpretation and validation of cluster analysis, Journal of Computational and Applied Mathematics. 20 (1987) 53–65. doi: 10.1016/0377-0427(87)90125-7. [DOI] [Google Scholar]
- [28].Bezdek JC, Pal NR, Some new indexes of cluster validity, IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics. 28 (1998) 301–315. doi: 10.1109/3477.678624. [DOI] [PubMed] [Google Scholar]
- [29].Sakellariou A, Sanoudou D, Spyrou G, Combining multiple hypothesis testing and affinity propagation clustering leads to accurate, robust and sample size independent classification on gene expression data, BMC Bioinformatics. 13 (2012) 270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Frey BJ, Dueck D, Clustering by passing messages between data points, Science. 315 (2007) 972–976. [DOI] [PubMed] [Google Scholar]
- [31].Shen R, Olshen AB, Ladanvi M, Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis, Bioinformatics. 25 (2009) 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Dempster AP, Laird NM, Rubin DB, Maximum likelihood from incomplete data via the EM algorithm, J Royal Stat Soc Series B. (1977) 1–38. [Google Scholar]
- [33].Fraley C, Raftery AE, How many clusters? Which clustering method? Answers via model-based cluster analysis., The Comp Journal. 41 (1998) 578–588. [Google Scholar]
- [34].Khakabimamaghani S, Ester M, Bayesian biclustering for patient stratification, Biocomputing 2016: Proceedings of the Pacific Symposium (2016) 345–356. [PubMed] [Google Scholar]
- [35].Lee D, Seung H, Algorithms for non-negative matrix factorization, Advances in Neural Information Processing Systems. (2001) 556–562. [Google Scholar]
- [36].Pontes B, Giraldez R, Aguilar-Ruiz J, Biclustering on expression data: A review, Journal of Biomedical Informatics. 57 (2015) 163–180. [DOI] [PubMed] [Google Scholar]
- [37].Cheng Y, Church G, Biclustering of expression data, Proceedings of the 8th International Conference on Intelligent Systems for Molecular Biology, La Jolla, CA (2000) 93–103. [PubMed] [Google Scholar]
- [38].Nguyen N, Caruana R, Consensus clusterings, in: Proceedings - IEEE International Conference on Data Mining ICDM, 2007: pp. 607–612. doi: 10.1109/ICDM.2007.73. [DOI] [Google Scholar]
- [39].Suzuki R, Shimodaira H, pvclust: An R package for hierarchical clustering with p-values, Bioinformatics. 22 (2013) 1–7. [DOI] [PubMed] [Google Scholar]
- [40].Bushel PR, Hamadeh HK, Bennett L, Green J, Ableson A, Misener S, Afshari CA, Paules RS, Computational selection of distinct class- and subclass- specific gene expression signatures, Journal of Biomedical Informatics. 35 (2002) 160–170. doi: 10.1016/S15320464(02)00525-7. [DOI] [PubMed] [Google Scholar]
- [41].Cabin RJ, Mitchell RJ, To Bonferroni or not to Bonferroni: when and how are the questions, Bulletin of the Ecological Society of America. 81 (2000) 246–248. doi: 10.2307/20168454. [DOI] [Google Scholar]
- [42].Bezdek JC, Ehrlich R, FCM: The fuzzy c-means clustering algorithm, Comp and Geosci. 10 (1984) 191–203. [Google Scholar]
- [43].Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubin GM, Sherlock G, Gene Ontology: tool for the unification of biology, Nature Genetics. 25 (2000) 25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Yazdani A, Yazdani A, Samiei A, Boerwinkle E, Generating a robust statistical causal structure over 13 cardiovascular disease risk factors using genomics data, Journal of Biomedical Informatics. 60 (2016) 114–119. doi: 10.1016/j.jbi.2016.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, Sham PC, PLINK: A Tool Set for Whole Genome Association and Population-Based Linkage Analyses, The American Journal of Human Genetics. 81 (2007) 559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Redei GP, Kruskal-Wallis test, Encyclopedia of Genetics, Genomics, Proteomics, and Informatics. (2008) 1067–1068. [Google Scholar]
- [47].Everitt BS, Landau S, Leese M, Stahl D, Measurement of Proximity, Cluster Analysis. (2011) 43–69. doi: 10.1002/9780470977811.ch3. [DOI] [Google Scholar]
- [48].Bazaraa MS, Sherali HD, Shetty CM, Nonlinear programming: theory and algorithms, John Wiley & Sons, Chicago, 2013. [Google Scholar]
- [49].Szklarczyk STRING v10: protein-protein interaction networks, integrated over the tree of life, Nucleic Acids Research. D1 (2015) 447–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Rand WM, Objective criteria for the evaluation of clustering methods, J Amer Stat Assoc. 66 (1971) 846–50. [Google Scholar]
- [51].R. R Development Core Team, R: A Language and Environment for Statistical Computing, 1 (2011). [Google Scholar]
- [52].Fraley C, Raftery AE, Murphy TB, Scrucca L, mclust Version 4 for R: Normal Mixture Modeling for Model-Based Clustering, Classification, and Density Estimation, Technical Report No. 597, Dept of Statistics, University of Washington; (2012). [Google Scholar]
- [53].Bodenhofer U, Kothmeier A, Hochreiter S, APCluster: an R package for affinity propagation clustering, Bioinformatics. 27 (2011) 2463–4. [DOI] [PubMed] [Google Scholar]
- [54].Thrun MC, Lerch F, Lotsch J, Ultsch A, Visualization and 3D printing of multivariate data of biomarkers, in: Proceedings of International Conference in Central Europe on Computer Graphics, Visualization, and Computer Vision, Plzen, 2016. [Google Scholar]
- [55].Thrun MC, Projection based clustering through self-organization and swarm intelligence: combining cluster analysis with the visualization of high-dimensional data., Springer Fachmedien, Wiesbaden, Germany, 2018. [Google Scholar]
- [56].Kaiser S, Santamaria R, Khamiakova T, Sill M, Theron R, Quintales L, Leisch F, DeTroyer E, biclust: BiCluster Algorithms, R Package Version 1. no. 1 (2015).
- [57].Golub T, Slonim D, Tamayo P, Huard C, Gaasenbeek M, Mesirov J, Coller H, Loh M, Downing J, Caliguiri M, Bloomfield C, Lander E, Molecular classification of cancer: class discovery and class prediction by gene expression monitoring, Science. 5439(1999) 531–7.. [DOI] [PubMed] [Google Scholar]
- [58].Monti S, Tamayo P, Mesirov J, Golub T, Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data, Machine Learning. 52 (2003) 91–118. [Google Scholar]
- [59].Cortes A, Brown MA, Promise and pitfalls of the Immunochip, Arthritis Research & Therapy. 13 (2011) 101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Welter D, MacArthur J, Morales J, Burdett T, Hall P, Junkins H, Klemm A, Flicek P, Manolio T, Hindorff L, Parkinson H, The NHGRI GWAS Catalog, a curated resource of SNP-trait associations, Nucleic Acids Research. 42 (2014) D1001–D1006. doi: 10.1093/nar/gkt1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Kirkpatrick S, Gelatt CD, Vecchi MP, Optimization by simulated annealing, Science. 220 (1983) 671–80. [DOI] [PubMed] [Google Scholar]
- [62].Lopez CE, Nembhard D, Cooperative workforce planning heuristic with worker learning and forgetting and demand constraints, in: IIE Annual Conference Proceedings, 2017: pp. 380–85. [Google Scholar]
- [63].Xiang Y, Gubian S, Suomela B, Hoeng J, Generalized simulated annealing for global optimization: the GenSA Package, R J. 5 (2013) 13–28. [Google Scholar]
- [64].Bader GD, Betel D, Hogue CWV, BIND: the Biomolecular Interaction Network Database, Nucleic Acids Research. 31 (2003) 248–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Chatr-Aryamontri A, Oughtred R, Boucher L, Rust J, Chang C, Kolas NK, O’Donnell L, Oster S, Theesfeld C, Sellam A, Stark C, Breitkreutz BJ, Dolinski K, Tyers M, The BioGRID interaction database: 2017 update, Nucleic Acids Research. (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Prasad TSK et al. , Human Protein Reference Database −2009 Update, Nucleic Acids Research. (2009) D767–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Hermjakob H, Montecchi-Palazzi L, Lewington C et al. , IntAct: an open source molecular interaction database, Nucleic Acids Research. (2004) D452–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Licata L, Briganti L, Peluso D, Perfetto L, Iannuccelli M, Galeota E, Sacco F, Palma A, Nardozza AP, Santonico E, Castagnoli L, Cesareni G, MINT, the molecular interaction database: 2012 update, Nucleic Acids Research. (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Schaefer CF, Anthony K, Krupa S et al. , PID: the Pathway Interaction Database, Nucleic Acids Research. (2009) D674–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Kanehisa M Furumichi M Tanabe, Sato Y, Morishima K, KEGG: new perspectives on genomes, pathways, diseases, and drugs, Nucleic Acids Research. (2017) D353–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Nishimura D, Biotech software and internet report, BioCarta, BIotech Software & Internet Report: The Computer Software Journal for Scient 2(3). (2004). 10.1089/152791601750294344. [DOI] [Google Scholar]
- [72].Fabregat et al. , The reactome pathway knowledgebase, Nucleic Acids Research. D1 (2015) 481–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Larochelle C, Alvarez J, Just W, How do immune cells overcome the blood-brain barrier in multiple sclerosis?, FEBS Letters. (2012). [DOI] [PubMed] [Google Scholar]
- [74].Isobe N, et al. , An Immunochip study of multiple sclerosis risk in African Americans, Brain. 138 (2015) 1518–30. [DOI] [PMC free article] [PubMed] [Google Scholar]