Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2012 Feb 8;32(6):1969–1973. doi: 10.1523/JNEUROSCI.3886-11.2012

When Up Is Down in 0g: How Gravity Sensing Affects the Timing of Interceptive Actions

Patrice Senot 1,2,✉, Myrka Zago 3, Anne Le Séac'h 1,2, Mohammed Zaoui 1, Alain Berthoz 1, Francesco Lacquaniti 3,4, Joseph McIntyre 1,2
PMCID: PMC6621712  PMID: 22323710

Abstract

Humans are known to regulate the timing of interceptive actions by modeling, in a simplified way, Newtonian mechanics. Specifically, when intercepting an approaching ball, humans trigger their movements a bit earlier when the target arrives from above than from below. This bias occurs regardless of the ball's true kinetics, and thus appears to reflect an a priori expectation that a downward moving object will accelerate. We postulate that gravito-inertial information is used to tune visuomotor responses to match the target's most likely acceleration. Here we used the peculiar conditions of parabolic flight—where gravity's effects change every 20 s—to test this hypothesis. We found a striking reversal in the timing of interceptive responses performed in weightlessness compared with trials performed on ground, indicating a role of gravity sensing in the tuning of this response. Parallels between these observations and the properties of otolith receptors suggest that vestibular signals themselves might plausibly provide the critical input. Thus, in addition to its acknowledged importance for postural control, gaze stabilization, and spatial navigation, we propose that detecting the direction of gravity's pull plays a role in coordinating quick reactions intended to intercept a fast-moving visual target.

Introduction

The task of intercepting an object in motion requires the prediction of its future movements to compensate for visuomotor delays. Accurate prediction may depend on one's ability to monitor the target's position, velocity, and perhaps even higher-order temporal derivatives. Given the limited capacity of the visual system to discriminate acceleration (Werkhoven et al., 1992), one might guess that humans would make systematic errors when attempting to intercept an accelerating target.

The lack of reliable real-time information about a visual target's acceleration does not, however, mean that the brain neglects acceleration altogether when performing tasks of interception. For instance, when asked to hit a ball, subjects tend to trigger the movement a bit earlier, for any given approach kinematics, when the target arrives from above, than from below (Senot et al., 2005). This timing shift is consistent with an a priori expectation that downward-moving objects accelerate under the influence of gravity (Lacquaniti et al., 1993; McIntyre et al., 2001; Zago et al., 2008). As such, it may reflect a strategy for anticipating the changes in speed most likely to occur during the time it takes neural signals from the visual system to have an effect on motor commands.

But what sensory information tells the CNS whether the target is moving with or against gravity? Signals from the inner ear are obvious candidates. Because otolith sensory organs respond differently according to the orientation of the head with respect to gravity (Fernández and Goldberg, 1976), they could define the direction of expected acceleration. Other sensory information could also be used to detect the gravitational axis, including contact cues between the body and the environment, proprioceptive cues about the orientation of body segments with respect to support surfaces (floor, chair, etc.) and efference copy of motor commands required to support a tilted head or outstretched limb against gravity's pull. Until now, however, the sensing of gravity's direction has only been explicitly linked to the sensation and control of one's own body (e.g., postural control or gaze stabilization). The implication of graviceptor signals in interceptive tasks, when the primary mover is a visually perceived external object, is, as yet, undemonstrated. Indeed, theories of direct perception-action coupling (Gibson, 1979) propose that complex multisensory processes based on internal models of physics would be inefficient and unnecessary.

To test for a direct influence of gravity sensing on hand–eye coordination, we used the varying gravitational conditions evoked by parabolic maneuvers in an airplane. Parabolic flight has previously been used to study gravity's influence on the conscious perception of body orientation, with human subjects sometimes reporting sensations of being turned upside-down in zero gravity (0g) (Simons and Gardner, 1963; Lackner, 1992). Here, we used parabolic flight to test whether mechanisms of gravity sensing could also play a role in a different class of neural processes, i.e., those that underlie rapid reactions to intercept a moving object.

Materials and Methods

Participants performed an interception task in a virtual environment presented in a head-mounted display. Real-time tracking of head orientation allowed for updating the visual scene according to the participant's direction of gaze; participants tilted the head upward to observe balls approaching from above and downward to observe balls rising from below. Participants pressed one button to launch the ball from a cannon then, after a random delay (200–1000 ms), pressed another button to trigger the movement of the racquet. The racquet movement was always the same and had to be initiated 57 ms before the arrival of the ball at the center of the interception zone. Temporal windows for success depended on the ball's acceleration and flight duration and ranged from 26 to 93 ms. Balls approached the interception point with constant acceleration of ±9.8 ms−2, or at constant velocity. The distance from cannon to interception point was 8 m, while initial velocity was adjusted so that the ball covered this distance with one of three different durations (750, 800, and 850 ms) regardless of the ball's acceleration (see Senot et al., 2005 for details).

The experiment was performed in normal gravity and in weightlessness, the latter achieved during parabolic maneuvers of an airplane (Pletser, 2004). In normal gravity, subjects sat on the floor with their knees bent. To intercept balls approaching from above, they leaned against a backrest and tilted the head to look upward toward the ceiling. When the ball approached from below, they leaned forward and tilted the head downward to look at the floor between their bent legs. In parabolic flight, the 22 s weightless phase of each maneuver is preceded and followed by an ∼20 s period of hypergravity (1.5–1.8 g). Before each hypergravity phase, subjects adopted the same posture as in normal gravity, appropriate to the direction of the ball's approach (above or below). On injection into weightlessness, the backrest (if present) was removed and subjects maintained approximately the same posture as in hypergravity, but with their buttocks floating several centimeters above the floor.

For a given gravitational condition, subjects performed all trials for balls approaching from above, then all trials for balls approaching from below, or vice versa, randomized across subjects. In weightlessness, subjects executed three to five trials per parabola. For those who performed the experiment in both gravity conditions, the order of trials in normal gravity or weightlessness was randomized across individuals. To learn the racquet's movement, subjects practiced on the ground, looking straight ahead to intercept balls that moved horizontally at constant speed, until they successfully intercepted the ball three times (typically 10–20 trials).

A total of 37 volunteers between 20 and 50 years of age (25 males, 12 females) performed the experiment as a part of this study (12 in normal gravity only, 7 in weightlessness only, and 18 in both gravity conditions). A local ethics board approved the protocol and subjects gave informed consent.

Statistical analyses were performed on the value of trigger time relative to impact obtained for each possible stimulus. Participants performed two to five repetitions for each of the nine possible ball kinematics within a given set of trials. Extreme trigger times were rejected as outliers based on the standard method of quartiles, computed participant-by-participant (Hill and Lewicki, 2007). Trigger times were averaged over the remaining repetitions of each stimulus for each subject and the effects of the different experimental factors were assessed by two different ANOVAs (Statistica; StatSoft). The first was performed on trigger times from all subjects, with the ball's approach direction (above or below), duration (750, 800, or 850 ms), and acceleration (accelerating, decelerating, or constant speed) treated as within-subject factors, while gravity (normal gravity or weightlessness) was treated as a between-groups factor. Because some participants performed the experiment in both gravity conditions, they contributed data to both the normal gravity and weightlessness samples. Thus, the sum of n = 30 for normal gravity plus n = 25 for weightlessness is greater than the number of different participants (n = 37) in this analysis. The second ANOVA was restricted to the participants who performed the experiment in both normal gravity and weightlessness (n = 18), with direction, duration, acceleration, and gravity treated as within-subject factors. We used Newmann–Keuls for post hoc testing and χ2 to compare success rates.

Results

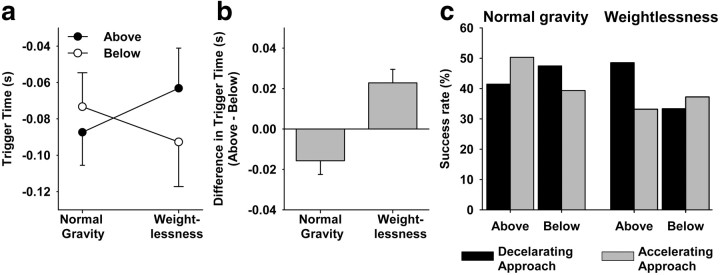
Figure 1a shows the average trigger time for balls coming from above or below in each gravity condition. Although intersubject variability was high, subjects responded earlier in normal gravity, on average, when the ball came from above (−87 ± 18 ms, mean ± SEM) compared with below (−73 ± 19 ms), consistent with our previous studies on the ground (Senot et al., 2005; Le Séac'h et al., 2010). This systematic bias was reversed in weightlessness, where subjects triggered the racquet earlier, on average, when the ball came from below (−93 ± 25 ms) compared with above (−63 ± 22 ms). Computing the difference between above and below on a subject-by-subject basis reduces intersubject variability and reveals more clearly the shift in relative timing that occurs between the two gravity conditions (Fig. 1b). The up/down asymmetry in timing was reflected in success rate as a function of the ball's acceleration and direction of flight (Fig. 1c). In normal gravity, participants succeeded more often for accelerating balls that approached from above than from below, and more often for decelerating balls that approached from below than from above. In other words, greater success was achieved for balls that complied with gravity's constraints than for those that did not. The opposite was true in weightlessness, where subjects had greater success for balls that moved coherent with a (nonexistent) upward gravitational pull than for those that accelerated downward as if in normal gravity.

Figure 1.

Figure 1.

Open in a new tab

Interception responses as a function of the ball's acceleration, direction of movement, and the gravitational context. a, Average trigger time with respect to the arrival of the ball (mean ± SEM). b, Average within-subject difference in trigger time between above and below (mean ± SEM) for subjects that performed the experiment in both gravity conditions. c, Success rate.

Statistical analyses confirmed these results. As in our previous experiments, we found significant effects of the ball's acceleration and flight duration on the timing of responses (Table 1). Once the effects of these different factors were taken into account, however, we found a highly significant cross-effect between direction and gravity (p < 0.001) that confirms the timing reversal displayed in Figure 1a. Post hoc analyses showed that subjects responded earlier for above versus below in normal gravity and earlier for below versus above in weightlessness (p < 0.05). There were no other significant cross-effects. Supplementary tests (e.g., nonparametrics, multivariate ANOVA, outlier detection; data not shown) were conducted to guard against errors due to nonnormality or nonsphericity of data distributions and yielded the same significant contrasts as the standard ANOVA shown in Table 1. In addition, the pattern of success rate, as a function of whether the ball accelerated in accord with normal gravity or not (Fig. 1c), changed significantly between 0g and 1g (χ2 analysis, p = 0.005).

Table 1.

Results of ANOVA analyses

Effect Gravity as a group factor
 Gravity as a repeated measure
F Significance F Significance
Approach acceleration F(2,106) = 580.47 p < 0.001 F(2,34) = 333.78 p < 0.001
Approach duration F(2,106) = 26.47 p < 0.001 F(2,34) = 10.33 p < 0.001
Acceleration × duration F(4,212) = 33.45 p < 0.001 F(4,68) = 19.67 p < 0.001
Direction F(1,53) = 7.68 p < 0.01 F(1,17) = 2.47 n.s.
Gravity F(1,53) = 0 n.s. F(1,17) = 0.84 n.s.
Direction × gravity F(1,53) = 23.45 p < 0.001 F(1,17) = 14.87 p < 0.01
Open in a new tab

Note that not all subjects showed a full reversal of response timing during parabolic maneuvers: 22 of 26 subjects responded earlier for balls that came from below than from above in weightlessness. Of the 18 subjects who performed the experiment in both gravitational conditions, 14 showed a shift toward earlier trigger times for below versus above in weightlessness compared with their performance in normal gravity.

Control tests

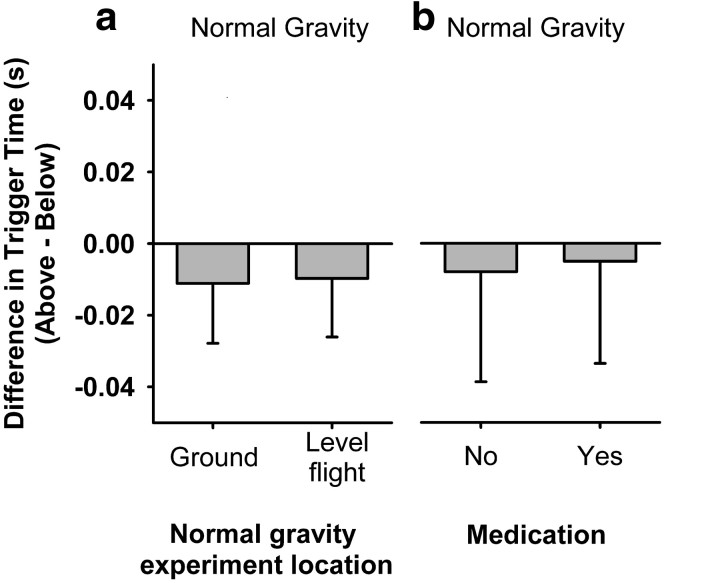
We tested whether response patterns could be attributed to factors other than the gravitational context itself. First, we asked whether the simple fact of performing the experiment in a flying airplane could produce the observed effects. For example, participants may have paid less attention to the task because of vibrations of the plane, noise, or the stress of parabolic flight. ANOVA applied to trigger time, including the factor experiment location (ground vs flight) showed no significant interaction between the direction and experiment location factors, nor was there a significant main effect of the latter on the overall trigger time (Fig. 2a). To test whether anti-nausea medication could explain the timing reversals, we asked a subset of participants to perform the experiment on the ground 30 min after the administration of an injected dose of scopalamine but before the take-off of the aircraft, and a second set of nonmedicated trials on a different day. A valid ANOVA cannot be performed for so few subjects, but we note that these subjects responded earlier, on average, for balls approaching from above versus below in normal gravity whether they were under the influence of anti-nausea medication or not (Fig. 2b).

Figure 2.

Figure 2.

Open in a new tab

Results of control tests. a, Effect of performing the experiment in normal gravity either on the ground or in level flight of the aircraft (n.s.). b, Effect of performing the experiment on the ground with or without the influence of anti-nausea medication (n.s.).

Discussion

Given our previous experiments on interception performed on the ground and during orbital spaceflight, the reversal of up/down timing patterns in parabolic weightlessness was quite astonishing. Suppression of the up/down differential would have been a more obvious result, since the effects of gravity on the body and other objects were removed. Because contact forces between the body and the plane were essentially zero and because there were no windows by which one could see the plane's trajectory, gravity's effects had disappeared within the local environment as far as available sensory information was concerned. Alternatively, one might predict that the up/down differential would be maintained, based on other sensory or cognitive cues. Indeed, some subjects, when lying supine, anticipate gravity's effects when said targets move in a head-to-feet direction (Miller et al., 2008) or downward in a virtual scene with strong up/down visual cues (Indovina et al., 2005; Moscatelli and Lacquaniti, 2011). Furthermore, astronauts who were seated upright in the space shuttle continued to anticipate the effects of gravity on a ball projected downward from the ceiling even after 14 d on orbit (McIntyre et al., 2001).

Why, then, did we observe a reversal of this up/down effect in parabolic flight, in contrast to our other studies in weightlessness? The answer most likely stems from the particular conditions of the parabolic maneuver, which is known to evoke reports of feeling flipped upside-down (Simons and Gardner, 1963; Lackner, 1992). The 22 s weightless phase of each parabola is bracketed by two phases of hypergravity (1.5–1.8 g), each lasting ∼20 s. This exposure to constant acceleration well above 1 g is relatively long for Earth-bound beings, unless they are accustomed to riding in jet airplanes or drag racers. It is conceivable, therefore, that the CNS interprets afferent signals under the a priori assumption that any constant acceleration lasting more than a few seconds must be that of normal Earth gravity (Merfeld et al., 2005). The unloading of the otoliths and other graviceptors when passing from hypergravity to 0g might therefore be sensed as negative gravity, i.e., a gravitational pull in the upward direction. This interpretation would be reinforced by other sensations, such as increased cranial blood pressure and the rise of internal organs within the body when gravity's pull is released. One would experience all of these sensations if the body were suddenly inverted in a 1g environment. The CNS might therefore associate these inputs with the more plausible situation of being upside down in a normal gravitational environment, rather than correctly interpreting these signals as an indication of weightlessness or freefall.

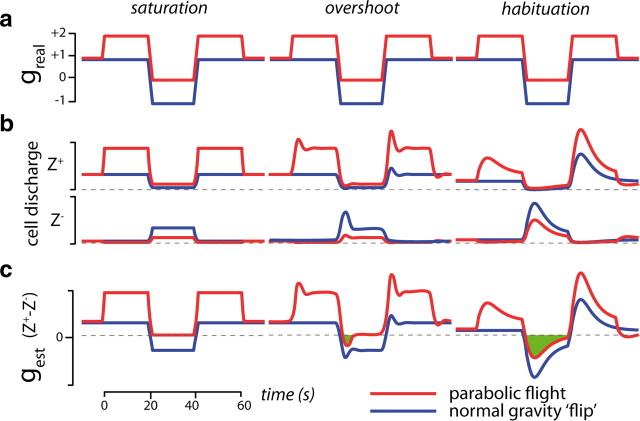
Numerous studies have demonstrated a dissociation between conscious visual perception processed by a ventral cortical stream and visually guided actions mediated by a dorsal cortical stream (Goodale and Milner, 1992), with the latter thought to be immune to optical illusions when memory is not involved (Bruno et al., 2008). So, even in light of the potential for inversion illusions in parabolic flight, our observations of timing reversals in an interception task are surprising. If a tight link between these phenomena exists, it could reflect top-down influences of multisensory cognitive context on visually guided actions (see below). A looser correlation could simply reflect the influence of common sensory signals on two separate processes. In either case, what might be the sensory signals driving those responses? Figure 3 depicts idealized properties of otolith signals that could conceivably underlie the effects of parabolic flight. For instance, the suppression of saccular activity due to negative acceleration tends to bottom out, such that there may be little difference between 0g and −1g discharge rates for cells preferentially tuned to upward acceleration (Z+ units; Fig. 3, left). While one would also experience such low Z+ firing rates when lying down, the CNS might nevertheless associate this state of minimal saccular activity, coupled with the absence of +1g excitation of utricular organs, with an upside-down posture in +1g. Dynamic properties of discharge rates might also lead to signals compatible with an upside-down posture. If Z+/− units exhibit phasic as well as tonic activity during changes in acceleration (Fig. 3, middle), the individual neurons and the combined estimate will briefly overshoot the 0 g level during the transition from hypergravity to hypogravity. This negative gravity state might then persist internally during the 22 s 0g phase because no otolith activations would contradict this interpretation. Habituation of afferent signals over a 22 s timescale would further blur the distinction between brief exposure to 0g and an equally brief upside-down flip in 1g, such that patterns of saccular activity could be quite similar in these two situations (Fig. 3, right). The fact that all three phenomena—saturation, overshoot, habituation—can be observed in data recorded from saccular afferents (Fernández and Goldberg, 1976) indicates that otolith signals, at least in theory, may be at the root of the timing reversals observed in parabolic flight. In this light, it is intriguing to note that otolith contributions to vestibulo-ocular reflexes change direction and increase in magnitude in upside-down animals (Brettler et al., 2000) in the same way that the differences in timing between above and below changed sign and increased in magnitude in 0g (14 ms for 1g vs 30 ms for 0g, p = 0.011) in our experiments. Asymmetry in otolith-mediated, optokinetic nystagmus can also be reversed both in 0g and in a head-down posture in humans (Clément and Lathan, 1991), giving further credence to the hypothesis that upside-down-like otolithic inputs in 0g could be the source of the timing reversal observed in our experiments.

Figure 3.

Figure 3.

Open in a new tab

Idealized otolith characteristics based on known physiological properties. a, Gravity profile for a 20 s upside-down handstand in normal Earth gravity (blue) and for a single cycle in parabolic flight (red). b, Fictive cell discharge rates for hypothetical saccular cells that are preferentially sensitive to upward (Z+) or downward (Z−) acceleration. c, Net gravitational estimate based on a simple subtraction of Z+ and Z− activities. Green shading highlights when the change from hypergravity to 0g might generate a net, transient signal consistent with negative acceleration.

From our experiments, the presence of gravity appears to be a sufficient condition to evoke up/down biases in interceptive responses, at least in some subjects. It is not, however, a necessary condition. Indeed, it is thought that a network of connections involving the insulae and temporoparietal junction of the brain integrates a variety of sensory modalities to define an up/down reference frame and then tunes fast interceptive responses within that context (Indovina et al., 2005). The integration of visual, tactile, and proprioceptive signals, in addition to other graviceptors, would explain why subjects may react to targets moving off the gravitational axis (Miller et al., 2008; Moscatelli and Lacquaniti, 2011) or in weightlessness (McIntyre et al., 2001) as if the targets were moving downward, as noted above. Idiosyncratic differences in the weighting of different sensory modalities could also explain why some subjects did not show a timing reversal in weightlessness, in much the same way that individuals depend differently on visual, graviceptor and idiotropic cues to define the perceived vertical (Dyde et al., 2006) and that not all subjects experience conscious illusions of being turned upside-down in weightlessness (Simons and Gardner, 1963; Lackner, 1992). In fact, according to one theory, vestibular signals are ambiguous anyway, such that additional sensory cues are required to determine up and down even in a normal Earth environment (Bortolami et al., 2006). Under this theory, proprioceptive cues or contact forces specific to weightlessness, rather than dynamical properties of vestibular neurons themselves, would be the source of the reversal in up/down catching behavior.

Can a case be made, therefore, for an effect of vestibular signals on interception responses? In our experiments, we allowed our participants to float above the floor of the aircraft during 0g phases, essentially eliminating contact cues in all directions. Moreover, the visual cues did not change between the different gravitational fields. This leaves the direct action of gravity on the body as the main parameter that changed between normal gravity and weightlessness. In this context, it is intriguing to note that, whereas healthy participants were prone to inversion illusions in parabolic flight, no such illusions were reported by a group of patients with bilateral labyrinthine defects (Graybiel and Kellogg, 1967). From that observation, and the plausible, vestibular-based mechanisms outlined above, one might surmise that otolith signals themselves are the most likely culprit behind the reversals of interception timing observed in our experiments.

Typically, one associates the sensing of gravitational acceleration with the detection and compensation of movements of the head and body in space. For instance, vestibulo-ocular reflexes act to stabilize gaze in the face of head movements (Green and Angelaki, 2003), integration of gravito-inertial cues contributes to spatial navigation (Israël and Berthoz, 1989; Mittelstaedt, 1999), and maintaining an upright posture is a primary function of the vestibular organs (Cathers et al., 2005) and other graviceptor cues. Gravity may also be taken into account in the optimal control of vertical limb movements (Berret et al., 2008; Crevecoeur et al., 2010) and gravity sensing may contribute to the adaptation of limb kinematics in 0g (Papaxanthis et al., 2005; Gaveau et al., 2011). Here, we have implicated gravity sensing in a different type of function, i.e., that of predicting the motion of a visually perceived external object. By comparing reversals in the timing of interceptive behaviors observed in parabolic flight to known dynamical properties of otolith receptors, we postulate a novel role of the inner ear in the tuning of fast, interceptive actions directed toward a moving visual target.

Footnotes

This work was supported by grants to J.M. from the Centre National d'Etudes Spatiales and to F.L. from the Italian Space Agency (Disorders of Cardiorespiratory and Motor Control and CRUising in Space with Out-of body Experiences Grants).We thank Novespace for technical assistance and M. Beraneck, I. Viaud-Delmon, and P.-P. Vidal for helpful discussions.

References

  1. Berret B, Darlot C, Jean F, Pozzo T, Papaxanthis C, Gauthier JP. The inactivation principle: mathematical solutions minimizing the absolute work and biological implications for the planning of arm movements. PLoS Comput Biol. 2008;4:e1000194. doi: 10.1371/journal.pcbi.1000194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bortolami SB, Rocca S, Daros S, DiZio P, Lackner JR. Mechanisms of human static spatial orientation. Exp Brain Res. 2006;173:374–388. doi: 10.1007/s00221-006-0387-9. [DOI] [PubMed] [Google Scholar]
  3. Brettler SC, Rude SA, Quinn KJ, Killian JE, Schweitzer EC, Baker JF. The effect of gravity on the horizontal and vertical vestibulo-ocular reflex in the rat. Exp Brain Res. 2000;132:434–444. doi: 10.1007/s002210000357. [DOI] [PubMed] [Google Scholar]
  4. Bruno N, Bernardis P, Gentilucci M. Visually guided pointing, the Müller-Lyer illusion, and the functional interpretation of the dorsal-ventral split: conclusions from 33 independent studies. Neurosci Biobehav Rev. 2008;32:423–437. doi: 10.1016/j.neubiorev.2007.08.006. [DOI] [PubMed] [Google Scholar]
  5. Cathers I, Day BL, Fitzpatrick RC. Otolith and canal reflexes in human standing. J Physiol. 2005;563:229–234. doi: 10.1113/jphysiol.2004.079525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Clément G, Lathan CE. Effects of static tilt about the roll axis on horizontal and vertical optokinetic nystagmus and optokinetic after-nystagmus in humans. Exp Brain Res. 1991;84:335–341. doi: 10.1007/BF00231454. [DOI] [PubMed] [Google Scholar]
  7. Crevecoeur F, McIntyre J, Thonnard JL, Lefévre P. Movement stability under uncertain internal models of dynamics. J Neurophysiol. 2010;104:1301–1313. doi: 10.1152/jn.00315.2010. [DOI] [PubMed] [Google Scholar]
  8. Dyde RT, Jenkin MR, Harris LR. The subjective visual vertical and the perceptual upright. Exp Brain Res. 2006;173:612–622. doi: 10.1007/s00221-006-0405-y. [DOI] [PubMed] [Google Scholar]
  9. Fernández C, Goldberg JM. Physiology of peripheral neurons innervating otolith organs of the squirrel monkey. I. Response to static tilts and to long-duration centrifugal force. J Neurophysiol. 1976;39:970–984. doi: 10.1152/jn.1976.39.5.970. [DOI] [PubMed] [Google Scholar]
  10. Gaveau J, Paizis C, Berret B, Pozzo T, Papaxanthis C. Sensorimotor adaptation of point-to-point arm movements after spaceflight: the role of internal representation of gravity force in trajectory planning. J Neurophysiol. 2011;106:620–629. doi: 10.1152/jn.00081.2011. [DOI] [PubMed] [Google Scholar]
  11. Gibson JJ. The ecological approach to visual perception. Boston: Houghton Mifflin; 1979. [Google Scholar]
  12. Goodale MA, Milner AD. Separate visual pathways for perception and action. Trends Neurosci. 1992;15:20–25. doi: 10.1016/0166-2236(92)90344-8. [DOI] [PubMed] [Google Scholar]
  13. Graybiel A, Kellogg RS. Inversion illusion in parabolic flight: its probable dependence on otolith function. Aerosp Med. 1967;38:1099–1103. [PubMed] [Google Scholar]
  14. Green AM, Angelaki DE. Resolution of sensory ambiguities for gaze stabilization requires a second neural integrator. J Neurosci. 2003;23:9265–9275. doi: 10.1523/JNEUROSCI.23-28-09265.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hill T, Lewicki P. Statistics: methods and applications. Tulsa, OK: StatSoft; 2007. [Google Scholar]
  16. Indovina I, Maffei V, Bosco G, Zago M, Macaluso E, Lacquaniti F. Representation of visual gravitational motion in the human vestibular cortex. Science. 2005;308:416–419. doi: 10.1126/science.1107961. [DOI] [PubMed] [Google Scholar]
  17. Israël I, Berthoz A. Contribution of the otoliths to the calculation of linear displacement. J Neurophysiol. 1989;62:247–263. doi: 10.1152/jn.1989.62.1.247. [DOI] [PubMed] [Google Scholar]
  18. Lackner JR. Sense of body position in parabolic flight. Ann N Y Acad Sci. 1992;656:329–339. doi: 10.1111/j.1749-6632.1992.tb25219.x. [DOI] [PubMed] [Google Scholar]
  19. Lacquaniti F, Carrozzo M, Borghese N. The role of vision in tuning anticipatory motor responses of the limbs. In: Berthoz A, Gielen C, Henn V, Hoffmann KP, Imbert M, Lacquaniti F, Roucoux A, editors. Multisensory control of movement. Oxford: Oxord UP; 1993. pp. 379–393. [Google Scholar]
  20. Le Séac'h AB, Senot P, McIntyre J. Egocentric and allocentric reference frames for catching a falling object. Exp Brain Res. 2010;201:653–662. doi: 10.1007/s00221-009-2081-1. [DOI] [PubMed] [Google Scholar]
  21. McIntyre J, Zago M, Berthoz A, Lacquaniti F. Does the brain model Newton's laws? Nat Neurosci. 2001;4:693–694. doi: 10.1038/89477. [DOI] [PubMed] [Google Scholar]
  22. Merfeld DM, Park S, Gianna-Poulin C, Black FO, Wood S. Vestibular perception and action employ qualitatively different mechanisms. I. Frequency response of VOR and perceptual responses during Translation and Tilt. J Neurophysiol. 2005;94:186–198. doi: 10.1152/jn.00904.2004. [DOI] [PubMed] [Google Scholar]
  23. Miller WL, Maffei V, Bosco G, Iosa M, Zago M, Macaluso E, Lacquaniti F. Vestibular nuclei and cerebellum put visual gravitational motion in context. J Neurophysiol. 2008;99:1969–1982. doi: 10.1152/jn.00889.2007. [DOI] [PubMed] [Google Scholar]
  24. Mittelstaedt H. The role of the otoliths in perception of the vertical and in path integration. Ann N Y Acad Sci. 1999;871:334–344. doi: 10.1111/j.1749-6632.1999.tb09196.x. [DOI] [PubMed] [Google Scholar]
  25. Moscatelli A, Lacquaniti F. The weight of time: gravitational force enhances discrimination of visual motion duration. J Vis. 2011;11:5. doi: 10.1167/11.4.5. [DOI] [PubMed] [Google Scholar]
  26. Papaxanthis C, Pozzo T, McIntyre J. Kinematic and dynamic processes for the control of pointing movements in humans revealed by short-term exposure to microgravity. Neuroscience. 2005;135:371–383. doi: 10.1016/j.neuroscience.2005.06.063. [DOI] [PubMed] [Google Scholar]
  27. Pletser V. Short duration microgravity experiments in physical and life sciences during parabolic flights: the first 30 ESA campaigns. Acta Astronaut. 2004;55:829–854. doi: 10.1016/j.actaastro.2004.04.006. [DOI] [PubMed] [Google Scholar]
  28. Senot P, Zago M, Lacquaniti F, McIntyre J. Anticipating the effects of gravity when intercepting moving objects: differentiating up and down based on nonvisual cues. J Neurophysiol. 2005;94:4471–4480. doi: 10.1152/jn.00527.2005. [DOI] [PubMed] [Google Scholar]
  29. Simons JC, Gardner MS. Wright-Patterson Air Force Base. Ohio: Aerospace Medical Research Laboratories; 1963. Weightless man: a survey of sensations and performance while free-floating. AMRL-TDR-62-114. [Google Scholar]
  30. Werkhoven P, Snippe HP, Toet A. Visual processing of optic acceleration. Vision Res. 1992;32:2313–2329. doi: 10.1016/0042-6989(92)90095-z. [DOI] [PubMed] [Google Scholar]
  31. Zago M, McIntyre J, Senot P, Lacquaniti F. Internal models and prediction of visual gravitational motion. Vision Res. 2008;48:1532–1538. doi: 10.1016/j.visres.2008.04.005. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES