Levodopa-Induced Dyskinesia Is Strongly Associated with Resonant Cortical Oscillations

Abstract

The standard pharmacological treatment for Parkinson's disease using the dopamine precursor levodopa is unfortunately limited by gradual development of disabling involuntary movements for which the underlying causes are poorly understood. Here we show that levodopa-induced dyskinesia in hemiparkinsonian rats is strongly associated with pronounced 80 Hz local field potential oscillations in the primary motor cortex following levodopa treatment. When this oscillation is interrupted by application of a dopamine antagonist onto the cortical surface the dyskinetic symptoms disappear. The finding that abnormal cortical oscillations are a key pathophysiological mechanism calls for a revision of the prevailing hypothesis that links levodopa-induced dyskinesia to an altered sensitivity to dopamine only in the striatum. Apart from having important implications for the treatment of Parkinson's disease, the discovered pathophysiological mechanism may also play a role in several other psychiatric and neurological conditions involving cortical dysfunction.

Introduction

The control of voluntary movements requires the coordinated action of sensorimotor circuits in the spinal cord and brainstem, basal ganglia, cerebellum, and frequently also large areas of the cerebral cortex (Swanson, 2000). Due to the complex interactions between these structures during planning and execution of movements, it has been highly difficult to link specific changes in neuronal activity patterns to the various aspects of motor dysfunction in diseases affecting the motor systems. In Parkinson's disease (PD), for instance, the understanding of the neurophysiological changes that are ultimately causing the symptoms of the disease is still very limited. In recent years, several studies have reported that the parkinsonian state is associated with a relative increase in the power of local field potentials (LFPs) below ∼30 Hz in the corticobasal ganglia network. However, although oscillations in this frequency range have been suggested to have a direct pathophysiological anti-kinetic effect, a causal relation to PD symptoms has been difficult to establish since similar LFP patterns are also present during inactive states in healthy subjects (Hammond et al., 2007; Fuentes et al., 2010). While the understanding of the electrophysiological mechanisms is still incomplete, the structural and biochemical mechanisms of PD—the gradual death of dopaminergic cells in the substantia nigra pars compacta (SNc) and the ventral tegmental area (VTA) of the midbrain—have been well established. After the early discovery of the essential role of dopamine in the pathophysiology of PD it was quickly realized that treatment with the dopamine precursor levodopa could be a useful therapy, and since then, this approach has remained the gold standard for symptomatic PD treatment. Unfortunately, in a majority of patients long-term treatment with levodopa is limited by the gradual development of severe motor complications, such as abnormal involuntary movements with hyperkinetic or dystonic features, collectively referred to as levodopa-induced dyskinesia (Fabbrini et al., 2007). Together with the identified critical role of dopamine in the striatum, the major input structure of the basal ganglia, this has led to the proposition that adaptive mechanisms in this structure induce a hypersensitivity to dopamine (for review, see Cenci and Konradi, 2010). Less attention has been paid to the slower, but still significant simultaneous loss of dopaminergic innervation in the cortex, even though these changes have been hypothesized to constitute an important factor underlying several symptoms of PD (Moore et al., 2008; Luft and Schwarz, 2009). Consequently, to identify neurophysiological mechanisms underlying parkinsonian symptoms as well as the motor dysfunction experienced in levodopa-induced dyskinesia, neuronal recordings should ideally be obtained from both striatal and cortical circuits over extended time periods during normal, parkinsonian, and dyskinetic states in awake, freely behaving subjects.

Materials and Methods

Animals.

Seven adult female Sprague Dawley rats (230–250 g, Taconic Inc.) were used in the study. The animals were kept on a 12 h light cycle and received food and water ad libitum. All experiments were approved in advance by the Malmö/Lund ethical committee of animal experiments.

6-Hydroxydopamine lesions.

Rats were anesthetized with Fentanyl/Medetomidine (0.3/0.3 mg/kg, i.p.) and fixed in a stereotaxic device (David Kopf instruments) with a horizontal cranium position. The animals received two injections of 6-hydroxydopamine (6-OHDA) hydrochloride (3.0 μg/μl free base, Sigma-Aldrich; dissolved in 0.02% ascorbate saline) into the medial forebrain bundle of one hemisphere at the following coordinates from bregma and cortical surface (Cenci and Lundblad, 2007): Injection site (i), 2.5 μl: tooth bar (TB), −2.3; anteroposterior (AP), −4.4; mediolateral (ML), −1.2; and dorsoventral (DV), −7.8; Injection site (ii), 2.0 μl: TB, +3.4; AP, −4.0; ML, −0.8; DV, −8.0. Moderate motor impairments including asymmetric posture and gait and reduced forelimb dexterity were apparent 2 weeks after lesioning. Only animals with nearly complete (>90%) loss of tyrosine hydroxylase (TH) immunoreactivity in the striatum were included in the study.

Implantation surgery.

Implantations were performed under Fentanyl/Medetomidine anesthesia (0.3/0.3 mg/kg, i.p.). Microwire electrodes were implanted in both hemispheres in the forelimb area of the primary motor cortex (MI; center coordinates: AP, +1.5; ML, ±2.8; DV, −1.0 from bregma and cortical surface; Gioanni and Lamarche, 1985) and the dorsolateral striatum (center coordinates: AP, +0.2; ML, ±3.8; DV, −3.5 from bregma and cortical surface; West et al., 1990). Furthermore, in animals receiving pharmacological intervention, a 20 gauge guide cannula (CMA Microdialysis AB) was implanted over the motor cortex adjacent to the recording area of the lesioned hemisphere. The tip of the cannula ended just superficial to the cortical surface where the dura had been locally explanted, ∼1.5 mm anterior of the cortical electrodes making sure that the volume injected would spread to the recorded area. The implant was fixated with dental acrylic which was attached to screws in the scull. These screws also served as connection points for the electrode ground wire. After surgery, the anesthesia was reversed by Atipamezole hydrochloride (5 mg/kg, i.p.) and buprenorphine (0.5 mg/kg, s.c.) was administered as postoperative analgesic. The animals were allowed to recover for 1 week after implantation before testing commenced.

Experimental procedure.

During recording sessions the animals were placed in a transparent cylinder (250 mm in diameter), and their behavior was documented via digital video recordings in parallel with the electrophysiological recordings (synchronized via an external pulse generator; Master-8, AMPI). The same paradigm was used in each experiment: First, the rat was recorded for 30 min to establish baseline conditions. Second, the rat was intraperitoneally injected with levodopa (levodopa methyl ester) and benzerazide (serine 2-(2,3,4-trihydroxybenzyl) hydrazide hydrochloride racemate). Dyskinesia developed 10 to 20 min post-levodopa injection and reached its peak severity ∼60 min post-levodopa injection. In experiments not involving further pharmacological intervention, the recordings continued until the dyskinesia diminished spontaneously (∼2 h post-levodopa injection). In experiments involving further pharmacological intervention, the rat received a 10 μl topical injection of either the dopamine type 1 receptor (D1R) antagonist SCH23390 (20 μg/μl) or vehicle (saline) onto the cortical surface at 60 min post-levodopa injection. The topical injection was made through the implanted guide cannula using a Hamilton syringe (∼5 μl/min), and the recordings continued for 60 min after topical injections.

Dyskinesia scoring.

The scoring of dyskinesias was done off-line according to standard methods for scoring of abnormal involuntary movements (AIMs) (Cenci and Lundblad, 2007). In summary, the three different types of AIMs: orolingual, forelimb, and axial dyskinesia were separately scored with respect to the severity of the dyskinesia for monitoring periods of 1 min. In addition, contraversive rotations with respect to the lesioned side were scored in the same manner, as rotational behavior is correlated with general dyskinetic symptoms in this model. First, AIMs were rated on a scale ranging from zero to three where zero equals no dyskinesia and three equals continuous dyskinesia. Second, the amplitude of the individual AIMs were also rated from zero to four to provide an extra dimension to the severity of the dyskinesia, where zero is the lowest and four the highest amplitude. The product of these two different measures for each type of AIM was then added together to produce a “total AIM value” for each scored time point. This combined value indicated the overall severity of the dyskinesia at any given time, and was graphically displayed with color coding for the different AIMs.

Tissue preparation.

To elicit dyskinesia before perfusion, rats were given a dose of levodopa (15 mg/kg) together with benserazide (12 mg/kg). One hour post-levodopa injection, corresponding to the time of peak dyskinesia, the rats were injected with a lethal dose of sodium pentobarbital (50 mg/kg) and transcardially perfused with 150 ml of 0.9% saline, followed by 300 ml of ice-cold 4% buffered paraformaldehyde. After fixation, the brain was removed and fixated in paraformaldehyde for 12 h. The brains were then transferred to a 20% sucrose solution in PBS at 4°C for cryoprotection overnight. The brains were sectioned using freezing sliding microtome to obtain coronal sections of 30 μm thickness. The obtained sections were stored in anti-freeze solution (30% ethylene glycol and 30% glycerol in 0.1 m phosphate buffer) at −20°C until used for staining.

TH staining and quantification.

The extent of the lesions was confirmed by TH immunohistochemistry as described in previous studies (Francardo et al., 2011). Briefly, the sections were washed three times in 0.02 m potassium PBS (KPBS) to rinse away the antifreeze. Subsequently, sections were quenched for 15 min in 3% hydrogen peroxide and 10% methanol in KPBS. The sections were then incubated in 5% normal goat serum (NGS) in KPBS with 0.25% Triton X-100 (KPBS-T) for 1 h, followed by incubation with primary anti rabbit anti-TH (1:1000; Pel-Freez) at 4°C overnight. On the next day, the sections were rinsed and incubated with the biotinylated goat anti-rabbit (BA1000) at 1:200 dilution in 5% NGS and KPBS-T. Thereafter, the sections were incubated for 1 h at room temperature in avidin-biotin-peroxidase solution (Vectastain Elite ABC; Vector Laboratories). The antibody bound was detected by using 3,3-diaminobenzidine and H₂O₂ (both from Sigma-Aldrich). For quantification of TH staining, digital photos of the individual sections were taken with a Nikon digital camera (DXM 1200F; Nikon Nordic AB) mounted on a Kaiser slimlite light box under identical illumination conditions. The optical density of TH-immunoreactive fibers was then measured according to previously described methods (Kirik et al., 1998) at two anteroposterior levels (+0.2 mm and +1.5 mm) using the NIH ImageJ program. For quantification of striatal TH staining in low magnification the optical density of the ipsilateral cortex was used as an estimate for TH background level staining and was consequently subtracted before side differences were calculated. The data are expressed as percentage of TH sparing of intact side.

c-Fos and D1R staining and quantification.

Immunofluorescence for c-fos and D1R was performed according to previously described protocols (Yung et al., 1995; Halász et al., 2002, 2006) with slight modification. Sections were rinsed in 0.02 m PBS, followed by two washes of Tris-buffer. The sections were then incubated in 5% NGS in PBS with 0.25% Triton–X (PBS-T) for 1 h. This was followed by overnight incubation at room temperature with one of the following antibodies: rabbit polyclonal antibody against c-fos (1:300; Santa Cruz Biotechnology), rabbit polyclonal antibody against D1R (1:300; Sigma-Aldrich). The antibodies against c-fos and D1R were detected by Alexa Fluor 594 goat-anti-rabbit (1:500; Invitrogen).

The total number of c-fos-positive cells and D1R-density was estimated by confocal laser scanning microscopy in immunofluorescent sections. Specifically, those cortical regions in the two hemispheres which corresponded to the electrode implantation sites were analyzed. Identical acquisition settings were used for both hemispheres, and any post-acquisition adjustments of brightness or contrast in the collected images were performed in an identical way for the two sides. Before quantification, the collected images were converted into bichromatic images. The person carrying out the analysis, who was blinded to which hemisphere the samples were collected from, then performed quantification through manual thresholding of fluorescence intensity. For c-fos quantification the number of cells displaying immunofluorescence above threshold levels was counted, whereas for D1R quantification the number of pixels above threshold levels was used as readout.

Electrodes.

Formvar-insulated tungsten wires (33 μm; California Fine Wire Co.) were arranged into four 4 × 5 arrays with 250 μm spacing in each dimension and cut to the length corresponding to the implantation site for each group. Each array consisted of 16 recording channels, two reference channels and one stimulation channel (not used in this study). Reference wires were deinsulated 300 μm at the tip to lower impedance and cut shorter than the recording wires, positioning them in the cell sparse regions superficial to the recording sites (the cortical surface and within the corpus callosum, for cortical and striatal electrodes, respectively). A 200 μm silver wire was used for ground connection. The wires were attached to board-to-board-connectors (Kyocera 5602) with conducting epoxy (Epotek EE 129-4) and linked to the acquisition device via a board-to-Omnetics connector adapter (Kyocera 5602; Omnetics).

Signal acquisition.

LFPs and single- and multiunit activity were recorded using a multichannel recording system (Neuralynx Inc.). LFPs were filtered 0.1–300 Hz, and digitized at 1017 Hz whereas action potentials were filtered at 600–9000 Hz and digitized at 32 kHz. Threshold for storage of spiking events was set to three SDs of the unfiltered signal.

Time-frequency analysis of LFP power.

Only experiments where high quality LFP recordings from all four brain structures (MI and striatum on both sides) were obtained for the whole recording session were included in LFP analyses (18 of, in total, 30 experiments). For each LFP recording, a spectrogram, i.e., a time series of power spectral densities (PSDs), was estimated with Welch's method (8 s Hann window with 50% overlap) using custom code written in Matlab (MathWorks). The spectrograms of the LFP recordings from all the functional electrodes within each structure were averaged to generate one spectrogram for each of the four structures. Channels with exceptional noise levels were excluded based on visual inspection. On average, 48.2 ± 7.8 channels were included per recording (left MI: 12.3 ± 3.4, right MI: 14.2 ± 0.6, left striatum: 10.9 ± 6.1, right striatum: 10.8 ± 2.6). To detect and reject LFP time windows containing artifacts, a flatness criteria (thresholded median variance over a 0.1 s window) was used. Furthermore, the 50 Hz and the 100 Hz components were removed from the PSDs due to power line noise. From these spectrograms, time-averaged PSDs during OFF/ON levodopa periods were obtained and denoted PSD_OFF and PSD_ON, respectively. Furthermore, the average power in a certain frequency band was obtained by averaging each PSD time series of the spectrograms over that frequency band.

Time-frequency plots of spectrograms (Fig. 1E,F; see Fig. 3B) were shown relative to the pre-levodopa baseline by normalizing the PSD time series with the corresponding PSD_OFF (indicated in figures by the unit dB_baseline). In addition, the resulting spectrograms were smoothed along the time and frequency axis with a three- and eight-point moving average, respectively, resulting in a time-frequency resolution of ∼16 s and 0.12 Hz.

Figure 1.

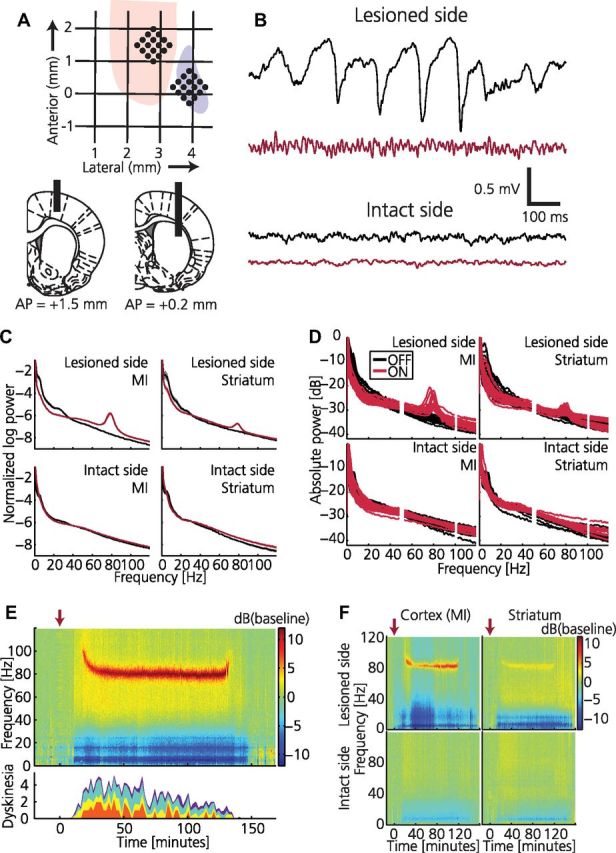
Dyskinesia is associated with high-frequency oscillations in cortical local field potential. A, Schematics illustrating positioning of recording electrodes relative to bregma. Top, Horizontal plane indicating anterior and lateral positions within forelimb representation in MI (pink) and striatum (purple). Bottom, Coronal plane indicating vertical positions for cortex (left) and striatum (right) together with AP positions. Electrodes were implanted bilaterally. B, Example traces of cortical LFPs recorded synchronously from the intact and lesioned hemisphere before (black) and after (red) levodopa administration. C, Average of normalized LFP power spectra for the intact and lesioned hemisphere before (black) and after (red) levodopa administration (n = 18). D, Normalized LFP power spectra shown for each experiment (50 and 100 Hz frequencies removed due to power line noise). E, Top, Spectrogram from LFP recording in lesioned MI showing a narrowband 80 Hz oscillation associated with the dyskinetic state (power spectrum normalized to pre-levodopa baseline; red arrow, levodopa injection). Bottom, Dyskinesia score (red, rotations; yellow, limbic; turquoise, axial; purple, orolingual). F, Example of spectrograms from parallel LFP recordings in all four structures.

Figure 3.

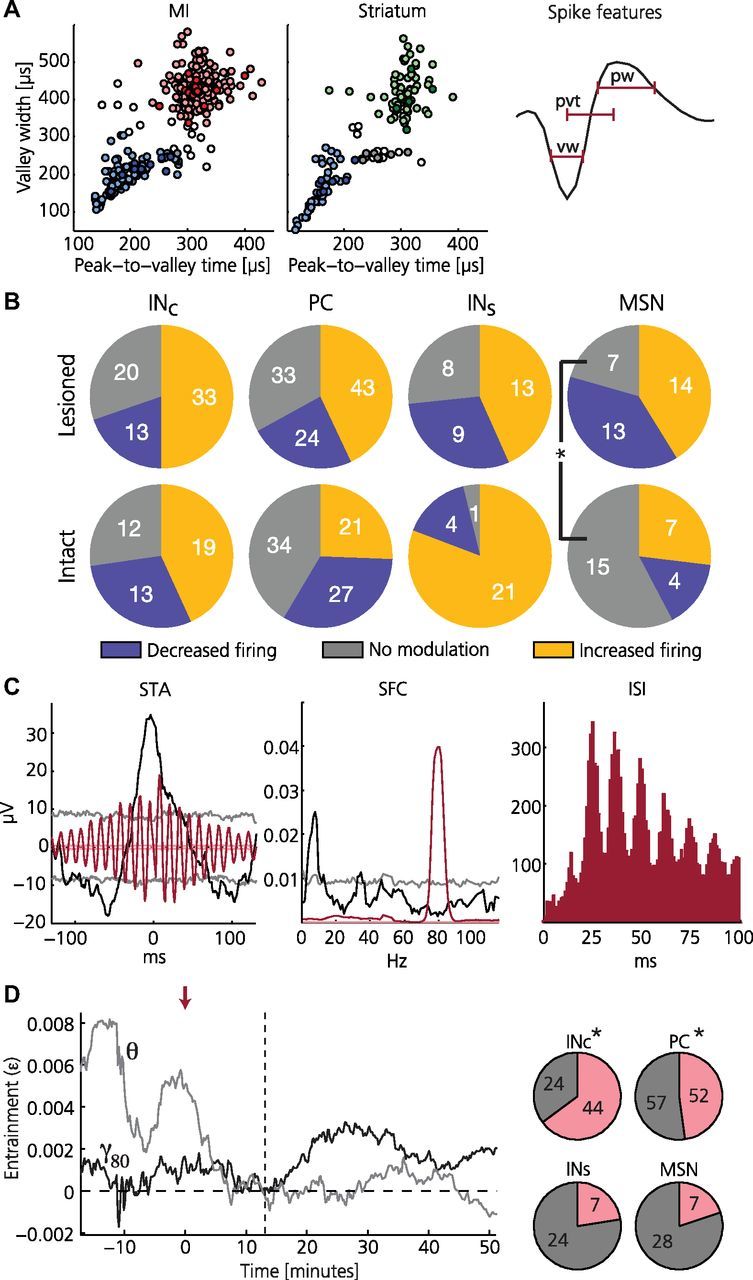
Individual neurons in the lesioned hemisphere show entrainment to resonant LFP oscillations. A, Classification into putative cell types for MI (left) and striatum (middle) based on spike shape features (right). For MI: red, pyramidal cells (PC); blue, interneurons (IN_c); uncolored, unclassified. For striatum: green, medium spiny neurons (MSN), blue, interneurons (IN_s); uncolored, unclassified. Darker colors mark significant entrainment to the 80 Hz band (γ₈₀; 75–90 Hz) after levodopa administration. B, Summary of firing rate modulations: fraction of cells displaying consistent increase or decrease in firing rates during the dyskinetic state compared with pre-levodopa administration is shown for the respective cell classes. Note that only putative medium spiny neurons show a significant difference between the lesioned and the intact side (more cells are modulated on the lesioned side; two-proportion z-test, p = 0.037, Bonferroni corrected for 12 tests). C, Example of a putative pyramidal cell in lesioned MI showing strong γ₈₀ entrainment and rhythmic firing after levodopa administration (note also pre-levodopa θ entrainment). Left: STA of LFP before (black) and after (red) levodopa administration (faded lines denote 95% confidence intervals). Middle, SFC before (black) and after (red) levodopa administration (peak values at 8 Hz and 79.5 Hz, respectively; faded lines denote 95% confidence intervals). Right: interspike interval (ISI) histogram revealing pronounced rhythmic firing at intervals of multiples of the 80 Hz period during dyskinesia. D, A majority of the cells in lesioned MI shifted from predominant θ to predominant γ₈₀ entrainment following levodopa administration. Left, Representative example of a putative interneuron showing a shift in preferred entrainment frequency. Index of entrainment (ε) is shown for θ (gray) and γ₈₀ (black) with ε = 0 corresponding to no entrainment (red arrow: levodopa injection; vertical dashed line: dyskinesia onset). Right, Charts summarizing the fraction of cells in lesioned cortex (top) and striatum (bottom) showing a shift in preferred entrainment frequency from θ to γ₈₀ following levodopa administration (pink). Notably, only cells in lesioned MI showed a significant bias for such a shift (asterisk denotes p < 0.05; chance level corresponds to 25%).

Plots of time-averaged PSDs (Fig. 1C,D) were normalized to the estimated mean variance of the pink noise background. In detail, for both PSD_OFF and PSD_ON, the variance of the pink noise background was estimated to be the power in those frequency bands where the PSD followed a 1/f-like trend (30–120 Hz, excluding 50 Hz, 75–90 Hz and 100 Hz). The normalization constant was then defined to the mean of these two values. In addition, average PSDs shown for individual experiments were smoothed along the frequency axis with an eight-point moving average (frequency bin resolution = 0.12 Hz).

Definition of pink decibels.

To measure the 80 Hz peak independently from the pink noise floor we first estimated the pink noise power

by fitting the constants a and b such that S_pink(f) fits the PSD optimally in the least-squares sense. The estimation of a and b was only based on frequency bands with a clear 1/f-like trend (30–120 Hz, excluding 50 Hz, 75–90 Hz and 100 Hz). This allowed us to describe PSD deviations from the pink noise floor conveniently in terms of the unit dB_pink according to

where S(f) and S_pink(f) have the dimension power per hertz and S_dB(pink) is expressed in the dimensionless unit dB_pink. Note that dB_pink can be viewed as a measure of the signal-to-noise ratio.

Frequency trend of the 80 Hz oscillation.

The exact frequency of the 80 Hz peak, denoted f_osc(t), was estimated to be the frequency within 75–90 Hz with maximal power (expressed in dB_pink). For time periods where the average power within 75–90 Hz was <3 dB_pink the peak frequency was considered to be undetectable and f_osc(t) was left undefined. f_osc(t) was calculated at 4 s intervals and smoothed by a 10 point moving average.

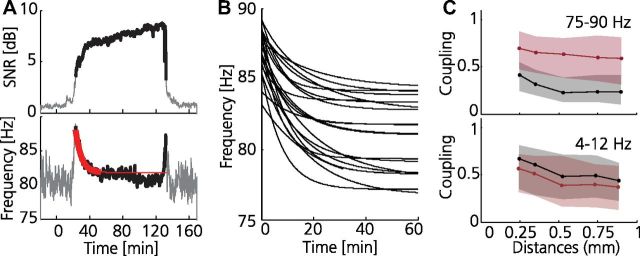
Typically a slow decrease in oscillation frequency was observed following the onset of the oscillation. To analyze this trend in more detail an exponential function was fitted to the period [t_on, t_on + 30 min], where t_on is the time at which the oscillation was first detected. The exponential function was defined to

where the constants a, b, and c were estimated such that the exponential function fit f_osc(t) optimally in the least-squares sense. With this definition, the onset oscillation frequency at t = t_on could be estimated to a + c, the asymptotical oscillation frequency to c, and the exponential decay of the oscillation frequency to b. The latter can be interpreted such that at time t = t_on + b, i.e., b min after oscillation onset, the oscillation frequency has decayed to a · exp(−1) + c. The reliability of the estimated parameters was assessed by the goodness of fit of the exponential function to f_osc(t) (mean squared error).

Relationship between 80 Hz power and dyskinesia.

The dyskinesia score was plotted as a function of 80 Hz power (expressed in dB_pink) to further illustrate the relationship between the two. Data from two time periods was included: a 40 min window starting immediately after levodopa administration and a second window starting immediately after D1-antagonist administration. The second window continued to the end of the recording (∼40 min). The relationship was clearly nonlinear with a fast rising threshold phase and a saturating plateau phase. A sigmoid function, defined by

was fitted to the data by estimating the optimal a, b, and c in the least-squares sense. The reliability of the estimated parameters was assessed by the goodness of fit (mean squared error).

Coherence.

Coherence between two simultaneously recorded LFP signals was computed using a multitaper method (Pesaran, 2008) implemented in the open-source data analysis toolbox Chronux 2.0 (http://chronux.org) (Mitra and Bokil, 2008). In a first step, a 5 min period was selected for analysis, during which the two LFP signals were segmented into nonoverlapping windows of equal length (4 s). Next, the multitaper method (7 tapers) was applied separately to each window, resulting in the cross-spectrum and the two auto-spectra, which were then used to compute the coherence for the current window. The final estimate of the coherence, C(f), was obtained by averaging the coherences over all windows. Both the averaging over the different time windows and the multitaper method have the advantage of effectively reducing the variance of the spectral estimates, and thus the coherence. Confidence limits (95%) for the coherence magnitude were estimated with a jack-knife procedure.

Coupling strengths and delays within structures.

The coupling strength and delay between two simultaneously recorded LFP signals in a certain frequency band [f_low, f_high] was calculated based on the coherence

where φ(f) denotes the so-called phase spectrum (Müller et al., 2003). Furthermore, the magnitude-squared coherence (MSC) was defined to

The coupling strength between the two LFP signals was then estimated to

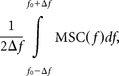where f₀ was that frequency within the range [f_low, f_high] for which MSC(f) reached its maximum, and Δf was the parameter determining the width of the integration integral, which was set to 0.5 Hz. The integral was normalized such that it, similar to the MSC itself, ranged between 0 and 1, and thus represented the average coupling strength between the two LFP signals in the frequency range of interest. The delay between the two LFP signals was estimated to (Müller et al., 2003)

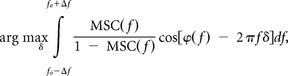i.e., the estimator evaluated the weighted goodness-of-fit of a line with slope δ to the phase spectrum φ(f) over the frequency range of interest, and chose to estimate the delay to that δ with the best goodness-of-fit. The delay estimation was only computed when the corresponding coupling strength was significant, i.e., when it exceeded the corresponding coupling strength calculated from the 95% confidence limit of the coherence.

Spike sorting and cell classification.

Action potentials were sorted manually into unit clusters using Offline Sorter (Plexon Inc.). Waveform features used for separating the units were, e.g., valley amplitude, peak amplitude or the first three principal components of all the 32-element vectors defining the sampled waveforms for a given dataset. A cluster was classified as single unit (SU) when <0.1% of the spikes in a defined cluster occurred within the refractory period (set to 1.6 ms), and as multiunit otherwise (Harris et al., 2000). Based on the features valley width, peak width, and peak-to-valley time of the average waveform of each SU, the SUs from striatum and motor cortex were further classified into two cell types each. The widths were defined as the full width at half maximum (FWHM). Striatal SUs were classified as either putative medium spiny neurons (MSN), interneurons (IN_S) or were left unclassified (Berke et al., 2004; Gage et al., 2010). Similarly, cortical SUs were classified as either pyramidal cells (PC), interneurons (IN_C) or were left unclassified (Barthó et al., 2004). The classification was performed by fuzzy k-means clustering (Duda et al., 2001) with probability of membership > 0.75, i.e., SUs with a probability of membership < 0.75 were labeled as unclassified. Table 1 summarizes the statistics of the waveform features of the cell types in the two structures.

Table 1.

Summary of spike shape features for each classified cell type (mean ± SEM presented)

Structure	Cell type	Number of cells	Peak width (μs)	Valley width (μs)	Peak-to-valley time (μs)
Striatum	MSN	61	164 ± 18	421 ± 56	305 ± 32
	IN	57	118 ± 16	148 ± 56	157 ± 24
	Unclassified	22	159 ± 20	258 ± 27	259 ± 29
Motor cortex	PC	194	162 ± 16	436 ± 42	318 ± 29
	IN	113	136 ± 18	199 ± 40	194 ± 35
	Unclassified	15	159 ± 17	311 ± 59	268 ± 57

MSN, Medium spiny neuron; IN, interneuron; PC; pyramidal cell.

Firing rate modulation.

Firing rate modulations relating to the dyskinetic state were evaluated by comparing firing rates during dyskinesia with firing rates during the pre-levodopa baseline. Firing rates were estimated with 10 s bins. If the cell fired <6 times during a 1 min window, data from that time period was excluded from the analysis. The firing rate distribution of the dyskinetic state was compared with the baseline distribution with a Mann–Whitney U test and was regarded as significantly modulated when p < 0.05. Differences in the number of modulated cells between the lesioned and the intact hemisphere were tested with a two-proportion z-test (p < 0.05).

Spike-field coherence.

The phase synchronization between spike times and LFP was measured by the spike-field coherence (SFC), which was defined to (Fries et al., 2001)

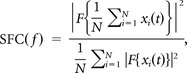where F denotes the multitaper spectral density estimation (time-bandwith product = 3, number of tapers = 5, Chronux toolbox, N the number of spikes, and x_i(t) the LFP segment corresponding to a short time window around the ith spike (±500 ms). Considering the definition of the spike-triggered average (STA)

the SFC can be rewritten to

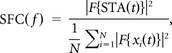i.e., the SFC can be interpreted as the normalized power spectrum of the STA. With this normalization SFC(f) ranges between 0 and 1, where 0 corresponds to the total absence of a phase relation between the spikes and the LFP component at frequency f, while 1 corresponds to the presence of a perfect phase relation, i.e., all spikes occur at the exact same phase of the LFP.

Since the spike and the LFP were recorded with the same electrode the spike was occasionally clearly present in the STA. Thus, the STA was interpolated on the interval [-3, 3] ms to minimize the influence of the spike artifact on the SFC and the PSD of the STA.

To assess the significance of the SFC, 200 surrogate spike trains were generated by independently dithering (Grün, 2009) all original spikes with uniform probability in the range ±5 s. The SFC corresponding to the original spike train was then considered significant for a certain frequency bin when it exceeded the 95^th percentile of the surrogate SFCs for that bin.

A neuron was considered to be entrained to a certain frequency band when the following two criteria were fulfilled: First, the SFC had to be significant for at least one 1 Hz-wide bin within the frequency band. Second, the band power of the STA during the ON period had to show a significant increase compared with the OFF period. An increase was judged as significant when it was larger than 95% of the changes seen on the intact side (where there was no detectable narrowband 80 Hz oscillation in the LFP). The rationale behind the second criterion was based on our observation that the SFC criterion alone was sometimes sensitive to noise in the γ₈₀ band (75–90 Hz). The likely reason for this is that the estimation of the power in the γ₈₀ band can be quite noisy due to the relatively low power in this band under normal, non-resonant conditions.

Instantaneous phase.

The time-dependent entrainment of SUs to certain LFP frequency bands was determined by evaluating the phase of the LFP at the time of each spike (Hurtado et al., 2005). For this purpose, the LFPs were first bandpass filtered (4–12 Hz for oscillations in the θ band, 75–90 Hz for the oscillation in the γ₈₀ band). In a second step, the complex-valued analytical signal z(t) was calculated from the filtered signal as implemented by the hilbert-function in Matlab's Signal Processing Toolbox. Next, the instantaneous phase of the LFP oscillation could be obtained as the angle of z(t),

When the LFP oscillation is interrupted or becomes very small in amplitude, the instantaneous phase becomes difficult to interpret, and so-called phase slips (i.e., jumps in the instantaneous frequency) can occur. To detect these phase slips, a first-order approximation of the instantaneous frequency f(t) was made from φ(t) according to

where φ̃(t) is the unwrapped instantaneous phase and Δt = t_i − t_i−1 is the sampling period. Values of φ(t) at which the corresponding f(t) exceeded the bandpass limits were discarded. Finally, the phase of the LFP oscillation at the time of spike j was determined through interpolation and denoted φ_j.

Time-dependent entrainment.

After determining the phases φ_j, the time-dependent entrainment was quantified based on

which is the distance from the origin of the complex plane after n steps (i.e., spikes) with step length 1 and step directions φ_j. It can be shown that when the step direction is random [i.e., when φ_j is drawn from a uniform distribution u(0, 2π)], the expectation value of the drift becomes E[d_random(n)] = $\sqrt{\pi n/4}$ (cf. random walks). To separate the part that corresponds to a direction bias from the purely random part of the drift, we defined d̂(n) = d(n)/$\sqrt{\pi n/4}$, which can be viewed as a measure of entrainment, since a value of d̂(n) > 1 would indicate that the phase angles were not drawn from a uniform distribution. A measure of entrainment would then correspond to the drift rate Δd̂(n)/Δn. After transforming n→t_n and interpolating so that d̂ becomes a time series with fixed sampling period Δt we obtained a time-dependent index of entrainment

with an ε > 0 indicating entrainment.

To test whether a class of neurons showed a biased pattern of shifting preferred entrainment frequency from θ to γ₈₀, we calculated the fraction of neurons that fulfilled the two criteria E[ε_θ(t) − ε₈₀(t)] > 0 during the OFF period and E[ε_θ(t) − ε₈₀(t)] < 0 during the ON period. Then we used the binomial cumulative distribution to calculate the probability to obtain these fractions by chance:

where x is the number of neurons in the class that fulfill the two abovementioned criteria and n is the total number of neurons in the class.

Statistical analysis.

Parameters in different groups, e.g., referring to baseline and dyskinesia, were compared using the two-sample Kolmogorov–Smirnov test (kstest2 function in Matlab, MathWorks) or the two-sided Mann–Whitney U test (ranksum function in Matlab). The correlation between different parameters was calculated using the Pearson correlation coefficient r and related p-value. A p-value <0.05 was considered statistically significant. All parameters are given in mean ± SD unless stated otherwise.

Results

In the present study, we have attempted to identify neurophysiological mechanisms underlying parkinsonian symptoms as well as the motor dysfunction experienced in levodopa-induced dyskinesia by performing chronic recordings in cortical and striatal circuits in the most widely used animal model of dyskinesia (Nadjar et al., 2009), that is, rats in which chronic unilateral lesions of the SNc/VTA dopaminergic cell-groups were induced by injecting the neurotoxin 6-OHDA into the medial forebrain bundle. When treated with levodopa, rats with unilateral 6-OHDA lesions display dyskinetic movements affecting the contralateral (parkinsonian) side of the body, as extensively illustrated in previously published studies (Cenci et al., 2002). Starting 2 weeks after lesioning, rats received daily intraperitoneal injections of levodopa to induce reproducible dyskinesia, and were then implanted with multielectrode recording arrays centered on connected regions of the primary motor cortex and striatum (forelimb representation, as defined by stereotactic coordinates (Gioanni and Lamarche, 1985; West et al., 1990; Anderson et al., 2010); Fig. 1A). One week after implantation recordings commenced where neuronal activity was recorded from the cortex and the sensorimotor-related part of the striatum in the lesioned as well as the intact hemisphere. At the beginning of each recording session, animals were allowed to adapt to the recording chamber for 15 min. During the subsequent 30 min a baseline recording was obtained, followed by levodopa administration at a dose tailored to promptly induce severe dyskinesia in each animal (15.6 ± 4.8 mg/kg, combined with a blocker of peripheral degradation of levodopa, Benserazide 12 mg/kg, i.p.). Between 10–20 min after levodopa administration, animals started displaying abnormal involuntary movements involving orolingual, forelimb, and axial muscles as well as contraversive rotations, which are typical dyskinetic behaviors in this animal model of PD (Cenci et al., 2002). The prevalence and severity of the different types of abnormal involuntary movements were monitored for different time periods using a validated rating scale (Cenci and Lundblad, 2007).

The dyskinetic state is signified by a resonant LFP oscillation at 80 Hz

In the current experiments, simultaneous electrophysiological recordings from the lesioned and nonlesioned hemisphere could be compared during different behavioral states (n = 5 rats). When analyzing the LFPs in the parkinsonian state, a first striking observation was the presence of transient high-voltage spindles in the cortical and striatal LFPs of the lesioned hemisphere (Fig. 1B, top; black trace) not only during time periods in which the animal was inactive, but also during relatively active periods. In the frequency domain, this activity resulted in an increase in LFP power below ∼30 Hz compared with the intact hemisphere (Fig. 1C, black traces). These findings suggest that transient LFP spindles are a specific physiological hallmark of the parkinsonian state, and as expected, LFP spindle activity diminished after levodopa administration (Dejean et al., 2008). However, in the transition from the parkinsonian to the dyskinetic state, levodopa proved to induce an even more striking change in LFP activity that was only observed in conjunction with dyskinetic symptoms. In all experiments (n = 18), the period of dyskinesia was always accompanied by a strong narrowband oscillation at ∼80 Hz in the motor cortex of the lesioned hemisphere (Fig. 1B–F). Generally, this oscillation was also observable in the striatum of the lesioned hemisphere, albeit at a considerably lower power (Fig. 1F). At no instance was the narrow-band oscillation detectable in non-dyskinetic animals either ON or OFF levodopa or in the intact hemisphere of any animal (Fig. 1D). However, a somewhat increased power in a broad frequency band above 30 Hz—a pattern typically seen in corticostriatal circuits during active periods and after levodopa administration in healthy subjects (Spooner and Winters, 1967; Wallach and Gershon, 1971; Costa et al., 2006; Dimpfel, 2008; Miller et al., 2009)—was observed in both hemispheres following levodopa administration (Fig. 1F). In the initial phase, the dyskinesia-associated oscillation was characterized by a slow gradual decrease in frequency from ∼100 Hz to 80 Hz (the time-frequency relation was well fitted with an exponential function with mean time constant 12 min; Fig. 2A,B), and the cessation of dyskinesia was often associated with a reverse increase in oscillation frequency. Yet, for the principal part of the dyskinetic period (lasting ∼2 h), the 80 Hz oscillation was found to be remarkably stable and similar between experiments (plateau value of fitted exponentials = 80.9 ± 2.7 Hz).The consistency of this oscillatory phenomenon in all animals recorded from may imply an inherent resonance of the cortical network (Wang, 2010) in the levodopa-treated state at ∼80 Hz. Because of the relatively homogenous cytoarchitectonical structure of the cerebral cortex, it would then follow that these oscillations could easily spread in the cortical sheet provided that the resonance frequencies of local circuits in adjacent areas are within the same frequency range. Indeed, when evaluating the LFP coupling strength between pairs of electrodes located 250–900 μm apart, we could observe a general increase in coupling strength in the 80 Hz band (γ₈₀; 75–90 Hz) following levodopa administration (Fig. 2C). Furthermore, the phase differences in the γ₈₀ band increased linearly with electrode spacing, corresponding to a lateral conduction velocity of 0.7 mm/ms [in agreement with previous estimates (Nowak et al., 1997)]. In summary, the LFP data suggest that synchronous abnormal activity patterns in the cerebral cortex may underlie the motor dysfunction induced by long-term levodopa treatment.

Figure 2.

Cortical oscillations associated with dyskinesia are tuned to 80 Hz. A, Example of power trend analyses of resonant oscillations during dyskinesia. Top, Signal-to-(pink)noise ratio (SNR) in the γ₈₀ band following levodopa injection at 0 min (SNR >3 dB shown in bold). Bottom, Peak oscillation frequency as a function of time (red, exponential function fitted to the 30 min following oscillation onset, defined as SNR >3 dB; fitting period indicated in bold; goodness-of-fit, 0.02 Hz²). B, Exponential functions fitted to 20 different recordings, aligned to oscillation onset (goodness-of-fit, 0.03 ± 0.01 Hz²); note the very similar time-frequency relation in all experiments. C, Coupling strength between LFP signals recorded from different electrodes in the motor cortex of the lesioned hemisphere as estimated from measures of coherence in two different frequency bands, plotted as a function of electrode separation (OFF and ON levodopa in black and red, respectively). Note the significantly increased LFP coupling strength in the 80 Hz band (γ₈₀, left) in the dyskinetic state (r_OFF = −0.21, r_ON = −0.11, p ≪ 0.001, two-sample Kolmogorov–Smirnov goodness-of-fit hypothesis test). Right, The θ band (4–12 Hz) included as a reference; in contrast to the γ₈₀, θ coupling was stronger in the non-dyskinetic state (r_OFF = −0.14, r_ON = −0.18, p < 0.001). Calculations were performed for a 5 min period during baseline and dyskinesia, respectively. The median (solid line) and the 25^th and 75^th percentile (shaded area) are shown for all recordings (n = 18).

Characterization of the neural firing patterns in the resonant state

Next, we therefore analyzed whether any evidence for abnormal firing patterns could be found in individual neurons (462 single units from 30 recordings in 6 rats; 15.4 ± 11.1 cells per session corresponding to 77 ± 92 cells from each animal). Based on their spike shape, cortical cells were classified as either putative pyramidal cells (PC) or interneurons (IN_C) (Barthó et al., 2004), and striatal cells were similarly divided into putative medium spiny neurons (MSN) or interneurons (IN_S; Fig. 3A; Table 1) (Gage et al., 2010). The subsequent analyses revealed that a majority of cells in the lesioned hemisphere showed either increased (47%) or decreased (25%) firing rates during the dyskinetic state compared with pre-levodopa administration (p < 0.05 Mann–Whitney). Importantly, however, similar dopamine-dependent alterations were also observed in the intact hemisphere, suggesting that this kind of rate modulations are less likely to cause the cortical LFP oscillation or dyskinetic symptoms (the only significant side difference found was for MSNs, for which a larger fraction of neurons tended to be modulated on the lesioned side; Fig. 3B). On the other hand, even in the absence of major changes in the firing rates of individual neurons, a transition into a rhythmic firing dynamic could still evolve on the network level. The temporal relationship between action potentials in individual neurons and the surrounding LFP oscillation was therefore investigated in further detail. These analyses revealed that a subgroup of cells in the lesioned hemisphere was clearly entrained to LFP oscillations in the γ₈₀ band in the dyskinetic state (Fig. 3A,C; PC, 12%; IN_C, 18%; MSN, 17%; IN_S, 22%; for inclusion criteria see Materials and Methods). Interestingly, a fraction of these cells were entrained to lower frequencies in the parkinsonian state (Fig. 3C, black trace). We therefore investigated temporal changes in preferred entrainment frequency of single cells by comparing the theta band (θ; 4–12 Hz) to the γ₈₀ band. Notably, although several cells in cortex and striatum were entrained to both bands it was only in lesioned MI that the majority of cells showed a clear transition in preferred entrainment frequency from the lower to the higher frequency band in response to levodopa administration (Fig. 3D; IN_C, p ≪ 0.001; PC, p ≪ 0.001, IN_S, p = 0.41; MSN, p = 0.68; tested with a binomial cumulative distribution function with p = 0.25), suggesting that these neurons have a particularly important role in the pathological synchronization of cortical networks both in the parkinsonian and in the dyskinetic state. Indeed, since even in strongly entrained cells action potentials would typically not occur in every cycle of the LFP oscillation, synchronization of relatively large networks of neurons is likely required to build up the strong oscillation observed in the LFP (Dejean et al., 2008; Wang, 2010).

Cortical histological adaptations resemble those of striatum

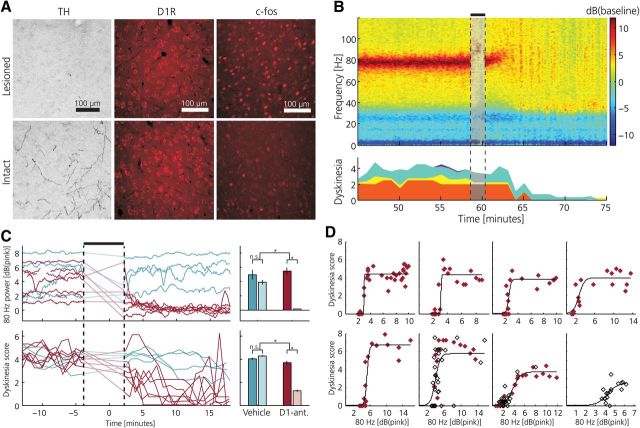
As the neurophysiological data indicated that exogenous dopamine administration in the parkinsonian state induced cortical resonance, the role of dopamine in the primary motor cortex was further investigated by using immunohistochemical techniques for the characterization of both presynaptic and postsynaptic changes (n = 6 rats). Quantitative evaluation of the staining density of tyrosine hydroxylase-containing axons and presynaptic terminals in the forelimb motor cortex showed a severe loss of dopaminergic innervation in all layers and in all animals (on average only 7.3% of intact side, Fig. 4A, left). In contrast, the expression of the dopamine type 1 receptor (D1R), which has been implicated in the regulation of forebrain excitability (Seamans and Yang, 2004), was not found to be different in corresponding areas between the two sides (p = 0.47, Mann–Whitney; Fig. 4A, center). This imbalance between presynaptic and postsynaptic elements of the dopaminergic transmission in the cortex mimics the changes that have been reported in the striatum (Nadjar et al., 2009; Cenci and Konradi, 2010; however, it should be noted that a comprehensive quantification of synaptic receptor densities would require more detailed analyses based on electron microscopic data). Thus, similar to the previously described striatal adaptations (Aubert et al., 2005), cortical networks are likely also subjected to dopamine sensitization. This was further supported by the finding that levodopa treatment induced an increased expression of the immediate early gene c-fos not only in the striatum but also in the motor cortex of the lesioned hemisphere (number of c-fos-positive cells were 218% of the intact side, p = 0.037, Mann–Whitney; Fig. 4A, right; for a further discussion on dopamine-dependent changes in cortical excitability see Seamans and Yang, 2004; Rotaru et al., 2007).

Figure 4.

Antagonizing D1-receptor activation in the primary motor cortex of dyskinetic animals disrupts cortical resonance and alleviates dyskinesia. A, Immunohistochemical analysis of dopaminergic markers comparing intact and lesioned MI at the time of peak dyskinesia. Left, Staining of TH-positive dopaminergic axons and terminals was markedly reduced in the lesioned hemisphere. Middle, D1R density in the lesioned hemisphere was unaltered after dopaminergic afferent denervation. Right, Expression of the immediate early gene c-fos after levodopa administration was relatively increased on the lesioned side. B, Topical application of the D1R antagonist SCH23390 to the cortical surface disrupts 80 Hz cortical resonant oscillation and alleviates dyskinetic symptoms. Left, Example of spectrogram from LFP recording in MI, power spectrum normalized to pre-levodopa baseline; D1R-antagonist injection denoted by black bar and faded colors. Dyskinesia score is shown at the bottom (red, rotations; yellow, limbic; turquoise, axial; purple, orolingual). C, Summary of all experiments (n = 11) showing γ₈₀ oscillations (top) and dyskinetic symptoms (bottom) following topical application of SCH23390 (red) or saline (blue), respectively (γ₈₀ power expressed relative to the pink noise background). Note the parallel decline in the power of the resonant LFP oscillation and the dyskinesia score in all experiments (traces during the period of drug application are linearly interpolated). Right, Average data from all experiments showing significant differences between D1R-antagonist vs vehicle treatment before (darker colors) and after topical application. Error bars denote SEM. *p < 0.05. D, Characterization of the relationship between γ₈₀ and severity of dyskinesia during the early dyskinetic phase (first 40 min following levodopa injection) and the cessation of dyskinesia following topical application of SCH23390. Each panel represents a single experiment (n = 5 rats) and displays the dyskinesia score as a function of cortical γ₈₀ power (each symbol denotes average over a 1 min period: filled, early dyskinetic phase; open, cessation of dyskinesia following SCH23390). The relationships were well fitted with sigmoid functions (average goodness-of-fit, R² = 0.72 ± 0.22). Notably, a similar relation between γ₈₀ power and the severity of dyskinesia is evident during the early phase of dyskinesia and following pharmacological γ₈₀ suppression.

A D1-antagonist applied to the cortical surface stops the oscillation and the dyskinesia

Finally, we performed experiments to test the hypothesis that the direct action of dopamine on receptors in the cortex is a critical component in the generation and maintenance of dyskinesia. For that purpose, a D1R antagonist (SCH23390, 200 μg in 10 μl saline) was topically administrated onto the cortical surface at 60 min after levodopa injection, corresponding to the expected time point of peak dyskinesia (n = 5 rats). We found that a few minutes after application of the antagonist both the 80 Hz oscillation and the dyskinetic symptoms were significantly reduced compared with control experiments using vehicle injections (Fig. 4B,C; p = 0.012 and p = 0.006 for pre- vs post-treatment group differences of γ₈₀ band power and dyskinesia score, Mann–Whitney, n = 7 and n = 4 experiments, respectively), while no significant changes in firing rates between the hemispheres were observed for any of the cell classes (two-proportion z-test: p > 0.018 corresponding to p > 0.154 after Bonferroni correction for multiple comparisons). However, although the antagonist suppressed the dyskinetic symptoms in all treated animals, the relatively local pharmacological blockade obtained by topical application was generally not sufficient to completely abolish dyskinesia. Thus, intermittent periods of dyskinesia and accompanying 80 Hz oscillation were observed in several experiments after D1R antagonist application. Interestingly, by specifically analyzing periods when animals displayed such moderate symptoms (which also occurred early in the on-set phase of the dyskinetic period) a clear relation between the power of γ₈₀ band oscillations and the simultaneous dyskinesia score could be established (Fig. 4D), in effect further corroborating the hypothesis that cortical resonance is causing dyskinetic symptoms.

Discussion

Previous studies have linked levodopa-induced dyskinesia to the supersensitivity of D1R-mediated signaling in the dopamine-denervated striatum (for review, see Cenci and Konradi, 2010). The present results reveal a previously unappreciated cortical phenomenon as being a key pathophysiological component in the generation of the abnormal involuntary movements. Although the observed resonant LFP oscillation at ∼80 Hz was many times stronger in the cortex, this rhythm was also detectable in the striatum concurrently with the cortical oscillation. This is a somewhat surprising finding, since it has generally been assumed that high-frequency oscillations in neuronal signaling to more distant targets are filtered out as a result of minor differences in axonal conduction velocities of individual fibers (Roberts and Robinson, 2008). An explanation may be offered by the characteristic anatomical connectivity of corticostriatal circuits: Because thousands of cortical neurons project onto single striatal neurons (Kincaid et al., 1998), even relatively weak coherent entrainment of some of the striatal-projecting cortical cells could drastically increase the probability of activating striatal neurons in specific phase relations to the cortical oscillation. Interestingly, in the subthalamic nucleus, which receives direct input from the same cortical areas through the hyperdirect pathway (Nambu et al., 1996), an almost identical oscillation (60–90 Hz) has been described in levodopa-treated PD patients implanted with deep-brain stimulation devices (Cassidy et al., 2002; Alonso-Frech et al., 2006) suggesting a related mechanism. However, because the subthalamic nucleus reciprocally can also modulate cortical activity, via connections to the output nuclei of the basal ganglia (that in turn influence motor nuclei in the thalamus), it cannot be ruled out that the oscillation may have multiple origins within the corticobasal ganglia-thalamic loop or that the subthalamic nucleus may in fact have an important role in driving the cortical oscillation (Williams et al., 2002). Nevertheless certain differences should be noted. While high-frequency oscillations in the subthalamic nucleus are also found in non-dyskinetic levodopa-treated patients the cortical 80 Hz oscillation that we here describe appears to be present only in association with dyskinetic symptoms suggesting a more direct causal pathophysiological link, which was also confirmed in the pharmacological experiments (Brown et al., 2002; Brown and Williams, 2005; Alonso-Frech et al., 2006). Based on our current findings, we therefore propose that a loss of cortical dopaminergic innervation represents a key predisposing factor for dyskinesia and that the ensuing supersensitivity to dopamine makes cortical circuits prone to network resonance when exposed to the systemic levodopa concentrations needed to obtain pro-kinetic effects in the basal ganglia. Consequently, an important objective for future studies should be to prevent or interfere with the mechanisms that underlie cortical resonant oscillations by means of pharmacological interventions (Bezard et al., 2004) or electrical stimulation (Hamani et al., 2008) of selected neuronal elements. Such interventions may in fact have even broader implications since similar oscillations have been suggested to be involved also in other psychiatric and neurological conditions that in part stem from cortical dysfunction (Wang, 2010; Yizhar et al., 2011).