Hippocampal Phase Precession from Dual Input Components

Abstract

Phase precession is a well known phenomenon in which a hippocampal place cell will fire action potentials at successively earlier phases (relative to the theta-band oscillations recorded in the local field potential) as an animal moves through the cell's receptive field (also known as a place field). We present a model in which CA1 pyramidal cell spiking is driven by dual input components arising from CA3 and EC3. The receptive fields of these two input components overlap but are offset in space from each other such that as the animal moves through the model place field, action potentials are driven first by the CA3 input component and then the EC3 input component. As CA3 synaptic input is known to arrive in CA1 at a later theta phase than EC3 input (Mizuseki et al., 2009; Montgomery et al., 2009), CA1 spiking advances in phase as the model transitions from CA3-driven spiking to EC3-driven spiking. Here spike phase is a function of animal location, placing our results in agreement with many experimental observations characterizing CA1 phase precession (O'Keefe and Recce, 1993; Huxter et al., 2003; Geisler et al., 2007). We predict that experimental manipulations that dramatically enhance or disrupt activity in either of these areas should have a significant effect on phase precession observed in CA1.

Introduction

Hippocampal place cells increase their firing rates when an animal is in a particular location within an environment. This region is referred to as the place field of a cell (O'Keefe and Dostrovsky, 1971; O'Keefe, 1976; O'Keefe and Nadel, 1978). One particularly fascinating feature of place cell coding is that of phase precession, in which a place cell will fire action potentials at progressively earlier phases, measured relative to the theta oscillations recorded in the local field potential, as the animal traverses the cell's place field (O'Keefe and Recce, 1993).

Previous models of phase precession include the “dual-oscillator model” of interference between two oscillating signals with different temporal frequencies (O'Keefe and Recce, 1993; O'Keefe and Burgess, 2005), and the “somatodendritic interference model” in which phase precession arises from the interactions between an oscillating somatic input and a second oscillating input of the same frequency but transformed by nonlinear dendritic properties (Kamondi et al., 1998; Magee, 2001; Lengyel et al., 2003; Losonczy et al., 2010; Leung, 2011). Other models have proposed that phase precession can arise from a ramp of excitation interacting with a single oscillating input (Harris et al., 2002; Mehta et al., 2002), asymmetries in local connectivity (Jensen and Lisman, 1996; Tsodyks et al., 1996; Wallenstein and Hasselmo, 1997), intrinsic temporal oscillations generated within CA1 (Geisler et al., 2007), short-term synaptic plasticity (Thurley et al., 2008), changes in network temporal dynamics driven by external input (Bose et al., 2000; Castro and Aguiar, 2012), or some combination of the aforementioned mechanisms (Baker and Olds, 2007).

We propose a model in which CA1 pyramidal cells are driven by dual input components arising from the two known anatomical inputs to CA1 (for review, see Ahmed and Mehta, 2009), CA3 and layer III of entorhinal cortex (EC3). Although EC3 input historically has been thought to play only a modulatory role in regulating CA1 output and plasticity (Levy et al., 1998; Golding et al., 2002; Remondes and Schuman, 2002; Judge and Hasselmo, 2004; Dudman et al., 2007), CA1 place cells retain spatial selectivity after disruption of input from CA3 (Brun et al., 2002; Nakashiba et al., 2008) suggesting that EC3 input can independently drive CA1 firing.

Excitatory drive from EC3 arrives in CA1 more than one-quarter theta-cycle before excitatory drive from CA3 (Mizuseki et al., 2009; Montgomery et al., 2009). We propose that this theta-phase offset, combined with a spatial offset between the input component receptive fields, generates phase precession. In our model spike phase is a function of animal location, in agreement with experimental studies of phase precession in CA1 (Huxter et al, 2003; O'Keefe and Burgess, 2005; Zugaro et al., 2005). Also, our model reproduces nonlinear phase advances that have been reported in the literature but are not easily reproduced by previous models (Skaggs et al., 1996) (see Fig. 6). Our results suggest that task or environmental factors driving different levels of activity in CA3 and EC3 may underlie different patterns of phase precession.

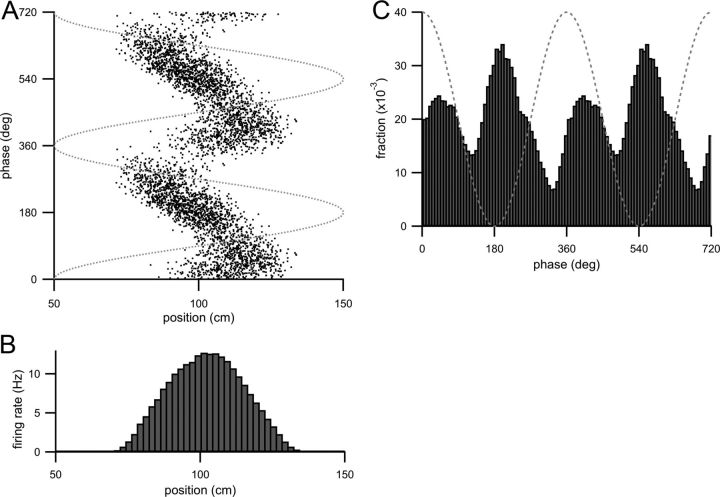
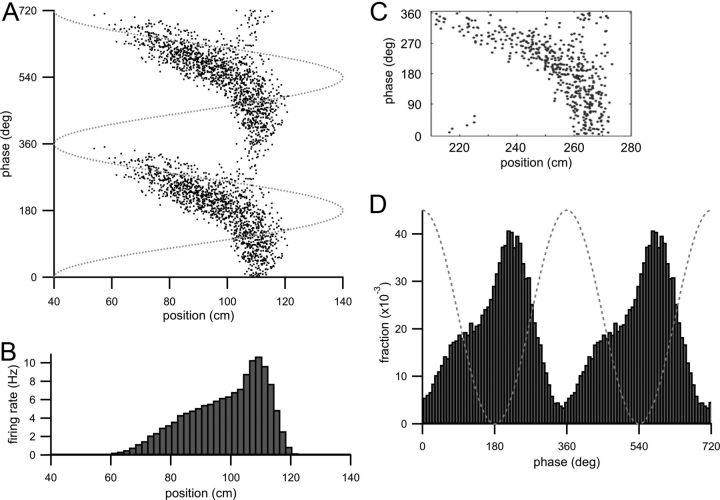
Figure 6.

Bilobed or boomerang-shaped spike raster from increasing the strength of the EC3 input component and also the theta modulation of both input components. Parameters are given in Table 1. A, Spike raster (theta phase of each action potential plotted as a function of animal position when the action potential was fired) of CA1 model cell spiking for increased EC3 input and with increased theta modulation of both input components. Dotted gray line is the theta oscillation. B, Firing rate histogram (calculated as in Fig. 1D) of model CA1 cell spiking with these parameters. C, Theta-phase histogram (fraction of spikes fired at a theta phase plotted as a function of theta phase) with these parameters. Two theta cycles are shown, and the dotted gray line is the theta oscillation.

Materials and Methods

The model CA1 pyramidal cell is a standard leaky integrate-and-fire model. The dynamics of the membrane potential are described by the following:

where C = 1 nF is the membrane capacitance, g_L = 50 nS is the resting membrane conductance of the neuron (in the absence of any excitatory synaptic input), g_E is the total excitatory synaptic conductance (determined by the input components as described below), E_L = −65 mV is the resting membrane potential, and E_E = 0 mV is the reversal potential of the excitatory synaptic current. If V depolarizes above a threshold (−52 mV), then an action potential is fired and the membrane potential is reset to −65 mV. The resting membrane potential is far below spike threshold and thus the resting membrane conductance prevents spiking when the animal is outside the place field. Any tonic level of synaptic inhibition may therefore be thought of as incorporated into the resting membrane conductance.

Royer et al. (2012) recently demonstrated that inactivation of either somatostatin-positive interneurons and parvalbumin-positive CA1 interneurons has a relatively small effect on the total phase advance observed across the place field, although parvalbumin-positive interneurons do appear to increase the rate of phase advance in the early parts of the CA1 place fields. For simplicity we have not attempted to include the effects of these or other interneuron types known for firing at specific theta phases (Somogyi and Klausberger, 2005; Klausberger and Somogyi, 2008; Royer et al., 2012). Instead, the driving excitatory influence of each of the input components (described below) should be considered to be a combination of excitatory synaptic input and any feedforward inhibition driven by that excitatory input.

We simulate the activity of a CA1 pyramidal neuron as the animal runs on a 200 cm long one-dimensional linear track. The model CA1 cell receives two components of synaptic input, one representing CA3 input and one representing EC3 input. The excitatory synaptic input rate arising from each input component is as follows:

⌊⌋₊denotes rectification and has no effect because b_i = 1 except in Figure 6, where b_i = 0.5. The parameter b_i controls how strongly the input rate is modulated at the theta frequency. A full list of input component parameters is given in Table 1.

Table 1.

Model parameters

Figure	ϕ1 (°)	ϕ2 (°)	b1	b2	x1 (cm)	x2 (cm)	α1 (Hz)	α2 (Hz)	σ1 (cm)	σ2 (cm)	k (°/cm)
1	260	100	1	1	90	110	280	280	21.2	21.2	0
2–3	Same as Figure 1
4	230	30	1	1	90	110	280	280	21.2	21.2	2.7
5	230	0	1	1	95	110	320	240	35.36 (21.2)	7.1	2.7
6	230	0	0.5	0.5	95	110	500	400	21.2	21.2	2.7
7A	Same as Figure 5
7B	Same as Figure 6

This table describes parameters for all figures. For Figure 5, σ₁ equals the value outside the parentheses for x < x₁ and the value inside the parentheses for x ≥ x₁.

The gray trace in Figure 1A is r₁, the CA3 input rate, for one run along the length of the track. A_i(x) may be thought of as describing the receptive field of each input component (for the purposes of this study, we reserve the term “place field” to refer to the range of track positions over which the model CA1 cell fires). Here A_i(x) is a Gaussian function of track position (dashed gray line and solid black line in Fig. 1A):

where x refers to the animal's position on a linear track. (In all figures, moving from x = 0 cm to x = 200 cm is running from left to right). The parameters α_i, x_i, and σ_i determine the amplitude, the center, and the width of the receptive field of input component i, respectively. The center of the EC3 component, x₂ = 110 cm is the same in all figures, while the center of the CA3 component is x₁ = 90 cm for Figures 1–4, and x = 95 cm for Figures 5 and 6. This spatial offset between receptive fields is a critical element of this model and we discuss below how such an arrangement might arise (see Discussion). The widths of the receptive fields are the same in all figures except for Figure 5 (see the addition of skewness into the receptive fields, below). The amplitudes of the synaptic input rates, α_1,2, were adjusted so that the peak firing rate of the model CA1 cell was between 10 and 15 Hz in all figures (except as noted in Fig. 2B–D). Although CA3 pyramidal neurons are known to have distinct place fields, principal neurons in EC3 have been reported to exhibit more spatially diffuse firing (Mizuseki et al., 2012), or even grid cell-like properties (Hafting et al., 2008). This model assumes a single spatially defined receptive field for the EC3 input component. Such a receptive field could arise if multiple grid cell-like EC3 neurons converge to a single CA1 cell (Solstad et al., 2006) or if the EC3 input is only strong enough to drive CA1 spiking in a specific subregion of space.

Figure 1.

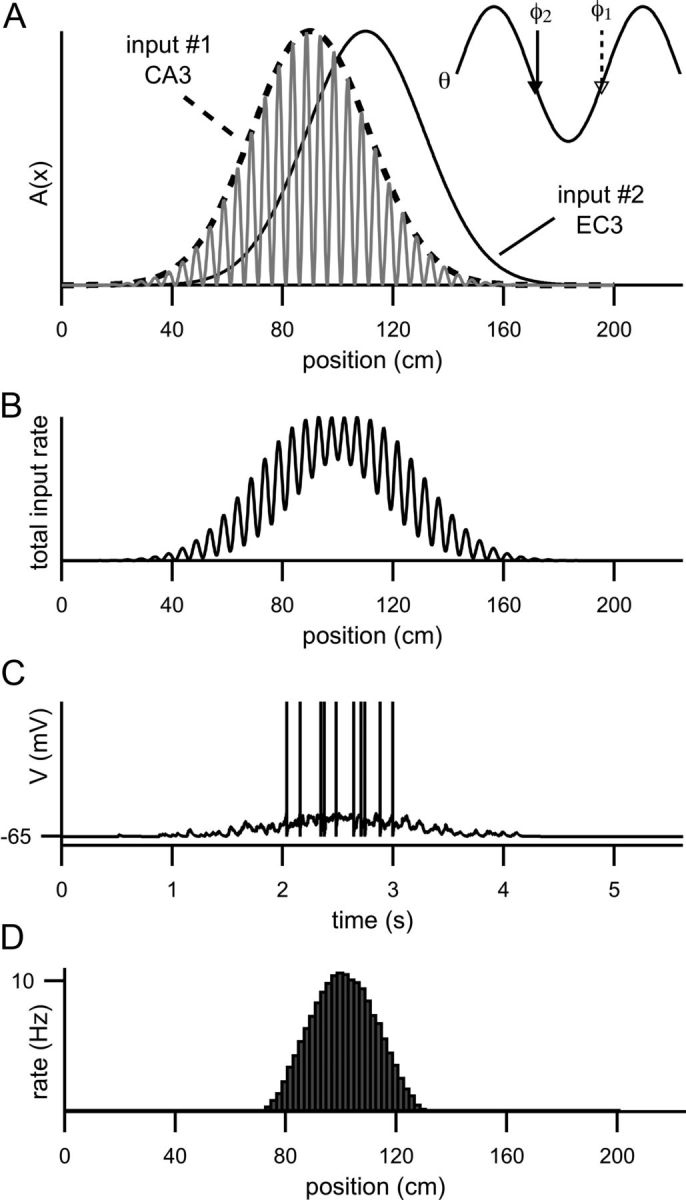
Two input components drive spiking in the model. A, The dashed line is A₁(x) and the solid line is A₂(x). These functions describe the receptive fields of the CA3 and the EC3 input components, respectively. The gray trace is the rate of synaptic input from CA3 (r₁) for one run through the place field (for clarity, the input rate from EC3 (r₂) is not shown). The inset shows 1.5 cycles of the theta oscillation with the phase of the CA3 input component (φ₁, dashed arrow) and the phase of the EC3 input component (φ₂, solid arrow) marked. Note that the phase of the EC3 component (φ₂) is advanced relative to the phase of the CA3 component (φ₁). B, Total synaptic input rate (r₁ + r₂) resulting from one run along the track in the preferred direction. C, Membrane potential as a function of time for one pass through the place field (while the animal runs at 40 cm/s). D, Average firing rate plotted as a function of position. Firing rate is calculated as the number of spikes fired in each bin divided by time spent in that bin (collected over 5000 runs). Each bin represents a 2 cm of track length.

Figure 2.

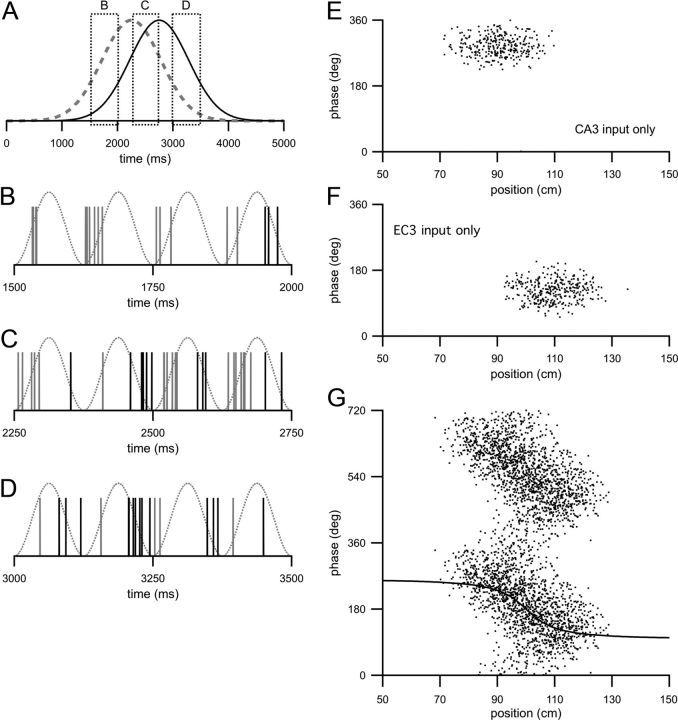
Model with spatially offset but nonprecessing input components. A, Traces are the relative strengths of the driving inputs from CA3 (dashed gray line) and EC3 (solid black line) as a function of time as the animal moves along the track length at 40 cm/s. Dotted boxes indicate regions of time that are expanded in B, C, and D. B, Spikes are synaptic inputs from CA3 (gray) and EC3 (black) resulting from one example run along the track in the preferred direction across the region indicated by the leftmost box in A. Note that the time axis is much expanded compared with that in A. The dotted trace is the theta oscillation. C, Same as B but for region indicated by center box in A. D, Same as B but for region indicated by rightmost box in A. B–D, the amplitudes (α₁, α₂) of the two input components are significantly decreased (this allowed individual synaptic inputs to be discernible) compared with other parts. E, Spike raster of the CA1 model cell when driven only by input from CA3. Each dot is the theta phase of an action potential plotted as a function of animal position at the time the action potential was fired. F, Spike raster of the model CA1 cell when driven only by input from EC3. G, Spike raster of the model CA1 cell when driven by both the CA3 and EC3 input components. The same data are plotted across two theta cycles for clarity. The solid line is the predicted spike phase plotted as a function of position. For clarity, the predicted phase is plotted over only one theta cycle. E–G, spike times were collected over 200 runs along the track in the preferred direction.

Figure 3.

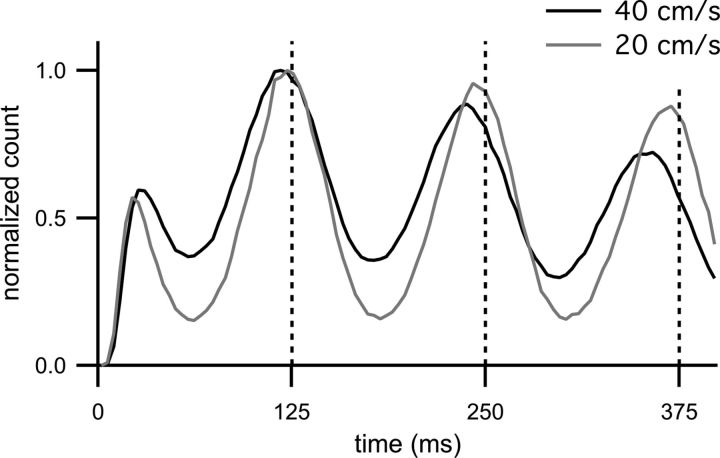
Autocorrelograms of model spike trains. The black trace is the autocorrelogram of spiking for the CA1 model (parameters as in Fig. 2G, running speed is 40 cm/s as indicated in the legend). Vertical dashed gray lines indicate multiples of the theta period. Note that the peaks of the autocorrelogram occur to the left (at shorter intervals) of the theta periods. The gray trace is the autocorrelogram with the same parameters, except with a running speed of 20 cm/s (as indicated in the legend). As was the case for a running speed of 40 cm/s, the peaks of the 20 cm/s autocorrelogram occur at shorter time intervals than the theta period, although the effect is less pronounced. Both histograms are normalized so that the bin with the maximum count is one (the bin at zero has been removed).

Figure 4.

Model with one precessing and one nonprecessing input component. A, Spike raster (action potential phase plotted as a function of animal position) showing model CA1 spiking when driven only by the CA3 input component (A₂ = 0). B, Spike raster of spikes fired by the model CA1 cell when driven only by the EC3 input component (A₁ = 0). C, Spike raster from model CA1 cell when driven by both input components. A–C, Dotted gray line is the theta oscillation and solid black line is the predicted spike phase. D, Average firing rate as a function of track position (calculated as in Fig. 1D).

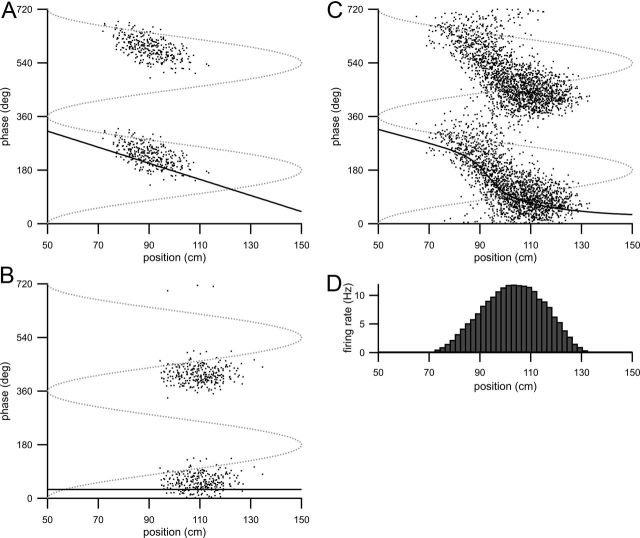
Figure 5.

Curved spike raster arises from increasing the strength of the CA3 input component relative to the EC3 input component. Parameters are given in Table 1. A, Spike raster (spike phases plotted as a function of animal location when the spike was fired) of CA1 model cell firing when the relative strength of the EC3 component is weakened. Dotted gray line is the theta oscillation. B, Firing rate histogram (calculated as in Fig. 1D) of model CA1 cell spiking with these parameters. C, Spike raster of an experimentally recorded cell with a curved spike raster, reprinted with permission from Figure 2A of Mehta et al. (2002). D, Each bin is the fraction of total spikes fired at a particular theta phase plotted as a function of that theta phase, referred to as the theta-phase histogram. Two theta cycles are shown, and the dotted gray line is the theta oscillation.

Both input components are temporally modulated at the same frequency as the theta oscillation (f = 8 Hz), but the phase (φ_i) of each input component is different. The theta oscillation is a cosine function, cos(2πft), and phases are defined relative to the theta oscillation (an input with phase 180° occurs at the trough of the theta oscillation). We vary the phase of the theta oscillation at the start of each trial (t = 0) to ensure that the animal enters the model place field at different theta phases. The phase of the CA3 input component, φ₁, is delayed relative to the phase of the EC3 input component, φ₂ (Fig. 1A, inset), in accordance with the known phase relationships between activity in CA3 and EC3 (Mizuseki et al., 2009), and also so that maximum CA1 spiking occurs close to the trough of the theta oscillation (defined here as 180°). Mizuseki et al. (2009) noted that CA1 neurons respond later (delayed by approximately one-half theta cycle) than would be expected based on the timing of presynaptic activity in CA3 and EC3 and also current-source density measurements in CA1. Here we include this phase delay by choosing φ₁ and φ₂ to be approximately a half-theta cycle later than the spike phases measured in CA3 and EC3 (Mizuseki et al., 2009), but do not attempt to propose a biophysical explanation for this delay. φ₁ = 260° in Figures 1–3 and 230° in all other figures. φ₂ = 100° in Figures 1–3, 30° in Figure 4, and 0° in Figures 5 and 6. It should be noted that, although EC3 input is advanced in theta phase relative to the CA3 input, the receptive fields are offset such that the animal enters the receptive field of the CA3 component before the receptive field of the EC3 component when the animal runs in the preferred direction (left to right).

The excitatory synaptic input to the model CA1 neuron is generated as a Poisson input train with underlying rate r₁+r₂ (the sum of the excitatory input rates arising from the two input components). Figure 1B shows r₁+r₂ for one run along the track. Each time a synaptic input arrives, g_E is instantaneously increased by 0.2 g_L (producing a 1 mV EPSP in the absence of any other synaptic input). In between synaptic inputs, the excitatory synaptic conductance exponentially decays to zero with a time constant of 2 ms. The trace in Figure 1C is the membrane potential of the model during one run along the track in the preferred direction. The histogram in Figure 1D shows the average firing rate of the model cell as a function of position when the animal runs in the preferred direction.

In Figures 4–6, we extend the range of phase precession to match experimentally published data by including phase precession in the CA3 input component (compare Figs. 2E, 4A). Phase precession is introduced into CA3 by substituting Φ₁(x) = k(x − x_o) + φ₁ for φ₁:

With this change, the CA3 input phase is a linear function of position and the parameter φ₁ is the CA3 input phase when the animal is at position x = x₀ = 80 cm. The rate of phase advance is k = 2.7°/cm (Figs. 4–6; Table 1). In Figure 5 only, skewness is introduced into the model firing rate profile to match the highly asymmetric firing rate profile of the data presented in Figure 5C. The receptive field of the CA3 input component is left-skewed by setting σ₁ = 35.36 cm for x < x₁ and σ₁ = 21.2 cm for x ≥ x₁, and the receptive field of the EC3 input component is narrowed by setting σ₂ = 7.1 cm.

We assume that both input components are active only when the animal runs left to right, reflecting the tendency of both CA3 and EC3 neurons to be direction-selective on a linear track (O'Keefe and Recce, 1993; Sargolini et al., 2006). Except as noted in Figure 3, the animal runs at a constant velocity of 40 cm/s.

Results

The model CA1 pyramidal cell receives two components of excitatory input, one originating in CA3 and one originating in EC3 (see Materials and Methods). In this study, the locations over which the input components are active will be called receptive fields to distinguish them from the place field of the CA1 cell. The receptive fields of these two input components are offset in space from each other (Fig. 1A, redrawn in Fig. 2A), and the activity of the two input components drives synaptic input at different theta phases (Fig. 1A, inset; also compare gray spikes with black spikes in Fig. 2B–D).

Figure 2A–D provides an intuitive explanation for how phase precession arises in this model. As the animal moves in the preferred direction, the excitatory drives from the CA3 input component and the EC3 input component rise and fall (Fig. 2A, dashed and solid black lines). Because of the spatial offset between the two input component receptive fields, the animal enters the receptive field of the CA3 input component before the receptive field of the EC3 input component when running in the preferred direction. Figure 2B shows the arrival times of synaptic input from CA3 (gray spikes) and EC3 (black spikes) for 500 ms as the animal enters the place field (Fig. 2A, leftmost box). The theta oscillation is plotted as the dotted trace. At this stage of the run, most of the synaptic input to the model CA1 cell comes from CA3 and therefore arrives at a relatively delayed phase of theta. (For Fig. 2B–D, the rate of synaptic input from both input components was dramatically decreased so that the timing of individual synaptic events relative to the theta cycle could be clearly observed.) Toward the center of the place field (Fig. 2A, center box) where the contributions of both input components are more equal, synaptic input arrives from both CA3 and EC3 (Fig. 2C). Because the number of synaptic inputs arriving from CA3 at a delayed theta phase (gray spikes) is approximately equal to the number of synaptic inputs arriving from EC3 at an advanced theta phase (black spikes), the average theta phase of the synaptic input received by the model CA1 cell in this panel is closer to the trough of theta. Spiking of the model CA1 cell driven by this synaptic input will therefore be, on average, at a phase midway between the EC3 and the CA3 input phases. Figure 2D shows the synaptic arrival times as the animal is exiting the place field (Fig. 2A, rightmost box). The majority of the synaptic input comes from EC3 (black spikes) and will drive model spiking at an advanced theta phase. Thus model CA1 spiking driven by these two input components will phase advance as the relative contributions of the two input components change over the breadth of the place field.

Phase precession occurs without requiring a phase advance incorporated into either input component. Figure 2, E and F, are spike rasters (each dot is the spike theta phase plotted against the location the spike was fired) of the CA1 cell spiking when driven by either the CA3 input component (Fig. 2E) or the EC3 input component (Fig. 2F) alone. When the model is driven by only one input component, average spike phase remains constant (although the rasters are shifted on both the phase and position axes depending on whether the model is driven by the CA3 or the EC3 component; Fig. 2, compare E, F). With input arising from both input components, CA1 model spike phases advance systematically as the animal moves across the place field (Fig. 2G; two theta cycles are plotted for clarity).

The average spike phase as a function of position can be predicted easily in this model. The rate of synaptic input driven by input component i is (with b₁ = b₂ = 1):

where A₁(x) and A₂(x) are Gaussian functions of track position (Fig. 1A, dashed line and solid line) differ only in their spatial position. We assign the phase of the CA3 input component to be φ₁ = 260° and the phase of the EC3 input component to be φ₂ = 100° (Fig. 1A, inset). With these phase assignments, CA1 activity peaks at 180° (the trough of the theta oscillation).

The sum of the two input components determines the total excitatory input rate and is A_tot cos (2π ft + ϕ) + A₁ + A₂ (Fig. 1B), where

and

The solid black line in Figure 2G is ϕ, the predicted spike phase (solid black line) plotted as a function of track position. In this model, spike phase is a sigmoidal function of position and the spike phases advance the most rapidly as the model transitions from being driven by the CA3 input component to being driven by the EC3 input component. At the entrances and exits of the place field, there is relatively little phase advance as CA1 spiking is essentially driven by only one of the input components.

In general there is good agreement between ϕ and the phase of model spiking, indicating that ϕ is a good predictor of spike phase (Fig. 2G, compare the solid line with the spike raster). The slight delay of the model spikes relative to ϕ arises from the integration time of the neuron. Because A₁ and A₂ are both functions of position, spike phase is itself a function of position. This dependency agrees with experimental evidence demonstrating that phase correlates strongly with proportion of place field traveled (O'Keefe and Recce, 1993; Huxter et al., 2003; Geisler et al., 2007). Because the total phase advance is determined by the difference between the two input component phases, the total phase advance will be unaffected by overall firing rate or animal running speed, as observed in previous studies (Huxter et al., 2003; Geisler et al., 2007).

The membrane potential (Fig. 1C) depolarizes as the animal approaches the place field and the total excitatory synaptic input to the model increases. This depolarization is very similar to the “ramp-like” depolarization reported by Harvey et al. (2009) and its shape depends primarily on how quickly the CA3 input component increases. Within the model cell place field, A_tot (the amplitude of oscillations in the input rate; Fig. 1B) determines the amplitude of membrane potential oscillations in the theta-band frequency range. Because A_tot is essentially zero outside the place field, the power of the cell's membrane potential oscillations in the theta range will be elevated when the animal is inside the place field, also consistent with the experimental observations of Harvey et al. (2009). For simplicity, this model was constructed so that the only source of theta-frequency oscillations is the excitatory drive of the dual input components. If additional sources of theta-modulated input are included, for example, a theta-modulated inhibition that is insensitive to location, the membrane potential theta-frequency oscillations will still be elevated within the place field but will return to a baseline value rather than zero outside the place field (data not shown).

A_tot also varies within the place field, predicting a variation in input amplitude that should, in principle, be experimentally detectable using intracellular recordings from CA1 pyramidal cells (such as in Harvey et al., 2009) to measure variations in the membrane potential oscillation amplitude as the animal enters specific subregions of the place field. In this model, the local minimum in membrane potential oscillation should correspond to the region of fastest phase advance. This location depends strongly on the exact arrangement and parameters of the input component receptive fields. For example, in Figure 1B A_tot has a local minimum in the center of the place field. In Figure 5, the local minimum of A_tot will be closer to the place field exit.

Phase precessing place cells, by definition, fire with a periodicity that is shorter than the period of the theta oscillation (O'Keefe and Recce, 1993). Indeed our model shows this effect, even though both input components oscillate at the same frequency (close inspection of the oscillations in the input rate and membrane potential in Figure 1, B and C, will reveal an oscillation frequency slightly higher than theta for much of the place field). The black trace in Figure 3 is the autocorrelogram of spikes fired by the model CA1 cell (parameters same as in Fig. 2). The peaks of the autocorrelogram occur at regular intervals shorter than the theta period (indicated by vertical dashed lines). Because spike phase is a function of position, the rate of phase advance, and therefore any periodicity in the model spiking, depends on the animal's running speed. The gray trace is the autocorrelogram of spikes fired when the running speed is halved (20 cm/s). The autocorrelogram peaks still occur at intervals shorter than the theta period, but the difference is less than for the 40 cm/s autocorrelogram. The dependence of the autocorrelogram peaks on running speed arises from the fact that phase is a function of position. These results match the experimental observations of Geisler et al. (2007) examining the relationship between the output oscillation of CA1 pyramidal cell spiking and running speed.

The maximum phase advance that can be achieved from simply summing excitatory inputs in this dual input component configuration is 180° (if the difference is >180°, the phase will appear to delay rather than advance as the animal runs). If the input components are exactly antiphase (180° out of phase) to each other, ϕ will equal either φ₁ (the CA3 input phase) or φ₂ (the EC3 input phase) depending on whether A₁(x) or A₂(x) is greater at that location. Under these conditions, the spike phase will abruptly step from φ₁ to φ₂ as the animal traverses the place field (although it is possible that theta-modulated inhibition could soften the sharpness of the transition). To avoid this we used inputs that were close to but not precisely antiphase to each other.

CA1 phase precession in rats and mice has been reported to extend for up to 360° (O'Keefe and Recce, 1993; although Schmidt et al. (2009) have pointed out that typically the range of phase advance is measured by examining the range of spike phases when pooled across multiple trials, and that when the phase advance is examined trial by trial, the total phase advance only averages 191.2°). We now extend the range of the phase advance exhibited by this model by considering the possibility that a portion of the phase precession observed in CA1 is inherited from an earlier stage of processing (Skaggs et al., 1996), namely CA3. Although, in theory, the full 360° of phase precession could be inherited from CA3 (making a mechanism for generating phase precession in CA1 unnecessary), it is unclear if simply summing inputs from phase-precessing CA3 neurons can account for the full range of phase precession as observed in CA1 (Geisler et al., 2010; Mizuseki et al., 2012). Moreover, in Figures 5 and 6 we show examples of spike raster shapes, similar to those reported in the literature, that can be reproduced by this modified version of the model but cannot be reproduced by simply extending the range of CA3 phase precession.

We incorporate phase precession into the CA3 but not the EC3 input component for three reasons. First, it is well documented that CA3 pyramidal cells phase precess (O'Keefe and Recce, 1993; Mizuseki et al., 2012), whereas neurons in EC3, in general, do not (Hafting et al., 2008; Mizuseki et al., 2009). Second, a previous analysis (Yamaguchi et al., 2002) of the probability density function of spike rasters suggested that while the spike rasters are well described by two components, only one of those components (most closely related to our CA3 input component) exhibits a position-dependent phase. Third, Mizuseki et al. (2012) recently demonstrated that the rate of phase advance of CA1 cells across the first half of their place fields is very similar to the rate of phase advance of CA3 cells over a similar fraction of their place fields but, importantly, these phase advances differ over the second half of their place fields where, in this model, the EC3 component begins to contribute.

To incorporate phase precession into the CA3 input component, we set the phase of this input to vary linearly with position (the solid black line in Fig. 4A is the predicted phase of the CA3 input component; also see Materials and Methods). Figure 4, A and B, illustrate spiking when the modified CA1 model is driven by either input component alone. The phases of CA1 spiking driven by the two input components at their receptive field centers are approximately in antiphase (Fig. 4, compare A, B). The parameters describing the spatial features of the receptive fields of the two input components are the same as in Figure 2. Phase precession in CA1 driven by both input components is shown in the spike raster in Figure 4C (with the predicted phase as the solid black line). Again, the phase advance has a sigmoidal shape (similar to Fig. 2G) but the first branch of the sigmoid exhibits the phase advance inherited from the CA3 input component.

The histograms in Figures 1D and 4D are the average firing rate as a function of track position. Both firing rate profiles are nearly identical because the amplitudes and widths of the input receptive fields are the same in both figures. These firing rate histograms are reminiscent of the “bell-shaped” firing rate profiles described by O'Keefe and Recce (1993) in their original discovery and description of the phase precession phenomenon, but in Figure 5 we show an example of an asymmetric firing profile (Fig. 5B).

With phase precession inherited from the CA3 input component as well as arising from the interaction between the two input components, the model fires over the same range of spike phases as reported for CA1 pyramidal cells in vivo. One salient feature of phase precession observed in CA1, but not well captured by our model thus far, is that the rate of phase advance is not constant across the breadth of the place field, and often spike rasters appear to curve downward (toward more advanced phases). This shape has been described as an acceleration in phase precession (Yamaguchi et al., 2002), a bimodal progression (Hafting et al., 2008), or a decrease in the precision of position coding by spike phase (Mehta et al., 2002). The effect seems to be quite variable from cell to cell, even when in the same environment. We now demonstrate that the model can reproduce a variety of spike raster shapes, similar to those observed in vivo, when we vary the receptive field parameters. These spike raster shapes arise from variability in the rate of phase advance across the place field and therefore (to our knowledge) are not easily reproduced by most previous models of phase precession.

Two examples of spike rasters that clearly demonstrate nonlinear phase advances are a “curved” spike raster shape (Mehta et al., 2002; Fig. 5C) and a “boomerang” shaped spike raster (Skaggs et al., 1996; Fig. 6A). These two examples were chosen in part because they reflect extreme ends of a spectrum of spike raster shapes produced by varying the strength of the EC3 input component relative to the CA3 input component. We now examine how varying the relative strength of the EC3 component relative to the CA3 component leads to these two different spike raster shapes and demonstrate that one method of quantifying these variations is by examining the theta-phase histograms of spikes fired by the model CA1 cell (compare Figs. 5D, 6C).

We chose the parameters for Figure 5A so that the spike raster had a curved shape like that reported in Figure 2A of Mehta et al. (2002) (reprinted with permission in Fig. 5C). This particular cell had an extremely asymmetric firing rate profile, replicated in the model by introducing a left skew into the receptive field of the CA3 input component and narrowing the receptive field of the EC3 component (see Materials and Methods). Previous work has proposed that such an asymmetry in the firing rate profile (Fig. 5B) arises through experience-dependent learning (Blum and Abbott, 1996; Mehta et al., 1997, 2000; Wallenstein and Hasselmo, 1997; Ekstrom et al., 2001; see Discussion). These parameter changes weaken the relative strength of the EC3 input component relative to the CA3 input component, and place the region of accelerated phase advance (the steeper leg of the sigmoidal shaped phase precession) toward the exit of the place field. This causes the spike raster to take on a shape in which the phase appears to curve downward as the animal moves through the place field.

The theta-phase histogram in Figure 5D is the (normalized) count of spikes fired at a particular phase, collected across the track. For these parameters, theta-phase histogram appears nearly unimodal with a peak close to the trough of the theta oscillation (180°). This phase distribution is similar to published theta phase distributions of CA1 pyramidal neurons in vivo for both anesthetized (Klausberger et al., 2003; Somogyi and Klausberger, 2005; Klausberger and Somogyi, 2008), and also awake and behaving rats (Skaggs et al., 1996; Mizuseki et al., 2009).

Increasing the degree of theta modulation (by setting b_1,2 = 0.5) instead of introducing a skewness produces a bilobed or boomerang-shaped spike raster. In Figure 6, the widths of the receptive fields of the two input components are identical but the amplitude of the CA3 input component is slightly larger than that of the EC3 input component. With these parameters, the spike raster has a bilobed appearance (Fig. 6A), quite different from the more linear shape in Figure 4A or the curved shape in Figure 5A. In the center of the place field the neuron appears to fire at two distinct phases of theta. Several such spike rasters have been experimentally observed by Skaggs et al. (1996), and a similar boomerang shape is observed in the population data of Allen et al. (2011). Because the spike raster almost appears to double back on itself, it is difficult to imagine a single process creating such a spike raster [although Kamondi et al. (1998) have noted that such a raster shape will arise from a neuron that fires in doublets].

Although this bimodality is not apparent in the firing rate profile of the model neuron (Fig. 6B), these parameters produce a distinctly bimodal theta-phase histogram (Fig. 6C). The second peak (closer to 0°) that appears on the descending phase of theta is driven by synaptic input primarily from the EC3 input component. Three studies (Skaggs et al., 1996; Maurer et al., 2006; Jezek et al., 2011) in rats have reported theta-phase distributions with a smaller second peak like that seen in Figure 6C (although Maurer et al., 2006 attributed the presence of such peaks to the firing of cells with “double” place fields). Also, dual peaks in the theta-phase histograms have been previously observed toward the centers of place fields in mice (Fig. 7B of Allen et al., 2011).

Figure 7.

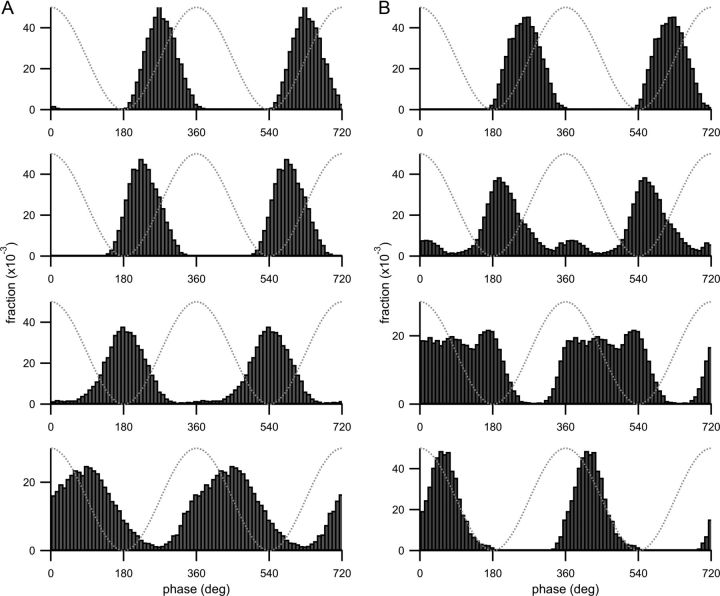
Theta-phase histograms from different place field subregions with model cell parameters used for Figures 5 and 6. For each panel, spikes were collected from a particular subregion of the place field and the theta-phase histogram (Figs. 5D, 6C) is plotted for those spikes. A, B, Top, Spikes from the first quarter of the place field were used. For the second, third, and fourth panels from the top, spikes from the second, third, and last quarter were used, respectively. Each histogram shows the fraction (plotted on the y-axis) of spikes collected from that subregion and fired at a particular theta phase (indicated on the x-axis). Two theta cycles are shown for clarity. Dotted gray lines are the theta oscillation. A, Parameters are the same as Figure 5 (curved spike raster). B, Parameters are from Figure 6 (boomerang-shaped spike raster).

Of particular interest is the fact that Skaggs et al. (1996) reported two theta-phase distributions from populations of cells recorded in two different mazes and the second peak is only visible in one, suggesting that differences in published datasets arise from differences in experimental or task conditions. The EC3 input component is relatively stronger in Figure 6 than in Figure 5 and drives the more salient early-phase peak in the theta-phase histogram in Figure 6C. It is possible that differences in experimental conditions affect the bimodality of the theta-phase histograms by modulating activity in EC3. The spike rasters reported by Skaggs do not all show the same spatial characteristics, even when recorded from nearby or overlapping track positions, suggesting that these different environmental conditions do not affect all CA1 neurons uniformly. The effect of increased activity in EC3 is therefore more likely to manifest as an increased probability of bimodal theta-phase histograms in the recorded population rather than a uniform increase in bimodality.

For the simulations presented here, phase precession is clearly observable in the spike rasters for all parameter sets examined, and the shape of the theta-phase histogram is easily predicted from visual inspection of the shape of the spike raster. However, under conditions in which phase precession is not easily observed, for example, if there is a significant background component of spikes whose phase is uncorrelated with animal location, examining the theta-phase histograms for different subregions of the place field may be a more sensitive method of examining the strength and spatial extent of the underlying input components (Allen et al., 2011; Royer et al., 2012). For the histograms in Figure 7, the place field, defined as the region over which the firing rate was greater than or equal to 1 Hz, was divided into four equal subregions. Each panel is the theta-phase histogram for spikes collected from one subregion. The model parameters were either the same as for the curved spike raster in Figure 5 (Fig. 7A) or for the boomerang-shaped spike raster in Figure 6 (Fig. 7B).

In the case of the curved spike raster (Fig. 5), CA1 spiking is primarily driven by the CA3 input component except at the place field exit. The dominance of the CA3 input at driving spiking is visible in the theta phase histogram (Fig. 5D), as the majority of spike phases are fired on the ascending phase of theta. The top three histograms in Figure 7A likewise cover a relatively delayed range of spike phases, whereas in the bottom histogram, the theta-phase histogram is broadened because the EC3 input component drives additional spikes at more advanced phases in this subregion. Also, there is a systematic shift to the left of the histogram peaks in the top three panels. This shift reflects the phase advance inherited from the CA3 input component.

The bimodality of the boomerang-shaped spike raster in Figure 6 may also be observed in the theta-phase histograms of Figure 7B. The peaks of the top two histograms in Figure 7B are shifted relative to each other, much like the peaks of the upper two histograms in Figure 7A, and this systematic shift continues in the third histogram of Figure 7B (compare the phase of the most prominent peak to the peaks of the two histograms above it). As in Figure 7A, this shift arises from the phase precession inherent in the CA3 input component. However, the second histogram of Figure 7B also contains indications of an additional more advanced peak. This additional peak is more prominent in the third histogram, and indicates that the EC3 component is more active at driving spikes than in Figure 7A. The additional peak (driven by EC3) does not shift between the second and third histograms because the EC3 input component does not phase precess.

The EC3-driven peak is visible in three out of four panels (as opposed to one out of four in Fig. 7A) because the receptive field of the EC3 input component is much wider in Figure 7B. The two distributions of CA1 spikes driven by each component do not combine as in the bottom histogram of Figure 7A, because spikes driven by the CA3 input component are still relatively delayed in the second and third histograms. However, in the bottom of Figure 7B, the theta-phase histogram appears unimodal and narrower than in the equivalent histogram in Figure 7A, because the synaptic input in Figure 7B was more strongly modulated by theta and therefore drove spiking over a narrower range of theta phases.

Two recent studies (Allen et al., 2011; Royer et al., 2012) provide evidence that there are two components of place cell spiking that may be independently modulated. Disruption of the connexin-36 protein results in what appears to be a preferential decrease of early-phase CA1 spiking (Allen et al., 2011). Although it is difficult to determine from the Allen et al. (2011) study if removal of connexin-36 expression resulted in a specific disruption of EC3 input or an enhancement of inhibition at advanced theta phases, these data are consistent with the connexin-36 knock-out decreasing the strength of the EC3 input component in this model. Royer et al., (2012) demonstrated that parvalbumin-positive (PV+) interneurons exert a greater inhibitory effect toward the entrance of a place field while somatostatin-positive (SOM+) interneurons have a greater influence toward the place field exit (where the EC3 component dominates in this model). These results suggest a significant role for EC3 input in driving CA1 firing in this portion of the place field, as SOM+ oriens lacunosum-moleculare (O-LM) interneurons inhibit distal CA1 dendrites (Freund and Buzsáki, 1996) where EC3 projections terminate. It will be interesting to observe if further experiments specifically targeting CA3 or EC3 output can provide more insight into the roles that these two input components play in phase precession and the encoding of information in CA1. Analyses such as the one described in Figure 7 will prove useful for determining the spatial extent and relative strengths of the two input components.

Discussion

We propose that CA1 pyramidal cell spiking is driven by dual input components (arising from CA3 and EC3 activity) that are offset from each other in both spatial position and theta phase. Phase precession arises as these two inputs interact and successively drive the neuron to fire. In this model, spike phase is a function of animal location, as suggested by a number of experimental studies (Huxter et al., 2003; O'Keefe and Burgess, 2005; Zugaro et al., 2005). In addition, the proposed configuration of inputs drives a membrane potential depolarization as the animal enters the place field followed by increased theta-frequency membrane potential oscillations once the animal is inside the place field, in agreement with recent intracellular recordings in behaving mice (Harvey et al., 2009). Finally, we demonstrate that varying parameters describing the relative strengths and spatial extent of the two input components can result in distinct spike raster shapes that are observed in the literature but have been difficult for previous models to reproduce. External environmental factors may determine the prevalence of these spike raster shapes in a given dataset by differentially modulating the activities of the two input components.

In the original dual-oscillator model (O'Keefe and Recce, 1993), phase precession arose through interference between oscillations of two different frequencies. Here the primary mechanism is the interaction between two oscillations of the same frequency but different theta phases. Although we have presented versions of the model in which the CA3 component precesses and therefore oscillates at a higher frequency than the EC3 component, the interference between the CA3 and EC3 input frequencies cannot alone explain the range of phase precession we observe.

Instead, our mechanism for phase precession is more similar to the “somatodendritic interference” effect reported by Kamondi et al. (1998) and Magee (2001). The major difference is that our model proposes that the two input components have separate and spatially offset receptive fields, whereas in previous works one oscillator is continually present and phase precession arises as the second oscillator changes in amplitude. The phase advance arising from somatodendritic interference (Magee, 2001; Losonczy et al., 2010) could contribute to the phase advance we attribute to the CA3 component. However, this previous model predicts a phase delay as the animal leaves the place field [although Mehta et al. (2002), Harris et al. (2002), and Losonczy et al. (2010) have proposed mechanisms that can prevent this delay] that is not observed in vivo. In our model spike phase always advances to the EC3 input component phase.

Our model requires that there be two sets of theta-modulated inputs with different theta phases and spatially offset receptive fields. If these conditions are met, this model could underlie phase precession observed in other parts of the brain, for example, CA3 or layer II of entorhinal cortex (EC2). It is possible for a local population of cells to comprise one of the required input components. However, the scarcity of local excitatory connections in CA1 (Amaral et al., 1991; Thomson and Radpour, 1991) suggests that the dual input components come from areas external to CA1.

The phase precession mechanism we have proposed relies on a spatial offset between the two input component receptive fields. Nevertheless, a mechanism must exist to ensure that these receptive fields are spatially contiguous. Dudman et al. (2007) have demonstrated that temporoammonic input can strengthen Schaffer collateral synapses onto the same CA1 pyramidal neuron in the absence of a somatic spike, provided that the inputs are paired at a precise temporal delay that could be introduced by the trisynaptic pathway (Judge and Hasselmo, 2004). Through this mechanism, EC3 input tuned for a particular location will selectively potentiate Schaffer collateral inputs that are active at the same location. Because this mechanism of plasticity does not require a somatic action potential (Golding et al., 2002; Dudman et al., 2007), this potentiation could occur upon introduction to a new environment, before either input component is strong enough to drive significant firing in the postsynaptic CA1 neuron.

Computational studies have demonstrated that Hebbian plasticity in the recurrent connections within CA3 (Blum and Abbott, 1996; Jensen and Lisman, 1996; Wallenstein and Hasselmo, 1997) can shift CA3 place fields in a direction opposite to the animal's direction of motion (Lee et al., 2004a). This shift can underlie the experience-dependent expansion of CA1 place fields that is observed experimentally (Mehta et al., 1997, 2000; Ekstrom et al., 2001) and would result in the receptive field of the CA3 input component being offset from the EC3 input component receptive field as required by our model.

This model also requires that EC3 input be able to independently drive firing in CA1 pyramidal cells. Although EC3 input to CA1 pyramidal cells previously has been considered to be modulatory (Levy et al., 1998; Remondes and Schuman, 2002) because of the relative difficulty in driving CA1 neurons to fire in vitro via stimulation of the temporoammonic pathway (Colbert and Levy, 1992; Empson and Heinemann, 1995; Levy et al., 1995; Soltesz, 1995) [although Yeckel and Berger (1995) and Milstein et al. (2011) have demonstrated superthreshold CA1 activation through stimulation of EC3 input in slice], evidence suggests strong excitatory distal input to CA1 pyramidal cells (Buzsáki et al., 1986; Brankack et al., 1993; Montgomery et al., 2009). It is possible that the firing patterns of EC3 neurons in vivo (Leung et al., 1995; Jarsky et al., 2005) or the specificity of their projections (Buzsáki et al., 1995; Naber et al., 1999) cause them to be more effective at invoking net excitatory drive (Buzsáki et al., 1995) than estimated in vitro. Also, previously activated CA3 input can enhance the efficacy of EC3 input (Ang et al., 2005; Jarsky et al., 2005), and this cooperativity between CA3 and EC3 input may be underestimated in slice.

CA1 and CA3 place cells respond differently to manipulations of environmental cues (Guzowski et al., 2004; Lee et al., 2004a, b; Vazdarjanova and Guzowski, 2004; Leutgeb et al., 2005). It is difficult to envision how these different response properties might arise if they represent sequential steps of spatial processing. Moreover, mice and rats can perform spatial tasks and CA1 pyramidal cells form place fields even when input from CA3 is disrupted (Mizumori et al., 1989; Brun et al., 2002; Nakashiba et al., 2008). This evidence suggests that spatial information arrives in CA1 via routes other than from CA3. A logical alternative source of input would be EC3. In addition, Chevaleyre and Siegelbaum (2010) have demonstrated that CA2 drives a strong but relatively uncharacterized pathway by which input from EC3 may reach CA1.

In this model, CA1 activity represents information directly transmitted from EC3 as well as more processed information from the trisynaptic pathway. Previous analyses of CA1 pyramidal cell spiking have concluded that position can be more precisely decoded from spikes fired during the descending half of the theta cycle (Huxter et al., 2008), or at the place field exit (Skaggs et al., 1996), whereas heading is better decoded from the ascending half of the theta cycle (Huxter et al., 2008). These conclusions could reflect different sources of information driving CA1 spiking at different theta phases.

Our model predicts that manipulations that significantly alter the ratio of activity between EC3 and CA3, such as disruption of the output from either CA3 (Brun et al., 2002; Nakashiba et al., 2008) or EC3 (Brun et al., 2008), will dramatically affect the theta-phase distribution of CA1 place field spikes. In particular, complete removal of input from CA3 eliminates phase precession in our model and shifts almost all CA1 spiking onto the descending phase of theta. It should be noted that because synaptic inputs from both EC3 and also CA3 are likely to shape the local field potential recorded in CA1, removing one input component could significantly alter both the shape and period of the theta oscillation. For this reason, it could be effective to use the range of spike phases recorded in the source of one input component as a reference. For example, Mizuseki et al. (2012) compared the phase advance in CA3 with the phase advance in CA1. Such measurements could be compared both before and after inactivation of EC3.

Our model also predicts that tasks that more strongly drive EC3 activity will result in more CA1 spiking at early/descending phases of theta. This effect could manifest as a higher percentage of cells with bimodal theta-phase histograms. One example where this could be observed is in “fragmented” CA1 place fields that are observed in mazes with repeating elements (Frank et al., 2000; Derdikman et al., 2009; Singer et al., 2010; Nitz, 2011; Mizuseki et al., 2012). If head direction-specific input from EC3 (Sargolini et al., 2006) drives or coordinates the development of these types of place fields (Mizuseki et al., 2012), our model predicts that these cells should exhibit more early-phase spiking than place cells with nonfragmented place fields or place cells in other mazes. Such a difference should be observable in theta-phase histograms collected from CA1 place fields formed in a variety of mazes. Examination of these theta-phase histograms and spike raster shapes provides a powerful way of dissecting the underlying contributions of CA3 and EC3.