Schaffer-Specific Local Field Potentials Reflect Discrete Excitatory Events at Gamma Frequency That May Fire Postsynaptic Hippocampal CA1 Units

Abstract

Information processing and exchange between brain nuclei are made through spike series sent by individual neurons in highly irregular temporal patterns. Synchronization in cell assemblies, proposed as a network language for internal neural representations, still has little experimental support. We use a novel technique to extract pathway-specific local field potentials (LFPs) in the hippocampus to explore the ongoing temporal structure of a single presynaptic input, the CA3 Schaffer pathway, and its contribution to the spontaneous output of CA1 units in anesthetized rat. We found that Schaffer-specific LFPs are composed of a regular succession of pulse-like excitatory packages initiated by spontaneous clustered firing of CA3 pyramidal cells to which individual units contribute variably. A fraction of these packages readily induce firing of CA1 pyramidal cells and interneurons, the so-called Schaffer-driven spikes, revealing the presynaptic origin in the output code of single CA1 units. The output of 70% of CA1 pyramidal neurons contains up to 10% of such spikes. Our results suggest a hierarchical internal operation of the CA3 region based on sequential oscillatory activation of pyramidal cell assemblies whose activity partly gets in the output code at the next station. We conclude that CA1 output may directly reflect the activity of specific ensembles of CA3 neurons. Thus, the fine temporal structure of pathway-specific LFPs, as an accurate readout of the activity of a presynaptic population, is useful in searching for hidden presynaptic code in irregular spikes series of individual neurons and assemblies.

Introduction

Brain nuclei continuously exchange information by sending spikes over a small fraction of connecting axons in rapidly changing combinatory patterns, usually interpreted as internal neural representations. It is still unknown how much of the neural code resides in units or assemblies' activities (Nicolelis et al., 1997; Harris, 2005). Although spike trains of single neurons are predominantly irregular, it has been proposed that at least part of the information flow is made through synchronous activity in cell assemblies (Stevens and Zador, 1998; Luczak et al., 2009; Kumar et al., 2010). The search for synchronous irregular activity in units is technically demanding (Ikegaya et al., 2004). An experimentally attractive complementary alternative is offered by ongoing local field potentials (LFPs), a mesoscopic variable that contains accurate spatiotemporal information of the synaptic activity of converging populations (Nunez and Srinivasan, 2006). The multiple presynaptic origins of LFPs have, however, limited their use to a few events and oscillations mostly in architectonically simple regions as the hippocampus (Buzsáki et al., 1983). Here, we use a novel approach to extract pathway-specific ongoing synaptic activity from spatial maps of irregular hippocampal LFPs (Korovaichuk et al., 2010) as a means to investigate the ongoing dynamics of one presynaptic population, the CA3 region, and its contribution to the elaboration of spike trains in postsynaptic CA1 units. Both pyramidal cells and interneurons in the CA1 receive excitatory inputs from several presynaptic nuclei, all of which can themselves initiate postsynaptic firing when sufficient synchrony occurs (e.g., following electrical stimulation) (Anderson et al., 1971). Although CA3 pyramidal cells usually fire within functional assemblies (Hájos and Paulsen, 2009; Takahashi et al., 2010), it is unknown whether the degree of synchronization is enough to fire CA1 pyramidal neurons during ongoing activity.

Among available computational techniques, the independent component analysis (ICA) (Choi et al., 2005) has spatiotemporal resolution sufficient to accurately separate different generators in irregular LFPs (Makarova et al., 2011). Hippocampal LFPs are particularly suited for ICA as the stratification of afferent axons from different presynaptic populations along principal cell dendrites facilitates spatial discrimination of the electrical current sources. We recently decomposed irregular hippocampal LFPs into several generators with subcellular spatial definition stable across animals (Korovaichuk et al., 2010; Makarov et al., 2010). Specifically, we identified the so-called Schaffer generator as corresponding to the ipsilateral input from the CA3 to CA1. In the present study, we explore the dynamical properties of presynaptic units composing this LFP generator. The low firing rate and functional clustering of CA3 pyramidal cells (Thompson and Best, 1989) allowed us discriminating elementary synaptic events in the Schaffer generator, which we term micro-field EPSPs (μ-fEPSPs). We use these to find correlated spikes between presynaptic and postsynaptic pairs of units within long spontaneous epochs. Paradoxically, during irregular hippocampal LFPs, the Schaffer μ-fEPSPs constitute a regular (oscillatory) succession of excitatory packages involving a variable contribution from individual presynaptic CA3 units. These μ-fEPSPs can effectively fire CA1 pyramidal cells and interneurons, revealing pathway-specific origin of some spikes as proposed in synfire chains (Abeles, 1991).

Materials and Methods

Experimental procedures.

The experiments were performed in accordance with European Union guidelines (86/609/EU) and Spanish regulations (BOE 67/8509-12, 1988) regarding the use of laboratory animals. The Research Committee of the Cajal Institute approved the experimental protocols. Female Sprague Dawley rats (200–220 g; n = 16) were anesthetized with urethane (1.2 g/kg, i.p.) and placed in a stereotaxic device. Surgical and stereotaxic procedures were performed as described previously (Canals et al., 2005). A concentric bipolar stimulating electrode was placed in the ipsilateral CA3 (septal pole) for orthodromic activation of the CA1 region [anteroposterior (AP), −3.2; lateral (L), 2.6; ventral (V), −3.3 mm]. A linear multisite silicon probe (NeuroNexus) connected to a multiple high-impedance headstage was lowered into the hippocampus (AP, 4.5–5.5; L, 2–3 mm). The probe recorded in 50 μm steps along the main axis of the CA1 pyramids, also spanning the DG/CA3 regions. Probes were soaked in DiI (Invitrogen) before insertion to identify postmortem the positioning in histological sections. A silver chloride wire in the neck skin served as a reference for recordings. Signals were amplified and acquired using Multi Channel Systems recording hardware and software (50 kHz sampling rate).

We studied the pharmacology of the Schaffer LFP generator by injecting drug solutions in the vicinity of a recording shank through a recording glass pipette (5–7 μm at the tip) using a Picospritzer (General Valve) (Canals et al., 2005). The pipettes were placed 300–500 μm from the recording shank in the stratum (st.) radiatum and the size of the microdrop was adjusted (∼50–100 nl) to limit the volume of the bathed tissue to <500 μm, as assessed by the selective modulation of evoked potentials in the desired group of recording sites. The used drugs were dissolved in aCSF to a final concentration ∼50 times higher than that usually used in vitro. Bicuculline methiodide (BIC) was obtained from Sigma-Aldrich, and 6,7-dinitro-quinoline-2,3-dione (DNQX) and 3-((±)-2-carboxypiperazine-4-yl)-propyl-1-phosphonic acid (CPP) from Tocris. A single injection ensured that the drug stably influenced recordings for at least 30 s. When assaying the effect of the drugs on the spike-triggered averages of raw and virtual Schaffer LFPs that required longer recording epochs (20–30 min), injection of microdrops in 5 min intervals provided reasonable long-term stability as witnessed by the steady effect on the evoked potentials. In another set of experiments, the Na⁺-channel blocker lidocaine (Braun) was ejected (2% v/v) in the CA3 pyramidal layer through the cannula of the concentric stimulating electrode, allowing the chemical blockade and electrical activation of the presynaptic region to be tested simultaneously.

In a series of experiments, microstimulation was applied via a glass pipette (5–7 μm at the tip) located in the CA3 pyramidal layer at the same coordinates as the bulk electrodes, further localized through the CA3 antidromic population spike following commissural activation. The stimulus intensity was varied in 1 μA steps and fEPSPs measured as the maximum amplitude from baseline. The threshold intensity was that producing 40–60% all-or-none miniature fEPSPs in the CA1 st. radiatum.

Independent component analyses of LFPs.

Recorded depth profiles of LFPs contain a time varying mixture of synaptic currents from multiple presynaptic origins. We used ICA to separate independent components, some of which were pathway specific (i.e., contained the postsynaptic activity elicited by a homogeneous population of presynaptic cells). Detailed signal treatment for ICA of LFPs has been described previously (Makarov at al., 2010), and the mathematical validation and interpretation in laminated structures is provided by realistic LFP model by Makarova et al. (2011). Briefly, the 32 LFP signals recorded simultaneously can be represented as the weighted sum of the activities of N neuronal sources or LFP generators as follows:

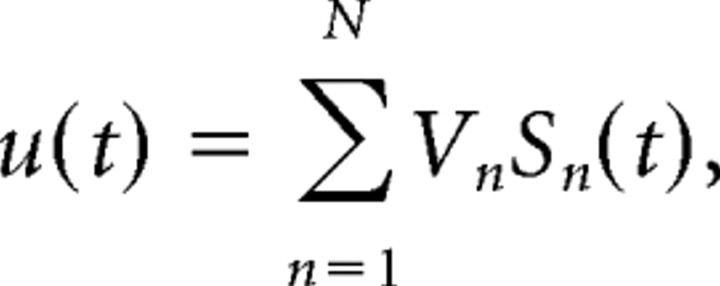where V_n and s_n(t) are the vector of the spatial weights and the time course of the nth LFP generator, respectively. Thus, the raw LFP observed at the kth electrode tip is a linear mixture of the electrical activity of several independent LFP generators describing transmembrane current source densities (CSDs) in principal cells, I_n = −σΔV_n (where σ is the conductivity of the extracellular space).

For the ICA, we used the infomax algorithm initially proposed by Bell and Sejnowski (1995) and implemented in the EEGLAB MATLAB toolbox (Delorme and Makeig, 2004). The routine returns the activations s_n(t) and the spatial weights V_n of up to 32 LFP generators [see MATLAB working code in the study by Makarova et al. (2011); http://www.mat.ucm.es/∼vmakarov/Makarova2011.html]. Only a few generators (e.g., four in Fig. 1A) have significant amplitude and distinct spatial distributions in the hippocampus (Korovaichuk et al., 2010). Once LFP generators have been extracted from the raw LFPs, they can be analyzed as if they alone were active. For example, we can construct virtual LFPs produced by a single generator based on its spatial weights and activation u_j(t) = V_js_j(t), and then evaluate the CSD created by this generator. The pathway specificity of some ICA-isolated components is assessed by their selective capturing of subthreshold evoked synaptic currents and cross-correlation to spike activity of presynaptic units (Korovaichuk et al., 2010) (see below).

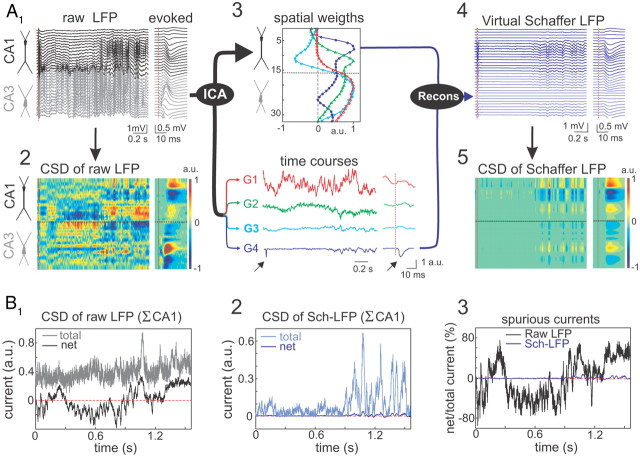
Figure 1.

Separation of pathway-specific LFP generators. A, Example of Schaffer-specific LFP extraction. A1, Raw LFPs across the CA1 and CA3 fields (black and gray traces, respectively). The dashed red line marks the time of a subthreshold stimulus applied to the ipsilateral CA3. The evoked pathway-specific (Schaffer) field potential is amplified in the right inset. A2, CSD of the evoked potential (right) yields the standard distribution of inward (blue) and outward (yellow-red) currents across the CA1 region, while that of raw LFPs (left) renders a complex poorly informative mixture. A3, ICA of LFPs provides four significant LFP generators, each defined by the curve of spatial weights (top panel) and a time course (bottom traces). Note that only the Schaffer generator (G4) captures the Schaffer-evoked activity (arrows). A4, The reconstructed (virtual) Schaffer LFPs for the raw LFP segment and evoked potential analyzed. The pronounced activity at electrodes 5–10 in the second half of the segment corresponds to a complex of sharp waves. A5, CSD of the virtual Schaffer LFPs provides precise spatiotemporal maps of inward/outward currents for unique spatially coherent membrane events. B, CSD of raw LFPs does not satisfy the zero-current criterion, while CSD of virtual LFPs does. The total and the net currents for a raw LFP segment (B1) and its Schaffer-specific component (B2) over the axis of CA1 pyramidal cells. B3, Deviation from zero of the net current (in percentage of the total current) highlights large peaks of spurious current in raw but not in pathway-specific LFPs.

Retrieval and quantification of μLFPs.

In addition to large well known sharp-wave events easily recognizable by the naked eye, we quantified smaller events (μLFPs) constituting the baseline activity of the Schaffer LFP generator. This activity reflects the synaptic bombardment received by CA1 units from CA3 pyramidal neurons. Conveniently, in parallel experiments we observed that the baseline for this LFP generator has high spatial coherence in the septotemporal axis (>0.8 between two shanks 500 μm apart). Its time structure consisted of a regular series of wavelets, suitable for mathematical discrimination and classification. Let v(t) be the Schaffer-specific LFP obtained from virtual LFPs at the electrode with maximal power. To identify elementary μLFPs, we used the wavelet transform of v(t) as follows:

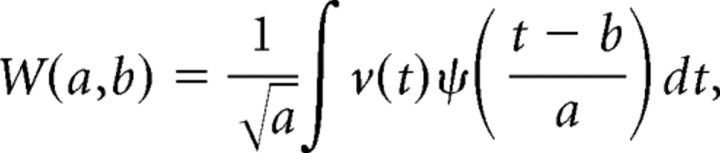where ψ is the Haar mother wavelet (well suited for detection of short pulses in a signal), a is the timescale, and b is the localization in time. We then rectified the wavelet coefficients using the following equation:

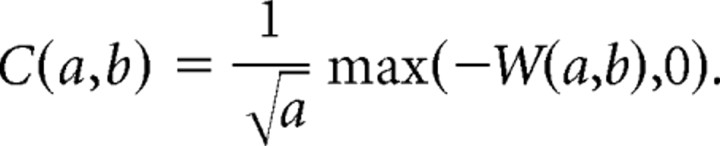The 2D surface obtained describes the local linear fit of the Schaffer-specific LFP by the pulse-like function (Haar) at the scale a and localization b. Large absolute values of C(a,b) at a given time instant and scale correspond to abrupt pulse-like transitions in v(t). Thus, we can associate such points in the (a,b)-plane with singular LFP events. Consequently, the local maxima

define the following: (1) the time instants of μLFPs (given by t_k = b_k − a_k/2), (2) their duration (given by a_k), and (3) amplitudes [given by A_k = C(a_k,b_k)]. We note that the identification of μLFPs is blind; hence their significant correlation with spikes of CA1 or CA3 units corroborates the reliability of the technique (see Results). To avoid contamination of the correlation of μLFPs to spikes by, for example, the large sharp waves, we rejected events within the 10% tails of the amplitude histogram.

Spike sorting.

We used wavelet-enhanced spike sorting method (Pavlov et al., 2007) that optimizes unit separation in linear multielectrode arrays. Three LFPs from contiguous electrodes were used to obtain local transmembrane currents in the vicinity of the central electrode. This procedure enables effective cancellation of extracellular currents parallel to the main axis (a strong source of contamination for spike sorting) and highlights the somatic transmembrane currents contributing to spikes. We note that no spectral filtering is required, which also saves original spike waveforms and consequently improves spike sorting (Pavlov et al., 2007). Next, a principal component analysis over collected spike waveforms was applied and has been used for extraction of the so-called representative waveforms. Then the parameters of the wavelet transform were tuned for best discrimination of the recorded data set (Pavlov et al., 2007). Finally, the most discriminative properties of spikes in the wavelet space were extracted. The extracted spike features were used for manual clustering.

Unit classification.

Units were classified into two subclasses, pyramidal cells and putative interneurons, according to the location of the recording site (within or outside the pyramidal body layers) and additional standard electrophysiological criteria (Csicsvari et al., 1998): (1) spike width (>0.4 and <0.4 ms for pyramids and putative interneurons, respectively); (2) mean firing rate (<1 vs >5 Hz); (3) relationship to theta rhythm (firing rate decreases for pyramidal cells and increases or remains unchanged for interneurons); (4) pattern of firing (isolated spikes vs bursting); (5) presence of complex spikes (in pyramidal cells only); and (6) the decay of autocorrelograms (fast vs slow). The total number of units used in this study is limited by the use of linear tracks of recording sites required to collect spatial maps of LFPs for ICA. Typically, one to three CA3 and one to two CA1 pyramidal cells were successfully isolated per recording.

Indexes of in-cluster firing, Schaffer-driven spikes, and spike transfer rate.

Temporal relationships between spikes of presynaptic and postsynaptic units and μLFPs were defined as coincidences with appropriate time windows for monosynaptic excitation (see below). Synchronous spikes sent by CA3 pyramidal cells within a functional cluster produce μLFP events, whereas firing of a unit outside a functional cluster does not yield strong enough (readable) μLFP. To quantify the “in-cluster” firings, we introduced the following index:

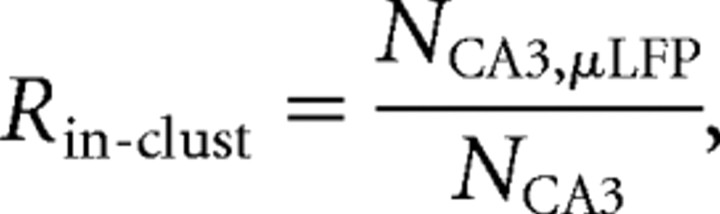where N_CA3 is the number of spikes of a CA3 pyramidal neuron and N_CA3,μLFP is the number of so called type I coincidences [i.e., the number of μLFP events synchronous with CA3 firings (0–8 ms latency)]. This index implicitly describes the variability of functional clusters (e.g., small R_in-clust value suggests that the neuron rarely participates in clustered firings, whereas R_in-clust ≈ 1 indicates that the neuron always fires synchronously with other neurons).

To quantify the ratio of spikes of CA1 pyramidal neurons temporally associated with μLFP events (i.e., with the Schaffer input to CA1), we introduced the index of Schaffer-driven CA1 spikes as follows:

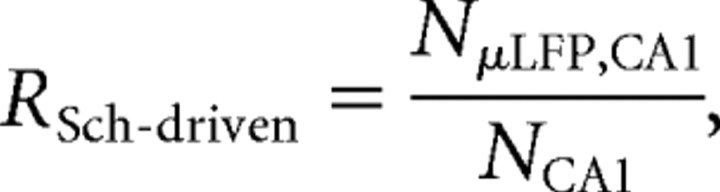where N_CA1 is the number of spikes of a CA1 pyramidal neuron and N_μLFP,CA1 is the number of so-called type II coincidences [i.e., the number of CA1 spikes synchronous with μLFP events (0–6 ms latency)]. Small R_Sch-driven value suggests that the Schaffer input has no effect on firing of CA1 cell, whereas R_Sch-driven ≈ 1 indicates that the output of the CA1 neuron is completely conditioned by the Schaffer input.

Spike transfer rate between connected presynaptic and postsynaptic units was evaluated by triple correlation or type III coincidences. It was built by cross-correlation of type I and type II coincidences, and represented as two-dimensional densitograms. Type III coincidences represent presynaptic CA3 spikes time-locked to μLFP events, which in turn drive postsynaptic spikes in CA1 cells, both within monosynaptic time windows (6 and 8 ms, respectively: for example, red square in Fig. 7C). The density of cell-to-cell efficient monosynaptic events was normalized to the density of casual events in a 30 × 30 ms time window b as follows:

Type III coincidences constitute a subclass of standard dual cross-correlations between full spike trains that sorts for analysis the postsynaptic spikes whose synaptic drive is exclusively due to Schaffer excitatory input, as determined by type II coincidences. This way of selecting postsynaptic spikes is akin to histograms of firing probability in evoked responses upon Schaffer electrical stimuli: those falling out of the evoked fEPSP time window are excluded since their synaptic trigger is unknown.

Figure 7.

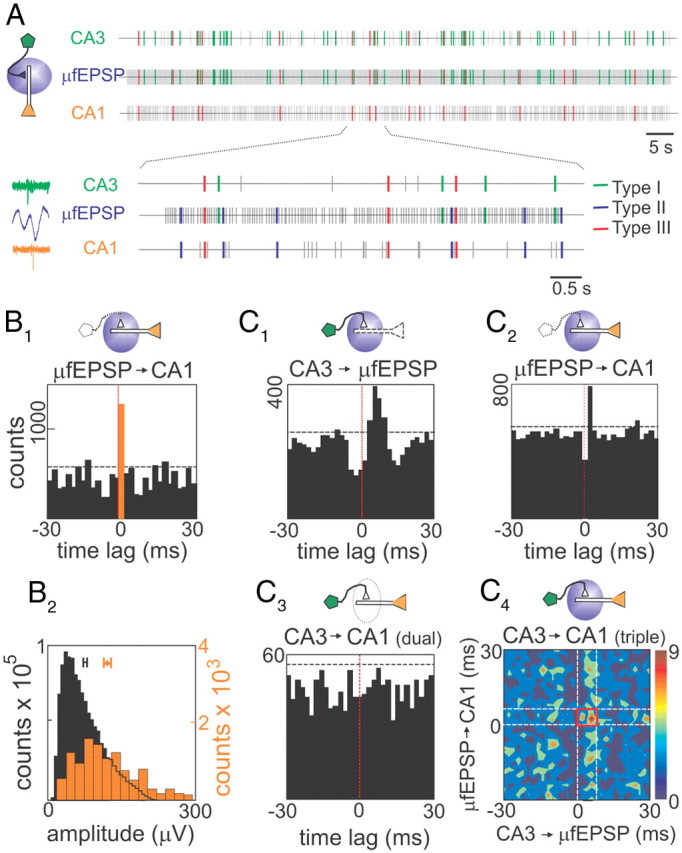
Spontaneous firing of CA3 pyramidal cells drives spikes in CA1 neurons. A, Point processes represent temporal series of spikes of a presynaptic CA3 pyramidal cell (top), μ-fEPSP events obtained from Schaffer-LFPs (middle), and spikes of a postsynaptic CA1 pyramidal cell (bottom). Plausible monosynaptic coincidences are color-coded: green ticks correspond to CA3 spikes→μ-fEPSPs; red ticks correspond to triple correlation CA3 spikes→μ-fEPSPs→CA1 spikes; and blue ticks (shown in the enlargement) correspond to μ-fEPSPs→CA1 spikes. The left inset illustrates typical triple coincidence (green, blue, and orange represent presynaptic spike, postsynaptic μ-fEPSPs, and postsynaptic spike, respectively). B1, Cross-correlation of μ-EPSPs to a spike train of a CA1 pyramidal cell. The orange bar corresponds to 0–2 ms time bin, the horizontal dashed line marks the significance level (α = 0.05), and the vertical red line marks zero time lag. The drawings above histograms indicate (by colored painting) elements along the synaptic chain used in cross-correlations. B2, The μ-EPSPs within the monosynaptic window were sorted out and its amplitude distribution (orange bars) plotted on top of the whole series (black bars). Note the significantly higher mean of the spike-sorted μ-EPSPs. C, Correlation analysis of a sample CA3–CA1 pyramidal cells pair. C1 and C2 correspond to cross-correlograms of type I and II coincidences, respectively. Both show significant peaks within monosynaptic time windows. C3 corresponds to standard cross-correlation between presynaptic and postsynaptic spike trains, whereas C4 shows densitogram for type III coincidences (color codes triple coincidences per square millisecond), which corresponds to a subpopulation of C3 selected by common presynaptic and postsynaptic spikes locked to μ-fEPSPs. The red square marks the time window (6 × 8 ms) considered for effective monosynaptic spike transfer. Note that, while dual correlation (C3) fails to show CA3 driving of CA1 spikes, this is unmasked in the triple correlation (C4).

Current source density analysis.

CSD analysis (Freeman and Nicholson, 1975; Mitzdorf, 1985) provides the magnitude and location of the net transmembrane current generated by neural elements contained within a small region of tissue. We used the one-dimensional approach, which estimates the CSD from the voltage and conductivity gradients along the cell axis, and assumes negligible net contributions in the XY-plane parallel to the cell body layer. This approach requires homogeneous activation in planar structures, which is customarily accepted for evoked potentials in the hippocampus whose variation along the longitudinal x-axis is negligible (Herreras, 1990). While this may not hold for ongoing LFPs whose current generators may be spatially restricted, it is not the case for the Schaffer LFP generator since the Schaffer collaterals produce homogeneous activation in the XY-plane, whether spontaneous or synchronous.

Correlations and statistics.

Averages of the LFPs triggered by spikes of single cells were built with at least 1500 spikes. Cross-correlation histograms (CA1, CA3 spikes, μ-fEPSP events) were built using a 2 ms time bin, and the significance level (α = 0.05) was determined by the surrogate test (1000 trains with randomly shuffled interevent intervals). To assess the statistical significance of the difference between two sample means, we used the standard Student t test. For dual and triple correlations, the chance ratio of coincident spikes was analytically estimated assuming a Poisson distribution of the number of events in a given time interval.

Results

Retrieval of Schaffer-specific LFPs

Segments of LFPs were recorded simultaneously along a linear track spanning the CA1 and CA3 fields of the rat hippocampus (Fig. 1A1). All results refer to irregular LFP activity (no theta rhythm). A CSD analysis of standard Schaffer-specific evoked field potentials revealed the subcellular spatiotemporal pattern of the transmembrane current along the main axis of principal cells (Fig. 1A1,A2, right panels) (Herreras, 1990). Active inward synaptic currents (sink) are surrounded by passive outward currents (sources), corresponding to the CA1 fEPSP produced by bulk subthreshold stimulation of the ipsilateral CA3 region. However, the CSD map for the ongoing LFPs (Fig. 1A1,A2, left panels) showed a poorly informative spatiotemporal mixture of sources and sinks induced by coactivation of several different afferent inputs.

The ICA separated the ongoing raw LFPs into contributing pathway-specific virtual LFPs (Fig. 1A3,A4). The LFP segment shown in Figure 1A1 receives contributions from four major LFP generators, each of which can be described by its distribution of spatial weights along the main axis of pyramidal cells (Fig. 1A3, top panel) and by its temporal dynamics (Fig. 1A3, bottom panel). The cross-animal stability, pathway specificity, and quantitative properties of these LFP generators have been described previously, both experimentally (Korovaichuk et al., 2010; Makarov et al., 2010) and using realistic simulations (Makarova et al., 2011). The Schaffer generator had a characteristic profile of spatial weights that matched the Schaffer-evoked fEPSP and it exclusively captured the evoked activity (Fig. 1A3, blue trace, arrows).

Disentangling raw LFPs into several component LFP generators enabled reconstruction of virtual LFPs produced by specific pathways. Figure 1A4 shows the virtual Schaffer-LFPs contributed to the raw LFPs shown in Figure 1A1. Subsequent CSD analysis of the reconstructed Schaffer-LFPs produced a clean spatiotemporal map of the transmembrane currents with a characteristic source–sink–source distribution, both for the evoked and ongoing activity (Fig. 1A5). The latter consisted of a highly stable baseline made of small amplitude regular events with occasional large sharp-wave events (Fig. 2A). Notably, only the CSD maps of virtual LFPs but not those of raw LFPs satisfy the criteria for CSD reliability. The net charge flow along the entire extension of the cell generator must be equal to zero (a 10% technical allowance is normally permitted) (Herreras, 1990). Figure 1B shows the test of the current conservation for CSD of a sample raw LFP (Fig. 1B1) and its Schaffer-specific component (Fig. 1B2). Strong deviation from zero of the net current for raw LFPs (up to 80%; Fig. 1B3) revealed the presence of strong spurious current, which practically vanishes (<6%) in the isolated Schaffer generator.

Figure 2.

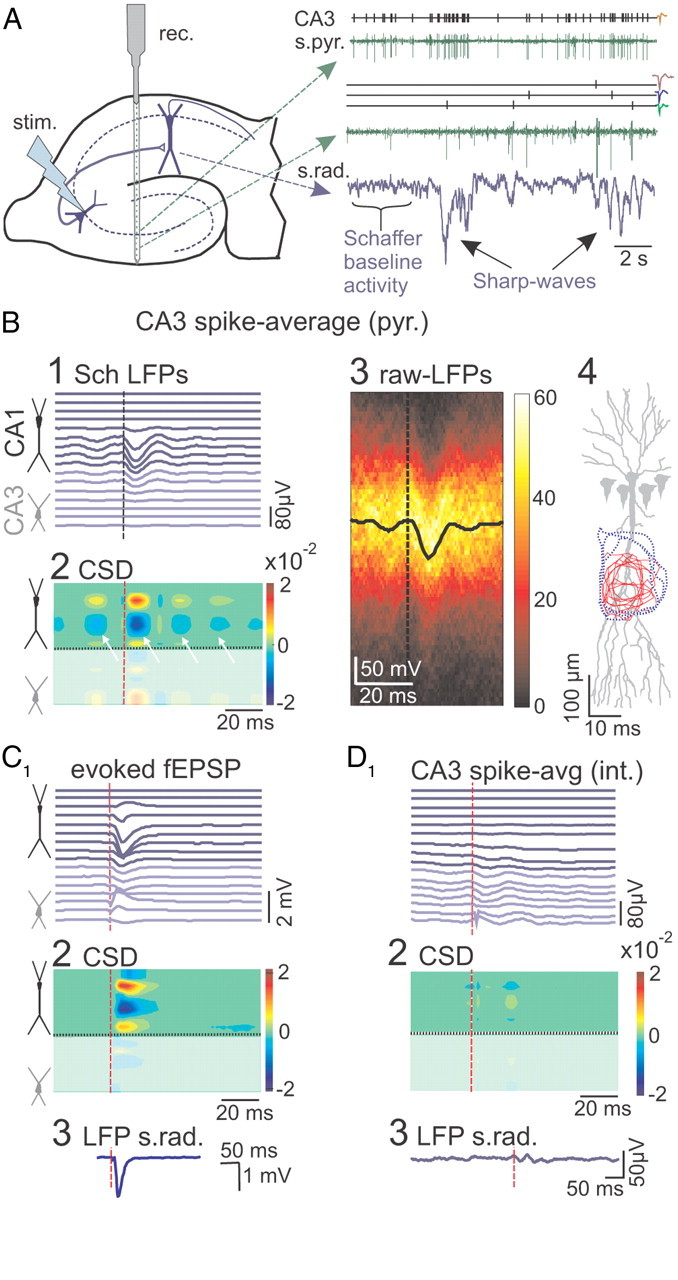
Ongoing activity of CA3 pyramidal cells cross-correlated with Schaffer LFPs. A, Sketch of the hippocampus indicating the positions of multisite recording (rec.) across the CA1 and CA3 fields and of stimulation (stim.) in the CA3 pyramidal layer. CA3 units were isolated in the st. pyramidale and radiatum. Sample of spike time series and of the point processes of isolated units are shown in green and black, respectively, along with the time course of the Schaffer generator in blue. This contains small-amplitude events forming the baseline activity and occasional large events (sharp waves). Spike waveforms of isolated units are shown on the right. B, Massive spike-triggered averaging of virtual Schaffer LFPs over firing of a CA3 pyramidal cell results in an fEPSP-like negative field potential profile centered on the st. radiatum that is preceded and followed by smaller potentials exhibiting an oscillatory gamma pattern (B1). CSD analysis of the spike-triggered average (B2) revealed a CA1 dendritic active sink (in blue) flanked by passive sources in the st. pyramidale and lacunosum (yellow/red). The arrows indicate the multiple secondary sinks. B3, The densitogram constructed with raw LFP epochs around 300 spikes of a single pyramidal cell (the color scale represents the counts per pixel). The spike-triggered average (in black) is identical with that obtained for the Schaffer-LFPs. B4, The space–time contours of the CA1 dendritic active sinks for individual CA3 pyramidal cells (red) are contained within those of the corresponding stimulus-evoked fEPSPs (blue). C, Subthreshold stimulation of the CA3 produced fEPSP depth profiles (C1), CSD distribution (C2), and maximum response in the st. radiatum (C3) matching the spike-triggered averages shown in B. D, Spike-triggered CA1 average built over spikes of CA3 interneuron showed no significant response. D1–D3 are as in C.

These results suggest that the time course of the Schaffer generator (Fig. 1A3, blue trace) follows the ongoing envelope of CA1 postsynaptic currents specifically produced by the firing of presynaptic CA3 pyramidal cells.

Presynaptic origin of the Schaffer LFP generator

To assess the cells of origin of the Schaffer-specific LFP generator, we correlated its temporal dynamics with the firing of the CA3 units (Fig. 2A). The firing of pyramidal cells in the somatic layer of CA3, and of putative interneurons within ±100 μm, was isolated and units were classified according to electrophysiological criteria (Fig. 2A) (see Materials and Methods). Spike-triggered averaged LFPs were constructed for the virtual Schaffer-specific LFPs (Fig. 2B1) and for the raw LFPs (Fig. 2B3). Averaging over spikes of single CA3 pyramidal cells yielded statistically significant responses similar to the evoked fEPSP for both the raw LFPs and the Schaffer generator in the CA1 (Fig. 2, compare B1, C1). The CSD of the spike-averaged Schaffer-LFP profiles (Fig. 2B2) revealed a short-latency (2–4 ms) current sink in the middle of the st. radiatum that was normally preceded and followed by smaller secondary sinks (Fig. 2B2, arrows). At the site of maximal amplitude, the response had latency to the peak of 12.1 ± 0.6 ms, amplitude of 50 ± 6 μV, and duration of 17.4 ± 0.4 ms (n = 67 pyramidal cells in 16 animals). The site of the inward synaptic currents coincided with those of subthreshold Schaffer-evoked fEPSPs within the territory of the Schaffer terminals (Fig. 2C2). Figure 2B4 shows the spatiotemporal contours of inward currents in CA1 obtained individually for 10 presynaptic CA3 pyramidal cells in three animals (red areas) and for the corresponding evoked subthreshold fEPSPs (blue areas). As expected, the territories of synaptic currents of individual neurons are smaller and lay inside the fEPSP areas produced by simultaneous activation of many neurons.

As mentioned above, the secondary peaks in the spike-averaged activity appeared regularly (interval, 22.8 ± 0.7 ms in n = 16 animals; Fig. 2B), and they were of similar duration to the main peak. Such an oscillatory pattern of postsynaptic currents cannot be explained by bursting of individual CA3 pyramidal cells, as we found no such trend in autocorrelation histograms. Rather, this pattern is inherited from the dominant gamma pattern in the Schaffer generator (see below; Fig. 4A). Moreover, a subgroup of local putative interneurons exhibited small-amplitude oscillatory responses (14 of 19; Fig. 2D), shifted by ∼10 ms from those of the neighboring pyramidal cells. Thus, consistent with previous reports on CA3 dynamics (Csicsvari et al., 2003; Hájos and Paulsen, 2009), the observed oscillatory tails in single-cell spike averages originate through the imperfect grouped firing of CA3 pyramidal cells forming functional clusters paced by local interneurons.

Figure 4.

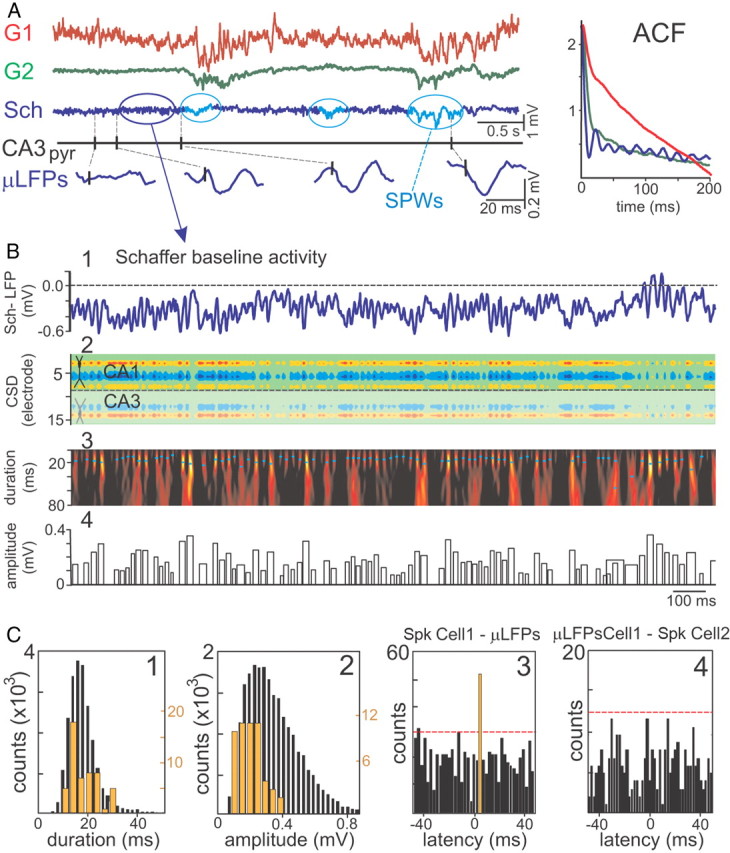
Schaffer LFPs are composed of elementary micro-field EPSPs triggered by CA3 pyramidal cells. A, Representative example of time courses of LFP generators and firing of a CA3 pyramidal cell. The generators G1 and G2 describe the activity across the fascia dentata and the CA1 st. lacunosum, respectively. The baseline activity of the Schaffer LFP generator (in blue) is formed by a temporal succession of small wavelets or μLFPs (enlargements at the bottom) in a global gamma pattern exclusive for this input. The presence of occasional sharp waves (SPWs) is highlighted (in cyan). Autocorrelations (ACF) of the time courses of the generators are shown in the right inset. B, Identification and quantification of μLFPs. B1, The virtual Schaffer-LFP in CA1, st. radiatum. Note the striking nonoverlapping succession of wavelets. B2, The CSD reveals a succession of inward currents with a spatial distribution matching that of Schaffer evoked and spike-triggered averages. B3, The Schaffer-LFP in the wavelet domain. High magnitude (color coded from black to yellow) at given time instant and scale (cyan dots mark maxima) corresponds to the presence of a pulse-like waveform or μLFP. B4, The width and height of the bar codify the duration and amplitude of detected μLFPs, respectively. C, The distributions of μLFPs durations (C1) and amplitudes (C2) are right-skewed (black bars). Some μLFPs are time-locked to the firing of a single CA3 pyramidal cell (samples in A). C3, Cross-correlation of the μLFPs and spikes of the CA3 pyramidal cell showed a significant peak (orange bar) at a latency compatible with monosynaptic excitation (dashed red line indicates the level of significance, α = 0.05). The subpopulation of spike-locked μLFPs presented similar durations as the whole population (orange bars, histogram in C1), whereas their amplitude was generally less disperse (orange bars, histogram in C2). C4, The subgroup of μLFPs time-locked to spikes in one CA3 pyramidal cell (cell 1, orange bar in C3) were cross-correlated with firings of another simultaneously recorded CA3 pyramidal cell (cell 2). The lack of significant correlation indicates exclusive cell 1-specific association with the group of postsynaptic μLFPs.

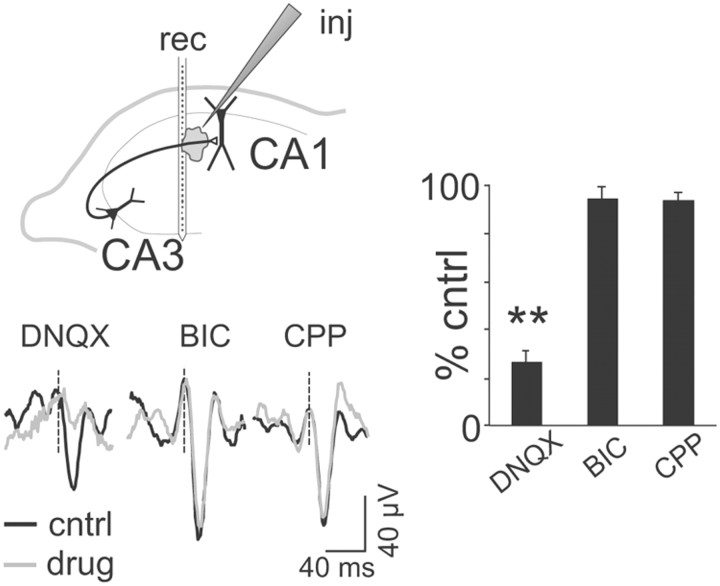
We confirmed the synaptic nature of the spike-averaged Schaffer-LFPs by local microinjection of antagonists of glutamate and GABA receptors in the vicinity of the electrode array at the level of the CA1 st. radiatum (∼50–60 pl). Only the non-NMDA antagonist DNQX (1 mm) blocked the spike-averaged responses (19.2 ± 2.2% of control; p < 0.05, t test), whereas the NMDA blocker CPP (1 mm) and the GABA blocker BIC (1 mm) had no such effect (n = 3 animals per drug; p > 0.05; Fig. 3). Hence, the ongoing firing of CA3 pyramidal cells produces small but discernible LFPs in the CA1 that are captured by the Schaffer LFP generator.

Figure 3.

Spike-triggered CA1 LFP averages are specifically blocked by non-NMDA glutamatergic blockers. The scheme illustrates the arrangement of electrodes: rec, linear recording probe; inj, injecting/recording pipette. Traces illustrate spike-triggered averages of Schaffer CA1 LFPs obtained for different CA3 pyramidal cells in control (black) and during local drug microinjection (gray). The histogram shows interanimal quantification of the amplitude of spike-triggered averages related to control conditions (**p < 0.01). Error bars indicate SEM.

Detection of elementary extracellular EPSPs in ongoing Schaffer-specific LFPs

Basal activity of the Schaffer virtual LFPs is dominated by an oscillatory gamma pattern, formed by small pulse-like events or μLFPs of variable amplitude and duration, akin to the spike-triggered average. This temporal pattern is exclusive for the Schaffer generator, which also includes occasional large sharp-wave events that emerged from the baseline during nontheta epochs (Fig. 4A, cyan ovals). The mean oscillatory frequency obtained from the autocorrelation function (Fig. 4A, ACF) of 10 min epochs in n = 5 animals was 45.2 ± 1.5 Hz. Some Schaffer μLFPs were clearly locked temporally to spikes of CA3 pyramidal cells (Fig. 4A, enlarged traces). Therefore, we assessed whether elementary postsynaptic events from single CA3 principal cells or their functional clusters could be discriminated in ongoing CA1 LFPs by studying the fine temporal nature of the Schaffer generator.

When considering a portion of Schaffer-specific LFP activity (Fig. 4B1), the CSD analysis returns a spatial distribution of currents (Fig. 4B2) akin to that of larger sharp-wave events, presynaptic spike averages, and evoked subthreshold fEPSPs. In the CSD map, we observe a sequence of current pulses corresponding to individual μLFP events. To detect these elementary events, we used the wavelet transform with the Haar mother wavelet (see Materials and Methods and the example of the analysis in Fig. 4B3,B4). The positions of the local maxima in the wavelet spectrum (Fig. 4B3, dots) correspond to time instants and the duration of elementary μLFPs, while the amplitude of the local maxima provides the amplitude of the elementary μLFPs (both plotted in Fig. 4B4).

Figure 4C (in black) shows histograms of the distribution of the duration (Fig. 4C1) and amplitude (Fig. 4C2) of μLFPs identified over a 10 min recording period. Both parameters exhibited a right-skewed distribution with modes at 16.4 ± 0.6 ms (mean, 19.5 ± 0.4) and 59 ± 3 μV (mean, 117 ± 4), respectively (n = 13 animals), similar to spike-averaged Schaffer-LFPs. Figure 4C3 illustrates the cross-correlation of firings of a single CA3 pyramidal cell with μLFP events. By analogy with the latency of evoked subthreshold fEPSPs (Herreras, 1990), we considered that μLFPs could be monosynaptically related with the firing of the presynaptic unit within a postspike time window of 2–6 ms. Notably, all CA3 principal cells (n = 67) displayed statistically significant peaks within this time window (Fig. 4C3, orange bar; surrogate data test at α = 0.05). The spike-locked μLFP events were sorted out as a group (the distributions of the durations and amplitude are shown in orange in Fig. 4C), and whereas the distribution of the durations of the spike-locked group coincided with the unsorted distribution, that of the amplitudes was sharper and centered on 0.2 mV. This suggests that the spike-locked Schaffer μLFPs constitute a subpopulation of the monosynaptic μ-fEPSPs, which are probably elicited by the CA3 neuron or the functional cluster to which it belongs.

To determine the degree of specificity of μLFPs to single CA3 pyramidal cells, we cross-correlated the subgroup of μLFPs sorted by time-locking to spikes of one pyramidal cell (those contributing to the orange bar in the example shown in Fig. 4C3) to spike trains of the other CA3 pyramidal cells isolated in the same recording session. We found significant correlations in 24 of 102 pairs of correlations (surrogate data test at α = 0.05). Figure 4C4 illustrates the more frequent case (78 of 102) of no significant sharing of μLFPs between two presynaptic CA3 pyramidal cells. Overall, the data support the cell specificity of the temporal relationship between CA3 spikes and μLFPs (failed cross-correlations) and also the presence of clustered firing by stable contribution of some cells to the same subgroup evoking μLFPs (significant cross-correlations).

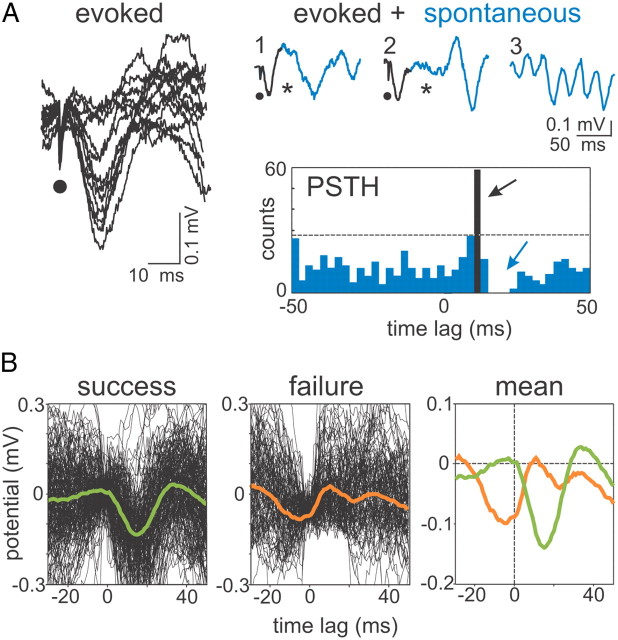
To confirm the identity of Schaffer μLFPs, we performed the following interference experiment. CA3-evoked fEPSPs in CA1 were produced by microstimulation in the CA3 pyramidal layer using a glass pipette 5–7 μm at the tip (Fig. 5A, left panel). By gradually decreasing the amplitude of the stimulus, we detected a threshold 52–63 μA (n = 4 animals), below which the evoked fEPSPs disappeared abruptly (0–100% responses occurred in <10 μA range). The waveform of minimal evoked fEPSPs was indistinguishable from that of spontaneous Schaffer μLFPs (Fig. 5A, right panel, black and blue sample traces, respectively), and no significant differences were detected between their respective amplitudes and durations (p > 0.05). In a representative poststimulus time histogram at threshold intensity (Fig. 5A, PSTH), both evoked fEPSPs (black bar; timing measured at the maximum negativity) and spontaneous μLFPs (blue bars) could be observed. Notably, the evoked minimal fEPSPs produced a time window (latency from fEPSP maximum value of 4.5 ± 0.3 ms and mean duration of 12.3 ± 1.4 ms; n = 4) during which spontaneous μLFPs did not appear (Fig. 5A, asterisks in raw traces and blue arrow in PSTH). We then averaged successful and failing responses separately (Fig. 5B). Strikingly, stimuli that failed to evoke a fEPSP had been delivered (by chance) at a precise instant of precedent spontaneous μLFPs (compare mean responses in Fig. 5B). The peak of the mean response was at 5.0 ± 1.4 ms before the stimulus onset and the duration of the averaged response was 24.3 ± 2.7 ms, similar to individual μLFPs. Thus, spontaneous μLFPs and minimal evoked fEPSPs have mutual blocking effect (i.e., both have narrow permissive time windows accurately marked by the occurrence of a previous event). Since both were initiated locally (i.e., far from the recording positions in the CA1), such mutual interference implies identity of action, and therefore fEPSPs and μLFPs are most likely one and the same entity. Hereafter, we refer to them as μ-fEPSPs.

Figure 5.

Spontaneous μLFPs and stimulus evoked μ-fEPSPs interact among each other in a similar way. A, Left, Microstimulation of the CA3 pyramidal layer at threshold intensity (∼40–60% of responses) evoked miniature all-or-none CA1 fEPSPs (13 superimposed responses). The dots indicate the time of stimulation. Right, Raw samples and peristimuli time histogram (PSTH) (n = 100 trials) of evoked fEPSPs (black traces and bar) and spontaneous μLFPs (blue traces and bars). The occurrence of CA3-evoked fEPSPs (black arrow) blocks (or delays) spontaneous μLFPs (blue arrow). The asterisks in raw samples 1 and 2 mark time intervals with missing spontaneous wavelets following evoked μ-fEPSPs; a typical segment of regular wavelet occurrence is included for comparison in trace 3. B, At threshold intensity, the CA3 stimuli either succeed (left; n = 61) or fail (middle; n = 39) to evoke a Schaffer μ-fEPSP. The means over successful and failed responses are shown in the right panel. Failure is caused by appearance within a narrow time window of a preceding spontaneous μLFP (peak at 5 ms before stimulus), which precludes excitation of evoked μ-fEPSPs.

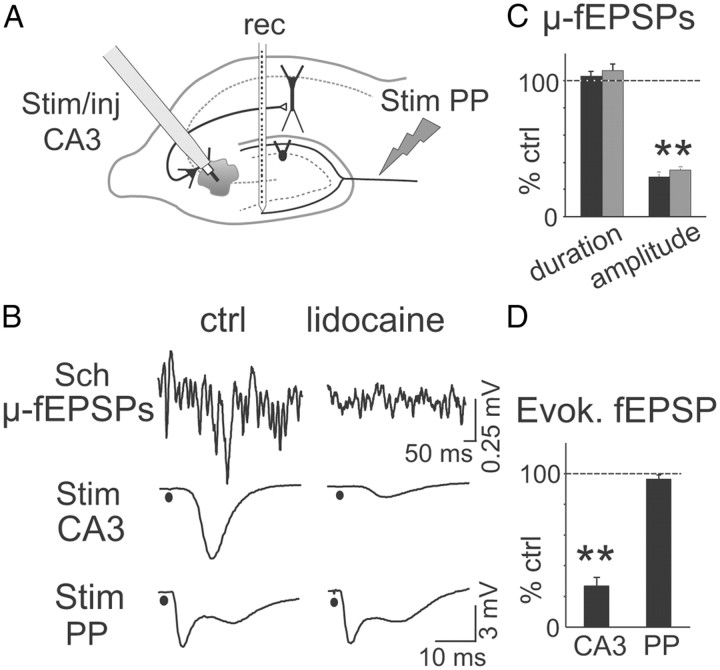
The common origin of spontaneous μ-fEPSPs and Schaffer-evoked responses was further assessed by local injection of small volumes of the anesthetic lidocaine in the CA3 pyramidal cell layer next to the stimulating site (see arrangement of electrodes in Fig. 6A). Three different volumes were essayed (0.2, 0.5, and 1 μl in n = 3 different experiments each). Lidocaine produced a rapid and simultaneous reduction of Schaffer-evoked fEPSPs (27.3 ± 5.9% of control value) and of spontaneous Schaffer μ-fEPSPs amplitude (29.5 ± 2.4 and 34.3 ± 1.5% of control, mean, and median, respectively; p < 0.01, t test) but not in duration, while it left unaffected perforant path-evoked responses in the DG (93.3 ± 1.8 of control) recorded simultaneously with a linear probe (representative experiment and population data are shown in Fig. 6B–D).

Figure 6.

Identity of Schaffer-specific ongoing μ-fEPSPs and CA3-evoked field responses. A, The common presynaptic origin of ICA-extracted ongoing μ-fEPSPs and CA3-evoked field responses in the CA1 was assessed by chemical and electrical interference at the presynaptic locus. The scheme indicates the arrangement of electrodes. Lidocaine was ejected in the CA3 cell body layer from the cannula of the stimulating electrode (Stim/inj) while delivering electrical pulses. Test stimuli were also applied to the perforant pathway (Stim PP). B, Sample traces, in control conditions (left) and after lidocaine injection (right), of (from top to bottom): ongoing Schaffer μ-fEPSPs separated by ICA, fEPSPs in the CA1 st. radiatum evoked by ipsilateral CA3 stimulus, and fEPSPs in the molecular layer of the DG evoked by PP stimulus. Note the selective reduction of spontaneous and evoked Schaffer-related events. C, Population data (n = 3 animals) of μ-fEPSPs amplitude and duration following lidocaine injection in percentage of the control values (black and gray bars correspond to mean and mode values; **p < 0.01). D, Quantification of the relative amplitude evoked fEPSPs for the same experiments (**p < 0.01). Error bars indicate SEM.

CA3 spike to μ-fEPSP to CA1 spike connections

Time series of elementary μ-fEPSPs permit information transfer from the CA3 to CA1 to be studied in detail. We now can test whether ongoing inputs from a single afferent pathway are strong enough to fire postsynaptic units in the CA1 region.

We examined spike trains of CA3 and CA1 pyramidal cells, and the temporal series of the elementary μ-fEPSPs produced by the CA3 population over CA1 (Fig. 7A). Since the spikes of the CA3 unit initiated some of these μ-fEPSPs and some μ-fEPSPs in turn contributed to the firing of the CA1 unit, we studied the dual and triple coincidences of the three elements in the synaptic chain using suitable time windows to ensure monosynaptic excitation. Accordingly, we marked the following temporal relationships (Fig. 7A): I, presynaptic CA3 spike to μ-fEPSP (green ticks); II, μ-fEPSP to postsynaptic CA1 spike or the so-called Schaffer-driven spikes (blue ticks); and III, CA3 spike to μ-fEPSP to CA1 spike (triple coincidence, red ticks). Type I temporal relationships were observed in all 67 CA3 pyramidal cells analyzed (Fig. 8), although only a fraction of the spikes had a monosynaptic association to μ-fEPSPs (23 ± 0.9%). Based on the previous results, this index is interpreted as the rate of recruitment of individual CA3 pyramidal cells into functional clusters responsible for μ-fEPSPs.

Figure 8.

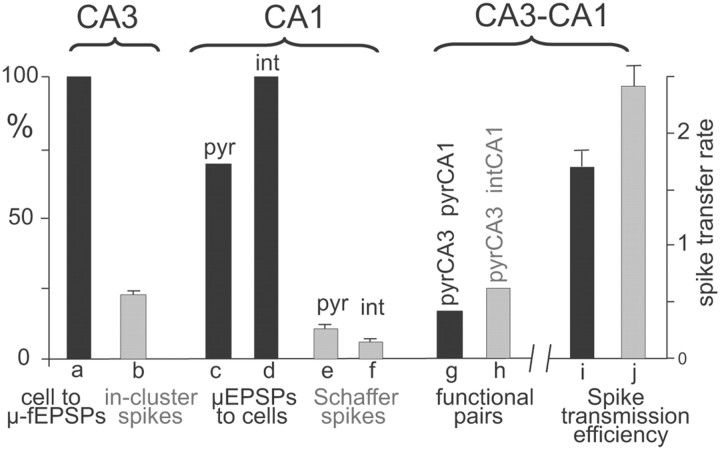
Dynamic properties of the Schaffer CA3–CA1 pathway. a, One hundred percent of the pyramidal CA3 units contribute to the generation of μ-fEPSPs in the CA1. b, Twenty-three percent of the spikes fired by individual CA3 pyramidal cells are synchronous with spikes of other cells forming a functional assembly, which jointly elicit μ-fEPSPs (in-cluster spikes). c, d, Seventy percent of the CA1 pyramidal cells and 100% of the CA1 interneurons fire spikes driven by monosynaptic μ-fEPSPs. e, f, The proportion of Schaffer-driven spikes constitutes, on average, 11 and 6% in CA1 pyramidal cells and interneurons, respectively. g, Seventeen percent of the CA3–CA1 pyramidal cell pairs are functionally connected, meaning that the postsynaptic cell fires spikes monosynaptically elicited by a CA3 assembly to which the presynaptic cell contributed with a spike. h, Twenty-five percent of CA3 pyramidal cell–CA1 interneuron pairs are functionally connected. i, j, The spike transfer rate between pairs of presynaptic (CA3 pyramid) and postsynaptic CA1 pyramidal (i) and interneuron (j) units (a/b ratios in main text).

Statistically significant type II temporal relationships were found in 20 of 29 CA1 pyramidal cells (or ∼70%; n = 9 animals). We examined μ-fEPSP to CA1 cross-correlation histograms that showed a statistically significant peak at a 2 ms time lag, corresponding to the Schaffer-driven spikes (Fig. 7B1). Such spikes constituted a substantial fraction of the firing of CA1 cells (11 ± 1%; range, 4–20%; typically 500–1500 spikes were analyzed per cell in a 10 min epoch). Hence, a significant share of the CA1 output is driven by the Schaffer input. Similar Schaffer-driven capabilities were found for all 11 putative interneurons recorded within 100 μm of the CA1 st. pyramidale. The proportion of Schaffer-driven spikes in these interneurons was 6 ± 0.8%.

The subpopulation of μ-fEPSPs temporarily associated with the Schaffer-driven CA1 spikes (Fig. 7B1, yellow bar) was sorted out and analyzed separately. They had mean amplitude significantly higher than the whole population (Fig. 7B2, compare black and orange histograms; p < 0.05, t test), indicating that synchronization of presynaptic CA3 neurons is required to fire CA1 pyramidal cells. Thus, CA3 pyramidal neurons can organize into functional clusters to transmit information to the CA1 output.

Some spontaneous μ-fEPSPs fulfill both type I and type II temporal relationships, which corresponds to a type III coincidence (Fig. 7A, bottom panel; red ticks and left inset). Such μ-fEPSPs are intermediate in terms of the CA3 to CA1 spike transmission, and hence, they can be used when searching for monosynaptically connected CA3–CA1 cell pairs. It should be noted that such connections are also functional [i.e., a spike fired by a CA3 cell (or the functional cluster to which it belongs) actively participates in the firing of a CA1 spike]. Figure 7C shows an example of the analysis for a CA3–CA1 pyramidal cell pair. Figure 7, C1 and C2, illustrates type I and II coincidences, both of which showed statistical significant bars. Figure 7, C3 and C4, illustrates the standard train-to-train dual correlation (Fig. 7C3) and its subclass type III coincidences (Fig. 7C4) selected by the interposing μ-fEPSPs. The density of events in the monosynaptic time window (red square) was normalized to chance value (R_{Spike-transfer} rate) (see Materials and Methods), which provides an estimate of the spike transmission efficiency in an assembly-to-cell CA3–CA1 monosynaptic chain. R_{Spike-transfer} > 1.2 (20% growth) was considered indicative of an effective functional monosynaptic connection in the CA3–CA1 neuronal pair. We identified 17 of 102 significant CA3–CA1 pyramidal cell pairs, with a mean. R_{Spike-transfer} = 1.69 ± 0.14. Note that the direct cross-correlation of presynaptic and postsynaptic spike trains (dual correlation) did not produce a significant peak (Fig. 7C3), whereas the triple correlation does (Fig. 7C4, red square), which is equivalent to increasing of the signal-to-noise ratio in the analysis. Furthermore, 12 of 48 CA3 pyramidal cell/CA1 interneuron pairs showed statistically significant spike transfer. The R_{Spike-transfer} index for these pairs was significantly higher than that observed for pairs of pyramidal cells (R_{Spike-transfer} = 2.4 ± 0.2; p < 0.05, t test), indicating a lower firing threshold for interneurons than for pyramidal cells in CA1 in response to the Schaffer input. Figure 8 summarizes our results on the dynamical properties of the information transfer in the Schaffer CA3–CA1 pathway.

Discussion

We studied the dynamical contribution of a single presynaptic component, the Schaffer input, to the spontaneous output of CA1 neurons through the temporal structure of the population synaptic envelope extracted from spatial maps of raw LFPs. Schaffer-LFPs show an ordered succession of μ-fEPSPs that appear to be generated by functional clusters of CA3 pyramidal neurons, to which individual units are recruited variably. Such pattern implies a hierarchical internal operation of the CA3 region based on sequential activation of pyramidal cell assemblies. A fraction of these excitatory packets readily induce firing of CA1 pyramids and interneurons, the so-called Schaffer-driven spikes, revealing the synaptic origin in the output code of single units. This finding experimentally supports the postulate that synchronous activity in cell assemblies is a network language for internal neural representation.

The ensemble gamma-frequency dynamics of spontaneous CA3 input to CA1

During ongoing activity, statistically significant temporal relationships between spikes in presynaptic and postsynaptic neurons may be lost due to the massive concurrent synaptic bombardment. To address this issue, we used an ICA of LFPs, which enables pathway-specific LFP generators to be dissected from raw LFPs. The optimization and experimental validation of this approach for hippocampal LFPs have been described previously (Korovaichuk et al., 2010; Makarov et al., 2010). We also discussed the biophysical foundations and the relationship of ICA-separated LFP generators to the spontaneous presynaptic multiunit activity and postsynaptic population currents (Makarova et al., 2011). Here, we demonstrated that the isolated Schaffer LFP generator is exclusively contributed by the postsynaptic transmembrane currents of CA1 pyramids provoked by spikes coming from CA3 pyramidal cells. The temporal envelope is formed by elementary μ-fEPSPs, which were discriminated, quantified, and used to identify monosynaptically connected CA3–CA1 cell pairs. In addition, Schaffer-LFPs contain electrographic events known to represent synchronous input from this pathway, such as sharp waves (Csicsvari et al., 2000) and the evoked field potentials produced by electrical shocks in the ipsilateral CA3 region (Korovaichuk et al., 2010).

The presynaptic origin of the Schaffer LFP generator was confirmed as follows: (1) the accurate localization of synaptic inward currents in the st. radiatum matched that of subthreshold Schaffer-evoked fEPSPs; (2) drug injections in the stratum radiatum demonstrated the non-NMDA glutamatergic profile of the synaptic currents at the postsynaptic side; (3) drug-induced local blockade of CA3 activity selectively disrupted spontaneous and evoked Schaffer events recorded in the CA1; (4) CA3–CA1 spike-LFP averages were raised solely by CA3 pyramids but not by CA3 interneurons or CA1 neurons; (5) field and CSD depth profiles of spike-triggered LFP averages matched CA3-evoked fEPSPs; and (6) spontaneous μ-fEPSPs in the CA1 were transiently occluded by remote minimal stimulation in the CA3 pyramidal layer.

We found that elementary μ-fEPSPs exhibited amplitudes and durations akin to CA1 LFP averages triggered by CA3 single-cell spikes. Whether firing of a single CA3 pyramid is enough to elicit elementary μ-fEPSP or synchronous firing of multiple CA3 pyramids is required could not be unequivocally established. A majority of CA1 pyramidal cells show Shaffer-driven spikes and it is very unlikely that a single CA3 spike depolarizes every target cell beyond threshold (Sayer et al., 1989), since it forms few contacts on each of them (Li et al., 1994). Our findings support the hypothesis that a functional cluster of synchronously firing CA3 pyramids generates an elementary μ-fEPSP, in agreement with previous findings on the dynamics of CA3 assemblies (de Almeida et al., 2007; Takahashi et al., 2010). The electrophysiological evidence for clustered excitation reported here included the fact that only a fraction of spikes of a single CA3 pyramidal cell are monosynaptically related to μ-fEPSPs. Hence, if the firing of a CA3 cell is not in synch with the other cells in the ensemble, no μ-fEPSP will be generated. Although CA3 units within functional assemblies tend to connect the same CA1 postsynaptic targets (Takahashi et al., 2010), the possibility exists that the recorded presynaptic unit is not directly involved in the firing of the postsynaptic cell, but in that case at least some of its partners in the assembly must be connected to initiate the μ-fEPSP.

One remarkable observation was the ordered succession of discrete μ-fEPSPs, which formed a global oscillatory gamma pattern. The mean duration of μ-fEPSPs coincides with the period of so-called slow gamma oscillations (40–50 Hz). In the case of randomly activated CA3 assemblies, one would expect variable overlapping of μ-fEPSPs, precluding their detection with a fixed duration. The variable contribution of individual CA3 pyramidal cells to CA1 μ-fEPSPs indicates that CA3 assemblies can be dynamically modulated in the composition of their contributing cells. In addition, the strikingly constant minimal amplitude of μ-fEPSPs across animals suggests a rather conserved average number of neurons, possibly related to a topological substrate such as the extensive recurrent connectivity that confers strong autoassociative properties to this region (Leutgeb et al., 2005). Together, these results indicate that functional clusters of CA3 pyramids are synchronized in a chain of one-at-a-time activations under supracluster oscillatory gamma dynamics. This finding is supported by several studies that point to interneuron subnetwork in the CA3 as a mediator of global gamma activity (Whittington et al., 1995; Csicsvari et al., 2003; Mann et al., 2005). Extrinsic inputs either directly to pyramids or via other interneuron subsystems may “release” ensembles of pyramids that send information packages to target neurons.

μ-fEPSPs link presynaptic and postsynaptic neurons

A major obstacle for quantifying the informational content in temporal spike series is the presence of multiple potential combinations of synaptic inputs that may initiate outgoing spikes. Studies correlating spike trains in CA3 and CA1 showed a significant drive of certain CA1 interneurons by CA3 pyramidal cells, but not of CA1 pyramids (Csicsvari et al., 1998, 2003). Such observations, compatible with a minor impact of individual inputs on the output of postsynaptic neurons, favor a stochastic mode of spike initiation whereby the output code is defined by the details of the synaptic noise during bombardment (Haider and McCormick, 2009). Nevertheless, we have shown that all CA3 pyramidal neurons contribute to monosynaptic μ-fEPSPs in CA1 and that ∼10% of spikes in 70% of CA1 pyramids are fired in response to input from this pathway. The presynaptic synchronization required is not excessively large as the spike-generating μ-fEPSPs were only twofold to threefold greater than the minimum quantum size, far below the amplitude reached during sharp waves when pyramidal cells are known to fire more frequently (Csicsvari et al., 2000). One may expect that the depolarization attained by such low-input synchronization remains below spike threshold. However, CA1 pyramids have an optimal geometry for dendrosomatic conduction (López-Aguado et al., 2002) and they exhibit rich dendritic electrogenesis, facilitating the initiation of local spikes (Canals et al., 2005). In earlier computational studies, we estimated that as few as six to seven local spikes in small dendrites may be sufficient to produce an axonal spike (Ibarz et al., 2006) (see also Kamondi et al., 1998).

Unveiling the presynaptic content in output codes: are all spikes the same?

Normally, the information transfer between nuclei is evaluated by correlating spike trains between presynaptic and postsynaptic neurons. In the CA3–CA1 connection, this has not been conclusive (Csicsvari et al., 2003). However, the availability of the mediating synaptic potentials allows the narrowing of the output of individual CA1 pyramids to those spikes specifically driven by the Schaffer input. The entire synaptic chain (triple correlations) thus revealed cell-to-cell specific impact to be explored in nonstimulated conditions. Also, the salience of functionally connected CA3–CA1 pyramidal cell pairs compared with the population can be continuously evaluated and used to quantify the routing and the modulation of information flow at the cell and population levels under different experimental situations such as induction of plasticity or animal behavior. For instance, in parallel studies to be reported separately, we have found sustained changes of ongoing Schaffer activity following LTP induction, which are specific for CA3–CA1 pairs of pyramidal cells in concordance with region-selective changes following learning experiences (Whitlock et al., 2006).

The identification of Schaffer-spikes in ongoing irregular series constitutes a first step for the semantic exploration of output codes in single cells. It is very common that irregularly firing cells display isolated spikes mixed up with burst firing. Although there is a single axon stemming out of the soma, it may give off collaterals that contact different cell types in different brain nuclei. Even if mixed messages pass to different target cells, the specialized postsynaptic machinery may be tuned to decode specific parts of them by the kinetic properties of different postsynaptic receptors and intrinsic channels. Furthermore, repeated irregular patterns of spikes have been proposed to represent reverberant activity in feedforward networks (Prut et al., 1998; Ikegaya et al., 2004; Takahashi and Sakurai, 2009). Some of the temporal relationships of presynaptic and postsynaptic spikes and μ-fEPSPs reported here are compatible with this model of network transmission. Even if an irregular fixed spike sequence carries no relevant information for a single target cell, its synchronous repetition over a cell assembly may do transmit a message. Thus, classifying spike sequences by their synaptic origin through pathway-specific LFPs may help finding physiologically relevant population codes. We propose that instant network activity should be studied by dissecting out the natural series of converging synaptic inputs and their relative participation in the elaboration of spike train series, as a useful approach to investigate neural and network mechanisms of learning.