Abstract
The influence of monetary loss on decision making and choice behavior is extensively studied. However, the effect of loss on sensory perception is less explored. Here, we use conditioning in human subjects to explore how monetary loss associated with a pure tone can affect changes in perceptual thresholds for the previously neutral stimulus. We found that loss conditioning, when compared with neutral exposure, decreases sensitivity and increases perceptual thresholds (i.e., a relative increase in the just-noticeable-difference). This was so even when compared with gain conditioning of comparable intensity, suggesting that the finding is related to valence. We further show that these perceptual changes are related to future decisions about stimuli that are farther away from the conditioned one (wider generalization), resulting in overall increased and irrational monetary loss for the subjects. We use functional imaging to identify the neural network whose activity correlates with the deterioration in sensitivity on an individual basis. In addition, we show that activity in the amygdala was tightly correlated with the wider behavioral generalization, namely, when wrong decisions were made. We suggest that, in principle, less discrimination can be beneficial in loss scenarios, because it assures an accurate and fast response to stimuli that resemble the original stimulus and hence have a high likelihood of entailing the same outcome. But whereas this can be useful for primary reinforcers that can impact survival, it can also underlie wrong and costly behaviors in scenarios of contemporary life that involve secondary reinforcers.
Introduction
In real life, stimuli rarely repeat with the exact same physical properties. Hence, it makes sense to generalize the same response to similar stimuli. This natural behavior has been studied extensively using characterization of responses around a conditioned stimulus (Guttman and Kalish, 1956; Solomon and Moore, 1975; Rescorla, 1976; Pearce, 1987; Shepard, 1987; Tenenbaum and Griffiths, 2001; Bouton, 2006). In the case of a stimulus that predicts aversive outcomes, one could expect a bias toward wider generalization. That is, applying the same behavioral response to stimuli that are even less similar to the original conditioned one (a “better safe than sorry” approach). Such a phenomenon was first described by Watson and Rayner (1920), Pavlov (1927), and others (Hearst, 1960; Dunsmoor et al., 2009; Schechtman et al., 2010), and was suggested as a possible cause and pathobiological marker for anxiety disorders (Lissek et al., 2010; Schechtman et al., 2010; Dunsmoor et al., 2011).
One possible fast and efficient way to produce a “fight-or-flight” response to two similar stimuli is to not discriminate them at the perceptual level to begin with. We have recently found evidence supporting this hypothesis and showed that people have a higher perceptual threshold (decreased sensitivity) for stimuli after aversive conditioning using primary reinforcers (Resnik et al., 2011). This might suggest that, in some cases, wider generalization occurs not only because we judge stimuli to likely belong to a set of situations with similar consequences (Shepard, 1987; Schechtman et al., 2010), but because aversive conditioning can also affect discrimination.
Extensive work on decision theories has focused on evaluation and assignment of value and choice behavior (Cohen and Blum, 2002; Rangel et al., 2008; Kable and Glimcher, 2009). Behavioral studies have provided detailed accounts of bias, and have generally shown that loss can bias behavior and modulate choice (Kahneman and Tversky, 1979; Green and Swets, 1989; Glimcher and Rustichini, 2004; Rangel et al., 2008; Sokol-Hessner et al., 2009). Recent imaging, lesion, and electrophysiological studies have identified potential neural networks that are associated with assigning subjective value and making choices, and hence might underlie such biases (Bechara et al., 1999; Breiter et al., 2001; Seymour et al., 2004; De Martino et al., 2006, 2010; Yacubian et al., 2006; Tom et al., 2007; Delgado et al., 2008; Guitart-Masip et al., 2010). However, relatively little work has attempted to directly identify the differences between primary and secondary reinforcers, and processing of value is probably mediated by shared but also different neural networks (Talmi et al., 2009; Delgado et al., 2011). Specifically, although secondary reinforcers bias choice and decision, it is not known whether they would compromise perception as primary reinforcers do (Resnik et al., 2011).
If monetary loss can alter perception, it would have implications for human life, and might result in compromised decisions for stimuli that are different from the original loss-related stimulus. It can also suggest that perceptual factors and sensory acuity contribute to choice bias (Kable and Glimcher, 2009). We therefore tested this hypothesis by associating tones with monetary loss and measuring changes in perceptual discrimination around the conditioned tone.
Materials and Methods
Thirty-nine healthy human participants (age range, 21–34 years; median age, 25 years; 17 females) were recruited through advertisement and were paid a minimum baseline amount for their participation. All experiments were conducted under a Helsinki protocol approved for R.P. and with signed consents by the participants. Subjects were told they could increase the baseline amount by playing correctly a game. Each participant first performed a discrimination task to find perceptual thresholds for three pure tones: 300, 500, and 700 Hz. Immediately afterward, participants underwent a conditioning paradigm (n = 14, mixed classical plus instrumental conditioning; n = 14, the same but while undergoing a functional scan; and n = 11, underwent only classical conditioning. The n = 14 that underwent the mixed paradigm in the scanner also performed a generalization paradigm in the scanner. All subjects then reperformed the discrimination task again for the three pure tones.
Discrimination tasks.
Discrimination tasks were performed outside the scan (before and after), and separately for 300, 500, and 700 Hz (in random order). All frequency discrimination thresholds were converted to a percentage of the original frequency for each subject: Δf/f, where f is the base frequency (i.e., 300/500 or 700 Hz), and Δf is the frequency difference at which a tone of f +Δf is correctly discriminated from f at 70.7% level in the discrimination task, by an adaptive “two-down, one-up” staircase converging procedure (Levitt, 1971). The task was a two-alternative forced choice (2AFC) that discourages bias (Macmillan and Creelman, 2004) and tests best for the sensitivity (criteria) of the subject. In each step, the two tones (f and f +Δf) are presented in a randomized order with a 1000 ms interval, and the subject is asked “Which tone had a higher pitch first/second?” No feedback was supplied. Notice also that there is little reason for bias, because it was very clear that this is a different task in a different context than the conditioning paradigm inside the magnet. The stimuli were pure tones with a duration of 250 ms and onset/offset ramps of 5 ms, for a total of 260 ms. Tones were delivered through headphones (HQ1400, Creative) at a 70 db SPL and were generated via Matlab on standard PC computers.
Conditioning paradigm.
One tone was randomly assigned as loss related, one as gain related, and one as neutral (counterbalanced across subjects). There were 35 presentations of each tone overall, and a combination of instrumental and conditional trials assured that the meaning of the tones remains the same action-wise, but retains the valence difference between loss and gain. In the instrumental task, subjects learned to associate a button to tone: one button, if pressed after the gain-related tone, resulted in a gain of 1 Israeli shekel; and the other button, if pressed after the loss-related tone, prevented loss of one-half an Israeli-shekel. Intermingled were classical-conditioning trials in which the subject was informed that the button is irrelevant (a message that appeared at the bottom of the screen during the trial “Helpless trial—keyboard deactivated”), and they would lose if they hear the loss-related tone or gain if they hear the gain-related tone.
Subjects received visual feedback telling them of the outcome of the trial (“earn #” or “lose #”). All trials last 2.5 s. Each trial started with the tone presented for 300 ms. In instrumental trials, response time was limited to 2.2 s, and immediately afterward appeared the feedback screen, and in classical trials there was a 2.2 s trace until the feedback screen appeared. Feedback screens were presented for 1.5 s. The intertrial interval ranged between 2 and 6 s (mean duration 4 s).
The three tones (300, 500, and 700 ms) are well differentiated and are much above the normal perceptual thresholds of ∼3–30 Hz in this range for naive subjects (Johnsrude et al., 2000; Ahissar et al., 2006), and subjects therefore rapidly and easily associate valence with tone, as shown by the learning curves. The neutral tone required no action and resulted in no outcome. We chose a ratio of 2:1 for gain/loss to overcompensate for intensity differences that might result from loss aversion. This is based on preliminary experiments in this setup that computed individual loss aversion (λ = −βloss/βgain, similar to loss aversion in prospect theory with the simplifying common assumptions of linear value function and identical weights for 0.5 probabilities). The median in our subjects (n = 11) was found to be 1.5 and the mean was 1.7 (Schechtman et al., 2010), highly similar to previous literature (Tom et al., 2007; Sokol-Hessner et al., 2009). In addition, loss aversion is less likely to play a factor with such small monetary amounts as we used here (Harinck et al., 2007).
To verify that our main perceptual result is not due to the mixture of classical and instrumental trials, we conducted an additional experiment (n = 11). In this experiment, everything was similar, but there were only classical conditioning trials, and just noticeable difference (JND) was measured before and after as described for the three tones (gain/loss/neutral).
Generalization paradigm.
Subjects (n = 14) were explicitly and clearly informed that a new game starts, where they can gain more money. In each trial, one tone was presented and the subjects were asked only one question: “Is this one of the tones you heard in the previous phase? Or a different new tone?”. Subjects were informed they would be rewarded for a correct response and not for a mistake, but did not receive feedback until the end. There were 16 possible tones overall: the loss-conditioned tone, the gain-conditioned tone, and −20%, −10%, −3%, +3%, +10%, +20% Hz around each of the two (hence, 6 × 2 + 2 = 14). Two additional tones (80 Hz and 900 Hz) were presented as control to further validate that the subjects comprehend the new task. There were 150 trials overall: 20 of each of the original 2 tones (2 × 20 = 40), 8 of each of the new tones around them (8 × 12 = 96), and 7 of each of the control (2 × 7 = 14), hence 40 + 96 + 14 = 150.
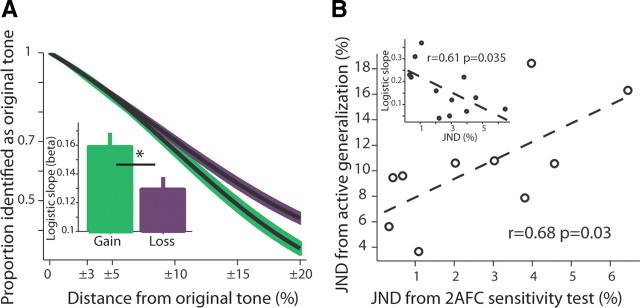
Notice that the two original tones have equal value now, and the subjects clearly understood this, as evident by their generalization behavioral function around each tone and their responses to the two control tones. Generalization here refers to (and measured by) the proportion of each tone identified as the original conditioned tone. Logistic fits were performed using Matlab “glmfit” function with “probit” link function (“logit” provided essentially identical results, as well as quantifying slopes by linear interpolation).
All behavioral results were highly similar for the n = 14 that performed the behavioral paradigm in a regular room and the n = 14 that performed it in the magnet (p > 0.5, ANOVA for the interaction of MRI/no MRI and JND changes described in the text), and all p values described as significant in the text are significant if performed separately for each group.
fMRI data acquisition and preprocessing.
Functional images were acquired by T2*-weighted gradient-echo echo-planar imaging [35 slices, flip angle = 75°, time repetition (TR) = 2000 ms, time echo (TE) = 30 ms, voxel size = 3 × 3 × 4 mm) on a 3 T MRI scanner (Tim Trio, Siemens). Anatomical images were acquired using a T1-weighted MPRAGE sequence (176 slices, flip angle = 9°, TR = 2300 ms, TE = 2.98 ms, FOV 256, voxel size 1.0 × 1.0 × 1.1 mm).
Data analysis.
We used Statistical Parametric Mapping (SPM8; Wellcome Trust Centre for Neuroimaging, http://www.fil.ion.ucl.ac.uk/spm) for image preprocessing—images were realigned to the first volume, unwarped, normalized to a standard EPI template based on the MNI reference brain, resampled to 2 × 2 × 2 mm voxels, and spatially smoothed with an isotropic 8 mm FWHM Gaussian kernel—and for estimation of statistical maps using a general linear model approach with six rigid-body realignment parameters as nuisance covariates. To delineate valence-related brain regions during the conditioning phases, three regressors were constructed for all trial types (i.e., “positive tone,” “negative tone,” and “neutral tone”). All regressors were modeled as box-car functions, from trial onset until the participant's response convolved with the hemodynamic response function. Feedback screens were modeled separately as epochs of 1.5 s. To identify brain areas mediating the observed behavioral effect of loss on discrimination thresholds, a second level random-effects analysis was conducted, using individual preconditioning and postconditioning just-noticeable-difference (JND) changes as covariates. Voxels in the obtained statistical map were considered significant if they exceeded a threshold of p < 0.0005 uncorrected and p < 0.05 corrected (FWE, small volume correction for multiple comparisons), and a minimum cluster size of 15 consecutive voxels (except small subcortical regions). We focused on frontal-lobe, temporal-lobe, and subcortical regions in this study, based on previous studies and our hypotheses.
ROI analysis (for regional correlations with JND changes and generalization).
The a priori anatomical ROIs were defined based on known anatomical landmarks according to the Talairach Daemon Atlas (Lancaster et al., 2000) using the SPM WFU PickAtlas tool (Maldjian et al., 2003), extracting the mean parameter estimates averaged across the whole ROI via SPM Marsbar toolbox. Anatomical ROIs were defined for the caudate, putamen, BA6, BA10, BA32, BA24, BA46, BA41, BA42, insula (BA13), and dorsomedial nucleus (DMN) of the thalamus, amygdala, and hippocampus. One regressor was constructed for each combination of “tone valence” × “tone distance” × “response accuracy” (i.e., “gain,loss” × “−20%,−10%,−3%,0%,3%,10%,20%” × “correct/incorrect”), and one regressor for the “control” tones (80 and 900 Hz). All regressors were modeled as box-car functions, from trial onset until the participant's response convolved with the hemodynamic response function. Parameter estimates (β values) were calculated by using a contrast of each regressor with the control regressor.
Results
Subjects performed a standard 2AFC for discrimination sensitivity (Green and Swets, 1989; Macmillan and Creelman, 2004) around three separate pure tones (300, 500, and 700 Hz), hence obtaining their JND for each tone (measured as sensitivity, Δf/f, − the percentage change they can detect). Then, they underwent a functional imaging scan while performing a behavioral paradigm in which one of the pure tones was associated with a monetary loss, another with monetary gain, and the third tone was unpaired (tones were counterbalanced across subjects for their valence). There were an equal number of presentations (35) of each of the three tones, and these were randomly intermingled. Half of the trials were instrumental where subjects had to learn which button, if pressed, results in gain of money for the gain-related tone; and which button, if pressed, would avoid losing for the loss-related tone. To make sure that the loss-related tone retains its valence throughout the experiment, half of the trials were classical conditioning, where the loss/gain/neutral tones were followed by announcement of the corresponding recompense. Once the conditioning and scanning was over, subjects physically relocated to another room and performed the 2AFC task for the three tones, again obtaining their JND (discrimination sensitivity) around each stimulus. We could therefore compare within subject the effect of monetary loss on changes in the sensitivity versus a baseline of monetary gain or mere exposure.
Although our experiment focused on loss conditioning, we took several measures to make the gain and loss of comparable intensity (as conditioning can affect loss aversion) (Guitart-Masip et al., 2010). First, we used small amounts, which are less subject to loss aversion (Harinck et al., 2007); second, we first quantified the loss-aversion factor in our setup and used a higher safety factor for the loss/gain ratio (1:2; see Materials and Methods); Finally, the use of an instrumental paradigm allowed us to measure and compare learning rates and reactions times as indication for differential intensity (Fig. 1A, n = 28, p > 0.1 interaction of learning rates and valence, F = 1.04, p > 0.1 main effect of valence, F = 0.91, 2-way ANOVA; p > 0.1 for reaction times, t = −1.7, paired t test).
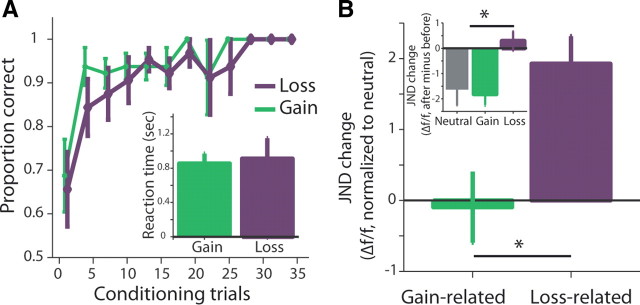
Figure 1.
Monetary loss decreases perceptual sensitivity for the conditioned stimuli. Subjects were tested for their discrimination threshold around three different pure tones; then underwent a conditioning session in which one tone was conditioned with monetary loss, one with gain, and one without outcome (neutral). After conditioning, they were tested again for changes in their discrimination threshold. A, Proportion-correct button press for loss-conditioned and gain-conditioned tones. There was no difference between the conditions and no interaction effect (n = 28). Shown are the means ± SEM. Inset, Reaction times for button press were not different for loss-related and gain-related tones. B, Group average changes (±SEM) in sensitivity for the loss-related and gain-related tones, compared with the neutral stimuli (n = 28). Data are the JND, presented as the percentage of the original tone (Δf/f) and obtained by a 2AFC adaptive test. Inset shows the non-normalized raw changes in JND (after − before; hence, a minus result is an improvement in sensitivity, n = 28).
As expected from previous perceptual studies, participants first had a normal JND for nontrained subjects (Johnsrude et al., 2000; Ahissar et al., 2006) but improved their discrimination for the neutral stimulus (Hawkey et al., 2004; Amitay et al., 2006; Resnik et al., 2011) (−1.63 ± 0.62, mean ± SEM; JND after − JND before, p = 0.002, t = −3.4, t test). We therefore used this improvement hereafter as a baseline for expected perceptual sensitivity at the second JND test. Subjects improved for the gain-related tone as well in a comparable way, and it was not significantly different from neutral (−1.73 ± 0.5, −0.1 compared with neutral, p > 0.5, t = 0.17, paired t test).
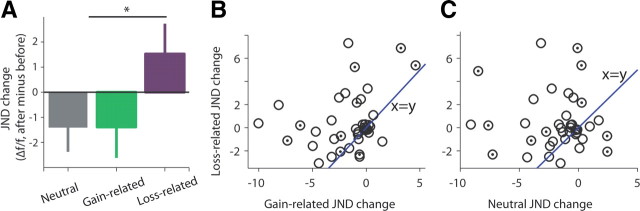
In contrast, subjects showed much less discrimination and sensitivity for the tone associated with loss (+0.29 ± 0.38), a mean of +1.93 when compared with neutral (Fig. 1B; p < 0.01, t = −2.8, t test). A full model showed an interaction of before/after × loss/gain/neutral (Fig. 1B, inset; p < 0.001, F = 5.1, two-way ANOVA). In an additional experiment, we validated that this increase in perceptual thresholds is not confined to the mixture of classical and instrumental trials that we used. The same result was obtained for a separate group of subjects (n = 11) that underwent only classical conditioning for the three tones (gain/loss/neutral) between the JND tests (Fig. 2A; neutral: −1.41 ± 0.96; gain: −1.39 ± 1.23; loss: +1.53 ± 1.2, p < 0.05, F = 3.9, ANOVA). Notice that even subjects that did improve their sensitivity for the loss-related tone, did so less than for the gain-related tone (Fig. 2B; p = 0.002, t = −3.4, paired t test) or for the neutral one (Fig. 2C; p = 0.003, t = −3.2, paired t test).
Figure 2.
Individual changes in JND after conditioning. A, Group average changes (±SEM) in sensitivity for the loss-related, gain-related, and neutral tones after classical conditioning only. Shown is the raw changes in JND (after − before; hence, a minus result is an improvement in sensitivity, n = 11), presented as the percentage of the original tone (Δf/f). B, C, Individual changes in sensitivity for loss-related stimuli versus gain-related (B) or neutral (C) stimuli. Empty circles are subjects from the combined classical plus instrumental conditioning paradigm (n = 28). Filled circles are subjects from the paradigm where only classical conditioning was used (n = 11).
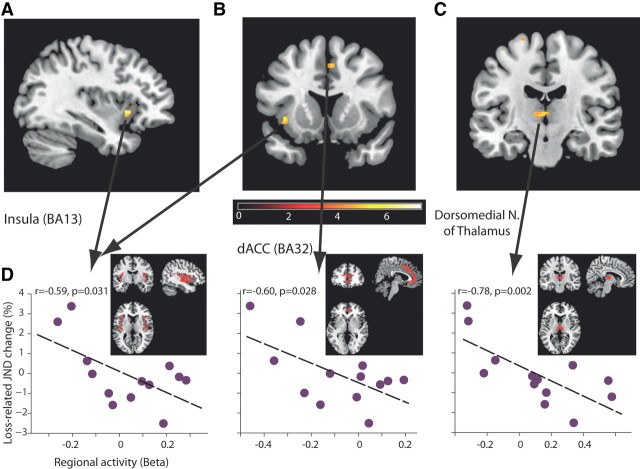
Our design and hypothesis were focused on the effects of loss on sensitivity, and we therefore used the individual changes in JND as a covariate with a loss > baseline contrast when analyzing the imaging data. Based on many previous studies, we performed a whole-brain analysis that focused on prefrontal cortices, striatum, insula, amygdala, hippocampus, and thalamus. This revealed that activities in several areas predicted the sensitivity changes for the loss-related stimulus, primarily in the insula (BA13; Fig. 3A), dorsal ACC (BA32; Fig. 3B), and the dorsomedial nucleus of the thalamus (Fig. 3C; Table 1; all imaging is p < 0.0005 uncorrected and p < 0.05 FWE corrected). Based on these findings, we extracted BOLD activations from the anatomical structures corresponding to the ROIs detected in the functional analysis, and confirmed an inverse relationship between mean anatomical ROI activations and changes in perceptual thresholds (Fig. 3D). This means that the higher the activity in these areas during the conditioning process, the more the subject improved for the loss-related tone. Notice that these are real predictions, because JND was measured outside and after the scan and the conditioning procedure. Although some studies report a loss-related decrease from baseline (Tom et al., 2007), we did not observe any activations in the complementing contrast of loss < baseline with JND changes as covariate.
Figure 3.
Neural networks in which activity inversely correlates and predicts the changes in sensitivity. A–C, Activation maps when using changes in JND (postconditioning − preconditioning) for loss-related stimuli as covariate with a loss > baseline contrast (all data presented are at p < 0.0005 uncorrected and p < 0.05 FWE corrected, k > 15). Shown are the insula (BA13, A, B); the ACC (BA32, B); and the dorsomedial nucleus of the thalamus (C). See Table 1 for the complete list. D, Individual correlations between whole regional activities based on anatomical ROI and JND changes for loss-related stimuli. Every data point is a subject. The same analysis was not significant for gain- or neutral-related stimuli in these regions (p > 0.1 for all, Pearson correlation; n = 14). Notice the significant correlations are not independent from the whole-brain analysis (A–C), because we inserted the changes in JND as covariate, yet we took the complete (much larger, shown in red) anatomical ROIs for each region for this post hoc analysis (insula: k = 1848; BA32: k = 1420; DMN: k = 244), so the significance is not a compulsory result.
Table 1.
Loss > Baseline contrast with individual changes in JND as covariate
| Region (BA) | Z-score | Talairach coordinates |
Cluster size | ||
|---|---|---|---|---|---|
| x | y | z | |||
| Left insula (13) | 4.23 | −37 | 13 | −4 | 25 |
| Right ACC (32) | 3.79 | 4 | 16 | 40 | 17 |
| DMN | 3.92 | −4 | −15 | 4 | 33 |
| Left superior frontal gyrus (6) | 4.17 | −20 | −10 | 69 | 20 |
| Left midbrain | 4.14 | −4 | −30 | −9 | 43 |
| Left cerebellum, culmen | 3.79 | −32 | −55 | −19 | 20 |
Activations in a loss > baseline contrast when adding individual changes in JND as covariate. Regions in bold are shown in Figure 3. All activations are at p < 0.0005 uncorrected and p < 0.05 FWE corrected, k > 15. No relevant activations were found in the complementing contrast, that of loss < baseline with JND as covariate.
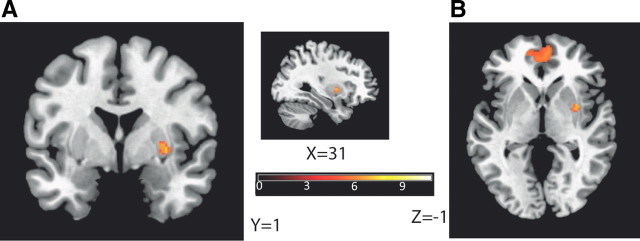
We further separated instrumental and classical acquisition trials for the same analysis and found that the insula, the amygdala, the entorhinal cortex, and the dorsolateral prefrontal cortex (BA46) were correlated with JND changes when instrumental trials were exclusively considered; and BA32 was correlated with JND changes when classical trials were exclusively considered (Table 2). These networks were specific to the loss-related changes, because none of these regions were identified when using the gain-related JND changes as covariate to the gain > baseline contrast. We verified and observed expected activations for the basic paired contrasts (Table 3), as of the striatum and BA10 in gain > neutral (Fig. 4) and gain > loss, and the right amygdala in loss > neutral, but also left amygdala in gain > loss (for detailed results, see Table 3).
Table 2.
Loss > baseline contrast in instrumental / classical trials only, with JND changes as covariate
| Region (BA) | Z-score | Talairach coordinates |
Cluster size | ||
|---|---|---|---|---|---|
| x | y | Z | |||
| Instrumental trials only | |||||
| L Insula | 3.72 | −40 | −16 | −1 | 19 |
| Inferior frontal gyrus (BA 46) | 3.38 | 40 | 37 | 11 | 18 |
| L Anterior entorhinal cortex (BA 34) | 3.51 | −24 | 5 | −15 | 16 |
| L Amygdala | 3.17 | −20 | −8 | −10 | 3 |
| L Midbrain | 4.27 | 0 | −26 | −7 | 79 |
| R Cerebellum culmen | 3.83 | 4 | −53 | −16 | 18 |
| R Superior temporal gyrus | 3.77 | 40 | 11 | −16 | 18 |
| Classical trials only | |||||
| R ACC (BA32) | 3.66 | 16 | 31 | 28 | 33 |
| R cerebellum | 3.69 | −20 | −81 | −35 | 147 |
| R midbrain | 3.38 | 40 | 37 | 11 | 18 |
Same as in Table 1 but for instrumental or classical trials only. L, Left; R, right.
Table 3.
Basic pairwise contrasts
| Region (BA) | Z-score | Talairach coordinates |
Cluster size | ||
|---|---|---|---|---|---|
| x | y | z | |||
| Gain > neutral | |||||
| R Putamen | 4.66 | 28 | 2 | 0 | 37 |
| L Hippocampus | 5.52 | −28 | −16 | −14 | 128 |
| BA10 | 4.65 | −4 | 46 | −7 | 734 |
| Gain < neutral | |||||
| Left insula (BA13) | 4.04 | −36 | 26 | 8 | 314 |
| L Precentral gyrus (BA44) | 3.88 | −50 | 14 | 7 | |
| R Insula (BA13) | 3.41 | 42 | 24 | 6 | 20 |
| R inferior frontal gyrus (BA45) | 3.41 | 48 | 18 | 5 | |
| Loss > neutral | |||||
| R Amygdala* | 2.96 | 24 | −8 | −10 | 8 |
| L Medial globus pallidus* | 2.81 | −16 | −4 | −1 | 8 |
| Loss < neutral | |||||
| L Inferior frontal gyrus (BA 47) | 3.43 | −34 | 25 | 1 | 37 |
| R Superior frontal gyrus (BA 6) | 3.94 | 22 | 7 | 64 | 31 |
| R Superior frontal gyrus (BA 6) | 3.9 | 4 | 10 | 53 | 73 |
| L Inferior frontal gyrus (BA 45) | 3.86 | −53 | 18 | 5 | 53 |
| L Middle frontal gyrus (BA 10) | 3.82 | −42 | 42 | 18 | 40 |
| R Thalamus, medial dorsal nucleus | 3.77 | 4 | −17 | 3 | 12 |
| Loss > gain | |||||
| No activations | |||||
| Loss < gain | |||||
| L Superior frontal gyrus (BA 9) | 4.63 | −12 | 48 | 23 | 125 |
| L Medial frontal gyrus (BA 10) | 3.9 | −12 | 51 | 16 | |
| L Anterior cingulate cortex (BA 32) | 4.65 | −2 | 47 | −2 | 750 |
| R Cingulate gyrus (BA 24) | 4.6 | 4 | −23 | 36 | 122 |
| L Hippocampus | 4.38 | −24 | −18 | −11 | 156 |
| L Amygdala | 4.33 | −22 | −2 | −10 | |
| R Caudate head | 4.07 | 8 | 18 | 5 | 161 |
Activations in all basic pairwise contrasts (without taking into account changes in JND). Regions in Bold for gain > neutral are shown in Figure 4. All activations are at p < 0.0005 uncorrected, k > 10. L, Left; R, right.
*First to emerge at p < 0.005.
Figure 4.
The striatum and BA10 are activated for a gain > neutral contrast. A, B, Right putamen (A) and prefrontal-cortex (BA10) (B) show activations in a gain > neutral contrast (without taking into account changes in JND). All activations are at p < 0.0001 uncorrected and p < 0.05 FWE corrected, k > 30 (Table 3).
Can the change in perception for loss-related stimulus affect future behavior? In our case, decreased sensitivity could mean that subjects would respond similarly to stimuli that resemble less the original loss-conditioned stimulus (wider generalization), even if it is a wrong “decision.” To test this, we had subjects perform a second phase of behavioral test. In this phase, that followed the acquisition stage, subjects were presented with a range of many pure tones, different in [±20%, ±10%, ±3%, 0%] from the loss-conditioned and the gain-conditioned original tones [i.e., (2 × 3 + 1) × 2 = 14 different tones), and in each trial (tone presentation) they were asked only one similar question: “Is this one of the tones you heard in the previous phase? Or a different new tone?” Subjects were clearly informed they would be rewarded for a correct response and not for a mistake, but did not receive feedback until the end. Notice that the gain- and loss-related original tones have equal value at this stage, and the optimal rationale behavior is to have an as narrow-as-perceptually possible behavioral function around them.
We found that subjects had wider behavioral curves around the loss-related tone (Fig. 5A, p < 0.01, t = 2.87, t test for logistic-fit slopes separately for gain and for loss; Inset shows mean ± SEM of individual logistic fits). Hence, subjects lost more money for the tones surrounding the original loss-related tone, and hence lost more overall. Importantly, there was a significant relationship between the width of the behavioral generalization curve and the individual JND for the loss-related tone (Fig. 5B; notice again that JND was measured after and outside the magnet and hence independent of the active generalization behavior). There was no such relationship for the gain-related tone (p > 0.1, Pearson correlation), and the interaction was significant in a full model (p < 0.05, interaction of gain/loss × JND type, F = 5.8, two-way ANOVA). This finding supports the notion that some of the behavioral generalization curve around the loss-related tone is due to the altered sensitivity.
Figure 5.
Generalization (mistaking other tones for the conditioned tone) is wider for loss-related stimulus and is partly explained by the changes in sensitivity. A, Behavioral function of responses identifying tones around (±3, ±10, ±20%) the loss-related and gain-related conditioned stimuli. The main plot shows a full logistic-fit model (±SEM in shaded color). The two models had significantly different β values (n = 14). The inset shows the average ± SEM of individual logistic fits per subject (smaller β mean wider function). B, There was a close relationship between the sensitivity (JND) of an individual subject and his/her generalization curve. Plotted is the JND from the 2AFC task (tested after subjects completed the generalization phase and were taken out of the magnet to a different room) versus the same measurement but calculated on the generalization curve (i.e., Δf/f at 0.707 proportion—same as the convergence of the 2AFC adaptive algorithm; see Materials and Methods; n = 12 for which both data points could be estimated). Obviously, the generalization had a larger JND, possibly due to the memory component (the 2AFC always presents the target and the test tone in immediate succession), but there was a significant correlation and explained variance. Inset, The same result was obtained when comparing the JND directly to the β (slope) from the logistic fit.
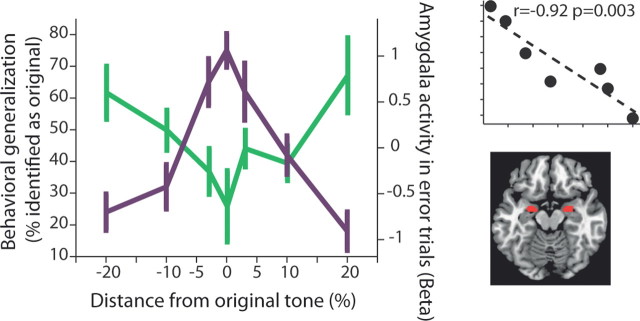
Finally, we tested whether activity of any of the regions were related to the behavioral generalization. We used predefined anatomical ROI for all of the areas that were identified in the aforementioned analyses, and tested for areas in which activity in error trials (i.e., when misidentifying a new tone as the original tone) was correlated with the behavioral generalization function. Only the amygdala showed such significant correlation (Fig. 6; p = 0.003, Pearson correlation; BA24 and BA6 had significant correlations as well, but did not pass correction for multiple comparisons). There was no significant relationship for correct trials (correctly identifying a new/original tone) and for incorrect or correct trials around the gain-conditioned tone (p > 0.1 for all, Pearson correlation). Only the putamen showed some correlation with correct responses of behavioral generalization around the gain-conditioned tone (r = −0.77, p = 0.042, but did not pass correction for multiple comparisons).
Figure 6.
Generalization (probability for mistaking a different tone for the conditioned tone) correlates with amygdala activity. We tested all the areas found in the aforementioned analyses, and obtained their activity in error trials: the trials when misidentifying a new tone as the original tone (i.e., the wider behavioral generalization function). We then correlated this activity with the behavioral responses. Three areas showed significant correlations (BA24 and BA6), but only the amygdala (right lower inset shows anatomical ROI) survived multiple-comparison correction (p = 0.003, r = −0.92; p < 0.05 for left and right amygdala separately as well). Shown is the raw behavioral data for loss-related generalization combined with amygdala activity (β) in error trials. Top right inset shows the correlation between the two lines.
We conclude that the amygdala became more active when a distant tone was misidentified as the loss-conditioned tone, with increasing activity the farther away the tone is.
Discussion
To the best of our knowledge, this is the first demonstration that monetary loss can modulate perception and influence our sensitivity and discrimination for stimuli that are associated with such losses. We further characterized a network of regions for which activity during the conditioning predicted the individual (per-subject) change in perception.
Monetary loss reduces perceptual sensitivity
We have previously shown that loss conditioning induces wider generalization, in the sense that subjects later identify a tone that is farther away from the aversive-conditioned tone as the original one (Schechtman et al., 2010). In principle, this reported behavior could be the result of a decision-making process and changes in production of choice behavior (e.g., choice bias). However, because there was no apparent reason for the subjects to behave this way and they lost more by doing so, and our task required memory-based discrimination, we suggested that it could also be the result of changes in perceptual discrimination. This suggestion obtained further support from our recent findings that following aversive conditioning with a primary reinforcer (odors or sounds), subjects indeed had decreased sensitivity (Resnik et al., 2011). The current study was designed to provide direct evidence that monetary loss also induces changes in discrimination thresholds, and, specifically, that it induces a decrease in sensitivity.
Another major goal of the current study was to obtain information about the underlying neural network. We identified regions that were previously shown to modulate learning in affective situations, such as the insula, the ACC (BA32), and the DMN—an area that receives and relays information across diverse “limbic” and prefrontal regions. We found that the higher the activity in these areas during the conditioning process, the more the subject improved for the loss-related tone. Because improvement is the expected baseline as occurred for neutral and gain-related tones (and observed in many perceptual studies) (Fahle and Poggio, 2002; Sagi, 2011), it suggests that higher activity in these areas allowed the subject to process the stimulus in the normal way for nonaversive stimuli, and improve for it. This is in line with the role of BA32 and the insula in emotional regulation (or “modulation of emotion”), and in inhibiting aversive responses that are mediated through the amygdala and related regions (Phelps et al., 2004; Ochsner and Gross, 2005; Quirk and Beer, 2006; Pessoa, 2008), possibly via the dorsomedial nucleus of the thalamus or direct projections. We therefore interpret this finding as if subjects with increased emotional modulation of the aversive response for the loss-related tone, could process better the stimuli, and hence improve on it. In contrast, subjects with an aversive response that was less modulated—i.e., there was lower activation in these regions—had abnormal or disturbed processing of the stimulus and eventually reduced sensitivity. More generally, a stimulus that is more aversive would be less regulated by these networks and the enhanced reaction would interfere with its normal processing, resulting in less sensitivity and overgeneralization.
Possible contribution of intensity and valence
Our findings cannot be explained by general attention resources, because subjects improved on the gain-related and neutral tones that were intermingled in the same session, and 2AFC tests are considered bias free for sensitivity (Macmillan and Creelman, 2004) and were performed after and outside the magnet and context. Importantly, our findings are most likely valence related, because we controlled for gain of comparable intensity. This was evidenced in the similar learning rates and reaction times. In addition, subjects' sensitivity improved similarly for the gain-related and the neutral tone. If the perceptual changes were due to intensity rather than valence, one would expect the same direction of changes for the gain-related tone (i.e., some deterioration compared with neutral), yet we observed the opposite. Further, our paradigm was designed to control for classical loss-aversion effects by taking a safety factor of 2:1 for gain/loss ratio (i.e., λ = 2). This was based on preliminary experiments that quantified the loss aversion in this setup [median 1.5; mean 1.7, n = 11 (Schechtman et al., 2010); and on previous literature (Tom et al., 2007; Sokol-Hessner et al., 2009)]. Finally, loss aversion is also less likely to play a factor with such small amounts (Harinck et al., 2007). Notice that we used gain-related stimuli as a control in our paradigm, and tuned and achieved comparable improvement in sensitivity between gain and mere exposure (neutral). We therefore cannot rule out the possibility that much larger monetary gains would alter perception as well and this should be tested in a separate study.
All in all, we conclude that in our study it is highly likely that the loss per se resulted in the relative increase in perceptual thresholds.
Active generalization is mediated by the amygdala
We initially used a mixture of classical and instrumental conditioning. Most relevant here is the possibility that the instrumental trials that allowed avoidance might have had an ameliorating effect (Kim et al., 2006). To address this, we included an equal number of classical trials that maintained valence. Moreover, notice that even if the instrumental trials indeed compromised the valence associated with the loss-related tone (because people could avoid losing money in half the trials), this should have reduced the effect size we observed and not increase the difference between gain/neutral and loss as we found. Final evidence was obtained by an additional group of subjects that underwent only classical conditioning, and for which the same trend of increased thresholds after loss conditioning and decreased thresholds after gain was found. Moreover, these subjects showed a larger increase (deterioration) in sensitivity for the aversive tone than the original group that underwent the mixed paradigm (compare Fig 1B, inset, right bar, Fig. 2A, right bar; but this was not significant).
Although the mixture of instrumental and classical conditioning does not affect the finding that loss affects perception, it might limit the interpretation of the imaging data, because learning could have been mediated by separate but interacting systems (Dayan et al., 2006; Rangel et al., 2008; Kable and Glimcher, 2009). We conducted the same covariate analysis on a model that separated instrumental and classical conditioning trials, and indeed found differential activity. The amygdala was not involved during classical trials of loss conditioning (Seymour et al., 2007; Delgado et al., 2011), but was involved during instrumental conditioning, in accordance with studies of active choice bias (Bechara et al., 1999; Breiter et al., 2001; Yacubian et al., 2006; Smith et al., 2009; De Martino et al., 2010). Based on this, we further found that amygdala activity was highly correlated with wider generalization (that includes choice behavior), in the sense that we observed increased activity when a tone was identified as the loss-conditioned tone, and the activity increased with the distance from it. In other words, more activity is observed when wrong decisions are made, with direct relationship to how “irrational” the decision is.
Conclusions and implications
Evolutionary-wise, it makes sense to have better detection for affective stimuli (Padmala and Pessoa, 2008), but it also makes sense to have less discrimination for risk-related stimuli (Resnik et al., 2011) (survival risk, not in its decision theory meaning), because it can assure a fast response for stimulus that resembles the original one and hence likely entails the same dangerous outcome. However, the fact that money, a secondary reinforcer, also induces these effects has wider implications in modern society. Here we showed that loss conditioning can alter perceptual thresholds and further result in compromised responses for other stimuli. This in turn increased loss of money despite the otherwise rationale behavior of the subjects. We therefore propose that the changes in perception we describe could compromise other decisions as well (Kable and Glimcher, 2009), and that choice behavior interacts with the altered perception.
Footnotes
The work was supported by a Minerva Foundation and European Union- International Reintegration grants to R.P. We thank Professor Elizabeth A. Phelps, Micah Edelson, and Dr. Avi Mendelsohn for discussions. We thank Dr. Edna Furman-Haran and Nachum Stern for fMRI procedures.
References
- Ahissar M, Lubin Y, Putter-Katz H, Banai K. Dyslexia and the failure to form a perceptual anchor. Nat Neurosci. 2006;9:1558–1564. doi: 10.1038/nn1800. [DOI] [PubMed] [Google Scholar]
- Amitay S, Irwin A, Moore DR. Discrimination learning induced by training with identical stimuli. Nat Neurosci. 2006;9:1446–1448. doi: 10.1038/nn1787. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Damasio AR, Lee GP. Different contributions of the human amygdala and ventromedial prefrontal cortex to decision-making. J Neurosci. 1999;19:5473–5481. doi: 10.1523/JNEUROSCI.19-13-05473.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouton ME. Learning and behavior: a contemporary synthesis. Sunderland, MA: Sinauer Associates; 2006. [Google Scholar]
- Breiter HC, Aharon I, Kahneman D, Dale A, Shizgal P. Functional imaging of neural responses to expectancy and experience of monetary gains and losses. Neuron. 2001;30:619–639. doi: 10.1016/s0896-6273(01)00303-8. [DOI] [PubMed] [Google Scholar]
- Cohen JD, Blum KI. Reward and decision. Neuron. 2002;36:193–198. doi: 10.1016/s0896-6273(02)00973-x. [DOI] [PubMed] [Google Scholar]
- Dayan P, Niv Y, Seymour B, Daw ND. The misbehavior of value and the discipline of the will. Neural Netw. 2006;19:1153–1160. doi: 10.1016/j.neunet.2006.03.002. [DOI] [PubMed] [Google Scholar]
- Delgado MR, Li J, Schiller D, Phelps EA. The role of the striatum in aversive learning and aversive prediction errors. Philos Trans R Soc Lond B Biol Sci. 2008;363:3787–3800. doi: 10.1098/rstb.2008.0161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado MR, Jou RL, Phelps EA. Neural systems underlying aversive conditioning in humans with primary and secondary reinforcers. Front Neurosci. 2011;5:71. doi: 10.3389/fnins.2011.00071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino B, Kumaran D, Seymour B, Dolan RJ. Frames, biases, and rational decision-making in the human brain. Science. 2006;313:684–687. doi: 10.1126/science.1128356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino B, Camerer CF, Adolphs R. Amygdala damage eliminates monetary loss aversion. Proc Natl Acad Sci U S A. 2010;107:3788–3792. doi: 10.1073/pnas.0910230107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunsmoor JE, Mitroff SR, LaBar KS. Generalization of conditioned fear along a dimension of increasing fear intensity. Learn Mem. 2009;16:460–469. doi: 10.1101/lm.1431609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunsmoor JE, Prince SE, Murty VP, Kragel PA, LaBar KS. Neurobehavioral mechanisms of human fear generalization. Neuroimage. 2011;55:1878–1888. doi: 10.1016/j.neuroimage.2011.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahle M, Poggio T, editors. Perceptual learning. Ed 1. Cambridge, MA: MIT Press; 2002. [Google Scholar]
- Glimcher PW, Rustichini A. Neuroeconomics: the consilience of brain and decision. Science. 2004;306:447–452. doi: 10.1126/science.1102566. [DOI] [PubMed] [Google Scholar]
- Green D, Swets J. Signal detection theory and psychophysics. Los Altos Hills, CA: Peninsula Publishing; 1989. [Google Scholar]
- Guitart-Masip M, Talmi D, Dolan R. Conditioned associations and economic decision biases. Neuroimage. 2010;53:206–214. doi: 10.1016/j.neuroimage.2010.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttman N, Kalish HI. Discriminability and stimulus generalization. J Exp Psychol. 1956;51:79–88. doi: 10.1037/h0046219. [DOI] [PubMed] [Google Scholar]
- Harinck F, Van Dijk E, Van Beest I, Mersmann P. When gains loom larger than losses: reversed loss aversion for small amounts of money. Psychol Sci. 2007;18:1099–1105. doi: 10.1111/j.1467-9280.2007.02031.x. [DOI] [PubMed] [Google Scholar]
- Hawkey DJ, Amitay S, Moore DR. Early and rapid perceptual learning. Nat Neurosci. 2004;7:1055–1056. doi: 10.1038/nn1315. [DOI] [PubMed] [Google Scholar]
- Hearst E. Simultaneous generalization gradients for appetitive and aversive behavior. Science. 1960;132:1769–1770. doi: 10.1126/science.132.3441.1769. [DOI] [PubMed] [Google Scholar]
- Johnsrude IS, Penhune VB, Zatorre RJ. Functional specificity in the right human auditory cortex for perceiving pitch direction. Brain. 2000;123:155–163. doi: 10.1093/brain/123.1.155. [DOI] [PubMed] [Google Scholar]
- Kable JW, Glimcher PW. The neurobiology of decision: consensus and controversy. Neuron. 2009;63:733–745. doi: 10.1016/j.neuron.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk. Econometrica. 1979;XLVII:263–291. [Google Scholar]
- Kim H, Shimojo S, O'Doherty JP. Is avoiding an aversive outcome rewarding? Neural substrates of avoidance learning in the human brain. PLoS Biol. 2006;4:e233. doi: 10.1371/journal.pbio.0040233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster JL, Woldorff MG, Parsons LM, Liotti M, Freitas CS, Rainey L, Kochunov PV, Nickerson D, Mikiten SA, Fox PT. Automated Talairach atlas labels for functional brain mapping. Hum Brain Mapp. 2000;10:120–131. doi: 10.1002/1097-0193(200007)10:3<120::AID-HBM30>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. J Acoust Soc Am. 1971;49(Suppl 2):467. [PubMed] [Google Scholar]
- Lissek S, Rabin S, Heller RE, Lukenbaugh D, Geraci M, Pine DS, Grillon C. Overgeneralization of conditioned fear as a pathogenic marker of panic disorder. Am J Psychiatry. 2010;167:47–55. doi: 10.1176/appi.ajp.2009.09030410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection theory: a user's guide. Ed 2. Hove, UK: Psychology Press; 2004. [Google Scholar]
- Maldjian JA, Laurienti PJ, Kraft RA, Burdette JH. An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. Neuroimage. 2003;19:1233–1239. doi: 10.1016/s1053-8119(03)00169-1. [DOI] [PubMed] [Google Scholar]
- Ochsner KN, Gross JJ. The cognitive control of emotion. Trends Cogn Sci. 2005;9:242–249. doi: 10.1016/j.tics.2005.03.010. [DOI] [PubMed] [Google Scholar]
- Padmala S, Pessoa L. Affective learning enhances visual detection and responses in primary visual cortex. J Neurosci. 2008;28:6202–6210. doi: 10.1523/JNEUROSCI.1233-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlov I. Conditioned reflexes. London: Oxford UP; 1927. [Google Scholar]
- Pearce JM. A model for stimulus generalization in Pavlovian conditioning. Psychol Rev. 1987;94:61–73. [PubMed] [Google Scholar]
- Pessoa L. On the relationship between emotion and cognition. Nat Rev Neurosci. 2008;9:148–158. doi: 10.1038/nrn2317. [DOI] [PubMed] [Google Scholar]
- Phelps EA, Delgado MR, Nearing KI, LeDoux JE. Extinction learning in humans: role of the amygdala and vmPFC. Neuron. 2004;43:897–905. doi: 10.1016/j.neuron.2004.08.042. [DOI] [PubMed] [Google Scholar]
- Quirk GJ, Beer JS. Prefrontal involvement in the regulation of emotion: convergence of rat and human studies. Curr Opin Neurobiol. 2006;16:723–727. doi: 10.1016/j.conb.2006.07.004. [DOI] [PubMed] [Google Scholar]
- Rangel A, Camerer C, Montague PR. A framework for studying the neurobiology of value-based decision making. Nat Rev Neurosci. 2008;9:545–556. doi: 10.1038/nrn2357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rescorla RA. Stimulus generalization: some predictions from a model of Pavlovian conditioning. J Exp Psychol Anim Behav Process. 1976;2:88–96. doi: 10.1037//0097-7403.2.1.88. [DOI] [PubMed] [Google Scholar]
- Resnik J, Sobel N, Paz R. Auditory aversive learning increases discrimination thresholds. Nat Neurosci. 2011;14:791–796. doi: 10.1038/nn.2802. [DOI] [PubMed] [Google Scholar]
- Sagi D. Perceptual learning in vision research. Vision Res. 2011;51:1552–1566. doi: 10.1016/j.visres.2010.10.019. [DOI] [PubMed] [Google Scholar]
- Schechtman E, Laufer O, Paz R. Negative valence widens generalization of learning. J Neurosci. 2010;30:10460–10464. doi: 10.1523/JNEUROSCI.2377-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seymour B, O'Doherty JP, Dayan P, Koltzenburg M, Jones AK, Dolan RJ, Friston KJ, Frackowiak RS. Temporal difference models describe higher-order learning in humans. Nature. 2004;429:664–667. doi: 10.1038/nature02581. [DOI] [PubMed] [Google Scholar]
- Seymour B, Daw N, Dayan P, Singer T, Dolan R. Differential encoding of losses and gains in the human striatum. J Neurosci. 2007;27:4826–4831. doi: 10.1523/JNEUROSCI.0400-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepard RN. Toward a universal law of generalization for psychological science. Science. 1987;237:1317–1323. doi: 10.1126/science.3629243. [DOI] [PubMed] [Google Scholar]
- Smith BW, Mitchell DG, Hardin MG, Jazbec S, Fridberg D, Blair RJ, Ernst M. Neural substrates of reward magnitude, probability, and risk during a wheel of fortune decision-making task. Neuroimage. 2009;44:600–609. doi: 10.1016/j.neuroimage.2008.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokol-Hessner P, Hsu M, Curley NG, Delgado MR, Camerer CF, Phelps EA. Thinking like a trader selectively reduces individuals' loss aversion. Proc Natl Acad Sci U S A. 2009;106:5035–5040. doi: 10.1073/pnas.0806761106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomon PR, Moore JW. Latent inhibition and stimulus generalization of the classically conditioned nictitating membrane response in rabbits (Oryctolagus cuniculus) following dorsal hippocampal ablation. J Comp Physiol Psychol. 1975;89:1192–1203. doi: 10.1037/h0077183. [DOI] [PubMed] [Google Scholar]
- Talmi D, Dayan P, Kiebel SJ, Frith CD, Dolan RJ. How humans integrate the prospects of pain and reward during choice. J Neurosci. 2009;29:14617–14626. doi: 10.1523/JNEUROSCI.2026-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenenbaum JB, Griffiths TL. Generalization, similarity, and Bayesian inference. Behav Brain Sci. 2001;24:629–640. doi: 10.1017/s0140525x01000061. [DOI] [PubMed] [Google Scholar]
- Tom SM, Fox CR, Trepel C, Poldrack RA. The neural basis of loss aversion in decision-making under risk. Science. 2007;315:515–518. doi: 10.1126/science.1134239. [DOI] [PubMed] [Google Scholar]
- Watson JB, Rayner R. Conditioned emotional reactions. J Exp Psychol. 1920;3:1–14. doi: 10.1037//0003-066x.55.3.313. [DOI] [PubMed] [Google Scholar]
- Yacubian J, Gläscher J, Schroeder K, Sommer T, Braus DF, Büchel C. Dissociable systems for gain- and loss-related value predictions and errors of prediction in the human brain. J Neurosci. 2006;26:9530–9537. doi: 10.1523/JNEUROSCI.2915-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]