Methods for Simultaneous EEG-fMRI: An Introductory Review

Abstract

The simultaneous recording and analysis of electroencephalography (EEG) and fMRI data in human systems, cognitive and clinical neurosciences is rapidly evolving and has received substantial attention. The significance of multimodal brain imaging is documented by a steadily increasing number of laboratories now using simultaneous EEG-fMRI aiming to achieve both high temporal and spatial resolution of human brain function. Due to recent developments in technical and algorithmic instrumentation, the rate-limiting step in multimodal studies has shifted from data acquisition to analytic aspects. Here, we introduce and compare different methods for data integration and identify the benefits that come with each approach, guiding the reader toward an understanding and informed selection of the integration approach most suitable for addressing a particular research question.

Introduction

The simultaneous recording and analysis of electroencephalography (EEG) and fMRI data in human systems, cognitive and clinical neurosciences has received substantial attention (Herrmann and Debener, 2008). Its significance is documented by the steadily increasing number of laboratories now using simultaneous recordings. Much of the motivation to explore the applicability of simultaneous EEG-fMRI comes from the selective view of brain functioning that the two recording modalities separately provide. fMRI suffers from an ill-posed temporal inverse problem, i.e., a map with regional activations does not readily permit inferences about “when” and in which order these activations have occurred (Logothetis, 2008). This is analogous to the well known spatial inverse problem in EEG, whereby one cannot infer with certainty the spatial location of sources in the brain from electrical potentials on the scalp (Michel et al., 2004; Grech et al., 2008). However, because the strengths and weaknesses of EEG and fMRI are complementary, simultaneous EEG-fMRI may achieve what seems otherwise largely impossible, namely the noninvasive recording of human brain activity with both high spatial and high temporal resolution.

The first applications of EEG-fMRI were born of a clinical interest in the improved localization of the neural sources of epileptogenic EEG activity for diagnosis and presurgical planning (Ives et al., 1993). Although the onset of pathological brain activity can clearly be inferred from EEG measurements, locations in the cortex from which these pathogenic neuronal events spread cannot unambiguously be derived from EEG alone. The simultaneous measurement and concurrent analysis of EEG and fMRI for presurgical evaluation of epilepsy provides insights beyond what is possible with separate recording protocols (Mulert et al., 2008; Gotman and Pittau, 2011). Based on this clinical line of research, then intrinsic brain states reflecting cognitive default modes were identified by assessing associations between spontaneous EEG oscillations and fluctuations of the fMRI signal in resting state (Laufs et al., 2003; Laufs, 2008). For example, negative correlations of fMRI activity in visual cortex with occipital alpha EEG (8–12 Hz) further corroborated the idea that these alpha oscillations correspond to an idling rhythm indicating cortical inactivation (Goldman et al., 2002; Moosmann et al., 2003). In more recent years, EEG-fMRI integration procedures have been developed to address basic research questions in cognitive neuroscience by applying simultaneous EEG-fMRI in the context of classical cognitive experiments (Mulert and Lemieux, 2009; Ullsperger and Debener, 2010).

One important challenge with simultaneous EEG-fMRI is the decreased signal quality potentially evident in both modalities. The necessity to introduce conducting materials for EEG recordings in the environment of the magnetic resonance system may interfere with image acquisition (Mullinger et al., 2008), and strongly degrades EEG signal quality due to the induction of electromagnetic currents (Kruggel et al., 2000; Debener et al., 2008; Yan et al., 2009). Most of the technical difficulties have now been solved, however, and commercial systems are readily available (Kruggel et al., 2001; Debener et al., 2007; Mullinger et al., 2011). Nevertheless, depending on the research question under investigation and the methods used for combined analyses, simultaneous EEG-fMRI does not necessarily yield both the spatial and the temporal resolution that might be desirable given the properties of each recording modality alone. Since the intrinsic features of the chosen analysis method strongly influence the putative outcome, the choice of the method used for data integration is of crucial importance.

Initial studies using both electrophysiology and hemodynamic data often focused on qualitatively or quantitatively comparing the outcomes of simultaneously acquired but separately analyzed EEG and fMRI data (Horovitz et al., 2004; Mulert et al., 2004). To take full advantage of the information from multimodal datasets, analytic approaches were needed that allowed more direct integration of information across modalities. The techniques currently available, however, differ in terms of their necessity for prior knowledge as well as their underlying biophysical and mathematical assumptions.

Asymmetric data integration

Asymmetric approaches for EEG-fMRI integration are characterized by a biased weighting of modalities in as much as information from one modality is used to guide the analysis of the other. Most influential of these approaches have been fMRI-informed EEG and EEG-informed fMRI.

fMRI-informed EEG

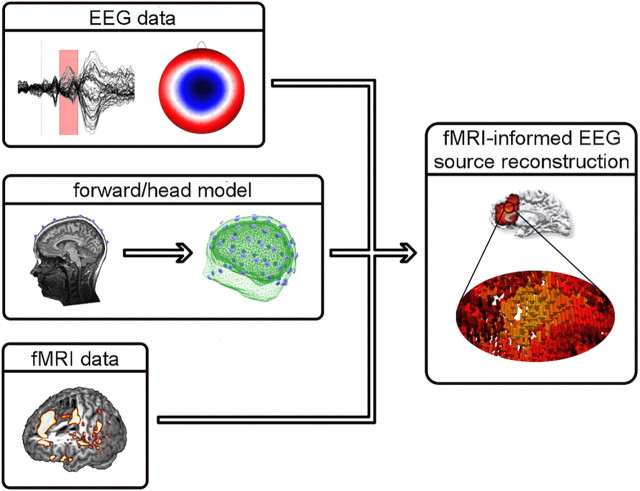
fMRI-informed EEG (Fig. 1) aims at alleviating the spatial EEG inverse problem by guiding electromagnetic source imaging using results obtained from fMRI (Heinze et al., 1994; Babiloni et al., 2000, 2002). To do this, the head geometry and most relevant biophysical characteristics of the brain (e.g., tissue conductivity) are first estimated to establish a forward model from which, given a simulated neural event, the paths of currents to the scalp can be calculated (Hallez et al., 2007). These forward models differ dramatically in terms of their neuroanatomical detail, ranging from simple interleaved spheres to individually approximated cortical representations computed from structural MR images. Given such a forward model and the measured data, source localization algorithms can then be applied that try to find the most optimal constellation of neural generators best explaining the observed scalp potential field. This inverse modeling step incorporates assumptions on how neuronal activity itself is approximated; e.g., either by a limited number of single equivalent current dipoles representing focal mass neuronal activity (Scherg and Berg, 1991; Mosher et al., 1992) or a large number of widely distributed current sources (Fig. 1; Hämäläinen and Ilmoniemi, 1994).

Figure 1.

Illustration of fMRI-informed EEG source reconstruction. To estimate the location and activity of active cortical patches in the brain that lead to measurable EEG signal changes on the scalp, forward or head models are constructed from individual MR images. Here, volumes representing skin, skull, and brain tissue have been extracted. Based on such a model and the EEG time courses as well as corresponding scalp topographies (the pattern of EEG activity as recorded on a participant's head), EEG sources can be inferred (inverse modeling). Statistical maps from a standard fMRI analysis are used to further constrain possible source constellations. The procedure used here for inverse modeling computes a high number of dipolar sources distributed across the brain, each of which is characterized by its position, orientation (pointing direction of an arrow), and strength (as indicated by coloring).

To derive concurrent spatiotemporal information from scalp-recorded EEG using information from fMRI, for example, the number of potential EEG generators (or equivalent current dipoles) can be inferred from the pattern of activations in fMRI maps. These dipoles are then seeded to locations in the brain corresponding to local fMRI maxima, subsequently allowing the time course of neural activity for each of these locations to be estimated. However, many researchers prefer so-called distributed source models which compute a reconstruction of neuroelectric activity at each point in a 3D grid of possible current sources (Hämäläinen and Ilmoniemi, 1994). In this context, the statistical maps of the fMRI result can be used to confine the putative source space by providing the probability of a particular region being the origin of the electrophysiological signal (Dale et al., 2000; Ou et al., 2010). Hence, whichever of these combinations is chosen, fMRI data help to reveal the locations while EEG-derived information provides the time courses of neural events at millisecond resolution (Vanni et al., 2004; Wibral et al., 2009, 2010).

Bledowski et al. (2006), for example, gathered EEG and fMRI data, albeit during separate sessions, while subjects performed a visual working memory task. Subsequent to a unimodal fMRI analysis, multiple discrete dipoles were seeded to the activation maxima as revealed from fMRI. Using this fMRI-derived source model, the time courses of relevant brain regions could be derived with high temporal resolution. Thereby, the sequence of neuronal processing stages during working memory retrieval could be studied concurrently at both the spatial and temporal scale, revealing serial and parallel processing elements in working memory.

Hence, although approaches for fMRI-informed EEG are used on simultaneously measured data, their strengths are most apparent in the context of separate recordings. As information derived from single trials is not taken into account, it is quite possible to work with EEG and fMRI data acquired under comparable, but not necessarily identical, experimental circumstances. This allows for an individual optimization of experimental conditions for each modality, for example by avoiding the otherwise inevitable gradient- and cardiac-related artifacts in the EEG when measured concurrently with fMRI. The validity of this approach strongly relies on the twin assumptions that the fMRI signal at a given location does carry information about the local dipole activity and that neural generators of scalp-recorded EEG/MEG do trigger a metabolic response (Wibral et al., 2010). While there is substantial evidence that under many circumstances there is indeed a tight coupling between electrophysiological and fMRI markers of neuronal activity (Logothetis and Pfeuffer, 2004), situations that violate such assumptions can easily be conceived. This would be the case, for example, when regions exhibiting an fMRI response remain electrically silent at the scalp (e.g., due to cortical “closed-field” geometry—a constellation of sources leading to a cancellation of current flow; Nunez and Silberstein, 2000) or when a stimulus-triggered synchronization of neuronal activity leads to a detectable electrophysiological response at no metabolic cost (which might be the case when the mean firing rate of the population does not change). Whereas the first situation is unproblematic for an fMRI-weighted source reconstruction, the latter is not: an fMRI-based weighting will adversely affect the reconstruction of sources in brain regions devoid of clear fMRI activations, eventually leading to gross localization errors. However, by carefully combining different methods for EEG source analyses, it might be possible to identify such ambiguous situations (Wibral et al., 2010).

EEG-informed fMRI

Elaborating on the idea of a direct coupling between EEG and fMRI, EEG-informed fMRI considers associations of changes over time between EEG and fMRI signals at a within-subject level (Fig. 2; Ullsperger, 2010). Here, EEG is preprocessed to a point where a specific EEG feature of interest over the time course of the recording can be extracted. In event-related designs this corresponds to the quasi-continuous stream of epochs surrounding the events of interest (e.g., the presentation of a stimulus or the occurrence of a behavioral response). Several features of the EEG are suitable, such as ERP amplitudes (Debener et al., 2005), ERP latencies (Bénar et al., 2007), EEG synchronization and phase coherence (Mizuhara et al., 2005; Jann et al., 2009), or the power within specific EEG frequency bands (Scheeringa et al., 2009). Whichever EEG-derived features are used, the basic assumption is that their fluctuations over time covary with fluctuations seen in the fMRI signal during the course of an experiment.

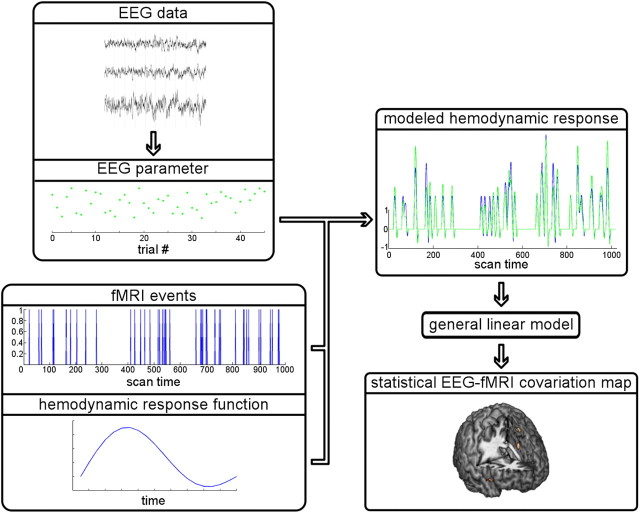
Figure 2.

Schematic of EEG-informed fMRI. For an event of interest (e.g., the occurrence of a response error), a parameter value of an EEG feature (e.g., the amplitude of an ERP) is extracted from every trial that includes this event. With respect to fMRI, the onsets of these events during the course of the experiment are known, and the fMRI signal changes caused by hemodynamic responses following the events are mathematically modeled. This is done via convolution: the multiplication and summation of a vector of zeros and ones representing the event onsets and the hemodynamic response function (mathematically modeled fMRI signal changes following an event). The result is the predicted time course of fMRI signal changes which can then be statistically compared with the observed fMRI signal for each voxel (volume element) of a brain scan. In the case of EEG-informed fMRI, not only is this model determined by event onsets and the hemodynamic response function (blue model prediction), but the expected hemodynamic responses are additionally parameterized using the extracted EEG feature: signal changes following events on trials with a large EEG response are scaled up as compared with trials with smaller EEG responses (green model prediction).

With this method, the processing of fMRI data simply follows standard procedures up to the point of first-level statistics, usually including slice-time correction, spatial realignment, spatial normalization, and smoothing (Strother, 2006). When setting up the regressors for first-level statistics (i.e., calculating statistical tests for a single subject), however, these regressors are not derived solely from the timing of stimulus onsets convolved with a modeled hemodynamic response. Rather, the modeled hemodynamic responses are additionally parameterized using the trial-wise extracted EEG feature, such that an enlarged potential amplitude in the single-trial EEG leads to an upscaling of the hemodynamic response function for a given event (Fig. 2). The resulting indices representing the model fit (beta estimates) are then tested at the group level either against other conditions or simply against zero to reveal brain regions exhibiting significant covariations and, thus, coupling of electrophysiological and hemodynamic responses.

Debener et al. (2005), for instance, used EEG-informed fMRI to test whether EEG correlates of performance monitoring (more specifically, the error-related negativity; ERN) predicts fMRI signal changes in the midcingulate cortex. For each erroneous response recorded during flanker task performance, the amplitude of the single-trial ERN was determined from EEG. This information was subsequently used for a parameterized analysis of the fMRI data. Indeed, this analysis scheme was able to prove the association of midcingulate activations with variations in ERN amplitudes while differentiating it from activity profiles of other frontal regions and the anterior insula. Moreover, single-trial amplitudes predicted task behavior in the subsequent trial, demonstrating that trial-by-trial fluctuations are not random noise but carry functional information. A similar analysis technique was developed by Eichele et al. (2005) to test the temporal sequence of ERP-related fMRI activations.

EEG-informed fMRI assumes only that the neural properties contributing to the signals captured by both modalities partly overlap and exhibit a linear association. In contrast to fMRI-informed EEG, no specific assumption is made about the spatial organization of activation patterns. This implies that this strategy can yield effects in brain structures or networks that are not necessarily the biophysical generators of, say, the ERP recorded at the scalp (Debener et al., 2005; Minati et al., 2008). One also has to bear in mind that single EEG epochs contain high levels of noise, and single-trial EEG analyses therefore have to rely on techniques that increase the signal-to-noise ratio of individual trials. In the frequency domain, the consideration of a narrow frequency band of the EEG can be thought of as a filtering mechanism. Alternatively a frequently used algorithm that enables the unmixing of spatiotemporally overlapping EEG signals before feature extraction is independent component analysis (ICA; James and Hesse, 2005; Onton et al., 2006). In any case, only a fraction of the ongoing brain activity can be used for an EEG-informed fMRI analysis at one time and the selection of the feature of interest is usually determined by the research question addressed. For example, whereas both ERP amplitudes and latencies have been shown to be correlated with hemodynamic responses, latencies are less likely to directly reflect activations of potential generators (Bénar et al., 2007).

Neurogenerative modeling

The methods described in the following section aim to benefit from the complementary information available from both modalities while avoiding an a priori bias of either (Valdes-Sosa et al., 2009; Riera and Sumiyoshi, 2010; Rosa et al., 2010). Although they require a certain amount of prior knowledge, these approaches follow logic comparable to that of EEG source modeling (Fig. 3). A forward model (or generative model) first concurrently specifies those physiological processes that give rise to EEG and those that give rise to fMRI data. Based on such forward computations, brain states can then be reconstructed from simultaneous EEG-fMRI recordings that best explain the observed data (the inverse modeling). Within such a framework, data integration relies on the ability to simulate the biophysical processes of electrophysiological and hemodynamic signal generation.

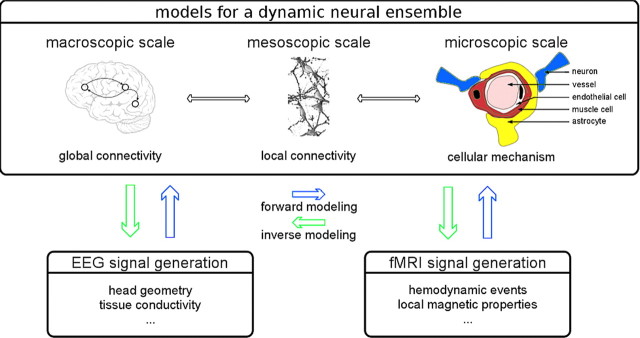
Figure 3.

Illustration of neurogenerative models for EEG-fMRI data analysis. This approach relies on mathematically modeling the dynamics of neural ensembles at various scales ranging from gross connectivity patterns to cellular events. In addition, biophysical forward models must specify the transformation of neural events to the measured EEG and fMRI signals. Based on these data, the result of a predefined neural activity pattern can be simulated (forward modeling) or, given a multimodal EEG-fMRI dataset, the most likely neural events can be inferred based on the observed EEG-fMRI signal properties (inverse modeling).

As the crucial element, a forward model for multimodal data incorporates assumptions about the link between electrophysiological and hemodynamic activities as well as the neurovascular coupling cascade (Logothetis and Wandell, 2004; Stephan et al., 2004; Raichle and Mintun, 2006), i.e., the sequence of neural events giving rise to changes in cerebral blood flow that in turn cause variations in fMRI signals. Hence, depending on richness of detail, different levels of description may be involved (Fig. 3; Rosa et al., 2010), ranging from cellular mechanisms mediating neurovascular coupling to connectivity patterns at a gross morphological level (Friston et al., 2008; Sotero and Trujillo-Barreto, 2008; Valdes-Sosa et al., 2009). Given real multimodal data, the second step of the procedure incorporates inverse modeling: estimating neural activity (e.g., EPSPs, along with other parameters) from the simultaneous EEG-fMRI observations. An intuitive approach is to repeatedly generate EEG-fMRI simulations and choose the one with the best fit to the observed data. However, computationally less demanding alternatives have been proposed that are already in use (Friston et al., 2008; Valdes-Sosa et al., 2009).

The interested reader might consider a recent study by Bojak et al. (2011) which elucidates the application of neurogenerative models. The authors used simulated data to investigate the plausibility of a neural population model for the analysis of simultaneous EEG-fMRI. Although confined to only few regions of the cortex, the authors were able to identify the effects of connectivity changes in the visual system on the activity pattern of simultaneous EEG-fMRI data. This study effectively demonstrates the relevance of such models for questions pertaining to the basic mechanisms of EEG and fMRI signal generation.

The conceptual similarity between EEG source reconstruction and EEG-fMRI data integration by means of biophysical modeling is obvious, as is the excelling need for prior information with the latter. Given that many aspects of the processes involved in fMRI and EEG signal generation are not yet fully understood, current models focus on specific aspects while strongly simplifying others. For example, the cellular mechanisms underlying neurovascular coupling have not yet been implemented in every detail (Riera and Sumiyoshi, 2010). Similarly, the reconstruction of neural activity using a brain-wide model has hitherto not been accomplished, which is not surprising given the complexity of the necessary models and the resulting computational demands. Thus, the ability to compare models of various complexity and differing physiological specificity should be considered one of the biggest strengths of the neurogenerative approach (Rosa et al., 2010).

Multimodal data fusion

Over the past years machine learning algorithms have successfully been applied to both EEG and fMRI data (Besserve et al., 2007; Pereira et al., 2009). Whereas unsupervised approaches are often used to decompose given datasets into latent variables, e.g., for artifact correction with EEG or the identification of functional networks from fMRI (Mennes et al., 2010; Joel et al., 2011), supervised approaches have drawn much attention due to their classification capabilities. An example is the prediction of the category of a presented stimulus from its evoked brain response (Mitchell et al., 2008; Haynes, 2009). When applied to EEG-fMRI data, most of these approaches hold the advantage of a genuine multivariate analysis scheme: the full spectrum of available information in multimodal datasets is explored. These “data fusion” methods use a common or symmetric model to jointly assess information from both modalities, whereas “integration” approaches usually overlay or bias one modality with the other.

Relevant methods for multimodal data fusion strongly differ in the degree to which they rely on physiological assumptions, require prior information, or share other similarities with the approaches discussed above. ICA, for example, is an unsupervised learning method which is used to discover hidden factors (independent components) from a set of observations such that the identified components are maximally statistically independent (not merely uncorrelated; Bell and Sejnowski, 1995; Hyvärinen and Oja, 2000). Here, it is assumed that the observed data originate from a linear mixture of these underlying independent components. A number of frameworks have been proposed to use ICA for multimodal data fusion. Taking joint ICA (Calhoun et al., 2006, 2009; Mijovic et al., 2012) as an example, the differing biosignal modalities are first processed separately, and ICA is subsequently applied to examine the relationships between data types (Fig. 4). Hence, fMRI statistical maps and ERP data of all subjects are merged into a single matrix and subjected to a joint ICA. Whereas in the unimodal case either temporally (EEG) or spatially (fMRI) independent components are revealed, this multimodal approach provides a joint spatiotemporal decomposition with joint independent components corresponding to electrophysiologically measured responses (indicating the timing of signal changes) alongside associated clusters of active regions (indicating spatial origins of signal changes). Using this technique, Calhoun et al. (2006) were able to examine the spatiotemporal dynamics of the auditory oddball response. Activations in auditory cortex and thalamus were mapped to the N1 auditory evoked potential, whereas brainstem, temporal lobe, and medial frontal activity showed a response profile corresponding to the P3 ERP.

Figure 4.

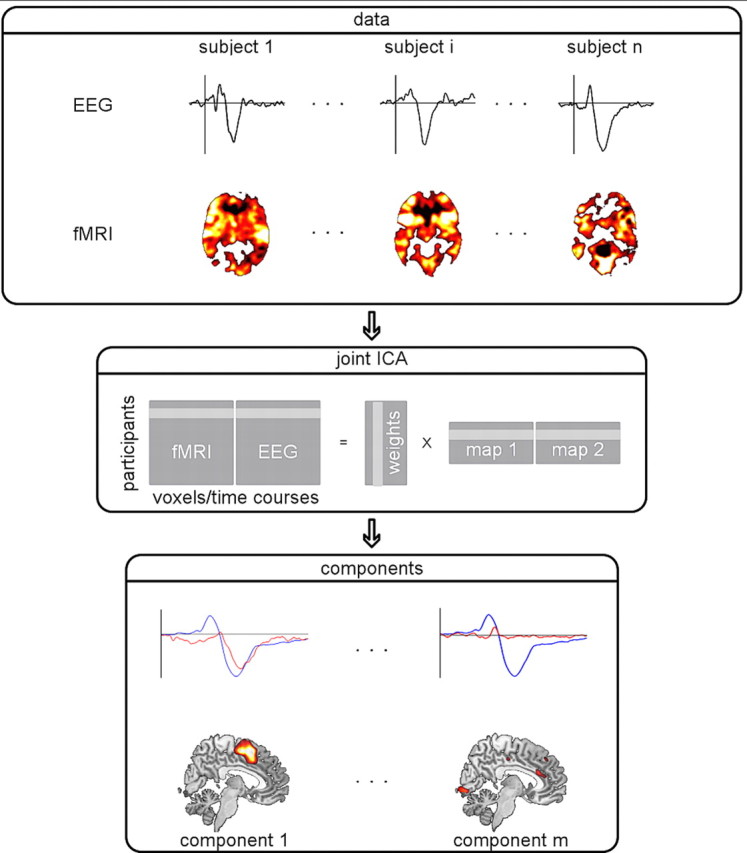
Schematic illustration of joint ICA. EEG and fMRI for a set of subjects are concatenated within the same matrix and subjected to a joint ICA. This procedure helps to capture the variance in brain responses across subjects and modalities on which basis a decomposition to independent components can be computed. The resulting components represent spatial (fMRI) and temporal (EEG) characteristics of brain responses. Here, the lower row shows the averaged ERP (blue) and time courses of two components (red) alongside their associated spatial maps.

Other methods extend the amount of data processed by additionally considering variations at the level of single trials, thereby not relying on prior information from within-subject statistics (Martínez-Montes et al., 2004; Goldman et al., 2009; Correa et al., 2010), or by first extracting components separately from each modality, and only then examining the pattern of cross-modal correlations (Eichele et al., 2005; De Martino et al., 2011; Huster et al., 2011).

Although the majority of algorithms applied here have a long history in computer science, their application to neuroscientific problems is a rather new development. Nonetheless, these methods have proven to be of high utility by providing unbiased and multivariate analysis schemes for simultaneous EEG-fMRI. In addition, many of these approaches are, or could be, easily generalized to frameworks that include other modalities, such as diffusion tensor imaging or genetic data (for review, see De Martino et al., 2010; Sui et al., 2012). On the other hand, as there is already a variety of different mathematical approaches for multimodal data fusion, the selection of a fusion model tailored for a specific research question might sometimes be difficult to accomplish. Moreover, some of the current approaches still rely on canonical models of the hemodynamic response or involve other physiological presumptions, thereby not yet taking full advantage of the full power of these algorithms.

Conclusion

Despite its rather recent development, a variety of differing methods have already been proposed for the concurrent analysis of EEG and fMRI data. The taxonomy applied here provides a natural starting point from which to better judge the potential advantages and limitations of such analysis approaches. However, a given procedure might very well share features of more than one of the categories proposed here. Ultimately, the method chosen will strongly depend on the research question addressed.

When one is primarily interested in the neural generators of scalp EEG phenomena, fMRI-informed EEG is the method of choice. This approach is founded on well established methods for EEG source reconstruction, and so constitutes the most direct technique for assessing related research questions. Additionally, it possesses high and well defined spatiotemporal resolution. It does not, however, take into account the variability of neural events seen across the course of an experimental session, and thereby neglects a potentially powerful source of information. Analyses based on EEG-informed fMRI, on the other hand, use this exact phenomenon and have already shown the ability not only to link physiological measures of different modalities with each other, but also to expose associations between physiology and variations in cognition, perception, and behavior. However, the temporal precision available with this technique is somewhat elusive, as it could potentially reveal neuroanatomical structures whose activity patterns are linearly linked to those of the generators, even though their engagement might precede or succeed the EEG event under investigation. Hence, EEG-informed fMRI seems most appropriate for revealing functional networks characterized by a linear relationship of cross-modal activity patterns identified at the single trial level. Neurogenerative models are particularly strong for testing hypotheses about the physiological mechanisms and biophysical properties underlying EEG and fMRI signal generation, as well as their interrelationship, making these models powerful tools in the field of theoretical neurobiology. Although the application of such models to whole brain analyses and complex experimental paradigms is currently lacking, its spatiotemporal resolution is in principle limited only by the precision of mathematical modeling and computational power. Finally, turning to the application of multivariate fusion methods for simultaneous EEG-fMRI, a definite recommendation is somewhat hindered by the algorithmic heterogeneity of this field. Associated approaches are well suited to address a variety of research questions as divergent as, for example, the identification of links between modalities, the prediction of behavior jointly from EEG and fMRI, or the exposure of hidden factors common to both modalities. Here, unsupervised learning algorithms with their data mining capabilities might thus constitute a counterpart to the model-driven neurogenerative approaches.