Microsaccadic Efficacy and Contribution to Foveal and Peripheral Vision

Abstract

Our eyes move constantly, even when we try to fixate our gaze. Fixational eye movements prevent and restore visual loss during fixation, yet the relative impact of each type of fixational eye movement remains controversial. For over five decades, the debate has focused on microsaccades, the fastest and largest fixational eye movements. Some recent studies have concluded that microsaccades counteract visual fading during fixation. Other studies have disputed this idea, contending that microsaccades play no significant role in vision. The disagreement stems from the lack of methods to determine the precise effects of microsaccades on vision versus those of other eye movements, as well as a lack of evidence that microsaccades are relevant to foveal vision. Here we developed a novel generalized method to determine the precise quantified contribution and efficacy of human microsaccades to restoring visibility compared with other eye movements. Our results indicate that microsaccades are the greatest eye movement contributor to the restoration of both foveal and peripheral vision during fixation. Our method to calculate the efficacy and contribution of microsaccades to perception can determine the strength of connection between any two physiological and/or perceptual events, providing a novel and powerful estimate of causal influence; thus, we anticipate wide-ranging applications in neuroscience and beyond.

Introduction

Fixational eye movements are critical for preventing and restoring vision loss during fixation (Riggs and Ratliff, 1952; Ditchburn and Ginsborg, 1953; Yarbus, 1957; Ditchburn et al., 1959), yet the relative importance of each eye movement type remains controversial, with the heart of the debate focusing on microsaccades, the fastest and largest fixational eye movement (Martinez-Conde et al., 2004, 2009; Collewijn and Kowler, 2008; Rolfs, 2009). Recent studies have linked microsaccade production to counteracting (i.e., reversing) adaptation and visual fading during fixation. Martinez-Conde et al. (2006) found increased microsaccade production before a peripheral target became perceptually visible and decreased microsaccade production before the target faded, and concluded that microsaccades enhance vision during fixation. Later studies disagreed with this interpretation, however (Collewijn and Kowler, 2008; Kowler and Collewijn, 2010; Poletti and Rucci, 2010; Kowler, 2011), with a recent review stating that “there is no compelling evidence (…) that microsaccades (or fixation saccades more generally) serve a necessary role (…) in keeping the visual world visible” (Collewijn and Kowler, 2008).

The main extant arguments against the perceptual significance of microsaccades are as follows: (1) fixational drift can restore vision just as effectively as, or more effectively than, microsaccades can (Collewijn and Kowler, 2008; Rolfs, 2009; Kowler and Collewijn, 2010; Poletti and Rucci, 2010; Kowler, 2011); (2) microsaccades are effective in a narrow range of directions, so only “a high rate of microsaccades in many directions [can] substantially improve overall visibility” (Collewijn and Kowler, 2008); (3) microsaccades have no impact on the visibility of foveal targets (Collewijn and Kowler, 2008; Kowler and Collewijn, 2010; Kowler, 2011); and (4) any visibility improvement due to microsaccades is an epiphenomenon, i.e., an accidental, rather than fundamental, function of microsaccades (Poletti and Rucci, 2010). Yet, no study has determined (1) whether drift restores vision more or less effectively than microsaccades, (2) whether microsaccade direction is critical to vision enhancement, or (3) whether microsaccades counteract fading in the fovea. At the core of this debate lies the difficulty of ascertaining the precise impact of microsaccades on vision versus that of other eye movements (Nachmias, 1961; Rolfs, 2009).

We recorded the eye movements of human observers while they reported when foveal and peripheral targets faded or intensified perceptually, both under Illusory fading and Real fading conditions (i.e., where targets faded and intensified physically). We developed a novel method, based on previous techniques to determine the strength of connection between two neurons (Levick et al., 1972; Mastronarde, 1987; Aertsen et al., 1989; Reid and Alonso, 1995; Alonso et al., 1996, 2001; Usrey et al., 1998, 1999), to calculate the efficacy and contribution of microsaccades to counteracting fading, using the subjects' reaction times from the Real fading condition to estimate the time window in which microsaccades and other ocular events could exert a causal influence on perception. Our results indicate that (1) microsaccades are the most important eye movement contributor to restoring vision during fixation, (2) microsaccades of all directions are equally effective, and (3) microsaccades restore both foveal and peripheral vision.

Materials and Methods

Subjects

Seven subjects (2 females, 5 males) with normal or corrected-to-normal vision participated in the experiments. Six subjects were naive and were paid $15/session. Experiments were performed under the guidelines of the Barrow Neurological Institute's Institutional Review Board (protocol number 04BN039). Written informed consent was obtained from each subject. For one subject, two experimental sessions were discarded due to pupil occlusion (which made the data too noisy for accurate microsaccade detection). Three other subjects lost five or less trials of data, out of 256 trials, due to pupil occlusion (the eye position was lost by the eye tracker); these data losses did not significantly affect the results.

Experimental design

Subjects rested their forehead and chin on the EyeLink 1000 (SR Research) head/chin support ∼57 cm away from a linearized video monitor (Barco Reference Calibrator V, 75 Hz refresh rate). The experiment consisted of five ∼1–1.5 h sessions, each including 64 randomly interleaved trials. The first session was counted as a training session and not included in the analysis.

Illusory fading condition.

While fixating a small red spot (0.05° diameter) on the center of the screen, subjects continuously reported whether a stimulus was faded/fading (button press) or intensified/intensifying (button release) (Martinez-Conde et al., 2006). To start the trial, subjects pressed a key and the stimulus appeared on the screen. The stimulus (Fig. 1A) was a two-lobe Gabor patch with a peak-to-trough width of 2.5° (Gaussian SDs of x = 1.5° and y = 1°; sine wave period of 5°; sine wave phase of 0). The Gabor had a maximum contrast of 40% from peak-to-trough and the same average luminance (50%) as the background. The Gabor was presented at random eccentricities of 0°, 3°, 6°, and 9° (measured from the center of the fixation point to the center of the Gabor). The position of the Gabor varied randomly across trials at one of the eight points of the compass to control for possible contrast adaptation effects across trials. The orientation of the Gabor also varied randomly between 0° and 360° in each trial to control for orientation adaptation effects. Figure 1B shows the distributions of the durations of faded and intensified periods. After 30 s, the stimuli disappeared and the trial ended. To disregard the potential effect of the initial stimulus onset transient at the start of each trial, we conducted analyses only on data recorded after the first second of the trial. A minimum average of two transitions per 30 s trial was imposed to ensure that the subjects experienced the illusion; one subject was discontinued after the training session due to this restriction.

Figure 1.

Experimental stimuli, subject reports, and performance. A, An epoch from an Illusory fading trial. Physical stimulus (top row; fixation dot not to scale), subject's perception of the stimulus (second row), and subject's report (third row). B, Distributions of the durations of fading and intensification percepts. C, Total amount of fading time across target eccentricities. D, Fading onset rate at each eccentricity. Asterisks indicate significantly higher fading onset rates at peripheral eccentricities for the pairs 0–3°, 0–6°, and 0–9° (one-tailed paired t test; *p = 0.012, **p = 0.0022, ***p = 0.0031). E, Subjects' performance in the Real fading condition. Shading and error bars indicate the SEM across subjects (n = 7).

Real fading condition.

Experimental details were as in the Illusory fading condition; however, the Gabor now physically faded and intensified. The Gabor always started at 40% contrast. Then, according to the times of transitions reported by the subject in prior randomly chosen Illusory fading trials, the Gabor faded/intensified in a step fashion to a lower/higher contrast randomly chosen from the following set: 0%, 10%, 20%, 30%, 40%. To avoid perceptual transitions due to illusory fading, which might interfere with the physical transitions, the Gabor moved at a constant speed (0.1 cycles/s) in a circular path of 1.25° radius. The parameters for the movement of the Gabor were the minimal values found to make the Gabor continuously visible at any given contrast.

Eye movement analyses

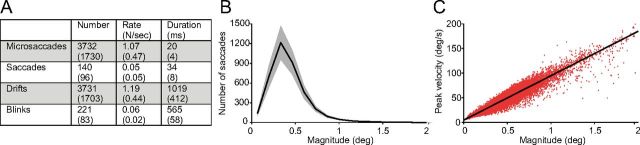
Eye position was acquired noninvasively with a fast video-based eye tracker at 500 Hz (EyeLink 1000; SR Research). EyeLink 1000 records eye movements simultaneously in both eyes (instrument noise 0.01° RMS). We identified and removed blink periods as portions of the raw data where pupil information was missing. We also removed portions of data where very fast decreases and increases in pupil area occurred (>50 units/sample; such periods are probably semi-blinks where the pupil is never fully occluded) (Troncoso et al., 2008a). We added 200 ms before and after each blink/semi-blink to eliminate the initial and final parts where the pupil was still partially occluded (Troncoso et al., 2008a). Saccades were identified with a modified version of the algorithm developed by Engbert and Kliegl et al. (Engbert and Kliegl, 2003; Laubrock et al., 2005; Engbert, 2006; Engbert and Mergenthaler, 2006; Rolfs et al., 2006) with λ = 4 (used for the velocity threshold detection) and a minimum saccadic duration of 6 ms. To reduce the amount of potential noise, we considered only binocular saccades, that is, saccades with a minimum overlap of one data sample in both eyes (Laubrock et al., 2005; Engbert, 2006; Engbert and Mergenthaler, 2006; Rolfs et al., 2006). Additionally, we imposed a minimum intersaccadic interval of 20 ms so that potential overshoot corrections might not be categorized as new saccades (Møller et al., 2002). Microsaccades were defined as saccades with magnitude <1° in both eyes. To calculate (micro)saccadic properties such as magnitude and peak velocity, we averaged the values for the right and left eyes. Figure 2 includes the descriptive statistics for microsaccades, saccades, drifts, and blinks (Fig. 2A), the magnitude distributions for microsaccades and saccades (Fig. 2B), and the peak velocity–magnitude relationship for microsaccades and saccades (Fig. 2C).

Figure 2.

Eye movements. A, Descriptive statistics for microsaccades (<1°), saccades (≥1°), drifts, and blinks. Numbers in parentheses indicate the SEM across subjects (n = 7). B, Magnitude distribution of microsaccades and saccades. Shading indicates the SEM across subjects (n = 7). C, Microsaccadic and saccadic peak velocity–magnitude relationship for all subjects combined. Each red dot represents a microsaccade or a saccade with peak velocity indicated on the y-axis and magnitude indicated on the x-axis.

Microsaccade correlations with illusory transitions

Let X_M, X_S, X_B, and X_R be the stochastic processes representing the onsets of microsaccade, saccade, blink, and intensification report (R). For example, if s₁, s₂, … s_k are the start times of all the microsaccades for a given subject, then X_M for that subject will be given by X_M(t) = 1 if t = s_i for some 1 ≤ i ≤ k and X_M(t) = 0 otherwise; similarly for saccades, blinks, and intensification reports.

We obtained correlations of microsaccades with reports of intensification for each subject, using ξ_MR(t) = ∑_n=−∞^n=∞ X_M(n + t)X_R(n) and then converting it to a rate (similarly for transitions to fading). For each subject, correlations were smoothed using a Savitzky–Golay filter of order 1 and a window size of 151 ms. Average correlations are the average of the smoothed correlations (Figs. 3, 4D).

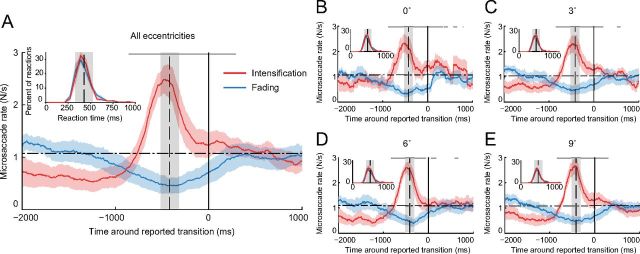
Figure 3.

Microsaccade rates relative to reported and perceptual transitions. A–E, Average microsaccade rates around reported transitions toward intensification versus fading in the Illusory fading condition. The solid vertical line indicates the reported transitions (t = 0). The horizontal dashed line indicates the average microsaccade rate. Target eccentricity is indicated at the top of each panel. The vertical dashed line and gray shading indicate the estimated time of the perceptual transitions (mean latency and 1 SD from the mean, extrapolated from the subject's detections of physical transitions in each inset). Insets, Reaction time distributions from correctly identified physical transitions (Real fading condition), for each eccentricity. In A, microsaccade rates depart from baseline ∼248 ms before the perceptual transitions (beginning of the vertical gray shading) and ∼764 ms before the reported transitions. Similar timing applies to each separate eccentricity in B–E. The gray dots and dashes (above the main red and blue traces) indicate the bins where microsaccade rates before transitions to intensification were significantly higher than microsaccade rates before transitions to fading (one-tailed paired t tests with Bonferroni correction, bin size = 20 ms, p value <0.01). Red and blue shading and error bars indicate the SEM across subjects (n = 7).

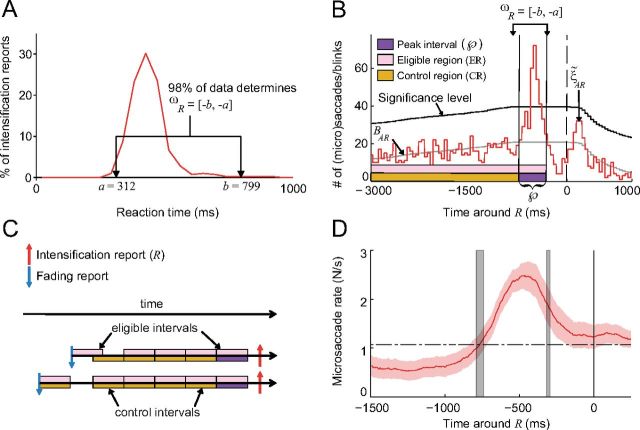
Figure 4.

The peak, control, and eligible intervals. A, One subject's reaction time distribution to physical intensifications during the Real fading condition, and ω_R (first approximation of the peak interval) for that subject. The average ω_R across subjects was [−801, −291] ± [21, 9] ms SEM. B, ξ̃_AR is the correlogram of all eye movements with Rs for the same subject from A, B_AR is the baseline, and the purple interval contained inside of ω_R is the peak interval. C, Examples of the peak, eligible, and control intervals for two Rs. D, Correlation of microsaccades with Rs (as in Fig. 3A) with gray vertical shaded lines indicating the average location of ([−786, −312] ± [24, 17] ms SEM). Red shading indicates the SEM across subjects (n = 7).

Contribution and efficacy

Correlograms and notation.

Again, let X_M, X_S, X_B, and X_R denote the microsaccade, saccade, blink, and intensification report (R) stochastic onset processes, and X_A = X_M + X_S + X_B that of all eye movements. Let N_* be the number of times * occurs. Let ξ_AR(t) = ∑_j=−∞^j=∞ X_A(j + t)X_R(j) be the correlation of X_A with X_R, and ξ̃_AR(n) = ∑_t=wn^t=w(n+1)−1 ξ_AR(t) be the correlogram of X_A with X_R (bin width, w = 50 ms). ξ̃_AR(n) refers to the bin value of ξ̃_AR at bin n, and ξ̃_AR(t) refers to the bin value of bin n, where wn ≤ t ≤ w(n + 1) − 1 (we adopt the same convention for any other function that is binned in time, such as B_AR, defined below).

Contribution and efficacy development.

The concepts of contribution and efficacy have been used to measure the strength of connection between two neurons (Levick et al., 1972; Mastronarde, 1987; Aertsen et al., 1989; Reid and Alonso, 1995; Alonso et al., 1996, 2001; Usrey et al., 1998, 1999). Here we show how to apply them to determine the impact of microsaccades on vision restoration after fading. We defined the contribution of microsaccades, 𝒞_R(M), as the percentage of intensification reports (Rs) caused by microsaccades, and the efficacy of microsaccades, ℰ_R(M), as the percentage of microsaccades which caused an R. That is:

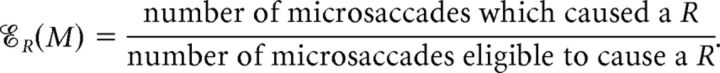To calculate the contribution and efficacy of microsaccades, along with those of other eye movements, we estimated the number of Rs caused by microsaccades, as well as those caused by saccades, blinks, and combinations thereof. Importantly, only eye movements occurring during a specific window of time in the faded region (i.e., the time in which the stimulus was reported as faded/fading) could cause a R. We call this window of time the “peak interval” (Usrey et al., 1999) because it corresponds to the peak of the correlogram between eye movements and Rs, and we denote it by . We estimated in two steps. First, we used the distribution of the subjects' reaction times to target intensifications in the Real fading condition (which we denote by Rrt) to estimate the reaction times in the Illusory fading condition. We required to be contained within the interval ω_R = [−b, −a] (where the interval [a, b] contains 98% of the data from Rrt, discarding the top and bottom 1%; Fig. 4A). We restricted to be contained in ω_R because eye movements in ω_R are the only ones that could have caused an R, as these are the only eye movements that occurred within the reaction times of the subject. Second, we further refined 's limits as follows. Let ξ̃_AR be the correlogram of all eye movement onsets (microsaccades, saccades, and blinks) with Rs. Also, let the baseline, B_AR, be the expected value of ξ̃_AR, assuming that the eye movements and Rs were independent (Mastronarde, 1987) (for an exact definition of the baseline, see Correlogram baseline and peak interval, below; Fig. 4B). We took as the interval of time inside of ω_R where ξ̃_AR was above B_AR (Levick et al., 1972; Mastronarde, 1987; Palm et al., 1988; Aertsen et al., 1989; Alonso et al., 1996; Usrey et al., 1998, 1999; Grün, 2009) and contiguous with the maximum bin closest to the Rs (for an exact definition of , see Correlogram baseline and peak interval, below; Fig. 4B). If no bin of ξ̃_AR within ω_R was significantly above B_AR, we took as nonexistent and the contribution and efficacy as zero for that subject.

To calculate the number of Rs caused by microsaccades, one cannot simply add the number of microsaccades that occurred within , for two reasons: First, because reaction times are broad, some s may have contained multiple microsaccades or combinations of microsaccades and other eye movements (i.e., blinks or saccades; Fig. 5). The simple addition of the number of microsaccades in could thus result in some Rs being counted as caused more than once, leading to an overestimate of microsaccadic contribution and efficacy. Second, some microsaccades that occurred within may not have caused a R; thus, counting them as causal would overestimate their contribution and efficacy.

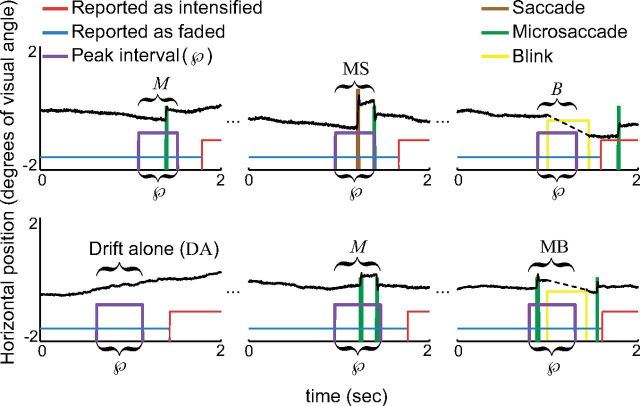
Figure 5.

Ocular events. Each row shows three 2 s epochs during the Illusory fading condition from one subject. The black trace indicates the eye's horizontal position. The blue and red pulses represent the subject's reports. The purple pulse indicates the location of the peak interval, in which ocular events can potentially cause Rs. Several types of ocular events are indicated above their peak intervals.

To account for the possibility that multiple eye movements may have led to a R, we defined the event M as an event that only microsaccades (one or more) occurred over a time interval of duration equal to 's duration (Fig. 5). We defined analogous events for saccades (S); blinks (B); microsaccades and saccades (MS); microsaccades and blinks (MB); saccades and blinks (SB); and microsaccades, saccades, and blinks (MSB) and calculated the contribution, 𝒞_R(E), and efficacy, ℰ_R(E), of each event E = M, S, B, MS, MB, SB, and MSB. That is, for each E, we calculated:

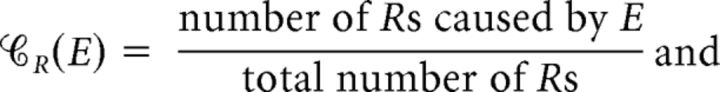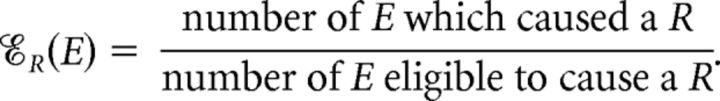The definitions of the ocular events E ensure a one-to-one correspondence between the caused Rs and the causal ocular events within ; thus, the numerators of ℰ_R(E) and 𝒞_R(E) represent the same quantity even though their semantics differ.

To account for the possibility that some Es that occurred within may not have caused an R, we used a control level (Mastronarde, 1987) to estimate the number of noncausal Es in . The control level is the probability that an E did not cause an R, despite being eligible to cause one. We estimated the control level using Es in the faded region before (we call this region the control region and denote it by CR; Fig. 4B). Es in CR did not cause an R because they were outside the reaction time window, but they were nevertheless eligible to cause an R because they occurred in the faded region. The control level was taken as the probability of an E occurring within the CR, P(E|CR), which we calculated by dividing the CR into control intervals of the same duration as (see Control and eligible intervals, below; Fig. 4B,C). If N_R was the total number of Rs, then the expected number of noncausal Es that occurred within was estimated as P(E|CR)N_R. The total number of Es that occurred in is P(E| )N_R; thus, we took the difference between P(E| )N_R and P(E|CR)N_R as our estimate of the causal number of Es, i.e., the numerator of both 𝒞_R(E) and ℰ_R(E). Therefore, the contribution and efficacy of an ocular event E are:

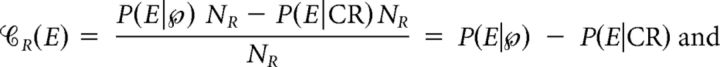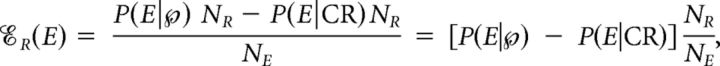where N_E is the number of Es that were eligible to cause a R. Eligible Es are those that occurred in the faded region before the termination of (we call this the eligible region and denote it by ER); Es that occurred after cannot be counted as eligible because the subject's reaction time was not fast enough for these Es to cause that specific R. We took N_E = P(E|ER)T_ER/d; where d is the duration of , P(E|ER) was estimated using eligible intervals in the same manner as P(E|CR) (see Control and eligible intervals, below; Fig. 4B,C), and T_ER is the amount of time spent in ER by the subject.

Correlogram baseline and peak interval.

We estimated the baseline, B_AR, using the data from the faded region before ω_R. We chose this region because microsaccades and other eye movements in this region are completely independent of the Rs as they occurred outside of the reaction time window in both directions. If I ϵ {0,1}^∞ indexes when X_A is in the faded region before ω_R, then we took the baseline rate to be

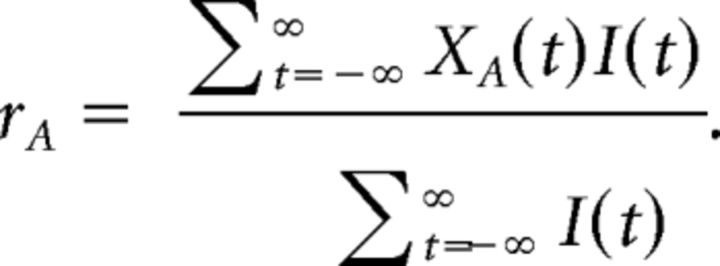r_A is the rate at which eye movements occurred during the faded region before ω_R. If s_n was the amount of time in bin n, the baseline value for bin n is B_AR(n) = s_nr_A. Let H = $\underset{n\in {\omega }_R}{\max }$ ξ̃_AR(n) (where n ϵ ω_R if bin n contains some time in ω_R) be the maximum of ξ̃_AR within ω_R. If H was significantly above B_AR (Levick et al., 1972; Mastronarde, 1987; Palm et al., 1988; Aertsen et al., 1989; Alonso et al., 1996; Usrey et al., 1998, 1999; Grün, 2009) (for significance definition, see Significance level, below; Fig. 4B), we let n₀ = max{n: n ϵ ω_R and ξ̃_AR(n) = H}. We defined the peak interval as all time, t ϵ ω_R, contiguous with n₀, such that ξ̃_AR(t) was above B_AR(t) and we denote it by . If no bin achieved significance, did not exist, and the contribution and efficacy were taken as 0.

Significance level.

We define here what it means for ξ̃_AR(n) to be significantly different from B_AR(n). Let D be the deviations of ξ̃_AR(n) from B_AR(n) in the faded region before ω_R where at least 10 Rs had data going back the same duration of time before the last fading occurred (this prevents the use of outliers and makes the definition of significance more stable). Let μ_D and σ_D be the mean and standard deviation of D, respectively. We declared ξ̃_AR(n) as significantly different from B_AR(n) if ξ̃_AR(n) − B_AR(n) was at least 5 SD (σ_D) above the mean (μ_D) (Fig. 4B) (Levick et al., 1972; Mastronarde, 1987; Palm et al., 1988; Aertsen et al., 1989; Alonso et al., 1996; Usrey et al., 1998, 1999; Grün, 2009).

Control and eligible intervals.

To calculate P(E|CR), where CR is the control region, we divided CR into control intervals of the same duration as (Fig. 4B,C). For each R, we divided the interval of data that began at the prior fading onset and ended at the start of into as many disjoint adjacent segments with the same duration as as possible. The control interval that was closest in time relative to a given R was always adjacent to . To avoid any bias, if there was more than one control interval for a given R, the control interval furthest in time from the R was randomly chosen as being adjacent to the prior fading onset or adjacent to the prior control interval (Fig. 4B,C). The same principle was used to calculate P(E|ER), only in this case, the interval that was closest in time relative to a given R was always (Fig. 4B,C).

Partitioning the microsaccadic event M.

We partitioned the event M in several different ways to investigate its contribution and efficacy as a function of microsaccade magnitude, number of microsaccades, and microsaccade direction. For example, in the case of microsaccade magnitude we defined M_i as the microsaccadic event with magnitude in the interval [0.25(i − 1), 0.25i] degrees, for i = 1, …, 4. Notice then, M_i ∩ M_j = φ for i ≠ j, and M = ∪_i=1⁴M_i, hence the M_i partition M. Similarly, {M¹,M^≥2}, {M_Oi}_i=1⁹, and {M_Ci}_i=1⁹ form partitions of M. To calculate the contribution and efficacy of any event E of a given partition, we used the same from the main analysis and applied the contribution and efficacy formulas to E. Next, we discuss how the contribution and efficacy of M relate to the contributions and efficacies of events which partition M.

The relations between the contribution and efficacy of M and the contributions and efficacies of the M_i.

Here we show how the contribution and efficacy of M are related to the contributions and efficacies of the M_i to understand why it is useful to partition M. Let N_Mi be the number of eligible M_i, N_M the number of eligible M, and w_i = N_MiN_M. Because the M_i partition M, it is easy to show that 𝒞_R(M) ≤ ∑_i=1⁴ 𝒞_R(M_i) and ℰ_R(M) ≥ ∑_i=1⁴ ℰ_R(M_i)w_i, and in both cases, equality occurs if and only if either P(M_i| ) > P(M_i|CR) for all i or P(M_i| ) ≤ P(M_i|CR) for all i. To show this for the efficacy, simply note that:

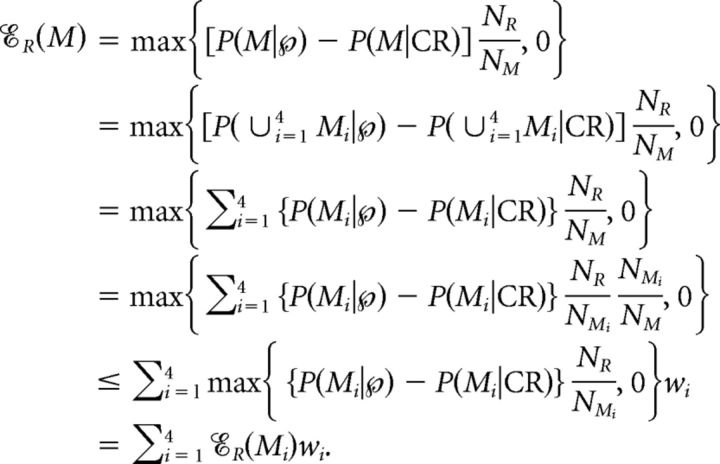Proof of the equality condition is easy and proof of the contribution bound is similar, so we omit them. Thus, 𝒞_R(M) is bounded above by the sum of all the 𝒞_R(M_i) and ℰ_R(M) is bounded above by a weighted average of the ℰ_R(M_i). We can see from these inequalities how the contributions and efficacies of the M_i affect 𝒞_R(M) and ℰ_R(M). For instance, suppose that P(M₁| ) < P(M₁|CR), P(M_i| ) > P(M_i|CR) for all i ≠ 1, and P(M| ) > P(M|CR). Then 𝒞_R(M₁) = 0 and ℰ_R(M₁) = 0, but this information is lost in 𝒞_R(M) and ℰ_R(M). Moreover, because P(M₁| ) < P(M₁|CR), the contributions and efficacies of the other M_i (i ≠ 1) are lessened and we get 𝒞_R(M) < ∑_i=1⁴ 𝒞_R(M_i) and ℰ_R(M) < ∑_i=1⁴ ℰ_R(M_i)w_i. In fact, if P(M₁| ) − P(M₁|CR) is extremely negative, then we may be left with a very small 𝒞_R(M) and ℰ_R(M), when in fact both may be large. As a concrete example, if P(M₁| ) − P(M₁|CR) = −50% and P(M_i| ) − P(M_i|CR) = −20% for i ≠ 1, then we would find 𝒞_R(M) = ∑_i=1⁴P(M_i|)−P(M_i|CR) = 10%, whereas microsaccades really contributed 60%. In our data, the occurrence of P(M_i|) < P(M_i|CR) happened five times in total for all subjects: P(M₁|) < P(M₁|CR) for four subjects and P(M₂| ) < P(M₂|CR) for one subject, so this happened for only small microsaccadic events. The effect of this is shown in Figure 7C where we find ∑_i=1⁴ 𝒞_R(M_i) = 49%, whereas 𝒞_R(M) = 45% (Fig. 6B). While this is not a very big difference, one should be careful to be sure that some elementary event like M₁ is not dragging the contribution and efficacy down of M and leading to false conclusions as in the example given above. Finally, notice that if M_i is a partition such that P(M_i|) ≈ P(M_j|) and P(M_i|CR) ≈ P(M_j|CR) for all i ≠ j, then the partition leads only to the information that there is no difference between the contributions and efficacies of the M_i.

Figure 7.

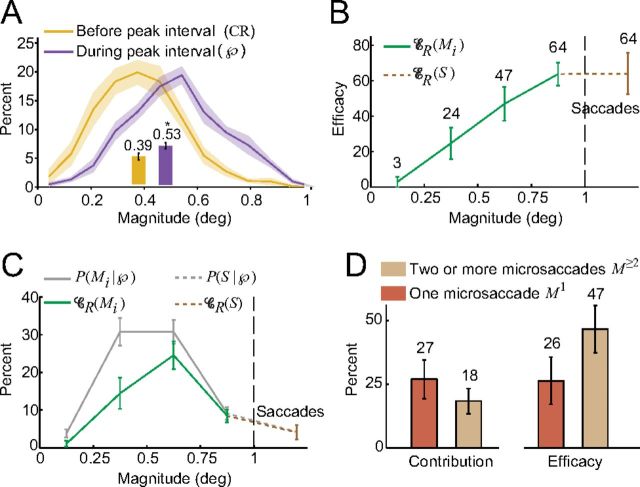
Microsaccade magnitude and single versus multiple microsaccades. A, Distributions of magnitudes of microsaccadic events in and in the CR (inset bars are the averages of the subjects' mean microsaccadic event magnitude). Microsaccadic events during are significantly larger than those before (*one-tailed paired t test, p = 0.0002). B, Efficacy of microsaccadic events of different magnitudes and saccadic events. B, C, M_i denotes the microsaccadic event M whose magnitude falls in the interval [0.25(i − 1), 0.25i] degrees, for i = 1, …, 4. C, Contribution of microsaccadic events of different magnitudes and saccadic events, and their probability of occurring within . D, Contribution and efficacy of microsaccadic events M with one microsaccade (M¹) versus two or more microsaccades (M^≥2). Shading and error bars indicate the SEM across subjects (n = 7 in A and C and contribution plot in D; see Table 1 for the number of subjects in B and efficacy plot in D).

Figure 6.

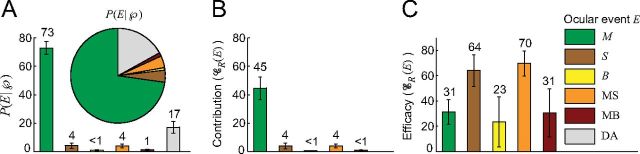
Contribution and efficacy for different ocular events. A, The bars and pie chart show P(E|), the probability of an event E occurring within the peak interval, for each event E. Because P(DA|) = 17%, the upper bound on the contribution of DA is 17%. B, The contribution, 𝒞_R(E), of each ocular event E. C, The efficacy, ℰ_R(E), of each ocular event E. Error bars indicate the SEM across subjects (n = 7 for A and B), see Table 1 for the number of subjects in each type of event in C).

Contribution and efficacy notes.

For the contribution and efficacy analyses, we discarded Rs when the duration of the prior faded period was too short to contain the entire ω_R period (13 ± 4% Rs discarded). In the Illusory fading condition, the average number of Rs (N_R) for the contribution and efficacy analyses was 288 ± 53 R. For all Illusory fading trials combined, each subject had a sufficient number of Rs to perform the contribution and efficacy analyses. To carry out the analyses on Illusory fading trials subject to a specific condition (for instance, only trials with the Gabor in the fovea), we required that at least 15 Rs occurred for this condition, otherwise the measurement became noisy due to insufficient data; in that case, we took both the contribution and efficacy as nonexistent (as opposed to 0). We also included a restriction on the number of ocular events (i.e., M, S, B, etc.). That is, to measure the efficacy of a particular ocular event E, we required that E occurred at least six times in the eligible region; otherwise, we took the efficacy of E as nonexistent. See Table 1 for the amount of eligible events across subjects. Finally, because we did not consider the significance of any ocular event E alone, we were not guaranteed that P(E|) > P(E|CR) for each type of event E and so in all cases (E = M, S, B, MS, MB, SB, MSB, M₁, M₂, etc.), we took 𝒞_R(E) = max{P(E|) − P(E|CR), 0} and ℰ_R(E) = max{P(E|) − P(E|CR), 0}N_R/N_E for each E because a negative contribution/efficacy has no meaning.

Table 1.

Number of eligible microsaccadic events of a given type

Ocular event (E)	Number of subjects with ≥6 eligible events	Average number (±SEM) of eligible events
M	7	667 ± 199
S	5	17 ± 5
B	4	25 ± 8
MS	4	33 ± 9
MB	4	17 ± 2
M1 (magnitude in [0, 0.25] degrees)	6	122 ± 47
M2 (magnitude in [0.25, 0.5] degrees)	7	350 ± 112
M3 (magnitude in [0.5, 0.75] degrees)	7	191 ± 57
M4 (magnitude in [0.75, 1] degrees)	7	42 ± 12
M1 (one microsaccade)	7	530 ± 179
M≥2 (two or more microsaccades)	6	157 ± 31
DA (drift alone)	7	969 ± 248
MC1 (θC in [0 10] degrees)	6	27 ± 6
MC2 (θC in [10 20] degrees)	6	34 ± 10
MC3 (θC in [20 30] degrees)	6	34 ± 12
MC4 (θC in [30 40] degrees)	6	36 ± 9
MC5 (θC in [40 50] degrees)	6	39 ± 12
MC6 (θC in [50 60] degrees)	6	35 ± 12
MC7 (θC in [60 70] degrees)	6	32 ± 12
MC8 (θC in [70 80] degrees)	6	38 ± 10
MC9 (θC in [80 90] degrees)	6	47 ± 14
MC10 (θC in [90 100] degrees)	6	43 ± 11
MC11 (θC in [100 110] degrees)	6	42 ± 12
MC12 (θC in [110 120] degrees)	6	39 ± 12
MC13 (θC in [120 130] degrees)	7	44 ± 15
MC14 (θC in [130 140] degrees)	6	46 ± 13
MC15 (θC in [140 150] degrees)	7	40 ± 12
MC16 (θC in [150 160] degrees)	7	41 ± 17
MC17 (θC in [160 170] degrees)	6	42 ± 16
MC18 (θC in [170 180] degrees)	6	33 ± 7
MO1 (θO in [0 10] degrees)	6	32 ± 8
MO2 (θO in [10 20] degrees)	7	66 ± 19
MO3 (θO in [20 30] degrees)	7	88 ± 24
MO4 (θO in [30 40] degrees)	7	104 ± 33
MO5 (θO in [40 50] degrees)	7	133 ± 45
MO6 (θO in [50 60] degrees)	7	98 ± 33
MO7 (θO in [60 70] degrees)	6	77 ± 24
MO8 (θO in [70 80] degrees)	7	70 ± 14
MO9 (θO in [80 90] degrees)	6	24 ± 6

The efficacy calculations in Figs. 6D; 7B,D; and 8B,C required that each subject had a minimum of six occurrences per ocular event type.

Contribution and efficacy sensitivity analysis

We made two classes of choices during the development of the contribution and efficacy analyses. The first class consisted of the fundamental definitions of quantities such as the baseline, peak interval, and control level. Inside of these definitions was a second class of choices: the numerical parameters chosen. We investigated the sensitivity of the algorithm to perturbations of these numerical parameters.

Parameters.

The numerical parameters chosen were as follows: (1) the bin width, call it β, chosen for the correlogram ξ̃_AR; (2) the number, call it η, of standard deviations (σ_D) above μ_D that ξ̃_AR(n) − B_AR(n) must achieve to deem that ξ̃_AR(n) was significantly above baseline; and (3) the percentage of reaction times, call it δ, to discard from each end of Rrt in determining the peak interval search range ω_R.

For the parameter δ, we only changed how much data to discard from the tail of Rrt and always discarded the top 1% throughout the sensitivity analysis. In what follows, we show the output of the algorithm for a range of each of these three parameters. This analysis determines the domain of parameters that give equivalent results, thus revealing the stability of the algorithm; it also provides insight into the role of each parameter. Here we first show how the parameters affect the baseline B_AR and significance level and then move to a discussion of the whole contribution and efficacy picture. The parameters always varied over the following values: β ranged from 10 to 300 ms in 10 ms steps, η ranged from 0 to 15 in 0.5 steps, and δ ranged from 0% to 10% in 0.5% steps, thus giving a total of 30*31*21 = 19,530 parameter combinations. We chose the maximum of each parameter range as larger than we deemed reasonable.

Baseline sensitivity.

To calculate the baseline B_AR, we used all the data in the faded region before ω_R to find the rate of events r_A and took the baseline value for bin n as B_AR (n) = s_nr_A, where s_n is the amount of time in bin n. Thus, B_AR depends only upon the location of ω_R and thus only upon δ. As δ increased, B_AR increased only moderately (data not shown). This increase occurs because as δ rises, a growing number of peak bins are excluded from ω_R. Thus, more peak bins are used to calculate B_AR. This led us to suspect that increasing δ greatly affects whether a bin achieved significance or not and we discuss this issue next.

Significance level sensitivity.

Recall that the deviations from baseline D, used in determining the significance level, were those deviations that occurred before the ω_R period, and that μ_D and σ_D are the mean and standard deviations of D. Increasing δ had the effect of greatly increasing σ_D (μ_D was relatively stable; data not shown). This occurs for two reasons. First, B_AR increases as discussed above and so ξ̃_AR is more likely to be further away from B_AR before the ω_R period. The second and main reason is that more and more of the deviations of ξ̃_AR from B_AR at peak bins are included in D, thus greatly increasing σ_D. Because the baseline B_AR and the standard deviations σ_D both increase as δ increases, it becomes progressively difficult, if not impossible, for a bin to achieve significance. Thus, we predicted that as δ increases, the number of significant peaks would decrease. This means that the average 𝒞_R(M) and ℰ_R(M) should also decrease, because if there is no significant bin for a given subject, then 𝒞_R(M) and ℰ_R(M) would be taken as zero for that subject. Once we had an idea of how δ would affect the overall algorithm, we fixed δ at 1%, varied β and η, and observed the effects.

Varying β and η with fixed δ = 1%.

Before proceeding, we must point out that the most important quantities which could change across parameter sets are: the contribution and efficacy values, in particular, 𝒞_R(M) and ℰ_R(M), the location and duration of both the peak interval and the peak interval search range ω_R (these change in an obvious way and so we do not discuss them), and the number of subjects which have a significant peak.

Because these are the most crucial quantities that can change, we focused on them. For 𝒞_R(M) and ℰ_R(M), we computed 𝒞_R(M) and ℰ_R(M) for each subject using data for all the Illusory fading trials and looked at how the averages of 𝒞_R(M) and ℰ_R(M) changed with the parameters.

𝒞_R(M) and ℰ_R(M) were equivalent for all parameters in the range of 10 ≤ β ≤ 240 ms and 0 ≤ η ≤ 9 with δ = 1%, and so the algorithm is stable in this region (data not shown). The behavior of 𝒞_R(M) and ℰ_R(M) is similar to that of the number of significant peaks. This is to be expected, however, because 𝒞_R(M) and ℰ_R(M) depend on whether there is a significant peak or not. As discussed above, if a peak is not significant, then 𝒞_R(M) and ℰ_R(M) are taken as zero. Thus, if a significant peak is lost among one of the subjects for a given parameter set, the average 𝒞_R(M) and ℰ_R(M) will decrease for that parameter set because a zero value will be added to the average. This point is illustrated next by varying all three parameters.

Varying β, η, and δ.

Here we varied all three parameters simultaneously. First, we looked at how the number of significant peaks changes with the parameters because 𝒞_R(M) depends on whether there is a significant peak or not. We found that as δ increases beyond 2%, the two dimensional region of stability for the number of significant peaks erodes away (data not shown). 𝒞_R(M) exhibits the same behavior, i.e., as the number of significant peaks goes, so does 𝒞_R(M) (data not shown). From this analysis, we concluded that the algorithm is most sensitive to δ and is generally insensitive to β and η. Intuitively, it makes sense that the algorithm is most sensitive to δ. If we shrink ω_R so much that it contains the peak of the intensification report reaction time distribution Rrt, then the algorithm becomes unstable at this point because it excludes the microsaccades that elicit a response within the reaction times of the subject. The sensitivity of the algorithm to the parameter δ provides validation that we are measuring the correct number of microsaccadic events that produce a perceptual response. In conclusion, the algorithm is most sensitive to the parameter δ and is stable over the parameter range: 10 ≤ β ≤ 240 ms, 0 ≤ η ≤ 9 SDs, and 0 ≤ δ ≤ 2%.

Results

Illusory fading condition

Subjects fixated a small red spot on the center of a computer screen and continuously reported, via button press, whether an unchanging visual stimulus (a two-lobe Gabor patch with 40% contrast), which was presented either foveally or peripherally, was faded (or in the process of fading) versus intensified (or intensifying) (Fig. 1A) (Martinez-Conde et al., 2006). The total amount of time the targets remained faded versus visible was comparable across all eccentricities (one-tailed paired t test, all p values >0.12; Fig. 1C), even though the rate of fading onsets was lower for foveal targets than that for peripheral targets (Fig. 1D). We recorded the subjects' eye movements simultaneously, and correlated microsaccades to the perceptual reports. In agreement with previous studies conducted with peripheral targets (Martinez-Conde et al., 2006; Troncoso et al., 2008a), we found that microsaccade rates increased before transitions to intensification and decreased before transitions to fading (Fig. 3). No previous study had analyzed the impact of microsaccade production on foveal visibility. Here we found that microsaccades restore the visibility of faded foveal targets (Fig. 3B) in comparable fashion to that of peripheral targets (Fig. 3C–E). These analyses indicate that microsaccades are relevant to human perception across the entire retina. The following sections consider all target eccentricities together.

Real fading condition

We pseudorandomly interleaved a condition in which the subjects indicated physical, rather than illusory, changes in target visibility. Visual targets faded and intensified physically, replaying the timing of transitions previously reported by the subject in randomly chosen Illusory fading trials. Subjects performed this task well (Fig. 1E), and their reaction times helped interpret the correlations of microsaccades with reported transitions in the Illusory fading condition (Fig. 3). Further, the subjects' reaction times in the Real fading condition provided tight estimates of reaction times in the Illusory fading condition, necessary for the contribution and efficacy calculations.

The rate of microsaccades decreased after physical changes in visibility, regardless of the sign of the change (data not shown). This observation is in agreement with previous studies showing that sudden physical changes cause a transient drop in the rates of saccades and microsaccades, followed by a temporary enhancement (Engbert and Kliegl, 2003; Troncoso et al., 2008b). This transient course of microsaccadic inhibition may indicate a fast reflex of the oculomotor system to sudden changes in visual input (Laubrock et al., 2005).

Contribution and efficacy calculations

The results show that microsaccades are the most important contributor to vision restoration after fading. Microsaccadic events occurred in 73% of s (Fig. 6A), and in only 28% of the control intervals. The difference between these two quantities (45%) provides a lower bound on the contribution of microsaccades, 𝒞_R(M), to perceptual intensification (Fig. 6B). That is, microsaccades caused a minimum of 45% and a maximum of 73% of all perceptual intensifications after fading. No other measured contributor caused >4% of perceptual intensifications.

The efficacy of microsaccades, ℰ_R(M), was 31%; that is, 31% of the microsaccadic events that occurred during a period of fading restored visibility (Fig. 6C). The efficacy of saccades, ℰ_R(S), (64%) was higher than that of microsaccades, in accordance with their larger size (Fig. 6B). The efficacy of microsaccades and saccades combined, ℰ_R(MS), was 70%. The high efficacy of saccades is not at odds with their low contribution to vision restoration (Fig. 6C): subjects performed the experiments under fixation conditions; thus, large saccades were rare, but effective when they did happen. Microsaccade contribution and efficacy did not vary significantly with eccentricity (data not shown).

Drift is ever-present (Cornsweet, 1956); thus, drift occurred in essentially every peak interval and every control interval. Due to the continuous nature of drift, one cannot determine its contribution and efficacy in the same manner as with transient eye movements such as microsaccades, saccades, and blinks. We defined drift alone (DA) as the event that only drift occurred over an interval of time with duration equal to 's duration. The probability of DA in was 17%, placing an upper bound on the contribution of DA to visual restoration (this upper bound did not vary significantly with eccentricity; data not shown). In other words, DA caused a maximum of 17% of all perceptual intensifications after fading (Fig. 6A). Because some of the Rs may indicate reporting errors rather than genuine perceptual intensifications, the actual contribution of DA is likely to be even smaller than 17%.

It is important to remember that only the ocular events that occurred within —but not the ocular events that occurred within the control region—restored visibility. Our results show that 73% of s contained microsaccades, whereas only 17% of s contained DA. In contrast, 70% of the control intervals contained DA, whereas only 28% of control intervals contained microsaccades. Thus, DA does not usually cause the reversal of fading.

Specific types of drift (i.e., drift with certain properties that are different in ) may be efficacious despite having a low contribution to vision restoration. Whereas our results provide an upper bound of 17% on the contribution of DA as a whole, future research outside of the scope of this project should determine the specific drift properties (if any) that cause perceptual intensification.

Microsaccade magnitude

Our results suggest that some microsaccades fail to restore vision. One reason could be that smaller microsaccades are less effective than larger ones. To test this hypothesis, we defined the magnitude of a microsaccadic event M to be the magnitude of the largest microsaccade that was part of M. We found that microsaccadic events within were 36% larger on average than those before (Fig. 7A). Further, microsaccadic efficacy grew linearly with microsaccade magnitude, at a rate of a 20% increase in efficacy for every 0.25° increase in magnitude (Fig. 7B). Microsaccades and saccades exhibit common dynamic properties (Ditchburn and Ginsborg, 1953; Zuber et al., 1965; Engbert and Kliegl, 2003; Rolfs et al., 2006, 2008a,b; Otero-Millan et al., 2008), and converging research findings support the idea of a common oculomotor origin for microsaccades and saccades (Otero-Millan et al., 2008, 2011a,b; Rolfs et al., 2008a; Hafed et al., 2009; Martinez-Conde et al., 2009). Our results show that microsaccades and saccades generate a continuum of vision restoration as a function of their size (Fig. 7B). As microsaccades grew in size, their contribution initially increased and then decreased (Fig. 7C) because larger microsaccades were relatively rare. See Materials and Methods, above, for additional details.

Number of microsaccades

We asked whether multiple microsaccades occurring in the same peak interval are even more effective than single microsaccades. We compared the efficacy and contribution of microsaccadic events with exactly one microsaccade to those of microsaccadic events with two or more microsaccades (three or four microsaccades occurred very rarely in any given peak or control interval). Microsaccadic events with two or more microsaccades were 1.8 times more efficacious than events with one microsaccade (Fig. 7D). However, they contributed 9% less than single microsaccade events because they were less frequent. See Materials and Methods, above, for additional details.

Microsaccade direction

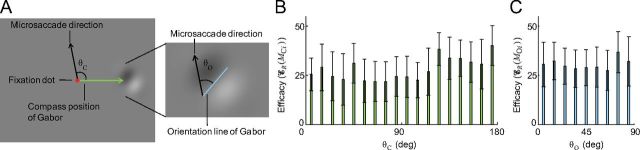
To test the hypothesis that only microsaccades with a narrow range of directions may improve visibility (Collewijn and Kowler, 2008), we defined the direction of a microsaccadic event M as the direction of the largest microsaccade which was part of M. We considered two aspects of microsaccade direction with respect to the fading target. First, the angle, θ_C, between the compass position of the Gabor patch and the direction of the microsaccade (Fig. 8A), with θ_C varying between 0° (toward the Gabor) and 180° (away from the Gabor). Second, the angle, θ_O, between the orientation of the Gabor and the direction of the microsaccade (Fig. 8A) with θ_O varying between 0° (parallel) and 90° (orthogonal). We found that microsaccadic efficacy did not vary as a function of θ_C or θ_O (Fig. 8B,C). Thus, microsaccades of all directions restore visibility equally effectively during fixation.

Figure 8.

Efficacy of microsaccades as a function of their direction. A, θ_C is the angle between the microsaccade direction and the compass position of the Gabor. θ_O is the angle between the microsaccade direction and the orientation of the Gabor. B, Efficacy of microsaccades did not vary as a function of their direction relative to the compass position of the Gabor (two-tailed paired t tests with Bonferroni correction and a family significance level α = 0.05). M_Ci denotes the microsaccadic event M whose θ_C falls in the interval [10(i − 1), 10i] degrees, for i = 1, …, 18. C, Efficacy of microsaccades did not vary as a function of their direction relative to the orientation of the Gabor (two-tailed paired t tests with Bonferroni correction and a family significance level α = 0.05). M_Oi denotes the microsaccadic event M whose θ_O falls in the interval [10(i − 1), 10i] degrees, for i = 1, …, 9. Error bars indicate the SEM across subjects (see Table 1 for the number of subjects in each type of event in B and C).

Discussion

The impact of microsaccades on vision and perception has remained controversial for over 50 years (Collewijn and Kowler, 2008; Martinez-Conde et al., 2009; Rolfs, 2009). The main current argument against the relevance of microsaccades to visual processing is that, in the absence of microsaccades, other sources of eye position variation suffice to achieve the same perceptual outcomes (Rolfs, 2009). Indeed, recent reviews have concluded that microsaccades do not have “special significance for visibility that cannot be matched or exceeded by slow or smooth eye movements” (i.e., drift) (Kowler, 2011) and that microsaccades perform no “visual task (…) [which can] not be done as well, or better, by (…) smooth eye movements or slow control” (Collewijn and Kowler, 2008). The idea is that, unless microsaccades serve a specialized role in vision that other eye movements do not address, their significance is vastly diminished. The logic of this line of reasoning is questionable. First, eye movement functions need not be a zero sum game, i.e., there is no reason to conclude that the impact of one eye movement type on vision must detract from the impact of other eye movements. In fact, our present results suggest that multiple eye movements can be more effective than single eye movements. Second, and most importantly, no study to date has quantified the effect of microsaccades on visibility versus that of other eye movements; thus, it has not been possible until now to conclude that microsaccades restore vision better or worse than other eye movements. Here we determined the direct microsaccadic impact on vision restoration, for the first time, and found the contribution of microsaccades to be much larger than that of drift alone (Fig. 6). Indeed, microsaccades were the most important eye movement contributor to restoring the visibility of faded targets during fixation.

Further, larger and multiple microsaccades were more efficacious than smaller or single microsaccades (Fig. 7). The higher efficacy of multiple microsaccades may be due to temporal summation. For example, microsaccade pairs might lead to a form of paired pulse facilitation similar to that shown for pairs of spikes in retino-geniculate synapses (Usrey et al., 1998). Larger microsaccades may be more efficacious than smaller ones due to their increased ability to bring the neuronal receptive fields to uncorrelated stimulus regions.

The claim that microsaccades cannot restore foveal vision (Collewijn and Kowler, 2008; Rolfs, 2009; Kowler and Collewijn, 2010; Poletti and Rucci, 2010; Kowler, 2011), if true, would argue against the overall significance of microsaccades to visual perception. Contrary to the assertion that foveal images do not fade “with or without microsaccades” (Kowler, 2011), we show here that fading does indeed occur in the fovea and that the total amount of fading time is equivalent across all eccentricities (Fig. 1C). Numerous authors have reported the fading of foveal targets previously (Darwin, 1795; Troxler, 1804; Krauskopf, 1963; Pessoa and De Weerd, 2003; Simons et al., 2006), including Troxler himself: “Troxler's effect has become associated almost exclusively with the disappearances of peripheral targets, but it is noteworthy that Troxler himself reported that the central fixation target disappeared after prolonged observation” (Wade and Tatler, 2005). No study to date has determined the impact of microsaccades on counteracting foveal fading, however. Thus, the significance of microsaccades for foveal vision has remained a point of contention in the literature. Here we show that microsaccades restore foveal and peripheral vision in analogous fashion (Fig. 3).

Fixational eye movements (including drift and microsaccades) may act in concert to prevent fading during fixation. Yet, visual stimuli still fade away in everyday vision (Darwin, 1795; Troxler, 1804; Coppola and Purves, 1996). When fading does occur, microsaccades restore visibility (i.e., counteract fading) most successfully. Because the ability of microsaccades to restore faded vision during fixation is not matched by that of other fixational eye movements, microsaccades may be considered special or unique in this regard, contrary to previous assertions (Collewijn and Kowler, 2008; Kowler, 2011). Future research should investigate the relative contributions of the various fixational eye movement types to the prevention of foveal and peripheral fading during fixation.

Why should the ability of microsaccades to restore faded vision exceed that of drift? One answer may be that, when a visual neuron has adapted to a particular stimulus (call it the adaptive stimulus), its responses to similar, subsequent stimuli will be weaker than in a nonadapted state (Sanchez-Vives et al., 2000). Drift movements move visual receptive fields slowly over a small region of space. Because nearby points of natural scenes are highly correlated with each other (Simoncelli and Olshausen, 2001), it follows that many visual neurons will continue to respond weakly and/or quickly adapt to new stimuli in their receptive fields due to drift. Conversely, microsaccades move receptive fields away from the adaptive stimulus quickly, and on a generally larger scale. Because of the larger distance covered by microsaccades, the new stimuli entering the receptive fields will be less likely correlated to the adaptive stimulus.

One might have expected microsaccade directions perpendicular to the target orientation to be most efficacious, and microsaccade directions parallel to the target orientation to be least efficacious (Collewijn and Kowler, 2008). Contrary to this idea, and in agreement with previous physiological analyses of microsaccade direction on the firing of V1 neurons (Martinez-Conde et al., 2000), we found microsaccades of all directions to be equally effective (Fig. 8). The explanation may lie in the aperture problem, i.e., the inability of a receptive field to distinguish between motion speed and motion direction (Martinez-Conde et al., 2000). According to the aperture problem, a visual neuron may not differentiate a slower microsaccade moving the target perpendicularly across its receptive field from a faster microsaccade moving the target obliquely to the receptive field.

Microsaccade research has been hampered not only by the extant controversies addressed above, but also by the long-lasting claim that microsaccades serve an accidental, rather than a fundamental, role in vision (Nachmias, 1961; Rolfs, 2009; Poletti and Rucci, 2010). Upon finding that microsaccade production did not increase after image fading, Poletti and Rucci (2010) recently concluded that counteracting fading cannot be a fundamental role of microsaccades. The logic in this reasoning is suspect, however, as it implies that for event A (i.e., microsaccades) to have a fundamental effect on event B (i.e., visibility), A must not only cause B, but the absence of B (i.e., fading) must also cause A. If true, it would follow that a retinal neuron cannot have a fundamental effect on the firing of an LGN neuron, unless the lack of firing of the LGN neuron, in turn, also drives the firing of the retinal neuron. This would result in the conclusion that, despite the many studies showing that retinal firing is precisely correlated to subsequent LGN firing (Levick et al., 1972; Mastronarde, 1987; Usrey et al., 1998, 1999), LGN firing is an accidental, rather than a fundamental, consequence of retinal firing.

The distinction between accidental and fundamental behaviors or physiological properties goes contrary to the fact that all nervous systems have evolved over time through a confluence of random (i.e., accidental) mutations, with no goal in mind. Accidental mutations that are valuable (or at least harmless) live on, whereas detrimental mutations are removed from the gene pool by natural selection. Thus, to call some functional properties fundamental and others accidental is to fall prey to the “illusion of design” (Dawkins, 1986), i.e., to allocate teleological meaning where there is none.

Poletti and Rucci's (2010) findings do not rule out that one function of microsaccades is to counteract fading. Rather, they argue against the existence of a mechanism that triggers microsaccades in response to fading [the question remains open, however: Engbert and Mergenthaler have reported that microsaccades are not randomly distributed in time, but triggered dynamically as a response to low retinal image motion (Engbert and Mergenthaler, 2006; Engbert et al., 2011)]. Whether or not fading triggers microsaccades, however, our results show that microsaccades restore faded vision in the fovea and the periphery; thus, counteracting fading is a function of microsaccades. Many other microsaccade functions have been proposed, including the control of fixation position (Ditchburn and Ginsborg, 1953; Cornsweet, 1956; Engbert and Kliegl, 2004), performance in high acuity visual tasks (Donner and Hemilä, 2007; Ko et al., 2010) and visual scanning of small regions (Haddad and Steinman, 1973), with support for and against each of them (Rolfs, 2009). Likewise, saccadic eye movements play multiple nonexclusive roles in vision, i.e., they correct gaze errors, foveate high interest targets, and search and integrate general information about the environment to stitch together each visual scene. Microsaccades and saccades share not only dynamic properties, but also a common oculomotor origin (Ditchburn and Ginsborg, 1953; Zuber et al., 1965; Engbert and Kliegl, 2003; Rolfs et al., 2006, 2008a; Otero-Millan et al., 2008, 2011a,b; Hafed et al., 2009; Martinez-Conde et al., 2009), lending further support to the idea that microsaccades serve a variety of important, nonexclusive functions during fixation, just as saccades do during visual exploration. Which of these microsaccadic and saccadic functions are fundamental, and which are byproducts, may be unanswerable and ultimately irrelevant to vision research.

Fixational eye movements are critical to natural vision (Martinez-Conde et al., 2004, 2009; Martinez-Conde and Macknik, 2008; Rolfs, 2009), and their importance in many visual and cognitive science studies, conducted under fixation conditions, cannot be overestimated. Therefore, the precise contribution and efficacy of microsaccades to vision is fundamental to the interpretation of previous and future neuroscience results (Martinez-Conde et al., 2009). Further, our method to calculate the efficacy and contribution of microsaccades on perception demonstrates how to quantify the strength of connections between many kinds of physiological and/or perceptual events where a causal relationship is suspected; thus, we anticipate wide-ranging applications in neuroscience.