Period Coding of Bmal1 Oscillators in the Suprachiasmatic Nucleus

Abstract

Circadian oscillators in the suprachiasmatic nucleus (SCN) collectively orchestrate 24 h rhythms in the body while also coding for seasonal rhythms. Although synchronization is required among SCN oscillators to provide robustness for regular timekeeping (Herzog et al., 2004), heterogeneity of period and phase distributions is needed to accommodate seasonal variations in light duration (Pittendrigh and Daan, 1976b). In the mouse SCN, the heterogeneous phase distribution has been recently found in the cycling of clock genes Period 1 and Period 2 (Per1, Per2) and has been shown to reorganize by relative day lengths (Inagaki et al., 2007). However, it is not yet clearly understood what underlies the spatial patterning of Per1 and Per2 expression (Yamaguchi et al., 2003; Foley et al., 2011) and its plasticity. We found that the period of the oscillation in Bmal1 expression, a positive-feedback component of the circadian clock, preserves the behavioral circadian period under culture and drives clustered oscillations in the mouse SCN. Pharmacological and physical isolations of SCN subregions indicate that the period of Bmal1 oscillation is subregion specific and is preserved during culture. Together with computer simulations, we show that either the intercellular coupling does not strongly influence the Bmal1 oscillation or the nature of the coupling is more complex than previously assumed. Furthermore, we have found that the region-specific periods are modulated by the light conditions that an animal is exposed to. Based on these, we suggest that the period forms the basis of seasonal coding in the SCN.

Introduction

Daily rhythms are governed by the suprachiasmatic nucleus (SCN), the primary circadian pacemaker in mammals, where 20,000 oscillators organize a coherent rhythm throughout the body (Klein et al., 1991; Reppert and Weaver, 2002). The SCN keeps track of the relative length of daylight throughout the year while simultaneously maintaining circadian rhythms, a task that is critical for seasonally breeding mammals. The coding mechanism of seasonal timing has been proposed by hypothesizing two oscillators whose periods are adjusted differentially by the duration of light (Pittendrigh and Daan, 1976b). These period-changing oscillators were found in the fruit fly Drosophila (Stoleru et al., 2007), but definitive parallel evidence has not been found in mammals (Helfrich-Förster, 2009). Nonetheless, phase redistribution of SCN oscillators by long and short photoperiods has been demonstrated in rodents in vivo (Schaap et al., 2003; VanderLeest et al., 2007) and in vitro by measuring electrical multiunit activities (Brown and Piggins, 2009) and by monitoring the luciferase reporter activities driven by the mouse Per1 promoter (Per1-luc) in cultured SCN explants (Inagaki et al., 2007; Naito et al., 2008). However, the day length-dependent period plasticity has not been clearly demonstrated. The difficulty of studying this period aspect with Per reporters [Per1 (Yamaguchi et al., 2003); Per2 (Yoo et al., 2004)] owes to their longer-than-behavioral period in vitro (Webb et al., 2009; Ko et al., 2010).

The essential components of the circadian clock circuit are negative- and positive-feedback regulations characterized by Per and Bmal1, respectively, which have recently been suggested to be independent (Relógio et al., 2011). In the mouse SCN, it has been noted that temporal expression patterns of Per1 and Bmal1 are not simply antiphasic under short and long photoperiods (Naito et al., 2008). We therefore chose to study Bmal1 dynamics in the SCN by using the transgenic mice expressing the Bmal1 promoter-driven luciferase reporter (Bmal1-ELuc) (Noguchi et al., 2010). We found that Bmal1 oscillations in the SCN are clustered and the phases of oscillators relate directly to regional heterogeneity of periods. With an experimentally determined period distribution, we could recapture most of the spatiotemporal phase dynamics using a phase oscillator model. Consistent with the idea that the period is region intrinsic, we discovered that the topographical structure of the clusters does not fall apart either during pharmacological blockade of neurotransmission or a surgical cut that divided the dorsal and the ventral regions of the SCN. We further observed the preservation of period and phase heterogeneities under complete physical isolation in SCN explants expressing Bmal1-ELuc but not in those expressing PER2::LUC. The ability of Bmal1 to oscillate almost freely in the culture system enabled us to extrapolate the role of intrinsic periods under various photoperiods present in the living animal. We showed that the Bmal1 oscillation periods in specific regions of the explanted SCN demonstrates aftereffects: modulations of behavioral periods observed in animals transferred from short or long photoperiods to constant darkness (Pittendrigh and Daan, 1976a).

Materials and Methods

Animals.

Bmal1-ELuc transgenic mice, which carry the 5′-flanking region (−816 to +99 bp) of the Bmal1 promoter linked to an ELuc reporter gene, were generated on the C57BL/6J background as described in previous publications (Nakajima et al., 2010; Noguchi et al., 2010), and C57BL/6J PER2::LUC knock-in mice were purchased from The Jackson Laboratory (Yoo et al., 2004). The breeding colony was kept on a 12 h light/dark (LD) cycle with food and water provided ad libitum. Adult animals (postnatal days 30–60) of either sex were used. The protocols for all animal experiments in this study were approved by the Animal Research Committees of the Osaka Bioscience Institute and Hiroshima University.

Entrainment and locomotor activity monitoring.

The times of light on/light off for equinox photoperiod (EP) (12:12 LD), short photoperiod (SP) (8:16 LD), and long photoperiod (LP) (16:8 LD) entrainments were as follows: 8:00 A.M./8:00 P.M., 10:00 A.M./6:00 P.M., and 6:00 A.M./10:00 P.M., respectively. The hour of midnight of each photoperiodic cycle was defined to be external time 0 (ExT 0). We have used ExT to designate an extrapolated time point of the light cycle during culture. The animals were kept individually in light-sealed cages that automatically control light (200 lux light on; 0 lux light off) and maintain a constant level of temperature (23.0 ± 1.5°C; mean ± SD), humidity (27.2 ± 5.1%), and environmental noise provided by a ventilating fan. Following EP entrainment, animals at ages 21–30 d were kept for 30 d during SP and LP entrainments. For free running under constant conditions, animals at ages 21–30 d were kept for 21 d under constant light (LL) and animals at ages 21–40 d were kept for a minimum of 5 d and a maximum of 30 d under constant darkness (DD) following EP. Lengthening of the behavioral period has been observed under 21 d in LL, and it was consistent with the period lengthening of bioluminescence activities in culture. The constant monitoring of temperature and humidity was done with a homemade unit using Arduino components (Seeed Technology). The locomotor activities were detected with a passive infrared sensor (BioTex) and counted for 1 min bins. The recorded activities were analyzed on Mathematica (Wolfram Research) with a custom-written package.

SCN explant culture, bioluminescence imaging, and pharmacology.

For imaging, coronal hypothalamic slices containing the SCN were prepared from different Bmal1-ELuc transgenic mice subjected to EP (n = 23 for control, including ones before pharmacological treatments; n = 19 for pharmacological treatments; n = 3 for surgical isolation), SP (n = 12), LP (n = 8), LL (n = 7), and DD (n = 3) conditions and from different PER2::LUC knock-in mice entrained under the EP condition (n = 8 for control; n = 2 for surgical isolation). The slicing was performed with a Microslicer (DSK) at 250 μm thickness. A trimmed SCN tissue was placed on a culture membrane (Millicell-CM; Millipore) and transferred to a 35 mm dish containing 1 ml of phenol red-free DMEM (Sigma-Aldrich) supplemented with B27 (Invitrogen), penicillin–streptomycin (25 U/ml; 25 μg/ml; Nacalai Tesque), and 100 μm beetle luciferin (Promega). The dish was sealed with vacuum grease to prevent evaporation. Stock aliquots of 0.5 and 1 mm tetrodotoxin (TTX) (Wako Pure Chemicals) and 10 mm gabazine (Sigma-Aldrich) were prepared in sterile distilled water at dilution ratio of 1:1000 and stored frozen until use. One microliter of the stock solution was added directly to the 1 ml culture medium. For mock experiments, only 1 μl of sterile distilled water was used instead. The slice culture was maintained at 35°C and observed continuously in either an integrated incubator-microscope system (LV200; Olympus) or a custom-built upright imaging system for 5–7 d. Time-lapse luminescence images were taken with either an LV200 or an FN1-R2. The LV200 consisted of a cooled CCD camera (Orca C4742-80-12AG; Hamamatsu) through a 40× objective (NA, 0.6; LUCPlan FLN; Olympus) and an incubator. The FN1-R2, our custom-made imaging system, was composed of a cooled CCD camera similar to the LV200 (Orca R2; C10600-10B; Hamamatsu), a combination lens system with a 20× objective (NA, 0.45; L Plan; Nikon) and a relay lens (0.55DS; Nikon) on a Nikon FN1 upright microscope, as well as a custom-made microincubator. Binning was set to 4 × 4 with an exposure time of either 15 min (Bmal1-ELuc) or 30 min (PER2::LUC) for each frame. Images were digitally acquired either with MetaMorph 7.1.1.0 (Molecular Devices) on a Windows system connected to an LV200 or with MicroManager 1.3.43 (University of California, San Francisco, San Francisco, CA) configured to run Hamamatsu DCAM driver on a Mac OS X system connected to FN1-R2. Each frame of the image was digitized through an in camera AD converter and stored in 16 bit grayscale TIFF format.

“Onigiri” section culture and bioluminescence photometry.

The SCN explants from mid to posterior coronal slices were surgically microsectioned in combinatorial shapes consisting of dorsal and ventral subregions and cultured separately. Due to the schematic resemblance of the microsections to an onigiri rice ball, we called the microsections “onigiri” sections (see Fig. 10A). The elementary onigiri sections were isolated dorsal (D), ventromedial (VM), and ventrolateral (VL) subregions of the whole (W) SCN. The ventral (V) onigiri section was cut in a shape that combined both VM and VL; the A-shaped dorso-ventrolateral (A) onigiri section combined D and VL; the T-shaped dorso-ventromedial (T) onigiri section combined D and VM. The onigiri sectioning was performed with a razor blade after the slice had been placed on a culture membrane in a moistened environment under a surgical microscope. The isolated onigiri section was then scooped onto the blade and transferred to another culture membrane on a separate dish. The sectioning and transfer of one section typically took 30–40 s. The D section was made near the bottom tip of the third ventricle so that connection between bilateral sides was preserved. The bilateral VL sections were combined and cultured in the same dish. The dishes were sealed with vacuum grease and given 1–2 h of stabilization before bioluminescence photometry. Twenty-four dishes on a rotating wheel were recorded sequentially through two photomultipliers with 15 min sampling intervals per channel (see Fig. 10B; LM-2400; Hamamatsu). Sections physically damaged during microsectioning were discarded from the recording. For photometry of onigiri sections from animals entrained under EP, we prepared 74 W, 33 D, 16 V, 24 VM, 25 VL, 13 A, and 10 T onigiri sections from Bmal1-ELuc transgenic mice and 44 W, 33 D, 15 V, 34 VM, 32 VL, 14 A, and 13 T onigiri sections from PER2::LUC knock-in mice. For other light conditions, we used Bmal1-ELuc mice and prepared 4 D, 4 VM, and 4 VL onigiri sections from four animals that experienced DD-free-run and prepared 6 D, 6 VM, and 5 VL onigiri sections from six animals that experienced LL-free-run.

Figure 10.

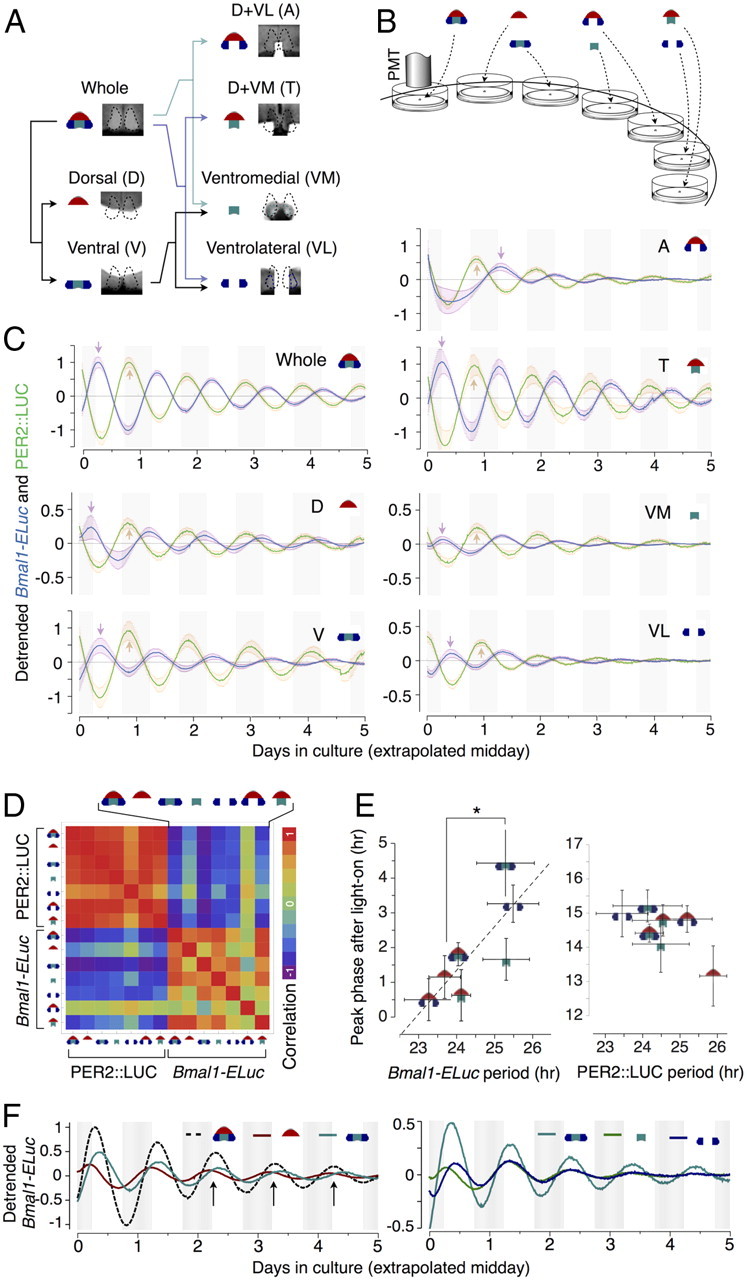
Isolated microsection (onigiri section) cultures demonstrate period heterogeneity as an intrinsic property of SCN subregions. A, The SCN in whole slice is drawn diagrammatically in an onigiri-like rounded triangle, which are subdivided into the D and the V regions. V is further divided into the VM and the VL, which includes portions of the dorsolateral region. In this scheme, we can probe all combinations of SCN subregions by combining D, VM, and VL appropriately. A T-shaped microsection (D+VM) and an A-shaped microsection (D+VL) complete all possible combinations, which we call onigiri sections. B, The onigiri sections were cultured and observed under the photomultiplier tube (PMT) for bioluminescence. C, The detrended ensemble averages of the reporter activities in onigiri sections show the phase relationship between Bmal1-ELuc and PER2::LUC are not always antiphasic and can vary from region to region, where the deviation from the antiphasic relationship is the highest in D. Note that there is an initial disturbance of oscillations in the Bmal1-ELuc rhythm of the A-shaped microsection, which we did not exclude when calculating correlations. D, The matrix of correlation coefficients among all onigiri section rhythms summarizes inter-microsection differences. Compared with the PER2::LUC, which are almost uniformly synchronized except for VL, Bmal1-ELuc shows a complex correlation structure. E, The arrival times of the first peak since culture, indicated as arrows in B, and the intrinsic periods show a strong positive relationship (r = 0.78) in Bmal1-ELuc samples (left), whereas a clear relationship does not exist in PER2::LUC (right). The onigiri sections are segregated into two groups by periods (*p < 0.05, Welch's t test). F, The peak times of the Bmal1-ELuc oscillation in the whole SCN explant corresponds to the crossing points between D and V oscillations (top, arrows), indicating the whole acts roughly like a simple weighted sum of the dorsal and the ventral. When the V is further dissected into VM and VL, an initial separation of phases appears, but this difference is only transient (bottom).

Serial cryosection immunohistochemistry.

Bmal1-ELuc mice were deeply anesthetized with pentobarbital and cardinally perfused with PBS followed by 4% paraformaldehyde (PFA) for 15 min. The brain was taken out and postfixed in 4% PFA for a minimum of 1 h and incubated in 30% sucrose–PBS for 12–32 h for cryoprotection. A temperature of 4°C was maintained throughout the process. It was then freeze-stored in the embedding material (Tissue-Tek OCT compound; Sakura Finetek) after intermediate treatments in a 1:1 mixture of 30% sucrose–PBS and OCT compound. Coronal cryosections of the brain of 30 μm thickness were prepared and transferred at room temperature to osmolarity-controlled (350 mOsm) PBS mixed with 0.2% Triton X-100 (PBST) and permeabilized for 1 h. The endogenous peroxidase activity of the tissue was removed in 0.3% H₂O₂ PBS for 30 min before blocking in PBST with 5% normal goat serum (PBST-NGS) for 1 h on a horizontal shaker. Blocked sections were incubated in selected primary antibody dissolved in PBST-NGS for 36 h at 4°C and washed overnight in PBST. Polyclonal antibodies were used against neuropeptides in the following concentrations: 1:2000 for arginine vasopressin (Millipore Bioscience Research Reagents), 1:1000 for vasoactive intestinal polypeptide (ImmunoStar), and 1:500 for gastrin releasing peptide (ImmunoStar). A second antibody kit (Vectastatin ABC kit Elite; Vector Laboratories) followed by diaminobenzidine stain visualized antibody binding. The slices were subsequently mounted on glass slides after dehydration in graded alcohols and clearing in xylene.

Immunofluorescence staining of cultured slices.

The culture membrane around cultured slices was cut out and washed in PBS. After overnight fixation in 4% PFA at 4°C, the slice was subjected to permeabilization in PBST for 24 h. Primary antibody concentrations and treatments were the same as above. The incubation medium containing second antibodies was filtered (0.22 μm pore size; Millex-GV; Millipore) before incubation to exclude possible aggregates of fluorophore conjugate. The sections were stained with anti-rabbit antibody conjugated either with Alexa Fluor 488 or 568 (1:500; Invitrogen) and mounted in Vectastain (H-1200 with DAPI; Vector Laboratories) after a wash in Tris-HCl.

Automated identification, phase extraction, and normalization of grid oscillations.

Raw images were median filtered to remove noise (Yamaguchi et al., 2003) and were convolved with a homogeneous kernel having a rough pixel dimension of the cell (called a “grid”). The overall dimensions of the images have been reduced such that one pixel is equivalent to a grid element (see Fig. 3A). The kernel had rough size dimensions that completely encompassed a single cell (∼10 μm diameter) (Klein et al., 1991): 5 × 5 pixels (15.4 × 15.4 μm²) for images taken from the LV200 and 7 × 7 pixels (16.7 × 16.7 μm²) for those from the FN1-R2. After convolution, the images were downsized to map each grid to a single pixel. This preprocessing was performed with an automated routine on NIH ImageJ, and subsequent processing was performed on Mathematica through custom-written packages.

Figure 3.

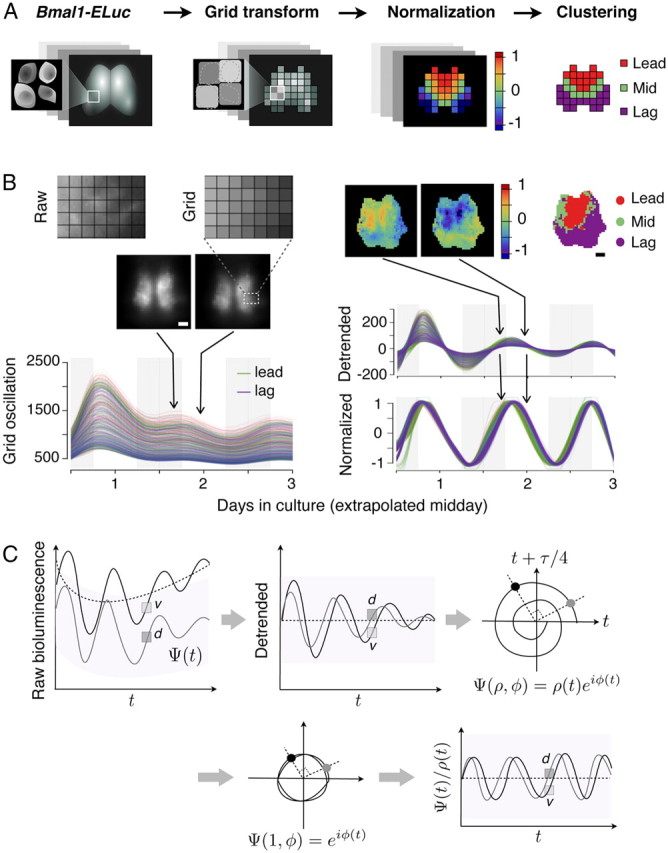
Grid-based image processing reveals spatial dynamics of Bmal1-ELuc. A, Schematic procedures of the image processing: a raw image is transformed into a set of grids. Oscillation of each grid is detrended by baseline subtraction and normalized. Partial correlations against the mean oscillation are compared and clustered by the multistep spectral clustering algorithm (see Materials and Methods). B, An example of a posterior-biased coronal slice culture. The center-of-mass position of the single-cell bioluminescence falls roughly into one grid element. The high baseline makes it difficult to see phase differences among oscillators (middle images, left). Detrending and subsequent normalization resolve relatively phase-leading and -lagging oscillators (top images, middle) that are clustered (top right). Cluster analysis summarizes locally synchronized oscillator activities over the recording duration (top right). C, The persistently high baseline bioluminescence of Bmal1-Eluc is estimated (top left) and removed to produce a detrended time series (top middle). The detrended series is projected to a phase space (top right) by dimensional embedding with time lag of 6 h (24/4 h). The oscillation Ψ is resolved into phase φ and amplitude ρ in the phase space, and the latter is adjusted to unity (bottom left) to produce normalized oscillation in time (bottom right). Scale bar, 100 μm.

Oscillators in the SCN are defined as the time series of the grids, which were obtained by progressive scanning over the image sequence, and active within-SCN grids were selected and indexed by reporter brightness; however, as a precaution, the number of grids were slightly overestimated to cover areas in which bioluminescent neurons are not visibly present. The grid oscillations were then detrended by removing the Hodrick–Prescott (H–P) baseline trend with a large penalty parameter to minimize loss of the oscillatory signal component (see Fig. 3C, top left). Possible generation of artifactual autocorrelation by detrending was found to be absent when randomly shuffled data and pseudorandom sequences were used. The time-dependent phase of each oscillator was extracted by dimensional embedding, which takes one-quarter of the 24 h period as the embedding lag (see Fig. 3C, top right) (Small, 2005). Finally, the sine of the time-dependent phase was calculated to produce normalized oscillations (see Fig. 3C, bottom right). The dimensional embedding was preferred to Hilbert transform mainly due to loss of recording length during convolution. The normalized oscillations were projected back to the original image geometry by reverse progressive scanning to generate imagery illustrating spatial phase dynamics.

Clustering of correlated oscillations.

We used two different clustering methods that are based on different characterizations of Bmal1 oscillations. For the variables that characterize each oscillator such as the period and mean phase, we used the simple hierarchical clustering algorithm by using the Ward's error sum-of-squares (ESS) criterion (Ward, 1963). For correlation that directly compares each pair of oscillations, we used a variant of the spectral clustering algorithm to segment a partial correlation matrix of all normalized oscillations and determine the objective number of clusters without considering the positions of oscillators in space. These two methods generated very similar results, and we also demonstrated that this coincidence was explainable by our hypothesis that the SCN oscillators are weakly coupled.

Ward's ESS is defined as the sum of the within-cluster variances: when the cluster C_k (k = 1, …,K) contains the data points {x_kj}, ESS for K clusters is computed as follows:

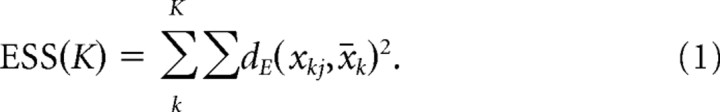where d_E is the Euclidean distance. x_k is the within-cluster mean as follows:

ESS(K) always decreases with the number of clusters, and the change in ESS at each stage is a measure for the information loss due to the merging of two clusters. To determine the most suitable number of clusters, we adopted a widely used method, which is computing the curvature of the ESS curve (Goutte et al., 1999). However, this scheme relies on a single parameter (e.g., period) characterizing the activity of each cell, and we cannot assume that the dynamics is close to pure harmonic oscillation. Therefore, using direct comparison of the activities, such as correlation, would be ideal, but we found that the correlation is often incompatible with distance-based clustering methods such as the Ward's method.

Hence, we applied the idea of the spectral clustering algorithm (von Luxburg, 2006), which is known to be good at finding segmentation of the given data, on correlations between normalized oscillations. Most of our data are composed of groups of oscillations separated by small gaps in phase, and we predicted that spectral clustering would be well suited for our purpose. Since in our data the mean oscillation dominated the correlations among oscillators, we chose partial correlation as the measure of similarity. Partial correlation between two signals x_i and x_j is defined by the following:

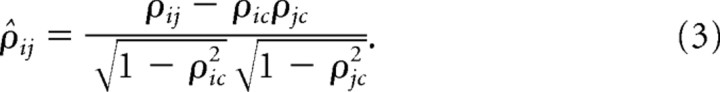ρ_ij is the correlation between x_i and x_j. ρ_ic (ρ_jc) is the correlation between x_i (x_j) and x_c, and x_c is the control signal representing the mean oscillation of the population.

By using the partial correlation matrix, we constructed a weighted undirected network in which nodes represent the cells in our data, and the weights between two nodes are the similarity in their activities given by the following:

and the graph Laplacian is defined as follows:

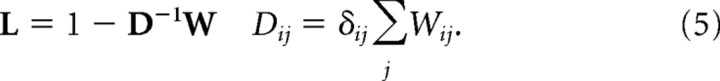The clusters are determined by the eigenvalues {λ_k} and eigenvectors {v_k} of L satisfying the following:

For the details of this procedure, we refer to the existing literature (von Luxburg, 2006). To determine the number of clusters, we used the multiscale criterion suggested by Azran and Ghahramani (2006). However, we used the full Laplacian (Eq. 6), while they only used D⁻¹W for the criterion. We also added one more cluster than the number determined by the criterion since the additional one usually became a “boundary cluster” that separates major clusters (the “mid cluster” in our analysis), and we found it useful for illustration (see Fig. 2B).

Figure 2.

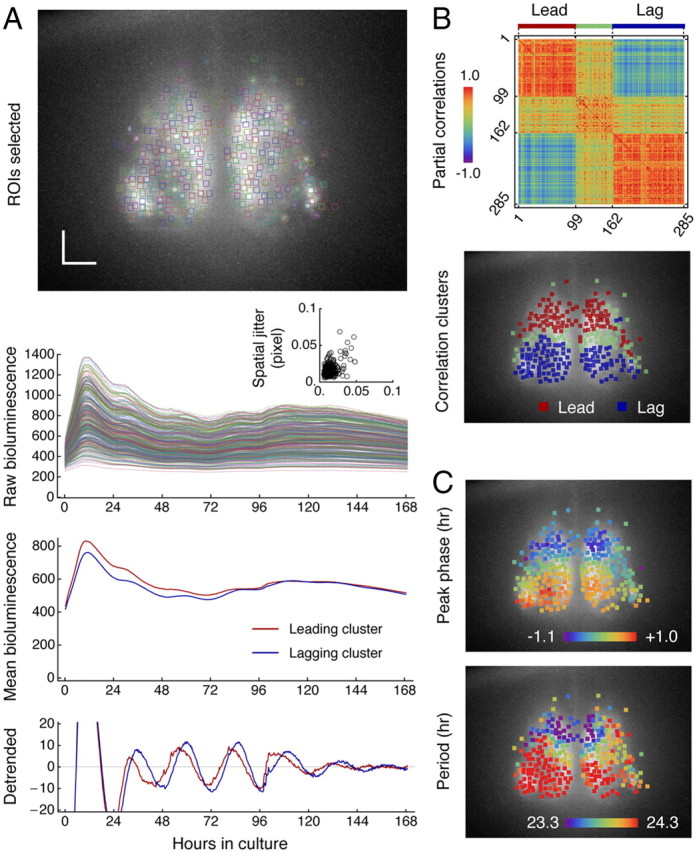
Clustered Bmal1 oscillations in cultured SCN indicate clustering in both phase and period. A, ROIs are selected for all identifiable neurons throughout the SCN explant (top image), and time-dependent changes of bioluminescence are tracked, colored in a consistent scheme (second row). The spatial jittering of neurons is constrained within 5% of a pixel dimension (inset). The spatial dimension of 1 pixel is 0.85 μm. The relative phase difference in mean oscillatory activities of leading (red) and lagging neurons (blue) (third row) becomes evident when the baseline bioluminescence is removed (bottom row). Scale bar, 100 μm. B, Partial correlations matrix (top) of all Bmal1 oscillations also shows clustered activities found via our correlation-based clustering algorithm (see Materials and Methods). The spatial distribution of the clusters (bottom) is discrete and associated with known dorsal and ventral regions. C, Phases (top) and periods (bottom) are heterogeneously distributed in clusters mirroring each other.

Linear relationship between phase deviation and intrinsic period.

Under no coupling or sufficiently weak coupling, the deviation of phase from the mean is attributable completely to intrinsic periods in such a way that the longer period oscillator would become phase lagged and the shorter advanced. Due to the nature of circadian oscillation, the difference between an experimentally determined intrinsic period and the mean period (ΔT) is always <24 h, and we can linearize the time-dependent phase deviation (ϕ) as follows:

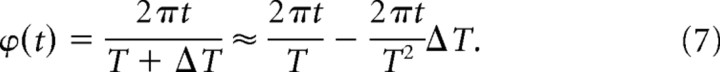Thus, given the recording duration t, the phase deviation becomes a linear function of period deviation. Since the slope of the phase deviation (Eq. 7) is linearly proportional to the recording duration, we have normalized it by dividing by the recording duration t, which we define as phase deviation per day (see Fig. 4D).

Figure 4.

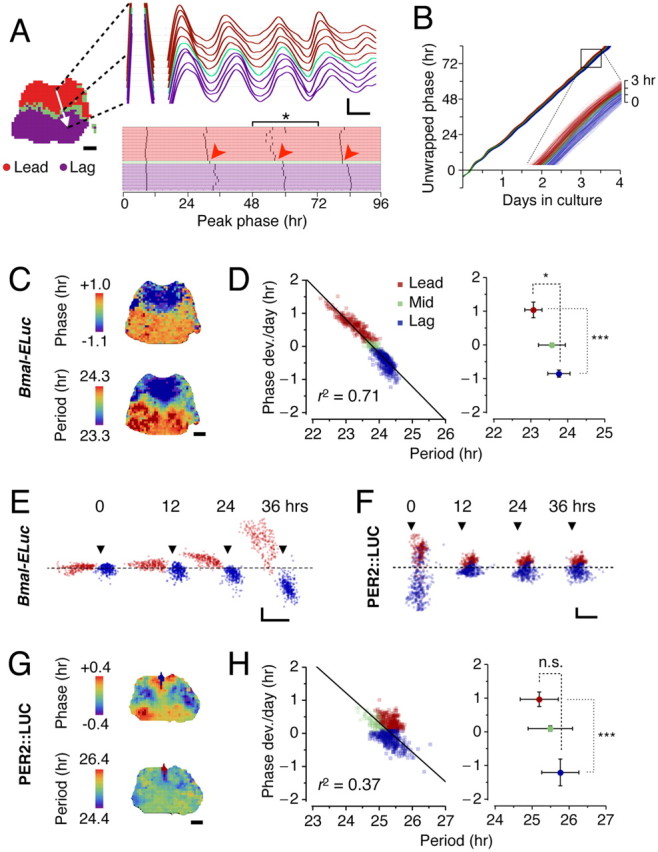
Clustering of correlated Bmal1 oscillations originates from period heterogeneity. A, Along a path from one cluster to the other (white arrow, left), correlation in oscillatory activities of Bmal1 in the neighbors sharply drops as the path crosses the border between the leading and the lagging clusters (top right), which results in disjoints (arrowheads) in positions of peak phase (bottom right). The scale bar of the slice image is 100 μm here and throughout. The calibration of the detrended oscillations represents 12 h (x-axis) and 10 bits of detrended bioluminescence (y-axis). B, The continuous phase evolution over time is illustrated by unwrapped phases that are highly linear (r² = 0.998 ± 0.002, mean ± SD; for n = 700 grids in the present sample; r² = 0.993 ± 0.009 in n = 23 explants), indicating the phase increases at a constant rate. The oscillators belonging to the phase-leading cluster (red) consistently have higher slopes than the ones in the phase-lagging cluster (blue) (inset magnifies the boxed, which spans 12 h in culture). C, The phase distribution (top) is markedly discrete throughout the SCN. Shown are the peak phases on the third day in culture (bracketed in A, *). The period distribution (bottom) exhibits discrete spatial patterning. D, Left, The time average of phase deviation shows a strong negative linear relationship with intrinsic periods (r = −0.84; p < 0.001 in the present sample), and the relationship is predicted by linearization of the mean period (coefficient of determination as goodness of fit, r² = 0.71) (solid line). D, Right, In Bmal1 oscillations, the leading and lagging clusters are resolved by both periods (*p < 0.05) and phase (***p < 0.001). E, Over time in culture, phase of each Bmal1 oscillator (y-axis) gradually moves away from the mean according to its intrinsic period (x-axis). Snapshots of phase versus period are shown at 0, 12, 24, 36 h in culture. The arrowheads indicate where the period equals 24 h, and the dashed line shows where the phase deviation is zero. The x- and y-axis calibrations represent 1 h, here and in F. This illustrates that the intrinsic period is the origin of tight correlation between the phase and the period. F, In Per2 oscillators, the gradual separation of phase is not evident. The arrowheads indicate where the period equals 25 h. G, Clustered Per2 oscillations is reflected in the discrete spatial phase distribution (top) but not in period (bottom). H, The leading (red) and lagging (blue) clusters are separated by phase but not by period; the relationship between phase and period is not clearly linear (r² = 0.37) (left). In all Per2 samples, the leading and lagging clusters are not resolved by period (p = 0.22, n = 8) but by phase (***p < 0.001) (right).

Simulation with population oscillator model.

The standard population oscillator model considers noise (ζ) and pairwise coupling (Γ) based on the phase differences between two oscillators (Pikovsky et al., 2001) as follows:

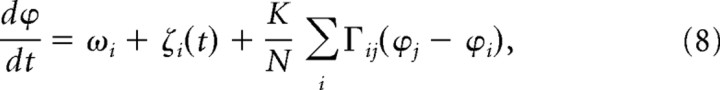where ω_i is the intrinsic frequency of an oscillator i, ζ_i is the noise, K is the coupling constant, N is the number of oscillators, and Γ_ij is the coupling function. The coupling can be considered all-to-all or global when all oscillator pairs are nonselectively considered. We simulated phase evolution of all oscillators based on experimentally determined parameters (ω_i, inverse of period multiplied by 2π) and initial conditions [ϕ_i(0), at the start of the recording] with various coupling constant K but without any noise (ζ = 0) (see Fig. 6B, top). In the cases in which no coupling is assumed, we have simply solved for dϕ_i/dt = ω_i with experimental ω_i and ϕ_i(0) values (see Fig. 6B, bottom).

Figure 6.

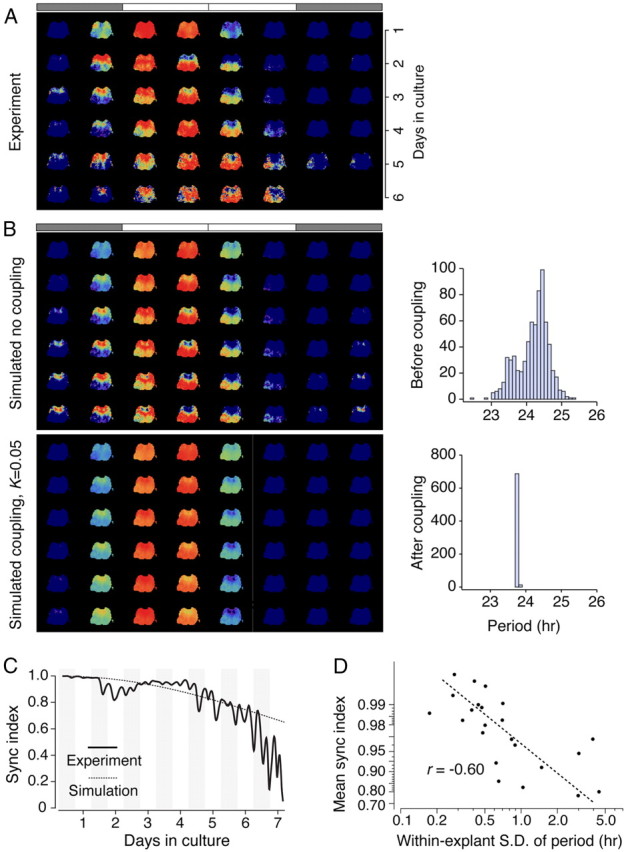
Computer simulations based on period distribution reproduce major spatial dynamics of Bmal1-ELuc oscillations. The experimentally observed spatiotemporal dynamics of Bmal1-ELuc oscillations (A) can be recreated using a phase oscillator model with only the initial phases and intrinsic periods extracted from the data without assuming any coupling (B). The experimentally determined period distribution is slightly binomial (B, top right), which reproduces later phase development when no coupling is assumed (B, top left); while a weak global coupling (coupling constant K = 0.05) fails to reproduce the experimental finding and brings the oscillators to synchrony (B, bottom left) and uniform period (B, bottom right). The bars on top of image sequence indicate the extrapolated 1 times of light on (white) and off (shaded) for 24 h. C, The phase oscillator model without coupling predicts temporal changes in the degree of synchronization (sync. index). The small fluctuations in the experimental data are due to imprecise phase extraction. D, The time-averaged synchronization index is negatively correlated with the width of the period distribution, quantified by the within-explant SD in all samples (r = −0.60; p < 0.005). The y-axis is plotted in reversed log scale.

Phase coherence evolution with zero coupling.

Suppose the phase is a linear function of frequency with distribution g(ω), with N → ∞, the summation of phase vector can be described by a continuous function as follows:

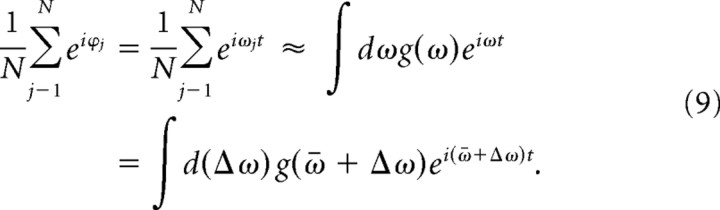If we assume the frequency distribution is Gaussian with dispersion D,

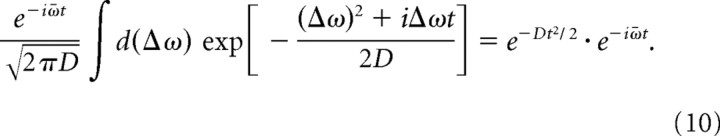Expanding Equation 10 in power series, we can demonstrate that the phase coherence decays quadratically without beating in the initial few cycles given a small dispersion D in the frequency distribution (see Fig. 6C).

Estimation of period via high-resolution Fourier method.

We used a modified periodogram method to estimate periods in both detrended bioluminescence and behavioral time series data. The primary peak spectrum is determined using fast Fourier transform, and a precise estimate of period is found through a high-resolution spectrum windowing centered at the peak. This method enables period estimation by enhanced spectral resolution not limited by sampling rate (resolutions of data sampling are 0.25 h for Bmal1-ELuc, 0.5 h for PER2::LUC, and 0.02 h for behavior). The modified periodogram correctly identifies the period in noisy data for a minimum of 3 d recording length, and the estimate becomes stable from 4 d recording length onward. We found that, compared with the mean interpeak interval estimation, this method estimates periods in the circadian range and is resilient against damping and noise.

Wavelet analysis for estimating the instantaneous period.

Continuous wavelet transform (CWT) was performed on Mathematica to track time-dependent changes in frequency components. A fundamental trade-off exists between temporal and frequency resolution of CWT (De Moortel et al., 2004). We used the Paul wavelet (m = 6) in preference to the Morlet wavelet for its superior temporal resolution. The Paul wavelet saves a larger portion of the transform of our circadian rhythm data inside the cone of influence by minimizing the edge effects due to the long periodicity of the data relative to the sample length. The scalogram, also known as CWT heat map (Meeker et al., 2011), was produced in the “rainbow” color scale with the peak positions denoted by a white line. The peak period component for each time point was found from 100 randomly selected oscillators (grids) per explant, and its variation over time was quantified by the temporal SD. For comparison across samples, we have pooled all oscillators in the period variability histogram (Meeker et al., 2011, and references therein) and also computed within-explant averages. The period change rate was calculated by finding a time derivative of a dominant instantaneous period divided by the time duration. It measures the degree of abrupt changes in the instantaneous period.

Measure of synchronization.

The Kuramoto synchronization index (SI), also known as phase coherence, measures the degree of order in a population of oscillators (Kuramoto, 1984; Pikovsky et al., 2001). It is the length of a vector sum average of all (N) phases at a time point that illustrates coherence of phases, defined by the following:

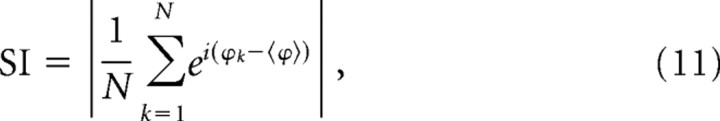where k is the index of an oscillator and 〈ϕ〉 is the mean phase of the whole population.

Quantification of cluster topography.

Clusters of correlated oscillations demarcate anatomical subregions of the SCN (see Fig. 8E). The center-of-mass (CM) position of a cluster C_k is defined as a vector sum average of oscillator positions (x_j) in the cluster minus the center of mass of the whole SCN explant.

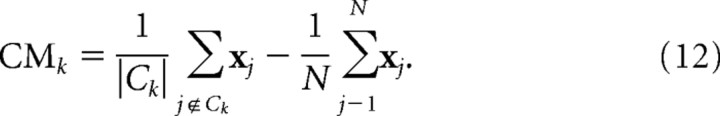Changes in CM can measure topographical changes of clusters after pharmacological treatments. In our experiments, drugs were applied to mid to posterior SCN explants, and changes in angular CM positions of clusters are compared (see Fig. 9B, middle). When CM is represented in polar coordinates, the angular position resolves the leading and the lagging clusters in the mid to posterior SCN explants (see Fig. 8B). We also assessed changes of the members of clusters after drug application, which can occur despite the macroscopic similarity in cluster positions. The overlap of cluster identities is defined as a percentage of the intersection of a cluster before the drug and a cluster after the drug divided by the mean number of elements of the two clusters. If members of a cluster do not change, the overlap is 100%. If members of the whole SCN are randomly sampled two times to the size of the cluster, the overlap of the two random samples will increase as the cluster size increases. Therefore, the overlap of a cluster has been compared with the chance level, estimated from overlap of random samples that has the size of the cluster (see Fig. 9B, right).

Figure 8.

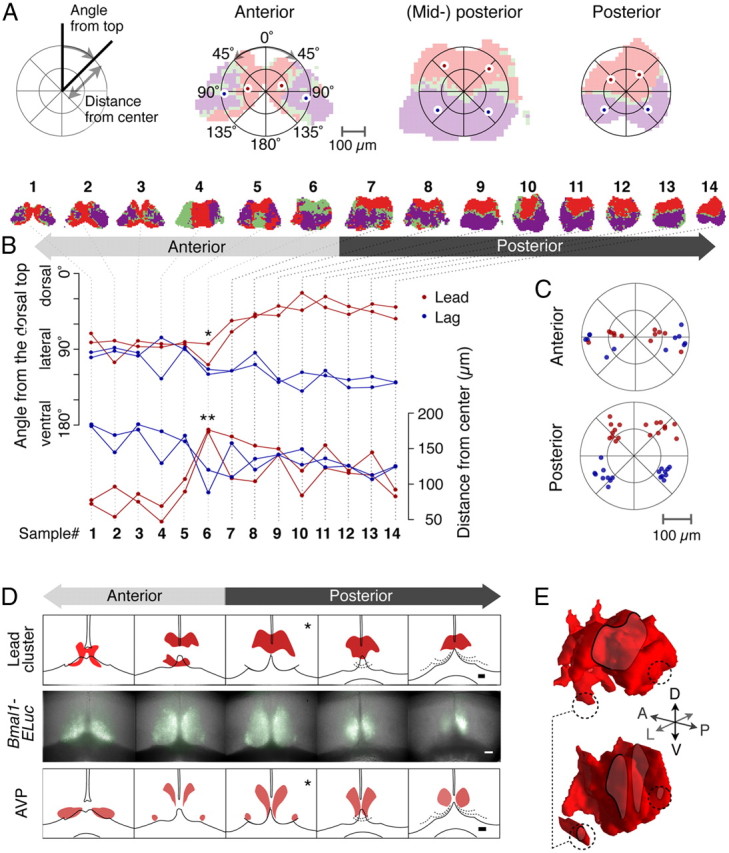
Characteristic cluster topographies summarized and compared with AVP immunostaining along the anterior–posterior axis. A, The cluster topography is quantitatively represented by the CM positions of the clusters on each unilateral side in polar coordinates. The origin is the CM of the whole SCN (left). Cluster CM positions in anterior, mid-posterior, and posterior SCNs are shown (right). B, Angular distribution of two major clusters along the AP axis shows an abrupt transition point (top, *). Radial distribution of the cluster CMs also reveals a strong transition (bottom, **). The top row shows shapes of clusters for 14 representative samples of 23 control recordings entrained under 12:12 LD. C, Cluster CM positions of all anterior (top) and posterior (bottom) samples. Two distinct patterns arise in the anterior and the posterior. D, The relative AP position of leading clusters (top row) can be estimated by the signature patterns of baseline Bmal1-ELuc expression (middle row). The patterns of Bmal1-ELuc are compared with the series of 30 μm thin sections, each 90 μm apart (bottom row), to identify their relative positions along the AP axis. Note the ventrolateral islands of AVP neurons are not included in the leading cluster (*). Scale bars, 100 μm. E, The leading clusters (top) and AVP immunostaining (bottom) along the AP axis are reconstructed in 3D (Fig. 7D) to reveal differences in spatial distributions (dashed circles).

Figure 9.

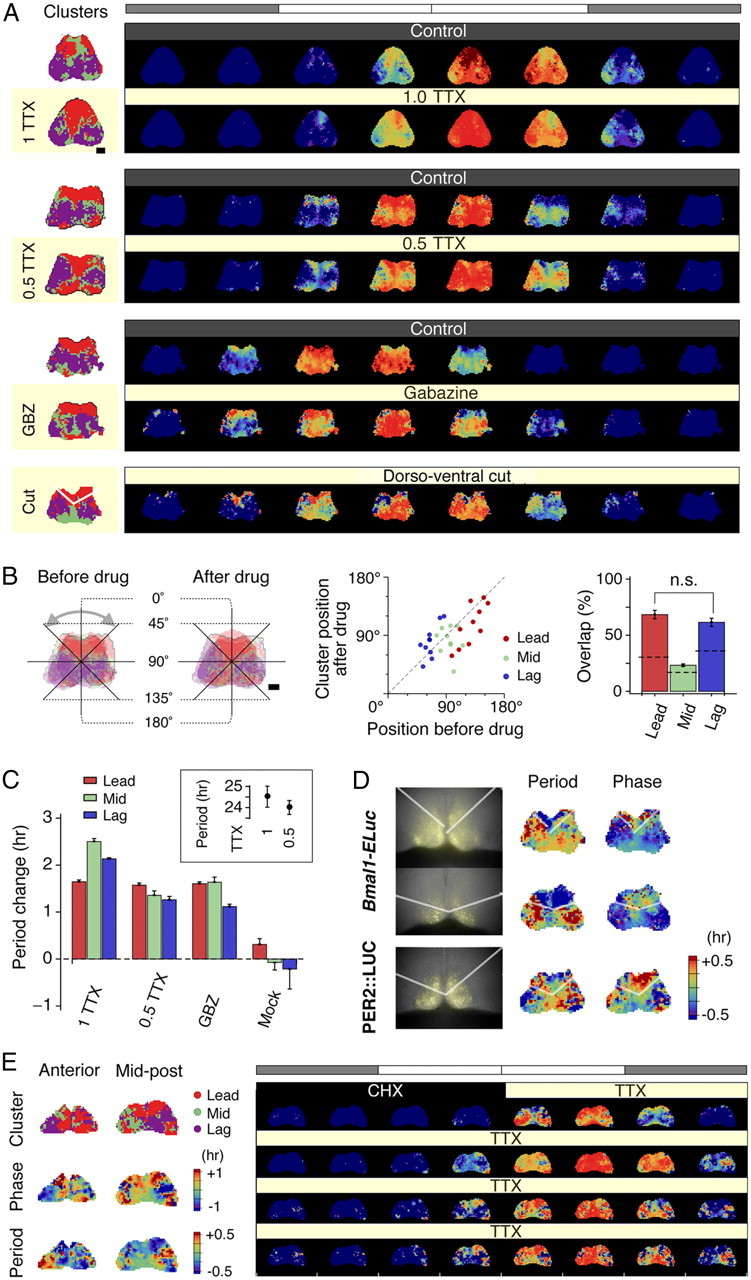
Clustering is robust against pharmacological and surgical isolations. A, Left column, Active oscillating grids of SCN explants are color labeled by phase clusters, which consistently identify the dorsal as the leading (red) and the ventral as the lagging (blue). This characteristic cluster topography remains undisturbed by inhibition of action potential by 0.5–1.0 μm TTX or by blockade of GABA_A-mediated synaptic transmission by 10 μm gabazine. Likewise, a surgical cut across the dorsoventral border of the SCN delineates the leading cluster in the dorsal SCN. A, Right column, Presented are normalized time-lapse image sequences for 24 h duration on the second (control) and the fifth (drug treatment) days in culture. The dorsal to ventral phase ordering pattern is unaltered after treatments of 0.5–1.0 μm TTX, 10 μm gabazine, or the surgical cut. The white and shaded bars on top indicate extrapolated times of light on and off, respectively. B, The change of topography before and after the application of TTX (left) is quantified by the angular position of the center of mass of each cluster on a unilateral side (middle), which we find significantly correlated (r = 0.58; p < 0.001). The cluster identities of oscillators overlap beyond chance levels before and after drug applications positions (p < 0.005, except for the mid cluster; the dashed line indicates the chance level) (right). C, The periods of Bmal1 oscillators increase after drug applications in all clusters (∼1.6 h on average under all drugs), while the periods do not alter after mock application (p < 0.001 compared with drug applications) in the imaging samples. The tendency of period increase under TTX is not statistically significant in a larger photometry sample set (p = 0.16, n = 12 for 1 μm; p = 0.44, n = 11 for 0.5 μm) compared with control (inset). Error bars indicate SEM. D, Surgically cut slices expressing Bmal1-ELuc (semitransparent white lines indicate where the cut is made; first column, top and middle rows) show divided groups of periods (second column), while the phase distribution is not as clear-cut (third column). In contrast, PER2::LUC-expressing cut slice (bottom row) shows less distinct groups of periods but better grouping of phases. E, Clusters (first row, left panel) retain their canonical topography during the action potential silencing by TTX, after the oscillator reset by CHX for 18 h, which, like phases (second row, left panel), coincide with the spatial distribution of periods (third row, left panel). The normalized time-lapse of the mid-posterior SCN (right panel) shows the progressive phase advance of the dorsomedial cluster and delay of the ventrolateral cluster, consistent with the idea of reemergence of the phase order by intrinsic periods. GBZ, Gabazine. Scale bar, 100 μm.

Statistical analysis.

The p values were calculated on Mathematica with HypothesisTesting package. Unless stated otherwise, we used Welch's t test, which does not assume equal variances. Mann–Whitney U test was used when normal distribution could not be assumed.

Results

Bmal1 oscillations in cultured SCN retain in vivo rhythm

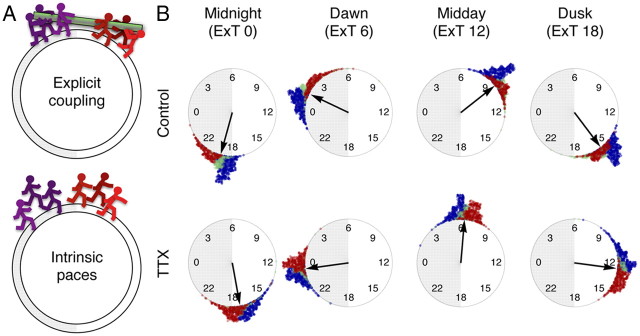
Transcriptional pathways of Bmal1, the positive loop component of the core clock, are different from those of Per genes that make up the core negative-feedback loop (Relógio et al., 2011). Unlike Per, light does not directly influence Bmal1 expression (von Gall et al., 2003). Transcriptional oscillations of Bmal1 reflect traces of activities of the core feedback loop and can therefore be thought to retain the inherent state of the circadian clock. If Bmal1 circadian oscillations in the single cell are more resistant to perturbations than Per2, studying its long-term oscillations could contrast single-cell dynamics against network dynamics and show how the dominant dynamical factor in single cells shapes overall heterogeneity in the network. The Bmal1-ELuc transgenic mouse carries an enhanced green-emitting luciferase (ELuc) (Nakajima et al., 2010) under the control of a 915 bp Bmal1 promoter fragment that reports Bmal1 transcription by bioluminescence (Noguchi et al., 2010). In Bmal1-ELuc mice, stable periodicity in behavioral circadian rhythms under constant darkness continued in oscillations of bioluminescence, when SCNs were explanted and kept in culture (Fig. 1A, left). A similar relationship could not be established, however, in PER2::LUC knock-in mice, where the SCN explants express longer than behavioral periods or sometimes show a “kink” or an abrupt lengthening of period (Fig. 1A, right). Notably, the Bmal1-ELuc oscillation period (T) in the anterior coronal section of the SCN was not found to significantly deviate from the behavioral free-running period (τ) (Fig. 1B, top), while T of PER2::LUC in the anterior SCN was significantly longer than τ (Fig. 1B, bottom). This indicated that oscillations of Bmal1 could be used as a means to study the organization of intrinsic periods in response to variable durations of light.

Figure 1.

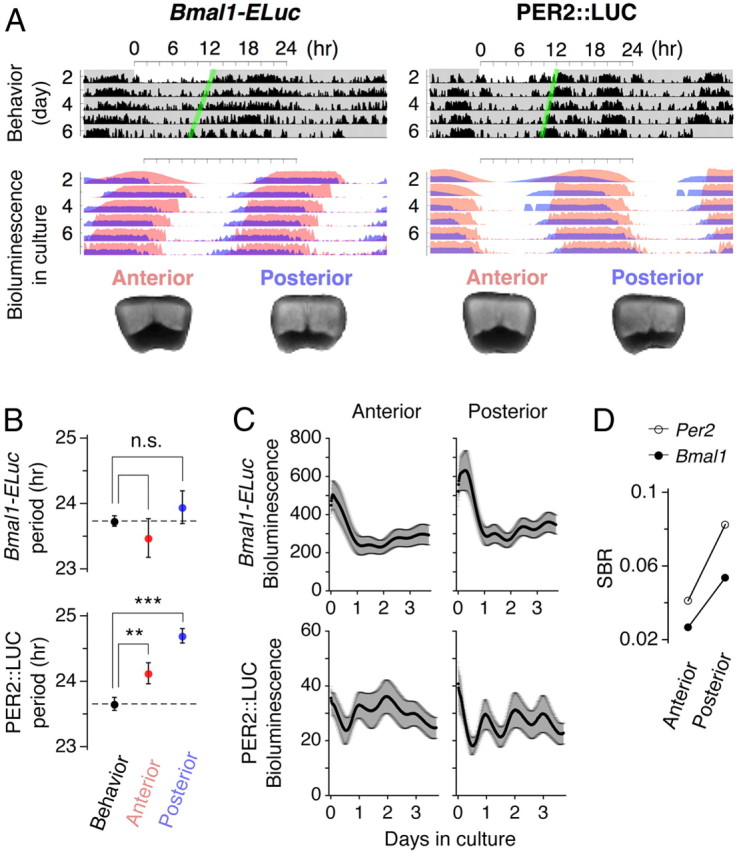
Weak correlation between locomotor activities and PER2::LUC bioluminescence rhythms highlights Bmal1-ELuc as a faithful reporter of intrinsic rhythms. A, Double plots of locomotor activities under constant darkness (top) and of bioluminescent reporter activities of cultured SCNs from the same animals (middle) and photos of corresponding slices (bottom) are shown. The Bmal1-ELuc reporter activity in culture appears to continue the locomotor rhythm (left), whereas PER2::LUC activity in culture deviates from the rhythmic pattern of the locomotor activity when the animal was alive (right). The double plot in culture represents normalized bioluminescence rhythms. The green lines are the guides marking the onsets of significant activity. The light red and light blue in the double plot denote the anterior and posterior SCN explants, respectively (bottom). B, The period of circadian locomotor activity under constant darkness (23.7 ± 0.1 h; n = 8) is statistically indistinguishable from that of Bmal1-ELuc rhythms in both anterior (23.5 ± 0.3 h; n = 39) and mid to posterior SCNs (23.9 ± 0.4 h; n = 43) (top); whereas the periods of locomotor (23.7 ± 0.1 h; n = 4) and PER2::LUC activities from both anterior (24.1 ± 0.2 h; n = 19) and mid to posterior (24.7 ± 0.1 h; n = 29) SCN cultures are significantly different (**p < 0.01; ***p < 0.001) (bottom). There was no significant difference in behavioral rhythm between wild-type and Bmal1-ELuc transgenic strains (p = 0.36; wild type, n = 6) or between wild-type and with PER2::LUC knock-in strains (p = 0.45). Statistical significance was determined by Welch's t test (see Materials and Methods). C, The peak-to-trough amplitude of Bmal1-ELuc bioluminescence is smaller in comparison with its respective baseline bioluminescence (top) than PER2::LUC (bottom). Note the difference in scales. Error bars indicate SEM. D, The SBR is higher in the posterior than the anterior SCN in both reporters, but Bmal1-ELuc is consistently low and ∼65% of PER2::LUC.

The ELuc provides bioluminescence signal over tenfold brighter than the conventional firefly luciferase (Nakajima et al., 2010), enabling us to shorten the sampling interval down to 15 min with a conventional cooled CCD camera and improve precision of period estimation. However, high baseline bioluminescence makes the oscillatory reporter activity difficult to assess directly. The relative amplitude of signal oscillation embedded on the baseline bioluminescence was smaller in Bmal1-ELuc compared with PER2::LUC (Fig. 1C). In addition, regardless of the reporter system, the signal oscillation had lower amplitude in the anterior than in the posterior SCN, leading to lower signal-to-background ratio (SBR) in the anterior SCN (Fig. 1D). The SBR was determined by the SD of the oscillatory signal divided by the mean bioluminescence and the Bmal1-ELuc's SBR was only 65% of PER2::LUC's SBR in both anterior and posterior SCNs. The low SBR resulted in visibly unclear Bmal1-ELuc oscillations in raw imaging data.

Clustering of Bmal1 oscillators

The Bmal1 oscillations of SCN neurons had high baseline bioluminescence in respective regions of interest (ROIs) (Fig. 2A, top and second rows). When the baseline was removed, phase-leading and phase-lagging subpopulations became much more visible (third and bottom rows). In the adult SCN samples we have used, there was little spatial jittering of neurons during culture (inset, second row) except for the first 24 h after preparation of culture. Heterogeneous phases of bioluminescence activities in SCN cultures have been observed using Per1 (Quintero et al., 2003; Yamaguchi et al., 2003) and Per2 reporter systems (Evans et al., 2011; Foley et al., 2011; Fukuda et al., 2011), which were previously interpreted as spatially propagating waves or tides that expand and recede back to their point of origin (Yan et al., 2007; Butler and Silver, 2009).

However, we found that the Bmal1 oscillation does not propagate continuously in space. Instead, the Bmal1 oscillators in the SCN were clustered and their activities were highly synchronized within clusters but not among members from different clusters. The direct comparison of similarity of oscillatory waves and classification by spatial clustering (see Materials and Methods) resulted in a clearly segmented matrix of partial correlation of each oscillator with one another (Fig. 2B, top). When the spatial positions of clustered oscillators were identified, we found that oscillators in the phase-leading cluster (red) are in the dorsal region and the lagging cluster (blue) in the ventral region of the SCN (Fig. 2B, bottom). The clustering represented actual division of rhythmic patterns and corresponded to both phases and periods (Fig. 2C).

Spatial visualization of phase evolution

The poorer SBR has hindered direct visualization of oscillations in the Bmal1-ELuc system, but it can be overcome by reprojecting normalized, background-free oscillations onto the original SCN geometry. However, the ill defined geometrical relationships among neurons make it difficult to achieve this. We circumvented these problems by regarding the square area (15 × 15 μm²) around each neuron as a grid element on a virtual scaffold (Fig. 3A,B). The neurons were effectively selected by convolution with a grid kernel that finds a spatial average around a dominant area of bioluminescence activities (see Materials and Methods). Although this method oversampled the number of oscillators compared with the traditional ROI method, the amount of false positives due to internal light scatter (Foley et al., 2011) was limited because the SCN is dense with neurons (Klein et al., 1991) and the method provided general spatiotemporal information consistent with results from the ROI method (Fig. 2). The fMRI-like pictures that the method generated enabled intuitive comparison of spatiotemporal dynamics from a large number samples.

Reconstructed SCN images from normalized oscillations immediately revealed clustered oscillatory activities, which were not evident in raw images since the uneven distribution of baseline bioluminescence does not coincide with the distribution of oscillator phase. For instance, a ventral neuron (“v”) (Fig. 3C) that apparently shows higher bioluminescence activity can be more advanced in phase than a darker dorsal neuron (“d”) (Fig. 3C). Detrending and normalization, performed by normalizing the amplitude in the phase plane, makes such relationship visible (see Materials and Methods). Use of this method and spatial clustering of correlated oscillations enabled us to classify and summarize spatial qualities with efficiency from a large dataset of SCN culture imaging.

Origin of the clusters of correlated rhythms

Our analysis showed the concerted oscillatory activities were clustered and did not propagate as waves. Instead, we found the apparent spatial succession in Bmal1-ELuc expression rhythm was epiphenomenal and oscillators in each different region paced almost independently and discontinuously. In the interpretations of both waves and tides, oscillations of two immediate neighbors are well correlated and the correlation decreases gradually as the physical distance between the oscillators increases. In Bmal1 oscillations, the correlation between two oscillators had spatial discontinuities and the correlation dropped suddenly at a particular distance between the two. Such points of discontinuity were evident in our data. For example, in the plot of the peaks of Bmal1-ELuc oscillations along a continuous path stretched from a phase-leading to a phase-lagging cluster (Fig. 4A), successive peaks were neighbored to each other as the path descended until it crossed a border between the leading and lagging clusters (marked by arrowheads) where the peaks separated abruptly despite their spatial closeness. The discontinuities occurred globally, as illustrated by discrete spatial distributions of phases and periods (Fig. 4C). Moreover, the spatial clustering pattern (Fig. 4A, left) matches with that of the phase (Fig. 4C, top) and also with the period (Fig. 4C, bottom), as confirmed by the ROI-based analysis (Fig. 2C). The strong relationships among the correlations, phases, and periods can indicate a simple underlying mechanism, and indeed we found a candidate.

Evolution of phases over time occurs on a line with a single slope, which is inversely proportional to the intrinsic period (Fig. 4B). Following this observation, if an oscillatory activity is driven mainly by the intrinsic period of the oscillator, its relative phase advance or delay with respect to the population average will depend only on its period difference from the mean, rendering a linear relationship between period and phase (see Materials and Methods). In the present Bmal1-ELuc recording sample, we verified existence of such linear relationship (r² = 0.71; Fig. 4D, left), and in all control Bmal1-ELuc recordings the phase-leading and -lagging clusters were statistically distinct, not only when the phases were compared (vertical comparison bar, ***p < 0.001, n = 23 explants; Fig. 4D, right) but also when the periods were compared (horizontal bar, *p < 0.05; Fig. 4D, right). The spread of phases around their mean (y-axis) grew linearly over time, as determined by periods (x-axis), because of the linear period-phase relationship (Fig. 4E).

Surprisingly, the same could not be observed in PER2::LUC samples (Fig. 4F). Although the phases distributed in groups (Fig. 4G, top), no reciprocal relationship in period could be determined (Fig. 4G, bottom; H, left). For all PER2::LUC imaging samples, phase-leading and -lagging clusters were distinguished only by phase (***p < 0.001; n = 8 explants), not by period (p = 0.22). This might explain why heterogeneity of period within the SCN has not been noted using Per reporters.

Stable periods of Bmal1 oscillations in SCN explants

We explained the formation of clusters by regionally distributed intrinsic periods. The period can be properly defined as an intrinsic property of an oscillation if it does not vary widely and arbitrarily over time. We transformed detrended oscillations with the Paul wavelet to estimate the instantaneous periods with high temporal precision (see Materials and Methods). This estimation showed that the periods of individual oscillators were stable and fluctuated within reasonable bounds (average temporal SD, 0.1 h) in Bmal1 as well as in Per2 samples (Fig. 5). In the scale map representation of period components of a randomly selected oscillator, a group of weak components could be found to occur circadianly, which were due to the nonsinusoidal curve shape of bioluminescence oscillations (Fig. 5A, left; B, left). The dominant period components were found in oscillators and were indicated as a line. In some SCN explants, a subpopulation of oscillators exhibited highly fluctuating dominant periods (Fig. 5A,B, second column), but in others almost all oscillators stayed stable (Fig. 5A,B, third column). Drifting of the dominant period component in the beginning of culture can be biased by abrupt increase of bioluminescence reporter signal and at the end of culture by the signal degradation and a relatively higher contribution of noise. The SD of period over time showed a distribution that is comparable with a previous study based on SCN explants expressing PER2:: LUC (Meeker et al., 2011). Although the distribution appears statistically similar in the two reporters, PER2::LUC data tended to have more explants having higher SD (Fig. 5C) and higher rate of period lengthening (Fig. 5D).

Figure 5.

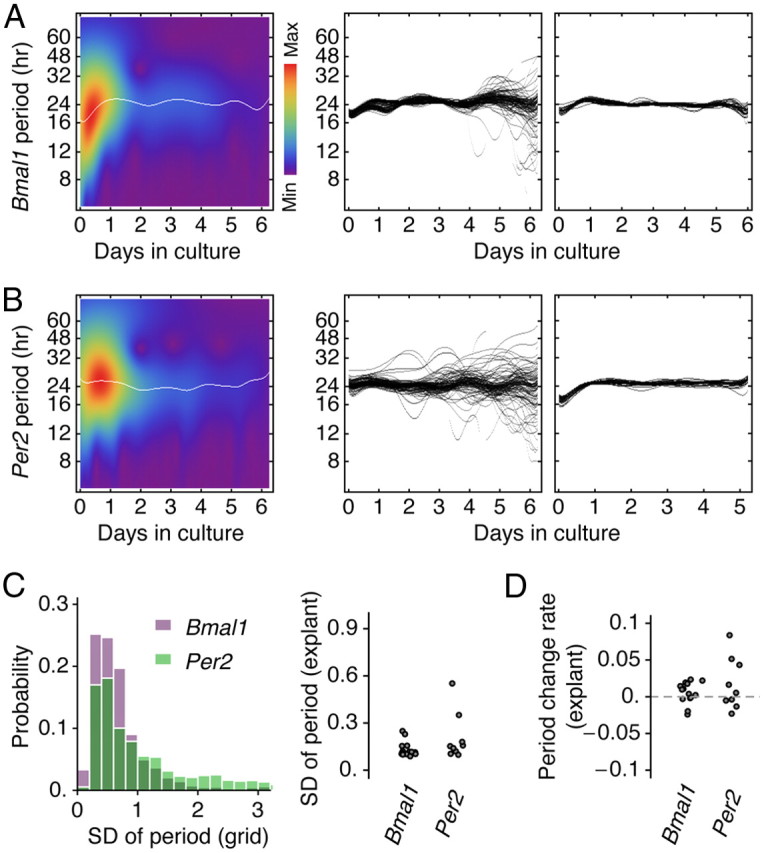
Stability of period over time estimated by wavelet analysis. A, The wavelet scale map of a randomly selected Bmal1 oscillator illustrates how a dominant period component (white line) along with other period components (blue to red) change over time (left). Within a SCN explant, a subpopulation of oscillators sometimes exhibited highly fluctuating dominant periods (middle) or most oscillators maintained a stable period (right). B, A similar observation could be made in SCN explants expressing PER2::LUC. C, The temporal SD of individual oscillations showed similar distributions in both Bmal1-ELuc and PER2::LUC reporter data (left). Although not statistically significant (p = 0.10), the within-explant averages indicated that PER2::LUC samples tended to have more explants with higher temporal SDs (right). D, The rate of period change in PER2::LUC samples also showed a tendency of more explants that increased period over culture duration, but it was not statistically significant compared with Bmal1 (p = 0.17).

Simulated recreation of spatiotemporal dynamics of Bmal1 oscillation in the SCN

Stability of periods of Bmal1 oscillations was in line with the linear phase evolution (meaning that the phase is progressing in a uniform manner through time) as shown in the unwrapped phase (Fig. 4B), which indicated little evidence of strong phase resets. This suggested that any purported network effects were minimal or at most subtle in the explant culture. To confirm that the period is the major determinant of the in vitro phase evolution, we reproduced the tissue-wide oscillations in silico by reconstructing grid elements with simulated oscillators having respective intrinsic periods and initial phases estimated from actual recording (reconstructed experimental images; Fig. 6A). The oscillations were obtained using a phase oscillator model with or without coupling (Kuramoto, 1984) (see Materials and Methods). Under no coupling, the simulation recreated the main features of the spatiotemporal evolution of Bmal1-ELuc expression (Fig. 6B, top left) and the period histogram remained identical with the experimental histogram (Fig. 6B, top right). A range of small global coupling (K) constant did not change this profile until it reached a threshold K ∼ 0.05, which brought the oscillators near complete synchronization (Fig. 6B, bottom left) and narrowed the period distribution to a sharp peak (Fig. 6B, bottom right). This suggests the coupling among Bmal1 oscillations is weak or is not globally strong at least.

The Kuramoto synchronization index (SI) measures the degree of synchronization at each point of time (SI = 0 for complete desynchronization and 1 for complete synchronization) (see Materials and Methods). The SI quantitatively demonstrated a good agreement between simulation and experiment throughout recording duration (Fig. 6C). The quadratic decaying profile of the SI can be explained analytically by assuming the oscillators with normally distributed periods and no coupling, which was exhibited in both model and experiment (see Materials and Methods).

Last, we found an inverse relationship between the within-explant SD of intrinsic periods and the time-averaged synchronization index (r = −0.6; p < 0.005; n = 23; Fig. 6D). This is consistent with the idea that the period drives the phase such that a wider period distribution will eventually create larger divergence of phases. These post hoc analyses indicated a potent contribution of cell-intrinsic properties in determining overall population dynamics in culture.

The three-dimensional distribution of clustered oscillations

The discrete spatial heterogeneity in the oscillator distribution was not an accidental feature of a particular coronal section. We found that the distribution has a structurally consistent topography throughout the anterior-to-posterior (AP) axis. There was a characteristic spatial distribution of leading and lagging clusters for each section along the AP axis (Fig. 7A, left). Also, the mean phase of the section tended to be advanced in the posterior relative to the anterior (reconstructed time-lapse images for the first day in culture, samples from different animals; Fig. 7A, right). We investigated how the clusters compared with the heterogeneous neuropeptide expression (Morin and Allen, 2006) by performing immunohistochemistry against three major neuropeptides in the SCN: arginine vasopressin (AVP), vasoactive intestinal polypeptide (VIP), and gastrin-releasing peptide (GRP) (Fig. 7B). We were unable to identify association of VIP- and GRP-containing neurons with any oscillatory clusters. However, we found the spatial pattern of AVP expression coincided with the region where the baseline bioluminescence was high (Fig. 7C), but it did not coincide completely with a cluster. Using defined AP positions in the immunostained serial cryosections as pointers (Fig. 7B), we have constructed a 3D distribution of AVP in the SCN and verified its integrity by comparing virtual sections of the 3D image with immunostained coronal, horizontal, and sagittal sections (Fig. 7D).

Figure 7.

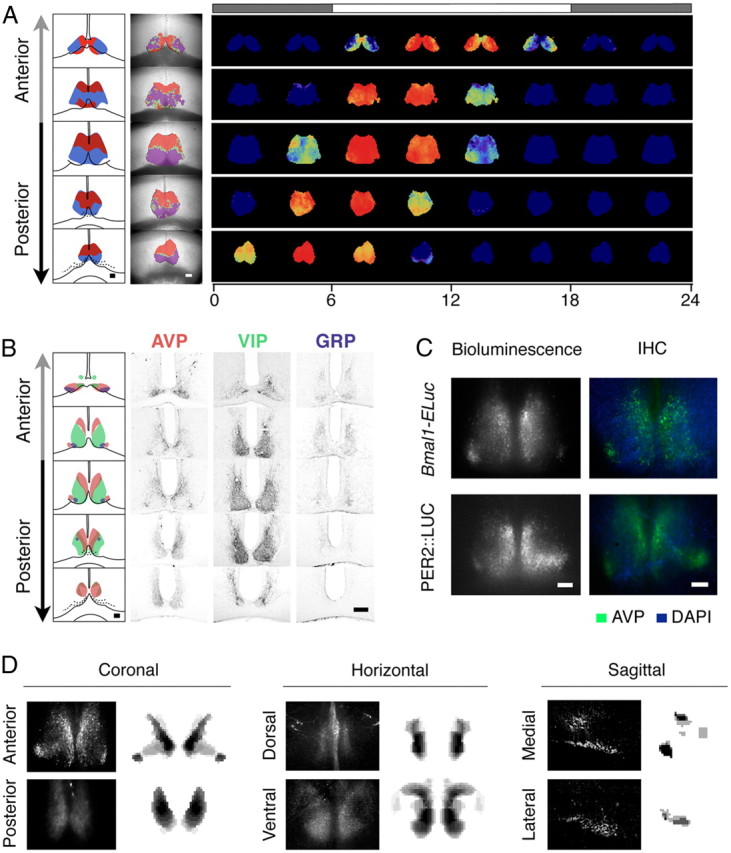
Distinct spatiotemporal dynamics of Bmal1 oscillations in anterior and posterior SCN cultures with positions outlined by characteristic morphology and AVP immunostaining patterns. A, Clusters of oscillations are identified by correlation (schematic, left column; actual, mid column), which summarizes the spatiotemporal dynamics of Bmal1-ELuc expression (first day in culture, right column). The top bar represents the extrapolated times of light on (white) and off (shaded). B, Neuropeptidergic immunostaining of AVP, VIP, and GRP does not reproduce the characteristic cluster patterns shown in A. The series of slices along the AP axis are separated by distance of 90 μm. C, Although AVP is not a faithful marker of a specific cluster, its immunostaining pattern (right) matches with the regional bias of baseline bioluminescence (left) in slices of both Bmal1-ELuc transgenic (top) and PER2::LUC knock-in (bottom) mice. D, The serial staining patterns of AVP in B are digitized and coronal, horizontal, and sagittal IHC patterns (left, black background) are compared with computer-generated virtual sections (right, white background). Scale bars, 100 μm. DAPI, 4′,6-Diamidino-2-phenylindole.

The anterior–posterior distribution of oscillatory clusters had two characteristic patterns in the anterior and posterior (Fig. 8A). In the posterior sections, a cluster of phase-leading oscillations appeared in the dorsal region followed by a cluster of phase-lagging oscillations in the ventral region, whereas, in the anterior sections, the phase-leading and -lagging cluster appeared in the medial and lateral regions, respectively. To characterize the cluster positions, we calculated the CMs of individual clusters on each unilateral side of the SCN and specified their positions in polar coordinates in terms of the distance from the CM of the whole SCN and the angle from the dorsal top (Fig. 8A, left) (see Materials and Methods). Through this quantification, we found that the transition between the anterior and (mid-to-) posterior patterns was notably sharp (Fig. 8B, * and **), and the anterior and the posterior had distinct cluster distributions (Fig. 8C). The approximate AP position of the culture explant was estimated by the similarity of the shape of the baseline Bmal1-ELuc bioluminescence with the AVP in serial sections (Fig. 8D). Based on this information, the clusters could be reconstructed in 3D (Fig. 8E, above) and compared with the AVP distribution in 3D (Fig. 8E, below), and finally we found that the pattern of the phase-leading cluster in 3D did not completely coincide with that of AVP immunostaining, especially on the ventrolateral edges (Fig. 8E, dashed circles).

Clustering is undisturbed by pharmacological decoupling

We performed pharmacological and surgical dissections on the SCN slices to further estimate the contribution of the intrinsic periods to cluster formation among Bmal1-ELuc oscillators in culture. Action potential silencing by sodium channel blocker TTX (0.5 or 1.0 μm, for additional blocking of persistent sodium currents) (Pennartz et al., 1997) did not disturb the internal circadian rhythms in the SCN not just in vivo (Schwartz et al., 1987) but also at the single-cell level (Welsh et al., 1995). Since the period of Bmal1 oscillation is an intrinsic property of a single cell, we anticipated that, with the circadian rhythms undisturbed under TTX application, the apparent phase relationship among Bmal1 oscillators would stay undisturbed as well. However, in Per1-luc-expressing SCN cultures, prolonged application of TTX caused loss of such relationship among oscillators, and the functional loss of network coupling was thought to be the culprit (Yamaguchi et al., 2003). To effectively decouple oscillators, we applied the GABA_A blocker gabazine (SR-95531) (10 μm), which suppresses synaptic transmissions among SCN neurons, which are mostly GABAergic (Klein et al., 1991). We also surgically cut the SCN slice into the dorsal and ventral regions to remove a network connection responsible for robustness from disturbances (Buhr et al., 2010).

Via our grid-based method, we could exhaustively compare oscillations before and after the drug application. The canonical ordering of the dorsal initiation and the ventral termination of Bmal1 expression was preserved regardless of pharmacological or surgical isolations (Fig. 9A, right), causing little changes in the cluster patterns (Fig. 9A, left). The clusters of correlated oscillations were calculated separately for the durations of control recording and chronic drug treatment. Topographical changes of clusters were quantified by the angular CM positions and the degree of overlap between pretreatment and posttreatment clusters (Fig. 9B) (see Materials and Methods). Quantitatively, the cluster positions did not deviate much after the drug application and stayed significantly correlated (r = 0.58; p < 0.001; n = 30 unilateral clusters from 5 explants; Fig. 9B, middle). Most members of clusters did not alter, and the overlaps were estimated to be 68 ± 4% in the leading cluster and 62 ± 4% in the lagging cluster, both significantly above chance levels (p < 0.0001 in leading clusters; p < 0.001 in lagging clusters; 5 explants; Fig. 9B, right). Despite minute changes in details, the overall cluster topography remained invariant. The detailed dynamics appeared to change following pharmacological isolation of oscillators. First, the period generally increased in imaging samples, while there was no significant change in period after mock treatment (Fig. 9C). This trend, however, was not found to be statistically significant in a larger set of photometry samples (p = 0.16, n = 12 for 1 μm TTX; p = 0.44, n = 11 for 0.5 μm TTX; Fig. 9C, inset). The increase did not spread the period distributions enough and failed to influence overall cluster topography. A surgical cut along the dorsoventral border similarly failed to disturb the cluster topography (n = 3). Interestingly, we found clear discontinuity in period and phase distributions in surgically separated Bmal1-ELuc samples (Fig. 9D, first and second rows), while we were unable to find a similar division in periods in a PER2::LUC sample (Fig. 9D, bottom row).

It has been suggested that the protein synthesis inhibitor cycloheximide (CHX) resets the molecular clock in single cells and recovery of the SCN after CHX washout corresponds to restarting the oscillations from the same initial state (Yamaguchi et al., 2003). The same study also suggested that TTX removes action potential-mediated network couplings. If phase ordering in culture is determined mostly by intrinsic properties of cells than synaptic influences, it should still occur under TTX after resetting by CHX. We therefore let the SCN culture recover under TTX (0.5 μm) to the wash medium after an 18 h CHX (10 μg/μl) treatment. As shown in Figure 9E, the canonical cluster topography was preserved under TTX (first row, left panel) and the period distribution mirrored the topographical phase pattern (second and third rows, left panel). Although the signal-to-background ratio was compromised after the CHX treatment, the dorsal-to-ventral phase ordering reappeared among clusters (mid-posterior SCN; right panel). This result contrasts with the previous interpretation of the CHX effect that the network, not single cells, retains the circadian state information that is used to restore the phases of component oscillators (Yamaguchi et al., 2003). At least in the Bmal1-ELuc system, it appears that the cell-intrinsic period, rather than the action potential-mediated coupling, is a critical factor for organizing phases in the SCN culture.

Heterogeneity of period is intrinsic to SCN regions

To further verify that the period is intrinsically determined in each SCN subregion regardless of synaptic couplings, we surgically microsectioned the mid coronal section of the SCN and monitored the oscillation of each region in isolation. In addition to the D and the V regions in the mid to posterior aspects that our clustering identifies, we have subdivided the ventral into the VM and VL (Fig. 10A). The VM includes the “central area” (Morin and Allen, 2006) identified by GRP immunoreactivity, a putative input pathway of the light signal. The SCN explant was thereby decomposed into three basic components, D, VM, and VL. To determine network effects between the regional components, we prepared six types of microsections (which we call “onigiri” sections), representing all possible ways to decompose the whole slice by physically removing one or two components while leaving the connections of the remainders intact. For example, removing VL from the whole slice to make a T-shaped onigiri section representing D+VM and removing VM leaves an A-shaped D+VL section (Fig. 10A, left). We then monitored bioluminescence from each onigiri section, expressing either Bmal1-ELuc or PER2::LUC, by photometry and detrended the population oscillation (Fig. 10B).

The averaged time series (peak amplitude normalized to the whole slice) showed approximately an antiphasic relationship between Bmal1 and Per2 in the whole slice. However, each onigiri section revealed a slight deviation from the relationship that was especially pronounced in D (Fig. 10C, “D,” second row, first column). The correlation matrix summarizes all phase relationships among onigiri sections using Bmal1-ELuc and PER2::LUC reporters, which shows the nearly, but not completely, antiphasic relationship between Bmal1 and Per2 is region dependent (Fig. 10D).

The arrival times of the first peak, inversely related to phases (Fig. 4), had a strong positive correlation with the intrinsic periods (r = 0.78; p < 0.05; n = 7 mean period–phase pairs) (Fig. 10E, left), whereas a similar relationship could not be found in PER2::LUC cultures (Fig. 10E, right), corresponding to the poor phase–period relationship observed in intact slice cultures (Fig. 4F–H). The onigiri sections containing D were marked by shorter periods (*p < 0.05, D, T, A, W, vs VM, VL, V; n = 10–33 sections) (see Materials and Methods) (Fig. 10E, left) and removing D diversified phases. In comparison, the relationship between D and V was straightforward. The oscillation of the whole slice behaved as if it were a simple sum of the separated D and V component oscillations (Fig. 10F, top). When the ventral subregions, VM and VL, were further dissected, the sum of the component oscillations coincided with the whole slice oscillation except for an initial phase separation that soon disappeared (Fig. 10F, bottom). This transient phase gap reflects a residual in vivo phase state in ventral subregions that eventually succumbs to the effect of intrinsic periods, which we found identical in both VM and VL subregions (Fig. 10E, left). Our findings with onigiri sections support the idea that the region-specific distribution of intrinsic period is the origin of clustering in the SCN explant culture.

Heterogeneous periods encode the light/dark cycle

If the intrinsic period is the important determinant of the entire phase evolution of an oscillator in vivo as in vitro, the period can be a reliable predictor for the future behavior of the SCN oscillation. Robust maintenance of period heterogeneity in culture suggests that the period clusters can serve as a memory of a particular “circadian state.” Reorganization of the phase distribution of circadian oscillations in the SCN by the day length variation has been known (VanderLeest et al., 2007; Brown et al., 2009). The question is whether there can be corresponding changes in the distribution of periods.

Our Bmal1-ELuc imaging data showed that, throughout various regimens of photoperiodic conditioning, the topographical distribution of periods remained unchanged (Fig. 11A). The cluster topography, directly related to the spatial period distribution, stayed similar regardless whether the animals were kept under DD (n = 3 explant imaging samples), EP (12:12 LD; the control condition), SP (n = 12), and LP (n = 8). This is comparable with a previous study that showed the period of the population PER2::LUC oscillation does not modulate significantly but tends to become longer after a short photoperiod (8:16 h light/dark cycle) and shorter after a long photoperiod (16:8 LD) (Mickman et al., 2008).

Figure 11.

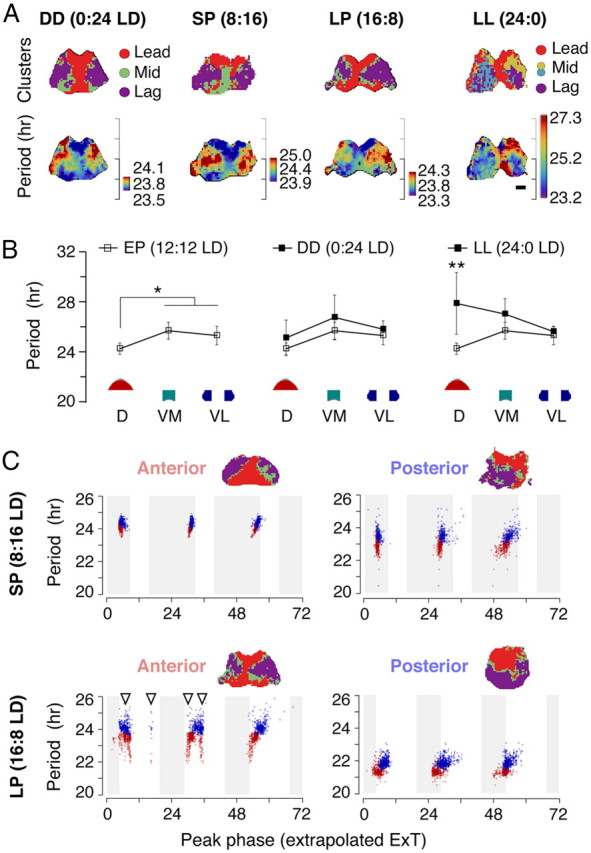
The periods change under all photoperiodic conditions while the corresponding clusters remain intact except for the constant light. A, The Bmal1-ELuc rhythms from SCN explants show preserved cluster topography from animals subjected to DD, SP (8:16 LD), or LP (16:8 LD) before culture. Prolonged exposure under LL breaks down the cluster topography (top row). The spatial pattern of period distribution remains similar to that of clusters as in control conditions (Fig. 3) except for the LL (bottom row). B, Onigiri section cultures show no significant difference in Bmal1-ELuc rhythms in SCN explants between the DD-free-run and EP (12:12 LD)-entrained animals (*p < 0.05, Welch's t test; n = 22, 14, and 14 from EP, and n = 4, 4, and 3 from DD, each for D, VM, and VL, respectively). This is in contrast with higher interculture variances seen in explants from LL-free-run animals, with a significantly increased mean value in D (**p < 0.01, Welch's t test; n = 6, 6, and 5, respectively, for D, VM, and VL). C, While the cluster topography remains unchanged (insets), the intrinsic period, in addition to the phase, shows plastic reorganization after SP and LP entrainments. Oscillators are brought in-phase after the SP entrainment, and the mean period remains close to 24 h in both the anterior and the posterior SCN explant cultures (top). The LP entrainment induces a divergent distribution of periods among the anterior and the posterior SCN while showing a bimodal phase distribution in the anterior (bottom). The oscillators with shortened periods gradually phase-advance under absence of external stimuli. The time on x-axis is in hours, with zero indicating midnight in ExT.

However, we observed that the cluster topography, robust against all the pharmacological and physical perturbations, broke down after animals had been kept under LL (n = 7) (Fig. 11A, far right); the noncanonical clustering was also characterized by a variable number of clusters (3, 3, 4, 4, 5, 9, and 10; compared with 3 in all EP controls). The within-explant mean intrinsic period increased in all cases (24.4 ± 0.7 h, mean ± SD; p = 0.02, n = 7 against 23 EP controls, Mann–Whitney U test), and in five of seven recordings the distribution became wider (within-slice SD, 3.03 ± 1.43 h, p < 0.01 against EP, in five samples, vs 0.19 ± 0.01 h in two samples). This is consistent with the report using Per1:GFP reporter mice that oscillators in the SCN desynchronize during free running under LL but is in contrast with the observation that periods in single cells do not alter (Ohta et al., 2005). This discrepancy can be due to a regional bias in period lengthening in addition to variance in samples. Whereas the intrinsic period distribution does not change significantly between EP-entrained and DD-free-run onigiri sections, the LL-free-run dorsal section displays significant lengthening of period compared with the corresponding EP entrained section (**p < 0.01; n = 6, 6, and 5, respectively, for D, VM, and VL; Fig. 11B). The observed loss of synchrony in LL samples may, therefore, be at least partially attributed to the widened period distribution.

Meanwhile, redistribution of intrinsic periods was observed in the SP and LP entrainments. The single-oscillator periods plotted against the peak timing showed that cellular intrinsic periods were modulated simultaneously with the phases (Fig. 11C). In the LP, the anterior SCN initially showed secondary peaks (Fig. 11C, bottom left, arrowheads) in the Bmal1-ELuc rhythm that dissipated over subsequent days in culture. These secondary peaks did not associate with a particular cluster, consistent with observations using the PER2::LUC reporter system (Inagaki et al., 2007). In the SP-entrained posterior SCN, although the initial oscillator phases were locked, the intrinsic periods were dispersed so that the phases will spread over time (Fig. 11C, top right).

From these, we found an interesting connection of the behavior and SCN rhythms, particularly between the mean of individual oscillator periods 〈T〉 and behavioral free-running period τ. As if the Bmal1 oscillation periods in the SCN anticipated the aftereffect, after the SP entrainment, the oscillators in the anterior (top left) had a tight period distribution with a substantially longer 〈T〉 (p < 0.05, Welch's t test; 25.1 ± 1.8 h, mean ± SD, in five anterior SCN explants, vs 23.2 ± 1.1 h in seven posterior explants), while, in the LP-entrained samples, 〈T〉 tended to be shorter in the posterior (p = 0.13; 23.1 ± 0.8 h, four anterior, vs 21.4 ± 2.5 h in four posterior explants). These connections between the photoperiodic conditions and the Bmal1 oscillator periods suggest that the period heterogeneity in the cultured SCN is not an accidental outcome of the in vitro condition but is reflective of the in vivo state before explantation.

Discussion

We have observed that oscillators in the cultured SCN explant attain cluster, or partial, synchronization. Absence of complete synchronization in our explant cultures indicates that the coupling among oscillators is not strong. The spontaneous clustering in the SCN bears a striking similarity to clustered contractions in the small intestine, where the heterogeneous distribution of intrinsic periods and weak couplings can entirely explain cluster synchronization (Ermentrout and Kopell, 1984). Furthermore, weak mutual entrainment can lead to separation of phases by intrinsic periods in a linear relationship (Winfree, 1967). These suggest that most of our experimental observations can be explained by weak interactions among heterogeneous SCN neural populations. Although weak coupling explains most of the observed data, it does not fully account for the orchestration of synchronization over time (Fig. 6C). Synaptic couplings can have large, population-wise consequences, as evidenced by loss of resistance to temperature forcing under TTX (Abraham et al., 2010; Buhr et al., 2010). Our simulation shows even a weak coupling beyond a small value can dramatically narrow period distribution to a single peak (Fig. 6B). Therefore, it is likely that some unknown form of interaction is present among SCN oscillators.

There has been an emerging hypothesis that the SCN network connectivity preserves phase information of individual oscillators (Yamaguchi et al., 2003). Our results, however, suggest that the precise nature of the network and couplings in the SCN still awaits clarification. The SCN is a phylogenetically ancient structure, and a direct analogy cannot be drawn from cortical networks. Similar to what we observed in the SCN, coordinated PER2::LUC rhythms in the presence of TTX are seen in other hypothalamic structures (Guilding et al., 2009). In particular, after resetting by CHX, the Bmal1 oscillators spontaneously form the canonical phase relationship (dorsal to ventral) during recovery under TTX. As an alternative explanation of the study by Yamaguchi et al. (2003), it was proposed that regionally distributed intrinsic periods create the observed phase distributions (Gonze et al., 2005), which is compatible with our findings. How action potentials couple SCN oscillators is as yet unclear. One possibility is that, unlike cortical networks, continuous presence of action potentials is not essential for intercellular communication. This is demonstrated by the electrical self-silencing of Per1 SCN neurons, which occurs at the supposed peak of their electrical firing (Belle et al., 2009). This could explain why the oscillator cluster structure is sustained even under action potential silencing, as it does not deviate severely from natural conditions.

The circadian oscillation itself occurs autonomously in a single cell. Dissociated single SCN neurons produce robust circadian rhythms (Welsh et al., 1995; Webb et al., 2009), and imaging studies reveal robust Per2 cycling in single non-neuronal cells (Welsh et al., 2004). The SCN cells without a network organization are functional as well, as they can restore circadian locomotor rhythm in SCN-lesioned hamsters (Silver et al., 1990). This leads us to picture the whole network dynamics as a collective phenomenon created by a population of autonomous oscillators, not that the network is the master coordinator of rhythms in individual oscillators. We visualize the oscillators as runners on a track (Fig. 12A). If the oscillators in the leading cluster (red) and the lagging cluster (blue) are organized through an explicit network coupling, like runners carrying a log in a line, there should be immediate desynchronization after application of TTX, which would sever coupling (Fig. 12B). However, the oscillators still maintain the ordered pace under the decoupling, implying that the intrinsic period is the dominant driving force of individual oscillations.

Figure 12.

A conceptual model of Bmal1 oscillatory dynamics in the SCN. A, The oscillator phases evolving in time are comparable with runners on a circular track. The clustered organization of Bmal1 oscillations depends less on the explicit coupling among oscillators, analogous to runners forced to carry a log and align themselves (top); rather, it occurs spontaneously by the intrinsic period distribution of all oscillators (bottom). B, The phase relationship between the leading and the lagging clusters remain invariant before (top) and after pharmacological or surgical isolations, as illustrated by the unchanged phase relationship on the fifth day of chronic TTX application (bottom). The phases of oscillators are represented as dots in colors, red for phase-leading and blue for lagging clusters, and the arrow indicates the mean phase with its length representing the degree of synchronization. The hour of day is expressed in extrapolated ExT.

Our studies with Bmal1 contrast potential differences with Per2 dynamics. Foley et al. (2011) reported cluster structures from PER2::LUC imaging that resemble patterns of baseline bioluminescence. The same study showed that the PER2::LUC activities coincide with expression of AVP, which we have also found not just in our PER2::LUC samples but also in Bmal1-ELuc samples (Fig. 7C). This indicates a strong association of AVP expression with the baseline expression of PERIOD and BMAL1. The similarity of AVP and baseline reporter expression patterns provides a clue to understand the differences in the two studies. Evans et al. (2011) found that the spatial expression of AVP is not associated with patterns of PER2::LUC activities, which we have also found in our study (Fig. 8E). Hence, the differences in clusters found in the study by Foley et al. (2011) and ours could be due to inclusion or exclusion of baseline activities.

Evans et al. (2011) also reported that the regional phase heterogeneity is not associated with the period. Consistently, in our PER2::LUC imaging samples, the period–phase relationship was absent or unclear (Fig. 4F–H), while our Bmal1-ELuc data showed a clear relationship between period and phase (Figs. 4D, 10E, left). In particular, the clusters in the PER2::LUC cannot be separated by intrinsic periods (Fig. 4H). This was also observed in surgically separated onigiri sections where the linear relationship between the period and the first peak phase was absent in the PER2::LUC samples (Fig. 10E, right) but present in the Bmal1-ELuc.

It remains unclear why the robustly maintained period heterogeneity in Bmal1-ELuc oscillations did not parallel in the PER2::LUC reporter condition. We suspect this could illustrate the potential independence of Per and Bmal1 pathways (Relógio et al., 2011). The circadian period of behavioral rhythms in the most widely used C57BL/6 mouse strain is ∼23.7 h, which was also true in our Bmal1-ELuc and PER2::LUC strains on the same background (Fig. 1B). In other studies, including ours, the SCN explant culture of PER2::LUC showed >24 h period length (Foley et al., 2011) regardless of the age of the animal or the thickness of the tissue preparation (Webb et al., 2009; Ko et al., 2010). The apparent dissociation of Per2 rhythms from behavioral rhythms can be related to differences in cellular pathways governing Per2 and Bmal1 dynamics. Conceptually, the circadian clock protein BMAL1, after forming a heterodimer with CLOCK or NPAS2, works as a substrate for expression of Per1, 2, and 3. However, it has not been defined precisely how each heterodimeric combination of PER1, 2, 3, and CRY1, 2 coordinates feedback to Bmal1 expression (Reppert and Weaver, 2002). Functionally, relative independence of the positive- and negative-feedback loops can enable cellular coding of the day length as suggested by the computational model of the fungal circadian clock (Akman et al., 2010). We speculate that the difference in susceptibility to outside influence of the two loops (von Gall et al., 2003) could be one factor that led to different behaviors of Bmal1-ELuc and PER2::LUC.

Contrary to simple mechanical clocks, which are robust pacemakers, the period of biological clocks can be plastic, or labile (Pittendrigh, 1960). We observed such lability through an internal reorganization of periods by day length. Single neurons are capable only of maintaining circadian rhythms, but their collective distribution of oscillations can represent photoperiod. Intrinsic periods of oscillators can store such extracircadian information since the phase redistribution is dependent upon the period distribution. An early model for the mechanism of this seasonal coding postulated that two heterogeneous oscillators, named morning (M) and evening (E) oscillators, decrease or increase their period lengths in response to light, respectively (Pittendrigh and Daan, 1976b). Our observations are comparable with the classical M and E oscillators model, in which the posterior SCN acts as the M oscillator as it is relatively phase advanced compared with the anterior under EP and its period modulates as a negative function of light duration, particularly in the LP (Fig. 11C, bottom left). There is no such correspondence in the anterior SCN, and period lengthens, rather than shortens, under the SP. Since external light stimuli are absent in the dish, the culture environment can be thought to emulate constant darkness and this lets us interpret the unusual period distributions of single oscillators as signatures of behavioral aftereffects. There are other examples that show period actively participates in formation of overall dynamics along with phase. In the Drosophila clock system, instead of adapting phases in response to light, a class of neurons modulates the period (Yoshii et al., 2009). Disorganized or short-period rhythms in mice lacking VIP receptors can be entrained robustly by artificial period lengthening with casein kinase 1 inhibition (Meng et al., 2010). However, we suspect that still an unknown coupling mechanism awaits discovery, which mediates both the adjustment of periods and maintains the stability of phase relationships in vivo.

We showed that distributed periods of individual neurons are a potent determinant of SCN dynamics. We further demonstrated the plasticity of intrinsic periods under summer or winter day lengths and found it to be region specific. Together, we propose that the heterogeneous distribution of intrinsic periods represents the internal state of the SCN and that this potentially plays an important role in the coding of light duration.