Biophysical Mechanisms of Multistability in Resting-State Cortical Rhythms

Abstract

The human alpha (8–12 Hz) rhythm is one of the most prominent, robust, and widely studied attributes of ongoing cortical activity. Contrary to the prevalent notion that it simply “waxes and wanes,” spontaneous alpha activity bursts erratically between two distinct modes of activity. We now establish a mechanism for this multistable phenomenon in resting-state cortical recordings by characterizing the complex dynamics of a biophysical model of macroscopic corticothalamic activity. This is achieved by studying the predicted activity of cortical and thalamic neuronal populations in this model as a function of its dynamic stability and the role of nonspecific synaptic noise. We hence find that fluctuating noisy inputs into thalamic neurons elicit spontaneous bursts between low- and high-amplitude alpha oscillations when the system is near a particular type of dynamical instability, namely a subcritical Hopf bifurcation. When the postsynaptic potentials associated with these noisy inputs are modulated by cortical feedback, the SD of power within each of these modes scale in proportion to their mean, showing remarkable concordance with empirical data. Our state-dependent corticothalamic model hence exhibits multistability and scale-invariant fluctuations—key features of resting-state cortical activity and indeed, of human perception, cognition, and behavior—thus providing a unified account of these apparently divergent phenomena.

Introduction

Human ongoing cortical activity during resting-state recordings is characterized by spontaneously fluctuating oscillations, particularly in the alpha (8–12 Hz) frequency band. Fluctuations of the alpha rhythm have traditionally been perceived as “waxing and waning,” akin to the fluctuating behavior of a random signal with a Gaussian amplitude distribution. Contrary to this prevailing notion, we recently demonstrated that spontaneous alpha activity bursts erratically between two distinct modes of activity (Freyer et al., 2009). A biophysical mechanism for this multistability has not been established and would have fundamental consequences for our understanding of spontaneous activity in the cortex as well as multistability as it occurs more generally in human perception (Ditzinger and Haken, 1989; Lumer et al., 1998; Haynes et al., 2005), decision making (Deco and Rolls, 2006), and behavior (Schöner and Kelso, 1988).

Spontaneous cortical activity recorded in electroencephalographic (EEG) data reflects the local spatial average of millions of cortical neurons. In contrast to biophysical models of synapses and spiking neurons, elucidating the causes of such large-scale data requires models of neuronal population dynamics that engage the cortex at the macroscopic scale (Freeman, 1975; Nunez, 2000). Two widely studied neural population models that yield alpha oscillations are the purely cortical model of Wilson and Cowan (1972) and the corticothalamic model elaborated by Lopes da Silva et al. (1974). These formative models established an important precedent for the crucial role that large-scale models of cortical rhythms play in elucidating causal mechanisms (Lopes da Silva et al., 1997). However, although they embody a number of basic neurophysiological processes, they lack important properties, such as conduction delays, spatial effects on the cortical sheet, detailed physiological parameterization, and validation across a variety of experimental settings. Hence, although they have explanatory power for particular phenomena, the potential to generalize these explanations across phenomena and hence provide a unifying framework is limited.

Recent progress in this field has focused on improving the physiological and anatomical foundation of these models as well as the range of healthy and pathological states that they describe (Deco et al., 2008). The biophysical model we study describes local “mean field” dynamics of populations of excitatory and inhibitory neurons in cortical gray matter interacting with neurons in relay and reticular nuclei of the thalamus (Robinson et al., 1997, 2001b). This activity is governed by physiologically based nonlinear differential equations that incorporate synaptic and dendritic dynamics, nonlinear firing responses, and axonal delays. The model has provided a unifying explanation of evoked potentials and a wide variety of states in wakefulness and sleep (Robinson et al., 2001b, 2002) and successfully predicted key features of human epileptic seizures (Robinson et al., 2002; Breakspear et al., 2006).

Despite these successes, the mechanisms of multistable fluctuations in healthy rhythmic activity have not yet been elucidated. To address this problem, we present a systematic analysis of spontaneous activity in this mean field model as a function of its dynamical stability and the nature of its stochastic inputs, constrained by detailed quantitative characteristics of multistability in empirical EEG data.

Materials and Methods

Corticothalamic neural field model

We studied a biophysical model that describes local mean field dynamics (Jirsa and Haken, 1996; Robinson et al., 1997; Deco et al., 2008) of populations of excitatory and inhibitory neurons in the cortical gray matter as they interact with neurons in the specific and reticular nuclei of the thalamus (Robinson et al., 2001b, 2002). A schematic overview of the model, showing the principle neural populations and their interconnections, is illustrated in Figure 1.

Figure 1.

Schema of principal neural populations and loops within the corticothalamic model. Connectivity and loops include intracortical (ee, ei, ie, ii), corticothalamic (re, se), thalamocortical (es, is), and intrathalamic (sr, rs). Arrows indicate excitatory feedback (blue) and inhibitory feedback (red).

The activity in each neural population is described by three state variables: the mean soma membrane potentials V_a(x,t) measured relative to resting, the mean firing rate at the cell soma Q_a(x,t), and the local presynaptic activity ϕ_a(x,t) where the subscript a refers to the neural population (e, excitatory cortical; i, inhibitory cortical; s, specific thalamic nucleus; r, thalamic reticular nucleus; n, nonspecific subcortical input). In broad terms, the differential equations that describe this model embody the conversion of each of these state variables into another through synaptodendritic filtering, neuronal activation, and axonal propagation within and between populations.

Presynaptic activity ϕ_a couples through synaptic transmission to postsynaptic potentials. The cell body potentials V_a fluctuate after these postsynaptic potentials have been filtered in the dendrites and summed at the cell soma. For excitatory and inhibitory neurons in the cortex, this is modeled using the second-order delay-differential equation (Robinson et al., 1997):

where a = e,i index the cortical population and the temporal differential operator

incorporates synaptic and dendritic filtering of incoming signals. For a single discrete input, this equation yields postsynaptic solutions with (bi)exponential rise and decay (the corresponding impulse response function is known colloquially as an alpha function). The quantities α and β are the inverse rise and decay times of the cell body potential produced by such an impulse at a dendritic synapse.

Note that input from the thalamus to the cortex is delayed in Equation m1 by half the corticothalamic “return time” t₀ (the time required for axonal signals to travel from cortex to thalamus and back), hence incorporating finite conduction velocities (Robinson et al., 2001b). For neurons within the specific and reticular nuclei of the thalamus, it is the input from the cortex that is time delayed and hence

for a = s,r. The effective synaptic strengths are given by ν_ab = N_abS_b, where N_ab is the mean number of synapses to neurons of type a from type b, and S_b is the magnitude of the response to a unit signal from neurons of type b.

After summation at the cell soma, changes in the local soma membrane potential V_a cause changes in the local firing rates Q_a according to the neuronal activation function Q_a(x,t) = S[V_a(x,t)], where S is a sigmoidal function that increases from 0 to Q_max as V_a increases. This is modeled as

where θ is the mean neural firing threshold, and σ is its SD. This incorporates the step-like function of an individual neural response smeared over a Gaussian distribution of firing thresholds and neuronal states (Marreiros et al., 2008).

The system of equations is closed by introducing the outward propagation of action potentials from the soma through axons, which then become presynaptic activity in distant regions. In the cortex, excitatory firing rates Q_e are propagated outward as ϕ_e according to the damped wave equation (Robinson et al., 1997):

The parameter γ_e = v_e/r_e governs the dispersion of propagating waves, where r_e and v_e are the characteristic range and conduction velocity of excitatory neurons, and ▿² is the Laplacian operator (the second spatial derivative). All other neural populations are approximated as having axons sufficiently short that they do not support wave propagation on the relevant scales for these populations. This gives ϕ_a = Q_a for a = i, r, s (Robinson et al., 1997).

The default values of all parameters were set to those values used in previously published studies (Robinson et al., 2002; Breakspear et al., 2006), which are strongly constrained by physiology (Robinson et al., 2004). For the present purpose, we focus on the global spatial mode, i.e., we investigate the case of spatially uniform activity. To this end, we set the spatial derivative ▿² in Equation m5 to zero, which removes spatial variation in the activity while still maintaining the intracortical spatial connectivity, including the finite axonal range and conduction velocity (elucidating the spatial properties of alpha bistability could be achieved within the full neural field framework by allowing the spatial derivative to be nonzero). This yields a set of eight first-order delay-differential equations (Robinson et al., 2002):

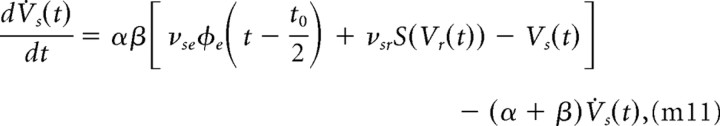These deterministic delay-differential equations allow the mathematical analysis of the attractors of the system and their bifurcations. To model the in vivo corticothalamic system, it is necessary to add stochastic terms that can embody a wide range of fluctuations, from thermal effects to synaptic inputs from brain regions not specified in the model. Stochastic fluctuations were modeled by introducing a noise term ϕ_n into the equations for the postsynaptic kernels in the excitatory neurons of the cortex (Eq. m9), specific (Eq. m11), or reticular (Eq. m13) nucleus of the thalamus. Hence, for example, Equation m11, expressing mean voltage fluctuations in the specific nucleus of the thalamus, becomes the stochastic delay differential equation:

where ν_sn indicates the synaptic strength of these synaptic inputs.

Large-scale fluctuations in electrical potentials, as recorded by EEG, are thought to primarily reflect summed synaptic currents in cortical pyramidal dendritic arbors induced by presynaptic inputs (Lopes da Silva et al., 1974; Nunez, 1995; Robinson et al., 2001a, 2004). Hence, we use the time series of ϕ_e to represent the cortical sources of scalp EEG. These time series were obtained from numerical integration of the corticothalamic model in the presence of stochastic fluctuations over long periods of time (4200 s). Numerical integration was performed using Heun's integration scheme, which is an extension of the Euler integration into a two-stage second-order Runge–Kutta integration scheme (Mannella, 2002). The analysis was repeated with other fixed step integration schemes, including the Euler method and the fourth-order Runge–Kutta scheme. All the phenomena reported here were observed with all of these schemes for sufficiently small time steps.

Electroencephalographic data

The activity of the model was compared with empirical distributions derived from human EEG data. Scalp EEG data were acquired from 16 healthy subjects (11 females; mean age, 25.3 years; range, 20–31 years) using BrainAmp amplifiers (hardware bandpass filter, 0.1–250 Hz; BrainAmp; Brain Products) and EEG caps (Easy-Cap; FMS) arranged according to the International 10–20 System, referenced against an electrode centered between Cz and Pz. Impedances of all electrodes were set below 5 kΩ. Written informed consent was obtained from each subject before their participation. Subjects were requested to rest with eyes closed while maintaining alertness. Acquisition times ranged in duration from 14 to 30 min. For detailed description of EEG data acquisition and preprocessing, please refer to the study by Freyer et al. (2009).

Parameter estimates for probability distribution functions and dwell-time distributions

Important properties of complex, correlated systems, such as the brain, can often be captured by a detailed characterization of the statistics of their macroscopic signals (Bramwell et al., 2000). Such an approach can uncover and constrain key underlying physical processes. Candidate quantities include the system power fluctuations and their temporal statistics (Freyer et al., 2009). Parameter estimates for the bimodal power fluctuations and for the cumulative distribution of the time the system dwelled in each of these two modes were hence derived from both the computational and empirical data to test whether the former embodied the key dynamical mechanisms observed in the latter.

Parameter estimates for exponential probability distribution functions.

Dynamic spectrograms were obtained by convolving the data with complex Morlet wavelets (center frequency, 1 Hz; bandwidth parameter, 10 s). Power at 10 Hz was estimated as the modulus squared of the corresponding wavelet coefficients. Frequency-specific probability distribution functions (PDFs) were then obtained by partitioning the fluctuations of power at 10 Hz into 200 equally sized bins and counting the number of observations in each bin.

For processes exhibiting Gaussian fluctuations in amplitude, the functional form of the corresponding power distribution follows an exponential PDF (Balakrishnan and Basu, 1996), P_x(x) = λe^−λx, where x is the power, and λ is the shape parameter that can be estimated from an empirical distribution by taking the log of the probability and estimating the slope of the resulting line. To gain a better insight into the functional form of the PDF—particularly the asymptotic scaling behavior of both tails—the fitted PDFs were formally evaluated in log–linear and log–log coordinates. For bimodal distributions, a second exponential distribution was estimated from the residuals, obtained after subtracting the primary mode. The resulting bimodal distribution can therefore be considered as a mixture of exponentials. As in the study by Freyer et al. (2009), we formally compared the bimodal to a unimodal fit using the Bayesian information criterion (BIC), which includes a penalty term for model complexity: Λ = n1n $\left(\frac{RSS}{n}\right)$ + k1n(n), where RSS is the sum of the squared residuals, n is the number of observations (discrete power bins), and k is the number of free parameters (k = 1 for the unimodal fit and k = 2 for the bimodal fit). Given two or more candidate models, the “best” model will yield the lowest value of Λ, reflecting small residual variance after penalization for the number of free parameters.

Parameter estimates for stretched-exponential dwell-time cumulative distribution functions.

After estimation of bimodal exponential distribution functions for the power fluctuations, the dwell-time distributions were characterized. These are the successive durations that the system resides in each of the two modes. Following Nakamura et al. (2007), the dwell times can be characterized by estimating their cumulative distribution functions (CDFs). For a simple (noise dominated) stochastic process, these can be expected to follow a simple exponential function P(X ≥ x) = exp(−ax). For more complex processes, these CDFs can be expected to develop long right-hand tails (Zaslavsky, 2002; Tsallis, 2006) such as power-law and stretched-exponential distributions. Indeed, viewing the dwell-time CDFs in log–log coordinates (Freyer et al., 2009) shows that the EEG data do not follow a power law distribution but rather a stretched-exponential form P(X ≥ x) = exp(−ax^b), where the right-hand tail of the distribution becomes heavier as the shape parameter b → 0. To estimate the parameters a and b, the equation can be rewritten as log(−log(P(X ≥ x))) = b log(x) + log(a). The parameters a and b were estimated from both the empirical and model data by means of a least-squares linear regression in log(x) − log(log(P)) coordinates.

Results

Multistable switching in empirically recorded alpha activity

We sought a mechanism for multistable alpha activity using a neural field model of large-scale brain dynamics (Robinson et al., 2001b, 2002). We evaluated the fundamental properties of the alpha activity simulated by this model according to three recently described (Freyer et al., 2009) key empirical observations. (1) The instantaneous power in the alpha band jumps spontaneously and erratically between distinct low- and high-amplitude modes. That is, power fluctuations are closely predicted as arising from two distinct probability distributions with partially overlapping tails (Fig. 2a,b). (2) Fluctuations of power within each of these modes follow an exponential probability distribution. Crucially, the SD of each mode scales in proportion to its mean: the widths of both modes are hence equivalent (scale-free) on logarithmic axes despite differences in their means of three orders in magnitude (Fig. 2c). (3) “Dwell times” of resting-state alpha activity within the two modes have long-tailed stretched-exponential distributions (Fig. 2d).

Figure 2.

Multistability in human EEG data. a, Exemplar time course of the power at 10 Hz (squared wavelet coefficients) shows erratic switching between low-power (black) and high-power (red) modes. b, Corresponding time–frequency plane. c, Probability distributions of power at 10 Hz (gray squares) are closely fitted by the sum (white line) of the two unimodal exponential distributions of low-power (black) and high-power (red) modes. A direct model comparison indicates the superiority of the bimodal fit compared with the unimodal fit [BIC difference (unimodal − bimodal) = 532]. Note that the width of each mode is constant on logarithmic axes, implying that the SD is scale free. The intersection of the exponential distributions provides the threshold used to partition the time series. d, Dwell-time cumulative distributions for the low-power (black) and high-power (red) modes closely follow long-tailed stretched-exponential forms (white lines). The parameter values of the stretched-exponential fits for the dwell-time CDFs of the low- and high-energy mode are a_low = 1.94, a_high = 1.78, b_low = 0.54, and b_high = 0.71. The gray line indicates a simple exponential form. Cumulative distributions were separately rescaled to have a mean value of one.

Spontaneous activity in the corticothalamic model

The neural field model we studied in the present report describes local mean field dynamics of populations of excitatory and inhibitory neurons in the cortical gray matter as they interact with neurons in the specific and reticular nuclei of the thalamus (Fig. 1). These dynamics are governed by physiologically derived nonlinear evolution equations that incorporate synaptic and dendritic filtering, nonlinear firing responses, corticothalamic axonal delays, and synaptic gains between presynaptic impulses and postsynaptic potentials (for detailed description and equations, see Materials and Methods).

Simulated data are obtained by integrating the corticothalamic model in the presence of nonspecific stochastic fluctuations of various forms. We modeled the effect of synaptic noise in the dendritic tree, because this is thought to be crucial to both background and evoked cortical responses (Faisal et al., 2008). Such inputs also mimic synaptic bombardment from thousands of neurons not explicitly modeled, such as from ascending subcortical nuclei. Synaptic and dendritic filtering of afferent inputs in this model are described by second-order delay differential equations that incorporate exponential rise and decay times of the cell body potential after synaptic impulses (see Materials and Methods, Eqs. m1–m3). Stochastic fluctuations were thus modeled by adding a noise term ϕ_n to the synaptic kernel of the equations for the neurons of the cortex or the specific or reticular nuclei of the thalamus (see Materials and Methods, Eq. m14). Following previous work (Robinson et al., 2004), we initially modeled ϕ_n as a simple uncorrelated noise process:

with mean ϕ_n⁽⁰⁾ and superimposed time-dependent fluctuations ϕ_n⁽¹⁾(t) drawn from a Gaussian distribution with zero mean and SD σ_n.

Consistent with previous reports (Robinson et al., 2001b), we observed spontaneous activity with a clear alpha component in the noise-driven model when the gains in the corticothalamic circuit were sufficiently high. Figure 3 illustrates an exemplar simulation using previously published parameter values for alpha activity (Breakspear et al., 2006), with stochastic fluctuations impinging on the specific thalamic nucleus. It can be seen that, although power in the alpha band fluctuates (Fig. 3a), it is nonetheless confined to a single-exponential distribution (Fig. 3b). Erratic jumping between low- and high-amplitude alpha was hence not observed with these parameter values regardless of the variance of the stochastic term, nor whether the noise impacted on thalamic or cortical populations. The behavior of the model in this dynamical regime thus accords with the widely held notion of the alpha rhythm as waxing and waning but conflicts with the more complex dynamics of actual empirical data.

Figure 3.

Fluctuations in alpha power in the noise-driven corticothalamic model in the presence of a global fixed point attractor. a, Noise-induced fluctuations in the expression of spontaneous alpha power. arb. u., Arbitrary units. b, Probability distribution of power at 10 Hz (gray squares) is closely fitted by a single-exponential distribution.

Given the inevitable presence of temporal variations of underlying state parameters in biological systems, the question also arises of whether a simple manipulation of these, and hence of the nonlinear flow in the neighborhood of the fixed point, could generate the observed phenomenon. To explore this possibility, while keeping the parameter centered at its previous value, we repeated the above simulation but added a mean-reverting stochastic process, η, to the fixed value of v_se:

where σ is the variance, τ is the correlation time of this process, and ξ(t) is a zero-mean Gaussian white-noise term. We used τ = 0.1 s and σ = 0.006 v_se, corresponding to a moderate perturbation without any long-term drift. Although some additional variability was present in the fluctuations of 10 Hz power—coincident with stochastic excursions in v_se—the envelope of these fluctuations was not qualitatively changed and hence still yielded a simple unimodal exponential PDF. The same outcome was observed for a variety of choices of the correlation time τ = 0.05 s and 0.025 s.

Multistable alpha activity in the corticothalamic model

Simulations based on these previously published parameters correspond to noise-driven fluctuations around a global fixed-point attractor—that is, when all simulations evolve toward a single asymptotically stable steady state, regardless of their initial conditions. Hence, the lack of multistability in this setting is not surprising. The occurrence of multistable fluctuations challenges the notion of noise-induced excursions around a stable fixed point because they suggest that the system evolves in a multi-attractor landscape (Friston, 1997; Deco et al., 2009a; Braun and Mattia, 2010). In the present study, we therefore sought to characterize noise-driven activity in regions of parameter space that support more complex dynamics. The dynamical landscape of the corticothalamic model was mapped using the default parameters given in Table 1 by systematically exploring values of the synaptic strength parameters ν_ab between pairs of neuronal populations. Following the approach adopted by Breakspear et al. (2006), bifurcation diagrams were obtained numerically using a continuation scheme (Engelborghs et al., 2002), keeping the parameters ν_ee, ν_ei, ν_es, ν_sr, ν_re, and ν_rs fixed and incrementally varying ν_se, which parameterizes the postsynaptic response of thalamic neurons to (time delayed) presynaptic input from cortical neurons.

Table 1.

Biophysical model parameters for spontaneous multistable alpha activity

Quantity	Value	Unit	Description
Qmax	250	s−1	Maximum firing rate
θ	15	mV	Mean neuronal threshold
σ	6	mV	Threshold SD
γe	100	s−1	Ratio conduction velocity/mean range of axons
α	60	s−1	Inverse decay time of membrane potential
β	240	s−1	Inverse rise time of membrane potential
t0	80	ms	Corticothalamic return time (complete return loop)
νee	1.06	mVs	Excitatory-to-excitatory (corticocortical) synaptic strength
νie	1.06	mVs	Excitatory-to-inhibitory (corticocortical) synaptic strength
−νei	1.8	mVs	Inhibitory-to-excitatory (corticocortical) synaptic strength
−νii	1.8	mVs	Inhibitory-to-inhibitory (corticocortical) synaptic strength
νes	2.20	mVs	Specific nucleus-to-excitatory (thalamocortical) synaptic strength
νis	2.20	mVs	Specific nucleus-to-inhibitory (thalamocortical) synaptic strength
νse	2.28	mVs	Excitatory-to-specific nucleus (corticothalamic) synaptic strength
−νsr	0.845	mVs	Reticular-to-specific nucleus (intrathalamic) synaptic strength
νsn	1.20	mVs	Nonspecific noise-to-specific nucleus synaptic strength
νre	0.91	mVs	Excitatory-to-reticular nucleus (corticothalamic) synaptic strength
νrs	0.41	mVs	Specific-to-reticular nucleus (intrathalamic) synaptic strength
νss	0	mVs	Specific nucleus self connection (intrathalamic)
νrr	0	mVs	Reticular nucleus self connection (intrathalamic)
χ	0.64		Ratio of multiplicative to additive noise
σn	0.56		SD of stochastic influence φn (fraction of the stable limit cycle attractor amplitude)

We hence observed a variety of bifurcations, most notably Hopf bifurcations heralding the transition from a linearly stable, damped equilibrium point to nonlinear periodic oscillations at a critical value of ν_se. Subsequent transitions to aperiodic activity were also observed but are not the focus of the present report. Supercritical Hopf bifurcations occur when stable periodic oscillations arise at values of ν_se above this critical value. Subcritical Hopf bifurcations occur in a different region of parameter space when unstable periodic oscillations arise at values of ν_se below this critical value. Subcritical Hopf bifurcations lead to a region of bistability in parameter space, in which damped equilibrium behavior coexists with large-amplitude periodic oscillations. These two attractors are separated in phase space by an unstable periodic orbit (Strogatz, 1994). Canonical examples (normal forms) of these bifurcations are shown in Figure 4, a and b.

Figure 4.

a, b, Canonical supercritical (a) and subcritical (b) Hopf bifurcations. Black and red denotes fixed-point and periodic solutions, respectively. Solid and dashed lines indicate stable and unstable solutions, respectively. Vertical gray lines indicate critical values of the tuning parameter. c, Bifurcation diagram for ϕ_e (excitatory synaptic states) obtained from Equations 6–13 using parameter values that yielded the main findings of this study. The instability corresponds to the appearance of an unstable 10 Hz mode and a range of values for ϕ_e, which are physiologically plausible. The gray line indicates the value of ν_se,(the synaptic strength of excitatory cortical projections to the specific thalamic nucleus) used in subsequent simulations.

In previous studies (Robinson et al., 2002; Breakspear et al., 2006), seizure activity was modeled as arising from a subcritical Hopf bifurcation with a large-amplitude periodic attractor. The present survey of parameter space yielded a subcritical Hopf bifurcation with a nonpathological limit-cycle amplitude for a physiologically plausible set of model parameters (Table 1, Fig. 4c). In the vicinity of this subcritical Hopf bifurcation, spontaneous switching between low- and high-amplitude activity was observed for stochastic fluctuations impacting on the specific nucleus of the thalamus (Fig. 5a). This switching corresponds to noise-induced jumps between the limit-cycle and fixed-point attractors that coexist in this region of parameter space. Bimodal activity was not observed in the presence of a supercritical Hopf bifurcation, nor if the stochastic term was introduced into the thalamic reticular nucleus or the cortex.

Figure 5.

Multistability in the corticothalamic model when driven by purely additive noise. a, Noise-induced switching between low- and high-amplitude fluctuations. arb. u., Arbitrary units. b, Probability distributions of power at 10 Hz (gray squares) shows a broad low-power exponential distribution and a high-power mode that is relatively narrow in these logarithmic coordinates. This is because the mean is shifted by two orders of magnitude but the SD is approximately equal to the low-power mode.

If, as in the present case, the stochastic thalamic input is purely additive, then the SD in the high-amplitude mode is approximately equal to the SD in the low-amplitude mode. Viewing the distributions in log(power)–log(likelihood) coordinates—which best illustrates the SD relative to the mean—reveals that the SD in the high-amplitude mode is very narrow relative to its mean for this purely additive form (Fig. 5b). That is, their means differ by more than two orders of magnitude, but their SDs are approximately equal because the noise-induced fluctuations are simply added to the states at each integration time step. In contrast, one of the key features of the EEG data is that the SD of each of the distributions scales proportionally to its mean, so that the SD of the high-power mode should hence be two orders of magnitude greater than that of the low-power mode. In log–log coordinates, this translates into two modes with distinct centers but equivalent width (Fig. 2c).

Multistability and scale-free SD with state-dependent noise

The failure of purely additive noise to adequately capture the proportional scaling between the mean and SD of each mode suggests the need for a state-dependent modulation of the nonspecific stochastic term. The noise term was hence modified to include an activity-dependent (multiplicative) component as well as the purely additive component:

where ϕ_n^(a) and ϕ_n^(m) are two independent (uncorrelated) stochastic terms, each drawn from a Gaussian distribution with zero mean and SD σ_n. The parameter χ controls the relative influence between the multiplicative term ϕ_n^(m) and the purely additive one ϕ_n^(a). The purely additive stochastic scenario (Eq. 1) is recovered for χ = 0. Note that, for the multiplicative (state-dependent) term, we used presynaptic input from the cortex ϕ_e delayed by the appropriate corticothalamic time delay t₀/2.

The biophysical correlates of these inputs are depicted schematically in Figure 6. Simulated with this functional form, the SD of the high-power mode does scale in proportion to its mean (Fig. 7c). Moreover, the dwell times of these modes both have long-tailed stretched-exponential forms (Fig. 7d). The corticothalamic model hence shows a striking concordance with empirical properties of the EEG (compare Figs. 2, 7). That is, across a broad range of physiological parameters, simulations of spontaneous activity meet all three empirical criteria: irregular switching between low- and high-amplitude alpha oscillations, proportional scaling between the mean and SD, and long-tailed stretched-exponential dwell-time distributions. These conditions impose the following constraints on parameter values. (1) As in the purely additive case, bimodal activity only occurs in the vicinity of a subcritical Hopf bifurcation. For this to occur, the SD σ_n of the stochastic influence has to be a fraction 0.1–0.6 of the amplitude of the large-amplitude limit-cycle attractor. For higher values of noise variance, the dwell times for the switching converge to simple exponential forms, consistent with a simple noise-dominated Poisson process. (2) Proportional scaling of the SD of the higher-power mode with its mean is not observed if χ < 0.25. In contrast, the SD of both modes scaled in proportion to their respective means for 0.25 < χ < 0.7. For χ > 0.7, the limit-cycle attractor exhibits very-high-amplitude excursions, inconsistent with a healthy resting-state waveform.

Figure 6.

Schema of stochastic inputs ϕ_n (green) into the specific nucleus of the thalamus and their multiplicative modulation by excitatory inputs from the cortex ϕ_e (blue). After synaptodendritic filtering, these inputs cause fluctuations in V_s, the mean membrane potential of thalamic neurons. Note that the arrows denote population projections, not single neurons: the two nonspecific noise inputs are uncorrelated at the population level.

Figure 7.

Multistability in the corticothalamic model when driven by state-dependent thalamic input. The characteristics of the model outcome show a remarkable concordance with empirical EEG data (panels as for Fig. 2). As in the data, the PDF (c) shows a clear bimodal distribution [BIC difference (unimodal − bimodal) = 323]. The parameter values of the stretched-exponential fits for the dwell-time CDFs of the low- and high-energy mode are a_low = 1.53, a_high = 1.29, b_low = 0.66, and b_high = 0.75, closely resembling the fitting parameters of the EEG data. arb. u., Arbitrary units.

We also integrated the system with the same random value for the multiplicative and additive noise terms at each time step, in which case Equation 3 can be simplified to

Using the same parameters used in Figure 7 again yields bimodal activity. However, the long right-hand tails of the dwell-time distributions are less pronounced than in the case of independent noise terms and thus gave a poorer fit to the data in Figure 2. This effect is expected because increasing the coherence between the two inputs (by setting them equal) effectively increases the noise amplitude and hence biases the switching process toward a simple noise-dominated Poisson process, consistent with point 2 above.

Discussion

The corticothalamic field model characterized in this study provides an explanation for three key features of ongoing neuronal activity as measured with EEG in humans during rest. When driven by thalamic fluctuations, spontaneous and erratic jumps between a high-amplitude 10 Hz oscillatory mode and low-amplitude irregular activity arise only in the presence of a particular type of dynamical instability, namely a subcritical Hopf bifurcation that emerges naturally with physiological parameters. Multistability is not observed in the absence of a nonlinear instability nor in the vicinity of other forms of instability, such as a supercritical Hopf bifurcation. Moreover, multistable bursting is only observed when stochastic fluctuations are introduced in the thalamic nucleus. Scaling of the SD of both modes in proportion to their respective means requires activity-dependent noise. This emerges when fluctuating presynaptic thalamic input is modulated by backward (corticothalamic) afferents from the cortex. Long-tailed stretched-exponential dwell-time distributions mandate low-amplitude fluctuations: when the stochastic influence is large, the dwell times follow a simple exponential form, consistent with a simple stochastic (e.g., Poisson) process. These findings establish a single candidate neurobiological mechanism for multistability and scale-free uncertainty—two widely studied attributes found in human perception (Ditzinger and Haken, 1989; Lumer et al., 1998; Haynes et al., 2005), cognition (Deco and Rolls, 2006), and behavior (Schöner and Kelso, 1988)—and hence unify these apparently divergent phenomena. They also place novel and strong constraints on the form and parameterization of our corticothalamic model. We now consider each of these three components of our study—namely, neural field modeling, multistability, and scale-free uncertainty—in more detail.

To our knowledge, this is the first biophysical model of the multistable dynamics that characterize alpha activity, the dominant rhythm of ongoing, or endogenous, cortical activity. The existence of two distinct morphologies of the alpha rhythm—a low-amplitude linear and high-amplitude nonlinear waveform—has been known for some time (Lopes da Silva et al., 1973, 1997; Stam et al., 1999; Breakspear and Terry, 2002). Several studies have focused on the contribution to this phenomenon of a nonlinear instability at 10 Hz (Robinson et al., 2002; Breakspear et al., 2006). For example, Stam et al. (1999) and Liley et al. (2002) were able to capture the nature of these two waveforms by simulating cortical activity on either side of a supercritical Hopf bifurcation in a corticothalamic neural mass and purely cortical neural field model, respectively. Valdes et al. (1999) inverted a neural mass model from exemplars of each of these two types of alpha activity, hence inferring the model parameters. They also argued that these two alpha morphologies represent cortical activity on either side of a supercritical Hopf bifurcation. This dynamical scenario suggests that the cortex alternates between each of these waveforms because an underlying state parameter stochastically wanders across the Hopf bifurcation boundary. However, the presence of burst-like switching between two completely distinct modes of alpha activity challenges this view (Freyer et al., 2009). Stochastic variation of an underlying state parameter in the region of a supercritical instability would yield a continuous mixture of the statistics of all visited states and is certainly not consistent with long-tailed dwell times in distinct modes separated by two orders of magnitude in power. Indeed, we did explore the effect of adding a mean reverting stochastic process to the bifurcation parameter. These simulations confirmed that mixing the dynamics in this way continued to yield unimodal exponential PDFs. Subcritical Hopf bifurcations have been proposed to account for the erratic nature of seizure activity (Robinson et al., 2002; Lopes da Silva et al., 2003; Suffczynski et al., 2004; Breakspear et al., 2006). In the present report, we show that a similar mechanism involving a physiological limit cycle also accounts for healthy spontaneous activity. This is achieved without any variation of the underlying parameters and hence spares our model of the additional complexity that this would require. In the setting of bistability, parameter-driven state changes would also yield hysteresis. Although there is evidence of this in seizure activity, there is no evidence in resting-state EEG recordings (Breakspear et al., 2006).

The mechanism of switching we establish draws on dynamical instabilities in the phase space of the system that are expressed by noise-driven excursions across the basin boundary separating the two coexisting attractors. Although there is a dynamical instability—as a result of separation of nearby phase space flows in the vicinity of the basin boundary—the system is structurally stable in the sense that small perturbations do not cause a sudden change in the overall attractor landscape. Indeed, we have contrasted our scenario with one in which the state parameters are themselves stochastically varied, possibly causing a sudden change in the attractor landscape and associated loss of structural stability. We were unable to generate the necessary bimodal dynamics in this setting and consider it an unlikely mechanism. It is crucial to note, however, that we have established sufficient conditions for these phenomena. There are other candidate mechanisms. For example, weakly coupled chaotic attractors exhibit a form of bursting known as intermittency (Ashwin et al., 1996). However, the dwell times in this setting follow a power law, not a stretched-exponential temporal pattern. In addition, although chaotic dynamics in our neural field model are possible (Breakspear et al., 2006), they are not consistent with the observed alpha rhythm. Also, intermittent bursting requires at least two coupled systems, whereas the present setting requires only one and is hence considerably more parsimonious. Noise-driven excursions around a hetereoclinic cycle are another theoretical mechanism for the transient expression of different dynamical forms (Ashwin and Field, 1999) and are closely related to the chimera states observed by Deco et al. (2009b). However, these dynamics, which typically require three or more coupled attractors, have a very characteristic (i.e., narrow) dwell time that scales logarithmically with the injected noise. Heteroclinic cycles do not express the long-tailed forms we observe in the data. Although we are confident that our sufficient conditions may also be superior to these other dynamical candidates for multistable alpha dynamics, a more systematic comparison may be better undertaken in a simpler dynamical setting and is indeed to be the subject of future work.

Our study also advances the rapidly emerging understanding of stochastic processes in the brain (Faisal et al., 2008; Ghosh et al., 2008; Deco et al., 2009a). For example, stochastic fluctuations in combination with time delays and empirically derived patterns of cortical connectivity endow simulated resting-state neuronal activity with fluctuations across a hierarchy of timescales, mirroring high-frequency oscillations in electrophysiological data as well as slow fluctuations (<0.1 Hz) of hemodynamic signals evident in functional neuroimaging data (Ghosh et al., 2008; Deco et al., 2009b). Interactions between stochastic processes and nonlinear dynamics have also been proposed to underlie many active cognitive processes such as decision making, perceptual multistability, and working memory (Friston, 1997; Wang, 2002; Deco et al., 2007; Braun and Mattia, 2010).

An important and novel contribution of the present study is that the proportional scaling of mean and SD observed empirically mandates a multiplicative interaction in the thalamus between nonspecific stochastic inputs and feedback from the cortex. This multiplicative term implies an interaction between stochastic and cortical inputs in the dendritic tree of thalamic neurons such as occurs when voltage-dependent NMDA receptors are effectively gated by fast AMPA receptors (Stephan et al., 2008). Such a proposed mechanism is consistent with known glutamate-mediated modulation of corticothalamic activity (McCormick, 1992) as well as functional accounts of feedforward and feedback circuits in the brain (Friston, 2005). The specific role of cortical feedback in our model also accords with a proposed network-wide “synaptic barrage” causing simultaneous increases in gain and variance at the scale of the cell membrane (Shu et al., 2003).

The proportional scaling of the SD and the mean (a constant coefficient of variation) mirrors several fundamental psychophysical processes from perceptual thresholds to optimal motor performance in the presence of uncertainty. As early as 1834, Ernst Weber observed that the relationship between the perceptual threshold for detecting change in a stimulus scales in a constant ratio with the stimulus intensity (Weber, 1834). In other words, the threshold of perceptual uncertainty is scale free. Such “signal-dependent” noise has also been proposed as a key feature of motor planning (Harris and Wolpert, 1998). If uncertainty in perceptual inference and motor planning is coded by the SD in states of the underlying neuronal population (Dayan and Abbott, 2001; Friston and Dolan, 2010), then “scale-free cognitive uncertainty” implies precisely the fixed ratio between mean and SD in neuronal states that we report. Although our study focuses on spontaneous activity, the central role of cortical feedback to the thalamus in our model argues that the same mechanism could underlie scale-free uncertainty in perception and behavior (Buonomano and Maass, 2009).

Although switching in the model and data both follow the same functional form, more frequent switching in the data marks a subtle deviation between the two (compare Figs. 2a, 7a). In this regard, it is interesting to note that switching between the fixed point and the limit cycle in the model was achieved with uncorrelated noise. However, because the stochastic term was introduced as a presynaptic input, and not added directly to the states V_a at each time step, it introduces a mean-reverting stochastic process [a relaxation process, a well-known example of which is the Ornstein–Uhlenbeck process (Uhlenbeck and Ornstein, 1930)]. The synaptic timescale constants α and β (Table 1) hence ensure that, at the level of the states V_s, the stochastic fluctuations are effectively autocorrelated and hence make an important contribution to slowing the mean switching rate. The other primary contribution comes from the strength of the nonlinear forcing term (deeper attractor basins would also slow the switching process). This affords an additional opportunity to more strongly constrain the parameters of the mean field model and hence exploit non-invasive data to make model-driven inferences on underlying physiology.

In summary, this neural field model exhibits three key empirical features of the human alpha rhythm, namely multistability, long-tailed dwell-time distributions, and proportional scaling between mean activity and its SD. This is achieved through a multiplicative interaction between stochastic inputs to the thalamus and nonlinear feedback from the cortex in the presence of a system instability (a subcritical Hopf bifurcation) that produces a bistable regime. Our findings further resolve the paradoxical coexistence between high-dimensional stochastic and low-dimensional nonlinear processes in large-scale neuronal systems: although moment-to-moment states are primarily driven by stochastic fluctuations—hence explaining their dominant role in the character of time series data (Stam et al., 1999; Breakspear and Terry, 2002) —these operate in a global nonlinear landscape containing multiple basins of attraction. The multiplicative interaction between these two processes plays a key role in our biophysical model of spontaneous cortical activity and provides an intriguing possibility to unify important features of human perception, cognition, and behavior.