Mixed Mode Oscillations in Mouse Spinal Motoneurons Arise from a Low Excitability State

Abstract

We explain the mechanism that elicits the mixed mode oscillations (MMOs) and the subprimary firing range that we recently discovered in mouse spinal motoneurons. In this firing regime, high-frequency subthreshold oscillations appear a few millivolts below the spike voltage threshold and precede the firing of a full blown spike. By combining intracellular recordings in vivo (including dynamic clamp experiments) in mouse spinal motoneurons and modeling, we show that the subthreshold oscillations are due to the spike currents and that MMOs appear each time the membrane is in a low excitability state. Slow kinetic processes largely contribute to this low excitability. The clockwise hysteresis in the I–F relationship, frequently observed in mouse motoneurons, is mainly due to a substantial slow inactivation of the sodium current. As a consequence, less sodium current is available for spiking. This explains why a large subprimary range with numerous oscillations is present in motoneurons displaying a clockwise hysteresis. In motoneurons whose I–F curve exhibits a counterclockwise hysteresis, it is likely that the slow inactivation operates on a shorter time scale and is substantially reduced by the de-inactivating effect of the afterhyperpolarization (AHP) current, thus resulting in a more excitable state. This accounts for the short subprimary firing range with only a few MMOs seen in these motoneurons. Our study reveals a new role for the AHP current that sets the membrane excitability level by counteracting the slow inactivation of the sodium current and allows or precludes the appearance of MMOs.

Introduction

In a recent work, we showed that spinal motoneurons of anesthetized mice display a subprimary firing range in response to a slow ramp of current (Manuel et al., 2009). This range is characterized by subthreshold oscillations at high frequency (100–150 Hz) that precede the firing of a full blown spike. In this regime, the discharge is very irregular, starts at frequencies as low as 2–3 Hz and increases with the current up to 40–70 Hz. We dubbed this firing behavior mixed mode oscillations (MMOs) as in physics, where MMOs refer to a dynamical regime where high-frequency oscillations of small amplitude alternate with low-frequency oscillations of large amplitude (i.e., the spikes). The subprimary range is followed by the classical primary range where there are no oscillations between spikes and the discharge is more regular. The subprimary firing range was never observed in cat motoneurons but has been recently described in rat spinal motoneurons (Turkin et al., 2010). It is likely that a substantial portion of the motor unit force is graded in this firing range. However, we do not know which ionic currents are responsible for the oscillations and shape the discharge in the subprimary range.

MMOs have previously been reported in interneurons (Llinás et al., 1991) and pyramidal cells of the frontal cortex (Gutfreund et al., 1995), stellate cells of the entorhinal cortex (Alonso and Klink, 1993; Klink and Alonso, 1993), magnocellular neurons of the supraoptic nucleus (Boehmer et al., 2000), trigeminal mesencephalic neurons (Wu et al., 2001), striatal fast spiking interneurons (Bracci et al., 2003), and vibrissa motoneurons (Nguyen et al., 2004; Harish and Golomb, 2010). In some cases, they were shown to be associated with a subthreshold resonance due to a slowly activating potassium current and enhanced by the persistent sodium current (Gutfreund et al., 1995; Wu et al., 2001, 2005). However, the frequency of the resonance in mouse motoneurons is too low (7–30 Hz) to account for the high frequency of oscillations (Manuel et al., 2009). Moreover, the resonance disappears when the membrane is depolarized toward the spike voltage threshold. In sharp contrast, the fast oscillations are absent at the resting potential and appear a few millivolts below the spike threshold (Manuel et al., 2009). Thus, MMOs in mouse motoneurons are not related to the subthreshold resonance. Our working hypothesis is that they are linked to the spiking mechanism itself and arise from the interplay between the sodium current and the delayed rectifier current.

We combined experimental (including in vivo dynamic clamp experiments) and theoretical studies (simulations and dynamical systems analysis) to elucidate the mechanisms underlying MMOs in mouse motoneurons. We show that high-frequency oscillations are indeed due to the fast currents involved in spike generation and that MMOs require a low membrane excitability, most likely due to a slow inactivation of the sodium current. We reveal a major role for the afterhyperpolarization (AHP) current, which paradoxically enhances membrane excitability by de-inactivating the sodium current and suppresses MMOs.

Materials and Methods

Experiments

Animal preparation.

Experiments were performed in vivo on 20 female adult CD1 mice weighing 22–42 g (from Charles River Laboratories or bred at Northwestern University). The same experimental protocol was used in Paris and in Chicago. Experiments yielded similar results, and the data were pooled together. In accordance with French legislation, the investigators had valid licenses to perform experiments on live vertebrates delivered by the Direction des Services Vétérinaires (Préfecture de Police, Paris, France). Experiments conducted at Northwestern University were performed under full approval from the Northwestern University Animal Care and Use Committee. At the onset of experiments, atropine (0.20 mg/kg, Aguettant) and methylprenidsolone (0.05 mg, Solu-Medrol, Pharmacia) were given subcutaneously to prevent salivation and edema, respectively. Fifteen minutes later, the anesthesia was induced with an intraperitoneal injection of sodium pentobarbitone (70 mg/kg; Pentobarbital, Sanofi). A tracheotomy was performed, and the mouse was artificially ventilated with pure oxygen (SAR-830/P ventilator, CWE). The end-tidal PCO₂ was maintained ∼4% (MicroCapstar, CWE). The heart rate was monitored (CT-1000, CWE), and the central temperature was kept at 38°C using an infrared heating lamp. A catheter was introduced in the external jugular vein, allowing for supplementary anesthesia by intravenous injections (6 mg/kg) whenever necessary (usually every 10–20 min). The adequacy of anesthesia was assessed on the lack of noxious reflexes and on the stability of the heart rate (usually 400–500 bpm) and end-tidal PCO₂. A slow intravenous infusion (50 μl/h) of a 4% glucose solution containing NaHCO₃ (1%) and gelatin (14%; Plasmagel, Roger Bellon) helped to maintain the physiological parameters. The sciatic nerve was dissected and mounted on a monopolar electrode for stimulation. The vertebral column was immobilized with two pairs of horizontal bars (Cunningham Spinal Adaptor, Stoelting) applied on the Th12 and L2 vertebral bodies, and the L3–L4 spinal segments were exposed by a laminectomy at the Th13–L1 level. The tissues in hindlimb and the spinal cord were covered with pools of mineral oil. After the surgery, the animal was paralyzed with Pancuronium Bromide (Pavulon, Organon SA, initial bolus: 0.1 mg, followed by a continuous infusion 0.01 mg/h). This preparation allowed us to maintain the animal in good physiological conditions for 6–10 h after the end of the surgery and to make stable intracellular recordings of motoneurons and dynamic clamp experiments. At the end of the experiments, animals were killed with a lethal intravenous injection of pentobarbitone.

Recordings.

Intracellular recordings of motoneurons were performed using micropipettes (tip diameter 1.0–1.5 μm) filled with KCl 3M (resistance 5–10 MΩ), an Axoclamp 2B amplifier (Molecular Devices) connected to a Power1401 interface, and the Spike2 software (CED). After impalement, identification of motoneurons rested on the observation of antidromic action potentials in response to the electrical stimulation of their axon in the sciatic nerve. All motoneurons retained for analysis had a resting membrane potential more hyperpolarized than −60 mV and an overshooting action potential. All recordings and dynamic clamp experiments were performed using the discontinuous current-clamp mode (7–9 kHz) of the amplifier because it allows for reliable measurements of the membrane potential, even when large currents are injected (Brizzi et al., 2004). The input resistance was determined from the responses to a series of small-amplitude square current pulses (−1.5 to + 1.5 nA) as in the study by Manuel et al. (2009).

Discharge properties.

The discharge properties were routinely investigated using triangular ramps of current with a velocity of 0.5–2 nA/s. Occasionally, slower ramps (down to 0.1 nA/s) or faster ramps (up to 10 nA/s) were applied to investigate the impact of the ramp velocity on the discharge pattern. The maximum intensity ranged from 2 to 15 nA, depending on the recruitment threshold of the motoneuron. I–F curves were obtained by plotting the instantaneous firing frequency versus the intensity of the injected current at spike time. The threshold of the first spike in the ascending ramp was determined as the point where the rate of rise of the voltage exceeded 10 mV/ms (Sekerli et al., 2004).

Dynamic clamp.

The dynamic clamp current was injected into the motoneuron soma through the recording micropipette. It was computed by a PC running RT-Linux (a Linux kernel modified to achieve real-time processing) and the dynamic clamp software MRCI (Raikov et al., 2004). The system allows the computation at a speed of 10 kHz of the equations modeling the persistent sodium current (I_Nap) or the AHP current. The equations used for I_Nap were as in the study by Manuel et al. (2007):

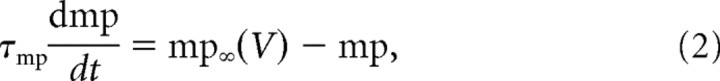and

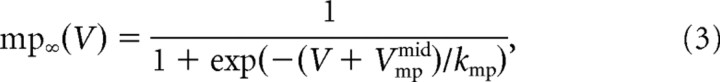where G_Nap is the maximal conductance of the current, mp is its activation variable, V_Nap its reversal potential, V is the membrane potential, τ_mp is the activation time constant, mp_∞(V) is the steady-state activation curve, V_mp^mid is the half-activation voltage, and k_mp determines the slope of the activation curve. We set V_Nap to 50 mV, τ_mp to 1 ms, k_mp to 2 mV. V_mp^mid was set at the mid-AHP following the first spike, i.e., below the spiking voltage threshold. G_Nap ranged from 0.02 to 0.06 μS.

For simplicity, the AHP current was modeled as an effective voltage-dependent current (Manuel et al., 2006), as follows:

where G_AHP was the maximal conductance, z(t) the voltage-dependent activation variable and V_AHP the reversal potential. We incorporated AHP summation in our model using the same formalism as in Meunier and Borejsza (2005). We instantaneously increased z from z_before to the following:

where 0 ≤ α ≤ 1, when the membrane voltage crossed the value 0 mV during the spike upstroke. We then let the activation variable relax exponentially with the time constant τ_z (i.e., z(t) = z_after · e^−t/τ_z) until the next spike occurred. In our experiments, α was fixed at 0.5, so that the first spike already recruited half of the maximal artificial conductance. The reversal potential (V_AHP) was always set to −100 mV. This value was chosen for technical reasons to ensure that the dynamic clamp generated current was always negative. G_AHP ranged from 0.1 to 0.5 μS (0 in the control condition), and τ_z was set to 10 ms, the mean value of the relaxation time constant measured in mouse motoneurons (Manuel et al., 2009).

Modeling

To make sense of the experimental data, we analyzed a single compartment conductance-based model of mouse motoneuron, using both numerical simulations and mathematical analysis based on classical techniques of dynamical systems theory.

Numerical simulations.

In its simplest form (basic model), our model incorporates only the two fast conductances that generate spikes (the transient sodium conductance and the delayed rectifier potassium conductance), and the slower AHP conductance. The equations of the model are as follows:

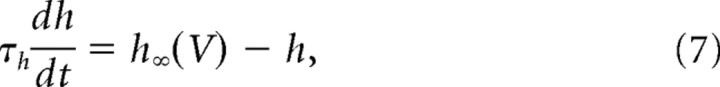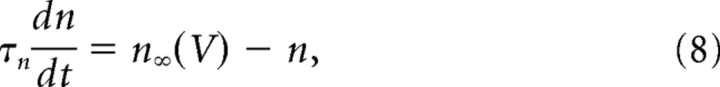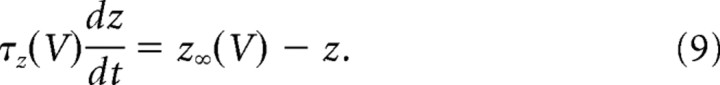The leak conductance G_l was set to 0.3 μS and the membrane capacitance to 0.8 nF, in accordance with the average values of the passive time constant τ_m and the input conductance measured in mouse motoneurons (Manuel et al., 2009). The reversal potential of the leak current was V_l = −66 mV. The steady-state activation and inactivation functions of the sodium conductance were as follows:

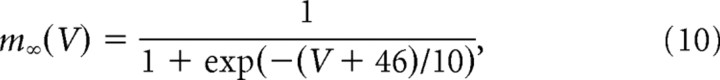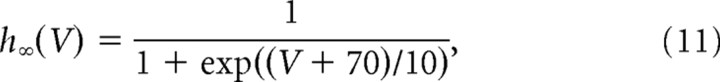and the activation function of the delayed rectifier conductance was as follows:

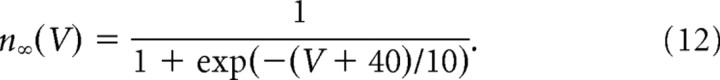The sodium conductance was assumed to activate instantaneously and to inactivate fast with the time constant τ_h = 1 ms. The delayed rectifier conductance activated with the same time constant τ_n = 1 ms. The AHP conductance was modeled by its effective voltage dependence as in dynamic clamp experiments. However, the activation variable z increased in the model with a time constant of 0.1 ms during spikes to avoid discontinuities in the dynamics. Values of the reversal potentials and maximal conductances of the spike-generating currents were V_Na = 50 mV, V_K = −90 mV. Values of G_Na, G_K, and G_AHP of 40, 3.5, and 0.3 μS were used, unless otherwise indicated.

We modified the balance between inward and outward currents, and thereby the membrane excitability, by increasing the transient sodium conductance, decreasing the delayed rectifier conductance, or adding a persistent component to the sodium current. This persistent sodium current had the same activation kinetics as the transient component, but its activation curve was shifted downward by 5 mV.

To account for hysteretic effects, we added to this basic model either a very slow inactivation process to the kinetics of sodium currents (both transient and persistent components) or added a very slow I_M-like potassium current. The slow inactivation of the sodium current was independent of the fast inactivation and was governed by the kinetic equation, as follows:

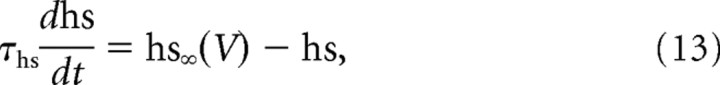where

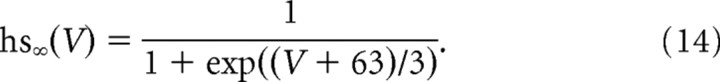and the time constant τ_hs was of the order of the second. The activation of the slow potassium current followed a similar equation, as follows:

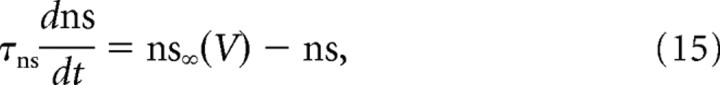where

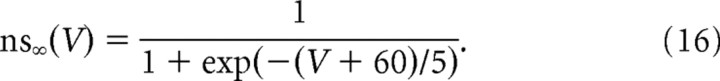Voltage fluctuations, as seen in experimental recordings, were incorporated by adding a Gaussian white noise component (SD σ = 0.2) mimicking synaptic background to the injected current. We checked that adding random fluctuations to the activation of the transient sodium conductance (channel noise) led to similar results.

In the noiseless case, the differential equations of the model were solved using the standard fourth order Runge–Kutta algorithm implemented in XPPAUT (Ermentrout, 2002). An Euler algorithm with a time step 10 times smaller was used when noise was added. XPPAUT was also used for the dynamical systems analysis (phase plane, bifurcation scheme) of the reduced model below.

Reduced model.

To further reduce the number of variables and simplify the mathematical analysis, we lumped together the sodium conductance inactivation variable h and the delayed rectifier activation variable n in a single recovery variable W with the dimension of a voltage. This led us to a model that had only three dimensions when slow kinetic processes were not taken into account. The reduction was performed as in the study by Abbot and Kepler (1990). We replaced the gating variables h and n by the potentials W_h and W_n via the change of variables h = h_∞(W_h), n = n_∞(W_n). We then substituted W_h and W_n with a single variable W, chosen so as to best approximate the impact of W_h and W_n on voltage evolution. We thus reduced the model to a three-dimensional system for the variables V, W, and z, as follows:

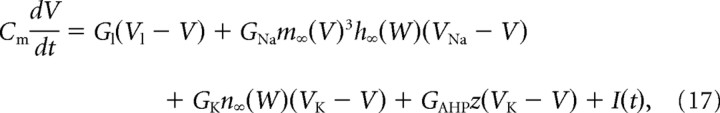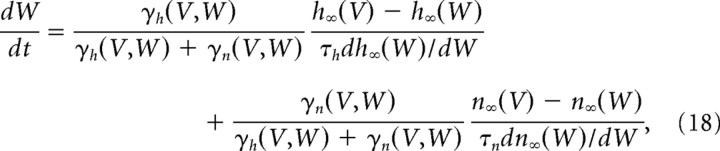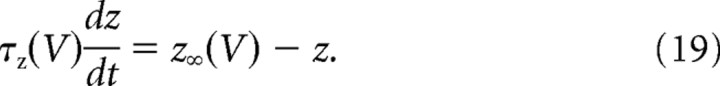In Equation 18,

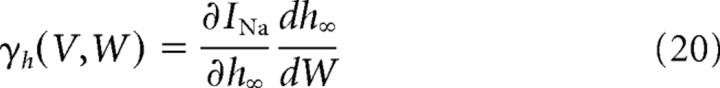and

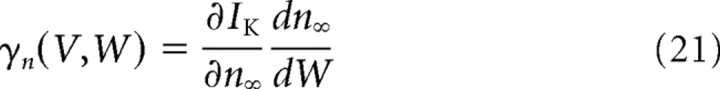are the derivatives of the currents I_Na(V, W) = G_Nam_∞(V)³h_∞(W)(V_Na − V) and I_K(V, W) = G_Kn_∞(W)(V_K − V) with respect to W.

They quantify how the voltage dependence of sodium current inactivation and potassium current activation make these currents change with the potential. We also introduce for later use the following:

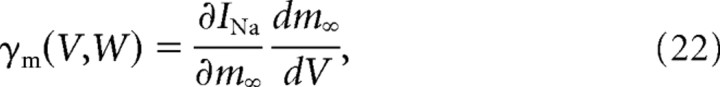which quantifies how the sodium current changes with the potential because of its voltage-dependent activation.

Mathematical analysis of the reduced model

The fixed points of the basic model (noiseless and without slow kinetic processes) are located in the z = 0 plane and given by the intersections of the two nullclines dV/dt = 0 and dW/dt = 0. The second nullcline is just the straight line V = W. Setting dV/dt = 0, z = 0, and W = V in Equation 17, one sees that the fixed point voltage is given by the steady-state current voltage equation, as follows:

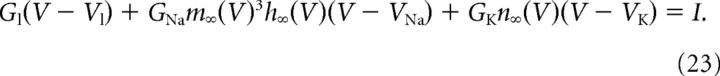This equation has either one solution (low excitability) or three (high excitability).

The characteristics of the subthreshold oscillations are derived from the linear stability analysis of the unique fixed point in the low excitability state, which becomes unstable at firing onset. Linearizing Equations 17–19 around this fixed point and computing the eigenvalues, we obtain a real negative eigenvalue in the z direction and two complex conjugate eigenvalues with positive real part in the V, W plane. The growth rate μ and frequency ν of fast oscillations are respectively given by the real and imaginary parts of these complex eigenvalues:

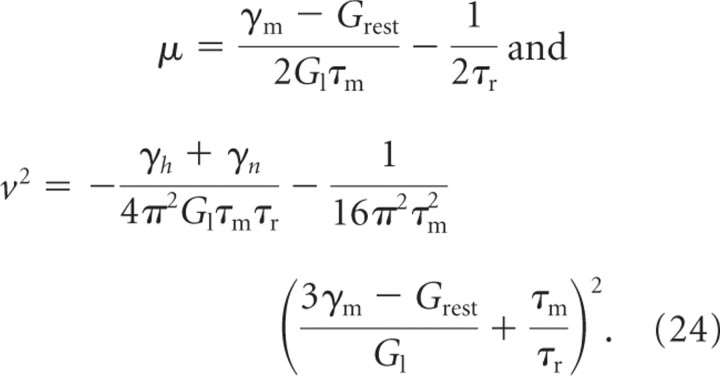In these equations

is the resting membrane conductance, the recovery time τ_r is the common value of τ_h andτ_n, and γ_m, γ_h, and γ_n are calculated at the fixed point (i.e., for V = W).

Results

Mixed mode oscillations and hysteretic firing patterns in mouse motoneurons

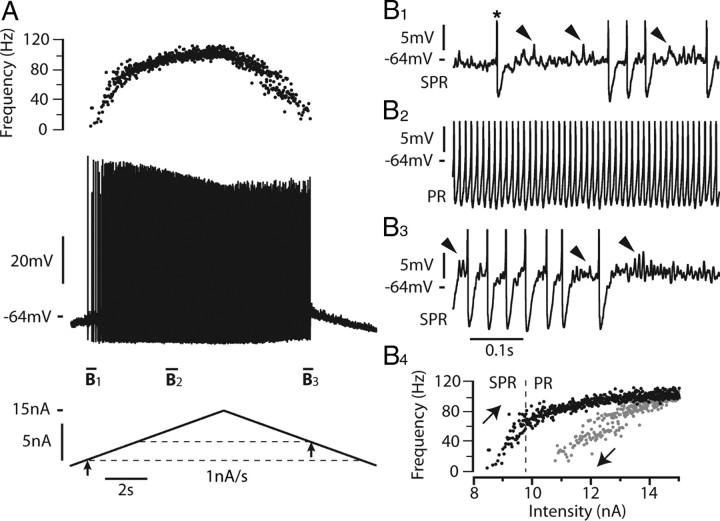
We investigated the mixed mode oscillations and the discharge pattern of 29 spinal motoneurons in response to triangular ramps of current. The most typical case, observed in 21 motoneurons, is shown in Figure 1. In response to a 1 nA/s ramp of current, the first spike was emitted when the current intensity reached 8.3 nA (recruitment current). The discharge then clearly displayed MMOs, which defined the subprimary firing range. In this range, each spike was followed by an AHP and then by a series of fast subthreshold oscillations superimposed on a voltage plateau (Fig. 1B1, arrows). The number of oscillations and, accordingly, the duration of each interspike interval were quite variable. In this motoneuron, the subprimary firing range lasted until the current reached 9.8 nA, i.e., over a current range of 1.5 nA. For higher current intensities, the fast oscillations disappeared (see enlargement in Fig. 1B2), indicating that the primary firing range was reached. The response to the triangular current ramp was asymmetrical. MMOs were present on most of the descending ramp (Fig. 1B3), and the derecruitment current was higher (10.8 nA) than the recruitment current. As a consequence, the I–F relationship displayed a clockwise hysteresis (Fig. 1B4). Moreover, the amplitude of the action potentials was not the same during the ascending and descending ramps of current. It substantially decreased during the ascending ramp and remained low during the descending ramp.

Figure 1.

Most motoneurons respond to a slow triangular current ramps with a discharge displaying MMOs and a clockwise hysteresis. A, Response to a 1 nA/s triangular ramp of current (15 nA amplitude). Instantaneous firing frequency (top trace), voltage response (middle trace), and injected current (bottom trace) are shown. The resting potential was −74 mV and the voltage threshold for the first spike (−64 mV) was reached when the current intensity was 8.3 nA (recruitment current, arrow below the ascending current ramp and lower dashed line). Note the decrease in spike amplitude during the ascending ramp and its stabilization at a low level during the descending ramp. The derecruitment current on the descending ramp was 10.8 nA, i.e., larger than the recruitment current (arrow on descending ramp and upper dashed line). B1, Magnification of the voltage trace near recruitment. The asterisk indicates the first spike on the ascending ramp. Spikes have been truncated to better see the voltage oscillations (some of them indicated by arrowheads) that appear in the interspike intervals after the AHP has fully relaxed. Note the firing variability that characterizes the subprimary range (SPR). B2, Increasing the injected current resulted in a primary firing range (PR) without oscillation between spikes and with less variability. B3, Magnification of the voltage trace near the derecruitment current. Firing becomes irregular again, and subthreshold oscillations reappear between spikes. B4, I–F relationship. Black and gray dots indicate the instantaneous frequency of each spike during the ascending and descending ramps, respectively. Note the clockwise hysteresis of the I–F relationship. The transition from the SPR to the PR occurred at 9.8 nA on the ascending ramp (dashed line). The input resistance of this motoneuron was 2.1 MΩ.

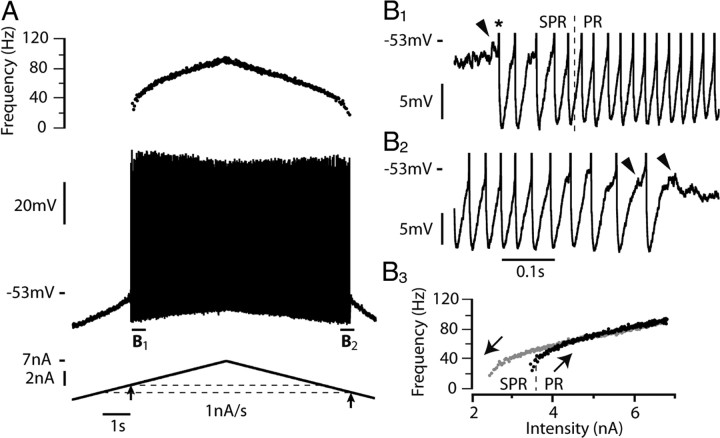
The eight other motoneurons exhibited different discharge properties as exemplified in Figure 2. The illustrated motoneuron was also submitted to a 1 nA/s ramp of current. Fast oscillations (Fig. 2B1, arrow) developed a few millivolts below the voltage threshold for the first spike (−53 mV). MMOs were present only during the first few interspike intervals of the ascending ramp over a current range of 0.3 nA (Fig. 2B1) and during the last intervals preceding derecruitment (Fig. 2B2). In sharp contrast with the motoneuron shown on Figure 1, the I–F relationship displayed a counterclockwise hysteresis, the derecruitment current (2.4 nA) being smaller than the recruitment current (3.4 nA) (Fig. 2B3). Moreover, spike amplitude varied little. The resting membrane potentials of the two motoneurons illustrated in Figures 1 and 2 were close (−74 mV and −76 mV, respectively). This indicates that their different firing patterns were due to genuine differences in their intrinsic membrane properties. It is interesting to note that the input resistance of motoneurons displaying a clockwise hysteresis was significantly smaller (3.7 ± 2.0 MΩ, N = 21) than the input resistance of motoneurons displaying a counterclockwise hysteresis (5.2 ± 1.2 MΩ, N = 7, Student's t test p = 0.02). The recruitment current was not significantly different between the two groups: 5.1 ± 3.7 nA (N = 21) in the motoneurons displaying a clockwise hysteresis and 3.8 ± 1.7 (N = 8) in those displaying a counterclockwise hysteresis (Student's t test p = 0.2). This is because the presence of the subthreshold oscillations made the timing of the first spike quite variable. The spike voltage thresholds were similar in the motoneurons displaying the clockwise hysteresis (−51 ± 10 mV) and in those displaying the counterclockwise hysteresis (−52 ± 10 mV).

Figure 2.

The discharge of a minority of motoneurons displays a counterclockwise hysteresis. A, Response of another motoneuron to a 1 nA/s triangular ramp of current (6.8 nA amplitude). Same arrangement as in Figure 1A. The resting potential was −76 mV and the voltage threshold for the first spike (−53 mV) was reached for a current intensity of 3.4 nA (recruitment current). Note that spike amplitude decreased much less during the ascending ramp than in Figure 1. The derecruitment current on the descending ramp was 2.4 nA, i.e., smaller than the recruitment current. B1, Magnification of the voltage trace near recruitment (truncated spikes). Voltage oscillations (arrowhead) appear before the first spike (asterisk) and remain present in the first few interspike intervals, giving rise to a small subprimary range (SPR). B2, Magnification of the voltage trace near the derecruitment current. B3, I–F relationship. Note the counterclockwise hysteresis. The transition from SPR to primary firing range (PR) occurred at 3.7 nA (dashed line). Note that a few subthreshold oscillations reappear. The input resistance of this motoneuron was 5.3 MΩ.

The fast subthreshold oscillations are due to the spike-generating currents

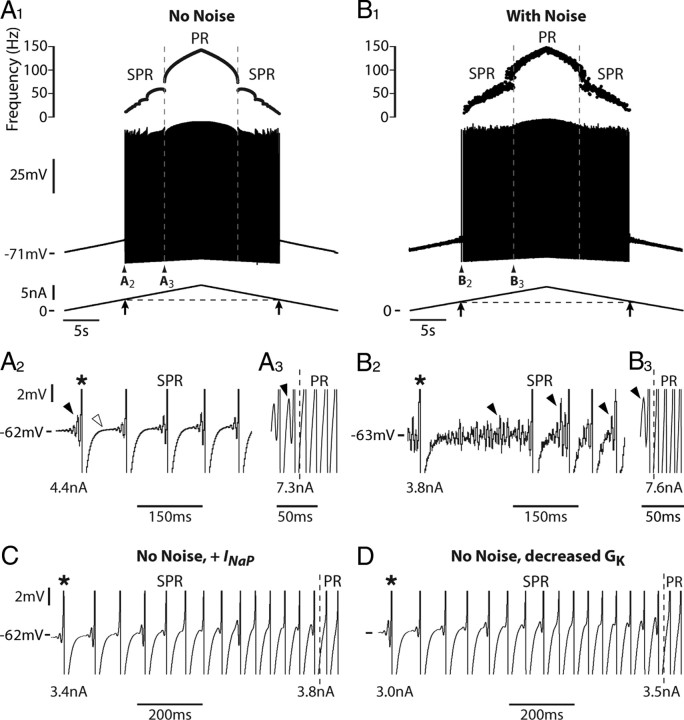
MMOs, associated with a subprimary firing range, do occur in our basic model that only incorporates the two (sodium and potassium) spike-generating conductances and the AHP conductance (see Materials and Methods). The voltage response of the model to a slow triangular current ramp (0.5 nA/s) is displayed in Figure 3A1. Near rest, the membrane voltage exhibits no oscillations. They appear before the first spike (recruitment current 4.4 nA), at a membrane potential of −62 mV, i.e., 3 mV lower than the spike voltage threshold (Fig. 3A2, filled arrowhead). As the AHP conductance is activated during the spike, this indicates that the subthreshold oscillations are not due to the AHP. In our model, they are caused by the spike-generating currents. After the first spike, the voltage reaches a stationary potential when the AHP has subsided (Fig. 3A2, open arrowhead). Fast oscillations emerge on top of it and grow in amplitude until a new spike is triggered. As the injected current increases, the number of oscillations between two successive spikes decreases, which accounts for the frequency steps observed in the subprimary firing range (see frequencygram in Fig. 3A1). The oscillations totally disappear when the injected current reaches 7.3 nA (Fig. 3A3). The high-frequency regime, starting at 74 Hz in the example illustrated, corresponds to the primary firing range. On the descending current ramp, MMOs reappear for 7.3 nA (Fig. 3A1, second vertical line), i.e., the same current as for the transition from the subprimary to the primary firing range on the ascending ramp. The derecruitment current (4.3 nA) is close to the recruitment current on the ascending ramp: the response is symmetrical and shows no significant hysteresis.

Figure 3.

MMOs and a subprimary firing range occur in the basic model. A1, Response of the model to a triangular current ramp (0.5 nA/s, 10 nA amplitude). Same arrangement as in Figure 1A. The dashed vertical lines indicate the transitions from subprimary range (SPR) to primary firing range (PR) on the ascending ramp (SPR width 2.9 nA) and from PR to SPR on the descending ramp. A2, Magnification of the voltage trace at firing onset (truncated spikes). Note that subthreshold oscillations (black arrowhead) appear before the first action potential (asterisk, recruitment current 4.4 nA). The open arrowhead points out to the voltage plateau that follows the AHP relaxation. A3, Magnification at the transition from the SPR to the PR (7.3 nA). Note that the time scale is three times faster than in A2. The oscillations (black arrowhead) totally disappear after the transition. B1, Same as in A1 with white noise added to the injected current. B2, B3, Magnification of the voltage trace at the firing onset (B2) and at the transition from the SPR to PR (B3). Note the fluctuations of the voltage and the substantial variations of interspike intervals in the SPR (B2). Subthreshold oscillations (black arrowhead) follow the AHP decay and progressively disappear during the SPR (B2). Recruitment current is 3.8 nA and transition from SPR to PR (dashed line) occurs at 7.6 nA. The SPR width is increased to 3.8 nA compared with A. C, Same as in A (no noise) except that a persistent component was added to the sodium current (I_Nap; conductance 0.5 μS). Magnification of the voltage response near firing onset. The recruitment current is 3.4 nA, i.e., smaller than in A, indicating an increased excitability. The transition from the SPR to the PR occurs at 3.8 nA. The width of the SPR is thus 0.4 nA, i.e., much smaller than in A. D, Same as in A except for the conductance of the delayed rectifier current (G_K), which was reduced to 3 μS (instead of 3.5 μS in A). Magnification of the voltage response near firing onset. The recruitment current is 3.0 nA, and the current at the transition from the SPR to the PR (dashed line) is 3.5 nA. Therefore, the width of the SPR is 0.5 nA, again much smaller than in A.

When white noise is added to the injected current (Fig. 3B) or sodium channel noise is incorporated in the model (data not shown), the recruitment current is lowered (Fig. 3, compare B2, 3.8 nA vs A2, 4.4 nA) because voltage fluctuations bring the membrane to the voltage threshold for spiking. This extends the subprimary range. Moreover, the discharge becomes particularly irregular in the subprimary range, and stacked bands are present in the frequencygram (Fig. 3B1, top) as in experimental recordings (see Fig. 6A for an example). They are due to variations of the number of oscillations from one interspike interval to the other (Fig. 3B2). However, as in the noiseless case, the discharge is quite symmetrical with similar behavior on the ascending and descending ramps.

Figure 6.

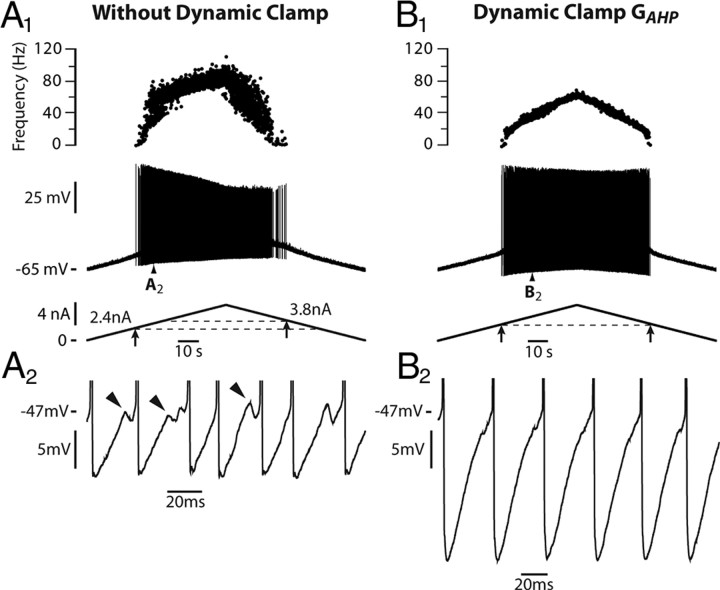
Increasing the AHP reduces both the MMOs and the clockwise hysteresis in a real motoneuron. A1, Response to a slow triangular ramp of current (0.1 nA/s, 6.7 nA amplitude). Same arrangement as in Figures 1A, 2A. Note the substantial decrease of spike amplitude during the ascending ramp. The discharge was asymmetric, the derecruitment current being larger (3.8 nA) than the recruitment current (2.4 nA), i.e., the I–F relationship displayed a clockwise hysteresis (data not shown). A2, Magnification of the voltage (truncated spikes) showing the fast subthreshold oscillations and the irregularity of the discharge. B1, Response when an artificial AHP (conductance 0.4 μS) was added to the natural one using dynamic clamp. Note that the spike amplitude remained nearly constant throughout the ramp and that the clockwise hysteresis disappeared (equal recruitment and derecruitment currents). B2, Magnification of the voltage trace showing that the subthreshold oscillations were much reduced compared with the large oscillations observed without the artificial AHP. Moreover the discharge became much more regular. The input resistance of this motoneuron was 5.0 MΩ.

MMOs require a low membrane excitability

The width of the subprimary firing range depends on the balance between the sodium and potassium currents. For instance, adding a persistent component to the sodium current reduces MMOs. When the persistent conductance is equal to 0.5 μS (1.25% of the transient conductance, set to 40 μS), the recruitment current is reduced from 4.4 to 3.4 nA because of the increased excitability (Fig. 3C). In parallel, the width of the subprimary range is strongly reduced (0.4 nA compared with 2.9 nA without persistent sodium current). Increasing the maximal conductance of the transient sodium current to 45 μS has a similar effect (data not shown). MMOs even disappear completely when the transient sodium conductance is increased beyond 60 μS. A decrease of the delayed rectifier current also reduces MMOs. Figure 3D shows that decreasing its conductance from 3.5 to 3 μS reduces the width of the subprimary range from 2.9 nA to 0.5 nA. At the same time, the recruitment current decreased from 4.4 to 3.0 nA, indicating an enhanced membrane excitability.

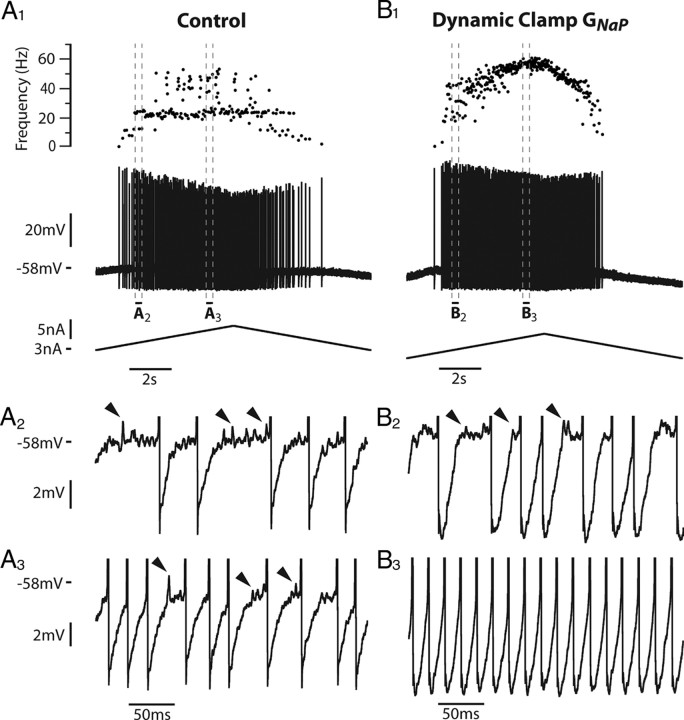
We tested experimentally in two motoneurons the prediction of the model that the persistent sodium current reduces the subprimary firing range. Using dynamic clamp, we added a fast activating inward current that mimicked the persistent component of the sodium current. In the case illustrated in Figure 4A, the motoneuron discharge remained in the subprimary firing regime during the whole current ramp in the absence of dynamic clamp: fast oscillations were present in almost all interspike intervals (Fig. 4A2,A3), and the discharge was very irregular (Fig. 4A1). When the artificial persistent inward current was added (Fig. 4B), the width of the subprimary range decreased (see the oscillations in Fig. 4B2), and a primary firing range appeared at the highest current intensities. In this range, the discharge was much more regular (see the frequencygram on the top of Fig. 4B1) and no oscillations could be seen in any interspike interval (Fig. 4B3). In the other motoneuron, the subprimary range also decreased at the benefit of the primary range when a persistent inward current was added by dynamic clamp. These experimental results are in keeping with our theoretical results.

Figure 4.

Adding an artificial persistent sodium current with dynamic clamp creates a primary firing range (PR) and decreases the subprimary range (SPR) in a real motoneuron. A1, Response of the motoneuron to a slow ramp of current (9 nA amplitude, 1 nA/s, control condition without dynamic clamp). The recruitment current was 3.5 nA. The discharge remained in the SPR during the whole ramp. Note the great variability in the frequencygram. A2, A3, Magnifications of the voltage trace (between the two pairs of dashed vertical lines in A1, truncated spikes) showing the fast oscillations (arrowheads), which account for the variability of the interspike intervals. B1, Response of the motoneuron in dynamic clamp (7 nA amplitude, 1 nA/s, artificial G_Nap = 0.025 μS). The recruitment current was reduced to 1.6 nA, indicating an increased excitability when the artificial persistent current was added. A firing range with little variability appeared in the frequencygram. B2, Magnification of the voltage trace at the beginning of the ramp (between the two dashed vertical lines in B1) showing the fast oscillations (arrowheads). B3, Magnification of the voltage trace for a higher current intensity (between the second pair of dashed lines in B1) showed no oscillations, as expected in the PR. A PR was thus created at the expense of the SPR, whose width decreased. This PR was observed despite the smaller ramp amplitude compared with control. It was entirely due to the addition of the artificial persistent sodium current. The input resistance of this motoneuron was 1.4 MΩ.

Altogether, our results show that MMOs are elicited by the spike-generating sodium and potassium currents, thus validating our working hypothesis. However, MMOs require a low membrane excitability, where the sodium current is sufficient to sustain a repetitive discharge but does not prevail too much upon the potassium current. Increasing the excitability reduces the subprimary firing range or even makes it disappear. In our basic model, the response to the triangular current ramps is symmetrical, and the recruitment and derecruitment currents nearly equal. This indicates that, in contrast with MMOs, the hysteretic behavior cannot be elicited by the fast spike-generating currents alone.

Slow inactivation of the sodium current accounts for the hysteretic properties of mouse motoneurons

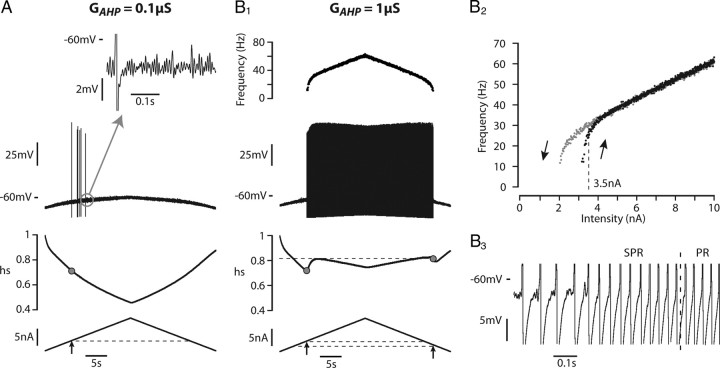
To account for the hysteretic properties of mouse motoneurons, we endowed the transient sodium current used in the model with slow inactivation properties (see Materials and Methods). In the example shown in Figure 5A, the discharge pattern of the model displayed a large clockwise hysteresis in response to a slow current ramp (0.5 nA/s) when the time constant of slow inactivation of the sodium current was set to 3 s: the derecruitment current was 3.6 nA larger than the recruitment current. Both the ascending and descending ramps displayed subprimary and primary firing ranges. However, the primary range was narrower during the descending ramp. The spike amplitude was reduced by 12 mV over the ascending ramp but remained nearly constant during the primary range on the descending ramp. The slow inactivation variable (hs, see Materials and Methods) progressively decreased from 0.90 at discharge onset down to 0.56 at the end of the ascending ramp, which accounts for this reduction of spike amplitude (Fig. 5A1). During the descending ramp, hs had increased to only 0.6 when derecruitment occurred, i.e., inactivation was much stronger at discharge termination (40%) than at discharge onset (10%). This asymmetry of inactivation between the ascending and the descending ramps readily accounts for the clockwise hysteresis of the I–F curve (Fig. 5A2). A clockwise hysteresis was observed in the I–F curve when the slow inactivation time constant was larger than 1.5 s. Figure 5C shows how the size of this hysteresis, defined as the difference between the derecruitment current on the descending branch and the recruitment current on the ascending one, varied with the time constant of the slow inactivation of the sodium current. It was maximal for 4 s. The hysteresis progressively decreased when the time constant was further increased to almost disappear for 60 s.

Figure 5.

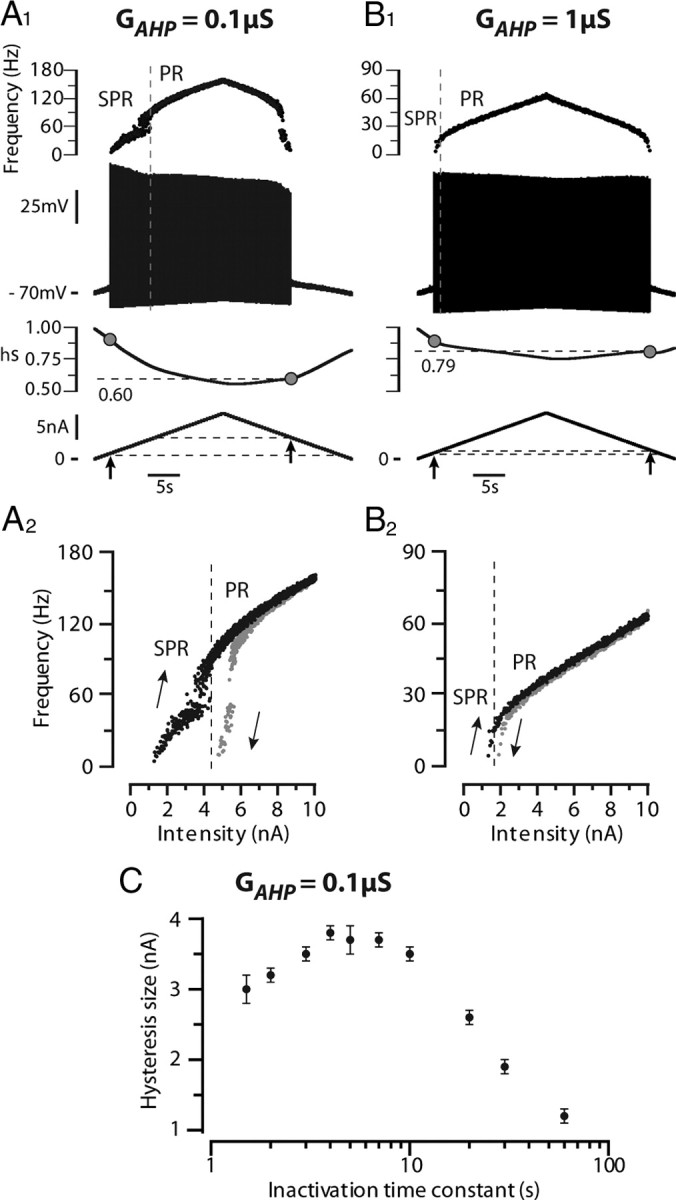
Adding a slow sodium current inactivation to the model creates a clockwise hysteresis. The transient sodium current was endowed with a slow inactivation process (3 s time constant) that added to the fast inactivation (1 ms) already present. The subsequent reduction in excitability was compensated by introducing a persistent sodium current (conductance 2.5 μS) with similar slow inactivaction. A1, Response to a slow triangular ramp of current (0.5 nA/s, amplitude 10 nA) when the AHP conductance was set to 0.1 μS. From top to bottom: instantaneous firing frequency, voltage response, slow inactivation variable (hs, see Materials and Methods) and injected current. Note the reduction of the spike amplitude during the ascending ramp. The gray dots on the inactivation curve point to the inactivation at firing recruitment on the ascending ramp and derecruitment on the descending ramp. PR, Primary firing range; SPR, subprimary firing range. A2, I–F curve. Note the large clockwise hysteresis of the I–F relationship. B1, B2, Response when the AHP conductance was increased 10 times (to 1 μS). Same arrangement as in A1 and A2. Note that the spike amplitude decreases much less, there is less slow inactivation, the subprimary range is narrower, and the hysteresis has almost vanished. C, Size of the hysteresis (i.e., difference between derecruitment and recruitment currents) plotted against the time constant of slow inactivation of the sodium current. The AHP conductance was 0.1 μS. Each point is the average of five simulations, and the vertical bar on each point is the SD. The abscissa is in logarithmic scale.

The clockwise hysteresis is sensitive to the ramp velocity. Increasing the ramp velocity 10 times (to 5 nA/s) while keeping the inactivation time constant fixed led to a more symmetrical I–F curve. Spike height was less reduced, and the primary range expanded at the expense of the subprimary range (data not shown). This is because slow inactivation varies much less during the 5 nA/s triangular ramp than during the 0.5 nA/s ramp, indicating again that MMOs (and the subprimary range) strongly depend on membrane excitability.

Adding a slow M-like potassium current that activates in the subthreshold voltage range with a time constant of 3 s also elicits a clockwise hysteresis of the I–F curve with a similar dependence on ramp velocity (data not shown). However, the amplitude of spikes does not decrease, contrarily to the effect of slow sodium current inactivation. This strongly suggests that the clockwise hysteresis observed in real motoneurons during slow ramps of current (Figs. 1, 6A) is largely due to the slow inactivation of the sodium current, although slow potassium currents may also play some part.

The AHP can paradoxically increase membrane excitability and reduce MMOs

The AHP interacts with the slow inactivation of the sodium current to set the excitability and thereby the firing pattern. Increasing 10 times the AHP conductance in the model dramatically changed the pattern of discharge (Fig. 5, compare A, 0.1 μS; B, 1 μS). The subprimary firing range and the hysteresis were nearly abolished (see I–F curve on Fig. 5B2). Moreover, the spike amplitude remained almost constant. Increasing the AHP de-inactivated substantially the sodium current: the slow inactivation variable decreased to only 0.76 at the end of the ascending ramp for the 1 μS AHP conductance (Fig. 5B1) versus 0.56 for the 0.1 μS AHP conductance (Fig. 5A1). Increasing the AHP conductance made the model more excitable, and consequently MMOs and hysteresis disappeared.

This prediction of the model was experimentally validated in two mouse motoneurons using dynamic clamp. In control conditions (Fig. 6A), the discharge of the illustrated motoneuron in response to a 0.1 nA/s triangular ramp of current was strongly asymmetrical: the derecruitment current was 1.4 nA larger than the recruitment current, the spike amplitude substantially decreased during the ascending ramp and remained low during the descending ramp. Figure 6B shows that adding an artificial AHP conductance of 0.4 μS (on top of the one naturally present) tended to suppress the MMOs (Fig. 6, compare B2, A2) and to make the discharge symmetrical (Fig. 6B1). Moreover, the spike amplitude remained nearly constant throughout current injection. Similar results were found in the other motoneuron. These experimental results are in keeping with the model and again strongly suggest that the sodium current is endowed with slow inactivation properties in mouse motoneurons. This inactivation lowers membrane excitability, favoring the appearance of MMOs, and it is largely responsible for the clockwise hysteresis of the I–F curve. Although the AHP current is hyperpolarizing and reduces the firing frequency, it favors primary range firing because it paradoxically increases the motoneuron excitability by de-inactivating the sodium current.

Origin of the counterclockwise hysteresis

The counterclockwise hysteresis appears in our model when the following conditions are met: the time constant of the sodium current slow inactivation is shorter than 1.5 s (and longer than 50 ms, i.e., five times the AHP time constant) and the AHP conductance is larger than 0.7 μS. In Figure 7A, the slow inactivation time constant was reduced to 0.6 s (i.e., five times less than in Fig. 5A) but the AHP conductance was kept at 0.1 μS (i.e., the same conductance as in Fig. 5A). The model fired only a few spikes during the ascending ramp (Fig. 7A), and the last spike was followed by long lasting subthreshold oscillations. This is because the inactivation time constant was small enough to allow for a strong inactivation of the sodium current (54% at the end of the ascending ramp), thus creating a low excitability state. When the AHP conductance was increased to 1 μS (Fig. 7B), it substantially de-inactivated the sodium current, and the model exhibited a sustained discharge (Fig. 7B1). However, the discharge pattern was not symmetrical: the derecruitment current was smaller (2.0 nA) than the recruitment current (3.1 nA), and the I–F curve displayed a counterclockwise hysteresis (Fig. 7B2). This is because de-inactivation of the sodium current by the AHP was larger at the discharge termination (hs = 0.79) than at the discharge onset (0.72). A small subprimary firing range occurred at the discharge onset (Fig. 7B3) during the dip displayed by hs (Fig. 7B1) and at discharge termination.

Figure 7.

Counterclockwise hysteresis in the model. A, The time constant of the slow inactivation of the sodium current was reduced to 0.6 s and the AHP conductance set to 0.1 μS. Top, Voltage response; middle, slow inactivation variable; bottom, injected current. A few spikes only were emitted and they were followed by sustained fast oscillations as shown on the enlargement of the circled area. B1, The AHP conductance was increased to 1 μS. Same arrangement as in Figure 7A1. Note that there is less slow inactivation than in A and that the discharge is sustained. The gray dots on the inactivation curve indicate the values of hs at recruitment and derecruitment. B2, I–F curve. Note the counterclockwise hysteresis. B3, Magnification of the voltage response at the transition from the subprimary range (SPR) to the primary firing range (PR).

A Shilnikov's homoclinic bifurcation underlies MMOs

The purpose of the present section is to understand, using dynamical systems theory, which mathematical scenario underlies the appearance of MMOs when the membrane is hypoexcitable, and what explains the switch from subprimary to primary range as the injected current is increased. For the sake of simplicity, we illustrate only what happens in the reduced model (see Material and Methods) and in the absence of noise. Adding a slow component to the inactivation of the fast activating sodium current, a slowly activating potassium current or a persistent sodium current does not qualitatively change the scenario that emerges from our analysis.

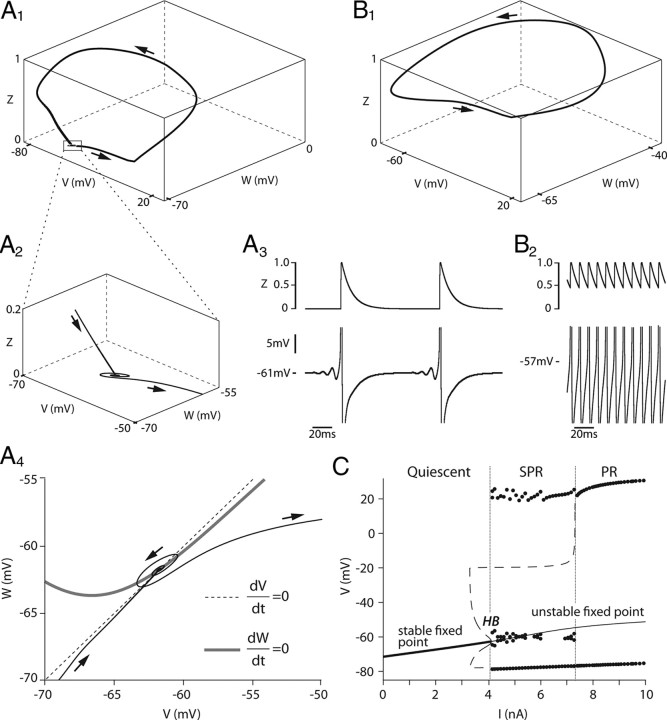
MMOs occur because two conditions are satisfied: (1) the model has a fixed point that is stable at the resting potential but, following a subcritical Hopf bifurcation, displays a spiral type instability in the subprimary range, and (2) this fixed point is revisited each time a spike has been fired. This is illustrated in Figure 8A. The tridimensional trajectory of our model during a typical period in the subprimary firing range is shown in Figure 8A1. After a spike is fired, the trajectory goes back to the V, W plane (see enlargement in Fig. 8A2) because the AHP has time to fully relax and its activation variable z decreases to 0 (Fig. 8A3). The trajectory reaches the fixed point of the model, i.e., the intersection of the two nullclines in the V, W plane (Fig. 8A4). However, because this fixed point is unstable, the trajectory of the model spirals away from it, and a new spike is fired (Fig. 8A1,A2). Fast oscillations are due to the existence of this unstable focus, and MMOs are associated with the existence of a trajectory that leaves this unstable fixed point but then returns to it because of the AHP decay. Such a trajectory is called a homoclinic trajectory. Accordingly, the mathematical scenario for the emergence of MMOs, where the fixed point becomes unstable through a subcritical Hopf bifurcation while a homoclinic trajectory arises, is called the Shilnikov's homoclinic bifurcation scenario. The transition from quiescence to MMOs is indicated in the bifurcation diagram of Figure 8C.

Figure 8.

The Shilnikov's homoclinic bifurcation scenario. A1, Trajectory of the reduced model during a typical period in the subprimary range (SPR). The trajectory [V(t), W(t), z(t)] is plotted in the three-dimensional V, W, z space. V is the voltage, W the recovery variable (see Materials and Methods), and z the activation variable of the AHP conductance. The arrows show motion direction on the three-dimensional trajectory. A2, Magnification of the trajectory (box in A1) when it revisits the unstable focus on the V, W plane. Note the spiral made by the trajectory around this focus. A3, Time evolution of the voltage (bottom trace) and of the AHP activation (z, top trace). Note the MMOs on the voltage. Note also that z fully relaxes to 0 during the interspike interval well before the next spike is fired. A4, The two nullclines dV/dt = 0 (dashed line) and dW/dt = 0 (gray line) are drawn in the V, W plane (i.e., the z = 0 plane). The trajectory spirals around the intersection of the two nullclines, i.e., the fixed point of the model. B1, Typical trajectory of the model in the primary firing range (PR). The trajectory stays away from the V, W plane where the unstable fixed point is located. B2, Time evolution of the voltage and z. Given the high discharge frequency, z has no time to relax between spikes. C, Bifurcation diagram of the model: the voltage of the stationary solution, both stable and unstable, is displayed as a function of the injected current. In the quiescent regime, the model displays a stable fixed point (solid line). This fixed point becomes unstable at 4.1 nA (first vertical line) through a subcritical Hopf bifurcation (HB) when it merges with an unstable, and thus not experimentally observable, periodic solution (thin dashed line). The model then displays MMOs with an alternation of subthreshold oscillations (the dots near the unstable fixed point indicate their minimum and maximum voltage) and full blown spikes (the series of upper and lower dots show their minimum and maximum voltage). The variations in the peak amplitude of spikes correspond to the successive frequency plateaus in the SPR. At 7.3 nA (second vertical line), the subthreshold oscillations and the unstable periodic solution disappear, and the model enters the PR.

The firing frequency increases with the injected current. The transition from the subprimary firing range to the primary range occurs at 7.3 nA (Fig. 8C). It occurs because the fixed point becomes more and more unstable (i.e., it takes less and less time to spiral away from it) and, importantly, because the AHP begins to saturate. When the interspike intervals become too small for the AHP to relax (Fig. 8B2), the fixed point is no longer reached before the emission of the next spike and the trajectory of the system stays away from it in the z direction (Fig. 8B1). MMOs are no longer present, and the primary range is reached.

The above scenario no longer occurs for high membrane excitability (larger ratio of sodium over potassium currents). The nullcline dV/dt = 0 then becomes strongly N-shaped and intersects the nullcline dW/dt = 0 in three points instead of one. The lower fixed point, stable at the resting potential, remains stable when the injected current is increased, and it disappears at discharge onset where it merges with the middle fixed point. Contrary to the hypoexcitable case, there is no current range where the model possesses a fixed point with a spiral instability, which is why no MMOs are observed.

Finally, the mathematical analysis allows us to compute the frequency of the fast oscillations, given by Equation 24 in Materials and Methods, and to understand which parameters determine them. The oscillation frequency is always high (typically 110 Hz for the standard value of parameters) and little depends on the voltage, in keeping with previous experimental results (Manuel et al., 2009). In contrast, it substantially depends on the passive membrane time constant and on the membrane repolarization kinetics (W variable). It increases by 50% every time τ_m is divided by two, and presents a similar, albeit lesser, sensitivity to the recovery time constant τ_r (the common value of τ_h and τ_n, see Materials and Methods).

Discussion

We show (1) that the fast subthreshold oscillations observed in spinal mouse motoneurons are due to the fast sodium and potassium currents involved in spike generation, and (2) that mixed mode oscillations occur each time the membrane is in a low excitability state. Slow inactivation of the sodium current largely contributes to this state. It reduces the sodium current available for spiking, giving rise to a large subprimary range with numerous oscillations between spikes. It also explains the clockwise hysteresis of the I–F curve observed in most mouse motoneurons. On the contrary, in motoneurons displaying a counterclockwise hysteresis of the I–F curve, it is likely that slow inactivation is substantially reduced by the AHP, thus resulting in a more excitable state. This could explain why these motoneurons display only a small subprimary firing range with few oscillations between spikes. Altogether, MMOs and a subprimary firing range arise when the AHP current does not sufficiently de-inactivate the sodium current and a low excitability is achieved.

Mechanism for MMOs

In our model, MMOs are explained by the Shilnikov's homoclinic bifurcation scenario. This is the first time to our knowledge that this scenario is invoked to explain MMOs in neurons. It relies on the separation of role between the fast spike-generating currents that are responsible for the high-frequency subthreshold oscillations and the much slower AHP that brings the fast currents back to equilibrium. Other neuron models do not display similar features and their MMOs are explained by different scenarios (Krupa et al., 2008; Rubin and Wechselberger, 2008; Harish and Golomb, 2009). For instance, MMOs can be obtained in the Hodgkin–Huxley model without AHP. They involve the generalized Canard scenario that requires two slow variables. This is achieved by slowing down the kinetics of the recovery variables h and n (Rubin and Wechselberger, 2008). This is not relevant for mouse motoneurons that are characterized by fast spike kinetics [mean half-width of 0.3 ms (Manuel et al., 2009)], indicating both a fast inactivation of the sodium current and a fast activation of the delayed rectifier current. In other models (Gutfreund et al., 1995), the subthreshold oscillations are at low frequency and directly associated with a membrane resonance involving a slow potassium current, at variance with mouse motoneurons where the low-frequency resonance and the fast oscillations are not linked. Rather similarly, Harish and Golomb (2009) explained MMOs in vibrissa motoneurons by noise-induced spikes on top of stable subthreshold oscillations. This is quite different from our scenario where the subthreshold oscillations are unstable and noise is not required to elicit spikes.

A matter of membrane excitability

A slow inactivation of the sodium current is likely responsible for the low membrane excitability of mouse motoneurons. Sodium channels are endowed with multiple time constants for their slow inactivation, ranging from 100 ms to 3 min (Hille, 2001), the molecular mechanisms of which are still largely unknown (Ulbricht, 2005). Slow inactivation of sodium currents has been implicated as a contributing factor to the firing rate adaptation of spinal motoneurons during sustained discharge (Kernell and Monster, 1982; Powers et al., 1999). In particular, a slow inactivation with a time constant of 130 ms accounts for the early phase of the spike frequency adaptation (Miles et al., 2005). Interestingly, frequency adaptation is accompanied by a decrease in spike amplitude (Powers et al., 1999). Moreover, the clockwise hysteresis of the I–F curve, observed in response to a slow triangular ramp of current, is characteristic of motoneurons with late firing rate adaptation [type 2 in the studies by Bennett et al. (2001), Button et al. (2006)]. When an inactivation process with a time constant larger than 1.5 s is incorporated in our model, the amplitude of the spikes decreases during the ascending ramp, a large subprimary firing range with MMOs is present, and the discharge displays a clockwise hysteresis pattern. These features are present when the ramp is slow (0.5 nA/s) and are substantially reduced when the ramp velocity is increased 10 times. This indicates that the slow inactivation of the sodium current likely decreases the membrane excitability at a level low enough to induce MMOs in mouse motoneurons. Frequency adaptation and MMOs thus appear as two facets of the same underlying biophysical mechanism.

Our simulations show that an M-like current, with the same time constant as the slow inactivation of the sodium current, also induces a clockwise hysteresis of the I–F curve. Such a current is present in turtle spinal motoneurons (Alaburda et al., 2002), and KCNQ channels, which underlie the M current, are expressed at the axon initial segment of mouse motoneurons where spikes are generated (Pan et al., 2006). The M-like current certainly plays a role in reducing the motoneurons excitability, but it cannot account for the reduction of spike amplitude.

The AHP, whose typical relaxation time constant is 10 ms in mouse motoneurons (Manuel et al., 2009), tends to oppose the slow inactivation of the sodium current. This de-inactivating effect increases the number of available sodium channels and makes the membrane more excitable, thus reducing MMOs. If the AHP is large enough, the membrane becomes too excitable to produce MMOs, as seen in our dynamic clamp experiments. This is perhaps why MMOs have never been observed in cat motoneurons: the mean AHP is 5.2 mV at the resting potential versus 2.8 mV in mouse motoneurons (Manuel et al., 2009). In line with this suggestion, MMOs tended to appear in experiments where the calcium chelator BAPTA was injected into a cat motoneuron to reduce the activation of SK channels (M. Manuel and D. Zytnicki, unpublished observations). Slow voltage-dependent potassium currents activated by the spikes, like a slow delayed rectifier current (not incorporated in our model), might add to the effect of the AHP and also contribute to the de-inactivation of the sodium current.

Our work suggests that MMOs depend on the excitability state. One may thus wonder whether barbiturate anesthesia, which alters the inactivation properties of sodium channels (Wartenberg et al., 1999), might induce MMOs. This is unlikely because MMOs have never been reported in motoneurons of barbiturate anesthetized cats. MMOs may also depend on neuromodulation, which increases membrane excitability. For instance, an enhancement of the persistent sodium current will suppress MMOs. Calcium persistent inward currents (PICs) also alter excitability. They have been observed in spinal motoneurons of decerebrate and unparalyzed cats (Conway et al., 1988; Hounsgaard et al., 1988; Lee and Heckman, 1998a,b), in turtle, mouse, and rat spinal cord slices (Hounsgaard and Kiehn, 1989; Carlin et al., 2000), and recently in spinal motoneurons of rats anesthetized with ketamine–xylazine (Button et al., 2006; Hamm et al., 2010; Turkin et al., 2010) and of mice anesthetized with fentanyl–midazolam (Meehan et al., 2010). Calcium PICs contribute to shape the I–F relationship and may create a counterclockwise hysteresis [types 3 and 4 in the study by Bennett et al. (2001)]. In our study, calcium PICs are likely to be depressed, since the barbiturate anesthesia we used is known to block L-type calcium channels (Guertin and Hounsgaard, 1999). This is probably why we did not observe any type 4 I–F relationship, i.e., a counterclockwise hysteresis with discharge acceleration on the ascending ramp (Bennett et al., 2001). However, when calcium PICs are present they do not preclude the existence of a subprimary firing range and subthreshold oscillations (Turkin et al., 2010).

Heterogeneities of the intrinsic membrane properties

In our sample, 28% of mouse motoneurons display a counterclockwise hysteresis without any acceleration of the discharge in the primary range [type 3 behavior described by Bennett et al. (2001)]. Note that this happens although PICs are strongly depressed. In this firing pattern, the action potential amplitude little decreases, the width of the subprimary firing range is quite small, and few fast oscillations are observed. In our model, this occurs when the inactivation time constant of the sodium current is smaller than in simulations leading to a clockwise hysteresis, and when the AHP conductance is larger and de-inactivates more the sodium current, thus increasing excitability. Excitability can also be enhanced in the model by moving the threshold of the slow inactivation toward more depolarized values. This suggests that slow inactivation might be less important and operate on a shorter time scale in motoneurons displaying a counterclockwise hysteresis than in those displaying a clockwise hysteresis. Altogether, the slow inactivation properties of the sodium current are likely to be heterogeneous in mouse motoneurons, which might well be responsible for their different firing patterns.

In rat lumbar motoneurons, I–F relationships with a clockwise hysteresis were observed in motoneurons with the smallest input resistance whereas counterclockwise hystereses were observed in those with the highest input resistance (Button et al., 2006; Turkin et al., 2010). Similar results were found in the present study. This suggests a possible relation between the physiological type of the motoneuron and the firing pattern. Experiments in unparalyzed animals should allow us to elucidate the functional consequences of the subprimary firing range of motoneurons on the contraction of their motor unit.