Feature-Specific Attentional Priority Signals in Human Cortex

Abstract

Human can flexibly attend to a variety of stimulus dimensions, including spatial location and various features such as color and direction of motion. Although the locus of spatial attention has been hypothesized to be represented by priority maps encoded in several dorsal frontal and parietal areas, it is unknown how the brain represents attended features. Here we examined the distribution and organization of neural signals related to deployment of feature-based attention. Subjects viewed a compound stimulus containing two superimposed motion directions (or colors) and were instructed to perform an attention-demanding task on one of the directions (or colors). We found elevated and sustained functional magnetic resonance imaging response for the attention task compared with a neutral condition, without reliable differences in overall response amplitude between attending to different features. However, using multivoxel pattern analysis, we were able to decode the attended feature in both early visual areas (primary visual cortex to human motion complex hMT+) and frontal and parietal areas (e.g., intraparietal sulcus areas IPS1–IPS4 and frontal eye fields) that are commonly associated with spatial attention. Furthermore, analysis of the classifier weight maps showed that attending to motion and color evoked different patterns of activity, suggesting that different neuronal subpopulations in these regions are recruited for attending to different feature dimensions. Thus, our finding suggests that, rather than a purely spatial representation of priority, frontal and parietal cortical areas also contain multiplexed signals related to the priority of different nonspatial features.

Introduction

The behavioral importance of locations has been hypothesized to be represented in topographical maps that can guide the allocation of spatial attention (Koch and Ullman, 1985; Wolfe, 1994; Itti and Koch, 2001). In this view, stimulus attributes such as color or motion can identify particular objects as being unique in a visual scene and cause the corresponding location in these maps to have increased activity that represents their “bottom-up” salience. Top-down influences related to the particular goals of the observer may also modulate activity in these maps, for example, by increasing the response at a task-relevant location while suppressing activity at other locations. These “priority maps” can be thought of as representing an abstract quantity reflecting the behavioral importance of locations, but, are hypothesized not to contain any information about the stimulus properties themselves. Instead, these properties must be recovered from representations in early visual areas.

The idea of a priority map has received considerable experimental support that implicates topographically mapped areas in the parietal and frontal cortex as possible neural substrates. In particular, single-unit physiology experiments with awake-behaving monkeys have found evidence that the frontal eye fields (FEFs) and the lateral intraparietal area (LIP) contain representations compatible with priority maps (Thompson and Bichot, 2005; Bisley and Goldberg, 2010). Concordantly, functional imaging studies in humans have found that corresponding frontal and parietal areas contain topographic representations related to saccade planning and attention (Silver and Kastner, 2009), suggesting that these areas in humans may also contain priority maps.

If signals in these frontal and parietal areas do indeed represent priority maps, what might they signal when a particular visual feature is prioritized rather than a particular location? Spatially superimposed displays in which two stimuli are shown in the same location but differ by a stimulus feature are particularly useful for demonstrating feature-based selection. Psychophysical studies have demonstrated that attending to one feature in such displays conferred improved sensitivity to that feature (Lankheet and Verstraten, 1995; Sàenz et al., 2003; Liu et al., 2007). Purely spatial priority maps as conceptualized in theoretical work (Koch and Ullman, 1985; Wolfe, 1994; Itti and Koch, 2001) would be expected to have heightened activity at the same location regardless of which feature is attended and would not contain information that could distinguish between the attended features. Alternatively, parietal and frontal areas may retain more detailed information about prioritized locations including basic stimulus attributes and thus could be used to prioritize stimuli not just in space but also along different feature dimensions.

To investigate how priority signals for features are represented, we conducted two experiments in which subjects attended to either direction of motion or color in a spatially superimposed stimulus while their brain activity was measured with functional magnetic resonance imaging (fMRI). Using multivariate pattern analysis, we were able to reliably decode which particular feature subjects were cued to prioritize (i.e., which color or which direction of motion). These results suggest that frontal and parietal areas contain representations that can be used to allocate feature-based attention.

Materials and Methods

Subjects

Six right-handed subjects (one female; mean age, 24 years) participated in the experiments; all had normal or corrected-to-normal vision. Two of the subjects were authors, and the rest were graduate and undergraduate students at Michigan State University, all of whom gave written informed consent and were compensated for their participation. The experimental procedures were approved by the Institutional Review Board at Michigan State University and adhered to safety guidelines for MRI research.

Visual stimuli and display

Visual stimuli consisted of moving dot patterns (dot size, 0.1°; density, 3.5 dots/deg²) in an annulus (eccentricity from 1° to 12°), presented on a dark background (0.01 cd/m²). Stimuli were generated using MGL (http://justingardner.net/mgl), a set of custom OpenGL libraries running in Matlab (MathWorks). Images were projected on a rear-projection screen located in the scanner bore by a Toshiba TDP-TW100U projector outfitted with a custom zoom lens (Navitar). The screen resolution was set to 1024 × 768, and the display was updated at 60 Hz. Subjects viewed the screen via an angled mirror attached to the head coil at a viewing distance of 60 cm.

Attention experiment: task and procedure

Attention to motion direction experiment.

The stimuli were composed of two overlapping dot fields (white dots, 48 cd/m²) that rotated around the center of the annulus (Fig. 1A). One dot field rotated in a clockwise (CW) direction, whereas the other rotated in a counterclockwise (CCW) direction at a baseline angular speed of 60°/s. A fixation cross (0.75°) was displayed in the center of the screen throughout the experiment.

Figure 1.

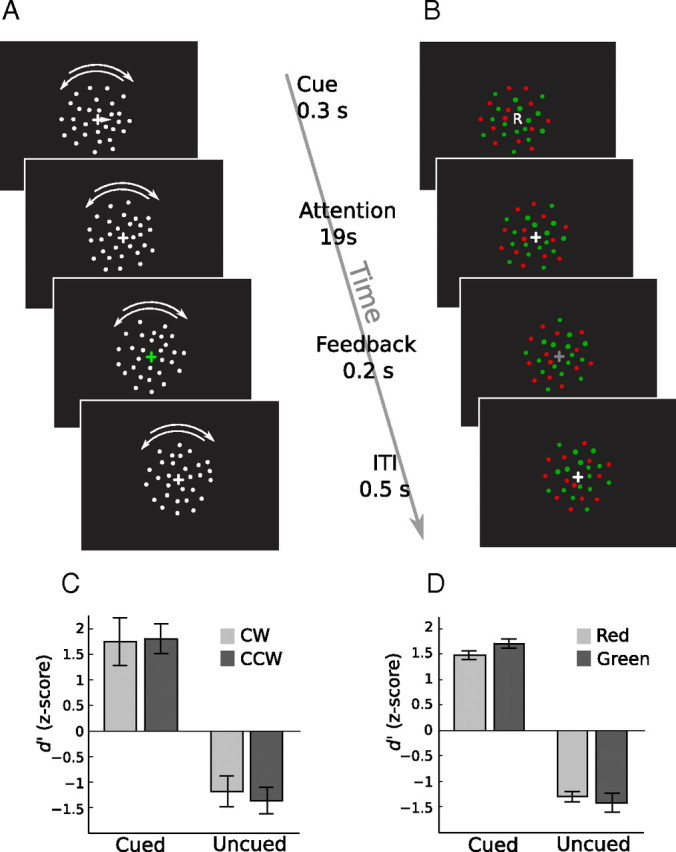
Schematic of the task and behavioral results. A, A trial in the motion experiment. B, A trial in the color experiment. The timing of events was identical for both experiments as indicated by the time line in the middle. ITI, Intertrial interval. C, Behavioral data in the motion experiment. A signal detection d′ value was calculated assuming subjects responded to either the cued dot fields or the uncued dot fields. Error bars denote ±1 SEM across subjects (n = 6). D, Behavioral data in the color experiment, in the same format as in C.

Subjects were cued to either attend the CW direction, attend the CCW direction, or attend neither (null) direction. At the beginning of each trial, an arrow cue (→, ←, ↔) was presented for 0.3 s, which instructed subjects to attend to the CW-rotating dot field, the CCW-rotating dot field, or neither. Trials were 20 s long, and the order was pseudorandomized such that the first trial in a run was always a null trial and each trial type was preceded and followed equally often by other trial types. Each scanning run contained six trials of each type, for a total of 18 trials (360 s/run). Each subject completed 10 of these runs in the scanner, for a total of 60 CW and 60 CCW trials.

On one-fourth of the CW and CCW trials (referred to as “task trials” below), subjects had to perform a speed-detection task that probed whether they were able to successfully direct attention to the cued direction. During task trials, both dot fields underwent brief speed increments (duration, 0.3 s) at random intervals (uniform distributed from 1.5 to 6.5 s). The timing of the speed-up events was randomized independently for the two dot fields. Subjects were instructed to press a button whenever they detected a speed-up in the cued dot field. The magnitude of the speed-up was controlled via a one-up, two-down staircase procedure to maintain performance at an intermediate level. Subjects had to respond within a 1.5 s interval after each speed-up target for the response to count as a hit, which caused a decrease in the magnitude of the speed increment; a miss or false alarm caused an increase in this value. At the end of a task trial, the fixation cross changed color briefly (0.2 s) to give performance feedback. Green indicated all targets were correctly detected, yellow indicated partial target detection, and red indicated none of the targets was detected. Subjects were instructed to always attend to the cued dot field and ignore the other dot field for the CW and CCW trials, regardless of the presence of the speed increment task. We did not include the detection task on all trials so that we could analyze perceptual effects in the absence of motor responses. However, we note that motor response per se cannot contribute to our ability to classify attentional states because the response was constant (the same single-button response for both attentional conditions). Subjects were not cued in advance about whether a trial contained the speed-detection task.

Attention to color experiment.

The design of this experiment (Fig. 1B) followed a similar format to the attention to direction experiment, except subjects were cued to direct attention to the color of the stimuli. Colored dots were shown in an annulus; half of the dots were red and half were green. All dots moved in a “random walk” manner, i.e., the location of each dot was displaced in a random direction at each screen update (speed, 4°/s). The red and green colors were set at isoluminance via heterochromatic flicker photometry. During this procedure, a red/green checkerboard pattern was counterphase flickered at 8.3 Hz in the same annulus, and subjects adjusted the luminance of the green color to minimize flicker (the red color was fixed). Each subject set the isoluminance point in the scanner for six times at the beginning of the scanning session. The average of the six settings was used as the luminance of the green color in the attention experiment.

Subjects were cued to attend to red, to green, or neither as indicated by “R,” “G,” or “N,” respectively, shown at the center of gaze at the beginning of each 20 s block. On one-fourth of the attending to red and green trials, small luminance increments were introduced to both dot fields at random intervals, and subjects detected the luminance increment in the cued color via a button press. The luminance increments were controlled by separate one-up, two-down staircase procedures for the red and green color. The fixation cross changed luminance at the end of the trial to give performance feedback: white, all targets detected; light gray, partial target detection; dark gray, no targets detected. Subjects completed 10 runs in the scanner for a total of 60 red and green trials each. Subjects were not cued in advance about whether a trial contained the luminance detection task.

Imaging data for the first null trial were subsequently discarded to avoid transient effects associated with the initiation of scanning. The motion and color experiments were run in separate sessions on different days. Before the scanning session, subjects practiced the attention task for at least 0.5 h in the psychophysics laboratory until they were comfortable with the task.

Motion–color experiment.

To evaluate the relationship between attention to motion and color, we ran a third session in which the motion and color experiments were conducted in a single session. Four of the six subjects participated in this experiment. The runs were identical to the original experiments. Subjects completed five motion runs and five color runs in an interleaved sequence.

Eye tracking.

To evaluate the stability of fixation, we monitored eye position outside the scanner while subjects performed the same tasks. Four of six subjects participated in the eye tracking session, with each subject performing two runs of the motion and color experiments. The position of the right eye was recorded with an Eyelink II system (SR Research) at 250 Hz. Eye position data were analyzed offline using custom Matlab code.

Functional localizer scan

In each scanning session, we also ran a “localizer” scan to identify voxels responding to the visual stimulus. Subjects were instructed to passively view the stimulus while maintaining fixation on a cross in the center of the screen. Moving dots stimuli alternated with blank fixation periods in 20 s blocks; a total of eight on–off cycles were presented in a scanning run. In addition, a 10 s fixation period was presented at the beginning of the run, the imaging data for which were subsequently discarded. The stimulus consisted of a single dot field with spatial characteristics matching that of the corresponding attention experiment. In the motion experiment, white dots moved in one of eight directions (0°-360° in 45° increments), changing direction every 1 s. In the color experiment, white dots underwent random walk motion. In the motion–color experiment, white dots moved in one of eight directions with random jitter (a combination of the linear motion and random walk).

Retinotopic mapping

For each subject, we mapped early visual cortex as well as several parietal areas that contain topographic maps in a separate scanning session. We used rotating wedge and expanding/contracting rings to map the polar angle and radial component, respectively (Sereno et al., 1995; DeYoe et al., 1996; Engel et al., 1997). Borders between visual areas were defined as phase reversals in a polar angle map of the visual field. Phase maps were visualized on computationally flattened representations of the cortical surface, which were generated from the high-resolution anatomical image using FreeSurfer (http://surfer.nmr.mgh.harvard.edu/) and custom Matlab code. Multiple runs of the wedge and ring stimuli were collected and averaged to increase signal-to-noise ratio. We incorporated an attentional tracking task in the mapping procedure, in which subjects tracked the moving stimulus with covert attention and detected a luminance decrement in the stimulus via button press. The amount of luminance decrement was controlled by an adaptive staircase procedure. We found that this attentional tracking task helped us identify topographic areas in the parietal areas (intraparietal sulcus areas IPS1–IPS4), consistent with recent reports (Silver et al., 2005; Swisher et al., 2007; Konen and Kastner, 2008). In a separate run, we also presented moving versus stationary dots in alternating blocks and localized the human motion-sensitive area, human motion complex hMT+, as an area near the junction of the occipital and temporal cortex that responded more to moving than stationary dots (Watson et al., 1993). Thus, for each subject, we indentified the following areas: V1, V2d, V2v, V3d, V3v, V3A/B, V4, V7, hMT+, lateral occipital cortex LO1, LO2, and four full-field maps in the IPS (IPS1–IPS4). We did not observe a consistent boundary between V3A and V3B; hence, we defined an area that contained both and labeled it V3A/B. We adopted the definition of V4 as a hemifield representation anterior to V3v (Wandell et al., 2007). LO1 and LO2 are two areas in the lateral occipital cortex that contain a hemifield representation (Larsson and Heeger, 2006).

Magnetic resonance imaging protocol

Imaging was performed on a GE Healthcare 3 T Signa HDx MRI scanner, equipped with an eight-channel head coil, in the Department of Radiology at Michigan State University. For each subject, high-resolution anatomical images were acquired using a T1-weighted magnetization-prepared rapid-acquisition gradient echo sequence (field of view, 256 × 256 mm; 180 sagittal slices; 1 mm isotropic voxels). Functional images were acquired using a T2*-weighted echo planar imaging sequence (repetition time, 2.5 s; echo time, 30 ms; flip angle, 80°; matrix size, 64 × 64; in-plane resolution, 3.3 × 3.3 mm; slice thickness, 3 mm, interleaved, no gap). Thirty-six axial slices covering the whole brain were acquired every 2.5 s. In each scanning session, we also acquired a two-dimensional T1-weighted anatomical image that had the same slice prescription as the functional scans but with higher in-plane resolution (0.82 × 0.82 × 3 mm). This image was used to align the functional data to the high-resolution anatomical images for each subject.

fMRI data analysis

Functional data were analyzed using custom code in Matlab. Data for each run were first motion corrected (Nestares and Heeger, 2000), linearly detrended and high-pass filtered at 0.01 Hz to remove low-frequency drift, and then converted to percentage signal change by dividing the time course of each voxel by its mean signal over a run. Data from the 10 attention runs were then concatenated for subsequent analysis.

Functional localizer.

A Fourier-based analysis was performed on data from the localizer scan. For each voxel, we computed the correlation (coherence) between the best-fitting sinusoid at the stimulus alternation frequency and the measured time series (Heeger et al., 1999). The coherence indicates how well the activity of a voxel is modulated by the experimental paradigm and hence serves as an index of how active a voxel responded to the visual stimulation. We used coherence as the sorting criterion in our classification analysis (see below).

Univariate analysis (deconvolution).

We fitted the time series of each voxel with a general linear model with two sets of regressors, corresponding to the two attentional conditions (i.e., CW and CCW in the motion experiment, red and green in the color experiment). Each regressor was composed of 15 columns of time-shifted 1, modeling the fMRI response in a 37.5 s window after the onset of a trial. The design matrix thus formed was pseudoinversed and multiplied by the time series to obtain an estimate of the hemodynamic response evoked by each of the two conditions. This deconvolution approach assumes linearity in temporal summation (Boynton et al., 1996; Dale, 1999) but not a particular shape of the hemodynamic response. To obtain a measure of response amplitude for an area, the deconvolved responses were averaged across the voxels in that area.

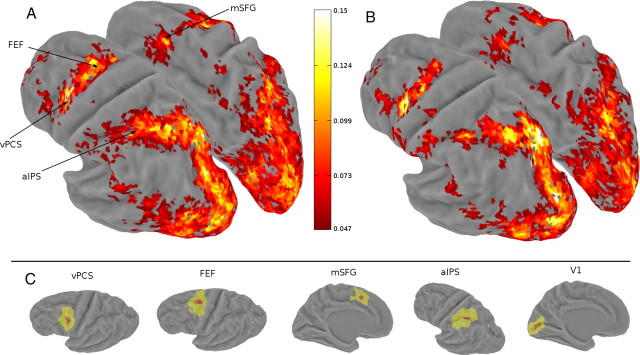
In addition to the visual and parietal areas defined by retinotopic mapping, we defined several other areas based on data from the attention experiment. We looked for voxels that showed significantly modulated response in the attention epochs relative to the null epochs, regardless of sign of the response (i.e., increases or decreases) or the relative amplitude of response in the two attention conditions (i.e., CW vs CCW, red vs green). This was done by using the goodness-of-fit measure, r², of the deconvolution model, which was the amount of variance explained by the model (Gardner et al., 2005). The statistical significance of the r² value was evaluated via a permutation test (Nichols and Holmes, 2002). Event times were randomized and r² values were recalculated for the deconvolution model. Ten such randomizations were performed; the resulting distributions of r² values for all voxels were then combined to form a single distribution of r², which we took as the distribution of r² values expected by chance. Note that each of the 10 distributions was computed for all voxels; thus, combining 10 of them produced a sufficiently large sample to estimate the null distribution. The p value of each voxel was then calculated as the percentile of voxels in the null distribution that exceeded the r² value of that voxel. Using a cutoff p value of 0.005, we defined four additional areas that were active during the attention epochs in both experiment: anterior intraparietal sulcus (aIPS), FEF, ventral precentral sulcus (vPCS), and medial superior frontal gyrus (mSFG) (see Fig. 2).

Figure 2.

Group r² map and averaged task-defined brain areas. A, Group-averaged (n = 6) r² map in the motion experiment, shown on an inflated Caret atlas surface. The approximate locations of the four task-defined areas (aIPS, FEF, vPCS, and mSFG) are shown by the arrowheads. Color bar indicates the scale of the r² value. B, Group-averaged (n = 6) r² map in the color experiment. Maps are thresholded at a voxelwise r² value of 0.047, corresponding to an estimated p value of 0.001 and a cluster size of five voxels. This corresponded to a whole-brain corrected false-positive rate of 0.005 according to AlphaSim (see Materials and Methods). C, Group-averaged task-defined areas, as well as V1, on the atlas surface (left hemisphere). Yellow indicates the union of each subject's area, and red indicates the intersection of each subject's area.

Multivariate analysis (multivoxel pattern classification).

For each voxel in an area, we obtained single-trial fMRI response by averaging the response in a 2.5–22.5 s time window after trial onset for each single trial (time points 2–9). This time window covered the duration of the trial with a shifted onset to compensate for the hemodynamic delay. This produced 60 responses (instances) for each attentional class (i.e., CW or CCW for the motion experiment and red or green for the color experiment) for each voxel. Each instance can be treated as a point in n-dimensional space, where n is the number of voxels. We used a binary linear discriminant analysis in which each novel instance was projected on to a weight vector, converting the n-dimensional instance to a scalar, which was then compared with a bias point to predict to which class the instance belonged:

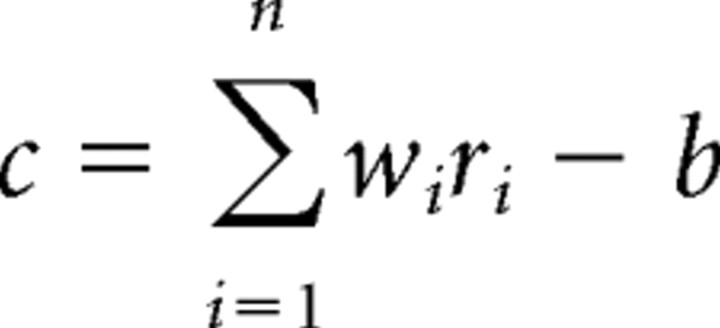The instance was predicted to belong to the first class (i.e., CW or green) when c was negative and the other class (CCW or red) when c was positive. r_i and w_i were response of the ith voxel (defined above) and classifier weight, respectively, and b was the bias point. The classifier weights (w⃗) were assigned using the following equation: w⃗=(m⃗₁−m⃗₂)(Σ + αI)⁻¹, where m⃗₁ and m⃗₂ were the means of the two classes of instance used to build the classifier, Σ was their combined covariance, I was the identity matrix, and α was a regularization parameter. The regularization parameter was set to the SD of the data across all instances and voxels and was used because Σ was underdetermined as a result of the larger number of voxels than instances used to build the classifier. b was set to the midpoint of the two distributions of projected instances.

To evaluate accuracy of the classifier performance, we performed a leave-one-out cross-validation procedure. A training dataset was first constructed by removing one instance, which was then used to train a classifier. The left-out instance was provided to the classifier as input and its output was recorded. This procedure was repeated for each instance of the data. The classifier accuracy was calculated as the number of correct classification over the total number of leave-one-out runs. To evaluate the stability of the classifier performance, we systematically varied the number of voxels (dimensions) used to construct the classifier, from 1 to 150 voxels (see Fig. 4). Voxels were sorted in descending order according to their coherence value in the functional localizer scan. The top n voxels were used in constructing a classifier of a particular size. Coherence value in the localizer scan gave us an independent measure of how active a voxel was and hence ensuring that our training and testing data were completely independent.

Figure 4.

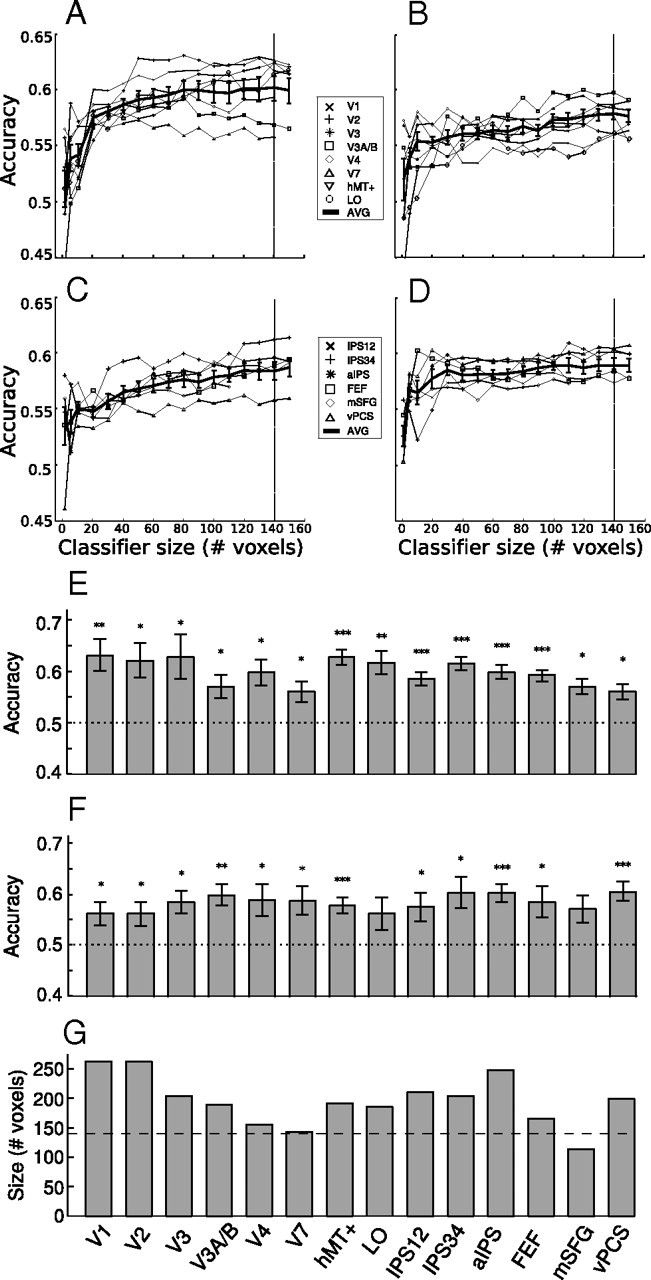
Multivoxel pattern analysis results. A, Mean classifier accuracy (n = 6) as a function of classifier size for the occipital areas in the motion experiment. B, Same data for the frontal and parietal areas in the motion experiment. “AVG” indicates the average across areas in that panel. C, D, Same data for the color experiment. Vertical line at 140 voxels indicates the final classifier size used for group averaging in E and F. Error bars in A–D indicate ±1 SEM across subjects. E, Mean classifier accuracy (n = 6) at 140 voxels in the motion experiment. Horizontal line indicates chance performance (50% correct), and error bars indicate ±1 SEM across subjects. Asterisks indicate the significance level in a t test of individual accuracies against chance (*p < 0.05, **p < 0.01, ***p < 0.001). F, Mean classifier accuracy (n = 6) at 140 voxels in the color experiment. Same format as in E. G, Average size in number of voxels for each area. Horizontal line denotes 140 voxels, which was adopted as the criterion to calculate group-averaged classifier performance.

Whole-brain multivariate analysis (“searchlight”).

In addition to the above region-based multivoxel pattern classification (MVPC) analysis, we also conducted the same analysis in the whole brain (Kriegeskorte et al., 2006). We restricted our search to the cortical surface instead of the whole volume. For each voxel in the gray matter (center voxel), we defined a small neighborhood containing all gray matter voxels within a 25 mm radius based on the distance on the cortical surface. This radius produced neighborhoods containing ∼100 voxels on average. MVPC analysis was then performed on each of such neighborhoods as above, and the resulting classification accuracy was assigned to the center voxel. Thus, for each subject, we generated a classification accuracy map of the whole brain; these maps were then averaged and thresholded for visualization (see below, Surface-based registration and visualization of group data).

Weight map analysis.

A correlation analysis was conducted to assess the similarity/dissimilarity of the voxel weights in the motion–color experiment, in which the attention to motion and attention to color runs were interleaved within a session. We concatenated separately all the motion runs and all the color runs and constructed a classifier for each experiment using all the instances (i.e., treating all data as training data). We calculated the correlation coefficient between the absolute weight values of corresponding voxels to assess their similarity. We then performed two permutation analyses to evaluate the statistical significance of this cross-experiment correlation.

In the first analysis, we wanted to determine whether the cross-experiment correlation was significantly different from the within-experiment correlation. We calculated the correlation values within the motion-only and color-only sessions, by splitting the data in half and training a classifier on each half of the data. The correlation between the absolute classifier weights on each of the two halves of the resampled data was then calculated. We repeated this procedure 1000 times, each time randomly selecting 30 of 60 instances to form one half (and the rest forming the other half), to compute a distribution of correlation values. Note that the generated correlations were based on the same amount of data as that in the cross-experiment correlations (30 instances of each attention condition). This resampling was performed for each area in each subject and generated a distribution of correlations between two halves of the data within motion and color experiment. The mean of the distribution was taken as the expected correlation within the motion and color classifiers.

In the second analysis, we wanted to determine whether the cross-experiment correlation was significantly different from chance. For this analysis, we randomly reassigned the event labels (CW, CCW, red, and green) to data from the motion-color session and then constructed two classifiers, one for the (nominal) motion experiment and one for the (nominal) color experiment, both of which now contained a random sample of all event types. We then computed the correlation between the absolute weights from the two classifiers and repeated the procedure 1000 times for each area in each subject. The mean of the distribution was taken as the expected chance level correlation between the absolute classifier weights.

Thus, for each subject, we obtained three correlations: observed cross-experiment correlation, expected within-experiment correlation, and expected chance correlation. We then applied Fisher's z-transform to the correlation values to convert them into normally distributed z-values. Finally, we compared the z-values for cross-experiment correlation with those of the within-experiment and chance correlations via one-tailed t tests to assess whether they were statistically different. We used one-tailed test because of a priori expectations regarding the direction of the difference between the correlation values, based on how they were generated. That is, the cross-experiment correlation should be larger than chance correlation but smaller than within-experiment correlation.

Surface-based registration and visualization of group data.

All analyses were performed on individual subject data, and all quantitative results reported were based on averages across individual subject results. However, to visualize the task-related brain areas, we also performed group averaging of the individual maps (see Figs. 2, 8). Each subject's two hemispherical surfaces were first imported into Caret and affine transformed into the 711–2B space of the Washington University at St. Louis. The surface was then inflated to a sphere and six landmarks were drawn, which were used for spherical registration to the landmarks in the population-average, landmark- and surface-based (PALS) atlas of human cerebral cortex (Van Essen, 2005). We then transformed individual maps to the PALS atlas space and performed group averaging, before visualizing the results on the PALS atlas surface. To correct for multiple comparisons, we thresholded the maps based on individual voxel level p value in combination with a cluster constraint.

Figure 8.

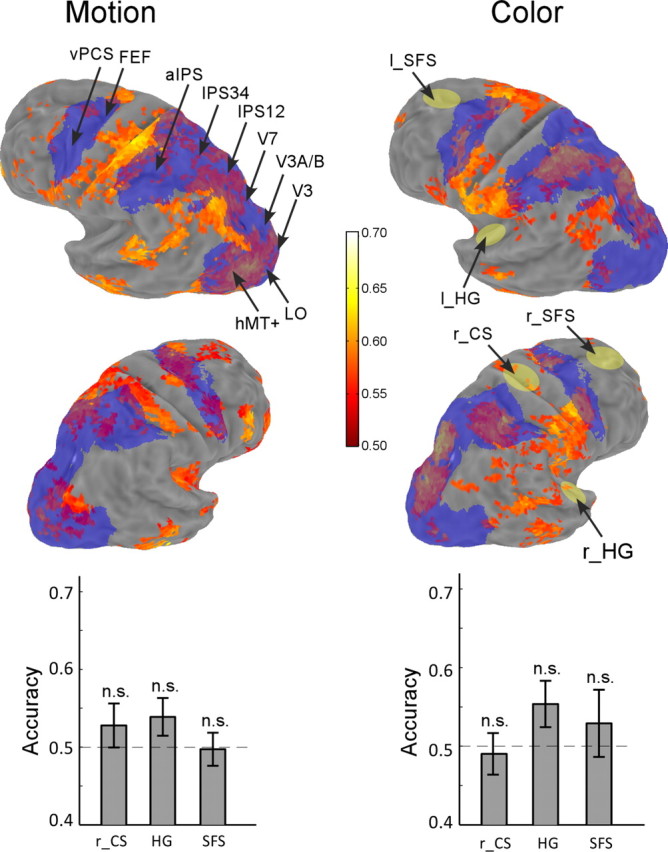
Verification of spatial specificity of classification results via whole-brain (searchlight) multivoxel pattern classification and analysis of control regions. Group-averaged classification accuracy for motion (left column) and color (right column) experiments. The map is shown on inflated Caret atlas surfaces, thresholded at an individual voxel level of p < 0.025 with a minimum cluster of 18 contiguous voxels (corresponding to a whole-brain false-positive rate of 0.01). Color scale represents the mean classification accuracy. Superimposed in blue on the surfaces are unions of the group-averaged brain areas defined by retinotopy and the attention task. The bottom graphs show classification accuracy in three control regions: bilateral Heschl's gyrus (HG), bilateral superior frontal sulcus (SFS), and right central sulcus (r_CS). Their locations are marked by yellow patches on the brain surface; n.s. indicates nonsignificant difference from chance (0.5). Left column, Motion experiment; right column, color experiment.

For the r² map (see Fig. 2), we derived a voxel-level p value based on aggregating the null distributions generated from the permutation test for each individual subject. Specifically, we randomly drew 10,000 r² values from the 10 randomization distributions for each subject and combined them. This combined distribution served as the null distribution for the averaged r² value across subjects. The p value of each individual voxel was thus the percentile of voxels that has a higher r² value in the null distribution. For the whole-brain classification accuracy map (see Fig. 8), we derived a voxel-level p value by performing a t test across subjects against chance accuracy (0.5). For both types of maps, we then performed 10,000 Monte Carlo simulations with AFNI's AlphaSim program to determine the appropriate cluster size given a particular voxel-level p value to control for the whole-brain false-positive rate.

To provide localization information about the task-defined areas (aIPS, FEF, vPCS, and mSFG), we averaged individually defined areas in the Caret atlas space and visualized them on the atlas surface (see Fig. 2C). We also calculated the Talairach coordinates of the averaged areas. We defined eight standard reference points in each subject's brain: anterior commissure, posterior commissure, the most anterior and posterior points, the most superior and inferior points, and the most left and right points. Individual brain was then transformed to the Talairach space (Talairach and Tournoux, 1988) via an affine transformation that minimized the squared error between the mapping of the eight reference points defined in the subject's brain with the coordinates of those points in the Talairach atlas brain.

Results

Behavior

Subjects were cued to selectively attend to one of two overlapping dot field stimuli that differed from each other by a single feature (Fig. 1): either direction of motion (CW or CCW) or color (red or green). To test whether subjects were able to successfully attend to the correct dot field, on one-fourth of the trials, brief increments in the speed (motion experiment) or luminance (color experiment) of the stimuli were presented at independent and random times on each of the two stimuli. The subject was instructed to press a button when they detected these changes only on the cued stimulus. The magnitude of the increment was controlled via an adaptive staircase procedure to ensure an intermediate and constant level of task difficulty across all conditions. The color and motion experiments were run in separate runs within which the cued direction of motion or color was randomized in interleaved trials with a null condition (subjects were cued not to attend to either stimulus).

Analysis of the subject's behavioral performance on the change detection task confirmed that subjects were able to selectively attend to the cued stimulus. From the subject's responses, we computed the signal detection theory measure of sensitivity (d′ value) to the stimulus changes (Fig. 1C,D), separately for each cued feature. Performance was excellent for the cued stimulus, and the subjects were equally sensitive to changes when either color or motion was cued (p = 0.55, two-way repeated-measures ANOVA). Furthermore, no difference in performance was observed between the two feature values, i.e., performance was equally good for red versus green and CW versus CCW (p = 0.22). Thus, any difference in fMRI responses reported below were not attributable to differences in task difficulty across conditions. We confirmed that the subjects were selectively attending only to the cued feature by also computing d′ for the uncued feature (which underwent stimulus changes independently). We found negative d′ values significantly different from the d′ for the cued stimulus (p < 0.0005 for both motion and color experiments, two-way repeated-measures ANOVA). The d′ for the uncued stimulus was negative because the majority of the correct responses to the cued target events were counted as false alarms to the uncued stimulus as the targets were relatively infrequent and the response window was short (1.5 s). Finally, eye tracking results showed that subjects maintained stable fixation during the attention epochs; thus, overt eye movements did not contribute to attentional effects.

Cortical areas modulated by feature-based attention

To define which cortical areas were modulated by feature-based attention, we performed an individual subject-based deconvolution analysis. We computed a deconvolved response for each of the two attention conditions and then obtained an r² value, which was the amount of variance in the time course explained by these average responses (see Materials and Methods). A high r² value indicated that activity in that voxel was modulated by the experimental paradigm. To visualize these data across subjects, we performed a spherical surface-based registration of each subject's brain to the PALS atlas space as implemented in Caret (Van Essen, 2005). We then transformed individual maps to the atlas space and averaged them together (Fig. 2). Note that we defined areas for each subject based on their retinotopy scans (see Materials and Methods) and individual r² maps and used the group-averaged atlas data for visualization purposes only.

In the motion experiment, attending to directions modulated brain areas in occipital, parietal, and frontal cortex (Fig. 2A). The occipital activity occupied the retinotopically defined visual areas (V1, V2, V3, V3A/B, V4, V7, hMT+, LO1, and LO2). The parietal activity ran along the IPS and extended to the posterior bank of the postcentral sulcus. The majority of this parietal activity coincided with the retinotopically defined IPS areas (IPS1–IPS4). Just anterior to the retinotopically defined IPS areas, we identified another area that might correspond to IPS5 and beyond (Konen and Kastner, 2008), but because we could not retinotopically map this area, we tentatively called it aIPS. In the frontal cortex, activity was found along the PCS and in the dorsomedial frontal cortex. We split the precentral sulcus activity into two areas: a dorsal portion that was located near the vicinity of the caudal part of the superior frontal sulcus and precentral sulcus, the putative human FEF (Paus, 1996), and a ventral portion (vPCS). These two regions appeared contiguous on the group-averaged r² map, but they formed primarily distinct clusters in individual subject maps. The dorsomedial frontal activation was located primarily in the posterior and medial aspect of the superior frontal gyrus. Its location is consistent with human pre-supplementary and supplementary motor area (Picard and Strick, 2001). The Talairach coordinates of these task-defined areas are listed in Table 1.

Table 1.

Talairach coordinates of task-defined areas

Area name	Left hemisphere	Right hemisphere
aIPS	−30, −29, 38	28, −37, 36
FEF	−20, −8, 45	21, −5, 44
vPCS	−36, −4, 39	41, 6, 32
mSFG	−6, 2, 52	3, 8, 50

The mean stereotaxic coordinates of the group-averaged area (see Figure 2C) are reported here.

In the color experiment, a similar set of areas were modulated by attending to colors as were modulated by attending to motion directions (Fig. 2B). This similarity was also observed in individual subject's data, as the same subject participated in both experiments. Because of this similarity, we defined the same set of areas based on individual r² maps (aIPS, FEF, vPCS, and mSFG) for both experiments. This was done by adopting a relatively low voxelwise threshold and defining areas based on overlapped activity in both r² maps. We were able to define all areas in all subjects, except mSFG in one subject. Hence, the mSFG results were based on five subjects. Activity patterns for both experiments were primarily symmetric for the two hemispheres; no obvious laterality was observed. Hence, in all analysis below, we combined data from corresponding areas across the two hemispheres.

The deconvolution analysis and retinotopic mapping allowed us to define 17 areas for each hemisphere: 13 from the retinotopic mapping session [V1, V2 (dorsal and ventral), V3 (dorsal and ventral), V3A/B, V4, V7, hMT+, LO1, LO2, IPS1, IPS2, IPS3, and IPS4] and four from the attention task (aIPS, FEF, vPCS, and mSFG). To assess the reproducibility of these areas with respect to sulcal landmarks across subjects, we examined their average location across subjects in the PALS atlas space. Figure 2C shows that these areas across subjects were found in overlapped regions in the atlas space. As a check of the quality of our surface registration, we also displayed the averaged V1 area on the atlas surface and found that it resided primarily in and around the calcarine sulcus, as was expected, given that calcarine sulcus was one of the landmarks used in surface-based registration. Although there was some variability across subjects in the location in the atlas space of the individually defined areas, (i.e., the union across subjects shown in yellow was larger than their intersection in red), this variability was comparable with topographically defined areas such as V1.

Average response across feature-based attention conditions

We first examined response amplitude averaged across all voxels in each defined area to determine whether there were any global differences in response magnitude between different feature-based attention conditions. Note that our whole-brain analysis based on r² values only required voxels to be significantly modulated by the experimental paradigm (see Materials and Methods). Importantly, it did not select voxels based on increases versus decreases in activity between attention and null epochs, nor on differences in amplitude between the two attention conditions (e.g., CW vs CCW). Therefore, it is informative to examine the time course data in the task-defined areas, in addition to the retinotopically defined areas. For this and subsequent analysis, we have combined the four retinotopically defined IPS regions into IPS12, which contained IPS1 and IPS2, and IPS34, which contained IPS3 and IPS4. We also combined LO1 and LO2 into one area, LO. This was done to improve signal-to-noise in the time course analysis and classifier performance in the multivariate analysis because the individual IPS and LO areas tended to be smaller and contained fewer voxels than other areas (see below, Multivoxel pattern classification: region based).

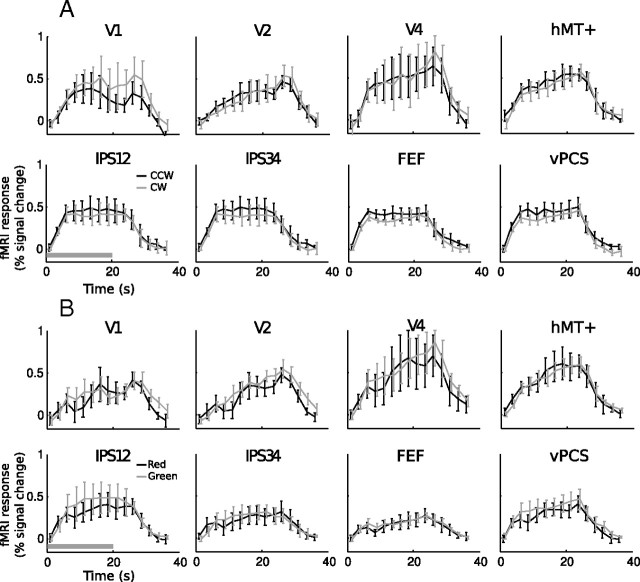
Average fMRI response amplitude showed a sustained increase above baseline for both attentional conditions. Time courses from a subset of brain areas are shown in Figure 3; data from all areas are similar. Given that the null epochs served as the baseline in our deconvolution analysis, the sustained elevated fMRI response shown in Figure 3 represents a higher response for the attention epochs relative to the null epochs. This increase was entirely attributable to attention, because the sensory stimuli were held constant throughout the experiment.

Figure 3.

Time courses in select brain areas. A, Mean time course (n = 6) of eight areas in the motion experiment. B, Mean time course (n = 6) of eight areas in the color experiment. The horizontal bar in the bottom left panel indicates the duration of a trial. fMRI responses are slightly shifted horizontally during plotting for better visualization. Error bars denote ±1 SEM across subjects.

Overall, there was little difference in response amplitude between attending to CW versus CCW (Fig. 3A, compare gray and black traces) and attending to red versus green (Fig. 3B). For each subject, we averaged the response amplitude in a time period 2.5–22.5 s after trial onset (the same time period used in the multivariate analysis, see below) and compared the two attention conditions across subjects. With only a few exceptions, response amplitude was not reliably different between the two attention conditions. In the motion experiment, attending to CCW yielded a larger response in FEF (p < 0.05, paired t test), whereas in the color experiment, attending to green yielded a larger response in V3 and V3A/B (p < 0.05 for both areas). Thus, attending to different features may lead to small differences in overall response amplitudes in certain brain areas, but in general, mean response amplitude within an area did not carry feature-specific information.

Multivoxel pattern classification: region based

Next we examined whether the pattern of the fMRI response across voxels in an area could distinguish which feature was attended, although the average response amplitude did not. We used a multivariate pattern classifier and cross-validation to assess whether attending to different features produced reliably different patterns of response. For each area, we sorted the voxels by how active they were in an independent localizer scan and constructed classifiers of different sizes by varying the number of voxels used (see Materials and Methods). We then computed classification accuracy as a function of classifier size (Fig. 4A–D). In general, classifier performance increased rapidly at small voxel numbers but much more gradually afterward, for both retinotopically defined occipital areas (Fig. 4A,B, motion and color experiments, respectively) as well as parietal and frontal areas (Fig. 4C,D).

Using 140 voxels as an arbitrary asymptotic classifier size, we plotted classification accuracy for each visual area and found that above-chance accuracy was achieved in both early occipital visual areas as well as parietal and frontal areas for both motion (Fig. 4E) and color (Fig. 4F) experiments (the exact choice of the cutoff classifier size is not critical). We used t tests to evaluate whether the mean accuracy was significantly greater than chance (0.5). The classifiers reliably decoded the attended motion direction in all areas (Fig. 4E) and the attended color in all areas except in LO and mSFG (Fig. 4F). Classifiers based on individual IPS areas (IPS1–IPS4) gave the same result as the combined ones, except that IPS2 did not reliably classify the attended color. Figure 4G shows the average size of all areas; all except mSFG was larger than 140 voxels, the criterion size in the accuracy result. The mSFG accuracy was based on all the voxels (∼110 on average). The relatively smaller size of the mSFG area and the fact we could not identify it in one subject could potentially account for its less reliable accuracy in the color experiment.

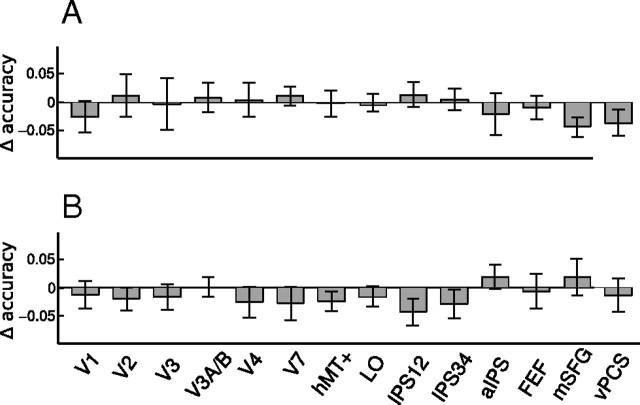
Because we used visual cues at fixation to direct subjects' attention, our classifier could be sensitive to differences in activity patterns attributable to the sensory response to the cue. This is unlikely because the cue was very small and only shown briefly at the beginning of a trial, whereas our classifier used the averaged response across the whole 20 s trial. If a sensory response to the cue could account for the classification results, one would expect classifier performance to be better in the early rather than the later part of the trial, because a sensory response to the cue should have dissipated in the later part of the trial. To test this prediction, we constructed classifiers using either the first half of the fMRI response, by averaging the first four time points (2.5–12.5 s), or the second half of the fMRI response, by averaging the last four time points (12.5–22.5 s). There was no significant difference in classification accuracy for the first half versus the second half of the trial (Fig. 5). Indeed, if anything, the second half could classify the attended feature slightly better than the first half. Thus, we can rule out the potential confound that a sensory response to the attention cue accounted for classification accuracy.

Figure 5.

Comparison of classifier performance based on first versus second half of the fMRI response in a trial. A, Mean difference (n = 6) in classifier performance (first half − second half) for the motion experiment. Error bars are ±1 SEM across subjects. B, Same results for the color experiment.

Weight map analysis

Next we asked whether the same set of voxels contributed to the decoding of attended directions and colors. The classification analysis showed that there were reliable patterns of activity in the same brain areas for attention to directions and colors. However, we wanted to determine how similar or different the patterns of activity were for directions and colors. To evaluate the relationship between these multivoxel patterns, we examined the weights assigned to each voxel by the classifier analysis. Classifier weights indicate how informative a particular voxel is for the pair of conditions being classified (e.g., CW vs CCW or red vs green). A voxel that responded similarly to both conditions would have a weight value near 0, whereas a voxel that responded very differently to the conditions would have a high absolute weight value. Thus, voxels that contribute to the classification accuracy for both color and motion experiments would be expected to have a high absolute weight value in both experiments (and voxels that do not contribute would have a low absolute weight value in both experiments).

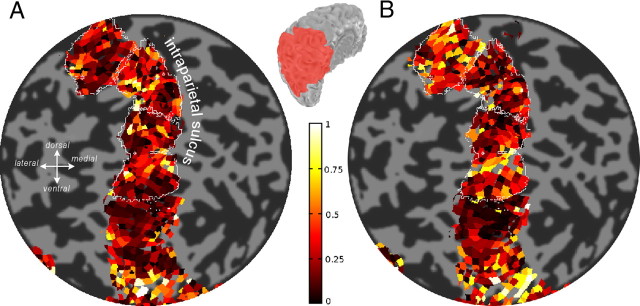
For this analysis, we repeated the two experiments in a single session (see Materials and Methods), so that functional data were acquired with the same slice prescription. This allowed us to establish a correspondence between individual voxels in the motion and color experiments with minimum spatial transformation of the imaging data. Figure 6, A and B, show the absolute classifier weight values for a single subject's parietal areas in the motion and color experiment, respectively.

Figure 6.

Classifier weight maps in a single subject, visualized on a flattened patch of the left posterior parietal cortex. A, Absolute weights for the motion classifier. B, Absolute weights for the color classifier. The thin white lines are the boundaries of three parietal areas in this hemisphere (top, aIPS; middle, IPS34; bottom, IPS12). IPS runs in the dorsoventral direction along the flat map. The inset indicates the location of the patch (in red) on a folded cortical surface.

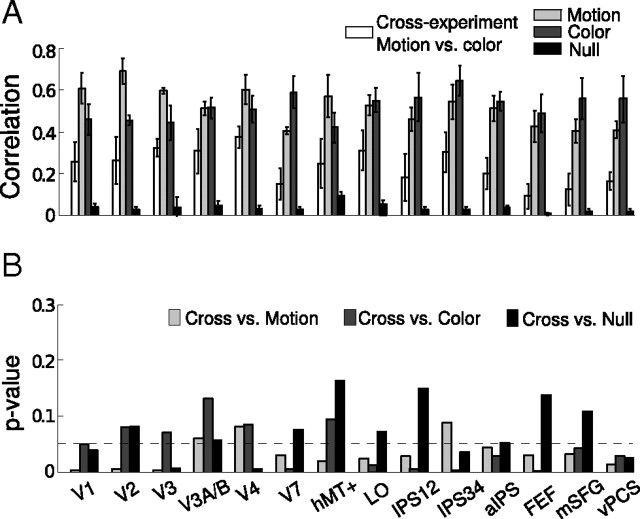
To evaluate the similarity of these weight maps, we ran a correlation analysis. For each area, we calculated a correlation coefficient between the absolute weights of the voxels in the motion and color classifier. The correlation value served as an index of the similarity between the weight maps across the motion and color experiments. There was a modest correlation, as shown in Figure 7A (cross-experiment motion vs color, white bars). We first assessed whether this correlation was significantly above chance, by performing a permutation analysis in which we randomized the labels of trials (whether they were CW or CCW, or red or green trials; see Materials and Methods) to generate a distribution of chance correlations (Fig. 7A, black bars). We took the means of these distributions to represent the estimated level of chance correlation. We then compared the cross-experiment correlation with these chance correlations and found them to be generally greater than chance (p values shown as black bars in Fig. 7B, t test).

Figure 7.

Correlation analysis of the weight maps. A, Mean correlations (n = 4) of the absolute weights between the motion and color classifier (white bars). Light gray bars plot the mean correlations between the absolute weights based on the split-half analysis of the motion experiment, whereas the dark gray bars plot the same results for the color experiment. The black bars plot the mean correlations of the null distributions based on randomly relabeling the events (see Materials and Methods). Error bars denote ±1 SEM across subjects. B, p values in one-tailed t tests comparing the cross-experiment correlation to the three correlations based on permutation analyses. The dashed horizontal line indicates the significance level of 0.05.

Having determined that there was indeed some significant similarity between the two weight maps, we next asked whether that similarity was complete or whether there was any significant difference between the two weight maps. To do this, we used the within-experiment correlation as a measure of the maximal correlation possible given the noise in the measurements and compared that with the correlation between the color and motion experiments. We performed a permutation analysis in which we split the data for the motion- and color-only session in half and generated a distribution of the within-experiment correlations (see Materials and Methods) (Fig. 7A, light and dark gray bars). We compared the cross-experiment correlations to the means of the distributions generated by the permutation analysis and found them to be generally smaller than the within-experiment correlation (p values shown as light and dark gray bars in Fig. 7B, t test). These results suggest that the degree to which voxels contributed to classification accuracy in the two experiments was partially but not completely correlated.

Multivoxel pattern classification: whole-brain searchlight

Given that signals from most areas defined by the univariate analysis can be used to classify the attended features, we wanted to confirm that classification accuracy was not attributable to some spatially unspecific signal in our data. We hence performed whole-brain MVPC analyses using a searchlight procedure (see Materials and Methods) to test the specificity of the classification results. Examination of the group-averaged map of classification accuracy showed above-chance performance in brain areas in occipital, parietal, and frontal cortex (Fig. 8), similar to the univariate analysis (cf., Fig. 2). Importantly, in both individual and group-averaged results, there were many cortical areas that did not show significant classification accuracy, thus ruling out the possibility that spatially unspecific signals drove classification accuracy in all areas of the region-based analysis.

We further confirmed the specificity of the classification analysis by performing region-based analyses on several regions that theoretically should not be involved in directing attention to visual features: motor cortex ipsilateral to the hand that the subjects used to perform the task (right central sulcus), bilateral early auditory cortex (Heschl's gyrus), and a region anterior to the FEF (bilateral superior frontal sulcus). For reference, the approximate locations on the atlas surface of these areas are shown in yellow in Figure 8. These areas all showed classification accuracy that was statistically indistinguishable from chance performance (t test, all p > 0.2), thus again confirming that classification accuracy in the region-based analysis was not attributable to an unspecific spatially global signal.

Checking the match between the region-based and whole-brain analyses revealed a general, although not perfect, correspondence between the two analyses. We superimposed the unions of each individually defined brain areas in the atlas space (Fig. 8, blue areas) on the whole-brain map. Significant classification was found in the whole-brain analysis within most of the areas from the region-based analysis, with the possible exception of right parietal regions in the motion experiment. This omission in the whole-brain analysis was likely attributable to the following two reasons. First, functionally defined regions do not completely overlap in the atlas space across subjects (Fig. 2); hence, averaging in the atlas space is less powerful than averaging the same functionally defined areas across subjects. Second, our region-based results combined voxels from corresponding areas in the left and right hemispheres, whereas the searchlight procedure was necessarily based on classification performance in local neighborhoods restricted within a hemisphere. Nonetheless, the overall results from the whole-brain analysis were primarily consistent with results from region-based analysis.

Although it is tempting to generalize the inference to new areas and compare results from the motion and color experiments in the whole-brain maps, the spatial specificity of the analysis is limited. Mislocalization of priority signals on the atlas map may easily occur attributable to the usual imperfections of group-averaged analyses such as imperfect segmentations, surface registrations, transformations according to aligning sulcal/gyral landmarks, and partial voluming attributable to the fact that voxels are in general larger than the thickness of the gray matter. Even more problematically, each voxel represents the classification accuracy for the whole surrounding region along the cortical surface: significant mislocalization may occur if, for example, a voxel is surrounded by two areas with weak priority signals. Classification accuracy then would be highest in the region in between the “actual” locations containing priority signals. Finally, the small number of subjects for this random-effects type analysis precludes any meaningful interpretation and extrapolation from the current dataset.

Discussion

We examined brain areas that carried a representation of attended feature in a feature-based selection task. Our univariate analysis showed that, compared with a baseline condition with identical sensory stimulation, the overall amplitude of neural response increased during attention to features. However, the mean response amplitude did not discriminate which feature was being attended. Using multivoxel pattern analysis, we were able to decode the attended feature in a number of frontal and parietal areas, as well as in visual areas. These frontal and parietal areas likely contain the control signals for maintaining attention to visual features.

Domain generality and specificity of attentional priority

That we could use signals from many parietal and frontal areas to decode the attended feature value, for both color and direction of motion, is consistent with growing evidence that these areas contain generalized control signals for guiding attention. Although we did not test for spatial attentional signals in our paradigm and thus did not directly determine whether the same areas control spatial and feature-based attention, many previous experiments have implicated the same areas such as FEF and IPS in the control of spatial attention (Silver et al., 2005; Szczepanski et al., 2010). Our results are thus suggestive of a general mechanism of attentional priority across spatial and feature-based attention.

A domain-general organization of attention priority signals is corroborated by previous studies that have directly compared brain activity between spatial and feature-based attention tasks (Wojciulik and Kanwisher, 1999; Giesbrecht et al., 2003; Egner et al., 2008), as well as between attention to different feature dimensions (Zanto et al., 2010). These studies have shown that primarily similar brain areas in the dorsal attention network show increased activity during different types of attention tasks. Finally, the process of shifting attention [a process likely to rely on different neural substrates than maintaining attention as studied here (Posner et al., 1984)] evokes transient activity in the medial superior parietal lobule (Serences and Yantis, 2006) that may also be organized in a domain-general manner (Greenberg et al., 2010).

Some domain specificity has also been suggested by subtle activity differences among different types of attention tasks (Wojciulik and Kanwisher, 1999; Giesbrecht et al., 2003; Egner et al., 2008; Zanto et al., 2010). Indeed, our whole-brain analyses resulted in some differences between maps for motion and color, suggesting some domain specificity outside of the topographic and functionally defined areas we studied in the region-based analyses. However, the variability inherent in basing comparisons on anatomical rather than function-based alignment for our relatively small number of subjects would suggest that further confirmation of these potential areas of domain-specific signals are required.

Feature selectivity: response amplitude versus patterns

Previous univariate analyses of task-specific responses may not be as diagnostic as examining specificity of signals using multivariate pattern analysis. For example, in direct comparisons (Shulman et al., 2002; Liu et al., 2003), attending to motion generally evoked larger responses than attending to color in the dorsal attention network, whereas the reverse contrast revealed very little activation in whole-brain analyses. Based on these results, one might conclude that the frontal and parietal areas do not participate in color-based selection, which leads to the puzzling question as to what areas control color-based attention. Our results showed that, despite showing lower amplitude response to color in previous experiments, these same areas contained color-specific signals. The larger response associated with attention to motion can be explained by a general preference for motion in these dorsal areas (Sunaert et al., 1999; Bremmer et al., 2001). However, such overall preference does not preclude the existence of color-selective signals in the same areas.

Similarly, previous studies on the effect of attention in visual cortex have emphasized cortical specialization during attention to different feature dimensions. For example, attention to color and motion activated V4 and hMT+, respectively (Corbetta et al., 1991; Chawla et al., 1999). Here we found that responses from both these areas carried information about the cued features, for both color and direction of motion. Thus, although these areas have an overall magnitude difference in response for attending to color versus motion, activity patterns in these areas are informative about feature values in both dimensions. These findings suggest that feature-based attentional modulation in visual cortex might be more widespread than suggested by studies using only univariate analyses (Kamitani and Tong, 2005, 2006).

Priority maps for visual features

Accumulating evidence suggests that areas such as the FEF and various areas in the intraparietal sulcus contain topographically organized control signals related to the locus of spatial attention. Perhaps the strongest support for this view comes from studies that showed subthreshold microstimulation of FEF improves behavioral performance for stimuli located in the movement field of neighboring neurons (Moore and Fallah, 2001), as well as increases firing rate of V4 neurons whose receptive fields overlap with the FEF movement field (Moore and Armstrong, 2003). These findings suggest that spatial attention is controlled via feedback connections from frontal and parietal areas to visual areas that link neurons with corresponding spatial receptive fields. Thus, spatial organization, as reflected in topographic maps in both frontal/parietal areas and visual areas, provides a common framework to implement top-down control.

The topographical organization of attentional control signals in frontal and parietal areas is consistent with theoretical proposals for priority maps (Koch and Ullman, 1985; Wolfe, 1994; Itti and Koch, 2001), which have praimrily focused on prioritizing spatial locations, based on either bottom-up salience or top-down goals. The notion of a spatial priority map can be traced to early theories of attention, such as the “master map of locations” proposed in the feature integration theory (Treisman, 1988). Theoretical and physiological evidence has supported the idea that frontal (Thompson and Bichot, 2005) and parietal (Bisley and Goldberg, 2010) areas contain representations of priority independent of the particular stimulus features that give rise to their priority. However, a purely spatial priority map cannot explain how attention is prioritized during nonspatial selection, when location information is irrelevant, as in the current experiments with superimposed features.

Previous neuroimaging evidence has not determined whether putative priority maps contain purely spatial information or whether they can also contain more general information such as prioritized features (but see Serences and Boynton, 2007 for preliminary evidence consistent with our result for directions). Increased dorsal frontal and parietal activity associated with attending to feature values and dimensions (Shulman et al., 1999, 2002; Liu et al., 2003) has been reported, but these responses may have been attributable to spatial rather than featural aspects of the tasks. Stimuli in these experiments appear in restricted spatial locations, and thus activity in parietal and frontal areas may be associated with attending to the stimulus location instead of the cued feature. Furthermore, a general increase in neural activity is also consistent with a number of other explanations such as arousal/effort and response anticipation.

We found that parietal and frontal areas contain nonspatial information about the priority of specific features, thus requiring the extension of the notion of these areas as spatial priority maps. Our data suggest that these areas can control feature-based attention by actively sending top-down biasing signals for a particular feature to the visual cortex, analogous to the case for spatial attention. These top-down signals would presumably result in the feature-specific modulation in the visual cortex (Maunsell and Treue, 2006) that was reflected in the reliable decoding of attended feature in the visual areas (see also Kamitani and Tong, 2005, 2006). By demonstrating feature specificity, these results showed that there are priority signals that reflect the distribution of attention in feature space. However, unlike priority maps for spatial attention, these signals do not form a topographic organization of space but are manifested as distinct patterns of activity representing prioritized features.

The organization of spatial and feature priority signals

If the dorsal frontal and parietal areas contain priority signals for both features and locations, how might these various signals be organized? A useful model in which spatial and feature information is represented in the same cortical area is the primary visual cortex. V1 has a topographic map of the visual scene. Superimposed on this overall spatial organization are maps that represent other features: orientation, direction, color, and spatial frequency (Blasdel and Salama, 1986; Shmuel and Grinvald, 1996; Hübener et al., 1997). These maps can be thought of as independent representations of the same stimulus along different dimensions, and indeed these separate maps sometimes form an orthogonal organization (Bartfeld and Grinvald, 1992; Hübener et al., 1997; Swindale, 2000). Perhaps areas in the dorsal attention network conform to a similar organization. This possibility is consistent with our weight map analysis, which showed that distinct groups of voxels contributed to the decoding of attended colors and directions. Although the spatial organization of priority signals may be static for some basic features, there are likely also dynamic aspects of the organization that can be reconfigured to address particular task demands. This is suggested by recent studies on category learning, in which subjects need to discriminate visual stimuli belonging to arbitrarily defined categories (Seger and Miller, 2010). Neurons in monkey LIP have been shown to exhibit category-selective responses after training and shift their selectivity after retraining on new category boundaries with identical stimuli (Freedman and Assad, 2006). Thus, although representations may differ in how fluidly they adjust to task demands, representing different feature dimensions with overlapped yet independent maps might be a common organizational theme for both the early sensory and higher-order association cortex. Such “multiplexed” maps may therefore represent a general strategy for efficient organization of task-relevant information necessary to achieve flexible attentional selection.