Frequency-Tuned Cerebellar Channels and Burst-Induced LTD Lead to the Cancellation of Redundant Sensory Inputs

Abstract

For optimal sensory processing, neural circuits must extract novel, unpredictable signals from the redundant sensory input in which they are embedded, but the detailed cellular and network mechanisms that implement such selective cancellation are presently unknown. Using a combination of modeling and experiment, we characterize in detail a cerebellar circuit in weakly electric fish, showing how it can carry out this computation. We use a model incorporating the wide range of experimentally estimated parallel fiber feedback delays and a burst-induced LTD rule derived from in vitro experiments to explain the precise cancellation of redundant signals observed in vivo. Our model demonstrates how the backpropagation-dependent burst dynamics adjusts the temporal pairing width of the plasticity mechanism to precisely match the frequency of the redundant signal. The model also makes the prediction that this cerebellar feedback pathway must be composed of frequency-tuned channels; this prediction is subsequently verified in vivo, highlighting a novel and general capability of cerebellar circuitry.

Introduction

One of the most influential theories of cerebellar function describes it as a learning device. The initial theories by Marr (1969) and Albus (1971), and later physiological investigations by Ito (1984), argue that synaptic connections between parallel fibers and Purkinje cells are modified by experience. A central component of this theory is that an error signal originating from climbing fibers selects parallel fiber (PF) inputs by weakening (via LTD) those inputs whose timing is not appropriate for the required motor output. Although this theory is still intensely debated, an elegant body of work (Roberts and Bell, 2000; Sawtell and Williams, 2008) on a cerebellar-like structure in mormyrid electric fish confirmed the importance of PF timing and synaptic depression in shaping an adaptive filter that cancels expected sensory input. A similar process takes place in the gymnotiform fish, and our study builds on these findings to reveal new properties of cerebellar circuits.

Apteronotus leptorhynchus continuously emits a high-frequency (600–1000 Hz) sinusoidal electric organ discharge (EOD) into its environment to sense its surroundings and communicate with conspecifics. Small objects such as prey create spatially localized low-frequency (<16 Hz) amplitude modulations (AMs) of the EOD (Nelson and MacIver, 1999), while tail bending or the presence of same sex conspecifics will generate spatially global AMs in the same low-frequency range. These AMs are linearly encoded by numerous electroreceptor afferents (Carr and Maler, 1986; Gussin et al., 2007) that project to various types of pyramidal cells within the electrosensory lateral line lobe (ELL) (Saunders and Bastian, 1984; Berman and Maler, 1999). One type of pyramidal cells—superficial pyramidal (SP) cells—have extended spiny apical dendrites in receipt of PF feedback emanating from cerebellar granule cells [eminentia granularis posterior (EGp)] (Sas and Maler, 1987). Global signals recruit the feedback pathway, whereas spatially localized signals do not. This feedback serves to actively cancel the response to global low-frequency signals (Bastian, 1986). SP cells can therefore eliminate the global low-frequency AMs due to, e.g., tail bending or communication signals, yet still extract the local AMs that signal the presence of prey and other local objects. Behavioral studies (Nelson and MacIver, 1999) suggest that this cancellation mechanism is essential for prey capture in the absence of vision.

The response of SP cells consist of both isolated spikes and spike bursts generated by complex somatodendritic dynamics (Lemon and Turner, 2000). PF–SP cell synapses are subject to correlative LTD, in which depression occurs when both presynaptic and postsynaptic burst firing occur within a certain time window (Harvey-Girard et al., 2010). We used this in vitro plasticity rule, together with the estimated distribution of conduction delays in the feedback pathway, to construct a minimal model of the cancellation mechanism. The inclusion of these two elements in a cerebellar feedback model allowed us to constrain other properties of the circuit and identify the required neural dynamics. In particular, the model predicts that the granule cell network generates narrowly tuned frequency filters, a prediction that we verified in vivo.

Materials and Methods

LIF model.

This model of a superficial E pyramidal cell in the centrolateral segment of the ELL is based on the leaky integrate-and-fire framework and replicates the model by Noonan et al. (2003). Specifically, the voltage evolves according to the following equation:

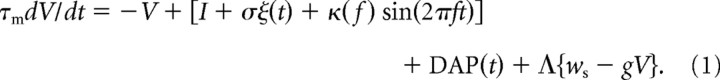When the membrane potential, V, crosses the threshold, V_thresh, a spike is recorded and V is reset to zero. V is maintained at zero for an absolute refractory period, τ_ref, after which V continues to evolve according to Equation 1. The voltages and currents have been normalized such that the voltage difference between the resting potential and the threshold voltage is unity. τ_m is the membrane time constant of the SP cell. These cells have an intrinsic burst mechanism, which has been studied previously and included as DAP(t). Feedforward electroreceptor input is modeled as an input bias current, I, with noise, σξ(t), and a sinusoidal modulation of amplitude κ(f) at the AM frequency f. Since electroreceptor input is strictly excitatory, the modeled feedforward input is rectified and […] in Equation 1 symbolizes rectification. Parallel fiber feedback is modeled as a constant input of strength Λ that excites SP cells directly and inhibits them disynaptically (see below). The PF–SP cell synapses are plastic and modeled as a series of weights, w_s, that are periodic with the AM stimulus and governed by burst-dependent learning rules. Disynaptic inhibition is modeled as a constant shunt, −gV.

During local stimulation, the strength of the feedback, Λ, is set to 0 since local stimulation does not drive the feedback (Chacron et al., 2003; Bastian et al., 2004). During spontaneous activity, the strength of the stimulus, κ(f), is also set to 0. Terms are further explained below. Parameter values for the model are summarized in Table 1. The code of this model is available online on the ModelDB database.

Table 1.

Parameter values for the model's Equations 1–7

Parameter	Value	Parameter	Value
Vthresh	1	g	1.44a
Λ	1 (global)	η2	1.8 × 10−3
τm	7 ms	η4	3.6 × 10−3
τref	0.7 ms	τw	980 s
I	0.58	wmax	1.5
σ	0.76	Lwidth4	100 ms
fcut	500 Hz	Lwidth2	10 ms

^ag = 1.5 if only the large-burst rule is used and g = 1.66 if only the small-burst rule is used (see Results).

Modeling the bursting dynamics.

Bursting in pyramidal cells is due to backpropagating dendritic spikes. DAP(t) in Equation 1 represents the depolarizing afterpotential, an injection of current into the soma of the neuron after an action potential is fired due to active channels in the cell's dendrites (Doiron et al., 2001). This effect has been modeled previously in E superficial cells by Doiron, Noonan, and colleagues (Doiron et al., 2001; Noonan et al., 2003). Their model was used in this paper with minimal parameter changes: A and γ have simply been increased to match the bursting behavior observed in vivo (Table 2).

Table 2.

Parameters used in the DAP component of the model normalized to the V_thresh of 1

Parameter	Value	Parameter	Value
A	0.6a (0.15)	B	2
α	20	β	0.35
τ	τm	rs	0.1τm
γ	0.2a (0.05)	D	0.1
E	3.5

^aChanges from Noonan et al. (2003); original values are given in parentheses.

Briefly, after the cell fires (V = V_thresh), and assuming the previous firing time is not too recent (see below), the cell will receive a DAP, i.e., a small current injection a short time later. This extra stimulation is modeled as a difference in α functions (Eq. 2 below): one generated by the soma and the other by the dendrites. If, however, the interval between this spike time and the previous spike time is less than the refractory period of the dendrite [i.e., t_n − t_n−1 < r_d(t_n⁺)], then the DAP is inactive for the current spike. The dendritic refractory period, r_d, is modeled as a dynamic variable that changes according to a secondary variable, b, which also controls the width of the dendritic α function. All spikes generated by the neuron are recorded, the most recent of which was at time t_n, and b updates whenever the neuron fires a spike. t_n⁺ refers to the time just after the most recent spike was fired and r_s is the somatic refractory period. The equations governing the DAP (Noonan et al., 2003) are as follows:

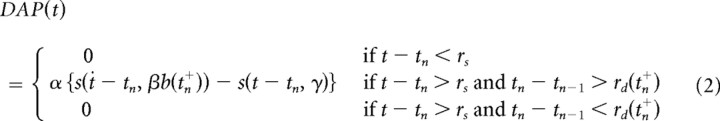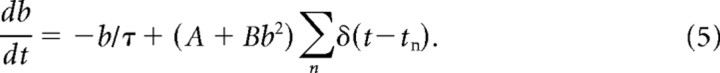The parameters used in the above equations are presented in Table 2.

Local stimuli inputs (feedforward).

The bias current, sinusoidal modulation and noise source in Equation 1 represent electroreceptor input. This approximation is effective because many afferents converge onto one pyramidal cell, their baseline firing rate is very high (∼200 Hz) and electroreceptors linearly encode AMs as a modulation of their baseline firing rate (Gussin et al., 2007). Since the electroreceptor input is strictly excitatory, the modeled feedforward input is rectified and […] in Equation 1 symbolizes rectification. The value of κ was fitted for each stimulus frequency to match firing and burst rates with experimental data (Table 3). The lower κ values at frequencies <4 Hz reflect the adaptation of the electroreceptors (Benda et al., 2005).

Table 3.

Value of κ for the different stimulation frequencies

Frequency (Hz)	κ	Frequency (Hz)	κ
0.5	0.25	12	0.39
1	0.27	16	0.39
2	0.31	20	0.39
4	0.39	32	0.39
8	0.39

Parallel fiber inputs (feedback).

We base our model of the feedback on the known circuitry of this pathway. The feedback pathway is initiated by a population of pyramidal cells of the ELL, called deep cells, which do not receive the canceling feedback input (Bastian et al., 2004). Deep cells drive granule cells in a caudal mass of cerebellar granule cells, the EGp, via neurons in the nucleus praeminentialis. Since the origin of the feedback—the deep pyramidal cells—is out of the feedback loop, it phase locks to the stimulus and drives the feedback at the stimulus's frequency. Similar to the model of Bastian et al. (2004), we model the feedback as a phase-locked input. However, Bastian's model did not take in account the delays inherent to the feedback loop. The effect of transmission delays is a crucial part of our model.

Based on the known sensory physiology and anatomy of the circuitry (see Results for more details), we estimated that the feedback has a wide range of delays that will cause it to return to pyramidal cells at diverse phases relative to the feedforward input. We estimate that this range of anatomical delays is sufficient to allow for subsets of PF input to be active at any given phase of the AM cycle, making the total PF input evenly distributed across phases. This was modeled by discretizing the feedback input into 2.5 ms non-overlapping segments, where each segment represents the beginning of the phase-locked response of a subset of PFs. Each segment is active at time t_s and is associated with a unique synaptic weight, w_s. The segment width (2.5 ms) being independent of stimulus frequency, the PF input will be divided into more bins over the period of low-frequency stimuli than over that of high-frequency stimuli (e.g., 100 parallel fibers bins for 4 Hz, 50 bins for 8 Hz, etc.).

In addition to directly exciting SP cells, parallel fibers also activate GABAergic interneurons that inhibit SP neurons (Maler, 2007). This inhibition is modeled as an extra shunting conductance, −gV, in Equation 1 that also varies with the PF feedback strength Λ. The disynaptic inhibition is kept constant across phase, as we have no experimental evidence that LTD occurs at these synapses (either on the input or output of the inhibitory interneurons). Thus, we begin with a uniform, naive distribution of parallel fiber input weights and rely on synaptic plasticity to shape the excitatory input and learn the appropriate balance between excitation and inhibition. The way we model inhibition differs from the Bastian et al. (2004) model because we tried to reflect more accurately the current knowledge of the circuitry. In the Bastian et al. (2004) model, PF feedback inputs were simply assumed to be net inhibitory arriving in phase with the feedforward signal and net excitatory in feedback that arrived in antiphase.

Note that another difference from Bastian's model is the way the two models handle different frequencies. Since Bastian's model did not take in account feedback delay, successful cancellation did not depend on stimulus frequency. Our model takes into account feedback delays and, depending on the stimulus frequency, a given delay will correspond to a different phase relationship between feedforward and feedback inputs.

Burst-dependent learning rule.

Burst-induced depression has been quantified in vitro using two-spike and four-spike burst pairs (Harvey-Girard et al., 2010). These rules were used to change the synaptic weights of the PF–SP synapse. To do so, bursts were categorized as small (two or three spikes) or large (four or five spikes). Even larger bursts were divided into smaller bursts for the purpose of applying experimentally known burst-based learning rules. For example, a six-spike burst is counted as a large four-spike burst followed by a small two-spike burst (note that large bursts have priority: we do not divide a six-spike burst into three two-spike bursts). Through the analysis of in vivo recordings, we determined that the interspike intervals (ISIs) within a burst are typically <15 ms in SP cells (data not shown) and used that criterion to identify bursts in the SP cell model. The timing, t_B, of the first spike in a burst determines the center of the temporal depression window function that is applied to the weights according to Equation 6. The strength and width of the depression rules are different for small and large bursts (η₂, L_width2 and η₄, L_width4, respectively).

During global stimulation, burst-induced depression decreases the synaptic weight of each segment according to a quadratic fit of the plasticity rule recently identified in vitro (Harvey-Girard et al., 2010). The strength of the burst-induced depression rules, η₂ and η₄, are kept constant across frequencies in the initial version of our model (see Fig. 4) but vary with higher frequencies in the final version (see Results and Fig. 5). Whenever the SP cell bursts, the synaptic weights were immediately depressed according to the following equation:

where η₂ and L_width2 were used if the SP cell burst was a small burst, and η₄ and L_width4 were used if the SP cell burst was a large burst. Once again, […] symbolizes rectification, which means this rule is applied to all segments that began at a time t_s as long as |t_s − t_B | < L_width2,4. Beyond this range, the weights are unchanged.

Figure 4.

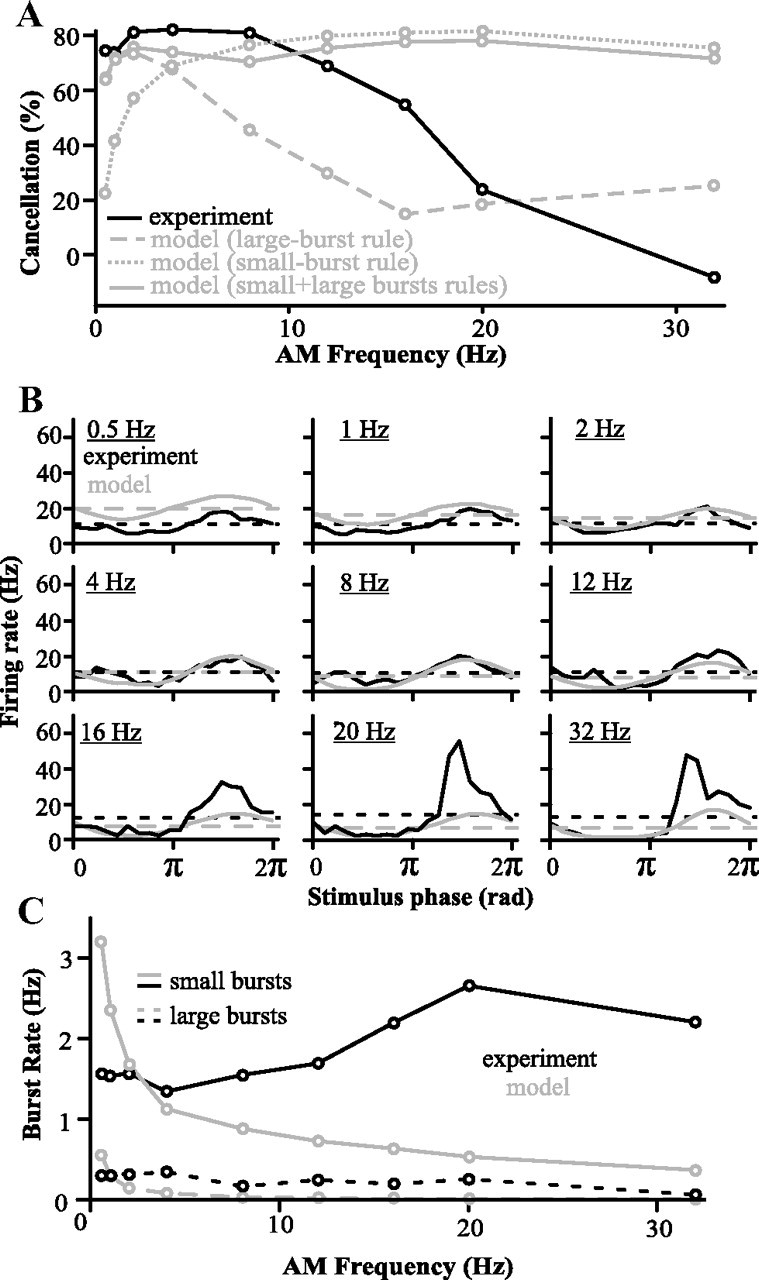
Comparisons between model and experimental responses when the model learned with the large-burst rule, the small-burst rule, or both. Note that, in this figure, parallel fiber activity is as yet unconstrained (compare to Fig. 6). A, Cancellation performance of the model compared to experimental data (n = 9 cells) (see Fig. 1). B, PSTH of the model and in vivo responses (global stimuli; n = 9 cells) when both large and small burst rule are used while the model is learning. Dashed lines represent average firing rate per second. C, Burst rates in model and in vivo responses (n = 9 cells) when both large and small burst rule are used while the model is learning. Note the difference in small burst rate at high AM frequencies.

Figure 5.

Frequency dependence of learning. The decreasing propensity for granule cells to burst at higher frequencies is implemented by changing the learning rule strength η. For each stimulus frequency, we determined the value of η that resulted in an optimal fit between model and experimental results. We plot here η as a percentage of the original values (0.0036 and 0.0018 for large- and small-burst rules respectively) (see Table 1).

However, a purely depressing rule would trivially decrease all weights to zero given sufficient time. We must therefore assume the existence of a mechanism counteracting this depression. Since an activity-dependent potentiation could not be identified in vitro (Harvey-Girard et al., 2010), a simple activity- and frequency-independent potentiating rule was added where all weights slowly relax back to w_max with a time constant of τ_w:

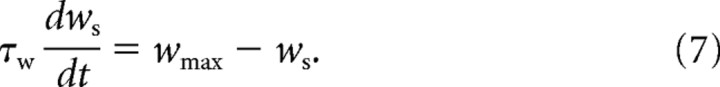During global stimulation, the synaptic weight of each segment will converge to a unique value specified by burst-induced depression and nonassociative potentiation. Synaptic depression parameters were experimentally derived, but the potentiation parameters can be adjusted. The strength of potentiation was set such that the model's response when stimulated globally closely matched the global experimental data after all weights attained their equilibrium value. The response of the model was always quantified after all weight values came to equilibrium. The global burst rates therefore represent the average rates required to balance the equilibrium weight distribution against increases from the potentiation rule.

Quantitative analysis.

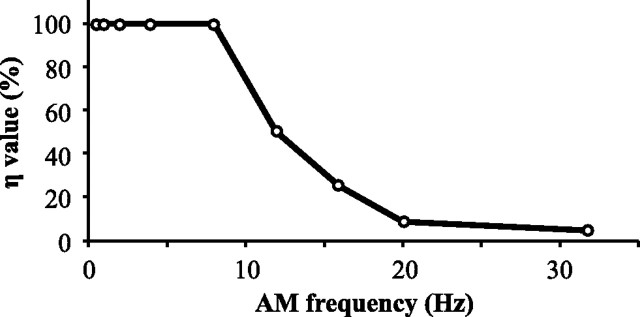
All model data for local stimulation were generated by collecting data over 1750 simulated seconds and the averaged response per period of stimulus frequency was calculated. For global stimulation, the system was allowed to come to equilibrium for 3500 s and then data were tabulated during the next 1750 s. There was no change in results if the model was allowed to come to equilibrium for 5250 s. As the feedforward transmission delays of the receptor afferents were not included in the model, the in vivo peristimulus time histogram (PSTH) data were shifted in phase to optimally overlap the experiment's PSTH for each stimulus frequency. The same phase shifts were used in both local and global PSTH plots. The disynaptic inhibition was fitted such that the model's average firing rate for 4 Hz matches the data's average firing rate. Cancellation at a given frequency is defined as follows (as a percentage): [1 − Amp_global(f)/Amp_local(f)] × 100. The amplitude at a given frequency was defined as the amplitude of a sine wave fitted to the model or experimental data's PSTH induced by that stimulus frequency. We show in Figure 1 that similar results can be achieved by quantifying the amplitude with the difference between the minimum of the PSTH and its maximum. Overcancellation can occur when the canceling feedback is stronger than the feedforward, causing the neuron to fire in antiphase to the stimulus. Therefore, if the phase of the sine wave fit is 90–270° shifted in phase in the global response compared to the local response, the cancellation (as a percentage) is calculated according to the following formula: [1 + Amp_global(f)/Amp_local(f)] × 100, so as to take values above 100%.

Figure 1.

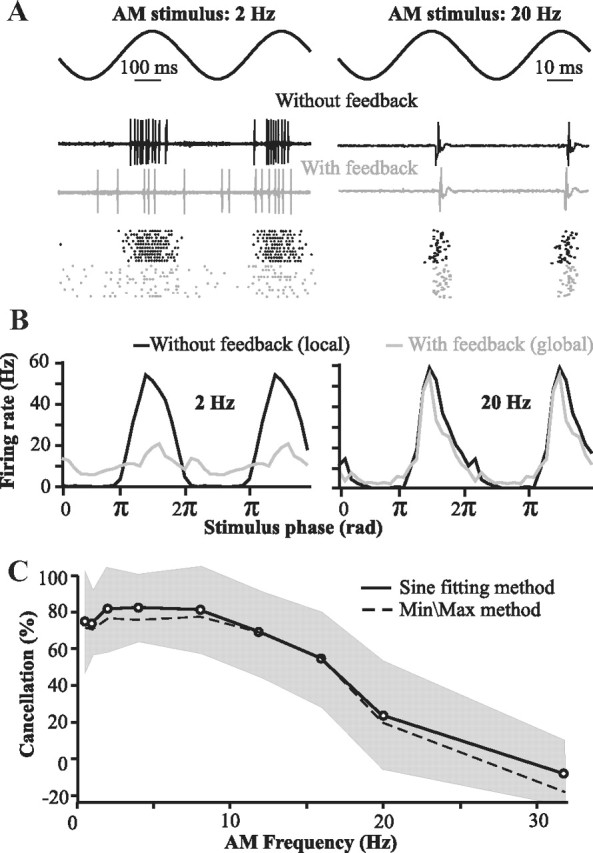
Properties of the system to be replicated by the model: local stimuli (no feedback) elicit a strong phase-locked response, whereas global stimuli—which do recruit the cerebellar feedback—elicit attenuated responses to low-frequency sine waves. This cancellation is due to feedback inputs. A, Examples of the responses of one neuron to sinusoidal stimuli of low or high frequencies (2 Hz or 20 Hz; top trace). The spike trains elicited by two cycles of the stimulus are displayed (middle traces) along with raster plots of the responses to many cycles (bottom plot). B, Average firing rate of superficial E-cells of the centrolateral segment of the ELL (n = 9 cells) elicited by one cycle of the stimulus (the data are duplicated on an adjacent cycle to improve visualization of the periodicity of the response). C, Cancellation of the stimulus response due to feedback as a function of stimulus frequency (mean ± SD; n = 9 cells). Cancellation is always calculated based on the ratio of the global PSTH's amplitude to the local PSTH's amplitude (see Materials and Methods). In the “Sine fitting method” (solid line), the PSTH's amplitude is calculated by fitting a sine wave (with the same frequency as the stimulus) through the mean firing rate data (e.g., see B). In the “Min/Max method,” the amplitude of the PSTH is the difference between its maximum (average of the highest 3 values) and minimum (average of the lowest 3 values). Both metrics achieve similar results; therefore, we use only the “sine fitting” method in subsequent graphs.

In vivo electrophysiology.

Details of the surgery and recording techniques are as described previously (Marsat et al., 2009; Marsat and Maler, 2010). Briefly, a craniotomy is performed on A. leptorhynchus of either sex under general anesthesia. During the experiment, the fish is awake but paralyzed with curare and locally anesthetized. Single-unit extracellular recordings from superficial pyramidal cells of the centrolateral of the electrosensory lateral line lobe were performed.

Stimuli consisted of amplitude modulations of the fish's own electric field. The stimulus was delivered through two large global electrodes placed on each side of the fish, thereby achieving a global stimulation. For local stimulation, a small dipole was placed in the center of the cell's receptive field. The distance between the dipole and the skin was adjusted to maximally stimulate the whole receptive field of the cell while avoiding stimulation of receptors outside the classical receptive field. The intensity of both local and global stimuli were adjusted so that the modulation was 10–15% of the fish's own electric field as measured near the cell's receptive field. In the experiment revealing the frequency selectivity of the feedback pathway, the training stimulus consisted of a normal global stimulus, to which a strong local stimulus of the same frequency and phase was added. As a result, the cell receptive field was stimulated at a stronger intensity than what would result from a normal global stimulus. The paradigm was shown to induce plasticity in the feedback pathway (Bastian, 1986), allowing the strength of the feedback to adjust to the strength of the feedforward input. This training stimulation at a single frequency was presented for 3 min, after which 15 s stimuli of two different frequencies (the training frequency and another one) were interleaved and played for 3 min in a normal global stimulation configuration. All experimental procedures were approved by the University of Ottawa Animal Care Committee.

Results

The role of cerebellar feedback to the ELL

Much is known about the different elements of this circuit and their role. ELL pyramidal cells can be differentiated into superficial (SP), intermediate, and deep varieties (Bastian and Nguyenkim, 2001). SP cells, but not deep ones, have extensive apical dendrites and express the NR2B subunit of the NMDA receptor as well as Ca²⁺ store proteins (Maler, 1979; Berman and Maler, 1999; Harvey-Girard et al., 2007). SP cells respond selectively to the low-frequency (<20 Hz) component of broadband noise stimuli delivered locally to their receptive field centers (Chacron et al., 2003). Furthermore, only SP cells have strong feedback inputs that underlie the cancellation of these low-frequency signals delivered globally (Bastian et al., 2004); therefore our study focuses on these cells. The goal of our model was to replicate the cancellation of low-frequency redundant signals observed in vivo during global stimulation (Fig. 1). Contrary to stimuli restricted to the center of the pyramidal cell's receptive field (classic receptive field), global stimuli effectively drive not only the classical, but also the nonclassical receptive fields via a cerebellar (EGp) feedback pathway (Chacron et al., 2003; Bastian et al., 2004). By comparing responses to local and global stimuli, we can quantify the canceling effect of the feedback. Under local stimulation, the cell responds strongly above its baseline rate at the stimulus peak but far below baseline at the trough. During global stimulation, the differential response is mostly eliminated for AM frequencies below 10 Hz (e.g., 2 Hz in Fig. 1A,B, left). However, we show that this cancellation is strongly frequency dependent and deteriorates drastically between 10 and 20 Hz (Fig. 1A,B, right, C). The main question motivating our modeling effort was to determine whether the recently characterized in vitro LTD rule (Harvey-Girard et al., 2010), together with known anatomical and physiological constraints, could explain this frequency-dependent cancellation.

Model replicates experimentally observed responses in the absence of feedback

Our first goal was to replicate the properties of SP cells when they are driven only by the feedforward sensory input, in particular the bursting dynamic that will be essential to the plasticity. We used the leaky integrate-and-fire formalism to model SP cells but added the burst-inducing depolarizing afterpotential (LIF-DAP model) that incorporates the effect of backpropagating dendritic spikes. This model is a reduction of biophysically realistic models (Doiron et al., 2001) and has previously been shown to capture the essential details of SP cells burst discharge and electrosensory stimulus encoding (Noonan et al., 2003). Baseline discharge was modeled by delivering a bias current to the LIF-DAP model (Fig. 2A) with noise added so as to match the SP cell's mean baseline discharge (mean 9.5 Hz, SD = 3.1, n = 9 neurons). SP cells are linearly modulated by sensory input (Bastian et al., 2004; Gussin et al., 2007). Thus, direct electroreceptor input to the SP cells was modeled by sinusoidally modulating the bias current. Since electroreceptors adapt to AM < 4 Hz (Benda et al., 2005), the strength of this modulated input was adjusted at these frequencies to match the experimentally observed firing and burst rates under local conditions (see Materials and Methods). As shown in Figure 2B, our LIF-DAP model matched the observed responses of SP cells to local stimulation for frequencies up to 32 Hz despite neglecting the effects of feedforward disynaptic inhibition (Berman and Maler, 1998a) or possible nonlinear biophysical dynamics.

Figure 2.

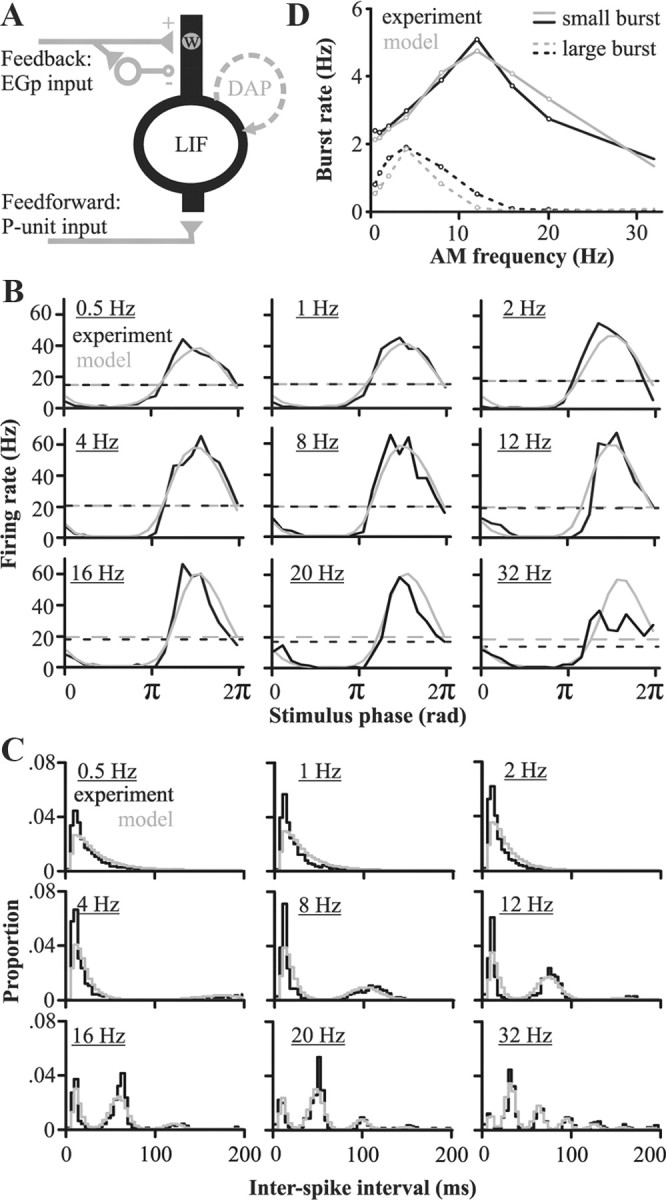
Model exploration: replication of pyramidal cells properties when stimulated locally (no feedback) and constraints imposed on the model during global stimulation (with feedback). A, Schematic of the main components of the model: an LIF model cell receiving feedforward input from the receptors and feedback inputs from the EGp. A DAP was added to replicate the neuron's burst propensity. The feedback inputs have a direct excitatory component delivered through plastic synapses (of weight w) and a disynaptic nonplastic inhibitory component. This feedback input is active only when modeling the response to global stimuli. B, Peristimulus time histograms comparing the response of in vivo (n = 9 cells) and modeled pyramidal cells elicited by local stimuli of different AM frequencies. Dashed lines represent the average firing rate. C, Interspike interval histograms of the model's responses and for experimental data (n = 9 cells) for AM rates ranging from 0.5 to 32 Hz. Bin width is 4 ms. Although ISIs >200 ms do occur, they are rare, and the histogram's area is normalized to 1 for ISIs <200 ms. D, Comparison of in vivo and modeled pyramidal cell responses (n = 9 cells) during local stimulation: burst rates as a function of stimulus frequency. Bursting is quantified by dividing the spike trains into small (2 or 3 spikes) or large bursts (4 or 5 spikes); longer bursts are taken as combinations of small and large bursts (see Materials and Methods).

The DAP dynamic causes both the cell's burst rate and number of spikes/burst to vary with stimulus frequency. Our model correctly captured the experimentally determined relationship between stimulation frequency and burst rate and spikes/burst (Fig. 2C,D). These bursts are important for both stimulus encoding (Gabbiani et al., 1996; Oswald et al., 2004; Marsat et al., 2009) and induction of LTD at the synapse between PF and pyramidal cells (Harvey-Girard et al., 2010). Note that in the latter case, small and large bursts result in different associative time windows for LTD (see below). Therefore, to parallel the in vitro experiments, bursts were divided into small (two or three spikes) and large (four or five spikes; see Materials and Methods). The match between spiking and bursting patterns in the model and experimental data is even clearer when comparing the ISI histograms (Fig. 2C). While our model relies on a bursting mechanism specific to cortical (Mainen and Sejnowski, 1996) and electrosensory (Lemon and Turner, 2000) pyramidal cells, our methodology of embedding bursting dynamics in a delayed feedback loop that includes cerebellar-like circuits and a correlative learning rule can clearly be applied to other systems.

Incorporating a feedback that cancels low-frequency coding

The crucial step in our study is to incorporate a feedback input that reflects two newly identified properties of the circuit: a distribution of delays in the feedback and a burst-dependent plasticity. The cerebellar feedback pathway to the ELL originates from nonplastic cells of the ELL that project bilaterally to the nucleus praeminentialis. From this nucleus, cells project bilaterally to the granule cells of the EGp, and these granule cells in turn project bilaterally to the SP cells of the ELL (Carr and Maler, 1986; Sas and Maler, 1987). This produces a wide range of feedback delays dependent on the length and conduction velocity associated with each possible trajectory. An additional source of delay arises from the spatial extent of the EGp (∼1200 μm) (Maler et al., 1991): cells at one edge of the EGp will incur an additional delay of 12 ms (given a conduction velocity of 0.1 m/s) (Roberts and Bell, 2000) compared to cells at the other edge. The delays resulting from the various possible trajectories thus likely vary from ∼20 to >70 ms. Furthermore, the origins of the feedback pathway—the deep cells of the ELL—have a variety of phase relationships with the stimulus depending on the side of the body they represent and on their functional type. Indeed, these cells can be divided in two types: E-cells, responding throughout the peak of the stimulus, and I-cells, responding throughout its trough (Bastian and Nguyenkim, 2001; Marsat et al., 2009).

Considering this variety of delays and phase relationships, and assuming that granule cells of the EGp phase lock to their input (D'Angelo et al., 2001), PF most likely provide feedback to SP cells at all possible phases of the low-frequency AMs that are canceled during global input. In addition, granule cells have been shown to phase lock to periodic inputs and to burst to sensory stimuli and be silent in the absence of stimulation (D'Angelo et al., 2001; Chadderton et al., 2004; Rancz et al., 2007; Sawtell, 2010). We therefore assumed in our model that (1) the array of PFs provide feedback to SP cells at all possible phases of the stimulus, and (2) EGp granule cells respond in a bursty manner, phase locked to low-frequency AM signals.

The feedback pathway provides direct excitatory and disynaptic inhibitory input to SP cells (Maler and Mugnaini, 1994), and both were replicated in our model (see Eq. 1 in the Material and Methods). The excitatory input was modeled as a feedback of strength Λ set to 1 during global stimulation, multiplied by the synaptic strength of the PF–SP cell synapse, w_s, that can be altered by the burst-induced plasticity identified experimentally (Harvey-Girard et al., 2010). The inhibition is also proportional to the feedback strength but is otherwise constant because no long-term plasticity is known at these synapses. The reversal potential of the inhibitory synapse (GABA_A receptors) is near the SP cell's resting potential (Berman and Maler, 1998b), so inhibition was modeled as a constant membrane conductance increase, g. The overall strength of the excitatory feedback was adjusted to be slightly larger than inhibition, consistent with in vivo and in vitro physiological studies (Bastian, 1986; Berman and Maler, 1998b).

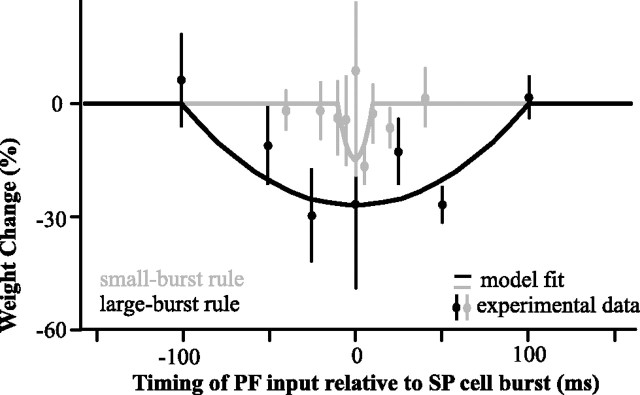
The strength of the synapses between PFs and SP cells were modeled as weights that span the stimulus period (2.5 ms bin widths; see Materials and Methods). They were initially all equal since the array of PFs provide inputs at all possible phases of the stimulus. If the SP cell bursts in close temporal proximity to the firing time of a given PF the corresponding synaptic weight will depress according to the depression rules identified in vitro (Harvey-Girard et al., 2010). The different rules identified for small and large bursts, are based on experiments that paired two-spike bursts or four-spike bursts presynaptically and postsynaptically. A variety of presynaptic and postsynaptic burst sizes can occur in vivo and the plasticity rule might therefore continuously interpolate between rules based on different burst sizes. For the sake of simplicity and to remain consistent with in vitro data, we restrict our model to the experimentally defined small-burst and large-burst categories. The corresponding plasticity rules were modeled as quadratics (Fig. 3) having different depression strengths and delay ranges. To prevent complete depression of all PF feedback, we included a recovery process by which all weights slowly relax back to their default value in an activity- and frequency-independent manner.

Figure 3.

Burst-induced depression measured in vitro (data points; mean ± SE, n = 7 cells for all points except for 100 ms, where n = 5) and applied to the PF–SP synapse of the model (lines) for small bursts and large bursts (gray and black respectively). The measured weight change is the result of 100 presynaptic and postsynaptic burst pairings. Note that the large-burst rule is not equal to the sum of two small-burst rules. Depression was induced in vitro by repeatedly pairing burst-like electrical stimulations to the PF and burst-like current injection in the SP cell's soma. The size of the EPSP elicited in the pyramidal cell by a test stimulation of the PF was then measured as the time lag between PF and SP burst stimulation was varied (see Harvey-Girard et al., 2010 for more details).

We initially only took into account large bursts and the plasticity they elicit, where the pairing time window for LTD is ±100 ms. By itself, this rule was only effective for canceling AM frequencies <5 Hz, because the plasticity time window was too broad to selectively target the positive phase of the AM of higher frequencies (Fig. 4A). For example, for an 8 Hz signal, a burst at the crest of the stimulus will depress weights 75 ms later, at its trough, and therefore reduce the excitatory feedback required to cancel the trough. Trying to use the narrower small-burst rule by itself—counting longer bursts as several small bursts—also failed to replicate the experimental results (Fig. 4A). It canceled high frequencies too much (see below), but also did not cancel low frequencies enough.

Using either depression rules alone, and the failure of the model that ensued, revealed the sensitivity of the system to this parameter. The inclusion of both burst rules acting simultaneously in the model allows cancellation to be effective at the appropriate range of frequencies and accurately reproduces the cancellation observed in SP cells at frequencies below 16 Hz (Fig. 4A). Therefore, the nonlinear dependence of the learning rule time window on the size of the burst is essential to adequately shape the feedback synaptic strength: the temporal precision associated with the small burst is required to cancel high frequencies, while the strong impact of large burst is required to cancel low frequencies. However, discrepancies between the model and the experimental data remain at very low (0.5 and 1 Hz) and at high (20 and 32 Hz) frequencies. At low frequencies, the model cancels as well as the real pyramidal cells, but the average firing rate is slightly higher in the model (Fig. 4B). This minor discrepancy may be due to intrinsic (Mehaffey et al., 2005) or feedforward inhibitory (Shumway and Maler, 1989) adaptation dynamics that were not included in our model. Nonlinear synaptic depression from very large bursts not included in the model may also be a factor. However, synaptic depression from large burst pairings has yet to be explored experimentally.

Model requires frequency-dependent parallel fiber input

The more serious discrepancy is that our model permits cancellation of not only low, but also high frequencies (16–32 Hz), which is not seen in vivo (Fig. 4B). Yet, under global stimulation, the model actually bursts less than that observed in vivo (Fig. 4C), implying that cancellation is failing in vivo despite SP cells producing enough bursts to drive plasticity. It seems paradoxical that bursting decreases with AM frequency yet cancellation remains strong. However, burst-induced depression has a constant time window, but period length decreases as the AM frequency of the stimulus increases. Thus, the proportion of PF segments affected by a single burst increases with AM frequency (i.e., a small burst will affect 20 ms/250 ms of the PF segments spread over a 4 Hz cycle and 20 ms/50 ms of the segments at 20 Hz). Therefore, fewer bursts per second are required to maintain the same weight distribution at high frequencies. The difference between the experimental cancellation and the model may come from the fact that our model thus far assumed that each burst in the SP cell is matched by a burst in all the PFs representing a given phase, thus that firing rate of granule cells is going up with stimulus frequency. No direct recording of Apteronotus's granule cells are available, but in vitro studies of mammalian granule cells have shown that their mean firing rate remains relatively constant across frequencies. Furthermore, they produce spike bursts in response to sinusoidal current injection, but the number of spikes per burst drops off with increasing frequency, and, after 10 Hz, the cells failed to produce bursts on every cycle [D'Angelo et al. (2001), their Fig. 2A]. It is therefore likely that, at higher AM frequencies, a burst in the pyramidal cells will not be matched by a burst in every PF representing a given phase and thus will not elicit depression in all the corresponding synapses.

We incorporated the declining probability of a presynaptic burst into the learning rule by optimally decreasing the parameter η as a function of frequency to reproduce the experimental data (Fig. 5). We found that an approximately exponential decrease in η above 8 Hz was necessary to obtain the decrease in cancellation at higher frequencies seen in vivo (Fig. 6). This addition allowed the model to match experimental data in terms of both bursting (Fig. 6B,C) and stimulus cancellation (Fig. 6A,D). Considering that the reduction of the PF input at higher frequencies was essential for the replication of the experimental data, such a reduction can be considered a prediction of our model. Further studies will be required to test whether the EGp granule cell burst size is inversely related to the stimulus frequency as predicted.

Figure 6.

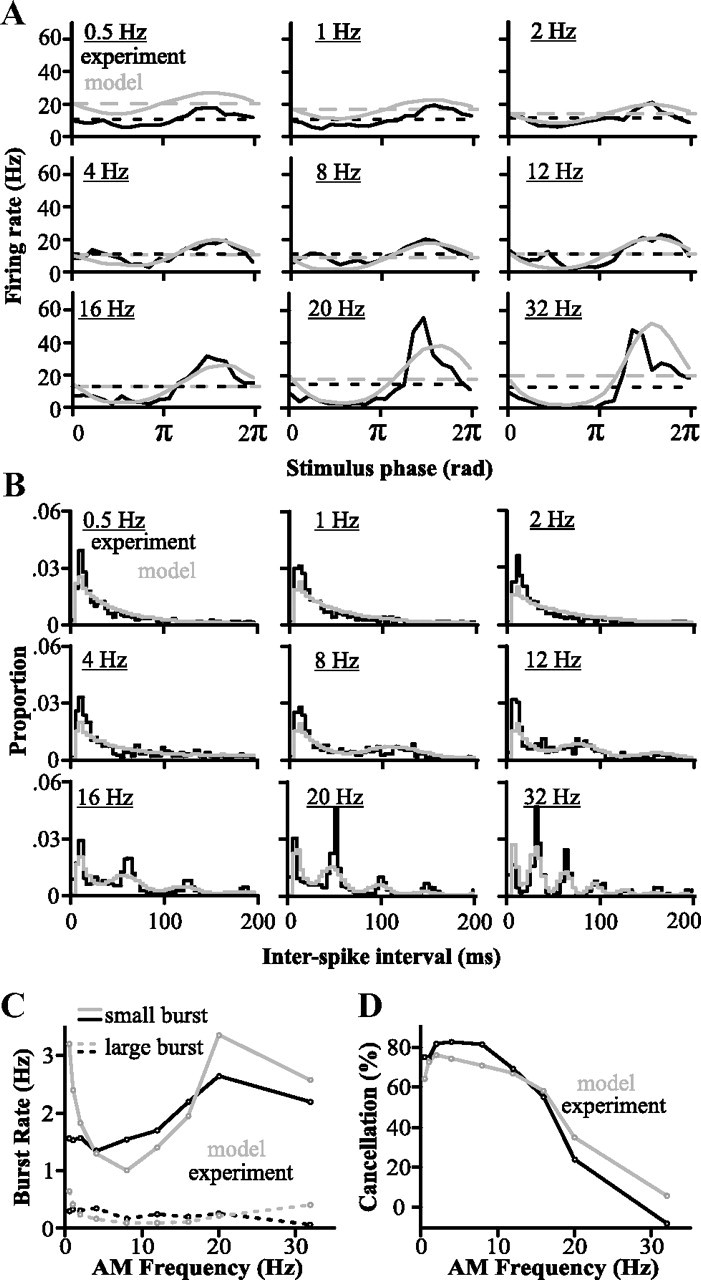
Comparison of the model with in vivo data showing its ability to replicate the feedback-induced cancellation. This model now includes the frequency dependence of granule cell bursting. A, PSTH of the model and in vivo responses to global stimuli of different frequencies (n = 9 cells). Dashed lines represent average firing rate per second. B, Interspike interval histogram of the model's responses and for experimental data (n = 9 cells). Bin width is 4 ms. C, Burst rates in model and in vivo responses (n = 9 cells). Bursting responses were segregated into small and large bursts as described previously (see also Materials and Methods). D, Cancellation measured for responses of this final version of the model correspond well to the in vivo data (n = 9 cells).

Independent parallel fiber frequency channels revealed in vivo

We have experimentally demonstrated that good cancellation of global frequencies <16 Hz can be achieved and our model faithfully captures this result. A key element of our model—the existence of PFs representing all phases for any stimulus frequency—is dependent on anatomical and physiological data demonstrating a wide range of PF feedback delays to SP cells. This implies, however, that a delay associated with a particular phase for one frequency may be at a different phase for another frequency. For example, a PF whose delay is associated with the peak of a 4 Hz AM will be associated with the trough of a 12 Hz AM. To keep the phase definition of each PF consistent, our model assumed that the weights learned at one frequency are independent of learning at another frequency. Our model therefore predicts the existence of independent frequency-tuned PF feedback channels to allow the burst LTD rule to select the right time delays necessary to cancel each frequency.

We tested the possible existence of independent frequency channels in the feedback pathway in vivo by taking advantage of the fact that the synaptic plasticity between parallel fibers and pyramidal cells also allows adjustment of the feedback strength relative to the feedforward input (Bastian, 1986). Two sinusoidal stimuli (2 Hz, 8 Hz) were presented individually to an E-type SP cell both locally and then globally to assess the initial degree of cancellation; cancellation was achieved for both frequencies (Fig. 7). Following a protocol introduced by Bastian (1986), we then paired the global presentation of one frequency (8 Hz in the example shown in Fig. 7) with the local presentation of the same frequency at an intensity such that the summation of both local and global AMs strongly drive the neuron to burst discharge.

Figure 7.

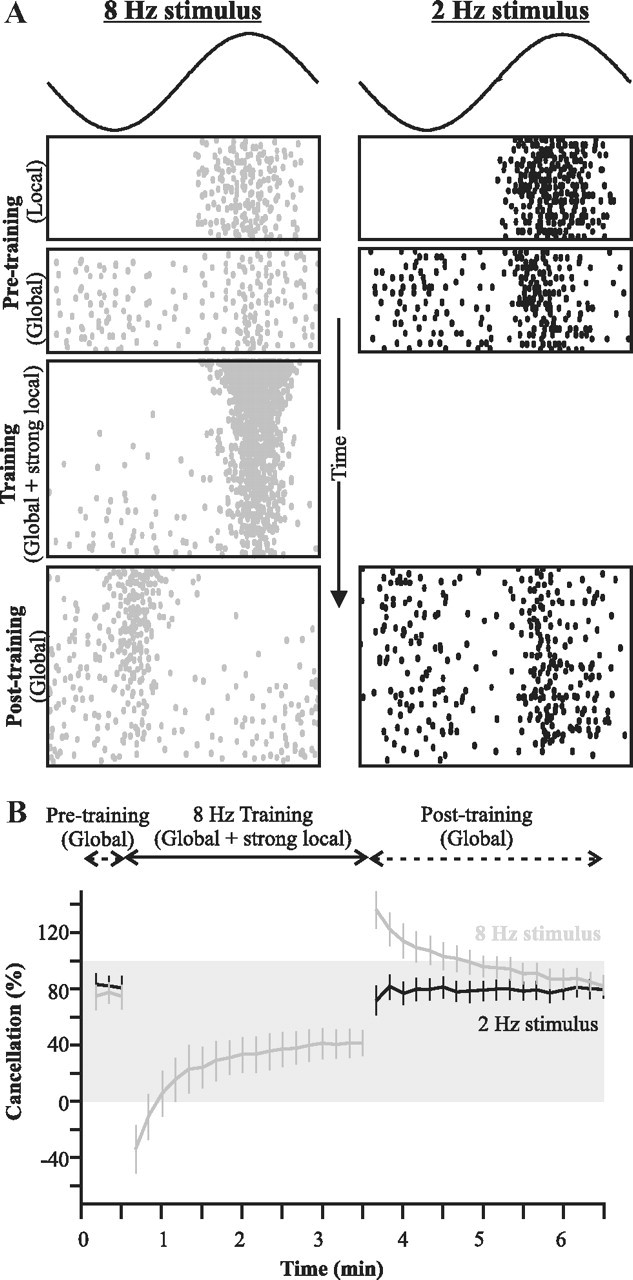
Frequency-specificity of parallel fiber inputs demonstrated in vivo. A, Raster plot showing, as a function of time, the response of a typical cell to the different steps of the experimental protocol: pretraining baseline for two AM frequencies delivered either locally (no feedback) or globally (thus recruiting feedback); training stimuli of a single frequency where a local stimulus is added to a global one; and posttraining responses to global stimuli revealing the effect of the induced plasticity on the response to the two frequencies. B, Quantification of the mean (±SE; n = 11 cells) canceling impact of the feedback. The gray shading highlights values of cancellation between 0 and 100%. Values below zero mean that the response is more strongly modulated by the stimulus than the uncanceled baseline (local stimulation), and thus that the response is not canceled but enhanced. Values above 100 indicate an overcancellation: cancellation is perfect (100%) when the response is flat across phases. But if the canceling feedback is too strong, the neuron will respond more strongly at the trough of the cycle than at the top (see Materials and Methods for details).

The response of the cell to the Global + Local training signal diminished as the number of presented cycles increased, presumably due to the strong evoked burst discharge inducing plasticity at PF synapses. Following the training protocol, the original stimuli were again presented globally to measure the change in cancellation. After training, the cell responded to that frequency in antiphase: the trough of the stimulus now elicited spiking, while its peak silenced the cell. This response is diametrically opposite to that expected from the anatomy and physiology of an E-cell, and cannot be due to the direct input from electroreceptors (Maler, 2007).

As previously shown by Bastian et al. (2004), this reversed response is due to the temporarily modified PF feedback synapses, which provide a feedback input too strong relative to the feedforward input and causes an overcancellation of the response. Most importantly, the global response to presentation of the 2 Hz AM was unchanged and cancellation remained similar before and after the training with 8 Hz. Additional experiments revealed that the opposite protocol (pairing of local and global AMs for the 2 Hz stimulus) produced exactly the same frequency-specific change in the feedback (data not shown). Similar results were also found when using frequencies of 5 Hz and 12 Hz (data not shown), thus confirming that our result applies to a wide range of low frequencies. A thorough quantitative characterization of the frequency-tuning curves of the EGp granule cell feedback is beyond the scope of this paper. We conclude that our prediction was verified: PF feedback cancellation input to SP cells is frequency specific.

Discussion

We developed a minimal yet sophisticated model of the cancellation mechanism via EGp constrained by neurophysiological and anatomical data: (1) the spiking response of SP cells to stimulation of their receptive field centers; (2) the dynamics and AM frequency dependence of the SP cells burst mechanism; (3) the delays in the PF feedback pathway; (4) the frequency-dependent adaptation of electroreceptor afferents; and (5) in vitro PF–SP cell synaptic plasticity rules: burst-dependent correlative LTD with a plasticity pairing window that is proportional to the number of spikes per burst. This cancellation model highlights the delicate frequency-tuned balancing act in which stimuli produce bursts, which drive learning, which in turn regulates bursting, and further emphasizes the intricate interplay of biophysical mechanisms at the cellular and systems level.

The model we have developed is minimal in the sense that we have not incorporated additional physiological data that might improve its performance. For example, facilitation of PF-evoked EPSPs has been observed in vitro (Lewis and Maler, 2002, 2004); thus, the presynaptic enhancement of PF-evoked EPSPs can drive SP cells and local interneurons more strongly. This effect would strengthen the cancellation at low frequencies and contribute to the cancellation decay at high frequencies by slightly decreasing the average feedback strength as PF bursts become more rare. However, the purpose of the model was to identify the necessary and sufficient features for redundant input cancellation, rather than focusing on the complex dynamics of short-term plasticity.

Remarkably, our minimal model was quantitatively consistent with the response of SP cells to stimulation of their receptive field center and to the development of cancellation following stimulation that recruits feedback (classical + nonclassical receptive field). The in vitro experiments had shown that large bursts produced long plasticity windows >±50 ms, while the small-burst windows were <±10 ms (Harvey-Girard et al., 2010). We found that the small bursts were sufficient to produce excellent cancellation for high-frequency inputs, but the plasticity window was too narrow to cancel low-frequency inputs. Conversely, the large temporal window associated with large burst could not achieve cancellation of high-frequency inputs. The use of different temporal plasticity windows for bursts of different sizes, and the dependence of burst size on the temporal frequency of the stimulus, was critical to adequately shape the canceling feedback across AM frequencies.

The fact that lower-frequency AMs elicit bursts with more spikes is by no means surprising, and these larger bursts can be expected to lead to more calcium entry in the postsynaptic cells via postsynaptic NMDA receptors (Berman et al., 2001; Harvey-Girard et al., 2007). Depending on the type and amount of calcium binding and sequestering proteins (Jande et al., 1981; Maler et al., 1984) and their competition with LTD-promoting second messenger systems (Harvey-Girard et al., 2007), this variation in Ca²⁺ influx could explain changes in the duration of the LTD window. It may be useful to look for such dynamic matching of LTD pairing windows in other sensory systems with a large range of input frequencies, e.g., in the vestibular system (Lisberger et al., 1983).

An additional constraint was necessary in our model to explain the deterioration of cancellation at AM frequencies >8 Hz. Mammalian granule cells (in vitro) only burst consistently on every cycle for frequencies ≤10 Hz, and the number of spikes/burst appears to be inversely proportional to frequency (D'Angelo et al., 2001). Incorporating such a frequency-dependent drop of PF bursting produced an excellent quantitative fit between model and experimental data. Our model thus predicts that, similarly to rat cerebellum, bursting in EGp granule cells of electric fish will decrease with stimulus frequency as described in Figure 5. Our results suggest that frequency-dependent burst size is a general consequence of the intrinsic properties of cerebellar granule cells (D'Angelo et al., 2001) in combination with the dynamics of granule cell circuitry (Dugué et al., 2009). Characterizing the properties of EGp granule cells in vivo will be required to confirm our predictions.

A major discovery presented here is the evidence of frequency tuning of the PF feedback. Recording of electrosensory afferent input to the EGp has revealed input tuned to high-frequency AMs but none to the frequency range important for cancellation (Bastian and Bratton, 1990; Middleton et al., 2006). We therefore hypothesize that frequency tuning is generated within the EGp granule cell network itself. The intrinsic dynamics of mammalian granule cells induce resonance in the theta range (3–12 Hz) (D'Angelo et al., 2001). The local Golgi cell inhibitory network is also associated with low-frequency oscillatory activity of granule cells (Dugué et al., 2009) and could allow the network to be tunable to specific frequencies. It has even been suggested that long-term plasticity in the cerebellar granule cell layer can induce “temporal matching” appropriate to the timing function of granule cells (De Zeeuw et al., 1998; D'Angelo et al., 2001). The temporal precision of granule cell discharge has been proposed to be important for the adaptive regulation of oscillatory motor output (D'Angelo and De Zeeuw, 2009) and may even be implicated in the frequency tuning of the vestibulo-ocular reflex (VOR) (Lisberger et al., 1983). Frequency specificity of the VOR is evident in the motor output, but there is no experimental evidence pinpointing the neurons and circuits responsible for this frequency tuning. Existing models of VOR adaptation do not explicitly posit the granule/Golgi cell network as a source of frequency tuning (Lisberger and Sejnowski, 1992; du Lac et al., 1995).

In contrast, our results suggest that frequency tuning originates in cerebellar granule cell networks. Furthermore, apart for the initial observation from Lisberger et al. (1983) and De Zeeuw et al. (1998), the functional consequences of frequency tuning of cerebellar circuitry on target cells remains an unexplored issue (D'Angelo et al., 2009). Therefore, a conceptually novel aspect of our study is to relate the frequency-tuning capacity of granular cell networks [as suggested, for example, by Dugué et al. (2009)] to the frequency specificity of cerebellar learning by showing how frequency channels in parallel fibers are involved in learning at the PF–SP synapse. The EGp is located superficially (Sas and Maler, 1987) with its granule cells directly accessible to patch recording (Sawtell, 2010), optical Ca²⁺ imaging, or experimental perturbation. The EGp may therefore be a convenient preparation to investigate the cellular and circuit mechanisms that generate frequency-tuned and precisely timed granule cell/parallel fiber output.

There have been two general approaches to cerebellar function. One emphasizes the role of PFs in a timing role for cerebellum (Meek, 1992; Kistler et al., 2000), while the other describes the cerebellum as an adaptive filter (Dean et al., 2010). It is clear from our results that these viewpoints are not contradictory. The PF feedback to ELL is presumably phase locked to low-frequency sensory input. We hypothesize that the synaptic and intrinsic dynamics of SP cells then make use of this precisely timed input to implement an adaptive filter that cancels redundant low-frequency signals. It appears that exactly the same principle may be operative in another well studied cerebellar-like structure: the ELL of mormyrid fish. The EOD of mormyrids consists of brief pulses with long and variable interpulse intervals and the EOD command nucleus sends corollary discharge to the EGp that, as in A. leptorhynchus, provides feedback to the ELL. This circuit is also used as an adaptive filter to cancel redundant sensory input (Roberts and Bell, 2000; Roberts and Portfors, 2008; Sawtell and Williams, 2008), and theoretical studies have implicated the mormyrid PFs in conveying the precise timing of the EOD corollary discharge to ELL neurons (Roberts and Bell, 2000). The PF–SP cell synapse analog in the mormyrid ELL obeys an anti-Hebbian spike timing-dependent plasticity (STDP) rule (Bell et al., 1997) instead of correlative burst-induced rules. Presumably the mormyrid STDP rule is matched to the pulsatile nature of the EOD, which simplifies the cancellation problem to one of causal matching of the time delay of sensory input following a corollary discharge.

Instead, Apteronotus operates its EOD continuously and the feedback to the ELL must synchronize directly with global stimuli of arbitrary frequency. Furthermore, Apteronotids cannot rely on a corollary discharge input to guide the timing of the feedback inputs. We propose that the need to cancel multiple frequencies requires independent frequency channels and multiple learning rules. Our results indicate that the precise timing of sensory or motor associated signals is a general function of parallel fibers of the cerebellum and related structures such as the ELL or the dorsal cochlear nucleus (Oertel and Young, 2004; Roberts and Portfors, 2008; Tzounopoulos and Kraus, 2009). The local circuitry and dynamics (synaptic and intrinsic) of the PF target varies, however, so as to implement the appropriate adaptive filter required for each system.

In summary, our study brings two new concepts to the theory of cerebellar function. First, a precise matching between the temporal window of plasticity and the burst dynamics can permit adaptive shaping of PF inputs by synaptic plasticity. Second, cerebellar granule cells are capable of providing frequency filters of incoming mossy fiber input. We suggest that granule cell frequency tuning may prove central to a better understanding of cerebellar circuits in general.

Notes

Three supplemental figures for this article are available at http://mysite.science.uottawa.ca/alongtin/bol_etal.html. They are particularly relevant to the third subsection of the results. The first figure provides a descriptive diagram and detailed information on the feedback pathway and latencies. The second is an explanatory diagram of phase relationships between feedback inputs, different pyramidal cells, and the requirements for cancellation. The third is an illustration that can help understand how the feedback was modeled. This material has not been peer reviewed.