Descending Corticospinal Control of Intersegmental Dynamics

Abstract

To make an accurate movement, the CNS has to overcome the inherent complexities of the multijoint limb. For example, interaction torques arise when motion of individual arm segments propagates to adjacent segments causing their movement without any muscle contractions. Since these passive joint torques significantly add to the overall torques generated by active muscular contractions, they must be taken into account during planning or execution of goal-directed movements. We investigated the role of the corticospinal tract in compensating for the interaction torques during arm movements in humans. Twelve subjects reached to visual targets with their arm supported by a robotic exoskeleton. Reaching to one target was accompanied by interaction torques that assisted the movement, while reaching to the other target was accompanied by interaction torques that resisted the movement. Corticospinal excitability was assessed at different times during movement using single-pulse transcranial magnetic stimulation (TMS) over the upper-arm region of M1 (primary motor cortex). We found that TMS responses in shoulder monoarticular and elbow–shoulder biarticular muscles changed together with the interaction torques during movements in which the interaction torques were resistive. In contrast, TMS responses did not correlate with assistive interaction torques or with co-contraction. This suggests that the descending motor command includes compensation for passive limb dynamics. Furthermore, our results suggest that compensation for interaction torques involves the biarticular muscles, which span both shoulder and elbow joints and are in a biomechanically advantageous position to provide such compensation.

Introduction

To make a movement, the CNS has to overcome the inherent complexities of the musculoskeletal system. For example, contraction of muscles spanning one joint generates passive interaction torques (rotational forces) that propagate to other joints. These torques can produce motion of other body segments without any voluntary contraction of the muscles spanning the other joints (see Fig. 1A) and can significantly contribute to the overall joint torques generated during reaching movements (Hollerbach and Flash, 1982; Graham et al., 2003). Thus, passive interaction torques must be taken into account during the planning or execution of goal-directed movements (Sabes and Jordan, 1997; Sabes et al., 1998; Dounskaia et al., 2002; Debicki et al., 2004; Gritsenko et al., 2009).

Figure 1.

Experimental procedure. A, Action of interaction torques. The arrows indicate the directions of joint torques and resulting joint rotations. When a single-joint muscle (red) spanning the shoulder joint contracts, this linear force is transformed into a rotational torque (τ_s) that flexes the shoulder joint. This action produces an interaction torque (τ_ei) at the elbow causing it to extend. Simultaneous contraction of the biarticular flexor muscle (orange) would both help with the shoulder flexion and counteract the elbow extension caused by the interaction torque. B, Experimental apparatus. The subject's right arm is supported by a robotic exoskeleton (KINARM) so that it allows for movement of shoulder and elbow joints in a horizontal plane. Visual targets are projected on the plane of movement. TMS coil position over M1 is maintained using Brainsight, which calculates relative distance between the coil and the subject's head using reflective markers (trackers). C, Target locations and movement directions for the assistive and resistive conditions. The curved arrows illustrate joint torque directions during voluntary movements in the two conditions. τ_e, Elbow torque; τ_ei, interaction torque acting on the elbow from the movement of the shoulder; τ_s, shoulder torque; τ_si, interaction torque acting on the shoulder from the movement of the elbow. The arrowheads of τ_si point in both directions because this torque changes direction during the assistive condition. The τ_si are smaller than τ_ei relative to the net or muscle torques at the corresponding joint. D, The integration method of calculating amplitudes of the MEPs in individual trials. The shaded area represents the area of integration. E, The peak-to-peak method of calculating MEP amplitudes in individual trials. The vertical gray lines show the bin within which the maximum and minimum of an MEP was determined.

Multiple levels of the motor system have been proposed to be involved in limb dynamics control. At the peripheral level, muscle properties and the anatomical organization of the musculoskeletal system may compensate for some of the dynamic properties of the limbs by resisting perturbations and stabilizing movements (Loeb et al., 1999; Gillard et al., 2000). Spinal neural circuitry can also compensate for intersegmental dynamics through homonymous reflexes of biarticular muscles (Lacquaniti et al., 1991; Prochazka et al., 1997) and through heteronomous reflexes that couple muscles spanning different joints (Gracies et al., 1991; McClelland et al., 2001). These spinal circuits together with the musculoskeletal system may form “motor primitives,” which can be used by descending structures as building blocks for complex behaviors (Bizzi et al., 1991; Giszter et al., 1993). This theory suggests that compensation for limb dynamics is accomplished largely at the spinal level to simplify control by the higher-level brainstem and cortical structures (Georgopoulos et al., 1982; Feldman, 1986; Schwartz et al., 1988; Caminiti et al., 1990; Bizzi et al., 2000). Another school of thought argues for dynamics compensation based on internal models (i.e., neural representations of the dynamic properties of the limb and its interaction with the environment) (Lackner and Dizio, 1994; Shadmehr and Mussa-Ivaldi, 1994; Wolpert and Kawato, 1998). This suggests that the descending motor command is not purely kinematic but includes information about limb inertial dynamics as seen in neural activity (Kalaska et al., 1989; Cisek et al., 1998; Gribble and Scott, 2002; Sergio et al., 2005; Hamel-Pâquet et al., 2006; Herter et al., 2007). Thus, limb dynamics can be counteracted either by phasic activation of specific muscle synergies [e.g., by using biarticular muscles (Lackner and Dizio, 1994; Almeida et al., 1995; Gribble and Ostry, 1999)] and/or by the regulation of whole-arm mechanical impedance and joint stiffness through co-contraction of antagonists (Lacquaniti et al., 1993; Milner and Cloutier, 1993; Burdet et al., 2001; Franklin et al., 2007).

There remains considerable debate as to the relative roles played by these different kinds of mechanisms in control of multisegmental dynamics. Here, we investigate the contribution of the descending pathways by measuring corticospinal excitability during reaching movements with different dynamic requirements. Some of these results have been previously presented in abstract form (Gritsenko et al., 2009).

Materials and Methods

Subjects and tasks.

Thirteen healthy subjects aged 21–35 participated in the study (five females; eight males). They all gave informed consent before their inclusion and were naive to the objectives of the study. The study was approved by the Human Research Ethics Committee of the Faculté de Médecine, Université de Montréal, and was performed in accordance with the ethical standards set by the Committee. One of the subjects was unable to perform the task with consistent success, so that >30% of her trials failed to fulfill the task criteria for moving to visual targets within the time constraints outlined below. Thus, her data were excluded from analysis.

During a single experimental session, subjects were seated facing a projection system with their right arm supported in a horizontal plane by a robotic exoskeleton KINARM (BKIN Technologies) (Fig. 1B). Custom-written software controlled the projection system and displayed visual targets in the plane of subject's movement through a semitransparent mirror. The mirror partially obscured the view of the subject's arm. Therefore, to enhance visual feedback about the movement, a circular cursor 1 cm in diameter overlaid the subject's fingertip location and tracked the movement. Subjects were required to point to one of three targets. The most proximal target (also 1 cm in diameter) was the starting position for the fingertip (Fig. 1B, T0 target), while the other two targets with a 2 cm diameter were the reach goals (Fig. 1B,C, T1 targets). The T0 target always appeared in the same location, and one of the two T1 targets appeared equidistantly from T0 in each trial. T1 locations were chosen so that the movements to these targets required either rotation of the shoulder and elbow joints in the opposite direction (i.e., shoulder flexion and elbow extension) (Fig. 1C, assistive) or in the same direction (i.e., shoulder and elbow extension) (Fig. 1C, resistive). During the assistive condition, active elbow extension was accompanied by a passive extension interaction torque caused by simultaneous shoulder movement, which helped with the desired elbow movement. In contrast, during the resistive condition, elbow extension was accompanied by a flexion interaction torque due to shoulder extension; this passive interaction torque resisted the desired elbow movement (Fig. 1C). During the experimental session, trials with each of the two T1 locations were presented in a randomized-block design. Before the start of the experimental session, subjects were given the opportunity to practice the task for 40 trials.

Each trial started with the appearance of the T0 target. The subjects moved their arm to place a cursor in this starting location. Next, 1.5 s later the T1 target appeared in one of the two locations. One-half of all subjects, group 1, were required to leave the T0 target within a 400 ms window after the T1 appearance and simultaneous T0 disappearance. The other one-half of the subjects, group 2, were required to wait 1.5 s until the T0 target disappeared, before starting their reach to the T1 target with the same time constraint. Once the subjects reached the T1 target, they received feedback about the speed of their movement. If the subject arrived to the T1 target within a 550–1100 ms time window, the target changed color to green, indicating that movement speed was correct. Otherwise, the target color changed to red or blue, indicating to the subject that his/her movement speed was too fast or too slow, respectively. This encouraged all subjects to perform movements to both targets with the same average speed. At the end of the trial, the T1 target was left on for another 2.5 s for group 1 subjects or for another 1 s for group 2 subjects, so that each trial lasted at least 5 s. This was done to ensure that the frequency of transcranial magnetic stimulation (TMS), which was applied in almost every trial (see below, TMS procedure), was well below 1 Hz and did not induce long-term changes in cortical excitability (Chen et al., 1997). We have verified that no long-term changes in corticospinal excitability were induced by the frequent TMS by comparing TMS responses that preceded the onset of movement in the first and last halves of the experiment for each subject. No significant differences between the amplitudes of the early and late responses were found (data not shown).

TMS procedure.

In 90% of all trials, corticospinal excitability was probed using single-pulse TMS of the primary motor cortex (M1) with a figure-of-eight coil (Magstim Company). Responses to TMS, motor evoked potentials (MEPs), were obtained from surface electromyogram (EMG) of the following six arm muscles that span the shoulder and elbow joints: long and short heads of biceps brachii (Bic), brachioradialis (Br), lateral and long heads of triceps brachii (TriLat and TriLong), clavicular head of pectoralis major (Pec), and posterior deltoid (Del). Bic and TriLong are biarticular muscles that span both shoulder and elbow joints, while Br and TriLat are monoarticular muscles that span only the elbow joint and Pec and Del are monoarticular muscles that span only the shoulder joint. Br was recorded only in 7 subjects [one of whom was subsequently excluded from analysis as described above (see Subjects and tasks)], while the rest of the muscles were recorded in all 13 subjects. EMG was captured using Meditrace adhesive electrodes (Tyco Healthcare Group) positioned over muscle bellies, which were identified based on anatomical landmarks and palpation during contraction. Before placement of EMG electrodes, the skin was rubbed with a mildly abrasive material dipped in medical alcohol. The TMS site over the motor cortex was chosen as a hot spot (Traversa et al., 1997; Ellaway et al., 1998) [i.e., the coil location that produced MEPs in biarticular muscles (long heads of biceps and triceps) with the lowest TMS setting at rest]. The coil was oriented at a 45° angle to the midline with the handle pointing posteriorly. The location of the coil over the hot spot was maintained using the Brainsight tracking system (Rogue Research).

At the start of each session, resting threshold was determined for each subject as the lowest TMS amplitude that caused MEPs >50 μV 50% of the time in either of the recorded biarticular muscles when the arm was at rest and supported by the exoskeleton. During the session, TMS was delivered at 90% of the determined resting threshold in eight of nine trials at different times before and during movement to the T1 target. The timing of the TMS pulse was randomly chosen to either precede or follow the start of subject's movement, which was detected on-line when the subject exited the T0 target. The TMS pulse preceding the start of movement was automatically triggered by the KINARM software 150 ms after the signal to start the movement (appearance of T1 target for group 1 subject or disappearance of the T0 target for the group 2 subjects). The TMS pulse following the start of movement was triggered either 1, 80, 160, 240, 320, 400, or 480 ms after the detected onset of movement in different trials. At the moment of TMS coil discharge, the Magstim stimulator generated a square pulse of 50 ms duration, which was recorded together with the rest of the analog signals and used to synchronize EMG. The order of trials with and without a TMS pulse and the timing of TMS pulses were block-randomized with 25 repetitions of each condition (8 TMS times plus no-TMS trial, 2 directions) for a total of 450 trials.

EMG data were filtered (325 Hz low-pass and 10 Hz high-pass filters) and amplified (500 gain) using Lynx-8 amplifiers (Neuralynx). Next, EMG and joint kinematics were sampled at 1000 Hz using an analog-to-digital PC card (National Instruments) and analyzed off-line using custom software written in Matlab (MathWorks).

MEP analysis.

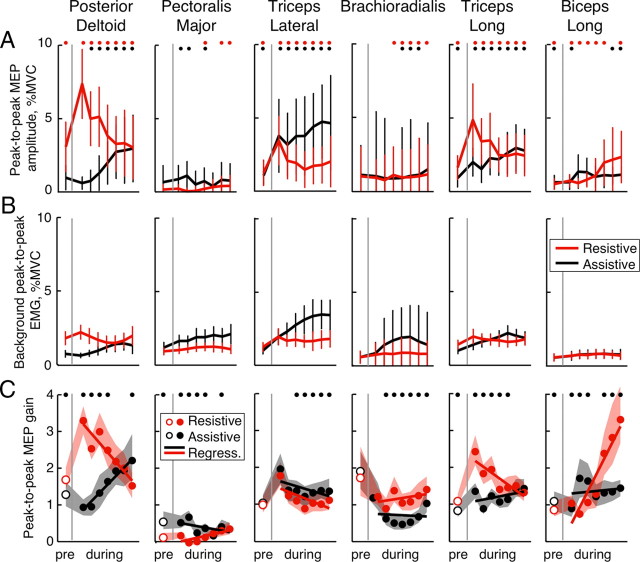
EMG recorded during trials with TMS was synchronized on the Magstim pulse, and the MEP amplitude was quantified in each trial using one of two methods. The first method, “integrated MEPs,” integrated rectified EMG within a time bin that started 5 ms after the TMS pulse and lasted until the end of the observed mean MEP. The end of the MEP was determined manually per muscle per subject from the mean rectified EMG trace averaged across all TMS trials plotted together with the mean background trace averaged across all non-TMS trials synchronized on the same times when TMS would be applied during movement (Fig. 1D). The second method, “peak-to-peak MEPs,” measured the difference between the maximum and minimum values of unrectified EMG within a time bin that started 5 ms after the TMS pulse and lasted 35 ms (Fig. 1E). The same two methods were also used to measure baseline EMG in control trials without TMS. These trials were synchronized to the start of movement, and the EMG within the same time epochs as those in TMS trials was analyzed using either integrated or peak-to-peak methods. Because the ongoing EMG during movements adds to the total value of the measured TMS responses, the MEP amplitudes were defined as the integrated or peak-to-peak MEPs minus integrated or peak-to-peak baseline EMG. To determine whether MEPs were evoked in any given condition, a t test was applied to the MEP amplitudes for each moment in time during movement, for each condition, and for each subject. Significant α was 0.0064 with Sidak–Bonferroni correction for multiple comparisons. The same statistical analysis was done across subjects, and its results are shown in Figure 7A as red and black dots demarcating significant MEP amplitudes for the resistive and assistive conditions, respectively.

Figure 7.

TMS responses across subjects. All plots show peak-to-peak EMG measurements taken at different times during a trial corresponding to vertical lines in Figures 2–5; columns show data for each muscle. The color of thick lines and symbols indicate resistive (red) and assistive (black) conditions; the vertical gray lines separate values before (pre) and during movement. A, Mean MEP amplitudes across subjects with pooled SD; dots demarcate values significantly different from zero. EMG was normalized to the MVCs of each subject before averaging. B, Background EMG across subjects with pooled SD, normalized to MVCs. C, The circles show MEP gains calculated based on the peak-to-peak MEP method shown in Figure 1E; the thick lines are regressions (Regress.) fitted to the gain values during movement (filled circles); the shaded areas show 95% confidence intervals. The open circles show mean gains before movement onset. The black dots demarcate significant differences (bootstrap procedure) (see Materials and Methods) between assistive and resistive conditions with power >0.8.

Responses to TMS measured from EMG are dependent on the excitability of motoneurons, which can be estimated from both the EMG activity preceding the TMS pulse, and at corresponding time periods in trials without TMS. This relationship between MEP amplitude and the motoneuronal excitability was largely linear in our experiments (data not shown). Therefore, the linear relationship was taken into account in the analysis of TMS responses by calculating “MEP gain,” defined as a ratio between the MEP amplitude and baseline EMG of control trials using the following formula: MEP gain = MEP amplitude/baseline EMG, where baseline EMG was calculated from trials without TMS as described above. According to this formula, a gain equal to 0 means that the mean EMG activity following the TMS pulse is equal to the mean background EMG (i.e., no MEPs were evoked).

All measures of MEP amplitude, gain, and baseline EMG were normalized to the maximal voluntary contractions (MVCs) recorded in the beginning of the session for each subject. The normalization measure was based on the maximal peak-to-peak EMG amplitude during three MVCs of each muscle, while the subject's arm was held against gravity in a posture similar to that assumed in the KINARM.

Statistical analysis of MEP gains calculated with the two methods was performed separately per condition per muscle using a bootstrap procedure (Efron and Tibshirani, 1993). Both single-trial MEP amplitude and baseline EMG values were resampled with replacement 500 times, and MEP gain was calculated for each sample according to the procedure described above. Resampling was done with preservation of data structure. This means that each bootstrap sample consisted of a certain number of elements drawn per subject, and the number of those elements was equal to the number of recorded trials per subject. The 95% confidence intervals were then calculated from the resulting distribution of MEP gains using a percentile method (Efron and Tibshirani, 1993). Comparison of MEP gains between conditions was done using a t test. Probability of making type I errors (p values) and type II errors (power) were calculated from the SEM of the bootstrap distribution. Significant α was 0.0064 with Sidak–Bonferroni correction for multiple comparisons. Only the significant differences between the resistive and assistive conditions with p < α and power >0.8 are marked with black dots on Figures 7C and 8C.

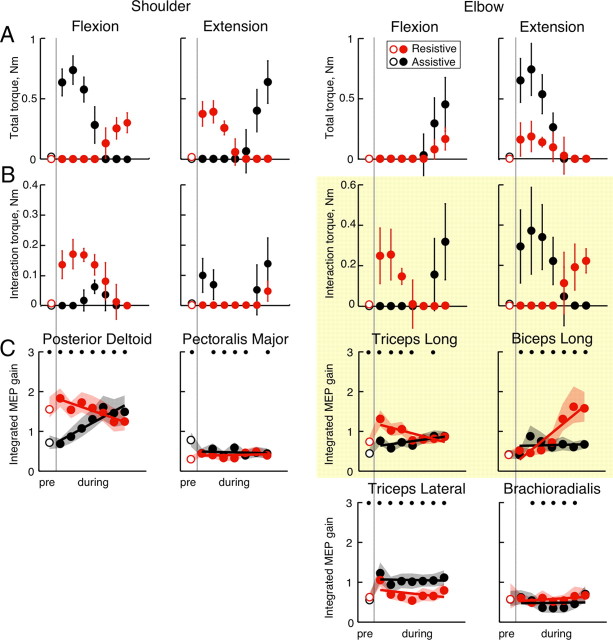
Figure 8.

Comparison of movement dynamics and MEP gain. The plots show joint torques in different directions (A, B) and MEP gains (C) before (pre) and during movement (separated by the gray line). The main result is highlighted by the yellow box. A, Columns show the total torque toward shoulder flexion, shoulder extension, elbow flexion, and elbow extension, during resistive (red) and assistive (black) conditions. B, Interaction torques in the same conditions. C, MEP gains calculated based on the integrated MEP method shown in Figure 1D. The symbols show mean gain values, the lines show regression lines, and the shaded areas show 95% confidence intervals. The black dots demarcate significant differences (bootstrap procedure) (see Materials and Methods) between assistive and resistive conditions with power >0.8.

Calculation of dynamics.

The kinematic data sampled at 1000 Hz were digitally low-pass filtered at 15 Hz to remove noise and used to calculate dynamics for comparison with the evoked TMS responses. Joint torques were computed using the following formulas from the literature (Sainburg et al., 1995, 1999; Shabbott and Sainburg, 2008):

where T_e and T_s are the net torques that caused recorded joint motion; T_ei and T_si are passive interaction torques; and T_em and T_sm are active muscle torques at the elbow and shoulder, respectively. Net joint torques were computed using the formulas adapted from Scott (1999) with terms describing the torque that results in the recorded acceleration of the joint (note that the robot torque was zero in our experiment) as follows:

where I_1,2 is link inertia; I_m1 is the shoulder motor inertia; m is link mass; c is the distance to the center of mass of the corresponding link; l is link length; θ is joint angle; θ̈ is angular acceleration; and the indexes 1 and 2 stand for proximal (shoulder) and distal (elbow) links and joints, respectively. Inertias, masses, and distances to the center of mass are combined values of the KINARM links, on which the subject's arm was resting, and the corresponding arm segments of the subject (Scott, 1999). Each subject's segment mass was estimated based on his/her height and weight (Winters and Woo, 1990). Inertia I of the subject's proximal and distal segments was estimated by modeling each segment as a cylinder with the mass m, length l, and small radius r as follows:

Passive interaction torques at the elbow and shoulder include all the terms from the dynamic equations in the study by Scott (1999) that describe the contribution from the attached segments (i.e., proximal segment action on the distal segment and vice versa). These were calculated according to the following formulas:

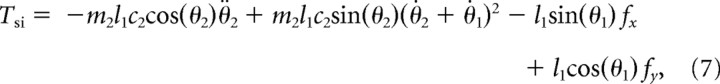where θ̇ is angular velocity; f_x and f_y are Cartesian projections of forces due to the additional KINARM links; and θ₅ is the angle of the lever at which the forces f_x and f_y were applied (Scott, 1999). These forces represent the action of the additional robot segments 3, 4, and 5 that make up the linkages from the robot motors to the arm segments 1 and 2 as follows:

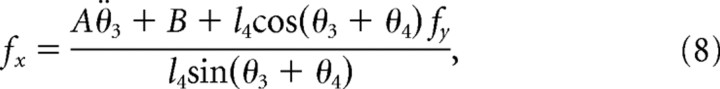where I_3,4 represents link 3 or 4 inertia; I_m2, elbow motor inertia; m, link mass; c, distance to the center of mass of the corresponding link; l, link length; θ, joint angle; θ̇, angular velocity; and θ̈, angular acceleration.

Statistical comparison of muscle torques between the assistive and resistive conditions was performed using repeated-measures (RM) t tests across subjects. First, the maxima and minima were found per trial for each condition (assistive and resistive). Second, the mean values over the 50 ms period centered on these values were calculated per trial and condition for each subject and averaged across trials. Third, a separate t test was done comparing the mean maxima and minima between conditions across subjects. Significant α was 0.0253 with Sidak–Bonferroni correction for multiple comparisons.

These muscle torques were compared with EMG bursts in the two conditions. Statistical comparison of EMG bursts between the assistive and resistive conditions was performed using RM t tests across subjects. First, the EMG in each trial without TMS was rectified and smoothed using a 60 ms moving-window averaging. Second, the values of the smoothed EMG trace that preceded by 150 ms the maxima and minima of muscle torques found above were selected per trial, EMG signal, and condition and averaged across trials. Third, a separate t test was done comparing these mean EMG values between conditions across subjects for each EMG signal. Significant α was 0.0253 with Sidak–Bonferroni correction for multiple comparisons.

For comparison with TMS responses, the net and interaction torques during the trials without TMS were averaged within the same time window and at the corresponding time intervals as baseline EMG (see above, MEP analysis). These torques were divided into the flexion and extension torques, and their absolute values were plotted separately in Figure 8 for comparison with the TMS responses in the muscles that act in the same direction around the corresponding joint. Quantitative comparison between these torque profiles and MEP gain profiles was performed by calculating in Matlab the partial correlation coefficient (R) and the goodness-of-fit statistics across subjects; significant α was 0.05. Each of the absolute torque profiles for flexion (F) and extension (E) directions were concatenated (appended, e.g., F followed by E or E followed by F), so that one mean trace for T_s, T_si, T_e, and T_ei was produced per condition (assistive or resistive) per subject. This was done so that a single coefficient could describe the correlation between MEP gain and torque in both flexion and extension directions. The muscle torques (T_em and T_sm) were not included in this comparison, because they are a dependent variable of total and interaction torques. These torque profiles were averaged across subjects and compared with the averaged concatenated MEP gain profiles of the corresponding muscle pairs. Thus, partial correlation was calculated between the mean EF T_si profile and the mean PecDel MEP gain profile (E T_si is matched with Pec and F T_si is matched with Del because the role of the muscle in this case is to counteract the interaction torques) controlling for the mean FE T_s profile. Similarly, partial correlation was calculated between the mean EF T_ei profile and the mean BrTriLat MEP gain profile, controlling for the mean FE T_e profile; and partial correlation was calculated between the mean EF T_ei profile and the mean BicTriLong MEP gain profile, controlling for the mean FE T_e profile.

Calculation of co-contraction.

Co-contraction was calculated as the amount of “wasted” contraction (Thoroughman and Shadmehr, 1999; Graham et al., 2003; Darainy and Ostry, 2008). The minimum value of mean rectified EMG profiles of each agonist and antagonist pair was calculated at a given point in time per condition (assistive or resistive) per subject. This resulted in co-contraction profiles for the shoulder monoarticular muscles Del and Pec, the elbow monoarticular muscles TriLat and Br, and the biarticular muscles TriLong and Bic. These co-contraction profiles were averaged across subjects, concatenated, and used for controlling for the partial correlation between interaction torques and MEP gains as described above. Thus, partial correlation was calculated between the mean EF T_si profile and the mean PecDel MEP gain profile controlling for the mean repeated PecDel co-contraction profile. Partial correlation was calculated between the mean EF T_ei profile and the mean BrTriLat MEP gain profile, controlling for the mean repeated BrTriLat co-contraction profile. Finally, partial correlation was calculated between the mean EF T_ei profile and the mean BicTriLong MEP gain profile, controlling for the mean repeated BicTriLong co-contraction profile.

Results

Kinematics and dynamics of movements

Subjects performed planar movements toward two equidistant visual targets, so that movement to one target required joint rotations in opposite directions [i.e., shoulder flexion and elbow extension (assistive condition)], while movement to the other target required joint rotations in the same direction [i.e., extension of both shoulder and elbow (resistive condition)] (Fig. 2). Figure 2 shows that joint excursions during movements toward the targets were unequal, so that in the resistive condition movements had smaller amplitudes of joint excursions with lower angular velocities (in local reference frames) than those in the assistive condition. Joint torques responsible for these differences (Fig. 3A) could be subdivided into passive interaction torques (Fig. 3B) and active muscle torques (Fig. 3C) to study the control mechanism of the neuromuscular system (Sainburg et al., 1995, 1999; Shabbott and Sainburg, 2008). Figures 2 and 3 show that larger muscle torques in the resistive condition produced much smaller joint movements than in the assistive condition. This is due to the changing role of the interaction torques acting on the elbow between conditions. Since the elbow interaction torques in the resistive condition are in the opposite directions to the desired joint excursions, they counteract the action of elbow muscle torques. In contrast, the elbow interaction torques in the assistive condition are largely in the same direction as the desired joint excursions, adding to the action of muscle torques. Note that the interaction torques at the elbow are approximately equal and opposite in sign in the assistive and resistive conditions. Interaction torque at the shoulder during both assistive and resistive conditions was found to be opposite to the desired shoulder rotation in the acceleration phase of the movement (Fig. 3B). During the deceleration phase of movement, the interaction torques at the shoulder followed the same assistive and resistive roles in the two conditions as at the elbow.

Figure 2.

Averaged movement kinematics of a representative subject. The thick lines show means during the resistive (red) and assistive (black) conditions; the shaded areas outline SD across 25 trials without TMS. The vertical gray lines indicate times of TMS across multiple trials; zero is the moment of exiting the T0 target. A, Angular position of shoulder and elbow joints. B, Angular velocity of shoulder and elbow joints. C, Angular acceleration of shoulder and elbow joints. All values are in the local joint-based reference frames.

Figure 3.

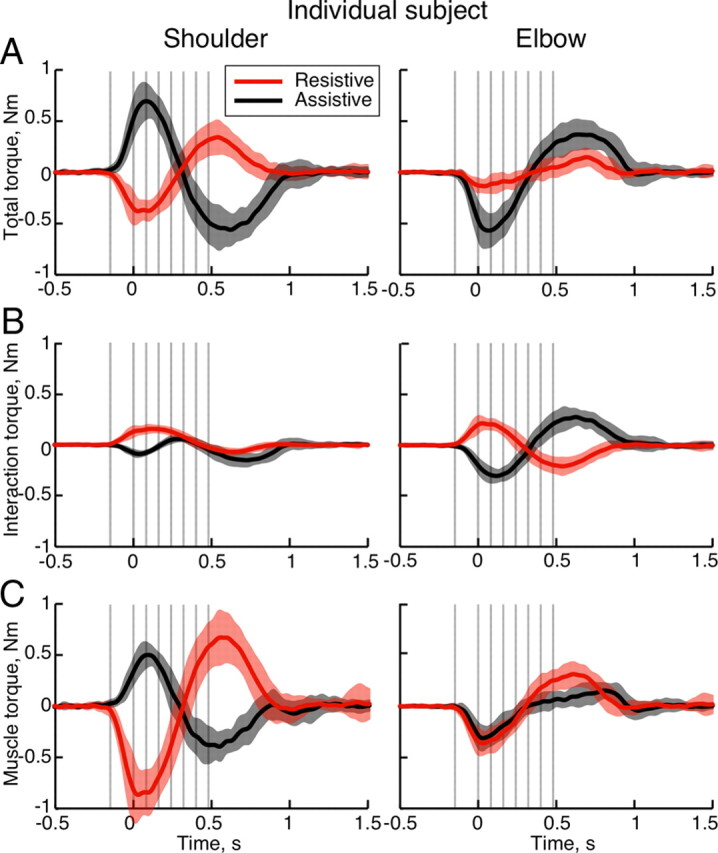
Averaged movement dynamics of a representative subject. The thick lines show means during the resistive (red) and assistive (black) conditions; the shaded areas outline SD across 25 trials. The vertical gray lines indicate times of TMS across multiple trials; zero is the moment of exiting the T0 target. A, Total torque at shoulder and elbow joints, proportional to angular acceleration. B, Interaction torque at shoulder and elbow joints. C, Active muscle torque at shoulder and elbow joints.

Electromyography

Muscle activity of four monoarticular (Pec, Del, TriLat, and Br) and two biarticular (TriLong and Bic) muscles was recorded during movements in the two conditions. A representative pattern of EMG in the two conditions for a single subject is shown in Figure 4(same subject as in Figs. 2 and 3). The EMG pattern of the monoarticular shoulder muscles followed the pattern of calculated muscle torques (Fig. 3C), in which their activity alternated between the initial acceleration by Pec followed by deceleration by Del in the assistive condition and the opposite pattern in the resistive condition (Fig. 4). In contrast, the EMG pattern of the monoarticular elbow and the biarticular muscles did not follow the pattern of calculated elbow muscle torques as closely as the shoulder muscles. The accelerating muscle torques that extended the elbow in the assistive condition were lower than those in the resistive condition, despite larger and faster elbow extension in the former compared with the latter condition (Fig. 3C) (t = −6.7; p < 0.0001). This is due to the opposing interaction torques from the shoulder acting on the elbow in the resistive condition. However, the corresponding burst of the TriLong in the beginning of movement was higher in the resistive than in the assistive condition in all but three subjects (Fig. 4) (t = 18.3; p < 0.0001). This shows that the biarticular TriLong muscle contracted more to produce the smaller and slower extension of both shoulder and elbow joints in the resistive condition compared with its contribution to the larger and faster elbow extension in the assistive condition. In contrast, the corresponding accelerating burst in TriLat was higher in the resistive than in the assistive condition in only 5 of 12 subjects (t = 8.2; p < 0.0001). This indicates that the contribution of the monoarticular TriLat to the acceleration action at the elbow is less dependent on interaction torques than that of the biarticular TriLong.

Figure 4.

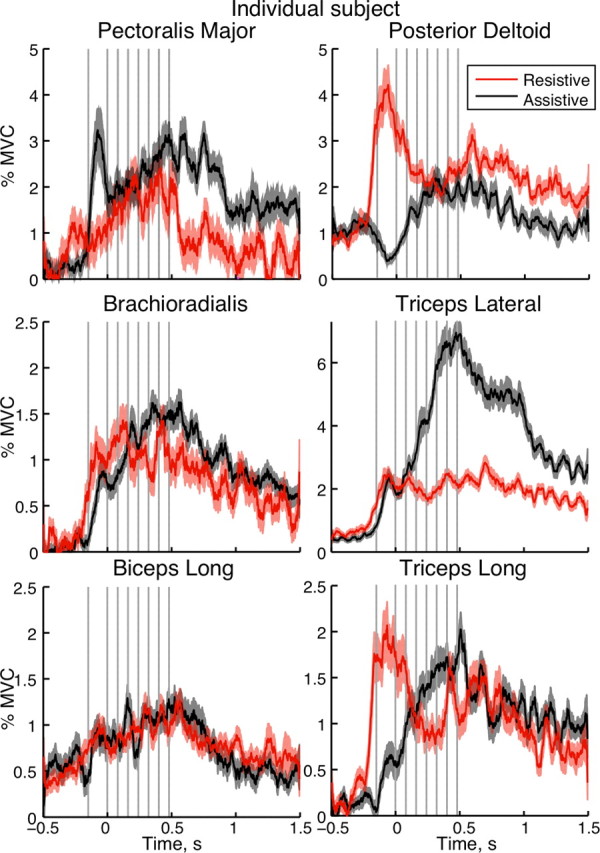
Averaged rectified EMG of a representative subject. The first and second rows show activity of monoarticular shoulder and elbow muscles, respectively; the third row shows activity of biarticular muscles. The thick lines show mean EMGs during the resistive (red) and assistive (black) conditions; the shaded areas outline SEM across 25 trials. First column, Flexor muscles; second column, extensor muscles. The vertical gray lines indicate times of TMS across multiple trials; zero is the moment of exiting the T0 target.

The EMG patterns of both flexors, Br and Bic, showed only deceleration bursts in the second part of the movements in the two conditions. The Br deceleration bursts were smaller in the resistive than in the assistive condition in 6 of 12 subjects (Fig. 4) (t = −10.7; p < 0.0001). In contrast, the Bic deceleration burst was larger in the resistive than the assistive condition in 4 of 12 subjects (Fig. 4) (t = 4.6; p = 0.0001). During the deceleration phase of movement, there were also bursts in both extensors, TriLong and TriLat, in all but one subject (Fig. 4). The EMG bursts in the monoarticular TriLat were smaller in the resistive than in the assistive condition in 6 of 12 subjects (t = −11.9; p < 0.0001). In contrast, the EMG bursts in the biarticular TriLong were larger in two subjects and smaller in three subjects in the resistive condition compared with that in the assistive condition (t = 0.1; p = 0.3963). At the same time, the decelerating muscle torque was significantly higher in all subjects at the corresponding time in the resistive condition compared with the assistive condition, due to the assistive decelerating interaction torques from the shoulder acting on the elbow (Fig. 3B) (t = 21.3; p < 0.0001). This shows that the monoarticular and biarticular muscles contribute differently to the decelerating action at the elbow.

The calculated joint muscle torques only show the difference between flexor torques generated by all flexor muscles and extensor torque generated by all extensor muscles that span the corresponding joint. This excludes equal torques of opposite direction that can arise during co-contraction. Figure 5 shows that the co-contraction of shoulder monoarticular muscles was higher in the resistive than in the assistive condition during the acceleration phase of movement (t = 4.3; p = 0.0002), but similar between conditions during the deceleration phase (t = 0.6; p = 0.3291). Similarly, the co-contraction of elbow monoarticular muscles was mostly larger in the resistive than in the assistive condition during the acceleration phase of movement (t = 4.7; p < 0.0001). However, it switched to being mostly larger in the assistive compared with the resistive condition during the deceleration phase (t = −7.3; p < 0.0001). A similar trend was observed for the co-contraction of biarticular muscles (acceleration phase of movement: t = 6.0, p < 0.0001; deceleration phase of movement: t = −4.0, p = 0.0004). This helps to explain the low deceleration muscle torque at the elbow during the assistive condition despite increasing EMG activity in the recorded muscles spanning that joint. Furthermore, it suggests that, during the deceleration phase of movement, co-contraction contributes to the dampening of assistive interaction torques, which amplify the desired movement.

Figure 5.

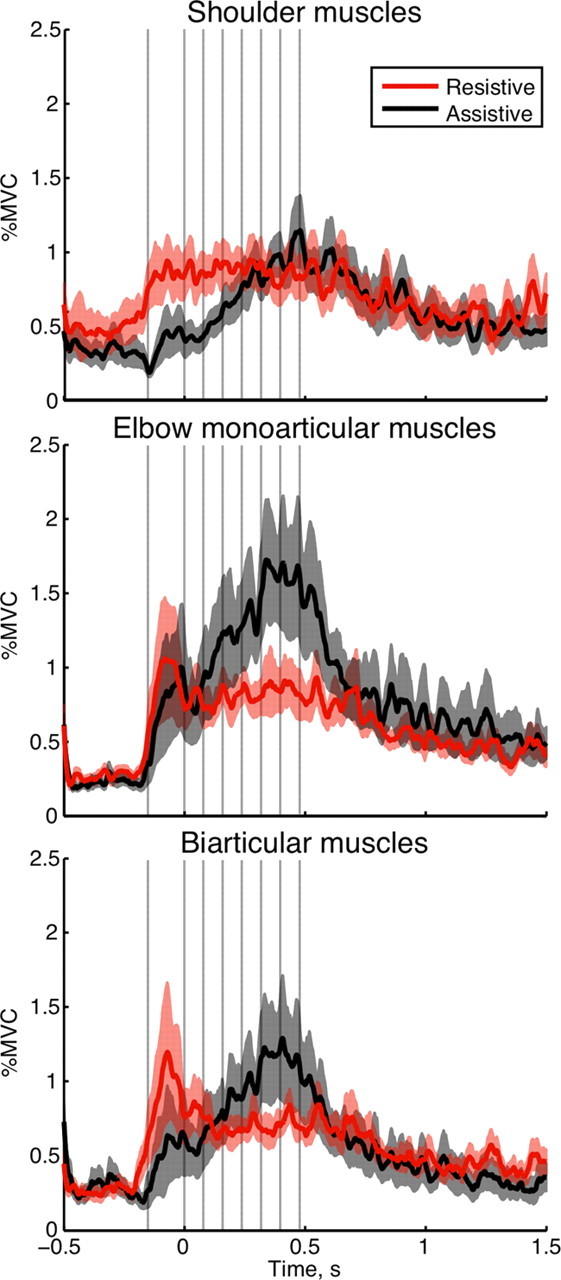
Co-contraction between antagonistic muscles across subjects. Top plot, Posterior deltoid with pectoralis major; middle plot, brachioradialis with triceps lateral; bottom plot, biceps long with triceps long. The traces show mean co-contraction in time during the resistive (red) and assistive (black) conditions; the shaded areas outline SEM across subjects. The vertical gray lines indicate times of TMS across multiple trials; zero time is the moment of exiting the T0 target.

Corticospinal excitability

TMS of M1 during movement evoked consistent MEPs in multiple muscles across multiple repetitions (Fig. 6). Pec was the only muscle in which MEPs were evoked infrequently, so that in the resistive condition no Pec MEPs were reliably evoked in any of the subjects, while in the assistive condition Pec MEPs were evoked in 5 of 12 subjects (including the subject in Fig. 6). The polarity of the MEPs was consistent across conditions in Pec, Del, and Bic muscles for all subjects, but less so in other muscles. The shape of the MEPs reversed in TriLat of four subjects, in TriLong of two subjects (Fig. 6), and in Bic of two subjects. In two of these subjects, the MEP reversal was accompanied by correlated EMG of TriLat and TriLong (R² = 0.34 and 0.48 per subject). This suggests that, in two subjects, changes in MEPs between the assistive and resistive conditions may be due to different recruitment of the synergistic muscles in the two tasks that is captured by the same recording electrode.

Figure 6.

Individual-trial MEPs of a representative subject during the assistive condition. The TMS time was at the moment of exiting the T0 target (time 0). The traces show nonrectified EMG in individual trials, a maximum of 25 trials is in each plot; the vertical gray lines show the time bin within which the MEP peaks were measured. Gray traces, MEPs in resistive condition, black traces, MEPs in assistive condition. y-axis scaling is matched between conditions for each muscle.

The amplitude of MEPs in all muscles depended on the time of TMS during movement and on the background EMG activity that is proportional to the motoneuronal excitability as illustrated in the population average in Figure 7. To measure corticospinal excitability that is independent from the motoneuronal excitability, we normalized MEP amplitudes (Fig. 7A) by the background EMG in trials without TMS (Fig. 7B). We call this measure the “MEP gain” (see Materials and Methods). In Del, TriLong, and Bic muscles, these MEP gains were dramatically different between the resistive and assistive conditions (Fig. 7C). At the beginning of movement, MEP gains in the monoarticular shoulder extensor Del and the biarticular extensor TriLong were larger in the resistive than the assistive condition. Near the end of movement, MEP gains of the biarticular flexor Bic were larger in the resistive condition than in the assistive condition The monoarticular elbow muscles Br and TriLat showed very little modulation of MEP gain during the movement (Fig. 7C). The pattern of MEP gain changes during movement is supported by a repeated-measures t test on regression slopes across subjects, which showed significant differences between resistive and assistive conditions in shoulder and biarticular muscles (t = 4.3, −4.0, −2.9, and 5.6; p = 0.0003, 0.0007, 0.0087, and p < 0.0001 for Del, Pec, Bic, and TriLong, respectively), but not elbow monoarticulars (t = 1.8 and −0.6; p = 0.0783 and 0.3273, for TriLat and Br, respectively). The same analysis was also performed using the integrated MEPs (Fig. 1D), instead of the peak-to-peak MEPs, with the same results for MEP gain of all muscles except Pec (Fig. 8C). The modulation during movement of Pec MEP gains was much lower when measured with the integrated method compared with that measured with the peak-to-peak method. This is likely due to the much lower MEP amplitudes evoked in Pec that were not significantly different from background EMG in most subjects, especially in the resistive condition (Fig. 7A, fewer significant MEPs in Pec).

The pattern of modulation of MEP gains described above was evident even before the onset of movement (Figs. 7C, 8C). The peak-to-peak MEP gains were larger in the resistive than the assistive condition before the onset of movement in 6 of 12 subjects for both Del and TriLong (Del: t = 5.1, p = 0.0001; TriLong: t = 3.3, p = 0.0036). This suggests that the corticospinal excitability in these muscles increased even before the availability of sensory feedback from movement in the resistive condition.

The temporal pattern of MEP gains reflects interaction torques

To help compare MEPs with limb dynamics in the assistive and resistive conditions, we averaged flexion and extension torques in control (no-TMS) trials at the same points in time before and during movement when MEPs were evoked in the TMS trials (Fig. 8). Because the interaction torque at the shoulder during the assistive condition was found to be opposite to the desired shoulder rotation in the acceleration phase of the movement (Figs. 3B, 8B), interaction torque compensation at the shoulder is needed during both conditions. TMS results show that the temporal profile of the MEP gain changes in Del muscle (Fig. 8C, first column) is very similar to the temporal profile of flexion interaction torque at the shoulder in both conditions (Fig. 8B). The modulation of MEP gain in Pec muscle was much lower than that of Del, but consistent with the potential role of shoulder muscles in interaction torque compensation. This modulation of Pec MEP gain was only seen in peak-to-peak and not in integrated MEP measurements (Figs. 7C, 8C, second column). Quantitative comparison between shoulder joint torques and the MEP gains of shoulder muscles revealed significant correlations only in the resistive condition in all subjects. The shoulder interaction torque and the concatenated MEP gain profiles of Del and Pec were significantly correlated (r = 0.74, p = 0.002, controlling for shoulder total torque; r = 0.77, p = 0.001, controlling for Del and Pec co-contraction) (see Materials and Methods). In contrast, shoulder total torque and the MEP gain profiles were not significantly correlated (r = −0.28, p = 0.305, controlling for shoulder interaction torque). This shows that the pattern of modulation of shoulder MEP gain is independent from the pattern of modulation of shoulder joint stiffness, as measured by the amount of co-contraction, and from the pattern of modulation of shoulder total torque that is proportional to the desired movement. Thus, the excitability of corticospinal projections to the shoulder muscles is timed and scaled together with the timing and scaling of interaction torque at the shoulder when it opposes the desired movement.

A similar analysis was performed on biarticular muscles. During the resistive condition, the patterns of both flexion and extension interaction torques at the elbow (Fig. 8B) are similar to the patterns of MEP gain changes in the biarticular extensor TriLong and the biarticular flexor Bic respectively (Fig. 8C, third and fourth columns). In contrast, during the assistive condition, the interaction torque at the elbow is in the same direction as the desired movement assisting motor execution (Fig. 8A,B, elbow). Consequently, the modulation of MEP gains in the biarticular Bic and TriLong muscles during the assistive condition is dramatically reduced (Fig. 8C). Quantitative comparison between elbow joint torques and the MEP gains of biarticular muscles found significant correlations only in the resistive condition in all but one subject. The elbow interaction torque and the concatenated MEP gain profiles of Bic and TriLong were significantly correlated (r = 0.62, p = 0.013, controlling for elbow total torque; r = 0.82, p < 0.0001, controlling for Bic and TriLong co-contraction). In contrast, elbow total torque and the MEP gain profiles were not significantly correlated (r = −0.14, p = 0.625, controlling for elbow interaction torque). This shows that, as for shoulder monoarticular muscles, the pattern of modulation of biarticular MEP gain is independent from the pattern of modulation of elbow joint stiffness and from the pattern of modulation of elbow total torque. Thus, the excitability of corticospinal projections to the biarticular muscles is timed and scaled together with the timing and scaling of the interaction torques, but only when they oppose the desired movement.

Surprisingly, the Br and TriLat MEP gains were either constant during the movements or were modulated the same way in both dynamic conditions (Figs. 7C, 8C). The correlation analysis on monoarticular elbow muscles found no significant partial correlations between their MEP gains and elbow torques. This shows that the excitability of corticospinal projections to the monoarticular elbow muscles is not modulated together with interaction torques. To summarize, this analysis suggests that M1 contribution to the control of biarticular and shoulder muscles involves compensation for interaction torques.

Discussion

Our results show that the excitability of corticospinal projections to the biarticular and shoulder muscles is modulated together with resistive interaction torques during movement. Despite notable intersubject variability, in all cases in which significant differences between the two dynamic conditions were found these differences were in biarticular and shoulder monoarticular muscles, and they were congruent with the proposed role of these muscles in interaction torque compensation. This suggests that the descending command along the corticospinal tract includes compensation for interaction torques, implicating cortical and/or subcortical pathways in dynamics compensation. Results further show that the modulation of the corticospinal excitability starts before the onset of movement and before the availability of afferent feedback, which suggest that the compensation for interaction torques may be in part predictive. Last, the corticospinal excitability was not modulated together with the co-contraction of agonist–antagonist pairs of muscles acting around each or both joints. This indicates that changes in joint stiffness as seen in co-contraction cannot explain the modulation of corticospinal excitability during movement. The observed intersubject variability may be the result of individual differences in the anatomical and functional organization of the cortical motor map, so that TMS activated different sets of corticospinal axons that modulated the activity of different combinations of muscles in different subjects. Alternatively, the variability may result from different muscle groups, not recorded in our study, being used for dynamics compensation.

Rationale for using TMS to measure corticospinal excitability

This study used TMS to investigate corticospinal excitability by measuring MEPs in six arm muscles. Several studies have shown that single-pulse TMS transsynaptically (i.e., indirectly) activates the corticospinal tract producing muscle responses that are proportional to cortical excitability (Hess et al., 1986; Rossini et al., 1988; Datta et al., 1989; Day et al., 1989; Roth et al., 1991; Saypol et al., 1991). Here, we have chosen to stimulate M1 at 90% of resting threshold with coil orientation at 45° to midline to preferentially activate the pyramidal tract neurons indirectly (Kaneko et al., 1996; Nakamura et al., 1996; Di Lazzaro et al., 1998). TMS with these parameters causes muscle responses that are proportional to underlying cortical activity, and these responses have been used to investigate corticospinal excitability during voluntary movements (Baker et al., 1995; Carson et al., 1999; MacKinnon and Rothwell, 2000; Morita et al., 2000; Di Lazzaro et al., 2003; Cros et al., 2007).

Corticospinal excitability was studied by comparing MEP amplitudes during movements with different interaction torques. MEP amplitude depends not only on the excitability of the corticospinal tract but also on the excitability of motoneurons, which are influenced by inputs from the spinal interneurons and monosynaptic projections from muscle spindle afferents. Therefore, we estimated motoneuronal excitability by averaging EMG in trials without TMS and used this measure to normalize MEP amplitudes and calculate MEP gain (see Materials and Methods). In agreement with our own measurements, a previous study reported a linear relationship between the background EMG and MEPs at various times during a voluntary movement (MacKinnon and Rothwell, 2000). In the MEP gain measure, this linear relationship was removed; thus, MEP gain is an estimate of the change in excitability of descending inputs to motoneurons in response to stimulation of M1. These descending inputs may include both direct corticospinal projections and multiple indirect pathways including intracortical, brainstem, and propriospinal interneurons (Burke and Pierrot-Deseilligny, 2010).

Corticospinal excitability correlates with resistive interaction torques

Passive inertial properties of the limb are known to be exploited by the motor system to make movements more efficient. For example, skilled throwers take advantage of interaction torques and minimize their energy expenditure while increasing the power of their movements compared with unskilled throwers (Debicki et al., 2004; Hore et al., 2005; Gray et al., 2006). Consistent with these studies, our results show reduced corticospinal input to the biarticular muscles and no significant correlations between corticospinal excitability and the interaction torques that are in the same direction as the desired movement. This suggests that the output from M1 is not counteracting the assistive interaction torques but instead allows these torques to contribute to the movement.

Several other studies have implicated M1 in the compensation for limb dynamics, showing that M1 neural activity is correlated with complex intersegmental dynamics of the multijoint limb (Cabel et al., 2001; Gribble and Scott, 2002; Kurtzer et al., 2006). Furthermore, it has been shown that M1 inactivation or lesion causes larger deficits in multijoint movements compared with single-joint movements (Lawrence and Kuypers, 1968; Martin et al., 1993) and that strokes in M1 or in its projections in humans cause deficits in intersegmental coordination, movement stability, and predictive scaling of force for grasping (Beer et al., 2000; Mihaltchev et al., 2005; Raghavan et al., 2006). At the same time, other studies argue that spinal mechanisms are not involved in limb dynamics compensation because short-latency spinal reflexes are downregulated in the acceleration phase of movement during exposure to novel loads (Shapiro et al., 2004) and they do not scale appropriately with inertial loads. In contrast, long-latency (presumably transcortical) reflexes do scale appropriately with inertial loads (Kurtzer et al., 2008, 2009; Pruszynski et al., 2009; Shemmell et al., 2009). Our results further support the involvement of M1 in limb dynamics compensation by showing that corticospinal excitability significantly correlates only with resistive interaction torques (Fig. 8). This suggests that the output from M1 is involved in the compensation for limb inertia by modulating activity of the appropriate muscle groups in accordance with the dynamic loads caused by the interaction between coupled limb segments (Sergio and Ostry, 1994; Almeida et al., 1995; Gribble and Ostry, 1998, 1999). Thus, our results support the hypothesis that the output of M1 contains information about the dynamic variables such as muscle forces (Scott and Kalaska, 1997; Cisek et al., 1998; Sergio and Kalaska, 2003; Sergio et al., 2005; Hamel-Pâquet et al., 2006; Trainin et al., 2007; Ajemian et al., 2008), rather than only kinematic variables such as movement direction (Georgopoulos et al., 1982; Schwartz et al., 1988; Caminiti et al., 1990; Fu et al., 1995; Bizzi et al., 2000; Mussa-Ivaldi and Bizzi, 2000). Our findings are also compatible with the “leading joint hypothesis” (Dounskaia et al., 2002), which proposes a hierarchical role for different joints in multijoint movements. In the movements studied here, the shoulder provides most of the power (Fig. 3C), while the elbow is either assisted by interaction torques or compensates for them. However, instead of a strict hierarchy we find that the compensation primarily involves the biarticular muscles, which are ideally situated to both provide power at the leading joint (shoulder) and stabilize the subordinate joint (elbow).

Corticospinal excitability does not correlate with co-contraction

Another way to compensate for interaction torques is to regulate whole-arm stiffness by coactivating muscles with antagonistic actions around one or more joints and increasing movement stability (Hogan, 1985; McIntyre et al., 1996; Milner, 2004; Franklin et al., 2007). We have investigated whether this mechanism is used for controlling limb dynamics during movements with assistive interaction torques, which amplify the desired motion in a positive-feedback manner. Our results show that the amount of co-contraction increases during the movement with assistive interaction torques, so that co-contraction is much higher for pairs of biarticular muscles and elbow monoarticular muscles toward the end of the movement (Fig. 5). This supports the theory of using arm stiffness to compensate for assistive limb dynamics. Surprisingly, however, we did not find a corresponding common increase in the corticospinal excitability in the antagonistic pairs of muscles during the assistive condition (Fig. 7C). This suggests that co-contraction does not cause the observed pattern of corticospinal excitability and strengthens our conclusion that the modulation of corticospinal excitability relates to interaction torque compensation.

Predictive versus feedback compensation for limb dynamics

The motor system has often been described as a hybrid feedback–feedforward system that includes both internal predictive signals and afferent feedback (for review, see Desmurget and Grafton, 2003). The idea of predictive limb dynamics compensation is supported by studies showing that the motor system can anticipate direction-dependent variations in hand acceleration (Flanagan and Lolley, 2001) and gravity-related loads (Gentili et al., 2007). Furthermore, limb dynamics prediction has even been observed in the absence of movement during motor imagery (Gentili et al., 2004) and in absence of interaction torques during single-joint movements (Almeida et al., 1995; Gribble and Ostry, 1999; Debicki and Gribble, 2005). These observations are further supported by our results showing that corticospinal excitability of projections to the shoulder muscles and the biarticular extensor muscle differs between assistive and resistive conditions even before movement onset (Figs. 7C, 8C).

At the same time, sensory feedback has also been shown to be involved in the compensation of limb dynamics, especially in learning novel dynamics (Sainburg et al., 1999; Verschueren et al., 1999; Bernardin et al., 2005). Furthermore, the absence of sensory feedback in deafferented subjects has been shown to cause deficits in intralimb coordination (Sainburg et al., 1993; Sarlegna et al., 2006). The present study found that joint stiffness (inferred from co-contraction levels) increased in the deceleration phase of movements in the assistive condition. This phase of movement is often suggested to rely more on feedback control rather than on predictive control (for review, see Meyer et al., 1988; Desmurget and Grafton, 2003). Thus, the gradually increasing co-contraction during the less stable movement suggests that the stiffness-based method of dynamics compensation may rely on sensory feedback rather than predictive pathways.