Counting Ion and Water Molecules in a Streaming File through the Open-Filter Structure of the K Channel

Abstract

The mechanisms underlying the selective permeation of ions through channel molecules are a fundamental issue related to understanding how neurons exert their functions. The “knock-on” mechanism, in which multiple ions in the selectivity filter are hit by an incoming ion, is one of the leading concepts. This mechanism has been supported by crystallographic studies that demonstrated ion distribution in the structure of the Streptomyces lividans (KcsA) potassium channel. These still pictures under equilibrium conditions, however, do not provide a snapshot of the actual, ongoing permeation processes. To understand the dynamics of permeation, we determined the ratio of the ion and water flow [the water-ion coupling ratio (CR_w-i)] through the KcsA channel by measuring the streaming potential (V_stream) electrophysiologically. The V_stream value was converted to the CR_w-i value, which reveals how individual ion and water molecules are queued in the narrow and short filter during permeation. At high K⁺ concentrations, the CR_w-i value was 1.0, indicating that turnover between the alternating ion and water arrays occurs in a single-file manner. At low K⁺, the CR_w-i value was increased to a point over 2.2, suggesting that the filter contained mostly one ion at a time. These average behaviors of permeation were kinetically analyzed for a more detailed understanding of the permeation process. Here, we envisioned the permeation as queues of ion and water molecules and sequential transitions between different patterns of arrays. Under physiological conditions, we predicted that the knock-on mechanism may not be predominant.

Introduction

Ion channels mediate ion flux with a high throughput, while at the same time retaining strict selectivity (Hille, 2001). The mechanisms underlying selective ion channel permeation are a fundamental issue in the field of neuroscience and have been studied extensively over several decades. Among these investigations, Hodgkin and Keynes (1955) proposed an insightful mechanism referred to as “knock-on,” which has maintained its relevance ever since.

The crystal structure of the potassium channel revealed a narrow and short stretch of the selectivity filter (Fig. 1A), where ions and water molecules cannot pass each other (single-file permeation) (Doyle et al., 1998). Multiple ions and water molecules occupy defined sites in the filter under equilibrium conditions (Morais-Cabral et al., 2001; Zhou et al., 2001). These distribution patterns suggest a picture in which the ion and water molecules during permeation generate a queue, and the ratio of the ion and water molecules undergoing permeation are thus countable.

Figure 1.

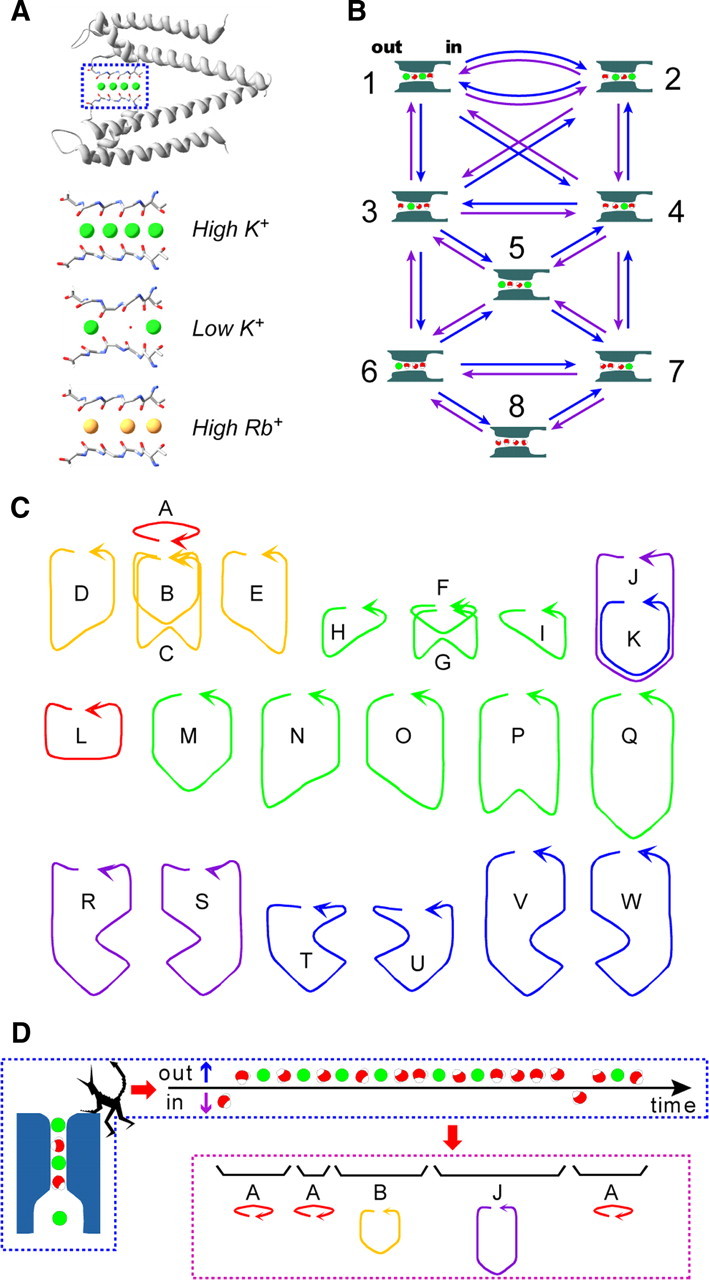
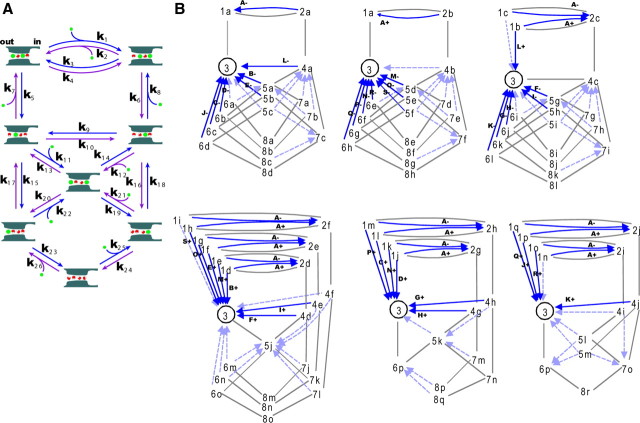
Permeation processes through the KcsA channel. A, The equilibrium ion distribution in the crystal structure of the KcsA channel. The selectivity filter (the boxed region in the top panel) is enlarged in the bottom under the different ionic conditions (Protein Data Bank accession codes: 1k4c, 1k4d, and 1r3i). There are four ion-binding sites in the selectivity filter, and the binding sites are named S1 to S4 from the outside (left) to the inside. The filter structure collapses at a low K⁺ concentration. Even at a high concentration of Rb⁺, the S2 site is left unoccupied. B, The discrete-state permeation model for the KcsA channel. The model involves eight K⁺ (green)-water (red) occupied states (diagrams with the state number; the left side is the extracellular space) in the selectivity filter and the transitions among them (arrows). The blue arrows indicate the transitions for efflux, and the violet ones indicate influx. C, The cyclic paths on the permeation diagram. For example, cycle A represents the transition between state 1 and 2, and cycle F represents the transition in states 3, 4, and 5. There are 23 cyclic paths for ion flux (alphabetical characters). They all involve two one-way cyclic paths with opposite directions. The arrows indicate the cycle direction for efflux (defined as + cycles). The cyclic paths are color coded to represent the water-ion coupling ratio. The red cycles indicate a 1:1 (water/ion) flux ratio; yellow, a 3:2 ratio; green, a 2:1 ratio; violet, a 5:2 ratio; and blue, a 4:1 ratio. D, A queue of ion and water flux and cycles on the diagram. From the observed queue of ion and water molecules, the demon assigns the queue to a series of cycles. Thus, ion and water flux can be regarded as random transitions among the cycles.

MacKinnon's group (Morais-Cabral et al., 2001; Zhou and MacKinnon, 2004) deciphered the permeation process as a series of transitions between two alternative arrays having ions and water molecules aligned one after the other: i-w-i-w and w-i-w-i (where i and w represent an ion and water molecule, respectively). These ion-distribution states were integrated into a discrete-state permeation model to express the permeation kinetics, and the eight state model became the canonical model for the K channels (Fig. 1B). Decoding the pattern of the dynamically permeating queue from the evidence based on still images was a most sophisticated achievement in the investigation of ion channel permeation. There is, however, a pitfall in this scenario. Permeation is intrinsically a dynamic process, while a crystal structure, being frozen, necessarily gives an ensemble average of the equilibrium ion distributions.

Here we present an approach to the study of the dynamic ion permeation processes through the open-filter structure in the steady state. In the ion channel, the high throughput of ion conduction accompanies water flux at a comparable rate (Hille, 2001). This high water flux is mandatory in a narrow no-pass pore, and we exploited this phenomenon of coupled water flux to understand the underlying processes of permeation.

To gain a realistic understanding of permeation, one can “watch” the exit of the selectivity filter with an imaginary microscope, assuming the point of view of Maxwell's demon located at the exit (Fig. 1D). The demon detects the output flow from the selectivity filter as a queue of ion and water molecules, and is able to count the individual particles. This queue is generated in the selectivity filter, where the ion and water molecules move by jumping state to state among the eight possible ion and water configurations (Fig. 1B). There are many cyclic paths (Figs. 1C, 2) on the diagram, and each cycle carries a defined number of ion and water molecules, such as 1:1 or 2:1. During steady permeation, these cycles contribute to the net flux of ion and water. Thus, the fractional contribution of the cycles reflects the ratio of the counted ion and water fluxes. Even without having such an imaginary microscope, the water-ion coupling ratio (CR_w-i = J_water/J_ion, where J_water and J_ion represent the flux of water and ion molecules per second) (Katchalsky and Curran, 1965; Schulz, 1980; Miller, 1982; Alcayaga et al., 1989; Dani, 1989; Ando et al., 2005; Oiki et al., 2010) can be measured electrophysiologically using the streaming potential (V_stream).

Figure 2.

A discrete-state permeation diagram and the expanded diagram for the KcsA channel. A, The permeation diagram used in this study with the name of the rate constants. This model involves cycles having different n_w-i values. B, The expanded diagram. The expanded diagram was constructed by defining state 3 as the starting state and all the states, except for state 3, were subdivided into substates, such as substate 8c. These diagrams include all of the 46 cyclic paths with one-way directionality. The arrows indicate the completing transitions for the one-way cycles, in which the solid arrows represent those of cycles generating the net cycle flux, and the cycle names are indicated with the + or − sign. The broken arrows indicate cycles of no net cycle flux. From the diagram, the one-way cycle fluxes for all the cyclic paths are readily calculated using matrix algebra.

Experiments were performed for the KcsA potassium channel, since various crystal structures exhibiting different ion distributions are available. We observed changes in the CR_w-i value at different K⁺ concentrations. These CR_w-i values were related to the underlying permeation processes using a theoretical method (Oiki et al., 2011). Here we envisioned how the ion and water molecules are queued during permeation and predicted how they are modified under physiologically relevant conditions.

Materials and Methods

Preparation of KcsA-reconstituted giant unilamellar vesicles.

The expression and purification of the KcsA channel were described previously (Iwamoto et al., 2006). The KcsA-reconstituted giant unilamellar vesicles (GUVs) were prepared according to the usual protocols (Delcour et al., 1989; Cortes et al., 2001) with some modifications. Purified KcsA channels (∼1 mg/ml) were reconstituted into azolectin (type IV-S; Sigma) liposomes with a protein/lipid weight ratio of 1:50. The proteoliposomes (∼5 mg) were collected by centrifugation (18,800 × g, 2 h) and resuspended in 100 μl of 10 mm HEPES, pH 7.5, containing 5% ethylene glycol. Five microliters of the suspension was dried for 6 h under vacuum on a clean coverglass surface. The dehydrated lipid film was rehydrated by 5 μl of the rehydration buffer (100 mm KCl, 1 mm MgCl₂, 10 mm HEPES, pH 7.5). GUVs suitable for the electrophysiological measurement were obtained after overnight rehydration at room temperature.

Apparatus for the V_stream measurement using the osmotic jump method.

The electrophysiological setup and the ultrafast solution exchange system for the osmotic jump method were the same as reported previously (Ando et al., 2005; Kuno et al., 2009), except for the configuration of the reference electrode. The reference electrode was set adjacent to the patch pipette electrode during the osmotic jump experiment. In this configuration, it is possible to avoid the establishment of a liquid junction potential between the two electrodes because they are always in the same solution (outflow).

Determination of the V_stream value.

The voltage command and the positioning of the double (or triple) barrel tube, from which the desired bathing solutions flowed out, were under the control of the program (Fig. 3A). A series of ramp commands was applied (Fig. 3E), and 30 I–V curves were obtained. To evaluate the V_stream values, linear regression of the time-dependent changes of reversal potential (V_rev) during the hyperosmotic pulse was performed, and the regression line was extrapolated to the time of an osmotic jump. Then, the value at the moment of the establishment of the osmolar gradient (ΔOsm) across the membrane was defined as the V_stream (Fig. 3G) (Ando et al., 2005). The osmolality of the solution was measured with an osmometer (Osmostat OM-6040; Arkray) and adjusted to the desired values by adding sorbitol. The K⁺ or Rb⁺ activity in the pipette solution and corresponding bathing solution (the outflows from barreled tube) were adjusted to the same values with a potassium-selective electrode (model 971901; Thermo Scientific).

Figure 3.

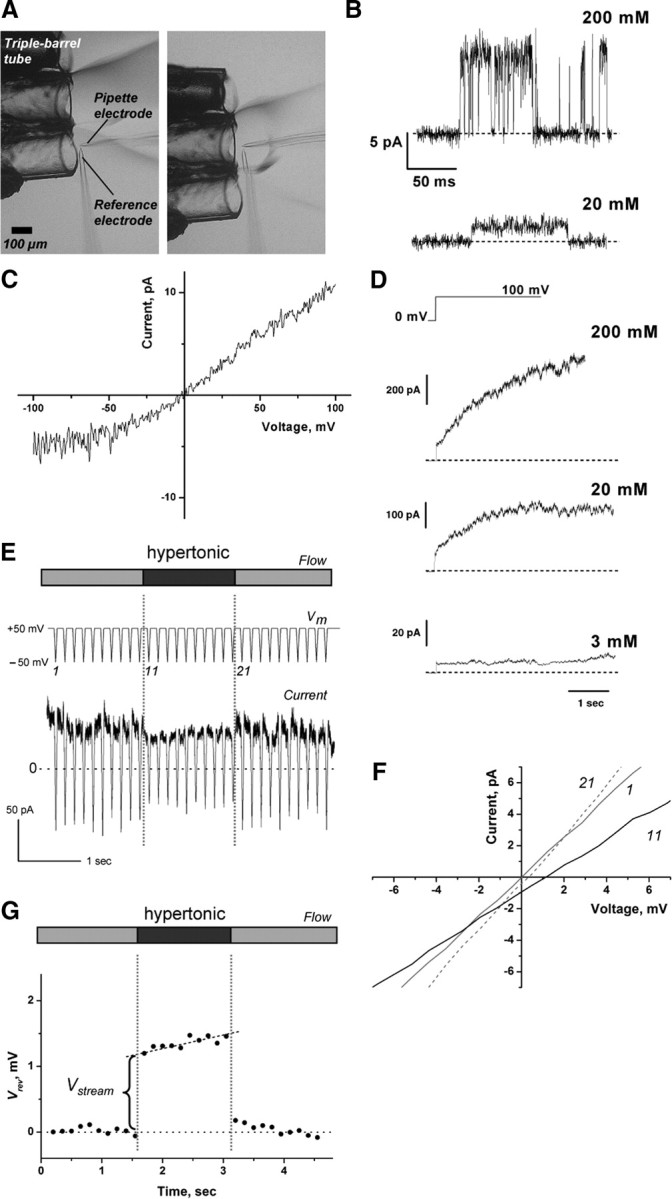
Measurements of the KcsA currents and the streaming potential. A, The osmotic pulse method. The configuration of the perfusion tubes and electrodes is shown. The outflow from each tube is different in osmolality. Rapid positional shifts of the tube lead to osmotic jumps within a few ms. The patch was stable even as it endured a 3 osmolar gradient (ΔOsm) across the membrane. B, The single-channel current of the KcsA channel for different K⁺ concentrations at pH 4.0. The current was measured at +100 mV. C, The single-channel current–voltage curve. A ramp voltage from −100 to +100 mV was applied during the open and closed states, and the difference in current was drawn. D, The macroscopic current upon voltage steps from 0 to +100 mV. The KcsA channel exhibits slow activation at positive potentials, and the time course of the activation differs significantly at different K⁺ concentrations. E, The protocol and evaluation of the V_rev. A train of the ramp voltage (+50 to −50 mV) was applied before, during, and after the osmotic pulse. A representative current trace elicited by a train of ramp commands synchronized with an osmotic pulse (in this case, 2.0 Osm/kg H₂O) is shown in symmetric 200 mm K⁺ at pH 4.0. A slight reduction in current amplitudes was observed during exposure to the hyperosmotic solution. This reduction appears to occur at the access resistance, which was augmented by a hyperosmotic solution with a higher resistivity (Kuno et al., 2009). F, The shifts of the I–V curves during the time course of the osmotic pulse. The I–V curves were drawn from the ramp current. The numbers on the I–V curves represent the number of the ramp commands. V_rev was obtained by linear regression of the I–V curves. G, A typical time course of V_rev during the command train. Osmotically driven water flux across the membrane toward the outside of the pipette leads to the condensation of K⁺ at the inner surface of the patch membrane, which generates a gradual positive shift in V_rev during the hyperosmotic period.

The diagram method for determining the cycle flux.

The eight state permeation diagram (Figs. 1B, 2A) is similar to that proposed by Molais-Cabral et al. (2001), in which either an ion or a water molecule occupies one of the four binding sites, and two ions are not allowed to occupy adjacent positions because of electrostatic repulsion. The 13 rate constants were set assuming that the potential profile of the permeation for K⁺ is symmetrical. We refer to this model as the “canonical eight state model.”

The steady-state probability of the states is calculated using the conventional method (Colquhoun and Hawkes, 1995). On the other hand, the net ion flux for the complicated eight state model needs cycle flux (the rate of completing a cycle) calculation (Oiki et al., 2011). Given the cycle flux, CR_w-i is readily calculated. The method for calculating the cycle flux is briefly described.

For a permeation diagram, the graphing procedure leads to the drawing of the expanded diagram (Fig. 2B), in which all of the cyclic paths in the original diagram with reversible plus (efflux) and minus (influx) cyclic fluxes are decomposed into one-way cyclic paths having distinct routes on the expanded diagram (Hill, 2004). The initial procedure is to draw the tree diagrams (Fig. 2B, gray lines), where all of the states are visited once without forming cycles. The states on the original diagram appear on each tree diagram, and they should be distinguished from each other by assigning the substate name (e.g., substates 8a–8r). From an end state of the branched paths, a one-way arrow (blue) is drawn to a state upstream of the tree branching. This generates a one-way cyclic path, and continuing this procedure generates the expanded diagram (Fig. 2B).

From the expanded diagram the transition matrix is formulated, such that the transition rate between the substates is assigned to be the same as that between the states on the original diagram. The total number of the substates was 100, and a 100 × 100 matrix was generated. The steady-state probabilities of the substates were readily calculated numerically from the inversion of the matrix.

On the expanded diagram, each arrow represents the completed transition for a one-way cyclic path, and the one-way cycle flux is calculated as the product of the probability of the substate at the tail of the arrow and the rate constant assigned for the arrow. For a case in which multiple cyclic paths are involved for a cycle of the defined name (such as cycle A), the products were summed up. The cycle flux κ is defined by the one-way cycle fluxes in both directions (J_κ = J_κ+ − J_κ−). Finally, for each cyclic path, the stoichiometric numbers of the ion and water transfer were assigned [n_i, n_w, and water/ion ratio (n_w-i)] (Ando et al., 2005), and the net ionic current and CR_w-i were calculated (Oiki et al., 2011).

The optimization of the rate constants.

Three different kinds of experimental data (CR_w-i, conductance, and ion occupancy) were used for optimizing the rate constants of the permeation model.

Estimation of the water-ion coupling ratio contributed from the wide pore region.

Osmotically driven water flux in the wide pore region outside of the single-file selectivity filter carries ions, and this may contribute to the measured CR_w-i. Levitt (1990) proposed a theoretical method for estimating the water-ion coupling in the wide pore region based on the continuum theory as follows:

where vol is the volume associated with the passage of one ion through the wide pore, η is the viscosity, a is the ion radius, L is the length of the wide pore, L_p is the hydraulic water conductivity of the rate-limiting process in the pore, R is the radius of the wide pore, α is the a/R, and

Dividing vol by the volume of a water molecule, the water-ion coupling in the wide pore region is calculated.

For the intracellular entryway toward the central cavity in the open channel of KcsA, the crystal structure indicates a geometry of ∼5–6 Å in terms of the radius, and 25 Å in length (Cuello et al., 2010). In the Levitt (1990) equation, the L_p for the rate-limiting conduction step represents the water flux in the entire pore, and therefore the L_p value of the selectivity filter should be used. Dani and Levitt (1981) further decomposed L_p as follows:

where f₀, f₁, f₂, etc. are the fractions of channels that contain 0, 1, 2, etc. ions, and L₀, L₁, L₂, etc. are the hydraulic water conductivity states for channels containing the 0, 1, 2, etc. ions. In the experimental condition for measuring the streaming potential, however, L₁ and L₂ are ignored since water flux for the ion-occupied pore ceases in the zero-current condition, and thus only the L₀ value is valid for calculating the L_p value (Dani and Levitt, 1981). For f₀, the probability of the channel being in the empty filter (state 8) is calculated from the permeation diagram using the optimized rate constants. Given the L₀ value, the water-ion coupling ratio in the wide pore can be estimated once the f₀ value is obtained.

Results

KcsA channel currents and the streaming potential as revealed by the osmotic pulse method

In the narrow pore where the single-file permeation takes place, ion flow and water flow drive each other. Even in the absence of differences in the electrochemical potential for a permeating ion, the net water flow driven by the osmotic difference across the membrane generates a net ion flow. The generated membrane potential is referred to as the V_stream (Miller, 1982; Alcayaga et al., 1989; Dani, 1989; Ismailov et al., 1997; Ando et al., 2005) and provides certain information on the underlying permeation processes, which is a prerequisite for determining how the ion and water molecules are queued.

To measure the streaming potential, the KcsA channel was reconstituted into GUVs and patch-clamping was performed (Chakrapani et al., 2007) (see Materials and Methods). A GUV membrane, on which the channels are oriented with the cytoplasmic domain inside (Chakrapani et al., 2007), was excised, and the inside-out membrane was exposed to acidic pH to elicit single and macroscopic channel currents (Fig. 3B–D). A train of 30 ramp voltages was applied (Fig. 3E) (Ando et al., 2005), and during the middle 10 ramps in the train, the patch membrane was exposed to a hyperosmotic solution (1:3 Osm/kg H₂O sorbitol; ΔOsm) for 1 s using a rapid perfusion system (Fig. 3A) (Ando et al., 2005). Figure 3E shows a representative current trace from such a train. From the current traces during the ramp voltage, the I–V curves were drawn (Fig. 3F) and the V_rev was measured. A typical time course of the changes in the V_rev values before, during, and after an osmotic pulse is depicted in Figure 3G. After the stable V_rev recordings were obtained under the steady iso-osmotic condition, V_rev jumped toward a positive potential upon the hyperosmotic pulse. A gradual but significant positive shift of V_rev during the hyperosmotic pulse and reversal of V_rev upon returning to the iso-osmotic solution were observed. The gradual shifts are consistent with our previous report on the human ether-à-go-go potassium channels (Ando et al., 2005) and stem from changes in the local K⁺ concentration at the surface of the patch membrane. The V_stream value was determined from the jump in the V_rev values at the beginning of the osmotic pulse (Fig. 3G).

Evaluation of the water-ion coupling ratio

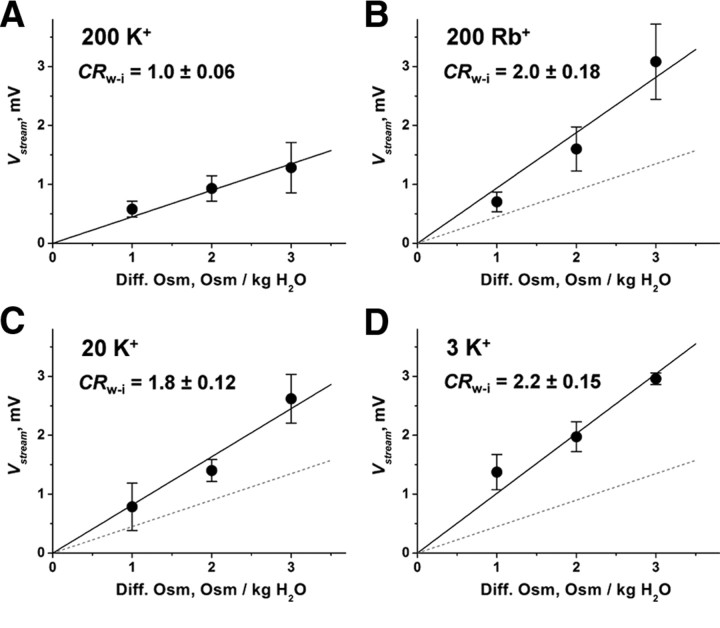
Figure 4A shows the ΔOsm dependency of the V_stream for the KcsA channel at 200 mm K⁺. The V_stream and ΔOsm exhibited a linear relationship. The slope value of 0.45 ± 0.03 mV/ΔOsm was obtained from a linear regression of the plots. This value is smaller than any previously measured. Such precise measurements rely on the setting of the appropriate reference points, such as the reference electrode and evaluation of the immediate V_stream value relative to the prejump (iso-osmotic) value (see Materials and Methods), while earlier methods needed corrections of several independent experimental parameters to reach the final determination.

Figure 4.

The streaming potential of the KcsA channel. ΔOsm dependency of the V_stream under various ionic conditions. From the slope, the CR_w-i value was calculated. A–D, The slope values were 0.45 ± 0.03 mV/ΔOsm for 200 mm K⁺ (A), 0.94 ± 0.09 mV/ΔOsm for 200 mm Rb⁺ (B), and 0.82 ± 0.05 and 1.01 ± 0.07 mV/ΔOsm in 20 mm K⁺ (C) and 3 mm K⁺ (D). The data represent the mean slope value ± the error of the slope.

The following equation relates the slope value to the ratio of the J_water and the J_ion (the CR_w-i) (Levitt et al., 1978; Rosenberg and Finkelstein, 1978):

where Δπ is the osmotic pressure, v_w is the molar volume of water, z is the ion valence, and F is the Faraday constant. The CR_w-i was determined to be 1.0 at 200 mm K⁺.

The CR_w-i value for Rb⁺ and K⁺ at different concentrations

Next, we evaluated the V_stream in the Rb⁺ solution, since Rb⁺ is known to permeate K channels with certain distinct conduction features (Eisenman et al., 1986; Hille, 2001; LeMasurier et al., 2001). Figure 4B shows the ΔOsm dependency of the V_stream at 200 mm Rb⁺. The slope value for Rb⁺ permeation (0.94 ± 0.08 mV/ΔOsm) was significantly higher than that for K⁺. The CR_w-i value was 2.0, indicating that two water molecules were carried with one Rb⁺ ion. The finding of an asymmetric distribution of Rb⁺ in the crystal structure (Fig. 1A) (Zhou et al., 2001; Lockless et al., 2007) and an interpretation posed by Morais-Cabral et al. (2001), which says that state 2 (Fig. 1B) might be destabilized in terms of the energy profile of the permeation, are consistent with our data.

Figure 4, C and D, shows the ΔOsm dependency of the V_stream for the low K⁺ concentrations. From the slope values, the CR_w-i was determined to be 1.8 and 2.2 in 20 and 3 mm K⁺, respectively. The results clearly indicate that the number of water molecules in a queue increased substantially at low K⁺ concentrations. In this way, we have experimentally counted the ion and water molecules in a streaming file through the open-filter structure of the KcsA channel.

The cycle flux and the CR_w-i value

From the obtained CR_w-i values, one may attain more intuitive insights into the underlying permeation process. The permeation process has been represented as random transitions among the ion-water-occupied states on a discrete-state permeation model (Läuger, 1980; Miller, 1999) (Fig. 1B) (Morais-Cabral et al., 2001). On this sort of permeation diagram, there are many cyclic paths (Fig. 1C). Starting from an arbitrary state, back and forth random transitions spontaneously return to the starting state and complete a cycle. For example, starting from state 3, a transition follows a route such as 3 → 4 → 5 → 3 and forms cycle F. By completing these cycles, n_w and n_i are carried forward (the ratio is n_w/n_i). The experimentally obtained CR_w-i values are, thus, most closely related to the contribution of the cyclic paths on the diagram, in which each path comprises a defined number of coupled ion and water transfer steps.

One can measure the cycle completion rate (cycle flux) by counting the number of times the random walk returns to an arbitrary state through a defined cyclic route in a given period of time (Hill, 1988; Oiki et al., 2011). The completion of each cycle can be regarded as an independent event, and the sum of the cycle fluxes generates the net flux (Fig. 2), as follows:

where J_κ is the cycle flux for cycle κ.

Each cyclic route (Fig. 1C) has its distinct stoichiometric number for each of the ion fluxes (n_i) and water fluxes (n_w) (Ando et al., 2005; Oiki et al., 2011). Thus, the stoichiometric ratio n_w/n_i (n_w-i) for each cycle can be defined, and these values of all of the cycles in the diagram determine the CR_w-i value, as follows:

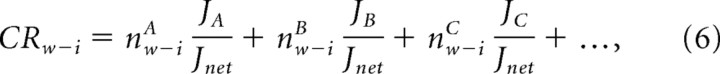where n_w-i^A, n_w-i^B, and n_w-i^C are the water-ion stoichiometry values for cycles A–C, respectively (Oiki et al., 2011). For example, if permeation occurs as the result of a transition between state 1 and 2, it generates the cyclic path of cycle A (Fig. 1B,C). Upon completion of cycle A, one ion and one water molecule are transferred. Cycle F, to take another example, transfers one ion and two water molecules. If the CR_w-i value is 1.5, then cycle A, cycle F, and the other cycles are mixed.

Based on the above theoretical considerations, the observed CR_w-i value can be interpreted in terms of which cycles were predominantly active in a given condition. In the high K⁺ (200 mm) condition, the CR_w-i value of 1.0 indicates that cycle A, having the n_w-i value of 1 (Fig. 1C), is predominant. The gradual increase in the CR_w-i value at the lower K⁺ concentrations indicates that the predominant cyclic path is shifted from cycle A to other cycles having higher n_w-i values. At 20 mm, cycles having the n_w-i value of 2, such as cycles F–I, contribute to the flux. At 3 mm, the CR_w-i value of 2.2 is attained only if cycles J, K, and others with a high n_w-i value (cycles R–W) are used. These semiquantitative clues are extended by quantitatively relating the CR_w-i values to the underlying process of permeation (Oiki et al., 2011).

Model optimization based on the CR_w-i values

T. L. Hill (1988, 2004) developed a diagrammatic method to calculate the cycle flux from the rate constants of the relevant permeation diagram. For the relatively complicated diagram of the KcsA channel, we have established a method of relating the rate constants and the cycle flux (Fig. 1B) (Oiki et al., 2011). Using the cycle flux, CR_w-i was eventually expressed with the set of rate constants. The net ionic current was also calculated from the cycle flux, which has otherwise typically been estimated with a Monte Carlo simulation (Morais-Cabral et al., 2001). Conversely, the rate constants have also been estimated from the experimental observables through fitting.

To optimize the rate constants, not only the CR_w-i values, but also the conductance data (LeMasurier et al., 2001) were used. Also, the K⁺ distribution in the filter at only the high concentration (Zhou et al., 2001) was included to optimize the rate constants. Three different kinds of experimental data thus were used to provide effective constraints on the process of the optimization (see Materials and Methods). The CR_w-i values were thereby accurately reproduced as a function of the K⁺ concentration using the optimized rate constants (Fig. 5A). The calculated current amplitudes and the ion-occupancy probability closely fit with the experimental data (Fig. 5B,C).

Figure 5.

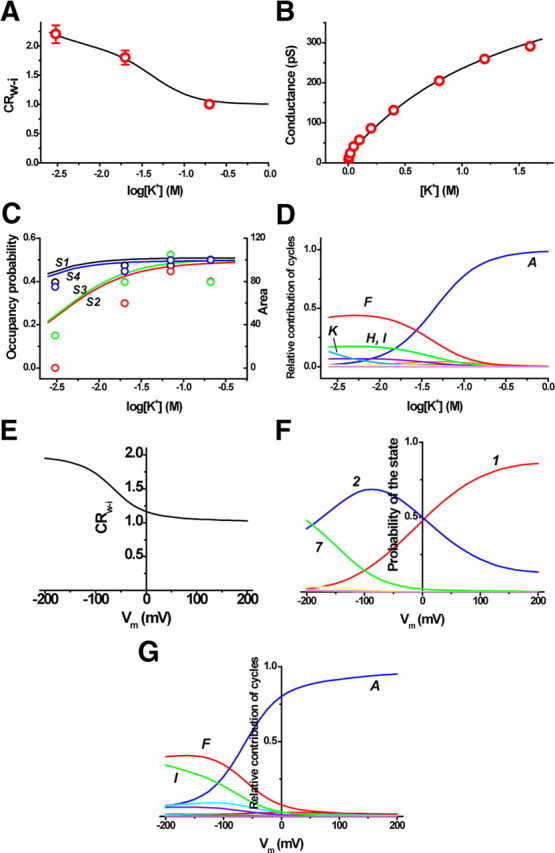
Experimental data and the underlying permeation processes. A, B, The experimental data of CR_w-i (A) and the conductance (B) as a function of the K⁺ concentration. The rate constants of the eight state permeation model were optimized to fit these experimental data. The lines indicate the fitted lines calculated from the cycle flux. C, The K⁺ occupancy on the four binding sites in the selectivity filter as a function of the K⁺ concentration. The ion distribution data of the crystal structure are represented as the area of the electron density (circles) superimposed through an appropriate scaling. Black (the symbols and the lines) indicates the S1 site, red indicates the S2 site, green indicates the S3 site, and blue indicates the S4 site. D, The current contributions from each cycle. The optimized rate constants were as follows (/s): k₁ = 5.0 × 10⁷, k₃ = 1.5 × 10⁸, k₅ = 2.5 × 10⁵, k₇ = 8.0 × 10⁸, k₉ = 3.5 × 10⁸, k₁₁ = 3.6 × 10¹⁰, k₁₃ = 1.0 × 10⁹, k₁₅ = 1.8 × 10¹⁰, k₁₇ = 1.8 × 10⁹, k₁₉ = 4.0 × 10⁸, k₂₁ = 1.44 × 10⁷, k₂₅ = 2.0 × 10⁶, and k₂₇ = 2.0 × 10⁹. E–G, The predicted features of permeation in an asymmetric condition of 4 mm K_out and 150 mm K_in at different membrane potentials; predicted curves for CR_w-i (E), the probability of the states (F), and the relative contributions of the cycles at different membrane potentials (G).

Before inquiring into the meaning of the CR_w-i values, the possible contribution of the wide pore region to the determination of the CR_w-i values must be taken into consideration. Osmotically driven water flow carries ions even outside of the single-file pore (see Materials and Methods), and here we can estimate the contribution of the wide pore to the obtained CR_w-i values. Based on the Levitt (1990) equation (Eq. 3), the L_p value for the empty selectivity filter (L₀) is necessary, while f₀ is calculated from the fitted rate constants as the probability of the empty pore (state 8) under the given conditions. For the KcsA channel, the L_p value is available (Saparov and Pohl, 2004), and the L_p value represents the selectivity filter. However, an extremely high L_p value, overwhelming the rest of the pore, does not satisfy the requirement of Equation 1, in which a rate-limiting L_p value is required. To approximate a realistic contribution of the entryway, we adopted the L_p values for the gramicidin channels, which exhibit single-file permeation (Levitt, 1984). Given the osmotic water permeability P_f value of 6.0 × 10⁻¹⁴ cm³/s for L₀ [L_p = (v_w/RT) P_f] (Dani and Levitt, 1981), and the probability of the empty channels (2.5 × 10⁻⁵ for 200 mm K⁺ and 0.044 for 3 mm K⁺), the coupling ratio in the wide pore was estimated to be 6.1 × 10⁻⁶ at 200 mm K⁺ and 0.01 at 3 mm K⁺. As far as the rate-limiting L_p value for the KcsA channel is on a similar order of magnitude as the gramicidin channel, the contribution of the wide pore region to the CR_w-i value is negligible.

The permeation-related parameters are estimated from the fitted rate constants. At the K⁺ concentration of 3 mm, the occupancy probability of K⁺ ions in the selectivity filter in the steady state was 0.44, 0.24, 0.24, and 0.44, respectively, at the S1, S2, S3, and S4 sites (Figs. 1A, 5C). On the other hand, the relative ion occupancy deduced from the area of the electron density in the crystal data differed significantly from those of the predicted values as the K⁺ concentration decreased. In particular, the occupancy probability of the S2 site is almost zero in the crystal structure. It has been reportedly established that the filter structure is collapsed at the S2 site in low K⁺ condition (Zhou et al., 2001). The ion distribution in the nonconductive conformation is irrelevant to an understanding of the permeation mechanism. In contrast, the values reported here reflect the ion occupancy undergoing permeation through the open-filter structure.

Visualization of the permeation process

From the cycle flux, the relative contributions of the current carried by the cycles were calculated as a function of the K⁺ concentration (Fig. 5D). In Figure 6A, the net flux is visualized as random transitions among the cyclic paths, and the relative contribution of each cycle flux is represented as the height of the cyclic paths raised from the footprint. At 200 mm K⁺, cycle A (the dark blue diamond) contributed predominantly to the net flux. In the concentration mid-range, cycle F (the red triangle) passing through state 5 (the double occupancy state at both ends) (Fig. 1B) overwhelmed cycle A, and cycles H (the light blue triangle) and I (green triangle) contribute significantly. Below 3 mm, not only cycle F, but other cycles (cycle K; the blue escutcheon) as well, significantly contribute to the net current.

Figure 6.

The visualized permeation processes. A, The relative contributions of the cycles at different K⁺ concentrations. The eight state diagram is shown as the footprint, above which the cyclic paths predominantly used in the permeation are demonstrated (the dark blue diamond for cycle A, the red triangle for cycle F, the light blue triangle for cycle H, the green triangle for cycle I, and the blue escutcheon for cycle K). The relative contributions of cycles are expressed as the level of height raised from the footprint. Cycles contributing to the net flux <0.01 are not shown. At 200 mm, the relative contribution of cycle A was 0.83, and that of cycle F was 0.15; at 20 mm, that of cycle A was 0.29, cycle F was 0.42, cycle G was 0.03, and cycles H and I were 0.11; and at 3 mm, that of cycle A was 0.04, cycle F was 0.34, cycle G was 0.09, cycles H and I were 0.18, cycle K was 0.13, and cycle L was 0.03. B, Predicted relative contributions of cycles at different membrane potentials in an asymmetric condition of 4 mm K_out and 150 mm K_in. At 0 mV, the relative contribution of cycle A was 0.62, cycle F was 0.22, cycle H was 0.01, cycle I was 0.11, and cycle L was 0.02; at −100 mV, that of cycle A was 0.34, cycle F was 0.38, cycle G was 0.02, cycle H was 0.03, cycle I was 0.22, and cycle L was 0.02.

Using the optimized set of the rate constants, we predicted the permeation features at physiologically relevant asymmetric ion concentrations, such as a 4 mm extracellular K⁺ concentration and 150 mm intracellular concentration (Figs. 5E–G, 6B). We obtained two important results. At 0 mV, the contribution of the cycles in the asymmetric condition (Fig. 6B) is similar to that at the symmetrical 200 mm K (Fig. 6A). At first, this result seemed counterintuitive, since the high K⁺ solution on one side exclusively governs the distribution. As the membrane potential became negative, the CR_w-i values increased significantly and the contribution of cycles F and I predominated (Fig. 5E, 6B). Near the resting membrane potentials, cycle A is no longer the predominant cycle. This behavior in an asymmetric condition has not been attained experimentally, since most of the measurements, including the V_stream, are performed under symmetrical conditions.

Discussion

In this study, we measured V_stream values as small as 0.5 mV. This value is the smallest reported since the first reports for the V_stream of the gramicidin channel in 1978 (Levitt et al., 1978; Rosenberg and Finkelstein, 1978). Before discussing the underlying permeation mechanism in our results, we will start by examining the experimental accuracy of the CR_w-i values and the validity of the permeation model.

Detecting such small changes in the V_stream value may be attributed to the setting of the most appropriate reference points, in contrast with the earlier methods in which various independent factors were collected to reach the results. For example, in our measurements the liquid junction potential arises between the different osmolality solutions from the double-barrel tube. By placing the reference electrode close to the patch electrode, this junction potential need not be a concern. Furthermore, the slowly developing concentration polarization, which contributes substantially to the steady-state V_stream measurements, was rendered irrelevant by measuring the voltage change immediately upon exposure to the osmotic gradient using the rapid osmotic jump method. The overall accuracy of the CR_w-i value was ∼0.1 (Fig. 4).

To interpret the CR_w-i value, the possible contribution of the intracellular entryway was considered, in which water flux carries the ions outside of the single-file region, and this generates water-ion coupling. We estimated the CR_w-i value of the wide pore region using the Levitt theory. The relevant L_p value for the empty pore (L₀) was taken from that of the gramicidin channel, which possesses a similar geometry of the single-file pore. Using the probability of the empty pore (f₀) at different K⁺ concentrations, the estimation revealed that the CR_w-i value for the wide pore is negligible in the KcsA channel.

The eight state permeation model is based on the ion distribution in the crystal structure of the KcsA channel (Fig. 1A,B). The eight states encompass all of the possible configurations of the ion distribution in the four binding sites of the selectivity filter provided that a positioning of the ions in adjacent sites is not allowed. During the permeation process, the ion and water molecules in the flow take one of the occupying states, and the transitions among the states generate the cyclic paths on the diagram, giving the cycle flux of a defined ratio of ion and water molecules in the flow (Fig. 1C,D). Thus, once the rate constants are given, CR_w-i as well as the ionic current and the ion occupancy probability are calculated.

Recently, computer simulations have suggested other arrays of ions and water molecules in the selectivity filter (Khalili-Araghi et al., 2006; Furini and Domene, 2009; Jensen et al., 2010; Nelson, 2011). Two issues were raised: may ions be located adjacently, and whether there are five sites rather than four sites in the selectivity filter. There is no experimental evidence for or against the competing proposals. The V_stream data potentially will provide clues to the answers to such questions. For example, the CR_w-i value at the higher level of the K⁺ concentration indicates the maximum number of ions loaded in the single-file region of the selectivity filter. These experiments are, however, outside the scope of the present investigation, and we reserve such experiments for future study and here use the canonical eight state model.

For the K⁺ permeation, we assumed a symmetrical energy profile, which is reflective of the nearly symmetrical distributions of K⁺ in the four binding sites of the selectivity filter (Zhou and MacKinnon, 2003) (see Materials and Methods). On the other hand, we obtained the CR_w-i value of 2.0 for Rb⁺, for which an asymmetric profile needs to be taken into account. Morais-Cabral et al. (2001) suggested that state 2 was destabilized based on the asymmetrical Rb⁺ distribution in the selectivity filter (Lockless et al., 2007). By integrating the CR_w-i value and the asymmetric distribution, our interpretation is that the destabilization of state 2 attenuates the cycle flux of cycle A, and the lower cycles, such as cycle F, are replaced, resulting in the higher CR_w-i values. The low occupancy probability of the S2 site suggests that state 3 (Fig. 1B) is also destabilized. These arguments are qualitative and introduce asymmetry (Treptow and Tarek, 2006) into the potential profile will be taken up in future investigation.

To attain a realistic picture of the ion permeation through the selectivity filter, we assume the view point of Maxwell's demon once again, situated at the outer pore taking note of the entering and exiting traffic of both the ion and water molecules. An example of the observed sequence is shown in Figure 1D. In a queue of ion and water molecules, the demon partitions the molecules into stretches of arrays and assigns them to a series of the cyclic paths. Accordingly, a long queue is transformed into a sequence of cycles. Random transitions among the states are integrated into cyclic paths, each of which has its own completion rate (cycle flux) and the stoichiometric number (n_i or n_w), so the permeation process can be regarded as random transition among the cycles. The sum of these contributed cycles constitutes a macroscopic observable, such as the current amplitude or the CR_w-i value (Eqs. 5, 6) (Oiki et al., 2011). Thus, the relative contribution of the cyclic paths in a given ionic condition and membrane potential affords an intuitive picture of permeation (Fig. 6). Using this method of coupling the electrophysiological experiments and the theoretical analysis, we obtained the viewpoint of the demon (i.e., counting ion and water molecules in a streaming queue through the open-filter structure).

Over the last several decades, a variety of experimental and theoretical studies have been performed on ion permeation (Hille and Schwarz, 1978; Läuger, 1980; Bernèche and Roux, 2001; Morais-Cabral et al., 2001; Thompson et al., 2009; Jensen et al., 2010). Among these studies, the “knock-on” mechanism still dominates as an explanatory account of the permeation processes (Bernèche and Roux, 2001; Jensen et al., 2010). One may define the knock-on mechanism as an electrostatic repulsion taking place among the ions permeating in and out of the pore in a manner that drives ion flux efficiently (Hille, 2001). The presence of multiple ions in the pore is a prerequisite for the knock-on mechanism. Cycle A (Fig. 1B) is the process that is most obviously accounted for by the knock-on mechanism. However, our results indicated that cycle A in fact occurs under limited conditions. As the K⁺ concentration was decreased, cycles not passing through the doubly occupied states increased significantly. Cycle K, for example, is comprised of a purely one-ion permeation mode in which there is no means available to affect the knock-on mechanism. Moreover, at an asymmetric concentration similar to physiological conditions, the lower cyclic paths that do not employ knock-on transitions (e.g., state 4 → 3 and state 7 → 4) become predominant. It is thus concluded that expressing these permeation processes as cyclic paths and fluxes is a practical method that provides a dynamic picture of permeation.

The interpretation put forward in this article is ultimately simple and straightforward. (1) The investigation of a dynamic process such as ion permeation requires the use of dynamic methods. Measuring the currents while carrying out the V_stream evaluation guarantees that the channel is in the open conformation. Based on the principle of the streaming potential, nonconductive states do not contribute to the determined value. (2) Not only ions, but also water molecules must be taken into account in elucidating the permeation mechanism. The macroscopic CR_w-i value provides the information on how the ion and water molecules are specifically queued in the selectivity filter. Thus, measuring the CR_w-i value corresponds to counting the individual movements of the ion and water molecules through the single-file pore. (3) A mesoscopic view using the cycle flux provides a more intuitive picture of the actual permeation process (Oiki et al., 2010). Generally, ion permeation through the channel is characterized by various levels of spatial and temporal events in the hierarchy of permeation processes (Dror et al., 2010; Oiki et al., 2010). On the one hand, the fine trajectories of ion and water movements in and around the pore have been examined extensively using computational methods (Bernèche and Roux, 2001; Jensen et al., 2010). On the other hand, the single-channel current data indicate the average number of transferred ions (LeMasurier et al., 2001). The approach used here carves out an important niche in the study of the permeation mechanism on a scale lying between the macroscopic current measurements and the elementary steps of ion transfer. The experimental observables were decomposed into linear combinations of cycle fluxes. The permeation was then visualized in the form of random transitions between and among the cycles, each of which exhibits a distinct pattern of ion and water interplay.

A conceptual framework is presented here along with methods for envisioning how the ion and water molecules form a single-file queue during the process of permeation. This method is promising for extension of the examination of the mechanism of ion selectivity, another fundamental issue in the field of neuroscience.