Single Synapse Information Coding in Intraburst Spike Patterns of Central Pattern Generator Motor Neurons

Abstract

Burst firing is ubiquitous in nervous systems and has been intensively studied in central pattern generators (CPGs). Previous works have described subtle intraburst spike patterns (IBSPs) that, despite being traditionally neglected for their lack of relation to CPG motor function, were shown to be cell-type specific and sensitive to CPG connectivity. Here we address this matter by investigating how a bursting motor neuron expresses information about other neurons in the network. We performed experiments on the crustacean stomatogastric pyloric CPG, both in control conditions and interacting in real-time with computer model neurons. The sensitivity of postsynaptic to presynaptic IBSPs was inferred by computing their average mutual information along each neuron burst. We found that details of input patterns are nonlinearly and inhomogeneously coded through a single synapse into the fine IBSPs structure of the postsynaptic neuron following burst. In this way, motor neurons are able to use different time scales to convey two types of information simultaneously: muscle contraction (related to bursting rhythm) and the behavior of other CPG neurons (at a much shorter timescale by using IBSPs as information carriers). Moreover, the analysis revealed that the coding mechanism described takes part in a previously unsuspected information pathway from a CPG motor neuron to a nerve that projects to sensory brain areas, thus providing evidence of the general physiological role of information coding through IBSPs in the regulation of neuronal firing patterns in remote circuits by the CNS.

Introduction

Burst coding is a phenomenon far from being completely understood, and is just a part of a central issue in neuroscience related to the understanding of the neural code in a broad sense. Burst firing is an important excitability property related to motor control in central pattern generators (CPGs) (Brocard et al., 2010; Selverston, 2010), to sensory information processing in visual and auditory centers (Reinagel et al., 1999; Eyherabide et al., 2008; Sabourin and Pollack, 2009), and is known to enhance signal detection in thalamocortical circuits (Steriade et al., 1993; Sherman, 2001).

Many studies have brought burst coding (Eyherabide and Samengo, 2010) to increased attention, especially for one of its most prominent features: bursting is an effective way for a system to code different types of information using (at least) two distinct timescales, one related to the bursting period and another to the intraburst spiking timescale (Kayser et al., 2009; Panzeri et al., 2010).

CPGs, such as those found in the crustacean stomatogastric nervous system (STNS), have been traditionally used to analyze how complex dynamics emerge in small circuits (Marder and Bucher, 2007). Bursting activity of pyloric CPG motor neurons of the stomatogastric ganglion (STG) is clearly associated with muscle contraction that is insensitive to small changes in intraburst spike timing (Morris and Hooper, 1997). Despite not expressing obvious motor information, intraburst spike patterns (IBSPs) presented by CPG neurons are characteristic of each neuron and change according to network connectivity (Szücs et al., 2003). Thus, in addition to motor information expressed in bursting, CPG neurons also have potential to express other kinds of information through IBSPs (Latorre et al., 2006). We investigated this matter by analyzing experimental data through an information theoretical tool that we developed specifically to compute information expressed within IBSPs.

We performed experiments on a pair of neurons of the blue crab STG pyloric CPG: the pyloric dilator (PD) neuron, which belongs to the pacemaker group, and the lateral pyloric (LP) neuron. These neurons are coupled with mutual inhibition and operate in antiphase (Selverston et al., 1976). Since the pacemaker receives the strongest feedback from the circuit through the inhibitory synapse from LP to PD, we choose to address the information flow in that direction. We found that the PD neuron is able to dynamically express information received from the previous LP burst. This is not only observed in the intact network, but also when PD is coupled to an artificial neuron that mimics LP activity.

Moreover, the information expressed in the IBSPs is inhomogeneous along the burst, revealing the ability of a single motor neuron to nonlinearly encode information through a single synapse. We also found that the informational content of IBSPs of the LP neuron not only affects PD dynamics, but also appears in the activity of the inferior ventricular nerve (ivn), a nerve that connects the STNS to the brain and has been shown to project into sensory areas of the brain in other crustacean species (Böhm et al., 2001). Our findings suggest that this nonlinear coding capability through spike patterns (Tiesinga et al., 2008) of motor neurons could be useful to higher levels of motor control mechanisms.

Materials and Methods

Animals.

We experimented mostly on adult blue crabs (Callinectes sapidus) of either sex from the southern coast of São Paulo state. A few experiments were done with California spiny lobsters (Panulirus interruptus), also of either sex, at the Institute for Nonlinear Science—University of California San Diego. All procedures followed the ethical principles suggested by the Society for Neuroscience and were approved by the Committee on Ethics in Animal Experimentation of the Federal University of São Carlos.

Preparations.

Dissection and preparation procedures were similar to those traditionally used in spiny lobsters or crab STNS preparations (Selverston et al., 1976). The STNS was removed from the crab stomach and pinned in a silicone elastomer-lined (Sylgard 184; Dow Corning) dish, filled with crustacean normal saline (in mm: 479 NaCl, 13 KCl, 14 CaCl2, 6 MgSO₄ 4 Na2SO4, 5 HEPES, and 5 TES; pH 7.4).

In addition to the STG, we removed the commissural ganglia (CoGs) and the oesophageal ganglia (OG), their connecting and motor nerves, and the ivn nerve, cutting it as close to the brain as possible (Fig. 1A). During all experiments, preparations were superfused with saline and maintained either at 23 ± 1°C (crabs) or 16 ± 1°C (lobsters).

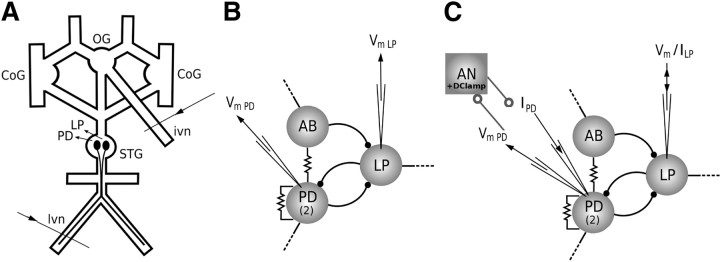
Figure 1.

Experimental procedures. A, Representation of the whole stomatogastric nervous system in the Petri dish: the two commissural ganglia (CoGs) and the OG are kept in the preparation to provide neuromodulation to the STG. In a set of experiments, extracellular signals are recorded from the lvn, which contains LP spikes, and from the ivn, which connects the STNS to the brain. B, Simplified scheme of the intact pyloric CPG. The pacemaker group is composed of two PD motor neurons that are connected to the anterior burster interneuron (AB) and to each other through electrical synapses. The LP neuron receives inhibitory synapses from the pacemaker group neurons and is the only presynaptic motor neuron to the pacemaker group. C, An inhibitory current I_LP is used to hyperpolarize LP while PD is connected to the AN, which mimics ISI variability, number of spikes per burst, and burst duration of the original LP. AN and PD real-time interaction is provided by a dynamic clamp protocol that injects IPSCs from the AN into PD according to a model of synaptic chemical inhibition. One PD neuron is impaled with two electrodes: one to record the membrane potential and the other to inject the artificial IPSCs.

Electrophysiology.

Extracellular signals were recorded from the lateral ventral motor nerve (lvn) and the ivn with stainless steel electrodes. Nerve signals were amplified by an A-M 1700 differential AC amplifier (A-M Systems).

Neurons were impaled with sharp glass microelectrodes (filled with 3 m K-acetate + 0.1 m KCl; resistance ∼30 MΩ) and intracellular signals were amplified using Neuroprobe 1600 amplifiers (A-M Systems).

Intracellular and extracellular signals were digitized at a 10 kHz sample rate by a Digidata 1322 ADC interface (Molecular Devices) using a dedicated acquisition software (Axoscope9; Molecular Devices). Neurons were identified by their characteristic bursting phase and by comparing their intracellular spike timings to the impulses recorded from their respective motor nerves.

A simplified version of the pyloric CPG consists of the pacemaker group, composed of the anterior burster interneuron (the only neuron in the pyloric CPG known to project to the anterior ganglia), two PD neurons, and the LP neuron, the only motor neuron from which PD receives presynaptic inputs (Fig. 1B).

Hybrid circuit experiments.

We used the dynamic clamp method to simulate an inhibitory synaptic connection between a computer model artificial neuron (AN) and the PD neuron (Fig. 1C). A Digidata 1200B data acquisition interface (Molecular Devices) was used to implement a protocol based on previous homemade implementations of the dynamic clamp (Pinto et al., 2001; Nowotny et al., 2006). In the original dynamic clamp protocol, a computer simulates synapses between neurons by monitoring their membrane potentials and generating the currents to be injected. The currents are calculated from equations modeling the voltage- and time-dependent synaptic conductances. We modified the protocol to simultaneously compute the membrane potential of AN from a mathematical model and simulate a synapse from AN to a biological neuron. Such a modification allowed the delivery of inhibitory currents to the PD neuron according to the behavior of a presynaptic AN membrane potential computed in real time.

Our AN neuron was either a real-time implementation of a whole-cell stochastic model of LP (stochastic AN) or simply a sequence of random spikes (random AN). Both were set to resemble the original LP mean behavior and its variability, as detailed below.

The stochastic AN is based on a stochastic LP model that was previously developed to reproduce the irregular behavior of biological LP neurons, which is absent in the Hodgkin–Huxley deterministic model (Carelli et al., 2005). Due to its stochastic nature, the model naturally presented spike timing variability from burst to burst. In our implementation of the stochastic LP model in the dynamic clamp, we were able to tune the stochastic AN to mimic the original LP variability in each preparation by changing the values of the following maximum conductances (G_i, range in mS/cm² in parenthesis): slow calcium (3.0 < G_Ca_s < 4.0), transient calcium (0.9 < G_Ca_t < 1.1), and calcium-dependent potassium (3.5 < G_K_[Ca] < 4.5). The tuning of these parameters was done by visual comparison between the membrane potential traces of the original LP and of the stochastic AN. All other parameters were kept the same as described in the original reference (Carelli et al., 2005). The dynamic clamp synapse from PD to the stochastic AN was set to shutdown AN when PD starts a burst. A typical value of this conductance was G_syn_PD→AN = 200 mS.

The random AN burst sequences were obtained from statistics during 5–10 min on the original PD/LP bursting behavior at each preparation regarding time of first and last spikes of LP after PD hyperpolarization (LP_start/LP_end), maximum and minimum number of spikes in a LP burst (max_spk/min_spk), and minimum interspike interval of LP (min_ISI). Values of these parameters varied widely among different preparations according to the pyloric rhythm natural variability. An example of a set is max_spk = 6, min_spk = 4, min_ISI = 15 ms, LP_start = 50 ms, LP_end = 400 ms. Next, we generated a long sequence of bursts in which, for each burst, we chose from flat random distributions, as follows: n_spk, the number of spikes of that burst (min_spk ≤ n_spk ≤ max_spk); the time of the first spike, t₁, in the range [LP_start, LP_start+ (LP_end − LP_start)/n_spk]; and the random sequence of spikes, with each t_i randomly chosen in the range [t_i + min_ISI, t_i + min_ISI + (LP_end − t_i − min_ISI)/(N_spk − i)], where 1 ≤ i ≤ (n_spk − 1). This sequence of random bursts was stored in a file to be used by the dynamic clamp to implement the random AN in real time. During the experiments with the random AN, the dynamic clamp detected each PD hyperpolarization and generated the artificial membrane potential according to the previously stored sequence of random bursts.

The synaptic strength from AN to the PD was adjusted in the dynamic clamp until inhibitory postsynaptic potentials, with amplitude similar to those produced by the activity of the original LP, were found in the PD trace [typical values of conductance used were in the range (50 mS ≤ G_syn_AN→PD ≤ 200 mS)]. Values of AN spikes per burst ranged from 4 ± 1 to 8.0 ± 0.8 in different experiments, corresponding to 10–25% of variation from burst to burst.

The experiments consisted of impaling the LP neuron with a single electrode and one PD neuron with two electrodes, one for current injection and the other for membrane potential recording. We simultaneously recorded PD and biological LP neurons with no artificial stimulation for ∼30 min. After that, we hyperpolarized the biological LP with a current of ∼−10 nA, and then connected the AN to the PD neuron by the artificial dynamic-clamp synapse, recording both PD and AN membrane potential as well as the current delivered to PD for ∼30 min.

LP and ivn recordings.

In the last set of experiments, we recorded long time series (∼30 min to 2 h) of lvn and ivn extracellular signals (Fig. 1A). LP spikes could be easily identified in the lvn trace because of their large amplitude and characteristic phase. The length of the ivn nerve is typically ∼8 mm (from the OG to the brain in blue crabs) and the extracellular electrode recording ivn activity was positioned ∼4 mm far from the OG.

Analysis method.

Studying the information conveyed by spike trains requires the identification of patterns that are usually defined before the analysis in terms of burst occurrences or certain spike/ISI sequences that can be associated with some specific stimulus features (Butts et al., 2007; Tiesinga et al., 2008; Eyherabide and Samengo, 2010; Kumar et al., 2010; Kreuz et al., 2011).

When dealing with sensory systems, an experimenter can readily infer what stimulus features are important (i.e., certain odor or sound frequency) and, based on previous knowledge of what is being coded, identify interesting patterns in the response spike train. However, studying information flow between two bursting neurons requires a different approach. In this case, both stimulus and response signals are sequences of spikes occurring in each neurons burst, so there is no simple criterion to determine which stimulus characteristics are important to be coded by the response neuron. Since we cannot adopt a relevance criterion, we use entropy to estimate which stimulus features are most informative.

We developed a method to extract all ISI patterns that occurred in a large number of sequential pairs of stimulus and response bursts. Then we computed the average mutual information to estimate how much the response IBSPs express information about stimulus IBSPs. This way we infer information flow between neurons while making the least number of assumptions about the code itself.

Information theory.

Information theory presents powerful concepts that can be applied to the study of neural coding (Shannon, 1948; Borst and Theunissen, 1999). If a specific event, x, occurs with probability p(x), the informational content of x (in bits) is defined as

For a series of discrete events, x, belonging to a set X = (x₁, x₂, …, x_n), the entropy of X, related to the degree of variability of the set, is defined as

A neuron is able to express information about stimuli if the variability of its response is somehow correlated to stimuli changes. The mutual information i between a stimulus s belonging to a set S and a response r belonging to a set R is defined as

where p(s,r) is the joint probability of finding the stimulus s and the response r. The average mutual information (AMI) is a measure of the mutual information of all possible pairs of (stimulus, response) defined by S and R:

Algorithm.

The two simultaneously recorded membrane potential time series of the stimulus (LP) and response (PD) neurons were treated using a simple algorithm that detects spikes (using derivative and amplitude threshold), providing a spike timing time series for each neuron. Burst occurrences were identified as any spike sequence between two large ISIs (≥0.2 s). Only stationary series with respect to the mean and standard deviations of number of spikes per burst, period, and burst duration of each neuron were considered for further analysis. After finding all bursts, pairs of stimulus (LP) and response (PD) bursts were collected by imposing that the LP burst must precede the PD burst. This constraint guaranteed a causality relation, allowing us to claim that information flows from the stimulus to the response neuron, despite the symmetry (S − R) of AMI measure.

Since the bursting period has some intrinsic variability, it is necessary to choose a time reference for each pair of stimulus and response bursts. We set the first PD spike as time reference (Fig. 2A). The same choice is often used in other techniques applied to pyloric neurons time series analysis (Ayers and Selverston, 1984; Canavier and Achuthan, 2010). The PD neuron is part of the pacemaker group, which strongly inhibits all other motor neurons, dictating the pyloric rhythm. Thus, the PD burst onset is important to determine when LP is allowed to fire. One consequence of this choice is that burst-to-burst natural fluctuations of the interval between the onsets of LP and PD will be reflected in the LP firing patterns extracted during the analysis. However, this choice is neither obvious nor unique, and all choices have different consequences. Other choices of the time reference can be used to explore complementary properties of information coding in the system. For example, they can be used to investigate how the interval between the onsets of LP and PD influences the results. Other parameters such as the start (s_LP) and end (e_LP) of LP burst and the end of PD burst (e_PD), are obtained from statistics over the whole series.

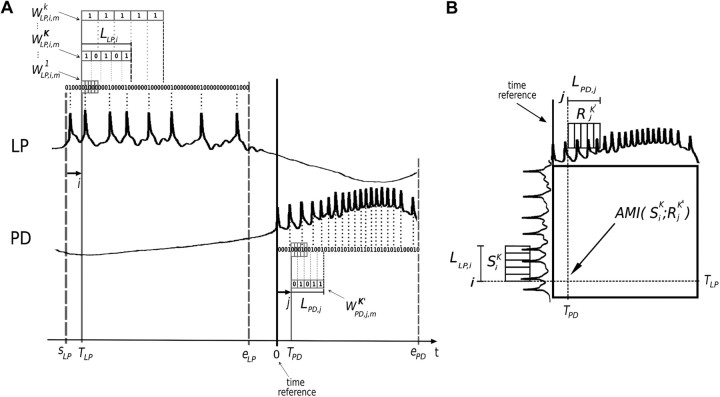
Figure 2.

Entropy maximization and AMI representation. A, Illustration of the mth pair of stimulus (LP) burst followed by the response (PD) burst. Time series are resampled into two binary strings in which a bit is set to one or zero according to spike occurrence, depicted above LP or below PD neuron trace, respectively. The time reference (thick vertical line) is set at the first spike of the PD burst for each pair of bursts. The start and end of LP (s_LP and e_LP, respectively) and the end of PD (e_PD) bursts are chosen according to statistics over the whole time series. Five bits words are formed beginning at the string bit pointed by i or j. The first stimulus word W¹_LP,i,m is composed of the sequence of five bits starting at the i pointer position. The resampling parameter k is used to select words of larger bins (W¹_LP,i,m, W²_LP,i,m, … , W^K_LP,i,m,… ); this way, the words represent a larger portion of the burst. Note that for very small k, the words have almost all bits equal to zero and for very large k, the words have almost all bits equal to one, producing small entropy values. k = K provides the stimulus set S_i^K = (W^K_LP,i,1, W^K_LP,i,2, … , W^K_LP,i,m, .., W^K_LP,i,N) that maximizes entropy. L_LP,i (L_PD,j) is the word duration associated with the stimulus (response) set. It measures the portion of the burst that S_i^K (or R_i^K′) represents and can vary along the burst. B, Schematic representation of AMI graphs: AMI(S_i^K, R_j^K') is computed for all possible pairs of pointers (i, j) according to the procedure described in A.

A string of zeros is associated with each burst of stimulus/response (each bit of the string has a time bin b₀=Δt, where Δt = 0.1 ms is the resolution of the data acquisition). When a spike is detected in a burst, the corresponding bit of the string is set to 1. Two pointers i and j are used to represent the displacement along the duration of the bursts, corresponding to the ith and jth bit of the stimulus and response strings, respectively.

For a pair of pointers (i, j), two sets of n bits words are extracted: a stimulus set S_i¹ = (W¹_LP,i,1, W¹_LP,i,2, … , W¹_LP,i,N) and a response set R_j¹ = (W¹_PD,j,1, W¹_PD,j,2, … , W¹_PD,j,N) (Fig. 2A), where N is the total number of bursts in the time series. The word W¹_LP,i,1 corresponds to the sequence of n bits starting at the ith bit of the LP string of the first pair of bursts. Analogously, the following word, W¹_LP,i,2, is an n bits word starting at the ith bit of the LP string of the second pair of bursts, and so on. The same logic applies to words of the response set.

The stimulus entropy H(S_i¹) is computed based on the probability of occurrence of every possible word in the set S_i¹. The same is done to compute the response entropy H(R_j¹) for the pointer j.

The following steps consisted in repeating the procedure of word extraction to calculate entropies for words with larger bins (Fig. 2A). This is achieved by using a resampling parameter k, so that the new bin is b = kΔt. The word W^k_LP,i,m is also an n bits word starting at the pointer i of the LP mth burst string, except that each bit is set to 1 if a spike occurs within the new bins. This procedure produces stimulus sets S_i^k = (W^k_LP,i,1, W^k_LP,i,2, … , W^k_LP,i,N) as function of k. Analogously, for a certain j pointer of the response strings, we computed a response set R_j^k = (W^k_PD,j,1, W^k_PD,j,2, … , W^k_PD,j,N) for every possible k value. From the probabilities of each word in the sets S_i^k and R_j^k′, we compute stimulus H(S_i^k) and response H(R_j^k') entropies.

The sets used to calculate AMI were chosen by looking for the value of k (k′) that correspond to the set S_i^k(R_j^k′) with the maximum value of entropy H(S_i^k)[H(R_j^k′)]. Considering K and K′, the values of k and k′ that respectively maximize the entropy of S_i^k and R_j^k′, we compute AMI(S_i^K, R_j^K') based on the joint probabilities of occurrence of all possible pairs of words (W^K_LP,i,m, W^K′_PD,j,m). AMI was calculated for all possible pointer values (i, j), leading to a matrix of AMI values (Fig. 2B).

In the analysis of LP/ivn time series, a slightly modified protocol had to be used, since the ivn nerve does not present burst activity. First, all LP and ivn spikes were detected and LP bursts separated. Each pair of stimulus and response consisted in one LP burst and the ivn spikes within the interval of [−2:2] s with respect to the first spike of each LP burst.

Then we calculated entropies and AMI values following the same steps previously described. In the AMI matrix obtained for LP/ivn, those regions with positive ivn time index correspond to information flow from LP to ivn and those with negative ivn time index correspond to information flow from ivn to LP.

Analysis.

To ease the interpretation of our results, instead of bin size we used the word duration L_LP,i = n.K.Δt, which is associated with the pointer i of the LP string for which K maximizes the entropy. In the graphs, we used l, which is L normalized by the burst duration. Also, instead of dealing with pointers, we used an equivalent but more intuitive timescale: t_LP is proportional to i and t_PD is proportional to j. In the results section, t will be referred to as “time index.”

All analyses were made with fixed n = 5, chosen by using a criterion of information gain over time. For each neuron and for n ranging from 2 to 12 bits, we calculated H_i(n)/L_i(n) along the burst. Typically, the values of n maximizing information gain over time for any index were <5 bits, so n = 5 seemed to be the best choice (data not shown).

Since data were acquired at 10 kHz, the maximum resolution is 0.1 ms. The analysis starts at the beginning of the burst (i = 1), with k = 1 (b₀ = 0.1 ms). Because this bin is too small, these words will be mostly populated by zeros and will form a set with low entropy. The value of k is increased unit by unit until it reaches a maximum value (typically >500) that corresponds to a word duration equal to the burst duration. In this case, the bin is too large, resulting in a set of low entropy because the words will be mostly populated by ones. The values of K, which maximize the entropy of a neuron in a given position of the burst, are strongly dependent on the bursting frequency and average spike number/burst in that specific preparation. In addition to the great variations of the values obtained for K (50–200), they typically correspond to word lengths of ∼20–30% of the total burst duration.

In addition to computing entropies and mutual information, we applied the method of surrogates (Theiler et al., 1992) based on randomly scrambling all stimuli of the stimulus/response bursts pairs to break the causal relation within pairs. The AMI of the surrogate set AMI_sur(S_i^K, R_j^K') is computed using joint probabilities of occurrence of all possible pairs of words (W^K_LP,i,R, W^K′_PD,j,m), where R is an index of the scrambled order of burst occurrences. Therefore, AMI_sur results must be due to statistical properties of IBSPs across the whole time series, disregarding causality.

To determine whether the results were statistically significant, we computed significance as sig = (AMI_rel − <AMI_surr>)/σ_surr, where <AMI_surr> is the mean and σ_surr is the standard deviation of AMI_surr results calculated for 20 surrogate datasets. All results reported in this manuscript were considered statistically significant if sig >7.

Instead of just computing AMI, we normalized it by the entropy of the response, which we called relative mutual information AMI_rel = AMI/H(R). It represents how much of the response neuron coding capability is dedicated to encode information about the stimulus.

Analysis programs were developed using C++ language and ran in free open source Ubuntu Linux 9.04 (Canonical) based AMD64 3200 MHz PCs or similar.

Results

In intracellular experiments made with the intact STG (Fig. 1A,B), we identified and impaled PD and LP neurons with microelectrodes and recorded long stationary time series of their antiphasic activity (Fig. 3A) for further analysis. Recording times varied from 30 min to 2 h, containing 1200–6000 pairs of bursts depending on pyloric rhythm. In a second set of experiments, we interfaced the PD neuron to a computer model neuron in real time while the real LP was maintained hyperpolarized (Fig. 1C). Finally, we performed experiments recording the extracellular activity at the lvn and at the ivn that connects the OG to the brain (Fig. 1A).

Figure 3.

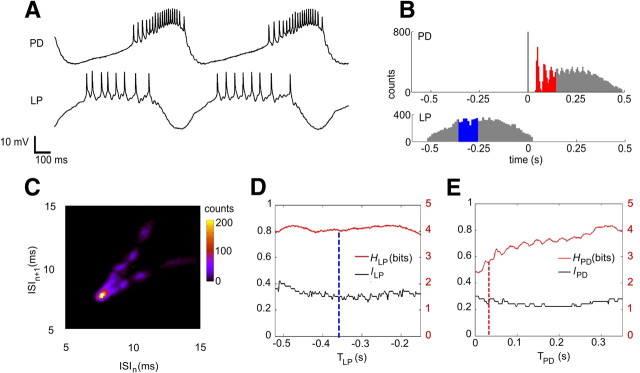
Time series, spike distributions, ISI signature, and entropies. A, Sample of LP and PD neurons time series presenting a typical antiphasic periodic bursting behavior. Spike rate of PD neuron is not uniform along the PD burst: from the beginning to the middle of the burst ISIs get progressively smaller and from the middle to the end of the burst, ISIs get progressively larger. B, Spike distributions of PD and LP using the first spike of each PD burst as time reference. The first spikes of PD occur in a well defined sequence that becomes less reliable along the burst. The distribution portion corresponding to the set of words of maximum local entropy for T_PD = 0.03 s is shown in red. Because of the time reference chosen, the distribution of LP spikes is much less precise. The distribution portion corresponding to the set of words of maximum local entropy for T_LP = −0.36 s is shown in blue. C, Intraburst ISI first return map showing clusters organized in a V-shape signature, characteristic of the PD. The clusters apparently present no inner structured pattern. D, Entropy H_LP (in bits, right y-axis) and l_LP (dimensionless, left y-axis); word duration is normalized by the LP burst duration. The blue dashed line is an example where T_LP = −0.36 s corresponds to H_LP = 4.0 bits and the set of words that maximizes entropy has a word duration l_LP = 0.3 (30% of LP burst). E, Same as D but for PD bursts. The red dashed line indicates T_PD = 0.03 s that corresponds to H_PD = 2.8 bits and the set of words that maximized the entropy has a word duration l_PD = 0.22 (22% of the PD burst). H_LP is approximately four bits along all LP burst while H_PD increases from 2.5 to four bits along the PD burst. The entropies are smooth but not homogeneously distributed along the bursts. l is also smooth for each neuron but there is no simple relation between H and l.

PD neuron is sensitive to previous IBSPs of the presynaptic LP neuron

In this section, we show a detailed analysis of data obtained in a single typical experiment. First, we calculated the spike distribution for all pairs of the PD burst preceded by an LP burst using the first PD spike as time reference (Fig. 3B). The first few spikes of the PD neuron presented a pattern consisting of a sequence of ISIs occurring in a reproducible manner with well defined means and deviations. The latter portion of the distribution shows that spike times are progressively less precise along the burst. The LP spike distribution presents no clear pattern because the natural fluctuations of the beginning of LP burst with respect to the first spike of the next PD contribute with additional variability to LP spike timing.

The use of more sophisticated tools allows one to distinguish other firing structures in a neuron burst. Previous studies revealed interesting patterns that can be seen in subsequent intraburst ISIs return maps of CPG neurons in crayfish (Segundo et al., 1998), lobster (Szücs et al., 2003), and leech (Campos et al., 2007), but cannot be recognized just by looking at spike distributions.

Some of these return map patterns have been referred to as ISI signatures of the neurons (Szücs et al., 2003; Latorre et al., 2006; Campos et al., 2007) because they are very similar for the same neuron type among preparations and distinct for different neuron types. In our experiments, we found that a blue crab PD neuron ISI signature has a typical structure of clusters organized in a V shape (Fig. 3C), which is similar to the one found for the lobster PD neuron.

The V-shaped pattern of ISI first return maps could be seen as a consequence of a well known progressive increase followed by a decrease of spiking frequency along the PD burst (Fig. 3A). Thus, the first return maps reveal a pattern that can be visually identified in the PD neuron membrane potential trace. However, both branches of the V-shaped signature clearly present clusters, a feature of the ISI first return map that would not be identified by simple visual inspection of the intracellular trace. The clusters' positions in the signature are sensitive to changes in the circuit connectivity (Szücs et al., 2003, 2005) and each cluster seems to have no inner structure. The ISI first return map of the blue crab LP neuron (data not shown) also resembles the LP signature found in the lobster (Szücs et al., 2003). It consists of a single comet-shaped cluster formed by apparently noisy deceleration of ISIs.

If we looked into the apparently noisy clusters of each neuron signatures, would we find even more structured patterns and could they be somehow correlated? We developed an information theoretical analysis tool that allowed us to unveil such fine patterns along the burst and to infer information coding capacity of these neurons.

In information theory (Shannon, 1948; Borst and Theunissen, 1999), the entropy (H) is a measure of variability and determines the maximum amount of information in a system. In our case, H is a measure of IBSPs variability along the burst (Fig. 3D,E).

Starting at the same given position within all bursts, which defines our time index (T), we choose a word of duration L and divide it into five bins. We build a set of words by assigning a bit one or zero according to the occurrence of a spike within each bin and then calculate the entropy of the set. After computing the entropy for different values of L, we find L_max as the one that maximizes the entropy as a function of T (Fig. 2A), ensuring that IBSPs have the greatest variability. We chose L to be a variable rather than a constant, as is usual in informational analysis, to allow a possibly inhomogeneous coding of information along the burst duration.

Both neurons present high entropy values (H_LP, H_PD) along their bursts, close to the maximum possible value of five bits (Fig. 3D,E). Entropy is clearly inhomogeneous throughout the PD burst and there is also some entropy fluctuation along the LP neuron burst. The parameter l_LP (l_PD), which is L_max normalized by the burst duration, presents small variations that are independent of those found in H_LP(H_PD). This fact justifies allowing different values of L along the bursts.

From the values of T and L, it is possible to find which spikes contribute to entropy maximization. For instance, the word duration maximizing entropy for the time index T_PD = 0.03 s is L_max,PD = 0.11 s, and the corresponding normalized value is l_PD = 0.22 (Fig. 3E). The spikes that lie within the [0.03:0.14] s interval of the PD histogram (Fig. 3B), where the second, third, and fourth spikes can be visually discriminated, code up to H_PD = 2.8 bits of information in their IBSPs (Fig. 3E).

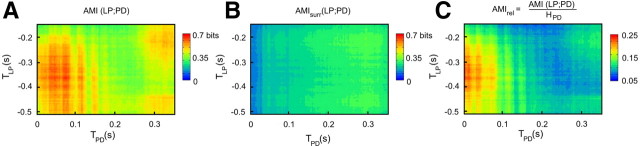
To infer how much PD and LP IBSPs variabilities are correlated along bursts, we computed their AMI and represented it in a 2D color map (Fig. 2B). In a typical experiment, AMI (Fig. 4A) is not uniform along PD and LP bursts, and its maximum value of 0.66 bits (Fig. 4A) corresponds to the first half of LP burst, starting at T_LP = −0.36 s (Fig. 3B, blue region), with the beginning of the PD burst at T_PD = 0.03 s (Fig. 3B, red region). The AMI peak represents a twofold increase with respect to the background values, in contrast to the entropies that do not present such abrupt behavior (Fig. 3D,E).

Figure 4.

Average mutual information. A, Matrix of local AMI values calculated for LP and PD in bits. T_LP and T_PD (in seconds) are the time indexes that vary along the neurons bursts. As the first spike of PD is used as time reference, T_PD is always positive and T_LP has negative values. There is a strong peak of 0.66 bits at (0.03, −0.36) s. B, AMI from LP to PD using surrogate sets where LP bursts order was scrambled. The surrogate matrix has a much lower amplitude, meaning that the peak observed in A is due to the causality relation between LP and PD: the PD neuron changes its IBSPs according to the input previously received from LP. C, AMI_rel = AMI/H_PD, which gives how much of the PD informational capacity is dedicated to encode LP stimuli.

AMI is symmetric with respect to stimulus and response (de Ruyter van Steveninck et al., 1997; Borst and Theunissen, 1999; MacKay, 2003). Therefore, it does not imply causality. To overcome this limitation, our method establishes a precedence relation of LP burst with respect to the following PD burst. Additionally, we calculate AMI for surrogate data (Theiler et al., 1992) where the order of LP bursts is scrambled, thus disrupting causality. AMI for the surrogate data (AMI_surr) (Fig. 4B) drops to only 10% of the original values. This means that the conspicuous AMI values of the original series are due to the causal relation (stimulus–response) between the LP IBSPs and the subsequent PD IBSPs. The AMI values are statistically significant (see Materials and Methods, above) at the peak and surrounding regions. By normalizing AMI to the response neuron entropy AMI_rel = AMI/H_PD, it is possible to infer how much PD is dedicated to code LP IBSPs. The peak of AMI_rel indicates that up to 25% of PD IBSPs can be predicted once LP IBSPs are known (Fig. 4C). Hence, AMI_rel takes into account fluctuations in response entropy, allowing direct comparison of AMI_rel results along PD burst. Clearly, the position of maximum values of the AMI_rel matrix indicates that information is mainly transmitted from the first half of the LP burst to the beginning of the PD burst.

The analysis of the information flow in the opposite direction, from a PD burst to the next LP burst (data not shown), produced statistically significant peaks in different regions of the AMI diagram, indicating that the sensitivity to presynaptic IBSPs is also a property of other bursting neurons and not only of the PD neuron.

Information flow from LP to PD is ubiquitous

It is widely known that pyloric neurons can present similar behavior in different preparations despite variations of their intrinsic excitability properties (Marder and Prinz, 2002; Goaillard et al., 2009). Is it possible for pyloric neurons of different animals to share a common information coding mechanism?

To address this question, we applied the same analysis to several LP/PD time series from experiments with Callinectes sapidus and Panulirus interruptus. We collected data from several crab preparations until having approximately a threefold natural variation of some important pyloric features, such as the pyloric period (from 0.44 ± 0.03 s to 1.3 ± 0.7 s) and number of spikes per burst of the LP neuron (from 4.4 ± 0.5 to 15 ± 3) and of the PD neuron (from 7.5 ± 0.5 to 20 ± 1). Despite such wide differences in pyloric general behavior, the results of AMI_rel were qualitatively very similar for different preparations.

Despite some differences in the overall conformation of AMI_rel hot spots along diagrams for different preparations, there are strong similarities in the position of AMI_rel peaks (Fig. 5). To observe the peak position more accurately, it is necessary to consider what portion of the burst corresponds to the maximum value of AMI_rel. The maximum values of AMI_rel can vary in each case, but for most preparations the position of the global peak is close to the beginning of both stimulus (LP) and response (PD) bursts. In Figure 5, above the AMI_rel graphs, the upper box represents the LP burst duration normalized to the pyloric period and the lower box represents the PD burst duration. The shaded regions in each pair of boxes represent the burst portions that correspond to the AMI_rel global peak. In this representation, it is clear that the peak of AMI_rel corresponds to the beginning (first few spikes) of LP and PD bursts in all six cases. From a total 16 time series from different crab (Fig. 5A-D) and lobster (Fig. 5E) preparations analyzed, 14 (87.5%) have their absolute or local maximum at the beginning of LP and 13 (81%) have absolute or local maximum at the beginning of LP with the beginning of PD. In all cases, AMI_rel peaks are statistically significant.

Figure 5.

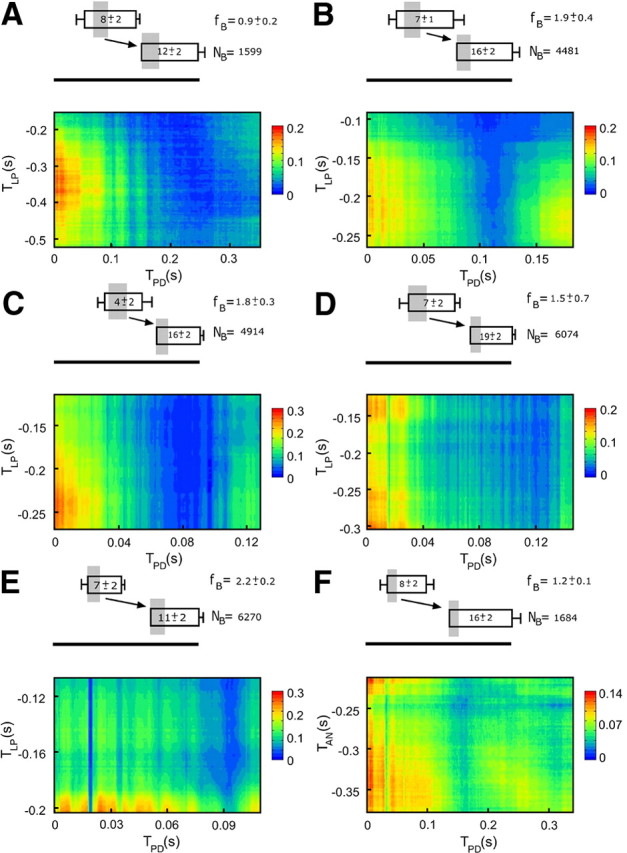
AMI_rel results in different preparations for experiments with LP and PD neurons. A–D, Preparations with the intact circuit of Callinectes sapidus. E, Preparations with the intact circuit of Panullirus interruptus. F, A hybrid circuit in which the LP neuron was replaced by an AN (prepared to mimic the original LP) and connected to PD through an artificial inhibitory synapse. Above each graph is a representation of the LP (upper box) and PD (lower box) average bursting duration and phases (time reference in the first spike of the PD bursts). The lateral bars represent SDs. The size of rectangles were normalized to the bursting period (horizontal bar with the same length for all maps). Bursting frequency (f_B in Hertz) and the number of pairs of bursts (N_B) used in the analysis are also indicated in each case. The average number of spikes/burst of each neuron is indicated inside each rectangle. Gray shading represents the portions of the bursts that correspond to the maximum peak of AMI_rel, and the arrow points the direction of information flow from LP to PD. AMI_rel peaks correspond to the beginning of both LP and PD bursts in all cases. Results are similar for different animals (with different LP and PD bursting phases, average spike numbers, and pyloric frequencies) and even among different species and are reproduced in hybrid circuit experiments.

A hybrid circuit where PD is connected to a model neuron through a single synapse presents similar results to those obtained for the intact circuit

The results presented so far indicate an information flow mechanism shared among different animals, but the question of whether such information flows through a single synapse or follows an indirect pathway using other connectivities across the STNS remains unanswered.

We investigated this matter by doing several experiments in which the PD neuron interacted with an AN in real time, while the LP neuron was kept hyperpolarized to a quiescent state. In this hybrid circuit, interaction was provided by a single inhibitory artificial synapse from AN to PD, implemented through a dynamic clamp protocol (Pinto et al., 2001; Nowotny et al., 2006). The AN was implemented either as a random spike generator or as a conductance-based model with additional stochastic dynamics (Carelli et al., 2005) and it was prepared to mimic the bursting phase and the average number of spikes/burst found in the original LP. The PD hyperpolarization onset determined when AN was allowed to burst and it was the only influence the biological circuit had over the AN. This way it was impossible for any CPG neuron to influence AN′s IBSPs.

The preparations used in the hybrid experiments showed variability regarding to the pyloric period (from 0.62 ± 0.03 s to 0.83 ± 0.05 s), number of spikes per burst of the PD neuron (from 7.4 ± 0.7 to 15 ± 2), and number of spikes per burst of the AN that mimicked the original LP (from 4 ± 1 to 8.0 ± 0.8). These fluctuations are comparable to those observed in intact circuit experiments. Moreover, of a maximum value of five bits, the entropy values obtained along the bursts of both random and stochastic AN were in the range of [2.2, 4.5] bits in different experiments, very similar to the range of [2.3, 4.6] bits obtained for the real LP in intact circuit experiments. Our hybrid circuit experiments presented AMI_rel results qualitatively similar to those found for the intact circuit: the peak of AMI_rel lies at the beginning of both stimulus and response neuron bursts (Fig. 5F). From a total of 16 experiments performed, 15 (94%) had an absolute maximum at the beginning of AN with the beginning of PD (statistically significant in all cases). Since AN entropy is typically high and AMI_rel also has very prominent values, the PD neuron IBSPs can reflect IBPSs variations of a presynaptic neuron, even if it they are completely artificially generated.

Information from the LP motor neuron is found in a nerve with fibers that project into sensory areas of the brain

Could the LP neuron be able to transmit information contained in its IBSPs to STNS neurons other than the PD neuron? If so, what could this information be used for?

We addressed this question by looking for information flow between the LP neuron and the ivn nerve that connects the OG to the brain (Böhm et al., 2001), using the same analysis technique for computing AMI_rel. Since the ivn signal is tonic, some adjustments were necessary as the original method was designed to separate the time series in pairs of bursts. Using the first spike of each LP burst as time reference, we collected all LP bursts with their corresponding portions of the ivn signal in the range of [−2:2] s with respect to the local time reference.

We computed AMI_rel between LP burst and ivn IBSPs (Fig. 6). The IBSPs corresponding to ivn spikes occurring before the LP burst were considered stimuli and the LP IBSPs were taken as responses. Conversely, if ivn IBSPs happened after LP IBSPs, LP was considered stimulus signal and ivn the response.

Figure 6.

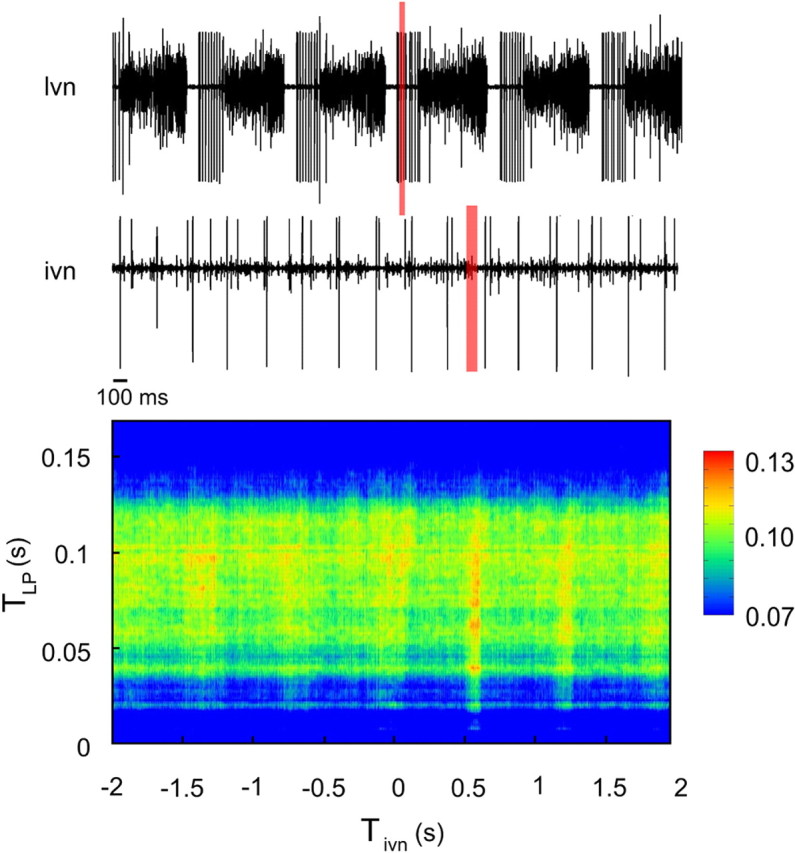
AMI_rel between LP neuron and ivn as a function of T_LP and T_ivn. The upper trace is the extracellular signal obtained from the lvn; we can clearly see and detect the LP spikes (big units). The lower trace is the extracellular signal recorded from the ivn. The peak of AMI_rel lies at T_ivn ∼0.6 s. The red shaded rectangles represent portions of the LP and ivn signals that correspond to the AMI_rel peak.

We found that part of the LP IBSPs is actually coded by ivn active units. The maximum AMI_rel region lies at a positive value of T_ivn, meaning information flows from LP to ivn (Fig. 6). The nerve takes approximately one pyloric cycle to express information received from the LP, ∼0.6 s after the LP burst. Since conduction velocity in the ivn is likely to be of the order of meters per second (for the superior oesophageal nerve, see Moulins et al., 1979; for the stomatogastric nerve, see Russell and Hartline, 1984), and the STG is only a few centimeters apart fror the ivn electrode, the nerve conduction velocity does not justify the delay found. This result suggests that the delay found is related to the way information is processed/coded, synapse by synapse, from the LP until it reaches the ivn. The most prominent values of AMI_rel correspond to a region near the beginning of the LP burst reaching a value of 12.5%. Three of 10 different crab preparations showed no significant AMI_rel values in any region of the graph. Nevertheless, the other seven cases (70%) presented an information flow from LP to ivn, with AMI_rel peaks ranging from 2.5% to 28.0% (all statistically significant).

Discussion

The study of complex burst dynamics is improving concomitantly with the development of dedicated analysis tools. For instance, phase response curves (PRCs) (Ayers and Selverston, 1984; Canavier and Achuthan, 2010) have greatly contributed to our understanding of synchronization in CPGs, considering neurons as periodic oscillators (Oprisan et al., 2004; Galán et al., 2005; Ermentrout et al., 2007; Schleimer and Stemmler, 2009). PRC methods target the phase shifts produced in periodic bursts by interacting neurons, disregarding any oscillations of intraburst ISIs. In fact, a few neurons' burst onsets and terminations dictate the constriction and dilation rhythm of pyloric muscles, so little attention has been traditionally paid to intraburst ISIs due to their lack of influence on motor activity.

Nevertheless, return maps of intraburst ISIs (Segundo et al., 1998) of CPG neurons reveal fine patterns that are sensitive to physiologically meaningful alterations of the circuit (Szücs et al., 2003, 2005; Campos et al., 2007). The shapes in first return maps were called neural signatures due to their reproducibility, typical of each neuron type. We found that the blue crab PD neuron has a very similar signature to the one previously reported for the lobster PD neuron (Szücs et al., 2003). This previous work described changes in the lobster PD neuron signature when the LP to PD synapse is artificially modified, meaning that PD's IBSPs are sensitive to LP activity or connectivity.

In the present work, we thoroughly investigated such relations, not only considering first-order ISI patterns, but also looking at a wide range of IBSPs using an information theoretical analysis tool. Although the method was developed to find and measure informational content of IBSPs, it may also have other applications due to its power to reveal hidden information in spike patterns.

In fact, we found that PD is able to express informational content of LP IBSPs that reaches significant amounts of its coding capacity. An even more interesting phenomenon is that usually the region of maximum AMI_rel corresponds to the beginning of both LP and PD bursts. Moreover, this result is robust in different preparations and even across different species.

Furthermore, wide variations in AMI_rel values were clearly not directly dependent on entropy variations of both neurons. If we think of the PD neuron as a simple integrator of synaptic inputs received in the hyperpolarization phase, then the dynamics observed during the depolarization phase should depend linearly on the inputs. If we observe that both entropies vary smoothly along the bursts, singular peaks can only be found in the AMI_rel graphs if the input information is coded into output through a nonlinear transfer function, which is in agreement with the predictions of previous work (Chacron et al., 2004).

PRC studies have described the effect of inhibitory pulses on PD phase by using its burst onset as time reference (Oprisan et al., 2004). The AMI_rel results are also consistent with those findings: the beginning of a LP burst (which usually comprises the first LP spike) is strongly correlated with the very beginning of the following PD burst. However, our analysis considers not only variations in PD phase relative to LP onset, but also the detailed spike timing within LP burst. If the PD neuron were only sensitive to phase variations, then the expected position of the AMI_rel peak would be at the very beginning of LP, and the peak region should be quite small, comprising only the first LP spike and not the subsequent ones. Our results reveal that not only phase, but also slight variations in ISI of a series of spikes are important to account for information expressed in the PD following burst.

Our results revealed correlations between LP and PD IBSPs in the intact circuit. However, they do not rule out the possible influence of a third element in both neurons activity. To clarify this issue, we showed that the PD response to an artificial neuron is quite similar to its response to LP in the intact network. The model neuron mimics, on average, the LP bursting phase and duration and its spike distribution is also similar to the original neuron. This way, spike timing is dictated only by parameters set before the experiment, based on statistics of the LP behavior. Therefore, PD's IBSPs variability in this case can only be affected by the AN spontaneous IBSPs variability. These results allow us to claim that the variations of the patterns of AN are reflected in the IBSPs of PD and that a single synapse is sufficient to account for the IBSP information coding mechanism found.

In crustacean CPG motor neurons, bursting is associated with coordination of muscle contraction, but intraburst ISI timescale cannot be directly associated with motor control. Morris and Hooper (Morris and Hooper, 1997; Hooper et al., 2007) showed that the cpv1b muscle contraction, controlled by the PD neuron through a graded synapse, is determined by spike number in such a way that small variations in frequency do not affect its contraction slope. Therefore, muscle contraction must be independent of information encoded in IBSPs. In contrast, in a different neuromuscular system (Zhurov and Brezina, 2006), the accessory radula closer muscle of Aplysia operates between the fast and slow regimens, presenting nonlinear contraction responses to different spike timings. The authors argue that such properties contribute to maintaining robust muscle contraction patterns in vivo. Therefore, although it is not the case for the pyloric PD neuron and cpv1b muscle (Morris and Hooper, 1997), in a system with nonlinear muscle properties, the IBSP information coding shown here could be directly involved in a mechanism of motor regulation.

If information expressed through IBSPs is not important for muscle contraction, does it have any relevance to the system at all? To address this question, we looked for information transmitted to another nerve that connects the STNS to the brain. In fact, ivn expresses information from LP IBSPs. In this analysis, the time reference is at the first spike of LP bursts; therefore, all information contained in IBSPs is only due to intraburst spike timing variability and not related to phase or pyloric period.

A previous study in crayfish (Böhm et al., 2001) showed that there are STNS neurons located within the OGs and CoGs that send fibers through the ivn. Arborizations of these neurons spread inside the protocerebrum and other areas, mainly the neuropils of the first and second antennae, leading to communication with important processing centers in the brain. As the STNS is known to be quite functionally invariant across species, ivn is a good candidate for a pathway that delivers information from the pyloric circuit to sensory areas of the brain. Although it is not possible to ensure, based only on information theoretical results, that the information conveyed would actually be used to affect behavior, it is consistent to assume that the pathway described makes information about pyloric neurons behavior available to the brain.

In the pyloric CPG of the STG, the intrinsic bursting capabilities of neurons interplay with synaptic connectivity, providing an autonomous way to generate output pattern. However, the CPG is controlled by higher centers and through sensory feedback that together regulate the bursting pattern (Selverston et al., 2000). Although neuromodulators, synapses, and cellular machinery of the STNS have been extensively studied, there is still no broad understanding of how the CPG is regulated. We propose the coding mechanism found as an alternate feedback pathway to help modulatory control.

Another important finding is that AMI_rel results are qualitatively similar across different preparations. The pyloric CPG can present a vast repertoire of rhythms in a single animal and across different specimens due to intrinsic variability in cellular excitability machinery, synaptic strength, and baseline neuromodulator concentrations. All animals used in our experiments were collected from their natural habitat, so we may consider the variability of pyloric activity observed to be representative of the dynamical repertoire that would be found in the natural environment (Goaillard et al., 2009). Our results revealed an information flow phenomenon that is ubiquitous among different preparations and for different species, despite striking differences in pyloric period, number of spikes per burst, or phase relations between LP and PD across different animals.

Recent experimental and theoretical works have shown that circuits with different cellular and network properties can present similar activity regarding bursting period and phase, meaning that they must be functionally equivalent (Marder and Prinz, 2002; Goaillard et al., 2009; Grashow et al., 2010). It has been proposed that such a remarkable phenomenon can be part of intricate mechanisms responsible for homeostasis maintenance. We showed that a subtle phenomenon, such as information transmission through IBSPs, is conserved despite differences in network properties, and even in circuits with functionally different activities. Thus, it could be considered evidence of another level of homeostatic regulation. We are currently investigating what ionic mechanisms might be responsible for the observed phenomena.

Previous studies have shown that sensory neurons can use temporal spike patterns and firing rate to code different signals simultaneously (Bair and Koch, 1996; Panzeri et al., 2010; Middleton et al., 2011). In the present work, we have shown that bursting motor neurons, usually seen as workhorses of muscle contraction, can also perform this task. They are able to use patterns of different time scales to simultaneously encode the conspicuous motor information and also information about how other CPG neurons are working. Furthermore, they may play a role in the regulation of neuronal firing patterns within the network or by the CNS.

These findings expand the view of the role attributed to CPG bursting neurons. As it happened with many other phenomena first observed in the STNS (Clarac and Pearlstein, 2007; Marder and Bucher, 2007), we hope our findings can lead to new insights in the investigation of neural coding in invertebrate and vertebrate nervous systems in the future.