Synaptic and Intrinsic Balancing during Postnatal Development in Rat Pups Exposed to Valproic Acid in Utero

Abstract

Valproic acid (VPA) is among the most teratogenic of commonly prescribed anticonvulsants, increasing the risk in humans of major malformations and impaired cognitive development. Likewise, rats exposed prenatally to VPA exhibit a variety of neuroanatomical and behavioral abnormalities. Previous work has shown that pyramidal neuron physiology in young VPA-exposed animals is marked by two strong abnormalities: an impairment in intrinsic neuronal excitability and an increase in NMDA synaptic currents. In this study, we investigated these abnormalities across postnatal development using whole-cell patch recordings from layer 2/3 neurons of medial prefrontal cortex. We found that both abnormalities were at a peak soon after birth but were gradually corrected as animals matured, to the extent that normal excitability and NMDA currents had been restored by early adolescence. The manner in which this correction happened suggested coordination between the two processes. Using computational models fitted to the physiological data, we argue that the two abnormalities trade off against each other, with the effects on network activity of the one balancing the effects of the other. This may constitute part of the nervous system's homeostatic response to teratogenic insult: an attempt to maintain stability despite a strong challenge.

Introduction

Valproic acid (VPA) and its sodium salt are used for the treatment of epilepsy, migraine, and bipolar disorder (Fairgrieve et al., 2000; Holmes et al., 2001; Contag and Bushnell, 2010; Galbally et al., 2010). Several case and population studies have together provided strong evidence that prenatal valproate exposure creates a vulnerability to structural malformations, developmental delay, mental disability, and autism (Christianson et al., 1994; Moore et al., 2000; Williams et al., 2001; Rasalam et al., 2005; Bromfield et al., 2008; Diav-Citrin et al., 2008; Tomson and Battino, 2008; Tomson et al., 2011). Nevertheless, valproate continues to be in common use, given the need to balance teratogenic risks with the risks of uncontrolled seizures or mood disorders. Understanding how valproate exerts its effects on the developing brain is important both as a means for understanding how the nervous system responds to environmental insults, and as an avenue toward discovery of effective therapies.

An animal model has been established in which pregnant rats or mice are administered VPA, typically given in a single dose around the time of neural tube closure (Rodier et al., 1996, 1997; Arndt et al., 2005). Some of the abnormalities exhibited by the resulting pups are anatomical in nature (e.g., diminished number of Purkinje neurons; Ingram et al., 2000); others are behavioral (e.g., increased repetitive behaviors; Schneider and Przewłocki, 2005). Notably, many of these abnormalities are similar to those observed in humans with autism (Markram et al., 2007). At the genetic and molecular levels, several candidates that might be important in VPA pathology have been identified, including the Hoxa1 gene, brain-derived neurotrophic factor, neuroligin 3, and proenkephalin (Stodgell et al., 2006; Schneider et al., 2007; Kolozsi et al., 2009; Roullet et al., 2010).

At a physiological level, previous work has shown that neocortical pyramidal neurons of 2-week-old VPA-exposed animals exhibit two strong abnormalities: impaired intrinsic excitability and excessive NMDA currents (Rinaldi et al., 2007, 2008a). Using whole-cell patch recordings from medial prefrontal cortex (mPFC), we confirmed these findings and went on to trace their postnatal time course. We found that both abnormalities were corrected over the first 5 weeks of life. The similarity in time course suggested that the two effects were coordinated. We explored this idea by fitting the physiological data to phenomenological model neurons (Brette and Gerstner, 2005) and examining the behavior of networks built from these model neurons. The results indicate that the particular way in which excitability is impaired, an increase in adaptive current, is well suited to counteract the network effects of excessive NMDA current. In other words, the coordinated effects maintain some balance in an otherwise imbalanced neural circuit.

Materials and Methods

Animals.

Pregnant Sprague Dawley rats were injected (intraperitoneally) with 500 mg/kg VPA sodium salt or saline at embryonic day 11.5. Male pups were used for physiological experiments at ages between postnatal day 4 (P4) and P38. All procedures were approved by the Institutional Animal Care and Use Committee at The Neurosciences Institute.

Cellular electrophysiology.

Brain slices were prepared and electrophysiological recordings made essentially as previously described (Desai and Walcott, 2006; Desai et al., 2006). Briefly, coronal sections of 350 μm thickness containing medial prefrontal cortex were cut on a vibratome in ice-cold artificial CSF (ACSF) containing the following (in mm): 126 NaCl, 3 KCl, 1 NaH₂PO₄, 25 NaHCO₃, 2 MgCl₂, 2 CaCl₂, and 25 dextrose. Osmolality was ∼310 mOsm. The pH was buffered to 7.4 by bubbling with 95% O₂/5% CO₂. Tissue was allowed to equilibrate for ≥1 h before the start of experiments and was used for ≤7 h after preparation. Slices were transferred one at time to a recording chamber mounted on a fixed-stage upright microscope and were perfused with warmed (31°C), oxygenated ACSF. The bath solution also contained 1 mm kynurenic acid and 50 μm picrotoxin (current-clamp recordings); 0.2 μm tetrodotoxin, 50 μm APV, and 20 μm bicuculline [miniature EPSC (mEPSC) recordings]; or 20 μm glycine and 50 μm picrotoxin (NMDA-AMPA ratio recordings). Layer 2/3 pyramidal neurons of dorsal prelimbic cortex were identified at 400× magnification using infrared differential interference contrast optics and an infrared-sensitive camera. Whole-cell patch recordings were obtained with pulled glass micropipettes (5–6 MΩ, 1 μm tip diameter). The internal solution for current-clamp and mEPSC recordings contained the following (in mm): 110 K-gluconate, 10 KCl, 10 (Na)phosphocreatine, 10 HEPES, 4 (Mg)ATP, 0.3 (Na)GTP, and 0.1% w/v biocytin. The internal solution for NMDA-AMPA ratio recordings contained the following (in mm): 110 Cs-gluconate, 10 CsCl, 5 QX-314, 10 (Na)phosphocreatine, 10 HEPES, 4 (Mg)ATP, 0.3 (Na)GTP, 5 EGTA, and 0.1% w/v biocytin. In both cases, osmolality was adjusted with sucrose to ∼290 mOsm and pH was adjusted with KOH to 7.4. Membrane potentials were corrected for liquid junction potentials (5 mV). Monosynaptic EPSCs were evoked using a concentric bipolar stimulating electrode placed within 50 μm of the soma. Synaptic recordings that showed evidence of polysynaptic or inhibitory contamination were discarded. Also discarded were recordings with series resistances >20 MΩ. Bridge and capacitance compensation were used as appropriate. All drugs and other chemicals were purchased from Sigma.

Adaptive exponential neuron model.

All computer simulations used the adaptive exponential integrate-and-fire (Brette-Gerstner) neuron model (Brette and Gerstner, 2005; Naud et al., 2008). The model has nine parameters: capacitance (C_m), leak conductance (g_L), leak reversal potential (E_L), threshold potential (V_T), threshold slope factor (Δ_T), reset potential (V_r), adaptation time constant (τ_w), subthreshold adaptation factor (a), and spike-triggered adaptation factor (b). The parameters determine temporal evolution of membrane potential V_m and adaptation current w, according to the following equations:

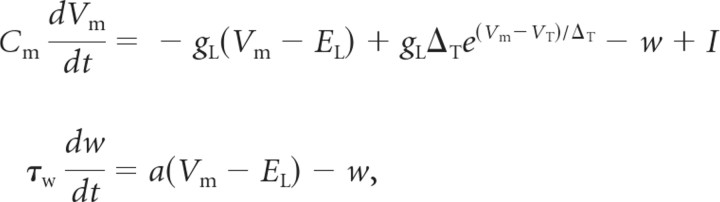where I is the total external current produced by current injection or by synaptic conductances. Every time V_m exceeds a cutoff of 0 mV, a spike is emitted, the membrane potential is reset to V_r, and the adaptation current is incremented by an amount b:

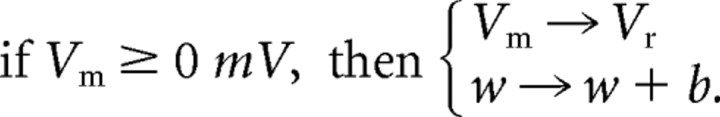Recordings from individual neurons were fitted to the parameters of the Brette-Gerstner model. First, responses to subthreshold current steps (−20 pA) were used to set the values of C_m, g_L, and E_L. Then, responses to suprathreshold current steps (1× to 2× rheobase) were used to fit the other six parameters (Δ_T, V_T, V_r, τ_w, a, b). This fitting was done by genetic algorithm optimization (Druckmann et al., 2007; Naud et al., 2008). The cost for each current step was computed based on six response features: number of spikes, adaptation ratio (number of spikes in second half of step divided by number of spikes in first half of step), first spike latency, first interspike interval, last interspike interval, minimum V_m after onset of spiking. Each of these features contributed a partial cost C given by:

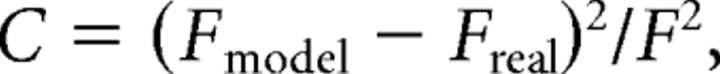where F_model was the value of that feature for the model parameters being tested and F_real was the value measured in the real neuron. The denominator F varied depending upon the feature being examined: F_real (number of spikes, first spike latency, first interspike interval, last interspike interval), 0.5 (adaptation ratio), or 2 mV (minimum V_m). For each current step, the cost was the weighted average of the six partial costs C. The number of spikes was given 3× and the adaptation ratio 1.5× the weight of the other features. Total cost for a given set of model parameters was the sum over the costs from all of the current steps. This total cost was what was minimized by the optimization. The genetic algorithm implementation we used was Matlab (MathWorks) function ga (population size 100, generations 500, crossover 0.6).

Simulated synaptic conductances.

AMPA and GABA inputs were modeled as exponential conductances with decay times of 5 and 8 ms, respectively. The AMPA reversal potential was 0 mV. The GABA reversal potential was −80 mV.

Each NMDA input was modeled by two first-order kinetic equations (Destexhe et al., 1994; Wang, 1999; Compte et al., 2000):

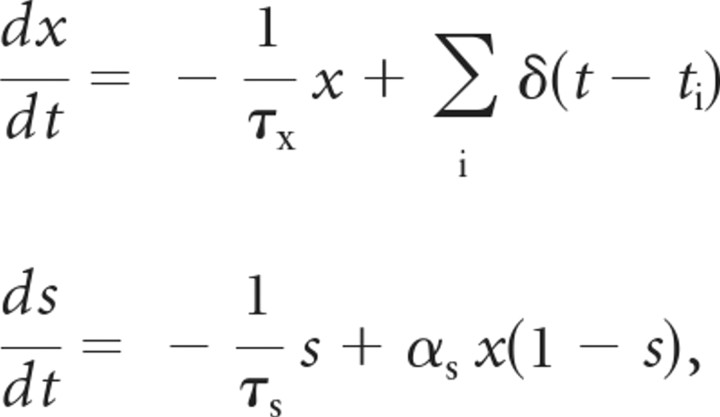where s is the fraction of open channels, x is an intermediate gating variable, δ(t) is the Dirac delta function, and the sum in the first equation is over spike times t_i. The time constants were τ_x = 2 ms and τ_s = 125 ms; the first controlled NMDA rise and the second controlled NMDA decay. The parameter α_s, which determines saturation properties, was 1 kHz. The NMDA current itself was given by:

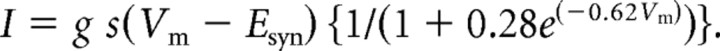where g is the unitary conductance and E_syn is the reversal potential (0 mV). The expression in curly brackets represents the magnesium block of NMDA receptors (Jahr and Stevens, 1990). AMPA and NMDA inputs were always coactivated. As described in Results, the NMDA unitary conductance g was varied so that the average NMDA-AMPA ratio varied between 0.5 and 0.75. We chose this kinetic formulation of NMDA conductance because it gave the NMDA current a smooth rising phase, and because the current produced by any one synapse saturated when presynaptic firing frequency became large. These properties are not only physiologically realistic, but important for network dynamics (Wang, 1999).

Single-neuron simulations.

The model neuron examined in Figure 7 (see below) had initial parameters similar to those of a control neuron: C_m = 100 pF, g_L = 5 nS, E_L = −65 mV, V_T = −50 mV, Δ_T = 4 mV, V_r = −55 mV, a = −2 nS, τ_w = 100 ms, and b = 50 pA. Inhibitory synapses had unitary conductance of 0.3 nS and fired at 10 Hz. AMPA synapses had a unitary conductance of 0.1 nS and fired at 5 Hz. NMDA synapses were coactivated with AMPA synapses; their unitary conductance was adjusted so that the NMDA-AMPA ratio varied between 0.5 and 0.75.

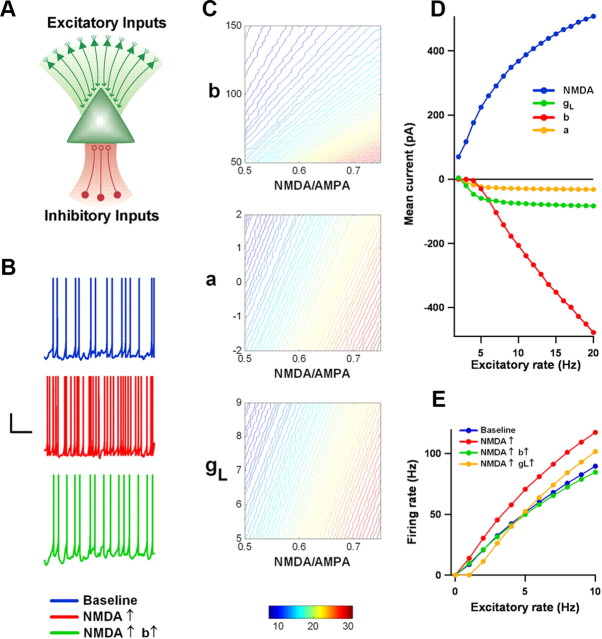
Figure 7.

Increasing the value of the spike-triggered adaptation parameter b offsets the effect on firing rate of increasing the NMDA-AMPA ratio. A, A single-model neuron received Poisson input from both excitatory and inhibitory synapses. The model neuron's parameters were initially similar to those of a control neuron, as described in Materials and Methods. B, Examples of the neuron's membrane potential in response to Poisson input in the baseline condition (blue), after the NMDA component of the excitatory synapses had been increased by 50% (red), and after b had been increased by 50 pA with the NMDA component remaining elevated (green). Calibration: vertical, 25 mV; horizontal, 200 ms. C, Firing rate of the model neuron as one varies NMDA-AMPA ratio and either b (pA), subthreshold adaptation parameter a (nS), or leak conductance g_L (nS). In these contour maps, when one of the latter parameters was varied, the others remained at baseline. Color scheme indicates firing rate in Hz. Note the broad range over which varying b maintains firing rate stability. D, As excitatory input rate increases, NMDA current increases dramatically, but the currents that flow as a result of leak g_L and subthreshold adaptation a do not. However, hyperpolarizing current due to suprathreshold adaptation b does grow in a similar manner. E, Consequently, increasing b effectively restores the neuron's input–output function following an increase in NMDA-AMPA ratio, whereas increasing g_L does not. Mean firing rate is plotted against excitatory input rate under baseline conditions, with an elevated NMDA component, and with both an elevated NMDA component and an increase in either b or g_L.

Network simulations.

The network model we used was adapted from that of Bazhenov et al. (2008). It contained excitatory and inhibitory layers, each of which was two-dimensional (see Fig.8A). The excitatory neurons were distributed uniformly on a 24 × 24 grid (576 neurons total), whereas the inhibitory neurons were distributed uniformly on a 12 × 12 grid (144 neurons total). Connectivity was local. Each excitatory neuron sent AMPA-NMDA projections to its 24 nearest excitatory neighbors (a 5 × 5 footprint, without autapses) and to its 9 nearest inhibitory neighbors (a 3 × 3 footprint). Each inhibitory neuron sent GABA projections back to its 25 nearest excitatory neighbors (a 5 × 5 footprint). Periodic boundary conditions applied. AMPA unitary weights onto excitatory neurons were 10% of the postsynaptic neuron's leak conductance. AMPA unitary weights onto inhibitory neurons were 1.67% of the postsynaptic neuron's leak conductance. GABA unitary weights onto excitatory neurons were 3× the AMPA weights. NMDA unitary weights were set relative to the AMPA unitary weights, as specified in Results. All neurons received an afferent excitatory current determined by an Ornstein-Uhlenbeck process. In most cases, the process had a mean of 40 pA, a SD of 40 pA, and a time constant of 5 ms. When recordings from older neurons (>P30) were used to build the network, the mean and SD were scaled by a factor of 2 to account for the large leak conductances and rheobase currents at this older age.

Figure 8.

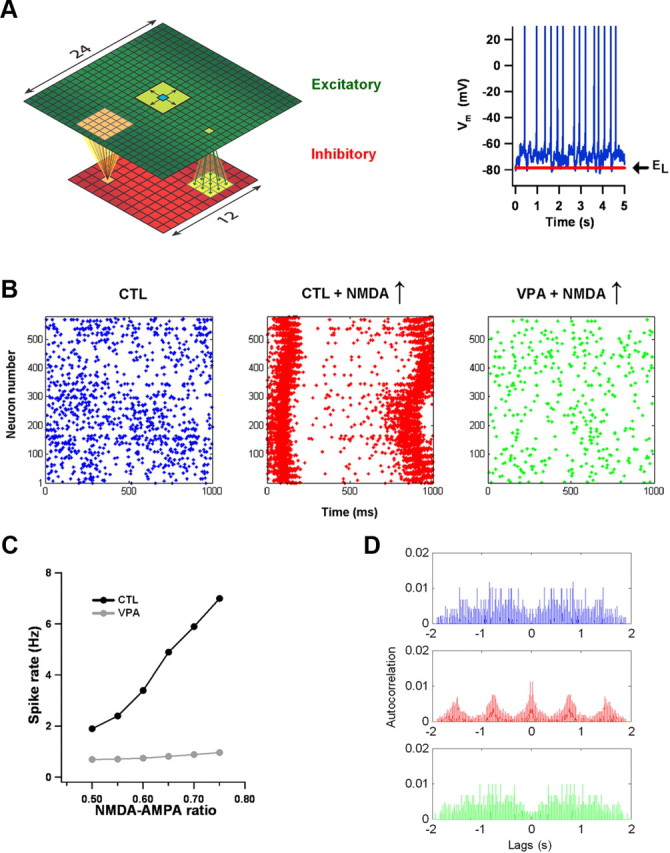
Effects of NMDA current and VPA intrinsic parameters on a cortical network model. A, The network consisted of two layers. One contained 576 excitatory neurons spaced uniformly on a 24 × 24 grid; the other contained 144 inhibitory neurons spaced uniformly on a 12 × 12 grid. Periodic boundary conditions applied. Connectivity was local and sparse, with excitatory neurons projecting to a small number of excitatory and inhibitory neighbors and inhibitory neurons projecting back to a small number of excitatory neighbors. All neurons received an afferent current. Under baseline (control) conditions, pyramidal neurons were depolarized above the leak reversal potential E_L and fired at a low rate. An example of one neuron is shown at right. B, Rastergrams of the spike times of excitatory neurons. When neuron parameters were drawn from fits to control data and the average NMDA-AMPA ratio was set to the control average of 0.5, spiking was dense but unstructured (left). Increasing the NMDA-AMPA ratio by 50% caused a sharp increase in spiking and periodic waves of activity (middle). Replacing the control parameters with VPA parameters restored unstructured activity (right). C, With control parameters, average firing rate was very sensitive to NMDA-AMPA ratio. But with VPA parameters, average firing rate was stable, as long as the ratio was kept within experimentally measured bounds. D, Plots of spike autocorrelation for the simulation data in the rastergrams shown in B. The top graph is for control conditions; the middle graph for control intrinsic parameters and elevated NMDA-AMPA ratio; the bottom graph for VPA intrinsic parameters and elevated NMDA-AMPA ratio. Values are normalized so that covariance at zero lag is 1, though the data points at zero lag are not shown to make the display clearer.

The parameters of the excitatory model neurons were drawn from fits to current-clamp recordings (see Fig. 6). Sixteen control recordings and 16 VPA recordings were fitted. For each type of network (control or VPA), the 16 sets of parameters were replicated 36 times and distributed randomly among the 576 excitatory neurons. The inhibitory neurons were uniform. Each was described by the Brette-Gerstner model with these parameters: C_m = 60 pF, g_L = 3 nS, E_L = −65 mV, V_T = −53 mV, Δ_T = 3 mV, V_r = −55 mV, a = 2 nS, τ_w = 20 ms, and b = 60 pA.

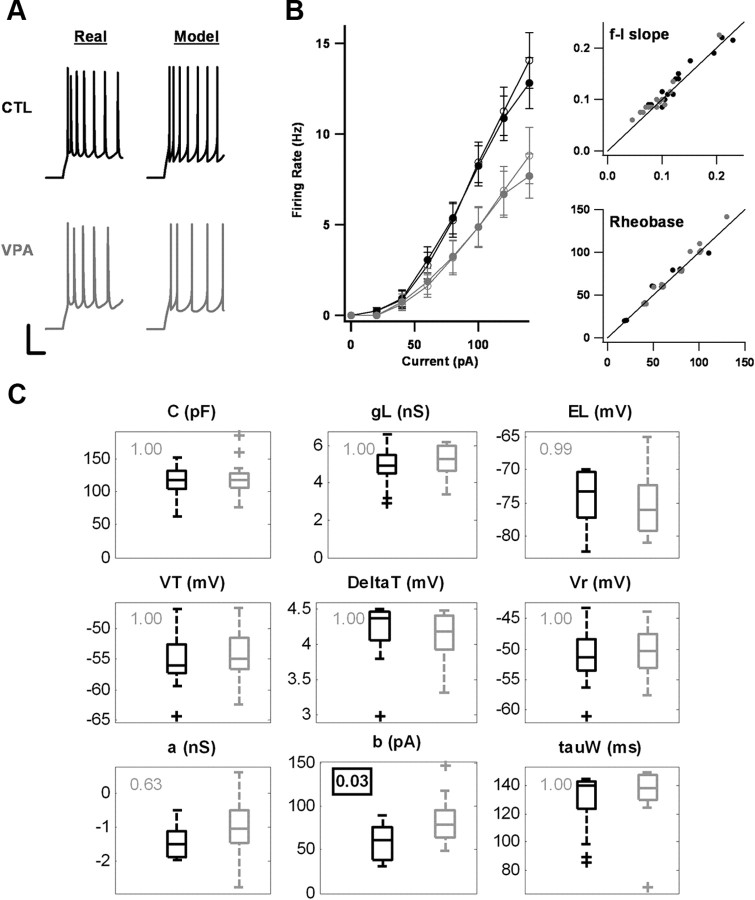
Figure 6.

Fitting the firing properties of P17–P18 neurons to the Brette-Gerstner neuron model. A, At left are examples of the responses of a control neuron and a VPA neuron to the injection of a 100 pA current step. At right are the responses of model neurons fitted to these recordings. Calibration: vertical, 25 mV; horizontal, 100 ms. B, Left, Average f–I curves of the model neurons (open circles) match those of the real neurons (closed circles). Control averages (n = 16) are in black, VPA averages (n = 16) are in gray. Error bars indicate SEM. Right, Scatter plots of the initial f–I slope (Hz/pA) and rheobase current (pA) for the 32 recordings. In both plots, the horizontal axis indicates measurements taken from real neurons, and the vertical axis indicates measurements taken from model neurons. Black dots are control data, gray dots are VPA data. The data points in the rheobase plot have been jittered (∼5 pA) to make overlapping points easier to distinguish. C, Box plots of the parameters of the Brette-Gerstner model for control (n = 16, black) and VPA (n = 16, gray) neurons. The parameters are capacitance C, leak conductance g_L, leak reversal potential E_L, effective threshold potential V_T, threshold slope factor Δ_T, reset potential V_r, subthreshold adaptation parameter a, spike-triggered adaptation parameter b, and adaptation time constant τ_w. The number at the upper left of each plot indicates the p-value (Bonferroni-corrected t test) of the comparison between the control and VPA means. Only the difference for b is significant.

Statistics.

Experimental measurements made on neurons from a given animal were first pooled and statistical analyses then performed on the resulting animal averages. This method of analysis (“by animal” rather than “by neuron”) obviates the potential problem of pseudoreplication, which can arise when recordings from a single animal are not statistically independent but are treated as such (Lazic, 2010). (It should be noted, though, that analyzing our data by neuron rather than by animal would not have changed any of the conclusions.) Where indicated, an ANOVA was run, with VPA exposure being one factor and age group another factor. The litter from which an animal had been taken was included as a random effect nested within the VPA exposure condition. Significant differences in the ANOVA were followed by two-tailed t tests with a Bonferroni correction for multiple comparisons. Significance was assessed at the 0.05 level. Statistical analyses were performed using the Matlab Statistics Toolbox (MathWorks).

Results

Whole-cell patch recordings were made from layer 2/3 pyramidal neurons of mPFC using tissue from animals aged between P4 and P38. Age-matched pairs of rats were used for recordings: one had been exposed prenatally to VPA (“VPA”), and the other had been exposed prenatally to saline (“Control”). Recordings from VPA and control slices were normally interleaved, ensuring that the two datasets were approximately the same size.

Development of intrinsic excitability

Intrinsic excitability was probed by injection of a family of current steps (−100 pA to 500 pA). To standardize measurements between neurons and across ages, neurons were tested from a fixed resting potential (−70 mV), which was maintained by a small offset current.

Intrinsic electrical properties of mPFC layer 2/3 pyramidal neurons in control animals did not reach a steady state until after the fourth week of life, with the most rapid development taking place in the first 3 weeks (Fig. 1). The nature of the changes and their time course was similar to what has previously been reported for other neocortical pyramidal neurons (Zhang, 2004; Oswald and Reyes, 2008). We found that as neurons grew larger and more branched, and the distribution and density of ion channels shifted, many physiological parameters evolved with time. These included both passive parameters (e.g., resting potential, input resistance, membrane time constant, sag potential) and active ones (e.g., spike threshold, spike shape, adaptation). Before P4, neurons generally could not fire action potentials in response to constant current pulses, and only by the beginning of the second week could they fire in a sustained manner.

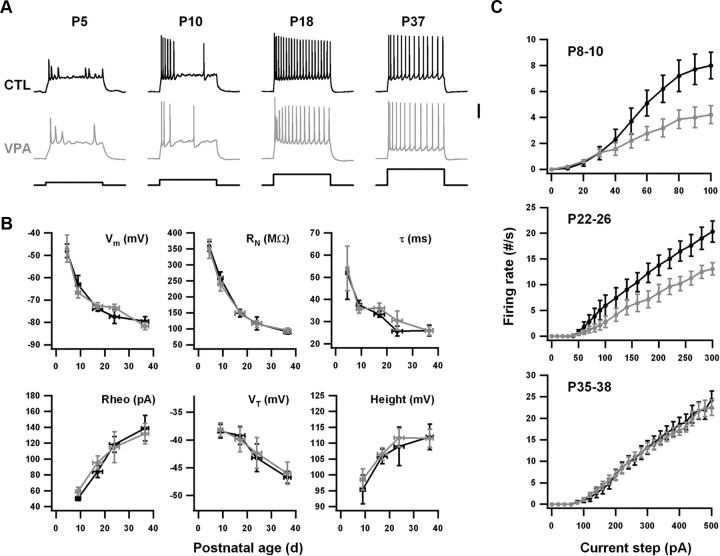
Figure 1.

Intrinsic excitability is reduced in VPA neurons during the early postnatal period but not the late postnatal period. Control (CTL) data are in black and VPA data are in gray. A, Examples of responses to current steps at four postnatal ages. Each step was 1 s long. Vertical scale bar: 25 mV for membrane potentials, 250 pA for current steps. B, Average measurements of resting potential (V_m), input resistance (MΩ), membrane time constant (τ), rheobase current (Rheo), threshold potential (V_T), and spike height (Height). Vertical error bars are SEM. Horizontal error bars indicate the age ranges into which data were grouped. The numbers of control and VPA animals in each age range were, respectively: 4 and 3 (P4–P5), 10 and 10 (P8–P10), 16 and 14 (P15–P19), 5 and 6 (P22–P26), 8 and 8 (P35–P38). On average, four neurons were recorded per animal. Age group was a significant main effect for every parameter (p < 0.001, ANOVA), but VPA exposure was not significant for any parameter. C, Firing rate-current (f–I) curves for three age groups, constructed by measuring the total number of spikes elicited by current steps (1 s long) of different amplitudes. Numbers of animals were as in B. VPA exposure was a significant effect for the youngest age group (p < 0.05, repeated-measures ANOVA), but not for the oldest.

The development of passive and subthreshold parameters in VPA pyramidal neurons closely paralleled that in control neurons, with no significant differences at any age (Fig. 1B, top row).

However, the development of active parameters differed between VPA and control neurons. The group of neurons from the youngest VPA animals (<2 weeks) was markedly less excitable than those from age-matched control animals. In particular, the numbers of action potentials generated by current steps were lower (Fig. 1C), which confirms a previously reported finding in early postnatal animals (Rinaldi et al., 2008a). This deficit was not caused by a general impairment in the ability of neurons to produce action potentials, since single-spike properties, such as rheobase and spike shape, were unchanged. Rather, the deficit was in the ability to fire sustained trains of action potentials in response to constant current (i.e., an excess of spike frequency adaptation).

As was true of control neurons, sustained firing in VPA neurons was strongly age dependent (Fig. 1A). It was only after the second week that neurons could fire throughout a 1-s-long current step, being subject to strong spike inactivation before then. Spike properties developed rapidly during the first month. As they did, differences between control and VPA neurons were gradually reduced (Fig. 1C). In fact, the differences disappeared altogether in adolescent animals (>1 month). Responses to current steps were indistinguishable between VPA and control recordings in these older animals, indicating that the early-life impairment in intrinsic neuronal properties of VPA animals was corrected over the course of postnatal development. The time course can be seen most clearly in Figure 2, in which the average slope of the firing rate–current (f–I) curves is plotted against age group. For control recordings, the slope decreased with age because of the decrease in resting input resistance with age. But for VPA recordings, the slope increased with age because the early impairment in intrinsic excitability was the more important effect. By ∼P30, the VPA slopes had caught up to the control slopes.

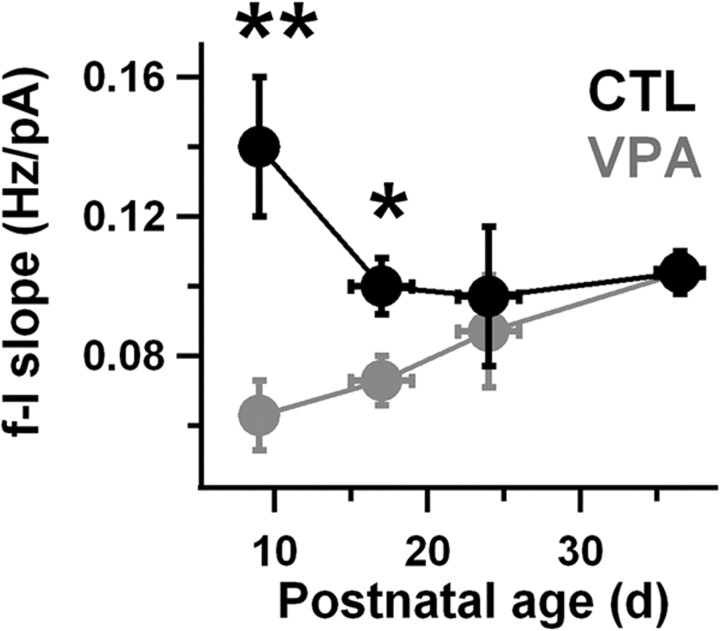
Figure 2.

VPA intrinsic excitability is restored to control levels after the third week of life. The initial slope of the firing rate-current (f–I) curve was measured for each neuron between rheobase and twice rheobase. A mean slope for each animal was calculated by pooling all measurements for neurons from that animal. These means were then divided based on VPA exposure condition and age group (as indicated by the horizontal error bars). Control (CTL) data are in black and VPA data are in gray. The numbers of control and VPA animals in each age range were, respectively: 10 and 10 (P8–P10), 16 and 14 (P15–P19), 5 and 6 (P22–P26), 8 and 8 (P35–P38). On average, four neurons were recorded per animal. For each age group and exposure condition, animals were drawn from 3 to 10 separate litters. Vertical error bars are SEM. VPA exposure was a significant main effect (p < 0.01, ANOVA). Bonferroni tests indicated a significant difference between VPA and control slopes for the two youngest age groups (**p < 0.01 and *p < 0.05).

Development of excitatory synaptic currents

Abnormalities in excitatory synaptic transmission have been reported in 2-week-old VPA animals (Rinaldi et al., 2007, 2008a). We examined this issue by evoking monosynaptic currents with extracellular stimulation and calculating the ratio of NMDA-mediated to AMPA-mediated currents at proximal synapses (Fig. 3A), which is a standard measure of glutamatergic synaptic transmission (see Myme et al., 2003, their Table 1).

Figure 3.

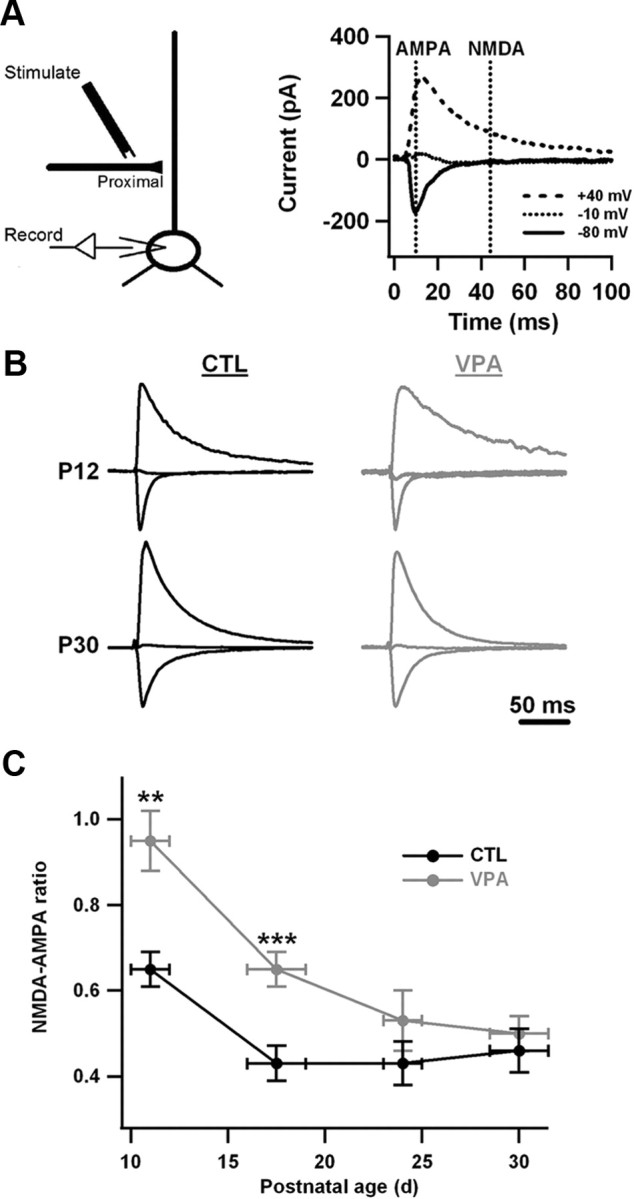
The NMDA-AMPA ratio is elevated in VPA neurons during the early postnatal period but not the late postnatal period. A, The ratio was estimated by stimulating proximal excitatory fibers while holding the postsynaptic neuron in voltage clamp at various potentials V_hold. At the most positive holding potential, the early response was mainly an AMPA current and the late response was mainly an NMDA current. The ratio of these two numbers is what was measured. B, Examples of evoked currents in control and VPA neurons at two ages. The holding potentials were varied as in A. Currents for each neuron have been normalized to the negative-going peak recorded at V_hold = −80 mV. Stimulus artifacts have been zeroed out. C, Average NMDA-AMPA ratio as a function of postnatal age. Horizontal error bars indicate the age ranges into which data were grouped. Vertical error bars are SEM. For control data, the numbers of animals were 7, 8, 3, and 6 for the four age groups shown. For VPA data, the numbers of animals were 6, 8, 3, and 6 for the four age groups shown. On average, four neurons were recorded per animal. For each age group and condition, animals were drawn from 2 to 5 litters. Differences between control and VPA measurements at P10–P12 and P16–P19 were significant (***p < 0.001 and **p < 0.01, Bonferroni test), but those at P23–P25 and P29–P32 were not.

The NMDA-AMPA ratio was much larger (∼50%) in VPA neurons than in control neurons early in postnatal development (<3 weeks, Fig. 3C). This agrees with the report of enhanced NMDA current in ∼P14 somatosensory neurons (Rinaldi et al., 2007). In both control and VPA neurons, the ratio decreased with age as AMPA transmission grew, but the decrease was much steeper in the VPA case, to the point that VPA-control differences were not significant beyond P23.

In principle, the difference in ratio could have been due to a difference in AMPA currents rather than in NMDA currents. To test this possibility, we measured AMPA-mediated mEPSCs from a holding potential of −70 mV (Fig. 4A). As has been reported in primary visual cortex (Desai et al., 2002), we found that mEPSC frequency in mPFC neurons increased dramatically during the second week of life, before reaching a plateau (Fig. 4C). In parallel, mEPSC amplitude decreased (Fig. 4C), likely reflecting both the increased cable filtering as dendritic trees grew and the effects of homeostatic processes (Desai et al., 2002; Pratt and Aizenman, 2007). AMPA mEPSC development in VPA neurons was indistinguishable from AMPA mEPSC development in control neurons, with a similar time course, frequency, and distribution (Fig. 4B,C). The kinetics of mEPSCs were also similar (Fig. 4D).

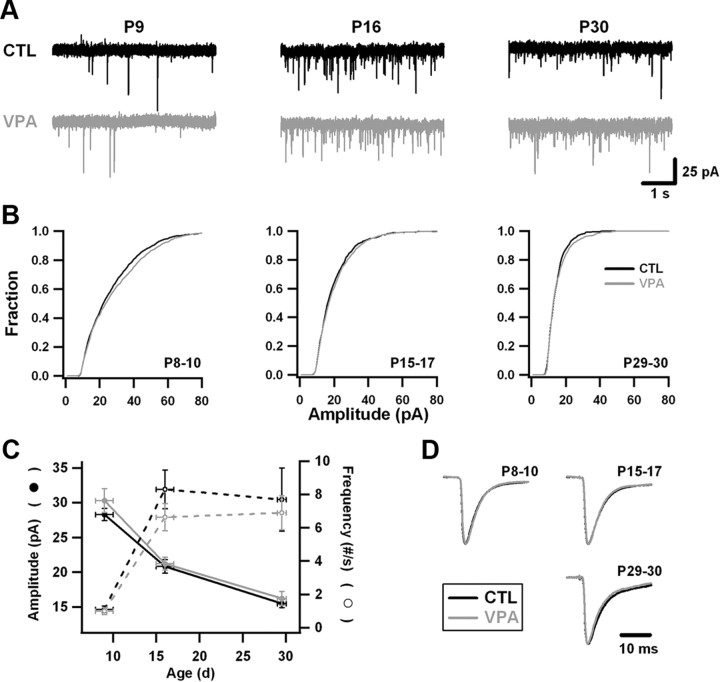
Figure 4.

Quantal currents mediated by AMPA receptors develop similarly in control and VPA cortex. A, Examples of voltage-clamp recordings of spontaneous excitatory currents in control and VPA neurons at P9, P16, and P30. B, Cumulative histograms of mEPSC amplitudes, constructed by randomly selecting 50 events from every recording. Data from control and VPA animals have been grouped into three age ranges: P8–P10 (n = 5 control; n = 5 VPA), P15–P17 (n = 6 control; n = 8 VPA), P29–P30 (n = 4 control; n = 4 VPA). On average, four neurons were recorded per animal. A Kolmogorov–Smirnov test (bin size = 2.5 pA) indicates that the amplitude distribution does not differ between conditions at any age (p > 0.2 for all groups). C, In both control and VPA neurons, mEPSC frequency increased and mEPSC amplitude decreased over the course of postnatal development. Plotted are average amplitudes and frequencies from animals grouped into the same age ranges as in B. Vertical error bars are SEM. VPA exposure was not a significant effect. D, Average (peak-scaled) mEPSC waveforms over development. Control and VPA waveforms from each age group have been overlaid. Rise and decay times did not differ significantly at any age.

Together the NMDA-AMPA ratio and mEPSC data indicate that NMDA currents are excessive in early postnatal VPA neurons, whereas AMPA currents are largely normal. The AMPA result is somewhat different from what has been reported for layer 5 pyramidal neurons in 2-week-old animals (Rinaldi et al., 2008a). We will address this discrepancy in the Discussion. Our data also indicate that the synaptic differences between VPA and control neurons are corrected over the first month of life.

Phenomenological neuron modeling

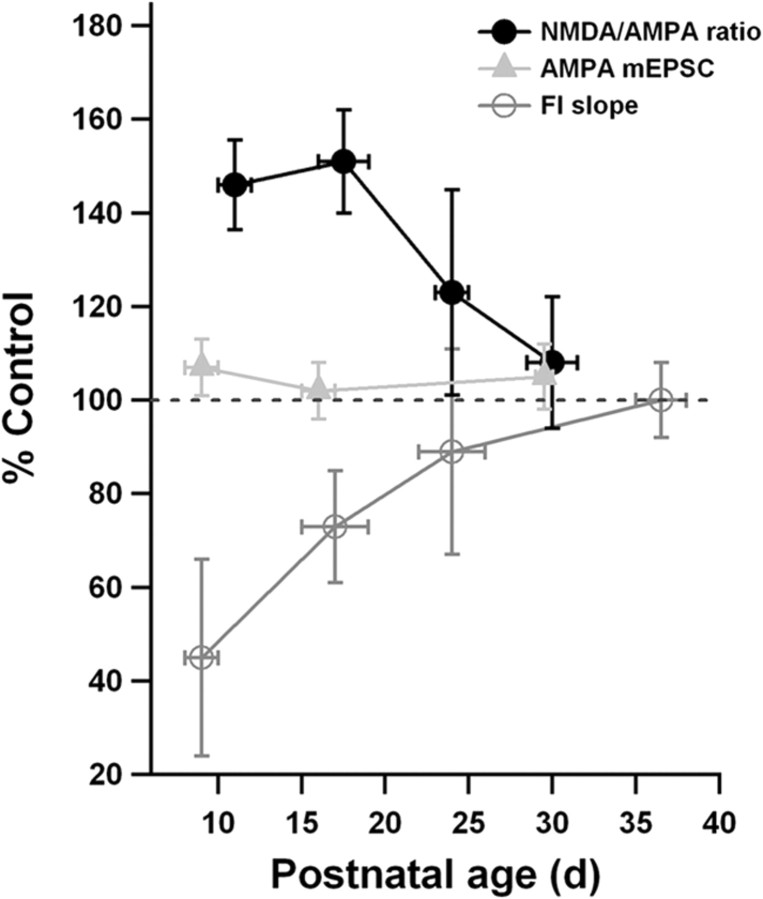
Figure 5 summarizes the experimental findings. What is striking is that the two physiological abnormalities appear to be complementary to each other. The impaired intrinsic excitability reduces neuronal firing, whereas the excessive NMDA current increases it. More importantly, the impairment in intrinsic excitability manifests as an increase in adaptation, rather than as a shift in input resistance or spike threshold. Adaptive currents, with their slow kinetics, have the right properties to offset the effects on neuronal and network dynamics of the slow synaptic currents produced by NMDA receptors (Wang, 1999; Faber, 2010). The fact that the developmental time courses of the two abnormalities parallel each other underscores the idea that they balance or trade off, with the one perhaps being the homeostatic response to the other (Desai, 2003; Turrigiano and Nelson, 2004; Watt and Desai, 2010).

Figure 5.

Summary of the experimental results. Average values measured in VPA animals at each age are plotted as a percentage of the average values measured in control animals at that same age. The three measurements shown are NMDA-AMPA ratio, AMPA mEPSC amplitude, and initial slope of the firing rate–current (FI) curve. The numbers of animals are the same as in the previous figures. Horizontal error bars indicate the age ranges into which data have been grouped. Vertical error bars were computed by assuming that, when taking a ratio, uncertainties propagate in quadrature.

We explored this idea by incorporating both abnormalities into simple computational models. Our choice of model neuron was driven by three important but competing needs: the model had to be simple enough so that its parameters could be adequately fitted using our data, efficient enough to permit simulation of large networks without requiring inordinate computing power, and realistic enough to represent the firing patterns observed in control and VPA neurons. Neither of the two most commonly used spiking neuron models—the leaky integrate-and-fire (LIF) neuron and the Hodgkin-Huxley neuron—could satisfy these needs well enough (Izhikevich, 2007). The LIF neuron is simple and efficient, but it cannot in its standard form capture many of the intrinsic firing properties observed in central neurons, such as spike-frequency adaptation and bursting. The Hodgkin-Huxley neuron is biologically realistic but its large number of adjustable parameters and its complexity make the fitting process extremely challenging (Druckmann et al., 2007) and limit the size of networks that can be simulated (Izhikevich, 2004). Instead, we chose to build our networks using adaptive exponential integrate-and-fire (Brette-Gerstner) neurons (Brette and Gerstner, 2005). This is one of a group of phenomenological neuron models introduced in recent years that are designed to combine simplicity and (a certain amount of) realism (Izhikevich, 2004, 2010). These models are similar to the LIF neuron but enhance it in two ways. First, they incorporate in the membrane potential equation a term that represents spike generation and that typically has a quadratic (Ermentrout, 1996; Latham et al., 2000), exponential (Fourcaud-Trocmé et al., 2003), or quartic (Touboul, 2008) form. Second, they include a second state variable (in addition to membrane potential) that broadly represents adaptation (Izhikevich, 2003, 2007). It is the inclusion of this second variable that gives the response properties of these models richness and allows them, despite their simplicity, to represent a surprising diversity of firing patterns.

The Brette-Gerstner neuron includes an exponential spike generation term and an adaptation variable w. It is defined by nine parameters: three determine passive properties (C_m, g_L, and E_L), three determine basic spike properties (V_T, Δ_T, V_r), and three determine adaptation (a, b, τ_w). We fitted 16 control recordings and 16 VPA recordings to the parameters of the model (Fig. 6). All of the neurons were from animals at P17–P18, an age at which differences between VPA and control neurons were still large and at which spike generation had matured sufficiently to be reasonably fitted by the model. As explained in Materials and Methods, the passive parameters were determined by responses to hyperpolarizing current steps whereas the other parameters were fitted to responses to suprathreshold current steps using a genetic algorithm. The resulting model neurons were able to capture the basic firing properties of the real neurons (Fig. 6B). In general, the fitted parameters were not unique: changing how different response features were weighted in the cost function produced appreciable differences in some of the parameter values. Nevertheless, the only significant difference between the control and VPA groups in any of the optimization runs was in the spike-triggered adaptation parameter b (Fig. 6C). This makes sense given that the measured VPA-control differences in the physiological data were limited to firing adaptation.

Spike-triggered adaptation versus NMDA

Before turning to the network model, it is worthwhile first to consider how spike-triggered adaptation and NMDA currents affect neuronal firing and how they interact. To do this we examined the responses of a single-model neuron to Poisson input from a large number of excitatory and inhibitory synapses (Fig. 7A) (See Materials and Methods for parameter values). The neuron's baseline intrinsic parameters—and hence its baseline intrinsic excitability—were similar to the average values obtained from the fits to control recordings. The baseline NMDA conductances were set so that the ratio of peak NMDA current to peak AMPA current at V_m = +40 mV was 0.5, which is close to the average NMDA-AMPA ratio recorded in control neurons at P17–P18. The presynaptic rates were chosen so that the postsynaptic neuron was, on average, depolarized to a few millivolts below threshold and V_m fluctuations were large enough to produce appreciable but irregular firing.

The baseline values produced a postsynaptic firing rate of ∼10 Hz (Fig. 7B). Increasing the NMDA-AMPA ratio by 50%, so that it was near the VPA average recorded at P17–P18, nearly tripled the firing rate. But this effect could be completely reversed if we simultaneously increased the value of b by 50 pA. The effectiveness of this intrinsic adaptation current, which decays with a time constant τ_w comparable in size to the NMDA decay time constant τ_s, in stabilizing postsynaptic firing could be seen even more clearly when we systematically varied the values of b and the NMDA-AMPA ratio, as in the top contour plot of Figure 7C. Note how broad the area is over which firing rate remained stable when b roamed over its experimentally determined range. By contrast, stability was much more limited when we attempted to counter the effects of elevated NMDA current by increasing subthreshold adaptation a or leak conductance g_L (Fig. 7C, middle and bottom). This was true even though we allowed both parameters to assume values at the top of the range more positive than the fitted values from any control or VPA recording.

The reason for this difference is that the amount of hyperpolarizing current due to b is sensitive to firing rate, whereas the amounts due to a and g_L are comparatively insensitive. Physically b is meant to represent the effects of something like a calcium-dependent potassium current—that is, a current that responds quickly to every spike and that can accumulate as firing rate grows. The parameter a instead represents voltage coupling, for example due to HCN channels. Its effect on adaptation current w is relatively slow (τ_w ≈ 100 ms), and action potentials are too brief for there to be much interaction. Instead, when the neuron is in an active state with a mean membrane potential V_mean, the role of a is simply to contribute an offset current:

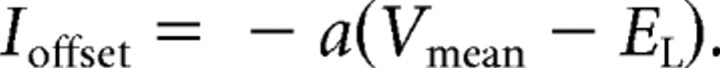Leak current also depends mostly on mean membrane potential; the current flow through leak channels due to action potentials is much smaller. These ideas are illustrated in Figure 7D, in which the presynaptic excitatory stimulation frequency was varied and the contributions to total current of NMDA, g_L, a, and b were plotted. As stimulation frequency increased, NMDA current increased dramatically, as one would expect. Spike-triggered adaptation current kept pace. However, leak and voltage-coupled adaptation currents did not.

As a result, increasing b is effective in restoring the neuron's input–output (I–O) function after an increase in NMDA-AMPA ratio, whereas increasing g_L or a is not (Fig. 7E). When the NMDA component is increased by some fraction, the proportional increase in excitation tilts the I–O curve upwards. Where suprathreshold adaptation controls the slope of the I–O curve (a multiplicative adjustment) and can respond appropriately, leak conductance and subthreshold adaptation merely produce lateral shifts in the I–O curve (an additive adjustment) (Silver, 2010).

Elevated NMDA effects on control and VPA networks

To explore the functional consequences of differences in control and VPA intrinsic and synaptic physiology, we built two-dimensional networks with local connectivity (Fig. 8A) (Bazhenov et al., 2008). This allowed us to study spatiotemporal aspects of network activity. The parameters of the inhibitory neurons were uniform, but the parameters of the excitatory neurons were drawn from the fits to our P17–P18 physiological data (Fig. 6). In this way, we built two networks: one with control intrinsic physiology, the other with VPA intrinsic physiology. The networks were made active by the injection into each neuron of an afferent current, generated by a noisy stochastic process. The current was chosen so that, under baseline (control) conditions, neurons were depolarized by ∼10 mV above rest, exhibited V_m fluctuations of several millivolts, and had firing rates of several Hz (Fig. 8A, right). How active in vivo cortical networks are under resting conditions is a matter of some uncertainty (Destexhe et al., 2003; Wehr and Zador, 2003; Zou et al., 2005; Haider et al., 2006; Higley and Contreras, 2006; Waters and Helmchen, 2006; Rudolph et al., 2007), but, for what follows, the precise choice of afferent current is not critical. In fact, we could obtain the same qualitative results even if the current's mean, SD, or both were doubled.

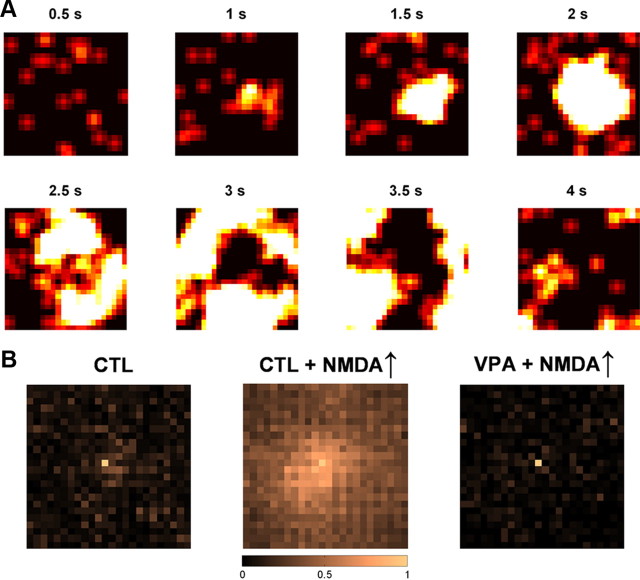
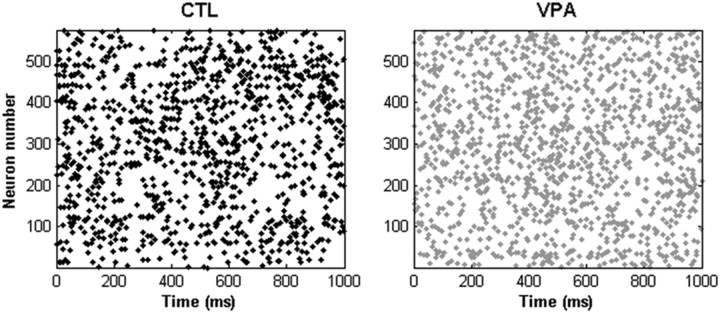
We examined how the two networks responded to increases in NMDA current. Initially, the NMDA-AMPA ratio at excitatory synapses was drawn randomly from a normal distribution with a mean of 0.5 and a SD of 0.15. That is, the ratio's distribution across each network approximately matched what had been measured in control neurons at this age. In this case, both networks exhibited dense and unstructured spike firing when subjected to the afferent excitatory input (Fig. 8B). This was appropriate, as the afferent input itself had no structure. For the control network, the average firing rate of excitatory neurons was ∼2 Hz. Increasing the NMDA amplitudes by 50%, so that the distribution matched what had been measured in VPA neurons at this age, produced three distinct but related effects in the control network: an increase in firing rate, periodic firing, and widespread spatial correlations. The increase in average firing rate of excitatory neurons is shown in Figure 8C. As average NMDA-AMPA ratio varied between 0.5 and 0.75, the rate grew linearly. When the ratio was pushed higher, growth became supralinear. More strikingly, increasing NMDA-AMPA ratio made the network vulnerable to periodic bouts of spatially extended activity. The temporal aspects can be seen in plots of spike autocorrelation (Fig. 8D). When average NMDA conductance was placed near the VPA average, control networks oscillated around 1 Hz. The frequency depended on NMDA decay time constant; the strength of the effect depended on NMDA amplitude. The spatial aspects are illustrated in Figure 9. When NMDA currents were elevated to VPA levels, small pockets of spiking activity grew into large clusters that quickly engulfed the whole network. Even on average, the network showed significant spatial correlations over hundreds of neurons (Fig. 9B). This is perhaps not unexpected given the importance of slow NMDA currents in generation of persistent and network activity (Wang, 1999).

Figure 9.

Spatially extended spiking activity provoked by excessive NMDA currents is suppressed by increased intrinsic adaptation. A, The network shown here was drawn from control recordings, but the NMDA-AMPA ratio was elevated as in VPA recordings. This produced traveling bursts of spiking activity. The heat maps show spike rates in the excitatory neuron layer (24 neurons by 24 neurons, as in Fig. 8A) in successive snapshots separated by 500 ms. When NMDA currents were large, small pockets of activity grew into large clusters that engulfed most of the network. B, Increasing intrinsic adaptation prevented the NMDA-induced waves of activity. Spatial crosscorrelation of firing rates under control conditions (left), after NMDA-AMPA ratio was increased by 50% (middle), and after control intrinsic neuronal parameters were replaced by VPA intrinsic neuronal parameters (right). The horizontal and vertical axes are each 24 neurons long. Values were scaled so that the value for the neuron at the center (autocorrelation) was 1. Firing rate was computed by dividing spike trains into 50 ms blocks.

The behavior of the VPA network was very different. All three effects of excessive NMDA currents were suppressed when we used fits to VPA recordings to define the excitatory neurons. Over the experimentally measured range of average NMDA-AMPA ratio at P17–P18 (0.5–0.75), average neuronal firing rates were mostly independent of its precise value (Fig. 8C). Instead, they were driven primarily by AMPA transmission and the afferent inputs. Only when the NMDA-AMPA ratio was pushed well outside of the range observed experimentally (>1.0) did the aberrant control-like network activity appear. Likewise, the periodic spiking seen in the control network was entirely absent in the VPA network (Fig. 8D), as were the spatially extended bouts of spiking activity (Fig. 9B).

This is remarkable because the control and VPA intrinsic parameters were quite similar in most respects. As noted, the only significant difference between them was in the parameter b, which on average was ∼25 pA larger in the VPA case (control 56.8 ± 4.8 pA versus VPA 82.3 ± 6.5 pA). That this increase was crucial was apparent when we ran the simulations on the control network again, leaving all of the parameters the same except for b, which we increased by 25 pA. Under these conditions, the firing rate and spatiotemporal effects were all absent (data not shown). Likewise, rerunning the simulations on the VPA network, with b reduced by 25 pA, caused the aberrant effects of excessive NMDA current to reappear. We can conclude that the changes in VPA intrinsic neuronal physiology, however subtle, are well placed to counter the changes in VPA NMDA synaptic currents.

The conclusion is supported by the fact that intrinsic differences between control and VPA neurons were confined to the early postnatal ages at which NMDA currents were different. We fitted 16 control and 16 VPA recordings obtained using tissue from older (>1 month) animals to the parameters of the Brette-Gerstner model. In this case, there were no significant differences in any of the parameters, including b (p > 0.6, t test). When the fitted parameters were placed into the two-dimensional networks, the behaviors of the control and VPA networks were indistinguishable (Fig. 10).

Figure 10.

Networks built using older recordings show no control-VPA differences. Recordings from animals older than P30 were fitted to the Brette-Gerstner neuron model and placed into the two-dimensional networks. Shown are spike rastergrams for the control network (left) and the VPA network (right).

It would be interesting—and would support the conclusion further—to perform network simulations using data from animals even younger than P17–P18. In particular, studying the age range around P10 would be useful given the fact that VPA intrinsic and synaptic abnormalities are larger than they are a week later. However, we were unable to obtain adequate fits between the ∼P10 experimental data and the Brette-Gerstner neuron model. In this age range, neuronal firing characteristics are still rather immature, as we noted earlier. For example, spike inactivation is common and spike broadening is pronounced. The Brette-Gerstner model, with its single adaptation current and its fixed voltage threshold, cannot capture these kinds of firing behaviors (neither can the Izhikevich model or other models of this class) (Izhikevich, 2010). In principle, one might be able to do so if one were to embellish the model with additional adaptation currents and/or conductances and a variable threshold. But such embellishment would mean introducing a new set of adjustable parameters, which would undermine the value of the approach.

Discussion

Young VPA rats (∼P14) have been the subject of an extensive and impressive series of physiological experiments (Rinaldi et al., 2007, 2008a,b; Markram et al., 2008). These have identified abnormalities in neuronal excitability, synaptic transmission and connectivity, and synaptic plasticity. One of the two motivations for our own experiments was to replicate, in layer 2/3 mPFC neurons, the findings on excitability and basal synaptic properties. Broadly speaking, we were successful at this. Our experiments on young animals (<P22) revealed impaired intrinsic excitability and excessive NMDA currents quite similar to those of the earlier studies. The one point of partial disagreement was in the amplitude and connectivity of AMPA synapses. Rinaldi et al. (2008b) performed recordings of pairs of connected layer 5 pyramidal neurons and found that, when neurons were within 50 μm of each other, AMPA connections were both weaker and more numerous in VPA tissue. Our recordings of AMPA-mediated mEPSCs did not show evidence of this; neither mEPSC amplitude nor mEPSC frequency was different when measured in VPA neurons. However, mEPSC experiments sample all of a neuron's synapses, not just those originating from nearby neurons. It may be that the excessive local connectivity observed by Rinaldi and colleagues is limited to the cortical microcolumn, and that our experiments, which were designed to give a broad-brush picture of layer 2/3 physiology, were unable to detect it.

The other, more pressing motivation for our experiments was to examine how VPA physiological abnormalities changed over postnatal time. Development is a long process and even when neurodevelopmental disorders are triggered prenatally, the outcome for any particular person depends on the interplay between individual experience and postnatal plasticity (Rice and Barone, 2000; Ospina et al., 2008; Fagiolini et al., 2009). We found that differences between control and VPA neurons decreased as animals matured, and disappeared altogether by ∼P30. This is an age in rats by which the most rapid part of prefrontal physiological development has ended (Zhang, 2004). We do not yet know how the correction happened, but clarifying the issue is an important task for future studies. It is also a difficult one because of the diversity of biophysical processes important for experience-dependent refinement of neural circuits (Nelson and Turrigiano, 2008).

Homeostatic compensation

Of special interest to the present study is what has been called “homeostatic plasticity,” the idea that there are regulatory mechanisms that maintain the stability and functionality of neural circuits in the face of challenges posed by developmental events, learning, and injury (Turrigiano, 2011). Examples include upregulation of excitatory synaptic currents in visual cortex following monocular deprivation (Desai et al., 2002) and downregulation of dendritic HCN channels in barrel cortex following whisker trimming (Breton and Stuart, 2009). Studies of homeostatic plasticity, comprised mainly of pharmacological manipulations in vitro and sensory manipulations in vivo, have demonstrated that the nature of compensatory changes depends upon brain area, developmental age, and cell identity. In some cases, multiple compensatory mechanisms are engaged simultaneously (Turrigiano, 2011).

This diversity indicates that the nervous system possesses many tools with which to respond to developmental challenges, and suggests there may exist “multiple solutions” that produce similar outcomes at both neuronal and network levels (Marder and Goaillard, 2006). Indeed, a number of examples of this sort have been identified, following genetic manipulations. To cite one, a reduction of dendritic H currents by HCN1 gene deletion is met by an increase in background GABA_A currents through a selective upregulation of GABA_A α5 subunit expression (Chen et al., 2010). The compensation is such that layer 5 pyramidal neurons of HCN1-knock-out mice exhibit normal synaptic summation, even though summation in wild-type neurons depends critically on the H current. To cite another, a functional knockdown of extrasynaptic GABA_A receptors in cerebellar granule cells is matched by an upregulation of a leak potassium conductance (Brickley et al., 2001). Here, the compensation not only maintains neuronal function but allows for normal motor function.

The present study suggests that physiological development of VPA cortex may represent a different example of homeostatic compensation—one in which the perturbation is produced not by genetic manipulation but by teratogenic insult. It is possible for NMDA synaptic currents and spike-triggered adaptation to be complementary in this sense, especially with respect to generation of network activity, because they share the same slow kinetics (Wang, 1999, 2001; Faber, 2010). The evidence is mixed about how effective the compensation is. On the one hand, neocortical slices taken from young VPA animals are hyper-reactive when subjected to strong electrical stimulation (Rinaldi et al., 2008b). On the other hand, young VPA animals are not at any greater danger of epileptic seizure than their control counterparts, and most of the reported behavioral effects of prenatal VPA exposure on rodents are mild (for review, see Markram et al., 2007).

The one consequence of excessive NMDA currents that intrinsic adaptation perhaps cannot compensate fully is enhanced synaptic plasticity, because of the particular importance of calcium influx through NMDA receptors (Rinaldi et al., 2008a). Even here tradeoffs are possible, especially for plasticity induced under naturalistic conditions (i.e., natural spike trains rather than stereotyped induction protocols). Whereas large NMDA currents bias synapses toward potentiation, spike-triggered adaptation biases them toward depression by reducing firing rates and temporal fidelity (Sourdet et al., 2003) and increasing membrane conductance (Delgado et al., 2010). Disentangling the two effects is difficult, but there are experimentally tractable ways of doing so. One way is to perform intracellular recordings from synaptically coupled pairs of neurons and to drive each with simulated inputs, introduced using dynamic clamp, to produce “in vivo-like” activity (Destexhe and Bal, 2009). If the spike trains of the coupled neurons are correlated, through correlations in the inputs, one would anticipate synaptic strengthening. The question would then be whether plasticity is stronger for VPA neurons because of increased NMDA currents, weaker because of increased adaptive currents, or the same because the two effects balance each other.

Valproate teratogenicity

Development of VPA physiology is important not only as an example of homeostatic regulation, but because of valproate's use in the treatment of epilepsy, migraine, and bipolar disorder (Fairgrieve et al., 2000; Holmes et al., 2001; Contag and Bushnell, 2010; Galbally et al., 2010). The risk of a malformation with valproate monotherapy has been estimated at ∼10%, compared with a risk of ∼4% with carbamazepine monotherapy and ∼3% with lamotrigine monotherapy (Bromfield et al., 2008; Tomson and Battino, 2008). At three years of age, children exposed to valproate in utero have IQ scores 6–9 points lower than those of children exposed to carbamazepine, lamotrigine, or phenytoin (Meador et al., 2009). And one in 10 valproate-exposed children meet the diagnostic criteria for autism, with many of the remainder experiencing speech delays and/or one or two autistic features (Moore et al., 2000; Rasalam et al., 2005).

The connection to autism especially has created considerable interest in the rodent model (Rodier et al., 1996; Arndt et al., 2005). When exposed to VPA near the time of neural tube closure, rats and mice exhibit neuroanatomical and behavioral abnormalities similar to those observed in people with autism. One outcome of the work on the VPA rodent as an autism model is a general theory of autism, proposed by Markram et al. (2007), called “Intense World Syndrome.” The theory postulates that the core pathology of the autistic brain is hyper-reactivity and hyper-plasticity of cortical circuits, leading to hyper-perception, hyper-attention, and hyper-memory. Previous physiological studies of early postnatal VPA cortex, cited above, supported this idea through the evidence they provided of excessive synaptic transmission and plasticity. By contrast, the results of the present study tend to weaken the argument, because we found that NMDA currents had been restored to control levels by ∼P30. However, it may be that excessive NMDA-dependent plasticity during early development creates hyper-connected circuits that display aberrant response properties in adulthood in the manner the intense world theory prescribes. A useful experiment would be to reduce NMDA transmission in young VPA cortex by application of an antagonist (Colonnese et al., 2003). If NMDA and adaptive currents are coupled in the manner we have suggested, both abnormalities might be reduced as a result. What would be especially important is if the behavioral effects observed in adult VPA animals were also mitigated.

A related idea about autistic pathophysiology is that an excitatory-inhibitory imbalance is involved (Rubenstein and Merzenich, 2003; Ramocki and Zoghbi, 2008). To date, this question has been addressed only indirectly in the VPA model. Gogolla et al. (2009) reported a loss of parvalbumin-staining neurons in parts of adult VPA mouse neocortex, with the deficiency confined to a single hemisphere. Gandal et al. (2010), also using adult VPA mice, reported a reduction of phase locking in the γ band (30–50 Hz) of the auditory evoked signal. Fast-spiking interneurons contain parvalbumin and are believed to be critical for the generation of γ oscillations (Cardin et al., 2009; Sohal et al., 2009). Examining inhibitory transmission using physiological recordings is therefore an important goal, though these reported effects suggest differences may be subtle.