Cellular and Network Contributions to Vestibular Signal Processing: Impact of Ion Conductances, Synaptic Inhibition, and Noise

Abstract

Head motion-related sensory signals are transformed by second-order vestibular neurons (2°VNs) into appropriate commands for retinal image stabilization during body motion. In frogs, these 2°VNs form two distinct subpopulations that have either tonic or highly phasic intrinsic properties, essentially compatible with low-pass and bandpass filter characteristics, respectively. In the present study, physiological data on cellular properties of 2°VNs of the grass frog (Rana temporaria) have been used to construct conductance-based spiking cellular models that were fine-tuned by fitting to recorded spike-frequency data. The results of this approach suggest that low-threshold, voltage-dependent potassium channels in phasic and spike-dependent potassium channels in tonic 2°VNs are important contributors to the differential, yet complementary response characteristics of the two vestibular subtypes. Extension of the cellular model with conductance-based synapses allowed simulation of afferent excitation and evaluation of the emerging properties of local feedforward inhibitory circuits. This approach revealed the relative contributions of intrinsic and synaptic factors on afferent signal processing in phasic 2°VNs. Additional extension of the single-cell model to a population model allowed testing under more natural conditions including asynchronous afferent labyrinthine input and synaptic noise. This latter approach indicated that the feedforward inhibition from the local inhibitory network acts as a high-pass filter, which reinforces the impact of the intrinsic membrane properties of phasic 2°VNs on peak response amplitude and timing. Thus, the combination of cellular and network properties enables phasic 2°VNs to work as a noise-resistant detector, suitable for central processing of short-duration vestibular signals.

Introduction

Processing of sensory signals in central networks is determined by intrinsic cellular properties and by the synaptic circuitry in which the neurons are embedded (Grillner, 2003). This is well documented in the acoustic system where inhibitory circuits along with intrinsic membrane properties shape the response dynamics of auditory signals (Grothe, 2003; Mathews et al., 2010). In contrast to the organizational complexity of auditory signal processing in a multitude of brainstem nuclei, the relatively simpler vestibulo-motor signal transformation along sequentially organized three-neuronal reflex pathways (Straka and Dieringer, 2004) is ideally suited to study how cellular and network properties contribute to the processing. The major computational step in transformation of head motion-related sensory signals into extraocular motor commands is performed by second-order vestibular neurons (2°VNs), which are distinguished in all vertebrates into subpopulations based on cellular properties (Straka et al., 2005). The different subtypes form the central neuronal elements of frequency-tuned parallel information streams (Straka et al., 2009) that are the functional basis for modifiable/nonmodifiable or linear/nonlinear vestibulo-ocular signaling pathways (Lisberger et al., 1983; Clendaniel et al., 2002; Ramachandran and Lisberger, 2008).

Computational models facilitate the understanding of how properties of neuronal populations interact with emerging properties of the circuits in which these neurons are embedded to produce a particular output. Even though many models explain on a systems level various aspects of vestibular-controlled eye movements (Anastasio and Robinson, 1989; Minor and Goldberg, 1991; Raphan and Cohen, 2002; Green and Angelaki, 2003; Ramachandran and Lisberger, 2006; Glasauer, 2007), a link with cellular vestibular models (Quadroni and Knöpfel, 1994; Av-Ron and Vidal, 1999) or implementation of distinct cellular properties and morpho-physiological aspects is rare (Cartwright et al., 2003). Cellular models of mammalian type A and B medial vestibular nucleus neurons, in contrast, primarily focus on the impact of ion conductances on vestibular signal processing (Quadroni and Knöpfel, 1994; Av-Ron and Vidal, 1999) but mostly lack implementation of emerging network properties through synaptic inputs of surrounding circuitry. However, several studies (Goldberg et al., 1987; Camp et al., 2006; Bagnall et al., 2008; Biesdorf et al., 2008) suggest that differential insertion of particular types of 2°VNs into local circuits is essential for dynamically adequate sensory-motor transformation and formation of parallel signaling pathways. Furthermore, a modeling approach is of clinical relevance, to investigate hypotheses on the pathogenesis of frequency-specific loss of vestibular function in patients suffering, for example, from gentamicin ototoxicity (Ishiyama et al., 2006).

The solid knowledge of cellular physiology and network connectivity of frog 2°VNs (Beraneck et al., 2007; Biesdorf et al., 2008; Pfanzelt et al., 2008) was used to construct conductance-based Hodgkin–Huxley-type spiking models that were supplemented by excitatory and inhibitory synaptic inputs to distinguish between contributions of cellular and network properties to signal processing and to test the simplest biophysical components that reproduce the diversity of 2°VN response dynamics in vitro. Extension to a population model further allowed making predictions on intrinsic and synaptic contributions to signal transformation during different stimulus paradigms including asynchronous afferent fiber input and synaptic noise.

Materials and Methods

Electrophysiology.

In vitro recordings of central vestibular neurons were performed in isolated brains of 12 adult male and female grass frogs (Rana temporaria) and complied with Principles of Animal Care (publication no. 86-23; revised 1985 by the National Institutes of Health). The experimental methods for the dissection of the frog whole-brain preparation were described previously in detail (Beraneck et al., 2007; Pfanzelt et al., 2008). Neurons were intracellularly recorded with sharp high-resistant glass microelectrodes (80–100 MΩ) and identified as 2°VNs by monosynaptic EPSPs after electrical stimulation of individual ipsilateral semicircular canal nerve branches (Straka et al., 1997). All 2°VNs were subdivided into either phasic or tonic neurons based on the responses to the injection of long, positive current steps (Straka et al., 2004). Neuronal filter properties of 2°VNs were determined by evaluating subthreshold and spike responses after intracellular injection of sinusoidally modulated currents (length T = 30 s) with quadratically increasing frequency (maximum f_max = 100 Hz) (ZAP stimuli): I_ZAP(t) = I₀sin(2πf(t)t/3) + I_hold, with f(t) = f_max(t/T)² (Beraneck et al., 2007). Intrinsic membrane properties were further analyzed using impedance magnitude functions obtained with piecewise nonlinear electrode compensation (Rössert et al., 2009b). The processing of synaptic signals in 2°VNs was studied by applying trains of single current pulses (0.2 ms) to individual ipsilateral semicircular canal nerves with intensities that ranged between 1.5 and 4× threshold for eliciting a postsynaptic field potential response in the vestibular nuclei. The stimulus trains consisted of pulses with interstimulus intervals that were sinusoidally modulated with a peak frequency of 70 Hz (Pfanzelt et al., 2008).

Computational models.

All time-domain simulations were performed using the NEURON simulation environment (Carnevale and Hines, 2009). To simulate tonic and phasic neurons, Hodgkin–Huxley-type models were constructed with regard to simplicity, fast simulation, and effective data fitting. Complexity was only added when needed to reproduce the observed behavior (Av-Ron and Vidal, 1999). The minimal models consisted of an initial compartment, termed soma, and a passive distal section (Rall, 1962) with nine compartments (N = 9). The model is described by the following equations (“time-domain” models):

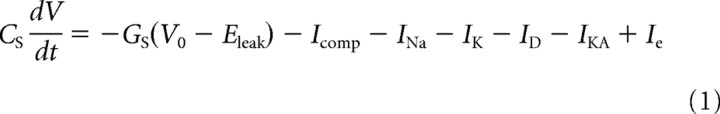for the soma, and

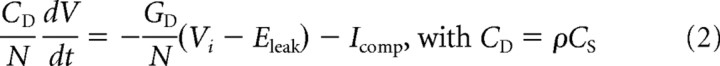for the distal compartments (i = [1,N]). V₀ is the membrane potential of the soma and V_i (i = [1,N]) is the membrane potential of one distal compartment. C_S and C_D, and G_S and G_D are the capacitance (C) and resting membrane conductance (G) of the soma (S) and the entire distal section (D), respectively; E_leak is the reversal potential of the leak current, ρ is the ratio between the total distal area and the area of the soma. I_Na and I_K are the sodium and delayed-rectifier potassium conductances responsible for action potential generation, I_D is a low-threshold potassium conductance responsible for the bandpass filtering properties in phasic neurons, and I_KA is an adaptation current responsible for the spike rate adaptation in tonic neurons. I_e is the current applied through the electrode. The area A of the cylindrical compartments is computed using a specific capacitance of C_m = 1 μF/cm² and the length and diameter are set to L = diam = $\sqrt{A/\pi }$. I_comp is the current from neighboring compartments and described by the following:

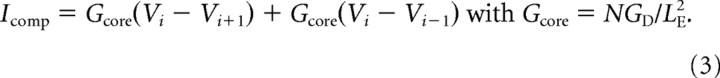The index i is 0 for the soma or 1 to N for the distal compartments. L_E is the electrotonic length (Rall, 1969).

The kinetics of the voltage-dependent Na⁺ current was modeled with equations given by Frankenhaeuser and Huxley (1964) for the amphibian sodium current, adjusted to a temperature of 14°C at which all neuronal recordings were made (Beraneck et al., 2007) using the temperature coefficient Q₁₀ and Kirchoff's law for the driving force as follows:

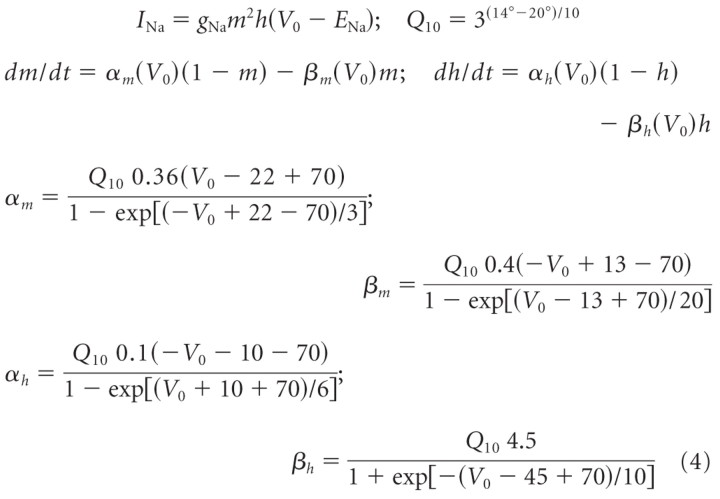E_Na is the sodium reversal potential; m and h are the voltage-dependent activation and inactivation gating variables, respectively; α and β are the respective rate constants of m and h; g_Na is the maximum sodium conductance.

To reproduce the typical class 1 excitability [definition by Hodgkin (1948); continuous spike frequency–current curve] as seen in tonic 2°VNs (Straka et al., 2004), a delayed-rectifier K⁺ (I_K) current with high activation threshold was necessary (Izhikevich, 2006; Prescott et al., 2008). Another indication for the presence of a high-threshold I_K channel was the absence of a resonance in tonic 2°VN impedance measurements during subthreshold membrane potential depolarization (Beraneck et al., 2007; Rössert et al., 2009b). Assuming identical delayed-rectifier K⁺ currents for tonic and phasic 2°VNs, the channel was modeled as a generic high-threshold potassium type (Prescott et al., 2008) using the Morris–Lecar formalism (Morris and Lecar, 1981) with b_n = −20 mV and g_n = 10 mV as follows:

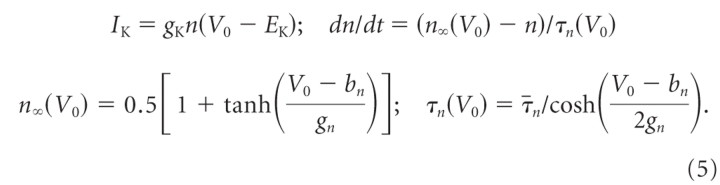E_K is the potassium reversal potential; n is the voltage-dependent activation-gating variable; n_∞ and τ_n are the corresponding voltage-dependent steady-state activation variable and time constant, respectively; g_K is the maximum conductance.

In phasic 2°VNs, a 4-AP-sensitive low-threshold Kv1.1 potassium channel is implicated in the particular response dynamics of these neurons (Beraneck et al., 2007). Since this channel is not yet fully characterized in frogs, it was modeled using the formalism for the similar low-threshold Kv1.1 potassium channel in mammalian ventral cochlear nucleus neurons (Rothman and Manis, 2003). The factor t_fac was added to the original formula to account for time constant adjustments as follows:

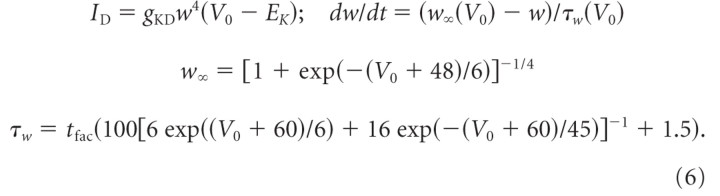E_K is the potassium reversal potential; w is the voltage-dependent activation-gating variable; w_∞ and τ_w are the corresponding voltage-dependent steady-state activation variable and voltage-dependent time constant, respectively; g_KD is the maximum conductance.

Tonic 2°VNs exhibit a spike rate adaptation during depolarizing current pulse injections (Straka et al., 2004). Although the definite mechanism for this adaptation remains unknown, the second, late afterhyperpolarization as generally seen in tonic 2°VNs (Straka et al., 2004) is very similar to that of mammalian type B MVN neurons (Johnston et al., 1994; Quadroni and Knöpfel, 1994; Peusner et al., 1998; Av-Ron and Vidal, 1999) and thus strongly suggests a potassium-mediated adaptation as in the latter neuronal type. It was therefore modeled as an abstract spike-dependent potassium conductance (Benda and Herz, 2003) that can be easily fitted to spike frequency data as follows:

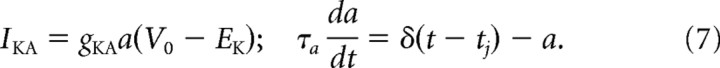Here, a is the activation-gating variable; δ(t − t_j) the Dirac function; and t_j, the time of the last spike. Thus, each time a spike occurs, the channel conductance is increased by g_KA and decays with the voltage-independent time constant τ_a.

Frequency-domain model formulation and fitting.

For phasic neurons, a phenomenological impedance function of a subthreshold model was fitted to frequency-domain responses obtained during different amplitudes of constant current injections (I_hold) (Rössert et al., 2009b). This model is similar to the “time-domain” model, but with only one active conductance I_D, which was assumed to be the dominant active conductance close to the resting potential. The total membrane current is the sum of the capacitive displacement current, the ionic current I_D, and the constant electrode holding current I_hold as follows:

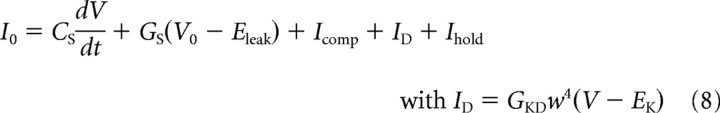for the soma and

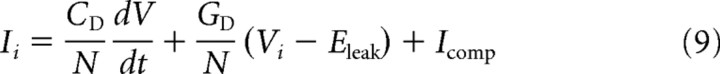for a distal compartment.

The corresponding admittance function can be described as follows. For a general derivation of frequency-domain model formulations, see Pfanzelt et al. (2008). A lower index V signifies that the formula is evaluated at a certain voltage, such as w_V = w_∞(V), as follows:

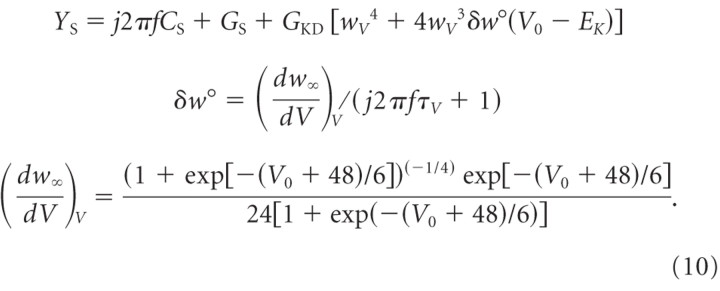The admittance Y_D of a single passive distal compartment is as follows:

The complete input admittance, Y₀, of the entire compartmental model as seen at the soma can be derived by reducing the network to an equivalent driving point admittance (Murphey et al., 1995). The complete input admittance can be derived by beginning at the distal end of the cable and working toward the soma as follows:

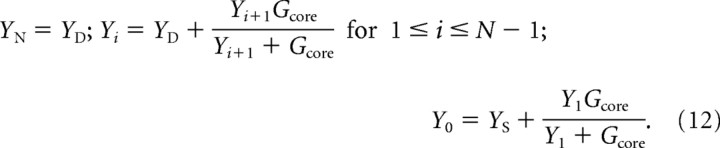The specific steady-state voltage V_i for each compartment at different holding currents I_hold was computed by means of a find root calculation. Finally, the inverse of the admittance, the impedance, was used and the magnitude of the impedance was fitted to the frequency response data of three representative phasic 2°VNs. The fitted parameters were L_E, ρ, C_S (in picofarads), G_S (in nanosiemens), G_D (in nanosiemens), g_KD (in millisiemens per square centimeter), and t_fac. The reversal potentials were set to E_K = −90 mV and E_leak = −70 mV. The fit was realized using the nonlinear least-squares fitting function “lsqnonlin” in MATLAB (The MathWorks). The resulting parameters for all phasic frequency-domain models are summarized in Table 1.

Table 1.

Model parameters

	LE	ρ	CS (pF)	GS (nS)	GD (nS)	gNa (S/cm2)	gK (S/cm2)	τ̄n (ms)	gKD (mS/cm2)	tfac	gKA (mS/cm2)	τa (ms)
Phasic impedance
PI1	0.68	3.71	195.81	45.44	10.70	—	—	—	1.51	1.06	—	—
PI2	0.95	6.99	90.93	9.42	65.80	—	—	—	5.13	0.84	—	—
PI3	0.67	1.76	127.77	27.26	6.30	—	—	—	10.00	1.10	—	—
Mean	0.77	4.15	138.17	27.37	27.60	—	—	—	5.55	1.00	—	—
SD	0.16	2.64	53.21	18.01	33.16	—	—	—	4.26	0.14	—	—
Tonic
T1	1.05	6.22	84.28	15.53	3.65	0.074	0.016	7.2	—	—	0.073	58.58
T2	0.67	6.86	93.13	36.56	5.99	0.108	0.013	3.1	—	—	0.123	51.08
T3	0.98	7.89	118.12	38.10	12.97	0.098	0.013	4.1	—	—	0.105	44.32
T4	1.22	8.46	75.76	32.50	8.05	0.125	0.009	2.9	—	—	0.106	46.04
T5	1.50	9.32	111.47	30.84	1.60	0.090	0.018	6.4	—	—	0.240	37.71
T6	0.91	6.41	62.80	17.74	4.34	0.106	0.010	6.0	—	—	0.171	65.18
T7	0.75	5.14	100.24	23.53	11.10	0.112	0.015	2.6	—	—	0.156	42.17
Mean	1.01	7.19	92.26	27.83	6.81	0.102	0.013	4.6	—	—	0.139	49.30
SD	0.28	1.44	19.60	8.98	4.12	0.017	0.003	1.9	—	—	0.055	9.68
Phasic
P1	1.66	4.47	39.39	35.88	8.75	0.102	0.013	4.6	3.43	1	—	—
P2	0.86	4.68	27.14	52.02	27.84	0.102	0.013	4.6	1.49	1	—	—
P3	0.79	2.54	32.32	18.97	12.58	0.102	0.013	4.6	2.71	1	—	—
P4	1.42	8.84	38.76	6.85	3.35	0.102	0.013	4.6	4.74	1	—	—
P5	1.05	2.22	23.28	38.80	20.09	0.102	0.013	4.6	0.71	1	—	—
P6	0.73	5.21	22.20	34.23	2.24	0.102	0.013	4.6	1.66	1	—	—
P7	1.41	9.04	41.64	35.03	30.84	0.102	0.013	4.6	4.40	1	—	—
P8	0.75	6.20	46.60	24.00	17.98	0.102	0.013	4.6	2.57	1	—	—
P9	0.70	6.13	12.26	27.85	13.26	0.102	0.013	4.6	7.08	1	—	—
P10	0.73	9.45	36.60	42.70	4.45	0.102	0.013	4.6	1.23	1	—	—
P11	1.09	9.73	56.85	4.41	12.86	0.102	0.013	4.6	8.19	1	—	—
P12	1.17	2.26	48.82	20.29	43.94	0.102	0.013	4.6	1.97	1	—	—
P13	1.15	2.48	21.75	18.46	9.89	0.102	0.013	4.6	1.96	1	—	—
P14	0.77	5.18	61.79	13.88	20.67	0.102	0.013	4.6	1.73	1	—	—
P15	0.88	8.65	74.77	29.45	7.76	0.102	0.013	4.6	1.86	1	—	—
P16	0.81	8.75	37.68	37.71	7.91	0.102	0.013	4.6	0.85	1	—	—
P17	1.10	9.21	22.99	43.65	12.20	0.102	0.013	4.6	0.75	1	—	—
Mean	1.00	6.18	37.93	28.48	15.09	0.102	0.013	4.6	2.78	1	—	—
SD	0.29	2.80	16.30	13.34	10.95	—	—	—	2.17	—	—	—

Parameters for the Hodgkin–Huxley-type models of phasic and tonic 2°VNs (see details in Materials and Methods). For both neuronal types, time-domain models have been fitted to frequency–current (f–I) and membrane potential decay responses (cells T1–T7 and P1–P17). In addition, frequency-domain models have been fitted to impedance magnitude measurements of three phasic neurons (cells PI1–PI3). The mean values (mean) and standard deviations (SD) are indicated for each fit method and cell type.

Time-domain fitting to experimental data.

The time-domain models of tonic and phasic 2°VNs were adjusted to experimental data using the simulated annealing algorithm implementation “simulannealbnd” in MATLAB (The MathWorks). The error function consisted of two parts. Similar to Pospischil et al. (2008), the first part was based on the firing behavior of the cells (f–I fit) and was the sum over the absolute values of the differences between several interspike frequencies: from onset of DC injection to the first spike (f₀), between the first and second interspike interval (f₁, f₂) and the mean of the firing frequencies after 150 ms of DC injection (f_∞) where spike rate adaptation was complete. If no spikes occurred to compute f₁ − f_∞, the corresponding values were set to 0, which corresponds to an interspike interval of infinity. The values were taken at 4–13 different DC levels, depending on the cell. The second part was the sum over the absolute values of the differences in the membrane potential at the end of small amplitude current injections (−0.3 to 0.3 nA) (V_decay fit). To prevent fitting of electrode artifacts, the first 1 ms after the stimulation was excluded from the fit. This led to an overall error function of the following:

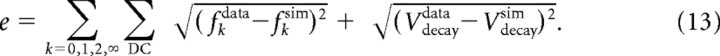The adjusted parameters for tonic neurons were L_E, ρ, C_S (in picofarads), G_S (in nanosiemens), G_D (in nanosiemens), g_Na (in siemens per square centimeter), g_K (in siemens per square centimeter), ¯τ_n (in milliseconds), g_KA (in millisiemens per square centimeter), and τ_a (in milliseconds); for abbreviations, see above. Because of the limited information content in the spiking data of phasic 2°VNs, the fitted parameters in the latter neurons were L_E, ρ, C_S (in picofarads), G_S (in nanosiemens), G_D (in nanosiemens), and g_KD (in millisiemens per square centimeter). For g_Na (in siemens per square centimeter), g_K (in siemens per square centimeter), and ¯τ_n (in milliseconds), the mean values from the tonic fit have been used. For t_fac, the mean from the frequency domain fit was chosen. The parameters for all tonic and phasic neurons are summarized in Table 1. Unless stated otherwise, the reversal potentials for all models were E_Na = 55 mV, E_K = −90 mV, and E_leak = −70 mV.

Model for synaptic activation.

To simulate synaptic activation of 2°VNs, dual-exponential conductance-based synapses were added to the soma of the compartmental models using the following equation: I_s = g_sF [exp(−t/t₂) − exp(−t/t₁)] (V₀ − E_s), with τ₁ as rise and τ₂ as fall time constant (Johnston and Wu, 1994). The index s is E for excitatory or I for inhibitory synapses. The peak conductance for a single synaptic event was defined by g_s; E_s indicates the reversal potential and V₀ the somatic membrane potential. The scaling factor F is defined such that the peak of the dual-exponential is 1. For excitatory synapses, values were τ₁ = 5 ms, τ₂ = 50 ms, and E_E = 0 mV (Pfanzelt et al., 2008). Disynaptic GABAergic and glycinergic feedforward inhibition (Pfanzelt et al., 2008) was combined into one inhibitory synaptic process with τ₁ = 5 ms, τ₂ = 150 ms, and E_I = −75 mV (Biesdorf et al., 2008). Synapses were implemented by the function “exp2syn” in the NEURON simulation environment. To mimic the monosynaptic excitation after electrical stimulation of vestibular nerve afferent fibers in the periphery a delay of 3.4 ms (Biesdorf et al., 2008), from the stimulus to the onset of the EPSP, was used. This delay is composed of stimulus utilization time for activation of vestibular afferents, conduction time from the site of stimulation in the periphery to central targets, and synaptic delay between vestibular afferents and 2°VNs (Straka et al., 1997). For the inhibition by local vestibular interneurons, a delay of 1.8 ms for one synapse (Holler and Straka, 2001) was used. Unless stated otherwise, g_E = 10 μS and g_I = 20/N nS, where N is the number of inhibitory interneurons. To simulate the synaptic activation by ipsilateral semicircular canal nerves, each single current pulse of the sinusoidally modulated stimulus train was assumed to trigger one synaptic event (Pfanzelt et al., 2008).

Spike rate analysis of responses after stimulation with pulse trains.

For individual tonic cells or models, the instantaneous firing rate (IF) was calculated as the inverse of the interspike interval and assigned to the time of the second spike of the interval to ensure a causal relationship between IF and input current (du Lac and Lisberger, 1995). The spike response transfer function for each frequency was calculated as ΔIF/ΔI, where ΔIF is the amplitude of the instantaneous firing rate IF and ΔI is the amplitude of the stimulation current I_e (Beraneck et al., 2004). The phase shift was calculated as the position of ΔIF with respect to the peak of the sine wave, provided that at least two spikes were triggered by the sine wave.

Population model.

For the population model, a total of 200 phasic, 200 tonic cells, or the combination of 100 tonic and 100 phasic neurons have been simulated. The parameters have been drawn from a lognormal distribution using the mean and SD values estimated in the time-domain fits (Table 1). The inhibition by local interneurons was implemented by adding inhibitory synapses to each phasic 2°VN from 10 randomly selected tonic 2°VNs. Instead of using a classical spike rate analysis to evaluate the responses of the tonic and phasic cell populations, a more biological relevant analysis was used: the functional output of each simulated tonic and phasic neuronal population was evaluated by calculating the postsynaptic conductance (with a normalized synaptic strength of 1) that is evoked by the spikes from the simulated two vestibular neuronal populations, respectively. The postsynaptic conductance was simulated with α functions [g_s = t/τ_synexp(−(t − τ_syn)/τ_syn)] (Dayan and Abbott, 2001) using two different time constants, τ_syn = 30 ms or τ_syn = 5 ms mimicking temporal evolution of the synaptic conductance. The resulting population responses were called computed postsynaptic conductance G_S.

The population model was stimulated in two ways. To simulate the responses to sinusoidally modulated pulse trains, each model cell was excited as described above with g_E = 15 nS for phasic and g_E = 5 nS for tonic neurons. To simulate noisy synaptic afferent inputs during sinusoidal head rotation, a sinusoidal current I(t) = I₀ + I_maxsin(2πft) was injected into each cell (Hospedales et al., 2008). For this set of experiments, only excitatory responses to ipsiversive rotations were considered; thus, all negative values of I(t) were set to zero. The maximum of I(t) was set individually for each neuron to 1.5 * the rheobase threshold (I_th), estimated before with current steps of 100 ms duration. Since many frog vestibular afferents show a low resting activity in vivo (Blanks and Precht, 1976) and many frog central vestibular neurons are silent or have a low resting discharge (Dieringer and Precht, 1977, 1979), continuous synaptic input appears to play a minor role in the frog vestibular system. However, to test the impact of spontaneous afferent activity, which for some fibers exceeds 10 spikes/s (Honrubia et al., 1981, 1989; Baird and Lewis, 1986; Myers and Lewis, 1991), two different parameter sets were used, termed “rectified” with I_max = 1.5 * I_th and I₀ = 0 to simulate no afferent resting activity and “continuous” with I_max = 0.75 * I_th and I₀ = 0.75 * I_th to simulate afferent resting activity. To add synaptic noise and unsynchronized responses from single afferent fibers, a noise current ε(t) = N(0,σ) filtered with τ = 2 ms (Hospedales et al., 2008) was added which resulted in a total excitatory current of I_S(t) = I(t) + ε(t). For the implementation of the noise current ε(t) in NEURON, see Arsiero et al. (2007). Unless stated otherwise, SD σ of the noise current was set to 60 pA (Hospedales et al., 2008). Even though this stimulation used a current-based synaptic model that neglects conductance fluctuations, this model has been proven exceptionally useful to provide insight into basic neuronal signal transmission during noisy input (Arsiero et al., 2007; Hospedales et al., 2008). To calculate the sensitivity of the population for several frequencies f, the population was stimulated with frequencies that varied from 0.1 to 100 Hz. After an onset latency of 1 s, the amplitude ΔG_S was estimated from the mean of 20 sinusoidal stimulus cycles.

Results

Differential organization of intrinsic properties of frog second-order vestibular neurons

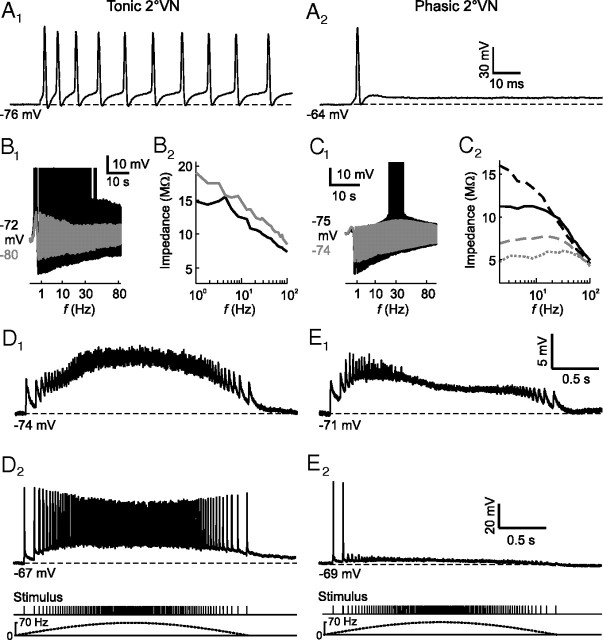
In frogs, 2°VNs form two well separated neuronal populations (tonic–phasic neurons) that differ in intrinsic and synaptic response dynamics (Straka et al., 2004; Pfanzelt et al., 2008). Tonic 2°VNs exhibit a sustained discharge (Fig. 1A₁) during long positive current steps with a relatively linear current–frequency relationship, whereas phasic 2°VNs fire only few spikes immediately after stimulus onset (Fig. 1A₂), consistent with different filter properties of the two neuronal types (Beraneck et al., 2007). These firing behaviors correspond to class 1 and class 3 excitability, respectively, as defined previously by Hodgkin (1948). Subthreshold responses (Fig. 1B₁, gray trace) and spike discharge (Fig. 1B₁, black trace) in tonic 2°VNs exhibit low-pass filter-like properties. In contrast, phasic 2°VNs have bandpass filter-like characteristics as evidenced by the presence of a membrane potential-dependent subthreshold response peak between 10 and 50 Hz (Fig. 1C₁, gray trace) that generates a particular frequency window for spike discharge (Fig. 1C₁, black trace). Moreover, depolarization causes an increase of the impedance in tonic (Fig. 1B₂) and a decrease in phasic 2°VNs (Fig. 1C₂) (Beraneck et al., 2007; Rössert et al., 2009b). The different, yet complementary filter properties thus render tonic 2°VNs suitable for integration and phasic 2°VNs for differentiation of synaptic inputs.

Figure 1.

Response profiles of tonic and phasic 2°VNs. A, Injection of positive current steps of 1.2 nA evoked a continuous discharge in tonic (A₁) and a single spike in phasic 2°VNs (A₂). B, C, Subthreshold responses (gray traces) and spike discharge (black traces, spikes truncated) of a tonic [I₀ = 0.5 nA, I_hold = 0 (gray trace) and I₀ = 1 nA, I_hold = 0 (black trace)] (B₁) and a phasic 2°VN [I₀ = 0.8 nA, I_hold = 0 (gray trace) and I₀ = 1 nA, I_hold = 0 (black trace)] (C₁) evoked by injection of sinusoidally modulated current (ZAP stimuli) with different amplitudes; impedance magnitude at different holding currents (I_hold) for the tonic 2°VNs [I_hold = 0 (black), I_hold = 0.5 nA (gray)] (B₂) and the phasic 2°VNs [I_hold = 0 (black), I_hold = −0.5 nA (black dashed), I_hold = 0.5 nA (gray dashed), I_hold = 1 nA (gray dotted)] (C₂) shown in B₁ and C₁, respectively. D, E, Typical subthreshold compound EPSPs (D₁, E₁) and spike discharge (D₂, E₂) evoked by stimulation of individual semicircular canal nerve branches with sinusoidally modulated trains of single electrical pulses (peak frequency, 70 Hz) of a tonic (D₁, D₂) and a phasic 2°VN (E₁, E₂). Pulse trains and corresponding sinusoidal modulation is shown at the bottom and apply to all responses in D and E. The calibration bars in A₂, E₁, and E₂, apply to A₁, D₁, and D₂, respectively.

The different intrinsic properties of tonic and phasic 2°VNs correlate with different dynamics of synaptic responses activated by vestibular nerve afferents (Pfanzelt et al., 2008). In tonic 2°VNs, the overall waveform of the compound EPSP, activated by sinusoidally modulated pulse trains, is approximately aligned with the stimulus frequency modulation (Fig. 1D₁;D₂, bottom trace) and spikes are continuously triggered above spike threshold (Fig. 1D₂). In phasic 2°VNs, the compound EPSP has a sharp rise and an early, slow decay, thus causing an advanced response peak relative to the envelope of the pulse train (Fig. 1E₁;E₂, bottom trace). In addition, spikes are triggered only by the first few pulses of the stimulus train (Fig. 1E₂). Physio-pharmacological analyses (Biesdorf et al., 2008; Pfanzelt et al., 2008) suggest that the dynamic response profile of phasic 2°VNs is caused by intrinsic membrane properties as well as emerging properties of the network in which the neurons are embedded. In particular, activation of local inhibitory vestibular feedforward circuits that are composed of tonic-type interneurons (Pfanzelt et al., 2008) might play a major functional role in generating the marked asymmetry of the responses in phasic 2°VNs.

Model of tonic second-order vestibular neurons

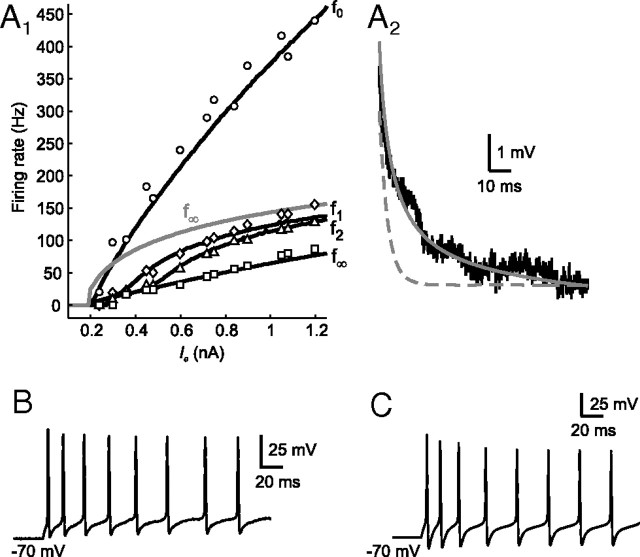
To establish the veracity of the modeling procedure, the fitting results for tonic 2°VN models were compared with the respective intracellular recordings. Figure 2, A₁ and A₂, shows a representative fit of a model cell to the two-part error function consisting of the adapting frequency–current (f–I) response (Fig. 2A₁, black lines) and membrane potential decay after depolarization (Fig. 2A₂, gray solid line). Based on underlying parameters, the spiking behavior of the model cell was reconstructed (Fig. 2C) and reproduced very well the typical firing characteristics of the fitted tonic cell during current step injection (Fig. 2B). The generated model allows studying the effect of the adaptation current I_KA characteristic for tonic 2°VNs. Removal of the latter current results in an f_∞ response (Fig. 2A₁, gray line) that is less linear. This general linearization effect of adaptation has been demonstrated analytically (Ermentrout, 1998). However, the firing behavior of tonic 2°VN models, classified as class 1 excitability (Hodgkin, 1948), remained unchanged after the removal of I_KA as indicated by the continuous f_∞ response (Fig. 2A₁, gray line) (Izhikevich, 2006).

Figure 2.

Comparison between tonic 2°VN data and model. A₁, Fit of a model (T1) (black lines) to frequency–current (f–I) responses of a tonic 2°VN (f₀, circles, f₁, diamonds, f₂, triangles; f_∞, squares); model f_∞ response (gray line) after removal of the adaptation current I_KA (g_KA = 0). A₂, Fit of a model (gray line) to the membrane potential decay (black line) of the same tonic 2°VN after injection of a current step of 0.15 nA; response of a simple RC model (gray dashed line; dendritic compartments removed before fitting to f–I response). B, C, Spike discharge of the fitted tonic 2°VN (B) and the generated model neuron (C) evoked by a depolarizing current step of 0.6 nA.

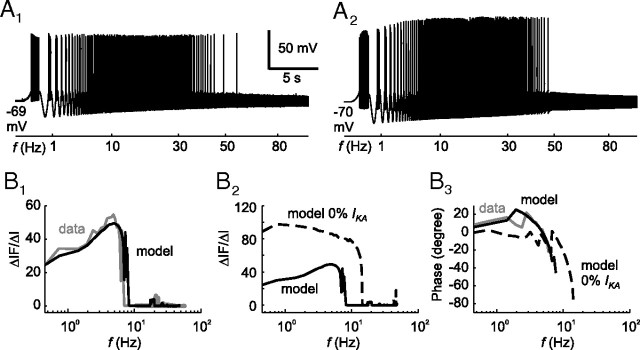
The necessity for generating a compartmental model and fitting with the two-part error function becomes obvious when a simple RC model (distal compartments were removed) was fitted to the frequency–current response. The membrane potential decay of the resulting RC model (Fig. 2A₂, gray dashed line) showed that the membrane time constant was underestimated. In contrast, the compartmental tonic 2°VN models that were fitted with the two-part error function not only reproduced the typical firing behavior during current step injections but also during stimulation with sinusoidally modulated currents with quadratically increasing frequency (ZAP stimuli). After ZAP stimulation, the tonic 2°VNs (Fig. 3A₁) and corresponding model (Fig. 3A₂) activated spikes at the lowest stimulus frequency and stopped firing at ∼50 Hz. This spiking behavior appeared to have simple low-pass filter characteristics; however, closer analysis of the spike rate function at each frequency (ΔIF/ΔI) (Fig. 3B₁) indicated that the neurons (black line) as well as the models (gray line) exhibited a resonant behavior with a peak at low frequencies of ∼5 Hz. This resonant behavior is attributable to the adaptation current I_KA, since removal of this current from the models (Fig. 3B₂, dashed line) resulted in an increased ΔIF/ΔI response with a typical low-pass behavior. However, the adaptation not only influenced the amplitude but also the phase (Fig. 3B₃). Both data and model responses (Fig. 3B₃, gray and black lines, respectively) showed a strong phase lead already at low frequencies, which was considerably reduced after removal of the adaptation current I_KA from the model (Fig. 3B₃, black dashed line). The somewhat surprising combination of low-pass subthreshold and resonant spike discharge is not unusual and likely caused by the presence of high-threshold calcium and calcium-dependent potassium currents (Ermentrout, 1998; Benda and Herz, 2003), as suggested earlier for chicken MVN neurons (du Lac, 1996). In corresponding mammalian type B MVN neuronal models (Av-Ron and Vidal, 1999), apamin-sensitive calcium-dependent (SK type) potassium channels (Serafin et al., 1991a,b; Johnston et al., 1994; Smith et al., 2002) cause a spike rate adaptation and resonance as in frog tonic 2°VNs. Similar spike shape and discharge behavior of the frog and rodent vestibular neuronal type, however, are at variance with their different computational roles in vestibular signal processing in frogs and rodents, respectively (Straka et al., 2005).

Figure 3.

Discharge dynamics of a tonic 2°VN and a tonic model neuron (T1). A, Spike discharge of the tonic 2°VN (A₁) and the corresponding tonic model neuron (A₂), evoked by injection of sinusoidally modulated currents (ZAP stimuli) with I₀ = 0.5 nA and I_hold = 0. B, Discharge behavior during ZAP stimulation (I₀ = 0.5 nA) analyzed at each frequency and plotted as spike rate (ΔIF/ΔI). B₁, Comparison between tonic 2°VNs (gray line) and tonic model neuronal responses (black line). B₂, Response of the model neuron (solid line) and after removal of the adaptation current I_KA (g_KA = 0) (dashed line). B₃, Phase shift of the responses of the recorded tonic 2°VNs (gray line), the tonic model neuron (black line), and the model neuron after removal of the adaptation current I_KA (g_KA = 0) (dashed line). The calibration bars in A₁ apply to A₂.

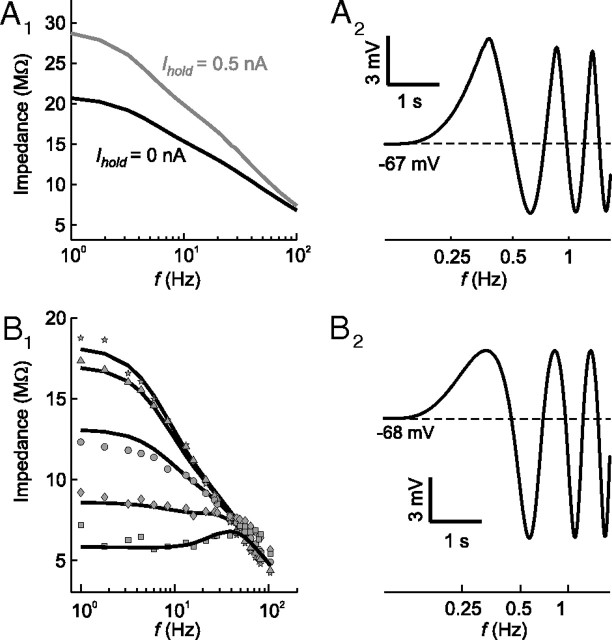
Apart from the reproduction of the typical firing pattern of tonic 2°VNs, the resulting models also showed the typical subthreshold response behavior: the impedance magnitude increased with membrane depolarization (Fig. 4A₁) and during ZAP stimulation the depolarizing response components were larger in magnitude compared with the hyperpolarizing half-waves as shown previously in electrophysiological recordings of these neurons (Fig. 4A₂) (Beraneck et al., 2007). In the model, this effect is caused by a window current of the standard fast sodium conductance, which originated from the overlap of activation and inactivation profiles (Fan et al., 1994; Parri and Crunelli, 1998), rather than from non-inactivating sodium or calcium conductances as previously suggested (Beraneck et al., 2007; Pfanzelt et al., 2008; Rössert et al., 2009b). However, the presence of the latter channels in tonic 2°VNs and a contribution to the described impedance increase with membrane depolarization cannot be entirely excluded, although there is no experimental evidence for this conductance in frog VNs so far. The most parsimonious assumption thus is the presence of a fast sodium window current that causes this particular polarization behavior, compatible with the absence of spontaneous discharge and plateau potentials in frog tonic 2°VNs (Straka et al., 2005). This latter response nonlinearity is usually indicative for the presence of persistent sodium currents, which have been shown in a subgroup of guinea pig type B MVN neurons (LTS-type) (Serafin et al., 1991b).

Figure 4.

Impedance dynamics and subthreshold responses of phasic and tonic model neurons. A₁, Impedance profiles of a tonic 2°VN model (T3) during injection of different holding currents [I_hold = 0 (black line) and I_hold = 0.5 nA (gray line)]. A₂, Response of the same tonic model neuron evoked by injection of sinusoidally modulated currents (ZAP stimuli) of I₀ = 0.2 nA at a depolarized membrane potential (I_hold = 0.33 nA). Note that the tonic model neuron was generated from data of a tonic 2°VN other than shown in Figures 2 and 3. B₁, Fit of a phasic model neuron (PI1) (black lines) to impedance magnitudes obtained from subthreshold responses of a phasic 2°VN at different holding currents [I_hold = 0 (circles), I_hold= −0.5 nA (triangles), I_hold = −1 nA (stars), I_hold = 0.5 nA (diamonds), I_hold = 1 nA (squares)]. B₂, Response of the same phasic model neuron evoked by injection of sinusoidally modulated currents (ZAP stimuli) of I₀ = 0.7 nA at a depolarized membrane potential (I_hold = 0.5 nA).

Model of phasic second-order vestibular neurons

At variance with the response properties of tonic 2°VNs, a major characteristic of phasic 2°VNs is a decrease in impedance magnitude with depolarization (Beraneck et al., 2007). This effect was well reproduced by including a low-threshold potassium channel (I_D) in the fitted frequency domain subthreshold models of phasic 2°VNs (Fig. 4B₁). The kinetics of the I_LT channel described by Rothman and Manis (2003) yields a good estimation for the assumed I_D channel in phasic 2°VNs. The resulting phasic subthreshold models reproduced the typical asymmetry of the sinusoidally modulated membrane potential (Fig. 4B₂) consisting of larger hyperpolarizing compared with depolarizing half-waves of the ZAP responses (Beraneck et al., 2007).

Moreover, with regard to other features, the fitting results of time-domain phasic models reproduced very well the intracellularly recorded responses of phasic 2°VNs. Figure 5A illustrates a representative fit of a spiking time-domain model to a phasic 2°VNs with the two-part error function of the frequency–current response (Fig. 5A₁) and membrane potential decay (Fig. 5A₂). The frequency–current response is limited to f₀, since the evoked discharge in phasic 2°VNs is generally restricted to a single spike at the beginning of the current step stimulus and thus f₁, f₂, and f_∞ are zero. The responses of the resulting model during current step injections (Fig. 5B₂) matches the typical class 3 excitability (Hodgkin, 1948; Izhikevich, 2006) of phasic neurons (Fig. 5B₁). Furthermore, the model responses during low- (Fig. 5D₁, black trace) as well as during higher-amplitude ZAP current injections that evoked a spike discharge (Fig. 5D₂, black trace) resembled the actual intracellular recordings (Fig. 5C₁,C₂).

Figure 5.

Comparison between phasic 2°VN data and model. A₁, Fit (black lines) to the frequency–current (f–I) response of a phasic model neuron (P8) (f₀, circles; f₁, diamonds; f₂, triangles; f_∞, squares). A₂, Fit (gray line) to the membrane potential decay (black line) after injection of a current step of 0.26 nA. B, Comparison between the evoked discharge of the phasic 2°VN (B₁) and the resulting phasic model neuron (B₂) during depolarization by a 1 nA current pulse. C, D, Subthreshold response (C₁, D₁) and spike discharge (C₂, D₂), evoked by sinusoidally modulated current injection (ZAP stimuli), of the same phasic 2°VN (C₁, I₀ = 0.9 nA, I_hold = 0; C₂, I₀ = 1 nA, I_hold = 0) and the corresponding model [D₁, I₀ = 0.9 nA, I_hold = 0 (black trace) and I₀ = 0.5 nA, I_hold = 0.6 nA (gray trace); D₂, I₀ = 1 nA, I_hold = 0 (black trace) and I₀ = 0.52 nA, I_hold = 0.6 nA (gray trace)]. E, Response peak frequency during ZAP stimuli at different holding currents (I_hold) and stimulus amplitudes [I₀ = 0.6 nA (circles), I₀ = 0.3 nA (triangles), I₀ = 0.1 nA (squares)]. The calibration bars in B₁, C₁, and C₂, apply to B₂, D₁, and D₂, respectively.

As shown in Beraneck et al. (2007), the response peak frequency of the ZAP stimulus-evoked responses in phasic 2°VNs is shifted to higher values with depolarization by, for example, constant current injection (Fig. 5D₁, gray trace). This depolarization-related shift in subthreshold response peak frequency consequently results in a shift of the discharge sensitivity to higher frequencies (Fig. 5D₂, gray trace). To further examine this dependency, the ZAP response peak frequency was evaluated in the phasic 2°VN model at different holding currents (I_hold) and ZAP stimulus amplitudes (I₀) (Fig. 5E), which illustrated the impressive depolarization-induced shift in ZAP response peak frequency. Furthermore, the response peak frequency depends on the amplitude of the ZAP stimulus because of nonlinear effects of the I_D channel. Interestingly, the differences between peak frequencies at different ZAP stimulus amplitudes become gradually smaller with increasing depolarizing holding currents, suggesting the presence of a particular parameter value where maximal potential deflections saturate.

A noticeable difference between phasic and tonic spiking models as indicated by the fitting results (Table 1) is the smaller conductance of the initial compartment of phasic 2°VNs (C_S = 37.93 ± 16.30 pF) compared with tonic 2°VNs (C_S = 92.26 ± 19.60 pF). A specific functional consequence is that the lower capacitance in combination with the low resistance in phasic 2°VNs causes the observed fast initial membrane dynamics that is necessary to trigger a spike before the membrane potential rise is shunted by the I_D channel. However, the deduction of specific morphological details (Edwards and Mulloney, 1984) is tedious since the initial compartment represents the soma and unknown parts of dendritic and axonal structures. Therefore, the assumption that the soma of phasic 2°VNs is smaller can only be made if the principal morphology of the two cell types is identical. However, different cell morphologies such as, for example, a bipolar morphology of phasic and a unipolar morphology of tonic 2°VNs would produce diverse effects including inverse soma ratios. Such differences in morphology between MVN neurons were also found in mammals where type A neurons are bipolar and type B neurons are unipolar (Serafin et al., 1993).

Synaptic activation of second-order vestibular neuronal models

The dynamics of synaptic signal processing by the two 2°VN models was determined by mimicking the respective activation with sinusoidally modulated synaptic stimulus trains applied to vestibular afferent fibers (Pfanzelt et al., 2008), exemplarily shown for one tonic and one phasic 2°VN model neuron (Fig. 6). The synaptically activated seven tonic model cells (Fig. 6A₁) were characterized as in the electrophysiological measurements, by a subthreshold EPSP compound response with an overall waveform that was aligned with stimulus frequency modulation (Fig. 6A₂) and by an activation of spikes with increasing synaptic conductance that started around the peak stimulus frequency and continued symmetrically until each stimulus pulse triggered a spike (Fig. 6A₃,A₄). In phasic 2°VN models, mimicking synaptic excitation from vestibular nerve afferents (Fig. 6B₁) evoked responses without the prominent early decay (Fig. 6B₂), which normally characterizes the subthreshold compound EPSPs of these neurons in electrophysiological recordings (Pfanzelt et al., 2008). Instead, a symmetrical response similar to that observed in tonic 2°VN models was elicited. With increasing synaptic conductance, spikes were evoked during the first single pulses of the pulse train only in 5 of 17 model neurons (Fig. 6B₃). In the remaining models and at high synaptic conductances, spikes were triggered by the first as well as the last single pulses (Fig. 6B₄). However, importantly, no phasic 2°VN model was encountered that elicited spikes around the center of the stimulus pulse train (Fig. 6B₃,B₄). Nonetheless, the incompatibility of the symmetric subthreshold response (Fig. 6B₂) and the activation of spikes by the last single pulses of the stimulus train with actual recordings required a modification of the synaptic environment of the phasic cell models. In agreement with anatomical and electrophysiological data (Straka et al., 1997; Biesdorf et al., 2008; Malinvaud et al., 2010), a synaptic inhibition through local GABAergic and glycinergic interneurons was added. As suggested previously by Minor and Goldberg (1991), this inhibition is mediated by tonic type 2°VNs that are activated by vestibular afferents (Fig. 6C₁). The insertion of all seven tonic 2°VN model cells as inhibitory interneurons (Fig. 6C₁) accounted for the skewed subthreshold response (Fig. 6C₂) and prevented spiking at the end of the synaptic stimulation (Fig. 6C₃,C₄), in conciliation with the recorded data (Pfanzelt et al., 2008). This indicates that the ipsilateral disynaptic inhibition contributes to a substantial extent to the particular response dynamics of phasic 2°VNs during activation of labyrinthine afferent inputs.

Figure 6.

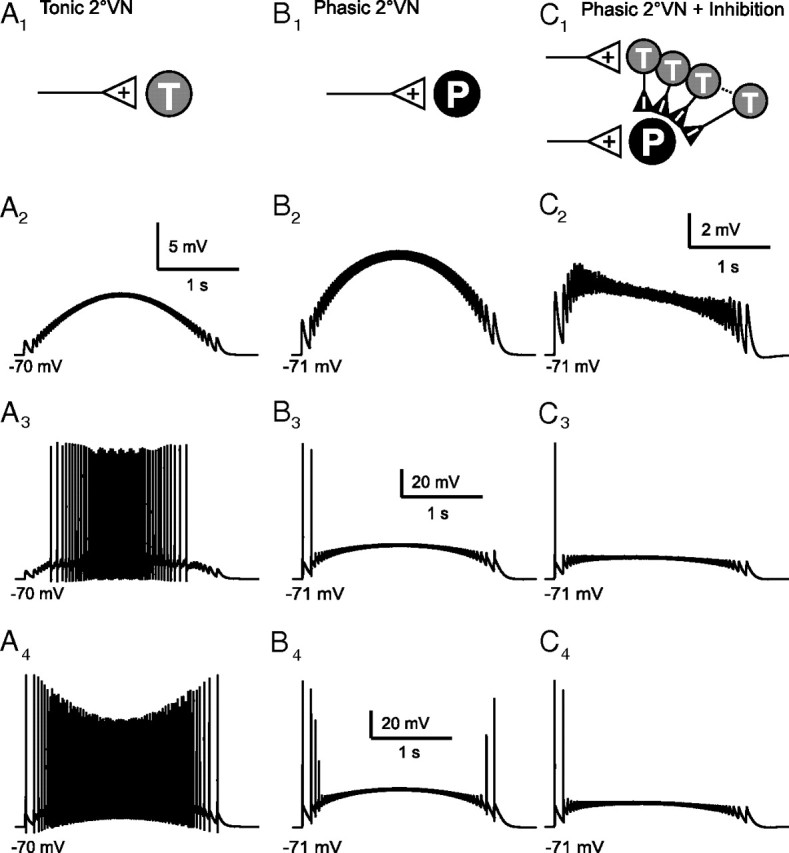
Synaptic subthreshold compound responses and spike discharge of tonic (T4) and phasic (P7) model neurons evoked by sinusoidally modulated pulse train stimulation (peak frequency, 70 Hz) for three cellular and network configurations: tonic (A) and phasic (B) model neuron with monosynaptic afferent vestibular nerve excitation only. C, Same phasic model neuron with monosynaptic excitation as in B and with disynaptic inhibition from all seven tonic model neurons; A₁, B₁, and C₁ indicate network configuration, respectively. Excitatory synaptic conductance increases from A₂–A₄ (A₂, g_E = 1 nS; A₃, g_E = 4 nS; A₄, g_E = 9 nS), B₂–B₄ (B₂, g_E = 4 nS; B₃, g_E = 26 nS; B₄, g_E = 35 nS), and C₂–C₄ (C₂, phasic, g_E = 4 nS; tonic, g_E = 4 nS; C₃, phasic, g_E = 26 nS; tonic, g_E = 7 nS; C₄, phasic, g_E = 35 nS; tonic, g_E = 9 nS). The calibration bars in A₂, B₃, and B₄, apply to B₂, to A₃ and C₃, and to A₄ and C₄, respectively.

Population responses of second-order vestibular neuronal models

Evaluation of the qualitative contributions of ion channels, inhibition, asynchronous afferent fiber input, and synaptic noise to the signal transmission in the central vestibular system was studied by generating a population model. The functional output of tonic and phasic cell populations (population response) was analyzed by determining the net normalized postsynaptic conductance (G_S) from either 200 phasic or 200 tonic 2°VNs or from converging 100 tonic and 100 phasic 2°VNs that activate a particular target neuron, respectively (e.g., extraocular motoneurons) (scheme depicted in Fig. 7B₁). This approach uses a linear summation of the vestibular network output and takes into account different modes of synaptic integration that were implemented in the model by different postsynaptic time constants (see Materials and Methods) (see below). Thus, for the evaluation of this postsynaptic conductance, no intrinsic properties of the target neurons had to be taken into account.

Figure 7.

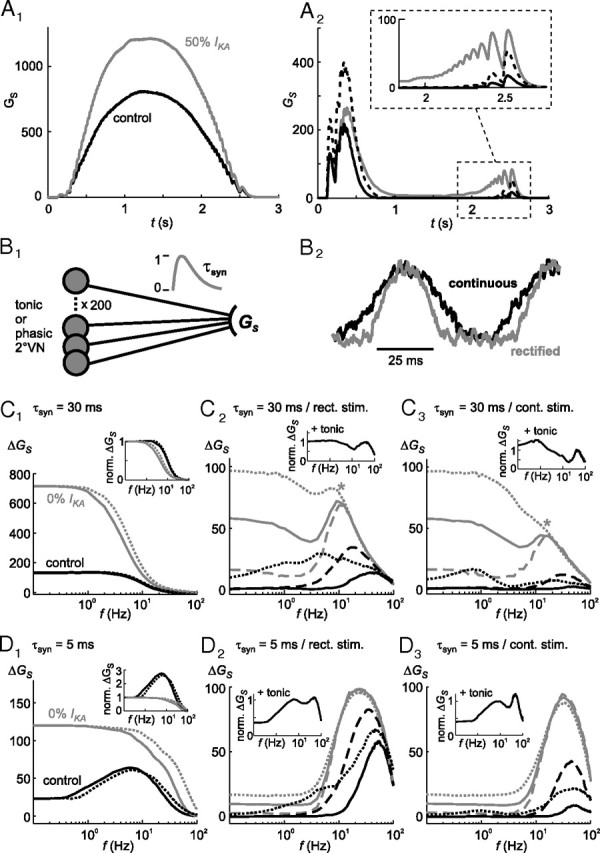
Role of ion channels, synaptic inhibition, noise currents, and postsynaptic time constants in shaping the dynamics of population model responses. A, Specific implication of altered parameters on the calculated postsynaptic conductance G_S of tonic (A₁) and phasic (A₂) model neuron populations during sinusoidally modulated pulse train stimulation; overlay of control responses (A₁, A₂, black lines), with reduced (50%) adaptation current I_KA in tonic population responses (A₁, gray line), with reduced (50%) low-threshold potassium currents (I_D) (A₂, black dotted line) and with reduced (50%) synaptic inhibition through local interneurons (A₂, gray line) in phasic model populations; inset in A₂ shows the response to the last pulse train stimuli at an extended time and amplitude scale; postsynaptic time constant τ_syn = 30 ms. B, Scheme depicting the estimation of the postsynaptic conductance G_S (B₁) and an example of noisy stimulation currents (f = 15 Hz) that mimic the activation with (continuous) or without afferent resting activity (rectified) (B₂). C, D, Calculated postsynaptic conductance amplitudes ΔG_S of tonic (C₁, D₁) and phasic vestibular population model responses (C₂, C₃, D₂, D₃) with large (τ_syn = 30 ms) (C) or small (τ_syn = 5 ms) (D) postsynaptic time constants; overlay of control responses (C₁–C₃, D₁–D₃, black lines), without adaptation current I_KA (g_KA = 0; gray lines) in tonic (C₁, D₁) population responses, with reduced (50%) low-threshold potassium currents (I_D; black dotted lines), with reduced synaptic inhibition (50%, black dashed lines), without synaptic inhibition (gray lines) and with normal (100%, gray solid lines), increased (200%, gray dotted lines) or without (0%, gray dashed lines) noise currents [ε(t)]; the insets in C₁ and D₁ represent responses that were normalized to control values at 0.1 Hz. The insets in C₂, C₃, D₂, and D₃ show the normalized combined output of 100 tonic and 100 phasic 2°VN model neurons onto a putative target neuron with short (C₂, C₃) or long τ_syn (D₂, D₃). Results from simulations with (continuous) and without afferent resting activity (rectified) are indicated by the dotted and solid lines, respectively, in the tonic (C₁, D₁) and in different plots in the phasic population (C₃, D₃, and C₂, D₂, respectively).

Excitation of the population model with a sinusoidally modulated train of single electrical pulses in each tonic 2°VN model cell resulted in a symmetrical postsynaptic population response (Fig. 7A₁, control) with a gain that increased considerably with reduction of the adaptation potassium current I_KA (Fig. 7A₁, 50% I_KA). In contrast, the phasic 2°VN model population caused a typical asymmetric postsynaptic response with a large transient response at the beginning and a small response at the end of the stimulus train (Fig. 7A₂, control). The postsynaptic activation at the end of the stimulus train is mediated by a small number of phasic model neurons with a particularly low I_D conductance in which the implemented feedforward inhibition was too weak to prevent spike generation by the last pulses of the stimulus train. Additional reduction of the I_D conductance in each of the model cells by 50% (Fig. 7A₂, black dashed line) increased the population response, both at the beginning and the end of the stimulus train. In contrast, reduction of the feedforward inhibition by 50% had a larger impact on the response component at the end of the stimulus train (Fig. 7A₂, gray line).

To simulate a more natural vestibular input (e.g., by asynchronously activated single afferent fibers and synaptic noise), a respective noisy sinusoidally modulated current was injected into each target cell (see Materials and Methods). Two different sets of stimulation currents were used, either mimicking inputs with (continuous) or without assuming afferent resting activity (rectified) (Fig. 7B₂) (see Materials and Methods). Figure 7C₁–C₃ illustrates the dynamics of the postsynaptic conductance amplitude ΔG_S with respect to the stimulus frequency for the tonic (Fig. 7C₁) and for the phasic model population (Fig. 7C₂,C₃). Under control conditions (Fig. 7C₁–C₃, black lines), the tonic neuronal population exhibited a typical low-pass filter behavior, whereas the phasic neuronal population showed the typical bandpass behavior, although with a rather small resonance during continuous stimulation. Notably, however, the low-frequency resonance observed in the firing rates of individual tonic 2°VNs (Fig. 3B₁) was absent in the input to the presumed postsynaptic target neurons. In contrast, removal of the adaptation current I_KA in tonic 2°VNs (Fig. 7C₁, gray lines) caused a considerably increased gain along with a shift of the cutoff frequency toward lower values (Fig. 7C₁, inset). Reduction of the low-threshold potassium current (I_D) to 50% in each phasic model neuron (Fig. 7C₂,C₃, black dotted lines) resulted in enhanced amplitudes during low stimulus frequencies and a large shift of the resonance peak toward lower frequencies. Reduction of the inhibition to 50% (Fig. 7C₂,C₃, black dashed lines) or 0% (Fig. 7C₂,C₃, gray solid lines) also caused a gain increase that, however, was accompanied by a small resonance shift to lower frequencies. Interestingly, without ipsilateral disynaptic inhibition, phasic model cells exhibited an activity at low stimulus frequencies, which was not the case during control conditions. This effect is primarily attributable to the noise current. Removal of this latter current, while maintaining 0% inhibition (Fig. 7C₂,C₃, gray dashed lines), caused a general decrease of the activity, specifically at low stimulus frequencies, leaving only few phasic 2°VNs with a particularly low I_D active. In contrast, amplifying the noise current to 200%, while maintaining 0% inhibition, strongly enhanced the postsynaptic conductance amplitude evoked at low stimulus frequencies and almost entirely removed the resonance peak (Fig. 7C₂,C₃, gray dotted lines). These results suggest that the observed response dynamics of phasic 2°VNs originates from a balanced interaction of the I_D channel, disynaptic inhibition, and noise current, with each of these parameters controlling a particular aspect of the response profile.

The impact of resting activity of vestibular nerve afferents on the response profile was tested by implementation of this parameter into the model. The difference between continuous (with afferent resting activity) and rectified (without afferent resting activity) stimulations in the tonic model population is restricted to a small response shift toward lower frequencies during continuous stimulation (Fig. 7C₁, compare dotted lines with solid lines). In contrast, the rectified stimulation in the phasic model population causes a substantially higher resonance at high frequencies, whereas the low frequency response remains unaltered (Fig. 7, compare C₂, C₃). This difference is attributable to the steeper stimulus current during the rectified compared with the continuous stimulation (Fig. 7B₂), which leads to a faster membrane potential change and thus to a more efficient activation of phasic 2°VNs.

As demonstrated above, the dynamics and frequency tuning of the postsynaptic input in presumed target neurons of tonic and phasic 2°VNs (e.g., extraocular motoneurons) are to a large extent determined by the combination of intrinsic and synaptic properties of the presynaptic 2°VNs. However, time constants of the synapses between 2°VNs and the target neurons can either reinforce or antagonize the presynaptic properties. In particular, reduction of the time constants of the activated model α-synapses from τ_syn = 30 ms to τ_syn = 5 ms (Fig. 7D) revealed how this parameter can change vestibulo-motor response dynamics. Shortening of the time constant unmasked a pronounced resonance in the tonic 2°VN-mediated postsynaptic population response (Fig. 7D₁, inset) similar to the low-frequency resonance in the firing rate of individual tonic 2°VNs (Fig. 3B₁). A similar effect was seen in the phasic 2°VN population response. The noise current eventually created voltage transients that were fast enough to trigger action potentials in phasic 2°VNs and as a consequence a postsynaptic conductance in the presumed target neuron. However, the magnitude of the postsynaptic time constant determined the degree of integration of the relayed signals. A long time constant caused substantial integration of the activated conductance during the depolarizing half-wave, visible as a high gain at frequencies <1 Hz (Fig. 7C₂,C₃, gray lines). Higher stimulus frequencies finally caused synaptic integration to exceed the cycle duration of the sinusoidally modulated stimulus waveform. Consequently, this increased the overall signal amplitude at the expense of postsynaptic signal dynamics, thereby decreasing the gain, seen as a dip at ∼3 Hz in the phasic 2°VN population response without feedforward inhibitory inputs and with a long τ_syn (Fig. 7C₂,C₃, gray lines). Above a particular stimulus frequency, action potentials are triggered independent of the amount of noise current in phasic 2°VNs, which caused a substantial gain increase above 3 Hz with maximal values at ∼10 Hz (Fig. 7C₂,C₃, gray asterisk). In contrast, a short time constant of the presumed postsynaptic target neuron limits the integration of the postsynaptic conductance. This results in particular low gains of the postsynaptic conductance for frequencies up to ∼3 Hz but causes an enhancement of the resonance peaks and a shift of the latter to considerably higher frequencies independent of other conditions (Fig. 7, compare plots in C₂, C₃; D₂, D₃).

Responses with rectified and continuous stimulations showed the same qualitative differences independent of the length of the time constant. Possible effects of postsynaptic signal convergence of tonic and phasic 2°VN populations on the response dynamics were evaluated by combining the output of 100 tonic and 100 phasic 2°VN model neurons, normalized to the maximum of each population response, onto a putative target neuron (Fig. 7C₂,C₃,D₂,D₃, insets). Although this approach revealed in general differences in the response dynamics that depended on the stimulus type (rectified/continuous) or postsynaptic time constant, a similar decline was always noticeable for intermediate frequencies between 10 and 30 Hz. This particular result is a clear prediction that can be tested in the future in, for example, abducens motoneurons after electrical stimulation with pulse trains as used for the evaluation of 2°VNs (Pfanzelt et al., 2008). Previously reported functional implications of the feedforward inhibition as found in frogs (Biesdorf et al., 2008) and monkeys (Goldberg et al., 1987) are cancellation of irregular afferent activity during the activation of a horizontal angular VOR (Minor and Goldberg, 1991) and the induction of homeostatic long-term depression (Menzies et al., 2010). However, the present findings in this study suggest, in addition, the implementation of a high-pass filter that possibly controls the resonance frequency of phasic 2°VNs.

Comparison of the consequences of short and long time constants of 2°VN synapses onto vestibular target neurons thus yields important information on how the processing of sensory signals in central vestibular neurons can be enhanced or antagonized at the next synaptic level within, for example, the vestibulo-ocular reflex pathway. A short postsynaptic time constant limits synaptic integration, thereby ensuring a more or less unaltered transformation of presynaptic into postsynaptic signals including particular expressions of response resonance phenomena. In contrast, a long synaptic time constant causes signal integration over longer time periods, thereby canceling or diminishing potential presynaptic response resonances observed in both tonic and phasic 2°VNs. The extension of the single-cell model to a population model proved to be extremely useful for an estimation of how the feedforward inhibition and potassium conductances control particular aspects of the sensory signal transformation in 2°VNs and the transmission to target neurons under seminatural conditions. The obtained results suggest a critical influence of synaptic noise as well as properties of the postsynapse on the timing and sharpness of effective vestibular signal processing.

Discussion

Frog phasic and tonic 2°VNs subdivide into separate subpopulations with different, yet complementary intrinsic membrane properties. Distinct cellular categorization and differential synaptic embedding into local circuits make the two cell types well suited to determine in a computational approach cellular and network contributions to sensory signal processing. Reproduction of distinctive neuronal and synaptic properties by compartmental Hodgkin–Huxley-type models revealed conductance and synaptic circuit configurations that might be the cause for the different functional modes of the two types. This allows making predictions on potential functional roles of ion channels, noise currents, synaptic inhibition, and postsynaptic time constants for sensory-motor transformation.

Potassium channels contribute to functional modes of phasic and tonic neurons

Different potassium channels of actual data and of constructed cellular models are important contributors to the differential filter characteristics of 2°VNs. In tonic 2°VNs, this channel is spike dependent and responsible for fast spike-rate adaptation. Compatible with the low-pass filtering of subthreshold responses in these neurons (Beraneck et al., 2007), this ion channel might also account for the low-frequency discharge resonance without influencing subthreshold and impedance responses and contributes to the linear current–firing rate relationship in rodent MVN neurons (du Lac and Lisberger, 1995; Bagnall et al., 2008). The highly adaptive discharge and bandpass filter-like responses of frog phasic 2°VNs are reproduced by a model with low-threshold Kv1.1 (I_D) potassium channels (Beraneck et al., 2007). Thus, the specific functionality of the two frog vestibular subtypes appears to depend, at least in part, on different potassium channels as is the case for GABAergic and non-GABAergic mouse MVN neurons (Gittis and du Lac, 2007). However, differences in, for example, persistent sodium conductances cannot be ruled out as additional biophysical component for the different response dynamics of the two cell types. Nonetheless, decomposition of the responses into contributions of different potassium channels meets the initial goal to determine in a first step the simplest biophysical components that explain the origin of the dynamic bandwidths of tonic and phasic 2°VNs.

Complementary interaction of cellular properties and synaptic networks

Intrinsic neuronal properties as well as contributions from feedforward and feedback circuits determine subthreshold response kinetics and discharge profiles (Kozlov et al., 2009). The pronounced subthreshold response peak asymmetry and temporally limited spike discharge in frog phasic 2°VNs (Figs. 1A, 6B,C) is caused by the combined influence of cellular and network characteristics (Pfanzelt et al., 2008). Although empiric experiments did not allow elucidating the respective functional roles of cellular and network properties, the present computational approach suggests that both components control different, yet complementary temporal aspects. The prominent I_D current in phasic 2°VNs essentially determines discharge threshold and sensitivity at response onset (Rössert et al., 2009a), whereas the feedforward inhibition builds up slowly and exerts its influence on later response components during any longer-lasting activation (Pfanzelt et al., 2008; Rössert et al., 2009a). Thus, delayed inhibitory inputs, presumably through tonic type 2°VNs, limit the discharge during extended sensory inputs, thereby complementing the effects of rapidly adapting I_D potassium conductances. Appropriate tuning of cellular and network properties allow phasic 2°VNs to mathematically differentiate afferent inputs or to serve as event detector for the typically short episodes of rapid body movements of frogs (Beraneck et al., 2007) and complies with the functional consequences of the inhibitory feedforward side loop (Minor et al., 1999; Straka and Dieringer, 2000).

The specific role of local inhibitory interneurons in bandpass filtering of vestibular nerve-activated excitation, however, depends on number and type of recruited afferent fibers. Preferred synaptic connections of thick, irregular firing vestibular afferents with the most phasic 2°VNs suggest that the latter neurons receive particularly dynamic inputs (Goldberg et al., 1987). Accordingly, cellular and circuit properties of phasic 2°VNs would reinforce highly dynamic acceleration-related head motion signals, compatible with an amplification of the response resonance when the input originated from afferent fibers with a low or no spontaneous activity and a resonance reduction when the input was evoked by afferents with a resting rate of >10 Hz (Fig. 7C,D). In contrast, physiologically matching synaptic connectivity between thinner vestibular afferents and tonic 2°VNs allow appropriate transformation of head position-related signals by neurons with more persistent cellular conductances such as frog tonic 2°VNs or rodent type A MVN neurons (Straka et al., 2005). Thus, a differential central vestibular organization supports parallel processing of sensory signals in dynamically distinct pathways (Straka et al., 2009) as in the visual (Shapley, 1990; Merigan and Maunsell, 1993), auditory (Cant and Benson, 2003), or somatosensory system (Johnson and Hsiao, 1992). However, the observed convergence of a larger spectrum of vestibular afferents onto 2°VNs (Goldberg, 2000; Straka and Dieringer, 2004) suggests some mixing of signal contents. The resulting convergence, however, might be only apparent since specific regional distributions of synapses from thin and thick fibers onto different somato-dendritic sites (Sato and Sasaki, 1993; Huwe and Peterson, 1995; Mensinger et al., 1997) allow integration or differentiation or any recombination of head motion-related signals depending on the synaptic time constant.

Critical parameters for vestibular sensory-motor transformation

Appropriate computational models allow the determination of respective implications of cellular and circuit properties and to make predictions on how individual components influence overall function. Calculations of postsynaptic currents of innervated target neurons help elucidate the contributions of different biophysical parameters to vestibular sensory-motor transformation. Activation of the respective model populations with noisy synaptic afferent input (Hospedales et al., 2008) essentially confirms the functional roles of cellular and network properties of phasic 2°VNs (Fig. 7). However, the dynamics of the constructed postsynaptic responses critically depends on the synaptic time constant that either reinforces or counteracts 2°VN filter properties. The discharge resonance at ∼5 Hz in tonic 2°VNs is only transmitted to postsynaptic targets if τ_syn is small, whereas larger time constants cause signal integration, thereby ensuring a linear low-pass filter-shaped synaptic transmission. On the presynaptic side, the adaptation conductance I_KA in frog tonic 2°VNs balances this critical relationship by increasing the cutoff frequency when τ_syn is large, which might also be the basis for the frequency-independent linear gain of mammalian vestibular reflexes (Sekirnjak and du Lac, 2002; Bagnall et al., 2008). After removal of the inhibition, phasic model population responses exhibit relatively high gains at low frequencies, which requires large synaptic time constants and noisy membrane potential fluctuations that create voltage transients that are fast enough to trigger action potentials. Functionally, the inhibitory side loop thus acts as high-pass filter, which controls the resonance frequency of phasic 2°VNs and leads, in combination with intrinsic membrane properties, to a sharpening of the bandpass properties of phasic population responses. Thus, the combination of intrinsic and network properties of phasic 2°VNs generates a noise-resistant detection system for short-duration vestibular signals.

Limitations of computational modeling

A major advantage of computational modeling is the possibility to extract testable predictions for empiric experiments. However, several limitations affect the interpretation of biophysical parameters and functional roles of model components, such as afferent resting rates, convergence of afferents through axo-dendritic and/or somatic synapses, or the morphological interpretation of particular parameters. Given the importance of resting rates for information content in vestibular nerve afferents (Sadeghi et al., 2007), a critical issue was the assumed level of spontaneous discharge. Responses, mediated by afferents with low (i.e., thick fibers), as opposed to those with high resting rates, match well the response dynamics of phasic model neurons, whereas the processing in tonic neurons is less influenced by spontaneous activity. Extraction of more precise predictions, however, requires additional data on synaptic connectivity patterns of dynamically different fiber types. Nonetheless, the model reproduces very well the dynamics of synaptic responses in 2°VNs and thereby helps identifying sets of parameters that might be critical for signal processing. The incorporation of more detailed data on afferent terminal organization will further test differential functional roles of cellular and circuit parameters in sensory signal transformation.

Another limitation of the current model is the interpretation of specific cellular parameters. Accurate implementation of spiking and passive membrane potential responses was only possible using a compartmental model. Since “distal compartments” reproduce responses of more distal cellular areas as seen from the recording site, the compartmental model represents the overall “electrotonic structure” but does not allow deducing specific morphological details (Edwards and Mulloney, 1984). The lower mean capacitance of phasic model neurons suggests that these neurons are smaller than tonic 2°VNs, at variance with previous assumptions (Straka et al., 2004). However, the lower value only indicates that the initial compartment, which represents the soma and unknown parts of dendrites and axon, is smaller. Larger morphological differences between the two frog 2°VN types are not unlikely, given the known bipolar and unipolar morphology of mammalian type A and B MVN neurons, respectively (Serafin et al., 1993). In addition, open low-threshold I_D potassium channels at resting membrane potential likely impair a comparison of resistance measurements and thus the inferred cell sizes of phasic and tonic 2°VNs. Nonetheless, the compartmental model facilitates the understanding of how different physiological parameters might shape the response dynamics but currently limit inferences on the magnitude of dendritic integration or specific functional effects of different synaptic sites in the absence of morphological details.