Analysis of Development of Direction Selectivity in Retinotectum by a Neural Circuit Model with Spike Timing-Dependent Plasticity

Abstract

The development of direction selectivity in the visual system depends on visual experience. In the developing Xenopus retinotectal system, tectal neurons (TNs) become direction selective through spike timing-dependent plasticity (STDP) after repetitive retinal exposure to a moving bar in a specific direction. We investigated the mechanism responsible for the development of direction selectivity in the Xenopus retinotectal system using a neural circuit model with STDP. In this retinotectal circuit model, a moving bar stimulated the retinal ganglion cells (RGCs), which provided feedforward excitation to the TNs and interneurons (INs). The INs provided delayed feedforward inhibition to the TNs. The TNs also received feedback excitation from neighboring TNs. As a synaptic learning rule, a molecular STDP model was used for synapses between the RGCs and TNs. The retinotectal circuit model reproduced experimentally observed features of the development of direction selectivity, such as increase in input to the TN. The peak of feedforward excitation from RGCs to TNs shifted earlier as a result of STDP. Together with the delayed feedforward inhibition, a stronger earlier transient feedforward signal was generated, which exceeded the threshold of the feedback excitation from the neighboring TNs and resulted in amplification of input to the TN. The suppression of the delayed feedforward inhibition resulted in the development of orientation selectivity rather than direction selectivity, indicating the pivotal role of the delayed feedforward inhibition in direction selectivity. We propose a mechanism for the development of direction selectivity involving a delayed feedforward inhibition with STDP and the amplification of feedback excitation.

Introduction

The development of visual functions, such as direction selectivity, is thought to require visual stimuli (Wiesel, 1982; Katz and Crowley, 2002; Hooks and Chen, 2007). Direction selectivity is the capacity of neurons to respond more significantly to moving visual stimuli in one preferred direction than in any other direction. Direction selectivity in the mammalian primary visual cortex (V1) is significantly reduced by visual deprivation (Cynader and Chernenko, 1976; Humphrey and Saul, 1998; Li et al., 2006). Recent reports indicate that repetitive retinal exposure to a moving bar in a specific direction induces the development of direction selectivity in ferret V1 (Li et al., 2008) and the developing Xenopus retinotectal system (Engert et al., 2002; Mu and Poo, 2006). The development of direction selectivity involves change in receptive fields, time profiles of input to direction-selective neurons, and time integration of the input through training. Furthermore, Mu and Poo (2006) hypothesized that the development of direction selectivity in the Xenopus retinotectal system is mediated by spike timing-dependent plasticity (STDP) (Mu and Poo, 2006), which involves bidirectional modifications in synaptic strengths depending on the relative spike timing between presynaptic neurons and postsynaptic neurons (Bi and Poo, 1998; Zhang et al., 1998; Froemke and Dan, 2002; Dan and Poo, 2004). However, the mechanism responsible for the development of direction selectivity remains unclear.

Although some neural circuit models have been proposed to explain the development of direction selectivity in V1 as a result of STDP (Buchs and Senn, 2002; Shon et al., 2004; Wenisch et al., 2005), the development of direction selectivity has not been directly compared with experimental results. We constructed a realistic neural circuit model of the Xenopus retinotectal system that could be quantitatively compared with various observed experimental features (Engert et al., 2002). To incorporate a synaptic learning rule, we simplified the detailed molecular STDP model (Urakubo et al., 2008, 2009) to produce a simple STDP model that retained the ability to reproduce the experimentally observed temporally asymmetric learning window (Fig. 1B; supplemental Fig. 7, available at www.jneurosci.org as supplemental material) (Froemke and Dan, 2002; Froemke et al., 2006; Urakubo et al., 2008). This simple STDP model can be used to test the development of direction selectivity. Our retinotectal circuit model reproduced several features of the development of direction selectivity. We propose that STDP at the synapse between the RGCs and the TNs combined with delayed feedforward inhibition leads to the amplification of the inputs from neighboring TNs, resulting in the development of direction selectivity. By contrast, only STDP without delayed feedforward inhibition resulted in the development of orientation selectivity. A part of this work was published earlier in an abstract (Honda et al., 2009).

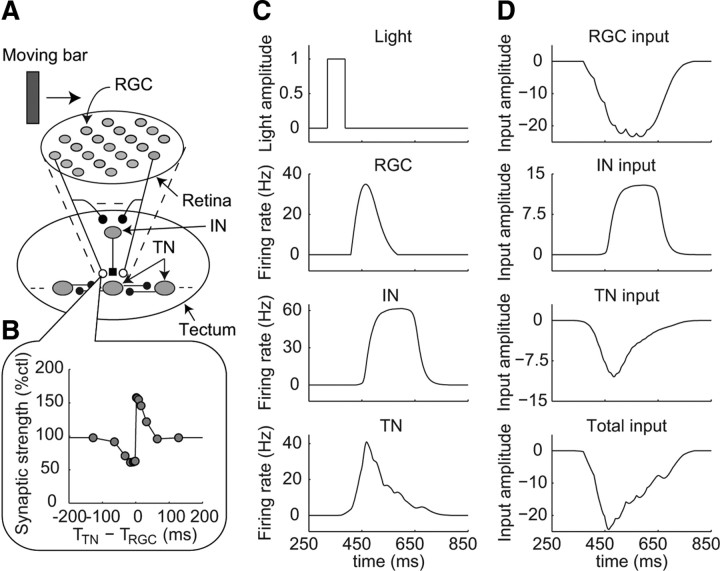
Figure 1.

Retinotectal circuit model. A, Structure of the neural circuit in the retinotectal circuit model. The model contains 185 RGCs, 37 INs, and 37 TNs. The RGCs have excitatory projections to both the TNs and the INs. Each IN has an inhibitory projection to the TN, which receives excitation from the same RGCs as each IN does. TNs have excitatory projections to neighboring TNs. Open circles represent excitatory synapses, which are modified through STDP, and filled circles represent excitatory synapses, which are fixed and not modified through STDP. Filled square represents an inhibitory synapse, which is fixed and not modified through STDP. B, Temporally asymmetric learning window reproduced using a simple STDP model that is included in the synapses from RGCs to TNs. A detailed description of the simple STDP model is provided in the supplemental material (available at www.jneurosci.org). C, D, Time profiles of the model responses to a fast-moving bar (0.3 μm/ms) before training. C, Light amplitude at the center of the receptive field of the RGC indicated by the arrow in A and firing rates of the RGC, the IN located in the center of the tectum, and the TN located in the center of the tectum, as indicated in A. D, Inputs to the TN located in the center of the tectum from the RGCs, IN, and neighboring TNs and the summation of these three inputs (total input), as indicated.

Materials and Methods

Retinotectal circuit model.

We developed a retinotectal circuit model by extracting essential knowledge to explain the development of direction selectivity from experimental findings for neural activity, connectivity, and receptive field properties (Fig. 1A; supplemental Fig. 1, available at www.jneurosci.org as supplemental material) (Rybicka and Udin, 1994; Engert et al., 2002; Tao and Poo, 2005; Akerman and Cline, 2006; Lien et al., 2006; Mu and Poo, 2006; Vislay-Meltzer et al., 2006; Pratt et al., 2008). A detailed description of the retinotectal circuit model is presented in the following sections; here, a brief overview is provided. For simplicity, we modeled one tectum receiving optic input from a contralateral eye. The retinotectal circuit model is comprised of three types of neurons, retinal ganglion cells (RGCs), interneurons (INs), and tectal neurons (TNs). In the retinotectal circuit model, synaptic strengths are modified through STDP only in the synapses between the RGCs and the TNs (Zhang et al., 1998; Engert et al., 2002), while other synapses are fixed. The synaptic strengths of TN–TN synapses have been experimentally reported to change in a spike timing-dependent manner (Pratt et al., 2008). However, the timing window has not been examined, and the STDP learning rule of TN–TN synapses remains unknown. In addition, the developmental stages of Xenopus investigated in our study (stages 42–45) (Engert et al., 2002) are earlier than those investigated by Pratt et al. (2008) (stages 45–49). For these reasons, we did not include the synaptic modification of TN–TN synapses into the retinotectal circuit model. White moving bar stimuli were presented to the RGCs, and the response properties of each neuron were examined. Unless specified, we simulated the time-varying firing rate of each neuron but not the membrane potential. Only for calculating the changes in synaptic strengths through STDP, we generated the spikes of RGCs and TNs from the firing rates of RGCs and TNs, respectively, according to the Poisson process (see below for details). For the numerical simulations, the fourth-order variable time-step Runge–Kutta method (Matlab function ode45) was used for stable and precise computation. The constructed programs are available for download (http://www.kurodalab.org/info/retinotectum/index.html).

Structure of the retinotectal circuit model.

Our retinotectal circuit model consisted of one retinal and two tectal layers (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). The retinal layer was a two-dimensional lattice in a circle with a radius of 65 μm, and one RGC was located at each lattice point (185 RGCs in total). The distance between nearest lattice points, or the distance between nearest RGCs, was 6$\sqrt{2}$ μm. The first tectal layer was a two-dimensional lattice in a circle with a radius of 30 μm, and one IN was located at each lattice point (37 INs in total). The distance between nearest INs was 6$\sqrt{2}$ μm. The second tectal layer was a two-dimensional lattice in a circle with a radius of 30 μm, and one TN was located at each lattice point (37 TNs in total). The distance between nearest TNs was 6$\sqrt{2}$ μm. The lattice orientations were the same across all three layers. To define the location of each neuron in each layer, we set two perpendicular-directed axes, the x-axis and y-axis along the lattice orientations. The coordinates of the neuron were represented as (x, y) (μm). The position of the neuron located at the center in each layer was represented as (0, 0). In supplemental Figure 1 (available at www.jneurosci.org as supplemental material), neurons were indicated with four different symbols (open circles, filled circles, open diamonds, and filled diamonds) to illustrate connectivity in the retinotectal circuit model. We assumed the distance between nearest RGCs was 6$\sqrt{2}$ μm based on the following experimental observations. It has been reported that a retinal area is 0.09 mm² and the number of RGCs is 2700 per retina in Xenopus tadpole at stage 45 (Gaze and Grant, 1992). From this observation, we estimated the distance between nearest RGCs to be 6 μm. On the other hand, we estimated the diameter of an RGC of Xenopus tadpole at stages 43–44 to be 11 μm based on the anatomical study of Huang and Moody (1993). Therefore, we set the distance between 6 and 11 μm. We confirmed that the development of direction selectivity by a fast-moving white bar (see below) can also be reproduced with the distance 10$\sqrt{2}$ μm, which is >11 μm (data not shown).

Experimental studies have shown that the RGCs send excitatory input to both the INs and TNs (Rybicka and Udin, 1994; Akerman and Cline, 2006; Lien et al., 2006), the INs send inhibitory input to the TNs (Rybicka and Udin, 1994; Akerman and Cline, 2006; Lien et al., 2006), and the TNs send excitatory input to the TNs (Pratt et al., 2008). Furthermore, each receptive field of a TN occupies most of the retinal area (50–80%) (Engert et al., 2002; Tao and Poo, 2005; Vislay-Meltzer et al., 2006). The total numbers of neurons that send excitatory input to one TN were assumed by the number of EPSCs evoked by one sweep of a moving bar (Engert et al., 2002). Based on these experimental findings, we determined the connectivity in the retinotectal circuit model. The IN located at the position (x, y) on the first tectal layer received excitatory input from 21 RGCs indicated by the same symbol, which were located within a circle with center (x, y) and a radius of 40 μm on the retinal layer, and sent inhibitory input to the TN located at the position (x, y) on the second tectal layer. The same 21 RGCs also sent excitatory input to the TN located at the position (x, y). The projections from RGCs to any IN and TN pairs are identical, regardless of the locations of the IN and TN pairs. The TN located at the position (x, y) received excitatory input from the neighboring TNs located within a circle with center (x, y) and a radius of 12.5 μm, regardless of the symbol. Therefore, the numbers of the neighboring TNs, from which the TNs received input, are gradually decreasing from the center to the edge of the second tectal layer. The directions of moving bars were chosen from 45°, 135°, 215°, or 305° from the x-axis.

Model of RGCs.

To simulate the response of the RGCs to moving bars, we made an RGC model based on a linear–nonlinear cascade model (supplemental Fig. 2, available at www.jneurosci.org as supplemental material) (Berry et al., 1999). To simplify the implementation of the model, only the OFF-center RGCs were modeled because the responses of the TNs to light decrements are much larger than those to light increments (Zhang et al., 2000; Engert et al., 2002). In the RGC model, the input was a visual stimulus and the output was the time-varying firing rate of the RGC. The visual stimulus was passed through a spatial and temporal linear filter. The description of this filtering process is as follows:

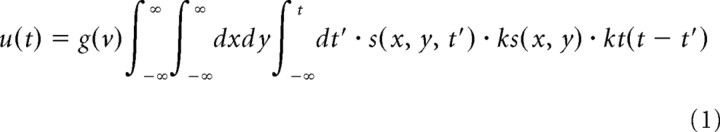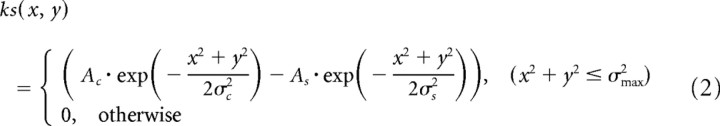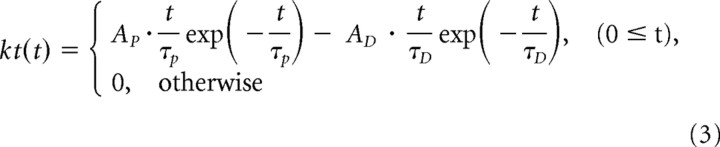where s(x, y, t) is the visual stimulus; ks(x, y) is the spatial linear filter given by the difference of Gaussian functions; kt(t) is the temporal linear filter given by the difference of α functions; u(t) is the output of the linear filters; g(v) is a gain factor (Eq. 5); A_c and A_s are the amplitudes of the positive and negative Gaussian functions, respectively; σ_c and σ_s are the widths of the positive and negative Gaussian functions, respectively; σ_max is the size of the spatial linear filter; A_P and A_D are the amplitudes of the positive and negative α functions; and τ_P and τ_D are the time constants of the positive and negative α functions, respectively.

Then, the output of the linear filters u(t) was rectified using a static nonlinear function F(u) to generate the output, or the firing rate of the RGC. If the visual stimulus provides a strong excitation, the negative feedback reduces the gain at the input and, consequently, the response to the subsequent stimulation. The equations describing this process are as follows:

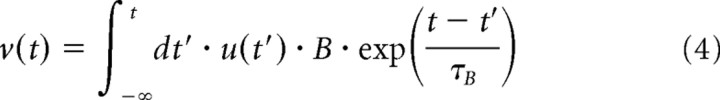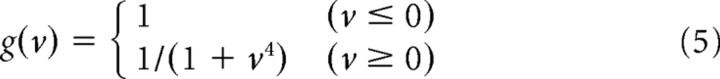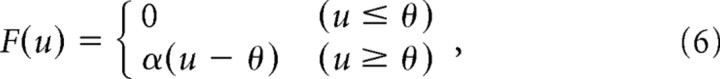where v(t) is the gain control filter and g(v) is the gain control function. These equations have four parameters: the time constant τ_B and the amplitude B of the gain control filter, and the slope α and the threshold θ of the rectifier F(u). Equation 4 denotes an exponential filter, which averages the output of the linear filter u over time, and Equation 5 denotes a decreasing gain control function, which uses the result v(t) to set the gain factor g(v). In Equation 6, the output of the linear filters u(t) is transformed into the firing rate. The model parameters are listed in Table 1.

Table 1.

Model parameters for RGCs

Parameters	Values
Ac	1 μm−2
As	0.6 μm−2
σc	15 μm
σs	20 μm
σmax	60 μm
AP	0.3 ms−1
AD	1 ms−1
τP	35 ms
τD	10 ms
τB	120 ms
B	15 ms−1
α	35 Hz
θ	0.07

Models of INs and TNs.

Each IN receives excitatory inputs from the RGCs. The firing rate of the ith IN r_i^IN was determined based on the input from the RGCs through a standard rate-model equation (Chance et al., 1999; Dayan and Abbott, 2001).

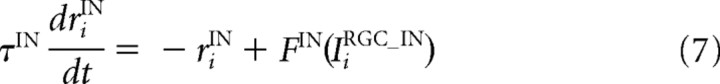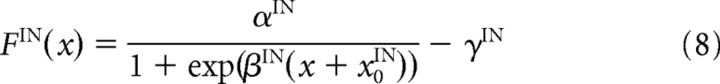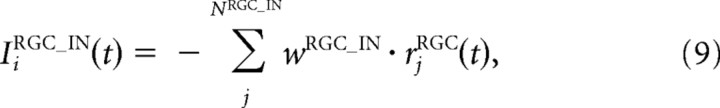where τ^IN is a time constant; F^IN is a sigmoidal activation function; α^IN, β^IN, γ^IN, and x₀^IN are constant values that characterize the activation function F^IN; N^RGC_IN is the number of RGCs projecting to one IN; I_i^RGC_IN is the input from the RGCs; w^RGC_IN is the synaptic strength from the RGCs to the INs; and r_j^RGC is the firing rate of the jth RGC and is equal to F(u) in Equation 6.

Each TN receives excitatory inputs from two types of neurons, RGCs and TNs, and inhibitory input from an IN. The firing rate of the ith TN r_i^TN is determined by the sum of these three types of inputs, as calculated using the following equations:

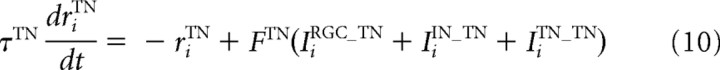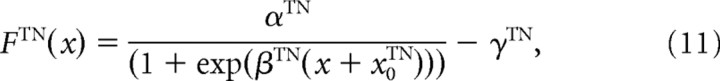where I_i^RGC, I_i^IN, and I_i^TN are the inputs from the RGCs, IN, and TNs, respectively. These inputs, in turn, are calculated using the following equations:

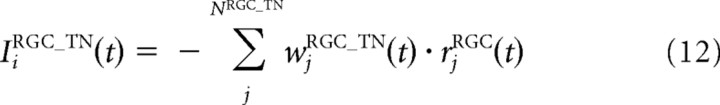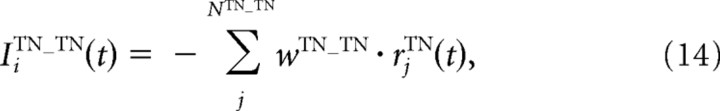where τ^TN is a time constant; F^TN is a sigmoidal activation function; α^TN, β^TN, γ^TN, and x₀^TN are the constant values that characterize the activation function F^TN; N^RGC_TN and N^TN_TN are the numbers of the RGCs and the TNs projecting to one TN, respectively; and w_j^RGC_TN, w^IN_TN, and w^TN_TN are the synaptic strengths from the RGCs, IN, and neighboring TNs to the TNs, respectively. Before training, synaptic strengths are the same values for all synapses with the same types. w_j^RGC_TN was modified through STDP depending on the following synaptic learning rule. The model parameters for the INs and TNs are listed in Table 2.

Table 2.

Model parameters for INs and TNs

INs		TNs
Parameters	Values	Parameters	Values
τIN	20 ms	τTN	4 ms
αIN	62 Hz	αTN	100 Hz
βIN	0.8	βTN	0.15
γIN	0 Hz	γTN	1.984 Hz
x0IN	16.6	x0TN	26
NRGC_IN	21	NRGC_TN	21
		NTN_TN	4–8
wRGC_IN	0.082 Hz−1	wRGC_TN(0)	0.082 Hz−1
		wIN_TN	0.21 Hz−1
		wTN_TN	0.043 Hz−1

Synaptic learning rule.

Synaptic modification was induced through STDP in the synapses from the RGCs to the TNs. As a synaptic learning rule, we used a simple STDP model, which was made by simplifying the detailed molecular STDP model (Urakubo et al., 2008, 2009). A detailed description of the simple STDP model is provided in the supplemental material (available at www.jneurosci.org). In the simple STDP model, the synaptic strengths were changed depending on the relative timing of the RGC spiking and TN spiking. Therefore, we generated the spike trains of the RGCs and TNs from the firing rates of the RGCs and the TNs according to the Poisson process with a bin width of 1 ms to compute the change in the synaptic strengths, respectively. The simple STDP model is based on the molecular mechanisms of STDP and reproduces a temporally asymmetric learning window through the allosteric kinetics of NMDA receptors.

Visual stimulation.

Visual stimuli drive the firings of the RGCs. We used fast- (0.3 μm/ms), medium-speed- (0.2 μm/ms), and slow- (0.1 μm/ms) moving white bars (20 μm in width and 280 μm in length) covering the receptive fields of all the neurons as the training and test stimuli. For training, a bar moving in a specific direction (trained direction) was swept repeatedly (1 Hz, 60 sweeps). For testing whether the centered TN showed direction selectivity, we fixed the synaptic strengths at the values obtained just after training and presented bars moving in four orthogonal directions relative to the trained direction (trained, 90°, 180°, and 270°) to avoid visual stimuli-induced changes in the synaptic strengths during the test.

Data analysis.

To quantify the direction and orientation selectivity of a neuron, we calculated the direction index and orientation index, according to Li et al. (2008):

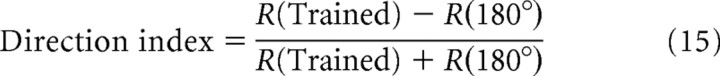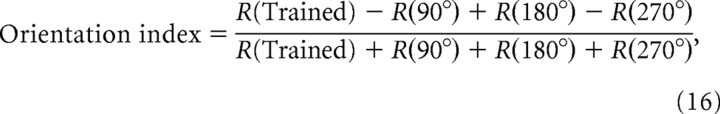where R(direction) represents the integrated total input (time integration of total input) evoked by one sweep of a moving bar in the indicated direction.

Results

Construction of the retinotectal circuit model

To understand the mechanism responsible for the development of direction selectivity through STDP in the developing Xenopus retinotectal system, we constructed a realistic neural circuit model of the retinotectal system using a simple STDP model (Fig. 1A,B) (see Materials and Methods). The simple STDP model was made using a simplification of a detailed molecular STDP model (Urakubo et al., 2008, 2009) to reduce the computational cost. We determined the structure of the neural circuit in the retinotectal circuit model by extracting essential knowledge to explain the development of direction selectivity from experimental findings (Rybicka and Udin, 1994; Tao and Poo, 2005; Akerman and Cline, 2006; Lien et al., 2006; Pratt et al., 2008). Visual information was received by the RGCs. The RGCs provided a feedforward excitation to both the TNs and the INs (Fig. 1A). Each IN provided a delayed feedforward inhibition to the TN, which received excitation from the same RGCs as each IN did. This delay was derived from larger time constant of inhibitory kinetics. The TNs received feedback excitation from neighboring TNs. In other words, a TN received excitatory input from two types of neurons, RGCs and TNs, and inhibitory input from an IN that was driven by the same RGCs. Only in the synapses between the RGCs and the TNs, synaptic strengths were modified through STDP according to the simple STDP model (Fig. 1B). As a visual stimulus, we used a bar moving at the same speed as that used experimentally by Engert et al. (2002). As the response of the retinotectal circuit model, we observed the inputs to one TN located at the center of the tectum, and the firing rates of each neuron projecting to the TN.

Before training, the firing rates of the RGCs increased after a moving bar passed through the center of the receptive fields of the RGCs because the RGCs were an OFF-center type. Successively, the firing of the RGCs induced an increase in the firing rates of the INs and TNs (Fig. 1C). We here defined the inputs from the RGCs, IN, and TNs as the RGC input, the IN input, and the TN input, respectively (Fig. 1D). The inputs in the retinotectal circuit model corresponded to the electric currents in a neuron, and negative inputs increased the firing rate of the neuron. The total input to the TN was the sum of inputs from the RGCs, the IN, and the neighboring TNs. We hereafter examined the inputs and quantitatively compared the results with experimental observations. The inputs to the TN were equal to the four orthogonal directions because of the symmetry of the neural circuit. The responses of the other neurons were similar to those of the neurons described above (data not shown).

Development of direction selectivity

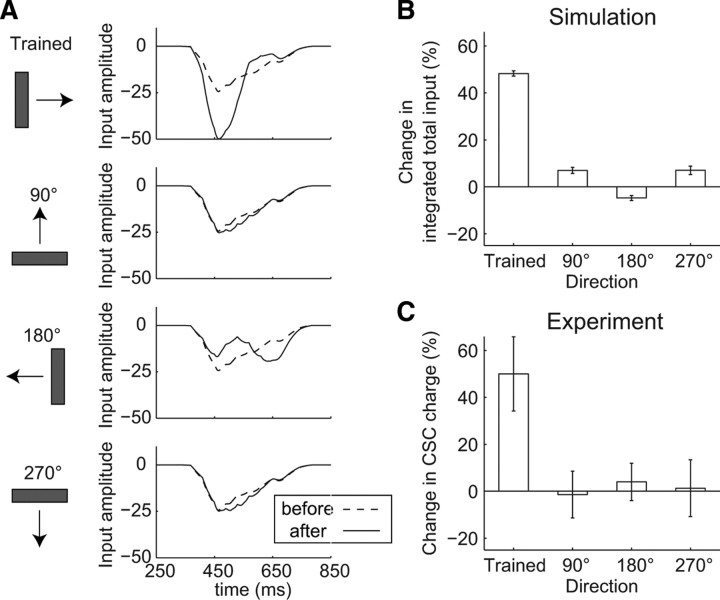
We explored whether the experimentally observed development of direction selectivity can be reproduced in our retinotectal circuit model (Fig. 2). We trained the retinotectal circuit model using 60 sweeps of a fast-moving bar in one specific direction (trained direction), and examined the time profiles of the total input to the TN produced by bars moving in four directions orthogonal to the trained direction before (Fig. 2A, dashed lines) and after (Fig. 2A, solid lines) training. After training, the peak amplitude of the total input in the trained direction increased, whereas the peak time of the total input remained the same (Fig. 2A). On the other hand, the peak time of the total input in the opposite direction to the trained direction (180° direction) was delayed, whereas the peak amplitude of the total input remained the same (Fig. 2A). This result is consistent with results observed experimentally (Engert et al., 2002). Those in the perpendicular directions to the trained direction (90° and 270° directions) remained unchanged. The time profiles for the firing rate of the TN in each direction were similar to those of the total inputs (data not shown). The integrated total inputs in the trained direction increased, whereas those in the other directions remained the same (Fig. 2B), consistent with the experimentally observed results (Fig. 2C) (Engert et al., 2002). Thus, the TN had begun to exhibit direction selectivity. In addition, once direction selectivity has developed, the suppression of inhibitory input reportedly leads to a reduction in direction selectivity in various brain areas including the tectum (Sillito, 1975, 1977; Glantz, 1998; Ramdya and Engert, 2008). Consistent with this finding, we confirmed that, in the retinotectal circuit model, suppressing the IN input led to an increase in the total inputs in all directions, resulting in a complete loss of direction selectivity (supplemental Fig. 4, available at www.jneurosci.org as supplemental material). The roles of the inhibitory input in the development of direction selectivity were also analyzed (see below, Fig. 7).

Figure 2.

Development of direction selectivity in the retinotectal circuit model. A, Time profiles of the total inputs to the centered TN evoked by bars moving in four orthogonal directions as a test stimulus before (dashed lines) and after (solid lines) training (one trial). B, C, Percentage changes in the integrated total input (time integration of total input) in each direction through training during the simulation (average of 5 trials ± SEM) (B) and during an experiment (mean ± SEM) (Engert et al., 2002) (C) (reproduced with permission from Nature).

Figure 7.

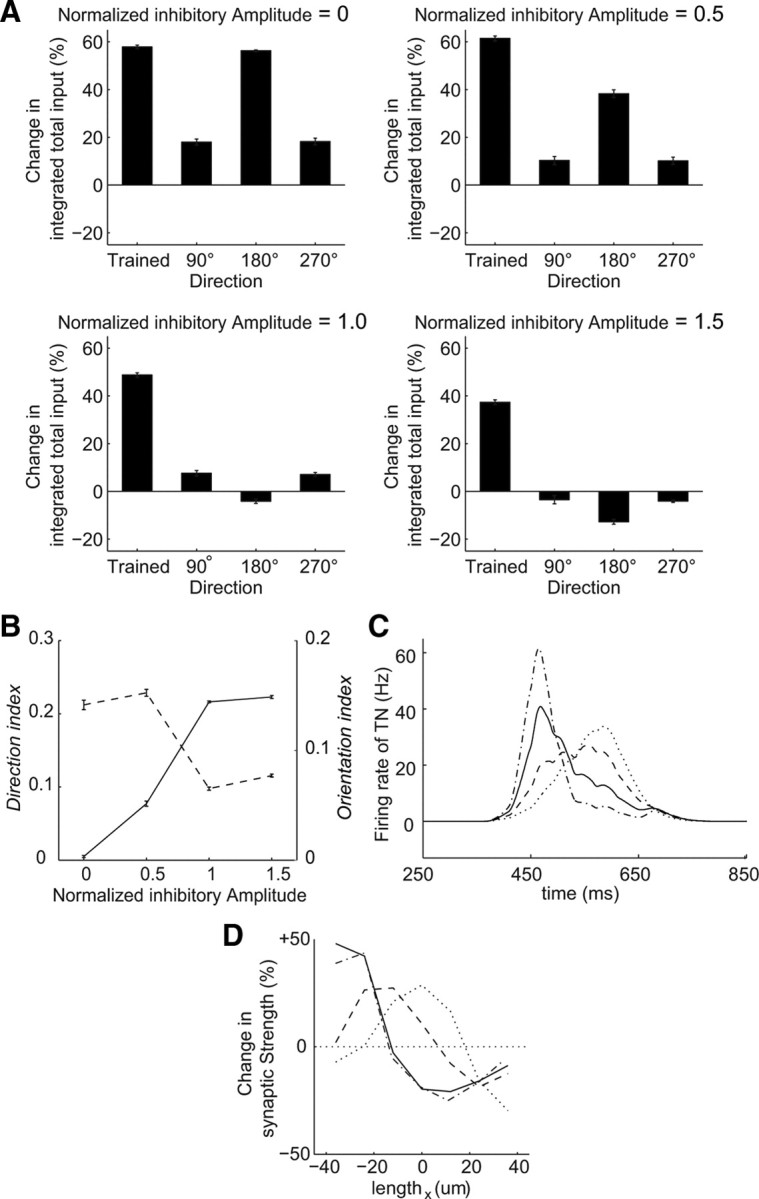
Delayed feedforward inhibition regulates the development of orientation and direction selectivities. A, Percentage changes in the integrated total input to the centered TN in each direction through training in the simulation (average of 5 trials ± SEM) in the cases of a normalized inhibitory amplitude = 0 (top left), 0.5 (top right), 1 (bottom left), and 1.5 (bottom right). The normalized inhibitory amplitude is the scale factor of synaptic strengths from the INs to the TNs. The above conditions in Figures 1–5 correspond to the case of the normalized inhibitory amplitude = 1.0. B, Direction (solid line) and orientation (dashed line) indices of the integrated total inputs against the normalized inhibitory amplitude (average of 5 trials ± SEM). C, Time profiles of the firing rate of the centered TN in the cases of the normalized inhibitory amplitude = 0 (dotted line), 0.5 (dashed line), 1 (solid line), and 1.5 (dotted-dashed line). D, Averaged changes in the synaptic strengths in the horizontal orientations against the trained direction (one trial). The line types correspond to those in C.

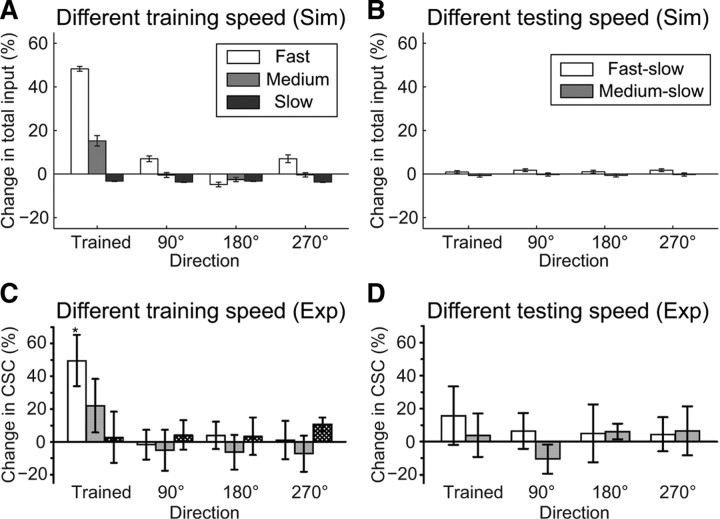
The development of direction selectivity depends on the speed of the moving bars (Engert et al., 2002). As in these previous experiments, we examined the dependency of direction selectivity on the speed of the moving bars using fast-, medium-speed-, and slow-moving bars as sets of training or test stimuli or both. When fast bars were used for both the training and test stimuli (Fig. 2), the integrated total inputs increased remarkably in the trained direction (Fig. 3A, white bars). When medium-speed bars were used for both the training and test stimuli, an increase in the integrated total input was observed in the trained direction, but the degree of the increase was smaller than that achieved with the fast bars (Fig. 3A, gray bars). When slow bars were used for both the training and test stimuli, the integrated total inputs were unchanged in all four directions (Fig. 3A, black bars). Thus, as the speed of the moving bars decreased, the increase in the integrated total inputs in the trained direction was reduced (Fig. 3A). When slow bars were used as the test stimulus after training with fast and medium-speed bars, the integrated total inputs were unchanged in all four directions (Fig. 3B). These results were consistent with the experimental results (Fig. 3C,D). Of note, the spike numbers of the TN produced by a sweep of moving bars were similar regardless of the speeds, but frequencies varied (supplemental Fig. 3, available at www.jneurosci.org as supplemental material), as observed experimentally (Engert et al., 2002). The mechanism of speed dependency is explained in the Discussion section.

Figure 3.

Speed dependency of moving bars during the development of direction selectivity. A, C, Percentage changes in the integrated total inputs in each direction through training. Fast- (0.3 μm/ms), medium-speed- (0.2 μm/ms), and slow- (0.1 μm/ms) moving bars were used for both training and test stimuli in the simulation (average of 5 trials ± SEM) (A) and an experiment (mean ± SEM) (Engert et al., 2002) (C) (reproduced with permission from Nature). B, D, Percentage changes in the integrated total inputs in each direction using slow test bars after training with fast (fast-slow) and medium-speed (medium-slow) bars in the simulation (average of 5 trials ± SEM) (B) and experimentally (mean ± SEM) (Engert et al., 2002) (D) (reproduced with permission from Nature).

Thus, our retinotectal circuit model appears to capture the essence of the development of direction selectivity in the retinotectal system (Figs. 2, 3). Therefore, we used this retinotectal circuit model with fast-moving bars for training and testing to explore the mechanism responsible for the development of direction selectivity.

Mechanism responsible for the development of direction selectivity

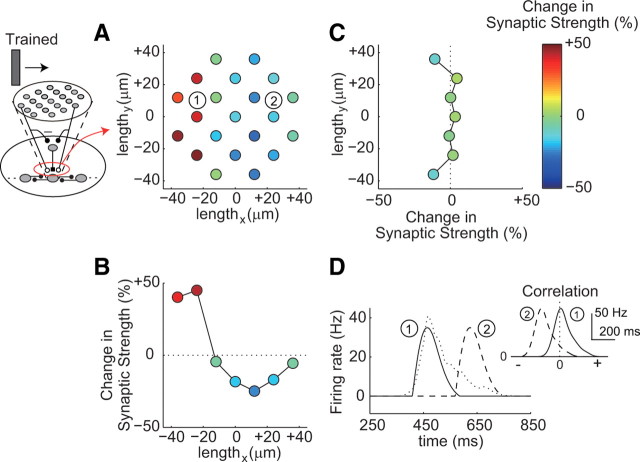
Asymmetric modification of synaptic strengths through STDP

Apparently, in the retinotectal circuit model, synaptic modification through STDP led to the development of direction selectivity, and we observed a change in synaptic strength from the RGCs to the centered TN (Fig. 4A–C). Before training, the synaptic strengths were the same. A bar moving from left to right was used as the training stimulus (Figs. 2, 4). As a result of the training, the synaptic strengths from the RGCs on the left side increased, whereas those on the right side decreased through STDP (Fig. 4A). Similarly, the averaged synaptic strengths along the trained direction were asymmetrically modified (Fig. 4B). We call such a spatial asymmetric change an asymmetric modification. In STDP, potentiation is induced when presynaptic spiking precedes postsynaptic spiking, whereas depression is induced when postsynaptic spiking precedes presynaptic spiking (Zhang et al., 1998; Bi and Poo, 2001; Dan and Poo, 2004). Here, RGC spiking and TN spiking corresponded to pre-spiking and post-spiking, respectively. RGC spiking before TN spiking led to potentiation, whereas RGC spiking after TN spiking led to depression (Fig. 1C). The firing of the RGCs on the left sides preceded that of the TN, and the firing of the RGCs on the right sides lagged behind that of the TN (Fig. 4D). The temporal order of the firing between the RGCs and the TN was also reflected by their cross-correlation (Fig. 4D, inset). Therefore, the asymmetric modification of the synaptic strengths was induced through STDP along the trained direction (Fig. 4B). In contrast, along the perpendicular orientation to the trained direction, the averaged synaptic strengths appeared to be unchanged regardless of the locations of the RGCs, because the increased and decreased synaptic strengths mutually cancelled each other (Fig. 4C). Such asymmetric modification of the synaptic strengths corresponds to the asymmetric modification of the tectal receptive field observed experimentally (Engert et al., 2002).

Figure 4.

Asymmetric modification of the synaptic strengths through STDP. A–C, Changes in the synaptic strengths (one trial). A, Changes in the synaptic strengths from each RGC to the TN. The coordinates show the relative position of each RGC to the TN. The circles indicate the locations of each RGC, and their color represents the amplitude of the change in the synaptic strengths. The trained direction is left-to-right. B, C, Averaged changes in the synaptic strengths in the horizontal (B) and perpendicular (C) orientations against the trained direction. D, Time profiles of the firing rates of two RGCs (solid and dashed lines) indicated in A and the TN (dotted line). An inset shows cross-correlations of the firing rates between each RGC and the TN. The numbers of the RGCs correspond to those in A.

Training induced changes in inputs

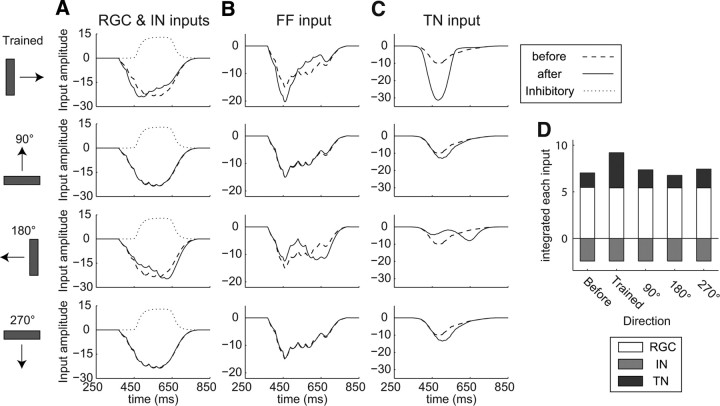
We next investigated the effect of asymmetric modification of the synaptic strengths on the changes in each input to the TN (Fig. 5). After training, the peak time of the input from RGCs to the TN (RGC input) in the trained direction was shifted earlier (Fig. 5A). This result arose because, in the trained direction, the RGC input to the potentiated synapses occurred at an earlier time, whereas that to the depressed synapses occurred at a later time through STDP (Fig. 4B). Although the integrated total inputs, the sum of RGC, IN, and TN inputs, increased in the trained directions (Figs. 2B, 3), the integrated RGC inputs in the trained direction remained the same (Fig. 5D). This means that STDP does not directly trigger an increase in the integrated RGC input or the integrated total input. In the 180° direction, however, the peak time of the RGC input was shifted later because the RGC input to the depressed and potentiated synapses occurred at an earlier and later time, respectively (Figs. 4B, 5A). The RGC inputs in the 90° and 270° directions remained the same because the averaged synaptic strengths along the perpendicular orientation were unchanged (Figs. 4C, 5A). The time profiles of the IN inputs to the TN and the integrated IN inputs also remained the same because of the fixed synaptic strengths (Fig. 5A,D). In the retinotectal circuit model, the feedforward input to the TN consisted of the RGC input and the IN input. Therefore, we here defined the FF input to the TN as the sum of the RGC and IN inputs. In the trained direction, the peak amplitude of the FF input increased because the peak time of the RGC input was shifted earlier and the overlap between the RGC input and the IN input was reduced (Fig. 5A,B). On the other hand, in the 180° direction, the peak amplitude of the FF input remained the same, because the peak time of the RGC input was delayed and the increased peak of the RGC input was masked by the IN input (Fig. 5A,B). In the 90° and 270° directions, the time profiles of the FF inputs remained the same (Fig. 5B). The TN input to the TN increased in the trained direction (Fig. 5C). The increased peak amplitude of the FF input exceeded the threshold for feedback excitation from the neighboring TNs, leading to the amplification of the integrated TN input (Fig. 5D; see below). In contrast, in the 180° direction, the peak time of the TN input was shifted later (Fig. 5C). The same peak amplitude of the FF input led to the same integrated TN input despite the time profile changes in both the FF and TN inputs (Fig. 5A–D). In the 90° and 270° directions, the time profiles of the TN input remained the same (Fig. 5C). In summary, the integrated TN input was remarkably increased only in the trained direction (Fig. 5D). The increase in the integrated TN input corresponds to the experimentally observed increase in the number of EPSCs in the trained direction (Engert et al., 2002). Thus, in the trained direction, the peak time of the RGC input shifted earlier as a result of STDP. Together with the delayed IN input, a stronger early transient FF input was generated, resulting in the amplification of the TN input through feedback excitation from the neighboring TNs (Fig. 5A–C). It is noteworthy that the increase in the integrated total input in the trained direction was derived from the increase in input from TN–TN synapses, whose synaptic strengths were fixed, but not from the increase in input from RGC–TN synapses, whose synaptic strengths were modified through STDP (Fig. 5D).

Figure 5.

Changes in time profiles of each input to the TN through training. A–C, Time profiles of RGC input (A), IN input (A), FF input (B), and TN input (C) to the TN evoked by fast-moving bars of four orthogonal directions before (dashed lines) and after (solid lines) training (one trial). The IN input is shown by the dotted lines (A). D, Contribution of each input to the integrated total input. White, Integrated RGC input; gray, integrated IN input; black; integrated TN input (1 trial).

Amplification of TN input through feedback excitation

We tried to examine the mechanism of the amplification of the TN input. Because of the complexity of the retinotectal circuit model, we analyzed the mechanism by making a simple retinotectal model. As mentioned, in the retinotectal circuit model, the total input was divided into two types of inputs, the FF input and the TN input (Fig. 6A). We made the simple retinotectal model, which is described by the feedforward input FFI(t) and one ordinary differential equation representing the firing rate of a TN r(t). FFI(t) in the simple retinotectal model corresponds to the FF input in the retinotectal model, and r(t) multiplied by a scale factor A_{t_t} corresponds to the TN input. In the retinotectal circuit model, the peak time and peak amplitude are considered as the critical factors for triggering the amplification of the TN input, which depend on training and directions of the moving bar. We used FFI(t), which is characterized by the peak time and peak amplitude of the FF input. The description of FFI(t) is as follows (Fig. 6B,C, top):

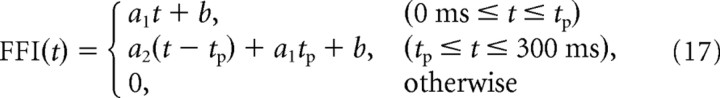where t_p is the peak time of FFI(t), a₁ (≤0) and a₂ (≥0) represent the slope of FFI(t) before and after time t_p, and b (≤0) is the minimum level of FFI(t). These parameters are subject to

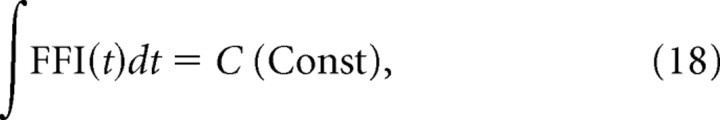because the integrated FF inputs remained the same before and after training in all four directions (Fig. 5D). The firing rate of the TN r(t) is described through the standard rate-model equation, similar to the neuron models in the retinotectal circuit model (Chance et al., 1999; Dayan and Abbott, 2001) (see Materials and Methods) as follows:

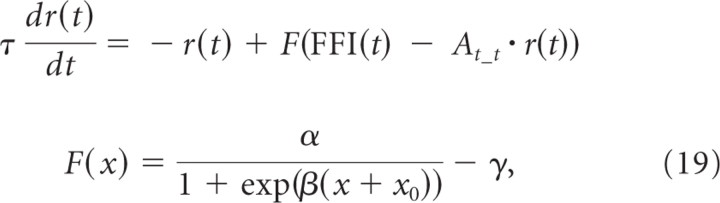where F is a sigmoidal activation function; τ is a time constant; A_{t_t} is the scale factor that determines the amplitude of the excitatory feedback; and α, β, γ, and x₀ are the constant values that characterize the activation function. We set C = 2400 ms, τ = 4 ms, A_{t_t} = 0.344 Hz⁻¹, α = 100 Hz, β = 0.15, γ = 1.984 Hz, and x₀ = 26. These values are the same as the retinotectal circuit model. A_{t_t} corresponds to the value obtained by multiplication of the synaptic strength between the TNs and the number of TNs projecting to the centered TN.

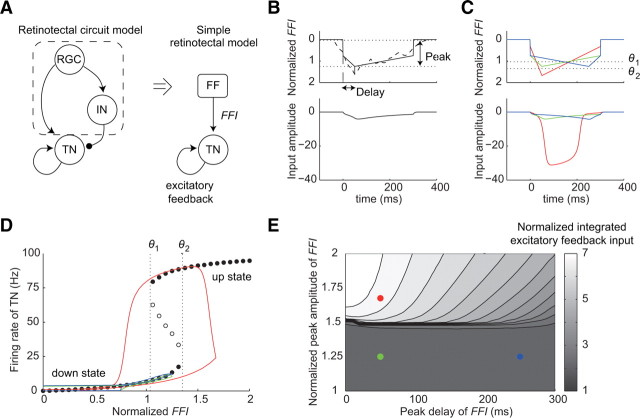
Figure 6.

Mechanism of amplification of the TN input. A, Schematic diagram of the simple retinotectal model (right). FFI in the simple retinotectal model corresponds to the sum of the RGC input and the IN input to the TN (left). B, Sample time profiles of FFI (top, solid line) and excitatory feedback input (bottom). Peak represents the maximum amplitude of FFI. Delay represents the duration between the peak time and the onset of FFI. Dashed line represents the FF input before training. C, Time profiles of FFI and excitatory feedback input. The green, red, and blue solid lines indicate the FFIs, which correspond to the FF inputs in Figure 5B in the trained direction before training, in the trained direction after training, and in the 180° direction after training, respectively. Dotted lines indicate the lower (θ₁) and upper (θ₂) transition thresholds of the excitatory feedback. D, Bifurcation diagram of the simple retinotectal model with respect to the parameter FFI. Solid and open circles indicate the firing rate of the TN at stable and unstable steady states, respectively. Each solid line indicates the superimposed firing rate profiles of TN against FFI. The line colors are consistent with those in C. Dotted lines indicate the lower (θ₁) and upper (θ₂) transition thresholds. E, Summary of the relationship among the peak amplitude of FFI, peak time of FFI, and integrated TN input. Solid circles indicate the point of the time profiles in C. The circle colors are consistent with those in C.

We set FFI with an early peak time and a medium peak amplitude (early-medium input) as the time profile for the FF input before training (Fig. 6C, top, green line). As the response after training in the trained direction, we examined the response to an early-strong input (Fig. 6C, top, red line) because the peak amplitude of the FF input increased (Fig. 5B). As the response after training in the 180° direction, we examined the response to a late-medium input (Fig. 6C, top, blue line) because the peak time of the FF input was delayed and the peak amplitude remained the same (Fig. 5B). In the trained direction after training, the excitatory feedback input was amplified because the FFI exceeded an upper transition threshold θ₂ of the excitatory feedback (Fig. 6C, red line). A bifurcation analysis indicated that the excitatory feedback generates a switch-like response and two stable steady states of the TN: the up state and the down state (Fig. 6D). When the FFI exceeded the threshold θ₂, the state of the TN was switched from the down state to the up state, resulting in the amplification of the excitatory feedback input (Fig. 6C,D, red line). On the other hand, in the 180° direction after training, the peak time of the excitatory feedback input was delayed, but the peak amplitude remained the same because the peak of the FFI did not exceed the threshold θ₂ (Fig. 6C, bottom, blue line). Thus, when the peak of the FFI was below the threshold θ₂, the state of the TN did not switch to the up state and the integrated excitatory feedback input was almost independent of the peak time (Fig. 6E).

Delayed feedforward inhibition regulates the development of orientation or direction selectivity

Inhibitory activity is essential for the development of visual neural circuits, such as ocular dominance plasticity (Huang et al., 1999; Hensch, 2005; Harauzov et al., 2010) and the refinement of receptive fields (Tao and Poo, 2005). We investigated the effect of delayed feedforward inhibition on the development of direction selectivity using our retinotectal circuit model. We defined a normalized inhibitory amplitude as the scale factor of the synaptic strengths from INs to TNs. The conditions described in Figures 1–5 correspond to the case of the normalized inhibitory amplitude equal to 1.0. We changed the scale factor and examined the training-induced changes in the integrated total input to the centered TN. We maintained the same spike numbers at the TN regardless of the amplitude of the delayed feedforward inhibition by varying the synaptic strengths from the RGCs to the TNs.

When the inhibitory amplitude was reduced, the integrated total inputs to the TN increased remarkably not only in the trained direction but also in the 180° direction (Fig. 7A, top). In the case of a complete reduction (normalized inhibitory amplitude = 0), the extent of the increase in the 180° direction was similar to that in the trained direction (Fig. 7A, top left). Such responses similar to both the trained and the opposite directions have been known as orientation selectivity (Hubel and Wiesel, 1959). In the case of a reduction by 50% (normalized inhibitory amplitude = 0.5), the extent of the increase in the 180° direction was smaller than that in the trained direction (Fig. 7A, top right). Thus, the reduction in the inhibitory amplitude resulted in the development of orientation selectivity rather than direction selectivity. In contrast, when the inhibitory amplitude was enhanced (normalized inhibitory amplitude = 1.5), the integrated total input in the 180° direction decreased, whereas that in the trained direction still increased (Fig. 7A, bottom right). We evaluated these properties using direction index and orientation index, measures of the degrees of direction and orientation selectivity, respectively (see Materials and Methods). As the inhibitory amplitude decreased, the direction index decreased, whereas the orientation index increased (Fig. 7B). This result indicates that the suppression of delayed feedforward inhibition leads to orientation selectivity rather than direction selectivity.

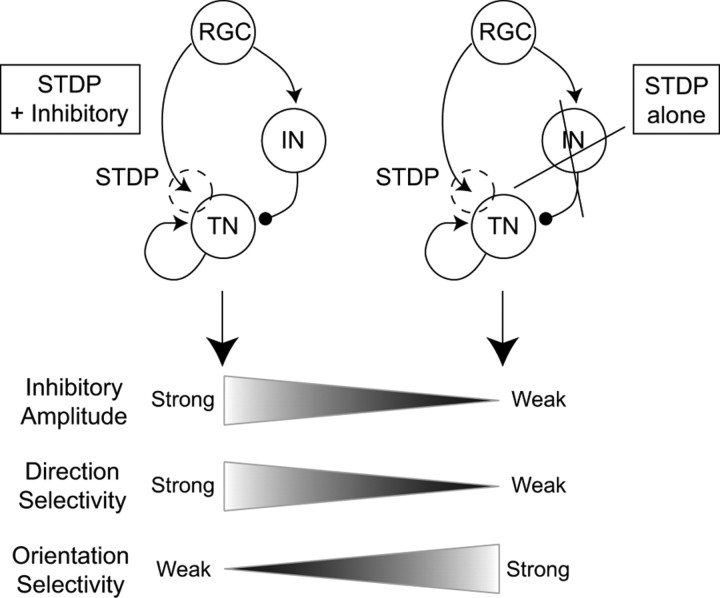
To understand the role of the delayed feedforward inhibition in the development of direction or orientation selectivity, we observed the time profiles of the firing rate of the TN. As the inhibitory amplitude was reduced, the peak time of the firing rate of the TN was shifted later (Fig. 7C). This outcome arose because the weak delayed feedforward inhibition from the IN did not suppress the feedforward excitation from the RGCs. The synaptic strengths from the RGCs, which fire slightly before the TN, increased through STDP. Therefore, with the reduction in the inhibitory amplitude, the peak of the averaged synaptic strengths moved from the left to the center (Fig. 7D; supplemental Fig. 7, available at www.jneurosci.org as supplemental material). In the case of a complete reduction in the inhibitory amplitude (supplemental Fig. 7A, available at www.jneurosci.org as supplemental material), before training, the peak amplitude of the FF input was below the threshold and the peak time was in the middle of the response duration. After training, both in the trained and 180° directions, the peak amplitude of the FF input exceeded the threshold and the peak time remained the same. As a result, orientation selectivity developed in the tectum (Fig. 7A). Thus, through STDP, a neural circuit consisting of feedforward and feedback excitation and delayed feedforward inhibition generates direction selectivity, whereas a neural circuit consisting of feedforward and feedback excitation without delayed feedforward inhibition generates orientation selectivity in the tectum (Fig. 8).

Figure 8.

Delayed feedforward inhibition tunes direction and orientation selectivity. In a neural circuit with feedforward excitation with STDP and feedback excitation, strong delayed feedforward inhibition leads to the development of direction selectivity (left), whereas weak delayed feedforward inhibition leads to the development of orientation selectivity (right).

Discussion

We have developed a realistic retinotectal circuit model with STDP. This retinotectal circuit model appeared to capture the critical features of the development of direction selectivity observed experimentally, such as the asymmetric modification of the tectal receptive field, the change in the time profiles of the total input, the increase in the number of EPSCs, and the speed dependency of the development of direction selectivity. Using this retinotectal circuit model, we proposed a mechanism responsible for the development of direction selectivity. A moving bar caused sequential firing of the RGCs, INs, and TNs, and repetitive exposure of the retina to the moving bar resulted in the asymmetric modification of the synaptic strengths through STDP (Fig. 4). In the trained direction, the asymmetric modification generated an earlier shift in the peak of feedforward excitation (Fig. 5A). Together with the delayed feedforward inhibition, a stronger early transient feedforward signal was generated (Fig. 5B), which exceeded the threshold of the feedback excitation from neighboring TNs and resulted in the amplification of the input to the TN and the development of direction selectivity (Figs. 5, 6). In the 180° direction, despite the shift in the peak time of the feedforward excitation, the shifted peak in the feedforward excitation was masked by the delayed feedforward inhibition and the integrated total input remained the same. In addition, the suppression of the delayed feedforward inhibition resulted in the development of orientation selectivity rather than direction selectivity (Figs. 7, 8).

Direction selectivity has been reported not only in the tectum of lower vertebrates (Sajovic and Levinthal, 1982; Hoshino and Matsumoto, 2003; Niell and Smith, 2005; Ramdya and Engert, 2008), but also in the mammalian V1 (Hubel and Wiesel, 1959, 1968). Cortical direction selectivity is usually explained by the Barlow–Levick-type model (Barlow and Levick, 1965), in which feedforward excitation generates the response of neurons in the preferred direction, whereas feedforward inhibition suppresses the excitation and the response in the opposite direction. However, the Barlow–Levick-type model is partly inconsistent with the features of cortical direction selectivity (Douglas and Martin, 1991; Suarez et al., 1995). To resolve this problem, feedback excitation from other direction-selective neurons has been additionally incorporated in some models (Douglas and Martin, 1991; Suarez et al., 1995; Maex and Orban, 1996). This structure (feedforward excitation, delayed feedforward inhibition, and feedback excitation) is consistent with the structure of the neural circuit in our retinotectal circuit model. In the retinotectal circuit model, the delay of the IN input against the RGC input was generated mainly by a larger time constant of inhibitory kinetics not by a lag of inhibitory evoked response. Consistent with this, experimentally, the decay time constant of IPSCs (27.1 ms) was larger than that of EPSCs (4.6 ms) in the tectum (Lien et al., 2006). Similarly, in mammalian visual cortex, the decay time constant of IPSCs (20.7–35 ms) was larger than that of EPSCs (2.6–11 ms) (Hestrin, 1992; Varela et al., 1999; Dong et al., 2004). Furthermore, STDP has also been observed in V1 (Sjöström et al., 2001; Froemke and Dan, 2002; Nevian and Sakmann, 2006; Corlew et al., 2007). Although the development of direction selectivity in V1 remains unclear, considering the similar structure of the neural circuit with STDP in V1, the direction selectivity in V1 may develop in a manner similar to that observed in the retinotectal circuit model.

Speed dependency

The development of direction selectivity depends on the speeds of moving bars both in experiments and simulations (Fig. 3). When medium-speed bars were used as training and test stimuli, the increase in the integrated total input was smaller than the increase obtained with fast bars (Fig. 3A, gray bars). This outcome occurred because, in the trained direction after training, the peak amplitude of the FF input obtained with the medium-speed bars was lower than that obtained with the fast bars although the peak amplitude still exceeded the threshold. When slow bars were used as both training and test stimuli, the synaptic strengths did not change and direction selectivity did not develop (Fig. 3A,C, black bars; supplemental Fig. 6A–C, available at www.jneurosci.org as supplemental material). The speed-dependent changes in the synaptic strengths in this retinotectal circuit model correspond to the speed-dependent changes in the tectal receptive field observed experimentally (Engert et al., 2002). When slow bars were used as the test stimulus after training with fast and medium-speed bars, direction selectivity was not observed (Fig. 3B,D). This outcome occurred because the peak amplitude of the FF input produced with the slow bars was lower than the threshold, even after training.

STDP in TN–TN synapses

The synaptic strengths of TN–TN synapses experimentally have been modified in a spike timing-dependent manner (Pratt et al., 2008). However, the developmental stages of Xenopus investigated in our study (stages 42–45) (Engert et al., 2002) are earlier than those investigated by Pratt et al. (2008) (stages 45–49). Therefore, we used the retinotectal circuit model without applying STDP to TN–TN synapses. If we apply the same STDP model not only to RGC–TN synapses but also to TN–TN synapses, all of the TN–TN synapses may be potentiated by the repetitive exposure of the retina to the fast-moving light bar. This corresponds to the situation in which burst firings in both pre-neurons and post-neurons lead to potentiation, regardless of the order of the firings in pre-neurons and post-neurons (Froemke et al., 2006; Urakubo et al., 2008). In this case with STDP at TN–TN synapses, stronger early transient feedforward signals and the decrease in the transition threshold of feedback excitation due to the potentiation of all TN–TN synapses are similarly likely to lead to the development of direction selectivity. Further study is necessary to address this issue.

Retinal direction selectivity

Some types of RGCs respond selectively to the direction of motion (Cronly-Dillon, 1964; Barlow and Levick, 1965; Oyster and Barlow, 1967; Pearlman and Hughes, 1976). In the rabbit retina, direction-selective RGCs account for ∼10% of all RGCs (Vaney, 1994; Vaney et al., 2001; Taylor and Vaney, 2003). Thus far, direction-selective RGCs have not been observed in Xenopus tadpoles. Therefore, these RGCs have been assumed not to exhibit a direction-selective response in a retinotectal circuit model. However, incorporating direction-selective RGCs into the retinotectal circuit model is likely to lead to similar results, and the mechanism we proposed in this study can similarly explain the development of direction selectivity.

Alternatively, the increase in the integrated total input in the trained direction may result from potentiation of all the synapses from direction-selective RGCs to the TN regardless of the location. In other words, only potentiation, but not asymmetric modification of the synaptic strengths through STDP, may be sufficient. If this is the case, when a slow bar is used as the test stimulus after training with fast and medium-speed bars, the integrated RGC input should increase in the trained direction; consequently, the integrated total input should also increase, unless the direction selectivity of the RGCs is dependent on speed. However, in the experimental observations, the input was not increased, suggesting that this case is unlikely. Thus, regardless of whether the RGCs show a direction-selective response, asymmetric modification through STDP is necessary for the development of direction selectivity.

Other models of the development of direction selectivity

Several visual neural circuit models with STDP have been proposed for the development of direction selectivity in V1 (Buchs and Senn, 2002; Shon et al., 2004; Wenisch et al., 2005). The structures of the neural circuits in the models of Buchs and Senn (2002) and Wenisch et al. (2005) differ from those in our retinotectal circuit model. In their models, direction selectivity developed as a result of essentially different mechanisms from those in our retinotectal circuit model. Using feedforward input from depressing and nondepressing synapses, Buchs and Senn (2002) proposed that a change in the degree of synaptic depression induces temporal advance in the response of neurons to drifting gratings in the preferred direction, resulting in the development of direction selectivity. In the model of Buchs and Senn (2002), only the feedforward excitation is modeled, whereas, in our retinotectal circuit model, the feedback excitation generated the direction selectivity. The model of Wenisch et al. (2005) is comprised of recurrent excitatory and inhibitory connections. The synaptic strengths from the recurrent excitatory connections have been modified by moving bars, resulting in the development of direction selectivity. In contrast, in our retinotectal circuit model, the synaptic strengths from the neighboring TNs were fixed and the change in the feedforward excitation triggered the development of direction selectivity. The model of Shon et al. (2004) used a neural circuit with a structure similar to that of the retinotectal circuit model and showed that asymmetric modification shifts the feedforward excitation earlier and broadens the timing between the excitation and inhibition in the preferred direction, resulting in the development of direction selectivity. The timing shift of the feedforward excitation is critical for the development of direction selectivity. On the other hand, in our retinotectal model, the amplification mechanism of the feedback excitation is important for reproducing the experimentally observed features of the development of direction selectivity. Thus, many alternative models are possible for the development of direction selectivity. Experimental findings of neural connectivity and changes in inputs through the development of direction selectivity are needed to constrain the models.

Future directions

We modeled our retinotectal circuit, based on the molecular mechanism of synaptic plasticity. The retinotectal circuit model appeared to be consistent with experimentally observed features of the development of direction selectivity. We used a simple STDP model that enabled us to coherently reproduce STDP. However, because of the implicit description of kinetic interaction in the simple STDP model, we could not directly compare the role of each molecule with the experimental result. By introducing our detailed molecular STDP model, where the kinetics of each molecule are explicitly described (Urakubo et al., 2008, 2009), we can examine the role of molecules including NMDA receptors, ionic channels, and the phosphorylation and dephosphorylation of signaling molecules and directly compare the molecular biological and pharmacological experimental results. Using such an approach, we can analyze the system characteristics of the development of visual and other functions through STDP.