Necessity is the Mother of Invention: Reconstructing Missing Sensory Information in Multiple, Concurrent Reference Frames for Eye–Hand Coordination

Abstract

When aligning the hand to grasp an object, the CNS combines multiple sensory inputs encoded in multiple reference frames. Previous studies suggest that when a direct comparison of target and hand is possible via a single sensory modality, the CNS avoids performing unnecessary coordinate transformations that add noise. But when target and hand do not share a common sensory modality (e.g., aligning the unseen hand to a visual target), at least one coordinate transformation is required. Similarly, body movements may occur between target acquisition and manual response, requiring that egocentric target information be updated or transformed to external reference frames to compensate. Here, we asked subjects to align the hand to an external target, where the target could be presented visually or kinesthetically and feedback about the hand was visual, kinesthetic, or both. We used a novel technique of imposing conflict between external visual and gravito-kinesthetic reference frames when subjects tilted the head during an instructed memory delay. By comparing experimental results to analytical models based on principles of maximum likelihood, we showed that multiple transformations above the strict minimum may be performed, but only if the task precludes a unimodal comparison of egocentric target and hand information. Thus, for cross-modal tasks, or when head movements are involved, the CNS creates and uses both kinesthetic and visual representations. We conclude that the necessity of producing at least one coordinate transformation activates multiple, concurrent internal representations, the functionality of which depends on the alignment of the head with respect to gravity.

Introduction

Fascinating theories have been proposed to describe how the CNS selects, combines, and reconstructs sensory information to perform targeted movements. According to various models: (1) networks of neurons create distributed representations of spatial information in different reference frames and for different sensory modalities, (2) the weighting of different sources of information is optimized to reduce uncertainty, (3) recurrent connections maintain coherency between redundant internal representations, and (4) these same connections allow for the reconstruction of sensory inputs that may be lacking (Droulez and Darlot, 1989; van Beers et al., 1999; Ernst and Banks, 2002; Pouget et al., 2002a). Recent experimental studies have proposed that visual targets may be represented in proprioceptive space and the unseen hand in visual space (Smeets et al., 2006), suggesting that the CNS indeed reconstructs information that is missing from the sensory array. In contrast, related studies (Sober and Sabes, 2005; Sarlegna and Sainburg, 2007) have shown that when both visual and kinesthetic feedback about the hand is provided, the CNS privileges the sensory modality directly comparable to the target, thus avoiding nonessential transformations that add noise (Soechting and Flanders, 1989).

We thus set out to reconcile theories about the weighting of multisensory information, based on the expected variance of each input, with models of recurrent networks that presuppose the free transformation of information across sensory modalities. In experiments where we asked subjects to orient the hand to an external target, we expanded on the aforementioned studies in two significant ways.

First, the design of those and many other experiments (Flanagan and Rao, 1995; Lateiner and Sainburg, 2003; Sober and Sabes, 2003) relied on conflict between visual and kinesthetic feedback about the hand. Because both information types were available simultaneously (to create conflict), a direct visual–visual or kinesthetic–kinesthetic target-hand comparison was always possible. In our experiments, rather than introducing conflict between the sensory signals describing the target or hand themselves, we instead introduced conflict between the reference frames used to encode their orientations in memory. With this technique, we could study situations where comparisons involving a single sensory modality were impossible, such as aligning the unseen hand to a visual target.

Second, subjects in the aforementioned experiments could easily use only egocentric information because no body movement occurred between target acquisition and the pointing response. And even if subjects were willing to accept the cost of computing exocentric representations of the target (Committeri et al., 2004; Burgess, 2006), they were given few external cues to do so. Here, we required subjects to tilt the head during an instructed memory delay, preventing them from using unprocessed egocentric inputs to align the hand with the externally anchored target. Furthermore, we encouraged the use of external reference frames (visual, gravitational) by providing a structured visual background while subjects tilted the head.

With these experiments, we examined situations in which a direct comparison of information in egocentric coordinates was or was not possible, thus allowing us to identify rules governing how the CNS performs cross-modal sensory reconstruction in tasks of visuomotor coordination.

Materials and Methods

Subjects performed a video game-like task of shooting a projectile out of a tool so that it passed between a set of oriented target beams. Since the projectile, as well as the tool, was long and narrow, the tool and the hand needed to be at the same orientation as the beams to achieve success, in much the same way that one must align the hand with an object to be grasped. The target orientation was presented either visually or kinesthetically and the orienting response of the hand was performed with visual feedback, kinesthetic feedback, or both. On some trials, subjects were required to tilt the head during an instructed memory delay and during this head movement we sometimes introduced an imperceptible sensory conflict between the visual and gravitational reference frames. We thus examined how visual and gravito-kinesthetic information is fused to guide the hand, and we compared these observations to the predictions of analytical models based on the idea that response variability should be minimized. The details of the experimental protocol are described below.

Experimental setup

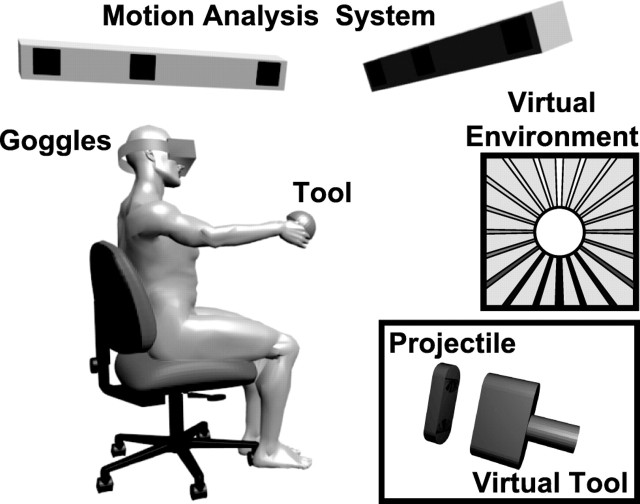
To select and modulate the sources of sensory information that subjects could use to accomplish the task, a fully immersive virtual-reality device was developed. The system consisted of the elements shown in Figure 1. A motion-analysis system with active markers (CODA; Charnwood Dynamics) was used to measure the three-dimensional position of 19 infrared LEDs in real time (submillimeter accuracy, 200 Hz sampling frequency). Eight markers were distributed ∼10 cm apart on the surface of stereo virtual-reality goggles (V8; Virtual Research) worn by the subjects, eight on the surface of a hemispherical tool (350 g, isotropic inertial moment around the roll axis) that subjects held in their dominant hand and three attached to a fixed reference frame placed in the laboratory. For the goggles and the tool, a numerical model of the relative positions of the LEDs was implemented in advance, so that an optimal matching algorithm could be used to effectively and robustly estimate the position and the orientation of the object, even in case of partially hidden markers. We exploited the redundancy of the high number of markers on the helmet and on the tool to reduce errors in the position and orientation estimation, resulting in a standard error in the measured viewpoint orientation below the visual resolution of the goggles (0.078°). To minimize the effect of the noise and computational delays of the system, a predictive Kalman filter was applied to the angular coordinates of the objects. The real-time position and orientation of the goggles were then used to update, at 50 Hz, the visual scene viewed by the subject in the virtual environment. Analogous data from markers on the tool were used to place a virtual tool in the scene that moved with the hand (Fig. 1).

Figure 1.

Experimental setup. A motion-analysis system was used to track, in real time, the position and orientation of virtual-reality goggles worn by the subjects and of a tool held in their dominant hand. The virtual-reality environment consisted of a cylindrical tunnel and a visual representation of the tool and projectile.

Virtual environment.

During the experiment, subjects were comfortably seated, so as to avoid problems with balance, but were not strapped to the chair to avoid unnatural somatosensory inputs about their position in space. Subjects observed a visual environment in the virtual-reality goggles. The virtual environment consisted of a cylindrical horizontal tunnel with walls characterized by longitudinal marks parallel to the tunnel axis (Fig. 1, right). These marks helped the subjects to perceive their spatial orientation in the virtual world. The color of these marks went from white on the ceiling to black on the floor to give an unambiguous cue as to which way was up in the virtual environment.

Experimental trials

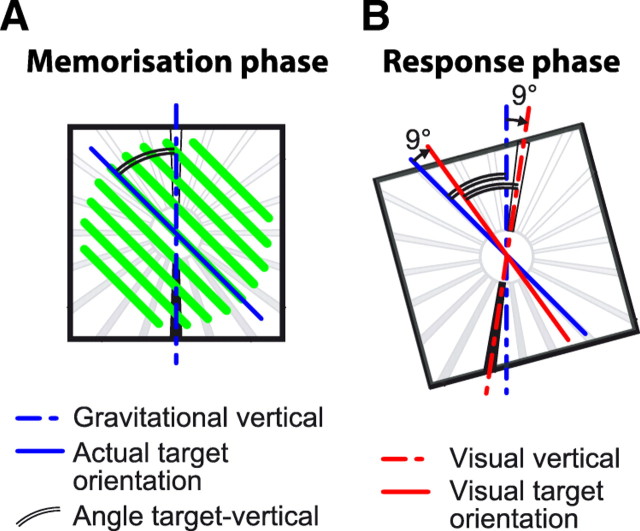
As shown in Figure 2, each trial of the task consisted of three phases, as follows: (1) observation and memorization of the target orientation, (2) head tilt, and (3) alignment of the tool to the remembered target orientation.

Figure 2.

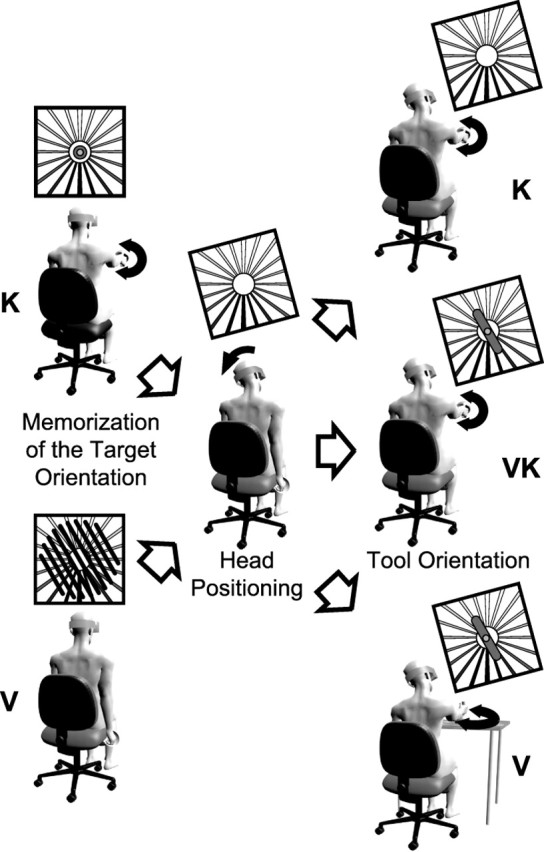
Experimental protocol. Each trial consisted of three phases. First, subjects acquired the target either visually (V) or kinesthetically (K) with the head in an upright position. Next, in the absence of visual feedback about the target, but with vision of a structured visual surround, subjects tilted the head to the right or to the left. Conflict between the kinesthetically and visually perceived head tilt could be introduced at this stage (see Materials and Methods). Finally, subjects aligned the tool to the remembered target orientation under visual control only (V), under kinesthetic control only (K), or both (VK).

Target presentation.

When the target was visual (V target presentation), parallel beams were displayed in front of the subject to define an orientation in the frontoparallel plane. These beams were always perpendicular to the tunnel's axis, but they could have different orientations with respect to the vertical. The subject had 2.5 s to memorize the orientation of the beams in the frontoparallel plane, after which they disappeared. Subjects kept their right arm by their side when the target was presented visually. Since in this phase the subject was not allowed to move the arm, the only available information about the target orientation was visual.

To present the target orientation kinesthetically (K target presentation), the target beams were not shown to the subject. Instead, we asked the subjects to raise their arm to hold the physical tool in front of them. A virtual tool in the form of a simple cylinder appeared in the visual scene, the movements of which reflected the position, pitch, and yaw orientation, but not roll angle, of the subject's hand. Roll movements of the physical handheld tool instead made the virtual tool change color. The tool turned from red to green as the hand approached the desired roll angle. The color gave only a measure of the absolute error between the actual and desired hand position, but not the direction of the error. Thus, subjects had to pronate and supinate the forearm to find the target orientation of the hand. Once the correct orientation was achieved, subjects had 2.5 s to memorize the limb posture, after which they were instructed to lower the arm. The only information available to memorize the roll orientation of the target was the proprioceptive feedback related to forearm pronation–supination. The target orientation was in this way presented kinesthetically, without any visual feedback about the desired orientation.

Response feedback.

When sensory feedback during the response phase was kinesthetic-only (K response feedback), the real handheld tool was represented by a cylindrical tool within the virtual environment (similar to the kinesthetic target presentation described above). Subjects received visual feedback about the tool's position and aiming direction in pitch and yaw, but not about its roll angle. In the visual-only condition (V response feedback), subjects saw a visual representation of the oblong tool (Fig. 1), but did not hold the real tool in their hand. Instead, they controlled the roll angle of the virtual tool by turning a control knob with the fingers. The rectangular extrusion of this tool allowed the subject to visually assess the orientation of the tool and projectile around the roll axis. In the combined visual and kinesthetic condition (VK response feedback), the subject both held the real tool in the outstretched hand and saw the oblong tool in the virtual world.

The three response feedback conditions (K, V, VK) could therefore be distinguished by the types of sensorimotor information available to the subject about the orientation of the response. In the K condition, the subject could use kinesthetic information, including cues about the orientation of the hand with respect to gravity, to align the outstretched hand and tool with the remembered target, but had no visual feedback about the roll orientation of the hand. In the V condition, the rotation of the knob changed the relative orientation of the tool. The ratio of knob rotation to tool rotation was 1:1, but the tool started out from an arbitrary starting orientation on each trial and it was usually necessary to move the fingers on the knob to perform the required rotation of the tool. In other words, there was no fixed mapping between the orientation of the knob, the orientation of the hand, and the orientation of the tool. Thus, in the V condition, the subject could compare the visual image of the tool with the remembered target orientation, but had no kinesthetic information about the orientation of the virtual tool with respect to the body or with respect to gravity. In the VK condition, subjects could use both visual and kinesthetic information to align the tool with the target orientation.

Trial sequence.

Subjects started each trial with the head in an upright posture. After 1 s in this position, the target orientation (visual or kinesthetic) was presented to the subjects at one of seven different orientations with respect to the vertical in the frontoparallel plane (−45°, −30°, −15°, 0°, +15°, +30°, +45°) for 2.5 s. Once the target was acquired, subjects had 5 s to tilt their head by 15° or 24°, to the right or to the left, depending on the trial. To guide subjects to the desired inclination of the head, visual feedback was provided by the virtual display: the color of the tunnel walls turned from red to green as the head approached the desired head inclination. Subjects initiated a rolling movement of the head and then adjusted the head tilt until the display became bright green. If the subject was not able to reach the desired head tilt in a predetermined amount of time (5 s), the trial was interrupted and was repeated later. After the 5 s delay period, including the head roll movement, a signal was given to the subject to align the tool with the remembered target orientation and to launch the projectile from the tool by pressing a trigger. Subjects were not constrained in terms of maximal execution time, and we observed response times of 8.6 ± 1.7 s on average. Note that subjects could not start tilting the head toward the required roll angle until after the target orientation was presented and removed. It was therefore impossible to mentally anticipate the effects of the head rotation while the target was still visible or while the hand was at the kinesthetically defined target orientation.

Training.

Subjects were trained before the experimental session to align the tool with the target orientation. During this training period, even though the target beams were invisible during the memory delay and response phase (as in the actual test trials), the target beams reappeared once the projectile was launched. In this way, the subjects could see whether the projectile was well enough aligned to pass between the beams. Subjects could thus learn to produce the correct roll orientation of the tool for each target orientation. After this initial training session, however, the beams no longer reappeared after the initial target acquisition and therefore subjects had no feedback about success during the remainder of the experiment. This choice was necessary to prevent adaptation to the sensory conflict applied in some trials (see below). Each subject performed training trials until he or she was able to easily perform the different parts of the task without procedural errors and with stable performance over several consecutive trials. Typically, subjects took ∼25 trials to satisfy these criteria, independent of the feedback conditions of the task to be performed.

Sensory conflict during tilting of the head.

To test for the relative effects of visual and kinesthetic information on the performance of this task in each condition, we used the virtual-reality system to introduce conflict between different sources of sensory information about head rotation in space (Viaud-Delmon et al., 1998). Tracking of the virtual-reality goggles was normally used to hold the visual scene stable with respect to the real world during movements of the head. This means that if the head was tilted x° clockwise, the visual scene rotated x° counterclockwise with respect to the goggles and head so that the visual horizontal and vertical remained aligned with the horizontal and vertical of the physical world. On certain trials, however, we introduced a gain factor in the updating of the visual display to break this one-to-one relationship between the roll motion of the head and the rotation of the visual scene. On half the trials where the subject tilted the head by 15°, a gain of 24/15 gave the visual impression of a 24° head roll angle, and thus the visual scene was tilted 9° with respect to gravity in the opposite direction of the head tilt (Fig. 3). Analogously, in half of the trials where the subject had to perform a 24° roll motion of the head, a gain of 15/24 generated a rotation of the visual field corresponding to a 15° tilt of the head, and thus the visual scene was tilted 9° with respect to gravity in the same direction as the head tilt.

Figure 3.

Potential effects of sensory conflict (scene tilt) applied during the movement of the head. In the memorization phase (left), subjects evaluated the orientation of the target (green beams). If a 24/15 gain between the actual and virtual head roll motion was applied when the subject tilted the head by 15° to the left (right), the gravitational and the visual vertical no longer matched and the visual scene was tilted 9° (24/15 × 15° − 15° = 9°) with respect to gravity in the opposite direction of the head tilt. If subjects used the memorized target angle with respect to the visual background, their responses would be deviated 9° in reproducing the earth-fixed target orientation. Conversely, if the target orientation was memorized and reproduced with respect to the body, gravity, or the physical world, no systematic deviation would occur.

The gain values were chosen during pilot experiments so that the tilting of the visual scene was large enough to produce measurable effects on the sensorimotor behavior, but not so large that the subject would be consciously aware of the sensory conflict. We verified that subjects were unaware of the conflict by interrogating each of them at the end of the experimental session.

It is worth mentioning that, in contrast to other studies incorporating conflict between visual and proprioceptive information (Gentilucci et al., 1994; Flanagan and Rao, 1995; Rossetti et al., 1995; van Beers et al., 1999; Ernst and Banks, 2002; Lateiner and Sainburg, 2003; Sober and Sabes, 2003, 2005; Sarlegna and Sainburg, 2007), the tilting of the visual scene used here did not generate any conflict between body-centered proprioception and retinotopic encoding of the tool's orientation. Although the visual background rotated 9°, the image of the tool in the goggles remained stable with respect to the physical world, and thus with respect to the body. For any given disposition of the hand in space, therefore, the orientation of the tool projected on the retina was the same as that which would be computed by integrating proprioceptive information along the kinematic chain between the hand and the eye, regardless of the amount of tilt applied to the visual background.

Subject groups and task conditions

A total of 120 volunteer subjects (60 males and 60 females) were recruited from the students and staff of the University Paris Descartes. The experimental protocol was approved by a local institutional review board (IRB), subjects gave informed consent in accordance with the Helsinki principles, and the experiments were conducted in accordance with local and international regulations on the use of human subjects.

Dynamic task with conflict.

The two possible target presentation methods (V or K) and the three possible response modes (V, K, or VK) combined to form a total of six different sensory feedback combinations (K–K, K–VK, K–V, V–K, V–VK, V–V). Sixty volunteer subjects were divided into six groups, each of which performed the experiment for one of these six possible combinations. Initially, each subject performed the task in only one of the six conditions to avoid priming, i.e., to avoid that the responses produced with one combination of sensory feedback could be affected by previous experience with another. A subset of five subjects performed the experiment in a second condition, however, after a delay of several months, as a means to test whether effects observed in the main experiment could be attributed to peculiarities of the different subject groups, rather than to the effects of sensory feedback conditions per se. In total, 56 stimuli [7 target orientations × 4 head-roll orientations × 2 levels of conflict (with or without)] were presented three times to each subject in pseudorandom order for a total of 168 trials each.

Static task without conflict.

An additional six groups of 10 subjects each performed the task without tilting the head, each for a single target–response condition. This protocol differed from the one described above by the fact that the subjects kept their head in an upright posture through the memory delay and response phases. These trials were performed with the gain applied to the rotations of the visual field equal to unity (i.e., no conflict), since the gain would have no effect in the absence of head tilt.

Data analysis

We analyzed the recorded data in terms of errors made in aligning the tool with respect to the oriented target at the moment when the subject pressed the trigger to release the projectile. Figure 4 shows typical responses from one subject who performed the experiment in one condition (V–V). The 168 individual responses performed in a single session are shown as the difference between the response and the target orientation expressed in the earth-fixed reference frame. We computed the constant error in each condition as the signed error in orientation of the tool with respect to the target, where positive errors correspond to counterclockwise rotations. We quantified the variable error as the standard deviation of repeated trials to the same target orientation in a given condition. To increase the statistical robustness of the variable error estimate, the responses following right and left head rotations of the same amplitude were combined (McIntyre et al., 1997) so that the response variability for each combination of target and head inclination was computed over six trials. To achieve the normal distribution required to perform an ANOVA, values of variable error (SD) were transformed by the function log(SD + 1) before performing the statistical tests (Luyat et al., 2005). Statistical analyses were performed on the constant and variable error by using mixed-model ANOVA with target modality (K, V) and response feedback (K, VK, V) as between-subject factors and with target orientation, head-roll amplitude, and the sensory conflict as within-subject factors. When significant effects were detected by ANOVA, statistically significant differences between levels of the independent factors were identified via the Newman–Keuls post hoc test. Planned comparisons of variable error for 0° targets versus all six other target orientations combined were also used to test for the presence of an oblique effect in each condition. All statistical analyses were performed with Statistica version 6.1 (StatSoft).

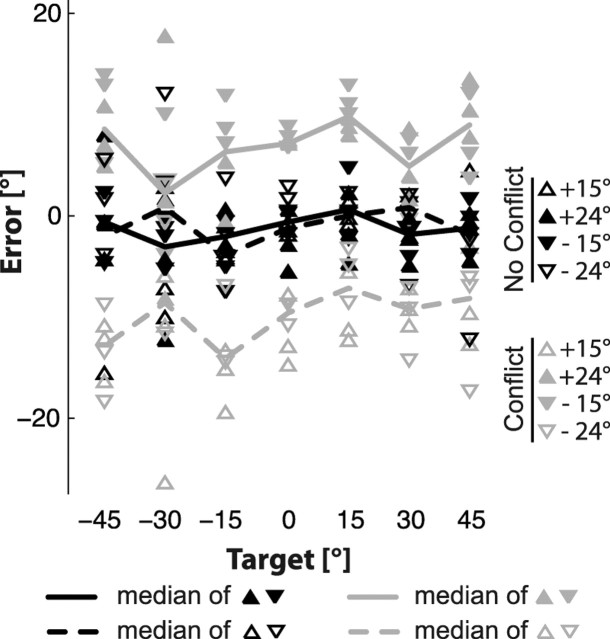
Figure 4.

Response deviations for a typical subject who performed the task in the V–V condition. For each target orientation (abscissa axis), the 24 individual responses are reported as the difference between the response and the target orientation expressed in the earth-fixed reference frame. Different symbols represent different conflict conditions and different directions of the head rotation. Solid and dashed lines pass through the median values for repeated trials that could be expected to yield clockwise (empty triangles) or counterclockwise (filled triangles) deviations due to the conflict (−15°and 24° combined; 15° and −24° combined). Data from trials without conflict are shown in black and trials performed with sensory conflict are shown in gray.

Quantifying the specific effect of conflict.

To focus on the specific effect of the sensory conflict that we imposed during the memory delay period, we collapsed data across target orientations, head tilts, and the different values for the gain applied to rotations of the visual scene, as follows: on a subject-by-subject basis, responses for trials performed with a +15° head tilt and gain of 24/15 and trials performed with a −24° head tilt and a gain of 15/24 (the cases where the visual scene was deviated clockwise by the conflict) were grouped together and the median response orientation was computed on a target-by-target basis separately for trials performed with and without conflict, as shown in Figure 4. The same procedure was performed for the trials performed after a −15° and +24° head rotation, since the corresponding gains (24/15 and 15/24, respectively) generate a counterclockwise deviation in both these conditions.

For each grouping of responses, we subtracted the median values for the no-conflict condition from the corresponding values in the conflict condition. This procedure accounted for intersubject differences and automatically compensated for the effects of target orientation, target presentation modality, and hand feedback that were independent of the head-roll movement. Then, the results of the clockwise and counterclockwise deviations were combined by inverting the sign of the former, so that the expected response deviations induced by the conflict were always positive. Finally, the deviations in each condition were averaged across the seven possible target orientations. These data were then subjected to a two-factor ANOVA with target presentation (K, V) and response feedback (K, VK, V) as independent factors to test for significant differences in response deviations between different experimental conditions. We also used Student's t test to determine whether the average deviation in each condition was statistically different from 0° and 9° (the theoretical extremes).

Modeling

The maximum likelihood principle (MLP) provides the mathematical basis for the notion that different sources of information can be combined in such a way as to minimize the variance of an estimated quantity. MLP predicts that two sources of information (e.g., X and Y) will be combined to form an optimal estimate of the true value (Z) according to the relative variance (σ²) of each estimate.

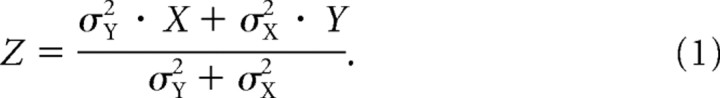The higher the variance of X, the greater the weight given to Y. We performed an analytical assessment of each of our experimental conditions, taking into account different sources of variance (noise) in each situation, to determine whether MLP provides an explanation for our empirical results.

In the context of neuroscience, Equation 1 is usually used to describe how multiple sources of information are combined to derive an optimal perception of a single quantity (van Beers et al., 1996, 1999; Ernst and Banks, 2002; Smeets et al., 2006). In a task of visuomotor coordination, however, such as aligning the hand to a target, two pieces of information are required to perform the task: the orientation of the target and the orientation of the hand. The solution for applying MLP to this situation is therefore somewhat ambiguous. Are separate estimates of target and hand constructed according to MLP and then compared, or is a more distributed mechanism used?

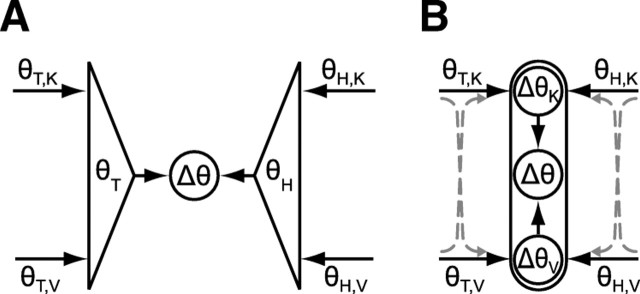
To address this question, we compared our empirical results with the predictions of two analytical models depicted in Figure 5, both based on MLP. In both schemes, subjects align the hand to the target using visual and/or kinesthetic information about the target (θ_T,V and θ_T,K) and visual and/or kinesthetic information about the hand (θ_H,V and θ_H,K). The two schemes differ, however, in the way these data are optimally combined.

Figure 5.

Two formulations of a maximum-likelihood model for the combined use of visual and kinesthetic information. In each model, the target is represented in both the visual domain (θ_T,V) and in the kinesthetic domain (θ_T,K). Similarly, the orientation of the hand is represented visually (θ_H,V) and kinesthetically (θ_H,K). Each internal representation is characterized by a corresponding variability (σ_θT,V², σ_θT,K², σ_θH,V², and σ_θH,K²). A, An optimal estimate of the target is compared with an optimal estimate of the hand to drive the response. B, Comparisons are performed separately in each sensory modality, and then an optimal combination of the individual comparisons is used to drive the response. Dotted arrows represent possible reconstructions of a kinesthetic representation from visual information and vice versa.

Difference between optimal estimates.

Figure 5A is based on the idea that the sensorimotor system optimally estimates both the target and the hand orientation, each defined by MLP. We applied Equation 1 to the estimation of the target orientation, where the two sources of information (X and Y) to be combined are visual (θ_T,V) and kinesthetic (θ_T,K):

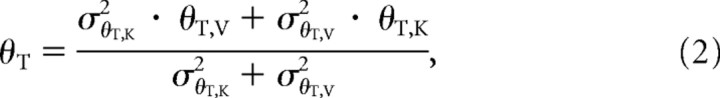and, similarly to the estimate of the hand position:

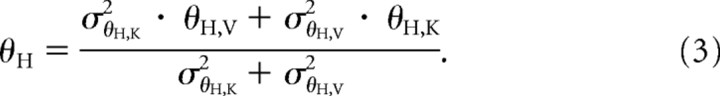The CNS will achieve the task by moving the hand until Δθ = θ_T − θ_H = 0.

Optimal fusion of individual differences.

Figure 5B depicts an alternative strategy in which the comparison of target and hand orientation is performed separately in each sensory modality, so that Δθ_V = θ_T,V − θ_H,V and Δθ_K = θ_T,K − θ_H,K. In this case, the variance of the comparison in each modality is given by the following:

and the final response is that for which the MLP-weighted sum of the individual differences goes to zero:

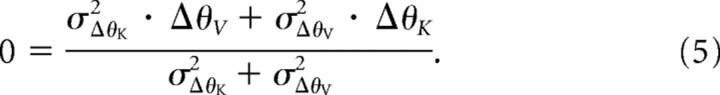Figure 5B raises the question, however, as to what happens when one or more sources of sensory information is absent. One option is to ignore the sensory modality that is lacking and simply carry out the task using the sensory modality that remains. This is a viable solution for comparisons where information about target and hand exists in at least one common reference frame (V–V, V–VK, K–K, K–VK), but cannot be applied in cross-modal comparisons (V–K and K–V). Alternatively, the CNS could reconstruct missing sensory information in one modality from equivalent information acquired in another. The dashed lines and arrows in Figure 5B represent the possibility that a kinesthetic representation of the target or hand could be reconstructed from visual information, or vice versa. Some such transformation would be necessary for cross-modal tasks such as V–K and K–V, and might be useful in other conditions as well.

Results

Here, we describe differences in response patterns for trials performed with the head in an upright position or following roll movements of the head without sensory conflict. We then examine multisensory integration by comparing trials with and without sensory conflict about the movement of the head. Finally, we compare the empirical results to the predictions of the MLP models in Figure 5.

Constant error

We first looked for patterns of constant error as a function of target orientation with and without head tilt. Figure 6A illustrates an apparent expansion of the responses away from the vertical for the target orientations closest to the vertical, also known as tilt contrast (Howard, 1982) and a slight attraction of responses toward 0° for the extreme (±45°) target values.

Figure 6.

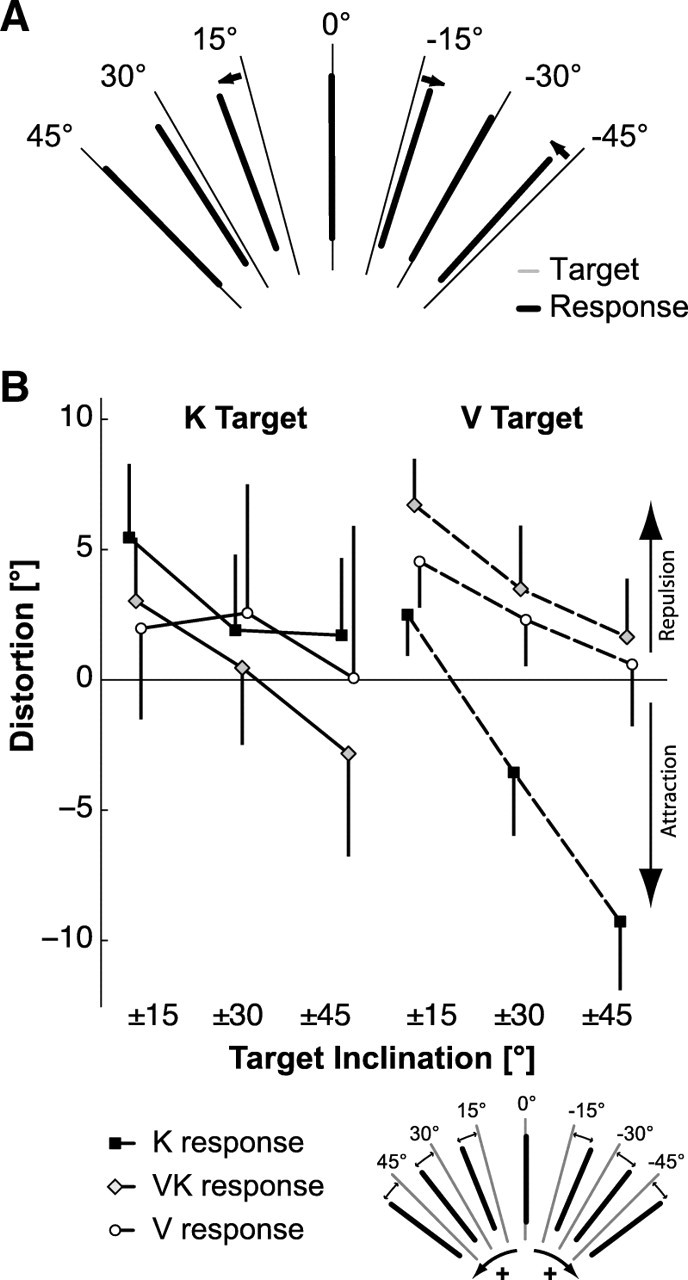
Constant error. A, Mean response to each target orientation for trials without conflict, averaged across all subjects, head tilts, target presentations, and response feedback conditions. Small arrows highlight the average responses that showed a notable deviation from the corresponding target value. B, Quantification of distortion of responses either toward (attraction) or away (repulsion) from the vertical meridian as a function of absolute target angle and sensory feedback conditions. Vertical whiskers represent the 0.95 confidence intervals. Inset, Sign convention for the quantification of the distortion.

We quantified this phenomenon via a distortion index computed as the average amount by which the responses were biased toward or away from the vertical for different absolute target angles. We performed this analysis only on trials performed without conflict. Positive and negative values indicate a repulsion from or attraction toward 0°, respectively. For example, a response of +16° to a target stimulus of +15° or a response of −16° to a target stimuli of −15° gives a repulsion value of 1°, indicating that these responses are oriented farther away from the vertical meridian compared with the target orientation. By grouping all target presentations and feedback modalities together, as shown in Figure 6A, we observed that the distortion significantly decreased for increasing absolute angles of the target (main effect of target absolute angle: F_(2,216) = 51.152, p < 0.001). The 4.0 ± 1.0° repulsion for the ±15° targets was larger (post hoc test, p < 0.001) than the repulsion for the ±30° targets (1.2 ± 1.3°), which was in turn significantly larger (post hoc test, p < 0.001) than the −1.7 ± 1.6° repulsion (attraction) observed for the ±45° targets. As can be seen in Figure 6B, the average of the distortion across all target angles was different depending on the combination of target modality and response feedback (target modality × response feedback interaction: F_(2,108) = 7.52, p < 0.0001). In particular, repulsion away from the vertical was significantly reduced when the target was visual and the response was performed with kinesthetic feedback only (i.e., for the V–K condition, post hoc comparisons between V–K, and all other conditions: p < 0.05). More specifically, although the V–K condition evoked a significant attraction toward vertical for the ±30° and ±45° targets, such attraction toward vertical was not apparent for any of the other experimental conditions.

Response variability

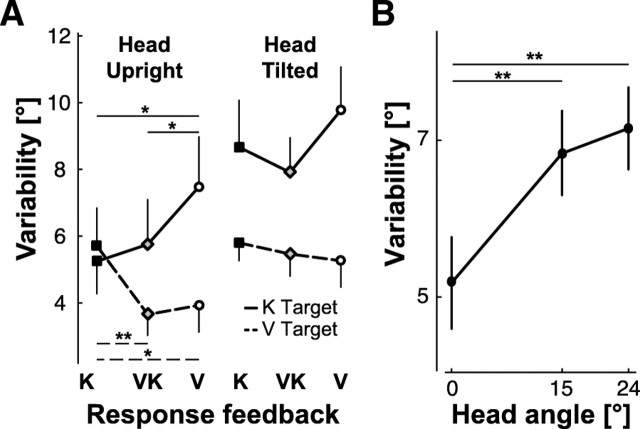
The analysis of variable errors revealed that, for all conditions and head inclinations combined, response variability depended on target orientation (target orientation main effect: F_(6,648) = 12.82, p < 0.001) and that, in particular, it was lower for vertical targets than for the six other orientations (all post hoc comparisons between the vertical and each other target orientation: p < 0.001). This is a very well known phenomenon called the oblique effect, which has been mainly observed for visual tasks (Appelle, 1972). Interestingly, this phenomenon was clearly modulated by the target modality and response feedback and by the tilting of the head. Cases where the planned comparison (see Materials and Methods) showed a significant difference between vertical and oblique targets at at least the p < 0.01 confidence level (p < 0.05, if Bonferonni correction is applied) are indicated by asterisks in Figure 7. In particular, having subjects hold the head upright and providing visual information about the target or response seems to have facilitated the appearance of the oblique effect.

Figure 7.

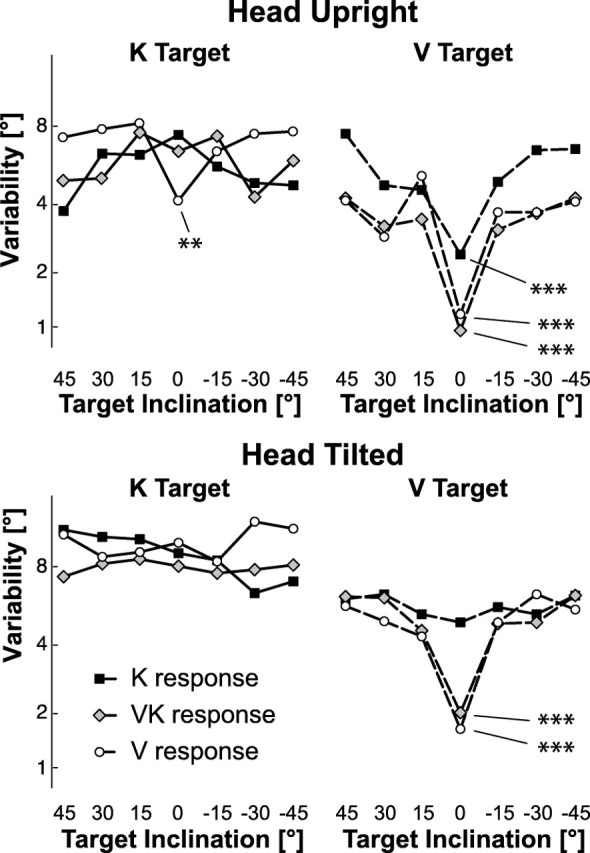
Response variability for trials without sensory conflict. Variable error is shown as a function of target orientation, sensory feedback conditions, and head tilt. Some conditions, but not all, manifest the so-called oblique effect in which variable error is lower for targets at 0° than for the other tested angles. Significant oblique effects are indicated by asterisks (**p < 0.01, ***p < 0.001) based on planned comparisons.

Independent of the oblique effect, we also wished to study the modulation of the response variability as a function of head tilt, target, and feedback conditions. The simple disappearance of the oblique effect, such as one might expect when the head is inclined with respect to gravity (Buchanan-Smith and Heeley, 1993; Lipshits and McIntyre, 1999; Luyat and Gentaz, 2002; McIntyre and Lipshits, 2008), could cause the overall average variable error to increase, potentially masking any additional increase or decrease of variability that moving the head or changing the feedback conditions might produce. Since modulation of variable error due to head tilt or feedback conditions could rely on mechanisms different from those that produce the oblique effect, we also performed a multifactor mixed ANOVA with repeated measures on data from which responses to 0° stimuli were excluded (Fig. 8). This analysis showed that the subjects were more precise when reproducing visual stimuli compared with kinesthetic stimuli (target modality main effect: F_(1,108) = 64.33, p < 0.001). The response precision clearly depended also on the combination of target and response modality (target modality × response feedback interaction: F_(2,108) = 7.50, p < 0.001) (Fig. 8A). In particular, variability increased (precision decreased) when the stimulus and response did not share a common sensory modality (V–K, K–V). Tilting the head also increased response variability (head roll main effect: F_(1,108) = 36.62, p < 0.001) and the variability increase appears to have been tightly related to the amplitude of the head rotation; i.e., the greater the roll motion of the head, the greater the variability (Fig. 8B). This effect appears to be independent of both the target modality and the hand feedback (no statistical interaction between the effect of the head roll movement, the target presentation, and the response feedback modality).

Figure 8.

Response variability as a function of sensory modality and head tilt. Vertical targets were excluded to emphasize effects of sensory modality and head movements on overall response variability, independent of the oblique effect. A, Effect of target presentation (K, V) and hand feedback (K, VK, V) on variable error. B, Effect of the amplitude of the head tilt on response variability. Vertical whiskers represent the 0.95 confidence intervals; significant differences between conditions are indicated with asterisks (*p < 0.05 and **p < 0.01) based on post hoc tests.

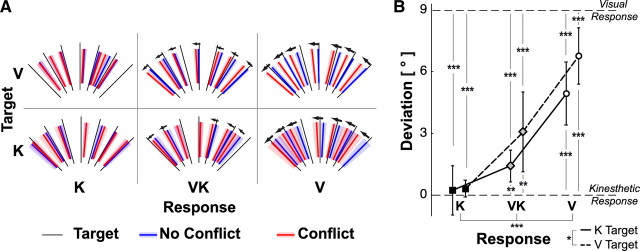
Sensory conflict about head tilt

Figure 9A shows a representative example of the effects of the sensory conflict applied during movements of the head on response orientations in terms of raw data. We compared results between trials with no sensory conflict about head tilt versus trials in which, after the roll movement of the head, the virtual visual scene was rotated 9° to the left with respect to the real world. The deviations that were reliably produced (Fig. 9A, small arrows) were all in the direction of the visual scene rotation (more so for the V response than the K response, with the average VK response in between). We then combined responses for the different head tilt directions and different directions of conflict (see Materials and Methods) and subjected these data to an ANOVA with target modality (V and K) and response feedback (V, VK, and K) as independent factors, (Fig. 9B). Interestingly, the effect of the conflict about the amount of head tilt on the responses mainly varied between the different hand feedback conditions (effect of the response feedback: F_(2,54) = 36.11, p < 0.001) and only slightly between the two types of target presentation (effect of the target modality: F_(1,54) = 4.78, p < 0.05). This indicates that there was a shift in the relative weight of the external visual versus gravito-kinesthetic information, depending primarily on the availability of visual or kinesthetic information for the control of the response, with a secondary influence of whether the target was visual or kinesthetic.

Figure 9.

Effect of conflicting information about head tilt. A, Colored lines indicate the response orientation for each target, averaged over all subjects, for each target modality (K, V) and for each feedback condition (K, V, VK) with (red) and without (blue) conflict. Arrows indicate detectable deviations between responses to the same target with and without sensory conflict applied during head movement and the shading around each line represents the corresponding response variability. Data shown here are for one possible value of sensory conflict (9° counterclockwise tilt of the visual scene). B, Deviations induced by the sensory conflict for the two target presentations (visual or kinesthetic) and for the three response feedback conditions (K, VK and V). Deviations of 0° are to be expected if subjects use only kinesthetic or gravitational information to align the response to the remembered target orientation. Deviations of 9° would be expected if subjects aligned the response to the remembered target orientation with respect to the visual scene. Vertical whiskers represent the 0.95 confidence intervals. Stars represent the significance of the main effects in the ANOVA and the results of the t test comparison with the nominal 0° and 9° values. (*p < 0.05, **p < 0.01, and ***p < 0.001).

When no visual information about the hand was present (K–K and V–K), responses followed the gravito-kinesthetic reference frame, with essentially no influence from the visual surround orientation. Indeed, the mean deviations in the K–K and V–K conditions (0.2° and 0.3°, respectively) did not differ significantly from the value of 0° that would be expected if the response was entirely kinesthetically driven (Student's t test for K–K: t₍₉₎ = 0.39, p = 0.70; for V–K: t₍₉₎ = 1.56, p = 0.15). At the other extreme, when no kinesthetic information about the response orientation was available (K–V and V–V), responses followed more closely (though not entirely) the visual surround. The mean deviations of 5° (K–V) and 6.7° (V–V) were both significantly different from 0° (K–V: t₍₉₎ = 6.30, p < 0.001; V–V: t₍₉₎ = 9.77, p < 0.001) and from the value of 9° that one would expect if the response was 100% aligned to the visual scene (K–V: t₍₉₎ = 5.17, p < 0.001; V–V: t₍₉₎ = 3.22, p < 0.01). In the cases where both visual and kinesthetic information about the hand were provided (K–VK and V–VK), responses fell midway between the predominantly visual and the purely kinesthetic conditions, with a mean responses deviation of 1.4° and 3.1°, respectively. The responses in these conditions were significantly different from both 0° (K–VK: t₍₉₎ = 3.64, p < 0.01; V–VK: t₍₉₎ = 3.10, p < 0.01) and 9° (K–VK: t₍₉₎ = 19.30, p < 0.001; V–VK: t₍₉₎ = 5.97, p < 0.001). These same tests were significant at p < 0.05 or better when Bonferroni correction (n = 6) was applied to account for the multiple t tests.

To rule out the hypothesis that different effects of conflict could be ascribed to intersubject differences and not to the different feedback conditions, we asked some of the subjects who had performed the V–K task to perform the V–V condition several months after the original experiment. Similarly, a few subjects who had performed the V–V task were asked to repeat the experiment in the V–K condition. The modulation of the responses of the five subjects involved in this additional experiment (individual results reported in Table 1) was very similar to those shown in Figure 9; the effect of the conflict about head tilt was 0.7 ± 0.9° and 7.0 ± 0.5° (mean ± SE) for V–K and V–V, respectively (main effect of feedback in the ANOVA for repeated measure: F_(1,4) = 80.05, p < 0.001). For all five subjects, the deviations induced by the tilt of the visual scene were greater for V–V than for V–K.

Table 1.

Responses deviation (in degrees) induced by the sensory conflict during tilting movements of the head for each of the subjects who performed the task in both V–K and V–V conditions

Subject	V–K (°)	V–V (°)	Δ (°)
S1	0.1	6.3	6.2
S2	0.1	7.5	7.4
S3	−0.8	7.0	7.8
S4	4.3	8.4	4.1
S5	−0.1	5.7	5.8
Mean	0.7	7.0	6.3
Main experiments	0.3	6.7	6.4

Δ, Difference between the effect of the conflict in the V–V and V–K condition. Mean and Main experiments; Comparison of the mean results of the additional and main experiments.

Finally, we note that no subject reported being aware of the sensory conflict about the head movement or the resulting artificial tilt of the visual scene. We further note that an ANOVA performed on the data from the main experiment indicated that there was no overall increase in within-subject response variability that could be attributed to the conflict itself; i.e., there was no main effect of the conflict (F_(1,54) = 1.74, p = 0.19) and no cross-effect between conflict and feedback condition (F_(2,54) = 0.66, p = 0.52) on the average variable error measured for each subject. Whereas tilting the visual scene affected the accuracy of the responses (constant error), it had no significant effect on the precision (variable error). These observations suggest that, although the artificially induced tilt alters the parameters of the sensory motor processing as desired, it does so without breaking the process itself, as would be essential for drawing valid conclusions from this type of experiment.

Computational models of sensor fusion

We performed an analytical assessment of each of our experimental conditions, taking into account different sources of variance (noise) in each situation, and compared model predictions to data according to the following reasoning. Kinesthetic representations are presumed to be referenced to egocentric proprioceptors and/or gravity (Soechting and Ross, 1984; Darling and Gilchrist, 1991) and would therefore be immune to the artificial deviation of the visual surround that we imposed during the head movement. The visual representation however, would be referenced both to the visual surround, to gravity, and to the head/retinal axis (Asch and Witkin, 1948; Witkin and Asch, 1948; Luyat and Gentaz, 2002; Jenkin et al., 2003, 2005; Dyde et al., 2006; McIntyre and Lipshits, 2008). Artificial tilt of the visual surround would cause the visual representation to deviate with respect to the physical vertical, although not necessarily by 100%. These assumptions are consistent with the experimental results in Figure 9, which shows the smallest deviations for K–K and the largest for V–V. The deviations induced by the artificial tilt of the visual field therefore provide an indicator of how the weighting of visual or kinesthetic information changes from one condition to another. Furthermore, if one adopts the premise that the oblique effect is the consequence of the use of visual information, as long as the retinal axis is aligned with the vertical (Buchanan-Smith and Heeley, 1993; Lipshits and McIntyre, 1999; Luyat and Gentaz, 2002; McIntyre and Lipshits, 2008), one can also ascertain what sensory information was reconstructed when the head was held upright (i.e., when no artificial tilt of the visual scene was imposed). We base this assertion on the fact that we saw a clear, strong oblique effect in the V–V comparison and no oblique effect for K–K. If a kinesthetic representation that manifests no oblique effect is added to a visual representation that does, one would expect the difference in variable error between vertical and obliques to be less strong compared with using vision alone. Therefore, an oblique effect of a strength that falls between these two extremes provides evidence for the combined used of visual and kinesthetic information.

What form for the MLP model?

We compared our experimental results with the predictions of the two computational models shown in Figure 5. Both models rely on weighting derived from MLP to combine multiple sources of information, and they will produce similar outcomes when visual and kinesthetic information is available for target and hand. But these models predict different outcomes when the target is presented in only one sensory modality or the other.

For Figure 5A, when the target is presented in only one modality, the CNS will presumably compute an estimate of the target orientation θ_T using the remaining information, giving, for example, θ_T = θ_T,K for K–VK and θ_T = θ_T,V for V–VK. In our experiments, subjects acquired the target position with the head in an upright position. Thus, there was no sensory conflict between the visual and kinesthetic reference frames and the target orientation θ_T would be the same whether it was acquired visually or kinesthetically (θ_T = θ_T,K = θ_T,V). The response predicted by the model of Figure 5A is therefore be given by θ_H such that:

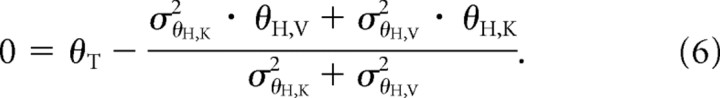This shows that MLP weighting in the response depends only on the variability of the hand feedback (σ_θH,K² and σ_θH,V²). Since these are presumably the same in both V–VK and K–VK (same feedback about the hand), this model predicts that the relative weight of visual or kinesthetic information will be the same in both conditions.

The model in Figure 5B predicts a different outcome when the target is available in only one sensory modality. According to this model, the CNS reconstructs missing information as necessary and then the target and hand orientation are compared in each sensory modality with the objective of reducing the weighted sum of these individual differences to zero (Eq. 5). Combining Equations 4 and 5 gives us the following:

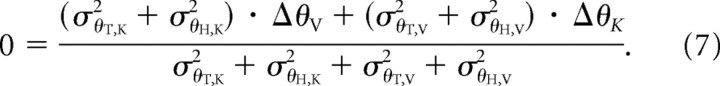Both the variance of the target and the variance of the hand feedback enter into the equation defining the optimal weighting. Equation 7 (Fig. 5B), in contrast to Equation 6 (Fig. 5A), therefore predicts that the choice of target modality can affect the final orientation of the hand.

Experimental evidence can thus be used to choose between the two models. We found a significant main effect of target modality on the amplitude of the deviations invoked by the head tilt and sensory conflict. Deviations were smaller when the target was presented kinesthetically than when it was presented visually (Fig. 9). When the head was held upright, we saw a strong oblique effect for V–VK but none for K–VK (Fig. 7). These data indicate a shift in the weighting between visual and kinesthetic information according to the modality of the target presentation. Since the model described in Figure 5A cannot explain the effects of target modality that were observed empirically here and in analogous experiments previously (Sober and Sabes, 2005; Sarlegna and Sainburg, 2007), we adopt the MLP formulation of Figure 5B for our subsequent analyses.

Criteria for reconstructing sensory information

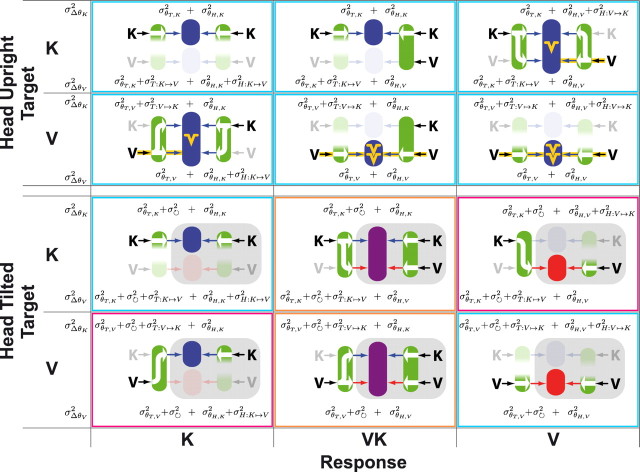
We next compared the predictions of the model in Figure 5B to the data for the six different combinations of target presentation and hand feedback, with and without head tilt. Figure 10 shows when visual or kinesthetic information about target and hand were used in each condition, based on the magnitude of the conflict-induced deviations (Fig. 9) and the strength of the oblique effect (Fig. 7). Figure 10 also shows potential sources of variability that, when used in conjunction with Equation 7, generate predictions about when the CNS does or does not reconstruct missing sensory information.

Figure 10.

Subsets of the neural networks that come into play for each combination of available target information (V, K) and hand feedback (K, VK, V) as a function of head tilt. Faded parts of the network are those that do not appear to be involved in the sensory information processing. White arrows indicate the reconstruction of missing sensory inputs that can explain the experimental results in each situation. For the head-upright condition, the deduction about information flow is based on the strength of the oblique effect (yellow symbols) that is ascribed to the visual acquisition of orientation (arrows on yellow background). For the head-tilted condition, the role played by each source of information is based on the effects of the imposed sensory conflict about head tilt (i.e., deviation of the visual scene). The color of the central region varies from blue to red, reflecting the amount of deviation induced by the tilting of the visual scene, which depends on the participation of different parts of the network in each condition (blue, no deviation; red, maximal deviation). Gray shading indicates elements of neural processing that occurred when the head was already tilted. The specific components contributing to the variance of the kinesthetic and visual comparisons (σ_ΔθK², σ_ΔθV²) are reported for each experimental condition (see Results). Border colors group together conditions that require similar assumptions to predict the experimental findings with the model of Figure 5B (see Results, Summary).

A first basic assumption is that cross-modal reconstruction adds significant amounts of noise to the variability in the perception of the target or hand orientation. This appears to be a reasonable assumption, based on Figure 7A; cross-modal conditions V–K and K–V, where at least one transformation was required, were significantly more variable compared with the unimodal conditions V–V and K–K, respectively. Under this assumption, the model of Figure 5B predicts that greater weight will be given to the sensory modality that permits a direct comparison, when possible, without the need for any reconstruction. For instance, to perform the task using a visual representation in K–K or a kinesthetic representation in V–V requires that both the target and hand be reconstructed in the missing modality. Each of these transformations will add noise to the reconstructed movement representation, creating a large imbalance between the variance of the direct comparison versus the variance of the reconstructed information. In the K–K condition,

where σ_{T:K ↦ V}² and σ_{H:K ↦ V}² represent the variance added by the transformation of the target and hand orientations, respectively, from kinesthetic to visual space. MLP would therefore favor the direct comparison, giving little or no weight to the noisier reconstructed information. The same reasoning can also be applied to V–V, V–VK, and K–VK when the head remains upright. The model of Figure 5B predicts that a direct comparison in the modality of the target would be used, rather than relying on a noisier reconstruction of the missing target information.

These model predictions were confirmed by empirical data for the unimodal tasks K–K and V–V. The lack of an oblique effect in K–K with the head upright and the lack of deviation caused by conflict during head tilt are entirely consistent using kinesthetic representations only, with no reconstruction of the target or hand in the visual domain. Similarly, the strong oblique effect in the head-upright position and the maximal capture by the deviation of the visual field is consistent using visual information without reconstituting the missing kinesthetic information in the V–V condition.

We also found no oblique effect in the K–VK condition when the head remained upright (Fig. 7), despite the availability of visual information about the hand, and the variable error for K–VK was the same as for K–K (Fig. 8A). Similarly, the oblique effect that we observed in the V–VK condition with the head upright was as strong as that observed for the V–V comparison and variable errors were similar for these two conditions. We also note that the pattern of attraction/repulsion from the vertical (Fig. 6B) was very similar between V–V and V–VK, both of which clearly differed from the pattern for V–K. We therefore conclude that when the head remained upright, the K–VK task was performed in kinesthetic space alone and that the V–VK task was performed in visual space alone (Fig. 5B).

For the cross-modal tasks V–K and K–V, the CNS could conceivably convert from the modality of the target acquisition to the modality guiding the hand, or vice versa. If one assumes the two transformations to be equally noisy, Figure 5B predicts that both reconstructions would be performed (e.g., for K–V), as follows:

since approximately the same variance would be added in both the kinesthetic and visual domains. In fact, when the head was held upright, we observed oblique effects in V–K and K–V that were weaker than that seen in V–V. As argued above, this indicates that both visual and kinesthetic information was used in these situations, as predicted by the model.

When performing cross-modal comparisons with the head tilted, however, we observed deviations induced by the conflict in the V–K condition similar to those found in K–K (i.e., little or no effect of conflict), indicating little or no use of visual information. Similarly, the effect of conflict in the K–V condition most closely resembled that observed in the V–V condition, indicating a high reliance on the visual modality, compared with K–V in the upright position. These results are compatible with the model of Figure 5B if one accepts the postulate that performing sensory transformations with the head misaligned with the vertical is noisier, i.e., that:

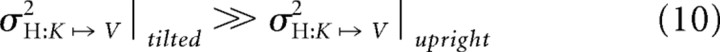and

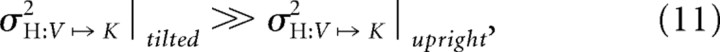such that MLP predicts little weight for information about the hand that is reconstructed when the head is tilted because it would not reduce overall variability.

The final discrepancy to be explained between model and data concerns the observations from V–VK and K–VK performed with the head tilted. In these cases, the deviation of the hand orientation due to conflict fell midway between the unimodal results (i.e., midway between V–V and K–K), as would be expected if both visual and kinesthetic representations were involved. This implies that, in both V–VK and K–VK with the head tilted, the CNS reconstructed the missing information about the target, in apparent contradiction to the prediction that such transformations are to be avoided. Model and data can nevertheless be partially reconciled if one also assumes that the act of turning the head adds noise to internal representations. This is a reasonable assumption considering that egocentric information from the sensory apparatus must either be updated to account for the intervening head movement or transformed into an external reference frame to correctly align the hand with the externally anchored target. If we explicitly include the noise added by the head movement (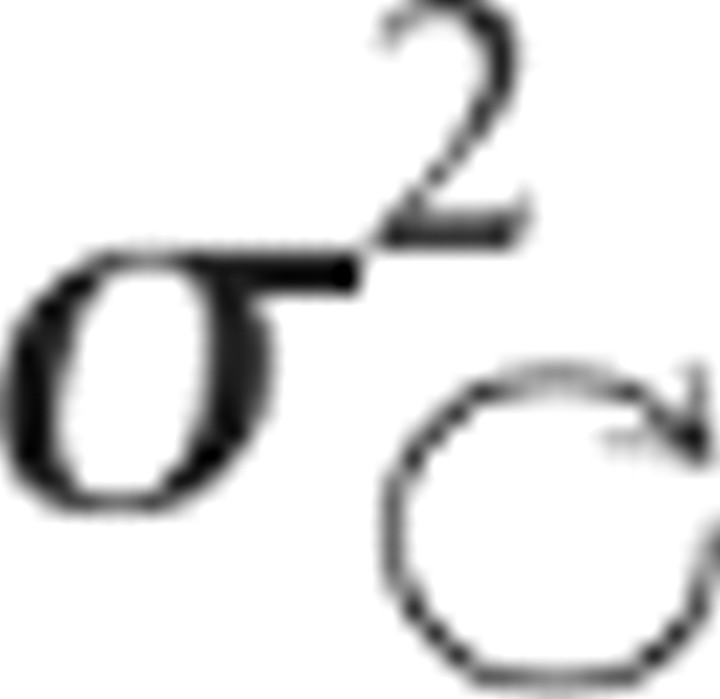) and sensory reconstruction (σ_{T:V ↦ K}²), we have, in the case of V–VK:

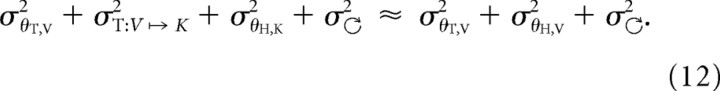The relative difference in variability in each domain will lessen in these conditions (compared with the case where no head movement occurs), leading MLP to predict a more graded use of information from both sensory modalities despite the cross-modal reconstructions that this implies. Model and data are reconciled even further if one postulates that accounting for head movements and reconstructing sensory information across modalities adds more-or-less the same amount of noise regardless of whether they are performed separately or together, i.e., that these two sources of noise do not add linearly.

This is not a far-fetched assumption, as the processing of egocentric information and the cross-modal transformations could be performed by the same neural network (see Discussion, below). In this case, the advantage for the direct comparison disappears, since approximately the same variability will be added to the sensor noise on both sides of the equation:

Summary

The outlines in each panel of Figure 10 summarize the results of the comparison between the empirical data and the predictions of Figure 5B. Conditions outlined in light blue can be explained by simply assuming that cross-modal sensory reconstruction adds noise. This favors the use of direct comparisons when possible (V–V, K–K, V–VK, and K–VK) and predicts a reciprocal reconstruction of both target and hand when at least one transformation cannot be avoided (V–K and K–V). To explain why the sensory modality of the hand was privileged in the cross-modal tasks (V–K and K–V) when the head was tilted (violet outlines), one must assume that cross-modal transformations are noisier when the head is not aligned with gravity. Finally, to explain why moving the head induced a combined use of both visual and kinesthetic information in V–VK and K–VK (orange outlines), even though a unimodal comparison without any reconstruction was possible, one must explicitly consider the noise engendered by head movement and whether the noise from multiple transformations adds linearly.

Discussion

In the literature, it has been proposed that the CNS gives more or less weight to different sensory information as a function of their respective variances (van Beers et al., 1996, 1999; Ernst and Banks, 2002; Smeets et al., 2006). Here we have conducted modeling and experiments that further test this hypothesis and explicitly consider if and when the CNS reconstructs information that is missing from the sensory array. Though our modeling is not fully quantitative, it makes clear predictions about the relative weight given to visual and kinesthetic information across different conditions, predictions that were confirmed by empirical data for only one formulation of the model (the optimal fusion of individual differences model shown in Fig. 5B) and only if one accepts certain assumptions about sources of noise. Although we have no formal proof that the model of Figure 5B is the only model that can explain the observed data, this model is based on solid theory (MLP) and the additional assumptions are motivated by well known experimental observations reported here and previously (Sober and Sabes, 2005; Sarlegna and Sainburg, 2007). This analysis suggests that, although optimal estimation provides a key concept for understanding multisensory integration, one must look beyond MLP alone to fully explain the observed behavior, as we discuss below.

Selective reconstruction of missing sensory inputs

The structure of an MLP model, often applied to the perception of a single quantity, can take on different forms when applied to tasks of eye–hand coordination, not all of which are consistent with experimental observations (Sober and Sabes, 2005; Sarlegna and Sainburg, 2007). For instance, Sober and Sabes remarked on the inability of MLP—presumably expressed in the form of Equation 6—to account for their results (Sober and Sabes, 2005). But MLP by itself does not dictate what happens when the target or hand are sensed in only one modality. Here we adopt an MLP model (Fig. 5B) that effectively requires the CNS to reconstruct missing target information to use the homologous information about the hand and vice versa. In the same vein, Smeets et al. (2006) demonstrated that a visual target will be represented kinesthetically and that the unseen hand will be represented visually in V–K-like conditions. Pouget et al. (2002b) demonstrated that visual representations may even be constructed when a task is performed without any visual inputs at all. We build on these previous studies by explicitly considering under what conditions the CNS does or does not reconstruct information that is missing and we ask how these transformations affect the outcome in the context of MLP. Note that this concept of sensory reconstruction and our experimental results are consistent with network models of concurrent representations in the CNS (Droulez and Darlot, 1989; Pouget et al., 2002a) and go further to show that the neural networks underlying these processes are not necessarily fully recurrent or always operational. It appears that missing sensory information is only sometimes reconstructed according to specific rules or conditions.

Transforming more than what's necessary

It has previously been suggested that the CNS avoids coordinate transformations as much as possible, due to the noise that such transformation engender (Sober and Sabes, 2005). For the unimodal comparisons in our experiments, cross-modal transformations were in fact avoided, privileging visual representations in V–V and kinesthetic representations in K–K. This makes eminent sense. Why reconstruct kinesthetic information from vision or visual information from kinesthesia when a direct unimodal comparison will suffice? The unnecessary transformations would only serve to increase response variability.

The same reasoning should apply when both visual and kinesthetic information about the hand are available (V–VK and K–VK), i.e., the comparison should be performed in the reference frame of the target. Indeed, Sober and Sabes (2005) and we found that the V–VK task was mainly performed visually, whereas K–VK was performed kinesthetically. An important distinction, however, is that we saw this to be true only if the head remained upright. When subjects tilted their heads to the side, we found that kinesthetic information was also used in V–VK and visual information was also used in K–VK. Note that moving the head prevents a simple, direct comparison of ego-centered kinesthetic or visual information.

In a similar vein, tasks for which target and hand are presented in different modalities cannot be accomplished by a direct comparison of egocentric information. But even though only one cross-modal transformation (i.e., the target into the modality of the hand, or vice versa) would have been sufficient to perform the task, the CNS happily reconstructed both target and hand in V–K and K–V, as long as the head remained upright. These findings are fully consistent with previous studies where the use of multiple internal representations was encouraged by the cross-modality of the task (Smeets et al., 2006) or by the fact that the limb used to define the kinesthetic target in a K–VK or K–K conditions (van Beers et al., 1996, 1999; Pouget et al., 2002b) was not the same as the one used to produce the kinesthetic response (thus preventing a direct comparison of proprioceptive information at the joint level).

We propose a working hypothesis, therefore, by which the CNS avoids sensorimotor computations when a direct, ego-centered comparison of target and response is possible. But once a transformation becomes inevitable, a broader slate of internal transformations are automatically used. This is a testable hypothesis, and we find parallels to this idea in electrophysiological studies conducted in nonhuman primates. Neural activation in the posterior parietal cortex of monkeys during visually guided reaching towards visual targets suggests that a direct comparison of target and hand in retinal space is performed without integration of kinesthetic information about the limb (Buneo et al., 2002). However, reaching to visually remembered targets in the dark activates distributed neural networks in parietal areas that simultaneously encode information in multiple reference frames (Avillac et al., 2005; Fattori et al., 2005). A property of this scheme is that, when the neural network that allows one to perform any one internal transformation is activated, it can be used to perform a number of multisensory reconstructions at little extra cost in terms of variability. This reasoning restores an MLP logic to our experimental observations, i.e., that head or body movements and cross-modality encourage the creation of concurrent internal representations of orientation through the reconstruction of missing sensory information.

Gravity provides a critical reference

When our subjects tilted the head, they were less likely to reconstruct missing sensory information about the hand (Fig. 10, V–K and K–V), in apparent contradiction with our hypothesis that moving the head encourages such reconstruction. In an experiment in which the head was held upright (Pouget et al., 2002b), turning the head left-to-right encouraged the reconstruction of target and hand in both visual and kinesthetic reference frames. We therefore conclude that the orientation of the head with respect to vertical, and not just the movement of the head, is a determining factor for what gets reconstructed. By this theory, had the target been acquired with the head tilted and the response been produced with the head upright, one would expect that the CNS would privilege the reconstruction of missing hand information.

Anatomical and electrophysiological evidence from monkeys (Bremmer et al., 2002; Schlack et al., 2002) and humans (Indovina et al., 2005) points to an interaction between vestibular and parietal cortex that could underlie the transformations between visual, gravitational, and kinesthetic reference frames. Furthermore, patients with vestibular deficits have difficulties integrating nonvestibular cues in tasks of spatial navigation (Borel et al., 2008), indicating that vestibular cues mediate the integration of visual and kinesthetic information. The fact that sensory information was more readily reconstituted when the head was held upright suggests that the functionality of the neural networks responsible for reconstructing the missing information (Pouget et al., 2002a; Avillac et al., 2005) is partially disrupted by the misalignment between gravity and the idiotropic vector (Mittelstaedt, 1983). This is perhaps why humans take pains to maintain the head in a stable vertical posture with respect to gravity (Pozzo et al., 1990; Assaiante and Amblard, 1993). The ontogenetic or phylogenetic evolution of the neural networks underlying the sensorimotor transformations would occur most often with the head upright, resulting in sensorimotor processes optimized for this situation. In our experiments, we find concrete evidence that gravity provides a stable reference frame used by the brain to perform sensorimotor integration and transformations (Paillard, 1991).

Conclusions

In this study, we have demonstrated that CNS favors direct comparisons of egocentric sensory information whenever possible, in accord with principles of maximum likelihood estimation, but does not avoid reconstructing missing information at all costs. On the contrary, it appears that when at least one transformation of orientation information is required, the reconstruction of other missing sensory information is better tolerated or even encouraged, perhaps because the additional reconstruction is no more costly in terms of noise. Nevertheless, the misalignment of the body with respect to gravity disrupts the transformation of information between visual and kinesthetic sensation.