Abstract
The primary auditory cortex (PAC) is central to human auditory abilities, yet its location in the brain remains unclear. We measured the two largest tonotopic subfields of PAC (hA1 and hR) using high-resolution functional MRI at 7 T relative to the underlying anatomy of Heschl's gyrus (HG) in 10 individual human subjects. The data reveals a clear anatomical–functional relationship that, for the first time, indicates the location of PAC across the range of common morphological variants of HG (single gyri, partial duplications, and complete duplications). In 20/20 individual hemispheres, two primary mirror-symmetric tonotopic maps were clearly observed with gradients perpendicular to HG. PAC spanned both divisions of HG in cases of partial and complete duplications (11/20 hemispheres), not only the anterior division as commonly assumed. Specifically, the central union of the two primary maps (the hA1–R border) was consistently centered on the full Heschl's structure: on the gyral crown of single HGs and within the sulcal divide of duplicated HGs. The anatomical–functional variants of PAC appear to be part of a continuum, rather than distinct subtypes. These findings significantly revise HG as a marker for human PAC and suggest that tonotopic maps may have shaped HG during human evolution. Tonotopic mappings were based on only 16 min of fMRI data acquisition, so these methods can be used as an initial mapping step in future experiments designed to probe the function of specific auditory fields.
Introduction
Over 100 years ago human primary auditory cortex (PAC, Brodmann's Area 41) was first identified based on its dense cellular structure (koniocortex) and myelination in postmortem tissue (Campbell, 1905; Fleschig, 1908; Brodmann, 1909; von Economo and Horn, 1930). Today PAC is still not routinely identifiable in the living human brain. The transverse gyrus of Heschl (HG, approximately medial two-thirds) located bilaterally on the temporal plane is an important but rough marker for PAC, not indicating exact architectonic borders (Rademacher et al., 2001). Complicating the matter, HG has high morphological variability across individuals and brain hemispheres. Duplications of HG, ranging from partial to complete, are common (estimated occurrence 41%, Rademacher et al., 1993), and architectonic evidence has not been clear about whether PAC occupies one or both divisions of duplicated Heschl's gyri. However, it is commonly assumed that PAC occupies only the first (more anterior) division of HG duplications (Rademacher et al., 1993; Penhune et al., 1996).
In the monkey, the primary auditory cortex is subdivided into three fields, A1, R, and RT, which together correspond to the architectonic core and each have primary-like features, including direct thalamic input (ventral medial geniculate nucleus, Rauschecker et al., 1997). The neurons of each field respond to tones over a limited frequency range and are spatially arranged according to preferred frequencies—tonotopy (Brugge and Merzenich, 1973; Morel et al., 1993; Kaas and Hackett, 2000). Along a posterior-to-anterior axis, there is a continuous mapping of preferred frequencies from high to low (A1), followed by a reversed mapping of low back to high (R), followed by a third smaller mapping of high back to low (RT). The borders between individual fields are marked by the reversals of the frequency gradients. These tonotopic fields have been imaged in the macaque using high-resolution functional MRI in good agreement with previous maps derived from single-neuron recordings (Petkov et al., 2006). Unlike in the human, the monkey temporal plane is relatively flat (no HG) (Hackett et al., 2001); thus, the monkey model does not allow direct prediction of human PAC location relative to HG.
Human tonotopic maps have been challenging to obtain thus far because of their small size relative to the spatial resolution of standard noninvasive neuroimaging techniques. Using fMRI, Formisano et al. (2003) and others (Talavage et al., 2004; Woods et al., 2009; Humphries et al., 2010; Striem-Amit et al., 2011) confirmed the presence in humans of at least two tonotopic maps with a mirror-symmetric “high-low-low-high” progression, likely homologs of areas A1 and R. The human data so far have not been clear about the spatial layout of tonotopic fields relative to HG, and no study has addressed the issue of PAC location across the common anatomical variants of HG. Here, we measured tonotopic maps individually in 10 human subjects using high-resolution fMRI (7 T) and found a striking and highly consistent relationship between the functional tonotopic maps of PAC and the underlying anatomical shape of HG.
Materials and Methods
Subjects
Ten subjects (5 male, 5 female, ages 20–35) participated after giving written, informed consent. No subject had a known hearing deficit or history of neurological or psychiatric illness. Experimental procedures were approved by the Ethics Committee of the Faculty of Biology and Medicine of the University of Lausanne.
MRI data acquisition
Blood oxygenation level-dependent (BOLD) functional imaging was performed with an actively shielded 7 T Siemens MAGNETOM scanner (Siemens Medical Solutions) located at the Centre d'Imagerie BioMedicale (CIBM) in Lausanne, Switzerland.
The increased signal-to-noise ratio and available BOLD signal arising from the use of ultrahigh magnetic field systems (>3 T) allow the use of smaller voxel sizes in fMRI. Also, the signal strength of venous blood is reduced due to a shortened relaxation time, restricting activation signals to the cortical gray matter and thus improving the spatial specificity of the BOLD signal (van der Zwaag et al., 2009; van der Zwaag et al., 2011). fMRI data were acquired using an eight-channel head volume rf-coil (RAPID Biomedical) and an EPI pulse sequence with sinusoidal readout (Speck et al., 2008) (1.5 × 1.5 mm in-plane resolution, slice thickness = 1.5 mm, TR = 2000 ms, TE = 25 ms, flip angle = 47°, slice gap = 1.57 mm, matrix size = 148 × 148, field of view 222 × 222, 30 oblique slices covering the superior temporal plane, first three EPI images discarded). The sinusoidal shape of the readout gradients reduces the acoustic noise produced by the scanner. A T1-weighted high-resolution 3D anatomical image (resolution = 1 × 1 × 1 mm, TR = 5500 ms, TE = 2.84 ms, slice gap = 1 mm, matrix size = 256 × 240, field of view = 256 × 240) was acquired for each subject using the MP2RAGE pulse sequence optimized for 7 T MRI (Marques et al., 2010). Anatomical images were used to coregister functional scans and to generate cortical surface representations.
Auditory stimuli
Sound stimuli were generated using MATLAB and the Psychophysics Toolbox (www.psychtoolbox.org) with a sampling rate of 44.1 kHz. Stimuli were delivered via MRI-compatible headphones (AudioSystem, Nordic NeuroLab) featuring flat frequency transmission from 8 Hz to 35 kHz. Subjects were instructed to keep their eyes closed during all scans.
To measure tonotopy (Fig. 1A), pure tone stimuli were presented to subjects in ordered progressions from low frequencies to high: 88, 125, 177, 250, 354, 500, 707, 1000, 1414, 2000, 2828, 4000, 5657, and 8000 Hz (half-octave steps). Starting with the lowest frequency, pure tone bursts of that frequency were presented for a 2 s block before stepping to the next higher frequency until all 14 frequencies had been presented. This 28 s low-to-high progression was followed by a 4 s silent pause, and this 32 s cycle was repeated 15 times per 8 min scan run. Each subjects participated in two 8 min scan runs, resulting in 30 frequency progressions per subject. Frequency progressions were designed to induce a traveling wave of response across cortical tonotopic maps: responses should peak first in regions preferring low frequencies and sequentially later in regions preferring higher frequencies. As described further below, cross-correlation was used to determine the time to peak of the response on a per-voxel basis. This procedure is equivalent to the phase-encoded mapping techniques shown to be highly efficient in visual retinotopic mapping (Engel et al., 1994; Sereno et al., 1995).
Figure 1.
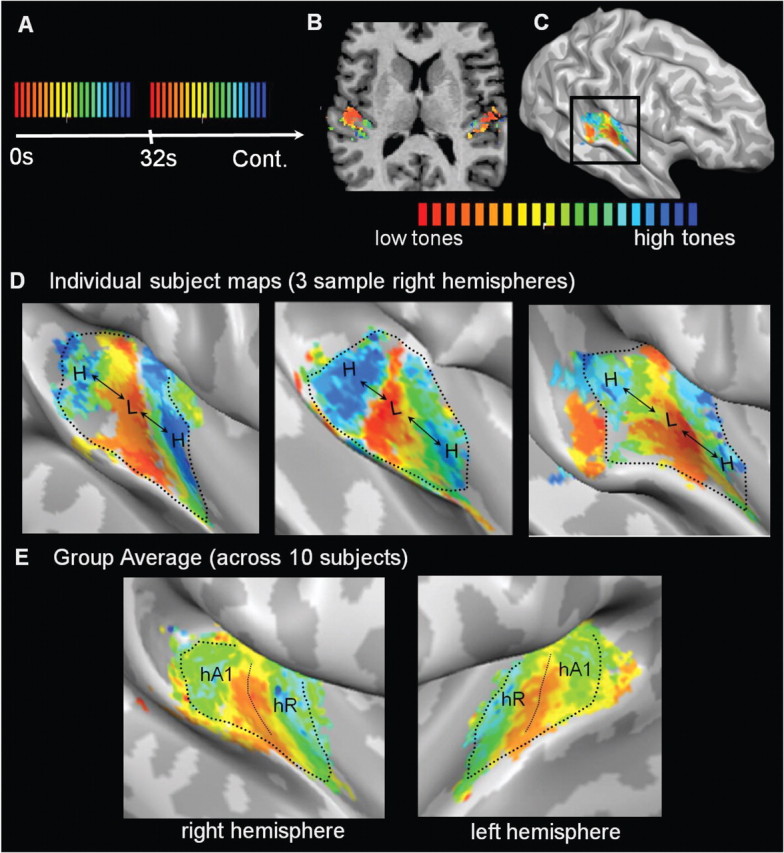
Tonotopic maps in auditory cortex. A, Sound stimuli were pure tone bursts presented in cycled progressions from low frequencies to high: 88 to 8000 Hz in half-octave steps. Each 28 s progression from low to high (red-to-blue color scale) was followed by a 4 s stimulus pause. Sound stimuli were designed to induce a traveling wave of response across cortical tonotopic maps: fMRI responses peak sooner in map regions preferring low frequencies and progressively later in regions preferring higher frequencies. Linear cross-correlation analysis was used to determine the temporal delay that best fit the observed fMRI response time course of each voxel and to assign a corresponding best frequency. B, Analyses were performed in each individual subject's (n = 10) volumetric space. C, Resulting color-coded frequency maps were projected onto each subject's cortical surface meshes. Surfaces were minimally inflated to expose the auditory cortex on the temporal plane. D, In 20/20 hemispheres, two primary mirror-symmetric tonotopic maps (high-to-low-low-to-high) were observed, and three sample right hemispheres are shown with a voxelwise threshold of p < 0.05 (FDR corrected). The posterior (high-to-low) and anterior (low-to-high) maps contain the regions hA1 and hR, respectively, and the low-frequency union between the two maps is the hA1–R border. Dotted lines indicate how surface patches containing the two maps were defined for the next step of analysis. E, Group averaged tonotopic maps across all 10 subjects after cortex-based alignment indicates the consistency of tonotopic map location relative to HG. Correlation threshold R > 0.15.
During each 2 s frequency block, eight tone bursts of the same frequency were presented. Tone bursts were either 50 ms or 200 ms in duration (interstimulus interval = 50 ms) and were alternated in pseudorandomized order during the 2 s block, resulting in a rhythmic pattern of tone onsets. This rhythmic pattern served to increase the perceptual salience of the stimuli over the regular pattern of background scanner noise.
Perceived volume (a perceptual rather than physical quality of sound) varies widely as a function of frequency, mostly due to peripheral sensitivities in the cochlea. After sound system calibration, sound intensities were adjusted according to standard equal-loudness curves (ISO 226, phon 65) to approximate equal perceived volume across all frequencies. Actual sound intensities (62–84 dB) matched the perceived volume of a 1000 Hz tone (reference frequency) at 65 dB. Sound levels were further attenuated (∼24 dB) by the required use of protective ear plugs. Background EPI scan noise was <104 dB as measured with an MR-compatible optical microphone (Sennheiser, MO 2000) and acoustic calibrator (Cesva Acoustic Instruments). Scan noise was attenuated +30 dB by the headphone ear cups and dense foam padding around the head used to stabilize position. Despite the moderate sound intensities, subjects reported hearing all tones over the background noise at a clear and comfortable level.
Five of the 10 subjects also participated in two additional scan runs (30 frequency progressions) in which tone frequencies progressed in reversed order from high-to-low to verify that the order of stimulus presentation did not alter the observed layout of the tonotopic maps. Data from one reversed-order scan run was discarded due to head motion (second run of subject no. 10).
Analysis
BrainVoyager QX software v2.3 (Brain Innovation) and MATLAB (R2008b) were used for data analysis and display. Standard fMRI data preprocessing steps included linear tread removal, temporal high-pass filtering, and motion correction. Spatial smoothing was not applied. Functional time-series were interpolated into 1 × 1 × 1 mm3 volumetric space in registration with each subject's 3D Talairach-normalized anatomical dataset. Functional-to-anatomical registrations were all visually inspected for verification. Cortical surface meshes were generated from the anatomical images using automated segmentation tools in BrainVoyager QX. The resulting surface meshes were minimally inflated (100 steps), just enough to allow viewing of the temporal plane while incurring the least amount of spatial distortion.
Statistical analyses (using linear cross-correlation) were performed in volumetric space (Fig. 1B) for each subject individually. A hemodynamic time course was predicted in response to the first 2 s sound block of each stimulus cycle. This cyclical model function was shifted successively in time in 2 s increments (corresponding to the TR) to generate 14 time-lagged functions. Linear cross-correlation was applied (between all 14 model functions and the measured fMRI time course) on a per-voxel basis. The time course was averaged from the two scan runs per experiment (240 volumes). Each voxel was then color coded according to the lag function resulting in the highest correlation value with its time course (winner-take-all). Correlation maps were projected onto partially inflated cortical surface meshes to facilitate viewing (Fig. 1C), and spatial smoothing of the maps was not applied. Individual subject correlation maps are displayed in Figure 1 with a statistical threshold of p < 0.05 corrected for multiple comparisons using the false discovery rate (FDR) method. Correlation values at this significance level were R > 0.17, 0.16, and 0.15 for the three data displays of Figure 1C.
Group-averaged tonotopic maps (Fig. 1E) were generated using cortex-based alignment (Fischl et al., 2004) as implemented in BrainVoyager QX. This is a nonrigid alignment of cortical surface meshes across individuals based on the gyral and sulcal folding patterns. Each subject's cortical surface meshes were aligned to a target mesh (separately for left and right hemispheres) and the target meshes were chosen from a subject with intermediate HG anatomy (subject 2, partial HG duplication in each hemisphere). All alignments were visually inspected. In all cases, the FTS (first transverse sulcus, anterior border of HG) aligned to the target FTS. In all cases when a single or partially duplicated HG was present, the HS (Heschl's sulcus, posterior border of HG) aligned to the target HS. In the three cases of complete duplications, it was HS2 (the more posterior of the two Heschl's sulci) that aligned with the target HS. Thus, in all cases, the sulci bordering the full Heschl's structure aligned. Following cortex-based alignment, individual-subject tonotopic maps were projected onto the target surface mesh so that all subject's maps were in a common, aligned coordinate space where tonotopic maps were subsequently averaged. The maps in Figure 1E are the result of a direct averaging of the lag and correlation values across the 10 subjects at each surface coordinate. Maps are displayed with a correlation threshold of R > 0.15, the average correlation value corresponding to p < 0.05 (FDR corrected) in the individual subject analyses.
Plots of primary auditory cortex (surface patches of Figs. 2 and 3)
Figure 2.
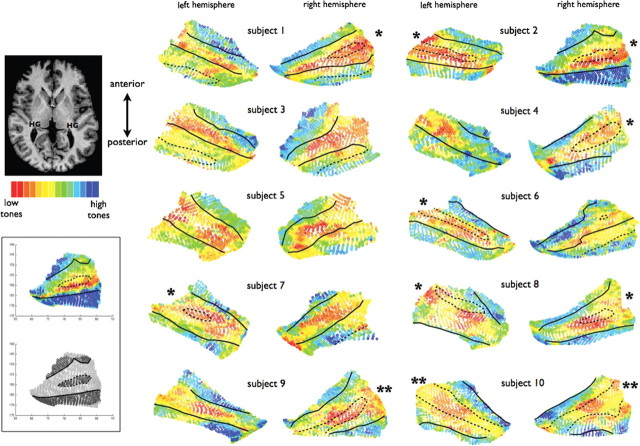
Spatial layout of PAC relative to HG. Surface patches containing the two primary mirror-symmetric tonotopic maps (“high-low-low-high, hA1 and hR) were selected from the cortical surface meshes (n = 20 hemispheres) and are plotted here with the borders of HG indicated (solid lines: anterior border = FTS; posterior border = HS). In 9/20 hemispheres, HG was a single gyrus with a smooth crown. In 8/20 hemispheres (partial duplications *), an SI was present on the gyral crown (dotted lines) splitting HG into two divisions that remained connected by a common medial stem. In 3/20 hemispheres (complete duplications **), a dividing sulcus was present that reached all the way down to the medial base of HG so that the two divisions did not remain connected by a common medial stem (also indicated with dotted lines). Note that in the case of complete duplications, there is a difference in the standard nomenclature and there are considered to be two Heschl's sulci (HS1 and HS2): the dividing sulcus (dotted line) is HS1 and the posterior border (solid line) is HS2. In some cases, the posterior end of the functional maps extended onto less prominent gyri of the planum temporale, which are also indicated by dotted lines (outside the posterior border of HG) when present. These plots reveal a continuous anatomical–functional relationship across the anatomical variants of HG, as described in Results. As shown in the lower left inset, gyral/sulcal borders were drawn corresponding to cortical surface transitions between convexity and concavity, as described in Material and Methods.
Figure 3.
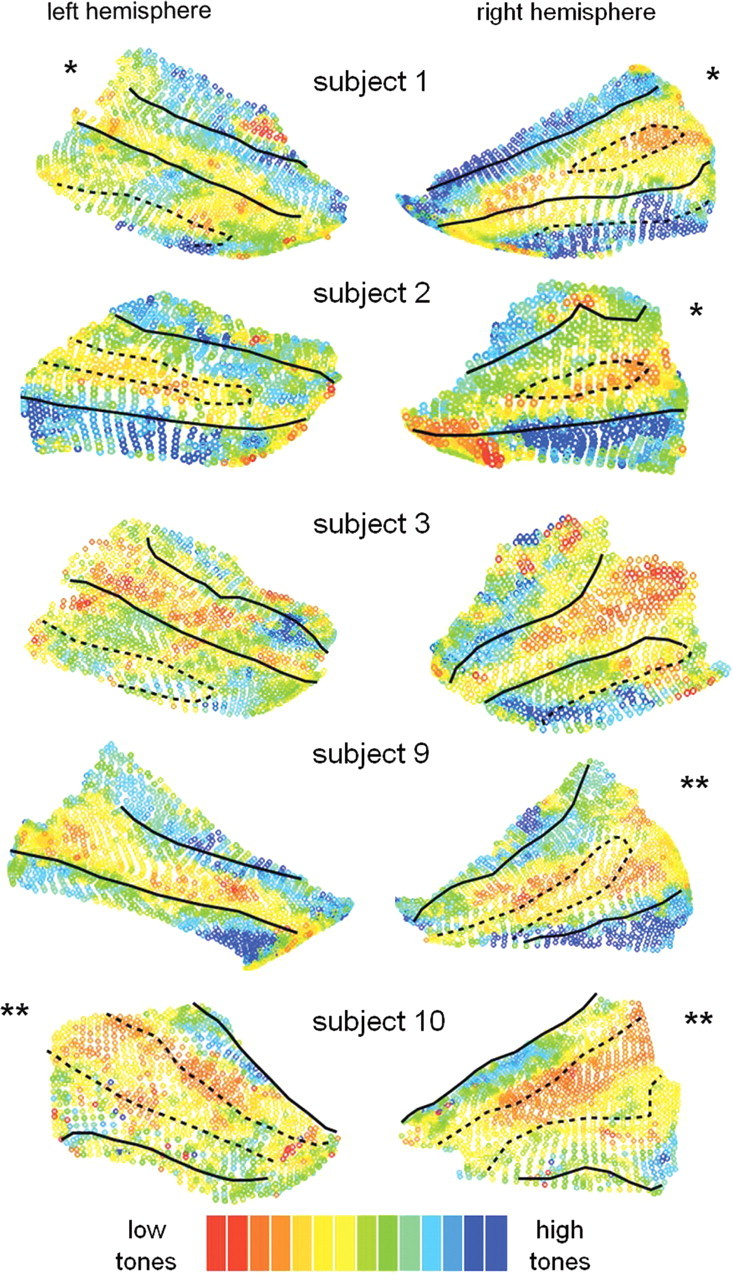
Results of separate scans run in five of the same subjects in which the tonotopic mapping stimuli were presented in reversed order (high frequencies-to-low, rather than low-to-high). A consistent anatomical–functional relationship is observed.
Two tonotopic gradients with mirror symmetry (“high-low-low-high”) were clearly observed in all hemispheres. Our goal was to evaluate the spatial layout of these two primary tonotopic fields relative to the underlying anatomy of HG in each subject. To this end, we manually selected contiguous patches of cortical surface containing the two primary gradients in each hemisphere (n = 20), and then plotted those surface patches with gyral borders overlaid (Figs. 2, 3) as described next.
How were the regions selected?
The selected regions were manually outlined on the (partially inflated) surface meshes using drawing tools within BrainVoyager QX. The selection is demonstrated with dotted lines on the individual subject surface maps in Figure 1D. As can be seen, the borders were drawn generously to include all voxels within a contiguous region that contained the primary two gradients. The exact borders were not dependent upon the particular correlation threshold used for display, since the overall pattern of the gradients was observable over a large range of display thresholds. Anterior and posterior borders were drawn along the length of the outer high-frequency representations. Lateral and medial borders were drawn to cover the full extent of the observable tonotopic pattern, which generally covered the full medial-lateral extent of HG. Considering that human PAC is expected only on the medial two-thirds of HG (at least approximately), it is highly likely that the full extent of A1 and R is included in these selections. It is also likely that the lateral edge of the selected regions includes some portion of lateral belt (nonprimary) fields, and also possible that the medial edge includes a small portion of medial belt fields. In the macaque, iso-frequency bands of the core gradients continue laterally and medially into the belt fields, so it is not expected that we can discern the lateral and medial borders of the primary core fields based solely upon tonotopic maps.
How were the regions plotted?
All vertices within the contiguous selected regions were exported and plotted. Specifically, five values were exported for each vertex: x, y, and z coordinates, a best-fitting lag value (1–14), and a curvature value. The coordinates were plotted in the x–y plane and collapsed across z-coordinates. Open circles show overlapping points in the collapsed z-dimension. A color scale indicates the best-fitting lag value of each point.
This 2D collapsed presentation (of partially inflated surface coordinates) was chosen, rather than standard flat maps, to minimize anatomical distortion due to continued inflation or complete flattening. In particular, we chose to collapse across the z-direction to preserve as well as possible x–y spatial relationships since there has been much interest in the particular orientation of the tonotopic gradients within the x–y plane (see Discussion). We find that previous human fMRI tonotopy studies have made this orientation difficult to interpret by display of data on highly inflated or fully flattened surfaces that had significant x–y spatial distortions. A disadvantage of our collapsed presentation is that the gradients are somewhat squeezed in the direction orthogonal to HG; however, as noted above, data points are plotted with open circles so that overlapping data points remain visible.
What statistical threshold was used?
Within the plotted surface patches (Figs. 2, 3), no statistical threshold was applied. This is because of the arbitrariness of selecting a voxelwise correlation threshold when the goal is to observe the pattern of data across all voxels within an area of interest. Thus, the plots of Figures 2 and 3 show data from all vertices within the contiguous selected regions, with no points excluded due to thresholding.
How were gyral borders drawn?
Curvature values were calculated as implemented in BrainVoyager QX and correspond to what is geometrically defined as mean curvature. Normal curvature is measured as 1/r, where r is the radius of an inscribed circle. A vertex on a 3D surface has an infinite number of normal curvatures, and the mean curvature is the average of the principal (max and min) curvatures. The units are 1/mm. Extracted curvature values identified each vertex as convex (gyral) or concave (sulcal) on a continuous negative-to-positive scale and are based on the original geometry of the surface mesh before inflation. To estimate gyral/sulcal borders, we plotted binarized curvature values and drew edges at the transitions from convexity to concavity. Edges were overlaid on the correlation maps, as demonstrated in the lower left inset of Figure 2.
Results
Anatomical variants of HG have been previously classified into three subtypes (Leonard et al., 1998; Abdul-Kareem and Sluming, 2008). In the first subtype, HG is single and has a smooth crown (single HG). It is bordered by the first transverse sulcus (FTS) on the anterior side and Heschl's sulcus (HS) on the posterior side. In the second subtype, HG is partially divided along its length by a sulcus intermedius (SI). The length of the SI can be short or long and its depth can vary, but the division is considered partial if the SI does not extend down to the medial base of HG, leaving the two divisions of HG connected by a common stem (partial duplication or common stem duplication). In the third subtype, HG is fully divided by a sulcus extending all the way down to its medial base, dividing the structure into two parallel gyri without a common medial stem (complete duplication). In case of complete duplications, the standard nomenclature of the sulci differs and there are considered to be two Heschl's sulci (HS1 and HS2): the dividing sulcus is called HS1 and the sulcus behind the posterior division is HS2. The 20 hemispheres in our study (which were not preselected for anatomy) had the following distribution of the three HG subtypes: 9 single gyri, 8 partial duplications, and 3 complete duplications.
In 20/20 individual hemispheres, we clearly observed two mirror-symmetric frequency progressions (high-low-low-high) in the region of HG. Figure 1D shows maps in three sample hemispheres (voxelwise statistical threshold p < 0.05, after FDR correction for multiple comparisons). The two mirror-symmetric maps correspond with those identified by Formisano et al. (2003) and are likely homologs of macaque areas A1 and R. The more posterior of the two maps (high-to-low) corresponds to A1 and the anterior map (low-to-high) corresponds to R. Here, we refer to these regions as human A1 (hA1) and hR. Additional smaller frequency progressions were in some cases observed posterior and anterior to the main two maps, and these may correspond to nonprimary auditory fields (Rivier and Clarke, 1997); however, these maps were less consistent and are not further addressed here. The spatial layouts of the two primary tonotopic maps relative to HG were consistent enough across subjects to be evident on group-averaged maps (n = 10) that were combined using cortex-based alignment (Fig. 1E).
Our goal was to evaluate the spatial layout of PAC relative to the underlying anatomy of HG in each subject individually. To this end, we outlined the “high-low-low-high” maps observed on each surface mesh (n = 20, see outlines on Fig. 1D) and plotted those contiguous surface patches with gyral borders overlaid (Fig. 2). Every surface voxel within each contiguous patch is displayed and color coded according to preferred frequency, with no points excluded due to thresholding. Cases of single gyri, partial duplications, and complete duplications are indicated. The plots in Figure 2 show several patterns of interest. First, it was evident in 20/20 hemispheres that tonotopic gradients ran perpendicular to the long axis of HG (correspondingly, map iso-frequency lines ran parallel to HG). Second, in cases of partial or complete duplications, PAC (the combined maps of hA1+hR) clearly spanned both anterior and posterior divisions of HG, not only the anterior division as commonly assumed. Third, consistent with previous architectonic reports, PAC was not always limited by the outer borders of HG. In some cases (subjects 1, 2, 3, 6, and 7), the posterior map (hA1) continued a variable extent beyond HS onto less pronounced gyri of the planum temporale.
Finally, and most surprisingly, there was a highly consistent relationship between the spatial layout of the maps and the underlying shape of HG. On all single HGs (9/20 hemispheres, subtype 1), the low-frequency union between the two maps (the hA1–R border) occurred on the crown of the gyrus. In all cases of partial duplications (8/20 hemispheres, subtype 2) the hA1–R border occurred either in or very near the SI. In all cases of complete duplications (3/20 hemispheres, subtype 3), the hA1–R border also occurred within the dividing sulcus (HS1), which thus appears to be a continuation of the pattern seen on partial duplications. As shown in Figure 3, reversing the order of stimulus presentation during mapping (tones presented from high frequencies to low) did not influence the spatial layout of the observed maps with respect to these observed patterns.
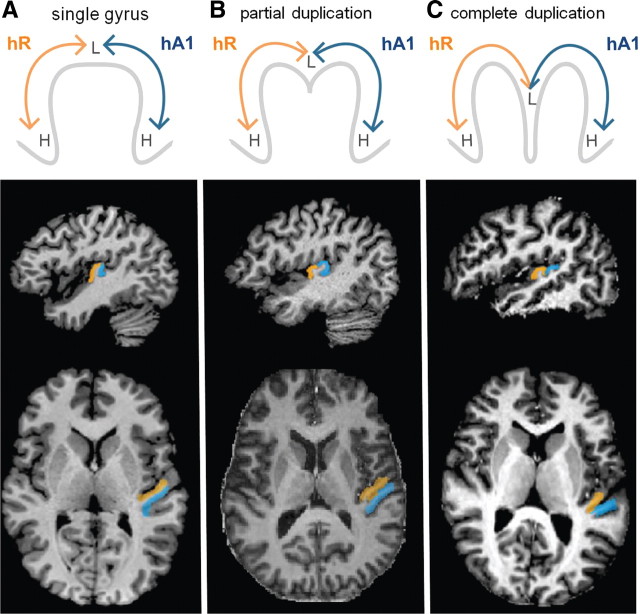
This precise anatomical–functional relationship reveals that the anatomical variants of HG are part of a continuum, rather than distinct subtypes as summarized in Figure 4. hA1 (the posterior high-to-low map) is located on the posterior side of HG when the gyrus is single (Fig. 4A) and on the posterior division of HG when the gyrus is duplicated (Fig. 4B,C). hR (the anterior low-to-high map) is likewise located on the anterior side or division of HG. The lower panels of Figure 4 show the actual locations of hA1 and hR in three sample subjects, as identified by their own functional tonotopic mappings. The regions correspond to the coordinates of the subject's “high-low-low-high” contiguous surface patches projected into each subject's own native anatomical space. The border between hA1 and hR was defined along the reversal between the two frequency gradients (as demonstrated on the group-average map in Fig. 1E).
Figure 4.
Heschl's gyrus variants are part of a continuum, rather than distinct subtypes. Top row, Diagrams of hA1 (blue) and hR (orange) locations on cross-sections of HG. hA1 is located on the posterior side or division of HG on single and duplicated gyri, respectively. hR is likewise on the anterior side or division of HG. L and H depict the location of low and high frequencies on the tonotopic maps. Middle and bottom rows, Actual hA1 and hR locations in axial and sagittal anatomical views from three sample subjects, as identified based on the functional tonotopy data. The regions were selected on the cortical surface meshes (as shown in Fig. 1) and projected into volumetric anatomical space. The hA1–R border between was defined along the gradient reversal (the low-frequency representation) at the center of the two maps.
Figure 5A shows the relationship between frequency representation and cortical curvature values across all PAC surface voxels of all single HG hemispheres (means and SE bars computed over all voxels of all 9 hemispheres combined, total number of voxels = 10,400). The curvature value of each voxel is a measure of the voxel's local concavity versus convexity on the cortical surface mesh before inflation. Negative values are convex (gyral) and positive values are concave (sulcal). There was a significant correlation between frequency and curvature values: correlation values, R, were computed over all voxels of each of the nine hemispheres separately (hence N = 9) and were significantly different from zero (mean positive correlation value R = 0.34; p < 0.0005, t test). Thus, we found a systematic relationship in that frequencies near the union of the mirror-symmetric maps (i.e., low frequencies) tend to occur on a gyrus (HG) and those frequencies farthest from the union (i.e., high frequencies) tend to occur in sulci. A similar relationship (Fig. 5B, number of voxels = 9763) was also observed in cases of partial duplications (N = 8, mean R = 0.34, p < 0.005, t test); however, the pattern was fully disrupted (Fig. 5C, number of voxels = 3932) in cases of complete duplications (N = 3, p > 0.05, mean R = −0.15, t test). Interestingly, the union of mirror symmetric retinotopic maps on a gyrus also occurs in the visual system at the V1/V2 border (Van Essen, 1997; Rajimehr and Tootell, 2009; see Discussion). The analysis here of map value versus curvature value is similar to that of Rajimehr and Tootell's (2009) quantification of this structure–function relationship in the visual cortex.
Figure 5.
Tonotopy relative to curvature of HG. Curvature index versus preferred frequency values of all surface voxels within the two primary tonotopic maps, across all subject's hemispheres with a single HG (A), partial duplication (B), and complete duplication (C). Positive curvature values indicate concavity (sulcal), and negative values indicate convexity (gyral). Systematically, low frequencies tend to be represented on a gyrus (HG) and high frequencies within adjacent sulci. Error bars indicate SEM. D, Diagram of a single gyrus showing how a fold between mirror symmetric maps brings equivalent topographic points on the two maps closer together in space. E, Actual tonotopy data on HG from a sample subject for comparison, sagittal slice view.
Discussion
These data reveal a striking and highly consistent relationship between the tonotopic maps of hA1 and hR and the underlying anatomy of Heschl's gyrus. These findings significantly revise HG as a marker for human PAC and suggest that tonotopic maps may have shaped HG during human evolution, as discussed below.
It is important to note that the mapping of human auditory cortex is not yet complete. Based on the monkey model, a third smaller primary field (RT) is expected anterior to R, as well as additional gradients outside the primary core (nonprimary belt fields). These additional fields have been imaged with fMRI in the macaque in good agreement with previous single-unit recordings (Petkov et al, 2006). Additional tonotopic fields have been imaged in the human as well, but they are seen less reliably than the main two gradients (Talavage et al., 2004; Woods et al., 2009; Humphries et al., 2010; Striem-Amit et al., 2011). We also observed, in some cases, additional frequency reversals anterior to hR (see Fig. 1D, example 1) and posterior to hA1 (Fig. 1D, example 3). Potential reasons that these fields are imaged less reliably in the human could be that these fields are small, less strictly tonotopic, not optimally driven by pure tones, and/or different from in monkeys.
It is also important to note that the lateral and medial boundaries of PAC are still unclear. Human PAC is expected on the medial two-thirds (approximately) of HG, with nonprimary architectonic regions occupying the lateral end of HG (Rivier and Clarke, 1997). In the macaque, iso-frequency bands of the core gradients continue laterally and medially into the belt fields, so it is not expected to be able to discern the lateral and medial borders of the primary core based solely upon tonotopic maps. The observed tonotopic patterns extended the full lateral–medial extent of HG. Thus, it is very likely that the lateral edges of the maps include some portion of lateral belt fields, and also possible that the medial edge includes a small portion of medial belt. A functional method of determining the human core–belt boundary remains to be demonstrated. A recent study estimates the core–belt boundary at a fixed spatial extent from the center of auditory activation (Chevillet et al., 2011), but this not does not reveal exact boundaries nor take into account individual differences.
PAC spans both divisions of duplicated Heschl's gyri
We find that human PAC covers both divisions of duplicated Heschl's gyri, not only the first (more anterior) division as commonly assumed (Rademacher et al., 1993; Penhune et al., 1996). This distinction affects a broad literature that uses anatomical criteria to estimate the size of human PAC (and the adjacent planum temporale) in relation to brain laterality, language and music abilities, and auditory-related pathologies, including dyslexia, autism, and schizophrenia (for review, see Abdul-Kareem and Sluming, 2008). By current convention, only the anterior division of duplicated HGs is included in PAC measurements (Rademacher et al. et al., 1993; Penhune et al., 1996; Leonard et al., 2001; Schneider et al., 2002; Emmorey et al., 2003; Wong et al., 2008; Gage et al., 2009; Schneider et al., 2009; Warrier et al., 2009; Hubl et al., 2010) with the posterior division assigned instead to the planum temporale (Dorsaint-Pierre et al., 2006). The criteria proposed by Penhune et al. (1996) (to consider only the anterior division as part of PAC if there is an SI extending half the length of HG) would wrongly exclude the posterior division of PAC (the entire hA1 subfield) in 7 out of 20 of our cases.
It is important to note that our study does not aim to propose a new set of anatomical criteria for estimating PAC size. We corroborate previous architectonic reports (Morosan et al., 2001) that PAC is not always contained within the anatomical borders of HG. In particular, PAC in many cases extended posteriorly onto the planum temporale. We concur with previous assertions that estimating PAC size based on gross anatomical landmarks is prone to error (Abdul-Kareem and Sluming, 2008).
Tonotopic gradients run across Heschl's gyrus
A leading model has been that tonotopic gradients run parallel to HG, rather than perpendicular. This model stems from architectonic reports (Hackett et al., 2001) that claim that human primary auditory cortex forms an elongated strip (posteromedial-to-anterolateral) along HG, the shape of which appears similar to the elongated auditory core in monkeys (posterior-to-anterior), which contains the three tonotopic fields A1, R, and RT. Thus, it was expected that human tonotopic gradients were rotated compared to the macaque and would be found running along (or parallel to) HG rather then across it. This model was somewhat supported by MEG measurements (Romani et al., 1982) and chronic microelectrode recordings (Howard et al., 1996) placing high frequencies medially on HG and low frequencies laterally on HG (thus potentially accounting for the low-to-high map of A1, but not R). Those recording methods were limited by poor localization accuracy and by limited sampling, respectively.
On the other hand, tonotopic gradients measured with fMRI have repeatedly appeared to run across HG, consistent with the posterior-to-anterior orientation in the macaque (Formisano et al., 2003; Talavage et al., 2004; Woods et al., 2009; Humphries et al., 2010; Striem-Amit et al., 2011). However, data have often been unclear and interpretation has been made difficult by display on highly inflated or fully flattened surfaces with distorted spatial relationships. For example, despite gradients appearing to run across HG, Formisano et al. (2003) concluded that gradient orientation was “posteromedial-to-anterolateral,” thus apparently confirming the model of parallel gradients. Our mappings lead us to strongly conclude that the primary tonotopic gradients run across HG, rather than along it, and that this orientation is highly consistent across individuals (n = 20 hemispheres) and across the morphological variants of HG.
It should also be noted that the gradients do not have to be strictly perpendicular and could be tilted in a number of orientations. The maps of hA1 and hR could run along an axis across HG that is tilted posteromedial (PM)-to-anterolateral (AL), or likewise, tilted posterolateral (PL)-to-anteromedial (AM). Another intriguing possibility is that the core axis is curved (as in the macaque, Kaas and Hackett, 2000) with the map of hA1 angled PM-to-AL and the map of hR angled PL-to-AM. Such a curved orientation would help explain why the low-frequency representation often appears wider laterally and could explain the earlier interpretation of MEG data. The exact orientation depends on how one establishes the starting (high) and end (low) points of the gradients, which is not obvious since the high- and low-frequency representations are not distinct points but rather iso-frequency bands that continue into nonprimary belt areas. The exact orientations may be clarified by future mapping studies that can distinguish core from belt regions, thus giving a better estimate of gradient starting and end points.
Measuring tonotopy with BOLD fMRI
In single-neuron recordings in animals, neuronal frequency tuning is characterized at threshold volume levels (characteristic frequency, CF), and tuning tends to broaden progressively as sound volume increases (Phillips et al., 1994). This leads to the question of how frequency tuning can be measured with fMRI, which requires the use of suprathreshold stimuli to illicit robust responses. Recent high-field fMRI studies (Petkov et al., 2006, 2009; Tanji et al., 2010) using suprathreshold stimuli (70–90 dB) have imaged multiple tonotopic fields in the macaque (including A1, R, RT, and belt areas) that matched the expected location, size, and gradient orientations known from previous electrophysiological and anatomical measures. As such, the BOLD response may be measuring (1) subtle preferences at high stimulus intensities and/or (2) the tuning of some neurons that remain sharp at high intensities. Such neurons have been reported in primary auditory cortex of the awake macaque (Recanzone et al., 2000) and in more recent studies that suggest the tuning is sharper in awake compared to anesthetized animals and more invariant to stimulus intensity (Sadagopan and Wang, 2008; Bartlett et al., 2011). Intracranial recordings on HG in alert humans show sharp frequency tuning at suprathreshold stimulus levels (Bitterman et al., 2008).
In the macaque, the cortical representation in A1 is ∼1 octave/mm. Given that our mapping stimuli (in humans) spanned 7 octaves (88–8000 Hz), associated maps would be expected to span at least 7 mm each (14 mm total for hA1 + hR), if not more considering human cortical expansion. The topological distance across our maps of hA1 + hR (angled across HG) was 27.6 ± 3.9 mm (mean ± SD), thus indicating sufficient space across HG to accommodate the expected length of two primary frequency gradients. In terms of limitations of fMRI imaging, there still remains an unknown impact of scanner noise on the cortical response to sound. The impact can be reduced with sparse scanning techniques (Petkov et al., 2009; Humphries et al., 2010) but with a significant trade-off in scan time. Also, it is unknown whether different physiological properties at different parts of the map differentially influence the BOLD response.
Comparison to architectonic measures of human PAC
After a century of mapping cortical architecture (Campbell, 1905; von Economo and Koskinas, 1925; von Economo and Horn, 1930; Galaburda and Sanides, 1980; Rademacher et al., 1993; Rivier and Clarke, 1997; Clarke and Rivier, 1998; Hackett et al., 2001; Morosan et al., 2001; Wallace et al., 2002; Sweet et al., 2005; Fullerton and Pandya, 2007), it appears that human PAC is not uniform, and multiple subdivisions have been proposed. The central regions of PAC show the strongest primary (koniocortical) features. von Economo and Horn (1930) noted that within PAC, the densest packing of granular cells is found on the crown of HG (referring to single gyri); and Hackett et al. (2001) found that the most prominent core region fell along the SI (referring to partial duplications). Our data suggest that this region of densest cellular structure (the crown of single gyri and the SI of duplicated gyri) may correspond to the low-frequency representation at the border between hA1 and hR.
Mirror-symmetric maps meet on a gyrus: parallel with visual cortex
Interestingly, the data reveal a previously unknown organizational parallel with the visual cortex: the union of mirror-symmetric tonotopic maps (the hA1–R border) occurs on the crown of the gyrus in humans, just as the union between mirror-symmetric retinotopic maps (the V1/V2 border) occurs on a gyrus in humans and macaques (Van Essen, 1997; Rajimehr and Tootell, 2009). This phenomenon in the visual system has been the primary argument for the hypothesis (Van Essen, 1997) that cortical folds occur as a result of axonal tension between highly interconnected regions during development. According to this hypothesis, interconnected mirror-symmetric maps are pulled together during development (Fig. 5D,E), resulting in compact cortical wiring. Indeed, monkey AI and R are highly interconnected between matching tonotopic locations (Morel and Kaas, 1992; Morel et al., 1993). While this hypothesis could explain the emergence of HG, it would not explain the variable existence of the SI. It is also possible that there are differences in cortical architecture (e.g., cell density, cortical thickness) linked to the region of low-frequency representation that make this region more likely to fold.
Heschl's gyrus is a cortical fold that is specific to human evolution: the macaque auditory cortex has mirror-symmetric tonotopy but is flat (no transverse gyri), chimpanzees may have a primitive transverse gyrus, and humans typically have 1–2 HGs per hemisphere (Hackett et al., 2001). Cats and rodents also have multiple tonotopic fields with gradient reversals (Schreiner and Winer, 2007, Hackett et al., 2011). Thus, mirror-symmetric tonotopy apparently preceded HG phylogenetically and may have guided the formation of HG during human evolution, as additional folding occurred to meet increased demand for cortical surface. It is not known whether HG duplications affect auditory processing. Interestingly, HG duplications are more common in the left hemisphere of expert phoneticians (Golestani et al., 2011) and in individuals with William's syndrome (Wengenroth et al., 2010).
Future directions
On a final note, the functional specializations of A1 and R remain unknown in monkey and human. Because tonotopic maps required only 16 min of fMRI data acquisition, these methods can be used as an initial mapping step in future studies of the specific auditory fields, much like the use of retinotopic mapping in visual cortex (Wandell and Winawer, 2011). Identification of these auditory fields is a necessary first step toward further study of the function, evolution, and plasticity of the human auditory cortex.
Footnotes
This work was supported by Swiss National Science Foundation Grant 3200030-124897 to S.C. and by the Centre d'Imagerie BioMèdicale of the Université de Lausanne, Université de Genève, Hôpitaux Universitaires de Genève, Lausanne University Hospital, Ecole Polytechnique Fédérale de Lausanne, and the Leenaards and Louis-Jeantet Foundations. We thank Artur Marchewka for assistance with pilot data collection.
The authors declare no competing financial interests.
References
- Abdul-Kareem IA, Sluming V. Heschl gyrus and its included primary auditory cortex: structural MRI studies in healthy and diseased subjects. J Magn Reson Imaging. 2008;28:287–299. doi: 10.1002/jmri.21445. [DOI] [PubMed] [Google Scholar]
- Bartlett EL, Sadagopan S, Wang X. Fine frequency tuning in monkey auditory cortex and thalamus. J Neurophysiol. 2011;106:849–859. doi: 10.1152/jn.00559.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bitterman Y, Mukamel R, Malach R, Fried I, Nelken I. Ultra-fine frequency tuning revealed in single neurons of human auditory cortex. Nature. 2008;451:197–201. doi: 10.1038/nature06476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodmann K. Vergleichende Lokalisationslehre der Grosshirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues. Leipzig, Germany: Barth; 1909. [Google Scholar]
- Brugge JF, Merzenich MM. Responses of neurons in auditory cortex of the macaque monkey to monaural and binaural stimulation. J Neurophysiol. 1973;36:1138–1158. doi: 10.1152/jn.1973.36.6.1138. [DOI] [PubMed] [Google Scholar]
- Campbell AW. Histological studies on the localization of cerebral function. Cambridge, UK: Cambridge UP; 1905. [Google Scholar]
- Chevillet M, Riesenhuber M, Rauschecker JP. Functional correlated of the anterolateral processing hierarchy in human auditory cortex. J Neurosci. 2011;31:9345–9352. doi: 10.1523/JNEUROSCI.1448-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke S, Rivier F. Compartments within human primary auditory cortex: evidence from cytochrome oxidase and acetylcholinesterase staining. Eur J Neurosci. 1998;10:741–745. doi: 10.1046/j.1460-9568.1998.00043.x. [DOI] [PubMed] [Google Scholar]
- Dorsaint-Pierre R, Penhune VB, Watkins KE, Neelin P, Lerch JP, Bouffard M, Zatorre RJ. Asymmetries of the planum temporale and Heschl's gyrus: relationship to language lateralization. Brain. 2006;129:1164–1176. doi: 10.1093/brain/awl055. [DOI] [PubMed] [Google Scholar]
- Emmorey K, Allen JS, Bruss J, Schenker N, Damasio H. A morphometric analysis of auditory brain regions in congenitally deaf adults. Proc Natl Acad Sci U S A. 2003;100:10049–10054. doi: 10.1073/pnas.1730169100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel SA, Rumelhart DE, Wandell BA, Lee AT, Glover GH, Chichilnisky EJ, Shadlen MN. fMRI of human visual cortex. Nature. 1994;369:525. doi: 10.1038/369525a0. [DOI] [PubMed] [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Ségonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM. Automatically parcellating the human cerebral cortex. Cereb Cortex. 2004;14:11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- Fleschig P. Bemerkungen über die Hörsphäre des menschlichen Gehirns. Neurol Zentralbl. 1908;27:2–7, 50–57. [Google Scholar]
- Formisano E, Kim DS, Di Salle F, van de Moortele PF, Ugurbil K, Goebel R. Mirror-symmetric tonotopic maps in human primary auditory cortex. Neuron. 2003;40:859–869. doi: 10.1016/s0896-6273(03)00669-x. [DOI] [PubMed] [Google Scholar]
- Fullerton BC, Pandya DN. Architectonic analysis of the auditory-related areas of the superior temporal region in human brain. J Comp Neurol. 2007;504:470–498. doi: 10.1002/cne.21432. [DOI] [PubMed] [Google Scholar]
- Gage NM, Juranek J, Filipek PA, Osann K, Flodman P, Isenberg AL, Spence MA. Rightward hemispheric asymmetries in auditory language cortex in children with autistic disorder: an MRI investigation. J Neurodev Disord. 2009;1:205–214. doi: 10.1007/s11689-009-9010-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galaburda A, Sanides F. Cytoarchitectonic organization of the human auditory cortex. J Comp Neurol. 1980;190:597–610. doi: 10.1002/cne.901900312. [DOI] [PubMed] [Google Scholar]
- Golestani N, Price CJ, Scott SK. Born with an ear for dialects? Structural plasticity in the expert phonetician brain. J Neurosci. 2011;31:4213–4220. doi: 10.1523/JNEUROSCI.3891-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackett TA, Preuss TM, Kaas JH. Architectonic identification of the core region in auditory cortex of macaques, chimpanzees, and humans. J Comp Neurol. 2001;441:197–222. doi: 10.1002/cne.1407. [DOI] [PubMed] [Google Scholar]
- Hackett TA, Barkat TR, O'Brien BMJ, Hensch TK, Polley DB. Linking topography to tonotopy in the mouse auditory thalamocortical circuit. J Neurosci. 2011;31:2983–2995. doi: 10.1523/JNEUROSCI.5333-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard MA, 3rd, Volkov IO, Abbas PJ, Damasio H, Ollendieck MC, Granner MA. A chronic microelectrode investigation of the tonotopic organization of human auditory cortex. Brain Res. 1996;724:260–264. doi: 10.1016/0006-8993(96)00315-0. [DOI] [PubMed] [Google Scholar]
- Hubl D, Dougoud-Chauvin V, Zeller M, Federspiel A, Boesch C, Strik W, Dierks T, Koenig T. Structural analysis of Heschl's gyrus in schizophrenia patients with auditory hallucinations. Neuropsychobiology. 2010;61:1–9. doi: 10.1159/000258637. [DOI] [PubMed] [Google Scholar]
- Humphries C, Liebenthal E, Binder JR. Tonotopic organization of human auditory cortex. Neuroimage. 2010;50:1202–1211. doi: 10.1016/j.neuroimage.2010.01.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaas JH, Hackett TA. Subdivisions of auditory cortex and processing streams in primates. Proc Natl Acad Sci U S A. 2000;97:11793–11799. doi: 10.1073/pnas.97.22.11793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leonard CM, Puranik C, Kuldau JM, Lombardino LJ. Normal variation in the frequency and location of human auditory cortex landmarks. Heschl's gyrus: where is it? Cereb Cortex. 1998;8:397–406. doi: 10.1093/cercor/8.5.397. [DOI] [PubMed] [Google Scholar]
- Leonard CM, Eckert MA, Lombardino LJ, Oakland T, Kranzler J, Mohr CM, King WM, Freeman A. Anatomical risk factors for phonological dyslexia. Cereb Cortex. 2001;11:148–157. doi: 10.1093/cercor/11.2.148. [DOI] [PubMed] [Google Scholar]
- Marques JP, Kober T, Krueger G, van der Zwaag W, Van de Moortele PF, Gruetter R. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. Neuroimage. 2010;49:1271–1281. doi: 10.1016/j.neuroimage.2009.10.002. [DOI] [PubMed] [Google Scholar]
- Morel A, Kaas JH. Subdivisions and connections of auditory cortex in owl monkeys. J Comp Neurol. 1992;318:27–63. doi: 10.1002/cne.903180104. [DOI] [PubMed] [Google Scholar]
- Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol. 1993;335:437–459. doi: 10.1002/cne.903350312. [DOI] [PubMed] [Google Scholar]
- Morosan P, Rademacher J, Schleicher A, Amunts K, Schormann T, Zilles K. Human primary auditory cortex: cytoarchitectonic subdivisions and mapping into a spatial reference system. Neuroimage. 2001;13:684–701. doi: 10.1006/nimg.2000.0715. [DOI] [PubMed] [Google Scholar]
- Penhune VB, Zatorre RJ, MacDonald JD, Evans AC. Interhemispheric anatomical differences in human primary auditory cortex: probabilistic mapping and volume measurement from magnetic resonance scans. Cereb Cortex. 1996;6:661–672. doi: 10.1093/cercor/6.5.661. [DOI] [PubMed] [Google Scholar]
- Petkov CI, Kayser C, Augath M, Logothetis NK. Functional imaging reveals numerous fields in the monkey auditory cortex. PLoS Biol. 2006;4:e215. doi: 10.1371/journal.pbio.0040215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkov CI, Kayser C, Augath M, Logothetis NK. Optimizing the imaging of monkey auditory cortex: sparse vs. continuous fMRI. Magn Reson Imaging. 2009;27:1065–1073. doi: 10.1016/j.mri.2009.01.018. [DOI] [PubMed] [Google Scholar]
- Phillips DP, Semple MN, Calford MB, Kitzes LM. Level-dependent representation of stimulus frequency in cat primary auditory cortex. Exp Brain Res. 1994;102:210–226. doi: 10.1007/BF00227510. [DOI] [PubMed] [Google Scholar]
- Rademacher J, Caviness VS, Jr, Steinmetz H, Galaburda AM. Topographical variation of the human primary cortices: implications for neuroimaging, brain mapping, and neurobiology. Cereb Cortex. 1993;3:313–329. doi: 10.1093/cercor/3.4.313. [DOI] [PubMed] [Google Scholar]
- Rademacher J, Morosan P, Schormann T, Schleicher A, Werner C, Freund H-J, Zilles K. Probabilistic mapping and volume measurement of human primary auditory cortex. Neuroimage. 2001;13:669–683. doi: 10.1006/nimg.2000.0714. [DOI] [PubMed] [Google Scholar]
- Rajimehr R, Tootell RBH. Does retinotopy influence cortical folding in primate visual cortex? J Neurosci. 2009;29:11149–11152. doi: 10.1523/JNEUROSCI.1835-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauschecker JP, Tian B, Pons T, Mishkin M. Serial and parallel processing in rhesus monkey auditory cortex. J Comp Neurol. 1997;382:89–103. [PubMed] [Google Scholar]
- Recanzone GH, Guard DC, Phan ML. Frequency and intensity response properties of single neurons in the auditory cortex of the behaving macaque monkey. J Neurophysiol. 2000;83:2315–2331. doi: 10.1152/jn.2000.83.4.2315. [DOI] [PubMed] [Google Scholar]
- Rivier F, Clarke S. Cytochrome oxidase, acetylcholinesterase, and NADPH-diaphorase staining in human supratemporal and insular cortex: evidence for multiple auditory areas. Neuroimage. 1997;6:288–304. doi: 10.1006/nimg.1997.0304. [DOI] [PubMed] [Google Scholar]
- Romani GL, Williamson SJ, Kaufman L. Tonotopic organization of the human auditory cortex. Science. 1982;216:1339–1340. doi: 10.1126/science.7079770. [DOI] [PubMed] [Google Scholar]
- Sadagopan S, Wang X. Level invariant representation of sounds by population of neurons in primary auditory cortex. J Neurosci. 2008;28:3415–3426. doi: 10.1523/JNEUROSCI.2743-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider P, Scherg M, Dosch HG, Specht HJ, Gutschalk A, Rupp A. Morphology of Heschl's gyrus reflects enhanced activation in the auditory cortex of musicians. Nat Neurosci. 2002;5:688–694. doi: 10.1038/nn871. [DOI] [PubMed] [Google Scholar]
- Schneider P, Andermann M, Wengenroth M, Goebel R, Flor H, Rupp A, Diesch E. Reduced volume of Heschl's gyrus in tinnitus. Neuroimage. 2009;45:927–939. doi: 10.1016/j.neuroimage.2008.12.045. [DOI] [PubMed] [Google Scholar]
- Schreiner CE, Winer JA. Auditory cortex mapmaking: principles, projections, and plasticity. Neuron. 2007;56:356–365. doi: 10.1016/j.neuron.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sereno MI, Dale AM, Reppas JB, Kwong KK, Belliveau JW, Brady TJ, Rosen BR, Tootell RB. Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science. 1995;268:889–893. doi: 10.1126/science.7754376. [DOI] [PubMed] [Google Scholar]
- Speck O, Stadler J, Zaitsev M. High resolution single-shot EPI at 7T. MAGMA. 2008;21:73–86. doi: 10.1007/s10334-007-0087-x. [DOI] [PubMed] [Google Scholar]
- Striem-Amit E, Hertz U, Amedi A. Extensive cochleotopic mapping of human auditory cortical fields obtained with phase-encoded fMRI. PLOS One. 2011;6:e17832. doi: 10.1371/journal.pone.0017832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweet RA, Dorph-Petersen KA, Lewis DA. Mapping auditory core, lateral belt, and parabelt cortices in the human superior temporal gyrus. J Comp Neurol. 2005;491:270–289. doi: 10.1002/cne.20702. [DOI] [PubMed] [Google Scholar]
- Talavage TM, Sereno MI, Melcher JR, Ledden PJ, Rosen BR, Dale AM. Tonotopic organization in human auditory cortex revealed by progressions of frequency sensitivity. J Neurophysiol. 2004;91:1282–1296. doi: 10.1152/jn.01125.2002. [DOI] [PubMed] [Google Scholar]
- Tanji K, Leopold DA, Ye FQ, Zhu C, Malloy M, Saunders RC, Mishkin M. Effect of sound intensity on tonotopic fMRI maps in the unanesthetized monkey. Neuroimage. 2010;49:150–157. doi: 10.1016/j.neuroimage.2009.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Zwaag W, Francis S, Head K, Peters A, Gowland P, Morris P, Bowtell R. fMRI at 1.5, 3, and 7 T: characterizing BOLD signal changes. Neuroimage. 2009;47:1425–1434. doi: 10.1016/j.neuroimage.2009.05.015. [DOI] [PubMed] [Google Scholar]
- van der Zwaag W, Gentile G, Gruetter R, Spierer L, Clarke S. Where sound position influences sound object representations: a 7-T fMRI study. Neuroimage. 2011;54:1803–1811. doi: 10.1016/j.neuroimage.2010.10.032. [DOI] [PubMed] [Google Scholar]
- Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
- von Economo C, Horn L. Über Winddungsrelief, Masse und Rindenarchitektonik der Supratemporalfläche, ihre individuellen und ihre Seitenunterschiede. Z Ges Neurol Psychiatr. 1930;130:678–757. [Google Scholar]
- von Economo C, Koskinas GN. Die Cytoarchitektonik der Grosshirnrinde des erwachsenen Menschen. Berlin: Springer; 1925. [Google Scholar]
- Wallace MN, Johnston PW, Palmer AR. Histochemical identification of cortical areas in the auditory region of the human brain. Exp Brain Res. 2002;143:499–508. doi: 10.1007/s00221-002-1014-z. [DOI] [PubMed] [Google Scholar]
- Wandell BA, Winawer J. Imaging retinotopic maps in the human brain. Vision Res. 2011;51:718–737. doi: 10.1016/j.visres.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warrier C, Wong P, Penhune V, Zatorre R, Parrish T, Abrams D, Kraus N. Relating structure to function: Heschl's gyrus and acoustic processing. J Neurosci. 2009;29:61–69. doi: 10.1523/JNEUROSCI.3489-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wengenroth M, Blatow M, Bendszus M, Schneider P. Leftward lateralization of auditory cortex underlies holistic sound perception in Williams syndrome. PLoS ONE. 2010;5:e12326. doi: 10.1371/journal.pone.0012326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong PC, Warrier CM, Penhune VB, Roy AK, Sadehh A, Parrish TB, Zatorre RJ. Volume of left Heschl's gyrus and linguistic pitch learning. Cereb Cortex. 2008;18:828–836. doi: 10.1093/cercor/bhm115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods DL, Stecker GC, Rinne T, Herron TJ, Cate AD, Yund EW, Liao I, Kang X. Functional maps of human auditory cortex: effects of acoustic features and attention. PLoS One. 2009;4:e5183. doi: 10.1371/journal.pone.0005183. [DOI] [PMC free article] [PubMed] [Google Scholar]