Intrinsic Reference Frames of Superior Colliculus Visuomotor Receptive Fields during Head-Unrestrained Gaze Shifts

Abstract

A sensorimotor neuron's receptive field and its frame of reference are easily conflated within the natural variability of spatial behavior. Here, we capitalized on such natural variations in 3-D eye and head positions during head-unrestrained gaze shifts to visual targets in two monkeys: to determine whether intermediate/deep layer superior colliculus (SC) receptive fields code visual targets or gaze kinematics, within four different frames of reference. Visuomotor receptive fields were either characterized during gaze shifts to visual targets from a central fixation position (32 U) or were partially characterized from each of three initial fixation points (31 U). Natural variations of initial 3-D gaze and head orientation (including torsion) provided spatial separation between four different coordinate frame models (space, head, eye, fixed-vector relative to fixation), whereas natural saccade errors provided spatial separation between target and gaze positions. Using a new statistical method based on predictive sum-of-squares, we found that in our population of 63 neurons (1) receptive field fits to target positions were significantly better than fits to actual gaze shift locations and (2) eye-centered models gave significantly better fits than the head or space frame. An intermediate frames analysis confirmed that individual neuron fits were distributed target-in-eye coordinates. Gaze position “gain” effects with the spatial tuning required for a 3-D reference frame transformation were significant in 23% (7/31) of neurons tested. We conclude that the SC primarily represents gaze targets relative to the eye but also carries early signatures of the 3-D sensorimotor transformation.

Introduction

The concept of a receptive field (RF) (i.e., that each stimulus location corresponds to a specific level of activity in a given neuron) is fundamental for spatial coding in sensory and sensorimotor structures (Kuffler, 1953; Mountcastle, 1958; Hubel and Wiesel, 1959). However, RFs are modulated by factors such as attention, motivation, and posture (Andersen and Mountcastle, 1983; Ben Hamed et al., 2002; Pessoa et al., 2002; Fahle, 2009), and stimulus location must be defined in some reference frame. In most experiments, the intrinsic reference frame is identified by measuring the RF at several distinct target and eye positions, and selecting the frame (e.g., eye or head) that provides the most coherent response (Stricanne et al., 1996). Eye-centered representations appear to persist through cortical and subcortical structures (Groh and Sparks, 1996; Cohen and Andersen, 2000) but often carry gaze position gain modulation (Andersen et al., 1985; Van Opstal et al., 1995), and some neurons show RFs fixed in head or intermediate frames (Jay and Sparks, 1987; Duhamel et al., 1997; Bremmer et al., 2001; Avillac et al., 2005).

This question becomes complex in structures like the superior colliculus (SC) that encode head-unrestrained gaze shifts (Munoz et al., 1991; Freedman et al., 1996; Klier et al., 2001). Here one needs to account for the following: (1) saccades are never perfectly accurate, so SC activity could relate to target location or gaze movement; (2) potential intrinsic frames now include eye, head, and body; (3) eye and head positions show natural variations, including torsional variations of ±10°, that influence location in eye and head frames (Glenn and Vilis, 1992; Crawford et al., 1999); (4) in this movement range, nonlinearities related to rotational geometry produce differences between linear gaze displacement and eye-fixed direction (Crawford and Guitton, 1997; Klier and Crawford, 1998). To date, the only study of the SC accounting for these factors used electrical stimulation (Klier et al., 2001), suggesting eye-fixed coordinates, but stimulation likely reveals downstream motor influence rather than the responses of neurons to their inputs (Smith and Crawford, 2005; Blohm et al., 2009), and cannot differentiate between target and movement coding.

We re-examined the question of SC receptive field/motor tuning and reference frame coding during head-unrestrained gaze shifts by combining standard RF mapping tasks, 3-D eye and head recordings, geometrically correct representations of target and gaze directions, and a new analytic technique (Keith et al., 2009) that exploits natural variations in eye and head position. We compared target (visual position) and motor (gaze movement) coding across four spatial models (eye-fixed, head-fixed, space-fixed, and linear gaze displacement), and also in intermediate frames. We also tested the prediction (Smith and Crawford, 2005) that neurons involved in a 3-D reference frame transformation should show gain fields orthogonal to their preferred visuomotor tuning. Our results indicate that, although individual neurons showed complex variations in RF shape, bandwidth, and intrinsic frame preference, at the population level the SC shows a statistically significant preference for target coding in eye coordinates, yet also shows early signs of a 3-D reference frame transformation.

Materials and Methods

Surgical procedures and 3-D gaze recordings

All protocols were in accordance with the Canadian Council on Animal Care guidelines on the use of laboratory animals and approved by the York University Animal Care Committee. The data were collected from two female Macaca mulatta monkeys (M1 and M2; 4.7 and 6.8 kg). Animals were prepared for chronic electrophysiological recordings and 3-D eye movement recordings. Each animal underwent surgeries described previously (Crawford et al., 1999; Klier et al., 2001, 2003). Briefly, under general anesthesia of 1–2% isoflurane after intramuscular administration of ketamine hydrochloride (10 mg/kg), atropine sulfate (0.05 mg/kg), and acepromazine (0.5 mg/kg) as a cocktail, we implanted the recording chamber, which was centered 5 mm anterior and 0 mm lateral in stereotaxic coordinates. A 19-mm-diameter craniotomy covered on the base of the chamber allowed access to both sides of the SC. A recording chamber was attached over the trephination with dental acrylic anchored by 13 stainless steel cortex screws that formed the skullcap. Two 5-mm-diameter sclera search coils were implanted in one eye of each animal to record 3-D eye movements. 3-D head movements were recorded by two orthogonal coils mounted on a plastic base that was fastened to a plastic platform on the skull cap during the experiment. Three-dimensional eye-in-space (gaze), eye-in-head (eye), and head-in-space (head) orientations were recorded and analyzed as described previously (Crawford et al., 1999).

Behavioral paradigms

We used one Pentium PC and custom-designed software to present stimuli, control behavioral paradigms, send digital codes to a Plexon computer, and deliver juice rewards to the monkeys. Stimuli were presented on a flat screen 60 cm in front of the animals and back-projected (WT600 DLP projector, NEC) onto the screen. Each monkey was seated in a primate chair modified to allow the head to move freely (Crawford et al., 1999) and fitted with a juice spout placed at their mouth for computer-controlled reward delivery (Crist Instruments). Animals were trained only with the head unrestrained, to promote the use of natural eye–head coordination patterns. Animals were trained to perform the following two paradigms.

The single-initial-target paradigm.

In this paradigm the initial-target position was always at the straight-ahead direction in laboratory (space) frame, the origin in the 2-D directional coordinates (Fig. 1A, ■). Nine to 15 secondary-target positions (Fig. 1A, ● for an example session) were organized into three concentric arcs about the initial target position. During experiments, these were spread to include the “hot spot” of a given neuron and as much of the neuron's entire receptive field as possible. Animals were trained to fixate the initial target position (Fig. 1A, ■) for 500 ms. Then the initial target disappeared and one of the secondary target positions (Fig. 1A, ●) appeared (in random order), requiring an immediate gaze shift. (We did not use a “memory delay” task because we wanted to reproduce behavior; Mays and Sparks, 1980a.) If the animal fixated within 12° of the new target location for at least 105 ms, they received a water/juice reward.

Figure 1.

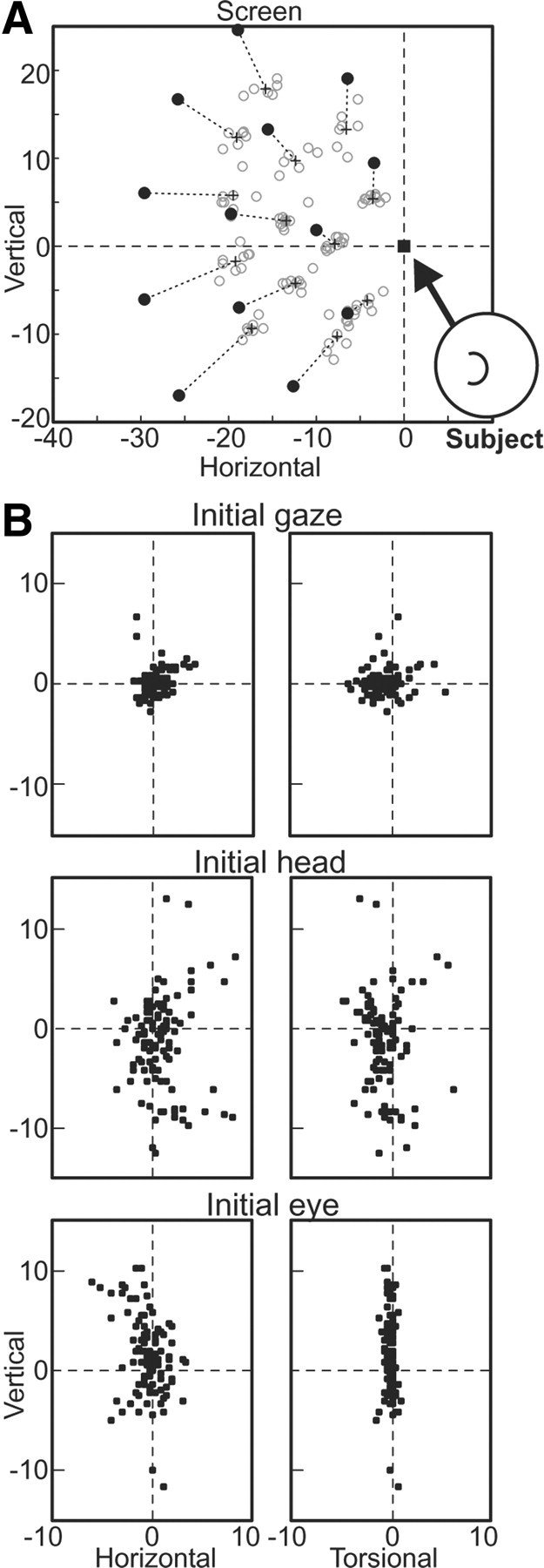
Experimental set-up and initial and final 3-D orientations for visual saccades made in head-unrestrained conditions. A, While the subject fixates the initial (home) target position (filled square), a saccade target appears at one of a set of positions (filled circles). The subject makes a saccade toward the saccade target and maintains fixation for at least 105 ms. Final gaze directions for all trials are indicated by open gray circles. The center-of-mass of the final gaze directions for all trials made to each saccade-target position are indicated by the cross, connected to the corresponding saccade-target position by a dashed line. B, The 3-D initial gaze (eye-in-space), head, and eye (eye-in-head) orientations are plotted for the same trials as in A.

We used this relatively large reward window to allow animals to naturally dissociate gaze position from target position, at their own discretion. This can be observed in Figure 1A, where the final gaze directions (gray open circles) are highly variable and tended to undershoot the visual target position (filled black circles) systematically (as shown by the + symbol, which marks the average final gaze position for trials made to each target position). This dissociation was necessary in order for us to distinguish neural responses to targets versus desired gaze positions (see below).

Another requirement of our methodology was a distribution of initial eye and head positions, which monkeys again provided naturally through their own variable behavior. Typical 3-D initial gaze, head, and eye positions during fixation of the initial target are shown for all trials of the example session in Figure 1B. Initial head position varied in all three dimensions across trials (Fig. 1B, second row), being unconstrained and chosen simply by what the monkey found comfortable. This head variability meant that initial eye position (Fig. 1B, bottom row) varies in a complementary fashion in the horizontal and vertical dimensions to keep initial gaze fairly close on the initial target (Fig. 1B, top row). The torsional values of eye position (eye-in-head) (Fig. 1B, bottom row) were restricted to Listing's plane (i.e., to have small torsional values), with the result that the torsional values of head and gaze were approximately the same (Fig. 1B, top and second rows). Such behavior has been described before (Freedman and Sparks, 1997; Crawford et al., 1999) and was typical of all of our recording sessions.

The three-initial-target paradigm.

In a variant on the above paradigm, we used three widely spaced initial target positions, each with five secondary target positions in an arc centered at the initial target position that passed through the hot spot of the neuron. The three arcs were identically spaced relative to each initial target position. In other respects, this paradigm was identical to the previously described single-initial-target paradigm. This paradigm was designed to test for gain-field effects of eye position, to differentiate eye-centered from fixed-vector spatial models, and to test a model that predicted that neurons involved in the nonlinear reference frame transformation for saccades should show gain-field effects for position components orthogonal to the main axis of the receptive field (Smith and Crawford, 2005).

Movement kinematics through time.

Figure 2A shows a typical hot-spot response of one of our neurons (described below) and the associated horizontal gaze kinematics plotted against time (Fig. 2B–D). Data are temporally aligned at the onset of the gaze shift to the secondary target. Note that this was the only gaze shift analyzed in this study. During our quantitative analysis of these data, gaze shifts were selected when gaze velocity exceeded 50°/s; the end was selected when velocity declined to <30°/s and every trial was visually inspected. Trials associated with errors or multiple step gaze shifts were removed from further analysis. Figure 2, C and D, again emphasizes the variability of eye, head, and, to a lesser extent, gaze positions, both before and after this gaze shift (key to the analysis provided below). After this first gaze shift, the animal fixated the secondary target for a variable period, longer than the 105 ms time window [320.4 ± 32.9 ms (±SD) for the example shown]. At this point, the animal received a reward, and then produced a return movement that was approximately toward center but had variable directions and amplitudes.

Figure 2.

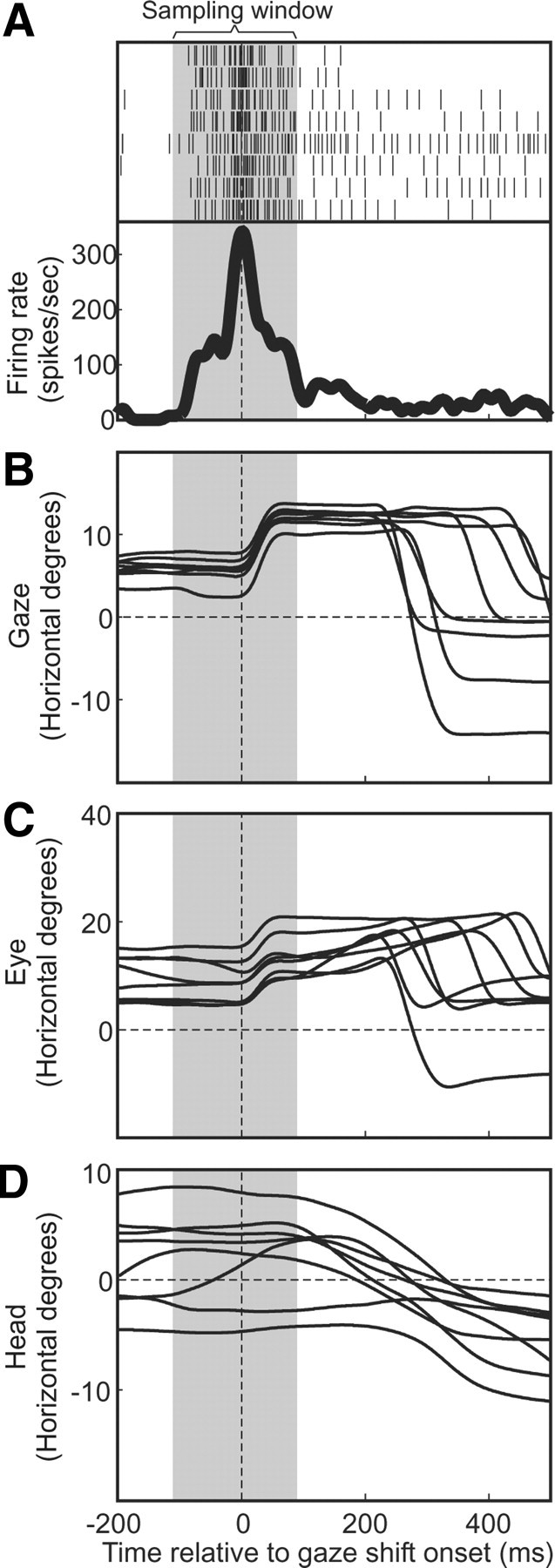
Typical “gaze saccade burst” and associated horizontal gaze, eye, and head positions, plotted as a function of time. Data from all eight trials to the neuron's optimal hot spot are aligned with gaze shift onset. A, The perisaccadic neural activity is plotted for all correct (rewarded) trials made to a single secondary-target position, the rasters (black vertical bars) for each trial plotted on each line, the average firing rate across these trials plotted below as a thick black curve. The sampling window (duration in which spikes were included in firing rate for each of these trials) is indicated by the vertical gray band. B–D, Horizontal gaze (eye-in-space) evolutions across the perisaccadic interval are plotted for each trial (B), as are eye (eye-in-head) position (C) and head position (D). Times in these panels are aligned by gaze shift onset (vertical dashed line).

Neural recordings and data inclusion criteria

Electrophysiology.

We recorded extracellular neural activity from the SC with commercially available tungsten microelectrodes (UEWLGGSMNN1E, FHC). A single electrode was backloaded into the guide tube, which was controlled by a hydraulic microdrive (MO-90S, Narishige International USA). We made one penetration per day into the intermediate and deep layers of the SC. The neural activity was amplified, filtered, and stored for off-line cluster separation applying principal component analysis with the Plexon MAP system. Neurons were randomly sampled from the SC such that once a neuron had a clear spiking activity, no attempt was made to preselect neurons for task-related responses. When gaze shift-related activity was identified, target stimulus positions were rapidly varied over the opposite visual hemifield to map out the spatial hot spot and the approximate extent of the neuron's receptive field. The stimulus locations for one of our two behavioral paradigms were then set to match this distribution, and recordings continued until the neuron could no longer be held. Since our paradigm did not allow the separation of visual and motor responses, we will henceforth refer to these as “visuomotor” neurons.

Figure 2A shows the typical bursting profile (aligned on gaze shift onset) for one neuron, showing eight trials toward the optimal target. As one can see, a robust burst was tightly linked to the onset of the first gaze shift to the secondary target, and there was only baseline activity for the return gaze shifts that followed. However, our data suggest that SC neuron responses are generally much longer and more idiosyncratic between neurons when the head is free to move than with head-fixed saccades, and there was no justification to exclude one part of the signal in favor of other parts in our data in our paradigm. Therefore, the duration of the sampling window used to quantify neural activity (Fig. 2, gray zone) was selected visually to cover the full duration of the “bursting” activity associated with the gaze shift. Overall, the selected windows typically started 50–100 ms before gaze onset and typically had durations of 200–300 ms.

Neuron inclusion criteria.

During the experiments, we recorded 203 isolated SC neurons from two animals (M1 = 127; M2 = 76), making head-unrestrained gaze shifts to visual targets from various initial starting positions (using both paradigms). The inclusion criteria were as follows: (1) off-line sorting (Plexon) of the isolated SC neuron had to remain isolated throughout the experiment; and (2) neural activity showed a temporal correlation to head-unrestrained gaze shifts made to stimuli at the secondary target positions (thus, we removed n = 105 neurons due to poor isolation and movement artifacts). Thus, we obtained clear data from a total of 98 neurons from two monkeys (M1 = 59; M2 = 39).

We then applied two further criteria: isolated SC neurons were required to pass the threshold of at least an 80% correct behavioral performance and have at least 4 gaze shifts to each visual target (the mean ± SD number of gaze shifts to each target was 9.3 ± 2.6), the maximum number of trials to one target being 20. The range of the number of correct gaze shifts analyzed in each neuron was 57–249, with the mean (±SD) being 131.1 ± 35.4. We also required a minimum firing rate of 50 spikes per second in the sampling window. (The number of targets for each fit across all neurons was as follows: mean ± SD 11.9 ± 2.1; minimum, 9; maximum, 15). These exclusion criteria left 63 neurons submitted for complete analysis using our newly published method (Keith et al., 2009). This comprised 32 neurons from the single-initial-target paradigm (mean number of gaze shifts ± SD, 107.5 ± 18.1) and 31 neurons from the three-initial-target paradigm (mean number of gaze shifts ± SD, 156.0 ± 31.9). Based on a combination of factors (stereotaxic coordinates of our depth of recordings, the visual responses that were encountered in more superficial recordings, electrical stimulation of the SC after recording sessions, and histological reconstructions), we estimate that 54% of these neurons were in the intermediate layers of the SC and 46% were within the deep layers.

Receptive field and reference frame analysis

Custom-designed programs written in Matlab 7.0 (Mathworks) were used to provide a 3-D analysis of the behavioral and neural data (Martinez-Trujillo et al., 2004; Constantin et al., 2009; Keith et al., 2009). We separately analyzed visual secondary-target position (T) and final gaze direction (G), which, as described above, were dissociated by the monkeys themselves (Fig. 1A). Both T and G were 2-D directional quantities defined initially in space (s) coordinates (i.e., in the coordinates of our eye coil system). These were then each transformed into three other frames: head (h), eye (e), or fixed vector (v). Transformation of T and G into eye and head coordinates was done using quaternion rotation (Martinez-Trujillo et al., 2004), whereas Tv/Gv was calculated from Ts/Gs as linear displacement relative to gaze in space coordinates (Keith et al., 2009). Note that e and v are both gaze centered, but not identical, and they only diverge for larger gaze shifts and position offsets (Hepp et al., 1993; Crawford and Guitton, 1997; Klier et al., 2001). Thus, in total, eight spatial representations were created (Ts, Th, Te, Tv, Gs, Gh, Ge, or Gv).

The fundamental goal of this article was to map the receptive field of each of our neurons in the spatial frame of each of these eight representations, and to see which one provided the best fit. It was shown in Keith et al. (2009) that the intrinsic reference frame of a neuron can be defined as the representation (i.e., Ts, Th, Te, Tv, Gs, Gh, Ge, or Gv) that provides the most coherent fit (i.e., the least variation in gaze-related activity for a given point in space). The amount of incoherence was quantified by the mean predictive sum-of-squares (PRESS) residual of the activity relative to the receptive field obtained with the best-fit kernel bandwidth (i.e., with the lowest PRESS), as described in detail previously (Keith et al., 2009).

To summarize the method: nonparametric fits of the neuron's firing rate (in our selected windows) were performed as a function of the 2-D position values of all trials using 2-D Gaussian kernels in each of the spatial representations described above. We used kernel bandwidths between 2° and 15° in 1° steps. (Note a kernel bandwidth of X° does not mean that the model is restricted to fitting separate X° patches, e.g., a 2° kernel bandwidth provides contours that spread well beyond ±4°.) The PRESS residual for each trial was obtained by fitting the data but excluding this trial, and then taking the residual between the fitted firing rate at the position value of that trial and the trials actual firing rate. The mean PRESS for a given kernel bandwidth and representation was the mean of the absolute values of these residuals. The best-fit bandwidth was that which produced the lowest mean PRESS across all bandwidths and representations. The best-fit representation produced the lowest mean PRESS. The spatial coherence of the data in the best-fit representation was then compared with those of the other representations for the same best-fit bandwidth. Because spatial coherence corresponded (inversely) with the spread of PRESS residuals (i.e., mean PRESS) a two-tailed Brown–Forsythe test was used to compare the best-fit representation with each of the other representations. (This test does not require normal distributions.) The Brown–Forsythe test was simply a t test in which the values being compared across representations were the absolute value difference between each PRESS residual and the median of PRESS residuals for each representation. A two-tailed test was used since the best-fit representation was not selected a priori. Each non-best-fit representation, which, when compared with the best-fit representation showed significantly greater spread of PRESS residuals (p < 0.05), could then be excluded as the intrinsic representation (sensory/motor position + reference frame) for the neuron.

To our knowledge, there is no alternative method in the neurophysiology literature that quantitatively identifies the intrinsic reference frame of neurons using continuous distributions of gaze and target position. For example, the covariance method used by Avillac et al. (2005) requires regularly spaced gaze and target positions. However, in this more restricted situation, our PRESS method produces exactly the same results as the covariance technique when our gain-field correction method is incorporated (Keith et al., 2009).

Additional analysis in the three-initial-target paradigm

Gain fields.

Our three-initial-target paradigm was designed to test whether the SC shows gaze position gain fields (Andersen and Mountcastle, 1983; Ben Hamed et al., 2002; Bremmer et al., 2002; Nagy and Corneil, 2010) orthogonal to the visuomotor tuning of its cells (Smith and Crawford, 2005). Since these target positions were set in a line in space (laboratory) frame (see Fig. 6A, squares), gain-field effects were examined only in one dimension, along a vector pointing between these initial target positions. Only first-order gain-field effects (i.e., linear gain fields) were examined (Andersen et al., 1985; Boussaoud and Bremmer, 1999). Here, we wanted to both identify and suppress gain-field effects for our reference frame analysis (e.g., when plotted in gaze-centered frames these three subsets would basically overlap, and gain modulation would be seen as noise that would bias against this fit). We eliminated such biases (for any frame) by removing significant linear gain-field effects as follows.

Figure 6.

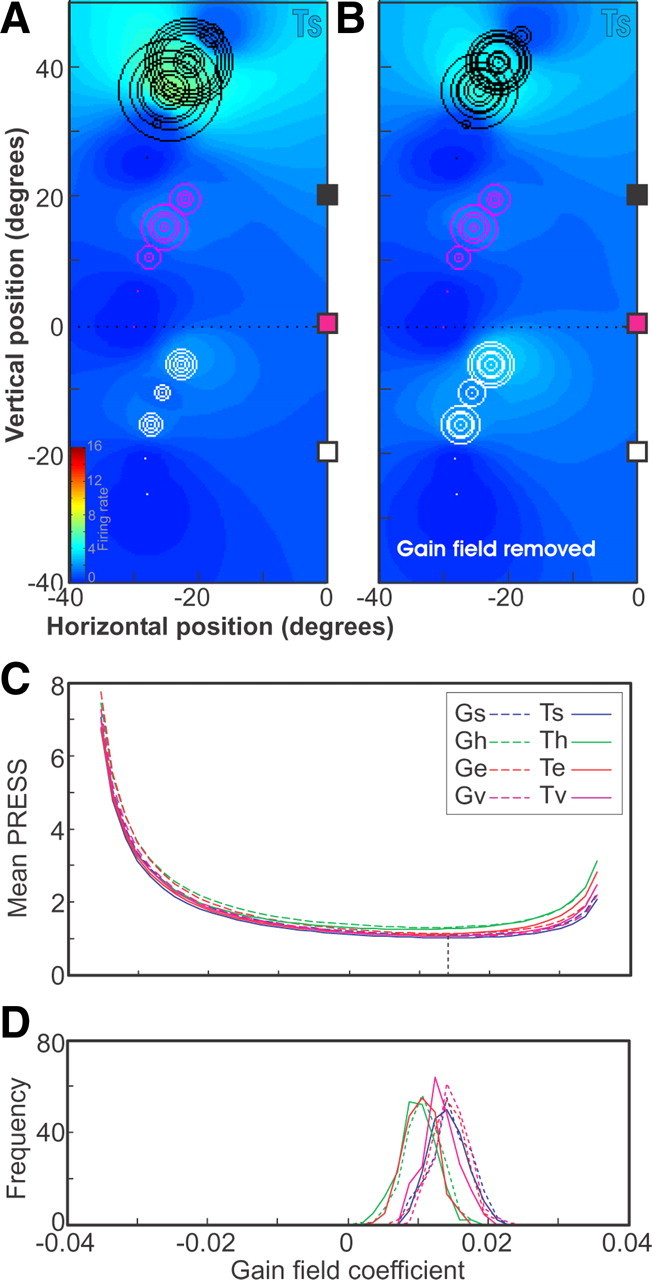
Gain-field statistics and removal. A, Mean PRESS values for the fits of G and T positions in s, h, e, and v frames for a range of linear gain-field coefficient values. The best-fit value, corresponding to the smallest mean PRESS, is indicated by the vertical dashed line. B, Histograms of best-fit linear gain-field coefficients for each position and reference frame for 200 random 80% subsets of trials. C, Fits of data plotted in terms of saccade-target position in Ts, where each trial is represented by a circle whose diameter is proportional to the number of spikes in the sampling window for the trial. Trials associated with the three different home-target positions (colored □) are plotted in different colors. D, Fits of the data for target in space frame where the gain-field factors have been divided out from the activity of each trial.

If F was the measured firing rate for a trial having initial eye position x along the direction vector connecting the three initial target positions, we represented this as a function of a firing rate without the gain field F*:

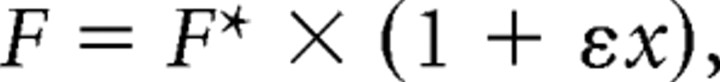where ε was the linear gain-field coefficient. The pregain firing rate F* then was as follows:

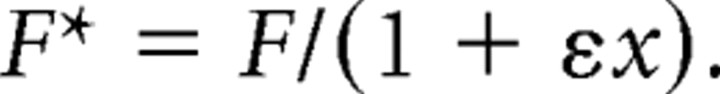We chose a range of linear gain-field coefficients, ε, to lie within the range of ±0.95/max(x), where max(x) was the maximum absolute value of position values across the set of trials for the neuron. This range prevented the inferred pregain firing rate F* from becoming negative. Intervals of coefficient values were chosen such that there were a total of 21 ε values. The gain-field coefficient chosen was the value for which the best-fit mean PRESS residual was smallest across all representations. This is illustrated in the Results (see Fig. 6).

Nonoverlapping distributions of secondary target positions.

As already stated, the data (secondary target or final gaze position) for the subsets of data associated with the three initial target positions more or less fully overlapped when plotted in eye frame, partially overlapped in head frame, and entirely separate in space frame (see Fig. 6A). This meant that the three subsets would be fitted independently in space frame and somewhat independently in head frame, and this independence produced a bias artificially increasing the coherence in space frame relative to head frame, head frame relative to eye frame. To avoid the effects of this bias when comparing coherence, we replaced the PRESS in space and head frames with the maximum PRESS produced in intermediate frames on the continuum connecting each frame with eye frame. This maximum PRESS provided a conservative minimum estimate for the unbiased PRESS residual of space and head frame.

Combining data from different neurons

Since the neurons in our population had widely varying receptive field sizes, they were best fitted at different kernel bandwidths. We combined the data from the different neurons in the following manner. For each neuron, the PRESS residuals obtained relative to fits obtained using the best-fit kernel bandwidth in each candidate reference frame were normalized relative to a common reference frame (we arbitrarily used target-in-eye frame, Te), whose mean PRESS residual was set to 1.0. Thus, the relative goodness of fit of the different candidate frames was preserved for each neuron by the relative mean PRESS values of these frames.

Although some neurons had more trials associated with them (depending on how many trials had to be eliminated from failure to meet the fixation and saccade requirements), we ensured that all neurons were given equal weight in the overall population evaluation of reference frame coherences. To do this, we combined the mean PRESS values from all neurons, each as single data points, and then performed a t test between the reference frame with the lowest population mean PRESS (i.e., lowest mean of neuron mean PRESS values) and each of the other reference frames in turn. Because this lowest-mean mean-PRESS frame was not determined a priori, we used a two-tailed t test in this comparisons.

Reference frame continuum analysis

The analysis described above, in which neural populations were tested relative to canonical representations, does not account for the following possibilities: (1) the data cluster into different groups along some dimension that we did not consider; and (2) the overall best fit is actually intermediate between some of these canonical frames (Pesaran et al., 2006; Blohm et al., 2009). These possibilities were addressed through the use of an “intermediate reference frame analysis.” For this, we performed fits and generated PRESS residuals for data plotted in intermediate frames that lay at regular intervals along continuums between (and beyond) each pair of the canonical reference frames, and kept the G and T representations separate. We then plotted the individual fits and compared the mean PRESS residuals for the combined population of 63 neurons along all such continua. The geometric and algebraic details of this use of intermediate reference frames is given in Keith et al. (2009).

Results

Receptive field mapping

The single-initial-target paradigm was used to map the receptive fields of SC neurons in terms of their gaze shift-related activity. As described in the Materials and Methods, the use of wide tolerance windows allowed monkeys to produce spreads of final gaze directions that often differed significantly from the visual secondary target positions (Fig. 1A), allowing our analysis to differentiate T and G representations. Also, the natural variation in initial head and gaze (Fig. 1B) allowed for differentiation among space, head, and eye reference frames. Figure 2 shows a typical saccade-related burst associated with gaze shifts to its optimal hot spot target, and the timing of the associated variable, natural distribution of gaze and head kinematics.

Figure 3 shows a complete receptive field/reference frame analysis for the neuron that was recorded during the same behavioral measurements shown in Figure 1. Each panel of Figure 3A plots the neuron's receptive field “fits” in one of our eight different spatial representations: the top row shows fits to secondary visual target position in four frames (Ts, Th, Te, and Tv); and the bottom row shows the equivalent fits to final gaze position after movements toward the target (Gs, Gh, Ge, and Gv). The inset in the top left panel shows the neural firing profile for all trials made to the hot spot target position in space coordinates. The activity is aligned to gaze shift onset (upward-pointing arrow), and the sampling window lies between the two vertical lines.

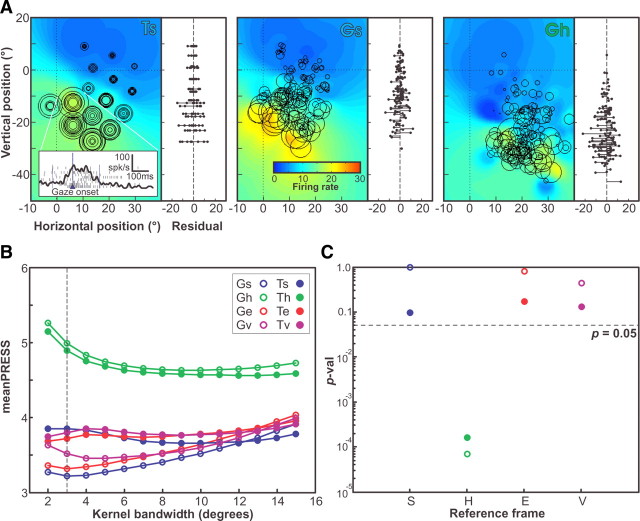
Figure 3.

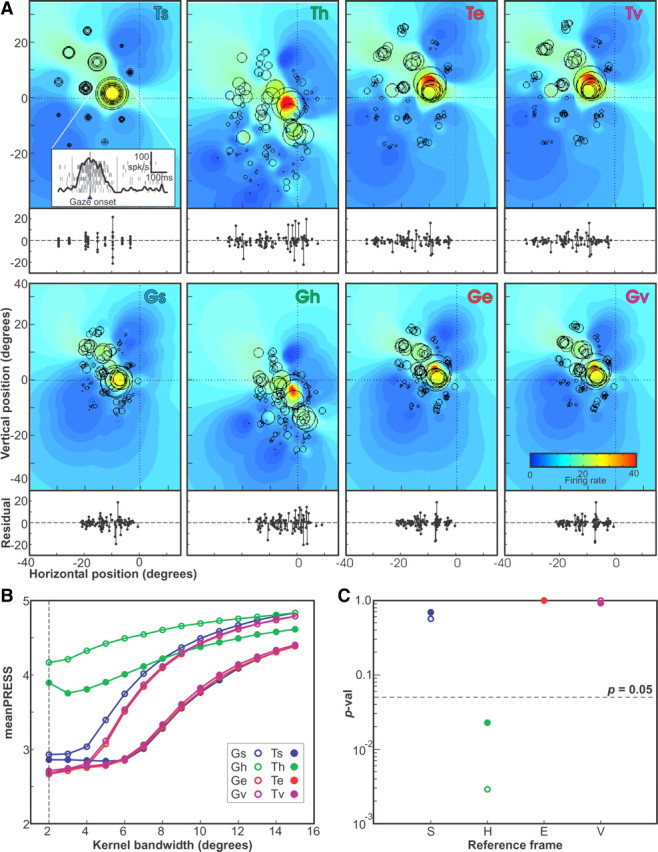
Receptive field analysis—example neuron 1 (104 trials). A, The activity of all trials for the example neuron are plotted using G or T positions in s, h, e, and v reference frames. Also shown are the receptive field fits obtained using the best-fit kernel bandwidth, as indicated by the colored field. Below each receptive field is a plot of the residual firing rates of the trails plotted as a function of horizontal position in each representation (final gaze or target position × reference frame). B, The mean PRESS values for the fits in the eight representations (two position values × four reference frames) for kernel bandwidths from 2° to 15° in 1° steps. The bandwidth that produced the overall best fit (smallest mean PRESS) is indicated by the vertical dashed line. C, The p values of the two-tailed Brown–Forsythe tests comparing the representation of best fit (target in eye) PRESS values obtained using the best-fit kernel bandwidth (2°) with the values in each of the eight representations in turn.

The color-coded field in each panel of Figure 3A is the fitted receptive field obtained from the best-fit kernel bandwidth (in this case, 2°) (Fig. 3B, dashed vertical line). Each panel also shows the actual activity (number of spikes in the sampling window) of each trial, represented by a black circle (○) whose size is proportional to activity, placed at the appropriate location for each spatial quantity (T or G) and reference frame (s, h, e, or v). This is a representative example of an SC visuomotor neuron with a closed RF, since, in all of the representations shown, the hot spot of the receptive field is bound on all sides by gaze shifts to targets with lower activation (Munoz and Wurtz, 1995; Marino et al., 2008).

These individual data points in Figure 3 (○) overlap in Ts coordinates (top left) because this represents the actual location of the targets in space. However, the size of these circles (neural activity) is quite variable for each position, suggesting that this may not be the most coherent receptive field map. In contrast, these data points are more spread apart in Gs because of the monkeys naturally variable gaze shifts, and they further spread apart in variable ways in the remaining panels because of variations in the monkey's initial gaze and head orientations (including torsional variability). However, it is hard to tell which plot is most coherent from this view.

To provide a more clear measure of coherence, we have provided the residuals of firing rates for individual trials below each colored receptive field in Figure 3A, plotted along the same horizontal scale. The provided stem plots represent the signed difference between the actual firing rate of the neuron for each trial, minus the predicted firing rate for the same 2-D point derived from our fit to that presentation. One trend is visually evident; the residuals increase (i.e., fit coherence gets worse) when data are transformed into head coordinates (Th and Gh) but then decrease when the data are transformed into eye centered coordinates (Te and Ge).

This result is more quantitatively reproduced in the mean PRESS residual plots for the fits obtained in all representations across all kernel bandwidths (2° to 15°) shown in Figure 3B. The best fits (smallest mean PRESS) occurred at a kernel bandwidth 2°. The absolute lowest residual (best fit) for this neuron occurred for the Te but fits were nearly as well for Ge, Tv, and Gv. The results of the two-tailed Brown–Forsythe test comparing the PRESS residuals in Te with all representations are shown in Figure 3C. For this particular neuron, only the head frame representations (Th and Gh) could be ruled out as candidates for the intrinsic reference frame of this neuron, as the mean PRESS for both of these representations was significantly greater (p < 0.05, two-tailed) than the representation of best fit (Te). The fact that qualitatively comparing the Te with the Th and Gh in terms of the spread of the residual plots of Figure 3A yields only a barely distinguishably larger spread in the head-frame representations demonstrates the superiority of this quantitative statistical method.

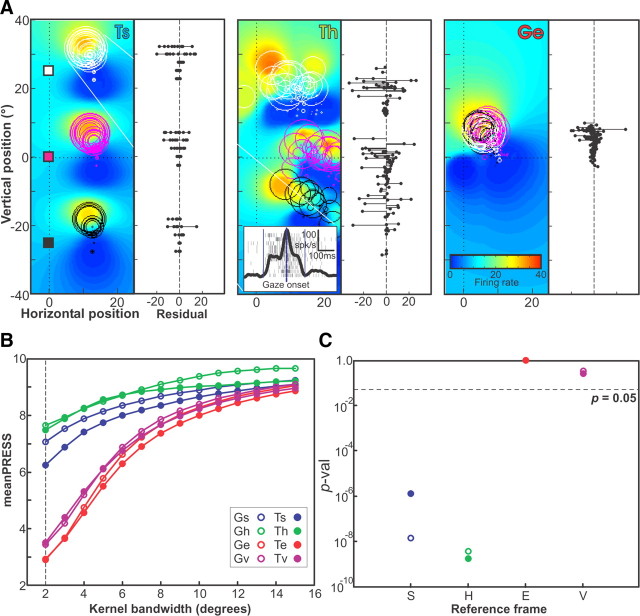
Figure 4 illustrates another representative neuron (an open RF), this time only plotting the RF data in the laboratory-referencing Ts representation and in the representations of best and worst fit. In this case, Gs provided the best fit, and Gh the worst. Note that in this figure, residuals are plotted along the side of the RF plots as a function of the same vertical scale. This neuron's best fit was in the Gs representation at a kernel bandwidth of 3°, where the Gs curve (blue open circles) has the lowest mean PRESS value at its minimum in Figure 4B. This neuron had no clear hot spot and was classified as an open RF (Munoz and Wurtz, 1995). The greater coherence in the Gs representation (Fig. 4A, middle) relative to Ts (Fig. 4A, left) and Gh (Fig. 4A, right) can be seen through the hotter colors in the lower region of the RF and a noticeably reduced spread in the residual plot. The best-fit Gs representation for this neuron showed significantly lower PRESS values (Fig. 4B) than the head-fixed representations (p < 0.001) (Fig. 4C), but for other representations the difference was sometimes marginal and never significant.

Figure 4.

Receptive field analysis—example neuron 2 (136 trials). A, The trial activities, represented as described in Figure 3, plotted in terms of target in space (laboratory) frame and in terms of Te, the representation of best fit. For each is shown the fitted receptive field obtained with the kernel bandwidth of best fit (2°), also as in Figure 3. Inset shows the rasters of all trials made to one saccade-target position, along with an integrated firing rate. Beside each receptive field is plotted the residual firing rates for all trials plotted as a function of vertical position in each representation. B, The mean PRESS values for fits obtained at kernel bandwidths of 2–15° in all eight representations (two positions × four reference frames), as in Figure 3. C, The p values of the Brown–Forsythe tests comparing the PRESS values of the representation of best fit with all eight representations.

As these examples illustrate, some reference frame fits could be excluded as candidates for intrinsic reference frame for some individual neurons. But note that the two examples shown are a representative selection from the population (for reasons that will become apparent below) but not necessarily a typical one. Most individual neurons did not show significant results for any particular reference frame. This may be limited by the number of trials we were able to collect while confidently holding the same neuron (which is a significant factor in head-unrestrained monkeys) or by the obtained distributions of initial positions. However, it has been argued that the reference frames of individual neurons are not particularly meaningful (Blohm et al., 2009), but rather it is the distribution of spatial coding in a population of neurons that is more important for understanding the transformations performed by that structure.

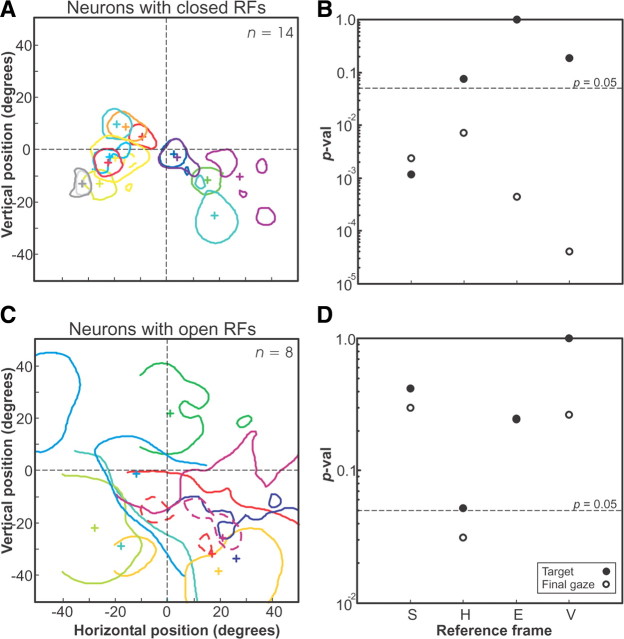
As a first step toward such a population analysis, we tested whether closed and open RF neurons showed significantly different reference frame coding schemes, or whether they could be treated as a single population for the sake of this analysis (Fig. 5). Only neurons with clear hot spots of activity were included in this analysis, where the hot spot was defined as activation of >50% of the maximum RF activation. Figure 5A illustrates the outlines of these receptive field hot spots for neurons that had closed RFs (n = 14), whereas Figure 5C shows the same for neurons with open RFs (n = 8). We then performed Brown–Forsythe tests between the best-fit and other representations for these two neuron subsets. For closed RF neurons (Fig. 5B), the best-fit representation was Te, and all representations other than Th and Tv had significantly larger PRESSs at the p = 0.05 level (two tailed) and could be excluded as intrinsic reference frame candidates. For the open RF neurons (Fig. 5D), the best fit was for Tv (fixed vector relative to initial gaze), and again the T fits were generally better than those for G. However, the statistical resolution here was poorer, and only one representation (Gh) could be excluded (p < 0.05). It is possible that there is a real difference between these populations that would show up in a much larger sample size. However, since we could not discriminate the best fit for the closed RF population (Te) or the open RF population (Tv) from each other in either of these separate analyses, we treated these populations together in our subsequent analyses.

Figure 5.

Hot spots of neurons with closed and open receptive fields. A, Closed receptive-field neuron hot spots for fits of target position in eye frame, along with the center of mass of each hot spot (+). Here, hot spots were defined as regions of >50% of maximum fit firing rate. Only those neurons having a hot spot are plotted (22 of 32 neurons). B, p values comparing the best-fit frame (Te) with each other frame for the population of neurons from A. C, Open receptive-field neuron hot spots (“holes” in these hot spots are indicated by dashed lines). D, The p values comparing the best-fit frame (Tv) for the population of neurons from C.

Gain-field analysis in the three-initial-position data

Before repeating our reference frame analysis for the three-initial-position dataset, we established (1) whether these data showed gaze position gain-field effects and (2) then suppress these effects. When an artificial network trained to convert a Te signal (likely to arise from visual inputs) into a 3-D Gv vector (a likely candidate to drive 3-D eye movements), some of its “hidden units” developed gaze position gain fields that were approximately orthogonal to the visuomotor tuning direction of the cell (Smith and Crawford, 2005). This is a geometric necessity to compensate for the nonlinear eye position dependencies of retinal projection (Crawford et al., 1997; Klier et al., 2001). Part of the motivation for our three-initial-positions paradigm was to see whether such signals emerge at the level of the SC.

As illustrated in Figure 6A, some of our neurons did show this effect. This figure plots the color-coded receptive field and individual trial responses in Ts coordinates, using the same conventions developed in Figures 3 and 4. Again, firing rates for individual trials are indicated by circles (white, magenta, and black circles) plotted at target locations in space. Typical for this paradigm, these targets were arrayed as equidistant arcs of several secondary target directions, and gaze shifts originated from three different initial target positions (corresponding white, red, and black squares). Note that there is directional modulation within the arcs (the lower targets give little or no response), but overall there was a much more robust response for the same directions (i.e., the black circles in the upper arc are largest) in saccades initiated from the upper target (black square), compared with the other saccades. This is a classic “gain-field effect.”

Figure 6, C and D, also illustrates the method that we used to establish whether gain fields were statistically significant, using this one neuron as an example. We first determined the best fit for gain-field coefficients (linear gain as a function of eye position along the three-initial-target line) in all representations (Fig. 6C, vertical dashed line). For this example neuron, the best-fit gain-field coefficient was 0.014. We then generated the 95% confidence interval (CI) for the best-fit gain-field coefficient by bootstrapping using 200 randomly chosen random samples of trials selected from the data with replacement Figure 6D. If the confidence interval for the best-fit gain-field coefficients did not include zero, then the gain field was considered to be significant. Applying this method to all of the 31 neurons tested in this way, 7 (23%) showed statistically significant gain-field effects (p < 0.05) along the axis of the three initial target positions, confirming that at least some neurons in the SC do possess such signals.

In those neurons that showed significant gain-field effects, we suppressed this effect by dividing out the gain-field coefficient from the pregain firing rates to obtain the corrected rates, F*. The result for our example neuron is shown in Figure 6D. This allowed us to proceed with our reference frame analysis without any bias arising from gain fields.

Reference frame analysis in the three-initial-position data

Having suppressed any gain effects from our three-initial-position dataset, we then applied the same reference frame analysis to these data as that described above for our other dataset. An example reference frame analysis for a neuron for which partial receptive field mapping was performed using the three-initial-target paradigm is shown in Figure 7. This neuron did not show a significant linear gain field across the three-initial-target positions. Figure 7A shows the receptive fields of the data plotted in Ts, Th (worst fit), and Ge (best fit) representations. As observed in Materials and Methods, in space coordinates (Fig. 7A, left) the trials for each initial-target position (colored circles and squares) were completely separated. In head coordinates (Fig. 7A, middle) there is some overlap, and in eye coordinates (Fig. 7A, right) there is complete overlap. Note the clear reduction in the residual distribution for the Ge panel. Quantitatively, the best fit for this neuron was obtained in the Ge representation (Fig. 7B) at a kernel bandwidth of 2°. Both space and head frame representations had significantly larger PRESS (p < 10⁻⁵) and therefore could be excluded as intrinsic reference frame candidates for this neuron. But note again that this is just one representative example; as with our first dataset, many of the individual neurons tested with the three-initial-position paradigm did not show a significant separation between frames of reference. We will describe the overall population fits for both of our datasets in the next section.

Figure 7.

Determination of intrinsic reference frame for example neuron with three widely spaced home-target positions (164 trials). A, Trial activity plotted in terms of saccade-target position in Ts, Th, and Ge, using the same conventions as in Figure 2. Fits of these data representations (colored fields) were made using the kernel bandwidth of best fit (2°). Shown in the inset are the rasters for all trials made to one saccade-target position, along with the integrated firing rate. Shown to the right of each receptive field are the residual PRESS values obtained for all eight representations (two positions × four reference frames) for each representation. B, The mean PRESS values obtained for all eight representations (two positions × four reference frames) for kernel bandwidths from 2° to 15°. C, The p values of the two-tailed Brown–Forsythe test comparing the PRESS residuals of the representation of best fit (Te) with each of the eight representations in turn, using the best-fit kernel bandwidth. Note that the best fit was obtained in Ge despite the fact that the trials were more closely packed in this representation than in either Ts or Th.

Summary of population data from both paradigms

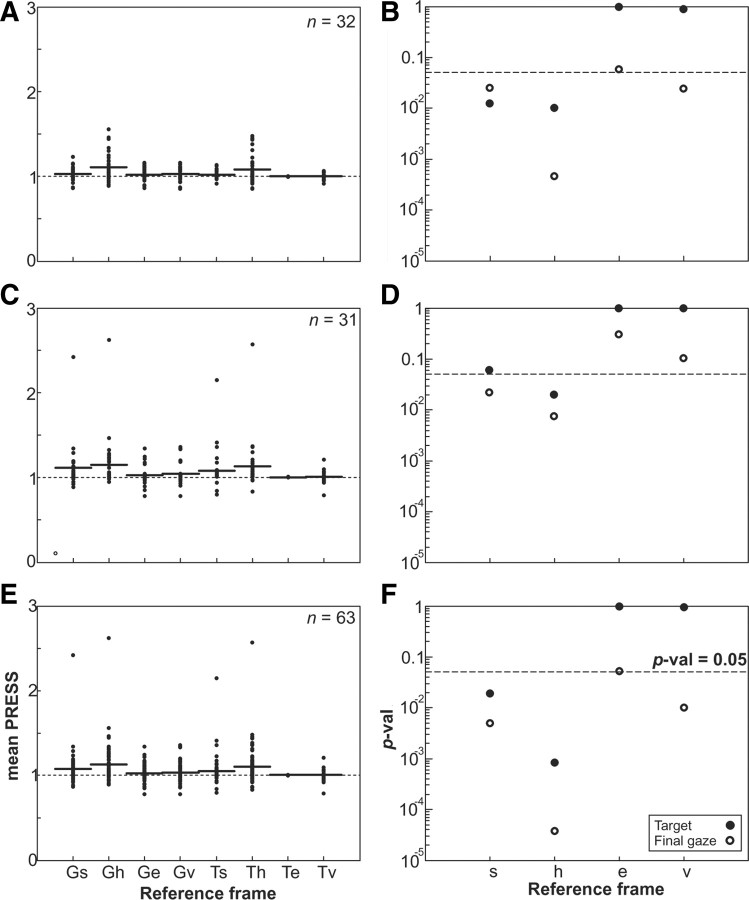
Figure 8A (left column) plots the mean root mean square (RMS) PRESS values for each individual neuron with the mean PRESS at each reference frame (Gs, Gh, Ge, Gv, Ts, Th, Te, and Tv) indicated by a horizontal line for the best-fit kernel bandwidth for each representation. The PRESS values were normalized relative to the spatial representation that provided the best fit. This shows the variability between neurons. The right column shows the population p values for the PRESS residuals for each representation relative to the spatial representation of best fit, as in Figure 5. Figure 8, A and B, quantifies all 32 neurons from the single-intial-target paradigm, including both the closed and open RF neurons illustrated in Figure 5 as well as other neurons with unclassified RF types. In this population, Te provided the best fit, although it was only slightly better than Tv. However, Te provided a significantly better fit compared with every other representation (except Ge, which was marginally nonsignificant: p = 0.058).

Figure 8.

Neuron population RMS PRESS and p values for neuron populations in different representations. A, C, E, RMS PRESS values are shown for all 8 representations (G and T × s, h, e, and v frames), normalized relative to target-in-eye representation values for 32 neurons whose receptive fields were mapped (A), 31 neurons with three widely spaced home-target positions (C), and the combined population of 63 neurons (E). For the neurons with three widely spaced home-target positions, the replacement PRESS values were used for space and head frames, described in the Materials and Methods and Appendix (supplemental material). B, D, F, The p values of a two-tailed t test comparing the PRESS residuals in each frame relative to the best-fit frame, which was target in eye frame are plotted for the receptive field-mapped neurons (B), the three home-target position neurons (D), and the combined population neurons (F).

The qualitative pattern (i.e., the relative ranking of the fits) was very similar for the 31 neurons from the three-initial-position paradigm (Fig. 8C,D). Again, Te provided the best overall fit but was not significantly better than the other gaze-centered (Tv/Ge/Gv) representations. Te provided a significantly better fit than the other head and space representations (Gs, Th, and Gh), except Ts, where the difference was marginally nonsignificant (p = 0.061).

Since the pattern of results for our two experimental populations (Fig. 8B,D) were very similar, we combined them for a grand total of 63 neurons (Fig. 8E,F). Not surprisingly, Te was again the best-fit representation for the combined population, with the other gaze-centered target representation (Tv) nearly indistinguishable. In this case, every other representation could be excluded (except perhaps Ge, which approached significance: p = 0.053). Thus, our analysis narrows the overall preference of the entire population to two candidates for the intrinsic reference frame (Te and Tv), and excludes all of the remaining representations of space (Ts, Gs), head (Th, Gh), and fixed vector (Gv).

Model fits to SC activity before versus after gaze saccade onset

In the previous analysis culminating in Figure 8F, we fit models to SC activity recorded over the entire perisaccadic burst (Fig. 2A). This raises the possibility that these data may have been contaminated by sensory and motor feedback signals during the gaze shift, and thus may not be “pure” SC signals. For example, eye and head position signals can alter visuomotor responses (Snyder et al., 1998; Xu et al., 2011) as fast as ∼60 ms after an eye movement (Xu et al., 2011). To address this issue, we separated all of our data trials in all cells into a pre-saccade onset burst (Fig. 2A, gray zone left of vertical blue dashed line) and a post-saccade onset burst (Fig. 2A, gray zone right of vertical blue dashed line). After subdividing these two datasets, we repeated the population analysis described in previous sections.

The results of this analysis are shown in Figure 9A (population analysis for data before gaze saccade onset) and B (population analysis for data after gaze onset). As in our previous results, in each of the new datasets the targets relative to eye representations (Te, Tv) remained the best fit and were statistically indistinguishable from each other. Target representation fits (T) were always superior to motor (G) fits. Again, the overall best eye-centered representation provided a statistically better fit than the space (Ts, Gs) and head frame (Th, Gh) representations (p < 0.05) in both datasets. Some minor jostling of the patterns occurred, and the level of significance is slightly reduced overall (e.g., Gv was no longer a significantly worse fit in Fig. 9A,B), but this is expected since we cut the total amount of data by approximately one half in each case. However, the overall pattern observed in the previous analysis of the complete burst (Fig. 8F) was retained in each of these new subsets. Moreover, there was no significant difference between these two (pre- and post-saccade onset) fit distributions. Most importantly, there was no significant change in the representation of best fit between pre-saccade onset activity, post-saccade onset activity, and the full burst. These results suggest that (1) the pattern we observed in the complete dataset (Fig. 8F) did not result from movement-related feedback signals, and (2) the presaccadic coding scheme was retained during the saccade.

Figure 9.

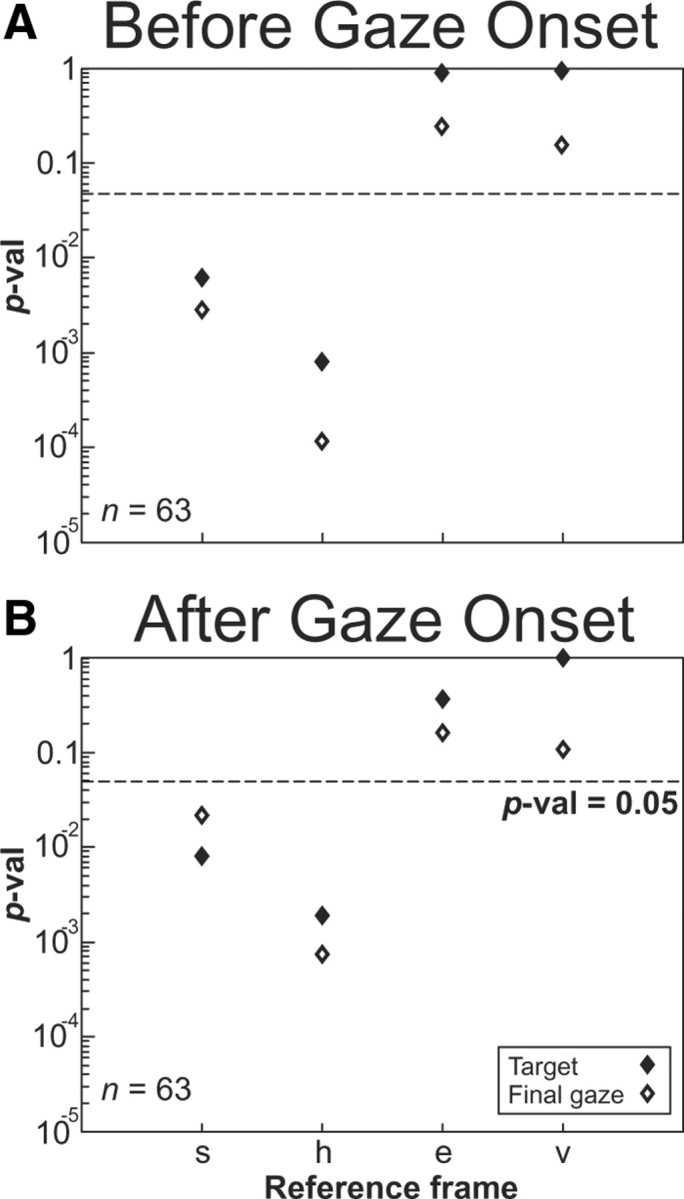
A, B, Analysis of full population of neurons showing two time windows of before gaze onset (A) and after gaze onset (B) with p values in each reference frame representations. The p values of a two-tailed t test comparing the PRESS residuals in each frame relative to the best-fit frame for the entire population of neurons before gaze onset (A) and after gaze onset (B). All conventions are the same as in Figure 8 except that the diamond symbols illustrate that the data were separated aligned either before or after gaze onset for target (closed symbols) and final gaze position (open symbols).

Intermediate reference frame analysis

Here we address the possibility that the best fits for our units may have been distributed along a continuum or continua of reference frames, rather than clustering about one or more cardinal frames. For this analysis, we kept the final-gaze (G) and secondary-target (T) representations separate (Fig. 10A,B), and focused on their frames of reference. As stated in the Materials and Methods, we only considered frames that lay along continuums between each pair of canonical reference frames. These intermediate frames were produced by scaling a fraction of the transformation that connected any two reference frames and extending beyond each of the reference frames [the algebra of this was given in Keith et al. (2009)]. We then compared the mean PRESS residuals for the combined population of 63 neurons along all such continua.

Figure 10.

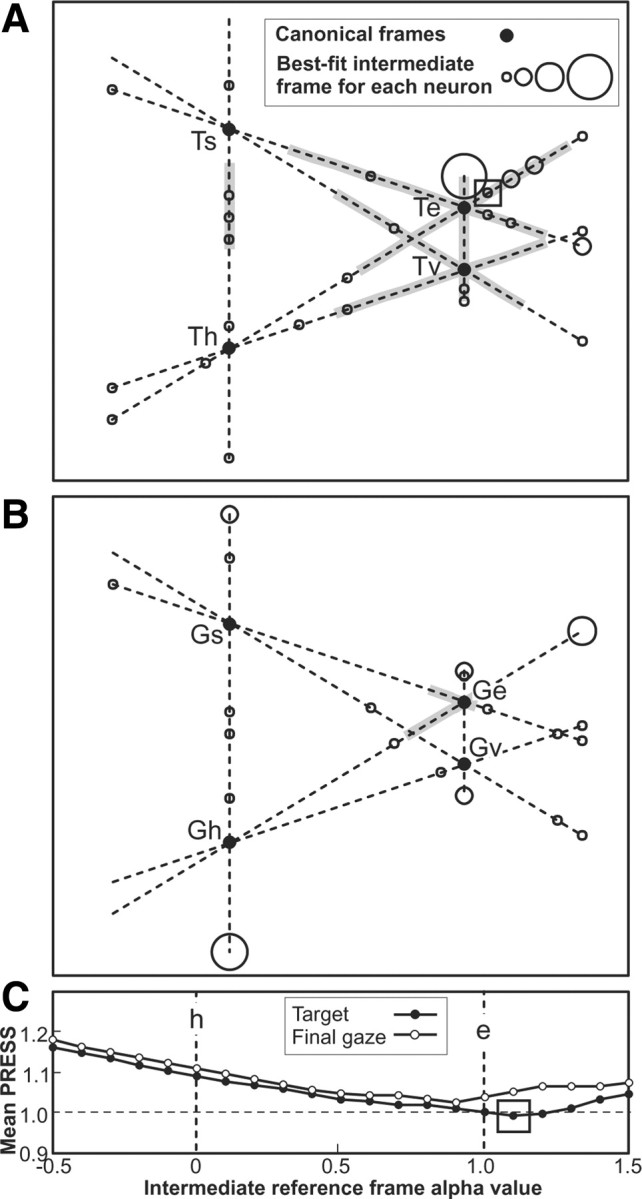
Best-fit intermediate reference frames for 63 neurons. A, The population mean PRESS values of best fits for all 63 neurons combined, for target and final gaze positions plotted in the intermediate reference frames at α intervals of 0.1 on the continuum between head and eye frames. The overall best-fit intermediate frame across all continua is indicated (□). B, C, For individual neurons, the best-fit intermediate reference frames are plotted in B if the best fit occurs for target-position intermediate frame, and in C if it occurs for final-gaze intermediate frame, from across all continuums between the four canonical reference frames: s, h, e, and v. Each neuron's best-fit intermediate frame is indicated by ○, a larger diameter circle indicating more than one neuron at the same frame. Overall best-fit for neuron population, as in A, is indicated (□). Confidence intervals along the continua correspond to intermediate frames that could not be excluded as the best fit (did not have a significantly greater PRESS than the best-fit frame at the p = 0.05 level), and are indicated by the gray zones.

In agreement with the results described above, we found that the overall best intermediate representation was Te. This overall best-fit representation is indicated by the box in Figure 10C, which shows the population mean PRESS along the example continuum from T (●) and G (○) between head and eye frames (h and e). The population mean PRESSs (data not shown) were somewhat higher along the other continua illustrated in the remainder of Figure 10.

Figure 10A documents the best fits for all individual neurons in an abstract space using lines to represent the continua between each of our canonical representations according to the scale from Figure 10C. The locations and distances between the canonical representations were approximately proportional to the mean shift in position for actual data points. Figure 10A plots neurons (○) that fit best for a T representation, whereas Figure 10B plots neurons (fewer in number) that showed a best fit for the G representation. In cases where neuron fits overlap, the diameter of the circle (○) indicates the number of neurons with that best-fit intermediate representation. The population best-fit intermediate representation was along the Te, also indicated in Figure 10A (□). As can be seen, the neuron best-fit representations were evenly distributed across much of each continuum, although they tended to cluster near Te/Ge and Tv/Gv canonical representations.

A 95% confidence interval was constructed along each continuum (Fig. 10A, indicated in gray; in some continuums there was no such interval), where the interval was defined as the intermediate representations for which the mean PRESS of the neuron population was not significantly greater (i.e., p > 0.05) than that obtained at the overall best-fit continuum (Fig. 10A, □). Note that only the canonical representations Te and Tv lie well within these 95% CIs, and Ge just lies at the border of the range, reproducing the results of the p values of Figure 8F in a schematic way. Note also that the confidence interval includes several intermediate representations between Ts and Th in Figure 10A. Although this does not statistically exclude the possibility that Tv is preferred or that the difference between units is meaningful, visual inspection of the plots suggests a distribution centered close to Te in Figure 10A, and to a lesser extent Ge in Figure 10B. We will return to the interpretation of these results in a broader context in the Discussion.

Discussion

Our primary aim was to determine the intrinsic reference frame of saccade-related activity in SC neurons. Using a combination of head-unrestrained 3-D recordings and a new analytic technique (Keith et al., 2009), we showed that, although individual SC neurons showed various intermediate reference frames, at the population level our sample of 63 neurons represented visual targets in a gaze-centered (either Te or Tv) reference frame, both before and during the gaze saccade. A secondary aim was to test whether these neurons showed gaze-position gain fields in the dimension orthogonal to their visuomotor tuning direction; we found that 23% of the neurons tested did show this effect. These results suggest that burst SC primarily uses a very early visual code (target relative to gaze) during direct, head-unrestrained gaze saccades, but these neurons also show multiplexed signals that could be early signs of a 3-D visuomotor transformation.

SC receptive fields during head-free gaze shifts

Freedman et al. (1997) used standard 2-D mapping to characterize SC RFs during head-unrestrained gaze shifts, but their focus was on a different question (gaze vs eye and head coding). Our analysis confirmed the existence of contralateral closed and open RFs of various shapes (Fig. 5) (Munoz and Wurtz, 1995; Marino et al., 2008). Typically, we found that a bandwidth of 2–3° was optimal to fit the contours of these ranges. Moreover, our examples (Figs. 3, 4, 6, 7) show variations in 3-D eye and head orientation (including torsion) blur RFs when they are plotted in the wrong frame. To our knowledge, no single-unit recording study, ever, has calculated the location of targets in rotating frames using the correct 3-D geometry: previous studies used linear approximations that distort in the head-free range (Crawford and Guitton, 1997; Klier and Crawford, 1998; Henriques and Crawford, 2001; Blohm et al., 2008).

Target versus gaze movement coding

The SC is involved in saccades and gaze control (Mays and Sparks, 1980b; Hepp et al., 1993; Tweed et al., 1998; Choi and Guitton, 2009), but it could either encode gaze kinematics (Sparks and Mays, 1980) or target information (Klier et al., 2001). Investigations of saccade dynamics during SC stimulation and recordings have suggested that the SC does influence velocity (Waitzman et al., 1991; Guitton, 1992; Van Opstal et al., 1995; Munoz et al., 1996). Head-restrained studies that dissociated target location from gaze kinematics by varying initial eye position (Sparks and Mays, 1980) or perturbing eye muscles have suggested that SC neurons correlate best to the former, rather than the latter. However, it has often been argued that “freeing” the head reveals a more natural spatial coding in areas like the SC (Guitton, 1992; Paré and Munoz, 2001; Klier et al., 2003; Choi and Guitton, 2009). Nevertheless, the current study also suggests that the saccade-related burst in SC activity primarily encodes visual target direction during head-unrestrained gaze shifts, despite considerable variations in eye/head kinematics. This is consistent with a role for the SC in higher-level functions such as target selection (Basso and Wurtz, 1998; McPeek and Keller, 2002; Müller et al., 2005; Shen and Paré, 2007) and attentional allocation (Kustov and Robinson, 1996; Carello and Krauzlis, 2004; Lovejoy and Krauzlis, 2010). However, since some of our neurons preferred G over T, our data do not exclude the possibility that the SC is partially involved in the early computations for gaze kinematics (and see the next section on Gain modulation). Moreover, this study only examined gaze and did not address the question of whether some neurons have a preference for eye or head movement (Guitton, 1992; Freedman et al., 1996) (but see Walton et al., 2007, 2008). Finally, we could not distinguish the “visual burst” from the “motor burst” (Munoz and Wurtz, 1995; Walker et al., 1995), so it is possible that these two responses might show different results. However, we were able to show that this coding scheme arose before gaze shift onset and persisted during the saccade, at least in this task and this undifferentiated population of 63 cells.

Gain modulation

A 3-D analysis has shown that the saccade generator must perform a nonlinear reference frame transformation from visual to motor coordinates to produce accurate movements in Listing's plane (Klier and Crawford, 1998; Henriques and Crawford, 2001; Klier et al., 2001), but the mechanism for this is almost entirely unknown. One possibility is that this is implemented by gain modulations along the gaze position component orthogonal to the main sensitivity vector of the saccade (Smith and Crawford, 2005). Gaze position gain effects have previously been observed in the SC for general combinations of eye position and saccade direction in the head-restrained monkey (Van Opstal et al., 1995; Paré and Munoz, 2001), but have not been tested specifically for saccades orthogonal to gaze position or in the head-unrestrained animal.

Our results showed that significant orthogonal position gain-RF modulation occurs in 23% (7/31) of SC neurons. This fraction was less than the fraction of neurons that show eye position gain modulation in all directions, 53% in SC (Van Opstal et al., 1995), 71% in posterior parietal cortex (Andersen et al., 1990), and 50% in the frontal eye fields (Cassanello and Ferrera, 2007), but comparable to the fraction (30%) of SC neurons that show collinear position gain-RF modulation (Van Opstal et al., 1995). This is consistent with the finding that the SC has an approximately equal probability of eye position gain modulation in different directions (Nagy and Corneil, 2010) and suggests that that eye position gain modulations extend to gaze in space (Brotchie et al., 1995). Our finding also supports neural network model predictions that SC neurons carry signals that could be used in a 3-D reference frame transformation (Salinas and Abbott, 2001; Smith and Crawford, 2005). This suggests that this transformation could begin within the SC.

Frames of reference in the SC population code

Previous head-restrained studies attempted to distinguish SC frames of reference by testing saccade-related activity from several widely spaced positions (Groh and Sparks, 1996; Werner-Reiss et al., 2003; Mullette-Gillman et al., 2005, 2009). Jay and Sparks (1987) showed that the RFs of visual SC neurons fit best to an eye-centered frame at the population level. Auditory responses of SC neurons showed that the population intrinsic reference frame of these neurons lay approximately midway between head and eye frame (Jay and Sparks, 1987), whereas motor responses to auditory signals fully compensate for eye position and are clearly in eye frame (Metzger et al., 2004). However, these head-restrained 2-D studies did not allow for testing between the larger number of representations (s, h, e, v) investigated in the current study, nor can one assume that the same neurons are activated in the same way during combined eye plus head gaze shifts. The current results eliminated most of these possibilities (Ts, Gs, Th, Gh), only leaving models that employ a gaze-centered frame.

Unfortunately, our results did not statistically separate the e and v models in the way that previous 3-D stimulation studies did (Klier et al., 2001; Constantin et al., 2004, 2007; Martinez-Trujillo et al., 2004). However, this is perhaps not surprising, given the size of gaze shifts we were able to test (limited by what our neurons responded to). In this range, the two models are very similar and likely within the range of noise coded by individual units. For example, the angular difference between Te and Tv positions for initial target positions that are displaced ±20° from the origin and the secondary target position is offset by 25° perpendicularly from these, is only 2°, which is hard to distinguish from noise, even in closed RFs. Moreover, now that the PRESS method has been fully described (Keith et al., 2009), it should be possible to optimize the behavioral aspects of such experiments to fit the analysis and specific neurons.

However, we think it is unlikely that the SC encodes Tv. First, Te is a known physiological signal (e.g., coded within the retina), whereas Gv is a theoretical motor variable that might only exist as the full ensemble of 3-D inputs to premotor neurons (Crawford and Guitton, 1997; Glasauer et al., 2001). Second, stimulation of the SC does not evoke gaze shifts that follow a code, but rather a Te (or Ge) code (Klier et al., 2001; Constantin et al., 2004). The variable fits that we observed in individual neurons might just be biological variability, and only the population level code (Te) might matter for behavior. Indeed, this is exactly what we found in our intermediate reference frame analysis: a distribution of coding schemes centered around Te. This agrees with the view that the final visuomotor reference frame transformation is performed at a lower premotor level (Klier et al., 2001), leaving a role for the SC in higher-level spatial functions such as target selection (Basso and Wurtz, 1998; McPeek and Keller, 2002; Müller et al., 2005; Shen and Paré, 2007) and attentional allocation (Carello and Krauzlis, 2004; Lovejoy and Krauzlis, 2010).

Notes

Supplemental material for this article is available at http://www.yorku.ca/jdc/documents/DeSouza_et_al_J_Neurosci_2011_Supplements.pdf. 3-D calculations associated with the PRESS method. This material has not been peer reviewed.