Aeroacoustic production of low-frequency unvoiced speech sounds

Abstract

A theoretical approach to describing unvoiced speech sound production is outlined using the essentials of aerodynamics and aeroacoustics. The focus is on the character and role of nonacoustic air motion in the vocal tract. An idealized picture of speech sound production is presented showing that speech sound production involves the dynamics of a jet flow, characterized by vorticity. A formal expression is developed for the sound production by unsteady airflow in terms of jet vorticity and vocal-tract shape, and a scaling law for the aeroacoustic source power is derived. The generic features of internal jet flows such as those exhibited in speech sound production are discussed, particularly in terms of the vorticity field, and the relevant scales of motion are identified. An approximate description of a jet as a train of vortex rings, useful for sound-field prediction, is described using the scales both of motion and of vocal-tract geometry. It is shown that the aeroacoustic source may be expressed as the convolution of (1) the acoustic source time series due to a single vortex ring with (2) a function describing the arrival of vortex rings in the source region. It is shown that, in general, the characteristics of the aeroacoustic source are determined not only by the strength, spatial distribution, and convection speed of the jet vorticity field, but also the shape of the vocal tract through which the jet flow passes. For turbulent jets, such as those which occur in unvoiced sound production, however, vocal-tract shape is the dominant factor in determining the spectral content of the source.

I. INTRODUCTION

This article presents a theoretical framework for describing the physics of sound production by vocal-tract airflow, which has long been known to be not only the primary mechanism of unvoiced consonant sound production, but also a secondary source of sound in voicing. While the discussion touches on issues related to flow-induced vibration of the vocal folds (phonation), it deals primarily with unvoiced sound production. This problem has been addressed in speech science only indirectly. The primary reason for this is that the physics of sound production and propagation in speech science has until recently focused on lumped-element models of primarily acoustic motion of the air in the vocal system. This approach has enabled a great deal of progress in understanding the mechanism of flow-induced vibration of the vocal folds and its attendant sound production, but not of purely aerodynamically produced speech sounds. Two elements have been largely missing in the speech science literature: first, a proper distinction between what constitutes “flow” and what constitutes “sound,” and second, aeroacoustic theory, which describes how airflows produce sound. The lack of a distinction between flow and acoustic modes of motion was, for example, a central failing in the work of Teager (1980, 1981), Teager and Teager (1983, 1990), and Kaiser (1983).

Consideration of these two points leads to a focus on vorticity, the flow quantity essential in understanding not only the dynamics of turbulent airflow motion, but also how that airflow produces sound. Even studies in speech sound production using more sophisticated flow models (Liljencrants, 1989; Alipour et al., 1996) have not focused on the role of vorticity or its central role in aeroacoustic theory. While McGowan (1988) was the first to incorporate concepts from aeroacoustics in discussing the production of speech sounds, he limited his discussion to voiced sounds. While the later, more comprehensive, contributions by Hirschberg and collaborators (Hirschberg, 1992; Pelorson et al., 1994; 1997; Hofmans, 2003; Lous et al., 1998) have successfully incorporated many of these ideas, they also focused largely on voiced sound production, and did not emphasize the distinction between the flow and sound modes of motion. Davies et al. (1993) addressed the effect of bulk air displacement from lungs through the vocal tract on sound propagation in the vocal tract by applying the acoustics of moving media to speech, but did not discuss directly the production of sound by airflow. Davies (1996) and Barney et al. (1997) used the aeroacoustic approach of Davies et al. (1993), but again were primarily interested in voiced sound production, and using the theory as a framework for data reduction. More recently, Zhang et al. (2002b) applied the aeroacoustic formalism of Ffowcs-Williams and Hawkings (1969) to voiced sound production, but did not consider unvoiced sound production. Zhang et al. (2002a) reported experimentally derived aeroacoustic source spectra of jets in a pipe, but these measured the direct radiation from the jet, not the interaction of the jet with changes in pipe shape, which, as described below, is the primary mechansim for unvoiced speech sound production.

A qualitative physical picture of unvoiced speech sound production has developed over a long time. Early contributions to speech science (e.g., Fant, 1960) noted the necessity of “turbulent” airflow for producing unvoiced sounds, but other than noting the random, broadband character of the source, they provided few details of the mechanism involved. Stevens (1971) incorporated many ideas from the aeroacoustics literature, notably the form of the acoustic spectrum from a turbulent jet and the notion that airflow produces the noise most efficiently in the presence of a “spoiler” or “obstacle,” so that the sound is produced not where the turbulent flow is formed, but instead where that turbulent flow interacts with an obstacle such as the teeth. In other words, the majority of sound radiation does not come directly from the turbulent jet itself, but from the interaction of the jet with its environment. Shadle (1985) confirmed the latter idea in a series of in vitro model experiments, but was unable to clarify the sound production mechanism when a distinct obstacle was not present. Later work by Shadle (1991) strongly suggested that the sound produced by airflow in the vocal tract is sensitive to the three-dimensional details of vocal-tract geometry, so that a simple axial area distribution may not be enough to characterize the vocal tract for the purposes of predicting unvoiced speech sounds. None of the above work directly addressed, or conclusively resolved, questions concerning the turbulent flow acoustic source characteristics (level, spectrum, spatial distribution) from first principles of air motion. These questions cannot be answered in terms of the traditional speech science approach to air motion in the vocal tract: either that (1) the flow is irrotational, quasisteady, and that the Bernoulli equation is sufficient to describe the relationship between pressure and particle velocity, or that (2) the acoustic excitation due to the flow is simply described by bandlimited white noise. The aerodynamics and its acoustic effect are far more complex, particularly when unvoiced sounds are produced.

From the very complexity of airflow dynamics arises the need for approximations, in order to make the problem tractable (even a numerical simulation is an approximation). Aeroacoustic theory provides a means for introducing reasonable approximations by providing formal expressions in which the nonacoustic motion is cast in the form of an acoustic source. The formal expression for sound pressure arising from aeroacoustic theory in fact represents a filtering of information concerning the airflow; an exact representation of the airflow is unnecessary and the form of the source term provides essential guidance concerning how to make valid approximations concerning the airflow.

This paper presents the essential ideas concerning fluid dynamics and aeroacoustics which are necessary not only for a fundamental understanding of the process of unvoiced speech sound production, but also for prediction of sound levels and spectral characteristics. First, an idealized picture of fluid motion in the vocal tract is presented. From this picture we see that, no matter what sort of sound is being produced, we have essentially two modes of motion involved, namely flow and sound. A qualitative discussion of the properties of these two modes is presented. The flow mode is seen to have a jet structure whose dynamics is dominated by vorticity, or air particle rotational motion. It is argued that characterizing aerodynamically generated speech sound production can be carried out in two steps: (1) a description of the production and evolution of jet vorticity, and (2) a description of how this motion produces sound.

The latter of these two issues is addressed first. Section II presents the integral expression for the aeroacoustic source at low frequencies. Note that the role of high-frequency, nonplanar acoustic modes in this context is not covered here but will be the subject of a subsequent paper. The implications of the formal expression concerning speech sound production are discussed. Then, a scaling law is derived for the sound-pressure fluctuation due to a vortex ring in an infinite tube. It is shown how the aeroacoustic source expression requires only limited information regarding the vorticity field. Guided by these considerations, Sec. III briefly discusses jet structure in order to define the relevant scales of motion from which order of magnitude estimates can be derived. Then, in Sec. IV the aeroacoustic source characteristics for an idealized vocal-tract flow are presented formally in terms of a model for the jet, resulting in an estimate for the shape of the aeroacoustic source spectrum. This theoretical treatment provides a framework for conclusively resolving the heretofore unanswered issues regarding unvoiced speech sound production—in particular, aeroacoustic source strength, spatial distribution, frequency content, and source impedance.

II. AEROACOUSTIC EXCITATION OF THE VOCAL TRACT

A. Nature of air motion in speech sound production

In examining the motion of air involved in speech sound production, it can be seen that at least two modes of motion are involved. For the moment, these can loosely be defined as being a flow mode and a sound mode. The flow mode essentially consists of the air being displaced from the lungs through the vocal tract and out of the mouth. Along the way, the kinetic energy of this motion can be harnessed to drive flow-induced vibration of soft tissues and/or an unsteady jet, both of which can acoustically excite the vocal resonator. Thus, the flow mode, which includes these jet- and flow-induced vibratory motions, can be seen as an intermediate mode of motion between the physiological inputs and the sound mode we perceive as speech.

Although this qualitative physical picture has implicitly existed since the beginnings of speech science, two questions have not been sufficiently addressed: (1) what is the nature of the flow mode and how can its behavior be predicted, or at least characterized, quantitatively, and (2) even if the flow mode motion is known perfectly, how does that mode convert some of its energy into sound? These questions have been answered, albeit in a greatly approximated way, for flow-induced vocal-fold vibration and its attendant sound production. In this description, the effects of the flow mode, especially the formation, convection, and dissipation of vorticity, which can have pronounced effects not only on the flow-induced vibration of the vocal folds (Pelorson et al., 1994; Lous et al., 1998; Hofmans, 2003), but also on aspirative and unvoiced sound production (Stevens, 1971; Shadle, 1985, 1991). Using a quasisteady Bernoulli model of the flow mode, where the effects of flow separation are incorporated as a lumped-element loss, as first done by Ishizaka and Flanagan (1972), seems to work well for simple models of vocal-fold vibration, but does not include a description of the vorticity dynamics relevant for unvoiced or aspirative sound production. Going beyond this simple description, or developing quantitative or predictive models of unvoiced speech sounds, means going beyond these simple quasisteady Bernoulli-equation descriptions of the flow mode.

A first step in this direction is a consideration of the properties of the modes of motion just described. First, we note that perhaps more precise, descriptive names for the modes are “convective” (or “incompressible”) and “propagative” (or “irrotational”). The propagative mode will be considered first because it is more familiar to speech researchers. Motion of air particles in the sound mode is characterized by propagative transfer of energy and momentum. In other words, these quantities are transmitted through air particles by the propagation of waves of compression/expansion. A fluid particle experiences no net displacement from its initial position during the passage of a sound wave. The only forces active in a sound field are pressure forces, which act uniformly on a fluid particle, producing no rotation upon it. A mathematical description of the sound mode must have these properties: (1) it must support volume fluctuations, and (2) it must be irrotational. The convective mode is by contrast characterized by transfer of energy and momentum through the actual displacement and rotation of air particles, which as a result end up far away from their initial location, as when air is displaced from the lungs and expelled out of the body. At air speeds observed in speech, which might locally approach 40 m/s (M=Mach number=0.12), these motions proceed without appreciable volume fluctuations, i.e., they are essentially incompressible. Therefore, a mathematical description of this mode in speech type air flows must (1) support air particle rotation, and (2) be incompressible.

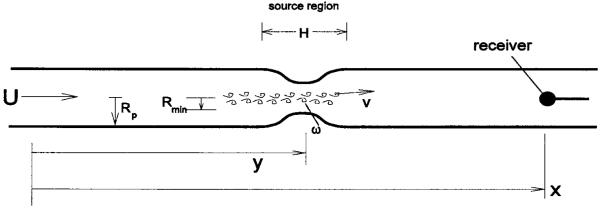
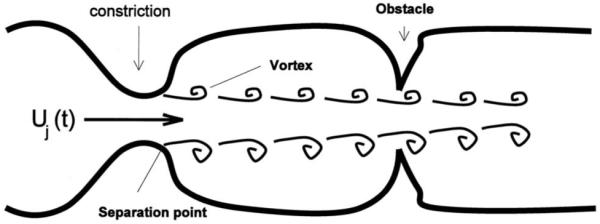
Figure 1 shows a sketch representing a vocal-tract airflow in which speech sounds are produced. This geometry has the generic features of all speech sounds, no matter their origin. First, a high-pressure reservoir (the lungs) to the left pushes air through the passage. Upon being accelerated through the leftmost constriction, the airstream decelerates and the flow becomes separated from the wall, forming a jet. This jet consists of a focused high-momentum region in the center, surrounded by stagnant air. These two regions are bounded by shear layers in which air particles undergo not only translation, but also rotation. Vorticity (in some sense, a measure of rotational motion) in the shear layer tends to coalesce into coherent structures (Cantwell, 1981; Hussain, 1986), which may or may not be “turbulent,” and which convect from left to right. The shear layer diffuses, through the action of viscous forces enhanced by coherent structure mixing, in the direction perpendicular to the flow, causing the jet to spread in the transverse direction. This process mixes the jet core flow and the stagnant region air, so that the momentum of the jet is ultimately spread out over the whole vocal-tract cross section. The presence of vorticity in the jet is a consequence of boundary layer separation (see Sec. II B 1) which injects into the bulk flow rotational motion formed in the thin viscous layer near the wall. Note that until the point of separation, the vorticity is confined to the boundary layers. Because vorticity corresponds to a definite amount of momentum [see, e.g., Batchelor (1968), or Saffman (1992)], it will persist even if the flow producing the jet is shut off. If, as is shown in Fig. 1, the jet encounters a change in duct area, the vortical structures in the jet will produce unsteady forces on the walls of the obstacle as they pass by it. These forces will excite (transfer energy) to the irrotational (acoustic) mode in the vocal tract.

FIG. 1.

Schematic of air motions in speech sound production. Air flowing from the lungs from left to right is forced through constriction at the right, at velocity U_j(t). The airstream separates at some point downstream of the location of maximum constriction, forming a jet. The jet boundaries consist of vortical flow, which quickly breaks down into coherent vortical structures. These structures convect from left to right at the local flow speed, a fraction of U_j. As the vortices convect through the vocal tract, they induce unsteady forces on the vocal-tract walls. These forces produce sound. For wall features such as the “obstacle” shown here, where the shape changes rapidly, these forces, and hence the sound produced, are particularly intense.

Contrast this picture with those which have propagated in the speech community, as seen in the work of Flanagan and Cherry (1969), Flanagan and Ishizaka (1976), or Stevens (1971) and Shadle (1985). In the first two, turbulent flow is treated as occurring only in those regions where the particle velocity of the airflow/sound field rises above a critical Reynolds number, above which a steady duct flow is usually turbulent. The source strength is prescribed as proportional to the square of the local particle velocity, and the spectral content is modeled as bandlimited white noise. Shadle (1985), following Stevens (1971), suggested modeling the aerodynamic source as a dipole in the vicinity of the obstacle, but was not able to resolve further questions regarding the spatial distribution of the source, particularly when no clear obstacle-type geometric feature was involved. Sondhi and Schroeter (1987) used a similar approach, but the same questions concerning the fundamental nature of the source were left largely unanswered. Furthermore, the notion that the jet has any definite structure, despite the “random” character of turbulent flow, and that this structure has any consequence for sound production, is largely missing from the speech literature. While Stevens (1971) and Shadle (1985) recognized that jets do have spatially distributed structure, they did not translate that realization into a concrete connection between that structure and sound production. Teager (1980, 1981), Teager and Teager (1983, 1990), and Kaiser (1983) also argued for the importance of jet structure in voiced sound production, but failed to provide a clear theoretical connection between jet structure and sound production. The spatio-temporal structure of internal flow jets is discussed in more detail in Sec. III.

The types of speech sound which are represented in Fig. 1 may be classified according to the behavior of both the constriction and the jet flow through that constriction. If the flow and the constriction are involved in flow-induced oscillation, then the sketch represents phonation, a trill, or a guttural sound. In the case of phonation, the sound produced at the obstacle is the source of aspirative noise, the “breathy” part of the voice. If the constriction is first closed and then suddenly opened, releasing a transient puff of air, then the sketch represents a plosive. On the other hand, if both the constriction geometry and the airflow through it are steady, then an unvoiced fricative is represented, while a voiced fricative is modeled by a steady constriction geometry and an unsteady periodic air flow due to the resonances of the voicing.

Speech sounds may be thought of as being produced by three mechanisms: (1) volume displacement due to vocal-tract wall motion, and (2) unsteady forces on the obstacle and the constriction walls (or, more generally, a change in duct geometry) induced by the unsteady motion of jet vorticity structures, and (3) direct radiation due to unsteady motion of the jet structures [see, e.g., the appendix of Zhang et al. (2002b)]. The second mechanism is the focus of this paper. Once the sound is produced, because the ends of the vocal tract do not perfectly absorb or allow perfect transmission of sound waves, some acoustic energy is reflected back into the tract, so that acoustic energy accumulates there in the form of standing waves. The standing wave structure at the open (mouth) end of the vocal tract is particularly important, since it transmits the oscillations inside the resonator to the outside world.

At this point in the discussion, it is possible to make more precise the sequence of events between diaphragm contraction and unvoiced sound production, as described in brief at the beginning of this section. First, the flow mode, which consists not only of the air displaced from the lungs, but also the unsteady jet motion formed at a constriction. Both of these motions, being essentially incompressible, are distinct from the sound field, and give up only a small fraction of their kinetic energy in generating it. Most of the kinetic energy of this convective mode of air motion is in fact either dissipated by viscosity with the aid of turbulence, or convected out the mouth by the airstream. The rotational (vortical) motions of the jet shear layers, which are shown below to be directly involved in sound production, are formed using energy taken from the airstream. Thus, the problem of unvoiced sound production may be seen more precisely to involve (a) how jet vorticity is formed and how it evolves, and (b) how this motion produces sound.

B. Acoustic pressure due to aerodynamic sources

To gain insight into the production of sound by vortical flow in the vocal tract, let us first look at the problem of sound production by vorticity convecting past an obstacle in an otherwise uniform cross-section pipe. Using this idealization of the vocal tract, an integral expression for the sound pressure can be derived. The integral expression is desirable because, in general, obtaining a high-fidelity description of the vorticity field is prohibitively expensive [see, e.g., Hardin and Pope, 1992; Hulshoff et al. (2001) for an example relating to duct aeroacoustics], if not impossible, motivating the use of an approximate description. The integral form works well in this context because it is relatively insensitive to errors involved in approximating the flow field. In addition, as will be shown, not all information regarding the vorticity field is relevant, so the formal result is informative in discriminating the aeroacoustically relevant information. The integral expression will then be used to demonstrate how the aeroacoustic source excitation of the vocal-tract pipe due to a single vortex ring may be determined.

1. Formal solution for sound pressure due to an aeroacoustic source

The problem under initial consideration is shown in Fig. 2. The air in an infinitely long pipe is in steady motion at speed U. The pipe has uniform cross section area A, except for a short section which contains a constriction. The steady airflow convects vortical disturbances through the constriction, a process which produces unsteady forces on the constriction walls, producing acoustic disturbances which radiate away from the constriction. If the duct shape, U, and the vortical disturbances are known, an expression is sought to describe the sound-pressure field at an observer location x due to the source processes at location y. The solution to problems of this type is the domain of aeroacoustics. Several texts on this subject are available for a more complete study (Goldstein, 1976; Dowling and Ffowcs-Williams, 1983; Blake, 1986; Lighthill, 1978; Howe, 1998).

FIG. 2.

Schematic of aeroacoustics problem: find the sound pressure at observer location, x, in an infinitely long duct of uniform cross section (radius R_p) containing a narrow constriction (radius R_min) of axial length H. The air in the pipe far away from the constriction is a combination of steady motion (velocity U) and the sound produced by an unsteady aerodynamic force on the constriction walls at source coordinate y. Forces are due to vorticity ω convected at local velocity v through the constriction.

For computing the sound field due to nonuniform flow in a duct, Howe (1975, 1998) has shown that a concise formulation may be derived using the acoustic total enthalpy B’≈p’/ρ_∞+U·u’ as the acoustic variable, where U is the steady flow speed and u’ is the particle velocity of acoustic disturbances. Here, and throughout the text, ρ_∞ is the ambient undisturbed air density. In speech-like geometries, the constrictions are rather severe, so that the steady flow speed in the unconstricted portion of the flow is extremely small. Thus, far from the region where the sound is produced, U is small, so B’≈p’/ρ_∞. Howe also showed that for low Mach number flows such as those seen in speech sound production, the convected wave equation for the low-frequency acoustic field variable B’ is given by

$$\frac{D^2{B}^{\prime }}{D{t}^2}-c^2\frac{{\partial }^2{B}^{\prime }}{\partial x^2}=\frac{\partial }{\partial x}{(\omega \times \mathbf{v})}_x,$$ (1)

where c is the speed of sound and DBₑ/Dt is the convective or material derivative of B’, following a fluid particle as it moves through space

$$\frac{D{B}^{\prime }}{Dt}=\frac{\partial B^{\prime }}{\partial t}+U\frac{\partial B^{\prime }}{\partial x},$$ (2)

where the first term represents the time rate of accumulation of total enthalpy at a fixed location in space and the second term represents the time rate of change of total enthalpy at a fixed location due to convection of total enthalpy fluctuations past that fixed point. Note that the effect of the latter term in the wave operator describes the convection of sound waves by motion of the medium.

The wave equation states that, if the right-hand side is zero, an acoustic disturbance will propagate such that its energy is conserved. In the quasi-one-dimensional propagation described here, energy of the disturbance will be conserved. If the right-hand side is nonzero, the disturbance will either gain or lose energy. If no disturbance exists (the “disturbance” has zero energy), then one will be generated. Because the terms on the right-hand side of Eq. (1) do work on the acoustic field, they are referred to as “sources” [although they may also act as “sinks” in an ambient sound field—see Howe (1980, 1998), Bechert (1980), Hirschberg (1992)].

The physical mechanism responsible for modifying the acoustic disturbance field is the axial component of the vector ω×v, the acceleration due to the motion of vorticity in the vocal-tract airflow. This term is central to the understanding of turbulent flow dynamics (see, e.g., Tennekes and Lumley, 1972), and relates not only to the direct radiation of sound from the jet (see Powell, 1964; Howe, 1998), but also to the aerodynamic forces induced on the vocal-tract walls by the jet (see Howe, 1998). Formulating the aeroacoustic problem in this manner has several advantages over the more commonly used one due to Curle (1955) [a development of Lighthill (1952, 1978)]. A discussion of these advantages is delayed until the solution for the sound field has been obtained, when they are more clear.

The solution of Eq. (1) for the sound-pressure fluctuation arising from the interaction of the jet and the constriction is found by convolving a tailored Green’s function with the source term ∂(ω×v)_x/∂x (see the Appendix for details)

$$p^{\prime }(x,t)=-{\rho }_{\infty }\frac{\mathrm{sgn}(x-y)}{2A(1+M)}{\int }_A{\int }_y[\omega \times \mathbf{v}\cdot {\mathbf{U}}^{\ast }]dAdy,$$ (3)

where sgn(x-y) is the signum function

$$\mathrm{sgn}(x-y)=\{\begin{array}{cc}1\hfill & \text{for}x-y>0\hfill \\ -1\hfill & \text{for}x-y<0,\hfill \end{array}\phantom{\}}$$

so that the acoustic pressure changes sign across the source, consistent with a dipole source. Here, A and M refer to the cross-sectional area and the steady flow Mach number, respectively, at the receiver location x where the sound pressure. Note that the integrand is written inside square brackets to denote that it is a function of source position y and retarded time t-|x-y|/(c(1+M)) it takes the signal to reach the observer at x from the source at y. This expression can also be written (Howe, 1998) as

$$p^{\prime }(x,t)=-\frac{\mathrm{sgn}(x-y)}{A(1+M)}{\int }_A{\int }_y\left[F\left(y\right)\right]dAdy,$$ (4)

where F is the axial component of the aerodynamic force on the constriction, which in Eq. (2) has been expressed in terms of the scalar product of jet flow vorticity acceleration ω×v and the quantity U*. Strictly speaking, U* is the ideal flow velocity field that would exist if the duct contained a unit speed steady airflow. It should be recognized that U* is not a flow which actually occurs—it arises in the expression from the correction to the retarded time in the Green’s function (see the Appendix), and so reflects the effect of source motion and diffraction around the change in vocal-tract shape. It should then be thought of as a property of the vocal-tract shape (Howe, 1975, 1998).

The integral solution of the convected wave equation shows that the force on the constriction (and hence sound production) occurs when vorticity moves across the streamlines of U*, or when v is not parallel to U*. The constriction drag force, and hence sound generation, is maximum for v oriented perpendicular to U*, and minimum (zero) when v and U* are parallel. (Streamlines are simply lines of tangency to the velocity field.) It should be stressed that, due to the contribution of vorticity, the streamlines of the flow v which is actually realized will have a very different geometry than that of an ideal flow such as U* (see, e.g., Saffman, 1992).

A few comments are in order regarding the relationship between Eq. (2) and the more commonly used expression [Eq. (3)] derived by Curle (1955) [see, e.g., Shadle (1985), Verge (1994), Hofmans (2003)], referred to hereafter as the Lighthill/Curle formulation. First, both express the dipole source in terms of the net force on a compact body, or, in this case, the vocal-tract walls. The difference is that the Lighthill/Curle formulation casts the force directly in terms of the net axial wall pressure force [see, e.g., Lighthill (1978)], while Howe (1975) writes the force in terms of the motion of separated flow vorticity and the duct shape. For the purposes of predicting unvoiced speech sound production, the advantage of the Howe formulation over that of Lighthill/Curle is due to three factors. First, the Lighthill/Curle result expresses the sound field in terms of integrals over the airflow Reynolds stresses and the pressure fluctuations on the vocal-tract walls. The Reynolds stresses occupy a much more extensive volume than the vorticity which may be thought of as “driving” this part of the flow. The vorticity occupies only a tiny fraction of the total volume of the vocal tract. Because the Howe formulation is given explicitly in terms of the vorticity, it requires integration over a much smaller volume than the Lighthill/Curle formulation (see also Powell, 1964). Second, Howe’s approach results in an expression for the sound pressure in terms of the separated flow vorticity away from the walls. In other words, the contribution of the vorticity in the wall boundary layers does not contribute to the sound field. (There will be no aerodynamic drag on the constriction, aside from a small skin friction drag, unless the flow separates, or unless it is placed in a separated flow.) These two factors result in a greatly reduced amount of flow information required to predict the sound field. Third, the integral in Eq. (2) depends not only on the jet flow, but also is an explicit function of the shape of the vocal tract, as reflected in U*. The shape of the vocal tract, and hence U*, may be specified with a good deal more precision than the vorticity acceleration ω×v (because of the expense in specifying ω to any level of precision). However, a simplified description of the vorticity field can still yield an accurate estimate of the acoustic source characteristics. This may be seen by inspection of Eq. (2): the dot product between ω×v and U* effectively reduces the amount of vorticity field information required because only those components of vorticity normal to the streamlines of U* will contribute to sound production. In this way, the sound production process may be thought to “filter” the vorticity field, the filter shape being determined by the shape of the vocal tract.

2. Relevance of formal result for unvoiced speech sound production

To proceed further in obtaining the acoustic pressure field due to the interaction of the nonuniform vocal tract with a full jet flow, it is necessary to determine at least approximate behavior for ω, v, and the angle between ω×v and U*. The reasoning used to choose scales for these quantities is explained in Secs. III and IV. However, even without that information several important points can be made at this stage. These relate (1) to the necessity of flow separation (jet formation) for unvoiced speech sounds to be produced at all; (2) to the extent to which a distinct obstacle is necessary for sound generation; and (3) to the suitability of the traditional speech science approximation of quasi-one-dimensional air motion for description of unvoiced speech sound production.

From the comments outlined above concerning Eq. (2), it is clear that, expressing the aerodynamic sound source in terms of the motion of free vorticity, the flow must separate somewhere in the vocal tract for sound to be produced. Since the vocal-tract wall lies on a streamline of U*, vorticity in boundary layers will not contribute to sound generation. This is equivalent to saying that the unsteady axial (drag) force resulting from the sum of the axial pressure force contributions on the vocal-tract walls is zero unless flow separation occurs [D’Alembert’s paradox—see the remarks of Teager (1980, 1981)].

In addition, from the conceptual picture given above, it is clear that it is not necessary for the jet to actually “impact” or “strike” the obstacle, as has been stated by Stevens (1971) and Shadle (1985). Indeed, a definite “obstacle” shape is not even necessary for sound to be produced by the jet. Shadle (1985) shows results for “no-obstacle” cases, where the jet flow passes through a change in the duct shape itself, including the open end of the tube. From inspection of Eq. (2), it is clear the crossing of U* streamlines by vorticity necessary for sound generation will occur for any change in duct shape, not just in the case of a definite obstacle. A clear theoretical example of this effect is given in Howe (1975), where Eq. (2) is derived for a simple reduction in cross-sectional area. [The same case was studied numerically, by Hulshoff et al. (2001)]. Here, there is no obstacle per se, only a change in duct area. A similar example can be seen in the whistler nozzle (Hirschberg et al., 1989), in which flow through two sudden changes in duct area can, under the proper conditions, lead to intense sound production without a direct impact of a jet on the pipe walls. Thus, it can be seen that the distinction Shadle (1985) made between the obstacle- and no-obstacle cases is in some sense an artificial one, at least in terms of the fundamental mechanism by which the sound is produced. In all cases, the aeroacoustic source is located wherever vorticity in a separated flow passes through a nonuniform duct.

It is also evident from the theoretical model of Howe (1975) that, because both the jet behavior and the streamlines of U* are determined by details of vocal-tract geometry, the traditional axisymmetric, quasi-one-dimensional representation of the vocal tract is likely not sufficient for prediction and study of unvoiced speech sound production. This point supports the observations of Shadle (1991), who noted the marked sensitivity of the sound produced by airflow through vocal-tract-like models to model geometry. The modeling efforts of Krane et al. (2005) and Sinder (1999) also demonstrate clearly that if the geometry of the flow passage is known precisely, Howe’s theory predicts the sound produced very well, whereas if a highly three-dimensional flow passage (such as the vocal tract) is approximated by an axisymmetric duct, the resulting prediction of sound is not entirely correct. It should be emphasized that this sensitivity to geometry impacts only the description of the aeroacoustic source, not the propagation of the sound field once generated. Thus, while the computation of aeroacoustic source characteristics does require a more detailed geometric description, the computation of the sound field by the traditional approach acoustic is quite sufficient, at least for low frequencies at which only plane waves propagate. At higher frequencies, nonplanar modes will propagate and will likely dominate the acoustic field. A treatment of the aeroacoustics of nonplanar mode generation in speech will be given in a subsequent paper.

3. Sound produced by single vortex ring passing an obstacle in an infinite tube

As an example of the process of unvoiced sound production, the sound produced by the convection of a single vortex ring through an axisymmetric constriction in an infinite pipe of otherwise uniform circular cross section will be discussed. The structure of a vortex ring is shown in Fig. 3. The ring consists of a circular tube of vorticity, such that the vorticity vector points in the azimuthal (θ) direction, the tube cross section has diameter δ_ʋ, and the ring has radius R_ʋ. The ring moves from left to right in motion induced by the vorticity in the ring itself (and its images in the duct walls), as well as the irrotational steady flow U. For more on how vorticity is convected, please see Saffman (1992). Using the definition of circulation, Γ, the volume integral of the vorticity is given by

$$2\pi R_{\upsilon }\Gamma ={\int }_0^{2\pi }{\int }_{A_{\upsilon }}\omega \cdot d\mathbf{A}d\theta$$ (5)

(where $A_{\upsilon }=\pi {\delta }_{\upsilon }^2$ is the area of the vortex ring normal to ω and θ is the coordinate tangent to the vorticity vector, i.e., tangent to the ring). The integral expression for the pressure fluctuation p’≈ρ_∞B’ far from the source region then becomes

$$p^{\prime }=-\frac{{\rho }_{\infty }\pi \mathrm{sgn}(x-y)R_{\upsilon }}{A(1+M)}[\Gamma ({\mathbf{e}}_{\theta }\times \mathbf{v})\cdot {\mathbf{U}}^{\ast }],$$ (6)

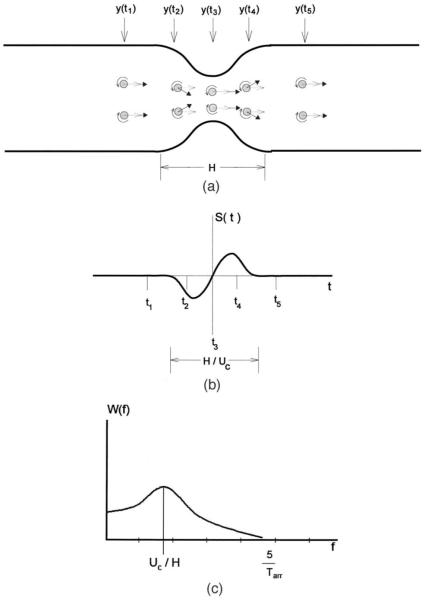
where e_θ is the unit vector in the vorticity direction. Note that the triple product in this expression is nonzero only where ω≠0, and the square brackets have the same meaning as in Eq. (2). If we assume the vortex takes an essentially axial path, then ω×v always points radially outward, and the vortex will generate sound if the radial component of U* is nonzero. As the vortex ring convects through the constriction, the radial component of U* points initially radially inward upstream of the point of maximum constriction, then radially outward downstream of this point. This behavior is shown in Fig. 4(a) as the vortex ring convects through the constriction, and the source strength takes the appearance of a single period of a sinusoid wave, as shown in Fig. 4(b). The sign change occurs when the vortex passes over the centerline of the obstacle.

FIG. 3.

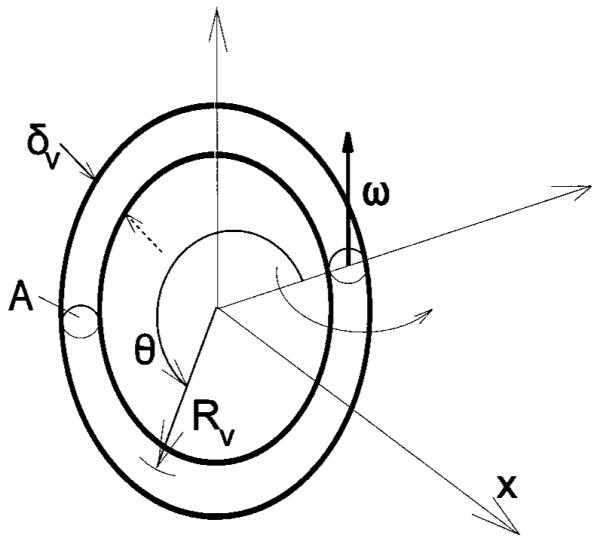
Structure of a vortex ring, showing the definitions of the vorticity vector and the coordinates used in Eqs. (4) and (5). The vorticity vector points in a direction tangent to the ring, as shown. The ring radius is R_ʋ, the core radius δ_ʋ, the cross-sectional area of the core A_ʋ=πδ_ʋ²,and θ is the azimuthal coordinate along the ring.

FIG. 4.

Aeroacoustic source behavior due to convection of single vortex ring through a constriction in an infinite pipe. Airflow is from left to right, vortex ring diameter is R_ʋ, vortex core diameter is δ_ʋ, and the axial length of the constriction is H. (a) Location y(t) of vortex ring, shown in cross section, at five instants t₁, t₂, t₃, t₄, and t₅ during vortex passage. Orientation of vectors ω, v, and U* are shown, ω in terms of its rotation sense in the plane of the page, v by lined arrowheads, and U* by solid arrowheads. Equation (2) states that the aerodynamic force on the constriction will be maximum when v is perpendicular to U*, and zero when they are parallel. (b) Waveform of aeroacoustic source strength due to vortex ring passage through constriction, with times indicated corresponding to vortex ring positions in Fig. 4(a). Duration of source is the time H/U_c that the vortex ring takes to convect through the constriction. Note that S(t)=0 when t=t₁, t₃ and t₅, because v and U* are parallel. The aerodynamic force changes sign as the vortex passes through the maximum constriction. (c) Spectrum of sound pressure due to the passage of a single vortex ring through the constriction. Peak occurs at U_c/H, the reciprocal of the time the source is “on.” Peak width is related to temporal extent of source signal, and becomes broader as U_c/H becomes smaller.

Because of the signum function in Eq. (6), the temporal pressure signature is a time-delayed image of the source signal for x>y, and an inverted, time-delayed image of the source for x<y. This behavior is consistent with dipole source behavior. The duration of the disturbance is roughly ℓ/U_c, where U_c is the convection speed of the vortex through the constriction, and ℓ is estimated by either H, the axial length of the constriction, or δ_ʋ, the radius of the vortex core. The choice of H or δ_ʋ as the length scale depends on which determines the duration of the interaction between the vortex and the change in vocal-tract shape. For cases where the vortex core is much smaller than the obstacle (δ_ʋ/H⪡1), then H is the proper choice. This corresponds, for example, to the case of the glottal jet produced in /h/ interacting with the bend in the vocal tract or anatomical features such as the epiglottis. In the opposite case, where the obstacle is “sharp” relative to the vortex core size (as in perhaps /s/ or /∫/) then δ_ʋ is the proper length scale. [In Fig. 4(a), the case δ_ʋ/H⪡1 is shown.) The aeroacoustic source spectrum, shown in Fig. 4(c), is a broad peak centered on f=U_c/ℓ, where ℓ is either H or δ_ʋ, as described above, with width approximately U_c/ℓ. Note that the breadth of the peak is due to the relatively short duration of the source. It is clear from this result that the frequency of the sound will increase as the axial extent of the vocal-tract shape change decreases or as the convection speed increases.

The amplitude of the peaks in the acoustic pressure signal may be estimated from the scales of motion. These are the axial length and height of the constriction, the vortex core radius and ring radius, the vortex circulation, and the vortex convection speed. Writing out the scalar product in Eq. (5), and using U*=U(x)/U=A/A(x) (Howe, 1975), we obtain

$$p^{\prime }\approx {\rho }_{\infty }\frac{\pi }{A}{R}_{\upsilon }\Gamma \upsilon \frac{A}{A\left(x\right)}\sin \alpha \left(t\right),$$ (7)

where α is the angle between the pipe axis (the direction of v, by assumption) and U*. Now, since ω∼U_c/δ_ʋ, then $\Gamma ~\omega {\delta }_{\upsilon }^2~U_c{\delta }_{\upsilon }$. Furthermore, A(x) may be estimated by its minimum, $A_{\min }=\pi R_{\min }^2$, and sin α may be estimated by (R_p-R_min)/(H²+(R_p-R_min)²)^1/2 , where R_p is the radius of the pipe away from the constriction, and R_min is the minimum radius in the constriction. Using these scales in Eq. (6), the acoustic pressure peak has amplitude proportional to

$$p^{\prime }~{\rho }_{\infty }\frac{R_{\upsilon }{\delta }_{\upsilon }}{R_{\min }^2}{U}_c^2\frac{R_p-R_{\min }}{{({(R_p-R_{\min })}^2+H^2)}^{1∕2}}.$$ (8)

From this expression it is clear that the sound pressure increases linearly with both R_ʋ and δ_ʋ, quadratically with U_c, and inversely with the square of R_min. In other words, sound production is greater for larger vortex rings (in terms of either its core size or its ring radius), faster convection speeds (i.e., the quicker it moves through the constriction, and the higher the frequency of sound generated), and larger radial changes of vocal-tract shape. These trends explain why the teeth, being the geometric feature in the mouth with by far the sharpest change in shape, are the primary geometric feature in the production of fricatives such as /s/, /∫/, or /z/, when the entire mouth is quite nonuniform in shape. It also explains why the vocal-tract walls near the constriction where the jet is formed are not typically as important in unvoiced sound generation—the shape does not change as drastically in that region.

A scaling law for the acoustic source energy as a function of vortex ring convection speed follows:

$$\frac{p^{\prime 2}}{{\rho }_{\infty }{c}^2}~{\rho }_{\infty }{U}_c^2{M}^2,$$ (9)

which shows that the sound power is proportional to the second power of the ring convection speed times the square of Mach number based on that speed. It is important to note that this particular scaling law (valid for the infinite pipe only) is given here for illustrative purposes; its form will change considerably in a finite-length pipe depending on source location and the local acoustic impedance of vocal-tract terminations.

Note that the velocity dependence for the dipole source energy ($U_c^4$ or $U_c^2{M}^2$) seen in Eq. (8) differs from that of the classical free-field aeroacoustic dipole source ($U_c^6$) (Curle, 1955; Howe, 1975, 1998). This behavior is true in general for aeroacoustic sources which generate one-dimensional plane waves, compared to the same compact source in free space. This is due entirely to the difference between the manner in which one-dimensional plane waves and three-dimensional spherical waves propagate, reflected in the difference in Green’s function for these two cases [see Howe (1975, 1998) for the equivalent Green’s function for three-dimensional wave propagation]. For a one-dimensional plane wave, the amplitude is independent of distance from the source, whereas it is inversely proportional to distance from the source for a spherical wave. In addition, the acoustic impedance for a one-dimensional plane wave is frequency independent, whereas the curvature of the spherical wave causes a frequency-dependent impedance, where the impedance becomes larger as frequency decreases. Thus, the source impedance is higher at low frequencies in a situation where spherical waves can propagate. This frequency dependence of the source impedance in free-field geometries is responsible for the higher value of velocity exponent in the scaling law for acoustic source power. This discussion emphasizes how the solution for the sound field given by Eq. (2) incorporates the source impedance.

Note also that the $U_c^4$ scaling for the aeroacoustic source strength appears to agree with that developed by Flanagan and Cherry (1969). Flanagan and Cherry used the correlation developed by Meyer-Eppler (1953), who measured the sound levels produced by flow through constricted pipes. Their scaling, while in principle correct, did not result from consideration of the physics of sound production by airflow, which the present theoretical development does. Note also that predictive models for unvoiced sound generation based upon Meyer-Eppler’s scaling found it necessary to develop a model for the source impedance, which the theoretical development does implicitly by inverting the wave equation with the Green’s function.

The efficiency of conversion of flow kinetic energy into sound-field energy may be seen from the ratio of the sound-field energy per unit volume, given in Eq. (8), and the flow kinetic energy per unit volume ${\rho }_{\infty }{U}_c^2∕2$. The ratio is proportional to M², which means that, since the Mach number of speech flows never exceeds 0.15, the aeroacoustic source is not a particularly efficient means of transforming flow energy into acoustic energy. This crucial realization was missing from the work of Teager (1980, 1981), Teager and Teager (1983, 1990), and Kaiser (1983). They based their arguments on Teager’s claims to have measured high-energy (relative to the sound field radiated from the mouth) jet-like air motion in the vocal tract, as opposed to the acoustic plane waves they claimed the traditional view predicted. Questions about Teager’s experimental method aside (see the commentary in Kaiser, 1983), he was in fact measuring the velocity distribution of the jet-like flow just above the glottis. As can be seen from the above discussion, this motion is to be distinguished from the sound field. However, lacking the theoretical underpinning for the distinction between convective and propagative motion, they argued for discarding the traditional plane-wave description of acoustic propagation in the vocal system. Here, it is argued that the traditional acoustic description is sufficient, with modifications due to the motion of the air (see, e.g., Davies, 1980; Davies et al., 1993). Furthermore, an intermediate mode of air motion is involved in sound production, namely the convective mode, and the specific manner in which this mode of motion is manifested in speech and how it produces sound needs to be clarified.

4. Effect of finite-length vocal tract

For a finite pipe such as the vocal tract, reflections at the pipe terminations must be incorporated into the analysis. For most unvoiced speech sounds, the constriction at which the jet is formed divides the vocal tract into a “front” and “back” cavity. Because the acoustic impedance of this narrow constriction is high, the front cavity is often treated as acoustically decoupled from the back cavity. This approximation works well for fricatives and plosives, but perhaps not as well for voiced fricatives. In our approximation of the acoustically relevant part of the vocal tract as a closed-open tube, the “closed” end can be thought to be located at the constriction where the jet is formed, while the “open” end may be thought to be located at the lips. In addition, the source is in general not located at the closed end of the front cavity, but somewhere inside it. Using the method of images (see Morse and Feschbach, 1953), the Green’s function may be constructed for a finite-length closed-open pipe, which represents the end reflections as virtual sources located outside the pipe itself (Pierce, 1989), as shown in Fig. 5

$$G(x,t\mid y,\tau )={\rho }_{\infty }\frac{c}{2A}\sum _{n=-\infty }^{\infty }{\gamma }^{n}H\left(t-\tau -\frac{x\pm 2n{L}_f}{c(1+M)}+\frac{{\varphi }^{\ast }\left(y\right)}{c(1+M)}\right),$$ (10)

where γ is the open-end pressure reflection coefficient, which takes a value between 0 and -1, and H(ξ) is the Heaviside function, which is equal to 1 for ξ>0 and 0 for ξ<0. The resulting expression for the sound at the open end is given by

$$p^{\prime }(x,t)=-\frac{{\rho }_{\infty }}{2A(1+M)}\sum _{n=-\infty }^{\infty }{\gamma }^n\times {\int }_{-\infty }^{\infty }{\int }_A{[\omega \times \mathbf{v}\cdot {\mathbf{U}}^{\ast }]}_{n}dAdy,$$ (11)

where the expression in square brackets is now evaluated at location x=x±2nL_f and retarded time t-(x±2nL_f)/(c(1+M)). Note that while the integral over source space, y, is from -∞ to +∞, observer space, x, is defined only over the interval 0<x<L. Thus, it can be seen that the effect of the open and closed ends of the tube is equivalent to the placement of time-synchronous virtual sources outside the vocal-tract domain. The net effect of these additional sources is the accumulation of sound at the resonance frequencies f_n=c(2n+1)/4L_f, where n=0,1,2,..., and L_f is the axial length of the front cavity. When the source is not located either at the inlet or outlet of the cavity, then a zero appears in the spectrum at approximately f_z=nc/(2L_s) (n=0,1,2,...), where L_s is the distance between the jet origin and the source location. The width of the resonance peaks depends on the value of γ: the higher γ is, the more acoustic energy radiates out the open end per round trip; the wider the resonance peaks, the lower the resonant levels become.

FIG. 5.

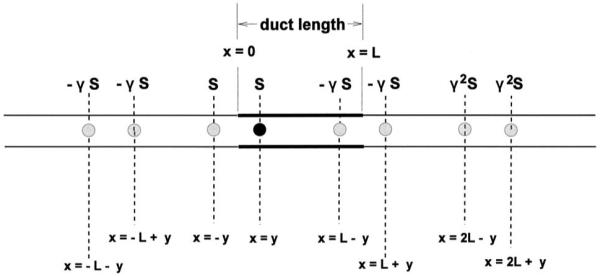
Treatment of acoustic effect of vocal-tract terminations as the superposition of image sources. Sound field in pipe of length L is equivalent to that due to the real source S, located at x=y, and its images, placed in an infinite pipe as shown. Note that the image sources shown are only the first few of the infinite series given in Eq. (9).

To this point, the open-end pressure reflection coefficient has been assumed frequency independent for clarity. In a more physically correct description, the reflection coefficient is frequency dependent, because the radiation efficiency of the open end of the tube increases with frequency. In this case, the product of the Heaviside function with the reflection coefficient is generalized to a convolution of the reflection coefficient time series with the Heaviside function. The net effect of the frequency-dependent reflection coefficient is that the amplitude of the resonance peaks at the tube exit decreases with the square of frequency. Thus, the acoustic spectrum in the tube due to an aeroacoustic source is the product of the Green’s function spectrum, which consists of resonance peaks with an inverse-frequency squared decay envelope, and the spectrum of the source. The form of the source spectrum is discussed in Section IV.

III. SOME PARTICULARS OF INTERNAL JET FLOWS

While the necessity of turbulent jets in unvoiced sound production has been acknowledged for some time, the relation between jet structure and sound radiation has never been made clear in a speech context. The results in Sec. II clearly show that the convection of vorticity through a nonuniform vocal tract will produce sound. Because the vocal tract is essentially nonuniform everywhere, it is necessary to determine where and how vorticity enters into the flow in a manner relevant to sound production. This last qualification is important, because vorticity is always present, at least on the vocal-tract walls where it is formed when the air is in motion. But vorticity will not be relevant for speech sound production unless it is injected into the flow away from the wall, as explained above in Sec. II B. Thus the issue may be summarized in three questions: (1) when and where do jets appear in speech-like flows; (2) for how much time and for what distance from the formation point does a jet persist, and (3) what range of length and time scales characterizes the jet motion. To answer these questions it is necessary to discuss some essentials of jet physics.

A particular point of emphasis in this discussion is that the jet, even when turbulent, is not simply random, but rather possesses a definite spatio-temporal structure. While this point has been recognized to some extent in the speech literature, it has yet to be fully integrated into models of speech sound generation. The variation of jet structure with flow speed, cross-sectional area, and other parameters has a definite pattern. Thus, while the physics of jet flows is rather subtle and complex, the features of jet-flow behavior relevant for production of sound by interaction between the jet and the vocal tract walls may be summed up in a few simple scaling laws.

A. Global jet structure

As described above in the Introduction, the generic flow pattern that arises in speech sound generation involves the formation and evolution of a jet, which may or may not be turbulent. A jet is quite simply a focused region of high-momentum air surrounded by stagnant air. The transition region in between the high-momentum and stagnant regions is the shear layer. This shear layer is characterized by a high transverse gradient in particle velocity, representing the change from the velocity found in the core flow of the jet and that in the surrounding stagnant region. It is also the region in which vorticity is present in the flow. Once formed, a jet does not persist for a great length downstream of its formation point. Instead, the jet spreads transversely with distance from its formation location. This occurs for two related reasons: diffusion (both “laminar” and “turbulent”) of the shear layer, and the setup of a recirculation in the stagnant region. This structure is shown in Fig. 6.

FIG. 6.

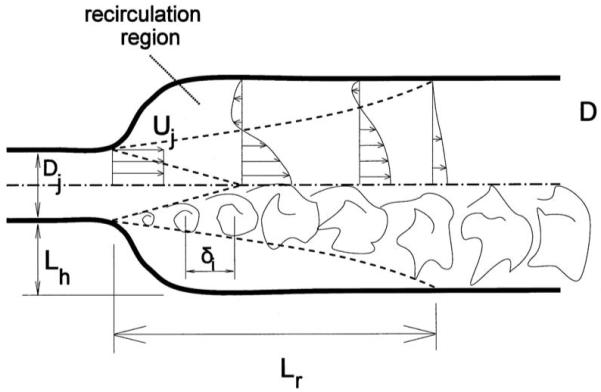
Schematic of global structure of a jet formed at a sudden expansion in a duct. The top half of the figure shows the distribution of particle velocity (and local momentum) as a function of distance from the centerline, at four axial locations. The bottom half shows the growth in size of the coherent structures through diffusion, as well as the breakdown of coherent structures. Note that the outer edge of the jet is curved due to the recirculatory flow caused by entrainment of stagnant region air by friction with the jet. D_j is the diameter of the duct at the jet formation location, U_j is the particle velocity at that location, L_h is the “step height,” L_r is the recirculation length, and δ_i is the spacing between shear layer coherent structures. Note that δ_i=U_c/f_us, where U_c is the convection speed of the vortical structure and f_us is the jet instability frequency. The relationship between L_s and L_r depends upon the Reynolds number U_jD_j/ν.

The first mechanism of jet spreading is the transverse spatial growth of the shear layer width with distance from the jet formation point. This spreading is governed by the rate of transverse diffusion of momentum. In other words, through diffusion the jet gives up its momentum to the stagnant region, so that the total momentum of the jet decreases (which is why flow separation acts as a dissipator of flow energy). Thus the jet is said to entrain the surrounding stagnant fluid. The rate of diffusion (or entrainment) depends on the local shear layer thickness—it is highest where the shear layer is thinnest, i.e., at the point of jet formation. In addition, the entrainment rate depends critically on whether the shear layer is laminar, turbulent, or something in between. For a laminar shear layer, the width δ_s grows as δ_s∼x^1/2. A turbulent shear layer tends to grow as δ_s∼x. Thus a turbulent shear layer diffuses much faster than a laminar one, due to mixing by the unsteady interaction of coherent structures, or regions over which vorticity is highly correlated (Hussain, 1986). A transitional shear layer is initially laminar, but becomes turbulent somewhere downstream of the formation point. The spreading rate is thus spatially dependent, i.e., the laminar and turbulent regions each have different rates of diffusion.

The second mechanism of jet spreading is a direct result of the entrainment of stagnant air mass in the confined stagnant region into the jet, an effect which is strongest near the jet origin. Note that the mechanism for entrainment is the one just described, in which fluid particles originally not in the jet have jet momentum transferred to them by diffusion. The entrained air moves with the jet along the jet boundary, producing a weak countercirculation near the walls to replace the stagnant air mass lost to entrainment. In this way a weak recirculatory flow is set up in the “stagnant” region. Further downstream, near the end of the recirculation zone, the countercirculation tends to spread the jet at an even faster rate than that arising from diffusion alone. Note that the spreading of the jet due to recirculation is not independent of the spreading by diffusion. Instead, jet spreading due to recirculation affects the rate of entrainment which drives the recirculation. This recursive relationship between recirculation and diffusion is typical of the nonlinear problems which arise in fluid dynamics.

If for any reason the recirculation is stronger on one side of the jet, then the jet to will tend to be pulled more strongly in that direction, so that the jet does not flow down the middle of the flow passage, but instead will cling to the wall on the side with stronger recirculation. This effect is typically observed in asymmetrical flow passages, such as those seen in the vocal tract. This phenomenon, the Coanda effect, is widely observed in nature and technology and has been proposed as an essential element in glottal flow behavior (Teager, 1980 and 1981; Teager and Teager, 1983 and 1990; Kaiser, 1983; Liljencrants, 1989), although recent experiments (Hofmans, 2003) seem to discount this notion, because the time for this flow pattern to manifest itself is much longer than a glottal pitch period. In unvoiced speech sound production, however, the time scale of the flow (the time the sound is being produced, during which the jet exists) is at least as long as the formation time for a Coanda flow pattern, so it is likely to be important for this class of sounds, particularly for fricatives.

Both mechanisms of jet spreading result in a recirculating region whose length L_r depends on the Reynolds number Re=U_jD_j/ν (U_j=jet velocity, D_j=diameter of vocal tract at jet formation location) and the change in radius L_H at the location at which the jet is formed, as shown in Fig. 6. For Re<200, L_r/L_H increases uniformly with Re. In the range 200<Re<2000, L_r/L_H is sensitive to the jet velocity profile shape and the level of flow disturbances. Above Re=2000, 6<L_r/L_H<12 (Blevins, 1984). These results for steady jet flows provide an estimate of the axial vocal-tract length a jet will persist. The spreading rate thus determines the recirculation zone length, the axial extent of the jet flow. This distance is the spatial extent over which vorticity has been injected into the flow and is able to participate in sound generation. If a change in duct area occurs downstream of the recirculation zone, then the jet vorticity will have largely reattached to the wall and will thus contribute little to sound production, as explained above.

B. Shear layer behavior

Because the acoustically relevant parts of the flow involve the vorticity concentrated in the separated shear layers, it is necessary to look more closely at free-shear layer dynamics. In general, the shear layer undergoes unsteady motion involving the coalescence of vorticity into concentrated coherent structures. While this motion is in some sense random in appearance, it has a definite temporal and spatial structure which may be described by scaling laws. This spatiotemporal structure varies with flow speed and duct area in a systematic way, allowing the scales of motion to be parametrized.

1. Shear layer formation—flow separation

Jet shear layers are simply the boundary layers which have been lifted off the wall. This process of flow separation is determined by the upstream development of the boundary layer and the shape of the wall (White, 1998; Panton, 1994; Batchelor, 1968; Bejan, 1984).

The pressure gradient force (a strong function of duct shape) and the velocity distribution of the boundary layer both determine whether the boundary layer will separate. Upstream of the constriction where a jet is formed, the vocal tract has a convergent shape, so that the flow accelerates as the minimum constriction area is approached. From the Bernoulli equation, it is clear that the static pressure decreases as the constriction is approached. The resulting pressure gradient force acts in the flow direction, augmenting the momentum in the boundary layer. Downstream of the minimum constriction area location, however, the flow begins to decelerate as the area widens, resulting in an increase in pressure with distance from the constriction, so that now the pressure gradient force progressively degrades the boundary layer momentum uniformly across the height of the boundary layer.

Although the deceleration associated with the adverse pressure gradient acts uniformly across the boundary layer, fluid particles in the outer stream have more kinetic energy to lose than those near the wall. In fact, the fluid particles near the wall are prevented from reversing course by being pulled along by the outer stream via the viscous drag in the boundary layer. If, however, the time scale of deceleration of the main flow, -(ρU_∞)/(∂p/∂x), is faster than the time for the deceleration to diffuse through the boundary layer, ${\delta }_s^2∕\nu$ (for a laminar boundary layer), then the fluid particles near the wall will reverse course, separating the boundary layer from the wall. In a steady flow, this process takes place over a finite length, so that separation occurs downstream of the location of minimum constriction. Because the process depends on the rate that momentum diffuses through the boundary layer, a turbulent boundary layer will take a longer length to separate, as the changes in the outer stream will be communicated to the flow near the wall much faster than in a laminar boundary layer. In practice, predicting the location of boundary layer separation and the manner in which the separated shear layer moves away from the wall is a difficult problem which must be solved numerically, even for highly idealized geometries.

2. Shear layer dynamics—coherent structures

How the shear layer behaves once it separates from the wall is a complex interrelationship between diffusion and the dynamics of the vorticity, which is often described in terms of the stability of the steady flow solution to perturbations in the flow (see, e.g., Drazin and Reid, 1982). Because the shear layer is highly unstable, shear layer vorticity quickly coalesces into concentrated, coherent regions of vorticity (Cantwell, 1981; Hussain, 1986). This process occurs over a range of frequencies centering on the most unstable frequency of the shear layer. In a shear layer, velocity fluctuations at a fixed point are typically caused by the passage of vortical coherent structures which convect at U_c, a fraction of the jet speed U_j, and have a length scale δ_i commensurate with the shear layer thickness δ_s. In this instance, then, the frequency of a velocity fluctuation measured at a fixed point is proportional to U_c/δ_i∼U_c/δ_s. Fluctuations with the highest amplitude will occur at the most unstable frequency of the shear layer.

Several instability modes are possible, and spatial structure of the jet is determined by the dominant mode exhibited. One of two modes in particular will be predominant. These are the symmetric (“varicose”) and antisymmetric (“sinuous”) modes, shown in Fig. 7. The symmetric mode occurs when the cross-sectional shape of the vocal tract at the constriction where the jet is formed is near circular. Examples of this geometry occur for production of /s/ or /∫/, and for whistling by blowing through rounded lips. The antisymmetric mode occurs when the constriction cross section is much wider than it is high, especially when shear layer thickness is close to the constriction radius (i.e., when the unseparated flow is fully developed) (see Bejan, 1984). A prime example of this geometric configuration occurring in speech is the glottal jet, which is also used in producing /h/. This case is probably the most extreme, since the jet used in /h/ is formed at the vocal folds; most constrictions at which jets are formed to produce unvoiced speech sound have an essentially elliptical shape.

FIG. 7.

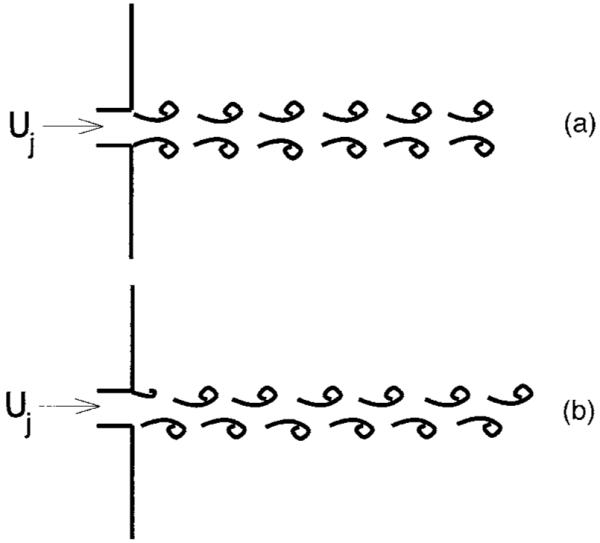
Jet instability modes. (a) Varicose (symmetric) mode, in which shear layer vorticity coalesces into vortex ring-like structures. (b) Sinuous (antisymmetric) mode, in which the shear layer vorticity coalesces into inclined vortex pair-like structures.

The “coherent structures” may be approximated as discrete vortex rings whose motion may be predicted from the vorticity distribution in the flow and the wall geometry (see Saffman, 1992). Typically, these structures convect at a fraction of the jet speed. If we consider an axisymmetric jet, the rings will be circular in shape. Otherwise, the rings will be roughly elliptical.

The vortex rings in a jet will interact with one another. For example, a ring may pass through the ring just downstream, and the two rings may pass through each other several times before merging. On the other hand, the rings themselves may instead develop azimuthally wavy structures that increase in amplitude through self-induction. These structures may then develop disturbances on yet smaller scales, until the smaller structures diffuse their kinetic energy to heat under the action of viscosity. Through this process of turbulent diffusion, what begins as a more or less coherent vortex ring becomes quite diffuse and disorganized. The degree to which turbulent diffusion dominates the dynamics of the jet depends on the Reynolds number of the flow, U_jD/ν, where U_j is the jet speed, D the diameter of the flow passage at the jet formation point, and ν the kinematic viscosity. The Reynolds number is a measure of the relative magnitudes of flow inertia to molecular dissipative (i.e., friction) forces. The higher the Reynolds number, the more inertia will dominate the dynamics, and the larger a range of spatial and temporal scales will develop (i.e., the spectrum of a flow quantity will be more broadband). Also, the higher the Reynolds number, the shorter the coherent structure lifetime, since turbulent diffusion will cause the coherent structures to lose their coherence more rapidly. At lower Reynolds number, however, the coherent structures may not even undergo the formation of smaller wavy structures, and will thus decay slowly through the action of viscosity. Thus, the coherent structures, while they will eventually lose their identity, may persist for a long time indeed, so that their effect on the flow is always felt.

When the jet is not axisymmetric, the tendency of the ring to deform rapidly from its initial coherent state is enhanced greatly (see, e.g., Saffman, 1992). In this case, the breakdown of coherent structures does not occur initially through small disturbances on the ring, but instead by the rapid deformation of the large structure of the ring itself. This greatly enhances the rate of turbulent diffusion, and hence jet spreading. For more on turbulent diffusion, and turbulent motion in general, see the discussions in Lugt (1983).

3. Scales of motion relevant for sound production

No matter how the turbulent diffusion process takes place, the process is (1) three-dimensional; (2) highly dissipative; and (3) involves vorticity dynamics. To abstract these motions into a simple model for sound generation is a formidable task unless certain simplifications can be made. First, a rationale for these simplifications comes from the aeroacoustic source expression [Eq. (2)]. First, note that no matter how three-dimensional the vorticity field, only vorticity which is oriented normal to the streamlines of U* will be involved in producing sound. In the axisymmetric vocal-tract approximation used in this paper, only the azimuthal component of the vorticity field is involved. Second, however the coherent structures evolve after forming, the initial coalescence of vorticity is preserved in some sense even while the structure is undergoing diffusion. Thus the initial spacing of coherent structures will determine the spacing of concentrations of vorticity throughout the jet. Furthermore, the coherent structures, while not truly axisymmetric, may be treated as such. Thus a jet may be modeled, for purposes of developing an aeroacoustic source model, as a train of vortex rings (axisymmetric jet) or as a train of inclined vortex pairs (planar jet).

At the Reynolds numbers and jet geometries seen in the production of unvoiced speech sounds, the jets are asymmetric and initially laminar. They will develop some coherence with length scale δ_i, which is proportional to the thickness of the jet (Bejan, 1984). Because vorticity is the curl of the velocity field, its magnitude is roughly the change in velocity through the shear layer divided by the shear layer thickness, U_j/δ_s. The circulation of a coherent structure is then roughly [see Eq. (4)] the vorticity times the area ${\delta }_s^2$ over which the structure is concentrated, so that

$$\Gamma ~\frac{U_j}{{\delta }_s}{\delta }_s^2~U_j{\delta }_s.$$ (12)

Coherent structures convect at a fraction of the jet speed, depending on the geometry, so that U_c∼U_j. The time spacing between arrival of vortices at a fixed location has order of magnitude δ_s/U_j. Thus, the frequency, f_arr, of vortex arrival at a fixed point in space is roughly the same as the instability frequency. For a jet in which the axisymmetric mode dominates, this may be given as

$$f_{us}~\frac{U_j}{D_j},$$ (13)

since δ_s∼δ_i∼D (Hussain, 1986), while for a jet in which the antisymmetric mode dominates, the result is given by

$$f_{us}~0.03\frac{U_j}{D_j}$$ (14)

[Sato (1960), Bjørnø and Larson (1984), Verge (1994)]. This can also be written as a rule in terms of the Strouhal number St= f_usD_j/U_j∼O(1) or O(10^-2), respectively. From these results, it is clear that for a jet in which the symmetric mode dominates, the most unstable frequency will be higher than for a jet of similar size and speed, but for which the antisymmetric mode dominates.

IV. UNVOICED SPEECH SOUND SOURCE CHARACTERISTICS

The aerodynamic source of unvoiced speech sounds arises from the convection of fluid particles possessing vorticity through the nonuniform potential flow associated with a nonuniform vocal-tract shape. The sharper the shape change, the more noise is produced, and the higher the frequency at which the sound is radiated. This much information is available using the approximate analysis presented above. It is possible to say more at this point about the shape of the source spectrum, using the same level of approximation in the previous sections.

In order to study the generic properties of the source spectrum, let us use the idealized flow pattern used in Sec. II B 4. The jet flow occurs in a tube of uniform cross section (radius R_p), with the exception of an obstacle of axial extent H and minimum radius R_min. The jet flow vortices convect in straight paths past the obstacle. The form of the source spectrum is simplified greatly if we further assume that the acoustic excitation may be concentrated in a point location. With this restriction, the expression for sound radiated in an infinite length tube becomes

$$\begin{array}{cc}\hfill p^{\prime }(x,t)=& \frac{-{\rho }_{\infty }\mathrm{sgn}(x-y)}{2A(1+M)}{\int }_{-\infty }^{+\infty }{\int }_A[(\omega \times \mathbf{v})\cdot {\mathbf{U}}^{\ast }\left(y\right)]dAdy\hfill \\ \hfill =& \frac{\mathrm{sgn}(x-y)}{A}S\left(y,t-\frac{\mid x-y\mid }{c(1-M)}\right),\hfill \end{array}$$ (15)

where S is the source strength located at x=y, the source location. The square brackets denote that the integrand is evaluated at the retarded time t-y/(c(1-M)). For a single vortex pair or ring passing through the source region, S has the form shown in Fig. 4(b), as described in Sec. II B 4. In the finite-length vocal tube case, the lip sound pressure will be the convolution of S(t) with the transfer function of the tube between the source location and the lips.

A. Relation between source expression for a jet to that for a single vortex

To describe the source function for the convection of a train of vortices of arbitrary arrival to the source region, the source function may be written as the convolution of the waveform W(t) for a single vortex, scaled by the source amplitude corresponding to each vortex, with an arrival function I(t), which is a series of delta functions whose phase is adjusted to the arrival time of the vortex

$$S(y,t)=W{\left(t\right)}^{\ast }I\left(t\right)={\int }_{-\infty }^{\infty }W\left(\tau \right)I(t-\tau )d\tau .$$ (16)

This behavior is shown in Fig. 8(a) for a single vortex ring and in Fig. 8(b) for a train of vortex rings which arrive at different times. In Eq. (15), W(t) is a normalized version of S(t) shown in Fig. 4(b), since it represents the contribution of a single vortex ring of unit circulation passing through the constriction at speed U_c∼U_j/2. As explained above, the characteristic time scale of this waveform is either H/U_c or δ_ʋ/U_c, the time during which a given jet vortex induces a force on the obstacle. This waveform also contains the information regarding both the shape of the obstacle and the vortex ring path, as explained in Sec. II. Thus, W(t) depends on both the vortex path and the shape of the vocal tract

$$W\left(t\right)={\rho }_{\infty }{R}_{\upsilon }\frac{\pi A}{A\left(x\right)}\frac{U_j}{2}\sin \alpha \left(t\right).$$

I(t) for a train of N vortex rings is given by

$$I\left(t\right)={\rho }_{\infty }\sum _{n=0}^N\delta (t-n{T}_{\mathrm{arr}}+{\theta }_n)\frac{{\left(U_j\right)}_n^2}{2}(T_{\mathrm{arr}}+{\Phi }_n).$$ (17)

Here, δ(t) is the Dirac delta function, T_arr the mean period of vortex ring arrival in the source region, and Φ the vortex arrival phase jitter. Note that T_arr=1/f_arr≈1/f_us, or the reciporcal of the jet instability frequency. Note also that the circulation of the nth vortex ${\Gamma }_n={\left(U_j\right)}_n^2\Delta t_n∕2$ is included in this function because it is proportional to the time Δt_n=(T_arr+Φ_n) since the last vortex arrived in the source region, and because the jet velocity may have changed since the vortex was injected into the flow at the jet formation point (which happens in voiced fricatives and plosives, as well as aspirative sounds in voicing). The vortex arrival phase jitter, Φ, may be considered as a random process of zero mean and a variance σ_Φ which depends on the jet Reynolds number and distance from the jet formation point. The larger σ_Φ becomes, the shorter the coherence time scale of the I(t) time series. Note that for the low-frequency sound production discussed in this paper, this model applies equally to the antisymmetric and axisymmetric jet modes discussed in Sec. III. Any differences in the distribution of vorticity between the two instability modes are manifested in the form of W(t).

FIG. 8.

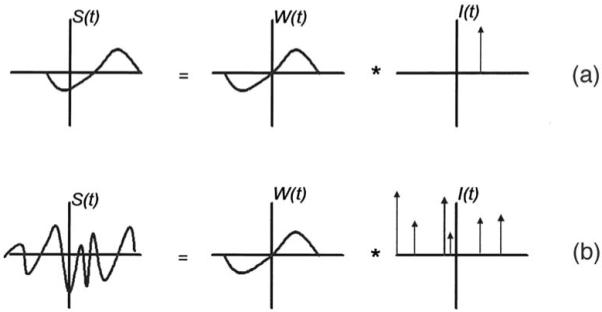
Aeroacoustic source expressed as a convolution of W(t) and I(t). W(t) is the spectrum of a unit-circulation vortex ring passing through the constriction at speed U_j, reflecting the shape of the duct and the path of the vortex. I(t) is a circulation-weighted function indicating the arrival in the source region of a vortex ring. (a) Single vortex ring. (b) Many vortex rings. The broadband behavior of S(t) arises due to the random phase of the time of arrival of each successive vortex ring into the source region.

B. Form of source spectrum for unvoiced speech sounds

Having expressed the aeroacoustic source time series as the convolution of a time series describing the passage of a single vortex ring and the statistics of arrival of a train of vortex rings, the aeroacoustic source spectrum due to a jet modeled as in Sec. III may now be studied. The spectral shape of W has been shown in Fig. 4(c). W(f) has a single peak centered at roughly U_c/ℓ, with a bandwidth of roughly that amount, as discussed in Sec. II B 3, where ℓ is either the constriction length H or the vortex core radius δ_i, as appropriate. (Note that here, the radius δ_ʋ of the vortex ring used to model the coherent structure of the jet has core size which is proportional to the coherent structure spacing δ_i∼δ_s .) In other words, the faster the vortex passes through the source region (either because of either high convection speed or narrow obstacle), the broader the peak.

The spectral behavior of I is shown in Fig. 9. The spectral shape of I(f) depends critically on the statistics of σ_Φ, demonstrated by the following limiting cases. Figure 9(a) shows the case for σ_Φ=0, where I(t) is periodic, and its spectrum is a series of sharp peaks occurring at harmonics of the vortex arrival frequency f_arr=1/T_arr= f_us. As σ_Φ increases, these peaks become broader, and the amplitude of the harmonics decays with frequency, until the spectrum becomes broadband with a peak at the mean vortex passage frequency, as shown in Fig. 9(b).

FIG. 9.

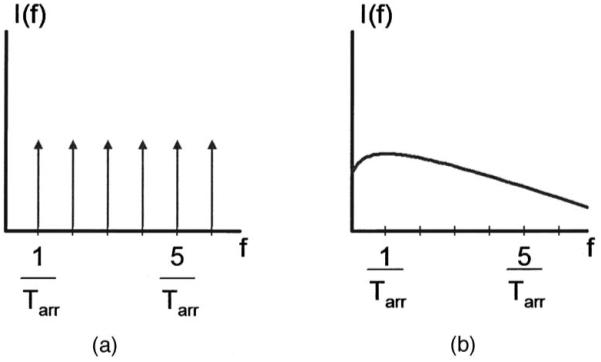
Frequency-behavior the arrival indicator function I, showing dependence on the variance of the random process describing the arrival phase Φ. (a) I(f) for σ_Φ⪡1 (highly periodic flow), as found in whistling, where the sound field becomes phase-locked to vortex shedding at the separation point, resulting in a spectrum composed of a fundamental (the jet instability frequency, 1/T_arr) and its harmonics. (b) I(f) for σ_Φ⪢1 (highly turbulent flow), as usual in unvoiced speech sounds, where the peak occurs at the jet instability frequency, but which exhibits no tonal quality.

Because the source function S(t) is the convolution of W and I, the spectrum of S is the product in frequency space of W(f) and I(f)

$$S\left(f\right)=W\left(f\right)I\left(f\right);$$ (18)

the vortex arrival spectrum could be said to filter the contribution due to a single vortex ring. The character of S(f) depends on which of W(f) and I(f) has narrower peaks, as shown in Fig. 10. If I(f) is more or less periodic, then I(f) will consist of narrow harmonic peaks and will dominate the spectral content of S(f). This behavior is illustrated in Fig. 10(a). On the other hand, if I(f) is broadband, and is wider than W(f), then W(f) dominates the spectral content of S(f). This behavior corresponds to the situation shown in Fig. 10(b). In practice, unvoiced speech sounds such as fricatives and plosives correspond more closely to the latter case. The former case is more akin to the occurrence of a strong flow-acoustic interaction such as whistling, where vortex shedding and the resonant sound field become phase locked (see Blake, 1986; Hirschberg et al., 1989), producing a highly periodic jet vortex structure. Other speech sounds which are likely to display this type of behavior are aspiration noise in voicing and voiced fricatives, although in these cases the sounds still maintain a broadband character because of two effects: first, the time scale of modulation of the jet velocity is much longer than the vortex shedding period; second, the amplitude of the jet modulation is small compared to the jet speed. The first effect applies to both voiced fricatives and aspirative noise because the modulation of the jet by the resonant sound field occurs at frequencies on the order of the voice frequency (∼100 Hz), while the jet instability is on the order of 1-10 kHz. In aspirative noise, however, the modulation of the glottal jet is complete (the jet shuts off either completely or close to completely once every pitch period), so the second effect applies only to voiced fricatives.

FIG. 10.

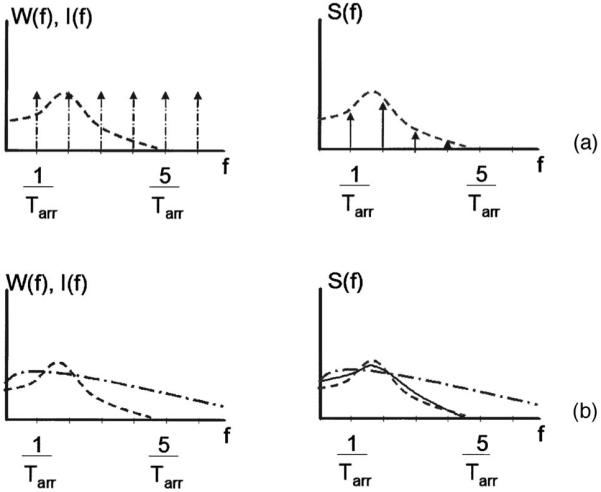
Aeroacustic source spectrum S(f) as a function of σ_Φ . Because S(f) is the spectrum of a single vortex filtered by the arrival function spectrum I(f), the statistics of the vortex ring arrival determine the character of the source spectrum. S(f) ―; I(f)-·-·, W(f) ---. (a) For σ_Φ⪡1, the jet is periodic, and I(f) exhibits tonal behavior, with tone levels modulated by shape of (W(f), reflecting both vortex path and wall shape. (b) For σ_Φ⊢1, I(f) is broad enough (flow is highly turbulent) that the shape of W(f) limits the shape of the source spectrum. In this case, the wall shape and vortex path dominate behavior of S(f).

V. SUMMARY

This paper presents an outline of the theoretical groundwork necessary for understanding and predicting the characteristics of aerodynamically generated speech sounds, using as much as possible the fundamental principles of air motion embodied in the fields of aerodynamics and aeroacoustics. The presentation focused initially on a generic picture of speech sound production, emphasizing that all speech sounds involve the unsteady flow through a constriction in the vocal tract, where a jet is produced. This jet interacts with the vocal-tract geometry downstream of its formation, inducing forces on the vocal-tract walls. These forces then produce sound. An expression for the sound field in terms of jet vorticity and the vocal-tract shape was then presented. The sound field was seen to be determined uniquely by the interaction of jet vorticity and the shape of the vocal tract, as reflected in both vorticity trajectories and the steady flow streamline shape. Thus, the aeroacoustic source characteristics depend on the shape of the duct, and are particularly powerful near “sharp” or discontinuous changes in areas such as those seen at the teeth. A definite “obstacle” is not necessary for sound generation, only the flow of jet vorticity through a change in vocal-tract area.

Jet motion relevant for sound production was shown to be characterized by the jet velocity and diameter, and by the temporal spacing of concentrations of vorticity (vortices). Using scales of motion characteristic of internal jet flows, a scaling law for aerodynamically generated speech sounds was derived by convolving the vortical source term of the wave equation with the Green’s function for plane-wave propagation in a duct.

An expression for the aeroacoustic source spectrum was developed as the convolution two waveforms. The first is a “shape” function, the sound source waveform due to the passage of a single, unit circulation vortex ring through the source region, which depends on the wall shape and vortex path. The second is an “arrival” function, a series of pulses, each of which indicates the phase of arrival of each vortex in the source region. Each pulse in this function is scaled by the aeroacoustic source strength of each vortex. The vortex arrival statistics determines whether the source spectrum is dominated by the vorticity field arrival statistics or the wall shape. If the vortex arrival time series is highly coherent and periodic, then it will dominate character of the source spectrum, which will consist of discrete peaks filtered by the shape function. On the other hand, if the vortex arrival time series is broadband, the wall shape will dominate the character of the source spectrum.

The results presented here represent a formal development of aeroacoustic source spectral characteristics for unvoiced speech sounds at low frequencies. For an application of these ideas to pipe flow noise prediction and to speech synthesis, see Krane et al. (2005), and Sinder (1999).

LIST OF SYMBOLS

A

vocal tract cross-sectional area

A_min

vocal tract cross-sectional area at axial location of maximum constriction

A_ʋ

cross-sectional area of vortex core=$\pi {\delta }_{\upsilon }^2∕4$

B

total enthalpy

B’

total enthalpy fluctuation

c

speed of sound

D _j

vocal-tract diameter at jet formation point

e_θ

unit vector in the direction of vorticity in vortex ring, points in θ direction

F(t)

aerodynamic force on vocal tract walls

f_arr

frequency of vortex ring arrival in source region

f_n

nth resonance frequency of vocal-tract acoustic pressure

f_us

shear layer instability frequency

f_z

frequency of zero of vocal-tract acoustic pressure

G

Green’s function=G(x,t;y,τ), the acoustic transfer function between source location y and receiver position x

H

axial length of constriction

H(t)

Heaviside function

I(t)

vortex ring arrival function, weighted by vortex ring circulation

L_h

transverse distance between jet formation point and wall downstream of jet formation point

L_f

axial length of front cavity, between jet formation point and lip termination

L_r

axial length of recirculation zone downstream of jet formation

L_s

axial distance between jet origin and source location

ℓ

length scale of airflow

M

Mach number ʋ/c

R_min

radius of minimum vocal-tract constriction

R_p

radius of duct away from constriction

R_ν

vortex ring radius

Re

Reynolds number Uℓ/ν

S(t)

aeroacoustic source strength

St

Strouhal number, f ℓ/U

T_arr

mean period for vortex rings arrival in source region

U

particle velocity of air in regions far from constriction

U*

velocity disturbance to unit incident flow, caused by change in vocal-tract shape

U_c

convection speed of vortex ring in jet

U_j

jet speed

u’

acoustic particle velocity

ʋ

air particle velocity

W(t)

source strength function for vortex ring of unit strength

x

observer position

y

source position

α

angle between U* and v for vortex ring in source region

Γ

vortex circulation, ($\pi {\delta }_{\nu }^2$)

γ

reflection coefficient of vocal tract terminations

Δt

time interval between vortex arrivals in source region=T_arr+Φ

δ(t)

Dirac delta function

δ_i

spacing between coherent structures in jet

δ_ʋ

vortex ring core diameter

δ_b

boundary layer thickness

θ

azimuthal coordinate, tangent to vortex ring

ʋ

air kinematic velocity

ρ

air density

ρ^∞

air density in jet

ρ’

acoustic density fluctuation

σ_Φ

variance of random process describing vortex arrival in source region

τ

source time

Φ

vortex arrival phase jitter

ϕ*

velocity potential of U*, U*=∇ϕ*

ω

vorticity, =∇×v

APPENDIX: GREEN’S FUNCTION SOLUTION TO CONVECTED WAVE EQUATION

The convected wave equation [Eq. (1)] may be solved using a Green’s function, which is defined by the following equation:

$$\frac{1}{c^2}\frac{D^{2}G}{D{t}^2}-\frac{{\partial }^{2}G}{\partial x^2}=\delta (\mathbf{x}-\mathbf{y})\delta (t-\tau ),$$ (A1)

and the appropriate boundary conditions. Here, G(x,t|y,τ) is the Green’s function, x is the location of the observer, t is the time when the observer feels the effect of the source, y is the location of the impulsive source, and τ is the time during which it is active. From this equation, it is clear that the Green’s function is the response of the wave equation to a spatially localized impulsive source, i.e., it is a spatially dependent impulse response function. In general, the solution to the boundary value problem has the form (Haberman, 1997)

$$\begin{array}{cc}\hfill B^{\prime }(x,t)=& {\int }_{-\infty }^t{\int }_A{\int }_0^{L}G(x,t\mid y,\tau )\nabla \cdot (\omega \times \mathbf{v})d\tau dAdy\hfill \\ \hfill & +{\int }_A{\int }_0^L[\frac{\partial B^{\prime }}{\partial \tau }(y,\tau =0)G(x,t\mid y,\tau =0)\phantom{]}\hfill \\ \hfill -& \phantom{[}{B}^{\prime }(y,\tau =0)\frac{\partial G^{\prime }}{\partial \tau }(x,t\mid y,\tau =0)]dAdy\hfill \\ \hfill -& c^2{\int }_{-\infty }^t[B^{\prime }(y=0,\tau )\frac{\partial G^{\prime }}{\partial y}(x,t\mid y=0.\tau )\phantom{]}\hfill \\ \hfill -& \phantom{[}\frac{\partial B^{\prime }}{\partial y}(y=0,\tau )G(x,t\mid y=0,\tau )]d\tau .\hfill \end{array}$$ (A2)

Note that the first integral gives the contribution due to the aeroacoustic source, and must be taken not only over the vorticity in the flow, but vorticity in the vocal tract wall boundary layers. The second and third integrals contain terms which are determined by the initial and boundary conditions for both G and the acoustic variable B’. It should be noted that the Green’s function is not unique in that there is considerable freedom in choosing what boundary conditions G satisfies. In particular it is sometimes possible to define a tailored Green’s function which simplifies greatly the form of Eq. (6). For more on solving boundary value problems using Greens’s functions, see Crighton et al. (1992), or Morse and Feschbach (1953).

All but the first term in Eq. (6) give the effect of boundary conditions for the finite-length vocal tract. For simplicity, let us first consider an infinite length tube. This tube is identical to that shown in Fig. 1, except that there are no lungs and no mouth opening. The solution for the finite-length vocal tract will then be constructed from the infinite tube solution using the method of images. A tailored Green’s function for the problem has been derived by Howe (1975), given by

$$G(x,t\mid y,\tau )=\frac{c}{2A}H\left(t-\tau -\frac{x}{c(1+M)}+\frac{{\varphi }^{\ast }\left(y\right)}{c(1+M)}\right),$$ (A3)

where H is the Heaviside function

$$H\left(f\right)=\{\begin{array}{cc}1,\hfill & f>1\hfill \\ 0,\hfill & f<1,\hfill \end{array}\phantom{\}}$$

ϕ* is the velocity potential of a unit steady irrotational flow velocity field U/U₁=∇ϕ*=U*, and A is the cross-sectional area of the pipe everywhere except in the region of the obstacle. This Green’s function describes low-frequency acoustic wave propagation in a nonuniform duct with a steady flow. Note that it differs from the free-space Green’s function for planar waves only in the correction factor ϕ */(c(1 +M)), which is a correction to account for both the diffraction through the potential flow disturbance due to the change in duct shape and the motion of vortical sources through this disturbance (Howe, 1975). Again, the convenience of using this tailored Green’s function is that the first term need only consider the vorticity that has been injected into the flow, away from the walls. In other words, the acoustic effect of incompressible wall pressure fluctuations (which sum to a net unsteady force on the vocal-tract walls) due to vorticity convection are lumped into the first integral containing only terms relating to the vorticity dynamics in the flow itself. Note that this Green’s function only accounts for the dipole source caused by aerodynamically generated forces on the walls, not for the direct radiation from the jet vorticity itself. The direct radiation is less efficient, by a factor of Mach number squared (Howe, 1975), so it is not considered here.

The solution for B’ is then found by convolving the Green’s function with the source term ∇·(ω×v)

$$B^{\prime }(x,t)=-\frac{\mathrm{sgn}(x-y)}{2A(1+M)}{\int }_A[\omega \times \mathbf{v}\cdot {\mathbf{U}}^{\ast }]dAdy,$$ (A4)

where sgn(x-y) is the signum function

$$\mathrm{sgn}(x-y)=\{\begin{array}{cc}1\hfill & \text{for}x-y>0\hfill \\ -1\hfill & \text{for}x-y<0\hfill \end{array}\phantom{\}},$$

so that the acoustic total enthalpy (and thus the pressure) changes sign across the source. In arriving at this form of the integral, use has been made of the property of convolution integrals

$$f^{\ast }\mathcal{L}\left\{g\right\}=\mathcal{L}{\left\{f\right\}}^{\ast }g,$$

and because ∇H(f)=δ(f)∇ f, g(f’)*δ(f-f’)=g(f), where $\mathcal{L}$ is any linear operator (such as ∇, in this case), and * denotes a convolution relationship [f *g=∫ f(t)g(t-τ)dτ], and δ(f) is the Dirac delta function.

Using the definition of total enthalpy, the solution may be rewritten in terms of sound pressure

$$\begin{array}{cc}\hfill p^{\prime }(x,t)\approx & {\rho }_{\infty }{B}^{\prime }(x,t)\hfill \\ \hfill =& -{\rho }_{\infty }\frac{\mathrm{sgn}(x-y)}{2A(1+M)}{\int }_A\int [\omega \times \mathbf{v}\cdot {\mathbf{U}}^{\ast }]dAdy.\hfill \end{array}$$ (A5)