Assessing the impact of the addition of dendritic cell vaccination to neoadjuvant chemotherapy in breast cancer patients: A model‐based characterization approach

What is already known about this subject

• Breast cancer is a widely studied disease, and tumour growth models have already been described in this setting.

What this study adds

• The quantification of the immunotherapy effect on tumour growth dynamics of nonmetastatic patients is a novelty in this area.

1. INTRODUCTION

Breast cancer (BC) is the most commonly diagnosed malignancy in developed countries1, 2 with a lifetime risk of developing being 1 in 8 women.3 Despite significant improvements in survival outcomes over the past 2 decades, BC remains the most common cause of cancer‐related mortality among women, accounting for 15% of all cancer‐related deaths.1

Different BC subtypes according to their genetic profile and molecular expression are defined, with important prognostic and predictive implications.4, 5, 6 The rate of pathological complete responses (pCR) after neoadjuvant chemotherapy (NAC) approaches 15% in luminal tumours and almost a 50% in Her‐2 pure BC.7 Although pCR has been identified as a surrogate endpoint for outcome in BC, triple negative (TN) and luminal tumours with low progesterone receptor expression represent an exception, having a worse long‐term outcome despite the achievement of pCR.8 Additionally, luminal tumours outcomes are generally good whether they achieved pCR or not. Moreover, a 15% discordance has been identified in pCR among the lymph nodes and the primary breast tumour in the same patient,9 suggesting that other surrogate endpoints could reflect better the biological heterogeneity of BC when related to outcome.

From a biological perspective, either resistance to NAC or the absence of targeted therapies could explain differences in pCR in BC subtypes. This, together with lack of maintenance therapy in TN BC, translates into distant relapse of the disease, and drives the need of looking for new therapeutic approaches.10 In this scenario, the immunotherapy is an adequate and innovative solution to train the patients' own immune system to target cancer cells.11, 12 Dendritic cells (DC) are 1 of the most potent antigen‐presenting cells and are capable of priming naïve T‐cells, activating the immune response.13, 14 Therefore, immunotherapy with DC‐based vaccines is a very attractive approach to treat cancer, offering the potential for high tumour‐specific cytotoxicity13, 15 and a synergistic effect when combined with chemotherapy. In this respect, an increasing number of clinical studies16, 17, 18 demonstrate that vaccination with DC is capable of inducing antitumour‐specific response in BC, while being safe and well tolerated.

Patient response is evaluated through the results obtained from tumour scans and measurements of circulating biomarkers, as well as with additional data from the disease progression. In general, each item from the battery of response data is reported in an isolated way, hampering the quantification of their impact to clinical outcome. This could be beaten by an integrated analysis of all the information available in the clinical setting.

Population disease progression and pharmacokinetic/pharmacodynamic (PK/PD) models as part of the pharmacometrics platform allow the integrated analysis of all the information, and provide a tool to predict outcomes, and to improve and optimise the therapies administered (dosing schedules). Once established and validated, mechanistic PK/PD models offer a series of in silico related possibilities covering from optimizing response follow‐up designs and exploring alternative therapeutic scenarios, to personalize treatments based on late predictions from early clinical longitudinal response.19 Even though BC is a widely studied disease, PK/PD modelling efforts in BC have been focused on advanced or metastatic stages of the disease, relating tumour size (TS) at a certain time point with survival.20, 21 However, modelling exercises applied to earlier stages of the disease can have a greater impact on the patients' outcome.

In this setting, the current work aims to develop a computational PK/PD model describing, mechanistically, the effect of immunotherapy in naïve locally Her‐2‐negative BC patients treated with autologous DC vaccines together with standard NAC and how such effects are modulated by patient's covariates, and translate either to TS, biomarker profiles, and beyond as predictors of progression‐free survival (PFS). The model is established based on data from 83 case–control patients, and was externally validated in a different cohort of 111 patients.

2. METHODS

2.1. Patient population

Eighty‐three treatment‐naïve patients were selected with locally or locally advanced BC and without overexpression of Her‐2 that could benefit from NAC. Thirty‐nine patients received DC vaccines together with NAC (21 of them from the multicentre phase II pilot clinical trial—EudraCT number 2009–017402‐3622; and 18 under compassionate use approved by the Spanish Institute of Health). Forty‐four patients, diagnosed and treated at the University Clinic of Navarra, with the same NAC schedule represented the control group. Table 1 provides a summary of patient characteristics.

Table 1.

Summary of patient characteristics corresponding to the study (control and vaccinated patients) and validation dataset

		Vaccinated (n = 39)	Control (n = 44)	Validation dataset * (n = 111)
Age (y) a		45.68 (36.15–74.48)	55.31(26–84.35)	47.6 (28.69–83.93)
Body mass index (kg/m 2 ) a		24.04 (17.41–35.93)	24.55 (18.92–42.74)	23.36 (18.19–39.88)
Subtype b	LA	10 (25.64)	13 (29.54)	27 (24.32)
	LB	12 (30.77)	18 (40.91)	60 (54.04)
	TN	17 (43.59)	13 (29.54)	24 (21.62)
Stage b	I	‐	2 (4.55)	‐
	II	25 (64.10)	26 (59.09)	111 (100)
	III	10 (25.64)	14 (31.82)	‐
	IV	4 (10.26)	2 (4.55)	‐
Hormonal status b	Menopausal	11 (28.20)	25 (56.82)	47 (42.34)
	Perimenopausal	2 (5.13)	2 (4.55)	6 (5.4)
	Premenopausal	26 (66.67)	17 (38.64)	57 (51.35)
	Pregnant	‐	‐	1 (0.9)
	Men	‐	‐	1 (0.9)
Tumour size diagnosis a	US (mm)	30 (0–100)	29.5 (0–84)	33 (0–111)
	MRI (mm)	54 (0–160)	42 (0–132)	62 (14–234)
Pathological response b Miller and Payne—T
I		3 (7.69)	3 (6.82)	‐
II		1 (2.56)	12 (27.27)	‐
III		15 (38.46)	16 (36.36)	‐
IV		8 (20.51)	7 (15.91)	‐
V		10 (25.64)	6 (13.64)	‐
Not available		2 (5.13)	‐	‐
Circulating biomarkers a
LDH diagnosis (IU/L)		207 (143–382)	225 (145–357)	165 (84–196)
CEA diagnosis (ng/mL)		1.2 (0.3–6.6)	2.05 (0.369–52.9)	2.03 (0.3–12.0)
CA15‐3 diagnosis (IU/mL)		18.7 (3.7–63.0)	18 (5.7–224.9)	15.5 (6.4–32.0)
PROGRESSION b		5 (12.8)	8 (18.18)	21 (18.91)
Median follow‐up (months)		64.60	66.14	113

^aShowing median (range).

^bShowing count (percentage).

^* No vaccination.

CA15‐3, carcinoma antigen 15‐3; CEA, carcinoembryonic antigen; LA, luminal A; LB, luminal B; LDH, lactate dehydrogenase; MRI magnetic resonance imaging; TN, triple negative; US, ultrasound.

All patients provided informed consent consistent with the International Conference on Harmonization of technical Requirements for Registration of Pharmaceuticals for Human Use—Good Clinical Practice and local legislation. The study was performed in accordance with the declaration of Helsinki and was approved by the institutional review board of the ethics committee.

2.2. Treatment

2.2.1. Chemotherapy

All patients received NAC with a sequential treatment consisting of 4 cycles of dose‐dense epirubicin plus cyclophosphamide with granulocyte‐macrophage colony‐stimulating factor support (schedule A), followed by a second schedule of 4 cycles each 21 days of docetaxel (schedule B) according to standard protocols. Changes to the original protocol in terms of drugs or dose administered were recorded, and permitted due to toxicity or specific patients' requirements.

2.2.2. Immunotherapy

In addition to the NAC treatment described above, 39 patients received vaccination with monocyte‐derived autologous DC loaded with autologous tumour lysate. The vaccination plan included at least 6 vaccines, with the first 1 administered between the last dose‐dense epirubicin plus cyclophosphamide and the first taxane‐based cycle of NAC. Vaccines were administered through intradermal injection every 3 weeks in the first 6 doses. Afterwards, 4 vaccines were administered every 2 months and, finally, quarterly until the end of the vaccines. DC vaccines were prepared according to the standard procedure23 under good manufacturing practices at the University Clinic of Navarra's Cell Therapy Area.

A schematic representation of the treatment program is provided in Figure 1A, along with the complete information of NAC received by the patients under study (Figure 1B), and from the validation dataset (Figure 1C).

Figure 1.

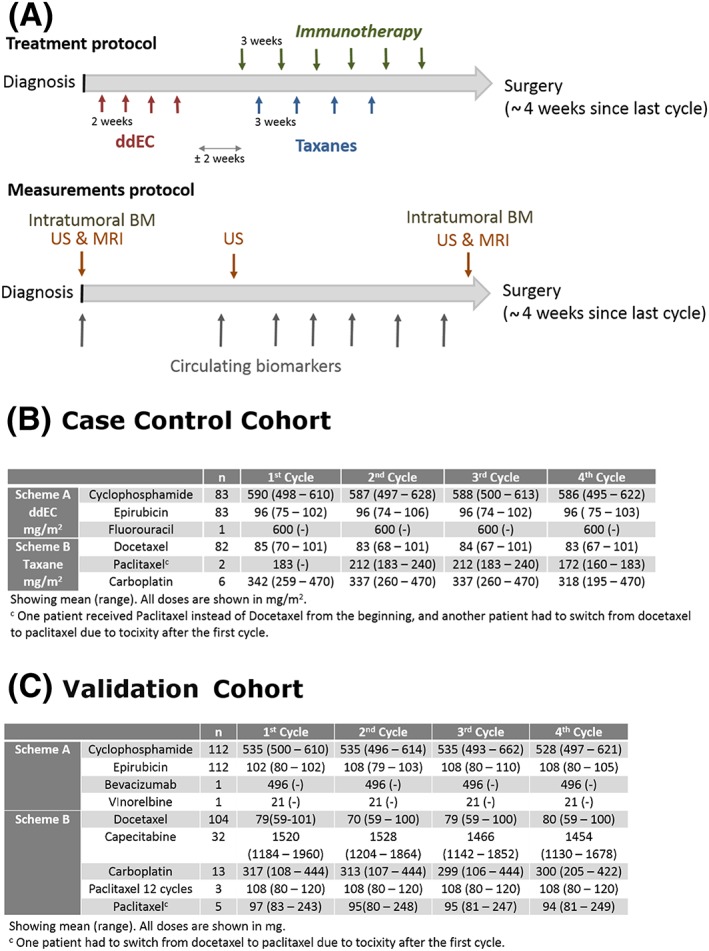
Information regarding treatment administered. Ai, NAC and IT administration schedules (upper); Aii, measurements sampling protocols (lower). B, C, Oncology treatments summarized as median (and range values in parenthesis) corresponding to the trial and validation datasets, respectively. Chemotherapy (CT), biomarkers (BM), ultrasound (US), magnetic resonance imaging (MRI)

2.3. Assessment of tumour dynamics

Tumour assessment was performed through imaging techniques, either through ultrasound (US; Mylab 60; Esaote, Genoa, Italy) or magnetic resonance imaging (MRI; Aera; Siemens, Erlangen, Germany) before the beginning of the NAC (US and MRI), between schedules (US), and at the end of the entire course of NAC, before surgery (US and MRI). The number of TS observations was 326, of which 206 were assessed by US, and 120 by MRI. The sum of the longest diameters was used for modelling purposes. The limit of quantification was set to 5 and 6 mm for US and MRI, respectively.

2.3.1. Measurement of circulating biomarkers

Blood samples for measurement of lactate dehydrogenase (LDH), carcinoembryonic antigen (CEA) and carcinoma antigen 15‐3 (CA15‐3) were collected from each patient before the beginning and between NAC cycles. Table 1 lists the median and range values of the circulating biomarkers. A description of the methodology used to quantify biomarker concentrations is provided in the Supplementary material S1.

2.4. Disease progression

PFS was defined as time to disease progression (TS increment or metastasis apparition) or death within 10 years after diagnosis. The Response Evaluation Criteria in Solid Tumours (RECIST)24 was used in the US and MRI performed.

2.5. Mixed‐effect modelling

In the context of longitudinal data analysis (multiple measurements are made on the same subject over time), parameters from a model can be estimated by mixed‐effect modelling techniques, using all the information collected from different individuals.

The advantages of using mixed effects in an analysis are that observations within a subject may be correlated and, in addition to the estimation of the model structural parameters, the existing interindividual variability can be estimated. The structural parameters follow a statistical distribution, which is often assumed to be log‐normal, so negative values can be avoided. This distribution describes the variation of the parameter values and, therefore, reflects the interindividual variability (IIV). The second level of variability is the residual variability, as it represents the underlying error of the measurements.25

The structural model is built based on the entire population under analysis, not on data from 1 particular subject, and therefore does not require rich data, nor is there a need for structured time schedules. This explains why sparse data can be used in the development of this kind of mathematical models.

2.6. Data analysis

A nonlinear mixed effects model, also known as the population approach,26 was used to study and establish the link between treatment, tumour progression, biomarker dynamics and PFS data, consisting of a structural model and a statistical model, therefore accounting for variability within the population.27

Longitudinal tumour and circulating biomarker data were logarithmically transformed. IIV was modelled exponentially implying a log‐normal distribution of the individual model parameters. Nondiagonal elements of the Ω variance–covariance matrix were tested for significance. Residual error was described with an additive model in the logarithmic domain. Data reported as below the limit of quantification (BLQ) of the analytical determination technique were also included in the TS analysis, treated as censored information and modelled accordingly.28 For the analysis of the data, the first‐order conditional estimation method with LAPLACIAN, available in the population analysis software NONMEM version 7.329 was used.

2.7. Tumour growth inhibition model

Equation 1 describes tumour dynamics (TA) as a function of 2 processes: (i) tumour progression (represented by the term K_P × TA accounting for an exponential growth governed by the first order rate constant [K_P]), and (ii) treatment induced tumour regression or lysis (LYSIS, represented by the term f [E_Drug] × TA × KLYS, where KLYS is a constant that modulates the lysis effect).

$$\frac{\mathit{dTA}}{\mathit{dt}}=K_P\times \mathit{TA}-f\left(E_{\mathit{\text{drug}}}\right)\times \mathit{TA}\times \mathit{\text{KLYS}}$$ (1)

At time of diagnosis, TA was assumed to be equal 1, and tumour lysis equal to zero. The parameters TS_US and TS_MRI were used to scale TA to describe tumour size observations obtained by US or MRI, respectively. This was possible due to the fact that measurements obtained by US and MRI were obtained at the same time and a correlation between them could be established.

The term f (E_Drug), represents both drug exposure and effects. Plasma or serum concentrations were not available for any of the drugs administered to patients. However, the current modelling strategy predicts drug exposure based on the K‐PD approach30 using the complete dosing history recorded for each patient, accounting for dose modifications, as shown in in equation 2.

$$\frac{d{C}_{{\mathit{TRT}}_n}}{\mathit{dt}}=-K_D\times C_{{\mathit{TRT}}_n}$$ (2)

Where C_TRTn represents the predicted active concentrations for the n NAC treatment. Although the parameter KD should be treatment specific and mimics the elimination rate constant of each of the drugs modelled, in our case and due to the lack of data regarding drug concentrations, drugs that were given simultaneously were grouped together, and treated as the same treatment in terms of efficacy, differing in dose intensity. Hence, based on the dosing records, drugs given to a patient at the same time were treated as the same drug. Therefore, with the available data, only 1 KD could be estimated because no differences between chemotherapy treatments is done. In order to modulate the effect of the drugs administered and their effect on tumour shrinkage, a constant (EFF) is introduced.

Vaccine exposure (θ_Vac) was arbitrarily set to 1 for those patients not receiving immune‐therapy treatment and estimated otherwise. Equation 3 shows the full model for drug effects.

$$\mathrm{f}\left({\mathrm{E}}_{\text{Drug}}\right)={\mathrm{K}}_{\mathrm{D}}\times {\mathrm{C}}_{\text{TRTn}}\times \mathrm{EFF}\times {\mathrm{\theta }}_{\mathrm{Vac}}$$ (3)

Where θ_Vac is the parameter accounting for the modulating effects of the vaccine on the tumour response elicited by chemotherapy.

As shown in equation 3, it is assumed that the rate of drug elimination (K_D × C_TRTn) is the driver of drug effect, and an EFF parameter is also estimated. As suggested by Jacqmin et al. in 2006,30 the elimination rate constant from the elimination compartment (Kd) estimates the time for equilibrium between the rate of drug administration and the observed response to drug action. However, the parameter EFF combines both PK and PD, and represents the apparent potency of the drug at steady state.

2.8. Biomarker model

The time course of circulating levels of LDH, CEA and CA15‐3 were described as a function of a zero order synthesis (K_in—modulated by tumour lysis), and a first order degradation processes (K_out), as shown in equation 4. The parameter θ_LYS accounts for the increasing levels of biomarkers as a function of tumour lysis.

$$\frac{d{\mathit{BM}}_m}{\mathit{dt}}=K_{{\mathit{\text{in}}}_m}\times \left(1+{\theta }_{\mathit{LYS}}\times \mathit{\text{LYSIS}}\right)-{K_{\mathit{\text{out}}}}_m\times {\mathit{BM}}_m$$ (4)

Where the suffix m corresponds to LDH, CEA or CA15‐3.

Tumour size and circulating biomarker data were analysed simultaneously. The same residual error was estimated for the 3 biomarkers.

2.9. Model for PFS

PFS was defined as time to disease progression or death within 10 years after diagnosis. Study withdrawals due to disease progression were considered informative dropouts, which were analysed simultaneously with TS and biomarker dynamics to describe the link between these and the probability of having disease progression.31

PFS was modelled as a time to event variable by means of a survival analysis, allowing identification of the underlying hazard function (instantaneous rate of event), from which the probability of remaining in the study can be obtained by integrating the hazard with respect to time. First, different distributions (exponential, Weibull, log‐logistic or Gompertz) were explored to see which better characterized the underlying hazard function.

Second, different expressions of tumour size and biomarker dynamics, along with other covariates that are shown in Table 1 were evaluated as potential modulators of the hazard.

2.10. Covariate selection

The stepwise covariate model building procedure implemented in Pearl Speaks NONMEM software32 was used to build the covariate model. The stepwise covariate model procedure is based on a forward inclusion followed by a backward deletion approach and, during these, the levels of significance used to incorporate the model and to keep a covariate in the model were set to 0.05 and 0.001, respectively.

Significant covariates were associated with the parameters using the general covariate model shown in Supplementary material S2.

2.11. Model selection criteria

Selection among models was based on: (i) the minimum value of the objective function provided by NONMEM, equal to −2 × log likelihood (−2LL); −2LL differences of 3.84, 7.88 and 10.83 are considered significant at the 5, 0.5 and 0.1% levels, respectively, for nested models differing in 1 parameter; (ii) precision of parameter estimates; and (iii) results from model performance judged by visual exploration of the goodness of fit plots.

2.12. Model evaluation

Parameter precision was further evaluated performing 200 nonparametric bootstrap analyses using Pearl Speaks NONMEM,33 stratified by treatment group to keep the same proportion of vaccinated vs control and listing the 2.5^th, 50^th and 97.5^th percentiles of each parameter distribution. Evaluation of the final model was based mainly on simulation‐based diagnostics. For the biomarker and tumour growth model, performance was evaluated by prediction‐corrected visual predictive checks (VPCs). A total of 500 datasets with the same study characteristics as the original were simulated. For the tumour size and biomarker variables the 2.5^th, 50^th and 97.5^th percentiles of the simulated observations were computed for all time intervals and the 95% prediction interval of each calculated percentile was obtained and plotted against the 2.5^th, 50^th and 97.5^th percentiles obtained from the raw data. For the PFS model, simulated event times were obtained following the MTIME method34 to create Kaplan–Meier VPCs.

2.13. Model validation

The model was externally validated using tumour size, circulating biomarkers, and PFS data gathered from 111 nonmetastatic BC patients treated and diagnosed at the University Clinic of Navarra. Patients from the validation dataset received similar NAC treatment, but none of them received immunotherapy. Table 1 also lists the characteristics of the population whose data were used for model validation.

The same procedure as that described for model evaluation through visual predictive checks was applied here to evaluate whether or not the model was capable of describing the data obtained from a population of patients different from the original.

3. RESULTS

3.1. General description of the data

Longitudinal raw data used in the current analysis as well as the schematic representation of how that information was integrated and linked together within the modelling framework is shown in Figure 2.

Figure 2.

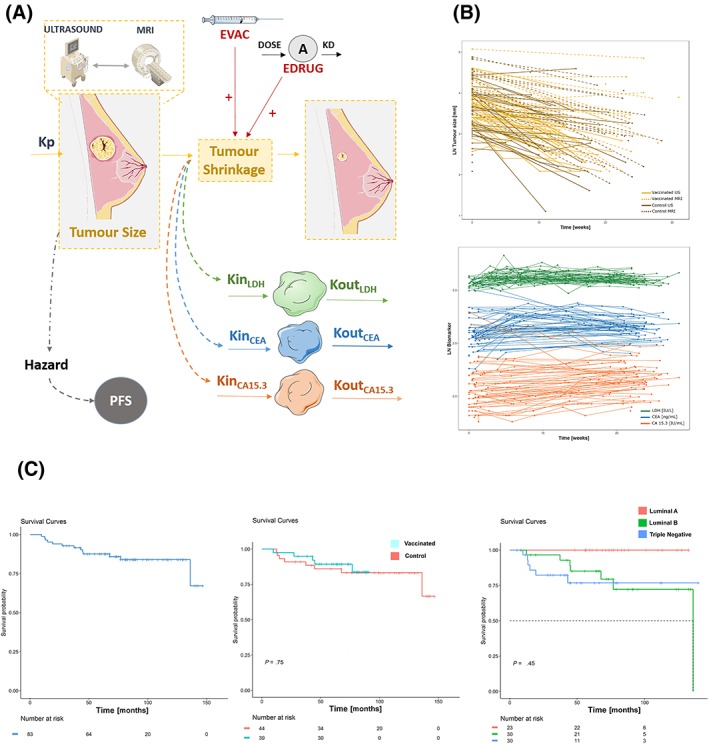
A, Schematic representation of the tumour growth inhibition model after NAC treatment and IT. K_P corresponds to proliferation rate constant; EVAC and EDRUG correspond to the vaccination and neoadjuvant chemotherapy effect, respectively. Tumour size affects progression‐free survival (PFS). LYSIS refers to the tumour shrinkage, which affects the elimination (Kout) of the biomarkers. B, Tumour size vs time profiles. Solid lines correspond to tumour size assessed by ultrasound, and dashed lines to magnetic resonance imaging. The light‐yellow colour represents control patients while the dark colour shows vaccinated patients. Middle panel, circulating biomarker vs time profiles: green (lactate dehydrogenase), blue (carcinoembryonic antigen) and red (carcinoma antigen 15‐3), and the PFS vs time profile is shown. LDH, lactate dehydrogenase; CEA, carcinoembryonic antigen; CA 15‐3, carcinoma antigen 15‐3. C, Raw PFS vs time profile is shown, stratified by treatment group and tumour subtype

Tumour size at diagnosis ranged from observations reported as BLQ to 100 mm (median = 30 mm) and BLQ to 160 (median = 54 mm) for US and MRI, respectively. Tumour size at diagnosis reported as BLQ were modelled accordingly. A decrease in TS during the treatment period occurred in the vast majority of the patients (95%), with 12% of the total measurements reported as BLQ at the time of surgery. Tumour regrowth after regression was not observed in any of the patients. The time‐course of circulating biomarkers showed a temporal increase over the values at diagnosis which was assumed to be the consequence of tumour lysis exerted by the treatment. All longitudinal continuous variables showed a moderate degree of IIV. As listed in Table 1 a small proportion of the patients experienced disease progression during the follow‐up period (8 patients out of 83 in the case–control groups).

3.2. Model for tumour size dynamics and circulating biomarkers

Disease initial status is represented by the typical baseline parameters with estimated values of 33.5 and 59.5 mm, for US and MRI, respectively, and their corresponding degree of variability, which was rather similar: 47 vs 42%.

Describing tumour shrinkage as a function of the total dose intensity administered provided a significantly better data description compared with when treatment effects were ignored (P < .001). Differences between schedules A and B could not be established (P > .05), indicating that both NAC schedules were equally effective with regard to TS reduction. The estimated IIV associated to the drug effect parameters was 49%. The parameter K_D representing the permanence of treatment effects in the body was estimated to be 2.23/week, corresponding to a half‐life of 2.2 days. A correlation between the rate of tumour decline and the initial tumour size could not be found.

As expected (due to the fact that there is 1 additional US measured around midterm of treatment) the modelling results were better when US data were described alone compared to the same approach applied to MRI. However, the pooled analysis provided better results in terms of data description, link to the clinical outcome and parameter precision.

Interestingly, and despite most of the patients did not show tumour increase during the treatment period, data supported the characterization of the progression of the disease (P < .001, according to the model selection criteria previously exposed). The estimate of first order proliferation rate constant (K_P) was low (2 × 10⁻⁴/week) and likely slowdown by the treatment. The K_P could only be estimated when the BM and TS data were simultaneously analysed. A model without K_P provided a worse fit (P > .05) than the final model.

Inclusion of vaccination effects in the model provided a significant improvement in data fitting (P < .01) and predicted almost a 20% further reduction in TS compared to the reduction achieved by NAC alone. This fact is confirmed by the finding that pCR rates in the breast were higher in the vaccinated cohort than in the control group (25.6% vs 13.6%; P = .04).

The circulating biomarkers showed different levels at diagnosis (ranging from 1.56 ng/mL to 234 IU/L), as well as different dynamics of turnover. Despite the differences in the biomarker specific parameter estimates, the magnitude of the tumour lysis effect of the rate of synthesis was not significantly different across the 3 biomarkers, although the model sustained the inclusion of IIV on this term, being the associated variability 45.5%.

For the 3 different biomarkers, a baseline parameter, synthesis rate and elimination rate were estimated. In normal conditions, the baseline can be described as the ratio between synthesis and elimination. However, at the time of diagnosis, these patients have their initial biomarker values already modified by the tumour (initial values were set as baseline), and therefore it does not correspond to the initial healthy value at which the system has to return (and therefore described by the ratio between synthesis and elimination). This fact explains why the model presented here described the data better than a model with only 2 parameters accounting for the biomarker dynamics.

Table 2 lists all model parameter estimates obtained with adequate precision. The model provided a very good description of TS (regardless the measurement method) and circulating biomarker data, both the typical profiles and the variability in the data (Figure 3A, B).

Table 2.

Population parameter estimates of the integrated model

Parameter	Estimate	2.5th–97.5th	IIV (SHR%)	2.5th–97.5th
Tumour size
TSU0 (mm)	33.5	31.2–37.4	47.3 (7.9)	31.6–48.3
TSM0 (mm)	59.5	54.9–67.9	42.5 (17.3)	33.6–52.1
Covariance			79.1
K D (/week)	2.23	2.13–40.95	NE	NE
EFF	0.028	0.024–0.037	49.2 (29.8)	34.0–54.2
KP (/week)	0.0002	0.0001–0.0003	NE	NE
θ VAC	1.17	1.02–1.23	NE	NE
KLYS	4.91	4.25–5.80	NE	NE
Biomarkers
BM0 LDH (IU/L)	234	202–235	16.6 (33.4)	10.6–16.88
BM0 CEA (ng/mL)	1.56	1.26–1.82	99.4 (33.4)	84.1–116.3
BM0 CA15‐3 (IU/mL)	19.8	16.9–22.8	66.6 (14.4)	56.7–85.1
KIN LDH (IU/week)	0.02	0.01–0.39	23.6 (57.4)	0.9–10.1
KIN CEA (ng/week)	0.013	0.012–0.027	89.1 (45.6)	80.9–122.6
KIN CA15‐3 (IU/week)	0.075	0.07–0.28	52.4 (35.4)	35.4–73.9
KOUT LDH (/week)	0.03	0.01–0.32	24.7 (55)	8.6–20.5
KOUT CEA (/week)	0.00096	0.0007–0.002	227.2 (40.1)	214.9–325.7
KOUT CA15‐3 (/week)	0.09	0.01–0.23	26.8 (56.5)	7.9–30.9
θ LYS	45.4	26.67–58.47	45.5 (33.5)	45.4–87.5
Progression‐free survival
BASE	5.67 × 10−4	1.19 × 10−4–9.29 × 10−4	NE	NE
BASE subtype LA	1.5 × 10−7	1.2 × 10−7–2.0 × 10−7	NE	NE
BETA	1.07	0.93–1.80	NE	NE
ALPHA	0.28	0.06–1.42	NE	NE

Residual error: US = 0.229; MRI = 0.302; biomarker: 0.173.

IIV, interindividual variation; SHR, Shrinkage; TSU0, TSM0, Tumour size at diagnosis by US or MRI, respectively; Kd, NAC elimination constant; EFF, parameter modulating NAC effect; KP, tumour growth constant; θ_VAC, parameter representing the DC vaccine effect; KLYS, tumour lysis constant.

NE, not estimated; BM0, biomarker at diagnosis; KIN, synthesis rate; KOUT, elimination rate; θ_LYS, parameter modulating the tumour lysis on the biomarker synthesis; BASE, baseline hazard; BASE subtype LA, baseline hazard for patients with Luminal A BC; BETA, shape parameter; ALPHA, parameter modulating the effect of tumour dynamics on the hazard. LDH, lactate dehydrogenase; CEA, carcinoembryonic antigen; CA 15‐3, carcinoma antigen 15‐3

Model equations:

$$\text{Tumour size}:\frac{\mathit{dTA}}{\mathit{dt}}=K_P\times \mathit{TA}-f\left(E_{\mathit{\text{drug}}}\right)\times \mathit{TA}\times \mathit{\text{KLYS}}$$

f (E_Drug) = K_D × C_TRTn × EFF × (1+ θ_VAC × C_VAC)

$$\text{Biomarkers}:\frac{d{\mathit{BM}}_m}{\mathit{dt}}=K_{{\mathit{\text{in}}}_m}\times \left(1+{\theta }_{\mathit{LYS}}\times \mathit{\text{LYSIS}}\right)-{K_{\mathit{\text{out}}}}_m\times {\mathit{BM}}_m$$

Progression‐free survival: h(t) = Base × BaseS × β × (Base × BaseS × t)^β − 1 × e^{−α × TA}

Figure 3.

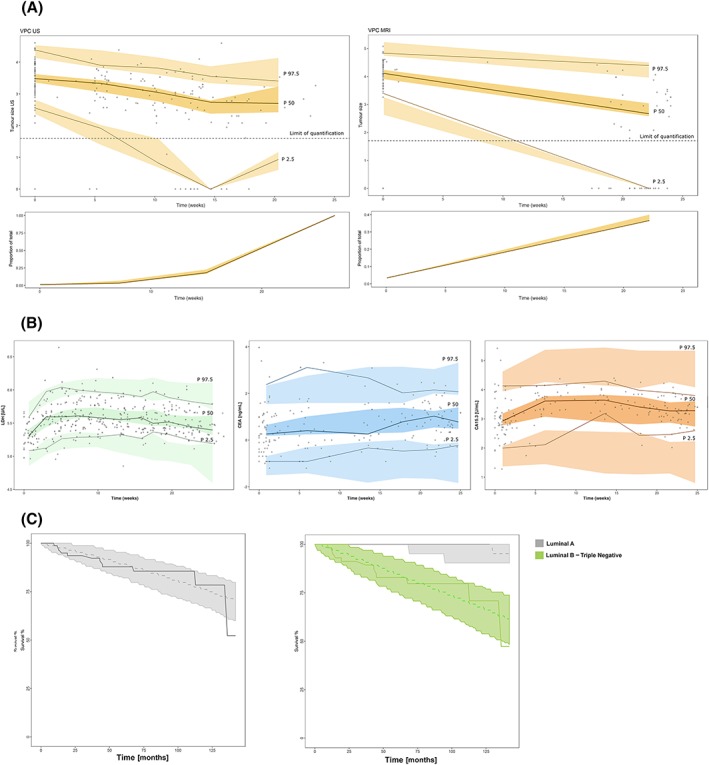
Results from simulation‐based model evaluation. (A, B upper panels) Points in black represent raw data, and coloured shaded areas represent the 95% confidence intervals of the 2.5^th, 50^th and 97.5^th percentiles obtained from 500 simulated datasets. A, Shows the tumour size assessed by ultrasound (US; left panel) and magnetic resonance imaging (right panel). The lower panels show the percentage of the below limit of quantification values. The solid line represents the observed proportion of below the limit of quantification values and the area is the 95% confidence interval predicted by the model. B, Biomarker prediction‐corrected visual predictive checks for lactate dehydrogenase, carcinoembryonic antigen and carcinoma antigen 15–3 (left to right). C, Kaplan–Meier curves for the progression‐free survival (PFS); the solid line represents the raw PFS profile and shaded areas cover the 95% confidence intervals of the model based simulated PFS profiles

3.3. Model for PFS

The probability of PFS in BC patients was best described by a parametric survival model using a Weibull distribution (P < .001). Simpler parametric distributions with 1 parameter, such as exponential models, or other 2‐parameter hazard distributions (log‐logistic, Gompertz), described the data less well (P > .05).

Among all the covariates and tumour related variables, the full TS profile predicted from diagnosis to surgery together with tumour subtype were the only covariates showing statistically significant effects on the hazard (P < .05). As a result, luminal A patients have better PFS. Biomarker dynamics were also tested as descriptors of the PFS data, ignoring TS dynamics, obtaining a worse description of the PFS (P > .05) than the description obtained when using the full TS profile over time.

Equation 5 represents the select model for the hazard.

$$h\left(t\right)=\mathit{\text{BaseS}}\times \beta \times {\left(\mathit{\text{BaseS}}\times t\right)}^{\beta -1}\times e^{-\alpha \times \mathit{TA}}$$ (5)

Where BaseS is the baseline hazard modified by tumour subtype, β is the shape parameter, and the parameter α modulates the effect of the dynamics of tumour activity on the hazard.

Parameter estimates are listed in Table 2. Results shown in Figure 3C indicate that the model describes well the PFS data. Additionally, the median predicted estimate of the 5‐year survival rate (87%) agrees well to observed (85%).

An exploration of the immunotherapy effects on PFS showed an increase on the 5‐year PFS compared to the control patients with increased vaccine effect, even though it was not statistically significant.

3.4. Model validation

A simulations‐based diagnosis (prediction‐corrected VPC) based on the model represented by the set of equations 1–5 and the parameter estimates listed in Table 2 was performed. As shown in supplementary material Figure S1 all response variables were well captured by the model confirming its model performance robustness.

4. DISCUSSION

BC is a global disease, with one of the highest incidences among all types of cancer. Even though it has been traditionally considered as a poorly immunogenic tumour, the number of clinical trials based on the application of DC immunotherapy is increasing in the metastatic setting.35, 36, 37, 38, 39 DC‐based vaccines induce antitumour specific responses while being well tolerated and safe. In this context, the current work aimed to provide an original mechanistic quantitative description of the effect of the administration of DC vaccines in the novel neoadjuvant scenario in BC patients.

Even though some modelling exercises have been applied to data obtained from BC patients,20, 21 this work reports for the first time a semi‐mechanistic modelling framework suitable for the quantification of the immunotherapy treatment given along with NAC to naïve early or locally advanced BC patients. The model built provided a better understanding of the relationship between TS, biomarker dynamics and PFS by integrating all the information available in the context of routinely available data in the clinical setting. Predictability of model readouts is warranted as the model has been externally validated in a cohort of 111 bc patients.

Tate et al.²⁰ developed a mathematical model that related survival with tumour size. The patients they used to build up their model were metastatic BC patients. They proposed an overall survival model related to tumour size at 1 discrete time point (6–8 weeks), and did not take biomarker dynamics into account. In contrast, our work has the novelty of being developed in the neoadjuvant scenario that takes the whole dynamics of the tumour size into account to explain PFS, along with the fact that biomarker dynamics are also included.

The whole time profile of TS was successfully described integrating information from 2 different imaging techniques (US and MRI), and thus increasing the available tumour size information. In fact, the TS estimation after NAC by standard imaging methods correlates poorly with the residual tumour, does not serve as a predictive factor for pCR and does not avoid breast surgery so far. By contrast, pCR is not the best endpoint for predicting survival in all BC subtypes, moreover regarding the addition of immune therapies that reflect better the benefit on survival than on tumour shrinkage.40 The implementation of this dynamic analysis provides more integrated information of the impact of tumour dynamics on PFS (Figure 4), based on TS rather than on RECIST based response criteria, which considers only 1 data point at one particular time. This is, to our knowledge, the first time that a modelling exercise combines different imaging techniques to model 1 variable like TS, optimising tumour information during the model‐building process.

Figure 4.

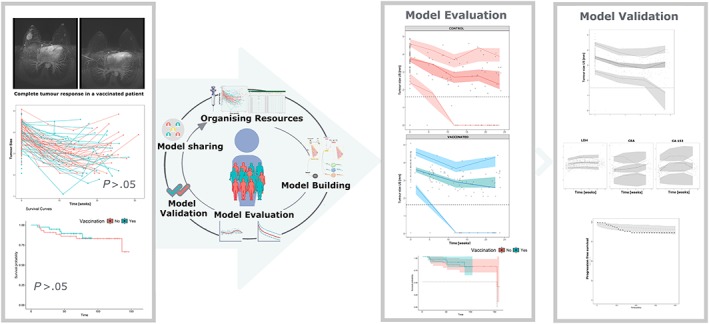
Summary of the model building process and representation of the potential benefits of the integrated pharmacokinetic/pharmacodynamic/disease progression models as part of the pharmacometric platform

Since clinical data are usually sparse, all the resources available should be used in the patient's favour. In this context, an innovative way of treating data obtained from different imaging techniques is shown here. These, addressed separately, give additional data to the clinicians, but maximize the information obtained when joined in the quantitative modelling exercise.

The magnitude of the immunotherapy effects could be precisely quantified using all longitudinal data available. Immunotherapy needs a longer median time to response (~4 months) than conventional chemotherapy.41 Our model predicts almost 20% shrinkage in TS when the vaccines are added to conventional NAC, and this value fits with the 18% ORR that has been described in a phase Ib clinical trial of TN metastatic BC patients treated with pembrolizumab.41 Even though the methodologies applied are different, other studies in which immunotherapy is used, reported an increase in complete responses after adding it to the NAC treatment,42 showing concordance with what it was obtained in this study.

Predicted TS dynamics helped to successfully describe the time course of LDH, CEA and CA15‐3 data by the proposed model. Despite none of the studied biomarkers resulted to be a better prognostic factor of PFS than tumour dynamics (P > .05), the stablished relationship between these and tumour progression is relevant, since the latter can be used as a surrogate of tumour activity, as shown by Buil‐Bruna et al.19, 43 This is particularly useful in cases when resources are limited or more readily available data can be used to infer more time and resource‐consuming information.

Ideally, we would have wanted the biomarkers to be used as a surrogate for the tumour, and therefore remove the need to obtain tumour measurements. However, in this particular case, the benefit of adding the biomarkers relies only in being able to estimate 1 parameter representing tumour growth (KP). Including biomarker data in our modelling framework was key to better characterize tumour dynamics, including proliferation, since biomarker data are more frequently obtained. Tate et al.,²⁰ in a modelling exercise perform in metastatic breast cancer, reported a tumour growth constant of 1.19 × 10⁻⁴/week, which is comparable to the 1 tumour growth constant estimated in our model (2 × 10⁻⁴/week). Therefore, in this case, biomarkers are not used as true biomarkers able to potentially replace tumour dynamics, but are included as additional data to support tumour dynamics description.

The parameter representing the permanence of NAC antitumoural effects in the body was estimated to be 2.23/week, which corresponds to a half‐life of 2.2 days. Therefore, the model predicts that the drug effect is gone in approximately 9 days. The estimated half‐life is higher than the reported in the prescribing information for the drugs, indicating a sustained and kinetically delayed response with respect to the plasma and tissue drug concentration vs time profiles.44

The analysis of PFS shown that the predicted time course of TS was the major factor contribution to the hazard. Given the fact that DC vaccines promoted tumour shrinkage, this provides a plausible mechanistic explanation for the greater PFS seen in the vaccinated patients. At a median follow up of 60 months, PFS for the control and the vaccinated groups were 80 and 88% respectively. Results obtained during the process of model building indicated that those effects were jeopardized when vaccination was introduced directly as a stratifying factor on the survival analysis, highlighting the benefit of using integrative computational methodologies. Further explorations of the model through simulations shown an improvement on PFS with increasing vaccine effects, which is line with previous studies not related to the modelling approach that have shown that immune activation against tumour suggest an improvement in survival.17, 45

The proposed model provides the basis of the improvement and optimization of the vaccine administration. Using the suggested framework, different administration schedules of the vaccines could be evaluated to select the most effective one. To do so, more data and a more refined model would be needed, but through this, the evaluation of shifting the timing of vaccine delivery would be possible, personalising treatment even more.

One limitation was, however, that some of the tumour size measurements overlap in time, and, by better characterising disease dynamics, more robust relationship could have been established. Although more repeated measures of imaging techniques could serve to better establish tumour dynamics, they are not recommended in the clinical practice. However, liquid biopsy such as circulating tumour DNA could solve this limitation and better predict PFS.46

Further studies will be needed to evaluate the safety of the vaccines, even though studies with similar treatment report them as safe.42, 47 An extended modelling framework with NAC and DC vaccination toxicity integrated with the current work will be helpful to completely understand the impact of this therapy on the patients.

The presented approach is in line with the concern regarding the development and application of pharmaco‐statistical models of drug efficacy and safety from clinical data, to improve drug development knowledge management and decision‐making (model‐informed drug development48); moreover, when we apply therapeutic strategies in which time effect reflects better the efficiency rather than criteria at 1 time point.24 This is an important pathway for lowering drug attrition rates, and dealing with new strategies for individualising medicine. The path exposed in this work can help us increase the potential knowledge that can be obtained from the typically available data in routine clinical practice.

Integrated population PK/PD/disease progression models as part of the pharmacometric platform provide a powerful tool to predict outcomes, so that the balance between efficacy and toxicity can be established. This work highlights the potential benefits (such as the quantification and identification of the vaccine effects, the establishment of not that evident relationships with PFS or the estimation of patient variability, therefore allowing individualization) of using pharmacometric techniques as a successful and accessible aid for clinical scientists in the optimization of current oncology therapies (Figure 4). The development and application of pharmaco‐statistical models of drug efficacy from clinical data is, therefore, a feasible and effective tool to improve drug development knowledge management and decision‐making.

To conclude, a semimechanistic validated modelling framework was developed to evaluate the increased effect of DC vaccines along with NAC on tumour shrinkage and to better understand the relationship between tumour size, biomarker dynamics and PFS. The identification and quantification of the immunotherapy effect was possible through a modelling strategy.

COMPETING INTERESTS

There are no competing interests to declare.

CONTRIBUTORS

B.P.S. built the dataset, performed the analysis and helped write and revise the manuscript. A.L.D.C. made the dendritic cell vaccines and helped revise the manuscript. A.E. collected data and helped revise the manuscript. L.J.P. collected data and helped revise the manuscript. S.I. made the dendritic cell vaccines and helped revise the manuscript. J.E. collected data and helped revise the manuscript. E.S. collected data and helped revise the manuscript. L.D.M. collected data and helped revise the manuscript. I.F.T. performed the analysis, and helped write and revise the manuscript. M.S. designed the clinical trial, collected data and helped write and revise the manuscript.

Supporting information

Data S1. Figure S1 shows the results from the validation exercise. Points in black represent raw data and coloured shaded areas represent the 95% confidence intervals of the 2.5^th, 50^th and 97.5^th percentiles obtained from 500 simulated validation datasets. (A) Tumour size assessed by ultrasound (left panel) and magnetic resonance imaging (right panel). (B) Biomarker prediction‐corrected visual predictive checks for lactate dehydrogenase, carcinoembryonic antigen and carcinoma antigen 15‐3 (left to right). (C) Kaplan–Meier curves for the progression‐free survival (PFS), dashed black line represent the raw PFS profile, and shaded areas cover the 95% confidence intervals of the model‐based simulated PFS profiles.

Data S2. Supporting information

Data S3. Supporting information

Solans BP, López‐Díaz de Cerio A, Elizalde A, et al. Assessing the impact of the addition of dendritic cell vaccination to neoadjuvant chemotherapy in breast cancer patients: A model‐based characterization approach. Br J Clin Pharmacol. 2019;85:1670–1683. 10.1111/bcp.13947