Population pharmacokinetic model and Bayesian estimator for 2 tacrolimus formulations in adult liver transplant patients

What is already known about this subject

• Tacrolimus is an immunosuppressant agent with a narrow therapeutic range

• Therapeutic drug monitoring is routinely performed using trough concentrations but area‐under‐the‐curve is theoretically a better marker of exposure.

• Several limited sampling strategies and Bayesian estimators have been developed to estimate exposure for tacrolimus in kidney transplantation.

What this study adds

• Separate population pharmacokinetic models have been developed for the early (day 7) and stable (week 6) periods post‐liver transplantation for Prograf and Advagraf.

• Bayesian estimators and limited sampling strategies have been developed to estimate accurately the tacrolimus exposure in liver recipients from 3 tacrolimus plasma concentrations.

• The tools developed for individual dose adjustment are available on‐line (www.pharmaco.chu‐limoges.fr).

1. INTRODUCTION

Tacrolimus (TAC) is a calcineurin inhibitor, largely used in combination with mycophenolate mofetil and corticosteroids in liver transplant recipients.1 It is characterized by a narrow therapeutic range and a large interindividual pharmacokinetic (PK) variability2 requiring individual dose adjustment using therapeutic drug monitoring (TDM). The TAC predose concentration (C₀) has been proposed as a predictive marker of its toxicity (e.g. nephrotoxicity and neurotoxicity3, 4) but its association with efficacy remains a matter of debate.5, 6, 7

Moreover, the last consensus conference has determined the interdose area under concentration curve (AUC) as the best exposure index that correlates with TAC efficacy.1 An AUC target range of 120–150 ng/mL^/h for the twice daily (TD) formulation was also suggested, without any specification as to kidney or liver transplantation. However, the studies referred to by the consensus conference were only performed in kidney transplant patients. Based on very large numbers of requests posted on our ImmunoSuppressive Bayesian dose Adjustment website (https://pharmaco.chu‐limoges.fr) for Prograf8 or Advagraf,9 we have proposed AUC target ranges in kidney transplant recipients for different therapeutic strategies (standard, minimization, maximization) and different post‐transplant periods. In the absence of studies or statistics in liver transplant recipients, no other specific AUC target can be proposed for liver transplant recipients.

One of the main objectives of population PK (POPPK) modelling is to design tools for routine drug dose adjustment.10 Accurate estimation of interdose drug exposure (AUC_0–12h or AUC_0–24h) can be obtained by combining a Bayesian estimator (BE) derived from a POPPK model and a limited sampling strategy (LSS).10 The development of such strategies has contributed to render the TDM of TAC based on AUC easier.8

POPPK models and BEs are most often built using a parametric POPPK modelling approach.3, 11, 12, 13, 14, 15 However, this approach assumes a specific and simple distribution of the PK parameters (gaussian, log‐normal etc.), while no such assumption is required when using a nonparametric approach.16 The nonparametric approach is theoretically a better choice when outliers or multimodal distribution of the parameters are observed16 or for complex PK.17 A previous report showed a multimodal distribution of TAC absorption parameters for the prolonged‐release formulation Advagraf, suggesting that a nonparametric approach would be appropriate in this case.3

The PK of TAC is influenced by several factors including TAC formulation, the type of organ transplanted, the time period post‐transplantation, haematocrit, albumin and cytochrome P450 3A5 genotypes.18 However, previous studies in kidney transplant patients12, 19 showed that a 1‐compartment model describing the absorption process with 2 γ‐distributions fitted TAC PK with excellent predictive performances (bias, precision and number of predictions out of the ±20% relative error interval were respectively: 0.89 ± 7.32%, 7.38% and 0/28 using iterative two‐stage Bayesian modelling in ITSIM; and − 2.62 ± 8.65%, 8.69% and 2/28 using Pmetrics),19 without including any covariate in the model.

Several POPPK models have been developed for TAC in kidney transplantation.3, 12, 18 In contrast, not much modelling work has focused on TAC for adult liver transplant recipients, whether in the stable19, 20 or early post‐transplant periods.15, 21, 22 In addition, only 2 studies used rich PK samples (with at least 9 samples)15, 19 and only 1 was developed for the Advagraf once daily (OD) formulation.20

The aims of this study were to develop POPPK models and BEs for the TAC OD (Advagraf) and TD (Prograf) formulations, in the early and late periods post liver transplantation using parametric and nonparametric modelling in parallel and to evaluate the performance of each method for predicting TAC AUC and dose requirements.

2. METHODS

2.1. Study design and patient population

The individual TAC blood concentration vs time data from 80 primary liver transplant recipients enrolled in a randomized, phase II, open‐label, multicentre prospective clinical trial were provided by Astellas. All patients included gave their written informed consent. Patients were undergoing primary whole or split liver transplantation and their age ranged between 18 and 65 years. Exclusion criteria included systemic infection requiring treatment, serum creatinine >175 μmol/L or concomitant medication known to affect the PK of TAC. The study was conducted in accordance with the Declaration of Helsinki, fifth revision (2000). Randomization was performed preoperatively on a 1:1 basis stratified by centre. Patients received a standardized immunosuppressive regimen with immediate‐release TAC (Prograf; Astellas Pharma Europe, Ltd., Staines, UK) or prolonged‐release TAC (Advagraf; Astellas Pharma Europe, Ltd., Staines, UK) and corticosteroids throughout the study. A summary of patient characteristics has been published previously.23

2.2. Study treatment

The first dose of TAC was administered orally within 6–12 hours (and no later than 18 hours, depending on the time of surgery) after skin closure, in the morning following transplantation. The initial dose of TAC was 0.1 mg/kg/day (0.05 mg/kg twice daily for the immediate‐release formulation). TAC OD was taken orally in the morning while TAC TD was taken in the morning and evening, on an empty stomach or at least 1 hour before or 2–3 hours after a meal. For both formulations, TAC dose was adjusted according to clinical signs and whole‐blood TAC C₀ levels.

2.3. Blood collection

Full PK profiles were collected from each patient under steady‐state conditions on day 7 (D7) and at week 6 ± 7 days (W6) after liver transplantation. Blood samples were drawn into EDTA tubes just before (C₀) and 0.5, 1, 2, 3, 4, 6, 8 and 12 hours after the morning dose of TAC TD, while additional time points were collected at 12.5, 13, 14, 15, 16, 18, 20 and 24 hours after dosing for TAC OD. All samples were stored at −20°C until analysis.

2.4. TAC assay

TAC concentrations were determined using a validated high‐performance liquid chromatography–tandem mass spectrometry assay method (lower limit of quantification = 0.1 ng/mL, intraday coefficient of variation (CV) = 17.6% and interday CV = 15.9%).24 The internal standard (20 μL, 50 ng/mL) was added to 1‐mL aliquots (whole‐blood calibration standards, quality control samples and study samples) then mixed briefly. Extraction of aliquots consisted in protein precipitation followed by solid phase extraction using C18 200 mg/3‐mL extraction cartridges. Eluates were evaporated under a stream of nitrogen at 40°C, and residues dissolved in a 50:50 mix (vol/vol) of acetonitrile and water, mixed and centrifuged, before being submitted to analysis.

2.5. PK modelling

The PK profiles obtained from the 80 patients were modelled using both parametric and nonparametric approaches in parallel and independent BEs were developed. As there are important changes in TAC PK over the first weeks post‐transplantation,12 PK profiles obtained at D7 and W6 were modelled separately and two independent BEs were developed (called early and stable periods post‐transplantation throughout the manuscript). The data set was split randomly into building (75%) and validation (25%) datasets using permutation tables at each period. Subsequently, 1‐ and 2‐compartment PK models with first order elimination associated with 1 or 2 γ‐distributions to describe the absorption process were compared using the Bayesian information criterion. Apart from the period post‐transplantation, no covariate data were available for this analysis.

2.5.1. Iterative 2 stage modelling (ITSIM)

The PK parameters were determined using an iterative 2‐stage Bayesian method implemented in our own computer program following a procedure described in previous papers.11, 12, 19, 25, 26 Briefly, the ITSIM program uses an expectation/maximization algorithm: the maximization step computes the kinetic curve of each patient by Bayesian estimation; the expectation step computes the population parameters from a weighted average of the individual parameters; the 2 steps are iterated until a good fit is obtained between the observed and computed concentrations. A combined error model was used to describe the residual variability.

2.5.2. Nonparametric modelling

The model was implemented in Pmetrics version 1.5.2.16 Pmetrics considers variability as originated from assay error (standard deviation, SD) and other random sources (λ). The global error term is defined by the equation = $\sqrt{{\mathit{SD}}^2+{\lambda }^2}$. A second‐degree polynomial error model depending on the concentration was used to describe the assay error (SD) while an additive (λ) error model was used to capture extra process noise.

2.6. Statistical analysis

All other statistical analyses were performed using R software version 3.3.1 (R foundation for statistical computing; http://www.r‐project.org) and graphs were drawn using GraphPad Prism version 5.00 for Windows (GraphPad Software, San Diego CA, USA, www.graphpad.com).

2.7. Evaluation of the model

Evaluation of the model was based: (i) on visual inspection of observed versus individual predicted concentration plots and weighted residual error versus individual predicted concentration plots; and (ii) on the likelihood of the model (Bayesian information criterion). The accuracy and robustness of the final model was evaluated using prediction‐corrected visual predictive checks (VPC). A total of 1000 replicates of the original dataset were simulated using the final model to generate expected concentrations and the 90% prediction intervals. The observed data were overlaid on the prediction intervals and compared visually. The prediction‐corrected VPC were based on the median, dose‐normalized concentrations.27

2.8. Building of Bayesian estimators

With each modelling approach, limited sampling strategies (LSS) combining a maximum of 3 TAC plasma concentrations (including predose concentration) restricted to the first 4 hours postdose were first investigated, as such combinations are more acceptable in routine practice. Secondly, unrestricted combinations of 3 sampling times were tested and the best LSSs, whether restricted or not, were selected by comparison of the interdose AUC prediction bias (mean prediction error) and precision (root mean squared prediction error, RMSE) in the validation datasets. The reference AUC was obtained using the linear trapezoidal rule (AUC_ref) applied to the full PK profiles. The number of predictions out of the ±20% relative error interval was also reported.

2.9. Dose adjustment

For each profile of the validation datasets, we calculated the theoretical doses to reach an inter‐dose AUC between 120 and 150 ng/mL h (AUC_0–12h) for TD, and between 240 and 300 ng/mL h (AUC_0–24h) for OD. The doses required were calculated using a proportionality formula (dose = target AUC × current TAC dose/estimated AUC), and those inferred from the AUC BEs were compared to those derived from the AUC_ref. Then, the Bayesian doses were compared with the reference doses in terms of (i) increase or decrease with respect to the dose received and (ii) absolute values.

3. RESULTS

Patient characteristics are described in the original study reports.23 At each post‐transplantation period (D7 and W6), 34 and 46 PK profiles were used for TAC OD and TD, respectively. At each period, the data set was split randomly into a building data set (n = 24 and 36 PK profiles of TAC TD and TAC OD respectively) and a validation data set (n = 10 PK profiles for each formulation). There was a significant difference (2‐way ANOVA) in the mean daily dose between TAC OD and TAC TD (p = 0.004) and between W6 and D7 (p = 0.008). The mean total daily dose was 16.2 ± 0.9 mg at D7 and 13.3 ± 0.9 mg at W6 for TAC OD, and 13.0 ± 1.1 mg at D7 and 10.6 ± 1.1 mg at W6 for TAC TD.

3.1. TAC exposure

Table 1 provides a summary of exposure parameters in the 2 post‐transplantation periods. The median whole blood C₀ values were numerically higher with TAC TD than TAC OD at both periods. There was only a strong correlation between AUC_0–24 and C₀ for TAC OD at W6 (r = 0.86) and between AUC_0–12 and C₀ for TAC TD at D7 (r = 0.81), while the correlation coefficient was lower for the other subgroups (OD D7, r = 0.18; TD W6, r = 0.67; Table 1).

Table 1.

Summary of exposure indices for tacrolimus twice daily (TD) and once daily (OD)

Exposure index	Median	Range	Correlation
TD/day 7
AUC0–12 (ng/mL h)	152.8	60.6–260.2	0.81
C0 (ng/mL)	8.2	3.8–16.1
TD/week 6
AUC0–12 (ng/mL h)	148.2	89.1–242.2	0.67
C0 (ng/mL)	8.5	5.5–12.1
OD/day 7
AUC0–24 (ng/mL h)	316.5	34.5–775.2	0.18
C0 (ng/mL)	8.6	0.8–55.0
OD/week 6
AUC0–24 (ng/mL h)	347.5	174.1–613.2	0.86
C0 (ng/mL)	9.3	3.9–21.9

AUC, area under the concentration–time curve; C0, trough concentration sampled in the morning.

3.2. PK models

For both the parametric and nonparametric approaches, a 1‐compartment model with first order elimination and 2 γ‐distributions to describe the absorption phase best described the TAC PK profiles for both OD and TD. The parameters estimated in this model were: a1, b1, a2, b2 (shape and scale of the 2 γ‐distributions), r (the fraction of dose absorbed following the first γ‐distribution), C₀ (the model estimated trough level for a theoretical dose of 1000 mg, the real trough level being calculated by dividing this C₀ value by 1000 and multiplying by the patient dose), F*AIV (the absolute bioavailability factor with respect to the IV route multiplied by the maximum concentration that would have been reached after a theoretical bolus IV of the reference dose) and α (the elimination parameter). For both approaches, the error model used was 0.0001 + 0.05C (C = drug concentration for OD and TD), but for Pmetrics an additional λ constant = 0.0005 was applied for both OD and TD. No measurements were below the limit of quantification.

The PK parameters were not significantly different between the 2 modelling approaches, the 2 formulations at the 2 periods post‐transplantation (Wilcoxon test, P = .2188, .1484, .7984 and .5737 respectively for TAC OD D7, W6 and TAC TD D7, W6; Table 2).

Table 2.

Parameters of the pharmacokinetic models developed using ITSIM and Pmetrics for tacrolimus (TAC) once daily (OD) and TD (twice daily) on day 7 (D7) and week 6 (W6)

	TAC OD D7				TAC OD W6
	ITSIM		Pmetrics		ITSIM		Pmetrics
	Median	Range	Median	Range	Median	Range	Median	Range
C 0 (μg/mL)	0.57	0.1–1.23	0.57	0.06–1.21	0.73	0.29–2.32	0.73	0.29–2.39
a1	4.88	1.59–9.89	7.26	0.06–11.94	6.00	1.00–12.05	7.00	0.56–12.94
b1 (/h)	6.33	1.36–12.48	13.8	0.23–14.93	6.82	1.52–14.48	9.49	0.57–14.93
a2	15.57	2.98–31.52	9.52	0.27–34.83	10.82	3.90–35.32	10.80	1.18–35.83
b2 (/h)	2.36	0.37–5.18	5.19	0.09–5.97	1.78	0.28–4.63	1.83	0.04–4.98
R	0.71	0.39–1.00	0.58	0.02–0.91	0.66	0.01–1.00	0.53	0.01–0.87
FAIV (ng/mL)	1.93	1.00–5.65	1.70	0.35–2.99	2.43	1.11–6.00	3.18	0.99–5.97
α (/h)	0.26	0.07–1.40	0.20	0.08–0.83	0.25	0.13–0.43	0.27	0.10–0.76
Vd/F (L)	515	177.0–1000.0	589	335–2857	412	167–901	314	167–1010
Cl/F (L/h)	48.5	19.2–91.7	48.7	18.9–91.3	35.1	15.8–80.1	35.3	15.7–81.5
C 0 (μg/mL)	1.27	0.53–3.53	1.30	0.62–3.46	1.66	0.83–8.52	1.60	0.75–8.65
a1	10.26	3.08–15.74	11.90	0.09–16.92	12.64	6.03–18.33	10.68	1.89–18.91
b1 (/h)	17.00	7.17–24.64	12.25	0.88–24.88	17.93	12.18–23.19	13.38	1.38–24.88
a2	11.83	7.95–14.28	13.1	5.05–14.95	10.25	5.04–15.23	8.17	1.73–14.93
b2 (/h)	9.25	2.56–20.77	12.81	3.09–20.91	7.24	1.89–10.07	5.90	0.35–9.95
R	0.58	0.01–1.00	0.55	0.07–1.00	0.74	0.06–1.00	0.56	0.06–1.00
FAIV (ng/mL)	3.12	1.27–9.96	3.60	2.25–9.95	4.98	0.97–9.53	6.30	1.75–9.95
α (/h)	0.39	0.10–0.68	0.44	0.21–1.00	0.44	0.25–0.77	0.55	0.26–1.00
Vd/F (L)	321	100–787	278	101–444	214	105–1030	159	100–571
Cl/F (L/h)	40.1	20.1–75.9	39.3	20.1–75.6	34.1	9.0–78.7	35.1	9.0–73.0

a1, b1, a2 and b2, shape and scale of the 2 γ‐distributions; r, the fraction of dose absorbed following the first γ‐distribution; C₀, the model estimated trough level for a theoretical dose of 1000 mg, FAIV, the absolute bioavailability factor with respect to the IV route multiplied by the maximum concentration which would have been reached after a theoretical bolus IV of the reference dose; α, the elimination parameter; D7, day 7; OD, Advagraf; TAC, tacrolimus; TD, Prograf; W6, week 6; Vd/F, apparent volume of distribution calculated as theoretical dose/FAIV; Cl/F, apparent clearance calculated as dose/AUC.

3.3. Model evaluation

The scatter plots of individual predicted (Figure 1) or population predicted (Figure 2) concentrations vs observed concentrations showed no major bias, whatever the modelling approach used. Weighted residuals vs individual predictions were homogeneously distributed over the concentration range (Figure 3).

Figure 1.

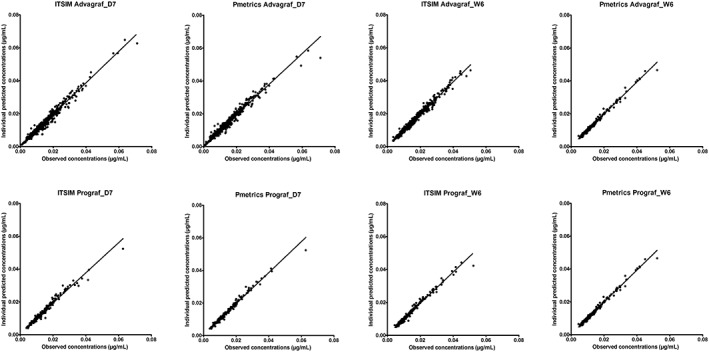
Scatter plots of individual model‐predicted concentrations vs observed concentrations obtained with the parametric (ITSIM) and nonparametric (Pmetrics) methods on day 7 (D7) and week 6 (W6) post‐transplantation, for the 2 formulations

Figure 2.

Scatter plots of model‐predicted concentrations vs observed concentrations obtained with the parametric (ITSIM) and nonparametric (Pmetrics) methods on day 7 (D7) and week 6 (W6) post‐transplantation, for the 2 formulations

Figure 3.

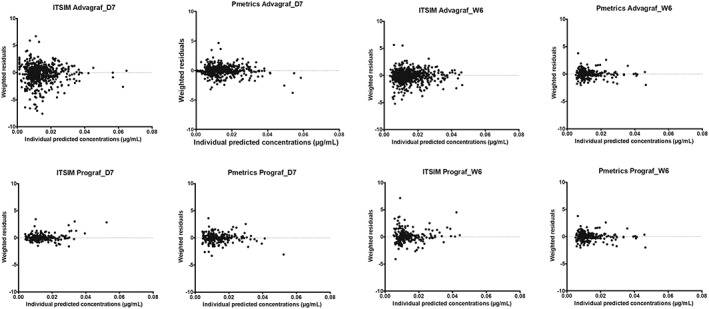
Weighted residuals (WRES) vs individual predicted concentrations obtained with the parametric (ITSIM) and nonparametric (Pmetrics) methods on day 7 (D7) and week 6 (W6) post‐transplantation, for the 2 formulations

The final models were evaluated using the dose‐normalized VPC, showing that the average prediction of the simulated data matched the dose‐corrected observed concentration–time profiles and that the variability was reasonably estimated whatever the modelling approach (Figure 4).

Figure 4.

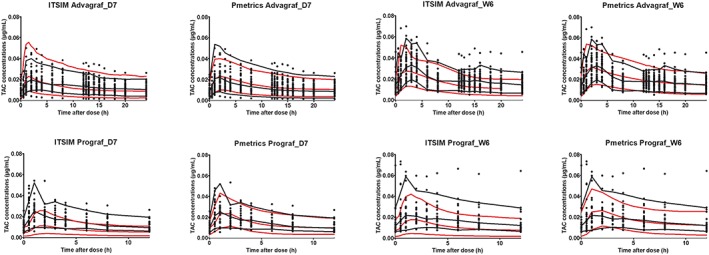
Visual predictive checks of the parametric (ITSIM) and nonparametric (Pmetrics) models on D7 and W6 post‐transplantation for the 2 formulations of tacrolimus (TAC). Percentiles (5, 50 and 95%) of predictions (grey dashed lines) are overlaid with the observations (symbols). Black lines are 95% confidence intervals for the observation percentiles. D7, day 7; W6, week 6

3.4. Bayesian estimators

The bias, RMSE and numbers of AUC estimates outside the ±20% interval are summarised in Table 3 for the best LSS for each formulation and period. The best LSSs developed were 0, 1 hour, 4 hours (restricted) and 0, 1 hour, 6 hours (not restricted) for TAC OD and 0, 1 hour, 3 hours (restricted) and 0, 2 hours, 6 hours (not restricted) for TAC TD. Bias values ranged from −11.2 to 8.3% and imprecision (RMSE) from 6.2 to 20.5%. Example of the best and the worse modelled profile using the best LSS for each combination of drug/period and each approach are presented in Figure 5.

Table 3.

Predictive performance of different limited sampling strategies (LSS) for Bayesian estimators derived from the parametric (ITSIM) and nonparametric (Pmetrics) models on day 7 (D7) and week 6 (W6) post‐transplantation, for the 2 formulations. In each situation are presented the best LSS restricted to the first 4 h post‐dose and the best LSS overall (unrestricted)

Model	Limited sampling strategy	Modelling software	Mean bias (%)	SD (%)	Range (%)	RMSE (%)	Number AUC estimates outside ±20% of the reference
TAC OD_D7	0, 1 h and 4 h	ITSIM	−5.60%	18.25%	−42.43% to 20.36%	18.19%	3/10
		Pmetrics	−11.21%	16.12%	−38.36 to 14.60%	18.96%	2/10
	0, 1 h and 6 h	ITSIM	−4.52%	7.80%	−19.75 to 9.39%	8.67%	0/10
		Pmetrics	−6.68%	16.08%	−41.48 to 14.27%	16.71%	1/10
TAC OD_W6	0, 1 h and 4 h	ITSIM	4.75%	9.01%	−6.95 to 22.49%	9.78%	1/10
		Pmetrics	1.14%	12.18%	−9.46 to 31.13%	11.61%	1/10
	0, 1 h and 6 h	ITSIM	−0.26%	7.63%	−11.29 to 11.09%	7.24%	0/10
		Pmetrics	−1.36%	8.99%	−16.27 to 13.91%	8.64%	0/10
TAC TD_D7	0, 1 h and 3 h	ITSIM	−2.42%	8.45%	−23.09 to 8.53%	8.38%	1/10
		Pmetrics	8.30%	19.80%	−16.09 to 56.50%	20.53%	1/10
	0, 2 h and 6 h	ITSIM	−2.30%	6.03%	−10.15to 8.27%	6.16%	1/10
		Pmetrics	−1.16%	17.11%	−17.21 to 37.79%	16.27%	1/10
TAC TD_W6	0, 1 h and 3 h	ITSIM	−0.65%	7.36%	−7.96 to 14.59%	7.02%	0/10
		Pmetrics	5.13%	12.51%	−25.06 to 17.76%	12.93%	1/10
	0, 2 h and 6 h	ITSIM	2.36%	11.46%	−12.40% to 29.39%	11.12%	1/10
		Pmetrics	3.83%	11.48%	−10.86 to 24.90%	12.25%	1/10

AUC, area under the curve; D7, day 7; OD, Advagraf; RMSE, root mean squared prediction error; SD, standard deviation; TAC, tacrolimus; TD, Prograf; W6, week 6, TAC, tacrolimus.

Figure 5.

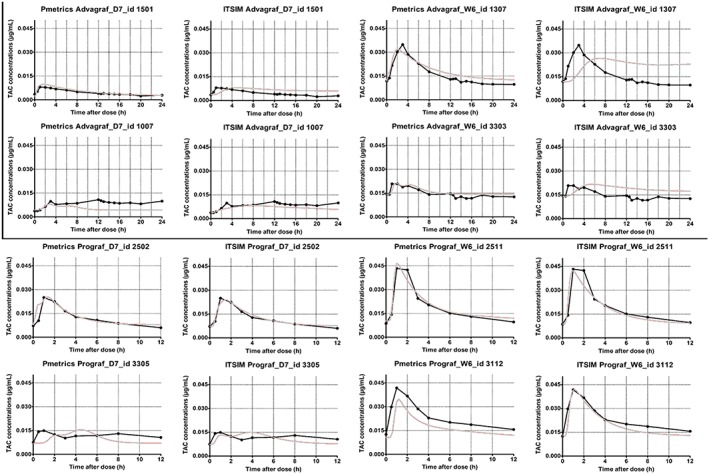
Best and worst modelled profiles using the best limited sampling strategy for each combination drug/period and each modelling approach (Pmetrics and ITSIM). TAC, tacrolimus; D7, day 7; W6, week 6

3.5. Dose adjustment

The TAC doses proposed based on the AUC estimates obtained using the 2 BEs were compared to the AUC_ref. Results of the best LSS for each formulation and period are presented in Table 4. The dose proposed for the 10 patients was less accurate at the early than the stable period (overestimation in 1–3 of 10 cases, depending on the LSS and the POPPK approach).

Table 4.

Comparison of the doses proposed to achieve area under the curve up to 12 hours (AUC_{0–12 h}) of 120–150 ng/mL h for TAC twice daily (TD) and AUC_0–24h of 240–300 ng/mL h for TAC once daily (OD) using Bayesian AUC estimates as compared to the reference, trapezoidal AUCs (only the best limited sampling strategies (LSS) for each period are presented)

	Patient		Proposed dose (mg)
	Number	Dose (mg)	Referencea		ITSIM		Pmetrics
TAC OD D7 LSS 0,1 and 6 h	1	4	4.5–6.0	↗	6.0–7.5	↗	8.0–10.0	↗
	2	17	13.5–17.0	=	14.0–17.5	=	16.0–20.0	=
	3	18	14.0–17.5	↘	14.5–18.5	=	16.0–20.5	=
	4	15	11.5–14.0	↘	12.0–14.5	↘	13.0–16.0	=
	5	15	15.0–19.0	=	16.0–20.0	↗	15.5–19.0	↗
	6	23	9.5–12.0	↘	10.5–13.0	↘	9.5–11.0	↘
	7	3	6.5–8.5	↗	6.0–7.5	↗	6.0–7.5	↗
	8	23	17.0–21.0	↘	17.0–11.5	↘	16.0–20.0	↘
	9	6	7.0–9.0	↗	8.0–10.0	↗	8.0–10.0	↗
	10	15	10.5–13.0	↘	10.5–13.0	↘	10.0–12.5	↘
TAC OD W6 LSS 0,1 and 6 h	1	11	9.0–11.0	=	9.5–11.5	=	8.5–10.5	↘
	2	22	18.0–23.0	=	19.0–24.0	=	16.0–20.0	↘
	3	15	9.0–11.5	↘	9.5–11.5	↘	8.5–11.0	↘
	4	20	10.0–12.0	↘	11.0–14.0	↘	11.5–14.5	↘
	5	25	15.5–19.5	↘	14.0–17.5	↘	13.5–17.0	↘
	6	12	8.0–10.0	↘	7.5–9.5	↘	8.5–11.0	↘
	7	19	11.5–14.0	↗	11.5–14.0	↘	11.0–14.0	↘
	8	6	4.0–5.0	↘	3.5–4.55	↘	4.0–4.5	↘
	9	25	10.5–13.0	↘	11.0–14.0	↘	11.0–14.0	↘
	10	8	6.0–7.5	↘	5.5–7.0	↘	6.0–7.5	↘
TAC TD D7 LSS 0,2 and 6 h	1	4	4.0–5.0	=	4.0–5.0	=	5.0–6.0	↗
	2	13	9.0–11.5	=	10.0–12.5	↘	11.5–14.5	=
	3	16	7.0–9.0	=	7.5–9.0	↘	7.0–9.0	↘
	4	10	10.5–13.0	↗	9.5–12.0	=	10.5–13.0	↗
	5	14	23.5–29.5	↗	24.5–30.5	↗	17.0–21.5	↗
	6	10	11.0–13.5	↗	11.0–14.0	↗	9.5–12.0	=
	7	12	10.0–12.5	=	9.5–12.0	=	9.5–12.0	=
	8	14	7.5–9.0	↘	7.5–9.5	↘	8.5–10.5	↘
	9	11	6.0–7.0	↘	6.5–8.0	↘	7.0–8.5	↘
	10	18	15.0–19.0	=	16.5–21.0	=	18.0–22.5	=
TAC TD W6 LSS 0, 1 and 3 h	1	9.5	10–12.5	↗	9.0–11.5	=	10.0–12.5	↗
	2	12	8.5–10.5	↘	8.0–10.0	↘	7.5–9.0	↘
	3	14	8.0–10.5	↘	8.5–10.5	↘	8.0–10.0	↘
	4	20	12.5–16.0	↘	11.0–14.0	↘	12.50–16.0	↘
	5	12	6.5–8.0	↘	6.5–8.0	↘	6.0–7.5	↘
	6	18	10.0–12.5	↘	10.0–12.5	↘	8.5–11.0	↘
	7	24	16.0–20.0	↘	16.5–21.0	↘	14.0–17.5	↘
	8	10	5.5–6.5	↘	5.5–7.0	↘	5.0–6.5	↘
	9	12	5.0–6.5	↘	5.5–7.0	↘	7.0–8.5	↘
	10	14	10.5–13.0	↘	10.5–13.3	↘	9.0–11.5	↘

^aReference, Trapezoidal method: proposed dose derived from the trapezoidal AUC_0–12 h for TD and AUC_0–24 h for OD; Poorly estimated doses are in bold characters; D7, day 7; OD, Advagraf; TAC, tacrolimus; TD, Prograf; W6, week 6.

In addition, to achieve the AUC_0–12h of 120–150 ng/mL h for TAC TD and AUC_0–24h of 240–300 ng/mL h both the ITSIM and Pmetrics methods predicted the same dosing changes (increase, decrease or no change) in 96 and 93% cases, respectively, and, the same dose in 94 and 85% of cases, respectively (Table 4).

4. DISCUSSION

In this study, full PK profiles collected at D7 and W6 after liver transplantation in 80 de novo liver transplant patients given either TAC TD or TAC OD were used to develop POPPK models and Bayesian estimators. They were able to accurately predict the interdose AUC using an LSS, and the dose required to reach a predefined AUC target range. Two independent modelling approaches were applied in this work, 1 using in‐house and the other public software. The goal was not to compare these methods but to implement both of them in our ImmunoSuppressive Bayesian dose Adjustment online service (https://pharmaco.chu‐limoges.fr) in order to make them available to the PK modelling community and for clinical care. A 1‐compartment structural model with first order elimination and absorption described by a double γ‐distribution accurately described the PK of TAC, regardless of formulation. A slight underestimation for the highest values can be observed for some patients on the individual prediction vs observation plots. Additionally, corrected VPC show that 1 patient taking 1 mg of Prograf and 1 taking 4 mg of Advagraf had concentration values largely over the 95% confidence interval of the simulated concentrations (based on the population parameters). Interestingly, these patients had high C₀ in comparison to their AUC values (C₀ = 9.6 ng/mL and AUC = 112 ng/mL h for the patient on Prograf and C₀ = 10.1 ng/mL and AUC = 253 ng/mL h for the patient on Advagraf). This underlines the usefulness of AUC estimation based on 3 observed concentrations and individual estimation of parameters using the Bayesian method (of note, VPC are based on population parameters and not individual parameters) in comparison to the C₀. In a previous study, we found that the same structural model also accurately described the PK of Envarsus (another once‐daily formulation of TAC) in liver transplant recipients.19 Several other structural models were proposed to describe the PK of TAC OD and TD in liver transplant patients.15, 20, 21, 22 For example, Moes et al. previously described the PK of TAC OD in stable liver transplant recipients using nonlinear mixed effects modelling (NONMEM). They developed a 2‐compartment model with 3 transit‐absorption compartments using sparse data within the first 6 hours after TAC dosing.20 Other studies based on extensive sampling data used elaborate models to adequately describe TAC absorption (in comparison to the classical first order absorption with or without lag time).10

In the present study, parametric and nonparametric methods gave similar results in terms of PK parameter estimates. On the basis of the few dose proposal discrepancies between Pmetrics and ITSIM, it seems that Pmetrics underestimated the AUC (= overestimated the dose) when the dose proposed was quite low and overestimated the AUC (= underestimated the dose) when the dose was quite high, as compared to ITSIM. The TAC PK parameters exhibited a high interpatient variability, which was well described using either POPPK modelling approach. The high variability we observed is in accordance with previous reports in paediatric or adult liver transplant recipients.28, 29, 30, 31 Moreover, we observed that PK parameter estimates were significantly different between TAC TD and TAC OD and between day 7 and week 6 for both formulations. Indeed, TAC PK is affected by several factors including time after transplantation, patient demographics and graft type. Additionally, in the first days after liver transplantation, the recovery of liver function influences TAC clearance in de novo liver transplant patients,31 which may explain the (relatively) lower accuracy of our Bayesien estimators at D7 in the present study. Moreover, corticosteroids used during the immediate post transplantation period are well known to affect the PK of TAC.10 Thus, because of these differences, we considered patients at day 7 and week 6 independently and developed different BEs for each formulation and each post‐transplantation period.

TAC TDM is generally performed based on C₀ measurements. However, a good correlation between C₀ and AUC is not always observed.12, 32 In our study, a better correlation was found at D7 for TAC TD and at W6 for TAC OD, while it was poor at W6 for TAC TD and on D7 for TAC OD, confirming that the relationship between trough levels and exposure is inconstant across time periods and formulations.10

To date, 2 LSSs have been proposed to estimate TAC AUC_0–12h or AUC_0–24h after the administration of the OD or TD formulations in adult liver transplant recipients.15, 20 Moes et al. investigated an LSS based on a POPPK model developed using NONMEM (version 7.2.1), in 49 stable liver transplant recipients given OD TAC. The predictive performance of different LSS schedules was evaluated in a cohort of 17 patients excluded from the development dataset because of missing covariates. Among selected concentration–time points, they found that the LSS 0, 2 h, 3 h was associated with the lowest AUC bias (0.46%) and imprecision (RMSE = 17.7%). Chen et al. developed a POPPK model with NONMEM using data from 125 Chinese liver transplant patients. They pooled 47 full PK profiles with TDM data to develop a 2‐compartment model with first‐order absorption and a lag time. The best LSS (0, 2 h, 4 h) was selected using the D‐optimal design but was only evaluated in patients from the development cohort (and not an external validation cohort, which is known to highly underestimate the bias and precision) showing bias of 3.5 ± 13.8% and precision of 12.6 ± 13.9% in the estimation of AUC_0–12h. 15 In the present study, the results of the Bayesian estimation of TAC AUC and of the dose required in the independent validation group showed that both ITSIM and Pmetrics have good predictive performance in term of bias and RMSE (<10% and <20% respectively is consensually accepted for MAP Bayesian estimation). The imprecision was overall lower in stable than in immediate post‐transplantation period for both TAC OD and TD. Because of the recovery of liver function, the PK of TAC is more complex in liver than in renal transplant recipients, rendering dose adjustment more difficult in the early period post‐transplantation.

For TAC in liver transplant recipients, the LSSs described in the literature include sampling times up to a maximum of 4 h post dose,14, 15, 19, 20 probably or explicitly because it is difficult to prolong patient stay at the hospital further for sample collection. However, this restriction could theoretically increase the bias and decrease the precision of AUC estimation for OD formulations. We observed a 2‐fold improvement in precision when allowing a sampling time at 6 h instead of 4 h for TAC OD, but only at D7. For the other 3 situations, the unrestricted selection of sampling times did not significantly improve estimation bias and RMSE, and it even led to worse results for TAC TD at W6.

In this study, we compared the ability of independent BEs to estimate the doses required to achieve a predefined target range (120–150 and 240–300 ng/mL h for TAC TD and TAC OD, respectively). The results obtained using both modelling approaches were excellent as compared to the trapezoidal AUC allowing the use of these models for routine dose individualisation and TDM based on the AUC. We hope that they may help to foster the use of AUC monitoring in liver transplant patients and to define AUC targets in this population, as we previously did in kidney transplant recipients.8, 9

This study has limitations. First, the model has been developed based on a relatively limited number of patients. The number of patients is a concern for many PK studies, but it is technically difficult and costly to increase the number of patients or full PK profiles per patient. As the early period post‐transplantation corresponds to the highest variability (unstable patients), a higher number of full PK profiles would have been better. However, as this phase 2 study was performed by a pharmaceutical company (and approved by the regulatory authorities), the reliability is high in terms of dosing time, blood collection times and concentration values, which limits random variability. Finally, the data splitting strategy employed confirmed the robustness and usability of the model. Second, the generalizability of the models for patients 1 year post‐transplant can be questioned and this has to be investigated in further studies.

In conclusion, we developed 2 different POPPK models and BEs able to accurately predict the interdose AUC of 2 TAC formulations in liver transplant patients. The tools developed with ITSIM are now available on the ImmunoSuppressant Bayesian dose Adjustment website (https://pharmaco.chu‐limoges.fr), while those developed with Pmetrics can be provided upon request, for research purposes only.

COMPETING INTERESTS

C.R., J.D., and C.M. have no competing interests to declare. J.B.W. has received honoraria from Chiesi. P.M. has received research grants and honoraria from Chiesi and Sandoz.

CONTRIBUTORS

J.B.W., C.R. performed the research, C.R., J.D. and J.B.W. analysed data, C.R. and J.B.W. wrote the paper, C.M., J.D., P.M. and J.B.W. designed the study.

Riff C, Debord J, Monchaud C, Marquet P, Woillard J‐B. Population pharmacokinetic model and Bayesian estimator for 2 tacrolimus formulations in adult liver transplant patients. Br J Clin Pharmacol. 2019;85:1740–1750. 10.1111/bcp.13960