 Metal–ligand covalency enables observation of coherent spin dynamics to room temperature in a series of vanadium(iv) and copper(ii) catechol complexes.
Metal–ligand covalency enables observation of coherent spin dynamics to room temperature in a series of vanadium(iv) and copper(ii) catechol complexes.
Abstract
Harnessing synthetic chemistry to design electronic spin-based qubits, the smallest unit of a quantum information system, enables us to probe fundamental questions regarding spin relaxation dynamics. We sought to probe the influence of metal–ligand covalency on spin–lattice relaxation, which comprises the upper limit of coherence time. Specifically, we studied the impact of the first coordination sphere on spin–lattice relaxation through a series of four molecules featuring V–S, V–Se, Cu–S, and Cu–Se bonds, the Ph4P+ salts of the complexes [V(C6H4S2)3]2– (1), [Cu(C6H4S2)2]2– (2), [V(C6H4Se2)3]2– (3), and [Cu(C6H4Se2)2]2– (4). The combined results of pulse electron paramagnetic resonance spectroscopy and ac magnetic susceptibility studies demonstrate the influence of greater M–L covalency, and consequently spin-delocalization onto the ligand, on elongating spin–lattice relaxation times. Notably, we observe the longest spin–lattice relaxation times in 2, and spin echos that survive until room temperature in both copper complexes (2 and 4).
Introduction
Magnetic transition metal complexes are a promising platform to create qubits, the smallest unit of quantum information science (QIS) systems. Within the broad scope of QIS there are numerous applications, most prominently, quantum computing which offers the potential to revolutionize our approach to certain computational problems.1–3 A second emerging area of QIS, well suited to molecular intervention, is quantum sensing, wherein quantum objects are used as environmental probes.4 Magnetic complexes comprise a highly promising platform to develop design principles for the foregoing applications owing to their wide range of tunability.5–7
To develop systems for QIS, it is essential to design qubits with long spin–spin and spin–lattice relaxation times, T2 and T1, respectively. In quantum computing, T2 represents the lifetime of information, while, T1 signals the maximum memory storage time, as well as the minimum possible time length between each computational cycle. For applications within quantum sensing, it is possible harness the sensitivity of the timescales of T1 and T2 to the local chemical and magnetic environment of the electronic spin to probe the local chemical environment. Both of these applications rely on an explicit understanding of how molecular factors influence T1 and T2 and is of intense current interest.8–12 Owing to the inherent chemical tunability of spins in transition metal complexes, investigating T1 and T2 in such species is a promising route to the requisite knowledge.
By modifying the chemical structure of molecules, it is possible to tune the specific lattice vibrations thereby engendering changes to T1. Prior research into molecular design of candidate qubits focused on lengthening T1 and T2 and increasing their persistence to higher temperatures. Specifically, the role phonons and local vibrational modes play in modulating spin dynamics of electronic spin qubits is of particular importance.13–19 In this study, we focus on a different parameter, modulating the covalency of the metal–ligand bond to control relaxation times. The identity of the spin-bearing orbital and its interaction with the lattice and intramolecular vibrations should guide the magnitude of T1. A nonbonding orbital, for example, should interact less strongly with lattice vibrations than a bonding (or antibonding) orbital, and thus display a longer T1. Within this framework, we hypothesize that tuning the covalency of metal–ligand bonding could likewise enhance T1. Despite this intuitive picture, significant experimental work remains to be done to test its validity.
Similarly, metal–ligand covalency could be envisioned to impact T2 by modulating the interaction of an electronic spin with nearby nuclear and electronic spins.20 When these environmental spins undergo flip-flop motions, such interactions shorten T2. Here, delocalization of the metal-based spin toward the ligand-based nuclear spins may engender stronger magnetic interactions that shut down flip-flop motions and lead to longer T2 times. Metal ions ligated by nuclear spin-free ligand shells completely eliminate such flip-flops, which enable near-millisecond-length T2 times.21,22 Yet that design principle is chemically limited, and hence, methods of enabling nuclear spins to be incorporated into the synthetic design are important.
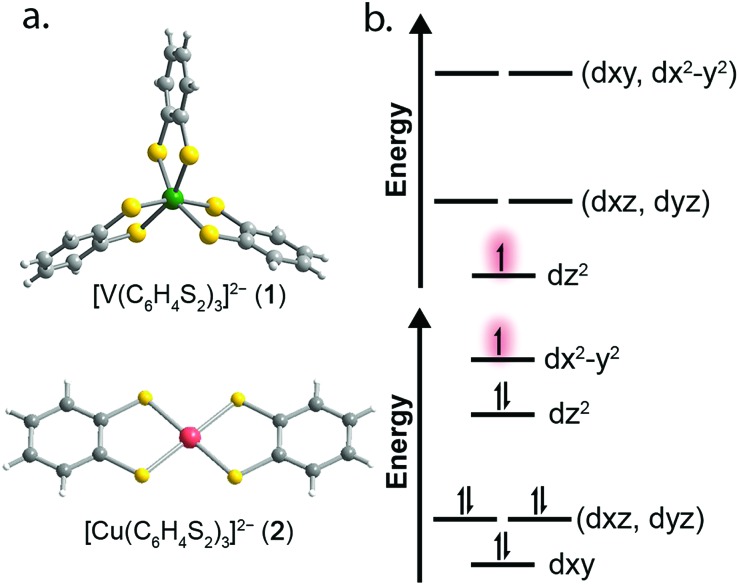
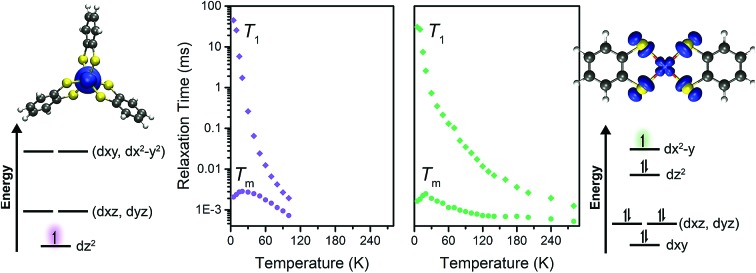
To test this hypothesis we synthesized and investigated the Ph4P+ salts of the dithiocatecholate complexes of vanadium(iv) and copper(ii):23,24 [V(C6H4S2)3]2– (1), [Cu(C6H4S2)2]2– (2), and the diselenocatecholate complexes [V(C6H4Se2)3]2– (3), and [Cu(C6H4Se2)2]2– (4) (Fig. 1). Here, we hypothesized that direct comparison of the V(iv) and Cu(ii) complexes would offer insight into the impact of changing the nature of the molecular orbital in which the electronic spin resides; a non-bonding, low-covalency dz2 orbital and an anti-bonding, high-covalency dx2–y2 orbital, respectively. Notably, in the V(iv) complex (1) the echo disappears beyond 100 K, whereas in the Cu(ii) complex (2) the spin echo persists until room temperature. We attribute this difference in behavior to a change in metal–ligand covalency. Investigation of 3 and 4 in concert with 1 and 2 allowed us to systematically test the role that more diffuse, 4p donor atoms play in modulating covalency and, thus, spin relaxation times. Note, because all complexes feature ligands that contain proton nuclear spins (1H, I = 1/2, 99.98% natural abundance) at nearly identical distances from the spin-bearing metal ion, the series provides a qualitative picture of the role of the variation in metal–ligand covalency on T2 times with a constant number of nuclear hyperfine interactions.
Fig. 1. (a) Molecular structures of the [VL3]2– and [CuL2]2– units as determined in the crystal structures of 1 and 2. Dark green, red, yellow, gray, and white spheres represent vanadium, copper, sulfur, carbon, and hydrogen atoms, respectively. (b) Qualitative d-orbital splitting diagrams for 1 (top), and 2 (bottom) highlight the nature of the orbital singly occupied by an unpaired spin.
Results and discussion
Correlating spin–lattice relaxation with structural changes necessitates a clear understanding of the structural similarities and differences between the compounds. Notably, the two classes of complexes have significantly different structures. The V4+ complex (1) is a hexacoordinate tris-chelate complex in a pseudo-octahedral geometry, while in 2, the Cu2+ ion resides in a four-coordinate, square planar geometry. In the solid state, the structure of 1 deviates from an idealized trigonal geometry owing to distortions in the arrangements of ligands. The average bond distances between the metal ions and the ligand donor atoms, 2.372(11) Å and 2.279(2) Å for V–S and Cu–S bonds, respectively, agree well with prior crystal structures of other dithiolate species.25 Comparison of the average M–L bond distances in 1 and 2 reveals that the metal–donor bond distances are all well below those computed using the Shannon–Prewitt ionic radii for Cu2+, V4+, and S2–, with larger deviations observed for 2 relative to 1.26 These short bond distances suggest enhanced metal–donor covalency in the copper complex relative to its vanadium counterpart. To further probe M–L covalency we investigated both complexes via X-band (∼9.5 GHz) continuous wave (cw) and pulse electron paramagnetic resonance (EPR) spectroscopy. As interactions between separate magnetic molecules engender spin–spin relaxation, we synthesized their closed-shell analogues: (Ph4P)2[Ti(C6H4S2)3] and (Ph4P)2[Ni(C6H4S2)2]. We then diluted complexes 1 and 2 in a matrix of their respective diamagnetic analogues at concentrations of 0.5%, yielding the compounds (Ph4P)2[V0.005Ti0.995(C6H4S2)3] (1′) and (Ph4P)2[Cu0.005Ni0.995(C6H4S2)2] (2′) (see ESI†).
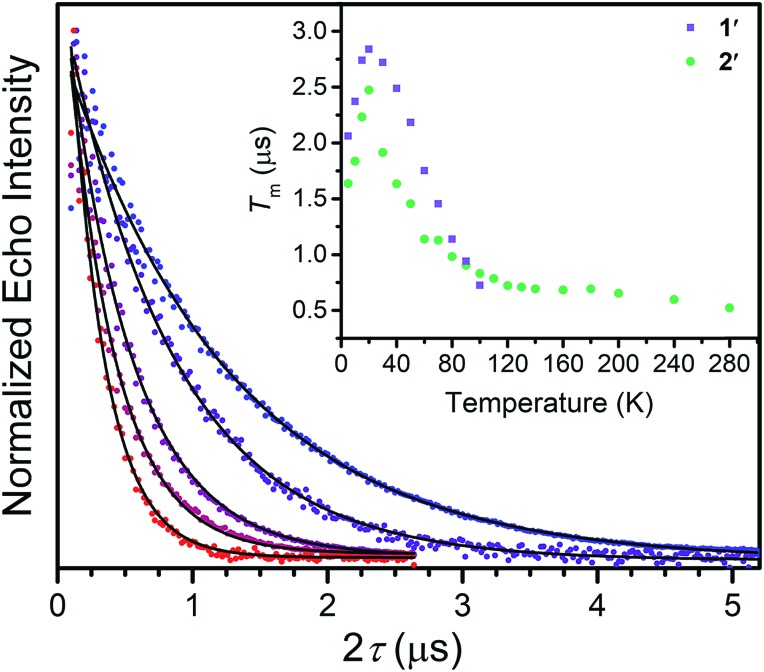
We investigated the diluted compounds by pulse EPR spectroscopy to probe the impact of covalency on spin dynamics. A direct measurement of T2 is often not possible. Instead the phase memory time, Tm, which encompasses all processes that contribute to electron spin decoherence, which include the T2 of the electron spin, is measured. Measurement of Tm proceeded via application of a Hahn-echo pulse sequence to 1′ and 2′ in the temperature range of 5–280 K (Fig. 2). At 5 K, both complexes feature Tm values of 1.5–2 μs, within the typical range for transition metal complexes. With increasing temperature from 5 K, T2 increases by ∼1 μs in both complexes. This lengthening occurs until 20 K, wherein Tm peaks for 1′ and 2′, reaching values of 2.84(1) and 2.48(2) μs, respectively. The origin of this behavior remains unclear but has been observed in other V(iv) catecholate complexes.19 Above 20 K, T2 begins to decrease, whereby 1′ features a more dramatic temperature dependence relative to 2′. By 100 K, 1′ possesses a Tm value of 0.72(6) μs, only slightly shorter than the Tm value of 0.83(1) μs for 2′ at 100 K. Interestingly, the echo is no longer detectible in 1′ above 100 K. In contrast, 2′ displays an echo until 280 K, permitting measurement of Tm at room temperature, with Tm = 0.51(1) μs at 280 K. The drastic discrepancies observed between 1′ and 2′, as well as the marginal decrease in Tm across such a wide temperature range in 2′ prompted us to delve deeper into their electronic structures and evaluate the impact of M–L covalency on T1 to account for the observed temperature dependences.
Fig. 2. Overlay of select Tm decay curves, in the temperature range of 20–280 K. The data was collected through application of a Hahn-echo pulse sequence. Inset: Temperature dependence of electronic spin phase memory times (Tm) for 1′ and 2′. Errors in the data are smaller than the dimensions of the data points.
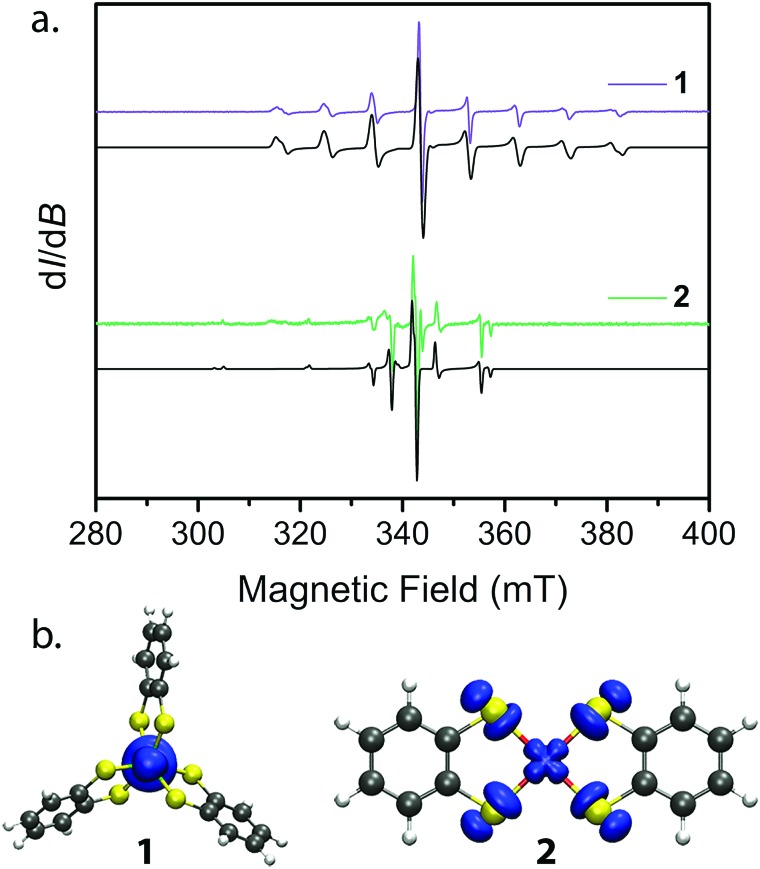
Towards that end, we examined the diselenocatecholate analogues of 1′ and 2′: (Ph4P)2[V0.005Ti0.995(C6H4Se2)3] (3′) and (Ph4P)2[Cu0.005Ni0.995(C6H4Se2)2] (4′) (see ESI† for full details). We initiated our investigation by analysis of their respective cw EPR spectra. 1′ and 3′ exhibit a collection of eight lines over 100 mT, consistent with electron–nuclear hyperfine coupling between the S = 1/2 spins and the 100% naturally abundant I = 7/2 51V nuclei (Fig. 3a). Complexes 2′ and 4′ display a more complex collection of resonances which are attributed to hyperfine coupling between the axial S = 1/2 spin with the two naturally abundant I = 3/2 nuclear spins of copper (63Cu and 65Cu, 69% and 31% natural abundance, respectively). Additional peaks in the spectrum of 4′ likely result from coupling to the Se–donor atoms (77Se, I = 1/2, 7.6% natural abundance, see ESI Fig. S5†). Simulations of all spectra proceeded with the program Easyspin27 and the spin Hamiltonian:
| Ĥ = gμBBS + IAS | 1 |
where g is the rhombic g-factor, μB the Bohr magneton, B the magnetic field, S the electronic spin, I the nuclear spin of the metal nucleus, and A the rhombic hyperfine coupling. Best simulations of the spectra for each complex yielded values that are reported in Table 1. The A and g parameters for 1′ and 3′ are within the expected values for trigonally symmetric pseudo-octahedral vanadium complexes.12,21 A cw EPR spectrum of 2 was previously reported,24 and the reported parameters reasonably reproduce our spectra with the inclusion of hyperfine coupling to both 63Cu and 65Cu nuclei. The additional complexity of the cw spectrum of 4′ is well-modelled with the inclusion of hyperfine coupling to a 7.6% natural abundance of 77Se nuclei. However, the simulation of 4′ is not a precise match, which may stem from non-collinearity of A and g, which has been previously reported in copper bis-diselenoate complexes.28
Fig. 3. (a) cw EPR spectra collected at 298 K for 1′ and 2′ (colored spectra) and their best simulations (black). Spin Hamiltonian parameters responsible for the simulations are reported in Table 2. (b) Plots of spin densities from the M06-L calculation for 1 and 2 with DMF as the solvent. The plots highlight the degree of spin delocalization onto the S-atoms in 2 and lack thereof in 1.
Table 1. Spin Hamiltonian parameters for simulating the cw EPR spectra of 1′–4′.
| 1′ | 2′ | 3′ | 4′ a | |
| g ∥ | 1.9878 | 2.085 | 1.950 | 2.082 |
| g ⊥ b | 1.9698 | 2.019 | 1.960 | 2.018 |
| 1.9698 | 2.019 | 1.955 | 2.018 | |
| A ∥ (MHz) | 0 c | 500 | 0 c | 460 (140) |
| A ⊥ (MHz) b | 258 | 115 | 255 | 145 (90) |
| 264 | 115 | 265 | 145 (90) | |
| α 2 | — | 0.51 | — | 0.39 |
| Spin density (M) | 0.935 | 0.756 | 0.949 | 0.732 |
| Spin density (E) d | 0.008 | 0.059 | 0.007 | 0.065 |
aHyperfine coupling constants in parentheses for 4′ correspond to 77Se hyperfine coupling.
bTop values for g⊥ and A⊥ are gx and Ax, bottom values are gy and Ay.
cNo features in the EPR spectrum corresponding to A∥ are apparent, inducing significant error in this value, and was held at zero for the simulation.
dSpin densities at the metal (M) and S/Se donors (E) were calculated using CASPT2.
Table 2. Fit parameters to the temperature dependence of T1 for 1′–4′.
| 1′ | 2′ | 3′ | 4′ | |
| A Dir (ms–1 K–1) | 4.7 ± 0.4 | 4.8 ± 0.8 | 0.51 ± 0.3 | 2.25 ± 0.8 |
| B Ram (ms–1) | 5 ± 2 × 105 | 1.4 ± 0.4 × 105 | 5.1 ± 2 × 105 | 2.1 ± 1 × 106 |
| C Loc (ms–1) | 5.4 ± 3 × 106 | 2.6 ± 1 × 106 | 3.1 ± 2 × 106 | 3.1 ± 2 × 106 |
| Θ Deb (K) | 98 ± 15 | 94.9 ± 9 | 71 ± 20 | 89 ± 6 |
| Δ loc (cm–1) | 275 ± 40 | 488 ± 72 | 161 ± 51 | 343.9 ± 80 |
The continuous wave EPR spectral simulations provide insight into the M–L covalency of 1–4. The magnitude of A is an important proxy of spin density at the metal nucleus, which is modified by covalency between the metal and ligands. This covalency is significantly dependent on the spin-bearing orbital. Only a small change is observed in A by changing the donor atom from S to Se in 1′ and 3′. Meanwhile, the same variation of donor atom in 2′ and 4′ results in a significant decrease in the magnitude and axiality of A. Of additional importance is the decrease in magnitude of A from 2′ to 4′; whereby the weaker hyperfine interaction in 4′ indicates relatively greater spin delocalization onto the C6H4Se22– ligand compared to C6H4S22–. To further bolster this argument, extraction of the covalency parameter α2, which relates to the σ bond strength of the dx2–y2 orbital, from the A and g parameters provides insight into the degree of spin-delocalization onto the catecholate ligands.29,30 This analysis, commonly performed in square planar Cu(ii) complexes,31–33 yields α2 parameters of 0.51 and 0.39 for 2′ and 4′, respectively. Here, a smaller α2 supports a greater degree of spin-delocalization onto the selenocatecholate ligand in 4′ relative to its sulfur analogue in 2′.
We employed both CASSCF/CASPT2 and DFT calculations on 1–4 to calculate the g-tensors and determine the amount of spin-density on the metal centers across the series. The calculated g-tensors agree well with the values extracted from the simulations of the cw spectra (see ESI Table S26†). The results of the MS-CASPT2 calculations, presented in Table 1, reveal significant spin densities residing on the S/Se donor atoms in 2 and 4, respectively. This showcases the strong covalency between the Cu2+ dx2–y2 orbital and S 3p and Se 4p orbitals. This result is in stark contrast with their vanadium counterparts, where spin density resides primarily in the dz2 orbital of the vanadium centre (Fig. 3b). The calculations are in good agreement with the natural bond orbital analysis computed with the M06-L functional and corroborate the α2 analysis extracted from the cw EPR spectra (see ESI Fig. S22 and Table S25†). The aggregate of this data support larger spin densities at the Se relative to S donors in 4 and 2, respectively. These results are broadly consistent with the qualitative electronic structures of Fig. 1:34 a (dz2)1 electron configuration in 1 and 3, wherein the dz2 orbital is relatively nonbonding, and a (dx2–y2)1 configuration in 2 and 4, wherein the spin-bearing dx2–y2 orbital directly engages the ligand orbitals. In summary, these data suggest: (1) enhanced M–L covalency for the copper-containing complexes 2 and 4 relative to 1 and 3; and (2) greater M–L covalency with the C6H4Se22– ligand relative to the C6H4S22– ligand.
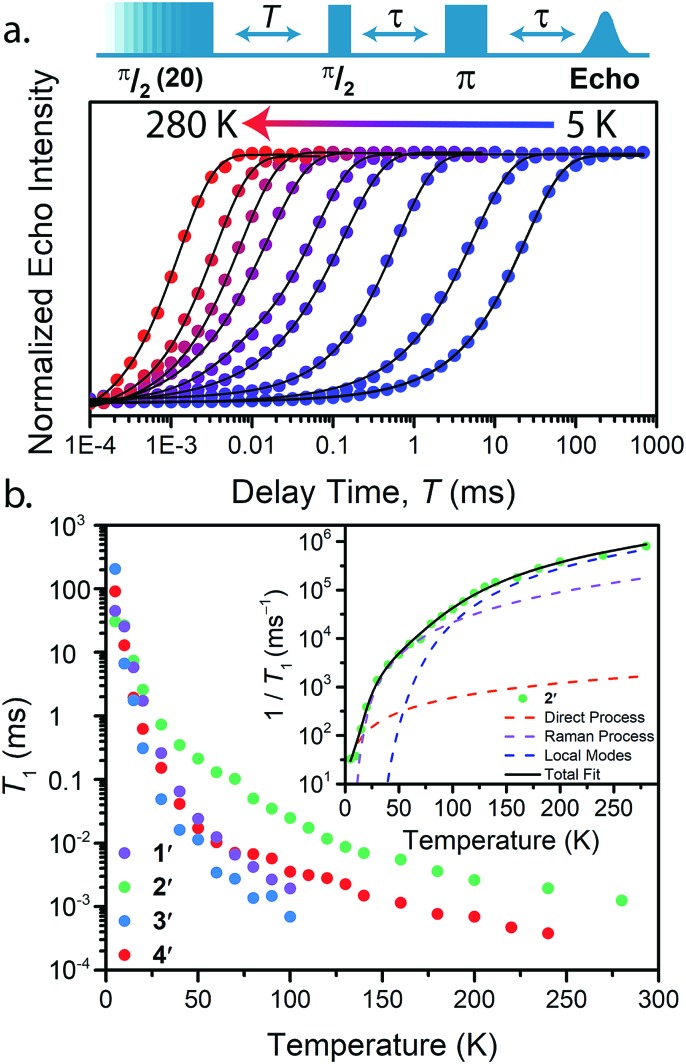
With these aspects of their electronic structures established, we explored the potential impact(s) on the spin–lattice relaxation times via saturation recovery experiments (Fig. 4a). In this experiment, a train of twenty consecutive 12 ns microwave pulses are applied to saturate the spin resonance corresponding to the MS = –1/2 to MS = +1/2 transition. Following saturation, a two-pulse Hahn-echo sequence is applied to detect the resurrection of the signal as a function of delay time, T. This pulse sequence differentiates itself from the commonly utilized inversion recovery experiment in that it seeks to eliminate the influence of spectral diffusion, or cross relaxation, which is often a prominent relaxation mechanism accounting for deviations from single exponential decay dynamics at low temperatures.35 Plotting the magnitude of the echo intensity as a function of delay time on a logarithmic scale results in the sigmoidal curves presented in Fig. 4a. Fitting these recovery curves to exponential decay functions, modified for the inclusion of spectral diffusion (see ESI†), provided the rates of recovery, which are equal to 1/T1.36 For all complexes, saturation recovery is slowest at 5 K and becomes faster with increasing temperature. In 1′ and 3′, the echo is detectable up to 100 K, beyond which the relaxation times became too fast for observation. In 2′ and 4′, however, a detectable echo persists until 280 K. The qualitative observation of slower relaxation at low temperature relative to high temperature is here quantitated. At 5 K, T1 values for 1′–4′ are 25(1), 30(1), 205(9), and 91(2) ms, respectively, while at 100 K, T1 is exponentially shorter, 1.9(1), 24.8(10), 0.7(1), and 3.5(1) μs for 1′–4′, respectively.
Fig. 4. (a) Select variable temperature saturation recovery curves for 3′. The data were collected via application of the pulse sequence depicted above the plot, in the temperature range of 5 to 280 K. (b) Summary of temperature dependent T1 data determined for 1′–4′. Inset: Fit to the temperature dependence of T1 for 2′, highlighting the relaxation mechanisms discussed in the text.
Analysis of the temperature dependence of T1 reveals three relaxation mechanisms that govern T1 for 1′–4′. The temperature dependence of T1 for all complexes was modeled to account for the influence of the direct, Raman, and local modes (Fig. 4b inset), using eqn (1) below.37
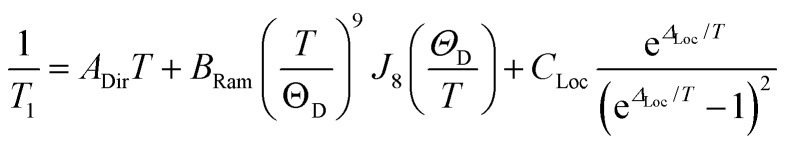 |
2 |
ADir, BRam, and CLoc are the coefficients for the direct, Raman, and local modes, respectively. T is the temperature, ΘD is the Debye temperature, J8 is the transport integral, and ΔLoc is the energy of the operative local vibrational mode. Our assignment of these processes, which models the data quite well, is guided by the known temperature ranges in which they occur. First, the direct process, which proceeds by the emission of a phonon is dominant below 10 K, and imparts a linear temperature dependence on T1. The direct process and spectral diffusion are often convoluted at these low-temperatures, but the use of a saturation recovery pulse sequence eliminates spectral diffusion from our model. Second, from 10 to 80 K, the Raman mechanism is typically observed, a two-phonon process involving the simultaneous absorption and emission of a phonon and imparts an exponential temperature dependence on T1.38 At higher temperatures, the influence of local vibrational modes begins to take effect, prompting our use of the local-mode term. This last term acts by modulating the MS energy levels, and is likely dominated by the first coordination sphere around the metal center.13 We eliminated a common high-temperature process, the Orbach process, from our model owing to the lack of low-lying accessible electronic states in dilute, uncoupled S = 1/2 systems.
The results of the foregoing mechanistic analyses of 1′–4′ point toward a picture of high-temperature relaxation governed primarily by metal–ligand interactions. First, the Raman process and local modes are considerably less operative (evidenced by smaller BRam) in the thiocatechol complexes 1′ and 2′versus their selenocatechol analogues 3′ and 4′. Second, the values of ΔLoc extracted from the fits are lower for the V(iv) complexes (275 and 161 cm–1 for 1′ and 3′) than the Cu(ii) complexes (488 and 343 cm–1 for 2′ and 4′, respectively). These observations are consistent with differences in metal–ligand interactions in 1–4. For example, the magnitude of BRam is strongly dependent on spin–orbit coupling and is concomitant with the observed differences in transitioning from S– (1 and 2) to their heavier Se–donor analogues (3 and 4).39 However, a more pronounced increase in BRam is observed between 2 and 4 relative to 1 and 3. Separately, ΔLoc is dependent on intramolecular vibration energies, and likely dominated by the inner coordination sphere and metal–ligand bond strength. The diminished influence of the local modes in 2 and 4 accounts for the persistence of T1 until room temperature.18
Our T1 analysis led us to believe that van der Waals phonon modes dominate T1 below 100 K and local modes of vibration dominate the T1 dynamics above 100 K. To support our analysis, we computed the phonon density of states and the local vibrational modes for 1–4, the results of which can be found in the ESI (Fig. S25 and S26†). Below 100 K, the Raman process dominates T1 relaxation and proceeds via coupling to low-energy phonon modes. The phonon density of states supports our observed trend in T1 relaxation below 100 K (Fig. S26†). Specifically, 3 and 4 possess a larger density of low-energy (<200 cm–1) phonon states compared to 2, and accounts for the longer T1 values for 2 in the 20–100 K range (see ESI† for further discussion). Likewise, the vanadium complexes 1 and 3 possess a significantly larger number of low-energy local vibrational modes relative to their copper counterparts. Additionally, the selenium–donor complexes 3 and 4 possess lower energy local vibrational modes in comparison to their sulfur–donor analogues. These observations corroborate the trend in ΔLoc extracted from our T1 analysis. We believe the higher energy vibrational modes in 2 relative to 4 accounts for the longer T1 in 2 at temperatures above 100 K.
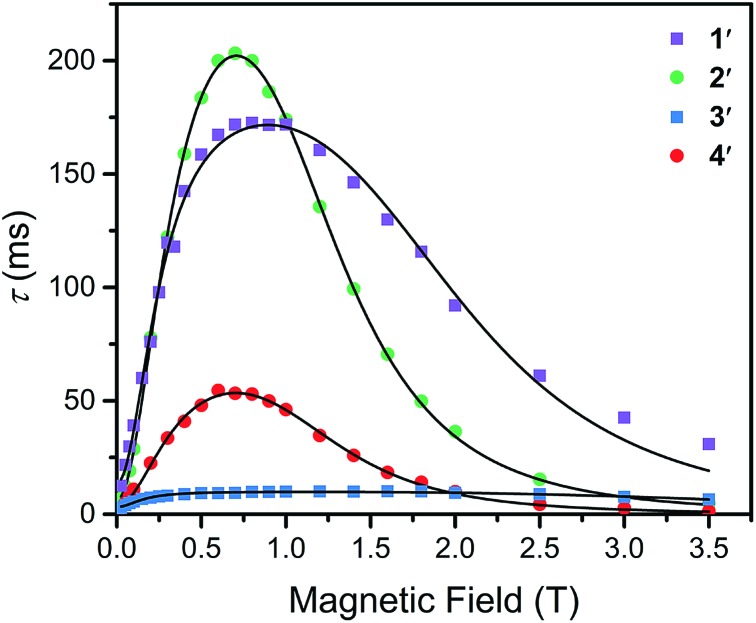
To further probe the impact of metal–ligand covalency on spin–spin interactions at low temperatures we acquired variable-field alternating current (ac) magnetic susceptibility data on 1–4 at 5 K from 25 mT to 3.5 T. We employed this technique to provide further insight into the spin relaxation dynamics operative at the lowest temperatures of measurement, specifically cross-relaxation and the direct process (Fig. 5 and S10–S13). Here, a peak in the out-of-phase magnetic susceptibility at a given oscillating field, frequency, static magnetic field, and temperature yields the rate of spin–lattice relaxation, 1/τ. This variable-field technique reveals additional mechanistic information that variable-temperature measurements does not.40–43 Close examination of the variable-field measurements performed at 5 K reveals a qualitatively similar field-dependence of τ for each compound. At low magnetic fields, τ increases with increasing magnetic fields until ∼0.75 T, beyond which it begins to drastically decrease with increasing magnetic fields. We modelled this data with the Brons–van Vleck model44 (eqn (2)) (see Table S23† for fit parameters):
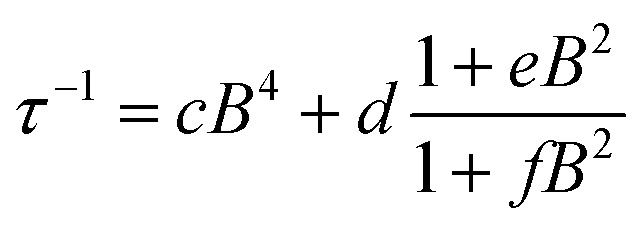 |
3 |
here, c is the coefficient for the direct process, d is the zero-field relaxation rate, e is dictated by the spin-concentration, and f relates to the internal magnetic field generated by dipolar coupled spins. This final parameter quantitates the ability of the external magnetic field to suppress cross-relaxation.
Fig. 5. Variable-field relaxation times (τ) extracted from alternating current magnetic susceptibility measurements performed on 1–4 at 5 K between 0.025 and 3.5 T. The solid lines are the best fits to the data according to eqn (3) in the text.
The Brons–van-Vleck model fits the data for 1–4 quite well and provides a mechanistic description of the variable-field data. First, the onset of the direct process at higher magnetic fields is responsible for the high-field hastening of relaxation, as it exhibits a B4 dependence owing to availability of a larger density of phonon states.45 Second, the low magnetic field behavior stems from shutting down dipolar induced (e.g. electron–electron and electron–nuclear) cross-relaxation pathways, leading to an increase in τ. This phenomenon is also observed in nitrogen vacancy centers in diamond.46 Finally, the plateau observed at ∼0.75 T in all compounds arises from the competition between subduing cross-relaxation at low fields and enabling the direct process at high fields.37
The more prominent decrease in τ at high-fields for 2 and 4, parameterized by c, are quantitated to be an order of magnitude more susceptible to the direct process relative to 1 and 3 (see ESI Table S23†). We hypothesize this behavior arises from stronger electron–nuclear hyperfine coupling in 2 and 4 relative to their vanadium counterparts, as mixing of magnetic sublevels enables the direct process.47,48 This will strongly affect the spin–lattice relaxation times at the lowest temperatures of measurement, and more critically at higher magnetic fields.
The ability of the external magnetic field to suppress cross-relaxation in these species relates to the internal magnetic field generated by the surrounding spin bath. We find f is considerably smaller in the vanadium complexes (212(62) and 122(23) T–2 for 1 and 3, respectively) relative to the copper complexes (389(50) and 162(30) T–2 for 2 and 4, respectively). The parameter f inversely scales with the number of nuclear spins that are coupled to electron spins by the hyperfine and dipolar interaction. For example, f is markedly smallest in 3, where the vanadium(iv) ion is expected to experience dipolar coupling to twelve catecholate 1H spins and six 77Se nuclei. Therefore, 3 exhibits the most pathways to undergo cross-relaxation. The more severe reduction in f between 2 and 4 relative to 1 and 3 is the result of the stronger 77Se hyperfine interaction arising from the strong Cu2+–Se covalency, thereby hindering the ability of the field to suppress cross-relaxation involving the 77Se nuclear spins. Our analysis corroborates the idea that hyperfine interactions enable the direct process to dominate at high magnetic fields and enable cross-relaxation pathways at low magnetic fields. Indeed, a recent theoretical study highlights the influence of hyperfine interactions on accelerating spin-relaxation, demonstrating its dominant influence at low magnetic fields.49 In summary, these results inspire the design principle of eliminating nuclear spins from ligands of qubit candidates due to their detrimental impact on both T1 and T2.50
The aggregate of our data thus far permits us to construct a cohesive picture of the temperature dependence of T1 and suggests metal–donor covalency and nuclear spin content as key design principles for elongating spin–lattice relaxation in qubit candidates. At the lowest temperatures, the vanadium complexes, 1′ and 3′, display a longer T1 than their copper analogues, 2′ and 4′. This observation is supported by the decreased susceptibility of the vanadium complexes to the direct process as determined by the variable-field ac susceptibility data and is a consequence of their weaker electron–nuclear hyperfine coupling. Above 10 K the copper complexes display longer T1 values than their vanadium counterparts, and the dithiolates possess longer T1 values than their selenium analogues. To understand the higher temperature dynamics, we must consider both the effective spin–orbit coupling experienced by the unpaired spin as well as the local modes of vibration.
Ligand-based spin–orbit coupling may become significant in governing T1 in highly covalent systems. In the selenium–donor complex 4, spin delocalization away from the metal could significantly weaken the effective spin–orbit coupling experienced by the electronic spin.51,52 This in turn suppresses the Raman process and yields longer T1's.53 However, 4 displays a faster spin–lattice relaxation rate than its sulfur analogue, 2. This unexpected hastening of relaxation time may be the result of the increased spin–orbit coupling from the selenium–donor atoms.54,55 This prompts us to conclude the heavy atom effect from donor atoms strongly affects T1 in highly covalent systems. Finally, the combined spin–orbit coupling of the metal-based spin with the low-energy vibrational modes in the vanadium(iv) complexes accounts for their fast T1 rates at higher temperatures. In contrast, reduction of spin–orbit coupling induced by metal–ligand covalency in the copper complexes, specifically 2, in combination with their higher energy local vibrational modes fortifies T1 up to room temperature.
Outlook
The systematic study reported herein provides the first direct evidence of a dependence of T1 on metal–ligand covalency. Specifically, longer T1 relaxation times for the sulfur donors in 1 and 2 in relation to their selenium analogues, 3 and 4. Importantly, such covalency appears to engender a significant role for spin-delocalization in copper complexes 2 and 4, enabling T1, and consequently, T2 to persist until room temperature. The significant role of M–L covalency ultimately dictates the potential for the observation of spin coherence at higher temperatures and must be carefully considered when designing molecular qubit candidates. Designing qubit candidates that persist to room temperature offers potential for creating designer qubits for quantum sensing applications within biology. Beyond quantum information science, these results may see impact in dynamic nuclear polarization where spin–lattice relaxation is an important parameter.56
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
We thank S. C. Coste, K. A. Collins, and D. W. Laorenza for helpful discussions and experimental assistance. This work was supported by Northwestern University, the State of Illinois, the Institute for Sustainability and Energy at Northwestern University, and the National Science Foundation CAREER Award No. CHE-1455017. (M. S. F., J. M. Z, and D. E. F.) and Award No. CHE-1565925 (M. R. W.). All synthetic work on qubit design was supported by CHE-1455017. X-ray crystallography was performed at the IMSERC at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF NNC).
Footnotes
†Electronic supplementary information (ESI) available: Methods and additional characterization and discussion. Crystallographic information of 1, 3–8 can be obtained from the Cambridge Structural Database CCDC 1877212–1877218. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc00074g
References
- Feynman R. P. Int. J. Theor. Phys. 1982;21:467–488. [Google Scholar]
- Lloyd S. Science. 1996;273:1073–1078. doi: 10.1126/science.273.5278.1073. [DOI] [PubMed] [Google Scholar]
- Nielsen M. A. and Chuang I. L., Quantum Information and Quantum Computation, 10th anniversary edn, Cambridge University Press, Cambridge, 2000. [Google Scholar]
- Wu Y., Jelezko F., Plenio M. B., Weil T. Angew. Chem., Int. Ed. 2016;55:6586–6598. doi: 10.1002/anie.201506556. [DOI] [PubMed] [Google Scholar]
- Aromí G., Aguilà D., Gomez P., Luis F., Roubeau O. Chem. Soc. Rev. 2012;41:537–546. doi: 10.1039/c1cs15115k. [DOI] [PubMed] [Google Scholar]
- Troiani F., Affronti M. Chem. Soc. Rev. 2011;40:3119–3129. doi: 10.1039/c0cs00158a. [DOI] [PubMed] [Google Scholar]
- Graham M. J., Zadrozny J. M., Fataftah M. S., Freedman D. E. Chem. Mater. 2017;29:1885–1897. [Google Scholar]
- Graham M. J., Zadrozny J. M., Shiddiq M., Anderson J. S., Fataftah M. S., Hill S., Freedman D. E. J. Am. Chem. Soc. 2014;136:7623–7626. doi: 10.1021/ja5037397. [DOI] [PubMed] [Google Scholar]
- Zadrozny J. M., Graham M. J., Krzyaniak M. D., Wasielewski M. R., Freedman D. E. Chem. Commun. 2016;52:10175–10178. doi: 10.1039/c6cc05094h. [DOI] [PubMed] [Google Scholar]
- Bader K., Dengler D., Lenz S., Endeward B., Jiang S.-D., Neugebauer P., van Slageren J. Nat. Commun. 2014;5:5304. doi: 10.1038/ncomms6304. [DOI] [PubMed] [Google Scholar]
- Zadrozny J. M., Freedman D. E. Inorg. Chem. 2015;54:1202–12031. doi: 10.1021/acs.inorgchem.5b02429. [DOI] [PubMed] [Google Scholar]
- Atzori M., Morra E., Tesi L., Albino A., Chiesa M., Sorace L., Sessoli R. J. Am. Chem. Soc. 2016;138:11234–11244. doi: 10.1021/jacs.6b05574. [DOI] [PubMed] [Google Scholar]
- Escalera-Moreno L., Suaud N., Gaita-Ariño A., Coronado E. J. Phys. Chem. Lett. 2017;8:1695–1700. doi: 10.1021/acs.jpclett.7b00479. [DOI] [PubMed] [Google Scholar]
- Atzori M., Tesi L., Benci S., Lunghi A., Righini R., Taschin A., Torre R., Sorace L., Sessoli R. J. Am. Chem. Soc. 2017;139:4338–4341. doi: 10.1021/jacs.7b01266. [DOI] [PubMed] [Google Scholar]
- Lunghi A., Totti F., Sanvito S., Sessoli R. Chem. Sci. 2017;8:6051–6059. doi: 10.1039/c7sc02832f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunghi A., Totti F., Sessoli R., Sanvito R. Nat. Commun. 2017;8:14620. doi: 10.1038/ncomms14620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atzori M., Benci S., Morra E., Tesi L., Chiesa M., Torre R., Sorace L., Sessoli R. Inorg. Chem. 2017;57:731–740. doi: 10.1021/acs.inorgchem.7b02616. [DOI] [PubMed] [Google Scholar]
- Escalera-Moreno L., Baldoví J. J., Gaito-Ariño A., Coronado E. Chem. Sci. 2018;9:3265–3275. doi: 10.1039/c7sc05464e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin C.-Y., Ngendahimana T., Eaton G. R., Eaton S. S., Zadrozny J. M. Chem. Sci. 2019;10:548–555. doi: 10.1039/c8sc04122a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi S., Tupitsyn I. S., van Tol J., Beedle C. C., Hendrickson D. N., Stamp P. C. E. Nature. 2011;476:76–79. doi: 10.1038/nature10314. [DOI] [PubMed] [Google Scholar]
- Zadrozny J. M., Niklas J., Pluektov O. G., Freedman D. E. ACS Cent. Sci. 2015;1:488–492. doi: 10.1021/acscentsci.5b00338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu C., Graham M. J., Zadrozny J. M., Niklas J., Krzyaniak M., Wasielewski M. R., Poluektov O. G., Freedman D. E. J. Am. Chem. Soc. 2016;138:14678–14685. doi: 10.1021/jacs.6b08467. [DOI] [PubMed] [Google Scholar]
- Sproules S., Weyhermüller T., DeBeer S., Wieghardt K. Inorg. Chem. 2010;49:5241–5261. doi: 10.1021/ic100344f. [DOI] [PubMed] [Google Scholar]
- Maiti B. K., Maia L. B., Pal K., Pkhira B., Avilés T., Moura I., pauleta S. R., Nuñez J. L., Rizzi A. C., Brondino C. D., Sarkar S., Moura J. J. G. Inorg. Chem. 2014;53:12799–12808. doi: 10.1021/ic501742j. [DOI] [PubMed] [Google Scholar]
- Machata P., Herich P., Lušpai K., Bucinsky L., Šoralová S., Breza M., Kozisek J., Rapta P. Organometallics. 2014;33:4846–4859. [Google Scholar]
- Shannon R. D. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1976;32:751–767. [Google Scholar]
- Stoll S., Schweiger A. J. Magn. Reson. 2006;178:42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- Kirmse R., Wartewig S., Windsch W., Hoyer E. J. Chem. Phys. 1972;56:5273–5278. [Google Scholar]
- Maki A. H., McGarvey B. R. J. Chem. Phys. 1958;29:31. [Google Scholar]
- Maki A. H., McGarvey B. R. J. Chem. Phys. 1958;29:35. [Google Scholar]
- Finazzo C., Calle C., Stoll S., van Doorlaer S., Schweiger A. Phys. Chem. Chem. Phys. 2006;8:1942–1953. doi: 10.1039/b516184c. [DOI] [PubMed] [Google Scholar]
- Hoffman S. K., Goslar J., Lijewski S., Zalewska A. J. Magn. Reson. 2013;236:7–14. doi: 10.1016/j.jmr.2013.08.009. [DOI] [PubMed] [Google Scholar]
- Moons H., Łapok Ł., Loas A., van Doorslaer S., Gorun M. S. Inorg. Chem. 2010;49:8779–8789. doi: 10.1021/ic100814j. [DOI] [PubMed] [Google Scholar]
- Figgis B. N. and Hitchman M. A., Ligand Field Theory and Its Applications, Wiley-VCH, New York, 2000. [Google Scholar]
- Hung S.-C., Grant C. V., Peloquin J. M., Waldeck A. R., Britt R. D., Chan S. I. J. Phys. Chem. A. 2000;104:4402–4412. [Google Scholar]
- Chen H., Maryasov A. G., Rogozhnikova O. Yu., Trukhin D. V., Tormyshev V. M., Bowman M. K. Phys. Chem. Chem. Phys. 2016;18:24954–24965. doi: 10.1039/c6cp02649d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eaton S. S., Harbridge J., Rindard G. A., Eaton G. R., Weber R. T. Appl. Magn. Reson. 2001;20:151–157. [Google Scholar]
- Fielding A. J., Fox S., Millhauser G. L., Chattopadhyay M., Kroneck P. M. H., Fritz G., Eaton G., Eaton S. S. J. Magn. Reson. 2006;179:92–104. doi: 10.1016/j.jmr.2005.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du J.-L., Eaton G. R., Eaton S. S. J. Magn. Reson. 1996;119:240–246. [Google Scholar]
- Tesi L., Lucaccini E., Cimatti I., Perfeti M., Mannini M., Atzori M., Morra E., Chiesa M., Caneschi A., Sorace L., Sessoli R. Chem. Sci. 2016;7:2074–2083. doi: 10.1039/c5sc04295j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atzori M., Tesi L., Morra E., Chiesa M., Sorace L., Sessoli R. J. Am. Chem. Soc. 2016;138:2154–2157. doi: 10.1021/jacs.5b13408. [DOI] [PubMed] [Google Scholar]
- Atzori M., Morra E., Tesi L., Albino A., Chiesa M., Sorace L., Sessoli R. J. Am. Chem. Soc. 2016;138:11234–11244. doi: 10.1021/jacs.6b05574. [DOI] [PubMed] [Google Scholar]
- Atzori N., Tesi L., Benci S., Lunghi A., Righini R., Taschin A., Torre R., Sorace L., Sessoli R. J. Am. Chem. Soc. 2017;139:4338–4341. doi: 10.1021/jacs.7b01266. [DOI] [PubMed] [Google Scholar]
- De Vroomen A. C., Lijphart E. E., H Prins D. Y., Marks J., Poulis N. J. Physica. 1972;61:241–249. [Google Scholar]
- De Vroomen A. C., Lijphart E. E., Poulis N. J. Physica. 1970;47:458–484. [Google Scholar]
- Jarmola A., Acosta V. M., Jensen K., Chemerisov S., Budker D. Phys. Rev. Lett. 2012;108:197601. doi: 10.1103/PhysRevLett.108.197601. [DOI] [PubMed] [Google Scholar]
- Abragam A. and Bleaney B., Electron paramagnetic resonance of transition ions, Clarendon Press, Oxford, 1970. [Google Scholar]
- Gómez-Coca S., Urtizberea A., Cremades E., Alonso P. J., Camón A., Ruiz E., Luis F. Nat. Commun. 2014;5:4300. doi: 10.1038/ncomms5300. [DOI] [PubMed] [Google Scholar]
- Lunghi A. and Sanvito S., arXiv preprint arXiv:1903.01424v1[quant-ph] 2018.
- Graham M. J., Yu C., Krzyaniak M., Wasielewski M. R., Freedman D. E. J. Am. Chem. Soc. 2017;139:3196–3201. doi: 10.1021/jacs.6b13030. [DOI] [PubMed] [Google Scholar]
- Stevens K. W. H. Proc. R. Soc. London, Ser. A. 1953;219:542–555. [Google Scholar]
- Kahn O., Molecular Magnetism, Wiley-VCH, 1993. [Google Scholar]
- Zhou Y., Bowler B. E., Eaton G. R., Eaton S. S. J. Magn. Reson. 1999;139:165–174. doi: 10.1006/jmre.1999.1763. [DOI] [PubMed] [Google Scholar]
- Schott S., McNellis E. R., Nielsen C. B., Chen H.-Y., Watanabe S., Tanaka H., McCulloch I., Sinova J., Sirringhaus H. Nat. Commun. 2017:15200. doi: 10.1038/ncomms15200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuire J., Miras H. N., Richards E., Sproules S. Chem. Sci. 2019;10:1483–1491. doi: 10.1039/c8sc04500c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni Q. Z., Daviso E., Can T. V., Makrhasin E., Jawla S. K., Swager T. M., Tempkin R. J., Herzfield J., Griffin R. G. Acc. Chem. Res. 2013;46:1933–1941. doi: 10.1021/ar300348n. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.