Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Mar 13;10(7):1477–1481. doi: 10.1021/acs.jpclett.9b00340

Gd(III)–Gd(III) Relaxation-Induced Dipolar Modulation Enhancement for In-Cell Electron Paramagnetic Resonance Distance Determination

Mykhailo Azarkh §, Anna Bieber §, Mian Qi †, Jörg W A Fischer §, Maxim Yulikov ‡, Adelheid Godt †, Malte Drescher §,*
PMCID: PMC6625747  PMID: 30864799

Abstract

graphic file with name jz-2019-00340c_0004.jpg

In-cell distance determination by electron paramagnetic resonance (EPR) spectroscopy reveals essential structural information about biomacromolecules under native conditions. We demonstrate that the pulsed EPR technique RIDME (relaxation induced dipolar modulation enhancement) can be utilized for such distance determination. The performance of in-cell RIDME has been assessed at Q-band using stiff molecular rulers labeled with Gd(III)-PyMTA and microinjected into Xenopus laevis oocytes. The overtone coefficients are determined to be the same for protonated aqueous solutions and inside cells. As compared to in-cell DEER (double electron–electron resonance, also abbreviated as PELDOR), in-cell RIDME features approximately 5 times larger modulation depth and does not show artificial broadening in the distance distributions due to the effect of pseudosecular terms.

Electron paramagnetic resonance (EPR) spectroscopy provides the means to determine distances between magnetically coupled electron spins. By combination of pulsed EPR techniques with site-directed spin labeling, distances in the range up to 8 nm, and under the very special condition of a perdeuterated biomacromolecule up to 16 nm, can be determined.1−10 Distance determination is based on the measurement of the dipolar coupling frequency, ωdd, which is inversely proportional to the cube of the distance between two magnetically coupled spins and can be performed in any kind of environment, including living cells. Because most cell components are diamagnetic, EPR-based distance determination inside cells is virtually background-free. Double electron–electron resonance (DEER or PELDOR)11,12 is the commonly used technique to perform such in-cell distance determination.13−19 In-cell EPR distance determination puts tight requirements on spin labels in terms of toxicity and stability. Complexes of Gd(III) with chelating ligands are ideal candidates for in-cell EPR and feature low toxicity, high stability, suitable spin relaxation times, and no orientation selection.18,20−25 Despite all these favorable properties of Gd(III)-based spin labels, conventional Gd(III)–Gd(III) DEER with rectangular pulses is still not the ideal technique for in-cell distance determination because of its low modulation depth and artifacts at short distances, e.g., below 3.4 nm if Gd(III)-PyMTA is used as the spin label.17,18,26,27 Though it is possible to increase the modulation depth and to reduce the artifacts at short distances by using chirp pulses28 and a dual-mode cavity,29 these improvements can be achieved only with an additional comprehensive and expensive equipment of the EPR spectrometer with a high-power microwave amplifier, an arbitrary-waveform generator, a broad-band, or a dual-mode cavity.

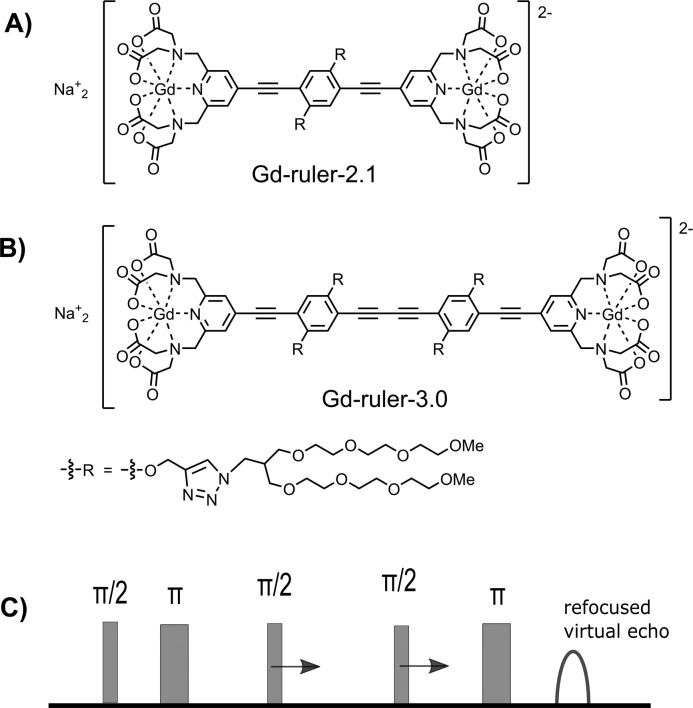
Alternatively, the downsides of conventional Gd(III)–Gd(III) DEER can be overcome in a related experiment abbreviated RIDME (relaxation-induced dipolar modulation enhancement).30−32 RIDME is a single-frequency technique and makes use of relaxation-induced spin flips, whereas DEER is a two-frequency technique which detects at the observer frequency while flipping coupled spins in a controlled way by a π-pulse at the pump frequency. Thus, RIDME is technically less demanding than DEER and has no limitations with respect to the excitation bandwidth. As an example, consider a rectangular pump pulse of 24 ns (excitation bandwidth of 40 MHz), which flips only a small part of the spins out of the 2 GHz-broad spectrum of Gd(III). While the contribution to the DEER signal is determined by this part of excited Gd(III) spins, the contribution to the RIDME signal is determined by the spins from the entire spectrum, which flip because of relaxation. Consequently, the modulation depth of in vitro Gd(III)–Gd(III) RIDME is increased by a factor of 10 compared to in vitro Gd(III)–Gd(III) DEER.26,33−35 These features of RIDME can also be beneficial for distance measurements inside cells. While the performance of Gd(III)–Gd(III) RIDME has recently been demonstrated for model systems in deuterated solvents at Q- and W-band frequencies,33−35 the in-cell application remained elusive. To the best of our knowledge, the only reported in-cell RIDME experiment was for trityl spin labels, which are S = 1/2 systems and have very different relaxation properties as compared to Gd(III) complexes.36 Here, we utilize stiff molecular rulers spin labeled with a Gd(III)-PyMTA complex (Figure 1A,B) and demonstrate that the 5-pulse dead-time free RIDME sequence32 (Figure 1C) is suitable for in-cell distance measurements between Gd(III)-based spin labels.

Figure 1.

Figure 1

Open in a new tab

Structural formulas of Gd-ruler-2.1 (A) and Gd-ruler-3.0 (B). (C) Dead-time free RIDME pulse sequence.

In-cell RIDME implies that the measurement is performed in protonated media, which results in shorter relaxation times, as compared to deuterated solvents. Additionally, RIDME features a steeper signal decay than DEER because of the hyperfine spin diffusion. Therefore, accurate choice of experimental conditions with respect to relaxation and spin diffusion is crucial to realize in-cell RIDME. The measurement of relaxation times for Gd-ruler-3.0 in H2O/glycerol (8/2 by volume) were performed in the temperature range between 10 and 30 K (Figure S1). The phase memory time decreases from 1.4 to 0.8 μs, and the ratio T2/T1 increases from 0.02 to 0.09 upon increasing the temperature. Though the highest ratio T2/T1 is favorable for RIDME, we performed all measurements at 10 K to have the longest phase-memory time. The pulse lengths were set at 8 and 16 ns for 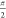Inline graphic and π, respectively. The mixing time of 8 μs provided a reasonable trade-off between the steepness of the RIDME background and the dipolar modulation depth. No proton electron spin echo envelope modulation (ESEEM) was observed for RIDME in protonated aqueous solution (the 1H nuclear frequency is approximately 48 MHz at 1.2 T). Neither was nuclear ESEEM observed from hyperfine and nuclear quadrupolar interactions with nitrogen atoms of the PyMTA ligand. Thus, no suppression of ESEEM effects was required. Consequently, the experimental RIDME data were processed as measured. Figure 2 shows the results of in vitro RIDME measurements in frozen protonated aqueous solutions (8/2 mixture of H2O and glycerol) for two molecular rulers that bear Gd-PyMTA as the spin labels with distances of 2.1 and 3.0 nm between the two Gd(III) ions.37−39 The RIDME form factors display modulation depths of 15% and 21% and visible oscillations, which indicate narrow distance distributions.

Figure 2.

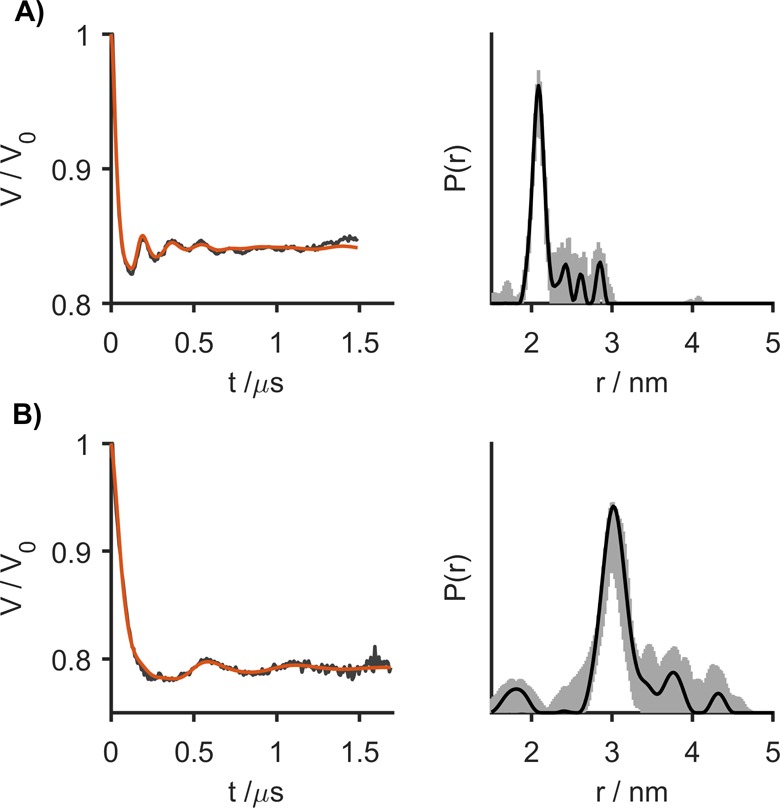
Figure 2

Open in a new tab

RIDME form factors (left) and corresponding distance distributions (right) obtained from frozen aqueous solutions of Gd-ruler-2.1 (A) and Gd-ruler-3.0 (B) in H2O/glycerol (8/2 by volume). Gray areas in the right panels show the uncertainty range (as defined in the Supporting Information) in the distance distributions.

For determination of the interspin distances from the RIDME data, it was taken into account that relaxation-induced spin flips with Δm ≥ 1 are possible for Gd(III) ions which have S = 7/2. Thus, apart from the fundamental frequency of the dipolar coupling ωdd, which corresponds to spontaneous spin flips with Δm = 1, overtones of this fundamental frequency occur, which originate from spin flips with Δm > 1. It has been shown for Gd(III) ions that only the first two overtones, i.e., 2ωdd and 3ωdd, contribute significantly to the RIDME form factor and that the overtone fractions can be assumed constant for distances above 3 nm, but they may vary if the distance is shorter.35

The RIDME data were processed with the OvertoneAnalysis software package, which explicitly includes the overtone fractions into the kernel function to extract the distance distribution by the Tikhonov regularization procedure.35 The fractions, which are represented by the coefficients P1, P2, and P3 (for the fundamental frequency ωdd and its overtones at 2ωdd and 3ωdd, respectively), were determined by their systematic variations toward a narrow single-peak distance distribution, as is expected for the studied Gd-rulers.26,35 We find the following overtone coefficients [P1P2P3]: [0.68 0.21 0.11] for Gd-ruler-2.1 and [0.4 0.3 0.3] for Gd-ruler-3.0. The sets of coefficients for the Gd-rulers in the protonated solution are different from the ones determined in the deuterated solution (cf. [0.8 0.2 0.0] for Gd-ruler-2.1 and [0.51 0.40 0.09] for Gd-ruler-3.0).35 From the comparison of the overtone coefficients for different solutions and different Gd-rulers, two observations follow: (i) Upon a decrease of the Gd(III)–Gd(III) distance but staying with the same solvent, P1 increases while P2 and P3 decrease.35 (ii) For the same Gd(III)–Gd(III) distance but changing from a protonated to a deuterated solvent, P1 increases and P3 decreases (P2 stays about the same). The distance distributions for both molecular rulers in aqueous solutions (Figure 2, right panel) were determined with the optimized overtone coefficients. The obtained distances are narrow and centered at 2.1 and 3.0 nm, in perfect agreement with the expectation.35

The origin of the different overtone coefficients in deuterated and protonated solutions still has to be investigated. For the moment, it is worth noting that some artifacts are possible in the RIDME experiment, which might affect the calibration of the overtone fractions. In particular, the echo crossing at zero time is very difficult to remove perfectly, and this might interfere with the calibration of the overtone fractions. Thus, the difference of these fractions between protonated and deuterated samples should be verified on a larger set of samples to be considered as an established fact.

After the proof-of-principle RIDME experiments in protonated media had been performed, Gd-ruler-3.0 was measured both in cell extract and inside oocytes of Xenopus laevis. The redox stability of Gd(III)-based spin labels allows for long incubation times.18,39 Thus, Gd-ruler-3.0 was incubated in the cell extract and inside oocytes for 2.5 h prior to shock freezing the sample for distance determination by RIDME. The form factors and the corresponding distance distributions are shown in Figure 3. In both cases at least one oscillation is clearly visible in the form factor. The accurate measurement of the second and further weak oscillations in the in-cell RIDME data is difficult because of the lower signal-to-noise ratio. The modulation depth of the in-cell measurement (13%, Figure 3B) is smaller than in the aqueous solution (21%, Figure 2B) and in cell extract (17%, Figure 3A), which is most likely due to the endogenous Mn(II) present in the cells (approximately 10 μM).18 Because endogenous Mn(II) ions contribute to the intensity of the RIDME signal but not to the modulation depth, the latter becomes diminished in in-cell measurements as compared with measurements in H2O/glycerol and in cell extract, in full analogy with in-cell DEER.18 The in-cell RIDME data for Gd-ruler-3.0 was analyzed using the same overtone coefficients as found for the protonated aqueous solution (vide supra). The resulting distance distribution is in agreement with the distance distribution determined in aqueous solution. This suggests that the overtone coefficients determined with a protonated aqueous solution can be used to determine Gd(III)–Gd(III) distance distributions for both in-extract and in-cell RIDME measurements.

Figure 3.

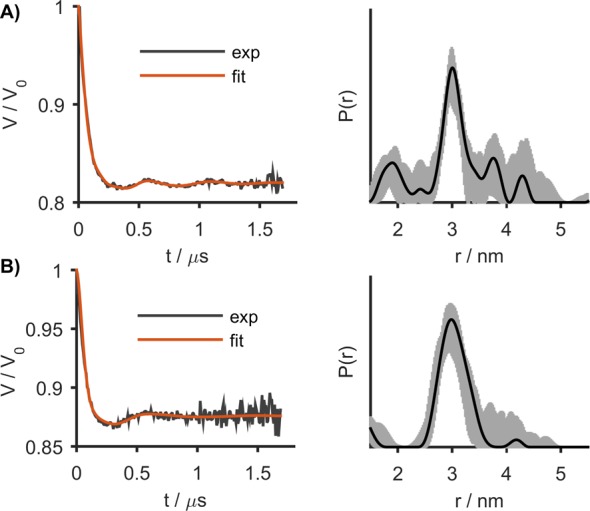
Figure 3

Open in a new tab

RIDME form factors (left) and the corresponding distance distributions (right) for Gd-ruler-3.0 in cell extract (A) and in oocytes (B). Gray areas in the right panels show the uncertainty range (as defined in the Supporting Information) in the distance distributions.

In general, in vitro RIDME measurements applied to Gd(III) spin-labeled compounds provide larger modulation depths and more accurate distance distributions than in vitro DEER measurements.34,35 In-cell measurements are performed under the challenging conditions of a protonated environment. In the presence of protons, the relaxation processes become faster and the hyperfine spin diffusion stronger. This results in a faster decay of the RIDME signal and shortens the length of the dipolar evolution time trace. If the experimental settings are chosen to maximize the length of the dipolar evolution time trace, i.e., low temperature and short mixing time, a RIDME time trace of at least 2 μs can be recorded, be it at the cost of the modulation depth. In this case, the modulation depths of in-cell and in vitro RIDME are in the range of 13–21%, which is still less than the modulation depth of 50% for RIDME measurements in deuterated solutions33 but is a significant improvement over an in-cell DEER measurement using the same Gd-ruler-3.0 (a modulation depth of about 4%).18

The overtone coefficients in a protonated aqueous solution and inside cells are the same for Gd-PyMTA spin labels at a given interspin distance. The distance distributions extracted from RIDME do not contain artifacts caused by pseudosecular terms, as opposed to DEER.20,26 We find that the overtone coefficients for aqueous solutions are significantly different for Gd(III)–Gd(III) distances of 2.1 and 3.0 nm, in agreement with what was reported for deuterated solvents.35 This implies that for broad distance distributions, which span distances below and above 3 nm, the dependence of the overtone coefficients on the interspin distance has to be included in the processing of the RIDME data.

In conclusion, we demonstrated for the first time the performance of Gd(III)–Gd(III) RIDME for distance measurements inside cells. It is suggested that the overtone fractions remain the same for samples in aqueous solution and inside cells, being primarily determined by the presence of protons in the medium. In the current state, Gd(III)–Gd(III) RIDME can be applied only to distance distributions where the overtone fractions can be assumed constant. Further methodological developments are required to account for variable overtone fractions during data processing and also to slow the decay of the RIDME signal during data acquisition. Along these lines, current developments of other Gd(III)-based spin labels40−45 and the application of shaped pulses46 are very promising. Giving its inherent advantages, i.e., precise distance determination and large modulation depth, RIDME has the potential to become a method of choice for in-cell distance measurements.

Acknowledgments

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement number: 772027 — SPICE — ERC-2017-COG). We thank Dr. Julia Cattani, Juliane Stehle, and Martina Adam for experimental contributions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00340.

  • Experimental details and additional figures (PDF)

Author Present Address

A.B.: Department of Molecular Structural Biology, Max Planck Institute of Biochemistry, Am Klopferspitz 18, 82152 Martinsried, Germany

The authors declare no competing financial interest.

Supplementary Material

jz9b00340_si_001.pdf (584.4KB, pdf)

References

  1. Distance Measurements in Biological Systems by EPR; Berliner L. J.; Eaton S. S.; Eaton G. R., Eds.; Biological Magnetic Resonance, Vol. 19; Kluwer Academics/Plenum Publishers: New York, 2000. [Google Scholar]
  2. Schiemann O.; Prisner T. F. Long-Range Distance Determination in Biomacromolecules by EPR Spectroscopy. Q. Rev. Biophys. 2007, 102, 377–390. 10.1017/S003358350700460X. [DOI] [PubMed] [Google Scholar]
  3. Jeschke G.; Polyhach Y. Distance Measurements on Spin-Labelled Biomacromolecules by Pulsed Electron Paramagnetic Resonance. Phys. Chem. Chem. Phys. 2007, 9, 1895–1910. 10.1039/b614920k. [DOI] [PubMed] [Google Scholar]
  4. Jeschke G. DEER Distance Measurements on Proteins. Annu. Rev. Phys. Chem. 2012, 63, 419–446. 10.1146/annurev-physchem-032511-143716. [DOI] [PubMed] [Google Scholar]
  5. Schmidt T.; Wälti M. A.; Baber J. L.; Hustedt E. J.; Clore G. M. Long Distance Measurements up to 160 A in the Groel Tetradecamer Using Q-Band DEER EPR Spectroscopy. Angew. Chem. 2016, 128 (51), 16137–16141. 10.1002/ange.201609617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Altenbach C.; Marti T.; Khorana H. G.; Hubbell W. L. Transmembrane Protein Structure: Spin Labeling of Bachteriorhodopsin Mutants. Science 1990, 248, 1088–1092. 10.1126/science.2160734. [DOI] [PubMed] [Google Scholar]
  7. Hubbell W. L.; Cafiso D. S.; Altenbach C. Identifying Conformation Changes with Site-Directed Spin Labeling. Nat. Struct. Biol. 2000, 7, 735–739. 10.1038/78956. [DOI] [PubMed] [Google Scholar]
  8. Klare J. P.; Steinhoff H.-J. Spin Labeling EPR. Photosynth. Res. 2009, 102, 377–390. 10.1007/s11120-009-9490-7. [DOI] [PubMed] [Google Scholar]
  9. Fielding A. J.; Concilio M. G.; Heaven G.; Hollas M. A. New developments in spin labels for pulsed dipolar EPR. Molecules 2014, 19 (10), 16998–17025. 10.3390/molecules191016998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Roser P.; Schmidt M. J.; Drescher M.; Summerer D. Site-Directed Spin Labeling of Proteins for Distance Measurements in Vitro and in Cells. Org. Biomol. Chem. 2016, 14 (24), 5468–5476. 10.1039/C6OB00473C. [DOI] [PubMed] [Google Scholar]
  11. Milov A.; Ponomarev A.; Tsvetkov Y. D. Electron-Electron Double Resonance in Electron Spin Echo: Model Biradical Systems and the Sensitized Photolysis of Decalin. Chem. Phys. Lett. 1984, 110 (1), 67–72. 10.1016/0009-2614(84)80148-7. [DOI] [Google Scholar]
  12. Pannier M.; Veit S.; Godt A.; Jeschke G.; Spiess H. W. Dead-Time Free Measurement of Dipole-Dipole Interactions Between Electron Spins. J. Magn. Reson. 2000, 142, 331–340. 10.1006/jmre.1999.1944. [DOI] [PubMed] [Google Scholar]
  13. Igarashi R.; Sakai T.; Hara H.; Tenno T.; Tanaka T.; Tochio H.; Shirakawa M. Distance Determination in Proteins inside Xenopus laevis Oocytes by Double Electron-Electron Resonance Experiments. J. Am. Chem. Soc. 2010, 132 (24), 8228–8229. 10.1021/ja906104e. [DOI] [PubMed] [Google Scholar]
  14. Krstic I.; Hänsel R.; Romainczyk O.; Engels J. W.; Dötsch V.; Prisner T. F. Long-Range Distance Measurements on Nucleic Acids in Cells by Pulsed EPR Spectroscopy. Angew. Chem., Int. Ed. 2011, 50, 5070–5074. 10.1002/anie.201100886. [DOI] [PubMed] [Google Scholar]
  15. Azarkh M.; Okle O.; Singh V.; Seemann I. T.; Hartig J. S.; Dietrich D. R.; Drescher M. Long-Range Distance Determination in a DNA Model System inside Xenopus laevis Oocytes by In-Cell Spin-Label EPR. ChemBioChem 2011, 12, 1992–1995. 10.1002/cbic.201100281. [DOI] [PubMed] [Google Scholar]
  16. Azarkh M.; Singh V.; Okle O.; Dietrich D. R.; Hartig J. S.; Drescher M. Intracellular Conformations of Human Telomeric Quadruplexes Studied by Electron Paramagnetic Resonance Spectroscopy. ChemPhysChem 2012, 13, 1444–1447. 10.1002/cphc.201100980. [DOI] [PubMed] [Google Scholar]
  17. Martorana A.; Bellapadrona G.; Feintuch A.; Di Gregorio E.; Aime S.; Goldfarb D. Probing Protein Conformation in Cells by EPR Distance Measurements using Gd3+ Spin Labeling. J. Am. Chem. Soc. 2014, 136 (38), 13458–13465. 10.1021/ja5079392. [DOI] [PubMed] [Google Scholar]
  18. Qi M.; Groß A.; Jeschke G.; Godt A.; Drescher M. Gd(III)-PyMTA Label Is Suitable for In-Cell EPR. J. Am. Chem. Soc. 2014, 136, 15366–15378. 10.1021/ja508274d. [DOI] [PubMed] [Google Scholar]
  19. Theillet F.-X.; Binolfi A.; Bekei B.; Martorana A.; Rose H. M.; Stuiver M.; Verzini S.; Lorenz D.; van Rossum M.; Goldfarb D.; Selenko P. Structural Disorder of Monomeric alpha-Synuclein Persists in Mammalian Cells. Nature 2016, 530, 45–50. 10.1038/nature16531. [DOI] [PubMed] [Google Scholar]
  20. Feintuch A.; Otting G.; Goldfarb D. Gd3+ Spin Labeling for Measuring Distances in Biomacromolecules: Why and How?. Methods Enzymol. 2015, 563, 415–457. 10.1016/bs.mie.2015.07.006. [DOI] [PubMed] [Google Scholar]
  21. Collauto A.; Feintuch A.; Qi M.; Godt A.; Meade T.; Goldfarb D. Gd(III) Complexes as Paramagnetic Tags: Evaluation of the Spin Delocalization over the Nuclei of the Ligand. J. Magn. Reson. 2016, 263, 156–163. 10.1016/j.jmr.2015.12.025. [DOI] [PubMed] [Google Scholar]
  22. Weinmann H. J.; Brasch R. C.; Press W. R.; Wesbey G. E. Characteristics of Gadolinium-DTPA Complex – A Potential NMR Contrast Agent. AJR, Am. J. Roentgenol. 1984, 142, 619–624. 10.2214/ajr.142.3.619. [DOI] [PubMed] [Google Scholar]
  23. Bousquet J. C.; Saini S.; Stark D. D.; Hahn P. F.; Nigam M.; Wittenberg J.; Ferrucci J. T. Gd-DOTA – Characterization of a New Paramagnetic Complex. Radiology 1988, 166, 693–698. 10.1148/radiology.166.3.3340763. [DOI] [PubMed] [Google Scholar]
  24. Cacheris W. P.; Quay S. C.; Rocklage S. M. The Relationship between Thermodynamics and the Toxicity of Gadolinium Complexes. Magn. Reson. Imaging 1990, 8, 467–481. 10.1016/0730-725X(90)90055-7. [DOI] [PubMed] [Google Scholar]
  25. Garbuio L.; Zimmermann K.; Häussinger D.; Yulikov M. Gd(III) Complexes for Electron-Electron Dipolar Spectroscopy: Effects of Deuteration, pH and Zero Field Splitting. J. Magn. Reson. 2015, 259, 163–173. 10.1016/j.jmr.2015.08.009. [DOI] [PubMed] [Google Scholar]
  26. Dalaloyan A.; Qi M.; Ruthstein S.; Vega S.; Godt A.; Feintuch A.; Goldfarb D. Gd(III)-Gd(III) EPR Distance Measurements – The Range of Accessible Distances and the Impact of Zero Field Splitting. Phys. Chem. Chem. Phys. 2015, 17, 18464–18476. 10.1039/C5CP02602D. [DOI] [PubMed] [Google Scholar]
  27. Yang Y.; Yang F.; Li X.-Y.; Su X.-C.; Goldfarb D. In-cell EPR Distance Measurements on Ubiquitin Labeled with a Rigid PyMTA-Gd(III) Tag. J. Phys. Chem. B 2019, 123, 1050. 10.1021/acs.jpcb.8b11442. [DOI] [PubMed] [Google Scholar]
  28. Doll A.; Qi M.; Wili N.; Pribitzer S.; Godt A.; Jeschke G. Gd(III)-Gd(III) Distance Measurements with Chirp Pump Pulses. J. Magn. Reson. 2015, 259, 153–162. 10.1016/j.jmr.2015.08.010. [DOI] [PubMed] [Google Scholar]
  29. Cohen M. R.; Frydman V.; Milko P.; Iron M. A.; Abdelkader E. H.; Lee M. D.; Swarbrick J. D.; Raitsimring A.; Otting G.; Graham B.; Feintuch A.; Goldfarb D. Overcoming Artificial Broadening in Gd3+-Gd3+ Distance Distributions Arising from Dipolar Pseudo-Secular Terms in DEER Experiments. Phys. Chem. Chem. Phys. 2016, 18, 12847–12859. 10.1039/C6CP00829A. [DOI] [PubMed] [Google Scholar]
  30. Kulik L. V.; Dzuba S. A.; Grigoryev I. A.; Tsvetkov Yu. D. Electron Dipole-Dipole Interaction in ESEEM of Nitroxide Biradicals. Chem. Phys. Lett. 2001, 343, 315–324. 10.1016/S0009-2614(01)00721-7. [DOI] [Google Scholar]
  31. Astashkin A. V. Mapping the Structure of Metalloproteins with RIDME. Methods Enzymol. 2015, 563, 251–284. 10.1016/bs.mie.2015.06.031. [DOI] [PubMed] [Google Scholar]
  32. Milikisyants S.; Scarpelli F.; Finiguerra M. G.; Ubbink M.; Huber M. A Pulsed EPR Method to Determine Distances between Paramagnetic Centers with Strong Spectral Anisotropy and Radicals: The Dead-Time Free RIDME Sequence. J. Magn. Reson. 2009, 201, 48–56. 10.1016/j.jmr.2009.08.008. [DOI] [PubMed] [Google Scholar]
  33. Razzaghi S.; Qi M.; Nalepa A. I.; Godt A.; Jeschke G.; Savitsky A.; Yulikov M. RIDME Spectroscopy with Gd(III) Centers. J. Phys. Chem. Lett. 2014, 5, 3970–3975. 10.1021/jz502129t. [DOI] [PubMed] [Google Scholar]
  34. Collauto A.; Frydman V.; Lee M. D.; Abdelkader E. H.; Feintuch A.; Swarbrick J. D.; Graham B.; Otting G.; Goldfarb D. RIDME Distance Measurements Using Gd(III) Tags with a Narrow Central Transition. Phys. Chem. Chem. Phys. 2016, 18, 19037–19049. 10.1039/C6CP03299K. [DOI] [PubMed] [Google Scholar]
  35. Keller K.; Mertens V.; Qi M.; Nalepa A. I.; Godt A.; Savitsky A.; Jeschke G.; Yulikov M. Computing Distance Distributions from Dipolar Evolution Data with Overtones: RIDME Spectroscopy with Gd(III)-based Spin Labels. Phys. Chem. Chem. Phys. 2017, 19, 17856–17876. 10.1039/C7CP01524K. [DOI] [PubMed] [Google Scholar]
  36. Jassoy J. J.; Berndhäuser A.; Duthie F.; Kühn S. P.; Hagelueken G.; Schiemann O. Versatile Trityl Spin Labels for Nanometer Distance Measurements on Biomolecules In Vitro and within Cells. Angew. Chem., Int. Ed. 2017, 56, 177–181. 10.1002/anie.201609085. [DOI] [PubMed] [Google Scholar]
  37. Qi M.; Hülsmann M.; Godt A. Spacers for Geometrically Well-Defined Water-Soluble Molecular Rulers and Their Application. J. Org. Chem. 2016, 81 (6), 2549–2571. 10.1021/acs.joc.6b00125. [DOI] [PubMed] [Google Scholar]
  38. Qi M.; Hülsmann M.; Godt A. Synthesis and Hydrolysis of 4-Chloro-PyMTA and 4-Iodo-PyMTA Esters and Their Oxidative Degradation with Cu(I/II) and Oxygen. Synthesis 2016, 48, 3773–3784. 10.1055/s-0035-1561660. [DOI] [Google Scholar]
  39. Yang Y.; Yang F.; Li X.-Y.; Su X.-C.; Goldfarb D. In-Cell EPR Distance Measurements on Ubiquitin Labeled with a Rigid PyMTA-Gd(III) Tag. J. Phys. Chem. B 2019, 123, 1050. 10.1021/acs.jpcb.8b11442. [DOI] [PubMed] [Google Scholar]
  40. Clayton J. A.; Qi M.; Godt A.; Goldfarb D.; Han S.; Sherwin M. S. Gd3+-Gd3+ Distances Exceeding 3 nm Determined by Very High Frequency Continuous Wave Electron Paramagnetic Resonance. Phys. Chem. Chem. Phys. 2017, 19, 5127–5136. 10.1039/C6CP07119H. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Mascali F. C.; Ching H. Y. V.; Rasia R. M.; Un S.; Tabares L. Using Genetically Encodable Self-Assembling GdIII Spin Labels to Make In-Cell Nanometric Distance Measurements. Angew. Chem., Int. Ed. 2016, 55 (37), 11041–11043. 10.1002/anie.201603653. [DOI] [PubMed] [Google Scholar]
  42. Yang Y.; Yang F.; Gong Y.-J.; Chen J.-L.; Goldfarb D.; Su X.-C. A Reactive, Rigid GdIII Labeling Tag for In-Cell EPR Distance Measurements in Proteins. Angew. Chem., Int. Ed. 2017, 56, 2914–2918. 10.1002/anie.201611051. [DOI] [PubMed] [Google Scholar]
  43. Welegedara A. P.; Yang Y.; Lee M. D.; Swarbrick J. D.; Huber T.; Graham B.; Goldfarb D.; Otting G. Double-Arm Lanthanide Tags Deliver Narrow Gd3+-Gd3+ Distance Distributions in DEER Measurements. Chem. - Eur. J. 2017, 23 (48), 11694–11702. 10.1002/chem.201702521. [DOI] [PubMed] [Google Scholar]
  44. Mahawaththa M. C.; Lee M. D.; Giannoulis A.; Adams L. A.; Feintuch A.; Swarbrick J. D.; Graham B.; Nitsche C.; Goldfarb D.; Otting G. Small Neutral Gd(III) Tags for Distance Measurements in Proteins by Double Electron-Electron Resonance Experiments. Phys. Chem. Chem. Phys. 2018, 20, 23535–23545. 10.1039/C8CP03532F. [DOI] [PubMed] [Google Scholar]
  45. Yang Y.; Yang F.; Gong Y.-J.; Bahrenberg T.; Feintuch A.; Su X.-C.; Goldfarb D. High Sensitivity In-Cell EPR Distance Measurements on Proteins Using an Optimized Gd(III) Spin Label. J. Phys. Chem. Lett. 2018, 9, 6119–6123. 10.1021/acs.jpclett.8b02663. [DOI] [PubMed] [Google Scholar]
  46. Doll A.; Qi M.; Pribitzer S.; Wili N.; Yulikov M.; Godt A.; Jeschke G. Sensitivity Enhancement by Population Transfer in Gd(III) Spin Labels. Phys. Chem. Chem. Phys. 2015, 17, 7334–7344. 10.1039/C4CP05893C. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz9b00340_si_001.pdf (584.4KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES