Handling Missing Data in the Modeling of Intensive Longitudinal Data

Abstract

Myriad approaches for handling missing data exist in the literature. However, few studies have investigated the tenability and utility of these approaches when used with intensive longitudinal data. In this study, we compare and illustrate two multiple imputation (MI) approaches for coping with missingness in fitting multivariate time-series models under different missing data mechanisms. They include a full MI approach, in which all dependent variables and covariates are imputed simultaneously, and a partial MI approach, in which missing covariates are imputed with MI, whereas missingness in the dependent variables is handled via full information maximum likelihood estimation. We found that under correctly specified models, partial MI produces the best overall estimation results. We discuss the strengths and limitations of the two MI approaches, and demonstrate their use with an empirical data set in which children’s influences on parental conflicts are modeled as covariates over the course of 15 days (Schermerhorn, Chow, & Cummings, 2010).

With new advances in statistical modeling techniques as well as data collection techniques, intensive longitudinal studies are becoming increasingly popular in the behavioral and social sciences to capture nuanced intra-individual changes as well as interindividual differences in intra-individual change. These designs also provide a renewed way of studying interrelations among change processes and the possible antecedents and determinants of interindividual differences in the change processes (Nesselroade & Baltes, 1979). Nevertheless, such intensive assessments often increase participant burden and consequently the likelihood of missing data due to participant noncompliance. Missing data also frequently arises within popular study designs. For instance, with event-contingent study designs, participants are only instructed to provide responses when a predefined event occurs, thus resulting in irregularly spaced data and substantial missingness in the data when used with discrete-time or regularly spaced models.

Determining appropriate responses to handle missing data requires knowledge of the three types of missing data mechanisms (Rubin, 1976), namely, missing completely at random (MCAR), missing at random (MAR), and not missing at random (NMAR). When missingness does not depend on any data, either observed or missing, it is defined as MCAR. MAR is delineated by missingness being related to the observed data, but not on the missing data (Fahrenberg & Myrtek, 2001). In contrast, NMAR refers to a situation when missingness depends on the value that would have been observed, but is currently missing. Appropriately responding to these different conditions is important as cross-sectional research has shown that inappropriately handling these various types of missingness leads to estimation problems, including bias in parameter point (Allison, 2003; Jones, 1996) and standard error estimates (Glasser, 1964), and reduction in power (Afifi & Elashoff, 1966), particularly in the case of NMAR.

Although extensive research has shown that missingness can cause bias within cross-sectional data, the impact of missingness on model estimation may be compounded when not accounted for in the estimation of intensive longitudinal data, given the time dependencies in the estimation. For instance, list-wise deletion, in which the entire observation would be dropped if any value of the variables is missing, is the default method of handling missing data in many software packages. However, list-wise deletion of intensive longitudinal data would alter the true time intervals between data points, resulting in bias parameter estimates (S. Liu & Molenaar, 2014) and low power. Additionally, most standard missing data handling tools were developed to handle missingness in cross-sectional data or longitudinal panel data (Eekhout et al., 2015; Graham, 2009; Landrum & Becker, 2001; M. Liu, Wei, & Zhang, 2006; Nakai & Ke, 2011; Wood, White, Hillsdon, & Carpenter, 2004). Given the increasing popularity of multivariate intensive longitudinal data analysis, more work needs to be done to examine ways to handle missing data in both dependent and covariate variables in the context of multivariate, multi-subject intensive longitudinal data under all three types of missing data mechanisms. We seek to fill this gap in the present article.

To motivate the missing data procedures considered in this article, we first describe an empirical example in which in fitting a multivariate, multi-subject time-series model, we face missingness in two time-varying covariates with the unknown missing data mechanism, while the missingness in the dependent variables of interest is likely MAR or NMAR. We then provide a brief review of the basic characteristics of the FIML and MI methods as well as the necessary adaptations when used to handle missingness in intensive longitudinal data.

MOTIVATING EXAMPLE

The current study was inspired by a previously published empirical study that explored the dynamics of inter-parental emotion states and behaviors at the ends of conflicts and associations with child emotions and behaviors during conflicts (Schermerhorn, Chow, & Cummings, 2010). Longitudinal data were collected from 111 cohabiting couples with a child of 8–16 years of age over 15 days. An event-contingent design was adopted in which the parents were asked to respond whenever or shortly after a conflict arose. In particular, the parents were asked to rate their own as well as their children’s emotional states and behaviors at each conflict. To analyze over-time and lagged dependencies in the couples’ dynamics and possible associations with child-related variable, Schermerhorn et al. (2010) considered the following model:

$$\left[\begin{array}{c}{w}_{it}\\ h_{it}\end{array}\right]=+\begin{array}{l}\begin{array}{cc}\left[\begin{array}{cc}{a}_{w\to w}& b_{h\to w}\\ b_{w\to h}& a_{h\to h}\end{array}\right]& \left[\begin{array}{c}{w}_{i,t-1}\\ h_{i,t-1}\end{array}\right]\end{array}\hfill \\ \begin{array}{cc}\left[\begin{array}{cc}{c}_{x1\to w}& d_{x2\to w}\\ c_{x1\to h}& d_{x2\to h}\end{array}\right]& \left[\begin{array}{c}x{1}_{it}\\ x{2}_{it}\end{array}\right]+\left[\begin{array}{c}{e}_{w,i,t}\\ e_{h,i,t}\end{array}\right]\end{array}\hfill \\ \begin{array}{cc}\left[\begin{array}{c}{e}_{w,i,t}\\ e_{h,i,t}\end{array}\right]& \sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\sigma }_{e_w}^2& {\sigma }_{e_{wh}}\\ {\sigma }_{e_{wh}}& {\sigma }_{e_h}^2\end{array}\right]\right)\end{array}\hfill \end{array}$$ (1)

where w_it and h_it represent the emotional rating, such as positive/negative emotion or conflict resolution, of wife and husband, respectively, from family i at the end of the tth conflict (i = 1,…, n; t = 1,…, T). The terms e_w,i,t and e_h,i,t are the residuals for wife and husband not accounted for by the hypothesized model, assumed to be multivariate normally distributed with zero means, variances ${\sigma }_{e_w}^2$ and ${\sigma }_{e_h}^2$, respectively, and covariance ${\sigma }_{e_{wh}}$. The hypothesized model is a vector autoregressive (VAR) model of order 1 with covariates, in which the dependent variables at the current time point are predicted by the dependent variables at the immediately preceding time point (i.e., a lag of 1). In the present context, the emotional states and conflict resolution behavior of each spouse at the end of the tth conflict were posited to be influenced by their own emotional states and resolution behavior at the t – 1th conflict, the strengths of which are captured in the auto-regression parameters, a_w→w and a_h→h. In addition, each person’s previous emotional states and resolution behavior at the previous conflict are also assumed to affect the partner’s emotional state and resolution behavior at the tth conflict, as governed by the cross-regression parameters, b_h→w and b_w→h. Two covariates are included in the dynamic model. The covariate, x₁, represents a child aggregate score on agentic behavior in the ith family, which includes actions such as helping out, taking sides, comforting the parents, and trying to make peace. The other covariate, x₂, is an aggregate measure of the child’s negative emotions and dysregulated behaviors, as averaged across actions such as anger, sadness, fear, as well as misbehaving, yelling at the parents, and aggression.

In this empirical study, a large portion (67% for all child-related variables) of the child-related covariates was missing because the children were not present when their parents were having conflicts (Schermerhorn et al., 2010). To handle the missingness, the authors previously recoded the child-related covariates from sum scores (ranging from 0 to 10) into dummy variable such that a child’s value on each covariate was coded as 0 both when the child did not display the behavior during the conflict and when the child was “missing” (i.e., not present at the conflict); each of the two covariates was coded as 1 when the child showed any level of that behavior. In other words, occasions on which the child was absent were treated to be the same as the occasions on which the child was present but did not display any of the specified actions (i.e., agentic behavior and negativity). This coding scheme has three primary drawbacks: (1) the data blurs the level of a child’s influence with presence or absence of the data, obscuring the ability to make meaning of the data; (2) it discounts potential effects of different levels of the child-related variables on dynamics at the family level, and (3) this data mechanism may be inappropriate as both the dependent and child-related covariates may be NMAR (e.g., the couples might be especially careful in ensuring that the child was absent when they anticipated discussing highly stress-provoking topics). Motivated by these empirical concerns, our goal in this study is to evaluate and compare the previous modeling results with new results obtained using two MI approaches we adapted for use with intensive longitudinal data, to be described in the following section.

Methods for Handling Missing Data and Issues

To understand our choices of missing data handling methods, a brief review of the contemporary methods of handling missing data and issues is in order. List-wise deletion, or complete case analysis, is perhaps the most commonly used method in handling missing data. It is also the default method in most statistical software packages (Ibrahim, Chen, Lipsitz, & Herring, 2005). With this method, only those subjects whose data are completely observed are included in the analysis. Model fitting procedures would be performed as if the data set after the removal of list-wise missingness is the complete data set. In the context of cross-sectional models, parameter point estimates are usually unbiased with list-wise deletion if the missingness occurs completely at random. However, with fewer observations in the data set, the standard error estimates may be biased, and power may also be reduced. More importantly, if the list-wise deletion method is applied to longitudinal data, the time intervals between observations will be incorrectly altered, which may result in biased point and standard error estimates.

A widely implemented approach to handling missing data is to use pattern-mixture models. Pattern-mixture models specify: $P(Y,R|X)=P(Y|R,X)P(R|X)$, where Y represents the dependent variable; R represents the missing data indicator matrix with entries consisting of 0s and 1s, corresponding to cases for which missingness is absent and present, respectively; and X represents covariates. With this method, the observed data depend on (are conditional on) the missing data patterns embedded in R, and R is postulated to depend only on the covariates, X (Little, 1993). Thus, a model is fit to observed data as grouped by missing data patterns, resulting in one set of parameter estimates for each group. In some applications, those parameter estimates are averaged (or weighted averaged) over groups to obtain the overall parameter estimates for all observed data, and some covariates of choice, i.e., X, are used to predict “membership” in the different groups of missing data patterns (Hedeker & Gibbons, 1997). Even though this method is based on a very intuitive way of decomposing $P(Y,R|X)$ and is very popular in structural equation modeling (Allison, 1987; Muthén, Kaplan, & Hollis, 1987), latent growth structural equation models (McArdle & Hamagami, 1992), and the random-effects literature (Hedeker & Gibbons, 1997), it is cumbersome to use with intensive longitudinal data because they are typically characterized by too many possible missing patterns to model. For instance, as few as seven measurement occasions of one variable will generate 128 (2⁷) possible missing data patterns, and the number of missing data patterns would increase substantially as the number of measurement time points increases. Therefore, it is often not practical to use pattern-mixture modeling in intensive longitudinal data analysis.

Data interpolation using splines or other nonparametric approaches (Chow & Zhang, 2008; De Boor, 1978; Kohn & Ansley, 1987; S. Liu & Molenaar, 2014; Wahba, 1990; H. Zhang, 1997) is another commonly adopted approach for handling missingness and/or irregularly spaced intensive longitudinal data for use with discrete-time (equally spaced) dynamic models (Tarvainen, Hiltunen, Ranta-Aho, & Karjalainen, 2004). Helpful interpolation tools include the na.approx() function in the zoo package in R (Zeileis & Grothendieck, 2005), which replaces all the missing values with linearly interpolated data, and the akima() function in the akima package (Akima, 1970, 1991), which interpolates any specified points between two observed data points using polynomials up to a cubic degree. Alternatively, S. Liu and Molenaar (2014) proposed using VAR models to interpolate missing data in multivariate time-series data and provided an R program, iVAR, for doing so.

Although practical and easy to implement, these interpolation approaches only take into consideration information from the times series of dependent variables and do not account for influences of the covariates. Approaches such as the iVAR are also confined by other constraints and assumptions, requiring, for instance, that the time-series process be stationary (i.e., with statistical properties that do not vary with time), the beginning of the time series be fully observed, and that the variables to be imputed conform to a multivariate normal distribution—thus limiting their utility in handling missingness in non-normal (e.g., categorical) covariates. Additionally, all these interpolation methods generate only one interpolated value for each missing observation; the interpolated data set is used in subsequent model fitting as if it were fully observed. As such, these procedures do not account for the uncertainty associated with the interpolated data, and may lead to underestimation of the standard errors. Finally, although not explicitly stated so, interpolating missing data based on information from the observed data assumes that the missing data mechanism can be adequately characterized as MCAR or MAR, and may not work under conditions of NMAR.

Other well-known methods for dealing with missing data include full-information maximum likelihood (FIML) and multiple imputation (MI) (Collins, Schafer, & Kam, 2001). Both methods have been shown to produce consistent estimates under certain conditions (i.e. MAR) for regression models (Thoemmes & Rose, 2014), but most of the work was targeted toward cross-sectional data (Allison, 2002; Horton & Kleinman, 2007; Ibrahim, 1990; Ibrahim et al., 2005; Little & Rubin, 2014; Schafer, 1997). S. Liu and Molenaar (2014) performed some comparisons of one possible MI approach and the iVAR approach in the context of time-series models and showed that the latter outperformed the former by a large margin. However, the specific MI procedure they considered did not take into account lagged information in imputing the missing data, thus bypassing key information on which one can readily capitalize in the imputation process; they also did not compare the approaches considered under NMAR—a condition under which MI methods may have some advantages over methods such as FIML. In the present article, we focus on comparing FIML and MI methods that are specifically adapted to tailor to characteristics of longitudinal data, especially intensive longitudinal data.

FIML

The FIML approach essentially handles missingness by performing parameter optimization using a raw data likelihood function constructed based on only the observed data (Arbuckle, 1996). In fitting models for intensive longitudinal data, the state-space framework provides a convenient platform for specifying any linear discrete-time longitudinal or dynamic model. The associated raw data likelihood function, often termed the prediction error decomposition function, can then be constructed using the observed data to perform FIML estimation (Chow, Ho, Hamaker, & Dolan, 2010; Harvey, 2001). The associated estimation procedures have been implemented in packages such as mkfm6 (Dolan, 2002), the SS fpack library in Ox (Koopman, Shephard, & Doornik, 1999), and the KFAS library in R (Helske, 2016). FIML remains one of the “gold standard” approaches for handling missing data in the dependent variables when the model is correctly specified, the data are MAR or MCAR, and the likelihood function has a close analytic form. However, this approach does not handle missingness in the covariates. One possible way to circumvent this problem is to include the covariates as dependent variables in the model, in which case the missingness can be handled via standard FIML estimation. Unfortunately, this method is not always practically feasible when many covariates are involved and some of them are non-normal or categorical in nature (i.e. sex, race). Moreover, in many cases, it may not be desirable to include covariates as additional dependent variables in the dynamic model due to the added computational costs and the fact that the dynamics of the covariates may not be the focus of direct modeling interest.

MI

MI, a commonly adopted approach for handling missingness, was first proposed by Rubin (1977), and elaborated in his work (Rubin, 2004). This method factors out $P(Y,R|X)$ in a way different from the pattern-mixture models, where $P(Y,R|X)=P(R|Y,X)P(Y|X)$. MI is based on the premise that in MI, m > 1 versions of multiple imputed data sets are first created by filling in the missing values using a missing data model of choice. These data sets are then analyzed as if they were complete data, using standard complete-data methods. Parameter estimates across the m imputations are then pooled for inferential purposes and the corresponding standard error estimates are adjusted to accommodate sources of variability both within and across imputations, thereby providing a way to quantify the missing data uncertainty. This method has the advantage of preserving the relations of the variables in the data while simultaneously accounting for the uncertainty about these relations (van Buuren & Groothuis-Oudshoorn, 2011). It has been widely applied in cross-sectional survey data (Rubin, 1996) and is one of the most popular missing data approaches (Allison, 2000; Harel & Zhou, 2007; Rubin, 1996; Schafer & Graham, 2002; Sinharay, Stern, & Russell, 2001; P. Zhang, 2003). Even though the underlying missing data mechanism may or may not conform to the MAR mechanism, inclusion of appropriate auxiliary variables – namely, observed variables that are not of substantive interest but may be related to aspects of the missing data mechanism – helps approximate a MAR scenario. The auxiliary variables are included in the imputation model only for the purpose of improving estimates of the missing data, reducing error variance, and increasing the precision of the parameter estimates (Thoemmes & Rose, 2014). The validity of including auxiliary variables has been assessed and proven both theoretically (Meng, 1994; Rubin, 1996; Schafer, 1997) and through simulation studies (Collins et al., 2001; van Buuren, Boshuizen, & Knook, 1999).

MI can be implemented with different techniques and software programs (e.g., King, Honaker, Joseph, & Scheve, 2001; Raghunathan, Lepkowski, Van Hoewyk, & Solenberger, 2001; Schafer, 1999; van Buuren & Groothuis-Oudshoorn, 2011). An extensive review of statistical computing software for MI packages for regression models has been provided by Horton and Lipsitz (2001). In this study, we compare two R packages that perform MI: MICE (van Buuren & Groothuis-Oudshoorn, 2011) and Amelia II (Honaker, King, & Blackwell, 2011). We provide a brief overview of their operating principles and imputation models here.

In the MICE package, MI is implemented via a chained equation approach. With this method, imputations are drawn by iterating over the conditional densities on a variable-by-variable basis by means of Markov chain Monte Carlo (MCMC) techniques (van Buuren & Groothuis-Oudshoorn, 2011). Let Y be the array of all dependent variables of interest for all individuals, and X be the array of covariates for all individuals. Let Y^obs and X^obs denote the observed data in the dependent variables and covariates, respectively, while Y* and X* denote their missing counterparts. θ is a vector of unknown parameters that completely approximates the multivariate distribution of Y and X. The ith iteration of the chained equation (i = 1,…, m) is a Gibbs sampler that draws successively from

$$\begin{gathered} {\theta }^{(i)}\sim P(\theta |Y^{obs},X^{(i-1)}) \\ {Y}^{\ast (i)}\sim P(Y|Y^{obs},X^{(i-1)},{\theta }^{\ast (i)}) \\ {X}^{\ast (i)}\sim P(X|X^{obs},Y^{(i)},{\theta }^{\ast (i)}) \end{gathered}$$ (2)

where the draw for the jth missing variable in Y*⁽ⁱ⁾, $Y_j^{*(i)}$, is conditional on all of the other non-missing variables in Y^obs, complete X⁽ⁱ⁻¹⁾ with missing covariates filled in with imputed values from the i – 1th iteration, and draws for θ*⁽ⁱ⁾ from the ith iteration. In a similar vein, the draw for the jth missing variable in X*⁽ⁱ⁾, $X_j^{*(i)}$, is conditional on all of the other non-missing variables in X^obs, complete Yⁱ with missing dependent variable values filled in with imputed values from the ith iteration, and draws for θ*⁽ⁱ⁾ from the ith iteration. The relations among the variables to be imputed and the corresponding “predictors” are assumed to follow an appropriate general or generalized linear model, depending on the distributional characteristics of the variables to be imputed (e.g., normal continuous data, ordinal, nominal). MICE provides considerable flexibility in customizing imputation models for different data characteristics and modeling purposes, and extensive graphical summaries of the MCMC process.

Amelia II is an MI program specializing in handling missingness in time-series data (Honaker & King, 2010; Honaker et al., 2011). Elements common to many intensive longitudinal models, such as polynomial time trends and lagged (previous) occasions of the variables to be imputed, are among the elements that can be used in the imputation model. As distinct from MICE, Amelia II performs imputations by assuming that the variables of interest, denoted herein as D = Y, X, are multivariate normally distributed with mean vector, μ, and covariance matrix, Σ. Thus, unlike MICE, the parameter vector needed to perform the imputations, θ, consists only of elements from a multivariate normal distribution, namely, elements in μ and Σ. Limited capacity is available for handling non-normal variables with missingness. That is, nominal, ordinal, and other non-normal (e.g., skewed) variables are handled by first drawing continuous-valued imputations from a multivariate normal distribution, and then performing heuristic transformations (e.g., square-root and log transformations, taking the continuous-valued draws as probabilities of success in a multi-nomial distribution to yield nominal imputed values; for further details, see Honaker et al., 2011). However, parameters that would otherwise define these non-normal distributions (e.g., the probability of each category in a multinomial distribution) are not estimated as in MICE.

With some of the simplification described above, Amelia II is able to gain some computational speed by replacing a full MCMC algorithm, which has more flexibility in handling a variety of posterior distributions for Y, X, and θ, with a faster, bootstrap-based expectation maximization (BEM) algorithm. The BEM operates as follows. A bootstrap procedure is first used to draw m samples of size n (the original sample size of Y and X ) with replacement from the data, D. Each of these boot-strapped data sets is used in the EM algorithm to obtain updated estimates of elements in θ. Following the parameter updates, missing observations in the original data set are then imputed separately using each of the m sets of parameter estimates from the EM, resulting in m multiply imputed data sets.

Pooling the estimates across MI replications for MICE and Amelia II

MICE and Amelia II can both be used to implement MI. Following the generation of m imputed data sets using either package, each of the m imputed data sets is then subjected to the same model fitting procedures as if it were fully observed, resulting in m sets of parameter estimates from fitting the model of interest. The m sets of estimates are then pooled into one final set of parameter estimates using Rubin (1996)’s pooling procedures. Specifically, the final point estimates are obtained as the average of the parameter estimates over the m MI replications as follows:

$$\begin{array}{l}\left(\begin{array}{c}\text{Posterior}\hspace{0.17em}\text{mean}\\ \text{of}\hspace{0.17em}\text{parameter}\hspace{0.17em}\text{estimates}\end{array}\right)\\ \hspace{0.17em}\hspace{0.17em}\text{=}\hspace{0.17em}\text{Average}\left(\begin{array}{c}\text{repeated}\hspace{0.17em}\text{complete}\hspace{0.17em}-\hspace{0.17em}\text{data}\\ \text{posterior}\hspace{0.17em}\text{means of}\hspace{0.17em}\text{parameter}\hspace{0.17em}\text{estimates}\end{array}\right),\end{array}$$

The final variances of the parameter estimates are computed as follows:

$$\begin{array}{l}\left(\begin{array}{c}\text{Posterior}\\ \text{variance}\hspace{0.17em}\text{of}\hspace{0.17em}\text{parameter}\hspace{0.17em}\text{estimates}\end{array}\right)\\ \hspace{0.17em}\hspace{0.17em}\text{=}\hspace{0.17em}\text{Average}\left(\begin{array}{c}\text{repeated}\hspace{0.17em}\text{complete}\hspace{0.17em}-\hspace{0.17em}\text{data}\\ \text{variance}\hspace{0.17em}\text{of}\hspace{0.17em}\text{parameter}\hspace{0.17em}\text{estimates}\end{array}\right)\\ \hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}\text{Variance}\left(\begin{array}{c}\text{repeated}\hspace{0.17em}\text{complete}\hspace{0.17em}-\hspace{0.17em}\text{data}\\ \text{posterior}\hspace{0.17em}\text{means}\hspace{0.17em}\text{of}\hspace{0.17em}\text{parameter}\hspace{0.17em}\text{estimates}\end{array}\right),\end{array}$$

from the sum of the average variances of the parameter estimates over the m imputations and the variances of the parameter estimates across imputations.

Goals of the Present Article

MICE and Amelia II are two commonly used tools to implement MI. They have some shared features, but also some key differences. Amelia II has some built-in modeling features that make it especially amenable to intensive longitudinal data. These features are not readily available in the MICE package, but users may construct their own lagged variables and polynomial time trends to be used in imputing intensive longitudinal data—a variation that has not been considered in previous studies using MICE for MI purposes (e.g., S. Liu & Molenaar, 2014) and is one of the key aspects to be evaluated in the present article. Also as noted, because the imputations in Amelia II are performed assuming that D is multivariate normally distributed and the other parameters involved in defining other non-normal distributions are not estimated directly, Amelia II may show some decrements in performance in cases where the distributions of Y and/or X deviate substantially from normality and the heuristic transformations implemented in Amelia II fail to capture the full range of plausible values in imputing the missing data– a scenario that may occur under NMAR conditions. In addition, although both MI and FIML have been widely applied in handling missing data, subtle differences between the two and the adaptations needed to deal with multivariate time series have not been tested in the presence of different missing data mechanisms, especially under NMAR.

The goal of this paper is to examine a full MI and a partial MI approach under different missingness conditions using two MI packages. Using a VAR model as the underlying model, we seek to evaluate the tenability and performance of: (1) a full MI approach, in which all missing variables are imputed simultaneously with MICE or Amelia II; (2) a partial MI approach, in which MI is only performed on the missing covariates while missingness in the dependent variables is handled via FIML estimation; (3) a naive list-wise deletion method. This is followed by an empirical demonstration of the different missing data handling approaches, and a discussion on the strengths and limitations of these approaches. We end with some practical guidelines for researchers interested in implementing these MI-based approaches and provide R code to illustrate their use with this article.

SIMULATION STUDY

The goal of the simulation study was to compare the performance of a full MI and a partial MI approach under different missingness conditions (MCAR, MAR, and NMAR) for a multivariate, multi-subject VAR model and using two MI packages: MICE and Amelia II. In the full MI approach, all missing variables were imputed simultaneously with MICE or Amelia II; in the partial MI approach, MI was only performed on the missing covariates, while missingness in the dependent variables was handled via FIML estimation. Results from complete data analysis and a naive list-wise deletion method for handling the missingness were also included to provide some baseline comparisons.

Simulation Design

We simulated two conditions with different sample configurations, namely, T = 15, n = 100, and T = 75, n = 100. The fewer measurement occasions in the first condition were selected to mirror the characteristics of the empirical study described under the motivating example, and is similar in sample size configuration to many other intensive longitudinal studies in the social and behavioral sciences (e.g., two-week daily diary). The second condition was selected to provide a longer time-series comparison to the first condition and, specifically, to shed light on the effects of different numbers of time points on parameter and standard error estimation in the presence of missingness.

The true parameter values of the dynamic model used in the simulation were set to typical ranges of parameter values observed in the motivating example as well as other empirical studies in psychology utilizing variations of the VAR model (Chow, Hamagami, & Nesselroade, 2007; Chow, Nesselroade, Shifren, & McArdle, 2004). The values of the model (Equation 1) were set as follows: $a_{w\to w}=0.4$, $a_{h\to h}=0.3$, $b_{h\to w}=-0.3$, $b_{w\to h}=-0.2$, $c_{x_1\to w}=0.3$, $c_{x_1\to h}=0.3$, $d_{x_2\to w}=-0.5$, $d_{x_2\to h}=-0.4$ and $\left[\begin{array}{cc}{\sigma }_{e_w}^2& \\ {\sigma }_{e_{wh}}& {\sigma }_{e_h}^2\end{array}\right]=\left[\begin{array}{cc}1& \\ 0.05& 1\end{array}\right]$.

We were interested in generating both continuous and categorical time-varying covariates that might be governed by their own intrinsic dynamics, but for whom the exact nature of the dynamics was unknown and thus not modeled by the researcher. To do so, we generated two covariates, $x_{1_{it}}$ and $x_{2_{it}}$, whose values depended on two completely observed auxiliary variables, $x_{3_{it}}$ and $x_{4_{it}}$. Both $x_{3_{it}}$ and $x_{4_{it}}$ were uniformly distributed over [−3,3]. The covariate $x_{1_{it}}$ was a binary variable generated based on a continuous but unobserved time-varying variable, θ_it, whose value at time t for child i was obtained as ${\theta }_{it}=.8\times {\theta }_{i,t-1}+.4\times x_{4_{it}}+{\epsilon }_{it}$; the value of $x_{1_{it}}$ was generated randomly from a Bernoulli distribution with the probability of getting a value 1 equals $\frac{1}{1+\text{exp}(-{\theta }_{it})}$. The covariate $x_{2_{it}}$ was a continuous variable predicted by one of the external variables, x₃, as $x_{2_{it}}=.6\times x_{3_{it}}+{\epsilon }_{it}$, where ε was distributed as N (0, 1).

To evaluate the performance of the MI approaches under different missingness conditions, missing data were generated following three possible missing data mechanisms: MCAR, MAR, and NMAR. Across all missingness conditions, each of the dependent and covariate variables was designed to have approximately 30% of missing data to mimic the proportion of missing data observed in many intensive longitudinal studies (Dunton et al., 2015; Jacobson, 2015, 2016; Kavanagh et al., 2011; Okifuji, Bradshaw, Donaldson, & Turk, 2011). Let $r_{w_{it}}$, $r_{h_{it}}$, $r_{x_{1_{it}}}$, $r_{x_{2_{it}}}$ be vectors of missingness indicators for the dependent variables and the covariates, respectively, such that r_it=1 if the corresponding variable for person i at time t is missing and 0 otherwise. Whether the probability distribution of r_it, $pr\left(r_{it}|.\right)$, is conditioned on observed or unobserved data determines the nature of the missingness conditions. The most general missing data model considered was an NMAR model in which we specified the probability of r_it as dependent on Y = h_it, w_it, the array of dependent variables, and X = x_j,it, j = 1,…, 4, the array of covariates.

The missing data models for the dependent variables we considered are expressed as follows:

$$\begin{gathered} \text{logit}\left(r_{w_{it}}=1|w_{it},x_{3_{it}},x_{4_{it}}\right)={\phi }_{0_w}+{\phi }_{1_w}\times w_{it}+{\phi }_{2_w}\times x_{3_{it}}+{\phi }_{3_w}\times x_{4_{it}} \\ \text{logit}\left(r_{h_{it}}=1|h_{it},x_{3_{it}},x_{4_{it}}\right)={\phi }_{0_h}+{\phi }_{1_h}\times h_{it}+{\phi }_{2_h}\times x_{3_{it}}+{\phi }_{3_h}\times x_{4_{it}}, \end{gathered}$$ (3)

where, under the NMAR condition, the log odds of the dependent variables being missing are functions of the dependent variables, w_it and h_it, and the two fully observed external covariates, $x_{3_{it}}$ and $x_{4_{it}}$. ${\phi }_{0_w}$ and ${\phi }_{0_h}$ are the intercept and ${\phi }_{1_w}-{\phi }_{3_h}$ are regression coefficients relating different predictors of missingness to the log odds of missingness. The φ values were chosen so that the percentages of missingness for the dependent variables were around 30% for all missingness conditions. This level of missingness is common for many ecological momentary assessment studies (e.g., Chow et al., 2005; Chow & Zhang, 2013). The range of the φ values was between −1 and .8. This most general condition, constituted by having nonzero values for all of the φ parameters, was NMAR because the missingness of the dependent variables depended not only on the two fully observed external covariates, but also on the values of the dependent variables, which might be missing. For instance, with ${\phi }_{1_w}=-.8$, the lower the value for w_it was, the more likely w_it would be missing. Put within the framework of our motivating example, this might correspond to cases where the wife might selectively report only the more severe conflict episodes, while the less-severe ones were dismissed as “petty disagreements” not deserving of further reports.

For the MAR condition, we simply set ${\phi }_{1_w}$ and ${\phi }_{1_h}$ in Equation 3 to zero so that the missingness of the dependent variables was only contingent on the two fully observed external covariates, $x_{3_{it}}$ and $x_{4_{it}}$. To simulate a MCAR condition, only the intercept terms, ${\phi }_{0_w}$ and ${\phi }_{0_h}$, were set to be nonzero in the model.

The missingness mechanisms for the covariates are specified as follows:

$$\begin{gathered} \text{logit}\left(r_{x_{1_{it}}}=1|w_{it},h_{it},x_{1_{it}},w_{it-1},h_{it-1},x_{1_{it-1}},x_{3_{it}},x_{4_{it}}\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\phi }_{0_{x_1}}+{\phi }_{1_{x_1}}\times x_{1_{it}}+{\phi }_{2_{x_1}}\times x_{1_{it-1}}+{\phi }_{3_{x_1}}\times w_{it-1} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\phi }_{4_{x_1}}\times h_{it-1}+{\phi }_{5_{x_1}}\times w_{it}+{\phi }_{6_{x_1}}\times h_{it}+{\phi }_{7_{x_1}}\times x_{3_{it}} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\phi }_{8_{x_1}}\times x_{4_{it}} \end{gathered}$$ (4)

$$\begin{gathered} \text{logit}\left(r_{x_{2_{it}}}=1|w_{it},h_{it},x_{2_{it}},w_{it-1},h_{it-1},x_{3_{it}},x_{4_{it}}\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\phi }_{0_{x_2}}+{\phi }_{1_{x_2}}\times x_{2_{it}}+{\phi }_{2_{x_2}}\times w_{it}+{\phi }_{3_{x_2}}\times h_{it} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\phi }_{4_{x_2}}\times w_{it-1}+{\phi }_{5_{x_2}}\times h_{it-1}+{\phi }_{6_{x_2}}\times x_{3_{it}} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\phi }_{7_{x_2}}\times x_{4_{it}} \end{gathered}$$ (5)

Similar to the missingness models for the dependent variables, the log odds of the covariates being missing are functions of both observed and unobserved variables under the NMAR condition. Specifically, the log odds of observing a missing value in a particular covariate at time t were conditioned on the values of the dependent variables at both time t and the previous time point, t – 1; the value of itself at times t; and the two fully observed external covariates, $x_{3_{it}}$ and $x_{4_{it}}$. For x₁, the value of itself at t – 1 was also included as a predictor of the log odds of missingness because we used an auto-regressive model to generate the values of x₁. ${\phi }_{0_{x_1}}$ and ${\phi }_{0_{x_2}}$ were the intercepts and ${\phi }_{1_{x_1}}$ through ${\phi }_{7_{x_2}}$ were regression coefficients relating different predictors of missingness to the log odds of missingness. Values of φs were set so that approximately 30% of the covariates were missing.

Under the MAR condition, the log odds of observing a missing value in the dependent variables and covariates were conditioned on $x_{3_{it}}$ and $x_{4_{it}}$, both of which were completely observed external/auxiliary inputs. The values of ${\phi }_{7_{x_1}}$, ${\phi }_{8_{x_1}}$, ${\phi }_{6_{x_2}}$, and ${\phi }_{7_{x_2}}$ were set at 0.6 and φ₀ = −1.1 to achieve the desired percentage of missingness. For the MCAR condition, all φ parameters in the missingness models were set to zero except for the intercepts ${\phi }_{0_{x_1}}$ and ${\phi }_{0_{x_2}}$. In that way, the missingness did not depend on any variables and was considered as completely random. We set both φ₀s = −0.7 to achieve around 30% of missingness.

MI Procedures

We tested three MI approaches in this simulation study: (1) full MI, where all missing values of the dependent variables as well as the covariates were imputed with MICE; (2) full MI with Amelia II; and (3) partial MI, wherein only covariates were imputed with MICE and missingness in the dependent variables was handled by the FIML procedure.

For both full MI and partial MI, we included all variables, with or without missing values, as predictors in the imputation model. This is in line with the general advice of including as many relevant variables as possible in MI (Collins et al., 2001). To be specific, when imputation was performed by MICE, both dependent variables, w and h, lagged dependent variables, both covariates, x₁ and x₂, lagged x₁, and both fully observed variables, x₃ and x₄, were included in the imputation model. With MICE, we used the default methods to generate the imputed data set, that is, the predictive mean matching method was used to impute the values of continuous-valued variables, and the logistic regression method was used for imputing the values of binary variables. With Amelia II, we used the same imputation model as that used in MICE. However, unlike MICE, with which we had to create the lagged variables by performing the lagging ourselves, in Amelia II, a lag argument can be invoked with the MI procedure to create these lagged variables automatically. For the ordinal binary variable in our data set, namely, x₁, where a zero represented the absence of the specified behavior and a one represented the presence of any level of the specified behavior, Amelia handled the imputations by first imputing the values as if it were continuous, and then translating the continuously imputed values back into the ordinal categories using binomial distribution (Honaker et al., 2011). This procedure was called by specifying the ords argument. Because the true missingness model is typically unknown in practice and the general practice in MI is to include as many plausible variables that may possibly be related to the missing data mechanism, we considered a more general imputation model than the true missingness model.

For the full MI approaches, the imputed data set in which all missing values were filled in with imputed data were used for model fitting as if there were no missingness. The ML parameter estimates were obtained by optimizing a log-like-lihood function, known as the prediction error decomposition function – computed using by-products of applying the linear Kalman filter to Equation 1 in state-space form (Chow et al., 2010; Harvey, 2001). This procedure was performed with a Fortran-based program, mkfm6 (Dolan, 2002). In addition, we wrote R wrapper functions to alternate between the MICE routine for performing MI and the call to mkfm6 to obtain parameter point estimates and standard error estimates.

For the partial MI procedure, missingness in the dependent variables was handled via FIML by mkfm6 wherein only the variables that were observed contributed to the calculation of the prediction error decomposition function at each time point, while missingness in the covariates were filled in with the MI method of choice (either via MICE or Amelia II) prior to model fitting in mkfm6 to circumvent the inability of standard FIML procedures to handle missingness in categorical covariates. The model fitting procedures as well as the procedure to pool the parameter estimates were identical to the full MI approach. In other words, the full and partial MI procedures are identical in handling missing covariates. Thus, our key interest in comparing the full and partial MI procedures was to examine whether using FIML to handle missing data in the dependent variables—as implemented in the partial MI approach—improves dynamic parameter estimates. Because Amelia II only handles imputation of categorical covariates heuristically, we only used MICE in handling missingness in the covariates so we could perform a more targeted comparison between the partial and full MI approaches in handling missingness in the dependent variables.

Estimation results of the full MI and partial MI approaches were compared in the Simulation Results section.

Five imputations were created by calling either the mice () function in the MICE package or the amelia() function in the Amelia II package. Increasing the number of imputations to beyond five did not lead to notable differences in the imputation and estimation results. Thus, we present only the results from using five imputed data sets in each Monte Carlo replication.

In the Appendix, we provide a set of R codes for setting up the imputation model and performing full or partial MI with MICE, generating the mkmf6 script to fit the specified state-space equation, and finally pooling the estimates across imputed data sets to obtain the final point and standard error estimates.

Performance Measures

We considered 2 (T = 15 and 75) × 3 (MAR vs. NMAR vs. MCAR) × 4 (Full MI with MICE, Full MI with Amelia II, Partial MI using MICE to handle the missingness in the covariates but FIML to handle the missingness in the dependent variables, and list-wise deletion of cases with missingness) = 24 conditions in our simulation study with n = 100 for all conditions. A total of 500 Monte Carlo replications were run for each condition. We employed a range of standard criteria commonly used in simulation studies to analyze the results of our simulation study. In particular, to assess the precision of the point estimates, we computed both the root mean squared errors (RMSEs) and biases. RMSE for a particular parameter was defined as the square root of the average squared difference between estimates for that parameter $(\widehat{{\theta }_h})$ and the true parameter value (true θ) across Monte Carlo runs $(\text{RMSE}=\sqrt{\frac{1}{H}{\sum }_{h=1}^H{(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )}^2})$. Bias was defined as the average difference between estimates of that parameter and the true parameter value across Monte Carlo runs $(\text{Bias}=\frac{1}{H}{\sum }_h^H(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )$. To evaluate the quality of standard error estimates, we computed difference of standard error (DSE), which was given by the difference between the standard deviation of each estimated parameter across Monte Carlo runs (i.e., the empirical standard error) and the average standard error estimate for that parameter across Monte Carlo runs $(\widehat{SE})$. In addition, we also compared the quality of the SE estimates to the “benchmark” standard error estimates obtained from the full data set by computing DSEfull, given by the difference between the average standard error estimates for a particular parameter (across Monte Carlo runs) obtained using the full data set with no missingness and the corresponding standard error estimate for that parameter obtained using any of the four missing data handling methods considered. Finally, we also calculated power as an index of positive detection rates and coverage rates as an overall measure of the quality of both the point and the SE estimates. Power was defined as the proportion of 95% confidence intervals that did not contain 0 across the Monte Carlo replications. Coverage rates were defined as the percentages of replications whose 95% confidence intervals for the parameters included the true parameter values. These empirical coverage rates help reveal whether the point and SE estimates collectively yield confidence intervals that provide the correct levels of coverage probability. Simulation results with power close to 1.0 and coverage rates close to the nominal rate of .95 would be considered as ideal.

SIMULATION RESULTS

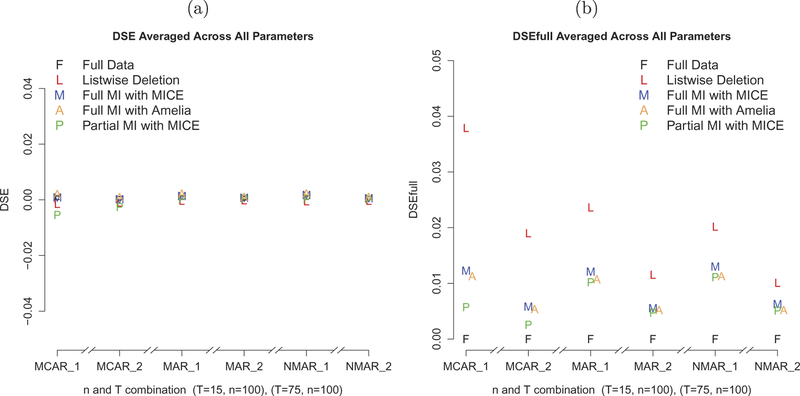
Simulation results are summarized in Figures 1–3, and detailed further in Tables 1–3. All three MI procedures (Full MI with MICE, Full MI with Amelia II, and Partial MI with MICE), but not the list-wise deletion procedure, yielded reasonable point estimates, as indicated by biases and RMSEs, across all missing data conditions (MCAR, MAR, and NMAR) and time point conditions (T = 15 and T = 75) considered in the present study. Increasing the number of total time points from 15 to 75 did not provide notable improvements in the accuracy of the point estimates. Small biases in SEs in comparison to the Monte Carlo SDs were observed for all simulation conditions, regardless of missing data handling techniques (see Figure 2a). However, when compared with SEs obtained using full data, inflation in SEs was noted with list-wise deletion. All three MI procedures improved the accuracy of SE estimates (as indicated by the smaller differences between SEs obtained using imputed data and SEs obtained using full data). DSEfulls were smaller with larger sample size condition (T = 75) for all missing data conditions and all missing data handling procedures (see Figure 2b).

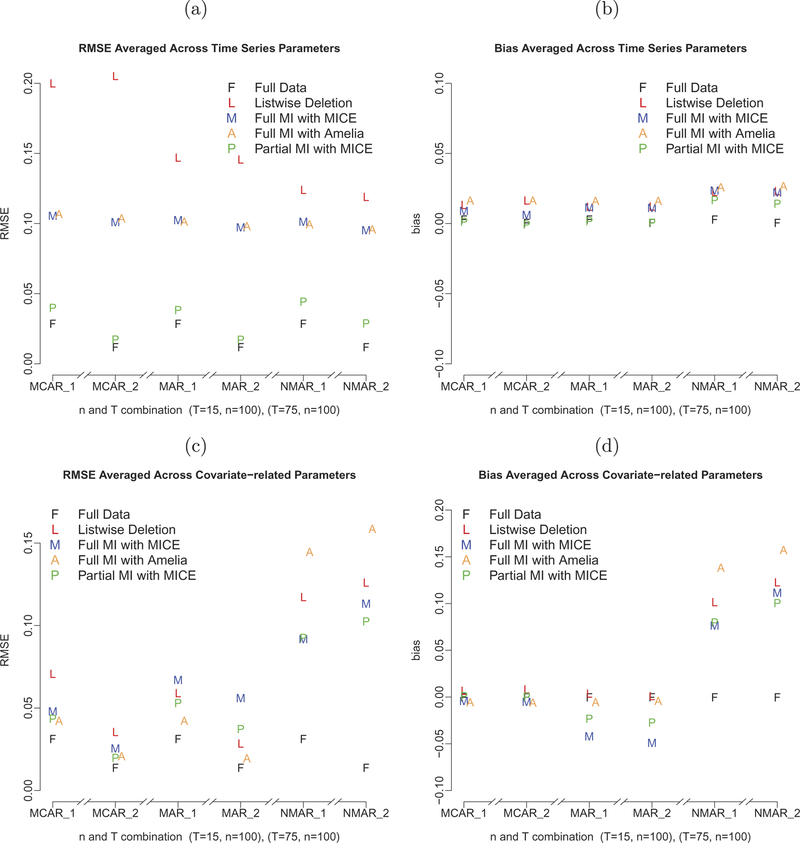
FIGURE 1.

A comparison of the accuracies of the point estimates: (a) RMSEs for the time-series parameters; (b) biases for the time-series parameters; (c) RMSEs for the covariate-related parameters; and (d) biases for the covariate-related parameters.

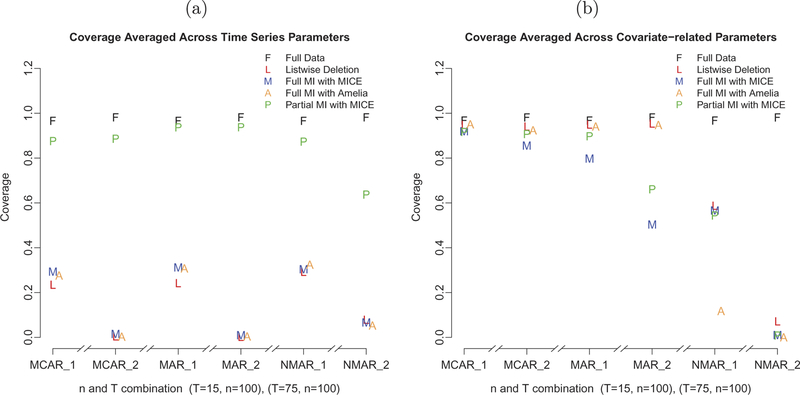
FIGURE 3.

A comparison of the coverages: (a) for the time-series parameter estimates; (b) for the covariate-related parameter estimates.

TABLE 1.

Summary Statistics of MCAR Condition Across 500 MC Replications (N = 100; T = 75)

	List-wise Deletion							Full MI with MICE
Parameter	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage
aw→w	−0.248	0.249	0.024	−0.001	0.014	1.000	0.000	−0.105	0.105	0.011	0.002	0.004	1.000	0.000
bh→w	0.173	0.175	0.027	−0.002	0.015	0.986	0.000	0.085	0.086	0.011	0.003	0.004	1.000	0.000
bw→h	0.114	0.116	0.022	−0.000	0.013	0.966	0.000	0.052	0.053	0.011	0.001	0.003	1.000	0.012
ah→h	−0.190	0.191	0.023	0.001	0.014	1.000	0.000	−0.084	0.085	0.011	0.003	0.004	1.000	0.000
cca→w	0.018	0.044	0.040	0.001	0.024	1.000	0.950	0.008	0.027	0.026	−0.002	0.008	1.000	0.908
dcn→w	−0.000	0.029	0.029	−0.002	0.017	1.000	0.938	−0.019	0.025	0.017	−0.001	0.006	1.000	0.794
cca→h	0.014	0.042	0.039	−0.001	0.022	1.000	0.932	0.007	0.026	0.025	−0.002	0.006	1.000	0.906
dcn→h	0.001	0.027	0.027	−0.001	0.015	1.000	0.942	−0.017	0.024	0.016	−0.000	0.005	1.000	0.814
${\sigma }_{e_w}^2$	0.322	0.326	0.048	−0.001	0.031	1.000	0.000	0.159	0.161	0.026	−0.001	0.009	1.000	0.000
${\sigma }_{e_h}^2$	0.158	0.163	0.043	−0.002	0.025	1.000	0.030	0.074	0.078	0.023	0.000	0.007	1.000	0.094
${\sigma }_{e_{wh}}$	−0.214	0.217	0.034	−0.003	0.019	0.998	0.000	−0.138	0.139	0.021	−0.001	0.008	0.958	0.000
	Full MI with Amelia II							Partial MI with MICE
Parameter	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage
aw→w	−0.103	0.103	0.010	0.002	0.004	1.000	0.000	−0.005	0.013	0.012	−0.002	0.001	1.000	0.878
bh→w	0.086	0.087	0.011	0.003	0.004	1.000	0.000	0.003	0.014	0.014	−0.002	0.002	1.000	0.890
bw→h	0.054	0.055	0.010	0.002	0.003	1.000	0.008	0.002	0.013	0.013	−0.003	0.001	1.000	0.880
ah→h	−0.083	0.084	0.011	0.003	0.004	1.000	0.000	−0.003	0.013	0.013	−0.002	0.001	1.000	0.908
cca→w	−0.011	0.027	0.024	−0.001	0.006	1.000	0.898	0.003	0.024	0.024	−0.003	0.004	1.000	0.904
dcn→w	−0.001	0.015	0.015	0.001	0.004	1.000	0.944	−0.001	0.016	0.016	−0.002	0.003	1.000	0.902
cca→h	−0.011	0.026	0.024	−0.001	0.005	1.000	0.908	0.002	0.023	0.023	−0.003	0.003	1.000	0.908
dcn→h	−0.001	0.015	0.015	0.000	0.004	1.000	0.944	−0.003	0.016	0.016	−0.002	0.003	1.000	0.914
${\sigma }_{e_w}^2$	0.183	0.184	0.025	0.001	0.010	1.000	0.000	0.007	0.024	0.023	−0.002	0.005	1.000	0.928
${\sigma }_{e_h}^2$	0.093	0.096	0.022	0.001	0.007	1.000	0.010	0.001	0.021	0.021	−0.001	0.003	1.000	0.926
${\sigma }_{e_{wh}}$	−0.115	0.117	0.021	−0.001	0.008	0.814	0.000	−0.010	0.023	0.020	−0.006	0.002	0.682	0.790

$\text{Bias}=\frac{1}{H}{\sum }_h^H(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )$, where H =total number of Monte Carlo replications, $\widehat{{\theta }_h}$ = estimate of θ from the hth Monte Carlo replications, true θ = true value of a parameter; $\text{RMSE}=\sqrt{\frac{1}{H}{\sum }_{h=1}^H{(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )}^2}$; SD = standard deviation of $\widehat{\theta }$ across Monte Carlo runs; DSE = deviance of average standard error estimate across Monte Carlo runs from SD; DSEfull = difference between average standard error estimate with missing data under each method and average standard error estimate with full data; Power/type I error = 1 – the proportion of 95% confidence intervals (CIs) that contain 0 across the Monte Carlo replications; Coverage = the proportion of 95% confidence intervals (CIs) that contain true θ across the Monte Carlo replications.

TABLE 3.

Summary Statistics of NMAR Condition Across 500 MC Replications (N = 100; T = 75)

	List-wise Deletion							Full MI with MICE
Parameter	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage
aw→w	−0.107	0.108	0.016	−0.000	0.007	1.000	0.000	−0.093	0.094	0.011	0.002	0.004	1.000	0.000
bh→w	0.165	0.166	0.017	0.001	0.007	1.000	0.000	0.128	0.129	0.012	0.003	0.005	1.000	0.000
bw→h	0.120	0.121	0.015	0.000	0.006	0.996	0.000	0.093	0.093	0.011	0.002	0.004	1.000	0.000
ah→h	0.073	0.075	0.017	−0.001	0.007	1.000	0.012	−0.071	0.072	0.011	0.002	0.004	1.000	0.000
cca→w	0.186	0.189	0.034	−0.000	0.017	1.000	0.000	0.105	0.108	0.028	−0.002	0.009	1.000	0.038
dcn→w	0.076	0.079	0.021	0.000	0.010	1.000	0.050	0.117	0.118	0.017	0.001	0.007	1.000	0.000
cca→h	0.174	0.177	0.033	−0.001	0.015	1.000	0.000	0.121	0.123	0.025	−0.001	0.007	1.000	0.002
dcn→h	0.055	0.059	0.021	−0.001	0.009	1.000	0.236	0.103	0.104	0.018	−0.000	0.007	1.000	0.000
${\sigma }_{e_w}^2$	0.153	0.156	0.029	0.001	0.014	1.000	0.000	0.138	0.140	0.024	0.000	0.009	1.000	0.000
${\sigma }_{e_h}^2$	0.051	0.058	0.028	−0.001	0.011	1.000	0.538	0.046	0.051	0.022	−0.000	0.006	1.000	0.452
${\sigma }_{e_{wh}}$	−0.147	0.149	0.022	−0.002	0.008	0.990	0.000	−0.086	0.088	0.020	−0.001	0.007	0.390	0.012
	Full MI with Amelia II							Partial MI with MICE
Parameter	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage
aw→w	−0.094	0.094	0.011	0.002	0.004	1.000	0.000	0.013	0.018	0.013	−0.000	0.003	1.000	0.816
bh→w	0.133	0.133	0.012	0.003	0.004	1.000	0.000	0.048	0.050	0.014	0.000	0.004	1.000	0.092
bw→h	0.091	0.092	0.011	0.002	0.003	1.000	0.000	0.040	0.042	0.013	−0.000	0.004	1.000	0.116
ah→h	−0.065	0.066	0.011	0.003	0.004	1.000	0.002	0.016	0.021	0.014	0.000	0.004	1.000	0.756
cca→w	0.195	0.196	0.024	−0.000	0.006	1.000	0.000	0.095	0.098	0.025	−0.001	0.007	1.000	0.032
dcn→w	0.130	0.131	0.016	0.000	0.005	1.000	0.000	0.104	0.105	0.016	0.001	0.006	1.000	0.000
cca→h	0.188	0.190	0.022	0.000	0.006	1.000	0.000	0.110	0.113	0.024	−0.000	0.006	1.000	0.000
dcn→h	0.116	0.117	0.016	−0.000	0.004	1.000	0.000	0.093	0.094	0.017	−0.000	0.006	1.000	0.000
${\sigma }_{e_w}^2$	0.145	0.147	0.023	0.002	0.009	1.000	0.000	−0.005	0.021	0.020	0.001	0.006	1.000	0.956
${\sigma }_{e_h}^2$	0.054	0.058	0.022	0.000	0.006	1.000	0.340	−0.022	0.030	0.021	0.000	0.005	1.000	0.804
${\sigma }_{e_{wh}}$	−0.077	0.080	0.019	−0.001	0.006	0.240	0.026	0.009	0.020	0.018	−0.001	0.005	0.800	0.918

$\text{Bias}=\frac{1}{H}{\sum }_h^H(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )$, where H = total number of Monte Carlo replications, $\widehat{{\theta }_h}$ = estimate of θ from the hth Monte Carlo replications, true θ = true value of a parameter; $\text{RMSE}=\sqrt{\frac{1}{H}{\sum }_{h=1}^H{(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )}^2}$; SD = standard deviation of $\widehat{\theta }$ across Monte Carlo runs; DSE = deviance of average standard error estimate across Monte Carlo runs from SD; DSEfull = difference between average standard error estimate with missing data under each method and average standard error estimate with full data; Power/type I error = 1 – the proportion of 95% confidence intervals (CIs) that contain 0 across the Monte Carlo replications; Coverage = the proportion of 95% confidence intervals (CIs) that contain true θ across the Monte Carlo replications.

FIGURE 2.

A comparison of the quality of SE estimates: (a) DSEs averaged across all parameter estimates; (b) DSEfulls averaged across all parameter estimates.

To facilitate the comparisons across missing data handling approaches, we aggregated the performance measures by parameter type. Specifically, we evaluated the performance measures as aggregated among all time-series parameters that govern the dynamics over time (including $a_{w\to w}$, $b_{h\to w}$, $b_{w\to h}$, $a_{h\to h}$, ${\sigma }_{e_w}^2$, ${\sigma }_{e_h}^2$,${\sigma }_{e_{wh}}$), and all the remaining parameters portraying the associations among the time-varying covariates and the dependent variables of interest. Figure 1a shows the RMSEs of all the time-series parameters (denoted as dynamic parameters in the figure) and their corresponding biases are shown in Figure 1b.

The accuracies of the point estimates for time-series parameters (as indicated by RMSEs and biases) were reasonable for all three MI approaches (full MI with MICE and Amelia II, and partial MI with MICE), but not for list-wise deletion, across all missing data and time point conditions considered in the present study. RMSEs were higher for list-wise deletion under the MCAR condition than under the MAR and NMAR conditions. This is because when list-wise deletion was implemented, the entire record for a time point was excluded from analysis if any of the dependent variables or covariates was missing. Under the MAR and NMAR conditions, missing values were more likely to occur at the same time point, when certain observed covariates (for MAR) or dependent variables (for NMAR) were at a higher level, whereas under the MCAR condition, missing values were more scattered for the four variables considered in the VAR model. As a result, more records were removed for the MCAR condition than the MAR and NMAR conditions, which led to more biased parameter point estimates. This type of “clustering” in missing responses is not uncommon in empirical ecological momentary assessment studies wherein participants tend to skip responses on multiple variables simultaneously (e.g., multiple variables in the same section of a survey, or an entire survey completely) on weekends, or when they feel too unmotivated to respond to researchers’ questions. For the same reason, larger inflation of SEs was also noted under the MCAR condition, as compared with the MAR and NMAR conditions (see Figure 2b).

As expected, compared with the list-wise deletion method, all three imputation procedures, including the partial as well as the full MI approaches with MICE and Amelia II, improved the accuracy of the parameters’ point estimates across all three conditions, especially for dynamic parameters. It can be seen from Figure 1a that the RMSEs of the dynamic parameters with list-wise deletion were noticeably larger than those obtained using any other imputation method across all imputation conditions. Even though differences seemed to be minor with aggregated biases for dynamic parameters (see Figure 1b), it can be seen from Tables 1–3 that the biases for each dynamic parameter were larger with list-wise deletion than all those obtained using any other MI procedures. This was likely because list-wise deletion altered the spacing between time points and led to biased estimates in the dynamic parameters. With MI approaches, the missing data points were filled in with imputed data, and the original spacing between the data points was preserved. Simulation results with regard to the time-series parameters were very close between full MI with MICE and full MI with Amelia II across the six conditions. Partial MI outperformed full MI in terms of RMSEs of the dynamic parameters across all missing data conditions (including NMAR), highlighting one advantage of the FIML method in handling missingness in the dependent variables in the specific time-series (VAR) model considered even under conditions where FIML alone has been found to be inadequate (specifically, under NMAR). Note also that using the FIML method alone—as opposed to the partial MI approach considered—would have led to considerable decrements in performance in the absence of better ways of handling missingness in the covariates (other than using, e.g., list-wise deletion).

A closer inspection of the parameter estimates without aggregation revealed that under MCAR and MAR conditions, the point estimates of the auto-regression parameters improved more than the cross-regression parameters under all MI approaches, compared with the estimates obtained from list-wise deletion in terms of both RMSEs and biases (see Tables 1 and 2 for MCAR and MAR results). In fact, under the MCAR and MAR conditions, the RMSEs of the point estimates of the auto-regression parameters with partial MI almost paralleled those from fitting the model to the full data. This indicated the relative difficulty in recovering the cross-regression parameters in comparison to the auto-regression parameters in the presence of NMAR.

TABLE 2.

Summary Statistics of MAR Condition Across 500 MC Replications (N = 100; T = 75)

	List-wise Deletion							Full MI with MICE
Parameter	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage
aw→w	−0.168	0.169	0.017	−0.001		0.007	1.000		0.000	−0.101	0.102	0.011	0.002
bh→w	0.105	0.107	0.019	−0.001	0.008	1.000	0.000	0.076	0.077	0.011	0.003	0.004	1.000	0.000
bw→h	0.072	0.074	0.016	−0.000	0.007	1.000	0.008	0.046	0.047	0.011	0.001	0.003	1.000	0.022
ah→h	−0.130	0.131	0.017	−0.000	0.007	1.000	0.000	−0.082	0.083	0.011	0.002	0.003	1.000	0.000
cca→w	−0.003	0.035	0.034	0.002	0.019	1.000	0.966	−0.103	0.106	0.025	−0.000	0.008	1.000	0.030
dcn→w	0.003	0.022	0.022	−0.000	0.011	1.000	0.948	−0.006	0.017	0.016	0.001	0.006	1.000	0.944
cca→h	0.008	0.036	0.035	−0.001	0.017	1.000	0.948	−0.080	0.084	0.025	−0.001	0.007	1.000	0.130
dcn→h	−0.004	0.021	0.020	0.000	0.010	1.000	0.954	−0.007	0.017	0.016	0.001	0.005	1.000	0.910
${\sigma }_{e_w}^2$	0.246	0.249	0.033	−0.000	0.017	1.000	0.000	0.169	0.171	0.024	0.000	0.009	1.000	0.000
${\sigma }_{e_h}^2$	0.122	0.126	0.030	−0.000	0.014	1.000	0.008	0.083	0.086	0.023	−0.000	0.006	1.000	0.046
${\sigma }_{e_{wh}}$	−0.162	0.164	0.023	−0.001	0.010	0.998	0.000	−0.113	0.115	0.019	−0.001	0.007	0.818	0.000
	Full MI with Amelia II							Partial MI with MICE
Parameter	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage	Bias	RMSE	SD	DSE	DSEfull	Power	Coverage
aw→w	−0.097	0.097	0.010	0.002	0.003	1.000	0.000	−0.008	0.014	0.012	−0.000	0.003	1.000	0.898
bh→w	0.082	0.082	0.011	0.003	0.004	1.000	0.000	−0.001	0.013	0.013	0.000	0.004	1.000	0.964
bw→h	0.050	0.051	0.010	0.002	0.003	1.000	0.012	−0.001	0.012	0.012	−0.000	0.003	1.000	0.952
ah→h	−0.077	0.078	0.011	0.002	0.003	1.000	0.000	−0.005	0.014	0.013	0.001	0.003	1.000	0.944
cca→w	−0.008	0.024	0.023	0.001	0.006	1.000	0.944	−0.065	0.069	0.023	0.001	0.007	1.000	0.220
dcn→w	0.000	0.015	0.015	0.001	0.005	1.000	0.962	0.002	0.015	0.015	0.001	0.005	1.000	0.964
cca→h	−0.008	0.024	0.023	−0.000	0.006	1.000	0.930	−0.045	0.050	0.023	0.000	0.006	1.000	0.498
dcn→h	0.001	0.015	0.015	−0.000	0.004	1.000	0.952	−0.001	0.015	0.015	0.001	0.005	1.000	0.960
${\sigma }_{e_w}^2$	0.175	0.176	0.024	0.001	0.009	1.000	0.000	0.016	0.027	0.021	0.001	0.006	1.000	0.914
${\sigma }_{e_h}^2$	0.089	0.092	0.022	0.000	0.007	1.000	0.016	0.007	0.022	0.021	0.000	0.005	1.000	0.940
${\sigma }_{e_{wh}}$	−0.109	0.111	0.019	−0.001	0.007	0.784	0.000	−0.004	0.018	0.018	−0.001	0.005	0.544	0.948

$\text{Bias}=\frac{1}{H}{\sum }_h^H(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )$, where H = total number of Monte Carlo replications, $\widehat{{\theta }_h}$ = estimate of θ from the hth Monte Carlo replications, true θ = true value of a parameter; $\text{RMSE}=\sqrt{\frac{1}{H}{\sum }_{h=1}^H{(\widehat{{\theta }_h}-\text{true}\hspace{0.17em}\theta )}^2}$SD = standard deviation of $\widehat{\theta }$ across Monte Carlo runs; DSE = deviance of average standard error estimate across Monte Carlo runs from SD; DSEfull = difference between average standard error estimate with missing data under each method and average standard error estimate with full data; Power/type I error = 1 – the proportion of 95% confidence intervals (CIs) that contain 0 across the Monte Carlo replications; Coverage = the proportion of 95% confidence intervals (CIs) that contain true θ across the Monte Carlo replications.

Interestingly, the point estimates for some of the covariate-related parameters were less biased with list-wise deletion than those obtained using the other missing data handling approaches under MAR conditions (see Figure 1c and 1d). This was the case for the parameters c_ca→w and c_ca→h associated with the binary covariate (see Table 2). This may be related to the over-parameterized nature of the imputation model for the covariates – the overly complex imputation model for the covariates might have injected too much noise and uncertainties into the imputed covariate values, creating slightly higher biases for these parameters under simpler missing data mechanisms. Under NMAR, the estimates from the full MI approach with Amelia II were characterized by distinctly higher biases, surpassing those associated from all other missing data approaches, including list-wise deletion. One possible reason might be Amelia II’s reliance on imputation procedures only for multivariate normal variables and heuristic data-driven transformations to handle the mapping of continuous imputed values to ordinary/other categorical responses. Thus, as conjectured, it is not able to handle imputations of missingness under more complex missingness mechanisms.

The SE estimates from all missing data approaches closely mirrored their corresponding empirical (Monte Carlo) SEs (see Figure 2a). The plot comparing these SE estimates to those obtained from the fully observed data set (see Figure 2b) suggested that all three MI approaches produced SE estimates that more closely mirrored those from the complete data set than list-wise deletion across all missing data and sample size conditions. In particular, positive biases in SE estimates compared to those from the full data set were observed with list-wise deletion data under all conditions, especially in the smaller T condition, thus indicating over-estimation in these SEs with list-wise deletion. A possible reason might be that list-wise deletion resulted in smaller sample size, which in turn led to more uncertainty in the estimates, thus leading to “overestimation” of the SEs compared to variability that existed in the full data. Positive biases in SE estimates were still observed in the other MI approaches considered, but to a lesser extent.

Even though the two full MI approaches produced better point estimates (in terms of biases and RMSEs) and SE estimates (in terms of biases of the SE estimates) for dynamic parameters across all conditions, the coverage rates remained substantially lower than the nominal value of .95 and close to the coverage rates from using the list-wise deletion method (see Figure 3a). In contrast, the partial MI coverage rates almost paralleled those from using completely observed data. Under MCAR and MAR conditions, coverage rates for the dynamic parameters were all over .9, whereas under NMAR conditions, the coverage rate as averaged across all dynamic parameters was still over .8 for the small sample size condition and around .5 for the larger sample size condition.

Coverage rates as averaged across all the covariate-related parameters were satisfactory with list-wise deletion (see Figure 3b) under MCAR and MAR conditions because the inflated SE estimates compensated for the biases in point estimates of the covariates. Unfortunately, none of the three imputation methods improved the coverage rates associated with the covariate-related parameters under NMAR conditions. In particular, in the larger sample size condition, because the SE estimates for all covariate parameters were very small (approximately 0.02), and all the point estimates were overestimated by around .1, the coverage for the covariate-related parameters was close to zero. Slightly better coverage rates (around .6) were observed in the smaller sample size NMAR condition, except for those obtained using Amelia II, highlighting, again, Amelia II’s more restricted capacity in handling the imputations, especially of categorical covariates.

Low coverage can occur either due to biases in the point estimates or due to anticonservative SE estimates (i.e., SE estimates that were too small compared with the true variability in the parameter estimates). Under both MI approaches—and especially when full MI was involved—the model used to impute the missing data was mildly mis-specified compared with the true missing data model. The discrepancy was more severe in the NMAR than in the other missing data conditions, and such discrepancies always produced some biases in the point estimates. Given that the quality of the standard error estimates from the MI approaches (full or partial) remained satisfactory across all sample size conditions, the poor coverage was more a direct result of the biases in the point estimates in situations where mis-specified imputation models were used to impute missing values. In larger sample size conditions, because the standard error estimates were also smaller, the coverage probability can and did in fact differ considerably from the nominal coverage rate, especially for the full MI approach compared with the partial MI approach.

With regard to power, for the sample sizes considered in the current simulation, the power estimates based on the 95% confidence level were well above .8 for all conditions and using any of the approaches considered (partial MI, full MI with MICE and Amelia II, and list-wise deletion methods), except for the process noise covariance parameter, whose true value was close to zero. With the MI approaches, the power estimates for all parameters were very close to 100% across all conditions. The advantages offered by the MI approaches in terms of power were more pronounced in conditions with smaller sample sizes and/or larger percentages of missingness, given the decrements in performance of the list-wise deletion method under such scenarios.

All else considered, the partial MI approach emerged as the preferred approach over the full MI approaches and list-wise deletion based on coverage, accuracy, and precision of the point estimates, especially those associated with the dynamic parameters. Our simulation results thus highlight some lesser-known advantages of the partial MI approach compared with the other full MI approaches, even under NMAR for both the covariates and the dependent variables. Of course, these results are restricted to the situations evaluated in the simulation study—that is, the true dynamic model is known and correctly specified, even though the missing data mechanisms may range from MCAR to NMAR.

EMPIRICAL ILLUSTRATION

We used the previously published data set of Schermerhorn et al. (2010) described in the Motivating Example section to illustrate the missing data handling methods considered in the simulation study. As noted earlier, the dependent variables of interest in this example were the husbands’ and wives’ conflict resolution ratings, whereas child aggregate agentic behavior and negativity were used as the time-varying covariates in the VAR model depicted in Equation 1. The goal of this illustration was to compare the results based on the missing data methods considered in our simulation study to the method used in the published paper. In particular, Schermerhorn et al. (2010) previously considered a hybrid FIML approach in which missingness in the dependent variables was handled by means of FIML, whereas the covariates were recoded as either 0 or 1, with 1 representing the presence of any level of the specified behaviors/emotions and 0 representing either the absence of the child during a particular conflict or the absence of the specified behaviors/emotions. In other words, missingness in the covariates was handled using MI, as opposed to being recoded as zero, in the new approaches. Recall that the full and partial MI approaches differ only in how missingness in the dependent variables was handled— namely, via MI and FIML, respectively. However, only 0.4% of the dependent variables were missing. Thus, the data set, as it stands, does not contain enough missingness in the dependent variables to warrant a meaningful comparison between the full and partial MI approaches. Thus, for demonstration purposes, we first compared the empirical modeling results from three approaches using the original data set: (1) using list-wise deletion; (2) full MI approach using MICE; and (3) FIML with the heuristic recoding scheme for the covariates considered by Schermerhorn et al. (2010). We then induced additional missingness by using a known NMAR mechanism to probabilistically remove approximately 30% of the dependent variable values from the original data set. Specifically, we let the probability of missingness to depend on the value of the dependent variable itself. Model-fitting results using the original data and those from the new data set with added non-ignorable missingness were compared.

Under the full MI method, estimation results were observed to stabilize with approximately 10 imputations, and increasing the number of imputations further did not change the corresponding parameter and SE estimates substantially. All variables we considered as relevant were included as predictors in the MI model, including husband’s and wife’s negative emotions after each conflict and after each previous conflict, husband’s and wife’s positive emotions after each conflict and after each previous conflict, husband’s and wife’s conflict resolution scores after each conflict and after each previous conflict, child agentic behavior, child negativity, husband’s and wife’s reported time length of the interaction, who initiated the problem, whether the problem was old or new, husband’s and wife’s reported hostility in marital relations, husband’s and wife’s self-reported Symptom Checklist-90 depression score, husband’s and wife’s self-reported depressive symptom scores, husband’s and wife’s reported marital satisfaction scores, and child age. Among these variables, whether the problem was new or old and whether husband or wife initiated the problem were dichotomous variables. The default imputation methods in the MICE package, namely, predictive mean matching method for continuous-valued variables and logistic regression method for binary variables, were used to generate the imputed data sets.

We used mkfm6 to fit the state-space model (Equation 1) with each of the 10 imputed data sets as if they were fully observed data. Ten sets of parameter estimates were obtained and pooled parameter estimates and SE estimates were calculated using R according to the method described in Section Methods for Handling Missing Data and Issues. Aside from the incorporation of alternative missing data handling techniques for the covariates, other settings (e.g., the specified VAR model, the ML estimation algorithm) were identical to those considered in the original study. Parameter estimation results are shown in Table 4.

TABLE 4.

Parameter Estimates for the Empirical Illustration

	Original method			List-wise deletion			Multiple imputation with MICE
Parameter	$\widehat{\mathrm{\theta }}$	SEθ	tvalue	$\widehat{\mathrm{\theta }}$	SEθ	tvalue	$\widehat{\mathrm{\theta }}$	SEθ	tvalue
aw→w	−0.091	0.043	−2.116*	−0.130	0.086	−1.512	−0.088	0.044	−2.000*
bh→w	0.056	0.043	1.302	0.134	0.085	1.576	0.055	0.043	1.279
bw→h	0.011	0.044	0.250	−0.076	0.089	−0.854	0.013	0.044	0.295
ah→h	−0.043	0.043	−1.000	0.034	0.088	0.386	−0.043	0.043	−1.000
$c_{x_1\to w}$	0.753	0.215	3.502*	2.311	0.634	3.645*	1.549	0.555	2.791*
$d_{x_2\to w}$	−0.733	0.166	−4.416*	−0.287	0.057	−5.035*	−0.506	0.089	−5.685*
$c_{x_1\to h}$	0.608	0.218	2.789*	1.470	0.655	2.244*	1.167	0.509	2.293*
$d_{x_2\to h}$	−0.698	0.168	−4.155*	−0.254	0.059	−4.305*	−0.429	0.087	−4.931*
${\sigma }_{e_w}^2$	7.652	0.233	32.841*	7.319	0.397	18.436*	7.476	0.239	31.280*
${\sigma }_{e_h}^2$	7.836	0.239	32.787*	7.805	0.424	18.408*	7.705	0.240	32.104*
${\sigma }_{e_{wh}}$	6.688	0.221	30.262*	6.722	0.388	17.325*	6.540	0.223	29.327*

^*p < .05

As shown in Table 4, the parameter estimates using the data re-coding procedure in the published study and the full MI approach were very close, while the list-wise deletion method produced substantially different estimates. For the dynamic parameters, the auto-regressive parameter for wives’ conflict resolution was observed to be statistically significant with both the original re-coding method and the full MI approach, but not with list-wise deletion. The significant negative auto-regressive parameter indicates that the wife’s conflict resolution score was influenced by her conflict resolution score at the end of the immediately preceding conflict, but in the opposite direction. That is to say, when the wife’s conflict resolution score was high at the end of one conflict, her conflict resolution score would tend to be low at the end of the next conflict. This significant auto-regressive parameter was not detected with the list-wise deletion method. The auto-regressive parameter for husbands was not significantly different from zero using any of the three missing data handling approaches, meaning husband’s conflict resolution scores were not predictable from his conflict resolution scores at the preceding time point. No significant cross-lagged regression parameters were found using all the missing data handling methods considered. Therefore, husbands’ conflict resolution scores were not predicted by wives’ conflict resolution scores at the end of immediate preceding time point and vise versa.

All three methods found significant influences of the child-related covariates on the dependent variables. To be specific, child agentic behavior was found to predict increases in both husbands’ and wives’ conflict resolution scores, while child negativity was associated with decreases in both husbands’ and wives’ conflict resolution scores. Even though all three methods yielded similar statistically significant findings and hence conclusions, the magnitudes of the parameter estimates were different. For instance, we can see from Table 4 that for child agentic behavior (x₁), both the magnitude of the parameter point estimates and the parameter SE estimates were larger with MI compared with those obtained using the original missingness recoding method, where child agentic behavior was dichotomously coded. The point estimate obtained under the full MI approach suggested stronger influence of child agentic behavior over parents’ emotion states, but also greater uncertainties in the parameter estimates due to missingness in the child agentic behavior. The reason for the difference is that the original method re-coded the child variables in a way that equated instances with no agentic behavior or negativity to instances with missing child covariate information. Process noises variance estimates were similar with all three methods.

We then compared these modeling results to those using the data set with added NMAR missingness in the dependent variables. Consistent with findings from our simulation study, when we imputed values of the missing dependent variables, using a slightly mis-specified model with either partial or full MI, we were able to obtain parameter estimates that were reasonably close to those obtained using the original data (i.e., with only .4% of missingness in the dependent variables), especially in comparison to estimates using list-wise deletion. However, contrary to our simulation results, which showed that partial MI provided more accurate dynamic parameter estimates than full MI, we did not observe large differences in the estimation results between the two approaches. One possible reason was that for this particular empirical data set, the dynamic parameters were either nonsignificant or marginally significant. Thus, our empirical analysis revealed additional factors (e.g., magnitudes or effect sizes of the dynamic parameters) that might dictate the relative performance of the partial and full MI approaches. Further investigation is needed to hasten our understanding of how effect size and its possible interaction effects with other factors affect the performance of the full and partial MI approaches.

In sum, the heuristic way of recoding missingness in the covariates on the associated child behaviors/emotions did not lead to different substantive conclusions than if the missingness were handled by means of full MI. However, using list-wise deletion altered the spacing between successive observations and greatly attenuated the magnitude of the autoregressive parameter for wife’s conflict resolution, leading to (possibly) erroneous conclusions concerning the (lack of) continuity in the wife’s conflict resolution ratings from one conflict to the next. The convergence in conclusions from all remaining missing data handling approaches suggested that incorporating more fine-grained variability (i.e., aggregate mean scores as opposed to binary responses) in child agentic and negativity did not yield distinctly different interpretations with regard to children’s roles on their parents’ conflict resolution. This suggested that the sheer presence of children’s agentic behavior and negativity was enough to have an impact on parents’ conflict resolution regardless of the extent and intensities of the behavior/ emotions.

DISCUSSION

In this study, we illustrated and examined the performance of partial MI and full MI approaches in the context of intensive longitudinal data analysis in fitting a bivariate VAR model with covariates. We evaluated the relative strengths and limitations of the two approaches in comparison to list-wise deletion under different missingness conditions and number of measurement occasion conditions in a simulation study. Four main findings emerged. First, consistent with previous findings with cross-sectional data (Little & Rubin, 2014), doing MI using a mildly mis-specified imputation model still led to better performance than list-wise deletion. By retaining the original spacing (e.g., the correct time intervals) between adjacent observations, both imputation approaches outperformed list-wise deletion by yielding smaller biases and RMSEs in the point estimates. Both MI approaches also performed better than list-wise deletion in SE estimation under all missingness conditions. Second, point estimates from the partial MI approach, especially those associated with the time-series parameters, were found to have better accuracy, precision, and coverage properties in general compared with the full MI approach. In contrast, the full MI approach was found to yield higher accuracy in SE estimation, particularly in situations involving non-ignorable missingness. Both approaches were found to yield reasonable results in handling percentages of missingness commonly encountered in empirical applications. Third, even though the full MI approach yielded more accurate SE estimates than the partial MI approach under the NMAR condition, SE estimates with the partial MI approach improved and became closer to the empirical SE under this condition with larger T. Finally, larger T did not help improve the accuracy of the point estimates of the list-wise deletion approach. For smaller T, the advantages of MI in improving parameter SE estimates are especially salient.

In our empirical illustration, the key results and conclusions obtained from using the full MI approach with MICE were consistent with the results reported earlier wherein the missing covariates were simply recoded as 0. However, list-wise deletion of observations with missing covariates did obscure the autoregressive effect in wife’s conflict resolution, as discrepant from the statistically significant autoregressive effect found using the other missing data handling approaches. Given the (somewhat unusually) small proportion of missingness in the dependent variables (approximately .4%), we did not find further differences, for example, between the partial MI and full MI approaches. However, we suspect more salient differences would emerge among the approaches in other empirical studies with slightly more realistic proportions of missingness (e.g., 30%, as considered in our simulation study). In addition, the specific empirical study considered in this article has covariates that may be tallied as sum scores while the child was present. Thus, it is still plausible to interpret missingness on the covariates as the non-occurrence of the specified behavior/emotions. In other studies, it may not always be theoretically plausible to recode the missing values on covariates as 0.

In general, results from this article demonstrated advantages of the MI approaches in handling missing data in intensive longitudinal studies. First, unlike list-wise deletion, MI approaches preserve the original observed time intervals, thus leading to more accurate parameter estimation in time-series models. Meanwhile, MI also takes into consideration the uncertainty of the imputed values by assimilating such uncertainty through the generation of multiple imputed data sets and including between-imputation variations in parameter estimates in the overall SE estimates. Second, MI approaches—including the full MI and partial MI approaches considered in the present study—are more flexible from the implementation and estimation standpoints compared with a full FIML approach or pattern-mixture modeling. Statistical packages for implementing MI procedures usually allow different imputation models to accommodate various data characteristics. In our simulation study, we included one continuous variable and one binary variable as the covariates of the dynamic model, and the estimation results were reasonable under both MI approaches. The number of measurement time points is also not a constraint with MI-based approaches. The two conditions we used in our simulation study have 15 and 75 time points for four variables, which would have yielded (2⁴)¹⁵ and (2⁴)⁷⁵ different missingness patterns if pattern-mixture modeling was used. Clearly, this would pose great computational challenges. Third, it is easier to include auxiliary variables with the MI approaches than an FIML approach (Collins et al., 2001). With MI, it is straightforward to include as many auxiliary variables as appropriate as part of the imputation model. In our simulation study, under the NMAR condition, we included two fully observed auxiliary variables in the imputation model, resulting in nine variables in total. The computational time (namely CPU time) for five imputations was 30 seconds on average with MICE and 4 seconds on average with Amelia II (using a PC with 3.60 GHz Intel Quad Core CPU) (N = 100, T = 75).

Our results helped clarify previous results concerning the inadequacies of the MI approaches for handling missingness in intensive longitudinal data in an important way. For instance, S. Liu and Molenaar (2014) claimed that imputing missing data in multivariate time series using VAR models yielded better estimates for the cross-lagged coefficients than an MI approach they considered. However, their true model was a time-series model and they did not incorporate lagged information in the imputation model for their MI procedure and neither did they include auxiliary variables. We did not consider the VAR-based imputation approach presented by S. Liu and Molenaar (2014) because this approach does not readily handle missingness in categorical (e.g., binary) covariates without some adaptation. Our view is that the MI approaches would perform equally well, if not better, if appropriate lagged dependent variables and auxiliary variables are included in the imputation model. Further studies are needed to verify this claim in cases that do allow the MI and the VAR-based imputation approaches to be compared directly.

It is important to point out that auxiliary variables should be carefully chosen when we perform MI, or biases may actually increase as opposed to decrease with the inclusion of auxiliary variable under certain conditions (Thoemmes & Rose, 2014). Kano (2015) demonstrated mathematically that including an auxiliary variable would increase estimation biases in a simple regression model under the following condition:

$$\left|{\rho }_{yr}\right|<\left|{\rho }_{yr}-{\rho }_{yx}{\rho }_{xr}\right|,$$

where $\left|{\rho }_{yr}\right|$ represents the absolute value of the correlation between a dependent variable (y) and a missingness indicator (r). ρ_yxρ_xr represents the product of the correlation between an auxiliary variable (x) and the dependent variable, and that between an auxiliary variable and the missingness indicator. Thus, increased estimation biases might be observed, for instance, when the auxiliary variable correlates positively with the dependent variable, but the two variables are correlated with the missing data indicator in opposite directions. In other words, estimation biases might emerge if values of the auxiliary and dependent variables change in the same direction but they contribute to missingness in mutually contradictory ways. Of course, the patterns of association among dependent variables, auxiliary variables, and the missingness mechanisms are often much more complicated in practice than the simple regression scenario considered by Kano (2015). It is also difficult, if not impossible, to falsify postulates concerning the nature of the missingness mechanisms. Thus, it is important to conduct sensitivity tests in empirical applications whenever possible to evaluate if and how inclusion of various auxiliary variables may change one’s estimation results (Thoemmes & Rose, 2014).

In addition to the choices of auxiliary variables to include in conducting MI, another important decision researchers need to make is how many replications are needed for the MI procedures. Rubin (2004) demonstrated theoretically that three to five imputations would be sufficient under most realistic circumstances, and this has been used as a general guidance by many researchers in deciding the number of imputations to use in empirical applications. However, with more complicated models and longitudinal data, some researchers have also proposed using a larger number of imputations to improve the stability of confidence interval estimation (Royston, 2004), obtain more accountable conclusions with empirical data (Spratt et al., 2010), to achieve more reliable model selection results with longitudinal data (Shen & Chen, 2013), and to improve power (Graham, Olchowski, & Gilreath, 2007). In the current study, we used five replications for the MI procedures in the simulation study. This appeared sufficient for the particular settings considered in this study (e.g., power was close to 100% across all the conditions considered; biases and other performance measures appeared satisfactory, except for coverage), and increasing the number of replications to 10 did not affect the results substantially. However, in other studies involving higher percentages or more complex patterns of missingness, smaller sample sizes, and weaker correlations, more number of replications may be needed (Lu, 2017).

The MICE package also provides functions to support missing data imputations for hierarchical (multilevel) data. Thus, one possible extension to the approaches evaluated in the present article is to use such multilevel functions to account for additional within-subject correlations among the repeated measures in the imputation process. However, the multilevel imputation options in MICE are currently available only for continuous data (van Buuren & Groothuis-Oudshoorn, 2011), and our simulations included both categorical and continuous covariates. Because our data generation mechanism was based on a group-based model that assumes homogeneity in all individuals’ change functions as well as missing data mechanisms, we found in a preliminary simulation study (not shown due to space constraints) that using multilevel imputations on only the continuous covariates did not lead to notable improvements in estimation quality compared to the approaches considered here. However, in other scenarios where heterogeneity in the missing data mechanism may be expected, using appropriate MI approaches that do account for multilevel data structures is critical. This is beyond the scope of the present article, but warrants more careful examination in future studies.

Admittedly, the results reported in the present study only pertain to the current model (i.e., bivariate VAR(1) model) and sample size configurations. Findings of the current study about the performance of partial MI and full MI may not generalize to studies involving other sample size configurations. For example, with higher percentages of missingness (than the 30% considered in our simulation study), more imputations may be necessary for the MI approaches to achieve stable estimation. Smaller sample sizes and shorter time series may also affect the results of the MI approaches. In addition, the two MI approaches considered in this study are both two-step procedures (i.e., with imputation followed by estimation of the modeling parameters as if the imputed data were observed). Such two-step procedures may not be adequate under more complex settings. Thus, further simulation studies are warranted to investigate the performance of the partial and full MI approaches under more complicated models (e.g., clustered data), and in comparison to other one-step (e.g., Bayesian) approaches that perform the imputation and parameter estimation simultaneously. Finally, we did not address the effect of mis-specification of imputation models on the results from MI in our simulation study. Even though the missing data mechanism in general is not directly falsifiable, especially in cases involving non-ignorable missingness, a seriously flawed imputation model that deviates substantially from the true missing data mechanism will very likely lead to biased estimates and improper interpretations (Barnard & Meng, 1999). Sensitivity test will be helpful in evaluating the reliability of MI under different scenarios.

Moving forward, several extensions to the present work are possible. For instance, it would be of interest to test and evaluate the performance of the MI approaches with other dynamic models, such as dynamic models involving latent variables, categorical dependent variables, and different patterns of association with auxiliary variables that could potentially be used for MI purposes. Nevertheless, the present work addressed some practical difficulties that researchers may encounter in handling missingness in intensive longitudinal data and showed that, with some adaptations, some of the common approaches for handling missingness in the dependent variables (specifically, FIML) can be combined with approaches for handling missingness in the covariates to ease computational burden and the need to devise MI models for missingness in all the variables for a full MI approach. We also demonstrated how lagged variables may be incorporated into an MI model to improve the estimation properties of models for intensive longitudinal data. We hope our work can help instigate further refinements and extensions of contemporary missing data handling techniques to better tailor to characteristics of intensive longitudinal data.

APPENDIX

R Code for Full/Partial MI, and Pooling Parameter Estimates

# Detailed demonstration of the method, together with simulated data set and #estimation program, mkfm6 (Dolan, 2002), is available on the website:
#https://quantdev.ssri.psu.edu/resources/handling-missing-data-modeling
#-intensive-longitudinal-data
# In this illustration, y1 and y2 represent the two dependent variables (DV)
# in the VAR model, x1 and x2 represent the covariates (COV).
# Each of them has T = 15 and N = 100, with around 30% of missing data.
# We also simulated two fully observed variables: ax1 and ax2.
# Data generating model we used follows the VAR model described in the
# paper.
# Read in the simulated data set.
data = read.table(“Simulate Data.txt”)
n = 100
nt = 15
# The first step is to define an imputation model, which includes both DVs,
# COVs, lagged DVs, lagged COVs if necessary, and all other auxiliary
# variables.
#Following steps will create a long/tall format data set with lag one DVs
# and COVs.
#The lagged variables can also be created using R functions of choice, such
# as lag().
#The number of lags to be included in the imputation model depends on
#the order of the assumed true model. For example, if the true model is a
# VAR at order one, only lag one variables are necessary in the imputation
# model.
y1 = data[,1:15]
y2 = data[,16:30]
x1 = data[,31:45]
x2 = data[,46:60]
ax1 = data[,61:75]
ax2 = data[,76:90]
y1.lag1 = cbind(rep(NA,n),y1[,c(1:(nt-1))])
y2.lag1 = cbind(rep(NA,n),y2[,c(1:(nt-1))])
x1.lag1 = cbind(rep(NA,n),x1[,c(1:(nt-1))])
x2.lag1 = cbind(rep(NA,n),x2[,c(1:(nt-1))])
y1.temp = reshape(y1, direction = “long”,varying = list(1:15))
y1.temp = y1.temp[order(y1.temp$id),][,2]
y2.temp = reshape(y2, direction = “long”,varying = list(1:15))
y2.temp = y2.temp[order(y2.temp$id),][,2]
x1.temp = reshape(x1, direction = “long”,varying = list(1:15))
x1.temp = x1.temp[order(x1.temp$id),][,2]
x2.temp = reshape(x2, direction = “long”,varying = list(1:15))
x2.temp = x2.temp[order(x2.temp$id),][,2]
y1.lag1.temp = reshape(y1.lag1, direction = “long”,varying = list(1:15))
y1.lag1.temp = y1.lag1.temp[order(y1.lag1.temp$id),][,2]
y2.lag1.temp = reshape(y2.lag1, direction = “long”,varying = list(1:15))
y2.lag1.temp = y2.lag1.temp[order(y2.lag1.temp$id),][,2]
x1.lag1.temp = reshape(x1.lag1, direction = “long”,varying = list(1:15))
x1.lag1.temp = x1.lag1.temp[order(x1.lag1.temp$id),][,2]
x2.lag1.temp = reshape(x2.lag1, direction = “long”,varying = list(1:15))
x2.lag1.temp = x2.lag1.temp[order(x2.lag1.temp$id),][,2]
ax1.temp = reshape(ax1, direction = “long”,varying = list(1:15))
ax1.temp = ax1.temp[order(ax1.temp$id),][,2]
ax2.temp = reshape(ax2, direction = “long”,varying = list(1:15))
ax2.temp = ax2.temp[order(ax2.temp$id),][,2]
# Note all categorical variables need to be specified using the as.factor
# function.
# In this simulated data set, COV x1 is a categorical variable. MImodel = data.frame(cbind(y1.temp,y2.temp, x1.temp,x2.temp, y1.lag1. temp,y2.lag1.temp,x1.lag1.temp,x2.lag1.temp, ax1.temp,ax2.temp))
MImodel[,3] = as.factor(MImodel[,3]) #specify x1 to be categorical MImodel[,7] = as.factor(MImodel[,7]) #specify x1.lag1 to be categorical
# The next step is to perform imputation using the specified imputation
# model.
# Number of imputation can be specified with the argument “m = “,
# which by default is 5.
library(mice)
m = 5 
imp = mice(MImodel,m = m)
# Initial list to store outputs
# Number of parameters estimated in this illustration is 11.
k = 11
# Parameter estimates from each imputation will be stored in matrix qhat. qhat = matrix(NA, nrow = m,ncol = k)
# Variances covariance matrix of parameter estimates from each imputation
# will be stored in a list u.
u = array(NA,dim = c(k,k,m))
# Perform model fitting with the m imputed data sets. for (i in 1:m) {
# Retrieve the ith imputed data sets
# data.impute = complete(imp,action = i)
# Arrange data for model fitting procedures as necessary.
# With Full MI, imputed data are used for all DVs and COVs.
# For Partial MI, we keep the missingness in DVs and use imputed data
# for COVs.
# Extract DVs and COVs from imputed data sets.
y1.imp = matrix(data.impute[,1],nrow = n,byrow = TRUE)
y2.imp = matrix(data.impute[,2],nrow = n,byrow = TRUE)
x1.imp = matrix(data.impute[,3],nrow = n,byrow = TRUE)
x2.imp = matrix(data.impute[,4],nrow = n,byrow = TRUE)
# Perform modeling fitting procedures with full or partially imputed
# variables with time series model fitting program of choice. In this
# paper, mkfm6(Dolan, 2002) was used to fit the VAR model.
# We also provided:
# - a R function to write out the data set in mkfm6 format, writemkfm.R;
# - a R function to write mkfm6 model script,compileKFscript.R; and
# - R functions to call mkfm6 through R (for PC users)
# These files are available on the website. To run the functions,
#please make sure all files are saved in the same directory.
# Create a name for new data set
datafile = sprintf(paste(“data%i”,”.txt”,sep = ““),i)
# Create a name for model script
fileKF = sprintf(paste(“mk%i”,”.txt”,sep = ““,collapse = ““),i)
filebat = sprintf(paste(“run%i”,”.bat”,sep = ““,collapse = ““),i)
#ne = 2 number of DVs
temp = cbind(y1.imp, y2.imp, x1.imp, x2.imp)
source(“writemkfm.R”) # function to write a data set in mkfm6 format
writemkfm(temp,ne,nt,datafile)
source(paste(“compileKFscript.R”,sep = ““)) #function to write
#mkfm6 model script
source(paste(“compilebat.R”,sep = ““))
system(sprintf(paste(“run%i”,”.bat”,sep = ““,collapse = ““),i),
wait = TRUE,intern = TRUE)
# Store model fitting results in qhat and u.
pars = scan(“pars.out”)
# program generated parameter point estimates.
qhat[i,] = pars[seq((k*k + 1),length(pars),2)]
# program estimated parameter variance covariance matrix.
u[,,i] = matrix(pars[1:(k*k)],ncol = k)
}
# Finally, pool results from m sets of estimations.
# Calculate average parameter point estimates across m sets of model fitting
# results
qbar <- apply(qhat, 2, mean)
# Calculate pooled standard error estimates
ubar <- apply(u, 1:2, mean)
e <- qhat - matrix(qbar, nrow = m, ncol = k, byrow = TRUE)
b <- (t(e) %*% e)/(m - 1)
vcov <- ubar + (1 + 1/m) * b #vcov is the pooled variance covariance
# matrix for parameter estimates
se = sqrt(diag(vcov))