Abstract
How cells utilize instructions provided by genes and integrate mechanical forces generated by tissue growth to produce morphology is a fundamental question of biology. Dermal bones of the vertebrate cranial vault are formed through the direct differentiation of mesenchymal cells on the neural surface into osteoblasts through intramembranous ossification. Here we join a self-organizing Turing mechanism, computational biomechanics, and experimental data to produce a 3D representative model of the growing cerebral surface, cranial vault bones, and sutures. We show how changes in single parameters regulating signaling during osteoblast differentiation and bone formation may explain cranial vault shape variation in craniofacial disorders. A key result is that toggling a parameter in our model results in closure of a cranial vault suture, an event that occurred during evolution of the cranial vault and that occurs in craniofacial disorders. Our approach provides an initial and important step towards integrating biomechanics into the genotype phenotype map to explain the production of variation in head morphology by developmental mechanisms.
Keywords: computational morphogenesis, finite volume method, intramembranous ossification, skull growth and evolution, craniosynostosis, brain, mouse model
1. Introduction
The evolutionary emergence of the head is central to the rise of the vertebrates and involves the evolution of key characters including a mineralized skull that protects and supports a cephalic nervous system and sense organs. The vertebrate cranial vault represents the cranial portion of the dermal skeleton that evolved to protect the rostral brain surface (Kawasaki et al. 2004). One of the fundamental questions underlying patterns of cranial vault shape variation across ontogenetic and evolutionary time is how organisms integrate genetic inputs and mechanical forces from growing soft tissues to produce skull morphology. Increase in brain size is evident across the evolution of vertebrates (O’Leary et al. 2007), and persistent loss of skull bones is demonstrated over the approximately 150 million years of synapsid evolution (Sidor 2001), yet remarkable accommodation of brain and skull is evident across living and extinct vertebrates (Richtsmeier and Flaherty 2013). Still, the mechanisms that direct the synchronization of these two tissues in development and in evolution is not understood.
The basic structure of the cranial vault is similar across mammals, consisting of plates of dermal bone that are not preformed in cartilage but form directly through intramembranous ossification, where the action of extracellular molecules (Long 2011; Westendorf et al. 2004; Cheng et al. 2003; Wan and Cao 2005; Aspenberg et al. 2001; Wan et al. 2007) and mechanical stimuli (Carter et al. 1988; Palomares et al. 2009; Maul et al. 2011; Sumanasinghe et al. 2006; Sato et al. 1999; Ikegame et al. 2001; Rauch et al. 2000) contribute to the condensation and direct differentiation of mesenchymal progenitors into osteoblasts that deposit bone matrix and mineralize that matrix. Cranial sutures are fibrous joints that form between dermal bones of the skull and consist of two osteogenic bone fronts and an intervening connective tissue containing undifferentiated mitotic mesenchymal cells. During development, sutures function as growth sites enabling cranial vault bones that are changing in shape and increasing in size to move away from one another over a rapidly expanding brain (Opperman 2000).
The laboratory mouse is currently the most extensively used experimental model for studying human development and disease and its value for investigating developmental mechanisms that foster phenotypic change is well recognized (Perlman 2016). We used the laboratory mouse to model the interaction of brain and cranial vault bones in embryonic development to help reveal how genetic programs that contribute to organ development use mechanical forces as feedback, providing both robustness to perturbations that could derail normal development, and flexibility to evolve new forms. Though molecular genetics has enumerated specific circumstances of cranial vault genesis and dysgenesis in experimental mice and in humans, understanding of the developmental interactions underlying fundamental similarity and diversity of cranial morphology across vertebrates cannot be achieved solely through experimental work.
Hybrid mechano-biological models for fracture healing exist (Bailón-Plaza and van der Meulen 2003; Geris et al. 2010), but there is no coupled mechano-bioregulatory model that considers brain growth and cranial vault bone formation. Using precise measures of brain and skull morphology collected from mouse embryos aged embryonic day 13.5 (E13.5) through birth (P0) (Aldridge et al. 2010; Motch Perrine et al. 2017), we built a reaction-diffusion-strain model of the development of the cranial vault that combines the influence of mechanical stimuli generated by a growing brain with a Turing reaction-diffusion (RD) model (Turing 1952) of molecular interactions. We used a Turing model to mathematically model the relationship between two interacting molecules that form a spatial pattern that results in cranial vault bone formation. We then conducted a structural analysis computing the estimated strain distribution resulting from rapid expansion of the growing brain across a layer of undifferentiated mesenchymal cells surrounding the brain. Finally, we use the model to investigate the distribution of molecules and cells and changes of the strain field over the domain across time to demonstrate formation of cranial vault bones and sutures. We conduct a parametric study adjusting model parameters according to published experiments where molecular variants cause cranial dysgenesis in laboratory mice. Our simulation gives results consistent with experimental observation revealing the generalizability of the model.
2. Materials and methods
2.1. Evidence-based assumptions for model development
This section provides the assumptions used during model development and the scientific evidence on which the assumptions are based. Intramembranous ossification, responsible for bone formation in the cranial vault, is controlled in part by a cascade of reactions of signaling molecules (e.g., Wnt, BMP, FGF) (Long 2011) that are locally produced and circulate in the extracellular space. The available evidence suggests that a spatial patterning of interacting molecules determines the locations of condensations of osteoblasts differentiated from mesenchymal cells. This patterning may be derived by the Turing mechanism (Turing 1952), a mathematical model describing the relation between two interacting molecules, an activator and an inhibitor. The Turing mechanism has explained biological pattern formation in diverse contexts (Garzón-Alvarado et al. 2013; Kondo and Shirota 2009; Raspopovic et al. 2014; Sugimura et al. 2007). From these data, we formulate the following simplifying assumptions: 1) a key molecule, the activator (e.g., BMP), activates the differentiation of mesenchymal cells into osteoblasts so that the patterning of the concentration of the molecule determines the location of primary ossification centers (A1a); and 2) the behavior of the activator is regulated by another molecule (the inhibitor) so that the regulatory loop of the two molecules can be modeled using a Turing’s reaction-diffusion model (A1b).
After the accumulation of cells that form the primary ossification centers, bone grows from these centers by a combination of the production and mineralization of osteoid by osteoblasts and continued differentiation of rapidly proliferating mesenchymal cells on the periphery of the condensation (Iseki et al. 1997; Rice et al. 2000; Ting et al. 2009; Yoshida et al. 2008). Osteoblasts in the ossification centers secret various extracellular molecules, some of which diffuse into the neighboring space allowing adjacent mesenchymal cells to differentiate into osteoblasts. Members of the bone morphogenetic protein family, BMPs, are important molecules in the morphogenetic signals underlying bone formation.
BMPs are secreted from undifferentiated mesenchymal cells and from differentiated osteoblasts (Lai et al. 2008), thus contributing to the formation and growth of primary ossification centers by promoting adjacent mesenchymal cells to differentiate along an osteogenic trajectory. From this information, we formulate and additional assumption: differentiated osteoblasts express the activator molecule that leads to bone growth (A2a).
In normal conditions, as dermal bones of the cranial vault approximate one another, they are separated by the space of cells that have not differentiated into osteoblasts, which are called sutures. Sutures enable growth of bones along the bony front, accommodating changes in size and shape of the growing brain, and allow the skull to deform during birth (Ting et al. 2009). Based on the experimental observation that noggin (inhibitor) specifically binds and inactivates several BMPs (activator) (Aspenberg et al. 2001), and inhibits bone formation, we formulate the following assumption about suture formation: the inhibitor molecule inhibits osteoblast differentiation contributing to suture formation and maintenance (A2b).
Experimental studies demonstrate that mechanical stimuli alter tissue differentiation and molecular expression during bone formation (Maul et al. 2011; Palomares et al. 2009; Subramony et al. 2013), in particular that tensile strain promotes the expression of BMPs (Ikegame et al. 2001; Rauch et al. 2000; Sato et al. 1999; Sumanasinghe et al. 2006), an appropriate example of an activator in our model. Our approach follows Carter et al. (1988) who tested the hypothesis that mechanical stress affects cell differentiation and suggested that hydrostatic stimuli, which is related to change in volume, may play an important role in tissue differentiation rather than shear stimuli. Volumetric strain is estimated in our study as the unit change in volume (e.g. dV/V where V represents the volume), which implies that it can also be related to the status or amount of cell proliferation (where increased cell proliferation results in increased accumulated volumetric strain). Cell proliferation is defined as the increase in the number and/or density of cells by continuous cell division and occurs prior to cell differentiation (Hall and Miyake 2000). From this information, we develop a third set of assumptions related to the role of mechanical stimuli produced by growth of the underlying brain in the process of cranial vault bones formation: 1) tensile volumetric strain promotes the expression of the activator (A3a); and 2) osteoblast differentiation occurs only after proliferation, in other words, cells can differentiate only where the accumulated local volumetric strain reaches a certain level (A3b).
2.2. Reaction-Diffusion-Strain (RDE) model
Using a set of assumptions based on scientific evidence (see A1–3 above) we coupled Turing’s reaction-diffusion equations with the mechanical effects of development to produce a reaction-diffusion-strain (RDE, where E represents Green-Lagrangian strain) model. The RDE model improves our previous work (Lee et al. 2017) by incorporating different length scales and responses to changing biomechanical conditions across developmental time, providing a flexible framework that accommodates interaction across levels at varying scales. The RDE model describes the behaviors of diffusible extracellular molecules contributing to cell differentiation using the reaction-diffusion system of activator-inhibitor type (Gierer and Meinhardt 1972). In this system, the activator promotes the production of itself (Fig. 1a-①) and the inhibitor (Fig. 1a-②), while the inhibitor inhibits activator signaling (Fig. 1a-③) thus establishing a regulatory loop. Differential speeds of diffusion of activator and inhibitor establish an inhomogeneous spatial pattern of concentration of molecules in a domain. At the cellular level, condensed activator initiates signaling pathways prompting differentiation of mesenchymal cells into osteoblasts (Fig. 1a-④). Differentiated osteoblasts express activator (Fig. 1a-⑤), prompting differentiation of adjacent mesenchymal cells into osteoblasts resulting in bone growth along the periphery of ossification centers. Concurrently, the inhibitor obstructs cell differentiation (Fig. 1a-⑥) contributing to suture formation between bones. At the tissue level, mechanical strain produced by continuous growth of the underlying brain affects the molecular and cellular processes. Based on the observation that tensile strain promotes activator production (Ikegame et al. 2001; Rauch et al. 2000; Sato et al. 1999; Sumanasinghe et al. 2006) (Fig. 1a-⑦ and ⑧) and that cells initiate differentiation when accumulated volumetric strain surpasses a threshold value (Fig. 1a-⑨), we added strain effects to the behaviors of key molecules and cells to build the RDE model.
Fig. 1.
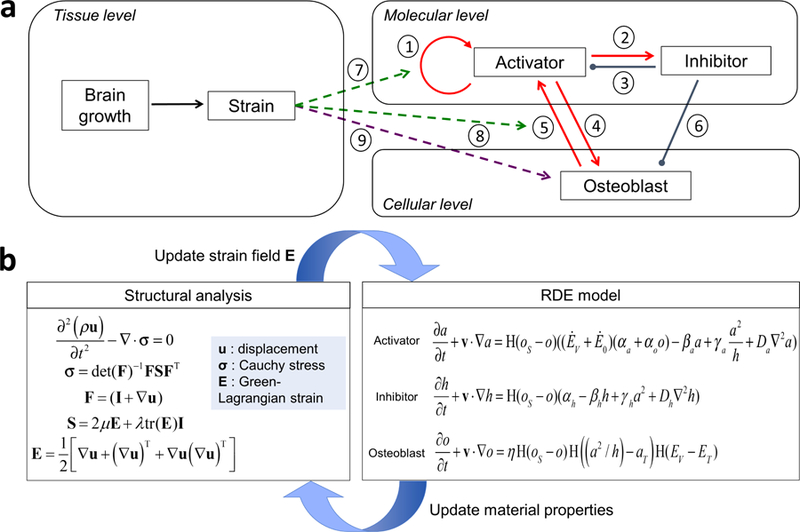
a Schematic diagram of the multi-scale reaction-diffusion-strain (RDE) model for cranial vault bone formation. b Schematic diagram showing the computational process. Structural analysis gives the strain field that is used to estimate the distribution of molecules and cells using the RDE model. Material properties of the domain are updated according to the distribution of cells, and then are used for structural analysis to estimate updated strain field.
2.2.1. Mathematical expression of the RDE model
Equations (1), (2) and (3) mathematically describe the coupled RDE model operating on a domain that considers groups of cells as a continuum.
| (1) |
| (2) |
| (3) |
The RDE model solves for the concentrations of activator, inhibitor, and differentiated osteoblasts, represented by a, h, and o, respectively. The terms v · ∇a, v · ∇h, and v · ∇o on the left hand side refer to the convection effect where each component moves with the bulk motion of the domain on which the component locates, where v represents the velocity of the moving domain and ∇ represents the gradient in space. The term H (oS ‒ o) multiplied with other terms on the right hand side is a rounded Heaviside step function (H (x) = 0 if x < 0 and 1 if x > 0) operationalizing the assumption that all behaviors of the components take place only in undifferentiated mesenchymal cells., where the variable oS represents the saturation concentration of osteoblasts that sets the upper limit of the generation of osteoblasts. The behaviors of the activator and inhibitor include their production , degradation (βaa and βhh), reaction , and diffusion (Da∇2a and Dh∇2h).
The parameters αa and αh quantify the production of activator and inhibitor from surrounding cells. The production of activator (αa + αoo) is assumed to be proportional to the local volumetric strain rate ĖV (details in section 2.2.2) plus Ė0, a constant that makes the production term positive, so that the strain field initially guides the distribution of activator. Once differentiation initiates, the production term also depends on the concentration of osteoblasts, o, so that the parameter αo quantifies the production of activator from differentiated osteoblasts. The activator in turn causes differentiation of cells near osteoblasts, resulting in bone formation and growth at the leading edge of the growing bone. βa and βh are constants quantifying degradation or depletion of each molecule by their excess. γa and γh are parameters associated with the non-linear interaction between activator and inhibitor. The interaction terms make the two equations coupled in a way that the activator promotes itself and the inhibitor (a2 in numerator in Eqs. (1) and (2)) but is constrained by the inhibitor (h in denominator in Eq. (1)). Da and Dh represent the diffusion rate of each molecule and ∇2 is the Laplace operator which describes spatial diffusion of variables. The rate of differentiation of mesenchymal cells into osteoblasts, , is promoted by activator and limited by inhibitor, so the ratio between the molecules determines the rate, based on whether it is higher than a threshold value, aT. Accumulated volumetric strain, EV (details in section 2.2.2), contributes to the rate, so that cells differentiate only after a threshold value, ET, is reached. The value η is a constant quantifying the amount of osteoblast generated by action of the molecules and mechanical strain.
It is convenient to non-dimensionalize the equations to reduce the number of parameters using a nondimensiona time (t*) and length (x*) scale and concentrations (a*, h*, and o*) where t* = βat, , , , , and . Adopting this convention, Eqs. (1) - (3) can be reduced to Eqs. (4) - (6).
| (4) |
| (5) |
| (6) |
where , , , , , , , and . The superscript * indicates that the value under it is non-dimensionalized. Non-dimensional parameters were chosen to satisfy conditions for pattern formation using a linear stability analysis (Murray 2002), which prevents the initial small perturbations on concentration of molecules from both decaying to remain homogeneous steady state and exponentially growing without achieving a stable inhomogeneous pattern. Exact values for the threshold of concentration of molecules ( and ) and for the limit of the strain (ET) were chosen by comparing the timing and location of appearance of primary centers of ossification in our computational results with their known locations in our experimental observations. The values of the non-dimensional parameters which are used in this study are given in table 1. The parameters can be associated with a particular length scale (either molecular, cellular or organ level) that enables one to devise experimental studies to measure their values in the future. The parameters A, B, G, D, αo, and are associated with the molecular level, and φ with the cellular level, and ET and with the tissue level.
Table 1.
Model parameters in non-dimensional reaction-diffusion-strain model.
| Non-dimensional parameters | Value | ||
|---|---|---|---|
| Molecular level | Production | A | 2.86 × 10‒3 |
| Degradation | B | 2.00 | |
| Interaction | G | 1.75 × 101 | |
| Diffusion | D | 3.00 × 102 | |
| Production from osteoblast | α0 | 4.00 × 102 | |
| Threshold | 2.68 × 10‒1 | ||
| Cellular level | Saturation | 1.43 × 10‒1 | |
| Coefficient | φ | 1.43 × 10‒1 | |
| Tissue level | Volumetric strain threshold | ET | 5.00 × 10‒1 |
| Strain rate constant | 3.00 × 10‒2 | ||
2.2.2. Kinematics
We compute the estimated strain distribution across the layer of undifferentiated mesenchymal cells surrounding the brain resulting from rapid expansion of the growing brain. Considering the group of cells as a continuum material, mechanical behavior of the material is governed by the balance of momentum:
| (7) |
with deformation gradient F = (I + ∇u) and second Piola-Kirchhoff stress S = 2μE +λtr (E) I. Parameters μ and λ are the material-dependent Lamé parameters which can be expressed in terms of Young’s modulus (E) and Poisson’s ratio (v) by and . The Green-Lagrangian strain tensor, E, is defined in terms of displacement (u) by:
| (8) |
In our simulation, all variables are treated as incremental values using the updated Lagrangian approach. In other words, displacement u is an incremental value calculated from the previous time step to the current time step, as is the deformation gradient F. The local volumetric strain rate is defined as . Accumulated volumetric strain EV is defined as, where Vn represents the volume of a cell or an element at the n-th time step. Here deformation gradient F0 is defined with the initial state as a reference. A local material property, p, is determined by, where pm and po indicates the property of mesenchymal cells and osteoblasts, respectively. The term H(oS ‒ o) multiplied with other terms on the right hand side is a rounded Heaviside step function (H (x) = 0 if x < 0 and 1 if x > 0) operationalizing the assumption that all behaviors of the components take place only in undifferentiated mesenchymal cells, where the variable oS represents the saturation concentration of osteoblasts that sets the upper limit of the generation of osteoblasts. Therefore, if the local concentration of osteoblasts is less than the critical saturation level the properties remain in the undifferentiated state. If the local concentration of osteoblasts is greater than the critical saturation level the properties are assigned to the differentiated state. Three material properties for structural analysis are defined in this way: Young’s modulus
| (9) |
Density
| (10) |
Poisson ratio
| (11) |
Values of 1000 kg/m3 for density (ρm), 20 kPa for Young’s modulus (Em), and 0.4 for Poissons ratio (vm) as estimated by Pillarisetti et al. (2011) were used for the material properties of the mesenchymal cells. Values of 2000 kg/m3 for density (ρo), 240 kPa for Young’s modulus (Eo), and 0.3 for Poissons ratio (vo) were used as estimates of the material properties of embryonic osteoblasts.
2.2.3. Computational implementation
Figure 1b is a schematic diagram showing the computational process. The governing equations for structural analysis (Eqs. (7) and (8)) are initially solved to estimate the strain field across the layer of undifferentiated mesenchymal cells surrounding the brain resulting from rapid expansion of the growing brain. With the strain field calculated, the RDE model (Eqs. (1) - (3)) is solved to estimate the distribution of activator, inhibitor, and osteoblast. As cell differentiation proceeds, the material properties of the domain change according to the distribution of osteoblasts. With the updated material properties (estimated from Eqs. (9) - (11)) of the domain, a new strain field is estimated and used again for the RDE model, forming an iterative loop of calculation.
2.3. Boundary valued problem informed by experimental data
We solve the model on a computational domain that represents a layer of cells surrounding the embryonic mouse brain. We required the domain to grow over time according to measures of the brain derived from experimental mouse embryos to investigate the effect of the non-uniform growth of the brain (Fig. 2).
Fig. 2.
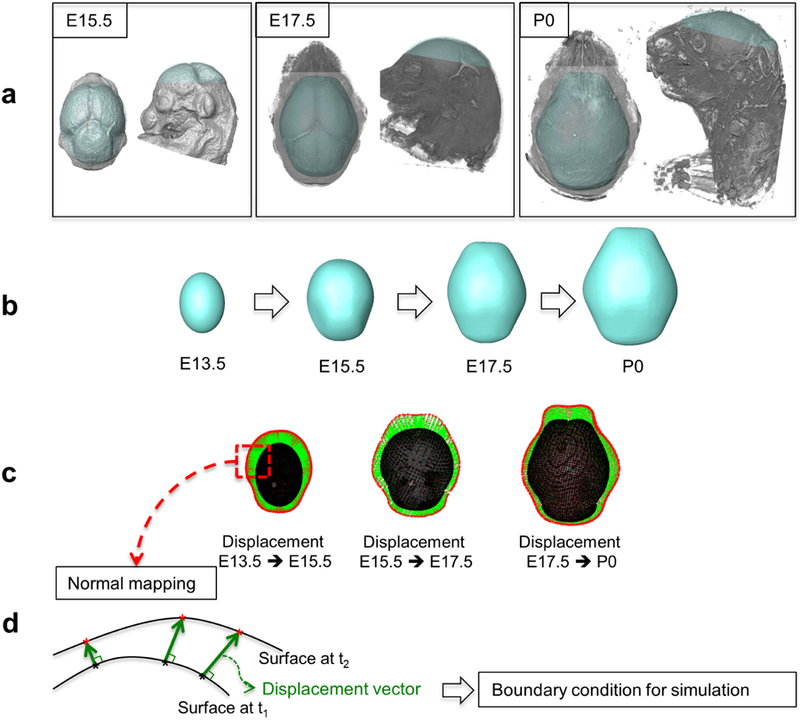
Process of establishing a computational domain that grows over time based on the data from experimental mice aged from embryonic day 13.5 (E13.5) to birth (P0). a µCT and MRM images of the mouse brain and cranial vault at E15.5, E17.5, and P0. b Simplified geometry of the brain and cranial vault, constructed from the µCT and MRM images. The brain shape at E13.5 is assumed as an ellipsoid. c Displacement vectors from points on the surface at the earlier time point to the surface at the later time point are computed using normal mapping method and represented with green arrows. d Schematic diagram of normal mapping. Displacement vectors (green arrows) are normal to the original surface at t1 at each point on the surface (black asterisks) and end on the target surface at t2 (red asterisks). The computed displacement vectors are used as boundary conditions for simulation to make the computational domain to grow over time.
2.3.1. Experimental data
To run our model we use precise, 3D measures of growing brain and skull acquired by high resolution micro-computed tomography (µCT) and magnetic resonance microscopy (MRM) images of embryonic mice heads from which forming bone and brain are segmented, respectively (Fig. 2a). Embryos used in our model are aged according to days post conception (e.g., embryonic day 14 is expressed as E14). Newborn mice are labeled postnatal day 0 (P0). See Appendix A for details of image acquisition. All mouse work was in compliance with animal welfare guidelines approved by the Pennsylvania State University Institutional Animal Care and Use Committees.
2.3.2. Computational domain
Figure 2 shows the process of establishing the computational domain. Using samples of µCT and MRM images of the mouse cranial vault and brain, respectively at several embryonic time points (Fig. 2a), we constructed a simplified surface that covers the brain and the cranial vault, and then made a thin volume around the surface for each embryonic time point (Fig. 2b). Each domain has three surfaces, 1) the inner surface that represents the surface of underlying brain, 2) the outer surface that sets the outer border of the layer of mesenchymal cells, and 3) the surface of the inferior base that connects the inner and outer surfaces. Assuming the brain shape at E13.5 as an ellipsoid, the displacement of each element between the sequential images is estimated using a normal mapping method (Fig. 2c and d). The estimated displacement was applied to the boundary condition for the inner and outer surfaces in our simulation and the base surface is constrained to only translate horizontally. Our model is run on a dynamic computational domain that grows continuously from E13.5 to P0 with the growth of the brain driving the growth of the cranial vault.
The initial mesh at E13.5 was generated using a commercial software ANSYS ICEMCFD (ANSYS, Inc., Canonsburg, PA, USA) and contains 4,978 hexahedral elements. During the simulation, we adapt the adaptive mesh refinement technique based on the gradient of osteoblast concentration to compensate the reduction in accuracy due to the mesh coarsening while the domain enlarges with growth, and to especially improve the resolution of calculation local to the growing bony front. This refinement resulted in an increase in the number of elements to 21,232 by P0.
The initial condition of the concentration of molecules was set as a random distribution of activator with ±0.5% of perturbation, but uniform concentration of inhibitor over the domain. Following experimental observations, it is assumed that the molecules and cells cannot move though the three surfaces of the domain. The RDE model is solved by the finite volume method using open-source code OpenFOAM (www.openfoam.org) to investigate the distribution of molecules and cells and changes of the strain field over time.
3. Results
3.1. Molecular signaling and local mechanical strain establishes primary ossification centers, subsequent bone growth, and suture location
Our time scale is based on chronological age estimates of mouse embryos used in analysis. At the initial time of computation, E13.5, the brain is growing, extracellular molecular signaling is active, but cranial vault bones are not yet mineralizing. At initiation, the concentration of activator is set nearly homogeneous with very small (±0.5%) random perturbations (Fig. 3a, at E13.5). No locations were specified as imminent ossification centers. By E14.5, through the combination of the reaction-diffusion process and the effects of mechanical strain, distribution of the molecules form six locations of high concentration of activator (Fig. 3a, at E14.5), initiating a signaling network that prompts local mesenchymal cells to differentiate into osteoblasts (A1a in section 2.1) when the accumulated local volumetric strain exceeds a certain threshold (A3b).
Fig. 3.
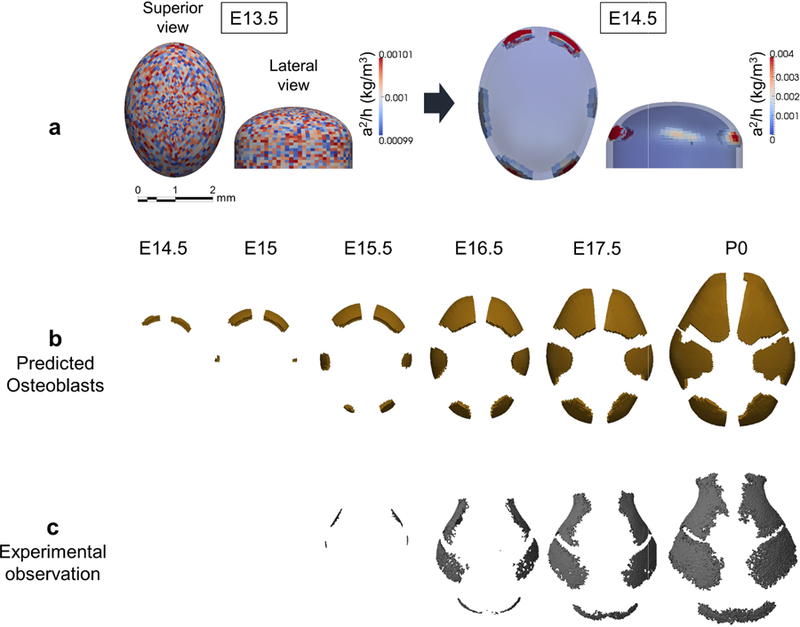
The RDE model predicts the location of primary centers of ossification and pattern of cranial vault bone growth. a Computational result of distribution of concentration of activator relative to inhibitor (a2/h) at E13.5 and E14.5. In superior view, anterior at top; in lateral view, anterior is left. b Computational prediction of distribution of differentiating osteoblasts and cranial vault bone formation by embryonic day. Superior view of skulls, anterior at top, posterior at bottom. Ossification centers for right and left frontal bones appear first (~ E14.5), followed by right and left parietal bones (~E15). Two more ossification centers representing the interparietal bone appear at E15.5. c Observed cranial vault bone formation and growth in embryonic mice (see Appendix A).
The number, location, and sequence of appearance of ossification centers of cranial vault bones in the simulation (Fig. 3b) agree well with experimental data (Fig. 3c). Turing’s model coupled with mechanical information is a rational computational approach for exploring processes fundamental to the development of the vertebrate cranial vault. Our model also reveals vault bone growth by the continued differentiation of osteoblasts at the leading edge of ossification centers that subsequently express activator into mesenchyme on the leading edge, as well as the placement and continued patency of cranial vault sutures. The mechanism underlying the spatio-temporal emergence of ossification centers, the relative growth of each bone element, the establishment of sutures, and localized absence of bone formation is revealed by the structural analysis (Fig. 4).
Fig. 4.
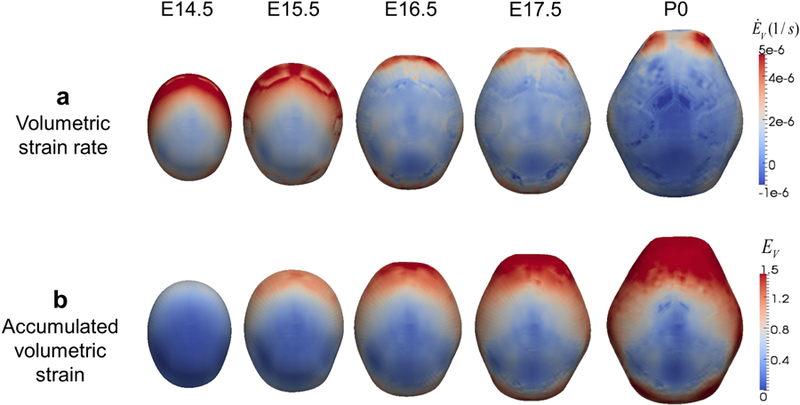
Mechanical strain estimated from structural analysis reveals mechanism of spatio-temporal pattern of bone formation. Computational estimation of volumetric strain rate ĖV (a) and accumulated volumetric strain EV (b) on the domain (shown from above; anterior at top, posterior at bottom) arranged by embryonic day.
The global distribution of volumetric strain rate (ĖV ) over time (Fig. 4a) results from non-uniform expansion of the domain and local strain rate increases at the growing bone fronts due to the change in material properties from undifferentiated cells to mineralizing tissue to bone. These impact the relative speed of growth of each bone and the final pattern of bone formation. The distribution of accumulated volumetric strain (EV ) (Fig. 4b) suggests that the lack of bone formation on the vertex of the domain and slowed growth at the posterior of the domain is due to relatively low local volumetric strain.
3.2. Parametric study predicts experimentally observed craniosynostosis
We conducted a parametric study to see the effects of variation of model parameters. For each of 6 non-dimensional parameters (A, B, G, D, αo, and φ), 9 levels of variation (from 0.2 to 1.8, with incremental of 0.2, times reference value) were tested and the results arranged in Fig. 5. Typical crania predicted in a range near the baseline values of parameters (blue brackets) imply our model is robust against minor molecular variation (individual variation of the normal condition). The model also predicts various phenotypes due to a major molecular change (mutation), including prematurely closing sutures (red brackets), an increase or decrease in the number of bones (green and cyan brackets) as in the formation of accessory or wormian bones, or in the cranial vaults of other species, and a decrease in size of specific bones (yellow brackets).
Fig. 5.
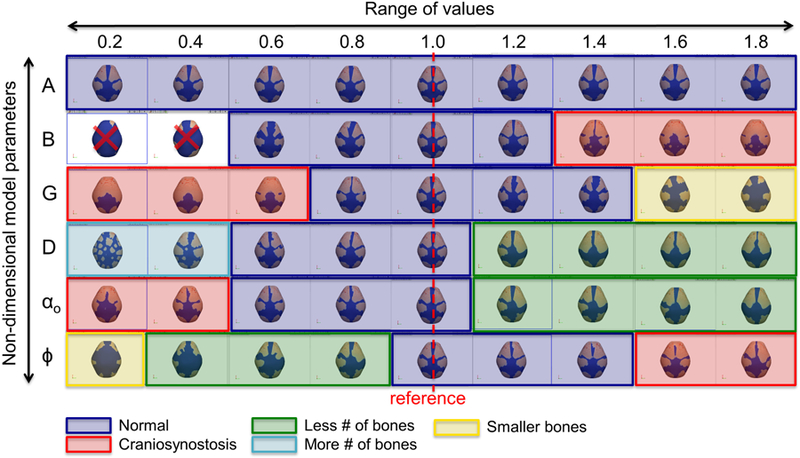
Result of parametric study. Various phenotypes including typical crania, prematurely closing sutures, an increase or decrease in the number of bones, and a decrease in size of bones are predicted.
Gdf 6 is a member of the bone morphogenetic protein (BMP) family and an appropriate candidate for activator in our model. Though BMPs promote bone formation, Gdf 6 knock-out embryos reveal differentiation of osteoblasts and bone formation in the coronal suture causing coronal suture fusion (Fig. 6a). We tested the ability of our model to reproduce this experimental observation by substituting Gdf 6 in the activator equation (Eq. (1)) of the model. Gdf 6 is expressed in mouse frontal bone primordia (Clendenning and Mortlock 2012), and is therefore controlled by αo that denotes the production of activator from osteoblast in the model. To simulate the Gdf 6−/− mouse, reference (2.0e4 [1/s]) is reduced (0.4e4 [1/s]), yielding a computational prediction of differentiated osteoblasts and eventual fusion of the coronal suture (Fig. 6b) that agrees with experimental observations (Fig. 6a).
Fig. 6.
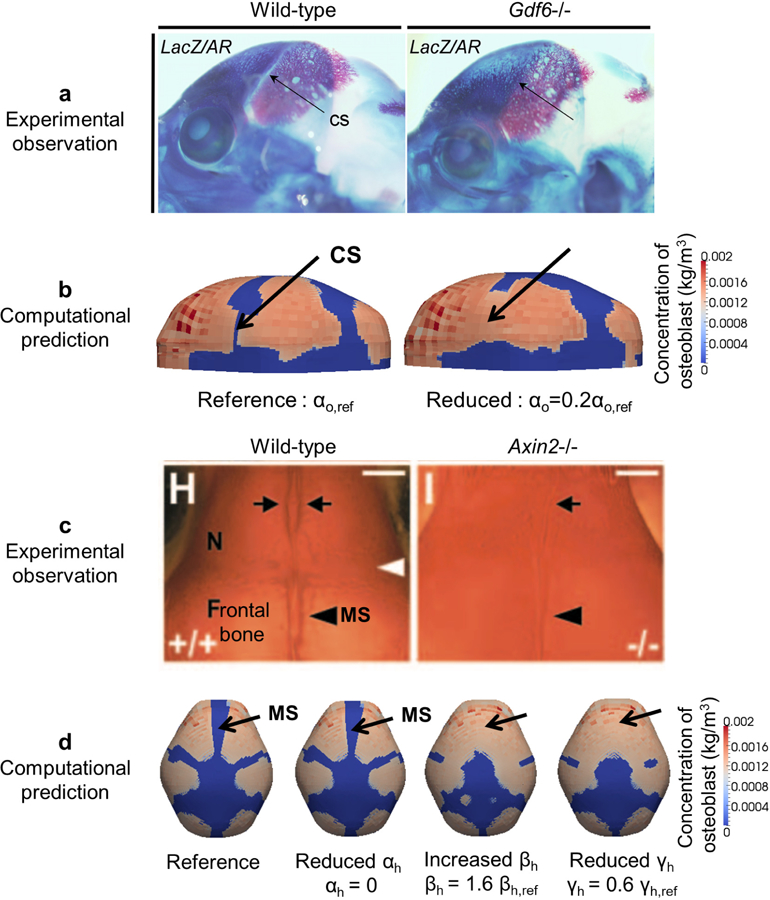
Comparison of experimental observations and predictions by the RDE model about cranial dysgenesis due to molecular variants. a Experimental observation of vault bones (stained by alizarin red) of a wild-type (WT) and Gdf 6−/− mouse. Lateral view, rostrum to left, eye at base of coronal suture (CS). CS is open in WT and closed in Gdf 6−/− mouse (adopted from Clendenning and Mortlock (2012)). b Computational prediction of distribution of osteoblasts with the reference value (left, CS patent) and the reduced value of αo (right, CS closed). c Experimental observation of alizarin-red stained cranial vault of WT and Axin2−/− mice (superior view, rostrum at top). Inter-nasal suture between arrows at top; metopic suture (MS) between frontal bones at bottom (adopted from Yu et al. (2005)). d Computational prediction of distribution of osteoblasts, forming bone, and morphology of MS with the reference value (far left), reduced value of αh, increased value of βh, and reduced value of γh.
Knock out of Axin2, a negative regulator of canonical Wnt pathways and therefore a member of the inhibitor group in our model, results in closure of the inter-frontal suture in mouse (Yu et al. 2005) (Fig. 6c). To adjust our model consistent with Axin2−/− mice, we modified model parameters related to the inhibitor by decreasing the production (αh), increasing the degradation (βh), and decreasing the interaction with activator (γh). The simulation results are consistent with experimental observations (Fig. 6c) showing inter-frontal suture fusion with changes of the parameters βh and γh (Fig. 6d). Changes in parameter αh does little to impact cranial vault morphology as shown in Fig. 5 where changes of the parameter A (αh/αa) across a wide range of values does not affect the typical cranial shape.
4. Discussion and Conclusions
Our model of cranial vault formation in the laboratory mouse corresponds largely with published experimental observations and current knowledge of the development of dermal bone. The number, location, and sequence of appearance of ossification centers in the simulation agree with current data, and with evidence that differentiating osteoblasts adding to the primary ossification centers come from the condensations, rather than being recruited from other mesenchymal populations surrounding the brain (Ting et al. 2009; Yoshida et al. 2008). Though our model does not include entrapment of osteoblasts into the mineralized matrix to become osteocytes, we consider the expansion of regions of high concentration of osteoblasts as representative of bone growth.
In the case of known human cranial vault disorders, there is a salient correspondence between our results and experimental findings pertaining to mechanisms underlying premature suture closure. Craniosynostosis, a relatively common congenital malformation, always involves the premature fusion of one or more of the cranial vault sutures and can include associated anomalies (Flaherty et al. 2016). The genetic and biomechanical basis for specific cases of craniosynostosis are the focus of current research (Al-Rekabi et al. 2016; Weickenmeier et al. 2017; Sewda et al. 2019). We evaluated our model by testing its ability to account for changes in vault development associated with known molecular variants (mutations) associated with craniosynostosis through a parametric study, where we adjusted model parameters according to published experiments. Clendenning and Mortlock (2012) concluded that Gdf 6 locally inhibits cell differentiation; a conclusion that contradicts previous studies and knowledge of Gdf 6 function. Importantly, our model implements the known function of Gdf 6 as a promoter of cell differentiation, one that interacts with the inhibitor to impede cell differentiation. The explanation proposed by our model is that low concentration of Gdf 6 reduces the concentration of inhibitor, allowing cell differentiation that leads to fusion of the coronal suture. Our explanation, including specific levels of inhibitor and timing of its variation, can be tested experimentally.
More broadly, we showed that changes in model parameters for most cases of computational craniosynostosis (Fig. 5, red brackets) match well with the reported experiments. For example, computational craniosynostosis occurs when the value of B is relatively large and the value of G is relatively small as occurs in cases where the interaction between Axin2 and Wnt is altered experimentally (Yu et al. 2005) and when the value of αo is relatively decreased as reported for the BMP ligand Gdf 6 (Clendenning and Mortlock 2012). Though our results match well with reported experiments where mutations on specific genes are associated with craniofacial malformations and disease, the source for many other craniofacial conditions remain unexplained. Given that the number of experiments that can be conducted with laboratory animals is finite, our approach provides a way to computationally test for the effects of specific genetic variants in given amounts across anatomical space and developmental time.
Many hypotheses pertaining to molecular changes associated with craniofacial disease can be generated from these data, but the model may be generalizable to larger questions of animal diversity. We know relatively little of the genetic mechanisms underlying the production of phenotypic diversity across evolutionary time. Since a finite set of families of genes shared by most animals regulate major aspects of body formation (Carroll et al. 2004), including organization of the vertebrate head, and substantial shifts in anatomy are accomplished by the regulation of genes in space and time over an individual’s lifetime, our model is potentially useful for questions of cranial vault evolution and for understanding the production of organismal differences across species.
The RDE model combines molecular and biomechanical regulation of cranial vault formation to predict the pattern of molecular signaling and cellular condensation that matches the positions of initial bone formation, patterns of cranial vault growth, and suture formation in experimental mice. Moreover, adjustment in model parameters consistent with experimental genetics reproduces sutural fusion seen in craniofacial disorders. Importantly, the multiscale computational framework that we introduce goes beyond enumerating specific cases and considers the emergent results of the hierarchical nature of genetic, cellular, and biomechanically driven coordination of cells and tissues applicable across species.
Our study reveals important inputs to formation of cranial vault bones, but we have not sought the identity of key molecular candidate pairs or the actual values of key parameters. The strength of our model lies in its generalizability as these details, when known for any specific case, can be used to tune the model to define and/or explore the function of certain parameters. Information provided by our model can facilitate targeted experiments designed to critically evaluate the role of specific molecular cues or cell behaviors on emergent 3-D cranial shapes. The structure of our model can be further modified by adding additional pairs of molecules (Marcon et al. 2016; Takagi and Kaneko 2002; Yang et al. 2002) when experiments implicate their identities.
Finally, we recognize that the primacy of either brain or skull in head development represents one of biology’s “chicken-and-the-egg” causality dilemmas, and that developing bones may influence the growing brain (Richtsmeier and Flaherty 2013). This can be resolved by a two-way coupling between brain and skull shape, where a non-linear viscoelastic medium represents a deformable brain on which volumetric expansion boundary conditions are applied. Further, the two-way coupling may expand our model to enable the study of differences in cranial vault morphology across vertebrate species, vault deformation caused by head constraint (e.g., intrauterine crowding), or change in the number and shape of bones and cranial vault sutures in the case of microcephaly or hydrocephalus. Importantly, our current model reveals that morphology, specifically change in morphology due to growth, is a fundamental mechanism of craniofacial development. Once refined, the model may help identify additional mechanisms underlying shape change in the evolution of the vertebrate skull and in craniofacial disease.
Acknowledgements
Computations for this research were performed on the Pennsylvania State University’s Institute for CyberScience Advanced CyberInfrastructure (ICS-ACI). We acknowledge Matthew Dolack for checking data on github.This work was supported in part through instrumentation funded by a National Science Foundation grant OCI0821527, a Burroughs-Wellcome Fund 2013 Collaborative Research Travel Grant, Pennsylvania Department of Health using Tobacco Cure Funds, and by the National Institutes of Health grants R01DE022988 and P01HD078233. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.Source code of the reaction-diffusion-strain model and an example case are available at https://github.com/PSUCompBio/skull-growth-modeling.
Appendix
A. Experimental data
High resolution micro-computed tomography (µCT) and magnetic resonance microscopy (MRM) images of embryonic mice serve as experimental data in our analyses. All use of mice was in compliance with animal welfare guidelines approved by the Pennsylvania State University Institutional Animal Care and Use Committees. µCT images with pixel size and slice thickness ranging from 0.0148 to 0.0168 mm were acquired by the Center for Quantitative Imaging at the Pennsylvania State University (http://eesl.iee.psu.edu/content/cqi) using the HD-600 OMNI-X high resolution X-ray computed tomography system (Varian Medical Systems, Inc., Lincolnshire, IL). Image data were reconstructed on a 1024 × 1024 pixel grid as a 16 bit tiff but were reduced to 8-bit for image analysis. Isosurfaces were reconstructed to represent all cranial bone at indicated ages based on hydroxyapatite phantoms imaged with the specimens using the software package Avizo 8.1.1 (FEI Company, Inc.). The minimum thresholds used to create the iso-surfaces ranged from 70 to 100 mg/cm3 partial density hydroxyapatite. MRM images were acquired by the High Field MRI Facility at the Pennsylvania State University (https://www.imaging.psu.edu/facilities/high-field). The fixed specimens were immersed in 2% Magnevist (Bayer Health Care, Wayne, NJ) phosphor-buffered solution (PBS) for 7–10 days depending upon the embryonic age of the specimen to reduce the T1 and T2 relaxation times. All MRM experiments were conducted on a vertical 14.1 Tesla Varian (Varian Inc., Palo Alto, CA) imaging system with direct drive technology. To prevent drying and to minimize magnetic susceptibility artifacts during scanning, specimens were immersed in fluorinert liquid, FC-43 (3M, St. Paul, MN). A standard imaging experiment with an isotropic resolution of 80 µm comprised a field of view of 15.4 × 14 × 11 mm3 and a matrix size of 192 × 132 (75% partial Fourier: 176) × 137. With eight averages and a repetition time of 75 ms (echo time 25 ms) the total scan time was 3 h. Matlab (The MathWorks, Inc., Natick, MA) was used for image post-processing. By zero-filling all directions by a factor of two, the pixel resolution of a standard imaging experiment was 40 µm3.
B. Assumption test
To test our assumptions and examine the effects of each in detail, we compare the simulation results of activator at E17.5 estimated using our computational model with and without each assumption (Fig. 7).
Fig. 7.
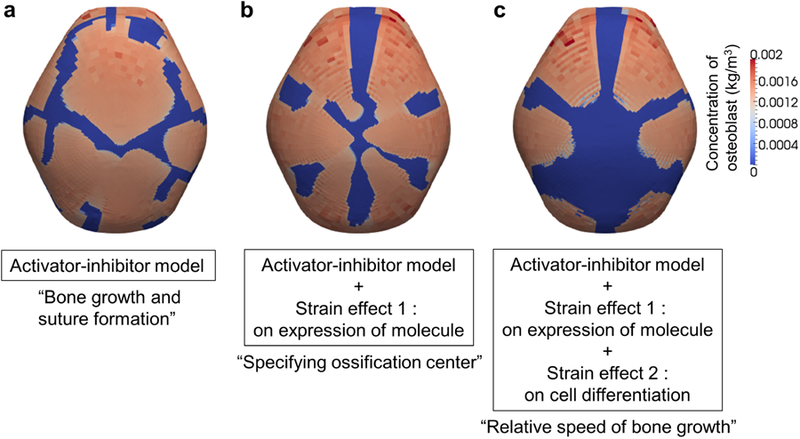
Distribution of osteoblasts at E17.5 from simulation results using various computational models. a Result using a model with only assumptions A1 and A2, without the assumption pertaining to mechanical effects. Bones grow and form sutures through reaction-diffusion process. b Result using a model with assumptions A1, A2, and only the assumption about the mechanical effect on production of activator (A3a). Locations of primary ossification centers are specified by the mechanical effect on the production of activator. c Result using a model with all assumptions A1, A2, and A3. Relative speed of bone growth is achieved by the mechanical effect on cell differentiation (A3b).
Figure 7a shows the results estimated using the model with only A1 and A2; mechanical effects on molecular expression and cell differentiation are not considered. As predicted, primary ossification centers form and bone grows from them with sutures forming between the bones. The effect of the inhibitor appears to play a role in suture formation. The number and locations of bones do not agree with experimental observations and reveal a disorganized pattern of bone formation. Figure 7b shows the results estimated using the model with only A1, A2, and A3a, excluding the assumption of the mechanical effect on cell differentiation. Six bones and associated sutures form in locations similar to our experimental observations as predicted. Consequently, the mechanical effect on the production of activator appears to play a role in specifying the number and location of the primary ossification centers. However, limiting the computation to these assumptions results in a similar growing speed across all bones so that their final volumes are similar, a result that does not match experimental observations. Figure 7c shows the result estimated using the model with all assumptions: A1, A2, A3a, and A3b. The results from the coupled model show that apical growth of the frontal and parietal bones is delayed, as observed in experimental animals. Moreover, growth of the inter-parietal bone is constrained superoinferiorly relative to the growth of the frontal and parietal bones, modeling what is observed in experimental data. The model reveals that localized restriction of growth of the interparietal is due to reduced accumulated volumetric strain apical to the bone (Fig. 4b). These results reveal the importance of local strain in determining the relative growing speed and final shape of each cranial vault bone.
Contributor Information
Chanyoung Lee, Department of Mechanical and Nuclear Engineering, Pennsylvania State University 341 Leonhard Building, University Park, PA 16802.
Joan T. Richtsmeier, Department of Anthropology, Pennsylvania State University 409 Carpenter Building, University Park, PA 16802
Reuben H. Kraft, Department of Mechanical and Nuclear Engineering, Pennsylvania State University 320 Leonhard Building, University Park, PA 16802
References
- Al-Rekabi Z, Cunningham ML, Sniadecki NJ (2016) Cell mechanics of craniosynostosis. ACS Biomaterials Science & Engineering 3(11):2733–2743, DOI 10.1021/acsbiomaterials.6b00557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aldridge K, Hill CA, Austin JR, Percival C, Martinez-Abadias N, Neuberger T, Wang Y, Jabs EW, Richtsmeier JT (2010) Brain phenotypes in two FGFR2 mouse models for Apert syndrome. Developmental dynamics : an official publication of the American Association of Anatomists 239(3):987–997, DOI 10.1002/dvdy.22218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aspenberg P, Jeppsson C, Economides AN (2001) The bone morphogenetic proteins antagonist noggin inhibits membranous ossification. Journal of Bone and Mineral Research 16(3):497–500, DOI 10.1359/jbmr.2001.16.3.497 [DOI] [PubMed] [Google Scholar]
- Bailón-Plaza A, van der Meulen MCH (2003) Beneficial effects of moderate, early loading and adverse effects of delayed or excessive loading on bone healing. Journal of biomechanics 36(8):1069–1077, DOI 10.1016/S0021-9290(03)00117-9 [DOI] [PubMed] [Google Scholar]
- Carroll S, Grenier J, Weatherbee S (2004) From DNA to diversity: molecular genetics and the evolution of animal design Blackwell Publishers, DOI 10.1093/jhered/esi101 [DOI] [Google Scholar]
- Carter DR, Blenman PR, Beaupré GS (1988) Correlations between mechanical stress history and tissue differentiation in initial fracture healing. J Orthop Res 6(5):736–748, DOI 10.1002/jor.1100060517 [DOI] [PubMed] [Google Scholar]
- Cheng H, Jiang W, Phillips FM, Haydon RC, Peng Y, Zhou L, Luu HH, An N, Breyer B, Vanichakarn P, Szatkowski JP, Park JY, He TC (2003) Osteogenic activity of the fourteen types of human bone morphogenetic proteins (BMPs). J Bone Joint Surg Am 85(8):1544–1552 [DOI] [PubMed] [Google Scholar]
- Clendenning DE, Mortlock DP (2012) The BMP ligand Gdf6 prevents differentiation of coronal suture mesenchyme in early cranial development. PloS one 7(5):e36,789, DOI 10.1371/journal.pone.0036789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flaherty K, Singh N, Richtsmeier JT (2016) Understanding craniosynostosis as a growth disorder. Wiley Interdisciplinary Reviews: Developmental Biology 5(4):429–459, DOI 10.1002/wdev.227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garzón-Alvarado Da, González A, Gutiérrez ML (2013) Growth of the flat bones of the membranous neurocranium: a computational model. Computer methods and programs in biomedicine 112(3):655–64, DOI 10.1016/j.cmpb.2013.07.027 [DOI] [PubMed] [Google Scholar]
- Geris L, Sloten JV, Oosterwyck HV (2010) Connecting biology and mechanics in fracture healing: an integrated mathematical modeling framework for the study of nonunions. Biomechanics and Modeling in Mechanobiology 9(6):713–724, DOI 10.1007/s10237-010-0208-8 [DOI] [PubMed] [Google Scholar]
- Gierer A, Meinhardt H (1972) A theory of biological pattern formation. Kybernetik 12(1):30–39 [DOI] [PubMed] [Google Scholar]
- Hall BK, Miyake T (2000) All for one and one for all: condensations and the initiation of skeletal development. Bioessays 22(2):138–147, DOI [DOI] [PubMed] [Google Scholar]
- Ikegame M, Ishibashi O, Yoshizawa T, Shimomura J, Komori T, Ozawa H, Kawashima H (2001) Tensile stress induces bone morphogenetic protein 4 in preosteoblastic and fibroblastic cells, which later differentiate into osteoblasts leading to osteogenesis in the mouse calvariae in organ culture. Journal of Bone and Mineral Research 16(1):24–32, DOI 10.1359/jbmr.2001.16.1.24 [DOI] [PubMed] [Google Scholar]
- Iseki S, Wilkie AOM, Heath JK, Ishimaru T, Eto K, Morriss-Kay GM (1997) Fgfr2 and osteopontin domains in the developing skull vault are mutually exclusive and can be altered by locally applied FGF2. Development 124(17):3375–3384 [DOI] [PubMed] [Google Scholar]
- Kawasaki K, Suzuki T, Weiss KM (2004) Genetic basis for the evolution of vertebrate mineralized tissue. Proceedings of the National Academy of Sciences of the United States of America 101(31):11,356–11,361, DOI 10.1073/pnas.0404279101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondo S, Shirota H (2009) Theoretical analysis of mechanisms that generate the pigmentation pattern of animals. Seminars in Cell and Developmental Biology 20(1):82–89, DOI 10.1016/j.semcdb.2008.10.008 [DOI] [PubMed] [Google Scholar]
- Lai TH, Fong YC, Fu WM, Yang RS, Tang CH (2008) Osteoblasts-derived BMP-2 enhances the motility of prostate cancer cells via activation of integrins. The Prostate 68(12):1341–1353, DOI 10.1002/pros.20799 [DOI] [PubMed] [Google Scholar]
- Lee C, Richtsmeier JT, Kraft RH (2017) A computational analysis of bone formation in the cranial vault using a coupled reaction-diffusion-strain model. Journal of Mechanics in Medicine and Biology 17(04):1750,073, DOI 10.1142/S0219519417500737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long F (2011) Building strong bones: molecular regulation of the osteoblast lineage. Nature reviews Molecular cell biology 13(1):27–38, DOI 10.1038/nrm3254 [DOI] [PubMed] [Google Scholar]
- Marcon L, Diego X, Sharpe J, Müller P (2016) High-throughput mathematical analysis identifies Turing networks for patterning with equally diffusing signals. eLife 5:e14,022, DOI 10.7554/eLife.14022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maul TM, Chew DW, Nieponice A, Vorp DA (2011) Mechanical stimuli differentially control stem cell behavior: morphology, proliferation, and differentiation. Biomech Model Mechanobiol 10(6):939–953, DOI 10.1007/s10237-010-0285-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motch Perrine SM, Stecko T, Neuberger T, Jabs EW, Ryan TM, Richtsmeier JT (2017) Integration of brain and skull in prenatal mouse models of Apert and Crouzon syndromes. Frontiers in Human Neuroscience 11:369, DOI 10.3389/fnhum.2017.00369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray JD (2002) Mathematical Biology : I. An Introduction, Third Edition, vol 17 Springer-Verlag New York, DOI 10.1007/b98868 [DOI] [Google Scholar]
- O’Leary DD, Chou SJ, Sahara S (2007) Area Patterning of the Mammalian Cortex. Neuron 56(2):252–269, DOI 10.1016/J.NEURON.2007.10.010 [DOI] [PubMed] [Google Scholar]
- Opperman LA (2000) Cranial sutures as intramembranous bone growth sites. Developmental Dynamics 219(4):472–485, DOI 10.1002/1097–0177(2000)9999:9999<::AID-DVDY1073>3.0.CO;2-F [DOI] [PubMed] [Google Scholar]
- Palomares KTS, Gleason RE, Mason ZD, Cullinane DM, Einhorn TA, Gerstenfeld LC, Morgan EF (2009) Mechanical stimulation alters tissue differentiation and molecular expression during bone healing. J Orthop Res 27(9):1123–1132, DOI 10.1002/jor.20863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perlman RL (2016) Mouse models of human diseaseAn evolutionary perspective. Evolution, medicine, and public health 2016(1):170–176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillarisetti A, Desai JP, Ladjal H, Schiffmacher A, Ferreira A, Keefer CL (2011) Mechanical phenotyping of mouse embryonic stem cells: increase in stiffness with differentiation. Cell Reprogramming 13(4):371–380, DOI 10.1089/cell.2011.0028 [DOI] [PubMed] [Google Scholar]
- Raspopovic J, Marcon L, Russo L, Sharpe J (2014) Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients. Science 345(6196):566–570, DOI 10.1126/science.1252960 [DOI] [PubMed] [Google Scholar]
- Rauch F, Lauzier D, Croteau S, Travers R, Glorieux FH, Hamdy R (2000) Temporal and spatial expression of bone morphogenetic protein-2, −4, and −7 during distraction osteogenesis in rabbits. Bone 27(3):453–459, DOI 10.1016/S8756-3282(00)00337-9 [DOI] [PubMed] [Google Scholar]
- Rice DPC, Åberg T, Chan YS, Tang Z, Kettunen PJ, Pakarinen L, Maxson RE, Thesleff I (2000) Integration of FGF and TWIST in calvarial bone and suture development. Development 127(9):1845–1855 [DOI] [PubMed] [Google Scholar]
- Richtsmeier JT, Flaherty K (2013) Hand in glove: brain and skull in development and dysmorphogenesis. Acta neuropathologica 125(4):469–89, DOI 10.1007/s00401-013-1104-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M, Ochi T, Nakase T, Hirota S, Kitamura Y, Nomura S, Yasui N (1999) Mechanical tension-stress induces expression of bone morphogenetic protein (BMP)-2 and BMP-4, but not BMP-6, BMP-7, and GDF-5 mRNA, during distraction osteogenesis. Journal of Bone and Mineral Research 14(7):1084–1095, DOI 10.1359/jbmr.1999.14.7.1084 [DOI] [PubMed] [Google Scholar]
- Sewda A, White S, Erazo M, Hao K, García-Fructuoso G, Fernández-Rodriguez I, Heuzé Y, Richtsmeier J, Romitti P, Reva B, Jabs E, Peter I (2019) Nonsyndromic craniosynostosis: novel coding variants. Pediatric Research DOI 10.1038/s41390-019-0274-2 [DOI] [PMC free article] [PubMed]
- Sidor CA (2001) Simplification as a trend in synapsid cranial evolution. Evolution 55(7):1419–1442, DOI 10.1111/j.0014-3820.2001.tb00663.x [DOI] [PubMed] [Google Scholar]
- Subramony SD, Dargis BR, Castillo M, Azeloglu EU, Tracey MS, Su A, Lu HH (2013) The guidance of stem cell differentiation by substrate alignment and mechanical stimulation. Biomaterials 34(8):1942–1953, DOI 10.1016/j.biomaterials.2012.11.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugimura K, Shimono K, Uemura T, Mochizuki A (2007) Self-organizing mechanism for development of space-filling neuronal dendrites. PLoS Comput Biol 3(11):e212, DOI 10.1371/journal.pcbi.0030212 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumanasinghe RD, Bernacki SH, Loboa EG (2006) Osteogenic differentiation of human mesenchymal stem cells in collagen matrices: effect of uniaxial cyclic tensile strain on bone morphogenetic protein (BMP-2) mRNA expression. Tissue engineering 12(12):3459–3465, DOI 10.1371/journal.pone.0120374 [DOI] [PubMed] [Google Scholar]
- Takagi H, Kaneko K (2002) Pattern dynamics of a multi-component reaction-diffusion system: differntiation of replicating spots. International Journal of Bifurcation and Chaos 12(11):2579–2598, DOI 10.1142/S0218127402006084 [DOI] [Google Scholar]
- Ting MC, Wu NL, Roybal PG, Sun J, Liu L, Yen Y, Maxson RE (2009) EphA4 as an effector of Twist1 in the guidance of osteogenic precursor cells during calvarial bone growth and in craniosynostosis. Development (Cambridge, England) 136(5):855–864, DOI 10.1242/dev.028605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turing AM (1952) The chemical basis of morphogenesis. Philosophical transactions of the royal society of London Series B, Biological sciences 237(641):37–72, DOI 10.1098/rstb.1952.0012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan DC, Pomerantz JH, Brunet LJ, Kim JB, Chou YF, Wu BM, Harland R, Blau HM, Longaker MT (2007) Noggin suppression enhances in vitro osteogenesis and accelerates in vivo bone formation. Journal of Biological Chemistry 282(36):26,450–26,459, DOI 10.1074/jbc.M703282200 [DOI] [PubMed] [Google Scholar]
- Wan M, Cao X (2005) BMP signaling in skeletal development. Biochemical and biophysical research communications 328(3):651–7, DOI 10.1016/j.bbrc.2004.11.067 [DOI] [PubMed] [Google Scholar]
- Weickenmeier J, Fischer C, Carter D, Kuhl E, Goriely A (2017) Dimensional, geometrical, and physical constraints in skull growth. Phys Rev Lett 118(24):248,101, DOI 10.1103/PhysRevLett.118.248101 [DOI] [PubMed] [Google Scholar]
- Westendorf JJ, Kahler RA, Schroeder TM (2004) Wnt signaling in osteoblasts and bone diseases. Gene 341:19–39, DOI 10.1016/j.gene.2004.06.044 [DOI] [PubMed] [Google Scholar]
- Yang L, Dolnik M, Zhabotinsky AM, Epstein IR (2002) Spatial resonances and superposition patterns in a reaction-diffusion model with interacting Turing modes. Phys Rev Lett 88(20):208,303, DOI 10.1103/PhysRevLett.88.208303 [DOI] [PubMed] [Google Scholar]
- Yoshida T, Vivatbutsiri P, Morriss-Kay G, Saga Y, Iseki S (2008) Cell lineage in mammalian craniofacial mesenchyme. Mechanisms of Development 125(9–10):797–808, DOI 10.1016/j.mod.2008.06.007 [DOI] [PubMed] [Google Scholar]
- Yu HMI, Jerchow B, Sheu TJ, Liu B, Costantini F, Puzas JE, Birchmeier W, Hsu W (2005) The role of Axin2 in calvarial morphogenesis and craniosynostosis. Development 132(8):1995–2005, DOI 10.1242/dev.01786 [DOI] [PMC free article] [PubMed] [Google Scholar]


