Positive reward prediction errors during decision making strengthen memory encoding

Abstract

Dopamine is thought to provide reward prediction errors signals to temporal lobe memory systems, but their role in episodic memory has not been fully characterized. We developed an incidental memory paradigm to 1) estimate the influence of reward prediction errors on formation of episodic memories, 2) dissociate this influence from surprise and uncertainty, 3) characterize the role of temporal correspondence between prediction error and memoranda presentation, and 4) determine the extent to which this influence is consolidation-dependent. We found that people encoded incidental memoranda more strongly when they gambled for potential rewards. Moreover, this strengthened encoding scaled with the reward prediction error experienced when memoranda were presented (and not before or after). This encoding enhancement was detectable within minutes and did not differ substantially after twenty-four hours, indicating that it is not consolidation-dependent. These results suggest a computationally and temporally specific role for reward prediction error signaling in memory formation.

Introduction

Behaviors are often informed by multiple kinds of memories. For example, a decision about what to eat for lunch might rely on average preferences that have been slowly learned over time and that aggregate over many previous experiences, but it might also be informed by specific, temporally precise memories (e.g., ingredients seen in the fridge on the previous day). These different kinds of memories prioritize distinct aspects of experience. Reinforcement learning typically accumulates information across relevant experiences to form general preferences that are used to guide behavior¹, whereas episodic memories allow access to details about specific, previously experienced events with limited interference from other, similar ones. Work from neuroimaging and computational modeling suggests that these two kinds of memories have different representational requirements and are likely subserved by anatomically distinct brain systems^2–4. In particular, a broad array of evidence suggests that reinforcement learning is implemented through cortico-striatal circuitry in the prefrontal cortex and basal ganglia^5–8 whereas episodic memory appears to rely on synaptic changes in temporal lobe structures, especially the hippocampus^9–15.

However, these two anatomical systems are not completely independent. Medial temporal areas provide direct inputs into striato-cortical regions^16–18, and both sets of structures receive shared information through common intermediaries^5–8,19. Furthermore, both systems receive neuromodulatory inputs that undergo context dependent fluctuations that can affect synaptic plasticity and alter information processing^20,21. Recent work in computational neuroscience has highlighted potential roles for neuromodulators, particularly dopamine, in implementing reinforcement learning. In particular, dopamine is thought to supply a reward prediction error (RPE) signal that gates Hebbian plasticity in the striatum, facilitating repetition of rewarding actions^5,6,22–24. In humans and untrained animals, dopamine RPE signals are observed in response to unexpected primary rewards¹⁷. But with experience, dopamine signals become associated with the the earliest cue predicting future reward⁵. Such cue-induced dopamine signals are thought to serve a motivational role²⁵, biasing behavior toward effortful and risky actions undertaken to acquire rewards^26–31.

While normative roles for dopamine have frequently been discussed in terms of their effects on reinforcement learning and motivational systems, such signals likely also affect processing in medial temporal lobe memory systems^32–36. For example, dopamine can enhance long term potentiation (LTP)³⁷ and replay³⁸ in the hippocampus, providing a mechanism to prioritize behaviorally relevant information for longer term storage³². More recent work using optogenetics to perturb hippocampal dopamine inputs revealed a biphasic relationship, whereby low levels of dopamine suppress hippocampal information flow but higher levels of dopamine facilitate it³⁵. Given that dopamine levels are typically highest during burst-firing of dopamine neurons³⁹, for instance during large RPEs⁵, this result suggests that memory encoding in the hippocampus might be enhanced for unexpectedly positive events.

However, despite strong evidence that dopaminergic projections signal RPEs^5,40,41 and that dopamine release in the hippocampus can facilitate memory encoding in non-human animals⁴², evidence for a positive effect of RPEs on memory formation in humans is scarce. Monetary incentives and reward expectation can be manipulated to improve episodic encoding, but it is not clear that such effects are driven by RPEs rather than motivational signals or reward value per se^21,33,43,44. The few studies that have closely examined the relationship between RPE signaling and episodic memory have yielded conflicting results about whether positive RPEs strengthen memory encoding^45–47. However, a number of technical factors could mask a relationship between RPEs and memory formation in standard paradigms. In particular, tasks typically have not controlled for salience signals, such as surprise and uncertainty, that can be closely related to RPEs and that may exert independent effects on episodic encoding through a separate noradrenergic neuromodulatory system^48–51. Thus, characterizing how RPEs, surprise, and uncertainty affect the strength of episodic encoding would be an important step toward understanding the potential functional consequences of dopaminergic signaling in the hippocampus.

Here, we combine a behavioral paradigm with computational modeling to clarify the impact of RPEs on episodic memory encoding, and to dissociate any RPE effects from those attributable to related computational variables such as surprise and uncertainty. Our goal was to better understand the relationship between reinforcement learning and episodic encoding at the computational level, which we hope will motivate future studies on the biological implementation of this link. Our paradigm required participants to view images during a learning and decision-making task before completing a surprise recognition memory test for the images. The task required participants to decide whether to accept or reject a risky gamble based on the value of potential payouts and the reward probabilities associated with two image categories, which they learned incrementally based on trial-by-trial feedback. Our design allowed us to measure and manipulate RPEs at multiple time points, and to dissociate those RPEs from other computational factors with which they are often correlated. In particular, our paradigm and computational models allowed us to manipulate and measure surprise and uncertainty, which have been shown to affect the rate of reinforcement learning^52,53 and the strength of episodic encoding⁴⁶. Again, surprise and uncertainty are closely related to RPEs in many tasks. However, they are thought to be conveyed through noradrenergic and cholinergic modulation^49,50,54, while RPEs are carried primarily by dopamine neurons⁵. We also assessed the degree to which relationships between encoding and each of these factors are consolidation-dependent by testing recognition memory either immediately post-learning or after a 24 hour delay.

Our results reveal that participants were more likely to remember images presented on trials in which they accepted the risky gamble. Moreover, the extent of this memory benefit scaled positively with the RPEs induced by the images. Notably, memory was not affected by RPEs associated with the reward itself (on either the previous or current trial), or by surprise or uncertainty. These results replicated in an independent sample, which also demonstrated sensitivity to counterfactual information about choices the participants did not make. Collectively, these data demonstrate a key role for RPEs in episodic encoding, clarify the timescale and computational nature of interactions between reinforcement learning and memory, and make testable predictions about the neuromodulatory mechanisms underlying both processes.

Results

The goal of this study was to understand how computational factors that govern trial-to-trial learning and decision-making impact episodic memory. To this end, we designed a two-part study that included a learning task (Fig. 1a–h) followed by a surprise recognition memory test (Fig. 1i).

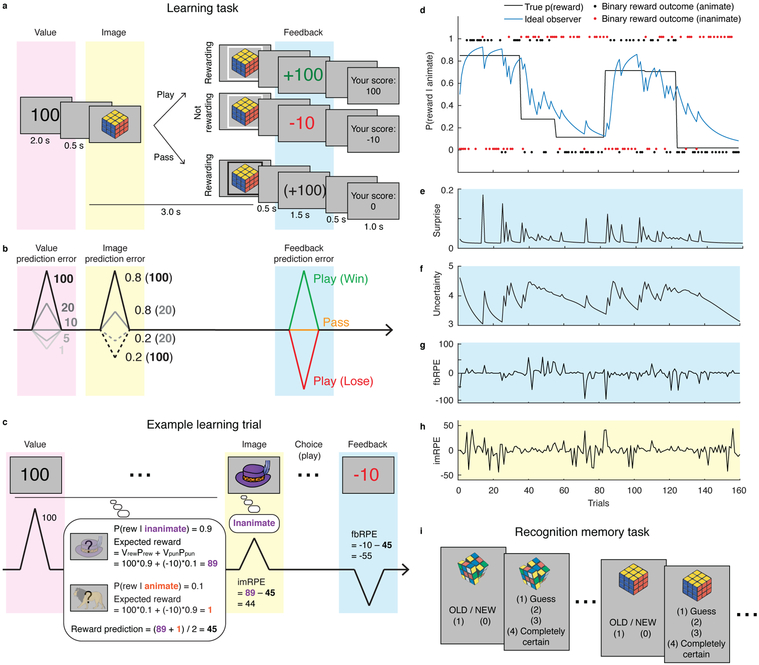
Figure 1.

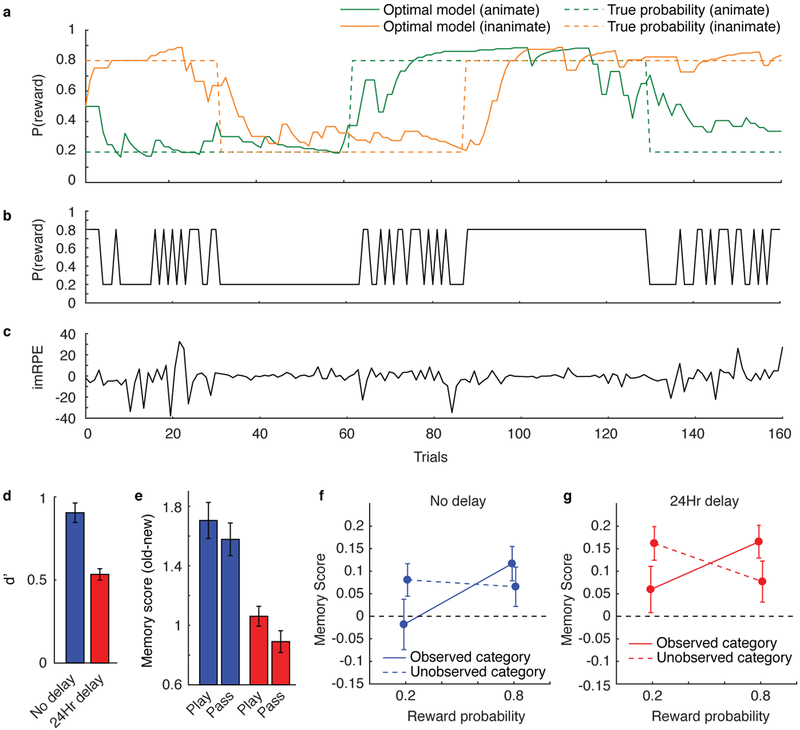
Dissociating effects of RPEs, surprise and uncertainty on incidental memory encoding. a, Task: On each trial, participants were first shown the value of a successful gamble for the current trial (e.g. 100). Next, a unique image belonging to one of two categories (animate/inanimate) was shown, which indicated the probability of reward. Participants made a play or pass decision. Then, participants were shown their earnings if they played (top and middle rows), or shown the hypothetical trial outcome if they passed (bottom row). At the end of each trial a cumulative total score was displayed. b, Manipulation of RPEs before, during, and after image presentation. For the image prediction error, we show example probabilities (0.8 and 0.2), and values (100 and 20). c, Types of RPE: The value RPE signals how the current value is better or worse than what is expected on average (10). The image RPE is computed as the difference between the expected reward of the current image category (e.g., 89) and the reward prediction, computed as the average expected reward of the two image categories (e.g., 45). The expected rewards are computed using the values and probabilities for reward/punishment (value: V_rew, V_pun, probability: P_rew, P_pun). The feedback RPE is computed as the difference between the expected and experienced outcomes. d, Model predictions: Reward probabilities were determined by image category, yoked across categories (i.e., p(rew | animate) = 1 – p(rew | inanimate)), and reset occasionally to require learning (solid black line). Binary outcomes (red/black dots), governed by these reward probabilities, were used by an ideal observer model to infer the underlying reward probabilities (blue line). e-g, Inputs to ideal observer model. The ideal observer learned in proportion to the surprise associated with a given trial outcome (e) and the uncertainty about its estimate of the current reward probability (f), both dissociable from RPE signals at time of feedback (g) and image presentation (h). Surprise is a probability, and uncertainty is measured in units of nats. i, Recognition memory: in a surprise recognition test, participants provided a binary answer (“old” or “new” image) and a 1–4 confidence rating.

On each trial of the task, participants decided whether to accept (“play”) or reject (“pass”) an opportunity to gamble based on the potential reward payout. The magnitude (value) of the potential reward was shown at the start of each trial (Fig. 1a, pink shading), whereas the probability that this reward would be obtained was signaled by a trial-unique image that belonged to one of two possible categories: animate or inanimate (Fig. 1a, yellow shading). Each image category was associated with a probability of reward delivery, which was yoked across categories such that p(rew|animate) = 1 – p(rew|inanimate) (these were decoupled in Experiment 2). Participants were not given explicit information about the reward probabilities and thus had to learn them through experience. They were instructed to make a play or pass decision during the three-second presentation of the trial-unique image and, after a brief delay, were shown feedback indicating the payout (Fig. 1a, blue shading). Informative feedback was provided on all trials, irrespective of play/pass decision, thereby allowing participants to learn the reward probabilities associated with each image category.

Thus, each trial involved three separate times at which expectations could be violated, yielding three distinct RPEs. At the beginning of each trial, participants were cued about the magnitude of reward at stake. On trials where larger rewards were at stake, participants stood to gain more than on most other trials, potentially leading to a positive RPE at this time (Fig. 1b, pink shading). This earliest PE is referred to as a “value RPE”, because it is elicited by the value of the potential payout of the trial relative to the average trial.

Next, when the image was presented, its category signaled the probability of reward delivery, yielding an “image RPE” relative to the reward probability of the average trial. On trials featuring images from the more frequently rewarded category, participants should raise their expectations about the likelihood of receiving a reward, leading to a positive image RPE (Fig. 1b, yellow shading). By contrast, on trials featuring images from the less frequently rewarded category, reward expectations should decrease below the mean, leading to a negative image RPE. For instance, if the reward probability was high for the animate category and low for the inanimate category, seeing an animate image should lead to a positive RPE, whereas seeing an inanimate image should lead to a negative image RPE.

Finally, feedback at the end of each trial indicated whether or not a reward was delivered and, if so, how large it was. This was expected to elicit another “feedback” RPE (Fig. 1b, blue shading). In summary, the paradigm elicits value, image, and feedback RPEs on each trial (Fig. 1c), allowing us to determine how each contributed to variation in incidental encoding of the images.

In addition to permitting dissociations among these three distinct RPEs, the paradigm can be used to distinguish RPEs from related computational factors. Specifically, although value RPEs were driven by the actual trial values, the other RPEs depended critically on task dynamics, which were manipulated via change-points at which reward probabilities were resampled uniformly, forcing participants to update their expectations throughout the task (Fig. 1d). This allowed for the dissociation of RPEs from surprise (how unexpected an outcome is) and uncertainty (about the underlying probabilities). All three factors were computed using a Bayesian ideal observer model that learned from the binary task outcomes while taking into account the possibility of change-points (see Methods; Bayesian ideal observer model). Qualitatively, surprise spiked at improbable outcomes, including—but not limited to—those observed after change-points (Fig. 1e); uncertainty changed more gradually and was typically highest during periods following surprise (i.e., when outcomes are volatile, one becomes more uncertain about the underlying probabilities; Fig. 1f); and feedback RPEs were highly variable across trials and related more to the probabilistic trial outcomes than to transitions in reward structure (Fig. 1g). Each of these computations was distinct from the image RPEs, which depended on the image categories (i.e., category signaling high versus low reward probability) more than on task dynamics (Fig. 1h).

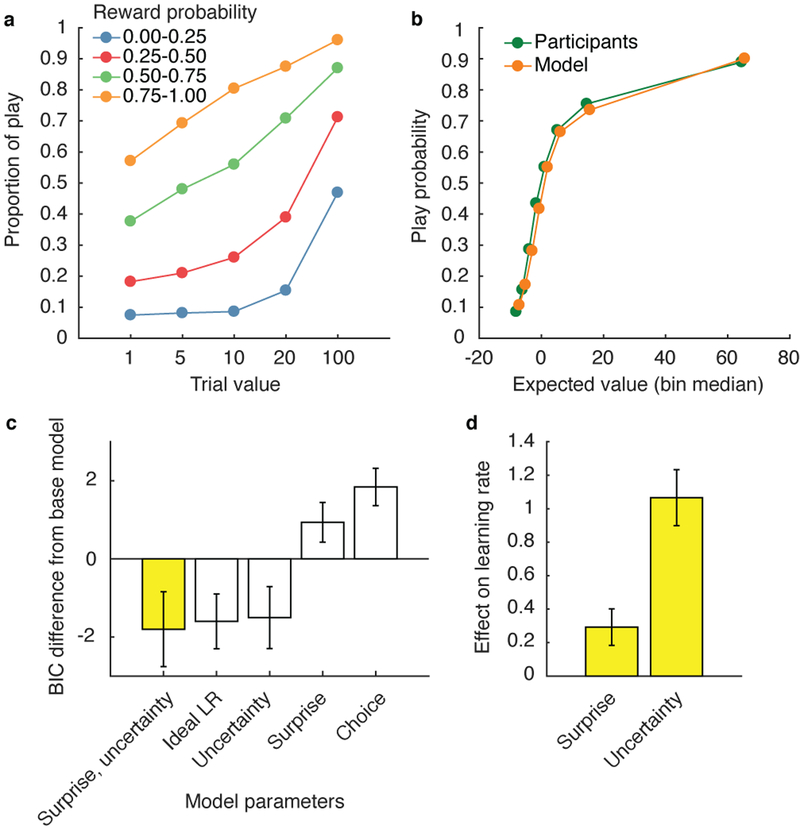
Analysis of data from 199 participants who completed the task online indicates that they (1) integrated reward probability and value information and (2) utilized RPEs, surprise, and uncertainty to gamble effectively. Participants increased the proportion of play (gamble) responses as a function of both trial value and the category-specific reward probability (Fig. 2a). To capture trial-to-trial dynamics of subjective probability assessments, we fit the play/pass behavior from each participant with a set of reinforcement learning models. The simplest such model fit betting behavior as a weighted function of reward value and probability, with probabilities updated on each trial with a fixed learning rate. More complex models (see Methods: RL model fitting) considered the possibility that this learning rate is adjusted according to other factors such as surprise, uncertainty, or choice. Consistent with previous work^50,53,55,56, the best fitting model adjusted learning rate according to normative measures of both surprise and uncertainty (Fig. 2b,c). Coefficients describing the effects of surprise and uncertainty on learning rate were positive across participants (Fig. 2d; surprise: two tailed t(199) = 2.34, P = 0.020, d = 0.17, 95% CI: 0.041–0.48; uncertainty: t(199) = 6.47, P < 0.001, d = 0.46, 95% CI: 0.74–1.39). In other words, in line with prior findings⁵³, participants were more responsive to feedback that was surprising or provided during a period of uncertainty. Thus, surprise and uncertainty scaled the extent to which feedback RPEs were used to adjust subsequent behavior.

Figure 2.

Participants’ behavior indicates an integration of reward value and subjective reward probability estimates, which were updated as a function of surprise and uncertainty (N = 199). a, Proportion of trials in which the participants chose to play, broken down by reward value and reward probability. b, Participant choice behavior and model-predicted choice behavior. The model with the lowest Bayesian information criterion (BIC), which incorporated the effects of surprise and uncertainty on learning rate, was used to generate model behavior (yellow bars in c, d). Expected rewards for all trials were divided into 8 equally sized bins for both participant and model-predicted behavior. c, BIC of five reinforcement learning models with different parameters that affect learning rate. d, Mean maximum likelihood estimates of surprise and uncertainty parameters of the best fitting model (first bar in c). Error bars indicate standard error across participants.

Participants completed a surprise memory test either five minutes (no delay, n = 109) or twenty-four hours (24 hour delay, n = 90) after the learning task. During the test, participants saw all of the “old” images from the learning task along with an equal number of semantically matched “new” foils that were not shown previously. Participants provided a binary response indicating whether each image was old or new, plus a 1–4 confidence rating (Fig. 1i).

Participants in both delay conditions reliably identified images from the learning task with above chance accuracy (Fig. 3a; mean(sem) d’ = 0.85(0.042), t(108) = 20.3, P < 0.001, d = 1.94, 95% CI: 0.77–0.93 for no delay and 0.51(0.032), t(90) = 15.9, P < 0.001, d = 1.94, 95% CI: 0.45–0.57 for 24 hour delay condition). Memory accuracy was better when participants expressed higher confidence (confidence of 3 or 4) versus lower confidence (confidence of 1 or 2; t(93) = 13.8, P < 0.001, d = 1.30, 95% CI: 0.64–0.86 for no delay and t(83) = 9.95, P < 0.001, d = .06, 95% CI: 34–0.51 for 24 hour delay).

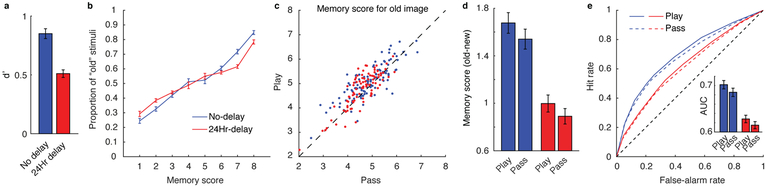
Figure 3.

Dependence of recognition memory strength on gambling behavior. a, Average d’ for the two delay conditions (no delay, N = 109; 24hr delay, N = 90). b, Average proportion of image stimuli that were “old” (presented during the learning task), separated by memory score. c, Mean memory score of “old” images for play vs. pass trials. Each point represents a unique participant. A majority of participants lie above the diagonal, indicating better memory performance for play trials. d, Mean pairwise difference in memory score between the “old” images and their semantically-matched foil images. e, ROC curves for play vs. pass trials. Area under the ROC curves (AUC) is shown in the inset. AUC was greater for play versus pass trials, indicating better detection of old vs. new images for play trials compared to pass trials. Error bars indicate standard error across participants. Colors indicate time between encoding and memory testing; blue = no delay, red = 24 hour delay.

To aggregate information provided in the binary reports and confidence ratings, we transformed these into a single 1–8 memory score, such that 8 reflected a high confidence “old” response and 1 reflected a high confidence “new” response. As expected, the true proportion of “old” images increased with higher memory scores, in a monotonic and roughly linear fashion across both delays (Fig. 3b). Thus, participants formed lasting memories of the images, and the memory scores provided a reasonable measure of subjective memory strength.

Recognition memory depended critically on the context in which the images had been presented. Memory scores were higher for images shown on trials in which the participants gambled (play) versus passed (Fig. 3c and Supplementary Fig. 1). Furthermore, the difference between memory scores for old versus new items was larger for play versus pass trials (t(199) = 3.30, P = 0.001, d = 0.23, 95% CI: 0.049–0.20) and this did not differ across delay conditions (t(198) = 0.41, P = 0.69, d = 0.058, 95% CI: −0.12–0.18) (Fig. 3d). Higher memory scores were produced, at least in part, by increased memory sensitivity. Across all possible memory scores, hit rate was higher for play versus pass trials, and the area under the receiver operating characteristic (ROC) curves was greater for play versus pass trials (Fig. 3e; t(199) = 3.53, P < 0.001, d = 0.25, 95% CI: 0.0066–0.023). We found no evidence that this play versus pass effect differed across delay conditions (t(198) = 0.36, P = 0.72, d = 0.051, 95% CI: −0.014–0.020).

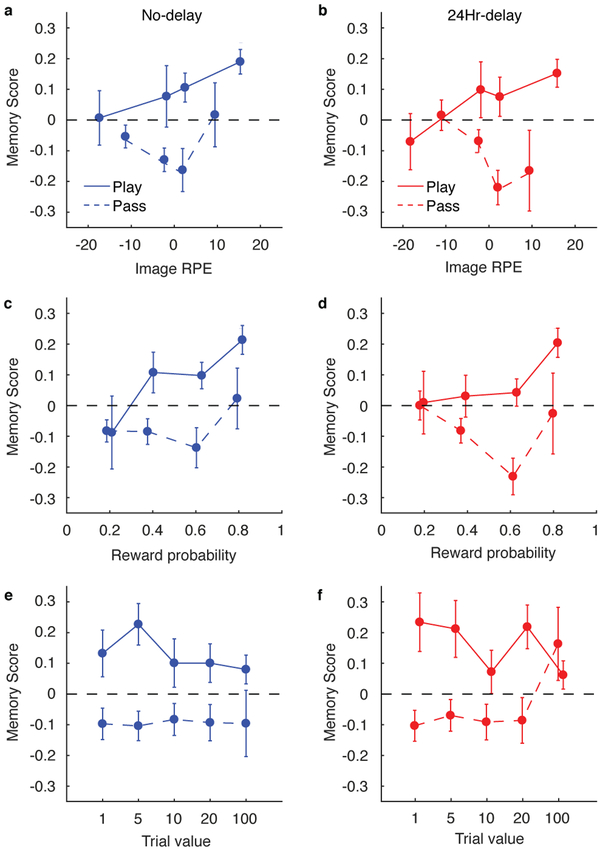
Next, we tested whether this memory enhancement could be driven by positive image RPEs (Fig. 1h), which would motivate play decisions (Fig. 2a). Indeed, the degree of memory enhancement on play trials depended on the magnitude of the image RPE. Specifically, memory scores on play trials increased as a function of the image RPE (Fig. 4a,b; t(199) = 4.33, P < 0.001, d = 0.31, 95% CI: 0.0032–0.0086), with no evidence of a difference between the delay conditions (t(198) = −0.11, P = 0.92, d = −0.015, 95% CI: −0.0057–0.0051). Moreover, this effect was most prominent in participants whose gambling behaviors were sensitive to trial-to-trial fluctuations in probability and value (Spearman’s ρ = 0.17, 95% CI: 0.033–0.30, P = 0.016, N = 200; see Methods; Descriptive analysis).

Figure 4.

Dependence of recognition memory strength on the RPE at time of image presentation, but not trial value. a,b, Positive association between subsequent recognition memory and RPE during image presentation for both no delay (a; blue) and 24 hour delay (b; red) conditions (no delay, N = 109; 24hr delay, N = 90). c-f, Positive association of recognition memory with reward probability estimates (c,d), but not with reward value (e,f) associated with the image. This suggests that the RPE that occurs during image presentation, but not the overall value of the image, is driving the subsequent memory effect. Error bars indicate standard error across participants. Colors indicate time between encoding and memory testing; blue = no delay, red = 24 hour delay.

To better understand this image RPE effect, we explored the relationship between memory score and the constituent components of the image RPE signal. The image RPE depends directly on the probability of reward delivery cued by the image category relative to the average reward probability. By contrast, variations in trial value should not directly affect the image RPE, because the participant already knows the trial value when the image is displayed. In other words, the participant knows the potential payoff—the value—at the outset of the trial (“I could win 100 points!”), but the probability information carried by the image can elicit either a strong positive (“and I almost certainly will win”) or negative (“But I probably won’t win”) image RPE.

Consistent with this conceptualization, subsequent memories were stronger for play trials in which the image category was associated with a higher reward probability (Fig. 4c,d; t(199) = 4.38, P < 0.001, d = 0.31, 95% CI: 0.25–0.67), but not for play trials with higher potential outcome value, which if anything were associated with slightly lower memory scores (Fig. 4e,f; t(199) = −1.99, P = 0.048, d = −0.14, 95% CI: −0.0020–0.0000). Reward probability effects were stronger in participants who displayed more sensitivity to probability and value in the gambling task (Spearman’s ρ = 0.18, 95% CI: 0.044–0.31, P = 0.010, N = 200).

To rule out the possibility that the effect of image RPE on subsequent memory is driven by a change in response bias rather than an increase in stimulus-specific discriminability, we repeated the same analysis using corrected recognition scores (hit rate – false alarm rate), rather than our memory score, as the metric for recognition memory. We found a positive effect of image RPE on corrected recognition, consistent with the idea that positive image RPEs enhancement memory accuracy rather than causing a shift in the decision criterion (t(199) = 2.04, P = 0.045, d = 0.14, 95% CI: 0.0000–0.0015; Supplementary Fig. 2).

Lastly, we tested for an effect of reward uncertainty on memory, noting that uncertainty about the trial outcome is greater at probabilities near 0.5 than for probabilities near 0 or 1. We found no effect of reward uncertainty on memory (Supplementary Fig. 3).

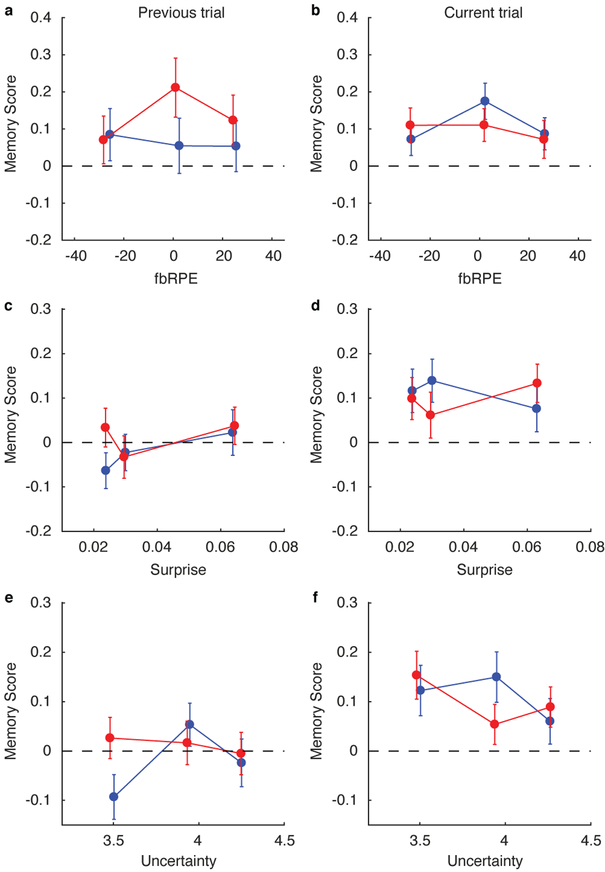
We found no evidence for an effect of feedback RPE, uncertainty, or surprise on subsequent memory. There was no evidence that memory scores were systematically related to the feedback RPE experienced either on the trial preceding image presentation (Fig. 5a; t(199) = −0.93, P = 0.36, d = −0.065, 95% CI: −0.0043–0.0016) or immediately after image presentation (Fig. 5b; t(199) = −1.26, P = 0.21, d = −0.089, 95% CI: −0.0021–0.0005). Similarly, we found no evidence that the surprise and uncertainty associated with feedback preceding (surprise: Fig. 5c and Supplementary Fig. 4, t(199) = 0.99, P = 0.32, d = 0.070, 95% CI: −0.97–2.94; uncertainty: Fig. 5e, t(199) = −0.82, P = 0.42, d = −0.058, 95% CI: −0.17–0.071) or following (surprise: Fig. 5d; t(199) = 1.53, P = 0.13, d = 0.11, 95% CI: −0.42–3.32, uncertainty: Fig. 5f; t(199) = −0.67, P = 0.51, d = −0.047, 95% CI: −0.18–0.091) image presentation were systematically related to subsequent memory scores, despite the fact that participant betting behavior strongly depended on both factors (Fig. 2c).

Figure 5.

No association between subsequent memory and RPE (a,b), surprise (c,d), or uncertainty (e,f) during the feedback phase of either the previous (a,c,e) or current trial (b,d,f). See Methods: Bayesian ideal observer model. Error bars indicate standard error across participants. Colors indicate time between encoding and memory testing; blue = no delay, red = 24 hour delay (no delay, N = 109; 24hr delay, N = 90).

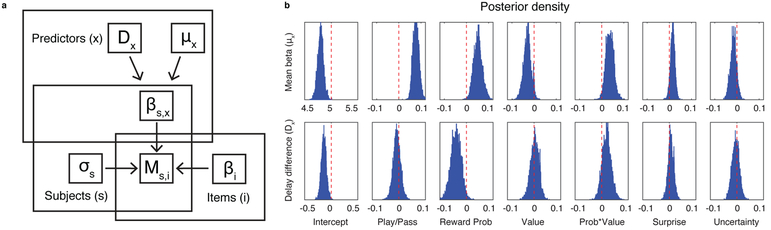
To better estimate the contributions of learning-related computations to subsequent memory strength, we constructed a hierarchical regression model capable of 1) pooling information across participants and delay conditions in an appropriate manner, 2) estimating the independent contributions of each factor while simultaneously accounting for all others, and 3) accounting for the differences in memory scores attributable to the images themselves. The hierarchical regression model attempted to predict memory scores by estimating coefficients at the level of images and participants, as well as estimating the mean parameter value over participants and the effect of delay condition for each parameter (Fig. 6a).

Figure 6.

Hierarchical regression model, which reveals effects of choice and positive RPEs on recognition memory encoding (N = 199). a: Graphical depiction of the hierarchical regression model. Memory scores for each participant and item (M_s,i) were modeled as normally distributed with participant specific variance (σ_s) and a mean that depended on the sum of two factors: 1) participant level predictors related to the decision context in which an image was encountered (i.e., whether the participant played or passed) linearly weighted according to coefficients (β_s,x) and 2) item level predictors specifying which image was shown on each trial and weighted according to their overall memorability across participants (β_i). Coefficients for participant level predictors were assumed to be drawn from a global mean value for each coefficient (μ_x) plus an offset related to the delay condition (D_x). Parameters were weakly constrained with priors that favored mean coefficient values near zero and low variance across participant and item specific coefficients. b: Posterior probability densities for mean predictor coefficients (μ_x; top row) and delay condition parameter difference (D_x; bottom row), estimated through MCMC sampling over the graphical model informed by the observable data (M_s,i).

Consistent with the results presented thus far, the hierarchical regression results support the notion that encoding was strengthened by the decision to gamble (play vs. pass) and by image RPEs, but not by the computational factors that controlled learning rate (surprise and uncertainty). Play trials were estimated to contribute positively to encoding, as indexed by uniformly positive values for the posterior density on the play/pass parameter (Fig. 6b top row of column 2; mean [95% CI] play coefficient = 0.078 [0.05, 0.1]; Supplementary Table 1). The reward probability associated with the displayed category was positively related to subsequent memory on play trials (Fig. 6b column 3; mean [95% CI] probability coefficient = 0.047 [0.01, 0.08]; Supplementary Table 1), as was its interaction with value (Fig. 6b column 5; mean [95% CI] probability*value coefficient = 0.042 [0.01, 0.07]; Supplementary Table 1). However, there was no reliable effect of value itself and, if anything, there was a slight trend toward stronger memories for lower trial values (Fig. 6b column 4; mean [95% CI] value coefficient = −0.03 [−0.05, 0.0001]; Supplementary Table 1); this did not replicate in our second experiment (see Experiment 2 below). The direction of the interaction between value and probability suggests that participants were more sensitive to image probability on trials in which there were more points at stake, consistent with a memory effect that scales with the image RPE (Fig. 1b, yellow shading). All observed effects were selective for old images viewed in the learning task, as the same model fit to the new, foil images yielded coefficients near zero for every term (Supplementary Fig. 5). Consistent with our previous analysis, coefficients for the uncertainty and surprise terms were estimated to be near zero (Fig. 6b rightmost columns; mean [95% CI] surprise and uncertainty coefficients = 0.012 [−0.01, 0.03] and −0.019 [−0.04, 0.01], respectively; Supplementary Table 1).

The model allowed us to examine the extent to which any subsequent memory effects required a consolidation period. In particular, any effects on subsequent memory that were stronger in the 24hr delay condition versus the immediate condition might reflect an effect of post-encoding processes. Despite evidence from animal literature that dopamine can robustly affect memory consolidation (e.g., Bethus et al., 2010), we did not find strong support for any of our effects being consolidation-dependent (note lack of positive coefficients in bottom row of Fig. 6b, which would indicate effects stronger in the 24 hour condition). As might be expected, participants in the no delay condition tended to have higher memory scores overall (Fig. 6b bottom of column 1; mean [95% credible interval] delay effect on memory score = −0.14 [−0.23, −0.05]; Supplementary Table 1), but their memory scores also tended to change more as a function of reward probability (Fig. 6b bottom of column 3; mean [95% credible interval] delay effect on probability modulation = −0.043 [−0.07, −0.01]; Supplementary Table 1) than did the memory scores of their counterparts in the 24hr delay condition. These results reveal the expected decay of memory over time, and suggest that the image RPEs were associated with an immediate boost in memory accuracy that decays over time.

It is possible that these memory effects may have been driven, at least in part, by anticipatory attention. Specifically, participants may have entered a heightened state of attention on play trials with large image RPEs, as they may have been eagerly anticipating feedback on such trials. While our paradigm did not include a direct measure of attention, we can address this question by determining which factors modulate the effect of feedback on trial-to-trial choice behavior. If a change in anticipatory attention affects the degree to which images are encoded in episodic memory, this increased attention should also lead to an increased effect of feedback on subsequent choice behavior. To test this account, we extended the best fitting behavioral model such that the learning rate could be adjusted on each trial according to the choice (play vs. pass) made on that trial as well as the image RPE received on play trials. Addition of these terms worsened the model fit (Supplementary Fig. 6a; t(199) = −7.40, P < 0.001, d = −0.52, 95% CI: −2.28 to −1.32), providing no evidence that choices or image RPEs influence the degree to which feedback influence subsequent choice. However, parameter fits within this model revealed a tendency for participants to learn more from feedback on play trials than on pass trials (Supplementary Fig. 6b; mean beta = 0.23, t(199) = 2.57, P = 0.011, d = 0.18, 95% CI: 0.054–0.41), whereas it revealed no consistent effect of image RPEs on feedback-driven learning (Supplementary Fig. 6b; mean beta = 0.16, t(199) = 1.29, P = 0.20, d = 0.091, 95% CI: −0.84–0.40). These analyses suggest that anticipatory attention likely mediated our play/pass effects at least to some degree, but they do not provide any evidence for a role of anticipatory attention in modulating the memory benefits conferred by large image RPEs.

In summary, behavioral data and computational modeling reveal important roles for surprise, uncertainty and feedback RPEs during learning. However, only decisions to gamble (play) and image RPEs influenced subsequent memory. The memory benefits conferred by gambling and high image RPEs were consolidation independent. To better understand the image RPE effect, and to ensure the reliability of our findings, we conducted a second experiment.

Experiment 2

Our previous findings suggested that variability in the strength of memory encoding was related to computationally-derived image RPEs and the gambling behavior that elicited them. However, the yoked reward probabilities in Experiment 1 ensured that the reward probabilities associated with the presented and not-presented image categories were perfectly anti-correlated on every trial. Thus, while an image from the high probability reward category would increase the expected value and hence elicit a positive image RPE, we could not determine if this was driven directly by the reward probability associated with the presented image category, the counterfactual reward probability associated with the alternate category, or—as might be predicted for a true prediction error—their difference. To address this issue, we conducted an experiment in which expectations about reward probability were manipulated independently on each trial, allowing us to distinguish between these alternatives.

In the new learning task, the reward probabilities for the two image categories were independently manipulated. Thus, during some trials both categories were associated with a high reward probability, on others both were associated with a low reward probability, and on yet others one was high and one was low (Fig. 7a,b). In this design, RPEs are relatively small when the reward probabilities are similar across image categories but deviate substantially when the reward probabilities differ across the image categories (Fig. 7c). Thus, if the factor boosting subsequent memory is truly an RPE, it should depend positively on the reward probability associated with the observed image category, but negatively with the reward probability associated with the other (unobserved) category.

Figure 7.

Task structure and results from Experiment 2. which allowed us to separately estimate the effects of both the observed and unobserved category probabilities on subsequent memory recall. a, Example task structure and model predictions. In the new learning task, the true reward probabilities of the two categories were independent, and restricted to either 0.2 or 0.8. The task contained at least one block (constituting at least 20 trials) of the four possible reward probability combinations (0.2/0.2, 0.2/0.8, 0.8/0.2, 0.8/0.8). b, Trial-by-trial reward probability, showing stretches of stable reward probability (0.2/0.2, 0.8/0.8), or varying reward probability (0.2/0.8, 0.8/0.2). c, The variability of image RPE, influenced by the reward probability conditions shown in b. d, Average d’ for both delay conditions (no delay, N = 93; 24hr delay, N = 81). e, Mean pairwise difference in memory score between the “old” images and their semantically-matched foil images. f,g, Interaction between image category and reward probability. There is a positive association between recognition memory and the reward probability of the currently observed image category, and a negative association between memory and the reward probability of the other, unobserved image category. Error bars indicate standard error across participants. In d-g, colors indicate time between encoding and memory testing; blue = no delay, red = 24 hour delay.

A total of 174 participants completed Experiment 2 (no delay, n = 93; 24 hour delay, n = 81) online. Participants in both conditions reliably recognized images from the learning task with above chance accuracy (Fig. 7d; mean(sem) d’ = 0.90(0.058), t(90) = 15.5, P < 0.001, d = 1.62, 95% CI: 0.79–1.02 for no delay and d’ = 0.53(0.035), t(81) = 15.4, P < 0.001, d = 1.62, 95% CI: 0.46–0.60 for 24 hour delay condition). We also observed a robust replication of the effect of gambling behavior on memory, as recognition accuracy was significantly better for images from play versus pass trials (Fig. 7e; t(173) = 3.93, P < 0.001, d = 0.30, 95% CI: 0.078–0.24). As in Experiment 1, we found no evidence that this effect differed by delay, t(172) = −0.31, P = 0.76, d = −0.047, 95% CI: −0.18–0.13).

The new experimental design permitted analysis of variability in memory scores for each old image as a function of its category’s reward probability (“image category”) versus the reward probability associated with the other, counterfactual category (“other category”). Based on the image RPE account, we expected to see positive and negative effects on memory for the image category and other category, respectively. Indeed, for both delays there was a cross-over effect whereby memory scores scaled positively with the reward probability associated with the image category (Fig. 7f,g t(173) = 2.38, P=0.019, d = 0.18, 95% CI: 0.043–0.46), but negatively with the reward probability associated with the other category (t(173) = −2,45, P=0.015, d = −0.19, 95% CI: −0.43– −0.046). These effects did not differ by delay (image category, t(172) = 0.27, P = 0.79, d = 0.041, 95% CI: −0.36–0.48; other category, t(172) = 0.43, P = 0.67, d = 0.065, 95% CI: −0.30–0.47).

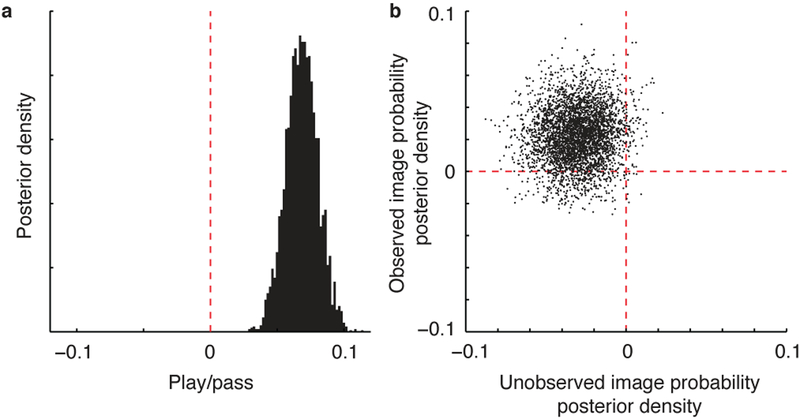
To better estimate the effects of image category, other category, and play/pass behavior on subsequent memory, we fit the memory score data with a modified version of the hierarchical regression model that included separate reward probability terms for the “image” and “other” categories. Posterior density estimates for the play/pass coefficient were greater than zero (Fig. 8a; Supplementary Table 1), replicating our previous finding. The posterior density for the “image category” and “other category” probabilities was concentrated in the region over which image category was greater than other category (mean [95% CI] image category coefficient minus other category coefficient: 0.052 [0.015,0.94]) and supported independent and opposite contributions of both category probabilities (Fig. 8b; Supplementary Table 1). These results, in particular the negative effect of “other category” probability on the subsequent memory scores (mean [95% credible interval] other category coefficient = −0.03 [−0.06, −0.001]), are more consistent with an RPE effect than with a direct effect of reward prediction itself. More generally, these results support the hypothesis that image RPEs enhance the degree to which such images are encoded in episodic memory systems.

Figure 8.

Hierarchical modeling results from Experiment 2 (N = 174). Memory scores depend on participant gambling behavior and the probabilities associated with both image categories. Memory score data from Experiment 2 was fit with a version of the hierarchical regression model described in Fig. 6a to replicate previous findings and determine whether reward probability effects were attributable to both observed and unobserved category probabilities. a, Posterior probability estimates of the mean play/pass coefficient. The posterior estimates were greater than zero and consistent with those measured in the first experiment. b, Image category probability (observed) coefficients, plotted against other category probability (unobserved) coefficients, revealing that participants tended to have higher memory scores for images that were associated with high reward probabilities (upward shift of density relative to zero) and when the unobserved image category was associated with a low reward probability (leftward shift of density relative to zero).

Despite the general agreement between the two experiments, there was one noteworthy discrepancy. While hierarchical models fit to both datasets indicated higher probability of positive coefficients for the interaction between value and probability (e.g., positive effects of reward probability on memory are greater for high value trials), the 95% credible intervals for these estimates in experiment 2 included zero as a possible coefficient value (mean [95% credible interval] probability*value coefficient = 0.007 [−0.019, 0.034]; Supplementary Table 1) indicating that the initial finding was not replicated in the strictest sense.

To better understand this discrepancy, and to make the best use of the data, we (1) extended the hierarchical regression approach to include additional coefficients capable of explaining differences across the two experiments and (2) fit this extended model to the combined data. As expected, this model provided evidence for a memory advantage on play trials, and an amplification of this advantage for trials with a high image RPE (Supplementary Fig. 7; Supplementary Table 1). In the combined dataset there was also a positive effect of the interaction between value and probability (Supplementary Fig. 7; mean [95% credible interval] probability*value coefficient = 0.02 [0.004, 0.04]; Supplementary Table 1), such that the positive impact of reward probability on memory was largest on high value trials, supporting our initial observation in Experiment 1. This finding is predicted by the RPE account, as the high reward probability category elicits a larger RPE when the potential payout is greater (“I could win 100 points, and now I almost certainly will”) as opposed to when the potential payout is low (“I could win 1 point, and now I almost certainly will”). We also observed that the reward probability effect was greater in the no delay condition (Supplementary Fig. 7; mean [95% credible interval] probability delay difference coefficient = −0.03 [−0.05, −0.002]; Supplementary Table 1), with no evidence for any memory effects being stronger in the 24 hour delay condition (Supplementary Table 1; all other delay difference ps > 0.19).

Using a similar approach, we also tested whether there was a negative effect of trial value on memory, which was weakly suggested by the results in Experiment 1. Using the combined dataset, we found no effect of trial value on memory (Supplementary Table 1).

Discussion

An extensive prior literature has linked dopamine to RPEs elicited during reinforcement learning^{5,6,22,24,29,40,57–59}, and a much smaller literature has suggested that dopamine can also influence the encoding and consolidation of episodic memories by modulating activity in the medial temporal lobes^21,42,60. To date, however, there has been mixed evidence regarding the relationship between RPE signaling and memory encoding. Here, we used a two-stage learning and memory paradigm, along with computational modeling, to better characterize how RPE signals affect the strength of incidental memory formation.

We found that memory encoding was stronger for trials involving positive image RPEs (Fig. 4a,b). This effect was only evident for trials in which participants accepted the risky offer, which is to say, trials in which the subjective prediction error could have plausibly been greater than zero. The effect was evident after controlling for other potential confounds (Fig. 6b column 3) and it was amplified for trials in which higher reward values were on the line (Fig. 6b column 5). The data also suggest that the effect may depend on the timing of the RPE; memory was enhanced by positive image RPEs, but we found no evidence of an effect of positive value or feedback RPEs. These results are all consistent with a direct, positive effect of RPE at the time of stimulus presentation on memory encoding. This interpretation is bolstered by the fact that individuals who were more sensitive to value and probability in the learning task (that is to say, those participants who were most closely tracking probability and value through the learning task) showed larger positive effects of image RPEs on memory. Experiment 2 further supported the RPE interpretation by demonstrating that memory benefits were composed of equal and opposite contributions of the reward probability associated with the observed image category and that of the unobserved, counterfactual, one (Fig. 7f,g, Fig. 8b). Together, these results provide strong evidence that RPEs enhance the incidental encoding of visual information, with positive consequences for subsequent memory.

We also found that participants encoded memoranda to a greater degree on trials in which they selected a risky bet (Fig. 3). This finding is consistent with a positive relationship between RPE signaling and memory strength, in that participant behavior provides a proxy for the subjective reward probability estimates (Fig. 2A). However, this effect was prominent in both experiments even after controlling for model-based estimates of RPE (Fig. 6b and Fig. 8a). Therefore, while we suspect that this result may at least partially reflect the direct impact of RPE, it may also reflect other factors associated with risky decisions. On play trials, participants view items while anticipating the uncertain gain or loss of points during the upcoming feedback presentation, whereas on pass trials participants know they will maintain their current score. A direct effect of perceived risk on memory encoding would be consistent with recent work that has highlighted enhanced memory encoding prior to uncertain feedback⁶¹, particularly when that feedback pertains to a self-initiated choice⁶².

One important question for interpreting these effects on memory encoding is to what degree they are mediated by shifts in anticipatory attention. Recent work by Stanek and colleagues demonstrated that images presented prior to feedback in a Pavlovian conditioning task showed a consolidation independent memory benefit when the feedback was uncertain. While we did not observe a memory benefit when feedback was most uncertain (note the lack of enhanced memory for intermediate reward probabilities in Fig 4c,d), it is possible that attention is modulated differently in our task, and that the memory benefits that we observed (on play trials and on trials including a large image RPE) might reflect these differential fluctuations in anticipatory attention. We attempted to minimize the influence of attention by 1) forcing participants to categorize the image on each trial, thus ensuring some baseline level of attention to the memoranda and 2) by presenting counterfactual information on pass trials that was nearly identical to the experienced outcome information. Indeed, we found that the best model of behavior relied equally on feedback information from play and pass trials and across all levels of image RPE (Fig. 2c), providing evidence that attention to feedback did not differ drastically across our task conditions.

A more nuanced analysis revealed that participants were slightly more influenced by outcome information provided on all play trials irrespective of image RPE. This suggests that anticipatory attention is elevated slightly on play versus pass conditions, but it does not imply a difference in attention on play trials with differing levels of image RPE (Supplementary Fig. 6b). Furthermore, there was no relationship between the degree to which participants modulated learning based on gambling behavior (play versus pass), and the degree to which they showed subsequent memory improvements on play trials (Supplementary Fig. 6c). Thus, while there do seem to be small attentional shifts that relate to gambling behavior, the size of such shifts is not a good predictor of which participants will experience a subsequent memory benefit. However, while our analyses suggest that the memory benefit conferred by positive image RPEs is not mediated by attention, we cannot completely rule out the possibility that attention may have fluctuated with RPEs in ways we could not measure. Future work with proxy measurements of attention (e.g., eye-tracking) can further address whether attention can be dissociated from RPEs, and if so, whether it modulates the relationship between RPE and memory.

At first glance our results appear incompatible with those of Wimmer and colleagues⁴⁵, who show that stronger RPE encoding in the ventral striatum is associated with weaker encoding of incidental information. We suspect that the discrepancy between these results is driven by differences in the degree to which memoranda are task relevant in the two paradigms. In our task, participants were required to encode the memoranda sufficiently to categorize them in order to perform the primary decision-making task, whereas in the Wimmer study, the memoranda were unrelated to the decision task and thus might not have been well-attended, particularly on trials in which the decision task elicited an RPE. Taken together, these results suggest that RPEs are most likely to enhance memory when they are elicited by the memoranda themselves, with the potential influence of secondary tasks eliminated or at least tightly controlled.

A relationship between RPEs and memory is consistent with a broad literature highlighting the effects of dopaminergic signaling on hippocampal plasticity^32,35,37 and memory formation⁴², as well as with the larger literature suggesting that dopamine provides an RPE signal^5,22 through projections from the midbrain to the striatum. It is thought that this dopaminergic RPE is also sent to the hippocampus through direct projections²⁰, although to our knowledge this has never been verified directly and should be a target of future research. Our results support the behavioral consequences that might be predicted to result from such mechanisms, but they also refine them substantially. In particular, we show that the timing of RPE signaling relative to the memorandum is key; we saw no effect of RPEs elicited by prior or subsequent feedback on memory (Fig. 5a,b), despite strong evidence that this feedback was used to guide reinforcement learning and decision making (Fig. 2). RPE-induced memory enhancement was selective to observed targets and did not generalize to semantically matched foils (Supplementary Fig. 5), as would be expected for a hippocampal mechanism¹², consistent with previous literature on the hippocampal dependence of recognition memory^63,64. However, other aspects of our results, such as the lack of consolidation dependence (Fig. 6b) deviate from previous literature on dopamine mediated memory enhancement in the hippocampus⁴², raising questions regarding whether our observed memory enhancement might be mediated through an alternative dopamine signaling pathway such as that targeting the striatum⁶⁵ or the prefrontal cortex^19,43,66. We hope that our behavioral study inspires future work to address these anatomical questions directly.

While our results are in line with some recent work relating positive RPEs to better incidental⁶¹ and intentional⁴⁷ memory encoding, they differ from previous work in that image RPE effects emerged immediately and were not strengthened by a 24 hour delay (Figs.4 and 6, Supplementary Tables 1 and 2). Previous work from Stanek and colleagues showed that memory encoding benefits bestowed by positive RPEs required a substantial delay period for consolidation⁶¹, consistent with rodent work delineating the mechanisms through which dopamine can enhance hippocampal memory encoding in a consolidation dependent manner⁴². However, it is unclear to what extent we should expect generalization of these results to our study, given the differences in experimental paradigm, timescale, memory demands, and species. The Stanek paradigm differed from ours in the timing and duration of image presentation, the relevance of the memoranda to task performance, and the nature of the task itself (our RPEs were elicited in a choice task, whereas theirs were elicited through a Pavlovian paradigm)⁶¹. Indeed, our results suggest that the timing of the RPE relative to image presentation is an important determinant of memory effects; in our study we demonstrate that the RPE elicited at the value time point 2.5 seconds prior to image presentation (pink shading on Fig. 1) had no appreciable effect on subsequent memory (Fig. 4e,f). The RPE-inducing stimulus in the Stanek paradigm was presented 1.4 seconds prior to the memorandum, somewhat intermediate in timing between our image RPE (synchronous with memorandum) and our value RPE (preceding memorandum). At the psychological level, it is clear that these timing differences are important, and it is possible that the strength of the encoding benefit, and even the consolidation dependence, may be sensitive to these small differences in relative timing. It should also be noted that the RPEs elicited at different times in our task occurred through the presentation of different types of information (e.g., reward magnitude, reward probability, actual outcome) and thus our claims about timing assume that these distinct RPEs are conveyed in a common currency.

At the level of biological implementation, the consequence of differences in timing may be enhanced by differences in dopamine signaling in operant versus Pavlovian paradigms, with the former eliciting dopamine ramps that grow as an outcome becomes nearer in time⁶⁷, and the latter eliciting the opposite trend in the firing of dopamine neurons⁶⁸. Thus, it is possible that our positive prediction error conditions elicit both a phasic dopamine burst and a ramp of dopamine as the outcome approaches, whereas the Stanek paradigm elicits a short phasic burst followed by a decrease in baseline dopamine. This signaling difference could be magnified by the differences in our presentation times, with our image present over the duration of the dopamine ramp, with the Stanek paradigm more precisely sampling the period during which a phasic spike in dopamine would be expected. While it is clear that patterns of dopamine signaling differ across these task designs, it is not clear whether such differences are effectively communicated to the hippocampus or whether they could alter the consolidation dependence of dopamine-induced memory encoding benefits. Future work should carefully examine the effects of relative timing and task design on the magnitude and consolidation dependence of RPE benefits to human memory encoding. We hope that the emergence of these timing and task dependencies from human studies inspires parallel studies in rodents to characterize the precise temporal dynamics through which dopamine signals can and do facilitate memory formation, and the degree to which these dynamics affect underlying mechanisms, in particular the role of consolidation.

Our results also provide insight into apparent inconsistencies in previous studies that have attempted to link RPE signals to memory encoding. Consistent with previous work (e.g.⁶⁵), our results emphasize the importance of choice in the degree to which image RPEs contributed to memorability. Indeed, for trials in which the participants passively observed outcomes, we saw no relationship between model derived RPE estimates and subsequent memory strength (Fig. 4a,b, dotted lines). This might help to explain the lack of a signed relationship between RPEs and subsequent memory strength in a recent study by Rouhani and colleagues that leveraged a Pavlovian design which did not require that explicit choices be made⁴⁶. In contrast to our results, Rouhani and colleagues observed a positive effect of absolute RPE, similar to our model-based surprise estimates, on subsequent memory. While we saw no effect of surprise on subsequent memory, other work has highlighted a role for such signals as enhancing hippocampal activation and memory encoding^69,70. One potential explanation for this discrepancy is in the timing of image presentation. Our study presented images briefly during the choice phase of the decision task. By contrast, Rouhani and colleagues presented the memoranda for an extended period that encompassed the epoch containing trial feedback, potentially explaining why they observed effects related to outcome surprise. More generally, the temporally selective effects of RPE observed here suggest that RPE effects may differ considerably from other, longer timescale manipulations thought to enhance memory consolidation through dopaminergic mechanisms^21,33,43,44.

In summary, our results demonstrate a role for image RPEs in enhancing memory encoding. We show that this role is temporally and computationally precise, independent of consolidation duration (at least in the current paradigm), and contingent on decision-making behavior. These data should help clarify inconsistencies in the literature regarding the relationship between reward learning and memory, and they make detailed predictions for future studies exploring the relationship between dopamine signaling and memory formation.

Methods

Experiment 1

Experimental procedure

The task consisted of two parts: the learning task and the memory task. The learning task was a reinforcement learning task with random change-points in reward contingencies of the targets. The memory task was a surprise recognition memory task using image stimuli that were presented during the learning task and foils.

Participants completed either the no delay or 24-hour delay versions of the task via Amazon Mechanical Turk. In the no delay condition, the memory task followed the learning task only after a short break, during which a demographic survey was given. Therefore, the entire task was performed in one sitting. In the 24-hour delay condition, participants returned 20–30 hours after completing the learning task to do the memory task.

A task of a specific condition (no delay or 24-hour delay) was administered at a time, and participants who agreed to complete the task online at the time of administration were recruited for that task condition. Data collection, but not the analysis was performed blind to the conditions of the experiments.

Participants

A total of 287 participants (142, no delay condition; 145, 24hr delay condition) completed the task via Amazon Mechanical Turk. Target sample sizes were chosen based on the results of an initial pilot study that used a similar design and was administered to a similar online target population. Randomization across conditions was determined by the day in which participants accepted to complete the human intelligence task posted on Amazon Mechanical Turk. Neither participants nor experimenters were blind to the delay condition. From the total participant pool, 88 participants (33, no delay; 55, 24hr delay) were excluded from analysis because they previously completed a prior version of the task or didn’t meet our criteria of above-chance performance in the learning task. To determine whether a participant’s performance was above-chance, we simulated random choices using the same learning task structure, then computed the total score achieved by the random performance. We then repeated such simulations 5000 times, and assessed whether the participant’s score was greater than 5% of the score distribution from the simulations. The final sample had a total of 199 participants (109, no delay, 90, 24hr-delay; 101 males, 98 females) with the age of 32.2 ± 8.5 (mean ± SD). Informed consent was obtained in a manner approved by the Brown University Institutional Review Board.

Learning task

The learning task consisted of 160 trials, where each trial consisted of three phases – value, image, and feedback (Fig. 1a). During the value phase, the amount of reward associated with the current trial was presented in the middle of the screen for 2 s. This value was equally sampled from [1, 5, 10, 20, 100]. After an interstimulus interval (ISI) of 0.5 s, an image appeared in the middle of the screen for 3 s (image phase). During the image phase, the participant made one of two possible responses using the keyboard: PLAY (press 1) or PASS (press 0). When a response is made, a colored box indicating the participant’s choice (e.g. black = play, white = pass) appeared around the image. The pairing of box color and participant choice was pseudorandomized across participants. After this image phase, an ISI of 0.5 s followed, after which the trial’s feedback was shown (feedback phase). The order of images was pseudorandomized.

Each trial had an assigned reward probability, such that if the participant chose PLAY, they would be rewarded according to that probability. If the participant chose PLAY and the trial was rewarding, they were rewarded by the amount shown during the value phase (Fig. 1a). If the participant chose PLAY but the trial was not rewarding, they lost 10 points regardless of the value of the trial. If the choice was PASS, the participant neither earned nor lost points (+0), and was shown the hypothetical result of choosing PLAY (Fig. 1a). During the feedback phase, the reward feedback (+value, −10, or hypothetical result) was shown for 1.5s, followed by an ISI (0.5 s), and a 1 s presentation of the participant’s total accumulated score.

All image stimuli belonged to one of two categories: animate (e.g., whale, camel) or inanimate (e.g., desk, shoe). Each image belonged to a unique exemplar, such that there were no two images of the same animal or object. Images of the two categories had reward probabilities that were oppositely yoked. For example, if the animate category has a reward probability of 90%, the inanimate category had a reward probability of 10%. Therefore, participants only had to learn the probability for one category, and simply assume the opposite probability for the other category.

The reward probability for a given image category remained stable until a change-point occurred, after which it changed to a random value between 0 and 1 (Fig. 1d). Change-points occurred with a probability 0.16 on each trial. To facilitate learning, change-points did not occur in the first 20 trials of the task and the first 15 trials following a change-point. Each participant completed a unique task with pseudorandomized order of images that followed these constraints.

The objective was to maximize the total number of points earned. Participants were advised to pay close attention to the value, probability, and category of each trial in order to decide whether it is better to play or pass. Participants were thoroughly informed about the possibility of change-points, and that the two categories were oppositely yoked. They underwent a practice learning task in which the reward probabilities for the two categories were 1 and 0 to clearly demonstrate these features of the task. Participants were awarded a bonus compensation proportional to the total points earned during the learning and memory tasks.

Computing the image reward prediction error (RPE)

The image RPE arises from the fact that the reward probabilities associated with the two image categories (animate/inanimate) differ. For instance, consider a trial in which the trial value was 100, the animate category was associated with a reward probability of 0.9, and an animate image was presented. The expected reward for that trial could be computed as follows:

$$expected\mathrm{ }reward\mathrm{ }=\mathrm{ }value\mathrm{*}p\left(rew\mathrm{ }\right|\mathrm{ }animate)\mathrm{ }–\mathrm{ }10\mathrm{*}(1-p\left(rew\mathrm{ }\right|\mathrm{ }animate\left)\right)\mathrm{ }=\mathrm{ }100\mathrm{*}0.9-10\mathrm{*}0.1=89.$$

In contrast, if the other (inanimate) category had been presented, the expected reward would be as follows:

$$expected\mathrm{ }reward\mathrm{ }=\mathrm{ }value\mathrm{*}p\left(rew\mathrm{ }\right|\mathrm{ }inanimate)\mathrm{ }–\mathrm{ }10\mathrm{*}(1-p\left(rew\mathrm{ }\right|\mathrm{ }inanimate\left)\right)\mathrm{ }=\mathrm{ }100\mathrm{*}0.1-10\mathrm{*}0.9=1.$$

We assume that participant reward expectations prior to observing the image category simply average across these two categories. Thus, in this case, the expectation prior to observing the animate image would have been (89*0.5 + 1*0.5) = 45. The image RPE was computed by subtracting the expected reward after the image category was revealed from the expected reward before it was revealed, in this case 89–45= 44.

Memory task

During the memory task, participants viewed 160 “old” images from the learning task intermixed with 160 “new” images (Fig. 1i). Importantly, we ensured that the new images were semantically matched to the old images. All 160 images in the learning task were those of unique exemplars, and the 160 lure images were different images of the same exemplars. Therefore, accurate responding depended on the retrieval of detailed perceptual information from encoding (e.g. “I remember seeing THIS desk”, instead of “I remember seeing A desk”).

The order of old and new images was pseudorandomized. On each trial, a single image was presented, and the participant selected between OLD and NEW by pressing 1 or 0 on the keyboard, respectively (Fig. 1i). Afterwards, they were asked to rate their confidence in the choice from 1 (Guess) to 4 (Completely certain). Participants were not provided with correct/incorrect feedback on their choices.

Bayesian ideal observer model

The ideal observer model computed inferences over the probability of a binary outcome that evolves according to a change-point process. The model was given information about the true probability of a change-point occurring on each trial (H; hazard rate) by dividing the number of change-points by the total number of trials for each participant. For each trial, a change-point was sampled according to a Bernoulli distribution using the true hazard rate (CP ~ B(H)). If a change-point did not occur (CP = 0), the predicted reward rate (μ_t) was updated from the previous trial (μ_t−1). When a change-point did occur (CP = 1), μ_t was sampled from a uniform distribution between 0 and 1. The posterior probability of each trial’s reward rate given the previous outcomes can be formulated as follows:

$$\text{p}\left({\mathrm{\mu }}_{\text{t}}{\text{|X}}_{1:\text{t}}\right)\propto \text{ p}({\mathrm{X}}_{\text{t}}|{\mathrm{\mu }}_{\text{t}})\sum _{{\text{CP}}_{\text{t}}}\sum _{{\text{μ}}_{\text{t}-1}}\text{p}\left({\mathrm{\mu }}_{\text{t}}{\text{|CP}}_{\text{t}},{\text{μ}}_{\text{t}-1}\right)\text{p}\left({\text{CP}}_{\text{t}}\right)\text{p}\left({\text{μ}}_{\text{t}-1}{\text{|X}}_{1:\text{t}}\right)\text{p}\left({\text{X}}_{1:\text{t}-1}\right)$$ (1)

Where p(X_t|μ_t) is the likelihood of the outcomes given the predicted reward rate, p(μ_t|CP_t, μ_t−1) represents the process of accounting for a possible change-point (when CP = 1, μ_t ~ U(0,1)), p(CP_t) is the hazard rate, and p(μ_t−1|X_1:t) is the prior belief of the reward rate.

Using the model-derived reward rate, we quantified the extent to which each new outcome influenced the subsequent prediction as the learning rate in a delta-rule:

$$\begin{gathered} {\text{B}}_{\text{t}+1}={\mathrm{B}}_{\text{t}}+{\mathrm{\alpha }}_{\text{t}}{\mathrm{\delta }}_{\text{t}} \\ {\mathrm{\delta }}_{\text{t}}={\mathrm{X}}_{\text{t}}-{\mathrm{B}}_{\text{t}} \end{gathered}$$ (2)

where B is the belief about the current reward rate, α is the learning rate, and δ is the prediction error, defined as the difference between the observed (X) and predicted (B) outcome. Rearranging, we were able to compute the trial by trial learning rate (Supplementary Fig. 8):

$$\text{α}=\frac{{\text{B}}_{\text{t}+1}-{\mathrm{B}}_{\text{t}}}{{\mathrm{X}}_{\text{t}}-{\mathrm{B}}_{\text{t}}}$$ (3)

Trial by trial modulation of change-point probability (i.e. surprise) was calculated by marginalizing over μ_t, which is a measure of how likely it is, given the current observation, that a change-point has occurred (Supplementary Fig. 8):

$$\text{p}\left({\text{CP}}_{\text{t}}{\text{|X}}_{1:\text{t}}\right)\propto \text{ p}({\text{X}}_{\text{t}}|{\mathrm{\mu }}_{\text{t}})\sum _{{\mathrm{\mu }}_{\text{t}}}\sum _{{\mathrm{\mu }}_{\text{t}-1}}\text{p}\left({\mathrm{\mu }}_{\text{t}}{\text{|CP}}_{\text{t}},{\mathrm{\mu }}_{\text{t}-1}\right)\text{p}\left({\text{CP}}_{\text{t}}\right)\text{p}\left({\mathrm{\mu }}_{\text{t}-1}{\text{|X}}_{1:\text{t}}\right)\text{p}\left({\text{X}}_{1:\text{t}-1}\right)$$ (4)

Uncertainty was determined by computing the entropy of the posterior probability distribution of the reward rate on each trial, measured in units of nats (Supplementary Fig. 8):

$$\text{H}\left(\text{t}\right)=-\sum \text{p}\left({\mathrm{\mu }}_{\text{t}}{\text{|X}}_{1:\text{t}}\right)\text{ln}\left(\text{p}\left({\mathrm{\mu }}_{\text{t}}{\text{|X}}_{1:\text{t}}\right)\right)$$ (5)

Descriptive analysis

Memory scores for each image were computed by transforming the recognition and confidence reports provided by the participant. On each trial of the recognition memory task, participants first chose between “old” and “new”, then reported their confidence in that choice on a scale of 1–4. We converted these responses so that choosing “old” with the highest confidence (4) was a score of 8, while choosing “new” with the highest confidence was a score of 1. Similarly, choosing “old” with the lowest confidence (1) was a score of 5, while choosing “new” with the lowest confidence was a score of 4. As such, memory scores reflected a confidence-weighted measure of memory strength ranging from 1 to 8. These memory scores were used for all analyses involving recognition memory.

For some statistical tests and plots (Figs. 4, 5, 7f,g) memory scores for target items were mean-centered per participant by subtracting out the average memory score across only the target items. Statistical analyses were then performed in a between-participant manner to assess the degree to which certain task variables affected mean-centered memory scores.

Relationships between computational factors and memory scores were assessed by estimating the slope of the relationship between each computational factor and the subsequent memory score separately for each computational variable and participant. Statistical testing was performed using one sample t-tests on the regression coefficients across participants (for overall effects) and two sample t-tests for differences between delay conditions (for delay effects).

In cases where reward probability was included in a statistical analysis, we used the reward probabilities estimated by the Bayesian ideal observer model described above, as these subjective estimates of the reward rate departed substantially from ground truth probabilities after change-points and were more closely related to behavior.

To generate the descriptive figures, we performed a binning procedure for each participant to ensure that each point on the x axis contained an equal number of elements. For each participant, we divided the y variable in question into quantiles and used the mean y value of each quantile as the binned value. To plot data from all participants on the same x axis, we first determined the median x value for each bin per participant, then took the average of the bin median values across participants. For some figures containing more than one plot, we shifted the x values of each plot slightly off-center to avoid overlap of points (Figs 5, 7f,g).

We were interested in testing whether participants who were sensitive to reward value and probability also had a strong image RPE on memory effect. In other words, participants that better adjusted their behavior using information about the trial value and probability will be more likely to remember items associated with higher RPEs. To quantify sensitivity to reward value and probability, we fit a logistic regression model on play/pass behavior that included z-scored versions of the reward probability (derived from the ideal observer model) and reward value as predictors for each participant. To find the effect of image RPE on memory, we fit a linear regression model on mean-centered memory score that included the image RPE as the predictor. We then computed the Spearman correlation between the coefficients of the two regression models.

Unless otherwise specified, statistical comparisons in the manuscript used a two-tailed t-test. Data distribution was assumed to be normal, but this was not formally tested. We used an alpha level of 0.05 for all statistical tests.

RL model fitting

We fit a reinforcement learning model directly to the participant behavior using a constrained search algorithm (fmincon in Matlab), which computed a set of parameters that maximized the total log posterior probability of betting behavior (Fig. 2c,d). Four such parameters were included in the model: 1) a temperature parameter of the softmax function used to convert trial expected values to action probabilities, 2) a value exponent term that scales the relative importance of the trial value in making choices, 3) a play bias term that indicates a tendency to attribute higher value to gambling behavior, and 4) an intercept term for the effect of learning rate on choice behavior. In fitting the model, we wanted to account for the fact that there may be individual differences in how a participant’s betting behavior is biased by certain aspects of the task. For instance, some participants may be more sensitive to trial value, while others may attribute higher value to trials in which they gambled. This was the rationale behind adding the second and third parameters. The overall, “biased” value estimated from gambling on a given trial was given by:

$$V_B\left(t\right)={B_{play}+(P}_{rew}\mathrm{*}{V}_t^k+\left(1-P_{rew}\right)\mathrm{*}{\left(-10\right)}^k)$$

Where B_play is the play bias term, P_rew is the reward probability inferred from the ideal observer model, V_t is the trial value (provided during the value phase), and k is the value exponent. This overall value term was converted into action probabilities (p(play|V(t)),p(pass|V(t))) using a softmax function. This was our base model.

Next, we fit additional RL models to the data by adding parameters to the above base model. These additional parameters controlled the extent to which other task variables affected the trial-to-trial modulation of learning rate, including surprise, uncertainty, the learning rate computed from the ideal observer model, and betting behavior. Specifically, learning rate was determined by a logistic function of a weighted predictor matrix that included the above variables and an intercept term. Therefore, it captured the degree to which learning rate changed as a function of these variables. The best fitting model was determined by computing the Bayesian information criterion (BIC) for each model, then comparing these values to that of the base model⁷¹.

To compare participant behavior to model-predicted behavior, we simulated choice behavior using the model with the lowest BIC, which incorporated surprise and uncertainty variables in determining learning rate (Fig. 2b). On each trial, we used the expected trial value (V(t)) computed above, and the parameter estimates of the temperature variable as inputs to a softmax function to generate choices.

Hierarchical regression model

Participant memory scores were modeled using a hierarchical mixture model that assumed that the memory score reported for each item and participant would reflect a linear combination of participant level predictors and item level memorability (Fig. 6a). The hierarchical model was specified in STAN (http://mc-stan.org) using the matlabSTAN interface (http://mc-stan.org)⁷². In short, memory scores on each trial were assumed to be normally distributed with a variance that was fixed across all trials for a given participant. The mean of the memory score distribution on a given trial depended on 1) a trial-to-trial task predictors that were weighted according to coefficients estimated at the participant level and 2) item-to-item predictors that were weighted by coefficients estimated across all participants. Participant coefficients for each trial-to-trial task predictor were assumed to be drawn from a group distribution with a mean and variance offset by a delay variable, which allowed the model to capture differences in coefficient values for the two different delay conditions. All model coefficients were assumed to be drawn from prior distributions and for all coefficients other than the intercept (which captured overall memory scores) prior distributions were centered on zero.

Experiment 2

Experimental procedure

In Experiment 2, the learning task was modified to dissociate reward rate from RPE. The reward probability of the two image categories (animate vs. inanimate) were independent and set to either 0.8 or 0.2, allowing for a 2×2 design (0.8/0.8, 0.8/0.2, 0.2/0.8, 0.2/0.2; Fig. 7a). Change-points occurred with a probability 0.05 on every trial for the two categories independently. Change-points did not occur for the first 20 trials of the task and the first 20 trials following a change-point. Tasks were generated to contain at least one block of each trial type in the 2×2 design. Each participant completed a unique task with pseudorandomized order of images that followed these constraints. The task instructions explicitly stated that the two image categories had independent reward probabilities that need to be tracked separately. Importantly, participants were also unaware that probabilities were either 0.2 or 0.8, and most likely assumed that the probabilities could be set to any value ranging from 0 to 1. The rest of the task, including the recognition memory portion, was identical to that of Experiment 1.

Participants

A total of 279 participants (157, no delay condition; 122, 24hr-delay condition) completed the task on Amazon Mechanical Turk. 105 participants (64, no delay; 41, 24hr-delay) were excluded from analysis because they previously completed a prior version of the task or didn’t meet our criteria of above-chance performance in the learning task. The criteria for above-change performance was identical to that of Experiment 1. Participants who completed Experiment 1 or any prior versions of the task were identified and excluded using the participant-unique identifier provided by Amazon Mechanical Turk, to ensure that participants were unaware of the surprise memory portion of the task. The final sample had a total of 174 participants (93, no delay, 81, 24hr-delay; 101 males, 71 females, 2 no response) with the age of 34.0 ± 9.1 (mean ± SD). Informed consent was obtained in a manner approved by the Brown University Institutional Review Board.