A Contemporary Look at Biomechanical Models of Myocardium

Abstract

Understanding and predicting the mechanical behavior of myocardium under healthy and pathophysiological conditions are vital to developing novel cardiac therapies and promoting personalized interventions. Within the past 30 years, various constitutive models have been proposed for the passive mechanical behavior of myocardium. These models cover a broad range of mathematical forms, microstructural observations, and specific test conditions to which they are fitted. We present a critical review of these models, covering both phenomenological and structural approaches, and their relations to the underlying structure and function of myocardium. We further explore the experimental and numerical techniques used to identify the model parameters. Next, we provide a brief overview of continuum-level electromechanical models of myocardium, with a focus on the methods used to integrate the active and passive components of myocardial behavior. We conclude by pointing to future directions in the areas of optimal form as well as new approaches for constitutive modeling of myocardium.

1. INTRODUCTION

Myocardium is the muscular tissue of the heart, possessing distinctive physiological, mechanical, microstructural, and electrical characteristics, and is a paradigm of functional efficiency. Heart failure (HF) typically occurs when the myocardium fails, becoming too stiff and not allowing enough blood to fill the ventricles during diastole, too dilated and not contracting properly during systole to meet ejection fraction demands, or regionally malfunctional due to the acute injury from lack of oxygen and infarction (1). Adverse effects can even occur as secondary effects due to diseased heart valves (2), pulmonary hypertension (3), bacterial or viral infections (4), cancer treatment (5), or unexpected pharmacological interactions (6). In the United States, HF afflicts approximately 6 million people, costs $34.4 billion each year, and continues to be the single most common diagnosis for individuals older than 65 (7). Because myocardium undergoes significant structural and biomechanical changes in patients with heart disease (1, 8, 9), a better understanding of myocardial biomechanics will reveal more details of the underlying pathophysiologies of disease, improve clinical treatment, and advance medical device design.

Clinical treatment of cardiac disease may involve changes in diet and lifestyle, reduction of risk factors, medication, and surgical intervention. Interventions include pacemaker leads mounted on the tissue, stents deployed to prop open narrowed or blocked blood vessels that deliver blood to the myocardium, cardiac ablation or resection performed to improve electrical properties, or injectable biomaterials introduced to alter the mechanical behavior of the failing tissue (10). In each of these cases that involves physical interactions between devices and tissues, modeling and simulation that incorporate biomechanical mechanisms play a vital role in determining the optimal designs of the devices and procedures. In essence, such designs depend on the critical link between the organ-level cardiac function and the behavior of the tissue at smaller scales (down to molecular levels) that could be provided by myocardium models.

As in many biomedical applications, the development of biomechanical models of myocardium relies on appropriate characterization of the structure–function relationship at the tissue level. As is the case for many other soft fibrous tissues, the major steps in determining a concise and robust constitutive model for the mechanical behavior of myocardium include (a) delineating its general characteristics, (b) establishing a consistent mathematical framework, (c) identifying a specific functional form that contains sufficient information to represent the three-dimensional (3D) mechanical properties and microstructure of the tissue, (d ) conducting efficient model parameter estimation using designed experiments, and finally (e) evaluating the predictive capability of the model (11–13).

Here, we review fundamental concepts relevant to the understanding and modeling of myocardial biomechanics. First, we provide a brief overview of myocardium structure and function, specifically myocytes, extracellular matrix (ECM), and tissue architecture. Then, we elaborate on the current constitutive approaches used in cardiac biomechanics. Finally, we review methods used to incorporate active behavior into the constitutive models.

2. MYOCARDIUM STRUCTURE AND FUNCTION

Myocardium is a very complex tissue with multiple highly interconnected length scales (Figure 1) in a well-refined structural and functional hierarchy, ranging from whole-heart biomechanics down to the basic functional unit for contraction, regulated by the actin–myosin cross-bridge cycling mechanism (14, 15). The effective mechanical behavior of myocardium at the organ and tissue scales strongly depends on the response of its constituents and their structural arrangement at the cellular and intracellular levels. For this reason, before proceeding with biomechanical models of macroscopic behavior of myocardium, we briefly review some of the pertinent studies on its microstructural characteristics. In this section, we aim to provide a sufficient level of understanding and cognizance of the microstructural details of myocardium relevant to tissue-level mechanical modeling. We refer the interested reader to other articles that review exclusively the diverse biological, electrical, and physiological aspects of myocardium (e.g., 16–19).

Figure 1.

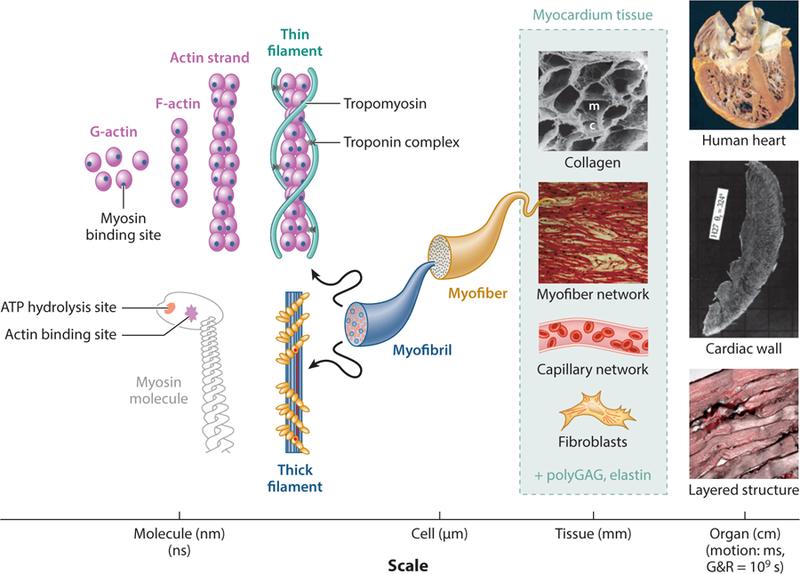
Structural hierarchy involved in myocardium tissue. Understanding of the tissue behavior at the mesoscale can better inform both the organ-scale behavior and the cellular and subcellular behavior. Abbreviations: ATP, adenosine triphosphate; c, capillary lacunae; G&R, growth and remodeling; m, myofiber lacunae; polyGAG, polyglycosaminoglycan. Images of the human heart, cardiac wall, collagen, and myofiber network are from References 24, 25, 26, and 27, respectively. The image of the layered structure is an unpublished image taken at the Willerson Center at the University of Texas, Austin.

2.1. Intra- and Extracellular Composition and Structure

Myocardium is a composite tissue that makes up the walls within the heart, consisting of cardiomyocytes and fibroblasts supported by the ECM and perfused by fluid delivered by blood vessels. Cardiomyocytes (myocytes) are the primary constituent, and in the mammalian heart they can be grossly approximated as large cylindrical rods with a length-to-diameter aspect ratio of up to seven to one (20). However, myocyte sizes and shapes are diverse and influenced by species, age, and disease. Myocytes have extensive sarcomeric units, and their intracellular ionic environment is highly controlled with ion channels. A rather strong and specialized intercellular connection, the intercalated disc, connects a large number of myocytes in series in supracellular structures. In addition to the physical mechanical connection provided by the intercalated discs, myocytes are extensively connected by gap junction channels that enable propagation of action potential to control the ionic environment and trigger coordinated muscle contraction (Figure 2a). Intercalated discs facilitate synchronized contraction among different myocytes for end-to-end transmission of force and action potential. Connected at intercalated discs, branching and merging into one another, the myocytes form a railway-like network of myofibers in cardiac tissue (21) and dominate heart composition (22), as they occupy approximately three-fourths of the tissue volume. Cardiac fibroblasts are much smaller and more numerous than myocytes, and they play a major role in the maintenance of the ECM, which provides mechanical support and anchors both to and in between cardiomyocytes.

Figure 2.

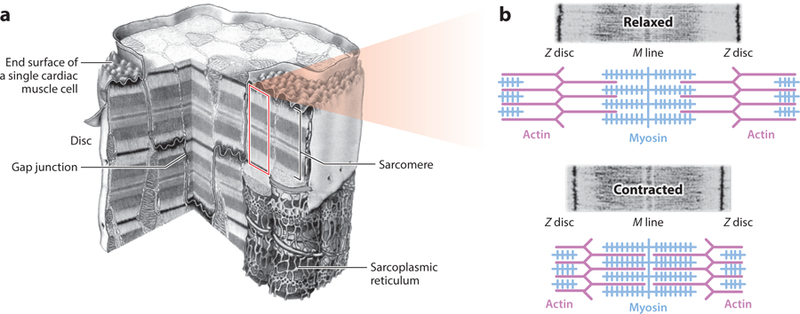
(a) Cutaway view of a cardiac myocyte, including several sarcomere units. (b) Machinery schematic for active muscle contraction via cross-bridge cycling. The central blue rods represent several myosin molecules (thick filament) with the actin binding site projecting out, surrounded by thin purple filaments. Titin proteins support the thick filament. Panel a adapted from Reference 23. Panel b adapted with permission from Pearson Education, Inc. Copyright 2004.

At the subcellular level, myocytes contain many myofibrils running in parallel along their longitudinal direction. When observed under microscope, the myofibrils reveal a distinct repeated pattern of bands. These systematic ensembles of bands form the basic functional units of the myocyte, the sarcomere, and the molecular mechanism for their contraction (Figures 1 and 2) (17). One sarcomere consists of several thick and thin filaments made of myosin and actin, respectively. Thin filaments are anchored at only one of their ends at a Z disc (with one Z disc anchoring multiple thin filaments) and run parallel to the thick filament toward the sarcomere center. Thick filaments are anchored at both ends to neighboring Z discs by the protein titin, which has exceptional elastic properties (up to 170% extension).

Actin thin filaments contain binding sites for myosin thick filaments, but at resting potential, the sites are blocked by the protein tropomyosin. Action potential changes negating the resting potential cause calcium ions (Ca²⁺) to flow into the cell and trigger abundant Ca²⁺ release from the sarcoplasmic reticulum inside the cell. Increased Ca²⁺ facilitates binding of Ca²⁺ to troponin C, leading to the exposure of the actin binding sites. Simultaneously, in the presence of adenosine triphosphate (ATP), energy is released, causing angular movement of these myosin heads. The myosin head binds to an adjacent position in the actin thin filament, resulting in relative sliding and generating a force that causes the sarcomere to shorten in length. This is known as the cross-bridge cycling mechanism of the sliding filament theory (Figure 2b). The power stroke of myosin heads causes actin to move relative to them, and the synchronous cross-bridge cycling of multiple filaments, sarcomeres, and myocytes results in effective contraction of the tissue and force propagation at the macroscopic scale.

Surrounding the myocytes and the myofibers, the ECM consists mainly of fibrillar collagen, elastin, and polyglycans (30) and is maintained by the fibroblasts in the tissue. It is composed of high-strength type I collagen (85%) and highly deformable type III collagen (15%) (31) in the form of endomysial, perimysial, and epimysial fibers. These fibers collectively form the scaffold required for supporting the myofibers and capillaries to maintain their arrangement and distribute the load across the tissue. Endomysial collagen surrounds the individual myofibers within the lamina, either as a fine weave running around the peripheral myofiber surfaces or as the transverse links connecting adjacent myocytes and often attached near Z discs (26, 32). Perimysial collagen, consisting mainly of type I collagen with high tensile strength (33), connects the adjacent laminae and also runs peripherally around a group of myofibers, bundling them together. This binding between layers is weaker near the midwall region due to longer perimysial collagen fiber lengths, allowing more freedom in comparison to subepicardium regions (25). Epimysial collagen is a sheath of connective tissue that surrounds the entire muscle (34; also see Figures 1 and 3 for graphical depictions of this arrangement).

Figure 3.

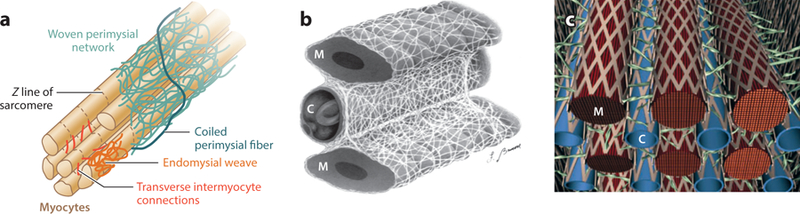
Different representations of the microstructural details of the collagen fiber arrangement in myocardium. (a) Arrangement of endomysial and perimysial collagen fibers with respect to myofibers. (b) Sheath-like arrangement of fine endomysial collagen fiber network. (c) Strut and weave representations of collagen fibers around myofibers (M) and capillary vessels (C). Panel a adapted from Reference 28. Panel b reprinted from Reference 29.

Lastly, two main representations have been proposed to describe the arrangement and interaction of collagen and myofibers. Earlier studies by Caulfield & Borg (35), Borg & Caulfield (36), and Borg et al. (37) introduced a “strut” representation for collagen fibers, connecting myofibers to myofibers perpendicularly (Figure 3c). The struts were perceived to connect myofibers to capillaries as well, such that they are attached perpendicularly to capillaries but tangentially to myofibers. This representation was helpful in explaining how strained collagen links maintain the patency of the capillaries in systole, whereas the links between myofibers become stretched in diastole and maintain the diastolic arrangement of the myofiber bundles. This strut theory was endorsed by others, until Macchiarelli et al. (29) and Intrigila et al. (26), using scanning electron microscopy and reticulum-staining techniques, described collagen as arranged in sheaths surrounding myofibers (i.e., as a weave instead of individual struts) (Figure 3b). The sheath representation is currently prevalent; however, a coexistence of sheaths and struts seems to be a plausible arrangement, which will require more comprehensive investigation of myocardium architectures and could be used for microstructurally based constitutive modeling, as discussed in the next section.

2.2. Tissue- and Organ-Level Architecture and Function

Histologically, myocardium has been observed to be composed of long myofibers, formed by myocytes arranged along their principal axis and coupled end to end (analogous to skeletal muscle fibers). Fiber orientation smoothly rotates throughout the ventricular wall (20) and is described with a helical angle. In addition, ventricular myocytes are organized by sheets in radial–tangential planes called myocardial laminae, each consisting of four to six layers of myocytes (Figure 4) (25). In an idealized description, these laminae at the midwall region are stacked at an angle relative to the longitudinal direction that helically varies along the radial direction. Nevertheless, this highly ordered structure is an idealization. Fiber and sheet organization is highly complex and regionally variable. There is no definite origin or termination point for myofibers; at best, they can be described as part of a 3D mesh. The relatively older approach put forward by Torrent-Guasp et al. (38) suggests an interesting helical pattern of the fibers, somewhat similar to the Gordian knot (39). In addition, the laminar structure has multiple branching points to encompass and accommodate the extracellular fibrous component of the tissue, and the ventricular wall is perfused by an extensive vascular network both between and across laminae (Figure 4) (40).

Figure 4.

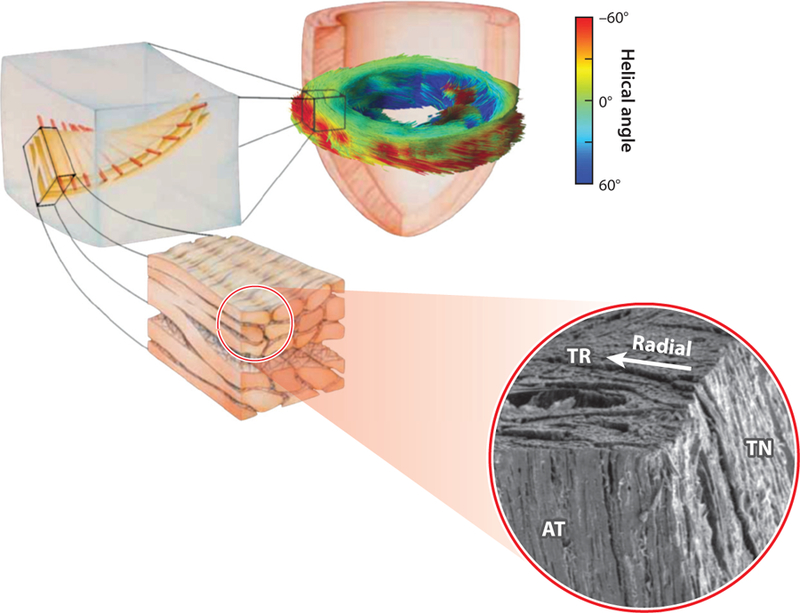
Schematic of cardiac microstructure showing transmural fiber orientation and branching sheet structures. Abbreviations: TR, transverse; AT, axial-transmural; TN, tangential planes. Combined figure adapted from References 25, 41, and 42.

With the advent of diffusion tensor magnetic resonance imaging (DT-MRI) that can capture myofiber directions in full 3D, a tremendous amount of information has become available. Consistent with the description obtained from electron microscopy of small cuboidal specimens, DT-MRI has revealed that laminar surfaces appear roughly as twisted surfaces going across the wall and stacked from apex to base (33). Anderson et al. (27) proposed two families of fibers: one tangential to the epicardial surface and another at approximately 40° to the epicardium running across the wall thickness without any orderly arrangement of supporting fibrous tissue. Interestingly, this description of cardiac fiber structure suggests that the septum, shared by the left ventricle (LV) and the right ventricle (RV), anatomically belongs to the LV. Different dominant muscle layers in the same heart at different transmural depths have also been observed using DT-MRI (43).

The ECM and the mechanical support it provides play important roles in development, remodeling, and signaling in myocardium. The ECM maintains the structural integrity of blood vessels and myocytes and facilitates the load transfer throughout the myocardial wall during active contraction (46). The triple-helical structure of collagen is known to be relatively stiff, such that a modest fibrotic increase in collagen content following pressure overload or myocardial infarction could lead to a substantial increase in local tissue stiffness (47). In addition to the role of the ECM in the overall stiffness of myocardium, its composition is an important factor in the structural anisotropy of myocardium. For instance, the development of large forces in the cross-fiber direction in contracting myocardium (Figure 5a) is still puzzling, while complex architecture of the ECM is suspected to be a key contributor to this behavior (45). Additionally, the transmural variation in ECM composition leads to differences in elastic anisotropy at various myocardial depths (22, 48).

Figure 5.

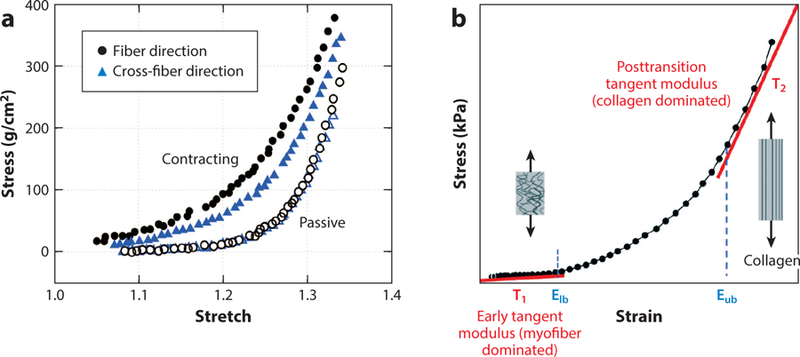
(a) Active contraction in fiber and cross-fiber directions observed by Lin & Yin (45) (using barium contracture in rabbit left ventricular tissue). (b) Stress–strain curve showing three distinct stiffness regions—myofiber dominated, transitioning, and collagen dominated—in the passive biomechanical response of myocardium. E_lb and E_ub represent the lower and upper bound strains of collagen recruitment, respectively. Panel b adapted from Reference 44.

As in the body’s connective tissues, the collagen fibrils in myocardium are initially coiled or crimped in a twisted configuration to enhance tensile strength at higher strains (34). Since this crimping does not initially bear load, it follows that the behavior of myocardium at low-strain regimes is governed by the myofiber response alone, whereas collagen fibers and their interactions with myofibers dominate the behavior at higher strains (Figure 5b). At slack length, collagen fibers of epi- and endocardium layers form a crisscross pattern, while at peak systole, the fibers become aligned along longitudinal and circumferential directions. This may be a well-designed mechanism to protect overstretching of the myocytes and minimize the amount of shear stress sustained during systole (49). Lastly, in rat papillary muscles, Robinson et al. (34) observed elastic fibers (elastin) helically running around the myocytes. These also suggested that, during the cardiac cycle, the elastin fibers facilitate diastolic expansion by storing energy during systole.

3. BIOMECHANICS OF PASSIVE MYOCARDIUM

There has been a long-standing interest in quantifying the forces and stresses acting in the myocardium for both a fundamental understanding of cardiac mechanics and clinical implications (e.g., 50–56). Three important reasons to quantify myocardium wall stresses in health and/or disease (53) are as follows: (a) The wall stress determines myocardial oxygen consumption; (b) the renormalization of the wall stress may serve as a feedback cue for myocardial remodeling in diseases characterized by abnormal loading of the ventricles, such as pulmonary hypertension and congestive HF; and (c) an understanding of ventricular mechanics may lead to insights into the fundamental principles underlying the general function of the heart. Given the tremendous advances in computational modeling, quantitative knowledge of the evolving changes and adaptations over time of the ventricular stress distribution (during the cardiac cycle) can be used as a target to guide the optimal design of medical devices by virtual prototyping (57, 58), as well as the design of ventricular interventions such as hydrogel injection (59, 60).

3.1. Constitutive Modeling: The Gateway to Cardiac Function Simulation

Constitutive modeling is the development of mathematical relationships between myocardial wall kinematics (the deformations of the tissue during the cardiac cycle) and wall stresses (the localized forces acting on a continuum element of the tissue). It is currently possible to quantify ventricular wall kinematics experimentally with diverse imaging techniques. Yet, ventricular wall stresses cannot be measured directly—they must be computed through constitutive relationships. In this section, we review constitutive models developed for the passive behavior of myocardium. We focus on contemporary models that consider myocardium to exhibit nonlinear and anisotropic behavior, consistent with its fibrous structure. Also, we restrict our attention to incompressible models of myocardium, with a brief discussion of the effect of compressibility in the last section.

The mechanical behavior of myocardium is usually approached by assuming it is pseudoelastic (11) and is therefore described by a pseudoelastic stored energy density function W (61). Before describing the existing forms of W in detail, we present a brief review of the basic relevant kinematic relations and stress definitions (for further details, see, e.g., References 62 and 63).

Upon application of external loading, a material point X in the reference configuration of the representative tissue element moves to a new point x = x(X, t ) at time t in the deformed configuration. The deformation gradient tensor F = Grad x characterizes the deformation of the material. The right and left Cauchy–Green tensors are defined as C = F^T F and B = F F^T, and the Green–Lagrange strain tensor is given by E = (C − I)/2, where I is the identity tensor. The second Piola–Kirchhoff stress tensor S can be described in terms of the stored energy density function W through

$$\mathbf{S}=2\frac{\partial W}{\partial \mathbf{C}},$$ 1.

and the Cauchy stress tensor is given by σ = J⁻¹ FS F^T, with J = det(F). Finally, for the case of nearly incompressible tissues, the above constitutive relation is replaced by

$$\mathbf{S}=2\frac{\partial W}{\partial \mathbf{C}}-p{\mathbf{C}}^{-1},$$ 2.

where p is the hydrostatic pressure and the incompressibility constraint J = 1 is enforced.

An established approach in constitutive modeling involves treating the tissue as a continuum and assuming that at any given point there exists both intracellular and extracellular space. This assumption implies that the variables of interest (e.g., strain and stress) are measured (or estimated) at a sufficiently large length scale in comparison to the underlying discrete structures. Within the realm of this assumption, the available models for constitutive behavior of the myocardium can be divided into two groups: phenomenological and structurally informed. We define phenomenological models as those that are based on general empirical observations of the material symmetry of the myocardium and that do not account for further specific compositional and structural information of the myocardium. In contrast, we define structurally informed models as those that contain quantitative information about the composition and microstructure of the myocardium, generally on a scale of less than 1 mm for human hearts. Both types of models are described below.

3.2. Phenomenological Constitutive Models

Phenomenological models aim to describe the lumped effects of different fibrous constituents (e.g., myo- and collagen fibers) inside a continuum element. On the basis of a chosen material symmetry, W for these models is often expressed in terms of kinematic invariants of the right Cauchy–Green deformation tensor C. The formulation of W based on these invariants offers a wide range of forms in correspondence with the anisotropy spectrum of the tissue. In addition, physical interpretations of the kinematic invariants allow W to be specified by including each individual term to represent a constituent or reflect an underlying mechanism. In contrast, it is sometimes more convenient to express energy in terms of the components of the strain tensor E because it is easier to control strain components in an experimental setup than to control deformation invariants. This approach also facilitates the identification of the specific form of the energy function, provided that the available mechanical data based on the strain components sufficiently cover the kinematic space. However, when choosing specific forms of W based on components of E, one must take extra care not to violate the principle of material frame indifference.

In the following subsections, we review both energy forms and categorize them into two classes: transversely isotropic and orthotropic models. For the sake of brevity, we describe the general form of energy for each category; Table 1 presents the specific forms of the energy function W for phenomenological models.

Table 1.

Summary of phenomenological constitutive models for passive behavior of myocardium^a

Invariant-based models: W = Ψ(Ii)
Isotropic W = Ψ(I1, I2 )	Fuchs et al. (64) Ψ = A (I1 − 3) + B (I2 − 3)	Guccione et al. (66) $\mathrm{\Psi }=A\left[e^{B\left(I_1-3\right)}-1\right]$
Transversely isotropic W = Ψ(I1, I2, I4 )	Humphrey & Yin (67) $$\begin{gathered} \mathrm{\Psi }=A\left[e^{B\left(I_1-3\right)}-1\right] \\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}+C[e^{D{\text{(}\sqrt{I_4}-1\text{)}}^2}-1] \end{gathered}$$	Humphrey et al. (68) $$\begin{gathered} \mathrm{\Psi }={\sum }_{i=1}^2{A}_i{\left(I_1-3\right)}^i \\ \hspace{1em}\hspace{1em}+{\sum }_{i=1}^2{B}_i{(\sqrt{I_4}-1)}^{i+1} \\ \hspace{1em}\hspace{1em}+C(I_1-3)(\sqrt{I_4}-1) \end{gathered}$$
	Lin & Yin (45) W = A (eQ − 1), Q = B1(I1 − 3)2 + B2(I1 − 3) (I4 − 1) + B3(I4 − 1)2
	Kerckhoffs et al. (69) $\mathrm{\Psi }=A\text{{}{e}^{\text{[}B\hspace{0.17em}{I}_1^2+C\hspace{0.17em}{I}_2-\text{(3}\hspace{0.17em}B\text{+}C\text{)(2}\hspace{0.17em}{I}_1-3\text{)]}}-1\text{}}+D\hspace{0.17em}\text{[}{e}^{E{\left(I_4-1\right)}^2}-1\text{]}$
Orthotropic W = Ψ(I1, I2, I4, I6, I8 )	Holzapfel & Ogden (70) $\mathrm{\Psi }=A[e^{B\left(I_1-3\right)}-1]+C[e^{D{\left(I_4-1\right)}^2}-1]+E[e^{F{\left(I_6-1\right)}^2}-1]+G[e^{H\hspace{0.17em}{I}_8^2}-1]$
	Schmid et al. (71) $\mathrm{\Psi }=A[e^{B{\left(I_1-3\right)}^2}-1]+C[e^{D{\left(I_2-3\right)}^2}-1]+{\sum }_i^{f,s,n}{E}_i[e^{F_i{\left(I_i-1\right)}^2}-1]$
Strain component–based models: W = Ψ(Eij )
Transversely isotropic	Yin et al. (72) $\mathrm{\Psi }=A[e^{B_1\hspace{0.17em}{E}_{11}^n+B_2\hspace{0.17em}{E}_{22}^n}-1]$	Guccione et al. (66) $\mathrm{\Psi }=A\left[e^Q-1\right]$, $$\begin{gathered} Q=B_1\hspace{0.17em}\text{tr}(\mathbf{E})+B_2\hspace{0.17em}{E}_{f\hspace{0.17em}f}^2 \\ \hspace{1em}\hspace{1em}+B_3(E_{ss}^2+E_{nn}^2+2E_{sn}^2)+B_4(E_{f\hspace{0.17em}s}^2+E_{f\hspace{0.17em}n}^2) \end{gathered}$$
	Hill et al. (73) $\mathrm{\Psi }=A\left[e^{B_1\hspace{0.17em}{E}_{11}^2}+e^{B_2\hspace{0.17em}{E}_{22}^2}+e^{B_3\hspace{0.17em}{E}_{11}\hspace{0.17em}{E}_{22}}-3\right]$
Orthotropic	Hunter et al. (74) $\mathrm{\Psi }={\sum }_{i,j}{A}_{ij}{E}_{ij}^2/{\left|B_{ij}-\left|E_{ij}\right|\right|}^{C_{ij}}\left(i,j=f,s,n\text{;}\hspace{0.17em}{A}_{ij}=A_{ji}\text{;}\hspace{0.17em}{B}_{ij}=B_{ji}\text{;}\hspace{0.17em}{C}_{ij}=C_{ji}\right)$
	Costa et al. (75) Ψ = A [eQ − 1], $Q={\sum }_{i,j}{B}_{ij}{E}_{ij}^2\left(i,j=f,s,n\text{;}\hspace{0.17em}{B}_{ij}=B_{ji}\right)$
	Schmid et al. (76) $\mathrm{\Psi }={\sum }_{i,j}{A}_{ij}[e^{B_{ij}{E}_{ij}^2}-1],\left(i,j=f,s,n\text{;}\hspace{0.17em}{A}_{ij}=A_{ji}\text{;}\hspace{0.17em}{B}_{ij}=B_{ji}\right)$

^aA, B, …, H are biomechanical material constants.

3.2.1. Invariant-based models.

To the best of our knowledge, Fuchs et al. (64) proposed the first (nonlinear) isotropic model for myocardial tissues that has the same form as the Mooney–Rivlin model used in the context of rubber elasticity (65). Also, Guccione et al. (66) studied the classical isotropic Fung model as the special case of their anisotropic model.

3.2.1.1. Transversely isotropic.

Myocardium exhibits a strongly anisotropic behavior arising mainly from the arrangement of myofibers and the collagen network (see Section 2). Transversely isotropic models were the first phenomenological models proposed to account for the anisotropy of myocardium. Following an idealization of the microstructure, these models lump all fiber types into an effective fiber constituent, identified by the local mean fiber direction f₀ in the reference configuration. Therefore, the energy function W takes the functional form W = ψ(I₁, …, I₅ ), where the invariants I₄ and I₅ account for the fiber contributions, defined as

$$I_4={\mathbf{f}}_0\cdot \mathbf{C}\hspace{0.17em}{\mathbf{f}}_0,\hspace{1em}{I}_5={\mathbf{f}}_0\cdot {\mathbf{C}}^2\hspace{0.17em}{\mathbf{f}}_0.$$ 3.

Stored energy density functions for transversely isotropic (phenomenological) models are commonly proposed in the reduced form of W = ψ(I₁, I₄ )—although this reduction has recently been debated (77), demonstrating the importance of the I₅ term under simple shear loading conditions. For the reduced form, the Cauchy stress tensor can be written as

$$\mathbf{\sigma }=-p\hspace{0.17em}\mathbf{I}+2W_1\hspace{0.17em}\mathbf{B}+2W_4\hspace{0.17em}\mathbf{f}\hspace{0.17em}\otimes \hspace{0.17em}\mathbf{f},$$ 4.

where f = F f₀ denotes the fiber direction in the deformed configuration, and W_i = ∂W/∂I_i.

Perhaps the first phenomenological model of this form was a simple generalized Fung-type model proposed by Humphrey & Yin (67). Thereafter, more involved choices of W were proposed; these include both polynomial forms, originally proposed by Humphrey et al. (68, 78), and exponential forms, such as those put forward by Lin & Yin (45) and Kerckhoffs et al. (69). Note that these models (45, 68, 78), in addition to the individual I₁ and I₄ terms, include coupling (i.e., a term with I₁ and I₄) to account for the interactions between the ground matrix and the fibers.

3.2.1.2. Orthotropic.

More recent histological studies of the microstructure of myocardial tissues indicate that the myocardium is a composite of layers (or sheets) of tissue separated by “cleavage planes” (see Section 2.1). Each sheet is composed of locally parallel muscle fibers in the sheet plane and is interconnected with a spatial network of collagen fibers. On the basis of this description, the microstructure of myocardium can be characterized by an orthonormal set of base vectors consisting of the unit vector f₀, aligned with the average fiber direction (or fiber axis); the unit vector s₀, which is in the plane of the sheet and orthogonal to the fiber axis; and the unit vector n₀, which is normal to the plane of the sheet. Figure 6a depicts the layered structure and the associated orthogonal set. In this review, we use the subscripts f, s, and n to denote the fiber, sheet, and normal directions, respectively.

Figure 6.

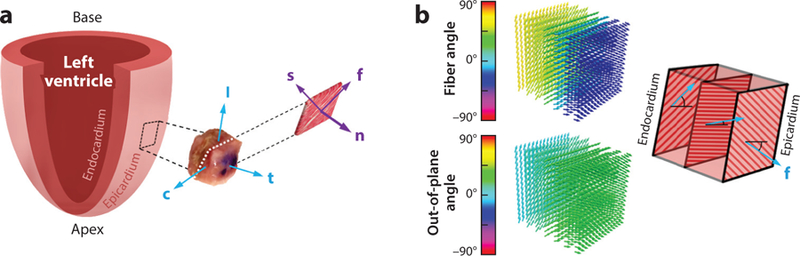
(a) Schematic representation of the fiber–sheet–normal microstructure. The mean myofiber direction is denoted by the vector f, the direction transverse to the fiber axis within the layers is denoted by s, and the direction normal to the layers is denoted by n. (b) Model of the heart wall as a layered structure, with each layer exhibiting transverse isotropy. Other vectors: c, circumferential direction; l, longitudinal direction; t, transmural direction. Panel a inspired by Reference 79. Panel b inspired by Reference 80.

Orthotropic phenomenological models (based on the above-mentioned description of myocardial microstructure) rely on the intuitive fact that the local effective behavior of the myocardium in the plane transverse to the fiber direction (i.e., the s₀–n₀ plane) is not isotropic. In the case of incompressible orthotropic materials characterized by the material directions (f₀, s₀, n₀ ), the stored energy density function W takes the functional form W = ψ(I₁, I₂, I₄, I₅, I₆, I₇ ), where I₆ and I₇ are two additional deformation invariants, defined as

$$I_6={\mathbf{s}}_0\cdot \mathbf{C}\hspace{0.17em}{\mathbf{s}}_0,\hspace{1em}{I}_7={\mathbf{s}}_0\cdot {\mathbf{C}}^2\hspace{0.17em}{\mathbf{s}}_0.$$ 5.

In this case, it is useful to introduce an additional (dependent) invariant I₈, defined as (81)

$$I_8^2={\left[{\mathbf{f}}_0\cdot \left(\mathbf{C}\hspace{0.17em}{\mathbf{s}}_0\right)\right]}^2=I_2+I_4{I}_6+I_5+I_7-I_1\left(I_4+I_6\right).$$ 6.

Reduced forms of W for orthotropic models are commonly employed and are given by W = ψ(I₁, I₂, I₄, I₆, I₈ ). For such a model, the Cauchy stress tensor can be written as

$$\begin{gathered} \mathbf{\sigma }=-p\hspace{0.17em}\mathbf{I}+2\left(W_1+I_1\hspace{0.17em}{W}_2\right)\mathbf{B}-2\hspace{0.17em}{W}_2\hspace{0.17em}{\mathbf{B}}^2 \\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}+2\hspace{0.17em}{W}_4\hspace{0.17em}\mathbf{f}\otimes \mathbf{f}+2\hspace{0.17em}{W}_6\hspace{0.17em}\mathbf{s}\otimes \mathbf{s}+W_8\left(\mathbf{f}\otimes \mathbf{s}+\mathbf{s}\otimes \mathbf{f}\right), \end{gathered}$$ 7.

where s = F s₀ denotes the fiber direction in the deformed configuration.

A prominent invariant-based orthotropic model was introduced by Holzapfel & Ogden (70) on the basis of the orthonormal material directions (f₀, s₀, n₀ ). An advantage of this model over earlier transversely isotropic models is that it can put into evidence (a) the nonisotropic behavior of myocardium in the plane transverse to the fiber direction and (b) the possible interaction between the fiber and sheet directions when compared with the simple shear experimental data of Dokos et al. (79). A similar constitutive form accounting for the contribution of the myocardial behavior in the n₀ direction was later developed (71). The energy forms consisting of (I _f, I_s ), (I _f, I_n ), (I_s, I_n ), or (I _f, I_s, I_n ) performed strikingly similarly, probably because of the interdependence between these invariants: I₁ = I _f + I_s + I_n.

3.2.2. Strain component–based models.

Constitutive models developed in terms of the components of the strain tensor (E_ij) are remarkably useful for experimental testing systems that provide data for fitting their parameters; however, they need to satisfy the principle of material frame indifference for applicability to all other deformations.

3.2.2.1. Transversely isotropic.

Yin et al. (72) proposed a simple Fung-type energy function for the biaxial behavior of myocardium, which consists of one exponential term as a polynomial function of strain components E₁₁ and E₂₂. The axes of the test apparatus, identified by the e₁ and e₂ directions, were taken to be aligned with the fiber and cross-fiber directions, respectively. Although aligning the material and apparatus axes facilitates parameter identification due to the minimization of in-plane shearing, it could severely limit the kinematic space within which the fitted model can reasonably predict the tissue behavior (82, 83). This point is discussed further in Section 3.4, below. In addition, Yin et al.’s model did not include the coupling term between the behaviors in two perpendicular directions, as was later demonstrated to be important for the biaxial behavior of the right ventricular free wall (RVFW) myocardium (73, 84).

Guccione et al. (66) proposed a transversely isotropic model for the 3D behavior of myocardium. The model uses an idealized cylindrical coordinate system ( f, c, r) representing fiber, cross-fiber, and radial directions and assumes that the behavior of the myocardium is the same in the cross-fiber and radial directions. The model accounts for coupling in the transverse plane, but not between the fiber and cross-fiber directions. Although subsequent experimental observations (25, 79, 85) revealed considerably orthotropic behavior of myocardium, this model offers a highly tractable implementation in organ-level finite-element simulations and has been extensively used for this purpose to date.

3.2.2.2. Orthotropic.

The so-called pole-zero model, presented by the Hunter group (41, 74), appears to be the first 3D orthotropic strain component–based model of myocardium. This model relies on the fiber–sheet–normal description of myocardium microstructure, and its W consists of six terms corresponding to contributions of the stretch along each material direction (i.e., the f₀, s₀, and n₀ axes) as well as the shearing within each material plane (i.e., f₀–s₀, f₀–n₀, and s₀–n₀ planes). In particular, the parameters A_ii (no sum) and A_ij (i ≠ j) correspond to the extensional stiffness along material axes and shear stiffness in the material planes, respectively. A peculiar feature of this model is that it exhibits inextensibility at some limiting strains (or poles), characterized by the parameter B_ij, which can occur in both stretching and shearing. Although myocardium commonly exhibits a strong stiffening effect (but not quite inextensibility) when subjected to large-strain equibiaxial loading (45, 86), whether an exponential function can sufficiently capture such stiffening is debatable.

Costa et al. (75) proposed a generalization of the Fung-type (exponential) model by Guccione et al. (66) to an orthotropic model to distinguish between the behaviors in two cross-fiber directions. This model requires seven parameters, and its exponential stiffening is consistent with the results of simple shear tests performed by Dokos et al. (79). However, as is the case for Guccione’s model (66), it is still worth investigating the necessity of including coupling terms between the stretching in the fiber and cross-fiber directions.

Finally, motivated by the simple shear experiments by Dokos et al. (79), Schmid et al. (76) adopted the fiber–sheet–normal functional form of the pole-zero model and presented new models by changing the descriptor function $a\hspace{0.17em}{E}^2/\left(b-{\left|E\right|}^c\right)$ in the pole-zero model to another function. The descriptor functions these authors proposed include the exponential form $a\hspace{0.17em}{e}^{b\hspace{0.17em}{E}^2}$ and a IntTan(b E² ), where the function IntTan(x) denotes the Taylor series of the indefinite integral of tan(x), truncated after the fifth term. The idea behind this form is to construct a descriptor that exhibits strong-enough stiffening at large stretches but does not have an infinite slope like the pole-zero function, which is difficult (and not advisable) to implement in computational analyses.

3.3. Structurally Informed Models

The phenomenological models reviewed in the preceding section offer a quantitative tool to describe the effective behavior of the tissue without taking into account statistical information about the compositional detail and structural and material properties of the myocardium constituents. For this reason, it is difficult to precisely infer from these models the micromechanical mechanisms that involve the coupling between myocytes and collagen fiber ensembles under physiological or pathological conditions.

In contrast, structurally informed models are based on descriptors that account for compositional and microstructural details (typically on a scale of less than 1 mm), which attempt to establish a link between the effective biomechanical behavior of myocardium and the underlying mechanisms taking place at the microstructural level. In practice, because of the profound complexity of myocardium microstructure, these models are developed following appropriate idealizations.

For the case of structural models, W is usually written as the sum of the mechanical contribution of the continuous ECM and its embedded fibers, including myo- and collagen fibers:

$$W={\mathrm{\Psi }}^g\left(I_1\right)+{\mathrm{\Psi }}^f\left(I_1\right)={\mathrm{\Psi }}^g\left(I_1\right)+{\mathrm{\Psi }}^m\left(\mathbf{E}\right)+{\mathrm{\Psi }}^c\left(\mathbf{E}\right)+{\mathrm{\Psi }}^i\left(\mathbf{E}\right),$$ 8.

where the contribution of the ground matrix W^g is isotropic and a function of I₁. The fiber contribution ψ ^f can be further split into terms describing the contributions of myofibers (m), collagen fibers (c), and the interactions between them (i), in the mechanical behavior of myocardium. Note that the mass/volume fraction for each constituent is commonly absorbed by the respective term in Equation 8. The effective energy contribution for each fiber type is the sum of the energies for all the fiber ensembles, weighted by the orientation distribution function R(N), where N is a unit vector identifying the span of fiber orientation in the reference configuration. The energy function for each fiber ensemble is commonly expressed in terms of deformation only along the fiber, denoted by w(I ^f ), where I ^f = N · C N is an invariant associated with the fiber deformation. As a result, the average of w(I ^f ) over all the fiber ensembles in the representative tissue element Ω may be written as

$${\mathrm{\Psi }}^f={\int }_{\Omega }R\left(\mathbf{N}\right)w\left(I^f\right)d\mathrm{\Omega }.$$ 9.

For the case of collagen fibers, they are known to be undulated in the zero-stress state, and given their negligible bending stiffness, they do not accommodate any applied loading until fully straightened. Thus, the actual (true) deformation in an individual fiber can be expressed as $I^t=I^f/{\lambda }_s^2$, where λ_s is the fiber slack stretch. With the use of a distribution function D(λ_s) to account for the gradual recruitment of undulated fibers in a statistical sense, the energy contribution of collagen fibers can be rewritten as

$${\mathrm{\Psi }}^f={\int }_{\mathrm{\Omega }}R\left(\mathbf{N}\right)w^{*}\left(I^f\right)d\mathrm{\Omega }={\int }_{\mathrm{\Omega }}R\left(\mathbf{N}\right){\int }_{x=1}^{\sqrt{I^f}}D\left(x\right)w\left(I^t\right)dx\hspace{0.17em}d\mathrm{\Omega },$$ 10.

where x is a dummy variable in the stretch space of each individual fiber, and w^∗ is the modified energy accounting for the recruitment. Below, we review some existing structural models in chronological order (Table 2).

Table 2.

Summary of structural constitutive models for passive behavior of myocardium^a

General form for structurally informed models W = Wg(I1 ) + W f (E, N, R, D)	Reference
ψg = 0, ψ f = ψm + ψc  ${\mathrm{\Psi }}^m={\int }_{-\pi /24}^{\pi /24}{R}_1{w}_1^{*}d\alpha$, ${\mathrm{\Psi }}^c={\int }_{-\pi /24}^{-\pi /24}{\int }_0^{2\pi }{\int }_0^{\pi }{R}_2{w}_{2}Jd\varphi \hspace{0.17em}d\theta \hspace{0.17em}d\alpha$  $w_k=A_k{ϵ}_k^2,\hspace{0.17em}{D}_k\left(x\right)=1/\text{(}\sqrt{2\pi }{\sigma }_k\text{)}{e}^{-\left(m_k-x\right)/2{\sigma }_k^2}$, k = 1, 2, ‹ is the fiber true strain	Horowitz et al. (87)
${\mathrm{\Psi }}^g=A[e^{B\left(I_1-3\right)}-1]$, ${\mathrm{\Psi }}^f={\int }_{R_i}^{R_o}w\hspace{0.17em}dR$  $w=C[{ϵ}^{D{\text{(}\sqrt{I^f}-1\text{)}}^2}-1]$	Humphrey & Yin (80)
ψg = 0,  ${\mathrm{\Psi }}^f={\int }_{-\pi /2}^{\pi /2}{R}_1{w}_1\hspace{0.17em}d\theta +{\int }_0^{\pi }{R}_2{w}_2\hspace{0.17em}d\theta +{\int }_0^{\pi }{\int }_0^{\pi /2}{R}_3{w}_3\hspace{0.17em}d\theta \hspace{0.17em}d\varphi$  $w_k=A_k{ϵ}^2/{\left(B-ϵ\right)}^C$, $k=1,2,3$, $ϵ=\left(I^f-1\right)/2$	Hunter et al. (74)
ψg = ϕg kg/2 (I1 − 3),  ${\mathrm{\Psi }}^m=\frac{{\varphi }^m}{H}\hspace{0.17em}{\int }_0^H{\int }_{-\pi /2}^{\pi /2}{R}^m\left(\theta ,z\right)w^m\left(I^m\right)d\theta \hspace{0.17em}dz$, ${\mathrm{\Psi }}^c=\frac{{\varphi }^c}{H}\hspace{0.17em}{\int }_0^H{\int }_{-\pi /2}^{\pi /2}{R}^c\left(\theta ,z\right)w^{*c}\left(I^c\right)d\theta \hspace{0.17em}dz$,  ${\mathrm{\Psi }}^i=\frac{{\varphi }^c}{H}\hspace{0.17em}{\int }_0^H{\int }_{-\pi /2}^{\pi /2}{\int }_{-\pi /2}^{\pi /2}{R}^m\left({\theta }^m,z\right)R^c\left({\theta }^c,z\right)w^{*i}\left(I^m,I^c\right)d{\theta }^m\hspace{0.17em}d{\theta }^c\hspace{0.17em}dz$,  $w^m=\frac{k_1^m}{2\hspace{0.17em}{k}_m^2}\text{[}{e}^{k_2^m{\left(\sqrt{I^m}-1\right)}^2}-1\text{]}$, $w^{*c}=\frac{k^c}{2}{\text{(}\sqrt{I^c}/{\text{λ}}_c-1\text{)}}^2$,  $w^{*i}=\frac{k_1^i}{2\hspace{0.17em}{k}_i^2}\text{{}{e}^{k_2^i\text{(}{I}^m+I^c-2\text{)}}-\text{[}{k}_2^i\left(I^c/{\text{λ}}_c^2-1\right)+1\text{]}{e}^{k_2^i\left(I^m-1\right)}\text{}}$	Avazmohammadi et al. (88)

^aThe reader is referred to the respective references for additional details on the constants and variables.

3.3.1. Horowitz model.

Building on the structural model by Lanir (89) for general connective tissues, Horowitz et al. (87) proposed a model that accounts for the distribution of both myo- and collagen fibers. The system of collagen fibers exhibits a “hairy” arrangement, connecting the myofibers to one another. All the fibers are assumed to behave linearly once recruited. The orientation of the fibers is described in spherical coordinates.

3.3.2. Humphrey model.

Motivated by the layered morphology of the myocardium, Humphrey & Yin (80) proposed a simple structural model that treats the heart as a layered composite, with each layer exhibiting transverse isotropy with in-plane fiber direction N (Figure 6b). An approximate linear transmural variation for the vector N allows the calculation of the average of w(I ^f ) over the thickness of myocardium. However, this model does not account for distribution of fibers within each layer, and assumes that the effect of gradual recruitment of fibers is negligible (w^∗ = w). The behavior of each layer is characterized by the phenomenological energy function of Humphrey & Yin (67). Sacks & Chuong (90) later proposed a similar constitutive model for RVFW myocardium, with the modification that the model makes use of the energy form of Humphrey et al. (68) for each layer instead.

3.3.3. Hunter model.

Hunter et al. (74) proposed a structural model that accounts for the distribution of fibers about the orthogonal fiber–sheet–normal microstructural directions and makes use of the pole-zero descriptor aE²/(b − E )^c to characterize the response of all families of fibers. The energy is written as the sum of the contributions of three families of fibrous connective tissues (mainly collagen); however, the effect of gradual recruitment of fibers is assumed to be negligible. The fiber orientation within each family has a Gaussian distribution about a mean direction, which is aligned with each of the microstructural directions (i.e., f₀ = N₁, s₀ = N₂, and n₀ = N₃).

3.3.4. More recent models.

Surprisingly, the area of structural modeling of myocardium seems to have been inactive after Hunter et al.’s (74) model, until recently. This may be due to persistent difficulties in achieving a thorough quantitative characterization of the collagenous ECM in myocardium, which has recently become more feasible through advances in imaging and image processing. For instance, Lee et al. (91) revisited the structural models by Horowitz et al. (87) and Eriksson et al. (92). Krishnamurthy et al. (93) studied the effect of fiber dispersion on myocardium active behavior. Avazmohammadi et al. (88) developed a structural model for the passive behavior of RVFW myocardium using histologically measured, 3D transmural orientation distributions for both myo- and collagen fibers. By taking advantage of these measurements, their model accounted for the contribution of both myo- and collagen fibers and the interaction among them in the mechanical behavior of myocardial tissues.

3.4. Optimal Design of Mechanical Tests: A Critical Need

Schmid et al. (71, 76) compared different material models by using three metrics: goodness of fit, determinability, and variability. Goodness of fit is a measure of how well the model fits the data. Determinability describes how sensitive the material parameters are to disturbances in the data. Finally, variability reflects how broadly a material parameter could vary between the individual fits. However, the core approach underlying contemporary studies on evaluating myocardium material laws is limited to finding a model that best fits the existing data. To date, this approach has been prevalent in the general field of tissue characterization, which, in our opinion, reflects a disconnect between the experiments and the a posteriori chosen model. As a result, the estimated parameters may not be able to sufficiently predict the behavior of the tissue in general loading conditions (not included in the original data) and may not be stable against the presence of noise, although they provide a “best” fit to the existing data.

While the form of the model is critical for the characterization of myocardium, a reverse approach may provide more robust results (i.e., choosing an appropriate model and determining what experiments are best to quantify the model), referred to as optimal loading paths. Indeed, although a complete suboptimal set of strain paths is sufficient to quantify a 3D form of W for myocardium and to provide an excellent fit of the form to those paths, it may fall short in adequately describing the behavior of myocardium under general boundary conditions during a cardiac cycle. Along these lines, Avazmohammadi et al. (13) proposed an approach that not only is based on the full 3D kinematic space but also (more importantly) uses the theory of optimal design of experiments to determine the optimal loading paths for a given model form. These authors demonstrated that carrying out such an analysis before performing the experiment is essential to secure sufficient predictive capability and determinability of the chosen model. Such attributes were not evaluated in previous 3D studies.

3.5. Is Fiber Structure Essential in Modeling Myocardium Mechanical Behavior?

The length scale of structural units in the myocardium, such as the collagen network and myocytes, ranges from nanometers to micrometers; thus, accurate modeling of the myocardium in sufficient detail is inherently a multiscale problem. Moreover, the structural characteristics of myocardium, such as the local orientation of the myo- and collagen fibers, are spatially heterogeneous and vary with position throughout the tissue from base to apex and from endocardium to epicardium. Therefore, the myocardium does not actually possess structural uniformity, which is essential to define a representative tissue element for an inhomogeneous specimen (94). In practice, many experimental analyses of the mechanical behavior of the myocardium (72, 79, 95) are performed on an intermediate scale, which consists of a cubic slice from base, equator, or apex. This intermediate scale is referred to as the mesoscopic scale. In the porcine heart, a representative cubic slice typically measures 3 × 3 × 3 mm (79), but these dimensions vary depending on the size of the heart wall. Unless the structural uniformity across the cubic samples is demonstrated, it is crucial to account for the variations of the directions of the local myo- and collagen fibers to obtain an accurate characterization of myocardium (92, 96–98).

4. ELECTROMECHANICAL MODELING OF MYOCARDIUM

The formulation of cardiac electromechanics can be presented through three distinct interconnected models and their governing equations (99, 100), namely (a) cell model equations characterizing the transmembrane current and action potential in terms of ion concentrations, (b) reaction–diffusion equations characterizing the propagation of electrical excitation, and (c) the equations of motion of continuum mechanics. These equations are incorporated with two sets of constitutive laws: (a) the stress–strain relations for the passive behavior of myocardium (covered in Section 3) and (b) the relationship among active tension, calcium concentration, and cell kinematics (101, 102). Reviewing the latter is beyond the scope of this review; instead, we focus on the available continuum-level methods to couple the mechanically active and passive behaviors of myocardium.

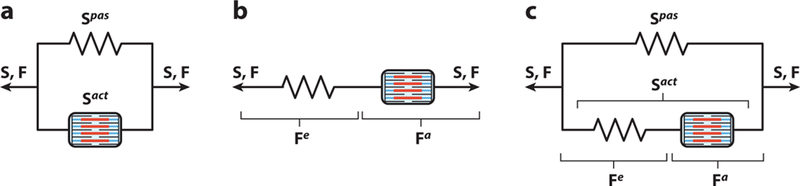
There are currently three common approaches to incorporating the active contraction into the mechanics of the myocardium: (a) active stress, (b) active strain, and (c) Hill’s three-element model. These approaches can be represented by different arrangements of passive (or spring) elements and contractile elements (Figure 7). We review each in turn below.

Figure 7.

Schematic representations of active contraction model. (a) Active stress model consisting of a contractile element in parallel with the passive spring element. (b) The active strain model consisting of a passive spring element in series with a contractile element. (c) Hill’s three-element model consisting of two spring elements in parallel and in series with a contractile element. Abbreviations: a and act, active; e, elastic; pas, passive; S and F, total stress and deformation gradient tensors, respectively.

4.1. Active Stress

The most common approach to account for active tension in myocardial mechanics is to linearly add the forces generated by muscle contraction to the passive forces, represented by parallel spring and contractile elements (Figure 7a). This additive decomposition of the total stress is expressed simply as (41, 45, 103–105)

$$\mathbf{S}={\mathbf{S}}^{act}+{\mathbf{S}}^{pas}={\mathbf{S}}^{act}+2\frac{\partial \hspace{0.17em}{W}^{pas}\left(\mathbf{F}\right)}{\partial \hspace{0.17em}\mathbf{C}},$$ 11.

where S^act and S^pas denote the active and passive parts of the total mechanical stress, respectively. In this model, both contractile and passive elements experience the same deformation (Figure 7a), which may not precisely represent the cross-bridge kinematics at the cellular level (Figure 2b).

4.2. Active Strain

A less common approach, called the active strain model (106–111), is inspired by the idea that production of active contraction is a dissipative process (unlike passive deformation, which is fully recoverable) (112). Rather than the stress, the total deformation instead follows a multiplicative decomposition, written as F = F^e F^a. The inelastic deformation F^a characterizes the muscle shortening, which is the result of the acto-myosin cross-bridge machinery (Figure 2b), and the elastic deformation F^e preserves the compatibility of the total deformation. The active contribution F^a needs to be constitutively provided as a function of the intracellular calcium concentration. The total stress in this case is given by

$$\mathbf{S}=2\frac{\partial \hspace{0.17em}W\left({\mathbf{F}}^e\right)}{\partial \hspace{0.17em}\mathbf{C}}.$$ 12.

In this approach, both contractile and passive elements experience the same stress but undergo different deformations (Figure 7b).

4.3. Hill Model

The third model, which can be considered a generalization of the two previous approaches, is inspired by the classical Hill model for excitation–contraction coupling (61, 113). This model consists of three elements (Figure 7c): one spring element and one contractile element in series (as in the active strain model), in parallel with another spring element (as in the active stress model). Accordingly, following a multiplicative decomposition for the deformation, and an additive decomposition for the stress, total stress can be expressed as (114–116)

$$\mathbf{S}={\mathbf{S}}^{pas}+{\mathbf{S}}^{act}\left(\mathbf{F},\hspace{0.17em}{\mathbf{F}}^a\right).$$ 13.

The parallel spring gives rise to the passive response of the tissue (i.e., the response when no active contraction is present). Together, the series and contractile elements characterize the mechanics of muscle activation. The series element accounts for the additional elastic stiffness that arises when the cross-bridges are engaged (117). The contractile element generates the active force, representing the kinetics of cross-bridge sliding (Figure 2b).

4.4. Structural Modeling of Myocardium Involving Active Contraction

Overall, constitutive biomechanical modeling of contracting myocardium and the underlying mechanisms have been scarcely studied. Pioneering research pertaining to the biaxial characterization of myocardium during active contraction traces back to Lin & Yin (45). A significant finding of this study was the development of remarkably large forces in the cross-fiber direction (Figure 5a) that could not be explained solely by myofiber dispersion about the mean fiber direction. Surprisingly, very few similar studies were conducted thereafter. Recently, however, Krishnamurthy et al. (93) took an important step by developing a biophysical model that integrates cross-bridge mechanics with the passive behavior of myofibers to explain the interaction between the fiber and transverse directions in the active state. In summary, there remains a pressing need for 3D characterization of the mechanical behavior of contracting myocardium, as well as for the development of integrated structural models that can identify the role of myo- and collagen fibers and their interaction in the contractile function of myocardium. Once implemented in an organ-level geometry, such models could provide new insights into the alterations of wall thickness during the cardiac cycle (21, 118).

5. FUTURE DIRECTIONS

5.1. Near-Term Landmarks

It should be clear from this review that comprehensive knowledge of the 3D mechanical behavior of myocardium is essential for understanding cardiac function in health and disease. Detailed tissue-level biomechanical models provide the mathematical framework for computational simulations that seek to link the structure and function of cardiac cells to the integrated behavior of the whole heart. While much progress has been made in such models, there remains a need for integrated approaches that enable (a) concise constitutive model forms to be developed on the basis of detailed tissue and cellular structural information, (b) identification of the optimal 3D tissue- and cellular-level experiments for model parameter identification, (c) experimental systems capable of conducting such 3D experiments, (d) comprehensive inverse finite element–based methods that fully integrate all experimental data to determine the best parameter estimates, and (e) greater use of Bayesian and related approaches to improve how we deal with the variation and uncertainty of the source data. Such integrated approaches will lay the groundwork for identifying, evaluating, and improving the optimal mathematical forms of the strain energy function when using a hyperelastic approach.

In the near term, a specific key issue to address is minimizing kinematic measures and material parameter covariances (119, 120). This review has demonstrated that much is to be gained from integrated studies on determination of an optimal form of a constitutive model (which entails minimal covariance between its constituent kinematic sets) in conjunction with optimizing the loading paths (which minimize the correlation between the material parameters). Concerning the latter, we have found that identifying optimal deformation modes (e.g., 82) is particularly critical for predicting tissue behavior under generalized deformation states not used in parameter estimation (13). More specifically, given that myocardial tissues undergo complex combinations of multiple deformation modes simultaneously in vivo, loading paths consisting of both simple shear and other 3D loading conditions are likely better choices for characterizing the myocardium response. However, it must be noted that the design of optimal loading paths is closely interlinked to the development of a constitutive model form, which is intrinsic to the nature of modeling non-linear materials. For planar tissues, we have recently developed such an integrated approach (121), and similar 3D works for myocardium remain to be explored. Overall, while we have conducted the first of such studies (13), this is only an initial step. For example, this comprehensive approach is indispensable for the case of treated diseased myocardium—such as hydrogel injection (10, 60, 122, 123)—where the local myocardium is subjected to more complex loading conditions. In addition, the development of appropriate instrumentation will be essential for the implementation of general loading paths and comprehensive exploration of optimal design of experiments.

After an appropriate constitutive law for myocardium is chosen, a remaining challenge is to reliably estimate the material constants such that they exhibit minimal dependence on the applied boundary conditions and experimental noise. This demand is especially prominent for in vivo applications, where the range of deformations can be dramatically limited compared with that experienced in vivo. Although many recent studies have explored the assimilation of different in vivo measurements to estimate these constants (124–128), another important aspect of such inverse problems that has not received adequate attention is the choice of optimization algorithm. Most studies so far have relied on either standard gradient-based optimization algorithms such as gradient descent and Levenberg–Marquardt, or gradient-free techniques such as genetic algorithms. However, the highly nonlinear nature of the forward problem and the presence of often strong statistical variation in the measurements demand the utilization of more robust algorithms that can (a) reduce the number of forward iterations and (b) directly account for the presence of the noise in the measurements. In this view, stochastic optimization methods such as Markov chain Monte Carlo (129) and Bayesian optimization algorithms (130, 131) that incorporate adjoint methods (132) offer scalability, higher speed, and enhanced robustness for identification of material constants.

Moreover, existing studies have modeled myocardium as an elastic material, whereas a few works have extended the invariant-based model to explore the viscoelastic behavior of myocardium (115, 133–135). Accounting for viscoelasticity is especially important for elastography applications to properly simulate the effects of acoustic wave dissipation. Finally, in our recent cardiac simulations, the effects of compressibility in myocardium in vivo (136) were profound. In particular, we found that the use of incompressibility can induce an up-to-twofold increase in the estimated contractile stresses. Such errors clearly indicate the need for greater fidelity in biomechanical modeling of the myocardium.

5.2. Greater Integration with the Underlying Structure and Insights into Growth and Remodeling

The morphology, structure, and functional mechanical properties of the myocardium are tightly interconnected. Clearly, existing structural approaches (87, 88) continue to rely on stochastic tissue-level structural data and approaches. Our ability to obtain cellular-level structural information (137) has greatly outpaced its use in biomechanical model development. Thus, a major challenge is to extend tissue-level stochastic approaches (87–89) to directly integrate detailed 3D structural information. Such approaches will enable a more direct connection between cellular and subcellular mechanisms and organ-level function.

These detailed structural approaches are especially necessary to describe growth and remodeling (G&R) (138). Roughly speaking, there are two types of mechanisms underlying G&R responses to environmental cues. The first type, associated with growth, induces changes in the mass and volume of fiber aggregates. The second type, associated with remodeling, alters the mechanical and structural properties of fiber ensembles. Despite significant progress in developing mathematical modeling that can reproduce the key manifestations of G&R events at both the tissue and organ levels, our understanding of how the mechanisms at smaller scales, such as hypertrophy, atrophy, and fibrosis, can collectively lead to anatomical and functional changes in the heart remains very limited. To improve our understanding of these mechanisms and of their underlying mechanical stimulants, it is essential to conduct theory-driven experiments that can relate the contribution of each type of mechanism (taking place at the cellular level) to measurable changes in behavior at the tissue level (47). A crucial step in this approach is to develop new classes of mesoscale constitutive models that, on the one hand, can directly account for changes in the ratio and mechanical and structural properties of different tissue constituents and, on the other hand, remain tractable for implementation in organ-level simulations.

The tissue models discussed in this review are but one aspect of many that are required to fully describe the physiological function of the heart and its pathophysiology, as well as to develop novel therapies. Coupling not only to realistic geometries at all scales but also to electromechanical events and blood flow both within the ventricles and in the myocardium itself, detailed subcellular mechanisms (e.g., ion channel function) must ultimately be described within a single complete functional computational model. Until that time, as the great Y.C. Fung stated, “Let’s enjoy the work” (139).