Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding

Abstract

Purpose

Diffusion encoding with asymmetric gradient waveforms is appealing because the asymmetry provides superior efficiency. However, concomitant gradients may cause a residual gradient moment at the end of the waveform, which can cause significant signal error and image artifacts. The purpose of this study was to develop an asymmetric waveform designs for tensor-valued diffusion encoding that is not sensitive to concomitant gradients.

Methods

The “Maxwell index” was proposed as a scalar invariant to capture the effect of concomitant gradients. Optimization of “Maxwell-compensated” waveforms was performed in which this index was constrained. Resulting waveforms were compared to waveforms from literature, in terms of the measured and predicted impact of concomitant gradients, by numerical analysis as well as experiments in a phantom and in a healthy human brain.

Results

Maxwell-compensated waveforms with Maxwell indices below 100 (mT/m)²ms showed negligible signal bias in both numerical analysis and experiments. By contrast, several waveforms from literature showed gross signal bias under the same conditions, leading to a signal bias that was large enough to markedly affect parameter maps. Experimental results were accurately predicted by theory.

Conclusion

Constraining the Maxwell index in the optimization of asymmetric gradient waveforms yields efficient diffusion encoding that negates the effects of concomitant fields while enabling arbitrary shapes of the b-tensor. This waveform design is especially useful in combination with strong gradients, long encoding times, thick slices, simultaneous multi-slice acquisition and large FOVs.

Introduction

Diffusion-weighted magnetic resonance imaging employs magnetic field gradients to sensitize the signal to the diffusive motion of signal-carrying spins. The gradients are assumed to be linear in space, but in practice, they are accompanied by so-called concomitant gradients, also referred to as Maxwell terms¹. In spin-echo sequences, diffusion-weighting is most commonly achieved with an identical pair of pulsed field gradients on either side of the refocusing pulse. This elegant symmetry ensures that the 0^th moment of the concomitant gradients caused by the first pulse is cancelled by the second pulse. Although the desired gradient waveform will be slightly perturbed by the concomitant gradients, they are too small to have a relevant impact on the b-value² and their 0^th moment will be zero. They can therefore be safely ignored.

In contrast to the symmetric case, compensation of concomitant gradients is not guaranteed for asymmetric gradient waveforms. Instead, asymmetric waveforms may cause a spatially dependent residual gradient moments at the end of the encoding. A residual moment causes a shift in k-space that may manifest as through-slice dephasing, image blurring², T₂*-relaxation³, and signal-dropout⁴, all of which reduce the accuracy of quantities or imaging biomarkers estimated from the data. Despite the potential problems, asymmetric waveforms are an appealing alternative to symmetric designs because of their superior efficiency. For example, asymmetry can be exploited in experiments that yield encoding periods of unequal duration (asymmetric timing) where gradients for diffusion encoding can be engaged during all of the available time, rather than inserting periods where the gradients are turned off^5,6. This facilitates a categorical improvement of the encoding efficiency (encoding strength per unit time) and can be used to reduce echo-times and thus improve the signal to noise ratio (SNR). Moreover, asymmetric designs can also be used to reduce eddy-currents⁷, enable motion and acceleration compensation⁸ and facilitate pore shape estimation^9,10.

Concomitant gradients are a well-known pitfall for applications that rely on strong gradients, and their effects have been described in several contexts^{1,2,4,11–15}. Two strategies have been applied to address the effects of concomitant fields in the context of diffusion-weighted imaging. The first is to correct the error by calculating the concomitant gradients at some location in space and subtract them from the desired waveform^2,4. This approach corrects the error in a single position in space, but data acquired at some distance from the selected point may still suffer from the error. The second strategy is to design waveforms that can be asymmetric but where the gradient moment from the concomitant gradients match on both sides of the refocusing pulse, or so-called waveform reshaping¹⁶. This approach has been applied for linear diffusion encoding (along a single spatial direction), however, it does not generalize to single-shot diffusion encoding along multiple directions.

We refer to single-shot diffusion encoding along multiple spatial directions as “tensor-valued” since it cannot be described by just a b-value and a direction vector, but is instead described by a b-tensor that also captures the shape of the encoding^17–20. Tensor-valued encoding can probe features of the tissue microstructure that cannot be probed by conventional encoding alone^21–29, e.g. microscopic anisotropy, orientation coherence and isotropic heterogeneity of tissue³⁰. It can also inform biophysical models^31–33. Waveforms that yield tensor-valued encoding have been proposed in both symmetric and asymmetric variants^34–37. Recently, Sjölund et al.⁵ proposed a numerical optimization technique that can generate arbitrary b-tensor shapes with asymmetric waveforms that enabled a significant reduction of encoding times and improved SNR compared to previous designs.

In this work we propose a waveform design that negates effects of concomitant fields while enabling arbitrary shapes of the b-tensor. We propose the scalar Maxwell index as a cost function for minimization during waveform optimization and show that Maxwell-compensated waveforms do not suffer errors due to concomitant gradients.

Theory

Approximation of concomitant gradients

The Maxwell equations dictate that linear magnetic field gradients, such as those used for diffusion encoding, are accompanied by spatially dependent concomitant gradients¹¹. The concomitant gradients depend on the main magnetic field (B₀) and the desired (subscript D) gradient waveform

$$g_{\text{D}}(t)=R{[\begin{array}{ccc}{g}_1(t)& g_2(t)& g_3(t)\end{array}]}^{\text{T}}={[\begin{array}{ccc}{g}_{\text{x}}(t)& g_{\text{y}}(t)& g_{\text{z}}(t)\end{array}]}^{\text{T}},$$ Eq. 1

where R is a rotation matrix that determines how the three-dimensional waveform shape (g_1,2,3) is translated to the physical gradient axes (g_x,y,z). To abbreviate the notation, we will only use the latter format, but we note that all subsequent expressions depend on R even if not explicitly stated. The concomitant (subscript C) gradient waveform (g_C) can be approximated with an expansion in B₀ at a given position ($\mathbf{r}={[\begin{array}{ccc}\hfill x\hfill & \hfill y\hfill & \hfill z\hfill \end{array}]}^{\mathrm{T}}$, z-axis is parallel with B₀)^1,11, according to

$$g_{\text{C}}(t,r)=G_{\text{C}}(t)r,$$ Eq. 2

where the concomitant gradient matrix is given by

$$G_{\text{C}}(t)\approx \frac{1}{4B_0}\left[\begin{array}{ccc}{g}_{\text{z}}^2(t)& 0_{}^{}& -2g_{\text{x}}(t)g_{\text{z}}(t)\\ 0_{}^{}& g_{\text{z}}^2(t)& -2g_{\text{y}}(t)g_{\text{z}}(t)\\ -2g_{\text{x}}(t)g_{\text{z}}(t)& -2g_{\text{y}}(t)g_{\text{z}}(t)& 4g_{\text{x}}^2(t)+4g_{\text{y}}^2(t)\end{array}\right].$$ Eq. 3

The actual (no subscript) gradient waveform, experienced by the spins, will not be the desired waveform, but rather the sum of the desired waveform and the concomitant waveform

$$g(t,r)=g_{\text{D}}(t)+g_{\text{C}}(t,r).$$ Eq. 4

Errors due to concomitant gradients may appear when the actual gradient waveform is not balanced, meaning it has a non-negligible 0^th moment at the time of the readout. This causes a shift in k-space. To capture the size of the k-space shift independent of the location we construct a concomitant moment matrix

$$K=\frac{\gamma }{2\pi }\underset{0}{\overset{\tau }{{\displaystyle \int }}}h(t)\cdot G_{\text{C}}(t)\text{d}t,$$ Eq. 5

where γ is the gyromagnetic ratio, and τ is the duration of the diffusion encoding. The sign function h(t) = (−1)^j(t) represents the spin-dephasing direction and assumes values of 1 or −1 for each encoding period $j(t)\in \mathbb{N}$, such that neighboring periods—separated by a refocusing pulse—have opposite signs. In this work we only consider spin-echo sequences, but this convention provides a straightforward generalization to experiments with an arbitrary number of refocusing pulses.

The residual 0^th moment vector (k) is the integral of the actual gradient waveform at any given position, according to

$$k(r)=\frac{\gamma }{2\pi }\underset{0}{\overset{\tau }{{\displaystyle \int }}}h(t)\cdot g(t,r)\text{d}t\underset{\text{If balanced}{g}_{\text{D}}}{\underbrace{=Kr}},$$ Eq. 6

which can be simplified to the expression on the right-hand side if the desired waveform is balanced, i.e., if the desired 0^th moment ${\mathbf{k}}_{\mathrm{D}}={\int }_0^{\tau }h(t)\cdot {\mathbf{g}}_{\mathrm{D}}(t)\mathrm{d}t$ is zero. Figure 1 visualizes the desired and concomitant gradient waveforms at multiple positions along with the resulting residual moment vectors. At the end of the gradient waveform, the residual 0^th moment (k) along an arbitrary direction (n, unit vector) is a scalar that carries information about the local shift in k-space at position r, according to

$$k(n,r)=n^{\text{T}}Kr.$$ Eq. 7

Figure 1 –

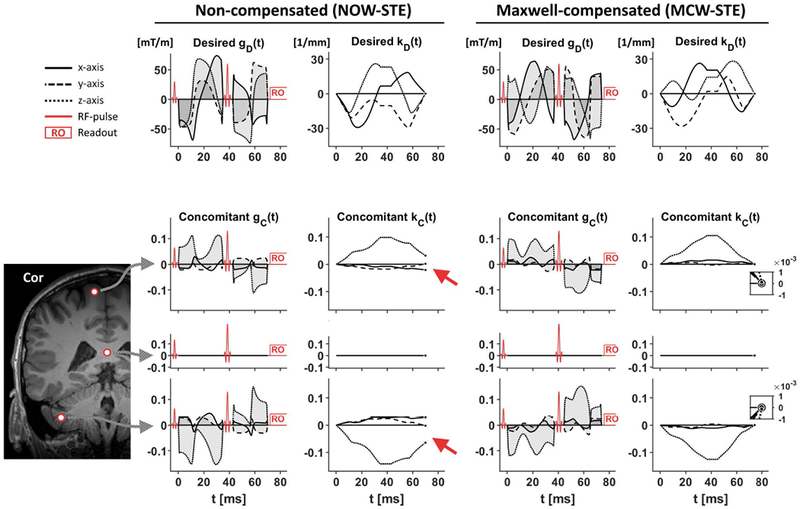
Desired gradient waveforms and their concomitant gradients at the three positions in the brain. Top row shows the desired gradient waveforms—non-compensated (left) and Maxwell-compensated (right) —and their moment vectors as a function of time. The intention is that the desired moment vector, k_D, should be zero at the end of the diffusion encoding, which is a trivial condition to fulfil in the absence of concomitant gradients. However, concomitant gradients may cause a residual gradient moment that persists after the end of the diffusion encoding (red arrows). The size and direction of the residual moment vector depends on the position in space, increasing in magnitude further away from the isocenter. By contrast, the Maxwell-compensated waveforms are designed to have concomitant gradients that exhibit a negligible residual moment. The inset plots in the rightmost column show that the residual moment after the diffusion encoding is negligible. The three positions (r) evaluated in this example are—from top to bottom—$[\begin{array}{ccc}\hfill 10\hfill & \hfill 0\hfill & \hfill 60\hfill \end{array}]\mathrm{mm}$, $[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}]\mathrm{mm}$ (isocenter) and $[\begin{array}{ccc}\hfill 50\hfill & \hfill 0\hfill & \hfill -80\hfill \end{array}]\mathrm{mm}$.

In summary, concomitant gradients are proportional to the square of the gradient amplitude and inversely proportional to the main magnetic field strength (Eq. 3). The residual moment caused by concomitant gradients has a non-trivial dependency on rotation and spatial position.

Signal error and artifacts caused by concomitant gradients

Several spatially varying artifacts may manifest when k ≠ 0. For simplicity, we will describe the relevant effects for an ideal spin-echo sequence with rectangular slice profiles and echo-planar imaging (EPI) readout; these are slice dephasing and blurring^2,13 as well as T₂*-weighting³.

Slice dephasing is caused by a residual moment along the slice encoding direction (n_s, unit vector normal to the slice plane), where the shift is $k_{\mathrm{S}}({\mathbf{n}}_{\mathrm{S}},\mathbf{r})={\mathbf{n}}_{\mathrm{S}}^{\mathrm{T}}\mathbf{Kr}$ (Eq. 7). Assuming approximately linear phase dispersion within each voxel¹² and a rectangular slice profile², the slice attenuation factor (AF_S) is given by

$${\text{AF}}_{\text{S}}(n_{\text{S}},r)=\left|\text{sinc}(n_{\text{S}}^{\text{T}}Kr\cdot T)\right|,$$ Eq. 8

where T is the slice thickness. Shifting the echo within the readout plane incurs blurring, as information about high spatial frequencies is shifted outside of the readout window. For EPI, any shift in the readout plane also incurs a spatially dependent T₂*-weighting, whenever the intensity-generating readout is performed at different time than at the time of the spin-echo echo³. This effect is most prominent for shifts along the phase direction due to the slower readout speed in that direction. The residual moment along the phase encoding direction (n_P) is given by $k_{\mathrm{P}}({\mathbf{n}}_{\mathrm{P}},\mathbf{r})={\mathbf{n}}_{\mathrm{P}}^{\mathrm{T}}\mathbf{Kr}$ (Eq. 7). Assuming negligible T₂*-relaxation during the relatively rapid readout of each k-space line, the attenuation factor (AF_P) can be approximated by the echo-shift in relation to the readout trajectory

$${\text{AF}}_{\text{P}}(n_{\text{P}},r)=\text{exp}\left(-\frac{\left|n_{\text{P}}^{\text{T}}Kr\right|}{\text{Δ}k}\cdot \frac{\text{Δ}t}{T_2^{\text{*}}}\right),$$ Eq. 9

where Δk = W/FOV_P is the inverse distance between two acquired k-space lines, where W is the parallel imaging factor and FOV_P is the field of view in the phase direction and Δt is the time between the acquisitions of two consecutive k-space lines. The total attenuation factor from both dephasing and T₂*-weighting is the product

$$\text{AF}(n_{\text{S}},n_{\text{P}},r)={\text{AF}}_{\text{S}}(n_{\text{S}},r)\cdot {\text{AF}}_{\text{P}}(n_{\text{P}},r).$$ Eq. 10

We conclude that spatially dependent signal errors can be caused by concomitant fields and will manifest as deleterious signal attenuation (AF < 1). This attenuation depends on the waveform and the T₂* of tissue as well as on imaging parameters such as slice position, angulation, in-plane acceleration, bandwidth and slice thickness.

Signal bias from diffusion-weighted images

In simulations we can calculate the relative signal bias as AF − 1 where the attenuation factor can be calculated independent of the effects of diffusion-weighting (Eq. 10). By contrast, in practical experiments the estimation of bias may be conflated with the diffusion weighting. The two effects can be separated by comparing a candidate waveform to a reference waveform that is not affected by concomitant gradients; all other variables kept equal. In a substrate that exhibits purely Gaussian diffusion, it is enough to compare the signal across identical b-values (and imaging parameters) to remove the effect of diffusion and relaxation weighting and retain only effects caused by the concomitant gradients. More generally, however, in the presence of microscopic or macroscopic diffusion anisotropy, the encoding must be matched with respect to the b-tensor. The b-tensor is calculated from the gradient waveform, according to^17,19

$$B=\underset{0}{\overset{\tau }{{\displaystyle \int }}}q(t)q{(t)}^{\text{T}}\text{d}t,$$ Eq. 11

where the dephasing q-vector is

$$q(t)=\text{γ}\underset{0}{\overset{t}{{\displaystyle \int }}}h(t\text{'})\cdot g_{\text{D}}(t^{\prime })\text{d}{t}^{\prime },$$ Eq. 12

and the b-value is simply b = Tr(B). Notably, this definition ignores the concomitant gradients because they have a negligible effect on the b-tensor². With matching b-tensors for a given waveform (i) and its reference (ref), the relative signal bias can be estimated by comparing the two, according to

$$\text{SB}=\frac{S_i(B)}{S_i(0)}\cdot \frac{S_{\text{ref}}(0)}{S_{\text{ref}}(B)}-1,$$ Eq. 13

where negative values of the relative signal bias reflect that signal is lost (AF < 1). Here, we do not impose the equality S_i(0) = S_ref(0) since this condition may be violated if the baseline signal differs across acquisitions, e.g. due to amplifier gain recalibration. We note that this estimation assumes that other effects—that also depend on the exact shape of the waveform—are negligible. Such effects include diffusion time^38–40, exchange⁴¹, flow⁴², and eddy-currents⁷.

Methods

Maxwell index

We seek a gradient waveform g_D for which K = 0 independent of the waveform rotation so that the signal bias is negligible. We propose to achieve this condition by minimizing the “Maxwell index” (m), herein defined as

$$m={(\text{Tr}(MM))}^{\frac{1}{2}},$$ Eq. 14

where

$$M=\underset{0}{\overset{\tau }{{\displaystyle \int }}}h(t)g_{\text{D}}(t)g_{\text{D}}^{\text{T}}(t)\text{d}t.$$ Eq. 15

We motivate this construct by noting that both M and K comprise the same self-squared and cross-terms found in ${\mathbf{g}}_{\mathrm{D}}(t){\mathbf{g}}_{\mathrm{D}}^{\mathrm{T}}(t)$, such that nulling the elements of M and/or K would satisfy our aim. In other words, K = 0 if ${\int }_0^{\tau }h(t)g_i(t)g_j(t)\mathrm{d}t=0$ for all axis combinations and waveform rotations. In the special case where the waveform is a one-dimensional trajectory (g_1D), this problem has a simple solution because K = 0 when ${\int }_0^{\tau }h(t)g_{1\mathrm{D}}^2(t)\mathrm{d}t=0$ independent of rotation¹⁶. However, in the general case, K is not invariant to rotation of the gradient waveform and is therefore a poor target for optimization. Instead, we propose to base the optimization target on m which is strictly positive and invariant to rotation. This means that for a given experimental setup, a waveform with a sufficiently small m will yield negligible effects due to concomitant gradients independent of rotation, FOV-orientation, and position within the FOV. Note that the diagonal elements of MM are strictly positive so that Tr(MM) is zero if and only if the eigenvalues of M are all zero, whereas Tr(M) may be zero when M has both positive and negative eigenvalues. See the Supporting Information for a more complete evaluation of m as the target for optimization.

Optimization of Maxwell-compensated waveforms

Tensor-valued diffusion encoding can be tailored to an arbitrary configuration of the imaging sequence and hardware capabilities using the numerical optimization framework by Sjölund et al.⁵. To achieve Maxwell-compensated waveforms (MCW) for arbitrary b-tensor shapes we introduce the Maxwell index (Eq. 14) as an additional constraint in the optimization framework. To allow arbitrary rotation of the waveform, we used the Euclidean norm and a heat dissipation factor of 1.

In principle, waveforms can be optimized at the temporal resolution employed by the gradient amplifier system (gradient raster time). However, with the current implementation, the optimization time increases rapidly with the number of waveform samples (N). Therefore, the optimization was limited to a relatively coarse temporal resolution and linear interpolation was used to resample the waveform to the gradient raster time. Although this approach facilitates fast optimization of waveforms, linear interpolation does not perfectly preserve Maxwell-compensation. We circumvent this problem by predicting the signal bias after interpolation in a worst-case scenario and increasing the temporal resolution until the bias is negligible. For the purposes of this paper, the worst-case scenario is taken to mean that we use the actual imaging parameters of the sequence but considers the rotation of the waveform that gives the largest signal bias within a sphere with a diameter of 0.5 m (centered on the isocenter) and a T₂* of 40 ms. Under these conditions, we consider a signal bias magnitude below 1 % (AF > 0.99) at the highest b-value to be negligible. Figure 2 shows that N = 100 is a sufficient temporal resolution for the waveform optimization and that the optimization should constrain the Maxwell index to be less than approximately 1000 (mT/m)²ms. To create additional headroom, we constrain all Maxwell-compensated waveforms to have m ≤ 100 (mT/m)²ms. We emphasize that these parameters can be tailored to any specific application and may therefore result in more or less conservative restrictions on the waveform design.

Figure 2 –

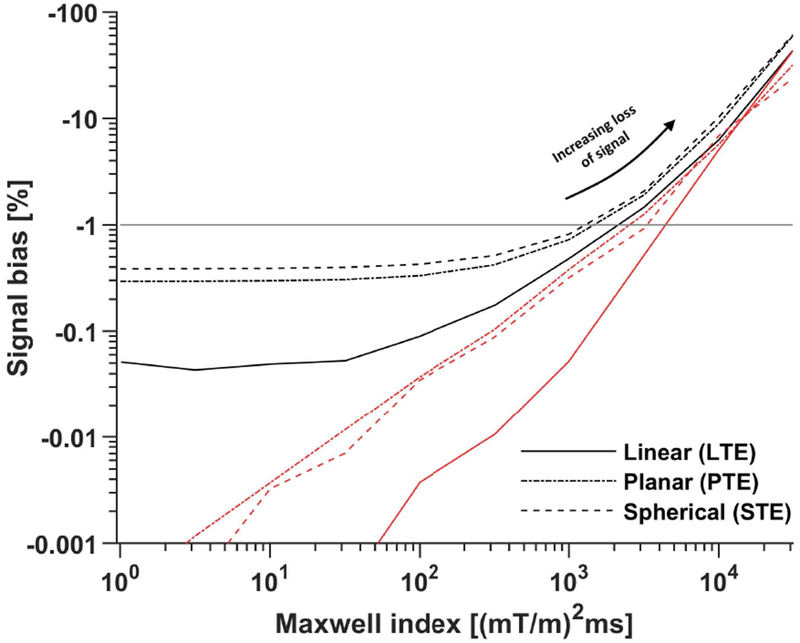
The signal bias (Eq. 13) depends on the Maxwell index constraint as well as the target b-tensor shape. The plot shows the simulated bias in the worst-case scenario when using interpolated (black) and original (red) waveforms optimized at a temporal resolution of N = 100 samples. It is clear that the interpolation worsens the Maxwell-compensation but does not elevate the signal bias beyond the tolerated level of −1 % (horizontal gray line). Furthermore, the signal bias becomes virtually independent of the Maxwell index when m is below approximately 100 (mT/m)²ms. This indicates diminishing returns for overly conservative optimization of m when the waveform must be interpolated in a later step. The median optimization time over 20 repeated optimizations for each m was between 2 and 30 s using an Intel Core i7-8750H.

Experimental validation of Maxwell-compensated waveforms

To verify that Maxwell-compensated waveforms (MCW) yield negligible signal bias due to concomitant gradients we tested the waveforms by performing diffusion-weighted imaging in an oil phantom and in a healthy brain in vivo. To include a wide range of b-tensor shapes, we optimized waveforms that yield linear, planar and spherical b-tensor encoding (LTE, PTE and STE, respectively) at b-values up to b = 2.0 ms/μm² while minimizing the encoding time (see Westin et al.¹⁷ for definitions of b-tensor shapes).

All experiments were performed on a 3 T MAGNETOM Prisma (Siemens Healthcare, Erlangen, Germany) with maximal gradient amplitude of 80 mT/m and maximal slew rate of 200 T/m/s. We used a prototype pulse sequence developed in-house⁴³, based on a diffusion-weighted spin-echo sequence. The imaging parameters were TR = 4.5 s, FOV = 220×220×175 mm³, slices = 35, resolution = 2×2×5 mm³, iPAT = 2 (GRAPPA), echo spacing = 0.65 ms, partial-Fourier = 7/8, and b-values of 0.1, 0.7, 1.4 and 2.0 ms/μm². This setup yielded a separation between the first and second encoding periods of approximately 8 ms during which the refocusing pulse is executed. Since the EPI-readout before the echo takes up more time than the selective excitation and navigators, the available time for diffusion encoding on either side of the refocusing pulse is asymmetric. For the current setup, δ₁ =δ₂ + 8 ms, where δ₁ and δ₂ are the durations of the encoding before and after the refocusing pulse. This timing asymmetry was used for all waveform optimization. TE was set to 102 ms, as determined by the waveform that required the longest encoding time to reach the maximal b-value. We found that all waveforms could be robustly executed on the scanner, without violating duty cycle or peripheral nerve stimulation limits, by limiting the maximal gradient amplitude to 75 mT/m and the maximal slew rate to 60 T/m/s in the optimization and execution.

The reference waveform was a pair of symmetric trapezoidal gradient waveforms on either side of the refocusing pulse, i.e. the Stejskal-Tanner design⁴⁴, also known as single diffusion encoding⁴⁵ that yields linear tensor encoding (SDE-LTE). For comparison, we also included numerically optimized waveforms without compensation⁵ (NOW) that yield linear, planar and spherical b-tensor encoding (NOW-LTE, NOW-PTE and NOW-STE). Finally, we included double diffusion encoding in an orthogonal configuration that yields planar tensor encoding (DDE-PTE). The DDE-PTE waveform required the longest encoding time to reach the maximal b-value, and therefore defined the TE that was used for all experiments. Note that all waveforms were executed in the timing for which they were optimized to retain the concomitant gradient characteristics that they exhibit at a minimal TE (Figure 3).

Figure 3 –

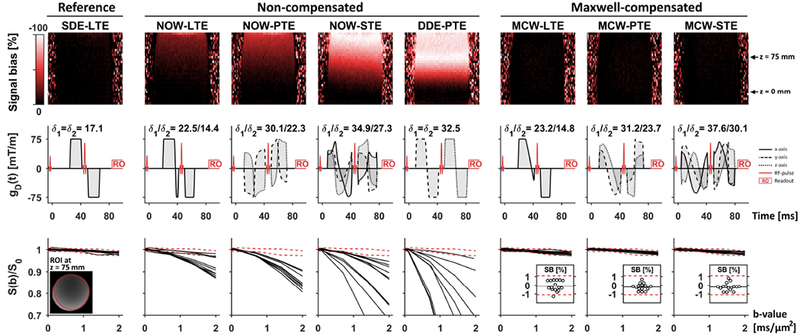
Diffusion-weighted signal in an oil phantom shows that non-compensated asymmetric gradient waveform designs exhibit gross signal bias (Eq. 13) due to concomitant gradients, whereas the Maxwell-compensated waveforms exhibit a negligible signal bias. The top row shows maps of the signal bias in coronal slices at the maximal b-value for the worst waveform rotation that was observed for each waveform type. The middle row shows the waveforms and timing used in the experiments. The bottom row shows the average signal in an ROI placed at z = 75 mm as a function of b-value for 16 rotations; broken red lines show the average reference signal ± two standard deviations. The signal bias is worst for DDE-PTE, reaching approximately –100 % (AF ≈ 0) in a large part of the volume. The signal bias is also visible for remaining non-compensated waveforms, albeit to a lesser degree. By contrast, the Maxwell-compensated waveforms showed no sign of concomitant gradient effects. The inset plots in the bottom row show the estimated signal bias (SB) in the ROI at b = 2 ms/μm² where horizontal black lines show the average signal bias across all rotations. All Maxwell-compensated waveforms had negligible signal bias and the distribution across rotations exhibited a variability that was similar to the reference sequence.

We predicted that none of the experiments would cause peripheral nerve stimulation above the permitted level. The prediction was performed in an in-house implementation of the SAFE model⁴⁶ and considered only the diffusion encoding gradient waveform and the EPI train.

A homogeneous oil phantom (cylinder with diameter 0.12 m, and length 0.20 m) was used to detect signal loss caused by concomitant gradients. Oil was chosen because it exhibits slow Gaussian diffusion (< 0.01 μm²/ms). Thus, signal attenuation due to diffusion encoding is small (in the order of 1 %) so that substantial signal attenuation can be attributed to concomitant gradient effects². We investigate the signal as a function of encoding strength for different waveform rotations and estimate the relative signal bias (Eq. 13) by comparing it to the reference sequence. Since the effect is expected to depend on waveform rotation we use 16 rotations of the waveform for each b-value. The same rotations were used for each b-value. We used axial slice orientation (${\mathbf{n}}_{\mathrm{P}}=[\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}]$, ${\mathbf{n}}_{\mathrm{S}}=[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}]$) and placed the phantom so that the cylinder was approximately parallel to the main magnetic field. The FOV was placed so that the center of the outermost slices were at z-coordinates −25 and 125 mm. The FOV was shifted in this manner to measure at relatively large distances from the isocenter, because the magnitude of the concomitant fields increases with distance from the iso center.

Brain imaging was also performed in a healthy volunteer (male, age 38 y). The study was approved by the Regional Ethical Review Board (Lund, Sweden), and informed consent was obtained prior to participation. Each waveform was executed in 8, 12, 18 and 24 rotations for the four b-values, respectively. The diffusion encoding directions were generated by electrostatic repulsion on the half-sphere^47,48. Each encoding direction corresponds to the symmetry axis of the b-tensors. Since spherical tensor encoding does not have a well-defined symmetry axis, we assigned g₁ (Eq. 1) to be the symmetry axis. An axial slice orientation was used, and the center of the FOV was placed in the plane of the isocenter (z = 0), which coincided with the corpus callosum as seen in a mid-sagittal view. The center of the outermost slices covered z-coordinates −70 and 80 mm. The total scan time for all seven waveform designs was 36 min. Image volumes were corrected for motion and eddy currents in ElastiX⁴⁹, using extrapolated references⁵⁰.

To establish the size of the signal error that may occur if concomitant gradients are ignored, we investigate the impact on the diffusion-weighted signal as a function of b-value at multiple locations in the brain parenchyma. We manually defined regions of interest in the cerebellum, posterior (close to the isocenter) and anterior corpus callosum, and in the superior white matter close to the cortex. To take the diffusion anisotropy into account, we compared the signal from non-compensated and Maxwell-compensated waveforms that yield identical b-tensors (Eq. 13). We also investigate the impact of concomitant gradients on parameter maps estimated by q-space trajectory imaging (QTI)^17,19. The QTI model was fitted to data acquired with SDE-LTE combined with either compensated or non-compensated variants of planar tensor encoding (MCW-PTE or DDE-PTE, respectively). We estimated parameter maps of mean diffusivity (MD), fractional anisotropy (FA)⁵¹, mean kurtosis (MK)^52,53, as well as the microscopic fractional anisotropy (μFA) and mean kurtosis decomposed into the isotropic (MK_I) and anisotropic (MK_A) components^17,22,25. The parameter bias caused by concomitant gradients in the non-compensated case was calculated as the difference in parameter values. To establish if the observed differences can be attributed to concomitant gradients, we predicted the error in the diffusion-weighted signal and QTI parameters by assuming that the signal from MCW-PTE was free from errors and multiplying it by the spatially-dependent attenuation factor estimated by Eq. 10 given the DDE-PTE waveform. Errors related to signal are presented as the signal bias (Eq. 13) and QTI parameter errors are presented as the difference.

We have modified the numerical waveform optimization⁵ to include Maxwell-compensation, and shared it at https://github.com/jsjol/NOW. We have also shared the SAFE peripheral nerve stimulation model at https://github.com/filip-szczepankiewicz/safe_pns_prediction, as well as tools for simulating and analyzing concomitant gradients and their effects as part of the multidimensional diffusion toolbox at https://github.com/markus-nilsson/md-dmri. These tools were implemented in Matlab (The MathWorks, Natick, MA, USA).

Simulated validation of Maxwell-compensated waveforms

To verify that Maxwell-compensated waveforms yield negligible signal bias due to concomitant gradients for a comprehensive set of rotations, we simulated the expected signal bias according to Eq. 10 and Eq. 13. The simulations used the same waveforms and imaging settings as the experiments. The worst signal bias within a sphere with a diameter of 0.2 m was calculated for three rotation modes. First, we investigated the effect of rotating the waveform assuming stationary axial slices. Second, the waveform was stationary but the FOV was rotated. Finally, both the waveform and FOV were rotated simultaneously but with independent rotation matrices. For each setup we use 10⁴ random rotations to yield a distribution of signal biases. We used boxplots to visualize the distribution of signal biases for each waveform and rotation mode.

Impact of constraining the Maxwell index on encoding efficiency

Constraining the Maxwell index in the waveform optimization is associated with a reduced diffusion encoding efficiency compared to optimization where the effects of concomitant gradients are ignored. We investigated how the maximal b-value depends on the Maxwell index by optimizing waveforms where m was constrained to be below values in the interval 1 to 10⁵ (mT/m)²ms. Optimization was also performed without constraining the Maxwell index. Thus, the range between extremely conservative to entirely unconstrained Maxwell indexes was investigated. The optimization settings were the same as for waveforms used in the experiments. The encoding efficiency was quantified in terms of the b-value that is achievable at a given constraint on the Maxwell index relative to the maximal b-value, b(m)/max(b).

Since the Maxwell index reflects a balance of the time-integral of the gradients squared on both sides of the refocusing pulse, we also investigated how the efficiency depends on the encoding time asymmetry. The timing asymmetry was defined as |δ₁ − δ₂|/(δ₁ + δ₂). The impact was also gauged in terms of the additional encoding time necessary to achieve the same b-value as for the non-compensated waveforms. We report the cost in terms of the additional encoding time required in absolute terms (c_abs = t_MCW − t_NOW) and relative terms (c_rel = c_abs/t_NOW) where t is the total duration of Maxwell-compensated (t_MCW) and non-compensated (t_NOW) waveforms.

Results

Measurements of the diffusion-weighted signal in oil using the Maxwell-compensated waveforms appeared to be unaffected by concomitant gradients and had the same signal behavior as the reference sequence (Figure 3). At the highest b-value, the average signal bias across rotations (one standard deviation) was −0.1 (0.6), −0.2 (0.4) and −0.2 (0.5) in percent for linear, planar and spherical tensor encoding, respectively. By contrast, non-compensated waveforms yielded gross signal bias; the worst case was observed for DDE-PTE where some rotations exhibited a complete signal dropout (SB ≈ −100 %) at a distance of approximately 75 mm from the isocenter. Figure 3 also shows that the effect increases with increasing b-value, and that it introduces rotational variance even if the diffusion itself is perfectly isotropic. Overall, the phantom experiments consistently verified that the Maxwell index is an appropriate target for optimization to alleviate the effects of concomitant gradients, and that ignoring such effects may have a marked effect on the diffusion-weighted signal.

The effects of concomitant gradients were also investigated in the brain in vivo. Figure 4 shows that non-compensated waveforms suffer a rotation dependent signal error that is large enough to affect the average signal, whereas the Maxwell-compensated waveforms exhibit no evident attenuation due to concomitant gradients. As in the oil, the effect depends on the rotation of the waveform and is larger for higher b-values. Therefore, the impact on parameters that correspond to the initial slope of S(b), such as the mean diffusivity, is likely smaller compared to parameters based on signal characteristics at high b-values, such as microscopic anisotropy and kurtosis parameters.

Figure 4 –

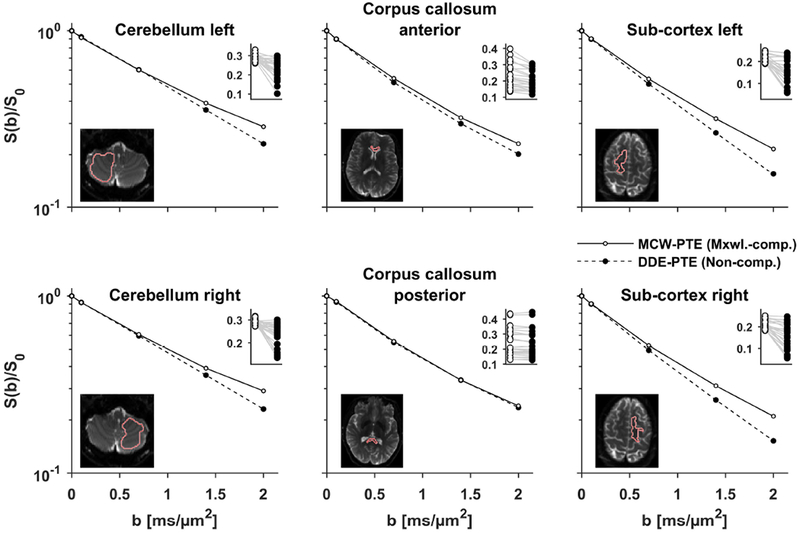
Plots show the signal vs b-value for planar tensor encoding produced by non-compensated (DDE-PTE, black markers) and Maxwell-compensated waveforms (MCW-PTE, white markers). In the main plots, the signal is averaged over directions, whereas the inset plots show individual directions at b = 2 ms/μm² where gray lines link signal pairs encoded with identical b-tensors (Eq. 11). At low b-values the two waveforms are similar, however at larger b-values, DDE-PTE suffers gross signal attenuation due to concomitant gradients. The effect is largest in the inferior and superior parts of the brain, i.e. the bias is largest along the z-axis. As expected from theory, the effect is negligible in the posterior corpus callosum because of its proximity to the isocenter.

The diffusion-weighted signal and QTI parameter maps for Maxwell-compensated and non-compensated waveforms are shown in Figure 5. The diffusion-weighted signal for DDE-PTE at b = 2 ms/μm² is visibly affected by signal dropout, most prominent along the inferior-superior direction, whereas MCW-PTE exhibited no such behavior. We emphasize that the top row of the figure only shows the signal maps for two rotations of the waveform, and that the artifacts produced by DDE-PTE take on different appearances depending on the rotation, as seen in the oil phantom where S(b) varies wildly depending on the waveform rotation (Figure 3). As expected, the differences in MD and FA were relatively small (see Supporting Information Figure S1), but gross parameter differences were observed in the μFA, MK_A (overestimated by 0.3 and 0.8, respectively) and MK_I (underestimated by 0.8). The underestimation of MK_I was severe enough to cause large regions in the parenchyma to exhibit negative values, which are not expected from the current experiments⁴³. The measured and predicted differences show a remarkable similarity, indicating that the difference between signal and QTI parameters based on DDE-PTE and MCW-PTE is indeed primarily due to the prominent concomitant gradients created by DDE-PTE.

Figure 5 –

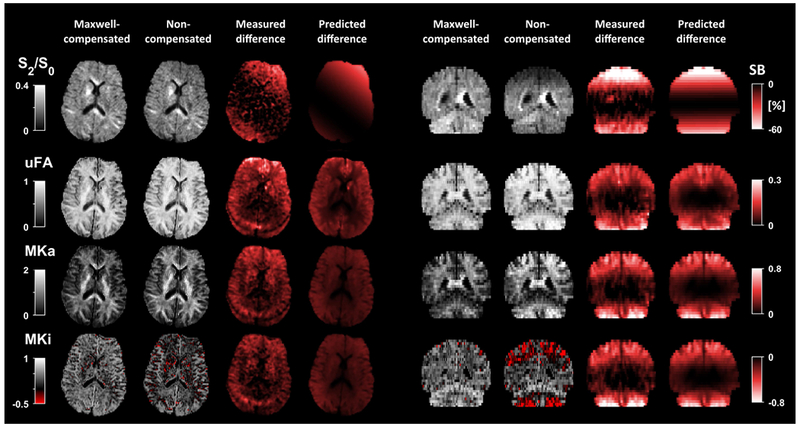
Diffusion-weighted data by non-compensated and Maxwell-compensated gradient waveforms shows that concomitant gradients can have a marked impact on signal and QTI parameters. The linear encoding used the Stejskal-Tanner design (SDE-LTE) in both cases, whereas the planar encoding was achieved by either non-compensated (DDE-PTE) or Maxwell-compensated (MCW-PTE) waveforms. The top row shows a comparison of the normalized signal (S₂/S₀) at b = 2 ms/μm² for identical b-tensors (Eq. 11), as well as the signal bias (SB, Eq. 13) where Maxwell-compensated data is used as the reference. The signal bias reaches values below −60 %, i.e., concomitant gradients in DDE-PTE can cause most of the signal to be lost in large portions of the brain. Data acquired with Maxwell-compensated waveforms showed no such artifacts. The impact of concomitant gradients on QTI parameters is shown as the difference between estimation based on non-compensated and Maxwell-compensated data. Generally, μFA and MK_A are overestimated, and MK_I is underestimated. This is expected since it is only DDE-PTE that is affected by concomitant gradients such that the divergence between the linear and planar encoding increases artificially^22,30. Notably, the bias in MK_I is severe enough to causes it to be negative in large portions of the brain. The measured and predicted signal bias, and parameter differences, were similar in both magnitude and spatial dependency, which indicates that they are caused primarily by concomitant gradients in DDE-PTE. The difference in MD and FA was relatively small since these parameters rely on data at relatively low b-values which is less affected by concomitant gradients (see Supporting Information Figure S1).

Simulations presented in Figure 6 show that the Maxwell-compensated waveforms can retain a negligible signal bias (magnitude is always below 1 %) due to concomitant gradients regardless of rotations of the waveform and/or FOV. By contrast, all non-compensated waveforms show a large variation of the bias depending on rotations.

Figure 6 –

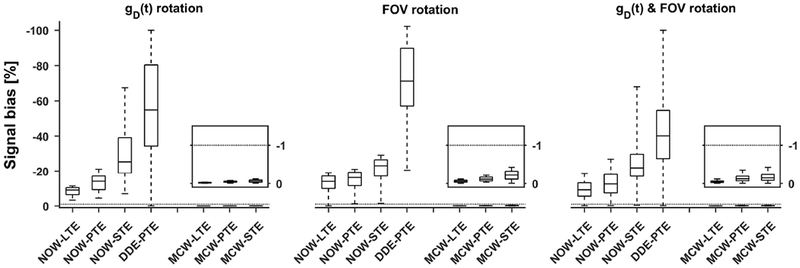
Simulation of signal bias (Eq. 13) for Maxwell-compensated and non-compensated waveforms that yield linear (LTE), planar (PTE) and spherical (STE) b-tensor encoding. The boxplots show the distribution of signal bias under 10⁴ random rotations of the waveform, FOV, or both; whiskers show extreme values, the box lines show 25, 50 and 75 percentiles. The simulated waveforms are identical to those used in the practical experiments (Figure 3) at b = 2 ms/μm². The non-compensated waveforms suffer from significant rotation dependent signal bias. Notably, DDE-PTE exhibits the worst overall signal bias. Throughout all examples the Maxwell-compensated waveforms exhibit negligible bias, regardless of b-tensor shape and rotation scheme; the simulation predicts that both the waveform and FOV can be arbitrarily rotated without discernible signal bias. The inset plots show a magnification of the bias for the Maxwell-compensated waveforms (y-axis covers the interval 0 to −1.5 %). The dotted line shows the level where 1 % of the signal is lost due to concomitant gradient effects.

The cost of imposing a constraint on the Maxwell index in the optimization of the waveforms is that the encoding efficiency, in terms of the achieved b-value per unit time, is reduced. Using the current premise, the efficiency was reduced by 7–23 %, depending on b-tensor shape (Figure 7). This translates to an extension of the required encoding time to reach b = 2 ms/μm² of approximately c_abs = 1–6 ms or c_rel = 2–8 %. Furthermore, the efficiency depends on the sequence timing asymmetry, where equal timing on both sides of the refocusing pulse yields the highest efficiency.

Figure 7 –

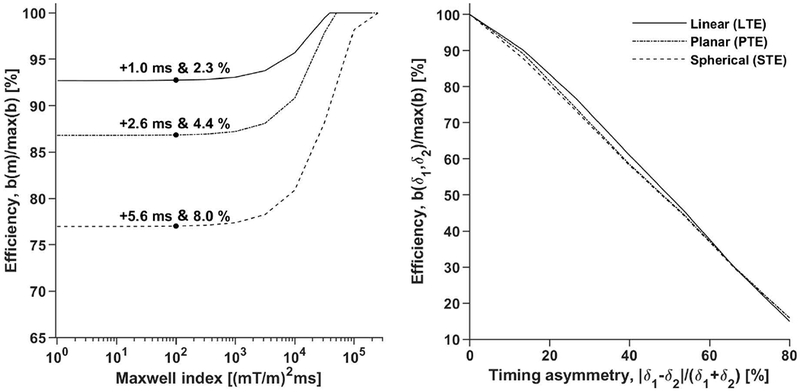
Introducing a limit on the Maxwell index reduces the efficiency of the diffusion encoding and the penalty depends on the timing asymmetry. The left plot shows that the impact on efficiency is independent of the Maxwell index for m below approximately 1000 (mT/m)²ms. The absolute and relative impact on the encoding duration (c_abs & c_rel) is stated for the experiment setup used in the practical experiments (δ₁ = δ₂ + 8 ms) at m = 100 (mT/m)²ms. For completeness, the same penalty is 3.6 ms or 7.9 % (data not shown), for STE when constraining the gradient waveform within a cube with sides of length 2×75 mT/m (max-norm optimization⁵) and disallowing arbitrary waveform rotation. The right plot shows that the efficiency depends heavily on the encoding time asymmetry of the sequence. As expected, equal gradient duration on either side of the refocusing pulse yields the highest efficiency.

Discussion

It is critical to consider signal errors and artifacts caused by concomitant gradients in diffusion encoding with asymmetric waveforms. We have proposed the Maxwell index as a target for waveform optimization and demonstrated that waveforms with Maxwell indices below approximately 100–1000 (mT/m)²ms exhibit negligible effects from concomitant gradients. This result generalizes to arbitrary rotations of the gradient waveform (encoding directions) and FOVs with arbitrary size and orientation. As such, the optimization is performed only once—under appropriate conditions—and will produce a waveform with negligible bias independent of how the FOV is placed and what diffusion encoding directions are used in any given subject. Additionally, we have presented a compact matrix formulation for the approximation of concomitant gradients for an arbitrary number of refocusing pulses and expanded the signal error prediction for slice selective spin-echo experiments to include the effect of T₂*-relaxation.

Investigations of concomitant gradient effects revealed that the impact of concomitant gradients is large for several asymmetric gradient waveform designs proposed in literature. Most prominently, DDE in a single spin-echo can be used to showcase the gross errors that can appear due to concomitant gradients. Figures 3 and 5 show examples of massive signal loss in both a phantom and in the human brain. Although we cannot rule out that the signal in the brain depends on effects that are not captured by the b-tensor, we expect that diffusion time dependency, exchange and flow are negligible compared to the gross signal loss predicted by theory and measured for non-compensated waveforms. Thus, it is reasonable to attribute the differences in diffusion-weighted signal and parameter maps in Figure 5 to concomitant gradients caused by the DDE-PTE waveform. As such, MCW-PTE is a viable alternative to DDE-PTE, since it is both robust to concomitant gradient effects and more efficient (shorter minimal TE for any given b-value). We stress that this issue with DDE is not present for imaging sequences where multiple refocusing pulses are used to make the diffusion encoding symmetric, such as in the double-spin-echo⁵⁴.

Maxwell-compensated waveforms are compatible with existing approaches for alleviating the effects of concomitant gradients. For example, it is possible to subtract the concomitant waveform for a given position (e.g., center of the slice) from the desired waveform such that the actual waveform is closer to the desired waveform, as described by Meier et al.⁴. The drawback of this approach is that the correction holds only for a single point in space, whereas remaining parts of the slice still suffer some error that may be non-negligible. Another drawback is that such single-point corrections may be incompatible with techniques that excite multiple slices simultaneously⁵⁵, although adaptions have been proposed⁵⁶. Another approach is post-hoc correction where signal is divided by the predicted attenuation factor in Eq. 10. This approach is limited by its requirement for very detailed knowledge of the sequence design as well as the T₂* of the tissue. Furthermore, if the error is so large that most of the signal is lost (Figure 3 and Figure 5) the reduction of SNR will be significant and unavoidable. Thus, we argue that Maxwell-compensated waveforms may be a preferable solution, especially for diffusion encoding at high gradient amplitudes and/or long encoding times^57,58, imaging of organs in large FOVs, simultaneous multi-slice imaging⁵⁹, super-resolution methods that employ thick slices and/or techniques based on rotated/oblique imaging stacks^60–63.

A special case of Maxwell-compensation can be achieved for waveforms that do not require rotation. For such a premise, it is enough to ensure that K = 0 (Eq. 5). This case is usually not useful since rotations are required to probe the orientation distribution function of anisotropic systems. However, for powder-samples (randomly oriented tissue) or for spherical tensor encoding, rotation of the encoding waveform may not be necessary^38–40. In such cases we may exploit the symmetries in Eq. 5 to design asymmetric waveforms that are Maxwell-compensated for a single stationary rotation. An example of this design principle was presented by Teh et al.⁶⁴ where cardiac diffusion imaging was performed with a waveform that was motion and acceleration compensated at the same time as it provided efficient spherical tensor encoding with K = 0. The benefit of using stationary waveforms for spherical encoding in combination with enclosing them in the cube rather than the sphere (max-norm vs. L2-norm⁵) will be investigated in future studies.

The drawback of Maxwell-compensation is a penalty to the encoding efficiency which manifests as a slightly longer encoding time. However, the penalty is rather small (1–6 ms), at least for the conditions used in this paper. Notably, the penalty grows with increasing timing asymmetry (Figure 7), although we note that this is true for symmetric designs too. Asymmetric designs that ignore concomitant gradients can be virtually independent of timing asymmetry, but the signal bias is expected to grow with increasing asymmetry.

The premise of this study is limited to that of brain imaging at a 3 T clinical MRI system with b-values up to 2 ms/μm². As such, we do not cover other relevant scenarios in detail. For example, we assume a T₂* of 40 ms to simulate tissue, which may not always be a representative. Thus, specific results of this study may not be immediately translatable to other systems, sequence designs, and tissues. However, we have shared the theoretical framework, waveform optimization tools and analysis software in open source so that it can be used to develop and test waveform and experiment designs in other scenarios. The proposed methods and tools can also be used to decide if Maxwell-compensation is at all necessary, or if the premise allows for the use of non-compensated waveforms due to, for example, very small FOVs. Finally, we have shown that any waveform with m = 0 yields K = 0 in support of the Maxwell index as an optimization target (Supporting Information). However, a better target cannot be ruled out. For example, such a target could include higher order spatial terms of the concomitant gradients¹ and/or encompass the effects of using asymmetric gradient coils⁴.

Conclusions

We proposed and demonstrated that the Maxwell index is a valid optimization target in the design of asymmetric gradient waveforms to yield negligible concomitant gradient effects. The design is applicable to arbitrary b-tensor shapes, sequence timing, and for any number of refocusing pulses larger than zero. The waveforms are Maxwell-compensated throughout the imaging volume independent of waveform rotation and FOV orientation. As such, this approach is especially relevant for diffusion imaging at high gradient strength, long encoding times, low main magnetic fields, large/oblique/off-isocenter FOVs, thick slices, and simultaneous multi-slice acquisition.

Supplementary Material

Supp info

Supporting Information Figure S1 – This figure shows the same analysis as Fig. 5 from the main manuscript but it also includes the MD and FA maps. The impact of concomitant gradients on parameters estimated mainly from data at low b-values is expected to be smaller than those that rely on high b-value data since $\mathbf{K}\propto {\mathbf{g}}_{\mathrm{D}}^2\propto b$.